机械原理典型例题 轮系
南京理工大学机械原理题库 轮系及其设计
07 轮系及其设计1.平 面 定 轴 轮 系 传 动 比 的 大 小 等 于 ;从 动 轮 的 回 转 方 向 可 用 方 法 来 确 定。
2.所 谓 定 轴 轮 系 是 指 ①, 而 周 转 轮 系 是 指 ②3.在 周 转 轮 系 中, 轴 线 固 定 的 齿 轮 为 ;兼 有 自 转 和 公 转 的 齿 轮 称 为 ; 而 这 种 齿 轮 的 动 轴 线 所 在 的 构 件 称 为 。
4.组 成 周 转 轮 系 的 基 本 构 件有: , , ;i k 1 与i k H1 有 区 别,i k 1 是 ;i k H1 是 ;i k H1 的 计 算 公 式为 , 公 式 中 的 正 负 号 是 按 来确 定 的。
5. 行 星 轮 系 齿 数 与 行 星 轮 数 的 选 择 必 须 满 足 的 四 个 条件 是①条件、 ②条件、 ③条件、 ④条件。
6.定 轴 轮 系 的 传 动 比 等 于 各 对 齿 轮传 动 比 的 连 乘 积。
- - - - - - - - - - - - - -- - - ( )7.周 转 轮 系 的 传 动 比 等 于 各 对 齿 轮 传 动 比 的 连 乘 积。
- - - - - - - - - - - - -- - - - - ( )8.行 星 轮 系 中 若 系 杆 为 原 动 件 可 驱 动 中 心 轮, 则 反 之 不 论 什 么 情 况, 以 中 心 轮 为 原 动 件 时 也 一 定 可 驱 动 系 杆。
- - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - ( )9.图 示 轮 系, 给 定 齿 轮1 的 转 动 方 向 如 图 所 示, 则 齿 轮3 的 转 动 方 向 。
(A )与ω1 相 同;(B )与ω1 相 反;(C ) 只 根 据 题 目 给 定 的 条 件 无 法 确 定。
机械原理轮系习题参考答案

一、解:(1)判断方向,蜗杆左旋用左手右旋用右手,四指握向蜗杆转动方向,拇指指向的反方向即为涡轮转向。
由此逆向判断图中蜗杆、涡轮和齿轮旋转方向如图中箭头所示。
手柄转向如图所示。
4001
601836186056341265432116=××=••=••=z z z z z z w w w w w w i 二、解:该轮系为周转轮系,由反转法对整个轮系加一个反向旋转角速度H w −,
由于齿轮4为定齿轮,角速度为零,即04=w ,所以H H i i 14
11−=; 又有 2.2)1(3423123
14−=•••−=z z z z z z i H
所以 2.32.211=+=H i
三、解:此轮系中假设轮1的方向向下,则行星轮2、2'和太阳轮4的转向都是
向下。
行星轮2、2'和行星架的角速度相同 在左边行星轮系中,1
3
1H 130z z H H −=−−=ωωωω 在右边行星轮系中,'2
444'2z z H ==ωωωω ∴4114ωω=i ==+4'2131z z z z z 25416
四、解:该轮系可以分为两部分,如图中虚线所分的左右两部分,左边为周转轮系,右边为定轴轮系;
分别求出两个轮系的传动比如下:
周转轮系:=H i 1414
1556601441===++z z n n n n H H ; 定轴轮系:7
63530566556====z z n n i ; 两轮系的关系是:
45n n =; 联立方程组求得min 9.741r n ≈; 转向与齿轮6转向相反。
机械原理典型例题第七章轮系1124

2019.11
例1. 在图示轮系中,已知:蜗杆为单头且右旋,转速 n1=1440r/min, 转动方向如图示,其余各轮齿数为: Z2 = 40 ,Z2‘ = 20,Z3 = 30 ,Z3 ' = 18 ,Z4 = 54 , 试: (1) 说明轮系属于何种类型; (2 ) 计算齿轮4 的转速n4;(3) 在图中标出齿轮4的转动方向。
解:
(1)1-2-3-4- H(5) 行 星 轮 系
i514 =(n1-n5)/(n4-n5)=1-i 15 =(-1) 2(Z2· Z4)/(Z1· Z3) =+ 16/25
故 i15 =1- i 514 = + 9/25 (2)5 、6 定 轴 轮 系
i56 =n5/n6= - Z6/Z5= - 1/5 (3) 混合轮系
=1-
i
B 2'4
=1+(Z3·Z4)/(Z2' ·Z3')=
+ 20
(3) 混 合 轮 系 i1B =i 12 ·i2'B =40 ×20=800
例3 图示轮系中,Z1 = Z3=25, Z5 = 100 ,Z2 = Z4 = Z6 = 20, 试区分哪些构件组成定轴轮系?哪些构件组成 周转轮系?哪个构件是转臂H?传动比i16 =?
3
2 2' 4
H 1
行星轮 — Z2,Z2' 联动关系 — n2=n 2' 系杆 — H 中心轮 — 1,3,4 3K-H 型周转轮系
解法一:
差动轮系1-2- 2‘-4-H
行星轮系1-2-3-H
i1H4
?
n1 ? nH n4 ? nH
? ? z2z3 = ? 174 z1z2 ' 33
机械原理-轮系例题
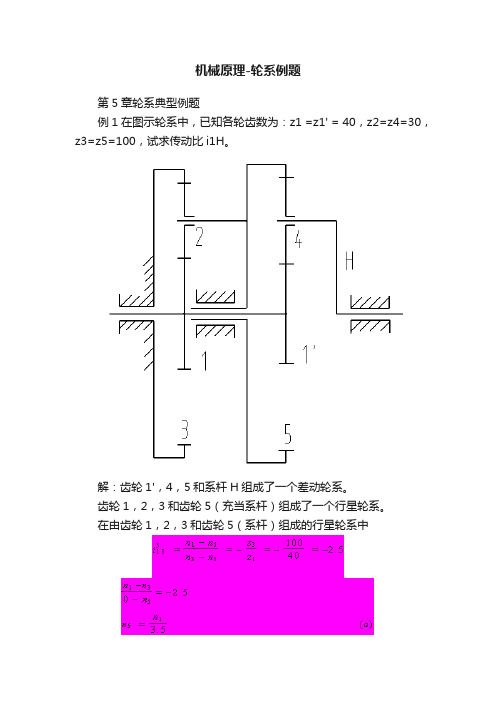
机械原理-轮系例题第5章轮系典型例题例1在图示轮系中,已知各轮齿数为:z1 =z1' = 40,z2=z4=30,z3=z5=100,试求传动比i1H。
解:齿轮1',4,5和系杆H组成了一个差动轮系。
齿轮1,2,3和齿轮5(充当系杆)组成了一个行星轮系。
在由齿轮1,2,3和齿轮5(系杆)组成的行星轮系中由于n 3=0,故有在由齿轮1',4,5和系杆H组成的差动轮系中即分析两个基本轮系的联系,可知n1= n1'(c)将(a),(c)两式代入(b),可得计算结果为正,表明从动系杆H和主动齿轮1的转向相同。
例2 在图示轮系中,已知各轮齿数为:z 1 = 90,z 2 = 60,z 2' = 30,z 3 =30,z 3' = 24,z 4 = 18,z 5 = 60,z 5' = 36,z 6 = 32。
运动从A,B两轴输入,由构件H输出。
已知n A=100r/min,n B=900r/min,转向如图所示。
试求输出轴H的转速n H的大小和方向。
解:齿轮3',4,5和系杆H组成了一个差动轮系齿轮1,2,2',3组成了一个定轴轮系,齿轮5',6组成了另一个定轴轮系。
对于齿轮3',4,5和系杆H组成的差动轮系,有即对于齿轮1,2,2',3组成的定轴轮系,有即对于齿轮5,6组成的定轴轮系,有即分析三个轮系之间的基本联系,有将该结果带入(a)式,可得化简整理后得计算结果为负,说明n H转向与n 5 相同,即n A,n B转向相反。
例3 在图示轮系中,已知齿轮1的转速为n 1 =1650 r/min,齿轮4的转速n4=1000r/min,所有齿轮都是标准齿轮,且z 2=z 5=z 6=20。
求各个齿轮中未知的齿轮齿数。
解:由齿轮1与齿轮3和齿轮6与齿轮4的同轴条件得齿轮1,2,3及系杆H1组成差动轮系;齿轮4,5,6及系杆H2组成行星轮系。
机械原理题目---轮系

机械原理题目---轮系案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作要求1)眼神关注客人,当客人距3米距离时,应主动跨出自己的位置迎宾,然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
《机械原理》典型例题

i2H 20
联立求解: i1H i12 i2H 40 20 800
nH方向
例5
装配用电动螺丝刀的传动简图,已知各轮齿数为 n1=3000 r/min,试求螺丝刀的转速。
1-2-3-H1行星轮系
i H1
13
n1 nH1 0 nH1
z3 z1
4-5-6-H2行星轮系
iH2
46
n4 nH2 0 nH2
(1)说明轮系属于何种类型;(2)计算齿轮4的转速n4;(3)在图中
标出齿轮4的转动方向。
解: (1) 定轴轮系。
(2)n4
z1 z2 z3 n1 z2 z3 z4
1 20 18 40 30 54
1440
8
r/min
例3
在图示轮系中, ,已知各轮的齿数,试判断该轮系 属何种类型,求齿轮4转速的大小和方向.
Hale Waihona Puke 解:3)当两电机反向转动时,为混合轮系
n1 735
差动轮系:
iaHb
na nH nb nH
zb za
定轴轮系:
i12
n1 n2
z2 z1
n2 nb
na nH zb
z1 z2
n1
nH
za
r/min na 735 r/min
nH 287 .4 r/min nH 与 na 转向相同
nH 0.832 r/min
由于1)和2)两种工作状况的输出转速很接近,因此即使有一个电 机发生故障,起重机通过变换电机的转向还能照常工作。
例7
i 例 已知各轮齿数,求传动比 AB
3
3
2
4
A
B
1
i1H4
n1 nH 0 nH
机械原理典型例题(第七章轮系)

C.一个差动轮系。
习题评讲
7-8:所示轮系中,已知Z1=Z2=Z3’=Z4=20, 轮1、3、3’与5同轴线。试求传动比i15。
3 2 4 5
解:假设1的方向向上,则得5的 方向与1的方向一致。
z2 z3 z4 z5 i15 (1) z1 z2 z3 ' z4
m
1
3'
z3 z5 (1) z1 z3 '
解: (1) 定 轴 轮 系1-2
i12=n1/n2= Z2/Z1=40( 向下)
(2) 周 转 轮 系 :2’-(3-3’)-4-H(B) iB2’4=(n2’-nH)/(n4-nH)
=1-n2’/nH=1- i2’H
=- (Z3·Z4)/(Z2’ · Z3’) 故 i2’H=1- iB2’4
=1+(Z3· Z4)/(Z2’ · Z3’)= +20
i1H n1 1980000 nH
t i1H / n1 1440min 24h
基本概念题
1.选择题:
1)图示轮系属于 B 轮系。
A. 定轴;
C. 行星;
B. 差动;
D. 混合
2)图示轮系,给定齿轮1的转动方向如图所
示,则齿轮3的转动方向 C A. 与ω1相同; 。 B. 与ω1相反;
2
由同轴条件,正确啮合条件
r3 r1 2r2
m1=m2=m3;m3’=m4=m5
z3 z1 2 z2 60 z5 z3 ' 2 z4 60
i15 9
r5 r3 ' 2r4
7-10:图示差动轮系中,设已知各轮的齿数Z1=15, Z2=25,Z2’=20,Z3=60,n1=200r/min, n3=50r/min。试求系杆H转数nH的大小和方向:1)当n1、 n3转向相同时;2)当n1、n3转向相同时。
轮系传动比计算经典例题

【例题】已知一行星轮系,太阳轮的齿数为 (Z_1),行星轮的齿数为 (Z_2),内齿圈的齿数为 (Z_3)。
行星架转速为 (n_H),太阳轮转速为 (n_1),求该行星轮系的传动比 (i_{1H})。
【解】
首先确定各构件的转速关系。
根据行星轮系的运动特点,我们有:
(n_1 + n_H = n_2 + n_3)
其中,(n_2) 为行星轮的转速,(n_3) 为内齿圈的转速。
由于内齿圈固定不动,所以 (n_3 = 0)。
将 (n_3) 的值代入上面的等式,得到:
(n_1 + n_H = n_2)
传动比 (i_{1H}) 定义为太阳轮转速与行星架转速之比,即:
(i_{1H} = \frac{n_1}{n_H})
将第2步得到的等式代入传动比的公式中,得到:
(i_{1H} = \frac{n_1}{n_1 - n_2})
由于行星轮的齿数与太阳轮和内齿圈的齿数有关,根据齿轮传动的原理,我们有:
(\frac{Z_1}{Z_2} = \frac{n_2}{n_1 - n_2})
将这个等式代入第4步得到的传动比公式中,得到最终的传动比公式:
(i_{1H} = 1 + \frac{Z_1}{Z_2})
这个公式是行星轮系传动比计算的基本公式,通过它可以方便地求出太阳轮与行星架之间的传动比。
轮系传动比计算经典例题

轮系传动比计算经典例题
经典的轮系传动比计算例题如下:
例题1:
一个车辆的发动机转速为6000 RPM,发动机输出轴上有一个直径为10 cm的轮,该轮与传动轴上的直径为20 cm的齿轮相联,传动轴上的齿轮与车轮相连,车轮直径为60 cm。
请计算该车辆的传动比。
解答:
首先,我们需要计算发动机输出轴上的轮的齿轮转速。
由于该轮和传动轴上的齿轮相联,它们的转速是相等的。
发动机输出轮的齿轮转速 = 发动机转速 = 6000 RPM
接下来,我们需要计算传动轴上的齿轮转速。
根据轮系传动比的定义,齿轮的转速与轮的直径成反比,即齿轮转速和轮的直径的比值是相等的。
传动轴上的齿轮转速 / 发动机输出轮的齿轮转速 = 发动机输出轮的直径 / 传动轴上的齿轮的直径
传动轴上的齿轮转速 = 发动机输出轮的齿轮转速 * (传动轴上的齿轮的直径 / 发动机输出轮的直径)
= 6000 RPM * (20 cm / 10 cm)
= 6000 RPM * 2
= 12000 RPM
最后,我们计算车轮的转速。
同样地,根据轮系传动比的定义,车轮的转速与齿轮的直径成反比。
车轮的转速 / 传动轴上的齿轮转速 = 传动轴上的齿轮的直径 /
车轮的直径
车轮的转速 = 传动轴上的齿轮转速 * (车轮的直径 / 传动轴上
的齿轮的直径)
= 12000 RPM * (60 cm / 20 cm)
= 12000 RPM * 3
= 36000 RPM
因此,该车辆的传动比为36000 RPM / 6000 RPM = 6。
机械原理题目---轮系
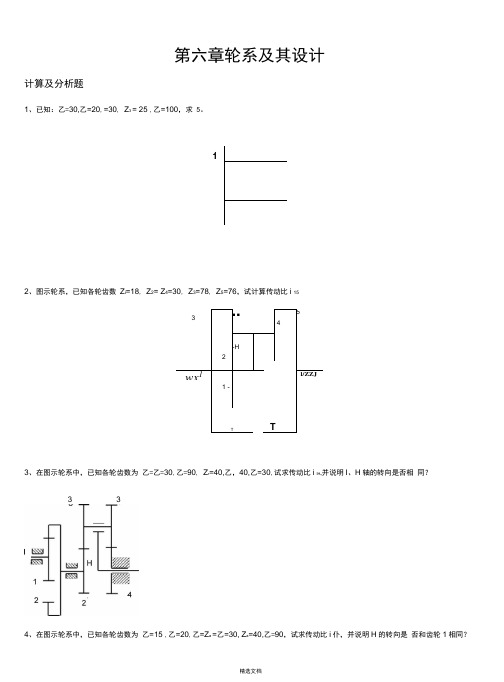
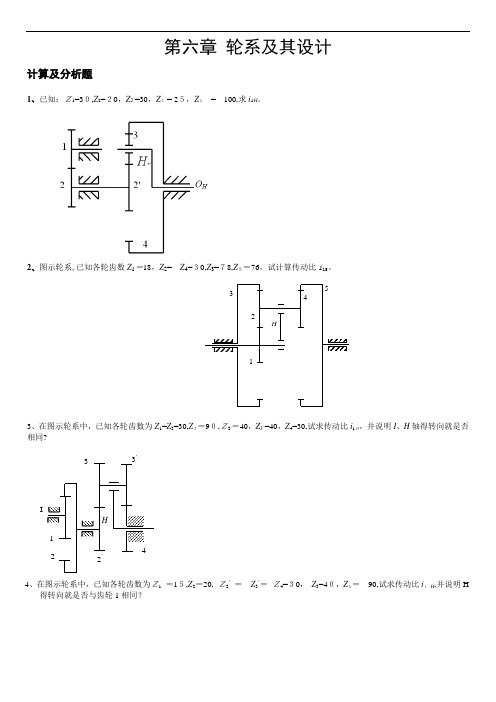
第六章轮系及其设计计算及分析题1、已知:乙=30,乙=20,=30, Z3 = 25 ,乙=100,求 5。
12、图示轮系,已知各轮齿数Z i=18, Z2= Z4=30, Z3=78, Z5=76,试计算传动比i 153、在图示轮系中,已知各轮齿数为乙=乙=30,乙=90, Z r=40,乙,40,乙=30,试求传动比i IH,并说明I、H轴的转向是否相同?3 34、在图示轮系中,已知各轮齿数为乙=15 ,乙=20,乙=Z a =乙=30, Z a=40,乙=90,试求传动比i仆,并说明H的转向是否和齿轮1相同?乙=30,乙=80,乙=25,乙=50,试求传动比i 15。
6、在图示轮系中,已知各轮齿数为乙=19,乙=76,乙=40 , Z3=20,乙=80 ,试求传动比i仆7、在图示轮系中,已知各轮齿数为乙=20 ,乙=25 ,乙=乙=30, Z3 = 20 ,乙=75,试求:(1)轮系的传动比i IH O(2)若n i=1000r/min,转臂H 的转速n H=?8已知图示轮系中各轮的齿数 乙=20,乙=40,乙=15,乙=60,轮1的转速为“=120r/min ,转向如图。
试 求轮3的转速氏的 大小和转向。
9、在图示轮系中,已知各轮齿数为 乙=Z B =乙=20,乙=40, Z 5= 60 , n i = 800r/min ,方向如图所示,试求n H 的大小及转向 10、在图示轮系中,已知各轮齿数为 乙=16 ,乙=24,乙=20 ,乙=40,乙=30 ,乙=20 ,乙=70试求轮系的传动比 5。
11、在图示轮系中,已知各轮齿数为 乙=15 ,乙=25,乙=20 ,乙=60,乙=10,乙=30, n i =200r/min , n 3=50r/min ,试求n i 、%转向相反时,n 5 =?。
a /小12、在图示轮系中,已知各轮齿数为乙=30,乙=25,乙=20,乙=75, n i=200r/min , n3=50r/min,试求:(1)n i与n3转向相同时,n H的大小和方向。
机械原理典型例题(第七章轮系)

3
自行车变速器
自行车的变速器是基于齿轮传动原理设计的。
数据分析及计算
通过数据分析和计算,可以更好地了解和优化齿轮传动系统的性能。
胶带传动原理
胶带传动是一种基于摩擦的传动方式,适用于轻载、低转速的传动。
胶带传动设计
胶带传动的设计要考虑传递力、张紧装置和传动比力的计算,可以确定轮胎传递给地面的力。
传动比计算
1 计算方法
传动比等于从动齿轮的齿数除以主动齿轮的齿数。
2 影响因素
齿轮传动的传动比受到齿数、齿轮模数等因素的影响。
3 传动比的重要性
传动比决定了齿轮传动系统的输出速度和扭矩。
齿轮传动的应用
1
机床
齿轮传动广泛应用于机床上,如铣床、车床、刨床等。
2
工程机械
挖掘机、推土机等工程机械中常使用齿轮传动。
机械原理典型例题(第七 章轮系)
本节将讨论机械原理中的轮系。我们将探索它的定义、分类以及在机械传动 和制造中的应用。
齿轮传动
一种效率高的传动方式
齿轮传动以齿轮的啮合为基础,具有高效率和较大的传递力。
常见的齿轮类型
齿轮传动包括直齿轮、斜齿轮、蜗轮蜗杆等不同类型,适用于不同的工程需求。
应用广泛
齿轮传动广泛应用于机械设备、汽车、船舶等领域。
《机械原理》轮系及其设计习题

《机械原理》轮系及其设计习题1.平 面 定 轴 轮 系 传 动 比 的 大 小 等于 ;从 动 轮 的 回 转 方 向 可 用 方 法 来 确 定。
2.组 成 周 转 轮 系 的 基 本 构 件有: , ,;i k 1 与i k H 1 有 区 别,i k 1 是 ;i k H 1是 ;i k H 1 的 计 算 公 式为 , 公 式 中的 正 负 号 是 按 来 确 定 的。
3.行 星 轮 系 中 若 系 杆 为 原 动 件 可 驱 动 中 心轮, 则 反 之 不 论 什 么 情 况, 以 中 心 轮 为 原 动 件时 也 一 定 可 驱 动 系 杆。
- - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - ( )4.图 示 轮 系, 给 定 齿 轮1 的 转 动 方 向 如 图 所示, 则 齿 轮3 的 转 动 方 向 。
(A )与ω1 相 同;(B )与ω1 相 反;(C ) 只 根 据 题 目 给 定 的 条 件 无 法 确 定。
5.在图示轮系中,根据齿轮1的转动方向,在图上标出蜗轮4的转动方向。
6.在图示的轮系中,已知各轮齿数为z z z z z 1235620=====,已知齿轮1、4、5、7为同轴线,试求该轮系的传动比i17。
7.图示磨床砂轮架微动进给机构中,z z z 12416===,z348=,丝杠导程s=4mm,慢速进给时,齿轮1和齿轮2啮合;快速退回时,齿轮1与内齿轮4啮合,求慢速进给过程和快速退回过程中,手轮转一圈时,砂轮横向移动的距离各为多少?如手轮圆周刻度为200 格,则慢速进给时,每格砂轮架移动量为多少?8.图示轮系中,已知各轮的齿数为z125 =,z 220=,z336=,z418=,z519=,z676=,求传动比i AB。
《机械原理》轮系典型例题

第7章 轮系典型例题一.简答题1.行星轮系齿数与行星轮数的选择必须满足的条件是什么? 答:传动比条件,同心条件,邻接条件,安装条件。
2.为什么要应用轮系?试举出几个应用轮系的例子。
答:一对齿轮难以获得较大的传动比,且不宜实现相距较远的两轴之间的传动,也不能改变从动轮的转向和实现运动的合成与分解等。
如:车床上的三星轮换向机构、汽车后轮传动装置、车床床头箱的调速装置等。
3.计算复合轮系的传动比时,能否对整个轮系加一个()H n -?为什么? 答:因为复合轮系中含有定轴轮系和若干基本周转轮系,由于定轴轮系和周转轮系传动比的计算方法不同,不同基本周转轮系的系杆转速不同,故不能加同一个H n 。
4.周转轮系中1n 与H 1n 的大小和方向是否相同?答:1n 与H1n 的大小不同,方向可能相同也可能不相同。
5.轮系如何分类?周转轮系又可作几种分类?具体如何分法?答:根据轮系在运转过程中各轮几何轴线在空间的相对位置关系是否固定分。
周转轮系分为两类,差动轮系及行星轮系。
具体分法:定轴轮系:轮系运动时,各轮轴线的位置固定不动。
周转轮系:轮系运动时,至少有一个齿轮的轴线是绕其他定轴齿轮的轴线转动。
其中,行星轮系自由度为1,差动轮系自由度为2。
复合轮系 :既有定轴轮系部分又有周转轮系部分、或者由几部分周转轮系所组成的复杂轮系为复合轮系或混合轮系。
二.分析与计算1.在图示轮系中,已知: 1430z z ==, 36100z z ==,1700 r min n =,311331100 2.540z n i n z ==-=-=- (1)由齿轮4、5、6和系杆组成行星轮系,齿轮6固定,60n =。
其转化机构传动比为H64H 4466H H 41001 2.540z n n n i n n n z -==-=-=-=--()H644H 46H 411 2.5 3.5z n i i n z ==-=-=--= (2)由题图可知:34n n =,联立解式(1)、(2)得()11H 344H H2.53.58.75n i i i n ==⋅=-⨯=- 1H 1H 700 r min 80 r min 8.75n n i ∴===--系杆的转向与齿轮1的转向相反。
机械基础轮系试题及答案

机械基础轮系试题及答案一、选择题(每题2分,共10分)1. 轮系中,若主动轮转速为n1,从动轮转速为n2,传动比i为:A. n1/n2B. n2/n1C. n1*n2D. n1-n2答案:B2. 轮系中,若主动轮齿数为Z1,从动轮齿数为Z2,传动比i为:A. Z1/Z2B. Z2/Z1C. Z1*Z2D. Z1-Z2答案:B3. 轮系中,若主动轮直径为D1,从动轮直径为D2,传动比i为:A. D1/D2B. D2/D1C. D1*D2D. D1-D2答案:B4. 轮系中,若主动轮扭矩为T1,从动轮扭矩为T2,传动比i为:A. T1/T2B. T2/T1C. T1*T2D. T1-T2答案:B5. 轮系中,若主动轮功率为P1,从动轮功率为P2,传动比i为:A. P1/P2B. P2/P1C. P1*P2D. P1-P2答案:B二、填空题(每题2分,共10分)1. 轮系中,传动比i的计算公式为_________。
答案:主动轮转速/从动轮转速或主动轮齿数/从动轮齿数或主动轮直径/从动轮直径2. 轮系中,若主动轮转速为n1,从动轮转速为n2,则传动比i=_________。
答案:n1/n23. 轮系中,若主动轮齿数为Z1,从动轮齿数为Z2,则传动比i=_________。
答案:Z1/Z24. 轮系中,若主动轮直径为D1,从动轮直径为D2,则传动比i=_________。
答案:D1/D25. 轮系中,若主动轮扭矩为T1,从动轮扭矩为T2,则传动比i=_________。
答案:T2/T1三、简答题(每题5分,共20分)1. 描述轮系中传动比的物理意义。
答案:传动比表示轮系中主动轮与从动轮转速或齿数或直径的比值,反映了轮系的减速或增速效果。
2. 轮系中,为什么主动轮与从动轮的转速比等于它们的齿数比?答案:因为轮系中齿轮的啮合关系使得主动轮与从动轮的齿数比决定了它们的转速比,即齿数多的轮转速慢,齿数少的轮转速快。
轮系传动比计算经典例题

轮系传动比计算经典例题(实用版)目录1.轮系传动比的定义与分类2.轮系传动比的计算方法3.经典例题解析正文一、轮系传动比的定义与分类轮系传动比是指在机械传动系统中,主动轮(驱动轮)的转速与从动轮(被驱动轮)的转速之比。
根据轮系结构的不同,轮系可以分为定轴轮系、动轴轮系和混合轮系。
1.定轴轮系:指轮系中各齿轮的轴线都固定不动的轮系。
2.动轴轮系:指轮系中至少有一个齿轮的轴线可以移动的轮系。
3.混合轮系:指轮系中既有定轴齿轮,又有动轴齿轮的轮系。
二、轮系传动比的计算方法轮系传动比的计算方法取决于轮系的类型。
以下是不同类型轮系的传动比计算方法:1.定轴轮系:设主动轮转速为 n1,从动轮转速为 n2,主动轮齿数为 z1,从动轮齿数为 z2。
则定轴轮系的传动比 i = n1 / n2 = z2 / z1。
2.动轴轮系:对于动轴轮系,需要先确定主动轮和从动轮的转速关系,然后再计算传动比。
具体的计算方法较为复杂,需要根据轮系的具体结构和齿轮的转速关系进行分析。
3.混合轮系:混合轮系的传动比计算方法与动轴轮系类似,需要根据轮系的具体结构和齿轮的转速关系进行分析。
三、经典例题解析以下是一个经典的轮系传动比计算例题:题目:图示为一电动卷扬机的传动简图。
z1 为单头右旋蜗杆,其余各轮齿数为:z2=42,z2"=18,z3=78,z3"=18,z4=55,卷筒 5 直径 d=400mm,电动机转速 n1=1500r/min。
求卷筒 5 的转速 n5 和重物移动速度 v。
解答:首先,根据蜗杆的性质,可以得出 z1=z2"=1。
然后,根据定轴轮系的传动比计算公式,可以得出:i = n1 / n5 = z2 / z1 = 42 / 1 = 42因此,n5 = n1 / i = 1500 / 42 ≈ 35.7r/min。
轮系例题
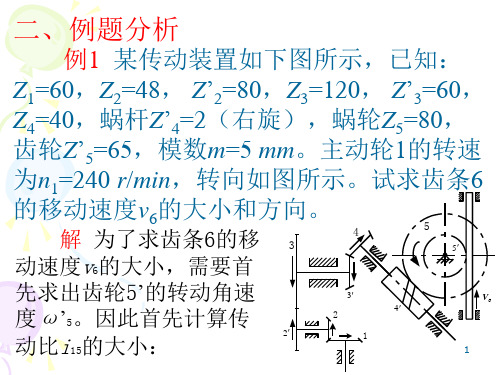
代入式(2)得:
1650 1000 z1 40
750 1000
z1
解上式得:Z1=25,则Z3=Z1+40=65。
6
二、例题分析
例4 下图的轮系中,已知各轮的齿数z1
= 20, z2 = 30, z3 = z4 =12, z5 = 36, z6 = 18, z7
= 68,解:求其该为轮双系重的周传转动轮比系。i1H1。-2-
Z2
Z3
H
Z5
Z1
Z4
Z6
14
二、例题分析
解:根据轮系传动的同心条件有:
Z3 (Z1 Z2 ) Z4 (28 20) 30 18
Z6 (Z3 Z4 ) Z5 (Z1 Z2 ) Z5 48 22 70
所求传动比i14的计算公式应为:
i41
i1H6
n1 nH n6 nH
(1)1 Z2Z6 Z1Z5
20 70 28 22
因为
n6 0
所以有 n1 nH 175
nH
77
16
二、例题分析
即:
77 nH 252 n1
(3)
将式(3)代入式(2)有:
25 77 21175 25n4 252 n1 252 n1
5 7
4h
6-7-H为星轮系,该行星轮系的转 化机构中,3-4-5-h构成了另一级 2
3
6
行星轮系。双重周转轮系的传动
H
比计算可通过二次转化机构解决。 1
第一次是在行星轮系1-2-6-7-H中
使系杆H固定形成转化机构,第二
次是在行星轮系3-4-5-h中使系杆h
机械原理典型例题第七章轮系

维护和故障排除的提示
维护
故障排除
1. 每年定期检查齿轮和轴承的磨损情况。 2. 保持清洁、润滑和防锈,防止腐蚀和水分蒸发。 3. 替换损坏的齿轮和轴承,保证传动的精度和
稳定性。
1. 发现异常声响和震动,检查是否有齿轮损坏 或轴承脱落。
2.பைடு நூலகம்发现漏油和渗油,检查是否有密封件老化或 磨损。
3. 发现偏移和不转动,检查是否有蜗杆摆动或 传动带变形。
3
自动变速器
由多个齿轮箱、液压泵和阀门组成,可实现自动换挡和动力输出。选用斜齿锥齿 轮和精密的精锻轮。
输入和输出轴之间的角度关系
螺旋锥齿轮
用于90度传动,耐用性强,精度 高,但成本高,安装要求高。
蜗轮蜗杆
用于30度传动,难滑动,传动效 率低,但减速比大,安全可靠。
锥齿轮
用于45度传动,传动效率低,制 造难度大,但适用范围广,传动 平稳。
机械原理典型例题第七章 轮系
了解轮系的组成部件,计算传动比和齿数,学习轮系类型和齿轮副的应用实 例,还有输入和输出轴之间的角度关系。
轮系简介
1 定义
轮系是由多个齿轮副组成的一种传动机构,常用于传递转矩和转速,改变旋转方向和旋 转轴。
2 特点
轮系具有紧凑的结构,高效的传动,可靠的性能,广泛的应用领域,例如汽车、机械、 航空等。
3 优点
轮系可以通过改变齿轮数量和齿轮副的组合方式来实现不同的传动比,方便进行维护和 故障排除。
组成部件
齿轮箱
包括齿轮、轴、轴承和密封件, 通常用于惯性负载、重载和交替 负载。
传动带
由织物、橡胶、聚合物等材料制 成,可承受高功率、高速和大转 角,一般用于小型和中型机械传 动。
机械原理题目---轮系【范本模板】

第六章 轮系及其设计计算及分析题1、已知:Z 1=30,Z 2=20,Z 2'=30,Z 3 = 25,Z 4 = 100,求i 1H .2、图示轮系,已知各轮齿数Z 1=18,Z 2= Z 4=30,Z 3=78,Z 5=76,试计算传动比i 15。
12 34 5 H3、在图示轮系中,已知各轮齿数为Z 1=Z 3=30,Z 2=90,Z 2'=40,Z 3’=40,Z 4=30,试求传动比i 1H ,并说明I 、H 轴的转向是否相同?4、在图示轮系中,已知各轮齿数为Z 1 =15,Z 2=20, Z 2’ = Z 3'= Z 4=30, Z 3=40,Z 5= 90,试求传动比i 1 H ,并说明H 的转向是否和齿轮1相同? 1I2 2’ 33’4H5、在图示轮系中,已知各轮的齿数为Z 1= 20, Z 2=30,Z 3=80, Z 4=25,Z 5=50,试求传动比i 15。
6、在图示轮系中,已知各轮齿数为Z 1=19,Z 2=76, Z 2'= 40,Z 3=20,Z 4= 80,试求传动比i 1H 。
7、在图示轮系中,已知各轮齿数为Z 1= 20,Z 2'= 25,Z 2= Z 3=30,Z 3’= 20,Z 4=75,试求:(1)轮系的传动比i 1H 。
(2)若n 1=1000r/min ,转臂H 的转速n H =?8、已知图示轮系中各轮的齿数Z 1=20,Z 2=40,Z 3=15,Z 4=60,轮1的转速为n 1=120 r/min ,转向如图。
试 求轮3的转速n 3 的122’ 34 53’ 45 123H1 2 32’ 3’4 H9、在图示轮系中,已知各轮齿数为Z 1= Z 3= Z 4=20,Z 2=40,Z 5= 60, n 1 = 800r/min ,方向如图所示,试求n H 的大小及转向。
10、在图示轮系中,已知各轮齿数为Z 1=16 ,Z 2=24, Z 2'= 20,Z 3=40,Z 3’= 30, Z 4= 20,Z 5=70试求轮系的传动比i 1H .11、在图示轮系中,已知各轮齿数为Z 1= 15,Z 2=25,Z 2’= 20,Z 3=60,Z 4=10,Z 5=30,n 1=200r/min,n 3=50r/min ,试求n 1、n 3转向相反时,n 5=?。
机械原理典型例题(第七章轮系)11-24

图示为里程表中的齿轮传动, 例4 图示为里程表中的齿轮传动,已知各轮的齿数为Z1 = 17,Z2 = 68,Z3 = 23,Z4 = 20,Z4' =19,Z5 , , , , , = 24。试求传动比i15。 。
解:(1) Z1、Z2 为 定 轴 轮 系。 :( ) i12=- Z2/Z1=-68/17=- 4 (2)Z3 –(Z4’-Z4)-Z5-H(2) 为 行 星 轮 ) 系, n3=0。 。 i53H=(n5-nH)/(n3-nH) =1-n5/nH=+(Z4Z3)/(Z5Z4’) i5H=1-i53H=1-(20×23)/(24×19) × × iH5=1/i5H=-114 (3) 混合轮系,n2=nH 混合轮系, i15=i12 i25=i12iH5=(-4)×(-114) × =456
H 14
=−
H i13 =
z 2 z3 174 =− z1 z2 ' 33
n3 − nH i = n4 − nH
H 34
行星轮 — Z2,Z2’ 联动关系 — n2=n2’ 系杆 — H 中心轮 — 1,3,4 , , 3K-H型周转轮系 型周转轮系
n1 − nH n = 1− 1 n3 − nH nH z3 = −5 z1
机械原理题目---轮系
第六章轮系及其设计计算及分析题1、已知:Z1=30,Z2=20,Z2’=30,Z3= 25,Z4=100,求i1H。
2、图示轮系,已知各轮齿数Z1=18,Z2=Z4=30,Z3=78,Z5=76,试计算传动比i15。
12345H3、在图示轮系中,已知各轮齿数为Z1=Z3=30,Z2=90,Z2'=40,Z3’=40,Z4=30,试求传动比i1H,并说明I、H轴得转向就是否相同?4、在图示轮系中,已知各轮齿数为Z1=15,Z2=20, Z2’=Z3’=Z4=30,Z3=40,Z5=90,试求传动比i1H,并说明H得转向就是否与齿轮1相同?1I2 2’33’4H5、在图示轮系中,已知各轮得齿数为Z1=20,Z2=30,Z3=80,Z4=25,Z5=50,试求传动比i15。
6、在图示轮系中,已知各轮齿数为Z1=19,Z2=76,Z2'= 40,Z3=20,Z4= 80,试求传动比i1H.7、在图示轮系中,已知各轮齿数为Z1= 20,Z2’= 25,Z2= Z3=30,Z3’= 20,Z4=75,试求:(1)轮系得传动比i1H.(2)若n1=1000r/min,转臂H得转速nH=?8、已知图示轮系中各轮得齿数Z1=20,Z2=40,Z3=15,Z4=60,轮1得转速为n1=120r/min,转向如图。
试求轮3得转速n3得大小与转向。
9、在图示轮系中,已知各轮齿数为Z1= Z3=Z4=20,Z2=40,Z5= 60,n1=800r/min,方向如图所示,试求n H得大小及转向.12 2’3453’H45123H1232’3’4H10、在图示轮系中,已知各轮齿数为Z 1=16 ,Z 2=24, Z 2’= 20,Z3=40,Z3'= 30, Z 4= 20,Z 5=70试求轮系得传动比i1H 。
11、在图示轮系中,已知各轮齿数为Z1= 15,Z 2=25,Z 2’= 20,Z3=60,Z 4=10,Z 5=30,n 1=200r/min ,n 3=50r/mi n,试求n1、n 3转向相反时,n 5=?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7-14:图示锥齿轮组成的差速器。已知Z1=48, Z2=42,Z2’=18,Z3=21,n1=100r/min, n3=80r/min,转向如图所示。求nH=?
2 1
2' H3
实际方向, n1与n3相反
i1H3
n1 n3
nH nH
z2z3 z1z2
49 48
n1 nH 49 n3 nH 48 100nH 49 80nH 48
轮 系, n3=0。
i53H=(n5-nH)/(n3-nH) =1-n5/nH=+(Z4·Z3)/(Z5·Z4’)
i5H=1-i53H=1-(20×23)/(24×19) iH5=1/i5H=-114 (3) 混合轮系,n2=nH i15=i12 ·i25=i12·iH5=(-4)×(-114)
=456
r5 r3 ' 2 r4 z5 z3 ' 2z4 60
7-10:图示差动轮系中,设已知各轮的齿数Z1=15, Z2=25,Z2’=20,Z3=60,n1=200r/min, n3=50r/min。试求系杆H转数nH的大小和方向:1)当n1、 n3转向相同时;2)当n1、n3转向相同时。
2 2' 3
i1H 3 nn13 nnH H
z2z3 z1z2'
5
H 1
1)若n1,n3方向相同 则n1=+200r/min,n3=+50r/min 代入上式得: 200 nH 5
50 nH
nH 75r / min
2)若n1,n3方向相反
则n1=+200r/min,n3=-50r/min
得:
200 nH 5
定轴
混合
行星
3)图示轮系属于
轮系。
A. 定轴; B. 差动; C. 行星; D. 混合。
行星 差动
行星
混合
混合
4)图示轮系是由
组成。
A.定轴轮系和行星轮系; B.定轴Y 轮系和差动轮系; C.一个定轴轮系和两个 行星轮系。
A.定轴轮系和行星轮 系; B.定轴轮系和差动轮 系; C.两个行星轮系。Y
例5:图a、b为两个不同结构的锥齿轮周转轮系,已知
Z1=20,Z2=24,Z2’=30,Z3=40,n1=200r/min, n3=-100r/min。求两轮系的nH=?
2' 3 H1
2'
3 2
H
2
a
i1H3
n1 nH n3 nH
z2z3 z1z2 '
200nH 8 100nH 5
nH13 800600r/min
A.蜗轮蜗杆和行星轮系; B.蜗轮Y 蜗杆和差动轮系; C.一个行星轮系。
4)图示轮系是由
组成。
A.定轴轮系和行星轮系;Y B.圆锥齿轮系和差动轮系; C.一个周转轮系。
A.定轴轮系和行星轮系; B.蜗轮蜗杆和差动轮系;Y C.一个差动轮系。
习题评讲
7-8:所示轮系中,已知Z1=Z2=Z3’=Z4=20, 轮1、3、3’与5同轴线。试求传动比i15。
1.选择题:
1)图示轮系属于 B 轮系。 A. 定轴; B. 差动; C. 行星; D. 混合
2)图示轮系,给定齿轮1的转动方向如图所
示,则齿轮3的转动方向 C 。
A. 与ω1相同;
B. 与ω1相反;
C. 只根据题目给定的条件无法确定。
3)图示轮系属于
轮系。
A. 定轴; B. 差动; C. 行星; D. 混合。
转化轮系中 n1与n3相
反
nH9.07r/min
+20
(3) 混 合 轮 系 i1B=i12·i2’B=40×20=800
例3 图示轮系中,Z1 = Z3=25,Z5 = 100,Z2 = Z4 = Z6 = 20,试区分哪些构件组成定轴轮系?哪些构件组成 周转轮系?哪个构件是转臂H?传动比i16 =?
解:
(1)1-2-3-4-H(5)行 星 轮 系
n1 nH n3 nH
1 n1 nH
i4H3
n4 nH n3 nH
1 n4 nH
H 1
z2z3 57
z1 z 2
6
z2 ' z3 57 z4z2 56
n1 157 21
nH
62
n4 157 1
nH
56 56
1-2-2‘-4-H,差动轮系
多种解法。
i14n n1 4n n1 4//n nH H 21 1//5 2 6588
解法一:
差动轮系1-2-2‘-4-H
行星轮系1-2-3-H
i1H4
n1 nH n4 nH
z2z3 = 174 z1z2 ' 33
i1H3
n1 nH n3 nH
1 n1 nH
z3 = 5
z1
i14
n1 n4
n1 n4
116
解二:
行星轮系3-2-2‘-4-H
行星轮系3-2-1-H
i
H 34
n3 nH n4 nH
z2z4 = 174
z3z2 ' 165
i3H1
n3nH n1nH
z1 z3
=1 5
i14
n1 n4
116
例7:已知Z1=1(右),Z1’=101,Z2=99,Z2’=Z4,Z4’=100,
Z5’=100,Z5=1(右),求i1;求当n1=1375r/min,输出轴H转一
i514=(n1-n5)/(n4-n5)=1-i15 =(-1)2(Z2·Z4)/(Z1·Z3)
=+16/25 故 i15=1- i514= + 9/25
(2)5、6 定 轴 轮 系
i56=n5/n6=- Z6/Z5=- 1/5 (3)混合轮系
i16=i15·i56=(9/25)×(- 1/5) =- 9/125 轮1和6的方向相反
1 b
i1H3
n1 nH n3 nH
z2z3 z1z2 '
200nH 8 100nH 5
nH2103015.38r/min
注意:
转化轮系传动比的“±”号的确定错误, 将导致整个计算结果的错误。
它不仅表明在转化机构中中心轮之间的 转向之间的关系,而且将直接影响到周 转轮系传动比的大小和正负号。
例4 图示为里程表中的齿轮传动,已知各轮的齿数为Z1 = 17,Z2 = 68,Z3 = 23,Z4 = 20,Z4' =19,Z5 = 24。试求传动比i15。
解:(1) Z1、Z2 为 定 轴 轮 系。
i12=- Z2/Z1=-68/17=- 4
(2)Z3 –(Z4’-Z4)-Z5-H(2) 为 行 星
- 50 nH
nH 8.33r / min
7-12:所示电动三爪自定心卡盘传动轮系中,
设已知齿数为Z1=6,Z2=Z2’=25,Z3=57,
Z4=56。试求:传动比i14。
i14=n1/n4
=i1H/i4H
3 2 2' 4 1-2-3-H, 行星轮系 3-2-2’-4-H, 行星轮系
i1H3
周的时间t。
1’ n1
5’
定轴: n2和n4’转向相反,n2’和n4转向相反
1
5
i1 2
n1 n2
Z2 Z1
i1 '4 '
n1' = n4'
Z 5'Z 4 ' Z 1'Z 5
H
n2
n1Z 1 Z2
n4'
n1'Z 1'Z 5 Z 5'Z 4 '
2' 2
4
3 4'
差动:
iH
2'4
n2' nH n4nH
z4 z2'
3 2
4 5
1
3'
i15 9
解:假设1的方向向上,则得5的
方向与1的方向一致。
i1 5
( 1) m
z2 z3 z4 z5 z1z2 z3 ' z4
( 1)2 z3 z5 z1z3 '
由同轴条件,正确啮合条件
m1=m2=m3;m3’=m4=m5
r3 r1 2 r2
z3 z1 2z2 60
解:
(1) 空间定轴轮系
(2)i14=n1/n4 = (Z2·Z3·Z4)/(Z1·Z2’ ·Z3’)
故n4 = 8 r/min ( 3)n4 方 向 ←。
例2.计算图示轮系的传动比i1H,并确定输出杆H 的转 向。已知各轮齿数Z1 = 1,Z2 = 40,Z2' = 24, Z3 = 72,Z3' = 18,Z4 = 114,蜗杆左旋,转向
机械原理典型例题(第七章) ——轮系
2011.11
例1. 在图示轮系中,已知:蜗杆为单头且右旋,转速 n1=1440r/min,转动方向如图示,其余各轮齿数为: Z2 = 40,Z2‘ = 20,Z3 = 30,Z3’ = 18,Z4 = 54, 试: (1) 说明轮系属于何种类型; (2) 计算齿轮4 的转速n4;(3) 在图中标出齿轮4的转动方向。
如图示。
解:
(1) 定 轴 轮 系1-2
i12=n1/n2= Z2/Z1=40( 向下) (2) 周 转 轮 系 :2’-(3-3’)-4-H(B)
iB2’4=(n2’-nH)/(n4-nH) =1-n2’/nH=1- i2’H =- (Z3·Z4)/(Z2’ ·Z3’)
故 i2’H=1- iB2’4 =1+(Z3·Z4)/(Z2’ ·Z3’)=
用箭头确定的构件的转向关系,是指转 化机构中各构件的转向关系,而非该周 转轮系中各构件绝对运动的转向关系。
