解决椭圆部分问题的新思路——化椭为圆
数学课件 椭圆化圆

去解决问题。 变化前后点的坐标对应变化:
(x, y) (x, y) ( x , y ) ab
(x, y) (x, y) (ax,by)
2、椭圆化圆的常见结论:
(1)原三点共线,后三点也共线:AB BC AB uBC
原直线平行,后直线也平行:AB//CD AB//CD
4
求 m 范围。
2、椭圆
x2 a2
y2 b2
1(a
b 0)
,过右焦点斜率2的直线与
椭圆交于 A, B ,若 AF 2FB ,求 e
3、椭圆 x2 y2 1 ,过点P(0,3) 直线与椭圆交于 A, B ,
4
(1)若 | PA |,求 范围;
| PB |
(2)求 SAOB 的最大值;
3
y0
2 1 0
0 x02
y02
3
所以点 P 轨迹方程为x2 y2 3
例5、求过椭圆 x2 y2 1 内长轴上一点 N(n,0) ,作直线
94
l 交椭圆于 P,Q(P在上方)两点,且PN 2NQ ,当三角形OPQ
面积最大时,求 l 方程(16重庆一诊) P(x1, y1)
3、椭圆化圆的应用
例1、求过椭圆x2
a2
y2 b2
1(a
b
0) 上一点P(x0,
y0 ) 的切线方程。
解:令
x
y
x a y b
化椭圆为 x2 y2 1
在
xOy 坐标系中:P( x0 ,
y0 )
P(
x0 a
,
y0 b
“化椭为圆”解决椭圆中的面积问题

龙源期刊网
“化椭为圆”解决椭圆中的面积问题
作者:王旭光
来源:《广东教学报·教育综合》2019年第46期
【摘要】在仿射变换下,图形的一些性质不会发生变化。
如,同素性、结合性、平行性、面积比等。
本文通过仿射变换“化椭为圆”来解决椭圆中的一些面积问题,在椭圆的教学和学习过程中,许多问题只能用解析幾何的方法来解决,计算量往往比较大,技巧也比较多。
而在解决圆的某些问题时,往往利用一些性质来处理,过程简明很多。
通过仿射变换正好可以“化椭为圆”,将椭圆中的面积问题转化到圆中来处理。
【关键词】仿射变换;椭圆;圆;面积
参考文献:
[1]吐尔洪艾尔米丁.仿射变换在椭圆面积中的应用[J].新疆师范大学大学学报(自然科学版),2009(1):44.。
仿射变换之化“椭”为“圆”的妙用

仿射变换之化“椭”为“圆”的妙用
白丽艳;殷秀仙;李江燕
【期刊名称】《玉溪师范学院学报》
【年(卷),期】2024(40)3
【摘要】仿射变换的一些重要性质在欧氏几何上有着很好的应用,以近几年高考真题为例,探讨研究了仿射变换在解决有关椭圆中求面积、直线斜率、最值、定值等一系列问题中的应用,化“椭”为“圆”,巧妙地解决圆锥曲线的相关问题,给出了不同题型下灵活运用仿射变换的具体方法.
【总页数】7页(P8-14)
【作者】白丽艳;殷秀仙;李江燕
【作者单位】玉溪师范学院数理学院
【正文语种】中文
【中图分类】O174.6
【相关文献】
1.也谈“RMI原理”与仿射变换下有关圆与椭圆的若干问题
2.走进大豆的微小世界——大豆干圆湿椭(圆)现象的实验探秘
3.妙用伸缩变换化椭为圆
4.化“椭”为“圆”,由“研题”到“命题”的探索——以椭圆中心三角形面积问题为例
5.对化椭为圆解法的探究
因版权原因,仅展示原文概要,查看原文内容请购买。
化“椭”为“圆”,由“研题”到“命题”的探索

化“椭”为“圆”,由“研题”到“命题”的探索作者:***来源:《数学教学通讯·高中版》2022年第04期[摘要] 橢圆与圆有很多相似之处,椭圆的很多性质都可以由圆类比得出. 文章主要借助于伸缩变换,化“椭”为“圆”,以椭圆中心三角形面积问题为例进行题源探究,并揭示了问题的本质,从命题者的角度来思考、设计题目,更好地把握命题规律,有利于学生学科素养的提高.[关键词] 椭圆;圆;三角形;面积数学家波利亚(George Polya,1887—1985)曾说过,“类比是一个伟大的引路人”. 椭圆是解析几何的重要内容,它的很多性质都可以由圆类比得出. 文章主要借助于伸缩变换,化“椭”为“圆”,以椭圆中心三角形面积问题为例进行了题源探究,并进一步对此类问题进行了命题研究. 通过化“椭”为“圆”,能够有效地降低题目难度,减少运算量,有助于学生系统掌握圆锥曲线问题,提高学科素养;教师通过命题的分析与研究,可以站在更高的视角看问题,提高课堂教学效果.[⇩] 伸缩变换在高中数学(人教A版选修4-4)中有伸缩变换的定义:设点P(x,y)是平面直角坐标系中的任意一点,在变换φ:x′=λ·x(λ>0),y′=μ·y(μ>0)的作用下,点P(x,y)对应到点P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换[1].对于椭圆E:+=1(a>b>0)和直线l:y=kx+m,在变换φ:x′=·x,y′=·y的作用下,分别化为E′:x′2+y′2=1和l′:by′=kax′+m. 椭圆在变换φ的作用下,有以下性质[2]:性质1 比值关系不变性:若A,B,C三点共线,伸缩变换后A′,B′,C′仍旧三点共线,同时对应的线段长度比值不变,特别地,当点B为线段AC的中点时,点B′也为线段A′C′的中点.性质2 位置关系不变性:伸缩变换前直线与椭圆的位置关系(相切、相交、相离)在伸缩变换后保持不变.性质3 面积关系确定性:伸缩变换前图形面积S与伸缩变换后图形面积S′满足关系S=abS′.[⇩] 问题探究设直线l:y=kx+m不过原点O,且与椭圆E:+=1(a>b>0)有两个不同的交点A,B,则称△OAB为椭圆的中心三角形. 由伸缩变换的性质可知,求解椭圆中心三角形的面积,完全可以转化为求解对应圆的中心三角形的面积.在伸缩变换φ的作用下得到:l′:by′=kax′+m与E′:x′2+y′2=1的交点为A′,B′,∠A′OB′=α,则S△A′OB′=sinα,S△AOB就转化为了S△A′OB′. 显然当α=90°时,S△A′OB′的最大值为;由伸缩变换的性质3可知S△AOB的最大值为,此时直线l′与圆E′的位置关系如图1所示. S△AOB的最大值取决于直线l与椭圆E的位置关系,即在椭圆已知的情况下,需要研究k,m对S△AOB的影响,有如下三种情况:(1)k确定;(2)m确定;(3)k,m存在线性关系.(1)当k确定时,不妨设k=k,直线l为一族平行线,在伸缩变换φ的作用下,l′:by′=kax′+m,当圆心O到l′的距离d=(α=90°)时,S△A′OB′有最大值,即S△AOB有最大值,如图2所示. 此时d==,即m=±,直线l′与圆x′2+y′2=相切,直线l:y=kx±,同时S△AOB 无最小值.(2)当m确定或k,m存在线性关系时,直线l过定点,不失一般性. 设直线l过定点P (s,t),在伸缩变换φ的作用下,对应的l′过点P′,. 由平面几何知识可知:①当OP′=≥,即2+2≥时,存在直线l′使得α=90°时,S△A′OB′有最大值,即S△AOB有最大值,此时圆心O 到l′的距离d=,直线l′与圆x′2+y′2=相切,如图3所示.②当OP′=<,即2+2<时,不存在直线l′使得α=90°,此时圆心O到l′的距离d≤OP′<,所以α为钝角. 由S△A′OB′=sinα知,当α取最小值时,S△A′OB′有最大值,也就是当弦心距d取最大值时,α取最小值,即d=OP′,OP′⊥A′B′,如图4所示. 所以sin==,cos==d,所以S△A′OB′的最大值为·2d=d,S△AOB的最大值为abd.由以上讨论可知,不论是平行直线族还是直线过定点,S△AOB的最值都与圆x′2+y′2=椭圆+=有关:如果平行直线族或定点在此圆(椭圆)外,S△AOB的最大值为;如果定点在此圆(椭圆)内,当OP′⊥A′B′时,S△AOB的最大值为abd.[⇩] 应用举例例1 (2014年全国Ⅰ卷理科第20题)已知点A(0,-2),椭圆E:+=1(a>b>0)的离心率为,F是椭圆的右焦点,直线AF的斜率为,O为坐标原点.(1)求E的方程;(2)设过点A的动直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.解析:(1)+y2=1.(2)设直线l:y=kx-2,作伸缩变换φ:x′=·x,y′=y.椭圆E:+y2=1,直线l:y=kx-2,点A(0,-2)在φ的作用下,得到:E′:x′2+y′2=1,l′:y′=2kx′-2,A′(0,-2). 根据上述分析可知,S△OP′Q′的最大值为,于是S△OPQ的最大值为×2×1=1,此时d==,解得k=±,所以直线l的方程为y=±x-2.例2 (2015年浙江卷理科第19题)如图5所示,已知椭圆+y2=1上两个不同的点A,B关于直线y=mx+对称.(1)求实数m的取值范围;(2)求△AOB面积的最大值(O为坐标原点).解析:(1)略.(2)作伸缩变换φ:x′=·x,y′=y.椭圆+y2=1,直线y=mx+,k=-在φ的作用下,得到:x′2+y′2=1,y′=mx′+①,kA′B′=-. 设P为AB的中点,根据性质1可知,P′为A′B′的中点,于是kOP′=,OP′:y′=x′②,联立方程①②得P′-,-,当P′在x′2+y′2=上,即m2=2时,S△A′OB′有最大值,如图6,于是S△AOB的最大值为=.[⇩] 命题探索通过前面的题源分析及示例,笔者尝试命制如下题目.1. 利用弦过定点构造条件改编2018年全国Ⅰ卷理科第19题如下:命题1:已知椭圆E:+y2=1,点M的坐标为(2,0),过M的直线l与E相交于A,B 两点,点B关于x轴的对称点为C,设O为坐标原点,求△OAC面积的最大值.命题设计分析:可以证明直线AC过定点P(1,0),作伸缩变换φ:x′=·x,y′=y.点M,P对应的坐标分别为M′(,0),P′,0,显然P′在圆x′2+y′2=上,因此S△OA′C′的最大值为,S△OAC最大值为=.通过改变M的位置控制题目难度,M的位置改变使得定点P的位置也发生了改变,导致P′位于圆x′2+y′2=内或外,从而S△OAC的最大值也发生了变化. 一般地:结论1:对于椭圆E:+=1(a>b>0),设M的坐标为(x,0),通过计算可知直線l过定点P,0,所以P′的坐标为,0.①当M的横坐标满足0<x≤a时,P′位于圆x′2+y′2=外,S△OA′C′的最大值为,S△OAC的最大值为.②当M的横坐标满足x>a时,P′位于圆x′2+y′2=内,由前面的分析可知,当OP′⊥A′C′时,S△OA′C′有最大值. S△OA′C′的最大值为,S△OAC的最大值为ab.2. 利用特殊图形构造条件如椭圆内接平行四边形,相似题目有2015年全国Ⅱ卷理科第20题、2021年佛山市高二期末考试第22题,题目如下:命题2:已知椭圆E:+=1,O为坐标原点,在椭圆上是否存在点A,B,C,使得四边形OACB为平行四边形,且面积为定值.命题设计分析:根据题意作伸缩变换φ:x′=·x,y′=·y.由伸缩变换的性质可知,平行四边形OACB所对应的四边形OA′C′B′是夹角为120°的菱形,因此SOA′C′B′=,于是S=×2×=3. 一般地:结论2:对于椭圆E:+=1(a>b>0),O为坐标原点,则在椭圆上存在A,B,C三点,使得四边形OACB为平行四边形,且面积为定值ab.伸缩变换使椭圆问题回归到圆上进行解决,搭建了两者的桥梁,借助于圆的丰富性质来解决椭圆问题,避免了复杂的计算. 同时从命题者的角度来思考、设计题目,更好地抓住问题的本质,把握命题规律,让教学游刃有余.参考文献:[1] 人民教育出版社. 数学选修4-4的“坐标系与参数方程”[M]. 北京:人民教育出版社,2008.[2] 魏国兵. 让椭圆“圆”形毕露——浅谈伸压变换在高考椭圆问题中的应用[J]. 数学教学,2014(05):13-16.。
简介“圆化法”

教学方法课程教育研究145学法教法研究在椭圆的解题过程中,我们常常遇到一些麻烦,比如:求椭圆的切线,求椭圆的弦长,还有椭圆中一个图形的面积,解决这些问题时,我们往往会算出一个冗长的包含二次根、二项式和分数的式子,这会让我们接下来的运算举步维艰。
于是我们想,能不能先将椭圆转化为一个圆,再利用圆特殊的几何性质进行分析呢?圆化法,即将椭圆通过投影的方法转化为圆,从而达到减少运算量并且更直接快速地解决问题的方法。
那么,我们该如何投影呢?可以从一道简单的例题入手:例题1(2011湖北)如图,直角坐标系xoy 所在的平面为α,直角坐标系(其中y 与重合)所在平面为β,(1)已知平面β内有一点,则点在平面α内射影P 的坐标为________(2)已知平面内β内曲线的方程是,则曲线在平面α内的投影c 的方程是________________分析:(1)已知那么即,又(2)把 代入方程得:由该题给我们提供了这样一个灵感:建立一个与直角坐标系xoy 所在的平面交线为y 轴的新坐标系平面,使两坐标系成某固定角度θ。
可使原坐标系系中的椭圆在新坐标系中射影为圆。
在新坐标系中每点坐标直线满足:。
即将原椭圆纵坐标不变,横坐标进行伸缩变换(类似于必修四中三角函数图象伸缩变换)。
这一方法在刚刚过去的2015湖北高考数学中同样有所体现。
例题2.(2015湖北)一种作图工具如图1所示,O 是滑槽AB 的中点,短杆ON 可以绕O 转动,长杆MN 通过处铰链N 与ON 连接,MN 上的栓子可以沿AB 滑动,且DN=ON =1,MN =3。
当栓子D 在滑杆AB 内做往复运动时,带动N 饶O 转动一周(D 不动时,N 也不动),M 处的笔尖画出的曲线记为C ,以O 为原点,AB 所在的直线为x 轴建立。
如图2所示的平面直角坐标系。
(Ⅰ)求曲线C 的方程;(Ⅱ)设动直线l 与两定直线和分别交于P ,Q 两点。
若直线l 总与曲线C 有且只有一个公共点,试探究:ΔOPQ 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由。
椭圆问题可转移到另一平面的圆中处理

椭圆问题可转移到另一平面的圆中处理
张小刚
【期刊名称】《中国科教创新导刊》
【年(卷),期】2007(000)006
【摘要】将椭圆问题转移到另一平面的圆中处理,是一种独特的方法.
【总页数】2页(P42-43)
【作者】张小刚
【作者单位】江苏省泰兴市第三高级中学,225400
【正文语种】中文
【中图分类】G623.5
【相关文献】
1.椭圆问题"圆"处理 [J], 张娜
2.巧用圆的性质处理椭圆问题 [J], 崔志刚
3.例析椭圆问题圆处理 [J], 宋波
4.巧用圆的性质处理椭圆问题 [J], 崔志刚;
5.从圆所在平面中找六点法画椭圆的规律 [J], 李广庆
因版权原因,仅展示原文概要,查看原文内容请购买。
谈椭圆化圆的方法、结论及运用

如 图1 ,在x O y 平 面 内设直 线 的斜 率为k , P ( s , t ) ,
则p( 一 s , 一 t ) , N ( O , t ) ,
( 1 ) 若A, B, c 三点共线 , 贝 , B , C 三点共线 ; 若A / / C D, 则4 B / / C D ;
1
c : = 1 通 过 矩 阵 = [ 【 0 2 。 ] J 变 化 得 到 椭 圆 2 + 4 = 1 , 那
根据矩 阵知识 ,椭 圆X 2 + : 1 通 过矩 阵 的逆矩 阵 一 :
得 。 , I Y I = r E , / l Y 。 I , 所以 。 , l y o I = I Y l , 将( y o ) 代人
一 ) ,
如果简单看待这个 问题 ,也 就是用 求轨迹方程类 型 中的相关动 点法求 轨迹 而已 但换 个角 度看 这个 问题 ,
1 D Ml = mI D A l 的几何意义就是 : 若O < m < l , 它是向礴由 方
向压缩 , 即对于 轴上方的点 向下压缩 , 对于确 下方 的点 向上压缩 , 而 轴上 的点保持不变 ; 若m > l , 也就 是相应拉 伸 ,这不正 是矩阵 中伸压变换 的本质吗 !无论O < m< l 或 m> l , 均将 圆转化 为了椭 圆. 那 自然联 想到 , 类 似此方 法 , 椭圆不是也 可以转 化为圆吗?
一
例1 ( 2 0 1 2 年湖 北理 2 】 题) 设A是 单位 圆 + = l 上 的任 意一点 , f 是过点A 与 轴垂直 的直线 , D 是直线Z 与 轴
点P ( , Y ) ,
的交点 , 点 在直线z 上, 且满足 l D MI = m I D A I ( m > O , 且
椭圆化圆优化解题

龙源期刊网
椭圆化圆优化解题
作者:徐才銮
来源:《理科考试研究·高中》2013年第10期
新课标数学选修4-4P4介绍了坐标的伸缩变换。
通过伸缩变换可以把曲线的方程化为简单形式,从而方便解题。
本文介绍用伸缩变换化椭圆为圆,来简化几类问题的求解。
一、最值问题
例1求椭圆x214+y2=1上的点到直线x+2y-4=0的最近距离和最远距离,并求出相应点的坐标。
解作伸缩变换x′=112x,
y′=y,则椭圆图1化为圆x′2+y′2=1,直线化为x′+y′-2=0。
如图1,过原点作与直线x′+y′-2=0垂直的直线y′=x′,交圆于A′和B′两点,可知点A′、B′到直线的距离分别最近、最远。
易得A′(212,212),B′(-212,212)。
那么由伸缩变换知原坐标系中,A(2,212),B(-2,-212)。
A、B两点到直线x+2y-4=0的距离dA=|2+2-4|15=2(2-2)15,dB=|-2-2-
4|15=2(2+2)15。
从而最近距离是2(2-2)15,最远距离是2(2+2)15,相应的两点分别是(2,212)和(-2,-212)。
点评本例的常规解法是设出与已知直线平行的椭圆的切线,代入椭圆方程,令判别式为零,解出参数,得到切线方程;再联立切线与椭圆的方程,解出切点;然后求出两个切点到直线的距离。
这种方法运算复杂。
而本文解法化为圆上两点到直线的距离问题,易得所求两点,回避了解复杂的方程(组),简捷获解。
高考数学复习:利用仿射变换解决椭圆

高考数学复习:利用仿射变换解决椭圆谈及利用仿射变换可以解决一些初等几何的问题,可以使问题变得更加简洁、透彻,对笔者启发很大,笔者通过自己的教学实践感觉到利用仿射变换,可以将椭圆的有关问题转化为圆的问题,从而可以借助圆当中的一些性质解决问题,使问题的解决过程大大简化,在利用仿射变换解决相关问题时,主要利用以下几个性质:性质1 变换后共线三点单比不变(即变换后三点的两个线段的比值和变换前的比值一样);性质2 变换后保持同素性和接合性(即变换前直线与曲线若相切,变换后仍相切); 性质3 变换前后对应图形的面积比不变;现以一些高考试题为例加以说明。
例1设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB 相交于点D ,与椭圆相交于E 、F 两点 ⑴若6=,求k 的值;⑵求四边形AEBF 面积的最大值。
分析:此例按照常规解法较为繁杂,但利用仿射变换将椭圆变换为单位圆,点A 、B 、D 、E 、F 分别变换为点A ’、B ’、D ’、E ’、F ’, 线段E ’F ’恰为圆的直径,根据性质1,D ’分线段E ’F ’的比与D 分线段EF 的比相同,利用圆当中的相交弦定理.....求得D ’点的坐标,再反求出D 点坐标,从而很容易求出k 值;利用性质3,可以求得四边形AEBF 与四边形A ’E ’B ’F ’的面积关系,由于四边形A ’E ’B ’F ’面积的最大值较易求出,这样也就很容易求得四边形AEBF 面积的最大值。
解:依题设得椭圆的方程为1y 4x 22=+ 作仿射变换,令x ’=2x ,y ’=y ,则得仿射坐标系x ’O ’y ’,在此坐标系中,上述椭圆变换为圆x ’2+y ’2=1,点A 、B 、D 、E 、F 分别变换为点A ’、B ’、D ’、E ’、F ’,且E ’F ’为圆的直径,E ’F ’=2,A ’(1,0),B ’(0,1)⑴根据性质1 ∵DF 6ED = ∴''''F D 6D E = ∴E ’D ’=712 D ’F ’=72 ∵E ’D ’·D ’F ’=A ’D ’ ·D ’B ’ A ’D ’+D ’B ’=A ’B ’=2∴A ’D ’=724 D ’B ’=723或A ’D ’=723 D ’B ’=724 ∴''''B D 34D A =或''''D 43A = 由定比分点公式可得:D ’(7374,)或D ’(7473,) ∴D 点坐标为(7378,)或(7476,) ∴k=83或k=32 ⑵设四边形AEBF 的面积为S ,四边形A ’E ’B ’F ’的面积为S ’,E ’F ’与A ’B ’的夹角为θ,则S ’=θ⋅⋅sin ''''B A F E 21=θsin 2≤2(当θ=2π时取“=”号,此时F ’ (2222,))由于椭圆的面积为πab=2π,圆的面积为πr 2=π根据性质3有π=π'S 2S ,故S=2S ’ ∴S ≤22 当且仅当F 坐标为(22222,),即k=21时取“=”号 说明:由上述证明过程可知,当D ’为A ’B ’中点是时四边形A ’E ’B ’F ’的面积取到最大值,根据性质1,当D 为AB 中点时四边形AEBF 的面积取到最大值。
大招7仿射变换

大招7仿射变换 大招总结仿射变换,通俗来讲,就是将一个空间内的图形按照一定法则变换,就会在另一个空间内得到与之对应的新图形.在高考数学解析几何题目中,我们可以利用仿射变换将一部分有关椭圆的问题转化为圆的问题,这样就可以借助圆中的特有的一些性质解决问题,从而使问题的解决过程大大简化.椭圆22221(0)x y a b a b +=>>,经过仿射变换x xa y yb '=⎧⎪⎨'=⎪⎩,则椭圆变为了圆222x y a ''+=,并且变换过程有如下对应关系:(1)点()00,P x y 变为00,a P x y b ⎛⎫' ⎪⎝⎭(2)直线斜率k 变为ak k b '=(3)图形面积S 变为aS S b''=(4)点、线、面位置不变(中点依然是中点,相切依然是相切)(5)弦长关系满足||A B AB ''=因此同一条直线上线段比值不变. 仿射变换一般而言主要应用于选填中快速得出结果,对于大题可以利用仿射变换快速得出结果但是容易丟掉步骤分,因此还是用正常方法写出过程.当出现以下几个场景的时候就可以联想仿射变换去处理:(1)面积问题(尤其是有一个顶点是坐标原点的时候);(2)斜率之积出现22b a-之类;(3)同一条线段的比例问题;(4)其他与之相关联的问题.典型例题例1.(2014-新课标)I 已知点(0,2)A -,椭圆2222:1(0)x y E a b a b+=>>的离心率为2F 是椭圆的右焦点,直线AFO 为坐标原点.+ (I)求E 的方程;(II)设过点A 的直线l 与E 相交于,P Q 两点,当OPQ ∆的面积最大时,求l 的方程. 分析:这里第二问出现OPQ ∆面积最大,因此可以联想仿射变换化椭为圆去做..解(I)设(,0)F c ,由条件知2c =得c =,又2c a =,所以2222,1a b a c ==-=,故E 的方程2214x y +=.(II)方法1:依题意当l x ⊥轴不合题意,故设直线:2l y kx =-,设()()1122,,,P x y Q x y 将2y kx =-代入2214x y +=,得()221416120k x kx +-+=,当()216430k ∆=->,即234k >时,21,22824314k k x k ±-=+ 从而2221224143||114k k PQ k x x k+⋅-=+-=+ 又点O 到直线PQ 的距离221d k =+,所以OPQ ∆的面积221443||214OPQk S d PQ k∆-==+,设243k t -=,则2440,144OPQt t S t t t∆>==++,当且仅当72,2t k ==±等号成立,且满足0∆>, 所以当OPQ ∆的面积最大时,l 的方程为:722y x =-或722y x =--. 方法2:作变换2x xy y'=⎧⎨'=⎩,椭圆E 变为圆:224x y ''+=,,此时P Q ''过点(0,4)A '-,此时,2OPQ OPQ S S ∆'∆+=因此OPQ S ∆最大时,OP Q S ∆''同样最大.1sin 2sin 22OP Q S OP OQ P OQ P OQ ∆''='⋅'∠''=∠''当且仅当2P OQ π∠''=时最大 设直线P Q ''方程为4y k x '=''-,那么O 到直线P Q ''距离2421d k '==+17722PQ k k k ⇒'=±⇒='=± ∴直线l 的方程为722y x =±- 总结思考:当过椭圆外一个定点P 作一条直线与椭圆交于,A B 两点时,AOB ∆面积最大值2ab,当且仅当经过仿射变换之后的A B ''与原点O 所构成的三角形为直角三角形时取到最大值.如果定点P 是圆内点,则有两种情况:(1)如果作仿射变换之后P '到圆心距离大于等于22a ,那么面积最大值仍然是;(2)2ab如果作仿射变换之后P '到圆心距离小于22a ,那么当OP A B '⊥''时面积取到最大值.例2.设1F 、2F 分别是椭圆2214x y +=的左、右焦点.(1)若P 是该椭圆上的一个动点,求12PF PF ⋅的取值范围;(2)设(2,0),(0,1)A B 是它的两个顶点,直线(0)y kx k =>与AB 相交于点D ,与椭圆相交于E 、F 两点.求四边形AEBF 面积的最大值. 解(1)由题意可知2,1a b ==,∵c ==∴12(F F 设 (,)P x y∴2212(,),)3,PF PF x y x y x y ⋅=-⋅=+-+()2221133844x x x =+--=-由椭圆的性质可知,2228384x x -⇒--*()212138[2,1]4PF PF x ∴⋅=-∈- (2)方法1:设()()1122,,,E x kx F x kx ,联立2214y kx x y =⎧⎪⎨+=⎪⎩消去y 整理可得()22144k x+=12x x ∴==(2,0),(0,1)A B∴直线AB 的方程为:220x y +-=根据点到直线的距离公式可知,点,E F 到直线AB 的距离分别为1212k h ++==2212k h +==∴12h h+=∴||AB ==∴四边形的面积为()1211||22S AB h h =+===4212214k k=++(当且仅当14k k =即12k =时,上式取等号,所以S 的最大值为22. 方法2:作变换2x xy y'=⎧⎨'=⎩之后椭圆变为圆,方程为224x y ''+=+此时(0,2),22,4B A B E F '''=''=当且仅当E F A B ''⊥''时面积取到最大此时1222ABBF AE B F S S '''==四边形四边形例 3.(2017-肇庆三模)已知圆221:(1)16F x y ++=,定点2(1,0),F A 是圆1F 上的一动点,线段24F A的垂直平分线交半径1F A 于P 点.(I)求P 点的轨迹C 的方程;(II)四边形EFGH 的四个顶点都在曲线C 上,且对角线,EG FH过原点O ,若34BG FH k k ⋅=-,求证:四边形EFGH 的面积为定值,并求出此定值.解(1)解:因为P 在线段2F A 的中垂线上,所以2||PF PA =. 所以211112||4PF PF PA PF AF F F +=+==>所以轨迹C 是以12,F F 为焦点的椭圆,且1,2c a ==,所以3b =。
用坐标伸缩变换解决椭圆问题

解 得 一5一
所 以 当 m > 1+ 时, 椭 圆 ① 内含于椭 圆 ②.
评析 用两 圆的位 置关系来 代 替两椭 圆的位 置
所以当 一5一√1 3 <m <一5+ ̄ / 1 3时已知直
线与椭 圆相交 .
2 2
关 系显 然 问题容 易解决 , 而坐标 伸缩 变换恰 好 沟通 了 两者 之间 的关 系 , 化繁为 简 , 安全可靠.
相应的圆 + Y =1 和直线 2 k x 一 √ my 一1 : 0 , 要
使 已知 的直线 与椭 圆有且仅 有一个 公 共 点 , 只要相 应
的直 线与 圆相切. P( m, ) 变 为 相 应 的 圆 , +y , 2:1和 定 点 P ( ,
解 令 , : ,y 车, 则已 知椭圆 和定点
f 1 的距 离小 于半 径 1 , 即 l 2×1—3×( 一1 )+, n l ,,
、
、 / / ( 1 —0 ) +( 一1— 0 ) < l , n一1 l ( , n>0 ) ,
解得 m > 1+ , 或 m < 1一 ( 舍去) ,
恩
< m <一5+
n Z
椭 圆方 程变为
所 在 直线的 方 程为y , 一 旱= 一 ( , 一 ) .
所 以以 P ( m, n )为 中点 的弦 所在 的直 线 方程 为
y
一
+ Y =1 D D 即 + 午 1 = 2 b ,
,
2
令 , _ , Y √ 2 y ,
7 3 0 0 7 0
宋
波
解 得 一 了 1 < < ÷ .
评析 以上 两例也可 以用一 元二 次方 程 的判别
解答题:利用“仿射变换”化椭为圆

浅谈仿射变换在解决椭圆问题中的应用一、仿射变换思想方法椭圆)0,0(1:2222>>=+b a b y a x C 中,令a x x =',by y =',,则椭圆方程变为单位圆 1'22=+y x C : ,该变换过程称为仿射变换。
相当于在xoy 与'''y o x 两个坐标系来研究问题,但圆中几何意义明显,便于计算。
但最后要还原到椭圆中去解决问题。
变化前后点的坐标对应变化:),()','(),(bya x y x y x =→ )','(),()','(by ax y x y x =→二、性质1、点线关系不变(1)同素性:在经过变换之后,点仍然是点,线仍然是线 (2)结合性:在经过变换之后,在直线上的点仍然在直线上 (3)原三点共线,后三点也共线;原直线平行,后直线也平行 2、原弦长||AB ,斜率k ,后弦长|''|B A ,22211||k k m AB ++=|''|B A (其中ba m =) 3. 直线与圆锥曲线的位置关系不变(相切、相交)已知直线0:=++C Bx Ax l ,椭圆1:2222=+b y a x C ,讨论直线与椭圆的位置关系。
由a x x =',byy =',仿射变换后,直线0:=++C Bx Ax l 变为0:'=++C Bbx Aax l 。
(此结论可以作为公式背下,提高平时做题的速度)椭圆变为1'22=+y x C : ,由直线与圆的位置关系易得答案。
例1 已知直线03=-+y x ,椭圆1422=+y x ,则直线与椭圆的位置关系是( ) A.相交 B.相切 C. 相离 D. 相切或相交解:由2'x x =,y y ='仿射变换后,直线03=-+y x ,椭圆1422=+y x 分别变为直线03''2=-+y x 、椭圆1''22=+y x ,而直线03''2=-+y x 到圆1''22=+y x 的距离15312|3|22>=+-=d ,所以直线和圆相离,由于仿射变换直线与圆锥曲线的位置关系不变,所以原直线和椭圆相离。
圆均匀压缩或伸长变为椭圆反之椭圆变为圆

探求椭圆与圆的内在联系 拓深椭圆概念的理解应用摘 要 本文通过挖掘椭圆与圆的概念以及方程形式之间的区别与联系,从圆入手,运用类比联想和投影转化的方法,揭示了椭圆与圆之间的内在联系,进一步拓深了椭圆概念的理解和应用。
关键词 椭圆 圆 方程 平行投影椭圆与圆之间存在着许多相互联系之处,当我们在研究椭圆问题时,若能挖掘椭圆与圆之间的内在联系,对我们加深椭圆问题的理解无疑是有好处的,本文就此问题作些探讨,以供参考。
1、概念判别(1)定义在平面上,到一个定点O 的距离等于定长R 的点的轨迹是圆,O 是圆心,R 是半径。
在平面上,到两个定点1F 、2F 距离之和等于常数(大于||21F F )的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。
(2)联系在平面上,取一条定长细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子移动笔尖,这时笔尖(动点)画出的轨迹是一个圆。
如果把细绳的两端拉开一段距离,分别固定在图板的两点处(如图1),这时画出的轨迹就是椭圆。
在讲解椭圆概念时,从学生比较熟悉的圆的概念出发,通过动态演示,对两点分离时所得图形的探究性学习,很自然地得出椭圆的概念,便于学生对概念的理解和掌握。
2、方程形式(1)标准方程圆方程:22020)()(R y y x x =-+-,其中),(00y x 为圆心,R 为半径。
椭圆方程:)0(1)()(220220>>=-+-b a by y ax x ,其中),(00y x 为椭圆中心,b a ,分别为椭圆的长短半轴长。
联系:在椭圆方程中,若取b a =,方程即为圆方程形式;两类方程都可转化为)0(022≠=++++AB E Dy Cx By Ax 的一般形式。
(2)参数方程圆方程:)2,0[,sin cos 00πααα∈⎩⎨⎧+=+=R y y R x x ,α为参数。
椭圆方程:)2,0[,sin cos 00πααα∈⎩⎨⎧+=+=b y y a x x ,α为参数。
椭圆变圆,避繁就简

椭圆变圆,避繁就简
柳华
【期刊名称】《科技信息》
【年(卷),期】2007(000)010
【摘要】把圆看成椭圆的特殊形式是大家所熟知的,那么在特定条件下若将椭圆看成特殊的圆是否合理呢?答案是肯定的.本文将给予论证并加以应用。
【总页数】1页(P199)
【作者】柳华
【作者单位】临沂市中医药职工中专学校,山东,临沂,276005
【正文语种】中文
【中图分类】O1
【相关文献】
1.齐差求辨出决策,避繁就简成判断——《决策心理:齐当别之道》读后 [J], 徐富明;李欧
2.伸缩变换椭圆变圆 [J], 朱东海
3.变圆心角增量等步长椭圆插补算法 [J], 方石银
4.数形结合避繁就简——借助函数的凸凹性巧解一类不等式的参数问题 [J], 龚敬辉
5.浅谈小学语文课堂如何返璞归真、避繁就简 [J], 张全
因版权原因,仅展示原文概要,查看原文内容请购买。
化椭为圆 其妙无穷

化椭为圆其妙无穷作者:王海军来源:《理科考试研究·高中》2020年第04期摘;要:直线与圆锥曲线的位置关系问题是近年来解析几何问题中的一个高频考点,尤其是与圆锥曲线有关的相交弦问题,此类问题计算量偏大,属于难点.基于圆的特性及椭圆和圆的内在联系,可以利用伸缩变换将椭圆变换为单位圆,把直线与椭圆的位置关系问题转化为直线与圆的位置关系问题,从而实现“椭圆问题圆解决”,使问题的运算量下降、难度降低.本文就“化椭为圆”法解决直线与椭圆相交问题举例说明.关键词:化椭为圆;转化与化歸;伸缩变换椭圆x2a2+y2b2=1a>b>0,经伸缩变换φ:x′=xa,y′=yb,得到x′2+y′2=1,有如下结论[1]:(1)伸缩变换前后,坐标成比例变换;(2)伸缩变换前后,直线斜率成比例变换:伸缩变换前,椭圆上任意两点AxA,yA,BxB,yB,连线的斜率(假定存在)k=yA-yBxA-xB,则伸缩变换后,k′=ab·k;(3)伸缩变换前后,直线与曲线的位置关系不变:设变换前直线与椭圆方程联立消去y 所得一元二次方程的判别式为Δ,则伸缩变换后Δ′=a2b2Δ;(4)伸缩变换前后,面积成比例变换:S′=1abS.题1;已知椭圆E:x236+y29=1和点P4,2,直线l经过点P且与椭圆交于A,B两点.当点P恰好为线段AB的中点时,求l的方程.分析;此问题是直线与椭圆相交的中点弦问题,解决此问题的方法有:①借助根与系数的关系,采用设而不求的数学思想;②代点相减法(点差法);③利用直线的参数方程法[2];④利用“化椭为圆”法.解析;利用伸缩变换φ:x′=x6,y′=y3,将椭圆E:x236+y29=1变换为圆E′:x′2+y′2=1,点P4,2变换为点P′23,23,所以kO′P′=1 .因为点P为直线与椭圆E相交弦AB的中点,所以P′23,23为圆E′的弦A′B′的中点.利用圆的性质可得kO′P′·kA′B′=-1.所以kA′B′=-1.即kA′B′=-1=2kAB.所以kAB=-12.所以直线的方程为y-2=-12(x-4).即y=-12x+4.通过上述解答可以得到一般的结论:已知椭圆E:x2a2+y2b2=1和点Px0,y0,直线l经过点P且与椭圆相交于A,B两点.当点P恰好为线段AB的中点时,直线l的斜率为k=-b2a2·x0y0.证明;利用伸缩变换φ:x′=xay′=yb将椭圆E:x2a2+y2b2=1变换为圆E′:x′2+y′2=1,点P (x0,y0)变换为点P′(x0a,y0b),所以kO′P′=y0bx0a=ay0bx0.因为点P为直线与椭圆E相交弦AB的中点,所以P′(x0a,y0b)为圆E′的弦A′B′的中点.利用圆的性质可得kO′P′·kA′B′=-1.所以kA′B′=-bx0ay0.所以kA′B′=-bx0ay0=abkAB .所以kAB=-b2a2·x0y0.评注;此解法采用伸缩变换“化椭为圆”的方法,基于圆的特性及椭圆和圆的内在联系,利用伸缩变换将椭圆变换为单位圆,把直线与椭圆的位置关系问题转化为直线与圆的位置关系问题,从而实现“椭圆问题圆解决”,使问题的运算量下降,难度降低.题2;已知点A0,-2,椭圆x2a2+y2b2=1(a>b>0)的离心率为32,F是椭圆的右焦点,直线AF的斜率为233,O为坐标原点.(1)求椭圆的方程;(2)设过点A的动直线l与椭圆相交于P,Q两点.当ΔOPQ的面积最大时,求l的方程.分析;第(2)问求当ΔOPQ的面积最大时l的方程,其常规解法是:设出直线的方程,利用韦达定理求出弦长以及点到直线的距离;再得出ΔOPQ面积的函数表达式;最后利用函数思想处理最值问题.虽然思路比较清晰,但是在这一过程中对数学运算的核心素养能力有较高的要求,同时还要求学生具有较强的分析问题、解决问题的能力.为了简便一些,下面就利用“化椭为圆”法求解此题.解析;(1)设Fc,0,直线AF的斜率为233,所以2c=233,解得c=3.又ca=32,所以a=2,b2=a2-c2=1.故椭圆的方程为x24+y2=1.(2)令φ:x′=x2,y′=y,则椭圆经过伸缩变换φ后得单位圆x′2+y′2=1.设θ为线段OP与OQ的夹角,则变换后△OPQ的面积S′=12sinθ≤12,当且仅当θ=π2时等号成立.此时,圆心到直线的距离为22.显然,当l⊥x轴时不符合题意.所以可设l′:y′=k′x′-2,则2k′2+1=22.则k′=±7=y′1-y′2x′1-x′2=y1-y2x12-x22=2(y1-y2)x1-x2=2k.所以k=±72.所以SΔOPQ=abS′=2×1×12=1.此时,直线l的方程为y=±72x-2.评注;此解法采用“椭圆化圆”法求解,与常规法相比“椭圆化圆”充分利用了“数形结合”的思想,降低了题目的思维难度,简化了运算的过程,充分体现了转化与化归思想的优越性,同时也培养了数学学科核心素养.题3;设A,B为椭圆x22+y2=1上满足ΔAOB的面积为64的任意两点,E为线段AB的中点,射线OE交椭圆C于点P,设OP=tOE,求实数t的值.分析;此题的常规解法是:设直线AB的方程y=kx+b,将其代入椭圆方程,利用判别式、根与系数的关系即可得到弦长AB;利用点到直线的距离公式求得ΔAOB的面积表达式;利用12AB·d=64得到k,b之间的关系;再由题设E为线段AB的中点,OP=tOE,点P在椭圆C 上,利用中点坐标公式即可得到点P的坐标;最后代入椭圆方程可得到k,b,t的关系式,再与上面得到的关系式联立即可得到t的值.很明显,常规解法涉及到的变量较多,运算量较大且不易求解,尤其是涉及k,b,t的关系,进而求t的值.下面利用“化椭为圆”法求解此题,以体现其优越性.解法1;令φ:x′=x2,y′=y,则椭圆经过伸缩变换φ后得单位圆x′2+y′2=1.SΔA′O′B′=12SΔAOB=12×64=34.即SΔA′O′B′=12·21-d2·d=34 .所以d2=14或34.即d=12或d=32 .所以t=OPOE=O′P′O′E′=1d .所以t=2或233.解法2;令φ:x′=x2,y′=y,则椭圆经过伸缩变换φ后得单位圆x′2+y′2=1.SΔA′O′B′=12SΔAOB=12×64=34 .所以∠A′O′B′=π3或2π3.所以d=OE=rsinπ6=12或d=OE=rsinπ3=32.所以t=OPOE=O′P′O′E′=1d=2或233.评注;此解法采用“化椭为圆”法求解,与常规法相比“化椭为圆”充分利用了“数形结合”的思想,降低了题目的思维难度,简化了运算的过程,其优越性不言而喻.椭圆与圆之间存在着许多内在联系,在学习和研究椭圆问题时,若能有意识地挖掘椭圆与圆之间的内在联系,利用伸缩变换将椭圆变换为单位圆,把直线与椭圆的位置关系问题转化为直线与圆的位置关系问题,从而实现“椭圆问题圆解决”.圆与椭圆的相互转化可以使我们领略知识之间并不是孤立的,这就促使我们在研究问题时,要善于转化,善于在知识之间建立合理的联系,善于将复杂问题合理地向简单问题转化,“化橢为圆”让学生多了一种选择,促进了学生数学思维的发展,有利于培养学生程序化思考问题的习惯,提升学生的数学运算能力,促使其形成一丝不苟、严谨求实的科学精神.学生数学学科素养的形成和发展,是在教师的启发和引导之下,通过自己的独立思考悟出来的,是一种逐渐养成的思维习惯和思想方法.数学之美,在于发现,因此有效挖掘题中所给信息,不仅是解题的需要也是优化知识结构、训练思维、提高数学素养的需要.参考文献:[1]侯宝坤.伸缩变换——兼谈化椭圆为圆问题[J].中学数学研究,2004(04):31-33.[2]王海军.聚焦“中点”多样解题[J].理科考试研究,2019,26(03),20-21.(收稿日期:2019-10-28)。
椭圆还圆法

题 目改 为 求 单 位 圆x 产 + y = l v  ̄P ( 02 ) 的直 线l 交圆 =  ̄ i z i
,
点A , B , △A O B 面积 最 大 时 直 线方 程 .
S Z X A , O W =1 I OA, l l 0B 1. s i
一
.
在单 位 圆 中。 ・ . ・ O P 上A B . I O A
卜1 0B l _ I OP A B I = 1 A B I .
r —— —— — —— — —
2 V 2. ( I) 求该椭圆的标准方
程:
且l A B l - VI O A l ‘ + l O B 广 .
( 2 ) 令
= x , 由 于仿 射 不 变 性 , 可知P ( 0 , 2 ) 变化为P
( O , 2 ) .
4 4
通 过 此 题 是 想 告 诉 我 们 出题 是 根 据 椭 圆 还 圆 法 。反 向转 化. 就 将 一 道 弱 智 的 题 变 成 一 道 巨难 的 解 析 几 何 难 题 . 同 时 我 们也 可知 道 高 考命 题 的方 式 、 背景, 加 深 对考 题 真 题 的 认 识 . 有 了对 椭 圆还 圆 法 全面 的认 识 , 那 么 到 底 什 么 时候 用 ?归 纳 了 以下 几 种 : 1 . 面 积 问题 : 2 . 线 段 成 比例 问题 : 3 . 斜 率 成 比例 问题 : 4 . 变 换 后 成 特 殊 几何 关 系 . 此种方法确实存在风险 , 但它能帮助我们快速获得结果 , 便 于检查 , 可 以用常规式子写 出过程 , 用 此 法 得 出结 果 . 优 秀 学 生参 加 自主 招 生 考 试 时 可 以随 意 使 用 .
解决椭圆部分问题的新思路——化椭为圆

解决椭圆部分问题的新思路—-化椭为圆-—山西大学附中 刘嘉信一、概念与基本的推导化椭为圆,顾名思义,就是把椭圆变成圆.那如何实现这一点呢?这里我们以中心在坐标系原点O 点,长轴在X 轴上的椭圆为例,看看如何将椭圆变成一个圆(在本文中默认a>b>0): 椭圆的标准方程为:)1......(12222=+by a x 将(1)式中左右两边同时乘以2a 可得: )2......(22222a yb a x =+ 我们可以设y ba z =,代入(2)式消去y 就有: )3......(222a z x =+这时,我们可以发现,(3)式中的形式就是xoz 坐标系里面的一个以坐标原点为圆心、以a 为半径的一个圆。
这时我们就把一个xoy 坐标系里面的椭圆成功的变成了一个xoz 坐标系里面的一个比较特殊的圆。
实际上,我们可以发现,这个方法的本质就是把y 轴人为地拉长为原来的y b a z =倍,变成xoz 坐标系。
二、应用无论什么理论,有实际的应用才有价值,那么那么这个方法到底有什么用处呢?我们知道,一般情况下,解决椭圆与直线关系等的问题时,我们需要联立、求解或者用韦达定理求解出21x x +或者是21x x ,较为繁琐,计算量较大,原因就是椭圆的几何性质太少,没有办法直接作出判断.但是,在我们把椭圆变成圆以后,我们就可以利用远的一些性质来解决一些问题.1、 判断直线与椭圆的位置关系.比如我们已知一条直线L:)1)......(0(0≠=++AB C By Ax 我们还知道一个椭圆C:)2......(12222=+by a x 我们可以用上面的方法,设y ba z =,代入(1)、(2)式得到: )3......(0=++C z aBb Ax )4......(222a z x =+这时候,我们就可以看出来:(3)式是xoz 坐标系里面的一条直线,而(4)式是xoz 坐标系里面的一个圆心为(0,0)、半径为a 的一个圆.这样我们就可以用点线距离和半径的关系来判断椭圆C 和直线L 的位置关系。
中小幼椭圆化圆公开课教案教学设计课件
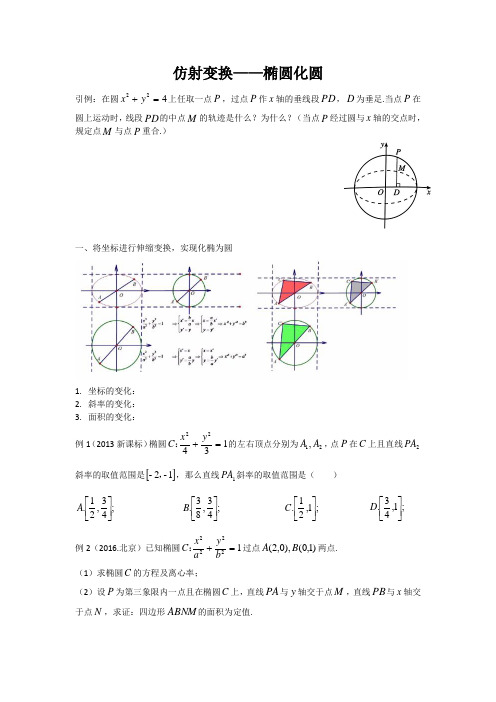
仿射变换——椭圆化圆引例:在圆422=+y x 上任取一点P ,过点P 作x 轴的垂线段PD ,D 为垂足.当点P 在圆上运动时,线段PD 的中点M 的轨迹是什么?为什么?(当点P 经过圆与x 轴的交点时,规定点M 与点P 重合.)一、将坐标进行伸缩变换,实现化椭为圆1. 坐标的变化:2. 斜率的变化:3. 面积的变化:例1(2013新课标)椭圆13422=+y x C :的左右顶点分别为21,A A ,点P 在C 上且直线2PA 斜率的取值范围是[]1-2-,,那么直线1PA 斜率的取值范围是( ) ;43,21.⎥⎦⎤⎢⎣⎡A ;43,83.⎥⎦⎤⎢⎣⎡B ;1,21.⎥⎦⎤⎢⎣⎡C ;1,43.⎥⎦⎤⎢⎣⎡D 例2(2016.北京)已知椭圆12222=+by a x C :过点)1,0(),0,2(B A 两点. (1)求椭圆C 的方程及离心率;(2)设P 为第三象限内一点且在椭圆C 上,直线PA 与y 轴交于点M ,直线PB 与x 轴交于点N ,求证:四边形ABNM 的面积为定值.例3(2014新课标1)已知点)2,0(-A ,椭圆12222=+by a x E :的离心率为23.F 是椭圆的右焦点,直线AF 的斜率为332,O 为坐标原点. (1)求E 的方程;(2)设过点A 的直线l 与E 相交于Q P 、两点,当OPQ ∆的面积最大时,求l 的方程.二、仿射变换后圆心角为直角问题例1(2011山东)已知直线l 与椭圆12322=+y x C :交于),(),,(2211y x Q y x P 两不同点,且OPQ ∆的面积26=∆OPQ S ,其中O 为坐标原点. (1)证明:2221x x +和2221y y +均为定值;(2)椭圆C 上是否存在点G E D ,,,使得26===∆∆∆OEG ODG ODE S S S ?若存在,判断DEG ∆的形状;若不存在,请说明理由.例2(2016浙江二模)已知椭圆12222=+b y a x C :经过点),(5456,其离心率为23,设M B A ,,是椭圆C 上的三点,且满足))2,0((,sin cos παα∈⋅+⋅=OB OA OM ,其中O 为坐标原点. (1)求椭圆C 的标准方程;(2)证明:OAB ∆的面积是一个常数.三、中点弦问题例1.(2015新课标2)已知椭圆)0(9:222>=+m m y x C ,直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点B A ,,线段AB 的中点为M .(1)证明:直线OM 的斜率与l 的斜率的乘积为定值;(2)若l 过点),3(m m ,延长线段OM 与C 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时l 的斜率;若不能,请说明理由.四、椭圆与圆结合的面积问题例1(2018武汉模拟)已知椭圆12222=+by a x C :的右焦点为)0,2(,离心率为36. (1)求椭圆的标准方程;(2)若直线l 与椭圆C 相交于B A ,两点,且以AB 为直径的圆经过原点O ,求证:点O 到直线AB 的距离为定值;(3)在(2)的条件下,求OAB ∆面积的最大值.五、定比分点和弦长公式例1(2011重庆)如图,椭圆O 的中心为原点,离心率22=e ,一条准线的方程是22=x . (1)求椭圆的标准方程;(2)设动点P 满足ON OM OP 2+=,其中N M ,是椭圆上的点,直线ON OM ,的斜率之积为21-,问:是否存在定点,使得PF 与点P 到直线102:=x l 的距离之比为定值;若存在,求点F 的坐标,若不存在,说明理由.例2(2016四川)已知椭圆12222=+by a x E :的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线3:+-=x y l 与椭圆有且只有一个公共点T(1)求椭圆的标准方程及点T 的坐标;(2)设O 是坐标原点,直线'l 平行于OT ,与椭圆E 交于不同的两点B A ,,且与直线l 交于点P .求证:存在常数λ,使得PB PA PT ⋅=λ2,并求λ的值.。
巧用圆的性质处理椭圆问题

巧用圆的性质处理椭圆问题
崔志刚
【期刊名称】《新高考》
【年(卷),期】2010(000)004
【摘要】圆在平面几何中占有重要的地位,同时,圆的性质在平面解析几何中也有广泛而灵活的应用.巧妙运用圆的性质,不仅使我们避免在解解析几何问题时因其求解过程繁杂冗长而陷入困境,还可使问题轻而易举获得解决,充分感受到平面几何的魅力.
【总页数】3页(P33-35)
【作者】崔志刚
【作者单位】无
【正文语种】中文
【中图分类】G623.502
【相关文献】
1.圆的性质——椭圆问题伸缩变换 [J], 葛桂华
2.巧用圆的知识妙解椭圆问题 [J], 陈惟前
3.巧用圆解椭圆问题 [J], 任伟芳
4.巧用圆的性质处理椭圆问题 [J], 崔志刚;
5.巧借圆的性质,妙解椭圆问题 [J], 王小妹
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解决椭圆部分问题的新思路——化椭为圆
——山西大学附中 刘嘉信
一、概念与基本的推导
化椭为圆,顾名思义,就是把椭圆变成圆。
那如何实现这一点呢?这里我们以中心在坐标系原点O 点,长轴在X 轴上的椭圆为例,看看如何将椭圆变成一个圆(在本文中默认a>b>0): 椭圆的标准方程为:
)1......(122
22=+b
y a x 将(1)式中左右两边同时乘以2
a 可得: )2......(22222
a y
b a x =+ 我们可以设y b
a z =,代入(2)式消去y 就有: )3......(222a z x =+
这时,我们可以发现,(3)式中的形式就是xoz 坐标系里面的一个以坐标原点为圆心、以a 为半径的一个圆。
这时我们就把一个xoy 坐标系里面的椭圆成功的变成了一个xoz 坐标系里面的一个比较特殊的圆。
实际上,我们可以发现,这个方法的本质就是把y 轴人为地拉长为原来的y b a z =倍,变成xoz 坐标系。
二、应用
无论什么理论,有实际的应用才有价值,那么那么这个方法到底有什么用处呢?
我们知道,一般情况下,解决椭圆与直线关系等的问题时,我们需要联立、求解或者用韦达定理求解出21x x +或者是21x x ,较为繁琐,计算量较大,原因就是椭圆的几何性质太少,没有办法直接作出判断。
但是,在我们把椭圆变成圆以后,我们就可以利用远的一些性质来解决一些问题。
1、 判断直线与椭圆的位置关系。
比如我们已知一条直线L :)1)......(0(0≠=++AB C By Ax
我们还知道一个椭圆C :)2......(122
22=+b
y a x 我们可以用上面的方法,设y b
a z =,代入(1)、(2)式得到: )3......(0=++C z a
Bb Ax )4......(222a z x =+
这时候,我们就可以看出来:(3)式是xoz 坐标系里面的一条直线,而(4)式是xoz 坐标系里面的一个圆心为(0,0)、半径为a 的一个圆。
这样我们就可以用点线距离和半径的关系来判断椭圆C 和直线L 的位置关系。
设d 为(0,0)到(3)表示的直线L ’的距离,则有:
2222a b
B A C
d +=既然知道了一个圆圆心与一条直线的距离和这个圆的半径,那么二者的
位置关系就十分好判断了。
2、 弦中点问题
弦中点问题是我起的一个名字。
在椭圆中这类问题可以用化椭为圆的方法来解决。
由于从xoy 坐标系变成xoz 坐标系以后,原来的弦的中点仍然是中点,所以我们就可以连接圆心(即坐标原点)和这个中点,制造出一个垂直(弦的垂直平分线)。
下面我举个例子:
【例1】已知椭圆C 的标准方程为:14
162
2=+y x ,求该椭圆所有的斜率为2的弦的中点的轨迹方程。
【解析】我们用上面的方法就可以把椭圆变成:1622=+z x 。
由于我们是要在xoz 坐标系里面做工作,所以必须把直线也变进来。
设这些弦所在的直线的方程为:b x y +=2,把y 代换成z 就有:b x z 24+=。
我们知道,圆里面弦的中点与圆心(这里是坐标原点)的连线与这条弦所在直线垂直,所以,很明显就有这些中点一定分布在直线x z 41-=上面,即x y 8
1-=。
因为弦的中点一定在椭圆内部,所以我们只需再加上范围即可。
不必再用原来的代入消元求解的方法,十分简洁。
【例2】已知椭圆C 的标准方程为:14
162
2=+y x ,P 、Q 为椭圆C 上的两点,直线OP 、OQ 的斜率的乘积为4
1-。
求|OP|+|OQ|。
【解析】设P ),(11y x ,Q ),(22y x
我们可以按照上面的方法把C 的方程变成1622=+z x ,于是在xoz 坐标系里面,有: 112y z =,222y z =。
因为OP 、OQ 过原点,所以11x y k OP =,2
2x y k OQ =;变成xoz 坐标系后,因为112y z =、222y z =,所以1111'22x y x z k k OP OP ==
=、2222'22x y x z k k OQ OQ ===。
又因为4
1-=⨯OQ OP k k ,所以有1''-=⨯OQ OP k k ,即在xoz 坐标系中,OP ⊥OQ ,所以||||21z x =。
所以:
20
1244)(4
3)(41)(414
1412221222221212222212122
222121=++=+++++=+++
=+++x x z x z x z x z x y x y x
三、注意
对于这种方法,我们必须注意两点:
1、 对于大多数给定某一个角度的题目,这个方法并不适用,因为角经过对y 轴的拉伸之后
就变了,失去了原来的集合性质,不适合用这种方法。
2、 对于求某一段距离的长的问题,如果用这种方法,就需要求出两个点的坐标,因为距离
经过变换以后也可能变得不同。
