《两直线夹角》(课件)
合集下载
2.5.1 直线间的夹角、平面间的夹角 课件(北师大选修2-1)
解：法一：以A点为坐标原点，建立直角坐标 系如右图所示，设B(1,0,0)，则C(1,1,0)， A1(0,0,1)，∴ AC ＝(1,1,0)， BA1 ＝(－1,0,1)， BA AC · 1 ∴cos〈 AC ， BA1 〉＝ | AC |· 1 | | BA 1，1，0· －1，0，1 1 ＝ ＝－ . 2 2× 2
2 3 1 ∴P0，0， ，E0， a， a 3 2
3 a . 2 1 3 2 3 (1)证明： BE ＝－a， a， a， PD ＝0，2a，－ a， 2 2 3 ∴ BE · ＝0＋a2－a2＝0. PD ∴ BE ⊥ PD ，∴BE⊥PD. 1 3 (2) AE ＝0， a， a， CD ＝(－a，a,0)． 2 2 1 2 a 2 2 AE · CD ＝ 则cos〈 AE ， CD 〉＝ ＝ ， 2a· 4 a | AE || CD | 2 即AE与CD的夹角的余弦值为 4
∵AB⊥BC，BB1⊥AB，BB1⊥BC， ∴ BA · ＝0， BB1 · ＝0， BB1 · ＝0， AB BC BC ∴ BA1 · ＝－a2. AC
又∵ BA1 · ＝| BA1 |·AC |· | cos〈 BA1 ， AC 〉， AC －a2 1 ∴cos〈 BA1 ， AC 〉＝ ＝－ . 2 2a· 2a ∴〈 BA1 ， AC 〉＝120° .
(4分)
x，y，z· 0，0，1＝0， ∴ x，y，z· 2，1，0＝0. y＝－ ∴ z＝0.
2x，
(6 分) ，0)，
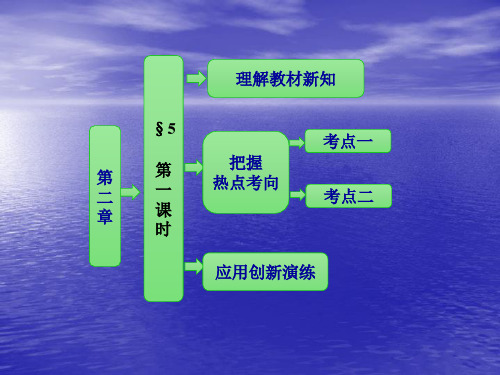
2 3 1 ∴P0，0， ，E0， a， a 3 2
3 a . 2 1 3 2 3 (1)证明： BE ＝－a， a， a， PD ＝0，2a，－ a， 2 2 3 ∴ BE · ＝0＋a2－a2＝0. PD ∴ BE ⊥ PD ，∴BE⊥PD. 1 3 (2) AE ＝0， a， a， CD ＝(－a，a,0)． 2 2 1 2 a 2 2 AE · CD ＝ 则cos〈 AE ， CD 〉＝ ＝ ， 2a· 4 a | AE || CD | 2 即AE与CD的夹角的余弦值为 4
∵AB⊥BC，BB1⊥AB，BB1⊥BC， ∴ BA · ＝0， BB1 · ＝0， BB1 · ＝0， AB BC BC ∴ BA1 · ＝－a2. AC
又∵ BA1 · ＝| BA1 |·AC |· | cos〈 BA1 ， AC 〉， AC －a2 1 ∴cos〈 BA1 ， AC 〉＝ ＝－ . 2 2a· 2a ∴〈 BA1 ， AC 〉＝120° .
(4分)
x，y，z· 0，0，1＝0， ∴ x，y，z· 2，1，0＝0. y＝－ ∴ z＝0.
2x，
(6 分) ，0)，
两直线夹角和到角
；
姿态享用。它们接受了残酷的现实，并学会把这看成生存的常态。他们的适应能力是很强的。适应能力强，这对人，对鸟，对任何生物，都是一个褒奖的词语。它们无师自通，就懂得了站在主人为它们架在笼中的假树杈上，站在笼子的中心位置，而不是在笼壁上徒劳地乱撞。就像主人所期待的 那样，优雅地偏头梳理它们的羽毛，如果有同伴，就优雅地交颈而眠。更重要的是，当太阳升起的时候，或者主人逗弄的时候，就适时适度地婉转歌唱，让人感觉到生活是如此的自由、祥和、闲适。而天空和扑翼这种与生俱来的事情，也就是多余的了。 但有一些鸟的适应能力却很差，这大抵是 鸟类中的古典主义者或理想主义者。它们对生命的看法很狭隘，根本不会随现实场景的转换而改变。在最初的惊恐和狂躁之后，它们明白了厄运，它们用最荏弱的姿态来抗拒厄运。他们是安静的，眼睛里是极度的冷漠，对小碟小碗里伸过来的水米漠然置之，那种神态，甚至让恩赐者感到尴尬， 感到有失自尊。鸟儿的眼睛里一旦现出这样的冷漠，就不可能再期待它们的态度出现转机，无论从小笼子换到大笼子，还是把粗瓷碗换成金边瓷碗，甚至于再赏给它们一个快乐的伙伴，都没有用了。这一切与它们对生命的认定全不沾边儿。事实上，这时候它们连有关天空的梦也不做了，古典主 义者总是悲观的，绝望的，它们只求速死。命运很快就遂了它们的心愿。 而我一直怀有敬意的，是鸟儿中的另一种理想主义，这种鸟儿太少，但我侥幸见过一只，因为总是无端想起，次数多了，竟觉得这鸟儿的数目似乎在我感觉中也多了。 我见到这只鸟儿的时候，它在笼中已关了很久了，我 无从得见它当初的惊恐和焦灼，不知它是不是现出过极度的冷漠，或者徒劳地撞击笼壁，日夜不停地用喙啄笼壁的铁枝。我见到它的时候，它正在笼子里练飞。它站在笼子底部，扑翼，以几乎垂直的路线，升到笼子顶部，撞到那里，跌下来，然后仰首，再扑翼……这样的飞，我从来没见过。它 在笼中划满风暴的线条，虽然这些线条太短，不能延伸，但的确饱涨着风暴的激情。它还绕着笼壁飞，姿态笨拙地，屈曲着，很不洒脱，很不悦目，但毕竟它是在飞。它知道怎样利用笼内有限的气流，怎样训练自己的翅膀，让它们尽可能地张开，尽可能地保持飞翔的能力。 在这样一只鸟的面前， 我感觉惭愧。一般我们很难看见鸟是怎样学飞的，那些幼鸟，那些被风暴击伤了的鸟，那些在岩隙里熬过隆冬的鸟，还有那些被囚的鸟。这是一件隐秘 的事。我们只看见它们在天空中划过，自由地扑翼，桀骜地滑翔，我们只羡慕上帝为它们造就了辽阔的天空。 但在看到那只在笼中以残酷的方 式练飞的鸟之后，我明白，天空的辽阔与否，是由你自己造就的，这种事情上帝根本无能为力。上帝只是说，天空和飞翔是鸟类的生命形式，而灾难和厄运也是世界存在的另一种形式。至于在灾难和厄运中你是否放弃，那完全是你自己的事情。 只要眼睛里还有蓝天? 兰心 人们常常爱将“遗憾” 两字挂在嘴边。 遗憾，一个颇为伤感的字眼，令人心碎。 十多年前的一个茫茫暗夜，津浦线的特快列车在广阔的华北平原上奔驰，在车厢黯淡的灯影下，我凭窗而坐，凝望着那一棵棵如风掠过的白桦树，蓦地，“遗憾”这两个字扑进眼帘。就在这一刹那，我在人生交叉点上作了一个重要的抉 择。而在往后的岁月里，因为这个决定，又引起了种种不同的遗憾，却是始料不及的。 曾经听过这样一个故事。 一位美国宾夕法尼亚艺术学院的教授，在不惑之年，竟然尝试去实现童年梦想，他不惜放弃优职高薪，从养狮开始到驯狮、驯虎豹，最终成为美国一代马戏大师。当他向万千观众致 谢时，盈泪的双眼，令他看不清那无数个兴高采烈的欢颜。在舞台探照灯的照耀下，他的梦想实现了，事业达到了顶峰。然而，这期间，结婚十几载的妻子因无法理解他的行动，离开了他。生命，最终留下了遗憾。 每个人都有自己遗憾的故事。 当我们站在母亲的墓前，咀嚼着“子欲养而亲不 在”的悲哀时；当空间与时间的不吻合而改变了一生的命运时；当一段美丽的情缘，最终刻在心坎上的，只是惆怅的回忆时；当滚滚红尘中，寻觅到一张亲切的面孔，却又在擦身而过的瞬间消逝时；当逝水年华，岁月蹉跎，留下了一个个苍白、空虚的印记时……遗憾带来的况味，竟是如此悲凉、 无奈。在这一瞬间，世界变得残缺不全，我们仿佛成了生命的弃儿，缘于那神秘的玄机不在自己的掌握之中。 叔本华说过，人们就像那些炼金者，原指望炼出金子，谁知却往往发现了一些更有价值的事物，如火药、药、化学化合物和一些自然原理。从这个角度去说，当人们感到遗憾时，可能有 另一种意想不到的收获出现。芳心虽然憔悴，灵魂却更为坚强。 ?谁说遗憾不是一种苦难？而在诗人的眼里，苦难也是美丽的。有遗憾，就意味着有惋惜、有追悔，心儿念念不忘的，仍是对憧憬的追寻，生活中也可能出现一个个感人至深的故事。哀莫大于心死，一旦伤痕化为云烟，深深的遗憾 也不会来光顾心房了。 一位朋友，夫妇俩年轻有为，事业有成，在上天的眷顾下，人生已经太完美，夫复何求之际，却令人感到寂寞，没有新鲜感可言。我想，他的遗憾，恰恰是因为没有遗憾吧？ 遗憾，令人流泪，也令心灵更加温柔。世上再没有一种东西，让你能如此快乐而忧伤。只要我还 有一双眼睛，这眼睛里装满了如洗的碧空，天色蓝得让瞳仁里满是细碎的小蓝点在跳跃，人生就依然有希望。那已逝去的无数个遗憾，点缀了平淡的日子；涟漪过后，更留下点点余韵，回味无穷。 如果说，人生是一本书，遗憾不啻是一串串省略号，空白之处，蕴含深刻的哲理；如果说，人生是 一出音乐剧，遗憾不啻是一个个休止符，无声之中，酝酿着新的活力！一瞬间的寂静，凝聚起下一个乐章的序幕。 ?我想，遗憾，在生命的历程里，扮演的，恰恰是这样一种角色吧？ 熬? 药? 吴克诚 所谓的药就是一些亡去很久的草。长得正好的草是不配叫药的，即使硬放进药屉，不久它也会 烂掉，因为它未经晒、烘、焙或炒——九九八十一劫，少了一劫，也不能成药。 所以药都身世沧桑。身世沧桑的药只能以文火慢熬。我喜欢这个“熬”，“煎药”的煎太轻薄，与药的身世不协调。 ?急火出菜，文火出药——饱经沧桑之心，除了以文火轻拢慢捻，是断不能把它再打开了——且看 文火不疾不徐在药锅底下缭绕，缭绕成花的瓣，那么锅中药就是瓣中蕊了。熬着熬着，蕊心舒开，尘封已久的沧桑便一丝一缕地倾吐出来。 越王勾践很善于用文火熬药。越国病入膏肓，他却不慌不忙，他用去二十多年的光阴，来熬一服复国之药。伍子胥在这方面可就逊色了，他输在一个“急” 字上，一急，药煳了。急火攻心，自己当然也在劫难逃。 沧桑是苦涩的，所以药都苦。 苦药祛病。 魏征是个善献苦药的人。唐太宗善喝苦药。虽然有时他也会紧皱眉头，但他最终还是咽了下去。商纣王咽不下去，渐渐就百病缠身了。病是潜伏着的阴谋，肉眼一时半会儿很难看到，它一旦显山 露水，就势如破竹了。 小孩子理解不了药的苦心，所以小孩子总拒绝好心好意的药。我甚至都拒绝走进父亲的药房——我至今仍记着那个春夜，月色正好，我溜进父亲的药房，倚着门，看他熬药。摇曳的烛影里，父亲被药拥着，也如一味药了。药香如蝶，满室翩跹。 父亲说：“过来啊，过来 叫药熏熏。”我可不愿让它熏，我一扭头，转身就跑，一地花影都被我踩碎了。 今夜，父亲故去已整整十年。当初那些被我踩碎的花影仍在。春夜也在。月也正好。可是再也不会有人唤我熏药了…… 当初面对那些苦药，我真不应拔腿就跑…… 从生到老，谁能离得了那些药？从生到老，谁能说 清，究竟要咽下多少药？ 我们这样近，我们这样远? ?冷夏 阳光像梦一样，安静的落入我平凡琐碎的生活深处，在这个春天的下午。 我坐在阳台上，手里捧着一本梭罗的《瓦尔登湖》。多少年来，每次阅读它，我都会闻到那片树林的青涩气，那面湖水波光淡然冷静，潮湿的新鲜的水气。我感 到一种非常遥远的愉快，可以在一本书里自由的跑步呼吸。 许多的事情，过去了就过去了，不可能重现。惟有音乐和文学，适合等待、遥望、冥想。 ?一直认为梭罗还活着，他活在一个地方，离我的住处遥远，离我的感觉很近的某个地方。对他文字的爱恋，就像我对生命的向往一样，永远不会 消失。 阳光穿透玻璃的窗子，使我感觉温暖。手禁不住要伸出去握住什么。这个多么重要，在我表面生活的背后，意识到自己蕴藏着丰富的情感，而这些情感一直活在心里。 ?梭罗的文字，是干净安静的雪，可以清凉燥渴的灵魂。可以听见来自纯粹生命深处的自然歌吟----“曾有个牧羊人活在 世上，他的思想有高山那样崇高，在那里他的羊群，每小时都给予他营养。” 那与我失之交臂的时光和旧梦，充满恍惚怅然的珍惜之感。 想到夏洛蒂.勃朗特、奥尔科特和奥思汀的时代，从古堡到庄园，马车的轱辘慢慢辗转，那些沐浴在舒适阳光里的蔓草丛生的小径，夏天开满野蔷薇，秋天以 山楂和黑莓著名，冬天最令人赏心悦目的是完全的寂静和无叶的安宁。 可以步履缓慢、从容。可以用一个上午的时间写一封并不长的信，用一个下午的时间眺望牧场上丝绒似的草坪和栅栏两侧的冬青。晚上坐在炉火旁怀揣着心事，躲避祖母探询的目光，阅读或编织。却努力等待着有马车夫忽然 的脚步声，急匆匆撩开寒冷的夜色带来了温暖克制的爱情的回音。 我合上《瓦尔登湖》，从阳台尽力向远方眺望。这个春天的午后和以往没有什么不同，宽阔的街道依然人群如织，车水马龙。很多次我试着站在高处，超越自己有限的目力，尽力透过繁华而富有生命的城市，透视那些纷纭热闹的 核心究竟是什么。 生存的紧迫和焦虑带来一张张匆忙麻木的面孔，不知道在那样面孔的身体里，除了对名利的疯狂追逐，是否还留有一点时间对珍贵东西的失落进行偶尔打捞，是否还留有一点空间可以温情的抗拒或冲淡什么。 世界嘈杂多变。人们拥有广泛的人际关系，却缺乏深刻的情感交流。 人们在虚拟的互联网上寻找知己，为或许根本不存在的爱情痛苦沉沦，而不在乎结局如何。人心越来越疲惫困顿，情感越来越冷酷灵活。 我对实际生活中过分热络的友情，对虚拟世界激情的可靠性一直保持平和的怀疑态度。 夜晚，当一切安静下来，我对自己说：写吧，无论写什么。文字是心 灵的古典音乐，是柏油路上的清泉。为了不失去它，用自己的方式来等待和怀念。喜欢阅读的人，也可以从我的文字中看见
姿态享用。它们接受了残酷的现实，并学会把这看成生存的常态。他们的适应能力是很强的。适应能力强，这对人，对鸟，对任何生物，都是一个褒奖的词语。它们无师自通，就懂得了站在主人为它们架在笼中的假树杈上，站在笼子的中心位置，而不是在笼壁上徒劳地乱撞。就像主人所期待的 那样，优雅地偏头梳理它们的羽毛，如果有同伴，就优雅地交颈而眠。更重要的是，当太阳升起的时候，或者主人逗弄的时候，就适时适度地婉转歌唱，让人感觉到生活是如此的自由、祥和、闲适。而天空和扑翼这种与生俱来的事情，也就是多余的了。 但有一些鸟的适应能力却很差，这大抵是 鸟类中的古典主义者或理想主义者。它们对生命的看法很狭隘，根本不会随现实场景的转换而改变。在最初的惊恐和狂躁之后，它们明白了厄运，它们用最荏弱的姿态来抗拒厄运。他们是安静的，眼睛里是极度的冷漠，对小碟小碗里伸过来的水米漠然置之，那种神态，甚至让恩赐者感到尴尬， 感到有失自尊。鸟儿的眼睛里一旦现出这样的冷漠，就不可能再期待它们的态度出现转机，无论从小笼子换到大笼子，还是把粗瓷碗换成金边瓷碗，甚至于再赏给它们一个快乐的伙伴，都没有用了。这一切与它们对生命的认定全不沾边儿。事实上，这时候它们连有关天空的梦也不做了，古典主 义者总是悲观的，绝望的，它们只求速死。命运很快就遂了它们的心愿。 而我一直怀有敬意的，是鸟儿中的另一种理想主义，这种鸟儿太少，但我侥幸见过一只，因为总是无端想起，次数多了，竟觉得这鸟儿的数目似乎在我感觉中也多了。 我见到这只鸟儿的时候，它在笼中已关了很久了，我 无从得见它当初的惊恐和焦灼，不知它是不是现出过极度的冷漠，或者徒劳地撞击笼壁，日夜不停地用喙啄笼壁的铁枝。我见到它的时候，它正在笼子里练飞。它站在笼子底部，扑翼，以几乎垂直的路线，升到笼子顶部，撞到那里，跌下来，然后仰首，再扑翼……这样的飞，我从来没见过。它 在笼中划满风暴的线条，虽然这些线条太短，不能延伸，但的确饱涨着风暴的激情。它还绕着笼壁飞，姿态笨拙地，屈曲着，很不洒脱，很不悦目，但毕竟它是在飞。它知道怎样利用笼内有限的气流，怎样训练自己的翅膀，让它们尽可能地张开，尽可能地保持飞翔的能力。 在这样一只鸟的面前， 我感觉惭愧。一般我们很难看见鸟是怎样学飞的，那些幼鸟，那些被风暴击伤了的鸟，那些在岩隙里熬过隆冬的鸟，还有那些被囚的鸟。这是一件隐秘 的事。我们只看见它们在天空中划过，自由地扑翼，桀骜地滑翔，我们只羡慕上帝为它们造就了辽阔的天空。 但在看到那只在笼中以残酷的方 式练飞的鸟之后，我明白，天空的辽阔与否，是由你自己造就的，这种事情上帝根本无能为力。上帝只是说，天空和飞翔是鸟类的生命形式，而灾难和厄运也是世界存在的另一种形式。至于在灾难和厄运中你是否放弃，那完全是你自己的事情。 只要眼睛里还有蓝天? 兰心 人们常常爱将“遗憾” 两字挂在嘴边。 遗憾，一个颇为伤感的字眼，令人心碎。 十多年前的一个茫茫暗夜，津浦线的特快列车在广阔的华北平原上奔驰，在车厢黯淡的灯影下，我凭窗而坐，凝望着那一棵棵如风掠过的白桦树，蓦地，“遗憾”这两个字扑进眼帘。就在这一刹那，我在人生交叉点上作了一个重要的抉 择。而在往后的岁月里，因为这个决定，又引起了种种不同的遗憾，却是始料不及的。 曾经听过这样一个故事。 一位美国宾夕法尼亚艺术学院的教授，在不惑之年，竟然尝试去实现童年梦想，他不惜放弃优职高薪，从养狮开始到驯狮、驯虎豹，最终成为美国一代马戏大师。当他向万千观众致 谢时，盈泪的双眼，令他看不清那无数个兴高采烈的欢颜。在舞台探照灯的照耀下，他的梦想实现了，事业达到了顶峰。然而，这期间，结婚十几载的妻子因无法理解他的行动，离开了他。生命，最终留下了遗憾。 每个人都有自己遗憾的故事。 当我们站在母亲的墓前，咀嚼着“子欲养而亲不 在”的悲哀时；当空间与时间的不吻合而改变了一生的命运时；当一段美丽的情缘，最终刻在心坎上的，只是惆怅的回忆时；当滚滚红尘中，寻觅到一张亲切的面孔，却又在擦身而过的瞬间消逝时；当逝水年华，岁月蹉跎，留下了一个个苍白、空虚的印记时……遗憾带来的况味，竟是如此悲凉、 无奈。在这一瞬间，世界变得残缺不全，我们仿佛成了生命的弃儿，缘于那神秘的玄机不在自己的掌握之中。 叔本华说过，人们就像那些炼金者，原指望炼出金子，谁知却往往发现了一些更有价值的事物，如火药、药、化学化合物和一些自然原理。从这个角度去说，当人们感到遗憾时，可能有 另一种意想不到的收获出现。芳心虽然憔悴，灵魂却更为坚强。 ?谁说遗憾不是一种苦难？而在诗人的眼里，苦难也是美丽的。有遗憾，就意味着有惋惜、有追悔，心儿念念不忘的，仍是对憧憬的追寻，生活中也可能出现一个个感人至深的故事。哀莫大于心死，一旦伤痕化为云烟，深深的遗憾 也不会来光顾心房了。 一位朋友，夫妇俩年轻有为，事业有成，在上天的眷顾下，人生已经太完美，夫复何求之际，却令人感到寂寞，没有新鲜感可言。我想，他的遗憾，恰恰是因为没有遗憾吧？ 遗憾，令人流泪，也令心灵更加温柔。世上再没有一种东西，让你能如此快乐而忧伤。只要我还 有一双眼睛，这眼睛里装满了如洗的碧空，天色蓝得让瞳仁里满是细碎的小蓝点在跳跃，人生就依然有希望。那已逝去的无数个遗憾，点缀了平淡的日子；涟漪过后，更留下点点余韵，回味无穷。 如果说，人生是一本书，遗憾不啻是一串串省略号，空白之处，蕴含深刻的哲理；如果说，人生是 一出音乐剧，遗憾不啻是一个个休止符，无声之中，酝酿着新的活力！一瞬间的寂静，凝聚起下一个乐章的序幕。 ?我想，遗憾，在生命的历程里，扮演的，恰恰是这样一种角色吧？ 熬? 药? 吴克诚 所谓的药就是一些亡去很久的草。长得正好的草是不配叫药的，即使硬放进药屉，不久它也会 烂掉，因为它未经晒、烘、焙或炒——九九八十一劫，少了一劫，也不能成药。 所以药都身世沧桑。身世沧桑的药只能以文火慢熬。我喜欢这个“熬”，“煎药”的煎太轻薄，与药的身世不协调。 ?急火出菜，文火出药——饱经沧桑之心，除了以文火轻拢慢捻，是断不能把它再打开了——且看 文火不疾不徐在药锅底下缭绕，缭绕成花的瓣，那么锅中药就是瓣中蕊了。熬着熬着，蕊心舒开，尘封已久的沧桑便一丝一缕地倾吐出来。 越王勾践很善于用文火熬药。越国病入膏肓，他却不慌不忙，他用去二十多年的光阴，来熬一服复国之药。伍子胥在这方面可就逊色了，他输在一个“急” 字上，一急，药煳了。急火攻心，自己当然也在劫难逃。 沧桑是苦涩的，所以药都苦。 苦药祛病。 魏征是个善献苦药的人。唐太宗善喝苦药。虽然有时他也会紧皱眉头，但他最终还是咽了下去。商纣王咽不下去，渐渐就百病缠身了。病是潜伏着的阴谋，肉眼一时半会儿很难看到，它一旦显山 露水，就势如破竹了。 小孩子理解不了药的苦心，所以小孩子总拒绝好心好意的药。我甚至都拒绝走进父亲的药房——我至今仍记着那个春夜，月色正好，我溜进父亲的药房，倚着门，看他熬药。摇曳的烛影里，父亲被药拥着，也如一味药了。药香如蝶，满室翩跹。 父亲说：“过来啊，过来 叫药熏熏。”我可不愿让它熏，我一扭头，转身就跑，一地花影都被我踩碎了。 今夜，父亲故去已整整十年。当初那些被我踩碎的花影仍在。春夜也在。月也正好。可是再也不会有人唤我熏药了…… 当初面对那些苦药，我真不应拔腿就跑…… 从生到老，谁能离得了那些药？从生到老，谁能说 清，究竟要咽下多少药？ 我们这样近，我们这样远? ?冷夏 阳光像梦一样，安静的落入我平凡琐碎的生活深处，在这个春天的下午。 我坐在阳台上，手里捧着一本梭罗的《瓦尔登湖》。多少年来，每次阅读它，我都会闻到那片树林的青涩气，那面湖水波光淡然冷静，潮湿的新鲜的水气。我感 到一种非常遥远的愉快，可以在一本书里自由的跑步呼吸。 许多的事情，过去了就过去了，不可能重现。惟有音乐和文学，适合等待、遥望、冥想。 ?一直认为梭罗还活着，他活在一个地方，离我的住处遥远，离我的感觉很近的某个地方。对他文字的爱恋，就像我对生命的向往一样，永远不会 消失。 阳光穿透玻璃的窗子，使我感觉温暖。手禁不住要伸出去握住什么。这个多么重要，在我表面生活的背后，意识到自己蕴藏着丰富的情感，而这些情感一直活在心里。 ?梭罗的文字，是干净安静的雪，可以清凉燥渴的灵魂。可以听见来自纯粹生命深处的自然歌吟----“曾有个牧羊人活在 世上，他的思想有高山那样崇高，在那里他的羊群，每小时都给予他营养。” 那与我失之交臂的时光和旧梦，充满恍惚怅然的珍惜之感。 想到夏洛蒂.勃朗特、奥尔科特和奥思汀的时代，从古堡到庄园，马车的轱辘慢慢辗转，那些沐浴在舒适阳光里的蔓草丛生的小径，夏天开满野蔷薇，秋天以 山楂和黑莓著名，冬天最令人赏心悦目的是完全的寂静和无叶的安宁。 可以步履缓慢、从容。可以用一个上午的时间写一封并不长的信，用一个下午的时间眺望牧场上丝绒似的草坪和栅栏两侧的冬青。晚上坐在炉火旁怀揣着心事，躲避祖母探询的目光，阅读或编织。却努力等待着有马车夫忽然 的脚步声，急匆匆撩开寒冷的夜色带来了温暖克制的爱情的回音。 我合上《瓦尔登湖》，从阳台尽力向远方眺望。这个春天的午后和以往没有什么不同，宽阔的街道依然人群如织，车水马龙。很多次我试着站在高处，超越自己有限的目力，尽力透过繁华而富有生命的城市，透视那些纷纭热闹的 核心究竟是什么。 生存的紧迫和焦虑带来一张张匆忙麻木的面孔，不知道在那样面孔的身体里，除了对名利的疯狂追逐，是否还留有一点时间对珍贵东西的失落进行偶尔打捞，是否还留有一点空间可以温情的抗拒或冲淡什么。 世界嘈杂多变。人们拥有广泛的人际关系，却缺乏深刻的情感交流。 人们在虚拟的互联网上寻找知己，为或许根本不存在的爱情痛苦沉沦，而不在乎结局如何。人心越来越疲惫困顿，情感越来越冷酷灵活。 我对实际生活中过分热络的友情，对虚拟世界激情的可靠性一直保持平和的怀疑态度。 夜晚，当一切安静下来，我对自己说：写吧，无论写什么。文字是心 灵的古典音乐，是柏油路上的清泉。为了不失去它，用自己的方式来等待和怀念。喜欢阅读的人，也可以从我的文字中看见
两直线夹角和到角
目标2： 直线l1与l2的夹角
如上图所示，l1到l2的角是θ1，l2到l1的 角是θ2＝π－θ1，当直线l1与l2相交但不 垂直时，θ1和π－θ1，仅有一个角是锐角， 我们就把其中的锐角叫做两条直线的夹
角. 当直线l1⊥l2时，直线l1和l2的夹角是
2
请大家根据直线l1到l2的角与l1与l2夹角的 定义过程中，寻求一下两种角的取值范围有 何不同?
1 tan 2 tan1 1 k 2 k1
l1到l2的角的取值范围是（0， )，
l1与l2的夹角的取值范围是(0，
2］
目标3： 直线l1到l2的角的公式
tanθ＝
k2 k1 1 k1k2
推导：设直线l1到l2的角为θ，l1：y＝k1x＋ b＝－1，则θ＝
2
如果1＋k1k2≠0
.
一 新知探究
O 如图，直线l1到l2的角是θ1，l2到l1的 角是θ2.
目标1： 1.直线l1到l2的角
两条直线l1和l2相交构成四个角，它们是两
对与对l2重顶合角时，所我转们的把角直，线叫l1做按逆l1到时l针2的方角向. 旋转到
注意：这一概念中l1、l2是有顺序的.
；单创:/News/Detail/2019-9-20/442424.htm
；
我也是服了！“ （9）“您就当浪子回头吧，兴许真考上了，您也是积德了。”我回复了微信，也不忘调侃地加了几个坏笑的表情。 （10）之后，因为工作的关系，我离开了那座城市，也与律师楼和老李少了很多的交集。 （11）青海茫崖的矿难，突然成为了这个国家的头条新闻。部分矿务局 领导受贿私自外包矿坑，私人小矿主违规野蛮开采，导致了一次灭顶的矿难。在矿难中死去的矿工遗孀，因为没有基本的合同和安全保险凭据，无法获得赔偿，更无人愿意替他们去争
两条直线的夹角(2020年整理).ppt
11.3-2两条直线的夹角
例2.已知直线l 经过点P(-2,1),与直线l0：3x-4y+5=0
的夹角为arccos 3 ，求直线l 的方程。 5
y
•P(2,1)
o
x
10:57:33
11.3-2两条直线的夹角
练习1
1.已知直线l经过原点，且与直线 y 3x 1
的夹角为
6
，求直线l的方程；
10:57:33
a2 + 12 ? 12 (- a)2
2
10:57:33
典型例题
11.3-2两条直线的夹角
例2.已知直线l 经过点P(-2,1),且与直线l0：3x-4y+5=0
的夹角为arccos 3 ，求直线l 的方程。
解:
5 1）直线斜率不存在时，验证知x+2＝0也满足题意;
2）当直线斜率存在时，设直线方程为y-1=k(x+2),
(3)l1 : y 3x 12,l2 : x y 0;
解：l1的方程化为一般式为：3x+y-12=0 根据 l1与l2的方程及两直线夹角公式可得:
cos 311 (1) 5
(1)2 32 12 (1)2 5
因为 0，,所2 以
arccos 5
5
即直线
10:57:33
l1和
l2的夹角为
为 l1与 l2的方向向量. 由向量的夹角公式得: cos
uur uur duur1 udur2
a1a2 b1b2
由cos cos
d1 d2
a12 b12 a22 b22
所以两直线的夹角公式: cos
a1a2 b1b2
问题:此时角 是唯一确定的吗?
两条直线的夹角
直线夹角 的大小. uur
uur
解:根据l1与l2的方程,取 d1 (b1, a1), d2 (b2, a2 )
为 l1与 l2的方向向量. 由向量的夹角公式得: cos
uur uur duur1 udur2
a1a2 b1b2
由cos cos
d1 d2
a12 b12 a22 b22
所以两直线的夹角公式: cos
典型例题
例1.求下列各组直线的夹角 ：
(2)l1 : 3x y 12 0,l2 : x 0;
解：（2）根据l1与l2的方程及两直线夹角公式可得:
cos 311 0 3 10
(1)2 32 12 02 10
因为 0，,所2 以
arccos 3 10
10
即直线
l1 和
l2 的夹角为
p
cos a =
= 0, \ a =
a2 + 12 ? 12 (- a)2
2
05:21:23
典型例题
例2.已知直线l 经过点P(-2,1),且与直线l0：3x-4y+5=0
的夹角为arccos 3 ，求直线l 的方程。
解:
5 1）直线斜率不存在时，验证知x+2＝0也满足题意;
2）当直线斜率存在时，设直线方程为y-1=k(x+2),
三、两直线夹角公式的推导 uur uur
两直线 l1、l2的夹角为 ;方向向量 d1、d2的夹角为
若 时: 若 为钝角时:
2
d1
于是得:cos cos
y
yd1
d2
d2
l2
d
x
2
l2
x
d1
o l1
高一数学-《夹角和距离公式》课件
角时可以在两条异面直线上分别取出两个向量，通过求这两个向量所成的角来求异面直线所
成的角，但需注意异面直线所成角范围(0°，90°]，注意这两个角相互转化时范围的不同．
知识要点二：线段的长度的求法
1．利用 a·a＝|a|2 求有关线段的长度；
2．利用两点间的距离公式来求．
知识要点三：对平面法向量的理解 1．所谓平面的法向量，就是指所在的直线与平面垂直的向量，显然，一个平面的法向 量有无数多个，它们是共线向量．由于过直线外一点作与已知直线垂直的平面有且只有一个， 因此，在空间中，给定一个点 A 和一个向量 a，那么以向量 a 为法向量且经过 A 的平面是唯 一确定的． 2．求平面法向量的方法 (1)方法一：找到一条与已知平面垂直的直线，则该直线的任意方向向量都是该平面的法 向量． (2)方法二：待定系数法 若要求出一个平面的法向量的坐标，一般要建立空间直角坐标系，然后用待定系数法求 解，一般步骤如下： ①设出平面的法向量为 n＝(x，y，z)． ②找出(求出)平面内的两个不共线的向量的坐标 a＝(a1，b1，c1)，b＝(a2，b2，c2)． ③根据法向量的定义建立关于 x、y、z 的方程组
答案：x＜－4
知识要点一：异面直线所成角的求法
1．几何法：即先根据异面直线所成角的定义，在给定的图形中找出或作出角，然后再
加以证明，最后在一个三角形中进行计算．上述过程即“作—证—求”三步．
2．向量法：即利用
cos θ＝|aa|·|bb|＝
x1x2＋y1y2＋z1z2 x21＋y21＋z21· x22＋y22＋z22
中的一个变量赋予一个特值，即可确定平面的一个法向量．赋的值不同，所求平面的法向量 就不同，但它们是共线向量．
3．应用平面的法向量解决线面平行、面面平行问题 (1)设直线 l 的方向向量是 a，平面 α 的法向量是 u，则要证明 l∥α，只需证明 a⊥u，即 a·u＝0. (2)若能求出平面 α、β 的法向量 u、v，则要证明 α∥β，只需证明 u∥v.
《直线间的夹角》课件1
D
C
AM
B
N
E
解: 分别以直线AE，AB，AD为x轴、y轴、z轴，
建立如图所示的空间直角坐标系，设CB=a，则A(0，
0，0)，E(2a，0，0)，B(0， 2a， 0)，C(0， 2a，a)，
D(0，0，2a)，所以M(a，a，a )
z
2
D
(Ⅰ)证:DM=(a，a，－1.5a)，
EB=(－2a，2a，0)， C DM ·EB =a (－2a) +a ·2a
l2
l1
B
A
C
3.空间直线夹角的解法
空间直线由一点和一个方向确定, 所以空间两条直线的夹角由 它们的方向向量的夹角确定.
3.空间直线夹角的解法
l2
s1 B l2 s2
s1 B
A
A
l1
s2 C
l1
C
已知直线l1与l2的方向向量分别为s1, s2
当0
s1, s2
2
时,
直线l1与l2的夹角等于
M A
+0=0 B y DM⊥EB，即DM⊥EB
E
x (Ⅱ)解:设平面MBD的法向量为n=(x，y，z)
DB=(0，2a，－2a)由n⊥DB， n⊥DM得
n n
DB = 2ay 2az DM = ax + ay
= 3 2
0 az
Байду номын сангаас
=
0
y x
= +
z y
3 2
z
x12 y12 z12 x22 y22 z22
练习1、求下列两个向量的夹角的余弦：
C
AM
B
N
E
解: 分别以直线AE，AB，AD为x轴、y轴、z轴，
建立如图所示的空间直角坐标系，设CB=a，则A(0，
0，0)，E(2a，0，0)，B(0， 2a， 0)，C(0， 2a，a)，
D(0，0，2a)，所以M(a，a，a )
z
2
D
(Ⅰ)证:DM=(a，a，－1.5a)，
EB=(－2a，2a，0)， C DM ·EB =a (－2a) +a ·2a
l2
l1
B
A
C
3.空间直线夹角的解法
空间直线由一点和一个方向确定, 所以空间两条直线的夹角由 它们的方向向量的夹角确定.
3.空间直线夹角的解法
l2
s1 B l2 s2
s1 B
A
A
l1
s2 C
l1
C
已知直线l1与l2的方向向量分别为s1, s2
当0
s1, s2
2
时,
直线l1与l2的夹角等于
M A
+0=0 B y DM⊥EB，即DM⊥EB
E
x (Ⅱ)解:设平面MBD的法向量为n=(x，y，z)
DB=(0，2a，－2a)由n⊥DB， n⊥DM得
n n
DB = 2ay 2az DM = ax + ay
= 3 2
0 az
Байду номын сангаас
=
0
y x
= +
z y
3 2
z
x12 y12 z12 x22 y22 z22
练习1、求下列两个向量的夹角的余弦：
两直线夹角课件
通过两直线的夹角，可以判断两条直 线是否平行、垂直或相交，从而确定 它们在几何图形中的位置关系。
通过两直线的夹角，可以构建出各种 几何图形，如三角形、四边形等。
计算角度
两直线夹角的大小可以通过几何计算 得到，可以用于计算其他角度或几何 量。
在解析几何中的应用
01
02
03
解析表达
两直线的夹角可以用解析 几何的方法表示，通过坐 标系和向量的运算来计算 。
02
两直线夹角的计算方法
利用三角函数计算直线夹角
总结词
通过利用三角函数中的正切、余切等函数，可以计算出两条直线线的斜率。然后，使用三角函数中的正切或余切函 数，将两个斜率相除，得到一个比值。最后，使用反正切函数来计算这个比值 对应的角度，即为两条直线的夹角。
电磁波的传播
在电磁学中，两直线夹角可以用于 表示电磁波的极化方向和传播方向 ，特别是在研究电磁波的干涉和衍 射等现象时。
04
两直线夹角的性质
直线夹角的性质定理
定理1
两直线夹角的大小与两直线的方向向量或方向模有关 ，具体为$theta = arccos(frac{overset{longrightarrow}{u} cdot overset{longrightarrow}{v}}{|overset{longrightarro w}{u}||overset{longrightarrow}{v}|})$，其中 $overset{longrightarrow}{u}$和 $overset{longrightarrow}{v}$分别是两直线的方向向 量。
利用向量计算直线夹角
总结词
通过向量的数量积和向量的模长，可以计算出两条直线的夹 角。
详细描述
两直线的位置关系-夹角课件
当两直线斜率不存在时，需要特别处理，因为公式中涉及斜率。
计算实例
实例一
实例三
设直线L1的斜率为2，直线L2的斜率 为3，根据夹角公式计算两直线的夹 角。
设直线L1和L2相互垂直，根据夹角公 式计算两直线的夹角。
实例二
设直线L1的斜率为不存在，直线L2的 斜率为-1，根据夹角公式计算两直线 的夹角。
两直线的位置关系-夹角ppt课 件
Байду номын сангаас
目录
CONTENTS
• 直线的基本性质 • 两直线的位置关系 • 两直线的夹角 • 两直线夹角的计算 • 两直线夹角的应用
01 直线的基本性质
CHAPTER
直线的定义
直线是无限长的，没 有起点和终点。
直线上的任意两点确 定一条唯一的直线。
直线是连续的，没有 中断。
解析几何中的曲线方程
利用两直线的夹角，可以推导出曲线 的方程，例如圆的方程、椭圆的方程 等。
在实际生活中的应用
建筑设计和施工
在建筑设计和施工中，两直线的夹角可 以用来确定建筑物的方向、角度等参数 。
VS
道路设计和导航
在道路设计和导航中，两直线的夹角可以 用来确定道路的方向、交叉点等参数。
谢谢
THANKS
截距式
$frac{x}{a} + frac{y}{b} = 1$，其中$a$是 直线在x轴上的截距，$b$是直线在y轴上的 截距。
直线的性质
直线是平面的，具有方向性。 直线上的任意两点到直线上任一点的距离相等。
直线可以无限延伸，具有连续性。
02 两直线的位置关系
CHAPTER
平行线
01
02
03
重合线
计算实例
实例一
实例三
设直线L1的斜率为2，直线L2的斜率 为3，根据夹角公式计算两直线的夹 角。
设直线L1和L2相互垂直，根据夹角公 式计算两直线的夹角。
实例二
设直线L1的斜率为不存在，直线L2的 斜率为-1，根据夹角公式计算两直线 的夹角。
两直线的位置关系-夹角ppt课 件
Байду номын сангаас
目录
CONTENTS
• 直线的基本性质 • 两直线的位置关系 • 两直线的夹角 • 两直线夹角的计算 • 两直线夹角的应用
01 直线的基本性质
CHAPTER
直线的定义
直线是无限长的，没 有起点和终点。
直线上的任意两点确 定一条唯一的直线。
直线是连续的，没有 中断。
解析几何中的曲线方程
利用两直线的夹角，可以推导出曲线 的方程，例如圆的方程、椭圆的方程 等。
在实际生活中的应用
建筑设计和施工
在建筑设计和施工中，两直线的夹角可 以用来确定建筑物的方向、角度等参数 。
VS
道路设计和导航
在道路设计和导航中，两直线的夹角可以 用来确定道路的方向、交叉点等参数。
谢谢
THANKS
截距式
$frac{x}{a} + frac{y}{b} = 1$，其中$a$是 直线在x轴上的截距，$b$是直线在y轴上的 截距。
直线的性质
直线是平面的，具有方向性。 直线上的任意两点到直线上任一点的距离相等。
直线可以无限延伸，具有连续性。
02 两直线的位置关系
CHAPTER
平行线
01
02
03
重合线
两条直线所成的角PPT教学课件
初三语文组
基本目标
• 感受诗词经典，追溯文化渊源; • 提高审美品位，积蓄典雅语言。
要点与方法：
• 节律是特征，朗读以凸显之。 • 意象是风景，想像以再现之。 • 情感是灵魂，体验以沟通之。 • 语言是珍品，玩味以珍藏之。
五个环节
• 一、朗读全诗，力求读准——感知作品 • 二、弄懂字词，理顺语句——疏通作品 • 三、揣摩意象，领略意境——领会作品 • 四、自我感受，独特体验——感悟作品 • 五、赏析技巧，品味语言——鉴赏作品
—骆宾王
触景生情：
昔人已乘黄鹤去， 此地空余黄鹤楼。 黄鹤一去不复返， 白云千载空悠悠。 晴川历历汉阳树， 芳草凄凄鹦鹉洲。 日暮乡关何处是？ 烟波江上使人愁。 —崔颢《黄鹤楼》
绘景言志：
东临碣石，以观沧海。 水何澹澹，山岛竦峙。 树木丛生，百草丰茂。 秋风萧瑟，洪波涌起。 日月之行，若出其中， 星汉灿烂，若出其里。 幸甚至哉，歌以咏志。 —曹操《观沧海》
y
x o
提问：１.解析几何中怎样判断两条直线的平 行和垂直？
直线的斜率 或 以方程的特点观察
２、区分以下两组直线的相交程度用什
么量刻画？
２
１
４３
两条直线所成的角
想一想 ？
观察下列两组相交直线，自己下定义以便区
分两组对顶角
l2
l4
2
3
1
4
甲
l1
2
3 1
4
乙
l3
一、概念的建立
1、l1到 l2角的定义
• 第二、“画意”揣摩。即探寻画面所蕴含 的意义及作者所要表达的思想感情，这是由画 面向画意的转化；越是客观本然，越是符合作 者本意就越好。
• 第三、“画源”追溯。一种情况是意象成 因的分析，如周振甫先生就曾对杜甫<春夜喜 雨>的意象形成，作过具体阐释。另一种情况 是对作者心路历程的追寻，即要知道作者是在 怎样的生活背景和心理情绪下写出这一作品的 。
《直线与平面的夹角》示范公开课教学PPT课件【高中数学人教】
知识梳理
题型一 用定义求线面角
【例1】在正四面体ABCD中，E为棱AD中点，连CE，求CE和平面BCD所成角 的正弦值． [思路探索] 可作出线面角，在三角形中解出．
解 如图，过A、E分别作AO⊥平面BCD， EG⊥平面BCD，O、G为垂足． ∴AO＝2GE，AO、GE确定平面AOD，连结 GC，则∠ECG为CE和平面BCD所成的角．
知识梳理
【例 3】(12 分)如图所示，正三棱柱 ABC－A1B1C1 的底面边长为 a，侧棱 长为 2a，求 AC1 与侧面 ABB1A1 所成角的正弦值．
审题指导 建立坐标系，用 sin θ＝|cosφ|＝求线面角．
知识梳理
【题后反思】 (1)用向量法可避开找角的困难，但计算繁琐，所以注意 计算上不要失误． (2)在求已知平面的法向量时，若图中有垂直于平面的直线时，可直接 确定法向量；当图中没有垂直于平面的直线时，可设出平面法向量的 坐标，用解不定方程组的方法来确定法向量．
知识梳理
公式cos θ＝cos θ 1 ·cos θ 2的理解 由0≤cos θ 2 ≤1，∴cos θ≤cos θ 1 ，从而θ1≤θ.在公式中，令θ 2 ＝90°，则cos θ＝cos θ 1 ·cos 90°＝0. ∴θ＝90°，即当AC⊥BC时，AC⊥AO. 此即三垂线定理，反之若θ＝90°，可知θ2＝90°，即为三垂线定理的逆 定理，即三垂线定理及逆定理可看成此公式的特例．
知识梳理
∵M 为 DC 的中点，∴CM＝12a
∴BM＝
a42＋a2＝
5 2a
又 ME＝12PD＝12a，∴BE＝ 54a2＋14a2＝ 26a
知识梳理
∴在 Rt△BME 中
cos∠MBE＝BBME ＝
高中数学必修二两条直线的位置关系(夹角)教案课时训练练习教案课件
两条直线的位置关系(夹角)教学目的：1. 明确理解直线1l 到2l 的角及两直线夹角的定义.2.掌握直线1l 到2l 的角及两直线夹角的计算公式.3.能根据直线方程求直线1l 到2l 的角及两直线夹角. 教学重点：两条直线的夹角. 教学难点：夹角概念的理解. 授课类型：新授课王新敞课时安排：1课时王新敞教 具：多媒体 教学过程： 一、复习引入：1．特殊情况下的两直线平行与垂直． 2．斜率存在时两直线的平行与垂直： 二、讲解新课：1.直线1l 到2l 的角的定义：两条直线1l 和2l 相交构成四个角,它们是两对对顶角,我们把直线1l 按逆时针方向旋转到与2l 重合时所转的角,叫做1l 到2l 的角.在图中,直线1l 到2l 的角是1θ, 2l 到1l 的角是2θ.1l 到2l 的角θ：0°＜θ＜1８0°.2．直线1l 到2l 的夹角定义:如图，1l 到2l 的角是1θ, 2l 到1l 的角是π-1θ,当1l 与2l 相交但不垂直时, 1θ和π-1θ仅有一个角是锐角,我们把其中的锐角叫两条直线的夹角.补充：当直线1l ⊥2l 时,直线1l 与2l 的夹角是2π. 夹角α：0°＜α≤90°.说明: 1θ＞0, 2θ＞0,且1θ+2θ=π 3．直线1l 到2l 的角的公式:12121tan k k k k +-=θ.推导:设直线1l 到2l 的角θ，222111:,:b x k y l b x k y l +=+=.如果.2,1,012121πθ=-==+则即k k k k如果0121≠+k k ,设1l ，2l 的倾斜角分别是1α和2α， 则2211tan ,tan k k ==αα.由图（1）和图（2）分别可知)()(122112ααπααπθααθ-+=--=-=或)tan()](tan[tan )tan(tan 121212ααααπθααθ-=-+=-=∴或于是121212121tan tan 1tan tan tan k k k k +-=+-=ααααθ 王新敞4．直线1l ，2l 的夹角公式: 12121tan k k k k +-=α 王新敞根据两直线的夹角定义可知，夹角在(0°，90°］范围内变化，所以夹角正切值大于或等于0.故可以由1l 到2l 的角取绝对值而得到1l 与2l 的夹角公式.这一公式由夹角定义可得王新敞三、讲解范例：例1 求直线23:,32:21-=+-=x y l x y l 的夹角(用角度制表示) 例2 求过点P （-5,3）且与直线x+2y-3=0的夹角为arctan2的直线l 的方程. 说明:上两例应用了两直线夹角公式,要求学生熟练掌握.例3 等腰三角形一腰所在直线1l 的方程是022=--y x ,底边所在直线2l 的方程是01=-+y x ,点(-2,0)在另一腰上,求这条腰所在直线3l 的方程例4 三角形的三个顶点是A (6，3)，B (9，3)，C (3，6)，求它的三个内角的度数. 四、课堂练习：1．求下列直线1l 到2l 的角与2l 到1l 的角：（1）1l ：y ＝21x ＋2；2l ：y ＝3x +7； (2) 1l ：x －y ＝5；2l ：x ＋2y －3＝0王新敞2.求下列两条直线的夹角：（1）y ＝3x －1，y ＝－31x ＋４；（2）x －y ＝5；y ＝４.(3)5x －3y ＝9，6x ＋10y ＋7＝0.3．已知直线l 经过点P （2,1），且和直线5x ＋2y ＋3＝0的夹角等于45°，求直线l 的方程.五、小结 ：通过本节学习，要求大家掌握两直线的夹角公式，并区分与1l 到2l 的角的联系与区别，能够利用它解决一定的平面几何问题王新敞六、课后作业： 七、板书设计（略）王新敞活动目的：教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的，每个人都要保护它，做到节约每一滴水，造福子孙万代。
直线与平面的夹角ppt课件
| CD n |
| a |
1
，又
| CD || n |
2a 2 2 2
)
ABC
6.（多选）已知正方体 ABCD A1B1C1D1 中，E，F 分别为 A1 D1 ，CC1 的中点，则(
A.直线 BE 与 B1 F 所成角为 90
B.直线 B1C 与 C1 D 所成角为 60
即
′
′
′
′
′
与平面
′
′
′
=2
′
，
中，sin ∠
′
′
=
是一个锐角，所以 ∠
′
′
1
2
′
′
所成角的大小为
=
，
π
6
π
6
，
.
1.在空间直角坐标系中，直线 l 的一个方向向量为 m (1, 0,3) ，平面 的一个
A)
法向量为 n (1, 5, 2) ，则直线 l 与平面 所成的角为(
A.
π
2
2
2ay 0,
n CA 0 ， n AP 0 ， a
可取 n (1, 0,1) .设直线 CD 与平面
a
2 x ay 2 z 0,
PAC 的夹角为 ，则 sin | cosCD, n |
0 90 ， 30 .故选 C.
.
设平面
则
′
⋅
′
⋅
′
′
=
′
的一个法向量为
− = 0,
=−
′
′
= 1，可得
=
(0,1,1)
.
= 0,
空间中直线与直线所成的角(夹角)
感谢您的观看
THANKS
详细描述
当两条重合的直线在空间中相交，它 们之间的夹角是0度。这是因为重合的 直线实际上是同一条直线，所以它们 在任何点处的角度都是相同的。
05
直线与直线所成的角的计算 方法
利用三角函数计算角度
总结词
利用三角函数计算直线与直线所成的角度，需要知道直线的 倾斜角，然后通过三角函数关系计算出两直线之间的夹角。
详细描述
首先，我们需要确定两条直线的倾斜角。然后，使用三角函数 中的正切或余切函数，通过两条直线的斜率来计算它们之间的 夹角。具体地，设两直线的斜率为k1和k2，夹角为θ，则有 tan(θ/2) = |k2 - k1| / (1 + k1 * k2)。
利用向量计算角度
总结词
通过向量的点积和模长来计算直线与 直线所成的角度。首先，我们需要将 直线表示为向量，然后利用点积公式 和向量的模长来计算两向量之间的夹 角。
夹角的几何意义在解 析几何、射影几何等 领域有着广泛的应用。
夹角的大小反映了直 线之间的倾斜程度。
03
直线与直线所成的角的实际 应用
空间几何问题
确定物体位置关系
在空间几何问题中，通过 计算两条直线所成的角， 可以确定物体之间的相对 位置关系。
判断形状和性质
通过分析直线之间的夹角， 可以判断几何形状的性质， 如平行、垂直、相交等。
通过作出的几何图形，利 用量角器或三角板测量夹 角的度数。
利用向量计算
通过向量的点积和模长， 利用向量公式计算夹角的 余弦值，从而得出夹角的 度数。
02
直线与直线所成的角的性质
角度的范围
01
02
03
04
直线与直线所成的角， 其角度范围在0°到180° 之间。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[练习] 光线从 A(-3,4) 射出，到 x 轴 上 B 点后，反射到 y 轴上点 C，再次反射，这时反射光线 恰好经过点D(-1，6)，求 BC 所在直线方程。
l1与l2夹角公式：
tan k2 k1
1 k1k2
(0 )
2
特别地, 当两直线垂直时,
即 k1k2
1 时,
θ
π 2
.
四、展示定理应用、形成技能技巧： 1.顺水推舟，直接应用：
[例1] 求直线 l1：y 2x 3,
l2 :
y x 3 的夹角， 2
l1 到 l2 的角，l2 到 l1 的角.
解：设夹角为，l1 到 l2 的角为1， l2 到 l1 的角为2 . 则由已知 k1 2,
k2
1,
tan
k2 k1 1 k1k2
1 2 12
3，
arctan 3
tan1
k2 1
k1 k1k2
3
1
arctan
3
tan 2
k1 k2 1 k1k2
3
2
arctan
3
.
[例2]1.求直线 3x 3y 6 0 和 3x y 2 0 的夹角.
2.直线l过原点且与直线 3x y 4 0 的夹角为π ,试求直线l的方程.
6
2. 纵横联系，综合应用：
[例3] 等腰三角形一腰所在直线 l1 的方程是 x 2 y 2 0, 底边所在直线 l2 的方程是 x y 1 0 , 点 (2，0) 在 另一腰上, 求这条腰所在直 线 l3 的方程 .
2
),
tan1 tan2
y
-2
2 o 1
l1 x
l3
l2
即 k1 k2 k2 k3 1 k1k2 1 k2k3
得：k3 2
y
-2
2 o 1
l1 x
l3
l2
又 l3 过点(2，0)，斜率为2，
l3 的方程为：2x y 4 0 .
[例4] 两直线 l1 : ax 2 y 2 0, 与 l2 : 2x 6 y c 0 交于 点 ( 1, m). 且 l1 到 l2 的角为 45o. 求a, c, m.
们把l1按逆时针旋 转到与l2重合时所
l1
转过的角叫做l1到
l2
l2的角.
θ1是l1到l2的角, θ2是l2到l1的角.
1
2
l1 l2
(θ1 0, θ2 0, θ1 θ2 π)
我们把其中不大于直角的角叫做这 两条直线所成的角Байду номын сангаас两直线的夹角).
l1到l2所成的角公式：
tan θ k2 k1 (0 θ π) 1 k1k2
解：设 l1 , l2 , l3 的斜率分别为 k1, k2 , k3 ,
如图，设 l3 到 l2 的角为2，l2 到 l1
的角为1，则1 2，
y
且
1，
2
( 0，
2
)
,
-2
2 o 1
l1 x
而
tan1
k1 k2 1 k1k2
,
l3
l2
tan 2
k2 1
k3 k2k3
,
1 2
且
1
,
2
(0，
一、复习旧知，以旧悟新： 1. 两条直线平行的充要条件？ 2. 两条直线垂直的充要条件？
二、设问置疑，导入课题：
我们已经研究过两条直线特殊的位 置关系：平行与垂直，那么两条直线在 一般相交的情况又是怎样的呢?
三、动手操作，探测公式：
如图, 两直线l1与l2相交构成四个角, 它们是两对对顶角, 为了区别这些角, 我