金属晶体配位数 计算
晶体配位数口诀

晶体配位数口诀晶体配位数口诀:体心立方有八,四方二十三,六方十九,圆柱十二,八方十六。
晶体是由许多称之为配位数的正方体组成的,每个正方体可以与周围其他正方体结合在一起,构成不同形状的晶体。
许多岩石和金属都是由晶体组成的,因此了解晶体的结构以及配位数很重要。
根据口诀提到的,晶体有八种基本的配位数,具体如下:体心立方的配位数为8;四方体的配位数为23;六方体的配位数为19;圆柱体的配位数为12;八方体的配位数为16。
这些配位数是按照不同形状的晶体确定的,它们是确定晶体结构的重要参数。
那么,这些配位数代表什么呢?它们代表了晶体的八种基本形状,这八种基本形状的晶体在自然界中最为普遍。
他们之间的不同之处在于配位数的不同。
例如,体心立方的配位数为8,它的形状就是一个普通的方块;而四方体的配位数为23,它的形状就是一个凹形;六方体的配位数为19,它就是一个不规则的六棱锥;圆柱体的配位数为12,它的形状就是一个圆柱;八方体的配位数为16,它的形状就是一个不规则的八棱锥。
除此之外,它们之间的差异还在于它们的表面空间,这意味着配位数为8的体心立方晶体表面有八个外表面,而配位数为16的八方体晶体则有16个外表面。
同样,它们之间的差异还在于它们的包围体积,这意味着体心立方的被包围的体积较小,而八方体的被包围的体积则较大。
此外,这些配位数也可以用来描述不同晶体的形状和结构。
例如,四方体的配位数为23,它的结构就是一个由四个连接的角落和一个连接的边构成的立方体;六方体的配位数为19,它的结构就是六个连接的角落和三条边组成的六棱锥状晶体;八方体的配位数为16,它的结构就是八个连接的角落和四条边组成的八棱锥状晶体。
通过以上分析,可以清楚地看出,配位数是描述晶体形状和结构的重要参数,它们之间的差异又主要是在于表面空间和包围体积。
因此,了解晶体的配位数是有助于理解晶体结构的重要参数。
晶体是自然界中最常见的物质,它们也是许多金属和石头的重要成分,因此了解晶体的结构和配位数也是研究、调查和分析岩石、金属和其他物质的重要参数。
高考化学:配合物和晶体中配位数的判断

配合物或晶体中配位数的判断配合物或晶体中一个微粒周围最近邻的微粒数称为配位数。
配位数这个概念存在于配位化学和晶体学中,定义有所不同。
配合物中的配位数是指直接同中心离子(或原子)配位的原子数目。
晶体学中的配位数是指晶体中一个原子周围与其等距离的最近邻的原子数目。
离子晶体中的配位数是指一个离子周围最近的异电性离子数目。
高中阶段判断配合物或晶体中配位数的方法可作如下小结。
一、各种典型配合物中配位数的判断1.配位数可以等同于中心离子(或原子)与配位原子形成的配位键键数,也可以等同于配位体的数目。
如[Ag(NH3)2]NO3、[Ag(CN)2]-、[Cu(NH3)4]SO4、[Cu(H2O)4]2+、[Zn(NH3)4]2+、[Zn(CN)4]2-、K3[Fe(SCN)6]、[Fe(CN)6]3-、[FeF6]3-等配合物或配离子中的中心离子与配位体的数目以及配位原子形成的配位键键数均相等,其中Ag+离子的配位数为2,Cu2+离子与Zn2+离子的配位数均为4,Fe3+离子的配位数为6。
一般规律:一般配合物的配位数可以按中心离子电荷数的二倍来计算。
又如Ni(CO)4、Fe(CO)5、Cr(CO)6等羰基化合物中Ni、Fe 、Cr原子的配位数分别为4、5、6。
[Co(NH3)4(H2O)2]Cl2、[CrCl(H2O)5]Cl2中Co2+离子与Cr3+离子的配位数均为6。
说明:羰基化合物中的中心原子呈电中性,此类配合物的配位数由化学式直接判断。
Co2+离子与Cr3+离子的电荷数分别为2、3,但配位数都是6。
所以,配合物的配位数不一定按中心离子(或原子)的电荷数判断。
2.当中心离子(或原子)与多基配体配合时,配位数可以等同于配位原子的数目,但不是配位体的数目。
如[Cu(en)2]中的en是乙二胺(NH2CH2CH2NH2)的简写,属于双基配体,每个乙二胺分子有2个N 原子与Cu2+离子配位,故Cu2+离子的配位数是4而不是2。
高三化学高考备考专题复习有关晶体的各类计算

位置 的原子数 例1、铝单质为面心立方晶体,其晶胞参数a=0.405nm,列式表示铝单质的密度
g·cm-3(不径必计的算关出结系果)
②若合金的密度为d g/cm3,晶胞参数a=________nm。
*(2)分数坐标:(0,0,0)-顶点
(1/2,1/2,0)
3、边长(晶胞参数)和半径关系
空间利用率
3 Po 顶10点0%
球半径r 与晶胞边长 a 的关系:
3、边长(晶胞参数)和半径关系
(1)球数:8×1/8 + 6×1/2 = 4
1 、 晶 体 中 的 微 粒 数 、 化 学 式 其中,密度公式中共有四个未知量:密度,微粒摩尔质量,晶 胞体积,NA,知道3个可求另一个,因此可能围绕密度出现4种题型。
在面心立方基础上,再插入4个球,分别占据8个小立 方体中4个互不相邻的体心,
S a a sin 60 3 a2 2
V晶胞 3 a2 2 6 a
2
3
2a3 8 2r3
V球球)
V球 V晶胞 100% 74.05%
7、空间利用率
(4)金刚石空间利用率:球体积占晶胞体积的百分比
8 4 πr 3 8 4 πr 3
3
3 100% 34%
实例
NaCl 型
AB CsCl 型
Na+:6 Na+:6 Cl-: 6 Cl-: 6
Cs+:8 Cs+:8 Cl-: 8 Cl-: 8
Na+:4 Cl-: 4 Cs+:1 Cl-:1
KBr AgCl、 MgO、CaS、 BaSe
CsCl、CsBr、 CsI、TlCl
ZnS型
Zn2+:4 Zn2+:4 Zn2+:4 ZnS、AgI、 S2-: 4 S2-: 4 S2-:4 BeO
fcc 110面配位数

fcc 110面配位数
fcc晶体结构中的(110)面是一个特定的晶体学术语,它指的是
面心立方晶体中的一个特定晶面。
在面心立方晶体结构中,每个原
子都位于一个面的中心和每个面的角上。
对于(110)面,它是指晶体
中的一个平行于晶体中心到相邻晶体中心的方向的平面,其具体的
配位数可以从不同角度来进行解释和计算。
从晶体学的角度来看,配位数是指晶体中每个原子周围最近邻
原子的个数。
在面心立方晶体结构中,每个原子周围最近邻原子的
个数可以根据晶体学的原理进行计算。
对于(110)面,配位数可以通
过在该平面上绘制晶体结构并计算每个原子周围最近邻原子的个数
来确定。
一般来说,(110)面的配位数是4,这意味着每个原子周围
有4个最近邻原子。
另一种角度是从金属结构的角度来看。
在金属学中,配位数是
指金属原子周围配位的配体或原子的个数。
对于(110)面,金属原子
周围的配位数可以通过绘制晶体结构并计算每个原子周围的配体或
原子的个数来确定。
一般来说,(110)面的金属原子配位数也是4。
总之,从晶体学和金属学的角度来看,(110)面的配位数都是4。
这种多角度的解释可以帮助我们更好地理解晶体结构中不同晶面的性质和特点。
典型金属的晶体结构

等径球最紧密堆积时,在平面上每个球与6个球相接触, 形成第一层(球心位置标记为A。此时,每3个彼此相接 触的球体之间形成1个弧线三角形空隙,每个球周围有6 个弧线三角形空隙,其中3个空隙的尖角指向图的下方 (其中心位置标记为B),另外3个空隙的尖角指向图的 上方(其中心位置标记为C),这两种空隙相间分布。
密排面
六方最紧密堆积
12
6354来自ABAB……的层序堆积
六方最紧密堆积
A B A B A
ABABAB…… 每两层重复一次
六方晶胞——六方密堆积
A
A密
B
排
B面
A
A
6.晶体结构中的间隙
刚球模型四面体间隙
刚球模型八面体间隙
四面体间隙:位于由 一个顶角原子和三个 面中心原连接成的正 四面体中心,数目为8。 rB / rA =0.225
82
62
3. 原子半径与点阵常数的关系
晶胞中棱边长度a,b,c称为点阵常数。如把原子看作半径为r的刚性球, 则可据几何关系求出点阵常数与r之间的关系。
体心立方
面心立方
密排六方
r 3a 4
r 2a 4
ra 2
4. 配位数与致密度
配位数和致密度定量地表示原子排列的紧密程度。 配位数(coordination number,CN):晶体结构中任一 原子周围最近且等距离的原子数。 致密度(K):晶胞中原子所占的体积分数,
密排六方(A3)hexagonal close-packed lattice→hcp
面心立方点阵
体心立方点阵
密排六方点阵
面心立方(face-centered cubic,fcc)
体心立方(body-centered cubic,bcc)
mg晶体配位数

mg晶体配位数
Mg晶体配位数是一种可以用来研究金属配位数的技术,可以帮助我们更好地了解金属在
晶体中的分布和排布。
Mg晶体配位数是利用Mg原子(质量数为24)构成结构中覆盖原
子的紧密度,而Mg原子作为配位原子占据了晶体空间中五六分之一的位置。
Mg晶体配位数可以用于分析金属的键强度,键长和晶体分析。
它是一种测量金属晶体固
态性质的有效依据,可以帮助我们分析有关金属的属性及性质,比如硬度和熔点。
此外,Mg晶体配位数还可以用于研究金属的化学性质。
比如,它可以帮助我们探索金属
的溶解度,并有助于更好地了解材料的铸造性能。
Mg晶体配位数可以帮助我们更准确地识别出金属以及其他有机物类型,还可以提供有关
物质性质之间关联性的进一步分析。
总而言之,Mg晶体配位数是一种可用于研究金属配位数的技术,可以用来研究金属的物
理性质和化学性质,探索金属的溶解度,帮助我们更好地了解金属在晶体中的分布和排布。
配位化学中的金属离子配位数的确定

配位化学中的金属离子配位数的确定配位化学是无机化学中的一个重要分支,研究的是金属离子与配体之间的相互作用及其结构性质。
在配位化学中,金属离子的配位数是一个关键的概念,它决定了配位化合物的结构和性质。
本文将探讨金属离子配位数的确定方法及其在配位化学中的应用。
一、配位数的概念与意义配位数是指金属离子周围配体的数目,也可以理解为金属离子与配体之间的化学键数。
配位数的确定对于揭示配位化合物的结构和性质非常重要。
在配位化学中,常见的金属离子配位数有2、4、6、8等。
二、确定金属离子配位数的方法1. 晶体结构分析法晶体结构分析是一种常用的确定金属离子配位数的方法。
通过X射线衍射技术,可以获得配位化合物的晶体结构信息。
在晶体结构中,金属离子与配体之间的距离和角度可以提供金属离子的配位数信息。
2. 磁性测量法磁性测量是另一种确定金属离子配位数的方法。
根据配位化合物的磁性性质,可以推断出金属离子的配位数。
例如,当金属离子的配位数为2时,通常表现为高自旋态,磁性较强;而当配位数为6时,通常表现为低自旋态,磁性较弱。
3. 光谱法光谱法也可以用于确定金属离子的配位数。
例如,红外光谱可以提供金属离子与配体之间的键合信息,从而确定配位数。
同时,紫外-可见光谱也可以用于研究金属离子的电子跃迁行为,进一步确定配位数。
三、金属离子配位数的应用金属离子配位数的确定对于了解金属配合物的结构和性质具有重要意义。
在实际应用中,金属离子的配位数决定了配位化合物的稳定性、光学性质、磁性性质等。
1. 稳定性金属离子的配位数与配位化合物的稳定性密切相关。
一般来说,金属离子的配位数越高,配位化合物的稳定性越高。
这是因为高配位数可以提供更多的配体与金属离子形成化学键,增强了配位化合物的稳定性。
2. 光学性质金属离子的配位数对配位化合物的光学性质有重要影响。
例如,金属离子在不同配位数下的配位化合物可以表现出不同的颜色。
这是因为金属离子的配位数改变了配位化合物的电子结构,导致其吸收和发射光谱发生变化。
高考化学:配合物和晶体中配位数的判断

高考化学:配合物和晶体中配位数的判断等离子体中,中心离子(或原子)同时以共价键和配位键结合,配位数不等于配位键的键数。
例如,[BF4B(OH)4AlCl4Al(OH)4等离子体中,中心原子与其配位原子之间的键数是4,但配位数却是6.这是因为这些离子中的中心原子与其配位原子之间的键数不仅包括配位键,还包括其他共价键。
二、晶体中配位数的判断晶体中的配位数是指晶体中一个原子周围与其等距离的最近邻的原子数目。
通常情况下,晶体中的配位数可以通过以下几种方法来判断:1.简单离子晶体中,离子的配位数等于其化合价。
例如,NaCl晶体中Na+离子的配位数为6,Cl-离子的配位数也为6.2.对于具有离子共价性质的化合物,其离子的配位数可以通过离子半径比来判断。
离子半径比越大,其配位数越小。
3.对于金属晶体,其配位数可以通过晶体结构中金属离子的配位数来判断。
例如,fcc结构中的金属离子配位数为12,hcp结构中的金属离子配位数为6.4.对于复杂晶体,配位数的判断需要通过晶体结构分析来确定。
总之,配位数是判断化合物或晶体性质的重要参数,通过对配位数的准确判断,可以更好地理解和解释其化学性质。
Na+离子的配位数都为6.或以正八面体的面心Na+离子分析,上、下、左、右、前、后各有一个Cl-离子,配位数为6.又如金属晶体中的面心立方堆积A1如图所示)。
典型代表Fe、Ni、Co,因立方体的面心原子都与中心原子形成金属键,以立方体的面心原子分析,上、下、左、右、前、后各有一个配位原子,故配位数为6.注意:在NaCl型离子晶体中,每个离子周围等距且紧邻的离子在上下、左右、前后各2个,共12个,这也不是真正的配位数。
因为是同电性离子。
化学中配位数是很重要的概念,特别是在配位化合物的研究中。
B、Al原子缺电子,它们形成的化学键既有共价键,又有配位键,配位数与配位键的键数不相等,配位数均为4.例如Al2Cl6中Al原子的配位数为4,酞菁钴的结构中钴离子的配位数也为4.然而,当中心离子(或原子)与不同量的配位体配合时,其配位数为不确定。
金属晶体堆积模型复习及计算

请计算:空间利用率?
以体心立方晶胞为例,计算晶胞中原子的 空间占有率。
小结:(2)钾型 (体心立方堆积)
配位数:8
(3)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。
微粒数为: 8×1/8 + 6×1/2 = 4
请计算:空间利用率?
B
此种立方紧密堆积的前视图A
7 1 9
6
5
8 2
3 4
10
11
12
这种堆积晶胞空间利用率高(74%),属于 最密置层堆集,配位数为 ,许多金属(如 Mg、Zn、Ti等)采取这种堆积方式。
回顾镁型的晶胞
1200
平行六面体
找铜型的晶胞
C B A
回顾:配位数 每个小球周围距离最近的小球数
=19.36g/cm3 1nm=10-9m=10-7cm
复习1pm=10-12m
练2:
现有甲、乙、丙、丁四种晶胞,可推知甲
晶晶体体体的中化的与学化的式学粒 为式子—为E—个F——D或—数—C——F比2——E—为;或——丁—C—1—晶—2:D1——体——;的—;丙化乙晶学 式为—X—Y——2Z——。
BA
甲
DC
乙
F
E
丙
Z X
Y
丁
练3: 甲
乙
丙
上图甲、乙、丙分别为体心堆积、面心立方堆积、 六方堆积的结构单元,则甲、乙、丙三种结构单
元中,金属原子个数比为——1—:—2:—3————。
乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数为12×1/6+2×1/2+3=6
金属晶体堆积模型及计算公式

----体心立方堆积:
5 8 1
6 7 2
4
3
这种堆积晶胞是一个体心立方,每个晶胞含 2 个原子,属于非密置层堆积,配位数 为 8 ,许多金属(如Na、K、Fe等)采取这种 堆积方式。
空间利用率的计算
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。 微粒数为:8×1/8 + 1 = 2
1200
平行六面体
每个晶胞含 2 个原子
铜型(面心立方紧密堆积)
7 6 5 1 8 9 4 2 3
12
10 11
这种堆积晶胞属于最密置层堆集,配位数 为 12 ,许多金属(如Cu、Ag、Au等)采取这 种堆积方式。
(3)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。 微粒数为: 8×1/8 + 6×1/2 = 4 空间利用率: 4×4лr3/3 (2×1.414r)3
分子间以范德 通过金属键形成的 华力相结合而 晶体 成的晶体
作用力
构成微粒 物 理 性 质 实例 熔沸点
共价键
原子 很高
范德华力
分子 很低
金属键
金属阳离子和自由 电子 差别较大
硬度
导电性
很大
无(硅为半导体) 金刚石、二氧化硅、 晶体硅、碳化硅
很小
无 Ar、S等
差别较大
导体 Au、Fe、Cu、钢 铁等
= 74.05%
堆积方式及性质小结
堆积方式 晶胞类型 空间利 配位数 用率 简单立 方堆积 简单立方 52% 68% 74% 74% 6 8 12 实例
Po Na、K、Fe
体心立方 体心立方 堆积 六方最 密堆积 六方
金属及各类晶体配位数计算图总结
立方ZnS型离子晶体:
所属晶系: 立方; 点阵: 立方F; 结构基元及每个晶胞中结构基元的数目: ZnS, 4个; Zn和S离子的配位数都是4;
CaF2型离子晶体:
所属晶系: 立方; 点阵: 立方F; 结构基元及每个晶胞中结构基元的数目: CaF2, 4个; Ca和F离子的配位数分别是8和4;
三、在配位化合物(简称配合物) 中
配位场理论认为中心原子的内层轨道受 周围配体的影响,也即关系到配位数。 例如,Ni2+离子与H2O和NH3等具有小的相 互排斥力的弱场配体,生成配位数为 6 的【Ni(H2O)6】2+和【Ni(NH3)6】2+等八面 体配离子;与Br-和I-等具有大的相互排斥 力的弱场配体则趋向于生成配位数为4的 【NiBr4】2-和【NiI4】2-等正四面体配离 子;与CN-等强场配体则生成配位数为4
3.典型结构的配位数 (1)六角密积和立方密积的配位数都是十二。即晶体中最
大配位数为十二。
(2)当晶体不是由全同的粒子组成时,相应的配位数要发
生变化—减小。由于晶体的对称性和周期性的特点,以
及粒子在结合成晶体时,是朝着结合能最小、最稳固的
方向发展。因此,相应的配位数只能取:
8(CsCl型结构)、6(NaCl型结构)、4(金刚石型结构)、
3(层状结构)、2(链状结构)。
4.氯化铯型结构的配位数
如图所示,大球(半径为R)中心为立方体顶角,小 球(半径为r)位于立方体的中心。 如果大球相切,则
立方体的边长为:
空间对角线的长度为: ak
a 2R
Cs
3a 2 3 R
RCl - 1.81 A rC s 1.69 A
o o
mn配位数

mn配位数
mn 配位数是指在晶体中,与某一原子最近邻的原子数。
晶体中的原子可分为晶体学上等价的原子和不等价的原子,晶体学上等价的原子可以有相同的配位数。
某一原子的配位数主要取决于晶体的结构,可通过对晶体结构的分析计算出来。
在离子晶体中,由于阴、阳离子的半径比不同,其配位数也不同。
当阴、阳离子的半径比大于0.414时,配位数为4;当阴、阳离子的半径比在 0.414到 0.732 之间时,配位数为6;当阴、阳离子的半径比小于 0.732 时,配位数为8。
在金属晶体中,由于金属原子的价电子可以脱离原子实而自由运动,在金属晶体中形成电子云。
金属原子在晶体学上等价的原子的配位数主要取决于金属原子的价电子数和金属晶体的结构。
例如,在体心立方晶格中,金属原子的配位数为8;在面心立方晶格中,金属原子的配位数为12。
在原子晶体中,由于原子间的共价键联系,原子间的配位数主要取决于共价键的性质和晶体的结构。
例如,在金刚石晶体中,碳原子的配位数为4;在二氧化硅晶体中,硅原子的配位数为4,氧原子的配位数为2。
总之,mn 配位数是晶体学中的一个重要概念,它与晶体的结构密切相关。
通过对晶体结构的分析,可以确定晶体中原子的配位数,这对于理解晶体的性质和应用具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金属晶体的空间结构
影响金属键强弱的因素
金属阳离子的半径 金属阳离子的电荷数 金属阳离子的堆积方式
半径越小,金属键越强 如碱金属 电荷越多,金属键越强;如 Al>Mg>Na
配位数
概念:一个粒子周围最近邻的粒子数称为配位数。
它可以描述晶体中粒子排列的紧密程度,粒 子排列越紧密,配位数越大,结合能越低, 晶体结构越稳定。
堆积模型
简单立方 体心立方 钾型 立方最密 镁型
采用这种堆 积的典型代 表
Po Na K Fe
空间利用率
52℅ 68℅
配位数
6 8 12
Mg Zn Ti
Cu Ag Au
74℅
74℅
面心立方最密 铜型
12
混合型晶体
C的杂化方式:SP
既有共价键又有金属键和范 德华力,属于混合型晶体 2
谢谢!
在提到配位数时应当分析其所处环境。
• • •
1、在晶体学中配位数与晶胞类型有关; 2、离子晶体中指一个离子周围最近的异电性离子的数目; 3、配位化学中,化合物中性原子周围的配位原子的数目。
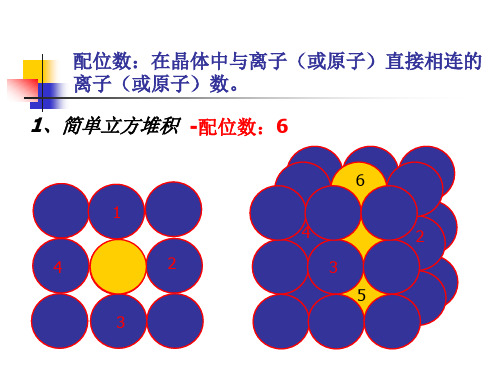
配位数:在晶体中与离子(或原子)直接相连的离 子(或原子)数。
金属晶体的原子堆积模型
非密置层,配位 数是4
密置层,配位数 是6
非密置层堆积——简单立方堆积
1、简单立方堆积
-配位数:6
1
6
1 2 4 3 5 6
2
4 3
2.体心立方堆积——钾型
2.体心立方堆积——钾型
-配位数:8
5
8
6 7 2 3
14Biblioteka 二.密置层堆积3. 六方最密堆积——镁型
配位数:12
6 5 10 7 1 8 9 4 11 2 3
12
4.面心立方最密堆积——铜型
