第五章 曲线运动知识结构图
人教版高一物理必修二第五章-《曲线运动》参考(14张)-PPT优秀课件

火星由于惯性,以 脱离砂轮时的速度 沿切线方向飞出, 切线方向即为火星 飞出时的速度方向
结 人教版高一物理必修二 第五章:5.1《曲线运动》参考课件(共14张PPT)【PPT优秀课件】-精美版 论
问 人教版高一物理必修二 第五章:5.1《曲线运动》参考课件(共14张PPT)【PPT优秀课件】-精美版 题 2
做曲线运动的物体运动轨迹弯曲方向与其所受合 外力方向有什么关系呢?
v1
G
v2
G
v
F
G v3
做曲线运动的物体所受合外力指向运 动轨迹凹的一侧
人教版高一物理必修二 第五章:5.1《曲线运动》参考课 件(共14 张PPT) 【PPT 优秀课 件】-精 美版
曲 人教版高一物理必修二 第五章:5.1《曲线运动》参考课件(共14张PPT)【PPT优秀课件】-精美版 线 运 动 的 特 点
1、曲线运动的轨迹是曲线;
2、曲线运动的运动方向时刻在改变;
物体沿圆周逆时针转动 且速度大小保持不变
v
B
A
v
3、曲线运动是变速运动,一定具有加速度,
合外力不为零
人教版高一物理必修二 第五章:5.1《曲线运动》参考课 件(共14 张PPT) 【PPT 优秀课 件】-精 美版
1、速度变化的运动必是曲线运动吗?
错
2、加速度变化的运动必是曲线运动吗? 错
3、曲线运动一定是变速运动?
对
4、变速运动一定是曲线运动?
错
5、曲线运动的速度一定变?
对
6、做曲线运动的物体所受合力一定不为零?对
7、物体在恒力下不可能做曲线运动?
曲线运动思维导图

投篮时的曲线运动
总结词
投篮时篮球的运动轨迹是一条抛物线, 因此投篮时的篮球运动也是一种曲线运 动。
VS
详细描述
投篮是篮球运动中的一项基本技术,当投 篮时,篮球沿着一条抛物线的轨迹飞向篮 筐。这个抛物线的轨迹是由篮球出手时的 角度、速度以及空气阻力等因素决定的。 为了提高投篮的准确性和命中率,球员需 要根据实际情况调整出手角度和力度,使 篮球能够准确地进入篮筐。
速度
描述物体运动快慢的物理量,等于位 移与时间的比值。
加速度
描述速度变化快慢的物理量,等于速 度的变化量与时间的比值。
加速度与力的关系
牛顿第二定律:物体受到的力与 加速度成正比,与质量成反比。
在曲线运动中,物体受到的力可 以分解为切向力和法向力,切向 力改变速度大小,法向力改变速
度方向。
曲线运动中,加速度的方向始终 指向曲线的凹侧。
曲线运动思维导图
contents
目录
• 曲线运动概述 • 曲线运动的物理量 • 曲线运动的规律 • 曲线运动的实例分析 • 曲线运动的思维导图总结
01 曲线运动概述
定义与特点
定义
曲线运动是指物体沿着弧线或曲 线的源自径运动,而不是直线运动 。特点
曲线运动的速度方向不断变化, 加速度与速度方向不在同一直线 上。
航天工程
01
卫星和火箭的发射、运行轨迹都是曲线运动,曲线运动在航天
工程中具有重要应用。
交通工程
02
车辆在行驶过程中会遇到曲线道路,曲线运动在交通工程中也
是必不可少的。
体育竞技
03
曲线运动在各种体育竞技项目中也有广泛应用,如田径、游泳、
自行车等。
如何更好地理解和掌握曲线运动
新人教版高中物理必修二第五章第一节《曲线运动》课件(共16张PPT)

•为了准确描述位移我们采用了什么数学手段? 建立坐标系
O
V0
s x
yx A
y
质点在某一点(时刻)的 速度方向是在曲线这一点 的切线方向。
曲线运动的特点
• 从运动学角度看:
① 曲线运动的速度方向时刻在改变, 因此一定是变速运动。
② 质点在某一点(时刻)的速度方向 是在曲线这一点的切线方向。
曲线运动
一、什么是曲线运动?
定义:质点的运动轨迹是曲线的运动
知识准备
• 运动学的基本概念
① 速度是矢量,既有大小又有方向。 ② 加速度是速度对时间的变化率,只要速度变
化就有加速度。
• 动力学的基本规律
① 力是改变物体运动状态的原因。 ② 牛顿运动定律。
• 平行四边行法则
一 曲线运动的位移
知识准备
F、v共线
F恒定 直线运动
F变化
匀变速直 线运动
变加速直 线运动
F恒定
匀变速曲 线运动
F、v不共线 曲线运动 F变化
变加速曲 线运动
课堂练习
• 下列关于曲线运动的说法,正确的是: A. 速率不变的曲线运动是没有加速度的 B. 曲线运动一定是变速运动 C. 变速运动事实上是曲线运动 D. 做曲线运动的物体一定有加速度
谢谢观赏
You made my day!
我们,还在路上……
• 如图所示,物体沿圆弧由A点滑到B点的过 程中速度大小保持不变,则:
A. 它的加速度为零
B. 它所受外力合力为零
A
C. 它做的是变速运动
D. 它做的是匀速运动
B
作业布置 完成本课练习
Thanks 谢谢您的观看!
新人教版高中物理必修2精品课件(第五章曲线运动 全套307张PPT)

第一节 曲线运动
学习目标
重点难点
1.知道曲线运动是一种变速运动,
1.曲线运动速度方
会在其轨道上画出速度方向.
向的确定,曲线运
2.通过研究蜡块的运动过程,体会 重点 动性质的理解.
建立直角坐标系研究曲线运动的
2.物体做曲线运动
方法.
的条件
3.知道物体做曲线运动的条件,认
1.运动的合成与分
(2)速度的分解:如图所示,物体沿曲线 运动到 A 点,速度大小为 v,与 x 轴夹角为 θ,则在 x 方向的分速度为 vx=vcos θ,在 y 方向的分速度为 vy=vsin θ.
[说明] 速度是矢量,速度的变化有三种情况 (1)速度方向不变,只有大小改变,物体做变速直线 运动. (2)速度大小不变,只有方向改变,物体做速率不变 的曲线运动. (3)速度的大小和方向同时变化,物体做曲线运动.
小试身手
4.(多选)某电视台举行了一项趣味游戏活
动:从光滑水平桌面的角 A 向角 B 发射一只
乒乓球,要求参赛者在角 B 用细管吹气,将
乒乓球吹进 C 处的圆圈中.赵、钱、孙、李四位参赛者
的吹气方向如图中箭头所示,那么根据他们吹气的方向,
不可能成功的参赛者是( )
A.赵
B.钱
C.孙
D.李
解析:根据物体做曲线运动的条件和特点,可知乒 乓球受到的合力指向曲线凹侧,故不可能成功的参赛者 是 A、B、D.
判断正误 1.地球围绕太阳的运动是曲线运动.( ) 2.研究风筝的运动时,可以选择平面直角坐标 系.( ) 3.当物体运动到某点时,位移的分矢量可用该点的 坐标来表示.( ) 答案:1.√ 2.× 3.√
小试身手 1.关于曲线运动的位移,下列说法正确的是( ) A.曲线运动的位移是曲线 B.只要曲线运动不停止,曲线运动的位移就一定越 来越大 C.曲线运动的位移不可能是零 D.做曲线运动的质点在一段时间内水平分位移是 4 m,竖直分位移是 3 m,则其位移大小为 5 m
曲线运动知识点总结(思维导图)
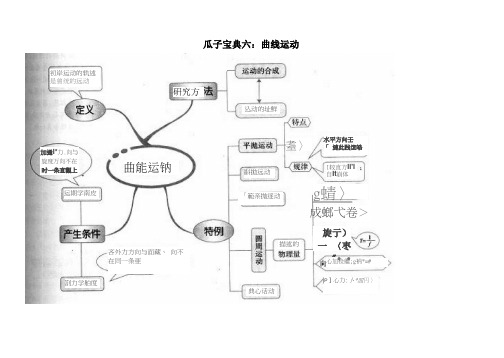
瓜子宝典六:曲线运动
初岸运动的轨述 是曾统的远动
硏究方
込动的址鮮
加通I*力.向与
旋度万向不在 时一条直觀上
运期学南皮
曲能运钠
吝外力方向与面藏、 向不 在同一条亜
剳力学舶度
耋〉
水平方向壬 「 速此践谊皓
斟拋远动 「範亲抛逐动
I较直方li'l 自It崩体
g蜻〉
成螂弋卷>
描述的
旋亍) 一 〈枣
心"加•检繼•;g衲*=#
典心话动
|P]心力:卜*皿円〉
ቤተ መጻሕፍቲ ባይዱ .Mgii!
不拒以興供KHI妬Q所 償的向心力的情AF做 tfMi&WM心的论幼
r I : Vi I wnm防止尸
◎.并H心度鈴
埃 連 崖 的 大 小 SUZ.II 違度、《1明、・"体定
不宣.«<•»««»« 心力的 大小侦定不*
㈤周达动
瑚之阳
悅哽P喧
一g
•时心ICit苴《1*由・? 应合力]
高一物理人教版必修二第五章第1节曲线运动(共40张PPT)

特别提示
1 物体的真实运动(相对于地面)是合运动。 2 运动的分解合成就是决定运动状态的物理量(速度、 加速度、位移)的分解合成。 3 分运动与合运动的等时性。 4 各分运动间的独立性。
30
二 运动的合成与分解
由分运动求合运动的过程叫做运动的合成 由合运动求分运动的过程叫做运动的分解
①画出它在各点的速度方向。
②画出它在各点的受力方向(不计空气阻力)。
③观察轨迹的弯曲与力的方向有什么关系?
A
A
B
B
C
C
关系:做曲线运动的物体,合力指向哪里,曲线向 哪里弯曲(合力的方向总是指向曲线的内侧)。
推广: 为什么空中飞行的导弹做的是曲线运动? 为什么导弹的轨迹是向下弯曲的?
合理猜想
设计实验
2 但人相对于地面的位移是5×1m+1m=6m。
39
(1)
运动的合成与分解
分运动
运动的合成 运动的分解
合运动
遵循平行四边形法则 具有等时性 (2)运动的合成与分解遵循平行四边形法则
40
α角最θ大=.a根rc据cocossθv船=v船/v水,船头与河岸的夹角应为
v水
此时渡河的最短位移:
s= L = Lv水
cos
v船
35
训练1 火车以 12 m/s的速度向东行驶,雨点的速度为 16 m/s,方向竖直向下,求:车中的人所观察到雨点的 速度,方向如何? 答案:20 m /s 方向竖直向下偏西37°
联系实际
V f
FG
Question1:
一物体由静止开始下落一段时间后突然受一恒 定水平向右风力的影响,但着地的前一段时间 风突然停止,则其运动轨迹可能是怎么样的? (其它力不计)
必修2 第五章 曲线运动讲解学习

必修2第五章曲线运动第五章 曲线运动s例6. D 例7. (1)船头垂直河岸渡河, 20 s ; (2)船头与上游河岸成60°角, 120m.5.1曲线运动曲线运动:导弹所做的运动;汽车转弯时所做的运动;人造卫星绕地球的运动;曲线运动中速度方向是时刻改变的。
一. 曲线运动的位移1. 坐标系的建立 直线运动:直线坐标系; 曲线运动:平面直角坐标系2. 曲线运动的位移OA ,l (,A A x y ),(,B B x y )等 二.曲线运动的速度 1. 曲线运动速度的方向(1) 实例:a :在砂轮上磨刀具时,刀具与砂轮接触处有火星沿砂轮的切线方向飞出;b .链球运动员选择脱手的时机 c. 小球曲线运动(2)曲线运动速度方向:质点在某一点(或某一时刻)的速度的方向是在曲线的这一点的切线方向。
(3)推理:a :只要速度的大小、方向的一个或两个同时变化,就表示速度矢量发生了变化。
b :由于做曲线运动的物体,速度方向时刻改变,所以曲线运动是变速运动。
c :曲线运动的一定有加速度,物体一定受到合外力。
合外力方向与速度方向不同。
2. 曲线运动的理论意义 割线−→−切线3. 运动速度的分解 (正交分解)cos x v v θ=, sin y v v θ= 22x y v v v =+三. 运动的合成与分解 1. 实验探究蜡块运动(1)实验分析分运动与合运动的关系 (2)蜡块位置、位移:x =v x t ,y =v y t2222x y s x y v v =+=+(3)蜡块运动轨迹:y xv y x v = 过原点的直线(4) 蜡块的速度 22x yv v v =+tan y xv v θ=2. 合运动与分运动 平行四边形法则 合成或分解:(1)位移(2)速度 (3)加速度3. 合运动与分运动的关系(1)等时性: 求运动时间可选择简单的分运动来计算 (2)独立性: 各分运动独自进行,不相互影响(3)等效性: 合运动与各分运动共同产生的效果相同,可相互替代4. 跨过定滑轮绳拉物体问题。
第5单元【曲线运动】物理知识结构图

物理知识结构图
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
Байду номын сангаас
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
物理知识结构图
返回上一层
新人教物理必修二第五章5.1曲线运动课件(共17张PPT)

观 察
观 察
轨迹是曲线的运动 叫做曲线运动
怎样确定做曲线运动物体在某一时刻的速度方向?
数学概念: 曲线的切线
B A
观察与思考 砂轮打磨下来的火星 (炽热颗粒)和墨水 它们沿着什么方向运动?
火星沿砂轮的切线方向飞出,墨水也沿着陀螺边缘的切线飞出
归纳总结
1.质点某一点(或某一时刻)的速度方向:
等于0°,也不等于180 °
归纳总结 F合(a)跟v在一直线上 → 直线运动
a 恒定
匀变速直线运动
a 变化
变加速直线运动
F合(a)跟v不在一直线上 → 曲线运动
a 恒定
匀变速曲线运动
a 变化
变加CD A、曲线运动一定是变速运动 B、变速运动一定是曲线运动 C、曲线运动的加速度一定不为零 D、曲线运动轨迹上任一点的切线 方向就是质点在这一点的瞬时速度 方向
练 习
2.物体在光滑水平桌面受三个水
平恒力(不共线)处于平衡状态,
当把其中一个水平恒力撤去时,
物体将 ABC
A、物体可能做匀加速直线运动
B、物体可能做匀减速直线运动
C、物体有可能做曲线运动
D、物体一定做曲线运动
练 习
3.如图,物体在恒力F 作用下沿曲线从 A
运动到B , 这时突然使它所受力反向
(大小不变),则物体以后的运动情
况C
A、可能沿曲线 Ba运动
c
b B
B、可能沿直线 Bb 运动
a
C、可能沿曲线 Bc运动 A
D、可能沿原曲线由 B 返回 A
不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月9日星期六2022/4/92022/4/92022/4/9 书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/92022/4/92022/4/94/9/2022 正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/92022/4/9April 9, 2022 书籍是屹立在时间的汪洋大海中的灯塔。
人教版必修二 第五章曲线运动第1节曲线运动(共34张PPT+素材)

即时练习
2.小球在水平桌面上做匀速直线运动,当它受到如图 所示方向的力的作用时,小球可能运动的方向是( D )
A、 Oa B、 Ob C、 Oc D、 Od
a v
O F
b c
d
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版必 修二 第五章曲线运动第1节曲线运动( 共34张P PT+素 材)
等时性:各个分运动与合运动总是同时开 始,同时结束,经历的时间相等。
等效性:分运动与合运动可以等效替代。
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版必 修二 第五章曲线运动第1节曲线运动( 共34张P PT+素 材)
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版必 修二 第五章曲线运动第1节曲线运动( 共34张P PT+素 材)
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版必 修二 第五章曲线运动第1节曲线运动( 共34张P PT+素 材)
四、物体做曲线运动的条件
F与V不共线
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版必 修二 第五章曲线运动第1节曲线运动( 共34张P PT+素 材)
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版必 修二 第五章曲线运动第1节曲线运动( 共34张P PT+素 材)
蜡块的合运动与分运动
1.合运动与分运动
如果物体同时参与了几个运动, 那么物体实际发生的运动就是合运动, 那几个运动就是分运动。
2.运动的合成与分解
知分运动求合运动叫运动的合 成,知合运动求分运动叫运动的分 解。
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版必 修二 第五章曲线运动第1节曲线运动( 共34张P PT+素 材)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二
运动合成与分解
合运动分运动,研究方法(建立直角坐标系)
运动的合成
1
分运动
(水平运动) (竖直运动)
平行四边形定则
运动的分解
合运动
(蜡块实际的运动)
2
位移 速度 加速度 力 关系(平行四边形定则)
注意:水平和竖直都是匀速直线运动,合运动是匀速直线 运动(速度与位移同向) 水平是匀速直线 竖直是初速度为零的匀加速直线运动合成轨迹如何?
第五章 曲线运动知识结构图 速度特点 一
曲线运动
研 究 方 法 化 曲 为 直
运动规律(性质)
做曲线运动条件
合运动分运动,研究方法(建立直角坐标系) 位移 速度 加速度 力 关系(平行四边形定则) 性质:等时性 等效性 独立性
二 运动合成与分解
思 想 迁 移
应 用
运动合成分解遵守原则 斜抛和平抛定义
B 火车转弯问题(火车匀速通过)不计摩擦
火车的拐弯处轨道面倾角为θ 两轨道间距为L,两轨高度差为h, 转弯半径为R,重力加速度g 求: (1)火车不挤压内外轨道速度?
(2)火车挤压内轨条件? (3)火车挤压外轨条件? 在以上问题中如果互动摩擦因数为 ,则火车不挤压内外轨道条件?
2 拱凹桥,超失重问题
f (Hz) n (r/s)
f=1/T
n=f
线速度方向沿着轨迹切线,角速度是矢量。
V=R
向心力:圆周运动中改变物体速度方向的力。 (下文详述) 向心加速度:向心力产生的加速度
例题 如果RA:RB:RC=2:1:1求:ABC,线速度之比?角速度之比?
注意: (1)同一个转轴上的物体角速度相同, (2)同一个皮带上的质点(或靠摩擦传动的两个轮子) 线速度大小一定相同. 例题 地球平均半径为6.4103km,物体位于北纬60度的质点 求:角速度多大? 线速度多大?
汽车以相同的速度通过以上 ABC三点,在那点最容易爆胎?
A
B
C
如果在c点速度足够大将出现什么现象? 离心运动和向心运动
3
六 圆周运动经典问题分析
1 水流星(单摆)——轨道模型 (1)要想做完整的圆周运动,在最高点 的最小速度多大? (2)要想做完整的圆周运动在最低点速度 多大?已知 R,g
2
轻杆—— 圆管模型 (1)要想做完整的圆周运动,在最高点的最小速度多大? (2)要想做完整的圆周运动在最低点速度多大?已知 R,g
2
匀速圆周运动 定义,受力条件,相应公式
(1)匀速圆周运动:质点在任意相等时间内通过的弧长相等。匀速指的是速率。 匀速圆周运动是变速运动,有加速度。 (2)受力条件:质点所受合力大小不变,方向始终指向圆心
3
变速圆周运动 定义,受力条件,特点
在圆周运动中速度与合力方向关系如何? 对于匀速圆周运动: (1) 合力大小不变 方向 始终指向圆心 与速度垂直 作用是改变速度的方向 变速圆周运动中 (2)合力大小方向都变 方向不指向圆心与速度不垂直 切向分力: 改变速度大小 法向分力:(提供向心力)改变速度方向
如图所示,匀速转动的水平圆盘上,沿半径方向两个用细线相连小物体A、B的质量均 为m,它们到转轴距离分别为20cm,。A、B与盘面间的最大静摩擦力均为重力的0.4倍 试求:(1)当细线上开始出现张力时,圆盘的角速度。 (2)当A开始滑动时,圆盘的角速度。 (3)当即将滑动时,烧断细线,A、B状态如何?
3
性质:等时性 等效性 独立性
(1)合运动与分运动所用时间相同
(2)两个分运动的共同运动效果和一个合运动的运动效果相同 (3)两个分运动是相互独立的,互相不影响。 4 运动合成与分解遵守原则
5
经典问题
(1)小船过河问题
(2)拉伸转动 问题 一个绳子(速度V1)连接一个实际运动的物体(V2) 物体匀速,求:绳子速度和运动物体速度的关系?
三
抛体运动
(曲线特例一)
研究方法和运动规律 位移,速度公式和影响因素 经典问题
描述圆周运动的物理量 V,,T,f,n,a向,F向定义特点 圆周运动 (曲线特例二)
四
匀速圆周运动 定义,受力条件,相应公式
变速圆周运动 定义,受力条件,特点
应 用
汽车,火车转弯问题 五 圆周运动实例 应 用 拱凹桥,超失重问题 离心和向心运动 水流星——轨道模型 轻杆—— 圆管模型 六 圆周运动经典问题 圆锥摆—— 圆锥模型 七 物体运动规律条件分析
4
圆锥摆—— 圆锥模型 (1)A,B不同个轨道区别? (2)求周期(已知 L,,g) (3)分析临界角速度? (已知,L)
5 临界问题
细绳一端系着质量为M=0.6kg 的物体,静止在水平圆盘上,另一端通过光滑的小孔吊 着质量为m=0.3kg的物体,M的中点与圆孔的距离为0.2m,并已知M与圆盘的最大静 摩擦力为2N,现使此圆盘绕中心轴线转动,问角速度在什么范围内可使m处于静止 状态?(取g=10m/s2)
合力与速度方向成锐角 是加速圆周运动 合力与速度方向成钝角是减速圆周运动 V O
V
五圆周运动实例分析
1 汽车,火车转弯问题 A 汽车转弯问题(汽车匀速转弯) (1)汽车匀速转弯请分析汽车所受向心力来源? (2)汽车质量为m,,转弯半径为R,求安全行驶速度? (3) 已经m,,R,路面倾角为,求安全行驶速度?
一
曲线运动
速度特点 质点在某一点的瞬时速度方向, 就是通过这一点的曲线切线方 向
曲线运动是一种变速运动(速度方向时刻变化)
1
2
运动规律(性质)
a Vt V t0F合 m3
做曲线运动条件 合力的方向(加速度的方向)与物体速度方向不在共线
我们只看速度方向与合力(或加速度)方向关系不 看二者大小关系。
问题1 : 当V船>V水 时和V船>V水时 (1)最短时间过河 (2)最短位移过河
三 抛体运动
1 斜抛和平抛定义
斜抛: (1)初速度倾斜 (2)只受重力作用 平抛: (1)初速度水平 (2)只受重力作用
近似处理:当 G>>f(重力远远大于阻力时候可以看成抛体运动)
2 研究方法和运动规律
规律:各种抛体运动都是匀变速运动(a=g) 匀变速直线:竖直上抛,竖直下抛运动(v向与g共线) 匀变速曲线:平抛,斜抛,斜下抛等等(v向与g不共线)
名称 线速度 角速度 周期 频率 转速
符号 V (m/s) (rad/s) T (s)
公式
定义
物理意义
质点经过弧长与时间比 运动的快慢 质点经过角度与时间比 质点转动的快慢
T 2
2 R v
质点运动一圈所用时间 转动的快慢 质点1s内完成周期数 1s内转动的圈数 转动的快慢 转动的快慢
光滑水平上一绳连接两个物体用轻绳子连接两个小球A,B如图,质量 分别为m,距离分别为L,转动角速度为, 绳子承受最大拉力为Fm 求:(1) OA,AB段绳子拉力之比? (2)转动最大速度为多大?
物体相对侧壁静止转动匀速转动与加速转动过程中受力分析?
平抛研究方法:(建立坐标系)画曲为直 (把上一节运动的分解运动到这里) 水平方向: 匀速直线运动 竖直方向: 竖直方向自由落体运动 (V0=0,a=g) 3 位移,速度公式和影响因素 y X
(速度方向与x轴交点为水平位移中点)
4
5典型问题(已知位移关系来接求解剩余关系)
四 圆周运动
1 描述圆周运动的物理量 V,,T,f,n,a向,F向定义特点
