“超级全能生”高考全国卷26省联考(甲卷)
“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案

“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案注意事项:1.本试题满分150分,考试时间150分钟;2.答题考生务必将自己准考证号填写在答题卡的相应位置;3.全部答案在答题卡,答在本试题卷上无效.一、现代文阅(3分)(一)论述类文本(本题共3小题,共9分)阅读下面的,宽1~3题。
展览通过实物、摹本、AR技术、仿制洞窟等方式将不便移动的壁画呈现在公众面前。
其中,大量数字化技术的运用对传统壁画临摹带来了新挑战。
人们不禁发问:当数字复制技术愈发成熟,古代壁画还需要临摹吗?过去,古代壁画临摹常常出于研究保护之目的,为历史而摹。
如山西永乐宫在进行整体搬迁保护工程前,组织中央美术学院师生进行了全部壁画临摹工作,以为后续搬迁工作服务。
这样的临摹,不仅对壁画保护具有重要意义,在这一过程中,通过对壁画形式语言结构的深入分析,也培养出了一批年轻的壁画研究人才。
另外,临摹流失海外的古代壁画也为还原文化遗产面貌提供了有益借鉴。
还有一批画家、学者是为艺术而摹。
出于对古代壁画艺术的崇敬向往,他们在临摹中更强调梳理壁画创作媒介、图像及方法。
如敦煌研究院,在临摹壁画艺术宝库作品时,探索出了一套从起稿、线稿、上色、画面整体调整到完稿的临摹技法体系。
又如段文杰先生临摹的《都督夫人礼佛图》,通过长达两年时间对唐人的研究,最终使本已残破的原壁画重绽光辉。
类似这样的“整理临摹”“复原临摹”等研究性临摹实践,在“客观临摹”的基础上,进一步凸显了当代研究者对壁画的理解感悟。
然而,这些实践成果的应用却面临着传播困境。
传统临摹作品虽具备较高的学术性,但因数量少、临摹耗时长等因素,大多用于研究、保护、教学工作,很少以展览、研究成果的形式走出洞窟,走向大众。
此时,数字技术的合理介入是满足公众诉求的必由之路,也是让静默千年的文化遗产“活”起来的必然要求。
数字复制、VR技术、3D动画复原演示、线上展览、配套互动游戏等高科技,为盘活传统壁画这个超级IP提供了无限可能,也为壁画保护提供了新思路。
“超级全能生”2019高考全国卷26省9月联考甲卷-语文试题(含详细答案)

“超级全能生”2019高考全国卷26省9月联考甲卷语文注意事项:1.本试题共8页,满分150分,考试时间150分钟。
2.答题前,考生务必将自己的姓名、准考证号等填写在答题卡的相应位置。
3.全部答案在答题卡上完成,答在本试题上无效。
4.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
5.考试结束后,将本试题和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
近年来,关于汉语在各国持续升温的报道不断见诸国内外媒体。
语言是民族的重要特征之一,语言的影响力和传播力也日益成为民族国家综合实力的体现。
海外“汉语热”实际上反映的是中国合作共赢、大国担当和文化自信的国际魅力。
互利共赢是重要动力汉语难学,但挡不住学习的热情,海外汉语热出现的根本原因是中国综合国力和国际影响力的大幅度提升,经济上的互利共赢是推动海外汉语热的根本动力。
首先,海外中资企业对熟悉汉语的当地员工的需求越来越大,尤其是对从事国际贸易的企业来说,懂汉语的员工在录用和薪酬方面往往都具有较大优势。
择业方面的语言优势以引领和示范作用影响着海外青年的外语学习选择。
其次,中国游客海外旅游数量屡破新高,而且展现出强大的消费能力,“学说中国话”成为外国商铺每天必须面对的市场现实。
经济搭台,文化唱戏,一些从业人员开始有意识地了解中国文化,了解中国人的生活习惯、行为方式甚至文化传统。
同时,一些有远见的海外家庭看好中国的发展前景,着手培养下一代的汉语语言能力,认为掌握汉语能让孩子站在更好的起点。
由于学习汉语的主要难点是汉字识别和四声发音,需要耳濡目染,因此懂汉语的家政服务人员格外受欢迎,成为高级私教,收入明显高于普通家政服务人员。
为了保持不间断的汉语语言学习环境,这些家庭还在生活中大量使用智能语音服务或其他支持中外互译的手机软件。
“超级全能生”2023届高三全国卷地区11月联考(甲卷)语文试题及答案 人教版高三

“超级全能生”2023届高三全国卷地区11月联考(甲卷)语文试题及答案人教版高三“超级全能生”2023高考全国甲卷地区11月联考语文注意事项:1.本试题卷共8页,满分150分,考试时间150分钟。
2.答题前,考生务必将自己的姓名、准考证号等填写在答题卡的相应位置。
3.全部答案在答题卡上完成,答在本试题卷上无效。
4.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
5.考试结束后,将本试题卷和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
已正式启动的碳排放权交易,对于我国“双碳”战略目标实现具有重要的里程碑意义,也向国际社会传递了强烈的信号。
当前的碳交易市场,我们可以理解为一个“非完全体”的碳交易市场。
其一是行业有限,首批被纳入碳排放配额管理的主要是发电企业。
其二是投资主体有限,目前参与碳交易的主要以企业为主,机构投资者和个人还没有被纳入投资群体。
其三是配额分配宽松,现行的配额机制还比较贴近企业的实际排放量,没有带来巨大的排放成本。
这种“非完全体”恰好适应了我国当前能源产业的发展状况,是未来完整碳交易市场和当前碳排放情况的有效链接。
其他国家刚开始推行碳交易市场的时候,也同样采取了这种软着陆的办法,给企业和市场一个适应的机会,相关机制也会根据实践逐步完善。
碳交易市场的到来,能够大力推动低碳产业的发展,促进其对高碳产业的替代。
碳交易的出现会让高碳产业的碳排放成本显著提升,低碳产业会因其成本优势逐步替代一部分份额,这样也会逼迫高碳产业开展节能减排转型,从而在整体上削减碳排放。
不仅如此,更重要的是,碳交易市场给绿色发展时代条件下实现区域平衡发展提供了新的思路。
正如《京都协议书》所规定的一样,国际碳交易市场上,发展中国家和发达国家存在着一个成本价差,而这个价差,是推动发达国家帮助发展中国家践行绿色发展规划、缩小经济差异的重要力量。
2024届超级全能生24省高三上学期1月高考全国卷联考全真演练物理试题(甲)

2024届超级全能生24省高三上学期1月高考全国卷联考全真演练物理试题(甲)一、单选题:本题共7小题,每小题4分,共28分 (共7题)第(1)题我国空间站在轨运行过程中,在通信传输方面有时需要借助于同步卫星,且两者之间距离越近信息传输保真度越高。
假设空间站A和同步卫星B都在赤道平面内运动,空间站的轨道半径r1=kR,R为地球半径。
已知地球自转的周期为T0,地表处重力加速度为g。
则()A.同步卫星的轨道半径B.同步卫星的轨道半径C.两次保真度最高的信息传输的最短时间间隔D.两次保真度最高的信息传输的最短时间间隔第(2)题如图所示,一根跨过光滑轻滑轮的轻质细绳两端各系一个小球a、b,b球的质量是a球的2倍,用手托住b球,a球静止于地面,细绳刚好被拉紧,突然松手,b球落地后立刻静止,a球上升的最大高度为h,则松手前b球距地面的高度为( )A.B.C.D.第(3)题如图所示,地面附近空间有水平向右的匀强电场,一带电微粒以初速度v0从M点进入电场,沿直线运动到N点,不考虑地磁场的影响。
下列说法正确的是( )A.该微粒带正电B.该微粒做匀速直线运动C.只增大初速度,微粒仍沿直线MN运动D.从M至N过程中,该微粒电势能减小,动能增加第(4)题甲物体的质量是乙物体的2倍,甲从H高处自由落下,乙从2H高处与甲物体同时自由落下。
不计空气的影响,在它们落地之前,下列说法中正确的是( )A.两物体下落过程中,在同一时刻甲的速度是乙速度的2倍B.两物体落地时速度相同C.下落1s末,它们的速度相同D.下落过程中甲的加速度是乙加速度的2倍第(5)题通电直导线ab的质量为m、长为l,用两根细线把导线水平吊起,导线上的电流为I,方向如图所示。
在竖直方向加一个方向向上的匀强磁场,导线处于平衡时悬线与竖直方向成,已知:,重力加速度为g。
则磁感应强度B的大小为( )A.B.C.D.第(6)题如图所示,一理想自耦变压器线圈AB绕在一个圆环形闭合铁芯上,左端输入正弦交流电压,、为相同的灯泡,其电阻均为且恒定不变,定值电阻的阻值为灯泡阻值的。
【高三】超级全能生2021届高考全国卷26省联考(甲卷)生物试题及答案

【高三】超级全能生2021届高考全国卷26省联考(甲卷)生物试题及答案超级全能生2021届高考全国卷26省联考(甲卷)理综生物1c0zkoao“超级全能生”2021高考全国卷26省联考(甲卷)科学综合-生物学时间:150分钟满分:300分第一卷(选择题,共126分)一、选择题(本大题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.以下关于细胞中化合物的陈述是正确的()a.核酸彻底水解后释放出的单糖不可以作为细胞的能源物质b、细胞膜的流动性与脂质有关,而稳定性与脂质无关c.将各种多糖分解为基本单元,都能与斐林试剂反应出现砖红色沉淀d、蛋白质可以控制细胞内外的物质,而不参与生物体内的物质运输2.下列各项关于细胞结构和功能说法,错误的是()a、植物细胞壁保持一定的细胞形状,动物细胞形态与细胞外液的浓度有关b.由于乳酸菌没有线粒体所以不能进行有氧呼吸c、花青素存在于植物细胞的大液泡中。
人类没有大液泡,但人类有含有色素的细胞d.核糖体、内质网、高尔基体参与了胰岛b细胞中胰岛素的合成和分泌3.黑蒙性白痴是黑蒙性白痴的家族遗传性疾病。
下图显示了该疾病的遗传谱系。
图中11-5个个体为纯合子。
下面的正确陈述是()a.ⅲ一8和ⅲ一9属于近亲结婚b、家族性遗传病属于多基因遗传,与环境密切相关c.该致病基因在这个群体中的基因频率是1/3d、 iii-8和iii-9想要一个没有致病基因的孩子的概率是5/94.下列有关免疫说法正确的是()a、淋巴细胞膜上有特定的受体,可以区分或识别“外来”细胞b.t细胞只存在于胸腺和骨髓c、效应B细胞(浆细胞)合成的抗体在体外被灭活d.体液免疫和细胞免疫是与生俱来的5.生根粉是一种新型、广谱、高效的植物生长调节剂。
能有效促进园林植物(包括花卉、盆景等)的扦插、移栽、幼苗生根,防止落果。
下面的陈述是正确的()a.生根粉的作用和细胞分裂素的作用相同b、生根粉对植物具有双重生理作用c.生根粉的作用和乙烯利(类似乙烯)混合使用效果更好d、生根粉与除草剂混合使用效果较好6.实验材料的选择对实验的成败影响很大,下列实验中,对实验材料的选择合理的是a、以酵母和小球藻为实验材料,验证了光合氧释放b.用艾滋病毒和大肠杆菌做实验材料,验证dna是遗传物质c、测定心肌细胞的静息电位d.研磨胡萝卜获得提取液,用斐林试剂检测其中的还原糖第二卷(非多项选择题,共174分)三、非选择题(包括必考题和选考题两部分。
“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案

“超级全能生”2019高考全国卷26省12月联考甲卷语文及答案注意事项:1.本试题满分150分,考试时间150分钟;2.答题考生务必将自己准考证号填写在答题卡的相应位置;3.全部答案在答题卡,答在本试题卷上无效.一、现代文阅(3分)(一)论述类文本(本题共3小题,共9分)阅读下面的,宽1~3题。
展览通过实物、摹本、AR技术、仿制洞窟等方式将不便移动的壁画呈现在公众面前。
其中,大量数字化技术的运用对传统壁画临摹带来了新挑战。
人们不禁发问:当数字复制技术愈发成熟,古代壁画还需要临摹吗?过去,古代壁画临摹常常出于研究保护之目的,为历史而摹。
如山西永乐宫在进行整体搬迁保护工程前,组织中央美术学院师生进行了全部壁画临摹工作,以为后续搬迁工作服务。
这样的临摹,不仅对壁画保护具有重要意义,在这一过程中,通过对壁画形式语言结构的深入分析,也培养出了一批年轻的壁画研究人才。
另外,临摹流失海外的古代壁画也为还原文化遗产面貌提供了有益借鉴。
还有一批画家、学者是为艺术而摹。
出于对古代壁画艺术的崇敬向往,他们在临摹中更强调梳理壁画创作媒介、图像及方法。
如敦煌研究院,在临摹壁画艺术宝库作品时,探索出了一套从起稿、线稿、上色、画面整体调整到完稿的临摹技法体系。
又如段文杰先生临摹的《都督夫人礼佛图》,通过长达两年时间对唐人的研究,最终使本已残破的原壁画重绽光辉。
类似这样的“整理临摹”“复原临摹”等研究性临摹实践,在“客观临摹”的基础上,进一步凸显了当代研究者对壁画的理解感悟。
然而,这些实践成果的应用却面临着传播困境。
传统临摹作品虽具备较高的学术性,但因数量少、临摹耗时长等因素,大多用于研究、保护、教学工作,很少以展览、研究成果的形式走出洞窟,走向大众。
此时,数字技术的合理介入是满足公众诉求的必由之路,也是让静默千年的文化遗产“活”起来的必然要求。
数字复制、VR技术、3D动画复原演示、线上展览、配套互动游戏等高科技,为盘活传统壁画这个超级IP提供了无限可能,也为壁画保护提供了新思路。
【附加15套高考模拟】“超级全能生”全国卷26省联考2020届高考数学(理)试题(甲卷)含答案
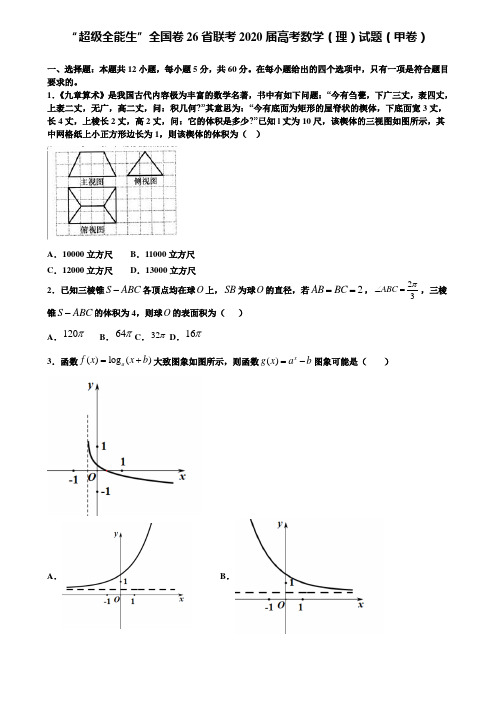
“超级全能生”全国卷26省联考2020届高考数学(理)试题(甲卷)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知l 丈为10尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为1,则该楔体的体积为( )A .10000立方尺B .11000立方尺C .12000立方尺D .13000立方尺2.已知三棱锥S ABC -各顶点均在球O 上,SB 为球O 的直径,若2AB BC ==,23ABC π∠=,三棱锥S ABC -的体积为4,则球O 的表面积为( ) A .120πB .64πC .32πD .16π3.函数()log ()a f x x b =+大致图象如图所示,则函数()x g x a b =-图象可能是( )A .B .C .D .4.已知函数()ln xf x x a =-,(0x >,01a <<)的两个零点为1x ,2x ,则( ) A .1201x x << B .121=x x C .121x x e<< D .12x x e>5.如图是一个射击靶的示意图,其中每个圆环的宽度与中心圆的半径相等.某人朝靶上任意射击一次没有脱靶,设其命中10,9,8,7环的概率分别为1P ,2P ,3P ,4P ,则下列选项正确的是( )A .12P P =B .123P P P +=C .40.5P = D .2432P P P +=6.已知双曲线C :22221(0,0)x y a b a b-=>>的左,右焦点分别为1F ,2F ,右顶点为A ,以A 为圆心,OA(O 为坐标原点)为半径的圆与双曲线C 在第一象限的交点为P ,若2PF PA ⊥,且122PF PF =,则双曲线C 的离心率为( ) A .15+ B .13+C .5D .37.某几何体的三视图如图所示,则该几何体的表面积为( )A .240B .220C .200D .260 8.若函数图象与函数的图象关于原点对称,则( )A .B .C .D .9.设锐角三角形ABC 的内角,,A B C 所对的边分别为,,a b c ,若2,2a B A ==,则b 的取值范围为( ) A .(0,4)B .(2,23)C .(22,3)D .(22,4)10.若81(1)2x ax x ⎫-⎪⎭展开式中含12x 项的系数为21,则实数a 的值为( ) A .3 B .-3 C .2 D .-211.将函数()2sin 2f x x =的图象向右平移ϕ02πϕ⎛⎫<<⎪⎝⎭个单位后得到函数()g x 的图象,若方程()()124f x g x -=的根1x ,2x 满足12min 6x x π-=,则ϕ的值是( )A .4πB .6πC .3πD .2π12.已知函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象过点3)B ,且在5(,)1212ππ上单调,把()f x 的图象向右平移π个单位之后与原来的图象重合,当1224,(,)33x x ππ∈且12x x ≠时,()()12f x f x =,则()12f x x +=( )A .3B 3C .1-D .1二、填空题:本题共4小题,每小题5分,共20分。
最新“超级全能生”全国卷26省联考届高考数学(理)试题(甲卷)及答案

“超级全能生”2016高考全国卷26省联考(甲卷)理科数学试卷一.选择题(本题共12小题,,每小题5分,共60分)1. 已知集合B ={1},C ={3},A B ={1,2},则()A 、AB =∅ B 、AC =∅ C 、A C ={1,2,3}D 、AC ={2,3}2. 若复数31z i =,22z i =+,则12z z =()A 、-1-2iB 、-1+2iC 、1+2iD 、1-2i 3. 掷一枚均匀的硬币4次,则出现正面的次数多于反面的次数的概率为() A 、12 B 、25 C 、516 D 、144. “0xy ≠”是“0x ≠”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 一个蜂巢里有1只蜜蜂,第一天它飞出去找回3个伙伴;第2天有4只蜜蜂飞出去各自找回了3个伙伴,...,如果这个找伙伴的过程继续下去,第6天所有的蜜蜂归巢后,蜂巢中一共有 只蜜蜂。
()A. 972B. 1456C. 4096D. 54606. 如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体表面积是()A. 80-2πB. 80C. 80+4πD. 80+6π 7. 对任意非零实数a,b,若的运算原理如图所示,则的值为()A.21+ B. 2 C.22 D. 212- 8. 下列函数中在3(,)44ππ上为减函数的是()A. tan y x =-B.cos(2)2y x π=--C. sin 2cos 2y x x =+D. 22cos 1y x =-9. 下列函数中满足121212()()()()22x x f x f x f x x ++<≠的是() A. ()f x ax b =+ B. ()f x x α= C. ()log (0,1)a f x x a a =>≠ D. 2()f x x ax b =++10. 双曲线22221(0,0)x y a b a b-=>>的一条渐近线的斜率为2,过右焦点F 作x 轴的垂线交双曲线与A,B 两点,△OAB (O 为坐标原点)的面积为45,则F 到一条渐近线的距离为() A. 3 B. 2 C. 5 D. 311. 半径为R 的球O 中有两个半径分别为23与22的截面圆,它们所在的平面互相垂直,且两圆的公共弦长为R ,则R= () A. 43 B. 5 C. 33 D. 4 12. 以下关于(0)x x ≥的不等式2ln(1)0x kx x ++-≥的结论中错误的是() .A.14k ∃≤,使不等式恒成立 B. 14k ∀≥,使不等式恒成立 C. 12k ∃≤,使不等式恒成立 D. 12k ∀≥,使不等式恒成立二、填空题(本题共4小题,每小题5分,共20分)13、等腰直角三角形的直角顶点位于原点,另外两个点在抛物线24y x =上,则这个等腰直角三角形的面积为14、若关于x 的不等式2x x mx -+>的解集为{}|10x x -<<,则二项式2016(1)mx +的展开式中的x 系数为15、等比数列{}n a 中,130,256,448,n n a a S T >==为数列{}n a 的前n 项乘积,则n T 当取得最大值时,n =16、已知向量(,),(1,1)a m n b ==,满足a b ≥2,且(2)0a a b -≤,则a b 的取值范围是 三、解答题(本题共6小题,共70分)17、(12分)△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若2sin sin 2sin()B C A C -=- (1)求cosA ;(2)若10,5a b c =+=,求△ABC 的面积。
超级全能生理综甲卷参考答案

“超级全能生”26省联考(甲卷)理科综合生物参考答案及评分标准一、选择题1.C2.B3.D4.A5.B6.C二、非选择题(一)必考题29. (9分)(1)DNA复制(1分)和蛋白质合成(1分)(或者答出“染色体复制”给2分)(2)b~c(或bc)(2分)c~d(或cd)(2分)(3)处于A峰值的细胞有三部分:停止分裂的细胞,在细胞周期中处于DNA复制前的细胞,刚形成的子细胞(3分,答对其中一点给1分,其他合理答案也得分)30.(10分)(1)信使RNA(或mRNA)(2分)翻译(2分)(2)苏氨酸和组氨酸(2分)ACA和CAC(2分)(说明:前后两空的氨基酸和密码子都能对应上得4分,不能对应的只能得第1空的分值)(3)因为3组和4组的核苷酸序列中含有终止密码(2分)31.(9分)(1)一(1分)符合(1分)(2)AABb、AaBb、AaBB、aaBb(每、写对一个得1分,共4分)(3)黄色:白色=1:1(3分)32.(11分)(1)水平(2分)属于(2分)(2)农作物、果树、河流中的绿色植物、其他野生的绿色植物(2分,答对2个以上给2分,只答一个给1分,其他合理答案也给分)(3)群落演替,属于次生演替(2分,只答次生演替给2分,只答群落演替给1分,)(4)(3分,只要符合图中所示生物的碳循环给分)(二)选考题39. (15分)(1)有氧或无氧(2分,只答有氧或无氧不得分)不需要(1分)(2)②灭菌(2分)稀释涂布(2分)重复试验可以减少误差(2分,其他合理答案得分)④5×109(2分)(3)后者计数比较大(2分,或前者计数比较小)菌落只是活酵母的数量,血球板计数是死活酵母菌都有(2分)40.(15分)(1)注射抗原(2分,答接种抗原或合理答案可得分)聚乙二醇(2分,或灭活病毒,其他合理答案均可)(2)抗体(2分)(3)小鼠抗体基因的识别抗原的区域人抗体基因的非抗原识别区域(每空2分,共4分,这两空的内容可以调换,文字必须合理可得分)限制性内切酶和DNA连接酶(2分,只答一个得1分)(4)目的基因(1分)将表达载体导入大肠杆菌,通过培养大肠杆菌来进行扩增(2分,可以答导入其他细菌或酵母菌,答PCR技术不能得分)化学参考答案及评分标准一、选择题7.A 8.B 9.C 10.A 11.B 12.C 13.D二、非选择题(一)必考题26.(14分,除标明分值外,其余每空均为2分。
2024届超级全能生24省高三上学期1月高考全国卷联考物理试题(甲)

2024届超级全能生24省高三上学期1月高考全国卷联考物理试题(甲)一、单选题:本题共7小题,每小题4分,共28分 (共7题)第(1)题如图所示,A、B、C三点把等量异种点电荷P、Q的连线平均分成了四份,过C点作两点电荷连线的垂线CD,有。
把另一个带正电的点电荷M沿连线由A点移动至C点,再沿垂线由C点移动至D点,移动过程中点电荷M的速率不变。
不考虑点电荷M对空间电场的影响,下列说法正确的是()A.B、D两点的电场强度大小为B.移动过程中点电荷M所受电场力先减小后增大C.移动过程中电场力对点电荷M先做正功后做负功再做正功D.移动过程中点电荷M的电势能先减小后增大第(2)题小滑块以一定的初速度沿粗糙斜面从底端C点上滑,到达最高点B后返回到底端。
利用频闪仪分别对上滑和下滑过程进行拍摄,频闪照片示意图如图所示,两图中最上端和最下端的滑块均为刚好运动到B、C两点时被拍摄到,A点为B、C间的一点。
若滑块与斜面间动摩擦因数处处相同,不计空气阻力。
关于图甲与图乙中滑块在A、B两点间( )A.摩擦力做功之比为1:1B.加速度大小之比为4:3C.运动时间之比为4:3D.过A点时的速度之比为4:3第(3)题如图所示,从我国空间站伸出的长为d的机械臂外端安置一微型卫星,微型卫星和空间站能与地心保持在同一直线上绕地球做匀速圆周运动。
已知地球半径为R,空间站的轨道半径为r,地球表面重力加速度为g。
忽略空间站对卫星的引力以及空间站的尺寸,则( )A.微型卫星的角速度比空间站的角速度要小B.微型卫星的线速度与空间站的线速度相等C.空间站所在轨道处的加速度与g之比为D.机械臂对微型卫星一定无作用力第(4)题某同学利用电压传感器来研究电感线圈工作时的特点。
图甲中三个灯泡完全相同,不考虑温度对灯泡电阻的影响。
在闭合开关S的同时开始采集数据,当电路达到稳定状态后断开开关。
图乙是由传感器得到的电压u随时间t变化的图像。
不计电源内阻及电感线圈L的电阻。
超级全能生甲卷语文

“超级全能生”26省联考(甲卷)语文参考答案及评分标准1. B。
不是“被强行纳入西学框架体系后,被解构、割裂”,而是并列关系,“或者被强行纳入西学框架体系,或者被解构”。
2. D。
A项“尽管这并不公平”错,原文并没有说科举制度不公平;B项利玛窦并不是在给欧洲人的信件中赞叹中国制度;C项“并没有任何作用”过于绝对。
3. D。
A项强加因果;B项“成为理论武器的是“平等的‘中国精神’”,不是科举制度;C 项法国和英国形成清新中国文明的潮流,并不是由于科举制度的影响。
4. B。
5. B。
六部中的民部,应为户部。
6. A。
原文并没有说李辅国推荐元载,只是在代宗面前称赞。
7(1)元载以为自己有清除恶人的功绩,贬低前贤,认为文才武略没有比得上他的。
(2)上封人李少良秘密将元载的丑恶行迹奏上朝廷,元载知道后,面奏代宗,将李少良等数人全都在朝廷打死。
译文:元载是凤翔岐山人,家境本来寒微。
元载自幼嗜好学习,喜欢写文章,性情敏捷聪慧,博览子部、史部书籍。
肃宗即位后,急于处置军务,命诸道采访使量才提拔属官。
元载升任洪州刺史。
两京收复,入朝任度支郎中。
元载智慧聪明有悟性,善于奏事对答。
肃宗嘉许他,把有关国计民生的事务委任他办理,让他充任使节赴江淮,总领漕运职务,不久加官御史中丞。
元载与幸臣李辅国亲善。
于是李辅国让元载兼京兆尹。
元载意在宰相,面见李辅国恳切要辞去京兆尹。
李辅国看出他的意愿,同意了。
第二天,拜元载同中书门下平章事。
十天后,肃宗病故,代宗即位。
李辅国权势更重,在皇上面前称赞元载。
元载能够探察皇上意图,因此很受恩宠,升任中书侍郎、同中书门下平章事,加集贤殿大学士,修国史。
李辅国死,元载又交结内侍董秀,多给他金帛,让暗自传达赛旨。
因此皇上有所关注,元载必先知道。
顺承意愿、探究微义,言谈中必定暗合,代宗因此更信任他。
内侍鱼朝恩依仗权势、自负恩宠,不与元载合作。
元载常常怕他。
大历四年冬,元载趁机密奏鱼朝恩专权,行为不轨,请将他除掉。
2024届超级全能生24省高三上学期1月高考全国卷联考全真演练物理试题(甲)

2024届超级全能生24省高三上学期1月高考全国卷联考全真演练物理试题(甲)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题目前,世界上正在研究一种新型发电机叫磁流体发电机,立体图如图甲所示,侧视图如图乙所示,其工作原理是燃烧室在高温下将气体全部电离为电子与正离子,即高温等离子体,高温等离子体经喷管提速后以速度进入矩形发电通道,发电通道有垂直于喷射方向的匀强磁场(图乙中垂直纸面向里),磁感应强度大小,等离子体在发电通道内发生偏转,这时两金属薄板上就会聚集电荷,形成电势差。
已知发电通道从左向右看长,宽,高,等离子体的电阻率,电子的电荷量。
不计电子和离子的重力以及微粒间的相互作用,则以下判断正确的是( )A.发电机的电动势为2500VB.若电流表示数为16A,则1s内打在下极板的电子有1010个C.当外接电阻为12Ω时,电流表的示数为5AD.当外接电阻为8Ω时,发电机输出功率最大第(2)题在超导托卡马克实验装置中,质量为m1的与质量为m2的发生核聚变反应,生成质量为m3的新核,同时放出质量为m4的X,若已知真空中的光速为c,下列说法正确的是( )A.该反应属于a衰变B.该反应释放的核能为(m1+m2-m3-m4)c2C.X为电子,最早由查德威克通过实验发现的D.该核反应是目前利用核能的主要方式第(3)题如图,潜艇从海水的高密度区驶入低密度区过程称为“掉深”。
图a,某潜艇在高密度区水平向右匀速航行;t=0时,该捞艇开始“掉深”,图b为其竖直方向的速度时间图像,水平速度v保持不变。
若以水平向右为x轴,竖直向下为y轴,则带艇“掉深”后的0~30s内。
能大致表示其运动轨迹的图形是( )A.B.C.D.第(4)题如图所示,一绝缘容器内部为长方体空腔,容器内盛有NaCl的水溶液,容器上下端装有铂电极A和C,置于与容器表面垂直的匀强磁场中,开关K闭合前容器两侧P、Q两管中液面等高,闭合开关后( )A.M处钠离子浓度等于N处钠离子浓度B.M处钠离子浓度小于N处钠离子浓度C.M处电势高于N处电势D.P管中液面高于Q管中液面第(5)题一艘摩托艇在水中沿直线匀速行驶,发动机的输出功率为P,摩托艇的速度为v,将摩托艇的输出功率增大为2P,此后摩托艇的最大速度为。
高考数学高三模拟试卷试题压轴押题 “超级全能生”高考全国卷26省联考甲卷文科数学试卷

高考数学高三模拟试卷试题压轴押题 “超级全能生”高考全国卷26省联考(甲卷)文科数学试卷一.选择题(本题共12小题,,每小题5分,共60分) 1. 已知集合B ={1},A B ={1,2},则A =()A 、∅B 、{2}C 、{1,2}D 、A C ={2}或{1,2} 2. 若复数1z i =-,22z i =+,则12z z =()A 、-1-2iB 、-1+2iC 、1+2iD 、1-2i 3. 掷一枚均匀的硬币4次,则出现“3次正面朝上,1次反面朝上”的概率为()A 、15B 、14C 、13D 、124. “0xy =”是“0y =”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 一个蜂巢里有1只蜜蜂,第一天它飞出去找回3个伙伴;第2天有4只蜜蜂飞出去各自找回了3个伙伴,...,如果这个找伙伴的过程继续下去,第6天所有的蜜蜂归巢后,蜂巢中一共有 只蜜蜂。
()A. 972B. 1456C. 4096D. 5460 6. 如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体表面积是()A. 80-2πB. 80C. 80+4πD. 80+6π 7. 对任意非零实数a,b,若的运算原理如图所示,则的值为() A.21+ B. 2 C.22 D. 212- 8. 下列函数中在3(,)44ππ上为减函数的是()A. tan y x =-B.cos(2)2y x π=--C. sin 2cos 2y x x =+D. 22cos 1y x =- 9. 下列函数中满足121212()()()()22x x f x f x f x x ++<≠的是()A. ()32f x x =+B. ()f x x =C. 1()()2x f x =- D. 2()1f x x x =++10. 双曲线22221(0,0)x y a b a b-=>>为等轴双曲线,过右焦点F 作x 轴的垂线交双曲线与A,B 两点,若|AB |=22,△OAB (O 为坐标原点)的面积为() A. 22 B. 23 C. 42 D. 4311. 半径为R 的球O 中有两个半径分别为23与22的截面圆,它们所在的平面互相垂直,且两圆的公共弦长为R ,则R=()A. 43B. 5C. 33D. 412. 以下关于(0)x x ≥的不等式2ln(1)0x kx x ++-≥的结论中错误的是(). A.14k ∃≤,使不等式恒成立 B. 14k ∀≥,使不等式恒成立 C. 12k ∃≤,使不等式恒成立D. 12k ∀≥,使不等式恒成立二、填空题(本题共4小题,每小题5分,共20分) 13、等腰直角三角形的直角顶点位于原点,另外两个点在抛物线24y x =上,则这个等腰直角三角形的面积为14、若关于x 的不等式2x x mx -+>的解集为{}|10x x -<<,且函数2()()f x x x m =-在x n =处有极小值,则n =15、等比数列{}n a 中,130,256,448,n n a a S T >==为数列{}n a 的前n 项乘积,则17T = 16、已知向量(,)(0,0),(2,3),(3,2)a m n m n b c =≥≥=-=-,满足a b ≥-3,且3a c ≤,则||a 的最大值为三、解答题(本题共6小题,共70分)17、(12分)△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若2sin sin 2sin()B C A C -=-(1)求cosA ;(2)若10,5a b c =+=,求△ABC 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“超级全能生”2016高考全国卷26省联考(甲卷)
文科数学试卷
一.选择题(本题共12小题,,每小题5分,共60分)
1.已知集合B ={1},A B U ={1,2},则A =()
A 、∅
B 、{2}
C 、{1,2}
D 、A C U ={2}或{1,2} 2.若复数1z i =-,22z i =+,则12z z =()
A 、-1-2i
B 、-1+2i
C 、1+2i
D 、1-2i 3.掷一枚均匀的硬币4次,则出现“3次正面朝上,1次反面朝上”的概率为()
A 、15
B 、14
C 、13
D 、12
4.“0xy =”是“0y =”的()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
5.一个蜂巢里有1只蜜蜂,第一天它飞出去找回3个伙伴;第2天有4只蜜蜂飞出去各自找回了3个伙伴,...,如果这个找伙伴的过程继续下去,第6天所有的蜜蜂归巢后,蜂巢中一共有
只蜜蜂。
()
A.972
B.1456
C.4096
D.5460
6.如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体表面积是()
A.80-2π
B.80
C.80+4π
D.80+6π 7.对任意非零实数a,b,若的运算原理如图所示,则
的值为()
A.
21
2
+ B.2 C.
22 D.212
- 8.下列函数中在3(,)44
ππ
上为减函数的是()
A.tan y x =-
B.cos(2)2y x π
=--
C.sin 2cos 2y x x =+
D.22cos 1y x =- 9.下列函数中满足121212()()
(
)()22
x x f x f x f x x ++<≠的是() A.()32f x x =+ B.()f x x =
C.1
()()2
x f x =- D.2()1f x x x =++
10.双曲线22
221(0,0)x y a b a b -=>>为等轴双曲线,过右焦点F 作x 轴的垂线交双曲线与A,B 两
点,若|AB |=22,△OAB (O 为坐标原点)的面积为()
A.22
B.23
C.42
D.43
11.半径为R 的球O 中有两个半径分别为23与22的截面圆,它们所在的平面互相垂直,且两圆的公共弦长为R ,则R=()
A.43
B.5
C.33
D.4
12.以下关于(0)x x ≥的不等式2ln(1)0x kx x ++-≥的结论中错误的是() .
A.14k ∃≤
,使不等式恒成立B.1
4
k ∀≥,使不等式恒成立
C.12k ∃≤
,使不等式恒成立D.1
2
k ∀≥,使不等式恒成立 二、填空题(本题共4小题,每小题5分,共20分)
13、等腰直角三角形的直角顶点位于原点,另外两个点在抛物线24y x =上,则这个等腰直角三角形的面积为
14、若关于x 的不等式2x x mx -+>的解集为{}|10x x -<<,且函数2()()f x x x m =-在x n =处有极小值,则n =
15、等比数列{}n a 中,130,256,448,n n a a S T >==为数列{}n a 的前n 项乘积,则17T =
16、已知向量(,)(0,0),(2,3),(3,2)a m n m n b c =≥≥=-=-r r r ,满足a b ≥r r g
-3,且3a c ≤r r g ,则||a r
的最大值为
三、解答题(本题共6小题,共70分)
17、(12分)△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若2sin sin 2sin()B C A C -=- (1)求cosA ;
(2)若10,5a b c =+=,求△ABC 的面积。
18.(12分)某毕业班统计全班40名学生报名参加学科竞赛和报名参加自主招生的数据如下:
(1)从该班随机选1名同学,求该同学仅报名参加其中一项的概率;
(2)从报名参加自主招生的同学中任取2人,求恰好1人两项都报名的概率.
19.(12分)已知三棱柱ABC —A 1B 1C 1,侧棱AA 1垂直于底面ABC ,∠2
ABC π
=,AB=BC=AA 1=4,D 为
BC 的中点.
(1)若E 为棱CC 1的中点,求证:DE ⊥A 1C
(2)若E 为棱CC 1上异于端点的任意一点,当三棱锥C 1-ADE 的体积为8
3
时,求异面直线DE
与AC 1所成角的余弦值.
20.(12分)已知直线l :y=x+1,圆O :223
2
x y +=
直线l 被圆截得的弦长与椭圆C :2222
1(0)x y a b a b +=>>的短轴长相等,椭圆的离心率e =2
(1)求椭圆C 的方程;
(2)过点M(0,-1
3
)的直线l 0交椭圆于A,B 两点,试问,在坐标平面上是否存在一个定点T,
使得无论l 0如何旋转,以AB 为直径的圆恒过定点T?若存在,求出T 的坐标;若不存在,请说明理由
21.(12分)已知函数1
()ln 1f x x x
=+-。
(1)求函数的单调性;
(2)证明:2ln[234(1)](*)2n n
n n N +⋅⋅⋅+<∈g
g g g
22.(10分)选修4-1:几何证明题选讲
如图所示,AB 为圆O 的直径,BC ,CD 为圆O 的切线,B 、D 为切点。
(1)求证:AD //OC
(2)若圆的半径为1,求AD ·OC 的值
23.(10分)选修4-4:坐标系与参数方程
已知A ,B(不与原点O 重合)分别在圆221:(2)4C x y -+=与圆222:(1)1C x y -+=上, 且OA ⊥OB.
(1)若以原点为极点,x 轴的正半轴为极轴建立极坐标系,当A 的极角为3
π
时,求A,B 的极坐标;
(2)求||||OA OB g 的最大值
24.(10分)选修4-4:不等式选讲
如果关于x 的不等式|3||4|||x x a -+-≤的解集为空集 (1)求实数a 的取值范围;
(2)若实数b 与实数a 取值范围完全相同,求证:|1|||ab a b ->-
超级全能生2016届高考全国卷26省联考(甲卷)
数学文 参考答案
1-5:DABBC 6-10:CCBDA 11-12:DB 13、16 14、2 15、1
16、 17、
18、
(2)设报名参加自主招生的同学中任取2人,恰好1人两项都报名的事件为B,设参加两项的2名同学分别为a,b,仅参加自主招生的4名同学分别为c,d,e,f..............(6分)
从报名参加自主招生的同学中任取2人有:
19、
20、
21、
22、
23、
24、。
