计量经济学案例分析一元回归模型实例分析
计量经济学实验一 一元回归模型
实验二一元回归模型【实验目的】掌握一元线性、非线性回归模型的建模方法【实验内容】建立我国税收预测模型【实验步骤】【例1】建立我国税收预测模型。
表1列出了我国1985-1998年间税收收入Y和国内生产总值(GDP)x的时间序列数据,请利用统计软件Eviews建立一元线性回归模型。
一、建立工作文件⒈菜单方式在录入和分析数据之前,应先创建一个工作文件(Workfile)。
启动Eviews软件之后,在主菜单上依次点击File\New\Workfile(菜单选择方式如图1所示),将弹出一个对话框(如图2所示)。
用户可以选择数据的时间频率(Frequency)、起始期和终止期。
图1 Eviews菜单方式创建工作文件示意图图2 工作文件定义对话框本例中选择时间频率为Annual(年度数据),在起始栏和终止栏分别输入相应的日期85和98。
然后点击OK,在Eviews软件的主显示窗口将显示相应的工作文件窗口(如图3所示)。
图3 Eviews工作文件窗口一个新建的工作文件窗口内只有2个对象(Object),分别为c(系数向量)和resid(残差)。
它们当前的取值分别是0和NA(空值)。
可以通过鼠标左键双击对象名打开该对象查看其数据,也可以用相同的方法查看工作文件窗口中其它对象的数值。
⒉命令方式还可以用输入命令的方式建立工作文件。
在Eviews软件的命令窗口中直接键入CREATE命令,其格式为:CREATE 时间频率类型起始期终止期本例应为:CREATE A 85 98二、输入数据在Eviews软件的命令窗口中键入数据输入/编辑命令:DA TA Y X此时将显示一个数组窗口(如图4所示),即可以输入每个变量的数值图4 Eviews数组窗口三、图形分析借助图形分析可以直观地观察经济变量的变动规律和相关关系,以便合理地确定模型的数学形式。
⒈趋势图分析命令格式:PLOT 变量1 变量2 ……变量K作用:⑴分析经济变量的发展变化趋势⑵观察是否存在异常值本例为:PLOT Y X⒉相关图分析命令格式:SCAT 变量1 变量2作用:⑴观察变量之间的相关程度⑵观察变量之间的相关类型,即为线性相关还是曲线相关,曲线相关时大致是哪种类型的曲线说明:⑴SCAT命令中,第一个变量为横轴变量,一般取为解释变量;第二个变量为纵轴变量,一般取为被解释变量⑵SCAT命令每次只能显示两个变量之间的相关图,若模型中含有多个解释变量,可以逐个进行分析⑶通过改变图形的类型,可以将趋势图转变为相关图本例为:SCA T Y X图5 税收与GDP趋势图图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。
《计量经济学》eviews实验报告一元线性回归模型详解

计量经济学》实验报告一元线性回归模型-、实验内容(一)eviews基本操作(二)1、利用EViews软件进行如下操作:(1)EViews软件的启动(2)数据的输入、编辑(3)图形分析与描述统计分析(4)数据文件的存贮、调用2、查找2000-2014年涉及主要数据建立中国消费函数模型中国国民收入与居民消费水平:表1年份X(GDP)Y(社会消费品总量)200099776.339105.72001110270.443055.42002121002.048135.92003136564.652516.32004160714.459501.02005185895.868352.62006217656.679145.22007268019.493571.62008316751.7114830.12009345629.2132678.42010408903.0156998.42011484123.5183918.62012534123.0210307.02013588018.8242842.82014635910.0271896.1数据来源:二、实验目的1.掌握eviews的基本操作。
2.掌握一元线性回归模型的基本理论,一元线性回归模型的建立、估计、检验及预测的方法,以及相应的EViews软件操作方法。
三、实验步骤(简要写明实验步骤)1、数据的输入、编辑2、图形分析与描述统计分析3、数据文件的存贮、调用4、一元线性回归的过程点击view中的Graph-scatter-中的第三个获得在上方输入Isycx回车得到下图DependsntVariable:Y Method:LeastSquares□ate:03;27/16Time:20:18 Sample:20002014 Includedobservations:15VariableCoefficientStd.Errort-StatisticProb.C-3J73.7023i820.535-2.1917610.0472X0416716 0.0107S838.73S44 a.ooao R-squared0.991410 Meandependentwar119790.2 AdjustedR.-squared 0.990750 S.D.dependentrar 7692177 S.E.ofregression 7J98.292 Akaike infocriterion20.77945 Sumsquaredresid 7;12E^-08 Scliwarz 匚「爬伽20.37386 Loglikelihood -1&3.3459Hannan-Quinncriter. 20.77845 F-statistic 1I3&0-435 Durbin-Watsonstat0.477498Prob(F-statistic)a.oooooo在上图中view 处点击view-中的actual ,Fitted ,Residual 中的第一 个得到回归残差打开Resid 中的view-descriptivestatistics 得到残差直方图/icw Proc Qtjject PrintN^me FreezeEstimateForecastStatsResids凹Group:UNIIILtD Worktile:UN III LtLJ::Unti1DependentVariablesMethod;LeastSquares□ate:03?27/16Time:20:27Sample(adjusted):20002014Includedobservations:15afteradjustmentsVariable Coefficient Std.Errort-Statistic ProtJ.C-3373.7023^20.535-2.191761 0.0472X0.4167160.01075S38.735440.0000R-squared0.991410 Meandependeniwar1-19790.3 AdjustedR-squa.red0990750S.D.dependentvar 76921.77 SE.ofregre.ssion 7J98.292 Akaike infacriterion20.77945 Sumsquaredresid 7.12&-0S Schwarzcriterion 20.S73S6 Laglikelihood -153.84&9Hannan-Quinncrite匚20.77545 F-statistic1I3&0.435Durbin-Watsonstat 0.477498 ProbCF-statistic) a.ooaooo在回归方程中有Forecast,残差立为yfse,点击ok后自动得到下图roreestYFM J訓YForea空巾取且:20002015 AdjustedSErmpfe:2000231i mskJddd obaerratire:15Roof kter squa red Error理l%2Mean/^oLteError畐惯啟iJean Afe.PereersErro r5.451SSQThenhe鼻BI附GKWCE口.他腐4Prop&niwi□ooooooVactaree Propor^tori0.001^24G M『倚■底Props^lori09®475在上方空白处输入lsycs…之后点击proc中的forcase根据公式Y。
最新计量经济学案例分析一元回归模型实例分析

案例分析1— 一元回归模型实例分析依据1996-2005年《中国统计年鉴》提供的资料,经过整理,获得以下农村居民人均消费支出和人均纯收入的数据如表2-5:表2-5 农村居民1995-2004人均消费支出和人均纯收入数据资料 单位:元 年度 1995199619971998199920002001200220032004人均纯收入1577.7 1926.1 2090.1 2161.1 2210.3 2253.4 2366.4 2475.6 2622.2 2936.4人均消费支出1310.4 1572.1 1617.2 1590.3 1577.4 1670.1 1741.1 1834.3 1943.3 2184.7一、建立模型以农村居民人均纯收入为解释变量X ,农村居民人均消费支出为被解释变量Y ,分析Y 随X 的变化而变化的因果关系。
考察样本数据的分布并结合有关经济理论,建立一元线性回归模型如下:Y i =β0+β1X i +μi根据表2-5编制计算各参数的基础数据计算表。
求得:082.1704035.2262==Y X∑∑∑∑====3752432495.1986.788859011.516634423.1264471222ii i i iX y x y x 根据以上基础数据求得:623865.0423.126447986.788859ˆ21===∑∑iii xyx β8775.292035.2262623865.0082.1704ˆˆ10=⨯-=-=X Y ββ 样本回归函数为:ii X Y 623865.08775.292ˆ+= 上式表明,中国农村居民家庭人均可支配收入若是增加100元,居民们将会拿出其中的62.39元用于消费。
二、模型检验1.拟合优度检验952594.0011.516634423.1264471986.788859))(()(22222=⨯==∑∑∑iii i yx y x r2.t 检验525164.3061 210423.12644710.623865011.166345 2ˆˆ222122=-⨯-=--=∑∑n x y iiβσ049206.0423.1264471525164.3061ˆ)ˆ()ˆ(2211====∑ie xVar S σββ6717.112525164.3061423.126447110137.52432495ˆ)ˆ()ˆ(22200=⨯===∑∑σββii e xn X Var S 在显著性水平α=0.05,n-2=8时,查t 分布表,得到:306.2)2(2=-n t α提出假设,原假设H 0:β1=0,备择假设H 1:β1≠067864.12049206.0623865.0)ˆ(ˆ)ˆ(111==-=ββββe S t)2(67864.12)ˆ(21->=n t t αβ,差异显著,拒绝β1=0的假设。
一元线性回归模型案例分析

一元线性回归模型案例分析一元线性回归是最基本的回归分析方法,它的主要目的是寻找一个函数能够描述因变量对于自变量的依赖关系。
在一元线性回归中,我们假定存在满足线性关系的自变量与因变量之间的函数关系,即因变量y与单个自变量x之间存在着线性关系,可表达为:y=β0+ β1x (1)其中,β0和β1分别为常量,也称为回归系数,它们是要由样本数据来拟合出来的。
因此,一元线性回归的主要任务就是求出最优回归系数和平方和最小平方根函数,从而评价模型的合理性。
下面我们来介绍如何使用一元线性回归模型进行案例分析。
数据收集:首先,研究者需要收集自变量和因变量之间关系的相关数据。
这些数据应该有足够多的样本观测值,以使统计分析结果具有足够的统计力量,表示研究者所研究的关系的强度。
此外,这些数据的收集方法也需要正确严格,以避免因相关数据缺乏准确性而影响到结果的准确性。
模型构建:其次,研究者需要利用所收集的数据来构建一元线性回归模型。
即建立公式(1),求出最优回归系数β0和β1,即最小二乘法拟合出模型方程式。
模型验证:接下来,研究者需要对所构建的一元线性回归模型进行验证,以确定模型精度及其包含的统计意义。
可以使用F检验和t检验,以检验回归系数β0和β1是否具有统计显著性。
另外,研究者还可以利用R2等有效的拟合检验统计指标来衡量模型精度,从而对模型的拟合水平进行评价,从而使研究者能够准确无误地判断其研究的相关系数的统计显著性及包含的统计意义。
另外,研究者还可以利用偏回归方差分析(PRF),这是一种多元线性回归分析技术,用于计算每一个自变量对相应因变量的贡献率,使研究者能够对拟合模型中每一个自变量的影响程度进行详细的分析。
模型应用:最后,研究者可以利用一元线性回归模型进行应用,以实现实际问题的求解以及数据挖掘等功能。
例如我们可以使用这一模型来预测某一物品价格及销量、研究公司收益及投资、检测影响某一地区经济发展的因素等。
综上所述,一元线性回归是一种利用单变量因变量之间存在着线性关系来拟合出回归系数的回归分析方法,它可以应用于许多不同的问题,是一种非常实用的有效的统计分析方法。
一元线性回归模型典型例题分析

第二章 一元线性回归模型典型例题分析例1、令kids 表示一名妇女生育孩子的数目,educ 表示该妇女接受过教育的年数.生育率对教育年数的简单回归模型为μββ++=educ kids 10(1)随机扰动项μ包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释.例2.已知回归模型μβα++=N E ,式中E 为某类公司一名新员工的起始薪金(元),N 为所受教育水平(年).随机扰动项μ的分布未知,其他所有假设都满足。
如果被解释变量新员工起始薪金的计量单位由元改为100元,估计的截距项与斜率项有无变化?如果解释变量所受教育水平的度量单位由年改为月,估计的截距项与斜率项有无变化?例3.对于人均存款与人均收入之间的关系式t t t Y S μβα++=使用美国36年的年度数据得如下估计模型,括号内为标准差:)011.0()105.151(067.0105.384ˆtt Y S +=2R =0.538 023.199ˆ=σ(1)β的经济解释是什么?(2)α和β的符号是什么?为什么?实际的符号与你的直觉一致吗?如果有冲突的话,你可以给出可能的原因吗?(3)对于拟合优度你有什么看法吗? (4)检验统计值?例4.下列方程哪些是正确的?哪些是错误的?为什么?⑴ y x t n t t =+=αβ12,,, ⑵ y x t n t t t =++=αβμ12,,,⑶ y x t n t t t=++= ,,,αβμ12⑷ ,,,y x t n t t t =++=αβμ12 ⑸ y x t n t t =+= ,,,αβ12 ⑹ ,,,y x t n t t =+=αβ12⑺ y x t n t t t =++= ,,,αβμ12 ⑻ ,,,y x t n t tt =++=αβμ12其中带“^”者表示“估计值”.例5.对于过原点回归模型i i i u X Y +=1β ,试证明∑=∧221)(iu XVar σβ例6、对没有截距项的一元回归模型i i i X Y μβ+=1称之为过原点回归(regression through the origin )。
计量经济学第二章 一元线性回归模型(1)(肖)

10
2.在经济学中,经济学家要研究个人
消费支出与个人可支配收入的依赖关系。
这种分析有助于估计边际消费倾向,就是
可支配收入每增加一元引起消费支出的平
均变化。
11
3.在企业中,我们很想知道人们对企
业产品的需求与广告费开支的关系。这种
研究有助于估计出相对于广告费支出的需
求弹性,即广告费支出每变化百分之一的
(2.3)
想想:结合表2.1的资料 ,怎样理解式(2.3)
变量Y 的原因, 给定变量X 的值也不能具
体确定变量Y的值, 而只能确定变量Y 的
统计特征,通常称变量X 与Y 之间的这种
关系为统计关系。
16
例如,企业总产出Y 与企业的资本投入
K 、劳动力投入L 之间的关系就是统计关 系。虽然资本K 和劳动力L 是影响产出Y 的两大核心要素,但是给定K 、L 的值并 不能确定产出Y 的值。因为,总产出Y 除 了受资本投入K、劳动力投入L 的影响外
在进入正式的回归理论之前,先斟酌一下变量y与变 量x可以互换的不同名称、术语。 Y 因变量 X 自变量
被解释变量 响应变量
被预测变量
解释变量 控制变量
预测变量
回归子
归回元
22
第二节
一、引例
一元线性回归模型
假定我们要研究一个局部区域的居 民消费问题,该区域共有80户家庭组成 ,将这80户家庭视为一个统计总体。
32
函数f (Xi)采取什么函数形式,是一个
需要解决的重要问题。在实际经济系统
中,我们不会得到总体的全部数据,因
而就无法据已知数据确定总体回归函数 的函数形式。同时,对总体回归函数的 形式只能据经济理论与经验去推断。
计量经济学一元回归实验报告
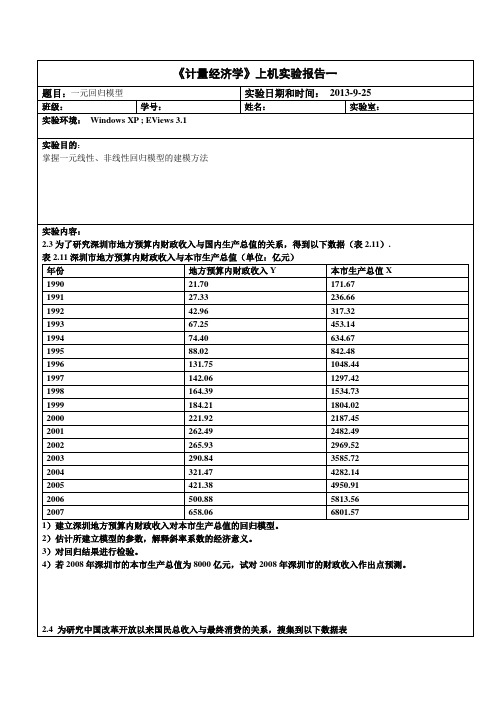
年份国民总收入X 最终消费Y 年份国民总收入X 最终消费Y1978 3645.217 2239.1 1993 35260.02 21899.91979 4062.579 2633.7 1994 48108.46 29242.21980 4545.624 3007.9 1995 59810.53 36748.21981 4889.461 3361.5 1996 70142.49 43919.51982 5330.451 3714.8 1997 78060.83 48140.61983 5985.552 4126.4 1998 83024.28 51588.21984 7243.752 4846.3 1999 88479.15 55636.91985 9040.737 5986.3 2000 98000.45 615161986 10247.38 6821.8 2001 108068.2 66878.31987 12050.62 7804.6 2002 119095.7 71691.21988 15036.82 9839.5 2003 135174 77449.51989 17000.92 11164.2 2004 159586.7 87032.91990 18718.32 12090.5 2005 184088.6 97822.71991 21826.2 14091.9 2006 213131.7 110595.31992 26937.28 17203.3 2007 251483.2 128444.61以分析国民总收入对消费的推动作用为目的建立线性回归方程,并估计参数2.计算回归估计的标准误差和可决系数3.对回归系数进行显著水平为5%的显著性检验4.如果2008年全国国民总收入为300670亿元,比上年增长9.0%,预测可能达到的最终消费水平。
实验步骤:(1)建立回归模型,应用EViews文件,由深圳市地方预算内财政收入(Y)和GDP的数据表,得散点图(如图1-1)。
计量经济学实验二-一元线性回归模型的估计、检验和预测

目录一、加载工作文件 (7)二、选择方程 (7)1.作散点图 (7)2.进行因果关系检验 (9)三、一元线性回归 (10)四、经济检验 (12)五、统计检验 (13)六、回归结果的报告 (15)七、得到解释变量的值 (15)八、预测应变量的值 (17)实验二一元线形回归模型的估计、检验和预测实验目的:掌握一元线性回归模型的估计、检验和预测方法。
实验要求:选择方程进行一元线性回归,进行经济、拟合优度、参数显著性和方程显著性等检验,预测解释变量和应变量。
实验原理:普通最小二乘法,拟合优度的判定系数R2检验和参数显著性t检验等,计量经济学预测原理。
实验步骤:已知广东省宏观经济部分数据如表2-1所示,要根据这些数据研究和分析广东省宏观经济,建立宏观计量经济模型,从而进行经济预测、经济分析和政策评价。
实验二~实验十二主要都是用这些数据来完成一系列工作。
表2-1 广东省宏观经济数据续上表续上表一、加载工作文件广东省宏观经济数据已经制成工作文件存在盘中,命名为GD01.WF1,进入EViews后选择File/Open打开GD01.WF1。
二、选择方程根据广东数据(GD01.WF1)选择收入法国国内生产总值(GDPS)、财政收入(CS)、财政支出(CZ)和社会消费品零售额(SLC),分别把①CS作为应变量,GDPS作为解释变量;②CZ作为应变量,CS作为解释变量;③SLC作为应变量,GDPS作为解释变量进行一元线性回归分析。
1.作散点图从三个散点图(图2-1~图2~3)可以看出,三对变量都呈现线性关系。
图2-1 图2-2图2-3 2.进行因果关系检验从三个因果关系检验可以看出,GDPS是CS的因;CS不是CZ 的因;GDPS不是SLC的因。
但根据理论CS是CZ的因,GDPS是SLC的因,可能是由于指标设置问题。
所以还是把CS作为应变量,GDPS作为解释变量;CZ作为应变量,CS作为解释变量;SLC作为应变量,GDPD作为解释变量进行一元线性回归分析。
计量经济学实验一一元线性回归完成版
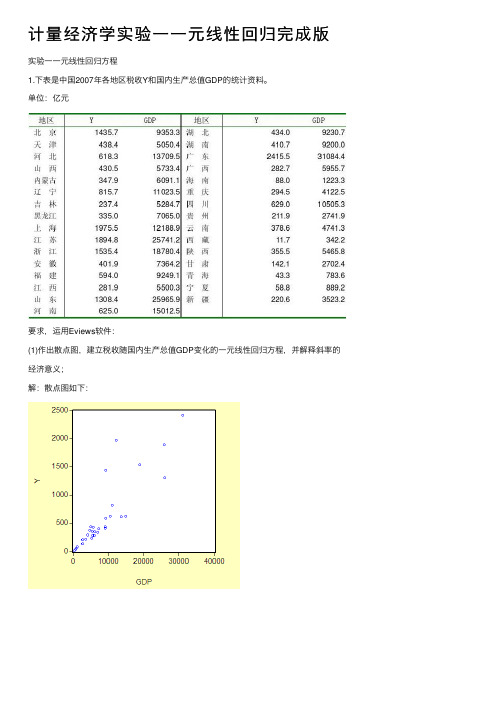
计量经济学实验⼀⼀元线性回归完成版实验⼀⼀元线性回归⽅程1.下表是中国2007年各地区税收Y和国内⽣产总值GDP的统计资料。
单位:亿元要求,运⽤Eviews软件:(1)作出散点图,建⽴税收随国内⽣产总值GDP变化的⼀元线性回归⽅程,并解释斜率的经济意义;解:散点图如下:得到估计⽅程为:0.07104710.62963=-y x这个估计结果表明,GDP 每增长1亿元,各地区税收将增加0.071047亿元。
(2) 对所建⽴的回归⽅程进⾏检验;解:从回归的估计的结果来看,模型拟合得较好。
可决系数20.7603R =,表明各地区税收变化的76.03%可由GDP 的变化来解释。
从斜率项的t 检验值看,⼤于5%显著性⽔平下⾃由度为229n -=的临界值0.025(29) 2.05t =,且该斜率满⾜0<0.071047<1,表明2007年,GDP 每增长1亿元,各地区税收将增加0.071047亿元。
(3) 若2008年某地区国内⽣产总值为8500亿元,求该地区税收收⼊的预测值及预测区间。
解:由上述回归⽅程可得地区税收收⼊的预测值:0.0710********.62963593.3Y =-= 下⾯给出税收收⼊95%置信度的预测区间:由于国内⽣产总值X 的样本均值与样本房差为()8891.126()57823134E X Var X ==于是,在95%的置信度下,0()E Y 的预测区间为593.3 2.045±593.3113.4761=±或(479.8239,706.7761)当GDP 为8500亿元时地区的税收收⼊的个值预测值仍为593.3。
同样的,在95%的置信度下,该地区的税收收⼊的预测区间为593.3 2.045593.3641.0421±=±或(-47.7,1234.3)。
资料来源:《深圳统计年鉴2002》,中国统计出版社解:(1)建⽴深圳地⽅预算内财政收⼊对GDP 的回归模型;得到回归⽅程:?0.134582 3.611151yx =-(2)估计所建⽴模型的参数,解释斜率系数的经济意义;X 的系数为0.314582,常数项为-3.611151。
一元线性回归模型案例

第二章一元线性回归模型案例一、中国居民人均消费模型从总体上考察中国居民收入与消费支出的关系。
表2.1给出了1990年不变价格测算的中国人均国内生产总值(GDPP)与以居民消费价格指数(1990年为100)所见的人均居民消费支出(CONSP)两组数据。
1) 建立模型,并分析结果。
输出结果为:对应的模型表达式为:201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出,拟合度较好,截距项和斜率项系数均通过了t 检验。
中国人均消费增加10000元,GDP 增加3862元。
二、线性回归模型估计表2.2给出黑龙江省伊春林区1999年16个林业局的年木材采伐量和相应伐木剩余物数据。
利用该数据(1)画散点图;(2)进行OLS 回归;(3)预测。
表2.2 年剩余物y 和年木材采伐量x 数据(1)画散点图先输入横轴变量名,再输入纵轴变量名得散点图(2)OLS估计弹出方程设定对话框得到输出结果如图:由输出结果可以看出,对应的回归表达式为:ˆ0.76290.4043t t yx =-+ (-0.625) (12.11)20.9129,146.7166, 1.48R F DW === (3)x=20条件下模型的样本外预测方法首先修改工作文件范围将工作文件范围从1—16改为1—17确定后将工作文件的范围改为包括17个观测值,然后修改样本范围将样本范围从1—16改为1—17打开x的数据文件,利用Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改为17—17,即只预测x=20时的y的值。
由上图可以知道,当x=20时,y的预测值是7.32,yf的分布标准差是2.145。
三、表2.3列出了中国1978—2000年的参政收入Y和国内生产总值GDP的统计资料。
做出散点图,建立财政收入随国内生产总值变化的一元线性回归方程。
实验3计量经济学实验一元线性回归模型

ˆ1 ~N(1,,
2
) (Xi X)2
三、知识点回顾
n 4、最小二乘估计量的性质及分布
随机干扰项 i 的方差 2 的估计 ˆ 0 和 ˆ 1 的方差表达式中都包含随机干扰项 i 的方差 2
,由于随机干扰项 i 实际上是无法观察测量的,因此其
量 Y 的平均值。
三、知识点回顾
1、四种重要的关系式
(2)总体回归函数(方程): E(YXi)01Xi
其中总体回归参数真值 0 , 1 是未知的;总体回归方程也是 未知的。
(3)样本回归函数(方程): Yˆi ˆ0 ˆ1Xi
在实际应用中,从总体中抽取一个样本,进行参数估计,从 而获得估计的回归方程,系数 ˆ 0 , ˆ1 为估计的回归系数;用 这个估计的回归方程近似替代总体回归方程,其中估计的回 归系数 ˆ 0 , ˆ1 是总体参数真值 0 , 1 的估计值;基于估计方程 计算的 Y ˆ i 就为 E (Y X i ) 的估计值; 由于我们从来就无法知道真实的回归方程,因此计量经济学 分析注重的是这个估计的回归方程和估计的回归系数;
据;普通最小二乘法给出的判断拟合程度的标准是:残差平
方和最小,即:m in Q ne i2n(Y i Y ˆi)2n Y i (ˆ0ˆ1 X i) 2
i 1
i 1
i 1
最小二乘法就是:在使上述残差平方和Q 达到最小时,确定
模型中的参数 ˆ 0 和 ˆ 1 的值,或者说在给定观测值之下,选
择出 ˆ 0 , ˆ1 的值,使残差平方和Q 达到最小。
接近,这也说明OLS估计值是非常有价值的。
三、知识点回顾
n 4、最小二乘估计量的性质及分布
一元线性回归模型案例

一元线性回归模型案例一元线性回归模型是统计学中最基本、应用最广泛的一种回归分析方法,可以用来探究自变量与因变量之间的线性关系。
一元线性回归模型的数学公式为:y = β0 + β1x,其中y表示因变量,x表示自变量,β0和β1分别为截距和斜率。
下面以一个实际案例来说明一元线性回归模型的应用。
假设我们有一组数据,其中x表示一个房屋的面积,y表示该房屋的售价,我们想利用一元线性回归模型来预测房屋的售价。
首先,我们需要收集一组已知数据,包括房屋的面积和售价。
假设我们收集了10个不同房屋的面积和售价数据,如下所示:房屋面积(x)(平方米)售价(y)(万元)80 12090 130100 140110 150120 160130 170140 180150 190160 200170 210我们可以根据这组数据绘制散点图,横坐标表示房屋面积x,纵坐标表示售价y,如下所示:(插入散点图)接下来,我们可以利用最小二乘法来拟合一条直线,使其能够最好地拟合这些散点。
最小二乘法是一种最小化误差平方和的方法,可以得到最优的拟合直线。
根据一元线性回归模型的公式,可以通过计算拟合直线的斜率β1和截距β0来实现最小二乘法。
其中,斜率β1可以通过下式计算得到:β1 = n∑(xiyi) - (∑xi)(∑yi)n∑(xi^2) - (∑xi)^2截距β0可以通过下式计算得到:β0 = (1/n)∑yi - β1(1/n)∑xi通过带入已知数据,我们可以计算得到斜率β1和截距β0的具体值。
在本例中,计算结果如下:β1 ≈ 1.0667β0 ≈ 108.6667最后,利用得到的斜率β1和截距β0,我们可以得到一元线性回归模型的具体公式为:y ≈ 108.6667 + 1.0667x我们可以利用这个回归模型进行预测。
例如,如果有一个房屋的面积为130平方米,那么根据回归模型,可以预测该房屋的售价为170 + 108.6667 ≈ 278.6667万元。
计量经济学实验报告一元线性回归模型实验

2013-2014第1学期计量经济学实验报告实验(一):一元线性回归模型实验学号姓名:专业:国际经济与贸易选课班级:实验日期:2013年12月2日实验地点:K306实验名称:一元线性回归模型实验【教学目标】《计量经济学》是实践性很强的学科,各种模型的估计通过借助计算机能很方便地实现,上机实习操作是《计量经济学》教学过程重要环节。
目的是使学生们能够很好地将书本中的理论应用到实践中,提高学生动手能力,掌握专业计量经济学软件EViews的基本操作与应用。
利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
【实验目的】使学生掌握1.Eviews基本操作:(1)数据的输入、编辑与序列生成;(2)散点图分析与描述统计分析;(3)数据文件的存贮、调用与转换。
2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测【实验内容】1.Eviews基本操作:(1)数据的输入、编辑与序列生成;(2)散点图分析与描述统计分析;(3)数据文件的存贮、调用与转换;2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
实验内容以下面1、2题为例进行操作。
1、为了研究深圳地方预算中财政收入与国内生产总值关系,运用以下数据:(1)建立深圳的预算内财政收入对GDP的回归;(2)估计模型的参数,解释斜率系数的意义;(3)对回归结果进行检验;(4)若2002年的国内生产总值为3600亿元,试确定2002年财政收入的预测值和预α=)。
测区间(0.052、在《华尔街日报1999年年鉴》(The Wall Street Journal Almanac 1999)上,公布有美国各航空公司业绩的统计数据。
航班正点准时到达的正点率和此公司每10万名乘客中投诉1(1)做出上表数据的散点图(2)依据散点图,说明二变量之间存在什么关系?(3)描述投诉率是如何根据航班正点率变化,并求回归方程。
计量经济学实验报告

计量经济学实验报告实验一:一元线性回归模型题目:已知某城镇居民年人均可支配收入X,研究它与人均消费性支出Y之间的关系。
实验目的:通过了解19805年~1998年的样本观测值,得到一元线性回归模型、以此得到1999、2000年的人均消费性支出的预测值。
实验时间:10月12日(星期三)实验地点:科技楼3楼实验内容:1,主菜单-File―New-Workfile打开工作文件范围选择框,选择Annual,分别输入1980,20002,主菜单-Quick-Sample在打开的当前的样本区间选择框中分别输入1980,1998。
3,主菜单-Quick-Empty Group打开空白表格数据窗口,分别输入变量Y,X的数据。
4,主菜单-Quick-Estimate Equation打开估计模型对话框,选择Least Squares,输入Y CX。
下面是Eviews的估计结果:得到回归方程为:Y =283.84+0.51X5,主菜单-Quick-Sample在打开的当前样本区间选择框中分别输入1980,20006,主菜单-Quick-Empty Group编辑变量X的数据,输入X1999,X2000年的实际值。
在回归模型估计结果显示窗口的命令行中,单击Forecast命令,预测结果变量名的缺省选择为YF,选择静态预测,点击ok。
得到1999,2000年的城镇居民年人均消费性支出预测值分别为1354.89和1424.05.实验二:二元线性回归方程模型实验目的:通过了解学生用于购买书籍及课外读物的支出与本人受教育年限和其家庭收入水平有关,了解预测当学生的受教育年限为10年,家庭月可支配收入为480元时,该学生全年购买书籍以及课外读物的支出。
实验时间:10月26日(星期三)实验地点:科技楼3楼实验内容:1,主菜单-File―New-Workfile打开工作文件范围选择框,选择Integer date,分别输入1,192,主菜单-Quick-Sample在打开的当前的样本区间选择框中分别输入1,18。
计量经济学 一元线性回归

随机变量; 研究的是非确定现象随机变量之间的关系,比如:农作物产量与气温、 降雨量及阳光等之间的关系。 ●(单向)因果关系:Y f (X ,u) ,其中 u 为随机变量。在计量经 济模型中,单一线性函数要求变量必须是单向因果关系。
在(单向)因果关系中,变量 Y 是不确定的,变量 X 是确定的 (或可控制的)。
E(Y | Xi ) f ( Xi )
这个函数称为回归函数。 回归函数分为:总体回归函数(population regression function,PRF)
样本回归函数(sample regression function,SRF)
二、总体回归函数(PRF)
例 2.1 一个假想的社区有 100 户家庭组成,要研究该社区每月家庭 消费支出 Y 与每月家庭可支配收入 X 的关系。 即如果知道了家庭的 月收入,能否预测该社区家庭的平均月消费支出水平。
关系,因此不线性相关并不意味着不相关;
③样本相关系数是总体相关系数的样本估计值,由于抽样波动,样本
相关系数是个随机变量,其统计显著性有待检验;
ቤተ መጻሕፍቲ ባይዱ
④相关系数只能反应线性相关程度,不能确定因果关系,即相关关系
并不意味着有因果关系,但有因果关系一定有相关关系。
统计依赖关系
正相关 线性相关 不相关 相关系数:
3000 亿美元? 旅游业的发展与这种决定性因素的数量关系究竟是什么? 怎样具体测定那个旅游业发展与这种决定性因素的数量关系? 应当考虑的问题:
(1)确定作为研究对象的经济变量 (如中国旅游业总收入)
(2)分析影响研究对象变动的主要因素 (如中国居民收入的增长)
(3)分析各种影响因素与所研究经济现象的相互关系 (决定相互联系的数学关系式)
一元线性回归模型案例分析
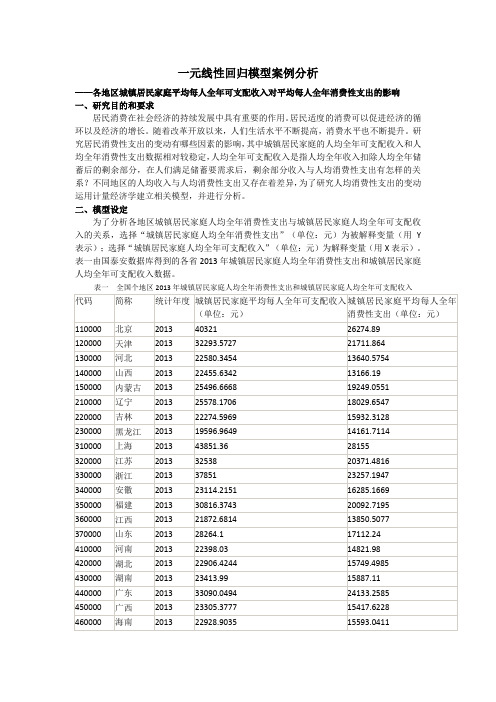
一元线性回归模型案例分析——各地区城镇居民家庭平均每人全年可支配收入对平均每人全年消费性支出的影响一、研究目的和要求居民消费在社会经济的持续发展中具有重要的作用。
居民适度的消费可以促进经济的循环以及经济的增长。
随着改革开放以来,人们生活水平不断提高,消费水平也不断提升。
研究居民消费性支出的变动有哪些因素的影响,其中城镇居民家庭的人均全年可支配收入和人均全年消费性支出数据相对较稳定,人均全年可支配收入是指人均全年收入扣除人均全年储蓄后的剩余部分,在人们满足储蓄要需求后,剩余部分收入与人均消费性支出有怎样的关系?不同地区的人均收入与人均消费性支出又存在着差异,为了研究人均消费性支出的变动运用计量经济学建立相关模型,并进行分析。
二、模型设定为了分析各地区城镇居民家庭人均全年消费性支出与城镇居民家庭人均全年可支配收入的关系,选择“城镇居民家庭人均全年消费性支出”(单位:元)为被解释变量(用Y 表示);选择“城镇居民家庭人均全年可支配收入”(单位:元)为解释变量(用X表示)。
表一由国泰安数据库得到的各省2013年城镇居民家庭人均全年消费性支出和城镇居民家庭人均全年可支配收入数据。
代码 简称 统计年度 城镇居民家庭平均每人全年可支配收入(单位:元) 城镇居民家庭平均每人全年消费性支出(单位:元) 500000 重庆 2013 25216.1271 17813.8642 510000 四川 2013 22367.633 16343.4513 520000 贵州 2013 20667.0748 13702.8708 530000 云南 2013 23235.5268 15156.1494 540000 西藏 2013 20023.35 12231.86 610000 陕西 2013 22858.3719 16679.6872 620000 甘肃 2013 18964.7783 14020.7206 630000 青海 2013 19498.54 13539.5 640000 宁夏 2013 21833.33 15321.1 650000新疆201319873.7715206.16为分析城镇居民家庭人均全年消费性支出(Y )与城镇居民家庭人均全年可支配收入(X )的关系,此案例用EViews 软件做计量分析。
一元线性回归模型案例分析

一元线性回归模型案例分析一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。
但是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也有明显差异。
例如,2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元,最高的上海市达人均10464元,上海是黑龙江的2.35倍。
为了研究全国居民消费水平及其变动的原因,需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费,由于各地区的城市与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。
而且,由于各地区人口和经济总量不同,只能用“城市居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异,并不是城市居民消费在不同时间的变动,所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入,其他因素虽然对居民消费也有影响,但有的不易取得数据,如“居民财产”和“购物环境”;有的与居民收入可能高度相关,如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大,如“零售物价指数”、“利率”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例分析1— 一元回归模型实例分析
依据1996-2005年《中国统计年鉴》提供的资料,经过整理,获得以下农村居民人均消费支出和人均纯收入的数据如表2-5:
表2-5 农村居民1995-2004人均消费支出和人均纯收入数据资料 单位:元 年度 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 人均纯收入 1577.7 1926.1 2090.1 2161.1 2210.3 2253.4 2366.4 2475.6 2622.2
2936.4
人均消费支出
1310.4
1572.1
1617.2
1590.3
1577.4
1670.1
1741.1
1834.3
1943.3 2184.7
一、建立模型
以农村居民人均纯收入为解释变量X ,农村居民人均消费支出为被解释变量Y ,分析Y 随X 的变化而变化的因果关系。
考察样本数据的分布并结合有关经济理论,建立一元线性回归模型如下:
Y i =b 0+b 1X i +m i
根据表2-5编制计算各参数的基础数据计算表。
求得:
082
.1704035.2262==Y X
∑∑∑∑====37
52432495.1986.788859011.516634423.1264471222i
i i i i
X y x y x 根据以上基础数据求得:
623865.0423
.126447986
.788859ˆ21
==
=∑∑i
i
i x
y
x β
8775.292035.2262623865.0082.1704ˆˆ1
0=⨯-=-=X Y ββ 样本回归函数为:
i
i X Y 623865.08775.292ˆ+= 上式表明,中国农村居民家庭人均可支配收入若是增加100元,居民们将会拿出其中的62.39元用于消费。
二、模型检验
1.拟合优度检验
952594.0011.516634423.1264471986.788859)
)(()(
2
2
222
=⨯==
∑∑∑i i
i i y
x y x r
2.t 检验
525164
.3061 2
10423
.12644710.623865011.166345 2
ˆˆ222122
=-⨯-=
--=
∑∑n x y i
i
βσ
049206.0423
.1264471525164
.3061ˆ)ˆ()ˆ(2
21
1==
==∑i
e x
Var S σ
ββ
6717
.112525164.3061423
.126447110137
.52432495ˆ)ˆ()ˆ(22
20
0=⨯===∑∑σββi
i e x
n X Var S 在显著性水平a=0.05,n-2=8时,查t 分布表,得到:
306.2)2(2
=-n t α
提出假设,原假设H 0:b 1=0,备择假设H 1:b 1¹0
67864.12049206
.0623865.0)ˆ(ˆ)ˆ(111==-=ββββe S t
)2(67864.12)ˆ(2
1->=n t t α
β,差异显著,拒绝b 1=0的假设。
3. F 检验
提出原假设H 0:b 1=0,备择假设H 1:b 1¹0
在显著性水平a=0.05,n-2=8时,查F 分布表,得到: F (1,8)=5.32。
7505.160525164.30618097.4921412
1ˆ2
221==-=
∑∑n e x F i i
β
160.7505>5.32,即F > F (1,8),差异显著,拒绝b 1=0的假设。
三、预测
当农村居民家庭人均纯收入增长到3500元时,对农村居民人均消费支出预测如下:
)(405.24763500623865.08775.292ˆ0
元=⨯+=Y
13257219
.84 423.1264471)035.22623500(1011525164.3061 )(11ˆ)(11ˆ)(S 2
22022200e =⎪⎪⎭
⎫ ⎝⎛-++⨯=⎪⎪⎭
⎫ ⎝⎛-++=-++=∑∑i i x X X n x X X n e σσ
在显著性水平a =0.05,n -2=8时, 025.0t =2.306 从而
)(S ˆ0
e 2
0e t Y α-=2476.405-2.306´84.13257219=2282.40(元) )(S ˆ0
e 2
0e t Y α+=2476.405+2.306´84.13257219=2670.41(元) []%9541.267040.22820=≤≤Y P
当农村居民家庭人均纯收入增长到3500元时,,农村居民人均消费支出在2282.40元至2670.41元之间的概率为95%。
四、利用计算机进行分析的步骤
以上分析内容可以借助计算机完成,下面以EViews3.0软件为例,介绍其分析过程。
1.设定工作范围
打开EViews ,按照以下步骤设定工作范围:
File®New®Workfile®Workfile Range®Annual®Start data(1995)®End data(2004)(图2-5、图2-6)®OK
图2-5 Workfile Range 对话框
图2-6 Workfile工作状态图
2.输入变量
在Workfile工作状态下输入变量X,Y
Objects®New Object®Type of Object(series)®Name for Object(X)(图2-7、图2-8)®OK。
同理,可输入变量Y。
图2-7输入变量X状态图
图2-8 Workfile工作状态图
3.输入样本数据
在Workfile工作状态下选中X、Y,右击鼠标,Open®as Group®Edit,输入数据(见图2-9)。
图2-9 Edit工作状态图
4.输入方程式
在Workfile工作状态下,选中Y、X,右击鼠标,Open®as Equation®Equation Specification®(Y C X)(图2-10)®OK,输出回归分析结果(见图2-11)。
图2-10 输入Y C X工作状态图
图2-11 回归分析表
输出结果的解释:
Variable 解释变量
Coefficient 解释变量的系数
Std.Error 标准差
t-Statistic t-检验值
Prob. t-检验的相伴概率
R-squared 样本决定系数
Adjusted R-squared 调整后的样本决定系数
S.E.regression 回归标准差
Sum squared resid 残差平方和
Log likelihood 对数似然比
Durbin-Watson stat D-W 统计量
Mean dependent var 被解释变量的均值 S.D.dependent var 被解释变量的标准差 Akaike info criterion 赤池信息量 Schwarz criterion 施瓦兹信息量 F-statistic F 统计量
Prob(F-statistic) F 统计量的相伴概率 由图2-11可以获得以下信息:
952594
.0623865.0ˆ8769.292ˆ210===r ββ 是b 0, b 1回归系数的估计量值,r 2是在双变量情况下,样本的可决系数
67889.12)ˆ( 599413.2)ˆ( 049205.0)ˆ(6704.112)ˆ(1
1
====β
ββ
βt t S S e
e
)ˆ(),ˆ(10ββe e S S 是10ˆˆββ,估计量的标准差,)ˆ(),ˆ(10ββt t 是1
0ˆˆββ,估计量的t 统计量。
F =160.7542是F 检验统计量的值 样本回归函数为:
i
i X Y 623865.08769.292ˆ+= 样本回归函数(Sample Regression Function ,SRT ) 5.预测
(1)扩展工作范围
在Workfile 工作状态下,Procs→Change Workfile Range→End data(2005)→OK 再选择Sample(1995 2005)( 图2-12) →OK
图2-12 工作范围图
(2)输入解释变量值
在Workfile工作状态下,X→Edit →(3500)。
(3)预测
在图2-11 Equation工作状态下,选择Forecast→OK(见图2-13),得到预测结果(见图2-14)
图2-13 设定预测状态图
图2-14预测结果输出图
在Workfile工作状态下,显示YF,可得到点预测值(见图2-15)
图2-15 预测值输出图
根据模型预测结果,当中国农村居民家庭人均纯收入达到3500元时,每个人将会拿出2476.41元用于消费。
