职高数学第三章函数习题集及答案
中职数学基础模块上册第三章函数的性质及应用举例

宁远职业中专学校2019年下期高一数学周测试题考试范围:函数的性质及其应用举例 总分:70分 适用班级:1901---1910班级: 姓名: 得分:一、选择题(每题4分,共20分)1、已知点A(m, -1)关于y 轴的对称点为B(3, n), 则m, n 的值分别为( ) A.m=3, n= -1 B.m=3, n=1 C.m= -3, n= -1 D.m= -3, n=12、下列函数中,既是奇函数,又是区间(0, +∞)内的减函数的是( )A. x y 1=B. 3x y =C. 22+=x y D.3+-=x y3、函数2x y =在其定义域内是( )A 、增函数B 、减函数C 、奇函数D 、偶函数4、若奇函数f(x)在[3, 7]上是增函数,且最小值为5,那么f(x)在[-7, -3]上是( ) A.增函数且最小值为-5 B.增函数且最大值为-5 C.减函数且最小值为-5 D.减函数且最大值为-55、已知)(x f 是偶函数且在(0,+∞)上是增函数,( ) A.)3()2()4(f f f <-<- B.)4()2()3(-<-<f f f C.)2()3()4(-<<-f f f D.)4()3()2(-<<-f f f二、填空题(每题4分,共20分)6、若)(x f 是奇函数,且3)4(=f ,则=-)4(f7、函数24)(2-+-=x x x f 在区间[1, 4]上的最大值是8、已知的定义域为则)(0,120,3)(2x f x x x x x f ⎩⎨⎧>+≤-= ,=-)]1([f f9、已知函数2)1(2)(2+-+=x a x x f 在区间]4,(-∞上是减函数,则实数a 的取值范围10、若函数2)(k kx x f +=的图像经过点(0, 4),且在R 上是增函数,则=k三、解答题(每题15分,共30分)11、某商店规定,某种商品一次性买10kg 以下按零售价格50元/kg 销售,若一次性购买量满10kg,可打 9折,若一次性购买量满20kg,可按40元/kg 的优惠价格供货。
中专函数考试题目及答案

中专函数考试题目及答案一、选择题(每题2分,共20分)1. 函数y=f(x)的定义域是所有实数,那么f(x)的值域是:A. 所有实数B. 非负实数C. 非正实数D. 所有整数答案:A2. 函数y=x^2在区间[0, +∞)上的单调性是:A. 单调递增B. 单调递减C. 先减后增D. 先增后减答案:A3. 下列哪个函数是奇函数?A. y = x^2B. y = x^3C. y = xD. y = -x答案:C4. 函数y=f(x)的图像关于原点对称,则f(x)一定是:A. 奇函数B. 偶函数C. 非奇非偶函数D. 线性函数答案:A5. 函数y=f(x)的图像关于y轴对称,则f(x)一定是:A. 奇函数B. 偶函数C. 非奇非偶函数D. 线性函数答案:B6. 函数y=f(x)的图像关于点(a, b)对称,则f(x)一定是:A. 奇函数B. 偶函数C. 非奇非偶函数D. 线性函数答案:C7. 函数y=f(x)的图像关于x轴对称,则f(x)一定是:A. 奇函数B. 偶函数C. 非奇非偶函数D. 线性函数答案:B8. 函数y=f(x)的图像关于直线y=x对称,则f(x)一定是:A. 奇函数B. 偶函数C. 非奇非偶函数D. 线性函数答案:D9. 函数y=f(x)的图像关于直线y=-x对称,则f(x)一定是:A. 奇函数B. 偶函数C. 非奇非偶函数D. 线性函数答案:A10. 函数y=f(x)的图像关于直线y=x+b对称,则f(x)一定是:A. 奇函数B. 偶函数C. 非奇非偶函数D. 线性函数答案:C二、填空题(每题3分,共30分)1. 函数y=f(x)在x=1处的导数为3,则f'(1)=______。
答案:32. 函数y=x^2+3x+2的极值点为______。
答案:-1.53. 函数y=sin(x)的周期为______。
答案:2π4. 函数y=e^x的导数为______。
答案:e^x5. 函数y=ln(x)的定义域为______。
中职数学第三章测试题及答案.docx

第三章函数测试卷一、填空题:(每空 2 分)1、函数 f ( x)1 的定义域是 。
x 12、函数 f ( x)3x2 的定义域是。
3、已知函数 f (x) 3x 2,则 f (0) , f (2) 。
4、已知函数 f (x)x 21,则 f (0), f ( 2)。
5、函数的表示方法有三种,即:。
6、点 P 1,3 关于 x 轴的对称点坐标是 ;点 M (2,-3 )关于 y 轴的对称点坐标是;点 N (3, 3) 关于原点对称点坐标是。
7、函数 f (x)2x 2 1 是函数;函数 f ( x) x 3x 是函数;8、每瓶饮料的单价为元,用解析法表示应付款和购买饮料瓶数之间的函数关系 式可以表示为 。
9、常用对数表中,表示对数与对数值之间的关系采用的是 的方法。
二、选择题(每题 3 分)1、下列各点中,在函数 y 3x 1的图像上的点是( )。
A .(1,2) B. (3,4 ) C.(0,1)D.(5,6) 2、函数 y 1的定义域为()。
2x 3A .,B.,33 , C. 3 , D.3 ,2 2223、下列函数中是奇函数的是( )。
A . y x 3B.y x 21 C. y x 3D. y x 3 14、函数 y 4x 3 的单调递增区间是 ()。
A .,B.0,C.,0D.0.5、点 P (-2 ,1)关于 x 轴的对称点坐标是( )。
A .(-2 , 1) B. ( 2, 1) C.(2 ,-1) D.(-2 ,-1) 6、点 P (-2 ,1)关于原点 O 的对称点坐标是( )。
A .(-2 , 1) B. ( 2, 1) C.(2 ,-1)D.(-2 ,-1) 7、函数 y2 3x 的定义域是()。
A.222D.2 ,B.,C.,, 33338、已知函数 f (x)x27 ,则 f (3) =()。
A.-16 C. 2三、解答题:(每题 5 分)1、求函数y3x 6 的定义域。
职高数学第三章函数习题集及答案

3.1函数的概念及其表示法习题练习3.1.11、求y=3x-1的定义域:2、指出下列各函数中,哪个与函数y x=是同一个函数:(1)2xyx=;(2)y;(3)s t=.3、已知f(x)=3x+6,求f(0)、f(2)、f(-2)。
参考答案:1、R2、(3)3、6、12、0练习3.1.21、利用“描点法”作出函数xy=的图像,并判断点(16,4)是否为图像上的点2、市场上苹果的价格是8元/kg ,应付款额y是购买苹果数量x的函数.请写出其解析法。
3、市场上中性笔的价格是2元/只,应付款额y是购买中性笔数量x的函数.请写出其解析法。
参考答案:1、作图略,在。
2、y=8x,(x为正整数)3、y=2x(x为正整数)3.2函数的性质习题练习3.2.11、判断函数y=-2x+3的单调性.23、判断函数y=8X+3的单调性.参考答案:1、减2、左增、右减3、增练习3.2.21、判断y=8X+3的奇偶性:2、判断y=4X 的奇偶性3、判断y=X 2的奇偶性 参考答案:1、非奇非偶函数2、奇函数3、偶函数3.3函数的实际应用举例习题练习3.31、.求()221,20,1,0 3.x x y f x x x +-<⎧⎪==⎨-<<⎪⎩的定义域; 2、求函数()221,0,,0.x x y f x x x -⎧⎪==⎨>⎪⎩的定义域;3、求函数() 1.6,010,2.812,10.x x y f x x x <⎧==⎨->⎩的定义域; 4、作出函数()1,0,1,0x x y f x x x -<⎧==⎨+⎩的图像 5、设函数()221,20,1,0 3.x x f x x x +-<⎧⎪=⎨-<<⎪⎩作出函数的图像.6、设函数7,03,4,310,1.51,10.x y x x x x <⎧⎪=+<⎨⎪->⎩作出函数的图像 参考答案:1、-2<=x<=32、R3、x>=04、略5、略6、略。
中职数学第3章《函数》单元检测试题及答案【基础模块上册】
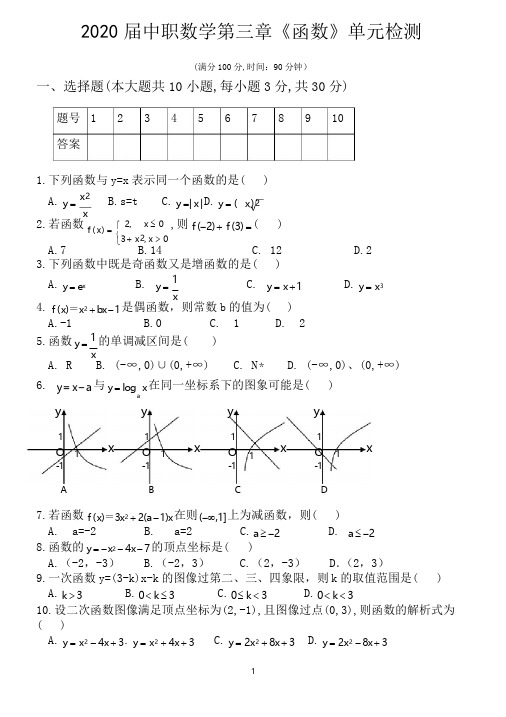
⎨12020 届中职数学第三章《函数》单元检测(满分 100 分,时间:90 分钟)一、选择题(本大题共 10 小题,每小题 3 分,共 30 分)题号 1 2 3 4 5 6 7 8 9 10答案1.下列函数与 y=x 表示同一个函数的是()A. y =x2xB.s=tC. y =| x |D. y = ( x ) 22.若函数 f ( x ) = ⎧ 2,x ≤ 0 ,则 f (-2) + f (3) = ()⎩ 3 + x 2, x > 0A.7B.14C. 12D.23.下列函数中既是奇函数又是增函数的是( )A. y = e xB. y =1xC. y = x + 1D. y = x 34. f ( x )=x 2 + bx - 1是偶函数,则常数 b 的值为( )A.-1B.0C. 1D. 2 5.函数 y = 1 的单调减区间是()xA. RB. (-∞,0)∪(0,+∞)C. N *D. (-∞,0)、(0,+∞)6. y = x - a 与 y = log x 在同一坐标系下的图象可能是() ay1O 1x-1y1O 1 x-1y1O x-1y1O 1 x-1A B C D7.若函数 f ( x )=3x 2 + 2(a - 1)x 在则 (-∞,1] 上为减函数,则( )A. a=-2B. a=2C. a ≥ -2D. a ≤ -2 8.函数的 y = - x 2 - 4 x - 7 的顶点坐标是( )A.(-2,-3)B.(-2,3)C.(2,-3) D .(2,3)9.一次函数 y=(3-k)x-k 的图像过第二、三、四象限,则 k 的取值范围是( )A. k > 3B. 0 < k ≤ 3C. 0 ≤ k < 3D. 0 < k < 310.设二次函数图像满足顶点坐标为(2,-1),且图像过点(0,3),则函数的解析式为 ( )A. y = x 2 - 4 x + 3 . y = x 2 + 4 x + 3 C. y = 2 x 2 + 8 x + 3 D. y = 2 x 2 - 8x + 33x -5 二、填空题(共 8 小题,每题 4 分,共 32 分)11.若函数 f ( x ) = ax - 2 ,且 f (2) = 4 ,则 a= 12.当 x= 时,函数 y = x 2 + 4 x + 3 有最小值13.函数 f ( x ) = x 2 - 2 x - 3 的递减区间是,递增区间是1 14.用区间表示函数 y = 的定义域为______________15.已知函数 f(x)=2x-1,则 f[f(2)]=16.若函数 f(x)=3x+m-1 是奇函数,则常数 m=17.已知二次函数 y = ( m - 3) x 2 + ( m - 2) x + 6 为偶函数,则函数的单调增区间为 18.函数 f(x)=(3k-6)x+2 在 R 上是减函数,则 k 的取值范围为三、解答题(6 小题,共 38 分)19.(8 分)求下列函数的定义域:(1) f ( x ) = 1 - x + 3 1 + x (2) f ( x ) =2 x - 1 x - 320.(6 分)f(x)是定义在(0,+∞)上的单调递减函数,且 f(x)<f(x-2),求 x 的取值范围.21.若函数 f(x)=3x-1,g(x)=x 2,求 g[f(x)]的值.22.(6 分)证明:函数 y=2x-3 在(-∞,+∞)上是增函数。
中职数学第三章测试题及答案资料讲解

第三章函数测试卷一、填空题:(每空2分)1、函数11)(+=x x f 的定义域是 。
2、函数23)(-=x x f 的定义域是 。
3、已知函数23)(-=x x f ,则=)0(f ,=)2(f 。
4、已知函数1)(2-=x x f ,则=)0(f ,=-)2(f 。
5、函数的表示方法有三种,即: 。
6、点()3,1-P 关于x 轴的对称点坐标是 ;点M (2,-3)关于y 轴的对称点坐标是 ;点)3,3(-N 关于原点对称点坐标是 。
7、函数12)(2+=x x f 是 函数;函数x x x f -=3)(是 函数;8、每瓶饮料的单价为2.5元,用解析法表示应付款和购买饮料瓶数之间的函数关系式可以表示为 。
9、常用对数表中,表示对数与对数值之间的关系采用的是 的方法。
二、选择题(每题3分)1、下列各点中,在函数13-=x y 的图像上的点是( )。
A .(1,2) B.(3,4) C.(0,1) D.(5,6)2、函数321-=x y 的定义域为( )。
A .()+∞∞-, B.⎪⎭⎫ ⎝⎛+∞⎪⎭⎫ ⎝⎛∞-,2323,Y C.⎪⎭⎫⎢⎣⎡+∞,23 D. ⎪⎭⎫ ⎝⎛+∞,23 3、下列函数中是奇函数的是( )。
A .3+=x y B.12+=x y C.3x y = D.13+=x y4、函数34+=x y 的单调递增区间是( )。
A .()+∞∞-, B. ()+∞,0 C. ()0,∞- D.[)∞+.05、点P (-2,1)关于x 轴的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)6、点P (-2,1)关于原点O 的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)7、函数x y 32-=的定义域是( )。
A .⎪⎭⎫ ⎝⎛∞-32, B.⎥⎦⎤ ⎝⎛∞-32, C. ⎪⎭⎫ ⎝⎛+∞,32 D.⎪⎭⎫⎢⎣⎡+∞,32 8、已知函数7)(2-=x x f ,则)3(-f =( )。
中职函数复习题及答案

中职函数复习题及答案一、选择题1. 函数y = f(x) = 3x + 2的值域是:A. (-∞, +∞)B. [2, +∞)C. (0, +∞)D. [0, +∞)2. 函数f(x) = x^2 + 1在x = -1处的导数是:A. 0B. 1C. 2D. -23. 如果函数f(x) = 2x - 3在区间[1, 4]上是增函数,那么f(1)和f(4)的大小关系是:A. f(1) < f(4)B. f(1) > f(4)C. f(1) = f(4)D. 不能确定二、填空题4. 函数y = 4x^3 - x^2 + 3x - 5的导数是_________。
5. 函数f(x) = sin(x) + cos(x)在x = π/4处的值是_________。
三、简答题6. 请简述函数的奇偶性,并给出一个奇函数和一个偶函数的例子。
四、计算题7. 计算函数f(x) = x^3 - 6x^2 + 11x - 6在x = 2处的值。
五、证明题8. 证明函数f(x) = x^3在R上是单调递增的。
六、应用题9. 某工厂生产一种产品,其成本函数为C(x) = 1000 + 50x,其中x是生产的件数。
如果每件产品的售价为200元,求该工厂的盈利函数,并计算当生产100件产品时的盈利。
七、解答题10. 已知函数f(x) = x^2 - 4x + 4,求其在区间[0, 3]上的最大值和最小值。
答案:1. A2. C3. A4. 12x^2 - 2x + 35. √26. 奇函数:f(x) = x^3,偶函数:f(x) = x^27. 88. 证明略9. 盈利函数为P(x) = 150x - 1000,当生产100件产品时的盈利为5000元。
10. 最大值为4,最小值为0。
本试题旨在帮助学生复习中职数学中的函数知识,包括函数的基本概念、导数、单调性、奇偶性、最值问题以及实际应用等。
通过这些练习,学生可以加深对函数概念的理解,并提高解决实际问题的能力。
中职数学基础模块(上册)基础练习-第三章函数

第三章 函数第三章 第一课时 函数的概念【基础知识·一定要看】1.函数的概念设A 、B 是非空的数集,如果按照某个确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有__________的数 f x 和它对应,那么就称:f A B 为从集合A 到集合B 的一个函数.记作: y f x ,x A .其中,x 叫做自变量,x 的取值范围A 叫做函数的定义域;与x 的值相对应的y 值叫做函数值,函数值的集合 {|}f x x A 叫做函数的值域. 2.求函数定义域的常用方法: (1)分母不为零;(2)偶次根式,则被开方数大于或等于零; (3)0的0次没有意义;(4)对数的真数大于零;(还没学)3.相同函数:个函数相等当且仅当它们的定义域和对应关系完全—致,而与表示自变量和函数值的字母无关.4.分段函数:如果函数y =f (x ),x ∈A ,根据自变量x 在A 中不同的取值范围,有着不同的对应关系,则称这样的函数为分段函数. 一、选择题1.在下面四个图中,可表示函数 y f x 的图象的可能是( )A. B. C. D.2.函数1()f x x的定义域是( ) A.[2,0)(0,)B.[2,) C.RD.(,0)(0,)3.下列每组中的两个函数是同一函数的是( )A.1y 与0y x ; B.y y x ;C.y x 与2y;D.y x 与y4. 23,12,1x x f x x x ,则(2)f 等于( )A.-2 B.0C.1D.65.函数 2112f x x x, 0,4x 的值域( )A. 0,4 B. 1,5 C. 1,4D.1,526.已知 2146f x x ,则 5f 的值为( ) A.26B.20C.18D.167.已知函数 2,32,3x x f x x x .则 3f f ( )A.1 B.4 C.9 D.16二、填空题8.函数()1f x 的定义域为 . 9.若 234f x x Bx ,且 112f ,则B = . 10.已知函数()y f x 的表达式4()1f x x,若()2f a ,则实数 a . 11.二次函数 22f x x x , 1,1x ,则函数 f x 在此区间上的值域为 . 三、解答题12.已知函数 1f x ax x过点(1,5),求a 的值.第三章 第二课时 函数的表示方法【基础知识·一定要看】1.函数的三种表示方法:①待定系数法:若已知f (x )的解析式的类型,设出它的一般形式,根据特殊值确定相关的系数即可.②换元法:设t =g (x ),解出x ,代入f (g (x )),求f (t )的解析式即可. 3.常见的几种基本初等函数①正比例函数(0)y kx k ②一次函数(0)y kx b k ③反比例函数(0)ky k x④二次函数2(0)y ax bx c a 一、选择题1.已知(21)44f x x ,则(1)f 的值为( ) A.2B.4C.6D.82.函数 y f x 的图象如图所示,则 9f ( ) A.5 B.4C.3D.23.已知 212f x x x ,则 f x ( ) A.2xB.21xC.21xD.22x4.已知 f x 是反比例函数,且(3)1f ,则 f x 的解析式为( ) A. 3f x xB. 3f x xC. 3f x xD. 3f x x5.若函数 f x 和 g x 分别由下表给出: 则 1g f ( ) A.4 B.3C.2D.16.已知 32f x x ,则 21f x 等于( ) A.32xB.61x C.21xD.65x7.已知()f x 是一次函数,且(1)35f x x ,则()f x 的解析式为( ) A.()32f x xB.()32f x xC.()23f x xD.()23f x x二、填空题8.已知 22143f x x ,则 f x .9.已知函数 f x 对于任意的x 都有 212f x x f x ,则 f x . 10.已知等腰三角形的周长为18,底边长为x ,腰长为y ,则y 关于x 的函数关系式为 . 三、解答题11.已知函数 224f x x x . (1)求 0f ; (2)求 f x 的解析式.第三章 第三课时 函数的性质【基础知识·一定要看】1.函数的单调性 ①单调函数的定义 自左向右看图象是上升的自左向右看图象是下降的②证明函数单调性的步骤第一步:取值.设12x x ,是()f x 定义域内一个区间上的任意两个自变量,且12x x ; 第二步:变形.作差变形(变形方法:因式分解、配方、有理化等)或作商变形; 第三步:定号.判断差的正负或商与1的大小关系; 第四步:得出结论. 2.函数的奇偶性 ①函数奇偶性的概念偶函数:若对于定义域内的任意一个x ,都有 f x f x ,那么 f x 称为偶函数. 奇函数:若对于定义域内的任意一个x ,都有 f x f x ,那么 f x 称为奇函数. ②奇偶函数的图象与性质偶函数:函数()f x 是偶函数 函数()f x 的图象关于y 轴对称; 奇函数:函数()f x 是奇函数 函数()f x 的图象关于原点中心对称;若奇函数()y f x 在0x 处有意义,则有(0)0f .③用定义判断函数奇偶性的步骤第一步:求函数()f x 的定义域,判断函数的定义域是否_______________,若不关于原点对称,则该函数既不是奇函数,也不是偶函数,若关于原点对称,则进行下一步;第二步:求()f x ,若 f x f x ,则()f x 是奇函数;若()f x =()f x ,则()f x 是偶函数;若()()f x f x ,则()f x 既不是奇函数,也不是偶函数;若()()f x f x 且 f x f x ,则()f x 既是奇函数,又是偶函数.1.若函数 1y a x b ,x R 在其定义域上是增函数,则( ) A.1aB.1aC.0bD.0b2.函数 f x 在R 上是减函数,则有( ) A. 25f fB. 25f fC. 25f fD. 25f f3.下列函数中,既是偶函数又在 0, 上单调递增的函数是( ) A.y xB.1y xC.21y xD.1y x4.若偶函数 f x 在 ,1 上是减函数,则( ) A. 2.513f f f B. 1 2.53f f f C. 3 2.51f f fD. 31 2.5f f f5.函数 f x 是定义在 0, 上的增函数,则满足 1213f x f的x 的取值范围是( ) A.12,33B.12,33C.12,23D.12,236.函数22y x x 单调减区间是( ) A.1,2B. 1,C.1,2D. ,【填空】7.已知 f x 是偶函数, 12f ,则 11f f .8.函数()y f x 是定义在R 上的增函数,且 29f m f m ,则实数m 的取值范围是 .9.函数()y f x 是定义在R 上的奇函数,当0x 时,3()f x x x ,则(2)f .10.已知 y f x 在定义域 0,1上是减函数,且 121f a f a ,则实数a 的取值范围 .11.已知函数2()()2f x x m .(1)若函数()f x 的图象过点(2,2),求函数y ()f x 的单调递增区间; (2)若函数()f x 是偶函数,求m 值.12.已知函数 1f x x x(1)判断 f x 的奇偶性并说明理由; (2)判断 f x 在 0,1上的单调性并加以证明.第三章 第四课时 函数的应用一、选择题1.据调查,某存车处(只存放自行车和电动车)在某天的存车量为400辆次,其中电动车存车费是每辆一次2元,自行车存车费是每辆一次1元.若该天自行车存车量为x 辆次,存车总收入为y 元,则y 关于x 的函数关系式是( ) A. 4000400y x x B. 8000400y x x C. 4000400y x xD. 8000400y x x2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P (千帕)是气球体积V (立方米)的反比例函数,其图像如图所示,则这个函数的解析式为( )A.69P VB.96P VC.69P VD.96P V3.某物体一天中的温度T 是时间t 的函数:3()360T t t t ,时间的单位是小时,温度的单位是C ,0 t 表示中午12时,其后取值为正,其前取值为负,则上午8时的温度为( ) A.18CB.8CC.0CD.4C二、填空题4.若某一品种的练习册每本2.5元,则购买x 本的费用y 与x 的函数关系是 . 5.某社区超市的某种商品的日利润y (单位:元)与该商品的当日售价x (单位:元)之间的关系为21221025x y x ,那么该商品的日利润最大时,当日售价为 元.三、解答题6.某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:(1)经过对上表中数据的探究,发现这种读物的投入成本 (元)是印数 (册)的一次函数,求这个一次函数的解析式(不要求写出的取值范围); (2)如果出版社投入成本48000元,那么能印该读物多少册?x x7.制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y (℃),从加热开始计算的时间为 min x .据了解,设该材料加热时,温度y 与时间x 成一次函数关系;停止加热进行操作时,温度y 与时间x 成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5min 后温度达到60℃.(1)分别求出将材料加热和停止加热进行操作时,y 与x 的函数关系式;(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1函数的概念及其表示法习题
练习3.1.1
1、求y=3x-1的定义域:
2、指出下列各函数中,哪个与函数y x
=是同一个函数:
(1)
2
x
y
x
=;(2
)y;(3)s t=.
3、已知f(x)=3x+6,求f(0)、f(2)、f(-2)。
参考答案:
1、R
2、(3)
3、6、12、0
练习3.1.2
1、利用“描点法”作出函数x
y=的图像,并判断点(16,4)是否为图像上的点
2、市场上苹果的价格是8元/kg ,应付款额y是购买苹果数量x的函数.请写出其解析法。
3、市场上中性笔的价格是2元/只,应付款额y是购买中性笔数量x的函数.请写出其解析法。
参考答案:
1、作图略,在。
2、y=8x,(x为正整数)
3、y=2x(x为正整数)
3.2函数的性质习题
练习3.2.1
1、判断函数y=-2x+3的单调性.
2
3、判断函数
y=8X+3的单调性.
参考答案:
1、减
2、左增、右减
3、增
练习3.2.2
1、判断y=8X+3的奇偶性:
2、判断y=4X 的奇偶性
3、判断y=X 2
的奇偶性
参考答案:
1、非奇非偶函数
2、奇函数
3、偶函数
3.3函数的实际应用举例习题
练习3.3
1、.求()221,
20,1,
0 3.x x y f x x x +-<⎧⎪==⎨-<<⎪⎩的定义域; 2、求函数()221,0,,0.x x y f x x x -⎧⎪==⎨>⎪⎩的定义域;
3、求函数() 1.6,010,2.812,10.x x y f x x x <⎧==⎨->⎩
的定义域; 4、作出函数()1,0,1,
0x x y f x x x -<⎧==⎨+⎩的图像 5、设函数()221,20,1,0 3.x x f x x x +-<⎧⎪=⎨-<<⎪⎩作出函数的图像.
6、设函数7,03,4,
310,1.51,10.x y x x x x <⎧⎪=+<⎨⎪->⎩
作出函数的图像 参考答案:
1、-2<=x<=3
2、R
3、x>=0
4、略
5、略
6、略。
