职高数学第三章函数习题集及答案
中职数学基础模块上册第三章函数的性质及应用举例

宁远职业中专学校2019年下期高一数学周测试题考试范围:函数的性质及其应用举例 总分:70分 适用班级:1901---1910班级: 姓名: 得分:一、选择题(每题4分,共20分)1、已知点A(m, -1)关于y 轴的对称点为B(3, n), 则m, n 的值分别为( ) A.m=3, n= -1 B.m=3, n=1 C.m= -3, n= -1 D.m= -3, n=12、下列函数中,既是奇函数,又是区间(0, +∞)内的减函数的是( )A. x y 1=B. 3x y =C. 22+=x y D.3+-=x y3、函数2x y =在其定义域内是( )A 、增函数B 、减函数C 、奇函数D 、偶函数4、若奇函数f(x)在[3, 7]上是增函数,且最小值为5,那么f(x)在[-7, -3]上是( ) A.增函数且最小值为-5 B.增函数且最大值为-5 C.减函数且最小值为-5 D.减函数且最大值为-55、已知)(x f 是偶函数且在(0,+∞)上是增函数,( ) A.)3()2()4(f f f <-<- B.)4()2()3(-<-<f f f C.)2()3()4(-<<-f f f D.)4()3()2(-<<-f f f二、填空题(每题4分,共20分)6、若)(x f 是奇函数,且3)4(=f ,则=-)4(f7、函数24)(2-+-=x x x f 在区间[1, 4]上的最大值是8、已知的定义域为则)(0,120,3)(2x f x x x x x f ⎩⎨⎧>+≤-= ,=-)]1([f f9、已知函数2)1(2)(2+-+=x a x x f 在区间]4,(-∞上是减函数,则实数a 的取值范围10、若函数2)(k kx x f +=的图像经过点(0, 4),且在R 上是增函数,则=k三、解答题(每题15分,共30分)11、某商店规定,某种商品一次性买10kg 以下按零售价格50元/kg 销售,若一次性购买量满10kg,可打 9折,若一次性购买量满20kg,可按40元/kg 的优惠价格供货。
职高函数试题及答案

职高函数试题及答案一、选择题(每题2分,共20分)1. 函数y=f(x)的定义域是:A. (-∞, +∞)B. [0, +∞)C. (0, +∞)D. [0, 1]答案:C2. 函数y=x^2-4x+c的顶点坐标是:A. (2, c-4)B. (-2, c+4)C. (2, c+4)D. (-2, c-4)答案:A3. 函数y=|x-1|+|x+3|的最小值是:A. 4B. 2C. 1D. 0答案:A4. 函数y=3x+2的值域是:A. (-∞, +∞)B. [2, +∞)C. (2, +∞)D. [0, +∞)答案:A5. 函数y=sin(x)的周期是:A. πB. 2πC. 3πD. 4π答案:B6. 函数y=ln(x)的定义域是:A. (-∞, +∞)B. (0, +∞)C. (-∞, 0)D. (0, 1)答案:B7. 函数y=e^x的导数是:A. e^xB. -e^xC. ln(e^x)D. 1/e^x答案:A8. 函数y=x^3-3x+1的单调递增区间是:A. (-∞, +∞)B. (-∞, 1)C. (1, +∞)D. (-∞, 0)答案:C9. 函数y=x^2-6x+8的对称轴是:A. x=3B. x=-3C. x=0D. x=6答案:A10. 函数y=cos(x)的值域是:A. (-∞, +∞)B. [-1, 1]C. (0, 1)D. [-2, 2]答案:B二、填空题(每题3分,共30分)1. 函数y=2x-3的反函数是y=____。
答案:(2y+3)/22. 函数y=x^2-6x+8的顶点坐标是(3, ____)。
答案:-13. 函数y=ln(x)的导数是y'=____。
答案:1/x4. 函数y=sin(x)+cos(x)的周期是____。
答案:2π5. 函数y=e^x的值域是____。
答案:(0, +∞)6. 函数y=x^3+2x^2-5x+1的单调递增区间是____。
中职函数第三单元题目难

中职函数第三单元题目难一、单选题1.函数f(x)=2x-sinx 的零点个数为( )A .1B .2C .3D .42.已知函数 f(x)={2x ,x ≥0,3−f(−x),x <0, 若函数 y =f(f(x))−a 有且只有1个零点,则实数a 的取值范围是( ) A .(−∞,−1)∪[2,+∞) B .(−∞,0)∪[4,+∞) C .(−∞,1)∪[4,+∞)D .(−∞,1)∪[2,+∞)3.已知函数 f(x)=lnx ,则函数 g(x)=f(x)−f′(x) 的零点所在的区间是( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)4.已知 a,b ∈R ,函数 f(x)={x,x <013x 3−12(a +1)x 2+ax,x ≥0 ,若函数 y =f(x)−ax −b 恰有三个零点,则( ) A .a <−1,b <0B .a <−1,b >0C .a >−1,b <0D .a >−1,b >05.函数f (x )=lnx ﹣ 2x的零点所在的大致区间是( )A .(0,1)B .(1,2)C .(2,e )D .(3,4)6.下列说法正确的是( )A .函数 y =f(x) 的图象与直线 x =a 可能有两个交点;B .函数 y =log 2x 2 与函数 y =2log 2x 是同一函数;C .对于 [a,b] 上的函数 y =f(x) ,若有 f(a)⋅f(b)<0 ,那么函数 y =f(x) 在 (a,b) 内有零点;D .对于指数函数 y =a x ( a >1 )与幂函数 y =x n ( n >0 ),总存在一个 x 0 ,当 x >x 0 时,就会有 a x >x n .7.若函数f (x )=ax +b 的零点为2,那么函数g (x )=bx 2−ax 的零点是( )A .0,2B .0,12C .0,−12D .2,128.已知函数f (x )= {(2a −1)x +4a,x <11+log a x,x ≥1 是R 上的减函数,则实数a 的取值范围是( )A .[ 16 , 13 )B .[ 13 , 12 )C .( 13 , 12) D .( 12,1)9.在某实验中,测得变量x 和变量y 之间对应数据,如表则x 、y 最合适的函数是( ) A .y=2xB .y=x 2﹣1C .y=2x ﹣2D .y=log 2x10.用二分法求方程log 8x −13x=0近似解时,所取的第一个区间可以是( ) A .(0,1) B .(1,2) C .(2,3) D .(2,4)11.已知关于 x 的方程 (12)x −x 13=0 ,那么在下列区间中含有方程的根的是( )A .(0,13)B .(13,12)C .(12,23)D .(23,1)12.已知函数 f(x)={log 12(x +1),x ≥0,f(x +1),x <0, 若函数 g(x)=f(x)−x −a 有且只有两个不同的零点,则实数 a 的取值可以是( ) A .-1B .0C .1D .2二、填空题13.已知偶函数 f(x) 是定义域为R 且最小正周期为2的周期函数.当 x ∈[2,3] 时, f(x)=(x −3)2 .若函数 F(x)=log a (|x|+1)−f(x)(a >1) 在R 上恰有6个零点,则实数a 的取值范围是 .14.函数 y =11−x的图像与函数 y =2sinπx(−4≤x ≤6) 的图像所有交点的横坐标之和等于 15.已知函数 f(x)={2x 2,x ≤0e x ,x >0 ,若方程 [f(x)]2=a 恰有两个不同的实数根m ,n ,则 m +n的最大值是 .16.用长度为28米的篱笆围成一边靠墙的矩形花园,墙长为16米,则矩形花园面积的最大值是平方米.三、解答题17.已知函数f(x)=xe x −ax −alnx +a.(1)若a =e ,判断函数f(x)的单调性,并求出函数f(x)的最值. (2)若函数f(x)有两个零点,求实数a 的取值范围.18.已知函数f(x)=|x﹣1|+|x+1|(x∈R)(1)画出函数图象,并写出函数的值域;(2)求使函数F(x)=f(x)﹣n有两个不同的零点时的n的取值范围.19.已知函数f(x)=ax 2+1x,其中a∈R.(1)若a∈(0,1],判断函数f(x)在(0,1]上的单调性,并用定义加以证明;(2)若a=1,不等式mf(x2)−f(x)>0在x∈[12,2]上恒成立,求实数m的取值范围.20.某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.∈EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.(1)设MN与AB之间的距离为x米,试将∈EMN的面积S(平方米)表示成关于x的函数;(2)求∈EMN的面积S(平方米)的最大值.21.在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价﹣供货价格)(1)求售价15元时的销量及此时的供货价格;(2)当销售价格为多少时总利润最大,并求出最大利润.22.某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.R,求圆形铁皮的半径R;(1)若漏斗的半径为√32(2)这张圆形铁皮的半径R至少是多少?答案1.A2.C3.B4.C5.C6.D7.C8.B9.D10.B11.B12.B13.3<a<514.1215.3ln2-2 16.9817.(1)解:易知函数的定义域为(0,+∞),当a=e时,f(x)=xe x−ex−elnx+e,所以f(x)=(x+1)e x−e−ex=(x+1)(ex−ex),当x∈(0,1)时,f(x)<0;当x∈(1,+∞),f(x)>0;所以f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;由此可得,f(x)的最小值为f(1)=e−e−eln1+e=e,无最大值.(2)解:因为f(x)=xe x−ax−alnx+a,所以f(x)=(x+1)e x−a−ax=(x+1)(ex−ax).当a≤0时,f(x)>0在(0,+∞)上恒成立,所以f(x)在(0,+∞)上单调递增,故可得函数f(x)至多只有一个零点,不符合题意;当a>0时,令e x−ax=0,设该方程的解为x0,则在(0,x0)上,f(x)<0;在(x0,+∞)上,f(x)>0,所以f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增;为了满足f(x)有两个零点,则有f(x0)=x0e x0−ax0−alnx0+a<0①因为x0是方程e x−ax=0的解,所以x0ex0=a,两边取对数可得lnx+x0=lna②,将②式代入①式可得f(x0)=a(2−lna)<0,所以a的取值范围为a∈(e2,+∞).且当a∈(e2,+∞)时,由②式得x0>1,f(1)=e−a+a=e>0,所以f(x)在(0,x0)上仅有1个零点;当x→+∞时,f(x)→+∞,故可得f(x)在(x0,+∞)上仅有1个零点;综上,若函数f(x)存在两个零点,则实数a的取值范围是(e2,+∞).18.(1)解:图象如图所示,由图象可知值域为[2,+∞)(2)解:由图象可得n>2故n的取值范围为(2,+∞)19.(1)解:当a∈(0,1],函数f(x)在(0,1]上的单调递减.用定义证明如下:设0<x1<x2≤1,则f(x1)−f(x2)=ax12+1 x1−ax22+1x2=(x1−x2)(ax1x2−1)x1x2,∵0<x1<x2≤1,∴x1−x2<0,0<x1x2<1,∵a∈(0,1],∴0<ax1x2<1,∴ax1x2−1<0,∴f(x1)−f(x2)>0,∴f(x1)>f(x2),∴当a∈(0,1],函数f(x)在(0,1]上的单调递减(2)解:若a=1,则f(x)=x 2+1x,∴f(x2)=x4+1x2,不等式mf(x2)−f(x)>0在x∈[12,2]上可化为m(x+1x)2−2m−(x+1x)>0①,令t=x+1x,x∈[12,2],则t∈[2,52],又①可化为mt2−2m−t>0在[2,52]上恒成立,故m>tt2−2=1t−2t在[2,52]上恒成立,因为y=t−2t在[2,52]为增函数,故y=t−2t,故ymin=1,所以(1t−2t )max=1,故m>1.综上,m的取值范围为(1,+∞)20.(1)解:①如图1所示,当MN在矩形区域滑动,即0<x≤1时,∈EMN的面积S= 12×2×x =x;②如图2所示,当MN在三角形区域滑动,即1<x<1+√3时,连接EG,交CD于点F,交MN 于点H,∵E为AB中点,∴F为CD中点,GF∈CD,且FG= √3.又∵MN∈CD,∴∈MNG∈∈DCG.∴MNCD=GHGF,即MN=2[√3+1−x]√3.故∈EMN的面积S= 12×2[√3+1−x]√3×x= −√33x2+(1+√33)x;综合可得: s ={x,(0<x ≤1)−√33x 2+(1+√33)x,(1<x <1+√3) (2)解:①当MN 在矩形区域滑动时,S=x ,所以有0<S≤1;②当MN 在三角形区域滑动时,S= −√33x 2+(1+√33)x .因而,当 x =1+√32(米)时,S 得到最大值,最大值S= 12+√33 (平方米).∵12+√33>1 , ∴S 有最大值,最大值为 12+√33平方米21.(1)解:每件商品售价x (元)与销量t (万件)之间的函数关系为t=20﹣x (0≤x≤20),设价格为y ,则y= 20t,x=15时,t=5万件,y=4万元;(2)解:总利润L=(x ﹣ 20t )t=xt ﹣20=x (20﹣x )﹣20≤ (x+20−x 2)2﹣20=80,当且仅当x=10元时总利润最大,最大利润80万元.22.(1)解:漏斗高h= 12R , 则体积V= 13 π( √32 R )2h ,所以R=2 √V π3(2)解:设漏斗底面半径为r (r >0),V= 13 πr 2√R 2−r 2 ,R= √9V 2π2r 4+r 2 ,令f (r )= 9V 2π2r 4 +r 2(r >0),则f′(r )= 2π2r 6−36V 2π2r 5,所以f (r )在(0, √18V 2π26 )上单调减,( √18V 2π26,+∞)单调增,所以当r= √18V 2π26 时,R 取最小值为 √9√3V 2π3.答:这张圆形铁皮的半径R 至少为 √9√3V 2π3。
中职数学第三章测试题及答案.docx

第三章函数测试卷一、填空题:(每空 2 分)1、函数 f ( x)1 的定义域是 。
x 12、函数 f ( x)3x2 的定义域是。
3、已知函数 f (x) 3x 2,则 f (0) , f (2) 。
4、已知函数 f (x)x 21,则 f (0), f ( 2)。
5、函数的表示方法有三种,即:。
6、点 P 1,3 关于 x 轴的对称点坐标是 ;点 M (2,-3 )关于 y 轴的对称点坐标是;点 N (3, 3) 关于原点对称点坐标是。
7、函数 f (x)2x 2 1 是函数;函数 f ( x) x 3x 是函数;8、每瓶饮料的单价为元,用解析法表示应付款和购买饮料瓶数之间的函数关系 式可以表示为 。
9、常用对数表中,表示对数与对数值之间的关系采用的是 的方法。
二、选择题(每题 3 分)1、下列各点中,在函数 y 3x 1的图像上的点是( )。
A .(1,2) B. (3,4 ) C.(0,1)D.(5,6) 2、函数 y 1的定义域为()。
2x 3A .,B.,33 , C. 3 , D.3 ,2 2223、下列函数中是奇函数的是( )。
A . y x 3B.y x 21 C. y x 3D. y x 3 14、函数 y 4x 3 的单调递增区间是 ()。
A .,B.0,C.,0D.0.5、点 P (-2 ,1)关于 x 轴的对称点坐标是( )。
A .(-2 , 1) B. ( 2, 1) C.(2 ,-1) D.(-2 ,-1) 6、点 P (-2 ,1)关于原点 O 的对称点坐标是( )。
A .(-2 , 1) B. ( 2, 1) C.(2 ,-1)D.(-2 ,-1) 7、函数 y2 3x 的定义域是()。
A.222D.2 ,B.,C.,, 33338、已知函数 f (x)x27 ,则 f (3) =()。
A.-16 C. 2三、解答题:(每题 5 分)1、求函数y3x 6 的定义域。
人教版(2021)中职数学基础模块上册第三章《函数》单元测试卷课件

9.函数y=2x-3的图象不经过 ( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【答案】 B 【解析】 过点(0, 3), ( 3 , 0)画直线得直线经过第一、三、四象限.
2
10.若函数在(0,+∞)上为减函数,则f(1)与f(2)的大小关系为
A.f(1)<f(2)
B.f(1)=f(2)
B.[-3,1]
C.[1,7]
D.[-5,-3]∪[1,7]
【答案】B 【解析】略.
6.函数y=2x2+1的值域是 A.[0,+∞)
() B.(1,+∞)
【答案】C 【解析】由2x2≥0,则2x2+1≥1.
C.[1,+∞)
D.(0,+∞)
7.若函数f(x)=3x,则下列说法错误的是 ( )
A.奇函数
B.偶函数
C.单调递增函数
D.图象必过坐标原点
【答案】B 【解析】由f(x)=3x,则f(-x)=-3x=-f(x),即函数f(x)=3x为奇函数.
8.函数f(x)=ax2+bx4-2,若f(2)=8,则f(-2)= (
A.8
B.10
C.-10
) D.-12
【答案】A 【解析】由f(-x)=f(x),则f(-2)=f(2)=8.
.
x 1
【答案】 {x | 2 x 2且x 1}
【解析】
由
4 x
x 1
2
0
0
,
则
2 x 1
x
2
.
20.若函数
f
(x)
x2
1, x
1
,则f(3)=
职高数学第三章函数习题集及答案

3.1函数的概念及其表示法习题练习3.1.11、求y=3x-1的定义域:2、指出下列各函数中,哪个与函数y x=是同一个函数:(1)2xyx=;(2)y;(3)s t=.3、已知f(x)=3x+6,求f(0)、f(2)、f(-2)。
参考答案:1、R2、(3)3、6、12、0练习3.1.21、利用“描点法”作出函数xy=的图像,并判断点(16,4)是否为图像上的点2、市场上苹果的价格是8元/kg ,应付款额y是购买苹果数量x的函数.请写出其解析法。
3、市场上中性笔的价格是2元/只,应付款额y是购买中性笔数量x的函数.请写出其解析法。
参考答案:1、作图略,在。
2、y=8x,(x为正整数)3、y=2x(x为正整数)3.2函数的性质习题练习3.2.11、判断函数y=-2x+3的单调性.23、判断函数y=8X+3的单调性.参考答案:1、减2、左增、右减3、增练习3.2.21、判断y=8X+3的奇偶性:2、判断y=4X 的奇偶性3、判断y=X 2的奇偶性 参考答案:1、非奇非偶函数2、奇函数3、偶函数3.3函数的实际应用举例习题练习3.31、.求()221,20,1,0 3.x x y f x x x +-<⎧⎪==⎨-<<⎪⎩的定义域; 2、求函数()221,0,,0.x x y f x x x -⎧⎪==⎨>⎪⎩的定义域;3、求函数() 1.6,010,2.812,10.x x y f x x x <⎧==⎨->⎩的定义域; 4、作出函数()1,0,1,0x x y f x x x -<⎧==⎨+⎩的图像 5、设函数()221,20,1,0 3.x x f x x x +-<⎧⎪=⎨-<<⎪⎩作出函数的图像.6、设函数7,03,4,310,1.51,10.x y x x x x <⎧⎪=+<⎨⎪->⎩作出函数的图像 参考答案:1、-2<=x<=32、R3、x>=04、略5、略6、略。
中职数学第3章《函数》单元检测试题及答案【基础模块上册】
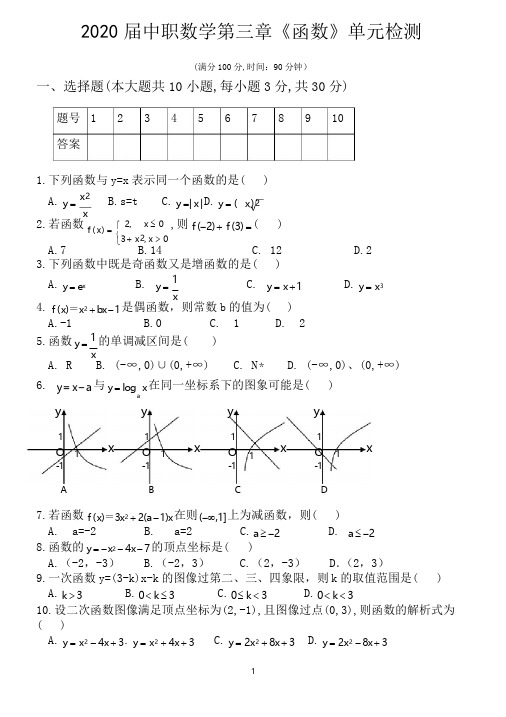
⎨12020 届中职数学第三章《函数》单元检测(满分 100 分,时间:90 分钟)一、选择题(本大题共 10 小题,每小题 3 分,共 30 分)题号 1 2 3 4 5 6 7 8 9 10答案1.下列函数与 y=x 表示同一个函数的是()A. y =x2xB.s=tC. y =| x |D. y = ( x ) 22.若函数 f ( x ) = ⎧ 2,x ≤ 0 ,则 f (-2) + f (3) = ()⎩ 3 + x 2, x > 0A.7B.14C. 12D.23.下列函数中既是奇函数又是增函数的是( )A. y = e xB. y =1xC. y = x + 1D. y = x 34. f ( x )=x 2 + bx - 1是偶函数,则常数 b 的值为( )A.-1B.0C. 1D. 2 5.函数 y = 1 的单调减区间是()xA. RB. (-∞,0)∪(0,+∞)C. N *D. (-∞,0)、(0,+∞)6. y = x - a 与 y = log x 在同一坐标系下的图象可能是() ay1O 1x-1y1O 1 x-1y1O x-1y1O 1 x-1A B C D7.若函数 f ( x )=3x 2 + 2(a - 1)x 在则 (-∞,1] 上为减函数,则( )A. a=-2B. a=2C. a ≥ -2D. a ≤ -2 8.函数的 y = - x 2 - 4 x - 7 的顶点坐标是( )A.(-2,-3)B.(-2,3)C.(2,-3) D .(2,3)9.一次函数 y=(3-k)x-k 的图像过第二、三、四象限,则 k 的取值范围是( )A. k > 3B. 0 < k ≤ 3C. 0 ≤ k < 3D. 0 < k < 310.设二次函数图像满足顶点坐标为(2,-1),且图像过点(0,3),则函数的解析式为 ( )A. y = x 2 - 4 x + 3 . y = x 2 + 4 x + 3 C. y = 2 x 2 + 8 x + 3 D. y = 2 x 2 - 8x + 33x -5 二、填空题(共 8 小题,每题 4 分,共 32 分)11.若函数 f ( x ) = ax - 2 ,且 f (2) = 4 ,则 a= 12.当 x= 时,函数 y = x 2 + 4 x + 3 有最小值13.函数 f ( x ) = x 2 - 2 x - 3 的递减区间是,递增区间是1 14.用区间表示函数 y = 的定义域为______________15.已知函数 f(x)=2x-1,则 f[f(2)]=16.若函数 f(x)=3x+m-1 是奇函数,则常数 m=17.已知二次函数 y = ( m - 3) x 2 + ( m - 2) x + 6 为偶函数,则函数的单调增区间为 18.函数 f(x)=(3k-6)x+2 在 R 上是减函数,则 k 的取值范围为三、解答题(6 小题,共 38 分)19.(8 分)求下列函数的定义域:(1) f ( x ) = 1 - x + 3 1 + x (2) f ( x ) =2 x - 1 x - 320.(6 分)f(x)是定义在(0,+∞)上的单调递减函数,且 f(x)<f(x-2),求 x 的取值范围.21.若函数 f(x)=3x-1,g(x)=x 2,求 g[f(x)]的值.22.(6 分)证明:函数 y=2x-3 在(-∞,+∞)上是增函数。
中职数学各章习题含答案

中职数学各章习题含答案中职数学各章习题含答案数学是一门重要的学科,它不仅是科学研究的基础,也是我们日常生活中必不可少的一部分。
对于中职学生来说,数学的学习更加注重实用性和应用性。
为了帮助中职学生更好地掌握数学知识,本文将为大家提供中职数学各章习题含答案。
第一章:整数与有理数1. 计算:(-3) + 5 - (-2) + (-4) = ?答案:-42. 计算:(-2) × (-3) × 4 = ?答案:243. 计算:(-5) ÷ 2 = ?答案:-2.54. 计算:(-2) ÷ (-4) = ?答案:0.5第二章:代数式与多项式1. 计算:(3x + 4y) - (2x - 5y) = ?答案:5x + 9y2. 计算:(2x + 3y) × (4x - 5y) = ?答案:8x² + 7xy - 15y²3. 计算:(3x - 2y) ÷ (x + y) = ?答案:3 - 5/(x + y)4. 计算:(2x + 3y)² = ?答案:4x² + 12xy + 9y²第三章:一次函数与一元一次方程1. 计算:解方程2x + 5 = 15答案:x = 52. 计算:解方程3(x + 2) = 15答案:x = 33. 计算:解方程2x - 3 = 5x + 2答案:x = -14. 计算:解方程2(3x - 1) = 4(2x + 3) - 4x 答案:x = -5第四章:二次函数与一元二次方程1. 计算:解方程x² - 6x + 8 = 0答案:x = 2, x = 42. 计算:解方程2x² + 3x - 2 = 0答案:x = -2, x = 0.53. 计算:解方程3x² - 4x + 1 = 0答案:x = 1/3, x = 14. 计算:解方程x² + 5x + 6 = 0答案:x = -2, x = -3第五章:函数与方程组1. 计算:解方程组2x + y = 53x - y = 1答案:x = 2, y = 12. 计算:解方程组x + y = 32x - y = 4答案:x = 2, y = 13. 计算:解方程组3x + y = 72x - 2y = 2答案:x = 2, y = 14. 计算:解方程组x + y = 22x + 3y = 7答案:x = 1, y = 1通过以上习题的训练,我们可以更好地掌握中职数学各章的知识点。
中职数学第三章测试题及答案资料讲解

第三章函数测试卷一、填空题:(每空2分)1、函数11)(+=x x f 的定义域是 。
2、函数23)(-=x x f 的定义域是 。
3、已知函数23)(-=x x f ,则=)0(f ,=)2(f 。
4、已知函数1)(2-=x x f ,则=)0(f ,=-)2(f 。
5、函数的表示方法有三种,即: 。
6、点()3,1-P 关于x 轴的对称点坐标是 ;点M (2,-3)关于y 轴的对称点坐标是 ;点)3,3(-N 关于原点对称点坐标是 。
7、函数12)(2+=x x f 是 函数;函数x x x f -=3)(是 函数;8、每瓶饮料的单价为2.5元,用解析法表示应付款和购买饮料瓶数之间的函数关系式可以表示为 。
9、常用对数表中,表示对数与对数值之间的关系采用的是 的方法。
二、选择题(每题3分)1、下列各点中,在函数13-=x y 的图像上的点是( )。
A .(1,2) B.(3,4) C.(0,1) D.(5,6)2、函数321-=x y 的定义域为( )。
A .()+∞∞-, B.⎪⎭⎫ ⎝⎛+∞⎪⎭⎫ ⎝⎛∞-,2323,Y C.⎪⎭⎫⎢⎣⎡+∞,23 D. ⎪⎭⎫ ⎝⎛+∞,23 3、下列函数中是奇函数的是( )。
A .3+=x y B.12+=x y C.3x y = D.13+=x y4、函数34+=x y 的单调递增区间是( )。
A .()+∞∞-, B. ()+∞,0 C. ()0,∞- D.[)∞+.05、点P (-2,1)关于x 轴的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)6、点P (-2,1)关于原点O 的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)7、函数x y 32-=的定义域是( )。
A .⎪⎭⎫ ⎝⎛∞-32, B.⎥⎦⎤ ⎝⎛∞-32, C. ⎪⎭⎫ ⎝⎛+∞,32 D.⎪⎭⎫⎢⎣⎡+∞,32 8、已知函数7)(2-=x x f ,则)3(-f =( )。
中职数学基础模块(上册)基础练习-第三章函数

第三章 函数第三章 第一课时 函数的概念【基础知识·一定要看】1.函数的概念设A 、B 是非空的数集,如果按照某个确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有__________的数 f x 和它对应,那么就称:f A B 为从集合A 到集合B 的一个函数.记作: y f x ,x A .其中,x 叫做自变量,x 的取值范围A 叫做函数的定义域;与x 的值相对应的y 值叫做函数值,函数值的集合 {|}f x x A 叫做函数的值域. 2.求函数定义域的常用方法: (1)分母不为零;(2)偶次根式,则被开方数大于或等于零; (3)0的0次没有意义;(4)对数的真数大于零;(还没学)3.相同函数:个函数相等当且仅当它们的定义域和对应关系完全—致,而与表示自变量和函数值的字母无关.4.分段函数:如果函数y =f (x ),x ∈A ,根据自变量x 在A 中不同的取值范围,有着不同的对应关系,则称这样的函数为分段函数. 一、选择题1.在下面四个图中,可表示函数 y f x 的图象的可能是( )A. B. C. D.2.函数1()f x x的定义域是( ) A.[2,0)(0,)B.[2,) C.RD.(,0)(0,)3.下列每组中的两个函数是同一函数的是( )A.1y 与0y x ; B.y y x ;C.y x 与2y;D.y x 与y4. 23,12,1x x f x x x ,则(2)f 等于( )A.-2 B.0C.1D.65.函数 2112f x x x, 0,4x 的值域( )A. 0,4 B. 1,5 C. 1,4D.1,526.已知 2146f x x ,则 5f 的值为( ) A.26B.20C.18D.167.已知函数 2,32,3x x f x x x .则 3f f ( )A.1 B.4 C.9 D.16二、填空题8.函数()1f x 的定义域为 . 9.若 234f x x Bx ,且 112f ,则B = . 10.已知函数()y f x 的表达式4()1f x x,若()2f a ,则实数 a . 11.二次函数 22f x x x , 1,1x ,则函数 f x 在此区间上的值域为 . 三、解答题12.已知函数 1f x ax x过点(1,5),求a 的值.第三章 第二课时 函数的表示方法【基础知识·一定要看】1.函数的三种表示方法:①待定系数法:若已知f (x )的解析式的类型,设出它的一般形式,根据特殊值确定相关的系数即可.②换元法:设t =g (x ),解出x ,代入f (g (x )),求f (t )的解析式即可. 3.常见的几种基本初等函数①正比例函数(0)y kx k ②一次函数(0)y kx b k ③反比例函数(0)ky k x④二次函数2(0)y ax bx c a 一、选择题1.已知(21)44f x x ,则(1)f 的值为( ) A.2B.4C.6D.82.函数 y f x 的图象如图所示,则 9f ( ) A.5 B.4C.3D.23.已知 212f x x x ,则 f x ( ) A.2xB.21xC.21xD.22x4.已知 f x 是反比例函数,且(3)1f ,则 f x 的解析式为( ) A. 3f x xB. 3f x xC. 3f x xD. 3f x x5.若函数 f x 和 g x 分别由下表给出: 则 1g f ( ) A.4 B.3C.2D.16.已知 32f x x ,则 21f x 等于( ) A.32xB.61x C.21xD.65x7.已知()f x 是一次函数,且(1)35f x x ,则()f x 的解析式为( ) A.()32f x xB.()32f x xC.()23f x xD.()23f x x二、填空题8.已知 22143f x x ,则 f x .9.已知函数 f x 对于任意的x 都有 212f x x f x ,则 f x . 10.已知等腰三角形的周长为18,底边长为x ,腰长为y ,则y 关于x 的函数关系式为 . 三、解答题11.已知函数 224f x x x . (1)求 0f ; (2)求 f x 的解析式.第三章 第三课时 函数的性质【基础知识·一定要看】1.函数的单调性 ①单调函数的定义 自左向右看图象是上升的自左向右看图象是下降的②证明函数单调性的步骤第一步:取值.设12x x ,是()f x 定义域内一个区间上的任意两个自变量,且12x x ; 第二步:变形.作差变形(变形方法:因式分解、配方、有理化等)或作商变形; 第三步:定号.判断差的正负或商与1的大小关系; 第四步:得出结论. 2.函数的奇偶性 ①函数奇偶性的概念偶函数:若对于定义域内的任意一个x ,都有 f x f x ,那么 f x 称为偶函数. 奇函数:若对于定义域内的任意一个x ,都有 f x f x ,那么 f x 称为奇函数. ②奇偶函数的图象与性质偶函数:函数()f x 是偶函数 函数()f x 的图象关于y 轴对称; 奇函数:函数()f x 是奇函数 函数()f x 的图象关于原点中心对称;若奇函数()y f x 在0x 处有意义,则有(0)0f .③用定义判断函数奇偶性的步骤第一步:求函数()f x 的定义域,判断函数的定义域是否_______________,若不关于原点对称,则该函数既不是奇函数,也不是偶函数,若关于原点对称,则进行下一步;第二步:求()f x ,若 f x f x ,则()f x 是奇函数;若()f x =()f x ,则()f x 是偶函数;若()()f x f x ,则()f x 既不是奇函数,也不是偶函数;若()()f x f x 且 f x f x ,则()f x 既是奇函数,又是偶函数.1.若函数 1y a x b ,x R 在其定义域上是增函数,则( ) A.1aB.1aC.0bD.0b2.函数 f x 在R 上是减函数,则有( ) A. 25f fB. 25f fC. 25f fD. 25f f3.下列函数中,既是偶函数又在 0, 上单调递增的函数是( ) A.y xB.1y xC.21y xD.1y x4.若偶函数 f x 在 ,1 上是减函数,则( ) A. 2.513f f f B. 1 2.53f f f C. 3 2.51f f fD. 31 2.5f f f5.函数 f x 是定义在 0, 上的增函数,则满足 1213f x f的x 的取值范围是( ) A.12,33B.12,33C.12,23D.12,236.函数22y x x 单调减区间是( ) A.1,2B. 1,C.1,2D. ,【填空】7.已知 f x 是偶函数, 12f ,则 11f f .8.函数()y f x 是定义在R 上的增函数,且 29f m f m ,则实数m 的取值范围是 .9.函数()y f x 是定义在R 上的奇函数,当0x 时,3()f x x x ,则(2)f .10.已知 y f x 在定义域 0,1上是减函数,且 121f a f a ,则实数a 的取值范围 .11.已知函数2()()2f x x m .(1)若函数()f x 的图象过点(2,2),求函数y ()f x 的单调递增区间; (2)若函数()f x 是偶函数,求m 值.12.已知函数 1f x x x(1)判断 f x 的奇偶性并说明理由; (2)判断 f x 在 0,1上的单调性并加以证明.第三章 第四课时 函数的应用一、选择题1.据调查,某存车处(只存放自行车和电动车)在某天的存车量为400辆次,其中电动车存车费是每辆一次2元,自行车存车费是每辆一次1元.若该天自行车存车量为x 辆次,存车总收入为y 元,则y 关于x 的函数关系式是( ) A. 4000400y x x B. 8000400y x x C. 4000400y x xD. 8000400y x x2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P (千帕)是气球体积V (立方米)的反比例函数,其图像如图所示,则这个函数的解析式为( )A.69P VB.96P VC.69P VD.96P V3.某物体一天中的温度T 是时间t 的函数:3()360T t t t ,时间的单位是小时,温度的单位是C ,0 t 表示中午12时,其后取值为正,其前取值为负,则上午8时的温度为( ) A.18CB.8CC.0CD.4C二、填空题4.若某一品种的练习册每本2.5元,则购买x 本的费用y 与x 的函数关系是 . 5.某社区超市的某种商品的日利润y (单位:元)与该商品的当日售价x (单位:元)之间的关系为21221025x y x ,那么该商品的日利润最大时,当日售价为 元.三、解答题6.某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:(1)经过对上表中数据的探究,发现这种读物的投入成本 (元)是印数 (册)的一次函数,求这个一次函数的解析式(不要求写出的取值范围); (2)如果出版社投入成本48000元,那么能印该读物多少册?x x7.制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y (℃),从加热开始计算的时间为 min x .据了解,设该材料加热时,温度y 与时间x 成一次函数关系;停止加热进行操作时,温度y 与时间x 成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5min 后温度达到60℃.(1)分别求出将材料加热和停止加热进行操作时,y 与x 的函数关系式;(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?。
中职数学基础模块上册第三章《函数》单元检测试题及参考答案

中职数学第三章《函数》单元检测(满分100分,时间:90分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.下列各组的两个函数,表示同一个函数的是( )A.x x y 2=与x y =B.2xx y =与x y 1= C.||x y =与x y = D.2)(x y =与x y =2.若函数22,0()3,0x f x x x ≤⎧=⎨+>⎩ ,则=+-)3()2(f f ( ) A.7 B.14 C. 12 D.23.下列函数中既是奇函数又是增函数的是( )A.23x y =B. xy 1= C. 1+=x y D.3x y = 4.一次函数y=2x+1的图像不经过的象限是( )A. 第一B. 第二C. 第三D. 第四5.函数1y x=的单调减区间是( )A. RB. (-∞,0)∪(0,+∞) C. N * D. (-∞,0)、(0,+∞) 6. y x a =-与log a y x =在同一坐标系下的图象可能是( )7.已知函数()21f x x +=,则)2(+x f =( )A. 2x +1B. 2x +5C. x +2D. x8.一次函数b kx y +=的图像关于原点对称,则二次函数c bx ax y ++=2)0(≠a 的图像关于( )对称。
A.x 轴B.y 轴C.原点 D .直线y=xA9.不等式022≥+-m x x 对于一切实数均成立,则m 的取值范围是( ) A.0>m B.0<m C.1≥m D.1≤m 10.设二次函数图像满足顶点坐标为(2,-1),且图像过点(0,3),则函数的解析式为( )A.342+-=x x y .342++=x x y C.3822++=x x y D.3822+-=x x y二、填空题(共8小题,每题4分,共32分)11.若函数2()34f x x x =+-,则()0f x ≥的解集为:12.设函数⎩⎨⎧>+≤-=)0(,2)0(,1)(2x x x x x f ,则)]2([-f f =13.函数y=24++x x 的定义域为 14.用区间表示函数y =13x -5 的定义域为______________15.已知函数f(x)=2x-1,则f[f(2)]= 16.若函数f(x)=3x+m-1是奇函数,则常数m=17.已知一次函数的图像过点(-1,2)、(2,-1),则其解析式为__________ 18.已知二次函数6)2()3(2+-+-=x m x m y 为偶函数,则函数的单调增区间为:三、解答题(6小题,共38分)19.判断函数1()f x x x=+的奇偶性。
(完整版)中职数学第三章习题及答案

第三章:函数一、填空题:(每空2分)11、函数f (x) —的定义域是 _____________________________ 。
x 12、函数f (x) 3x 2的定义域是______________________________ 。
3、已知函数f(x) 3x 2,贝U f (0) _____ , f (2) _______ 。
4、已知函数f (x) x21,则f(0) _______ , f ( 2) _________ 。
5、函数的表示方法有三种,即:______________________________________ 。
6点P 1,3关于x轴的对称点坐标是 ____________ ;点M (2, -3)关于y轴的对称点坐标是_________ ;点N(3, 3)关于原点对称点坐标是______________ 。
7、函数f(x) 2x2 1是 ___________ 函数;函数f(x) x3 x是______________ 函数;8、每瓶饮料的单价为2.5元,用解析法表示应付款和购买饮料瓶数之间的函数关系式可以表示为___________ 。
9、常用对数表中,表示对数与对数值之间的关系采用的是___________ 的方法。
二、选择题(每题3分)1、下列各点中,在函数y 3x 1的图像上的点是( )。
A. (1, 2)B. (3,4)C.(0,1)D.(5,6)2、函数 1y的疋义域为( )。
2x3f 333 f 3A. B. ,£ C., D.-22223、下列函数中是奇函数的是( )。
A. y :x 32B. y x 1C.3y x3D.y x 14、函数y 4x3的单调递增区间是()0A. B. 0, C.,0 D. 0.5、点P(-2,1) 关于x轴的对称点坐标是( )。
A. (-2, 1)B. (2, 1)C.(2,-1)D.(-2, -1)6、点P(-2,1) 关于原点0的对称点坐标是( )0A. (-2, 1)B. (2, 1)C.(2,-1)D.(-2, -1)7、函数y 23x的定义域是( )。
2021高职高考数学复习第三章函数:考题直通

A.[ 3 , ) 4
B.[ 4 , ) 3
C.(, 3] 4
D.(, 4] 3
【答案】C 由3 4x 0得 : x ,选C.
8.(2019年)函数y=lg(x+2)的定义域是 ( )
A.(-2,+∞)
B.[-2,+∞)
C.(-∞,-2)
D.(-∞,-2]
【答案】A 要使函数有意义,只要x+2>0,求得x>-2.∴函数y=lg(x+2)的定 义域为(-2,+∞),故选A.
12.(2015年)已知函数f(x)是奇函数,且f(2)=1,则[f(-2)]3= ( )
A.-8
B.-1
C.1
D.8
【答案】B ∵函数是奇函数,且f(2)=1, ∴f(-2)=-1, [f(-2)]3=(-1)3=-1.
13.(2016年)函数f(x)是偶函数,y=f(x)的图象经过点(2,-5),则下 列等式恒成立的是 ( ) A.f(-2)=5 B. f(-2)=-5 C. f(-5)=2 D. f(-5)=-2
考题直通
一、选择题
1.(2018年)已知函数f
(
x)
x x
3, x 0 2 1, x 0
,
设c
f (2),则f (c)
A.1
B.0
C. 1
D. 2
【答案】 B Q 2 0,c f (2) 2 3 1,Q 1 0, f (c) f (1) (1)2 1 0,选B.
A.4
B.-4
C.2
D.-2
【答案】C 由题意可知, f(x)=3x2+bx-1是偶函数,则b=0, 所以f(x)=3x2-1
f(-1)=3×(-1)2-1=2,故选C.
中职数学第三章测试题及答案

第三章函数测试卷一、填空题:(每空2分)1、函数11)(+=x x f 的定义域是 。
2、函数23)(-=x x f 的定义域是 。
3、已知函数23)(-=x x f ,则=)0(f ,=)2(f 。
4、已知函数1)(2-=x x f ,则=)0(f ,=-)2(f 。
5、函数的表示方法有三种,即: 。
6、点()3,1-P 关于x 轴的对称点坐标是 ;点M (2,-3)关于y 轴的对称点坐标是 ;点)3,3(-N 关于原点对称点坐标是 。
7、函数12)(2+=x x f 是 函数;函数x x x f -=3)(是 函数;8、每瓶饮料的单价为2.5元,用解析法表示应付款和购买饮料瓶数之间的函数关系式可以表示为 。
9、常用对数表中,表示对数与对数值之间的关系采用的是 的方法。
二、选择题(每题3分)1、下列各点中,在函数13-=x y 的图像上的点是( )。
A .(1,2) B.(3,4) C.(0,1) D.(5,6)2、函数321-=x y 的定义域为( )。
A .()+∞∞-, B.⎪⎭⎫ ⎝⎛+∞⎪⎭⎫ ⎝⎛∞-,2323, C.⎪⎭⎫⎢⎣⎡+∞,23 D. ⎪⎭⎫ ⎝⎛+∞,23 3、下列函数中是奇函数的是( )。
A .3+=x y B.12+=x y C.3x y = D.13+=x y4、函数34+=x y 的单调递增区间是( )。
A .()+∞∞-, B. ()+∞,0 C. ()0,∞- D.[)∞+.05、点P (-2,1)关于x 轴的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)6、点P (-2,1)关于原点O 的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)7、函数x y 32-=的定义域是( )。
A .⎪⎭⎫ ⎝⎛∞-32, B.⎥⎦⎤ ⎝⎛∞-32, C. ⎪⎭⎫ ⎝⎛+∞,32 D.⎪⎭⎫⎢⎣⎡+∞,32 8、已知函数7)(2-=x x f ,则)3(-f =( )。
职高高一数学第三章函数复习题精编版

职高高一数学第三章函数复习题精编版MQS system office room 【MQS16H-TTMS2A-MQSS8Q8-MQSH16898】复习题3第三章函数班级__________姓名___________学号________一、 选择题:1、函数2231)(x x x f -+=的定义域是()A 、{x|-2<x<2}B 、{x|-3<x<3}C 、{x|-1<x<2}D 、{x|-1<x<3}2、已知函数11)(-+=x x x f ,则f(-x)=() A 、)(1x f B 、-f(x)C 、-)(1x f D 、f(x) 3、函数f(x)=342+-x x ()A 、在(2,∞-)内是减函数B 、在(4,∞-)内是减函数C 、在(0,∞-)内是减函数D 、在(+∞∞-,)内是减函数4、下列函数中既是奇函数又是偶函数的是()A 、y=3xB 、y=x 1C 、22x y =D 、x y 31-= 5、奇函数y=f(x)(x ∈R)的图像必经过的点是()A(-a,-f(a))B(-a,f(a)) C(a,-f(a))D(a,)(1a f ) 二、填空题 (1)设f(x)=,0,32,0,3{2>+≤-x x x x 则f(-2)=_______________. (2)函数y=21x -的定义域为_______________.(3)设f(x)=542-x ,则f(2)=______________,f(x+1)=_______________.(4)函数y=22-x 的增区间为____________________.(5)已知f(x)=,0,3,0,3{3>-≤-x x x x 则f(-2)=____________,f(2)=_______________.3.设函数f (x )=722-x ,求f(-1),f(5),f(a),f(x+h)的值.4.求下列函数的定义域:(1)f(x)=112-+x x ;(2)f(x)=x x 322+. 5.讨论下列函数的奇偶性:(1)f(x)=3-52x ;(2)g(x)=212+-x x (3)f(x)=x(2x +1)6.设f(x)=⎪⎪⎩⎪⎪⎨⎧--,23,2,2x x .0,01,1≥<≤--<x x x(1)写出函数的定义域;(2)求f(-2),f (-21),f(3)的值; (3)作出函数f (x )的图像.7.为了鼓励居民节约用水,某市改革居民用水的计费方法,每月的收费标准如下:月用水量不超过203m 时,按2元/3m 计费,每月用水量超过203m 时,其中的203m 按2元/3m 计费,超过的部分按元/3m 计费,设每户月用水量为x 3m ,应交水费为y 元。
第三章函数测试卷及答案

第三章函数测试卷一、选择题(本大是20个小题,每小题3分,共60分)1.已知函数 )(x f 的图像关于原点对称,)(x g = )(x f +4,且)2(g =5,则)2(-g = ( )A.-3B. 3C. 5D.-52.已知函数)(x f =21-+x x ,则)0(f ,)3(f 的值分别是 ( ) A. 21,4 B. 21-,4 C. 21,-4 D.21-,-43.设函数769)3(2++=x x x f ,则=-)3(f( ) A. 15 B. 16 C. 10 D. 224.已知函数⎩⎨⎧<-->+-=)0(3)0(12)(x x x x x f ,则[]}{)3(f f f 等于 ( )A.-3B. 3C. -9D. 95.已知32)(2+-=x x x f ,若)1()(+=x f x g ,则=)0(g ( )A. 4B. 3C. 5D. 66.函数2515)(2-+-=x x x f 的定义域是 ( )A. )5,(--∞B. ),5(+∞C.[]5,5-D. ∅7.下列函数中,在区间)2,0(上是增函数的是 ( )A.x y -=3B.x y 1= C x y -= D.22+=x y 8.若抛物线k x x y +-=232与x 轴没有公共点,则k 的取值范围是( ) A.),3(+∞ B. ),31(+∞ C.)31,(-∞ D. 无法确定9.函数)11(2<≤-=x x y 的奇偶性是( )A.奇函数B.偶函数C.既是奇函数又是偶函数D.既不是奇函数又不是偶函数10.若函数5)1(3)(2+-+=x a x x f 在区间(]1,∞-上是减函数,则a 的取值范围是 ( )A.{}5-B.(]5,-∞-C.{}5D. [)+∞,511.已知函数)(x f 为偶函数,若点),(b a 在)(x f 的图像上,则下列各点一定在)(x f 的图像上的是 ( )A.),(b a -B. ),(b a -C.),(b a --D.),(a b12.给出下列函数:①11+•-=x x y ②3232-++=x x y③ 12-=x y ④x x y +=21其中非奇非偶的函数的个数为 ( )A. 1B. 2C. 3D. 413. 已知二次函数1)(2++=bx ax x f 的对称轴方程是1=x ,且过点)7,1(-,则a 与b 的值分别是A. 2,-2B. 2,-4C. -2,4D. -2,214.设函数34)(2+-=x x x f ,[]4,1∈x ,则)(x f 的最小值为 ( )A. -1B. 0C. 3D. -215.下列表示同一函数的是 ( ) A. 11+•-=x x y 与12-=x y B.()()353)(+-+=x x x x f 与5)(-=x x g C.()522-=x y 与52-=x y D. x y =与33x y =16. 已知函数)(x f 是()+∞∞-,上的偶函数,当0≥x 时,)1()(+=x x x f ,则当0≤x 时,)(x f 的解析式为 ( )A.)1()(x x x f --=B.)1()(x x x f -=C.)1()(x x x f +-=D.)1()(+=x x x f17.如果二次函数)(x f 的顶点是()1,3-,并且它的图像经过点()4,0,那么这个二次函数的解析式是 ( )A.1)3(31)(2+-=x x fB.1)3(31)(2++=x x f C.3)3()(2++=x x f D.5)3()(2--=x x f18.已知函数)(x f 是奇函数且在R 上是增函数,则不等式0)()1(≥+x f x 的解集为 ( )A. (]1,0-B.[)+∞,0C.(]1,-∞-D.(][)+∞⋃-∞-,01,19.设函数11)(22+-=x x x f ,则=)21()2(f f ( ) A. 1 B. -1 C.53 D.53- 20.若不等式022<++c bx x 的解集是()4,0,函数c bx x x f ++=2)(2的对称轴是 ( )A.2=xB. 4=xC.25=xD. 23=x 二、填空题(本天题5个小题,每小题4分,共20分)21.函数44)(22-+-=x x x f 的定义域是 .22.已知3)12(x x f =+,则=-)3(f .23.函数362)(2+-=x x x f 在区间[]4,2-上的最大值是 .24. 已知函数b a bx ax x f +-+=53)(2是偶函数,且其定义域为[]a a ,1-,则b a +=25.已知函数⎪⎩⎪⎨⎧<-≥+=),0(,),0(,1)(2x x x x x f 则5)(=x f 的解集是 . 三、解答题(本大题5个小题。
中职数学第三章函数测试题

中职数学第三章函数测试题work Information Technology Company.2020YEAR2第三章单元测试试卷姓名: 班别:一、选择题1. 下列函数中,定义域是[0,+)的函数是( ).A .y =2xB .y=log 2xC . y=x 1D .y=x2. 下列函数中,在(-∞,0)内为减函数的是( ).A .y= -x 2+2B .y =7x +2C .x y 1-=D . y=2x 2-13. 下列函数中的偶函数是( ).A . y =x +1B .y =-3x ²C .y =∣x-1∣D . y =x 32 4. 下列函数中的奇函数是( ).A .y =3x -2B .y=x 3C .y=2x 2D . y=x 2-x5. 下列函数中,在(0,+∞)内为增函数的是( ).A .y= -x 2B .y=x 1C .y=2x 2D .y =x ⎪⎭⎫ ⎝⎛216. 下列图象表示的函数中,奇函数是( ).二、填空题7. 已知函数f (x )的图象(如图),则函数f (x )在区间(-1,0)内是 函数(填“增”或 “减”),在区间(0,1)内是 函数(填“增”或 “减”).y x O y x O y x O y x O A B C D y x O -1 2 1 -2 3 第7题图 x 1 5 2 3 4 y = f (x ) O y 第11题O y x -1 3 -2 1 2 y = f (x ) 第12题图 -338. 根据实验数据得知,在不同大气压下,水的沸点T (单位:︒C)与大气压P ((5)在此函数关系中,自变量是 ,因变量是 ;(2)当自变量的值为2.0时,对应的函数值为 ;(3)此函数的定义域是 .9. 已知g (x ) =125+-x x ,则g (2)= ,g (0)= ,g (-1)= . 10. 函数15-+=xx y 的定义域是 . 11. 设函数f (x )在区间(-∞,+∞)内为增函数(如上第11图),则f (4) f (2)(填“>”或“<”).12. 设函数f (x )在区间(-3,3)内为减函数(如上第12图),则f (2) f (-2)(填“>”或“<”).三、解答题13. 求下列函数的定义域:(1)f (x )=log10(5x-2) (2) f (x(3)f (x )= x x -++121. (4) ()12-=x x f14. 利用定义判断下列函数的奇偶性:(1(3)f (x )= x 2-1 (4)f (x )=2x 3-x .15. 255ml的雪碧每瓶2.6元,假设购买的数量x瓶,花了y元,(1)请根据题目条件,用解析式将y表示成x的函数;(2)如果小林要买5瓶雪碧,共要花多少钱?(3)如果小林有50元,最多可购买了多少瓶雪碧?米,深为6米的长方体蓄水池,池壁每平方米的16. 修建一个容积为80003造价为a元,池底每平方米的造价为2a元,请将总造价y表示为底的一边长x米的函数;17、某地出租车按如下方法收费:起步价10元,可行3km(不含3km);3km到7km(不含7km)按1.6元/km计价(不足1km,按1km计算);7km以后按2.4元/km(不足1km,按1km计算),试写出以行车里程为自变量,车费为函数值的函数解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1函数的概念及其表示法习题
练习3.1.1
1、求y=3x-1的定义域:
2、指出下列各函数中,哪个与函数y x
=是同一个函数:
(1)
2
x
y
x
=;(2
)y;(3)s t=.
3、已知f(x)=3x+6,求f(0)、f(2)、f(-2)。
参考答案:
1、R
2、(3)
3、6、12、0
练习3.1.2
1、利用“描点法”作出函数x
y=的图像,并判断点(16,4)是否为图像上的点
2、市场上苹果的价格是8元/kg ,应付款额y是购买苹果数量x的函数.请写出其解析法。
3、市场上中性笔的价格是2元/只,应付款额y是购买中性笔数量x的函数.请写出其解析法。
参考答案:
1、作图略,在。
2、y=8x,(x为正整数)
3、y=2x(x为正整数)
3.2函数的性质习题
练习3.2.1
1、判断函数y=-2x+3的单调性.
2
3、判断函数
y=8X+3的单调性.
参考答案:
2、左增、右减
练习3.2.2
1、判断y=8X+3的奇偶性:
2、判断y=4X 的奇偶性
3、判断y=X 2
的奇偶性
参考答案:
1、非奇非偶函数
2、奇函数
3、偶函数
3.3函数的实际应用举例习题
练习3.3
1、.求()221,
20,1,
0 3.x x y f x x x +-<⎧⎪==⎨-<<⎪⎩的定义域; 2、求函数()221,0,,0.x x y f x x x -⎧⎪==⎨>⎪⎩的定义域;
3、求函数() 1.6,010,2.812,10.x x y f x x x <⎧==⎨->⎩
的定义域; 4、作出函数()1,0,1,
0x x y f x x x -<⎧==⎨+⎩的图像 5、设函数()221,20,1,0 3.x x f x x x +-<⎧⎪=⎨-<<⎪⎩作出函数的图像.
6、设函数7,03,4,
310,1.51,10.x y x x x x <⎧⎪=+<⎨⎪->⎩
作出函数的图像 参考答案:
1、-2<=x<=3
2、R
3、x>=0
4、略
5、略
6、略
(注:文档可能无法思考全面,请浏览后下载,供参考。
)。
