初一数学(七下)几何证明题
初一数学图形与证明试题答案及解析

初一数学图形与证明试题答案及解析1.如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是()A.30°B.25°C.20°D.15°【答案】B【解析】如图:根据题意可得:a∥b,∴∠3=∠1=20°,∵∠ABC=45°,∴∠2=∠ABC-∠3=45°-20°=25°,故选:B.【考点】1.平行线的性质;2.直角三角板的性质.2.(4分)如图所示的长方形或正方形三类卡片各有若干张,请你用这些卡片,拼成一个面积是2a2+3ab+b2长方形(要求:所拼图形中每类卡片都要有,卡片之间不能重叠。
)画出示意图,并计算出它的面积。
【答案】见解析【解析】因为第一类图形面积为ab,第二类图形面积为b2,第三类图形面积为a2,而要拼成的长方形的面积2a2+3ab+b2,所以需要第一B类卡片3张,第二类卡片1张,第三类卡片2张.试题解析:如图:因为第一类图形面积为ab,第二类图形面积为b2,第三类图形面积为a2,所以需要第一B类卡片3张,第二类卡片1张,第三类卡片2张,可以拼成一个长为2a+b,宽为a+b的长方形,所以长方形面积为(2a+b)(a+b)=2a2+3ab+b2.【考点】整式的运算.3.有两根13cm,15cm的木棒,要想以这两根木棒做一个三角形,可以选用第三根木棒的长为()A.2cm B.11cm C.28cm D.30cm【答案】B【解析】因为两边长13cm,15cm,所以第三边x的长满足:15-13<x<15+13,即2<x<28,所以选项A、C、D错误,B正确,故选:B.【考点】三角形的三边关系.4.(9分)如图,已知∠AOB是直角,∠BOC=600, OE平分∠AOC,OF平分∠BOC.(1)求∠EOF的度数;(2)若将条件“∠AOB是直角,∠BOC=600”改为:∠AOB= x0,∠EOF=y0,条件不变.①则请用x的代数式来表示y.②如果∠AOB+∠EOF=1560.则∠EOF是多少度?【答案】(1)45°;m(2)①y=x,②52°.【解析】(1)根据角平分线的定义和角的和差倍分的关系即可求得∠EOF的度数;(2)①把(1)中的数字换成字母即可解得x与y的关系;②根据x+y=156°,y=x即可解得x、y的值.试题解析:(1)∵∠AOB=90°,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.∴∠EOF=∠EOC-∠FOC=∠AOC-∠BOC= (∠AOB+∠BOC)-∠BOC=∠AOB=×=90°=45°.(2)①∵∠AOB=x°,∠EOF=y°,OE平分∠AOC,OF平分∠BOC.∴∠EOF=∠EOC-∠FOC=∠AOC-∠BOC= (∠AOB+∠BOC)-∠BOC=∠AOB.即y=x.②∵∠AOB+∠EOF=156°.则x+y=156°,又∵y=x.代入解得x=104°,y=52°.即∠EOF=52°.【考点】角平分线的性质;角的计算.5.如图,要使图中平面展开图按虚线折叠成正方体后,相对面上的两个数相等,则x-2y=________.【答案】-6.【解析】由题意知:x=2,y=4,所以x-2y=2-8=-6.【考点】正方体的平面展开图.6.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE= °.【答案】10.【解析】∵AE是△ABC的角平分线,∴∠EAC=∠BAC=64º,∵∠C=36°,AD⊥BC,∴∠DAC=54º,∴∠DAE=64-54=10º.【考点】角分线和直角三角形两锐角互余的应用.7.如图,AB∥CD,∠CED=900,EF⊥CD,F为垂足,则图中与∠EDF互余的角有().A.4个B.3个C.2个D.1个【答案】B.【解析】因为∠CED=900,所以∠EDF+∠ECD=90°,因为EF⊥CD,所以∠EDF+∠FED=90°,因为AB∥CD,所以∠ECD=∠AEC,所以图中与∠EDF互余的角有∠ECD,∠FED,∠AEC,共3个.故选:B.【考点】互余的定义;平行线的性质;垂直的定义.8.如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.(1)求∠COD的度数;(2)求∠BOF的度数.【答案】(1)144°;(2)63°【解析】(1)先根据互余的关系求出∠COE=54°,然后利用∠COD=∠DOE+∠COE计算即可;(2)先根据互余的关系求出∠AOD=54°,再求出∠BOD和∠DOF,利用角的和差关系即可求出∠BOF.试题解析:(1)∵∠AOC=90°,∴∠COE=90°﹣AOE=90°﹣36°=54°,∴∠COD=∠DOE+∠COE=90°+54°=144°;(2)∵∠DOE=90°,∠AOE=36°,∴∠AOD=90°﹣36°=54°,∵∠AOB=90°,∴∠BOD=90°﹣54°=36°,∵OF平分∠AOD,∴∠DOF=∠AOD=27°,∴∠BOF=36°+27°=63°.【考点】1.余角和补角;2.角平分线的定义.9.如图,线段AD=18cm,线段AC=BD=12cm,E、F分别是线段AB、CD的中点,求线段EF的长.【答案】12cm【解析】先利用线段的和差故选求出BC的长,从而可得(AB+CD)的长,然后根据线段中点的性质,可得AE与AB的关系,FD与CD的关系,再根据线段的和差关系解答即可.试题解析:根据图形可知:AC+BD=AC+(CD+BC)=AC+CD+BC=12+12=24cm,由AD=18cm,得18+BC=24,解得BC=6cm.所以AB+CD=AD﹣BC=18﹣6=12cm.因为E、F分别是线段AB、CD的中点,所以AE= AB,FD= CD.所以AE+FD= AB+ CD=(AB+CD)=×12=6cm,所以EF=AD﹣AE﹣FD=18﹣6=12cm.【考点】两点间的距离.10.如图,把一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2=.【答案】25°.【解析】如图:因为直尺的对边平行,所以∠1的内错角=∠1=20°,所以∠2=45°-20°=25°.【考点】平行线的性质.11.(本题满分12分)如图(1),四边形ABCD中,AD∥BC,点E是线段CD上一点,(1)说明:∠AEB=∠DAE+∠CBE;(2)如图(2),当AE平分∠DAC,∠ABC=∠BAC.①说明:∠ABE+∠AEB=900;②如图(3)若∠ACD的平分线与BA的延长线交于点F,且∠F=600,求∠BCD.【答案】(1)见解析;(2)见解析;(3)∠BCD=600【解析】(1)如图(1),过点E作EF∥BC,交AB于F.根据平行线的性质可证得结论;(2)①如图(2),根据平行线的性质和互为补角,角平分线的性质可证;②根据平行线的性质和角平分线的性质,可求结果.试题解析:解:(1)如图(1),过点E作EF∥BC,交AB于F.∵EF∥BC,AD∥BC∴EF∥AD∥BC∴∠DAE=∠AEF,∠CBE=∠BEF∴∠AEF+∠BEF=∠DAE+∠CBE∵∠AEB=∠AEF+∠BEF∴∠AEB=∠DAE+∠CBE.(2)如图(2)∠ABC+∠BAC+∠ACB=180°∵∠ABC=∠BAC,∠ACB=2∠DAE∴2∠ABC+2∠DAE=180°即∠ABC+∠DAE=90°∠ABC=∠ABE+∠CBE由(1)得∠AEB=∠DAE+∠CBE∴∠ABE+∠AEB=90°.(3)∠ACB=180°-∠ABC-∠BAC=180°-2∠BAC∵∠BAC=∠F+∠ACF∴∠ACB=180°-2(∠F+∠ACF)=180°-2×60°-2∠ACF∵CF平分∠ACD∴∠ACD=2∠ACF即∠ACB=180°-2×60°-∠ACD得∠ACB+∠ACD=60°即∠BCD=60°.【考点】平行线的性质,角平分线的性质,互为补角12.(3分)已知∠AOB=40°,∠CDE的边CD⊥OA于点D,边DE∥OB,那么∠CDE= .【答案】50°或130°.【解析】根据题意,作出草图,如图,DE∥OB,由平行线的性质可得∠AED=∠AOB=40°,又因CD⊥OA,可求得∠1=50°,∠2=130°,∠CDE可能是∠1也可能是∠2,所以∠CDE等于50°或130°.【考点】平行线的性质.13.有如下命题:①负数没有立方根;②同位角相等;③对顶角相等;④如果一个数的立方根是这个数本身,那么这个数是1或0,其中,是假命题的有()A.①②③B.①②④C.②④D.①④【答案】B【解析】因为负数有一个负的立方根,所以①为假命题;因为两直线平行,同位角相等,所以②为假命题;对顶角相等,所以③为真命题;因为如果一个数的立方根是这个数本身,那么这个数是1或0或﹣1,所以④为假命题.故选B.【考点】命题与定理.14.如图,钟表8时30分时,时针与分针所成的锐角的度数为.【答案】75°.【解析】8点30分,时针和分针中间相差2.5个大格,∵钟面12个大格,第相邻两个数字之间的夹角为30°,∴8时30分时,时针与分针的夹角是2.5×30°=75°.【考点】钟面角.15.如图,把弯曲的河道改直,能够缩短航程,这样做根据的道理是.【答案】两点之间线段最短.【解析】由两点之间线段最短可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理:两点之间线段最短.【考点】线段的性质:两点之间线段最短.16.如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是()A.70° B.65° C.55° D.22.5°【答案】C【解析】根据平行线的性质可由EG平分∠BEF,得∠BEG=∠GEF,再根据平行线的性质:两直线平行,内错角相等,由AB∥CD,求得∠BEG=∠2,再根据等量代换可求∠2=∠GEF,因此由三角形的内角和定理知∠1=70°,∠1+∠2+∠GEF=180°,可得∠2=55°.故选C.【考点】平行线的性质17.如图,∠AOC=90°,ON是锐角∠COD的角平分线,OM是∠AOD的角平分线,那么,∠MON= °.【答案】45°【解析】根据ON是锐角∠COD的角平分线,OM是∠AOD的角平分线,得出∠AOM=∠MOD,∠CON=∠NOD,又∠AOC=90°即可得出∠AOM=∠MOD=45°+∠COD.进而求出∠MON的度数为45°.【考点】角平分线的定义18.把命题“同角的余角相等”改写成“如果…那么…”的形式.【答案】如果两个角是同一个角的余角,那么这两个角相等.【解析】根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”,【考点】命题与定理.19.(7分)如图所示,O是直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.(1)求∠COD的度数.(2)判断OD与AB的位置关系,并说出理由.【答案】(1)45°(2)OD⊥AB.理由见试题解析。
七年级数学典型几何证明50题
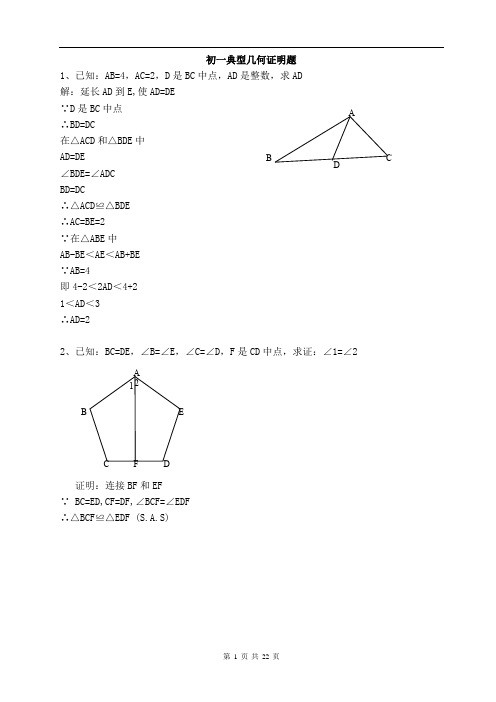
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
春七年级数学下册相交线与平行线几何证明题(含答案)

2018年春七年级数学下册相交线与平行线几何证明题1.如图,已知AD//BE,∠1=∠2.求证:∠A=∠E.2.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.求∠PAG的度数.3.如图,已知AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.4.如图,AB∥CD,BE,DE分别平分∠ABF,∠FDC,试问∠E与∠F之间的数量关系如何?请说明理由.5.如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.求证:CD⊥AB.6.如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?7.如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:8.如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.9.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.10.(1)如图1,已知任意三角形ABC,过点C作DE∥AB,求证:∠DCA=∠A;(2)如图1,求证:三角形ABC的三个内角(即∠A,∠B,∠ACB)之和等于180°;(3)如图2,求证:∠AGF=∠AEF+∠F;(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F的度数.11.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?(3)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?(4)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?12.如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140º,求∠BFD的度数.13.如图,已知∠1 =∠2,∠3 =∠4,∠5 =∠6.求证:ED∥FB.14.如图,已知∠BAP+∠APD=180°,∠1 =∠2.求证:∠E =∠F.15.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)说明:∠O=∠BEO+∠DFO.(2)如果将折一次改为折二次,如图-2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.16.如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,(1)若∠AEF=50°,求∠EFG的度数.(2)判断EG与FG的位置关系,并说明理由.17.(1)如图(1),已知任意三角形ABC,过点C作DE∥AB.求证:∠DCA=∠A;(2)如图(1),求证:三角形ABC的三个内角(即∠A.∠B、∠ACB)之和等于180°;(3)如图(2),求证:∠AGF=∠AEF+∠F;(4)如图(3),AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°.求∠F.18.如图,已知∠1=250,∠2=450, ∠3=300,∠4=100.求证:AB//CD.19.如图,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明。
(完整版)七年级数学几何证明题

七年级数学几何证明题1. 如图,在ABC中,D在AB上,且△ CAD^P A CBE都是等边三角形, 求证:(1)DE=AB(2)Z EDB=602. 如图,在A ABC中, AD平分/ BAC DE||AC,EF丄AD交BC延长线于F。
求证:/ FAC" B3. 已知,如图,在厶ABC中,AD,AE分别是△ ABC的高和角平分线,若/ B=30/ C=50°求:(1),求/ DAE的度数。
(2)试写出 / DAE与 / C - / B 有何关系?(不必证明)B D C4、一个零件的形状如图,按规定/ A=9Oo,/ C=25o,Z B=25o,检验已量得/运用三角形的有关知识说明零件不合格的理BDC=150,就判断这个零件不合格,由。
5、如图,已知DF // AC, / C=Z D,你能否判断CE // BD?试说明你的理由6、如图,△ ABC中,D在BC的延长线上,过D作DE丄AB于E,交AC于F.已知/ A=30 ° ,Z FCD=80° ,求/D。
7、如图,BE平分/ ABD , CF平分/ ACD , BE、CF交于G, 若/ BDC = 140。
,/ BGC = 110。
,则 / A ?C 8、如图,AD丄BC于D, EG丄BC于G,Z E =Z 1,求证AD 平分/ BAC9、如图,直线。
丘交厶ABC的边AB AC于D E,交BC延长线于F, 若/ B= 67°,/ ACB= 74°,/ AED= 48°,求/ BDF的度数•10、如图,将一副三角板叠放在一起,使直角的顶点重合于O,贝U/ AOC/ DOB11、如图,将两块直角三角尺的直角顶点C叠放在一起•(1)若/ DCE=35,求/ ACB的度数;(2)若/ ACB=140,求/ DCE的度数;(3)猜想:/ ACB与/ DCE有怎样的数量关系,并说明理由12、已知:直线AB与直线CD相交于点0,/ BOC= 45°,(1) 如图1,若EO丄AB,求/ DOE的度数;(2) 如图2,若EO平分/ AOC,求/ DOE的度数.13、已知AOB , P为OA上一点.(1)过点P画一条直线PQ,使PQ // OB ;(2)过点P画一条直线PM,使PM丄OA交0B于点M ;(3)若AOB 40 ,贝U PMO ?14、如图。
七年级下册数学期末考试几何大题证明必考题
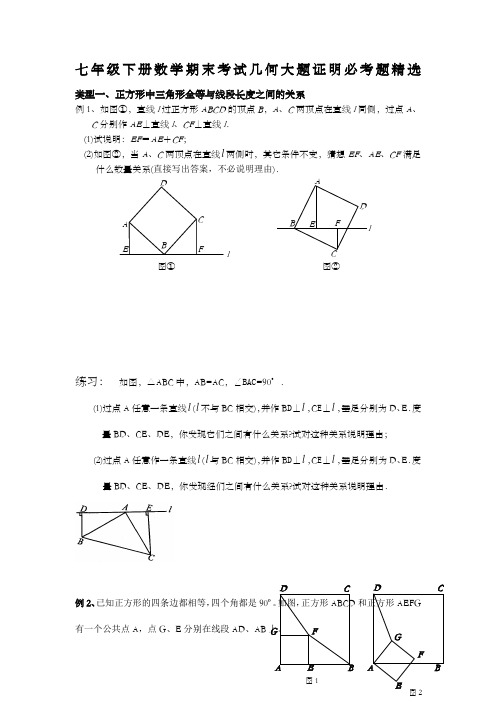
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
A E B 图1D CG FA BD CG FE图2(1)如图1, 连结DF 、BF ,说明:DF =BF ; (2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上画出示意图,并请求出这个大正方形的面积.附加:如图,△ABC 与△ADE 都是等边三角形,连结BD 、CE(1)BD 与CE 相等吗?请说明理由.A BCFDE GP32B(2)你能求出BD与CE的夹角∠BFC的度数吗?(3)若将已知条件改为:四边形ABCD与四边形AEFG都是正方形,连结BE、DG交点记为点M(如图).请直接写出线段BE和DGF例3、正方形四边条边都相等,四个角都是90o.如图,已知正方形ABCD在直线MN 的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.(1)如图1,当点E在线段BC上(不与点B、C重合)时:①判断△ADG与△ABE是否全等,并说明理由;②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;(2)如图2,当点E在射线CN上(不与点C重合)时:①判断△ADG与△ABE是否全等,不需说明理由;②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.图 2FG DA图 1FDA类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论.(4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o ,R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.CBAPDE2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的; (3)说明图(5)所得结论为什么是正确的.ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形,将一块含30o 角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立C图1吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
初中数学-几何证明经典试题(含答案)

初中数学-⼏何证明经典试题(含答案)初中⼏何证明题已知:如图,O 是半圆的圆⼼,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF 已知:如图,P 是正⽅形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三⾓形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正⽅形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正⽅形.4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(⼆)A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF 1、已知:△ABC 中,H 为垂⼼(各边⾼线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初⼆)2、设MN 是圆O 外⼀直线,过O 作OA ⊥MN 于A ,⾃A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初⼆)3、如果上题把直线MN 由圆外平移⾄圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初⼆)4、如图,分别以△ABC 的AC 和BC 为⼀边,在△ABC 的外侧作正⽅形ACDE 和正⽅形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的⼀半.经典题(三)1、如图,四边形ABCD 为正⽅形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初⼆)2、如图,四边形ABCD 为正⽅形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初⼆)3、设P 是正⽅形ABCD ⼀边求证:PA =PF .(初⼆)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)E1、已知:△ABC 是正三⾓形,P 是三⾓形内⼀点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初⼆)2、设P 是平⾏四边形ABCD 内部的⼀点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初⼆)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平⾏四边形ABCD 中,设E 、F 分别是BC 、AB 上的⼀点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初⼆)经典难题(五)1、设P 是边长为1的正△ABC 内任⼀点,L =PA +PB +PC ,D求证:≤L<2.2、已知:P是边长为1的正⽅形ABCD内的⼀点,求PA+PB+PC的最⼩值.3、P为正⽅形ABCD内的⼀点,并且PA=a,PB=2a,PC=3a,求正⽅形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(⼀)1.如下图做GH⊥AB,连接EO。
初一数学几何证明题答案

初一典型几何证明题1、已知: AB=4,AC=2,D是BC中点, AD是整数,求AD解:延长A D到 E,使AD=DE∵D是 BC中点A ∴BD=DC在△ ACD和△ BDE中AD=DE∠BDE=∠ADC B CDBD=DC∴△ACD≌△ BDE∴AC=BE=2∵在△ ABE中AB-BE<AE<AB+BE∵AB=4即 4-2<2AD<4+21<AD<3∴AD=22、已知: BC=DE,∠B=∠E,∠ C=∠D,F 是 CD中点,求证:∠1=∠2A21B EC F D证明:连接BF和 EF∵BC=ED,CF=DF∠, BCF=∠EDF∴△BCF≌△ EDF 第1页共22 页∴BF=EF,∠CBF=∠DEFB E连接在△ BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在△ ABF和△ AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ABF≌△ AEF。
∴∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=D,E EF证明:连接EF ∵AB∥CD共22 页第9页∴∠B=∠C∴△BEM≌△CFM( SAS)∵M是 BC中点∴CF=BE∴BM=CM在△BEM和△CFM中BE=CF∠B=∠CBM=CM7. 已知:如图所示,AB=AD,BC=DC,E、F 分别是DC、BC的中点,求证:AE=AF。
证:连接AC DE=BF∵在△ ADC和△ABC中∴△ADE≌△ ABF(SAS)AD=AB ∴AE=AFDC=BCAC=AC∴△ADC≌△ ABC(SSS)D∴∠B=∠ DE∵E、F 分别是DC、BC的中点AC又∵ BC=DCF∴DE=BFB∵在△ ADE和△ABF中AD=AB∠D=∠B8. 如图,在四边形ABCD中, E是AC上的一点,∠1=∠2,∠3=∠4,求证 : ∠5=∠6.证明:∵在△ADC和△ ABC中∴△DEC≌△ BEC(SAS)∠BAC=∠DAC ∴∠DEC=∠BEC∠BCA=∠DCAAC=AC∴△ADC≌△ ABC(AAS)D∵AB=AD,BC=CD在△ DEC与△ BEC中A12E5634CCE=CEB∠BCA=∠DCABC=CD9. 如图,在△ABC中, AD为∠ BAC的平分线,DE⊥AB于 E,DF⊥AC于 F。
七年级下几何证明题

第4题H2DC 几何说理题1、填空完成推理过程: 如图,∵AB ∥EF (已知)∴∠A+=1800() ∵DE ∥BC (已知) ∴∠DEF=() ∠ADE=()2.如图,EF ∥AD ,∠1=∠2,∠BAC=70°.将求∠AGD 的过程填写完整.因为EF ∥AD ,所以∠2=. 又因为∠1=∠2,所以∠1=∠3. 所以AB ∥. 所以∠BAC+=180°. 又因为∠BAC=70°, 所以∠AGD=.3.已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.4.已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.5.已知:如图,AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数 6、直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.49、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37o ,求∠D 的度数.50、如图,已知:21∠∠=,50=D ∠,求B ∠的度数。
51、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.52、AB//CD,EF ⊥AB 于点E ,EF 交CD 于点F ,已知∠1=600.求∠2的度数.53、如图,AB∥CD,BF∥CE,则∠B 与∠C 有什么关系?请说明理由.54.如图,已知:DE∥BC,CD 是∠ACB 的平分线,∠B=70°,∠ACB =50°,求∠EDC 和∠BDC 的度数.55.如图AB∥CD,∠NCM=90°,∠NCB=30°,CM 平分∠BCE,求∠B 的大小.56、如图,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?DEB CAENMCD BANMFDCBA57、如图,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.58、如图,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .59、如图所示,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.60、如图,在△ABC 中,∠ABC =80°,∠ACB =50°,BP 平分∠ABC ,CP 平分∠ACB ,求∠BPC 的度数.61、如图,点D 是△ABC 内一点,∠A =65°,∠1=20°,∠2=25°,求∠BDC 的度数。
专题1.11 《平行线》几何模型1(知识讲解)七年级数学下册基础知识专项讲练(浙教版)
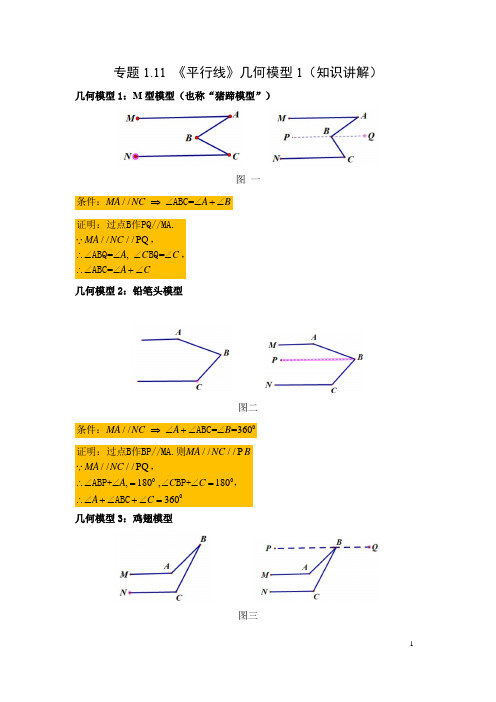
专题1.11 《平行线》几何模型1(知识讲解)几何模型1:M 型模型(也称“猪蹄模型”)图 一//=MA NC A B ⇒∠∠+∠条件:ABC ////PQ =,==MA NC A C C A C∴∠∠∠∠∴∠∠+∠证明:过点B 作PQ//MA.,ABQ BQ ,ABC几何模型2:铅笔头模型图二0//==360MA NC A B ⇒∠+∠∠条件:ABC000////P ////PQ ,180,180360MA NC BMA NC A C C A C∴∠∠=∠∠=∴∠+∠+∠=证明:过点B 作BP//MA.则,ABP+BP+,ABC几何模型3:鸡翅模型图三//-=MA NC A B ⇒∠∠∠条件:C////PQ ////PQ ,,,MA NC MA NC A C C B CBQ A C B∴∠∠∠∠∴∠=∠∠∴∠-∠=∠证明:过点B 作PQ//MA.则,ABQ=BQ=,ABQ-几何模型4:折鸡翅模型图四//MA NC A B ⇒∠=∠+∠条件:C ////PQ ////PQ ,,,MA NC MA NC A C C ABC CBQ A ACB C∴∠∠∠∠∴∠=∠∠∴∠==∠+∠证明:过点B 作PQ//MA.则,ABQ=BQ=,ABQ-几何模型5:多个M 型模型12121//......n n MA NB P PPAQ Q Q B -⇒∠+∠++∠=∠+∠+∠++∠条件: 证明思路参考几何模型1几何模型6:多个铅笔头模型12121//......n n MA NB P P P A Q Q Q B -⇒∠+∠++∠=∠+∠+∠++∠条件: 证明思路参考几何模型2类型一、M 型模型1(2020·宁波市惠贞书院七年级期中)如图,//AB EF ,设90C ∠=︒,那么x ,y ,z 的关系式______.【答案】90x y z +-=︒【分析】过C 作//CN AB ,过D 作//DM AB ,根据平行线的性质可知//////AB CN DM EF ,然后根据平行线的性质即可求解;解:如图,过C 作//CN AB ,过D 作//DM AB ,∴//////AB CN DM EF ,∴1x =∠,23∠∠=,4z ∠=,∴90BCD ∠=︒,∴1290∠+∠=︒,∴390x +∠=︒,∴3490x z +∠+∠=︒+,∴90x y z +=︒+,∴90x y z +-=︒.故答案为:90x y z +-=︒.【点拨】本题考查了平行线的性质,两直线平行同位角相等,两直线平行内错角相等,正确理解平行线的性质是解题的关键;举一反三:【变式1】(2020·四川成都市·天府四中七年级期中)如图,//,,3527'EE MN CA CB EAC ⊥∠=︒,则MBC ∠=____________________.【答案】5433'【分析】过C 点做EF 的平行线,利用平行线的性质,即可证明.解:过C 点做EF 的平行线,GH//,EF MN////,EF GH MN ∴3527'EAC ACH ∴∠=∠=,又,CA CB ⊥90,ACB ∴∠=︒5433',HCB ACB ACH ∴∠=∠-∠=︒又//,GH MN5433'HCB CBM ∴∠=∠=.故答案为:5433'.【点拨】本题考查了通过平行线的性质求解角度问题,解题关键在于过中间的点作已知直线的平行线.【变式2】(2019·辽宁大连市·七年级期末)阅读材料:如图1,点A 是直线MN 上一点,MN 上方的四边形ABCD 中,140ABC ∠=︒,延长BC ,2DCE MAD ADC ∠=∠+∠,探究DCE ∠与MAB ∠的数量关系,并证明.小白的想法是:“作ECF ECD ∠=∠(如图2),通过推理可以得到CF MN ,从而得出结论”.请按照小白的想法.....完成解答:拓展延伸:保留原题条件不变,CG 平分ECD ∠,反向延长CG ,交MAB ∠的平分线于点H (如图3),设MAB α∠=,请直接写出H ∠的度数(用含α的式子表示).【答案】阅读材料:40∠=︒+∠ECD MAB ,见解析;拓展延伸:120CHA α=∠︒-. 【分析】(1)作ECF ECD ∠=∠,DG MN ,BH MN ,由平行线性质可得180MAD ADG ∠+∠=︒,结合已知2DCE MAD ADC ∠=∠+∠,可证180CDG DCF ∠+∠=︒,进而得到DG CF ,从而CF BH ,140BCF MAB ABC ∠+∠=∠=︒,将180180BCF ECF ECD ∠=︒-∠=︒-∠代入可得40∠=︒+∠ECD MAB .(2)过H 点作HP∴MN ,可得∴CHA=∴PHA+∴PHC ,结合(1)的结论和CG 平分∴ECD 可得∴PHC =∴FCH =120°-3MAB 2∠,即可得120CHA α=∠︒-.解:【阅读材料】作ECF ECD ∠=∠,DG MN ,BH MN (如图1).∵DG MN ,∴180MAD ADG ∠+∠=︒.∴()180CDG MAD ADC ∠+∠+∠=︒.∵2DCE MAD ADC ∠=∠+∠,∴2180CDG DCE ∠+∠=︒.∴180CDG DCF ∠+∠=︒.∴DG CF .∵DG MN ,∴MN CF .∵BH MN ,∴CF BH .∴BCF CBH ∠=∠,MAB ABH ∠=∠.∴140BCF MAB ABC ∠+∠=∠=︒.∵180180BCF ECF ECD ∠=︒-∠=︒-∠,∴40∠=︒+∠ECD MAB .【拓展延伸】结论:120CHA α=∠︒-.理由:如图,作ECF ECD ∠=∠,过H 点作HP∴MN ,∴∴PHA=∴MAH=1BAM 2∠,由(1)得FC∴MN ,∴FC∴HP ,∴∴PHC=∴FCH ,∴40∠=︒+∠ECD MAB ,CG 平分∴ECD , ∴∴ECG=20°+1MAB 2∠,∴∴FCH=180ECG ECF ︒-∠-∠=180°-(40MAB ︒+∠)-(20°+1MAB 2∠)=120°-3MAB 2∠ ∴∴CHA=∴PHA+∴PHC=1MAB 2∠∠+(120°-3MAB 2∠)=120°-MAB ∠即:120CHA α=∠︒-.【点评】本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角(补角)相等进行推导.余角和补角计算的应用,常常与等式的性质、等量代换相关联.解题时注意方程思想的运用. 类型二、铅笔头型模型2 (2020·山东聊城市·七年级期末)直线AB 、CD 被直线EF 所截,AB∴CD ,点P 是平面内一动点.(1)若点P 在直线CD 上,如图∴,∴α=50°,则∴2= °.(2)若点P 在直线AB 、CD 之间,如图∴,试猜想∴α、∴1、∴2之间的等量关系并给出证明;(3)若点P在直线CD的下方,如图∴,(2)中∴α、∴1、∴2之间的关系还成立吗?请作出判断并说明理由.【答案】(1)50;(2)∴α=∴1+∴2,证明见解析;(3)不成立.理由见解析.【分析】(1)由题意直接根据平行线的性质可直接求解;(2)由题意过P作PG∴AB,则PG∴AB∴CD,利用平行线的性质即可求解;(3)根据题意过P作PH∴AB,则PH∴AB∴CD,利用平行线的性质进行分析即可求解.解:(1)∵AB∥CD,∠α=50°∴∠2=∠α=50°,故答案为:50;(2)∠α=∠1+∠2.证明:过P作PG∥AB,∵AB∥CD,∴PG∥AB∥CD,∴∠2=∠EPG,∠1=∠FPG,∵∠α=∠EPF=∠EPG+∠FPG,∴∠α=∠1+∠2;(3)不成立.理由:过P 作PH ∥AB ,∵AB ∥CD ,∴PH ∥AB ∥CD ,∴∠2=∠EPH ,∠1=∠FPH ,∵∠α=∠EPF =∠EPH ﹣∠FPH ,∴∠α=∠2﹣∠1,故不成立.【点拨】本题主要考查平行线的性质,注意掌握并灵活运用平行线的性质是解题的关键. 举一反三:【变式1】(2020·河北邢台市·八年级月考)如图1,四边形MNBD 为一张长方形纸片.(1)如图2,将长方形纸片剪两刀,剪出三个角(BAE AEC ECD ∠∠∠、、),则BAE AEC ECD ∠+∠+∠=__________°.(2)如图3,将长方形纸片剪三刀,剪出四个角(BAE AEF EFC FCD ∠∠∠∠、、、),则BAE AEF EFC FCD ∠+∠+∠+∠=__________°.(3)如图4,将长方形纸片剪四刀,剪出五个角(BAE AEF EFG FGC GCD ∠∠∠∠∠、、、、),则BAE AEF EFG FGC GCD ∠+∠+∠+∠+∠=___________°.(4)根据前面探索出的规律,将本题按照上述剪法剪n 刀,剪出()1n +个角,那么这()1n +个角的和是____________°.【答案】(1)360;(2)540;(3)720;(4)180n.【分析】(1)过点E作EH∴AB,再根据两直线平行,同旁内角互补即可得到三个角的和等于180°的2倍;(2)分别过E、F分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;(3)分别过E、F、G分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;(4)根据前三问个的剪法,剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.证明:(1)过E作EH∥AB(如图②).∵原四边形是长方形,∴AB∥CD,又∵EH∥AB,∴CD∥EH(平行于同一条直线的两条直线互相平行).∵EH∥AB,∴∠A+∠1=180°(两直线平行,同旁内角互补).∵CD∥EH,∴∠2+∠C=180°(两直线平行,同旁内角互补).∴∠A+∠1+∠2+∠C=360°,又∵∠1+∠2=∠AEC,∴∠BAE+∠AEC+∠ECD=360°;(2)分别过E、F分别作AB的平行线,如图③所示,用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°;(3)分别过E 、F 、G 分别作AB 的平行线,如图④所示,用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°;(4)由此可得一般规律:剪n 刀,剪出n+1个角,那么这n+1个角的和是180n 度. 故答案为:(1)360;(2)540;(3)720;(4)180n .【点拨】题主要考查了多边形的内角和,作平行线并利用两直线平行,同旁内角互补是解本题的关键,总结规律求解是本题的难点.举一反三:【变式2】(2020·湖北随州市·七年级期末)已知12l l //,点A ,C 分别在直线1l ,2l 上,点B 在直线1l 与2l 之间,90BCN BAM ∠<∠≤︒.(1)如图1,求证:ABC BAM BCN ∠=∠+∠.阅读并补齐下列推理过程过点B 作//BG NC ,因为12l l //,所以//AM _____(______________)所以ABG BAM ∠=∠,CBG BCN ∠=∠(_______________________)所以ABC ABG CBG BAM BCN ∠=∠+∠=∠+∠.解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,在学习中要注意体会.(2)如图2,点D ,E 在直线1l 上,DBC BAM ∠=∠,BE 平分ABC ∠,求证:DBE DEB ∠=∠.(3)在(2)的条件下,过点B 作BF 平分CBE ∠,请直接写出使//BF AM 时,BAM ∠与BCN ∠之间应具备的关系.【答案】(1)BG ,平行于同一条直线的两条直线平行,两条直线平行内错角相等;(2)见解析;(3)3BAM BCN ∠=∠【分析】(1)添加平行线,根据平行于同一条直线的两条直线平行,再利用平行线的性质进行角的等量代换;(2)与(1)同理,通过添加平行线,根据平行于同一条直线的两条直线平行,再利用平行线的性质、角平分线的定义进行角的等量代换;(3)在(2)的条件下,根据已有的数量关系,加上平行线得到的内错角相等进行等量代换即可.解:(1)BG ,平行于同一条直线的两条直线平行,两条直线平行内错角相等;(2)过点B 作BG //NC ,12//l l ,AM //BG ∴DEB EBG ∴∠=∠,CBG BCN ∠=∠,由(1)知,ABC BAM BCN ∠=∠+∠,又DBC BAM ∠=∠,ABC DBC BCN ∴∠=∠+∠,ABC ABD DBC ∠=∠+∠,ABD BCN ∴∠=∠,∴ABD CBG ∠=∠, BE 平分ABC ∠,ABE CBE ∴∠=∠,DBE EBG ∴∠=∠,DEB DBE ∴∠=∠(3)BAM 3BCN ∠=∠,理由如下:∴DBC =∴DBE +∴EBF +∴FBC ,∴BF∴AM ,∴∴EBF =∴DEB ,∴BF 平分∴CBE ,∴∴CBF =∴EFB ,而由(2)知:∴DBE =∴DEB ,∴∴DBC =3∴FBC ,∴CN∴AM ,∴CN∴BF ,∴∴FBC=∴BCN,∴DBC=3∴BCN,而∴BAM=∴DBC,∴∴BAM=3∴BCN【点拨】本题考查平行线的推论和性质,熟练掌握平行线的性质,并灵活进行等量代换是关键.。
北师大版七年级数学下册几何常见模型练习题(有答案)

全等三角形判定的三种类型已知一边一角型一次全等型1.已知,如图△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.2.如图,在△ABC中,D是BC边上的一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.求证:AD是△ABC的中线.两次全等型3.如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC =∠BEC.4.如图,在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,AE⊥BD于F交BC于E.(1)求证:∠ABD=∠CAE.(2)求证:∠ADB=∠CDE.(3)直接写出BD、AE、ED之间满足的数量关系.已知两边型一次全等型5.如图,点B,F,C,E在直线l上(点F,点C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)指出图中所有平行的线段,并说明理由.两次全等型6.如图所示,AB=CB,AD=CD,E是BD上任意一点,求证:AE=CE.7.如图:已知AE交BD于点C,∠DAC=∠EBC=∠BAC,AB=AC.试说明:DC与BE有怎样的数量关系.已知两角型一次全等型8.如图,已知∠BDC=∠CEB=90°,BE、CD交于点O,且AO平分∠BAC,求证:OB=OC.三角形中的四种常见说理类型说明相等关系1.如图,△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC上的点,且AE=AF,求证:DE=DF.说明位置关系说明平行关系2.已知△ABC为等边三角形,点P在AB上,以CP为边长作等边三角形△PCE.求证:AE∥BC.说明垂直关系3.如图,△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,且BD=CF,BE=CD,G是EF的中点,求证:DG⊥EF.说明倍分关系说明角的倍分关系4.如图,△ABC中,AB=AC,BD⊥AC于D.猜想:∠DBC与∠BAC之间的数量关系,并予以证明.说明线段的倍分关系5.如图,△ABC中,AB=AC,AD和BE是高,它们相交于H,且AE=BE.(1)求∠C的度数.(2)求证:AH=2BD.说明和、差关系6.如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.线段垂直平分线与角平分线的应用类型典例例1.已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.(1)求证:AE=BF;(2)求线段DG的长.利用线段垂直平分线的性质求线段的长1.如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.利用线段垂直平分线的性质求角的度数2.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连接AD.(1)若△ADC的周长为16,AB=12,求△ABC的周长;(2)若AD将∠CAB分成两个角,且∠CAD:∠DAB=2:5,求∠ADC的度数.利用线段垂直平分线的性质解决实际问题3.某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?利用线段垂直平分线的性质说明线段的数量关系4.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P放在射线OM上,两直角边分别与OA,OB交于点C,D.(1)证明:PC=PD.(2)若OP=4,求OC+OD的长度.利用线段垂直平分线的性质说明线段的位置关系5.如图所示,AD为△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,EF交AD于点M,求证:AM ⊥EF.全等三角形判定的三种类型1.证明:如右图所示,∵BD=DC,∴∠3=∠4,又∵∠1=∠2,∴∠1+∠3=∠2+∠4,即∠ABC=∠ACB,∴△ABC是等腰三角形,∴AB=AC,在△ABD和△ACD中,∴△ABD≌△ACD(SAS),∴∠BAD=∠CAD,∴AD平分∠BAC.2.证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠F=90°,在△BED和△CFD中,,∴△BED≌△CFD,∴BD=CD,∴AD是△ABC的中线.3.证明:在△ACD和△ACB中,,∴△ACD≌△ACB,(ASA)∴BC=CD,在△DCE和△BCE中,,∴△DCE≌△BCE(ASA),∴∠DEC=∠BEC.4.(1)证明:∵AE⊥BD,∴∠AFB=∠BAC=90°,∴∠ABD+∠BAF=90°,∠BAF+∠CAE=90°,∴∠ABD=∠CAE.(2)证明:过C作CM⊥AC,交AE的延长线于M,则∠ACM=90°=∠BAC,∴CM∥AB,∴∠MCE=∠ABC=∠ACB,∵∠BAF=∠ADB,∠ADB+∠F AD=90°,∠ABD+∠BAF=90°,∴∠ABD=∠CAM,在△ABD和△CAM中,,∴△ABD≌△CAM(ASA),∴∠ADB=∠M,AD=CM,BD=AM,∵D为AC中点,∴AD=DC=CM,在△CDE和△CME中,,∴△CDE≌△CME(SAS),∴∠M=∠CDE,∴∠ADB=∠CDE.(3)解:结论:BD=AE+DE.理由:∵△CDE≌△CME,∴ME=DE,∵AM=AE+ME=AE+DE,∵BD=AM,∴BD=AE+DE.5.(1)证明:∵BF=CE,∴BF+FC=FC+CE,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SSS);(2)解:结论:AB∥DE,AC∥DF.理由:∵△ABC≌△DEF,∴∠ABC=∠DEF,∠ACB=∠DFE,∴AB∥DE,AC∥DF.6.证明:在△ABD与△CBD中,∴△ABD≌△CBD(SSS),∴∠ABD=∠CBD,在△ABE与△CBE中,△ABE≌△CBE(SAS),∴AE=CE.7.解:DC=BE,∵∠EBC=∠BAC,∠ACD=∠BAC+∠ABC,∠ABE=∠EBC+∠ABC,∴∠ACD=∠ABE,在△ACD和△ABE中,,∴△ACD≌△ABE(ASA),∴DC=BE.8.证明:∵∠BDC=∠CEB=90°,∴CD⊥AB,BE⊥AC,∵AO平分∠BAC,∴OD=OE,在△BDO和△CEO中∴△BDO≌△CEO(ASA),∴OB=OC.三角形中的四种常见说理类型1.证明:连接AD,∵AB=AC,D是BC的中点,∴∠EAD=∠F AD,在△AED和△AFD中,,∴△AED≌△AFD(SAS),∴DE=DF.2、证明:∵△ABC与△PCE为等边三角形,∴AC=BC,EC=PC,∠BCA=∠PCE=60°,∴∠BCP=∠ACE,在△BCP和△ACE中,,∴△CBP≌△CAE(SAS),∴∠CAE=∠B=60゜=∠ACB,∴AE∥BC.3.证明:连ED,DF,∵AB=AC,∴∠B=∠C,在△BED和△CDF中,,∴△BDE≌△CFD(SAS),∴DE=DF,∵G是EF的中点,∴DG⊥EF.4.解:∠DBC=∠BAC.设∠C=β,∵AB=AC,∴∠ABC=∠C=β,∴∠BAC=180°﹣2β,∠BAD=∠ABC+∠C=2β,∵BD⊥AC,∴∠ABD=90°﹣2β,∴∠DBC=90°﹣β,∴∠DBC=∠BAC.5.(1)解:∵AE=BE,BE⊥AC,∴∠BAE=45°,又∵AB=AC,∴∠C=(180°﹣∠BAE)=(180°﹣45°)=67.5°;(2)证明:∵AB=AC,AD⊥BC,∴BC=2BD,∠1+∠C=90°,∵BE⊥AC,∴∠2+∠C=90°,∴∠1=∠2,在△AEH和△BEC中,,∴△AEH≌△BEC(ASA),∴AH=BC,∴AH=2BD.6.证明:如图,在AC上截取AE=AB,∵AD平分∠BAC,∴∠CAD=∠BAD,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴DE=BD,∠AED=∠ABC,∵∠AED=∠C+∠CDE,∠ABC=2∠C,∴∠CDE=∠C,∴CE=DE,∵AE+CE=AC,∴AB+BD=AC.线段垂直平分线与角平分线的应用类型例1.(1)证明:连接AD、BD,∵AD是∠BCA的平分线,DE⊥AC,DF⊥BC,∴DE=DF,∵DG是AB边的垂直平分线,∴AD=DB,在Rt△AED和Rt△DFB中,,∴Rt△AED≌Rt△BFD(HL),∴AE=BF;(2)由(1)得:CE=CF==7,∴AE=EC﹣AC=1,∵∠ECD=∠EDC=45°,∴DE=CE=7,由题意可得:AG=BG=5,∴AD2=AE2+DE2=50,∴DG2=AD2﹣AG2=25,∴DG=5.1.解:∵DE是BC的垂直平分线,∴CD=BD,∴△ACD的周长=AC+AD+CD=AC+BD+AD=AC+AB,由题意得,,解得.∴AB和AC的长分别为8.5cm,5.5cm.2.解:(1)∵DE是AB的垂直平分线,∴AD=BD,又∵△ADC的周长为16,∴AD+CD+AC=16,即BD+CD+AC=BC+AC=16,又AB=12,∴AB+BC+AC=16+12=28,则△ABC的周长为28;(2)∵AD=BD,∴∠BAD=∠ABD,∵∠CAD:∠DAB=2:5,设一份为x,即∠CAD=2x,∠DAB=∠ABD=5x,又∠C=90°,∴∠ABD+∠BAC=90°,即2x+5x+5x=90°,解得:x=7.5°,∵∠ADC为△ABD的外角,∴∠ADC=∠DAB+∠ABD=5x+5x=10x=75°.3.解:如图,这所中学建在P点位置(点P为△ABC的外心).连结AB、BC、AC,作AB和BC的垂直平分线,两垂直平分线相交于点P,则点P到点A、B、C的距离相等.4.证明:(1)如图,过点P作PE⊥OA于点E,PF⊥OB于点F,∴∠PEC=∠PFD=90°.∵OM是∠AOB的平分线,∴PE=PF,∵∠AOB=90°,∠CPD=90°,∴∠PCE+∠PDO=360°﹣90°﹣90°=180°.而∠PDO+∠PDF=180°,∴∠PCE=∠PDF在△PCE和△PDF中∴△PCE≌△PDF(AAS)∴PC=PD;(2)∵∠AOB=90°,OM平分∠AOB,∴△POE与△POF为等腰直角三角形,∴OE=PE=PF=OF,∵OP=4,∴OE=2,由(1)知△PCE≌△PDF ∴CE=DF ∴OC+OD=OE+OF=2OE=4.5.证明:∵DE⊥AC于点E,DF⊥AB于点F,∴∠AED=∠AFD=90°,∵AD为三角形ABC的角平分线,∴∠EAD=∠F AD,而AD=AD,∴△AED≌△AFD∴ED=DF,AE=AF∴△AEF为等腰三角形,AM为∠BAC的平分线∴AM是△AEF的高,即AM⊥EF.。
初一数学几何证明题答案

初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23、4、 证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDFBC DF ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
已知:∠1=∠2,CD=DE ,EFP 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-ABBA CDF2 1 EA在AC 上取点E , 使AE =AB 。
∵AE =AB AP =AP ∠EAP =∠BAE ,∴△EAP ≌△BAP ∴PE =PB 。
PC <EC +PE∴PC <(AC -AE )+PB ∴PC -PB <AC -AB 。
8. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE 证明:在AC 上取一点D ,使得角DBC=角C ∵∠ABC=3∠C∴∠ABD=∠ABC-∠DBC=3∠C-∠C=2∠C ; ∵∠ADB=∠C+∠DBC=2∠C; ∴AB=AD∴AC – AB =AC-AD=CD=BD在等腰三角形ABD 中,AE 是角BAD 的角平分线, ∴AE 垂直BD∵BE ⊥AE∴点E 一定在直线BD 上,在等腰三角形ABD 中,AB=AD ,AE 垂直BD ∴点E 也是BD 的中点 ∴BD=2BE ∵BD=CD=AC-AB ∴AC-AB=2BE9. 如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .P DACB解:延长AD 至BC于点E,∵BD=DC ∴△BDC是等腰三角形∴∠DBC=∠DCB又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2即∠ABC=∠ACB∴△ABC是等腰三角形∴AB=AC在△ABD和△ACD中AB=AC∠1=∠2BD=DC∴△ABD和△ACD是全等三角形(边角边)∴∠BAD=∠CAD∴AE是△ABC的中垂线∴AE⊥BC∴AD⊥BC10. 如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA证明:∵OM平分∠POQ∴∠POM=∠QOM∵MA⊥OP,MB⊥OQ∴∠MAO =∠MBO =90 ∵OM =OM∴△AOM ≌△BOM (AAS ) ∴OA =OB ∵ON =ON∴△AON ≌△BON (SAS ) ∴∠OAB=∠OBA ,∠ONA=∠ONB ∵∠ONA+∠ONB =180 ∴∠ONA =∠ONB =90 ∴OM ⊥AB11. 如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB . 证明:在AB 上取F ,使AF =AD ,连接EF ∵AE 平分∠DAB ∴∠DAE=∠FAE 在⊿ADE 和⊿AFE 中AD =AF ∠DAE=∠FAE AE = AE∴⊿ADE ≌⊿AFE (SAS ) ∴∠ADE=∠AFE∵AB 如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立若成立PEDCBA{{请给予证明;若不成立请说明理由.(1)证:∵DE ⊥AC 于E ,BF ⊥AC 于F , ∴∠DEC=∠BFA=90°,DE ∥BF , 在Rt △DEC 和Rt △BFA 中, ∵AF=CE ,AB=CD , ∴Rt △DEC ≌Rt △BFA (HL ) ∴DE=BF .在△DEM 和△BFM 中 ∠DEM=∠BFM ∠DME=∠BMF DE=BF∴△DEM ≌△BFM(AAS) ∴MB=MD ,ME=MF(2) 证:∵DE ⊥AC 于E ,BF ⊥AC 于F , ∴∠DEC=∠BFA=90°,DE ∥BF , 在Rt △DEC 和Rt △BFA 中, ∵AF=CE ,AB=CD , ∴Rt △DEC ≌Rt △BFA (HL ) ∴DE=BF .在△DEM 和△BFM 中 ∠DEM=∠BFM ∠DME=∠BMF DE=BF{{∴△DEM≌△BFM(AAS)∴MB=MD,ME=MF13如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.证:∵∠CEB=∠CAB=90°∠ADB=∠CDE在△ABD中,∠ABD = 180°-∠CAB-∠ADB 在△CED中,∠DCE = 180°-∠CEB-∠CDE ∴∠ABD =∠DCE在△ABD和△ACF中∠DAB=∠CAFAB=AC∠ABD =∠DCF∴△ABD≌△ACF(ASA)∴BD=CF∵BD是∠ABC的平分线∴∠FBE =∠CBE在△FBE和△CBE中∠FBE =∠CBEBE=BE∠BEF =∠BEC∴△FBE≌△CBE(ASA)∴CE=FE CF=2CE∴BD=2CEFEDC BA{ {14. 如图:DF=CE,AD=BC,∠D=∠C。
七年级数学证明题试题及参考答案

七年级数学证明题试题及参考答案七年级学习的一个难点就是证明题,这类的证明题有哪些值得推荐的呢?下面就是学习啦给大家的七年级证明题内容,希望大家喜欢。
如图AD//BC,∠A=∠C。
试说明AB//DCps:写过程..∵AD//BC∵∠A=∠ABF(两直线平行,内错角相等)∵∠A=∠C∵∠C=∠ABF∴AB//DC(同位角相等,两直线平行∵AD//BC(已知)∴∠A+∠ABC=180°(两直线平行,同旁内角互补)∵∠A=∠C(已知)∴∠C+∠ABC=180°(等式的性质)∴AB//DC(同旁内角互补,两直线平行))在正方形ABCD中,p(p靠近是D点)CD上的一点,BE⊥AP于E,DF⊥AP于F,说明△AFD≌△BEAD--------C111111∠BAE与∠DAF互余∠ADF与∠DAF互余所以∠BAE=∠ADF又待证明的两三角形都是Rt三角形,且AB=DA根据角角边定理,两三角形全等∠A=75°第二题是不是有问题啊∠GQD是30°吗应该是∠GQH=30°吧还有不懂怎么算的你追问一下我们QQ聊补充回答:∵GA//ED∴∠EBF=∠FHG=30°(两只线平行,同位角相等)∴∠FBA=∠ABD=(180°-30°)÷2=75°∵∠AHB=∠FHG=30°(对顶角)∴∠a=180°-75°-30°=75°#FormatImgID_0#还有一题等等啊补充回答:∵MN⊥CD∴∠MHD=90°∵∠GQD=130°∴∠GQH=180°-130°=50°∴∠HGQ=180°-90°-50°=40°∴∠AGH=90°∴∠EGA=180°-90°-40°=50°一、选择题(共27小题)1.﹣2的倒数是( )A.﹣B.C.2D.﹣22.﹣7的倒数是( )A.﹣B.7C.D.﹣73.﹣5的倒数是( )A.﹣5B.C.D.54.﹣2的倒数为( )A.﹣B.C.2D.15.﹣3的倒数是( )A.B.﹣3C.3D.6.﹣6的倒数是( )A.B.﹣C.6D.﹣67.与﹣3互为倒数的是( )A.﹣B.﹣3C.D.38.﹣的倒数等于( )A.B.﹣C.﹣2D.29.2的倒数是( )A.B.﹣C.±D.210.3的倒数是( )A.B.﹣C.﹣3D.311.﹣3的倒数是( )A.﹣3B.3C.D.﹣12.xx的倒数是( )A.B.﹣C.|xx|D.﹣xx13.﹣的倒数是( )A.﹣4B.4C.D.﹣14.﹣3的倒数是( )A.3B.C.﹣D.﹣315.﹣2的倒数是( )A.B.﹣C.2D.﹣216.﹣6的倒数是( )A.﹣6B.6C.D.17.﹣5的倒数是( )A.5B.﹣5C.D.﹣18.﹣的倒数是( )A.B.﹣2C.2D.﹣19.﹣的倒数是( )A.3B.﹣3C.﹣D.20.的倒数是( )A.2B.﹣2C.D.﹣21.有理数﹣的倒数是( )A.B.﹣C.D.﹣22.﹣2的倒数是( )A.2B.C.﹣D.﹣0.223.﹣的倒数是( )A.﹣3B.3C.﹣D.1、运送29.5吨煤,先用一辆载重4吨的汽车运3次,剩下的用一辆载重为2.5吨的货车运.还要运几次才能完?还要运x次才能完29.5-3*4=2.5x17.5=2.5xx=7还要运7次才能完2、一块梯形田的面积是90平方米,上底是7米,下底是11米,它的高是几米?它的高是x米x(7+11)=90*218x=180x=10它的高是10米3、某车间计划四月份生产零件5480个.已生产了9天,再生产908个就能完成生产计划,这9天中平均每天生产多少个?这9天中平均每天生产x个9x+908=54089x=4500x=500这9天中平均每天生产500个4、甲乙两车从相距272千米的两地同时相向而行,3小时后两车还相隔17千米.甲每小时行45千米,乙每小时行多少千米?乙每小时行x千米3(45+x)+17=2723(45+x)=25545+x=85x=40乙每小时行40千米5、某校六年级有两个班,上学期级数学平均成绩是85分.已知六(1)班40人,平均成绩为87.1分;六(2)班有42人,平均成绩是多少分?平均成绩是x分40*87.1+42x=85*823484+42x=697042x=3486x=83平均成绩是83分6、学校买来10箱粉笔,用去250盒后,还剩下550盒,平均每箱多少盒?平均每箱x盒10x=250+55010x=800x=80平均每箱80盒7、四年级共有学生200人,课外活动时,80名女生都去跳绳.男生分成5组去踢足球,平均每组多少人?平均每组x人5x+80=2005x=160x=32平均每组32人8、食堂运来150千克大米,比运来的面粉的3倍少30千克.食堂运来面粉多少千克?食堂运来面粉x千克3x-30=1503x=180x=60食堂运来面粉60千克9、果园里有52棵桃树,有6行梨树,梨树比桃树多20棵.平均每行梨树有多少棵?平均每行梨树有x棵6x-52=206x=72x=12平均每行梨树有12棵10、一块三角形地的面积是840平方米,底是140米,高是多少米?高是x米140x=840*2140x=1680x=12高是12米猜你感兴趣:1.初一英语语法习题答案2.七年级语文试题及答案3.初一语文试卷4.初一几何证明题答案5.初一上册几何证明题。
初一下册数学角度几何解析题以及练习题(附答案)-七年级下册几何求角度数

七年级下册数学几何解析题以及练习题(附答案)宇文皓月9.(2011·扬州)如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A 、B 两岛的视角∠ACB =________.答案 105°解析 如图,∵(60°+∠CAB )+(45°+∠ABC )=180°,∴∠CAB +∠ABC =75°,在△ABC 中,得∠C =105°.12.如图所示,在△ABC 中,∠A =80°,∠B =30°,CD 平分∠ACB ,DE ∥AC .(1)求∠DEB 的度数;(2)求∠EDC 的度数.解 (1)在△ABC 中,∠A =80°,∠B =30°,∴∠ACB =180°-∠A -∠B =70°.∵DE ∥AC ,∴∠DEB =∠ACB =70°.(2)∵CD 平分∠ACB ,∴∠DCE =12∠ACB =35°. ∵∠DEB =∠DCE +∠EDC ,∴∠EDC =70°-35°=35°.13.已知,如图,∠1=∠2,CF ⊥AB 于F ,DE ⊥AB 于E ,求证:FG ∥BC .(请将证明弥补完整)证明 ∵CF ⊥AB ,DE ⊥AB (已知),∴ED∥FC( ).∴∠1=∠BCF( ).又∵∠1=∠2(已知),∴∠2=∠BCF(等量代换),∴FG∥BC( ).解在同一平面内,垂直于同一直线的两条直线互相平行;两直线平行,同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC,求证:∠A+∠B+∠C=180°.分析:通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一平角,依辅助线分歧而得多种证法,如下:证法1:如图甲,延长BC到D,过C画CE∥BA.∵BA∥CE(作图所知),∴∠B=∠1,∠A=∠2(两直线平行,同位角、内错角相等).又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换).如图乙,过BC上任一点F,画FH∥AC,FG∥AB,这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗?请你试一试.解∵FH∥AC,∴∠BHF=∠A,∠1=∠C.∵FG∥AB,∴∠BHF=∠2,∠3=∠B,∴∠2=∠A.∵∠BFC=180°,∴∠1+∠2+∠3=180°,即∠A+∠B+∠C=180°.15.(2010·玉溪)平面内的两条直线有相交和平行两种位置关系.(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD.又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.解(1)不成立,结论是∠BPD=∠B+∠D.延长BP交CD于点E,∵AB∥CD,∴∠B=∠BED.又∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.(2)结论:∠BPD=∠BQD+∠B+∠D.(3)设AC与BF交于点G.由(2)的结论得:∠AGB=∠A+∠B+∠E.又∵∠AGB =∠CGF ,∠CGF +∠C +∠D +∠F =360°,∴∠A +∠B +∠C +∠D +∠E +∠F =360°. 14.把一副经常使用的三角板如图所示拼在一起,那么图中∠ADE 是度. 2.如图,在△ABC 和△ABD 中,现给出如下三个论断:①AD =BC ;②∠C =∠D ;③∠1=∠2。
初中数学几何证明题

24.如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠△ABC外有一点F,使FA⊥AE,FC⊥BC.〔1〕求证:BE=CF;〔2〕在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.24、如图,在△ABC中,∠ACB=90°,AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG。
求证:〔1〕AF=CG;〔2〕CF=2DE△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC〔或AC的延长线〕相交于点F.〔1〕如图1,假设DF⊥AC,垂足为F,AB=4,求BE的长;〔2〕如图2,将〔1〕中的∠EDF绕点D顺时针旋转一定的角度,DF扔与线段AC相交于点F.求证:1CF2BE AB+=;〔3〕如图3,将〔2〕中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,假设DN=FN,求证:3()BE CF BE CF+=-.25.如图1,在△ABC中,∠ACB=90°,∠BAC=60°,点E角平分线上一点,过点E作AE的垂线,过点A作AB的线段,两垂线交于点D,连接DB,24题图点F 是BD 的中点,DH ⊥AC ,垂足为H ,连接EF ,HF 。
〔1〕如图1,假设点H 是AC 的中点,AC=23,求AB ,BD 的长。
〔2〕如图1,求证:HF=EF 。
〔3〕如图2,连接CF ,CE ,猜测:△CEF 是否是等边三角形?假设是,请证明;假设不是,请说明理由。
图1图2△ABC 中,∠B=45°,∠C=30°,点D 是BC 上一点,连接AD ,过点A 作AG ⊥AD.在AG 上取点F ,连接DF.延长DA 至E ,使AE=AF ,连接EG ,DG ,且GE=DF.〔1〕假设22=AB ,求BC 的长;〔2〕如图1,当点G 在AC 上时,求证:CG BD 21=; 〔3〕如图2,当G 在AC 的垂直平分线上时,直接写出CGAB 的值. △ABC 是等腰三角形,∠BAC=90°,CD=1/2BC ,DE ⊥CE ,DE=CE ,连接AE ,点M 是AE 的中点.(1)如图1,假设点D 在BC 边上,连接CM ,当AB=4时,求CM 的长;〔2〕如图2,假设点D 在△ABC 的内部,连接BD ,点N 是BD 中点,连接MN ,NE ,求证MN ⊥AE ;〔3〕如图3,将图2中的△CDE 绕点C 逆时针旋转,使∠BCD=30°,连接N D C F A GBD ,点N 是BD 中点,连接MN ,探索ACMN 的值并直接写出结果 24.如图,ABC ∆中,︒=∠60A ,在AC 上截取AB AD =,E 为AB 上一点,且CD BE =,过点E 作BD 的垂线,分别交BC BD 、于F 、G ,连接EC 交BD 于H 。
初一数学图形与证明试题答案及解析

初一数学图形与证明试题答案及解析1.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”. 则半径为2的“等边扇形”的面积为【答案】2【解析】根据扇形的面积公式S=lr,其中l=r,求解即可.解:∵S=lr,∴S=×2×2=2,故答案为2.本题是一个新定义的题目,考查了扇形面积的计算,注:扇形面积等于扇形的弧长与半径乘积的一半.2.如图,直线,∠1=40°,∠2=75°,则∠3等于()A.55°B.60°C.65°D.70°【答案】C.【解析】如图:∵直线l1∥l2,∠1=40°,∠2=75°,∴∠1=∠4=40°,∠2=∠5=75°,∴∠3=65°.故选C.【考点】1.三角形内角和定理;2.对顶角、邻补角;3.平行线的性质3.如图,C、D是线段AB上的两个点,CD="8" cm,M是AC的中点,N是DB的中点,MN="12" cm,那么线段AB的长等于 cm.【答案】16【解析】由CD=8cm,MN=12cm,可得MC+DN=4cm,由M是AC的中点,N是DB的中点可得AC+DB=2MC+2DN=8cm,即可求得AB=AC+CD+DB=16cm.【考点】比较线段的长短4.在一块长为,宽为的长方形草地上,有一条弯曲水泥小路,小路任何地方的水平宽度都是1个单位,则草地面积为_________.【答案】(ab-b).【解析】∵小路任何地方的水平宽度都是1个单位,∴通过平移把小路变成长为b,宽为1的面积相等的矩形,所以草地面积为(ab-b).【考点】1.图形的平移规律;2.矩形面积的计算.5.下列命题中,①对顶角相等.②等角的余角相等.③若,则.④同位角相等.其中真命题的个数有()A.1个B.2个C.3个D.4个【答案】B【解析】①对顶角相等,正确;②等角的余角相等,正确;③若|a|=|b|,则a=b,错误,如|-2|=|2|,但-2≠2;④同位角相等,错误,如图,∠1与∠2是同位角,但∠1≠∠2;故2个正确;故选B.【考点】真命题与假命题.6.下列长度的3条线段,能构成三角形的是()A.1,2,3B.2,3,4C.6,6,12D.5,6,12【答案】B【解析】三角形中任意两边之和大于第三边,任意两边之差小于第三边.A、1+2=3;C、6+6=12;D、5+6=11<12.故选B.【考点】三角形三边关系.7.已知点P是线段AB的中点,若AB=6cm,则PB= cm.【答案】3【解析】根据线段的中点平分线段的长度.根据点P是线段AB的中点,则PB=AB==3cm.【考点】两点间的距离.8.如图,若PE平分∠BEF,PF平分∠DFE,∠1=35°,∠2=55°,则AB与CD平行吗?为什么?【答案】见解析.【解析】先根据角平分线的性质得出∠BEF与∠DFE的度数,再由等式的性质得出∠BEF+∠DFE=180°,从而根据同旁内角互补,两直线平行得出结论.试题解析:AB∥CD.理由:∵PE平分∠BEF,PF平分∠DFE,∠1=35°,∠2=55°,∴∠BEF=2∠1=70°,∠DFE=2∠2=110°(角平分线的定义),∴∠BEF+∠DFE=70°+110°=180°(等式的性质),∴AB∥CD(同旁内角互补,两直线平行).【考点】平行线的判定9.下列命题中是假命题的是()A.对顶角相等B.同位角相等C.邻补角互补D.平行于同一条直线的两条直线平行【答案】B.【解析】根据正确的命题叫真命题,错误的命题叫做假命题可知:选项A,对顶角相等是真命题;选项B,同位角相等是假命题,只有两直线平行,同位角才相等;选项C,邻补角互补是真命题;选项D,平行于同一条直线的两条直线平行是真命题;故答案选B.【考点】真假命题.10.已知等腰三角形的一边长为4,另一边长为8,则这个等腰三角形的周长为.【答案】20.【解析】分两种情况:第1种情况,腰长为8,底边长为4,等腰三角形的周长为20;第2种情况,腰长为4,底边长为8,这种情况不存在,故答案为20.【考点】分类讨论;等腰三角形的性质.11.下列说法中:①因为对顶角相等,所以相等的两个角是对顶角;②在平面内,不相交的两条直线叫做平行线;③过一点有且只有一条直线与已知直线垂直;正确的有().A.个B.个C.个D.个【答案】C.【解析】①说法错误,因对顶角有特殊的位置关系,相等的角不一定是对顶角;②是平行线的定义,正确;③是垂线的性质,正确,故选C.【考点】1.对顶角的理解;2.平行线意义;3.垂线性质.12.如图,下列不能判定∥的条件是( ).A.B.C.D.【答案】B.【解析】选项A,根据同旁内角互补,两直线平行可判定∥;选项B,根据内错角相等,两直线平行可判定AD∥BC,不能判定∥;选项C,根据内错角相等,两直线平行可判定∥;选项D,根据同位角相等,两直线平行可判定∥.故答案选B.【考点】平行线的判定.13.如图,下列说法错误的是()A.∠A与∠B是同旁内角B.∠3与∠1是同旁内角C.∠2与∠3是内错角D.∠1与∠2是同位角【答案】D【解析】根据同位角、内错角、同旁内角的定义可知:∠A与∠B是同旁内角,所以A说法正确;∠3与∠1是同旁内角,所以B说法正确;∠2与∠3是内错角,所以C说法正确;∠1与∠2是邻补角,所以D说法错误,故选:D.【考点】1.同位角;2.内错角;3.同旁内角.14.如图,等边三角形ABC的边长为10厘米.点D是边AC的中点.动点P从点C出发,沿BC的延长线以2厘米/秒的速度作匀速运动,设点P的运动时间为t(秒).若△BDP是等腰三角形,则为t= .【答案】【解析】过点D作DG⊥BC,利用等边三角形的性质得出BD=5,再利用含30°的直角三角形得出BG=,即可得出PC的长度.过点D作DG⊥BC,如图:∵等边三角形ABC的边长为10厘米,点D是边AC的中点,∴BD=5,∠DBG=30°,∴BG=,∴PC=-5=,可得t=.【考点】等边三角形的性质;等腰三角形的判定15.(3分)下面是一个正方体纸盒的展开图,请把-10,7,10,-2,-7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数。
2022-2023学年人教版数学七年级下册期末几何解答题专题练习

2022-2023学年人教版七年级下学期期末数学几何解答题专题练习1、如图,AB∥CD,∠A=∠C,BE平分∠ABC交AD的延长线于点E,(1)证明:AD∥BC;(2)若∠ADC=118°,求∠E的度数.2、如图,已知∠1=∠BDC,∠2+∠3=180°.(1)AD与EC平行吗?试说明理由.(2)若DA平分∠BDC,CE⊥AE于点E,∠1=80°,试求∠F AB的度数.3、小聪把一副三角尺ABC,DCE按如图1的方式摆放,其中边BC,DC在同一条直线上,过点A向右作射线AP∥DE.(1)如图2,求∠P AC的度数;(2)如图3,点Q是线段BC上一点,若∠AQB=53∠PAQ,求∠QAB的度数.4、已知:在四边形ABCD中,AD∥BC,AE平分∠DAB交BC于点E,点M为线段BC上一点,且AM∥DC.(1)如图(1),若点M与点E重合,求证:∠C=∠BAE;(2)如图(2),若AN平分∠BAM交BC于点N,且∠NAE=25°,求∠C的度数;(3)在(1)的条件下,F为线段BA的延长线上一点,∠DCB=75°,若∠DCB的三等分线与∠F AD的角平分线交于点P,请直接写出∠APC的度数.5、直线AB∥CD,BE﹣EC是一条折线段,BP平分∠ABE.(1)如图1,若BP∥CE,求证:∠BEC+∠DCE=180°;(2)CQ平分∠DCE,直线BP,CQ交于点F.①如图2,写出∠BEC和∠BFC的数量关系,并证明;②当点E在直线AB,CD之间时,若∠BEC=40°,直接写出∠BFC的大小.6、如图1,AB∥CD,点E在AB上,点H在CD上,点F在直线AB,CD之间,连接EF,FH,∠BEF=α,∠FHD=β.(1)直接写出∠EFH的度数为;(2)如图2,若HM平分∠CHF,MN平分∠BEF,证明:∠EFH+2∠M=180°;(3)如图3,若∠BEN=1n∠BEF,∠MHC=1n∠FHC,则∠M=.(用含有n,α,β的式子表示)7、如图,已知A(0,a),B(b,0),且满足|a−4|+√b+6=0.(1)求A、B两点的坐标;(2)点P(m,n)在线段AB上,当PB=2P A时,求P点的坐标;(3)若点M(c,6),△ABM的面积记作S△ABM,当S△ABM>10时,直接写出c的取值范围.8、在平面直角坐标系中,已知点A(a,0),B(0,b),若a,b满足(a﹣b+6)2+|2a﹣3b+14|=0.(1)求点A,B的坐标;(2)将线段AB向右平移2个单位至CD,线段CD与y轴交于点E,求点E的坐标;(3)点P为直线CD上一动点,连接BC,PB,若4≤S△BCP<6,则点P的横坐标x P的取值范围是.9、如图,已知AB∥CD,M,N分别是直线AB,CD上一点,点E在直线AB,CD之间.(1)如图1,求证:∠BME+∠DNE=∠MEN;(2)如图2,F是EM上一点,NE平分∠FND,FH平分∠NFE,试探究∠NHF与∠BME 之间的数量关系?并证明你的结论;(3)如图3,P为直线MN上一动点(不与点N重合),过点P作PG⊥MN交直线CD 于点G,∠PNG的角平分线和∠PGC的角平分线交于点O,则∠O的度数为(直接写出结果).10、平面直角坐标系中,A(a,0),B(0,b),a,b均为整数,且满足b=√2a−4−√4−a,点C在y轴负半轴上且S△ABC=10,将线段AB平移到DE,其中点A的对应点是点D.(1)请直接写出点A ,B ,C 的坐标;(2)如图(1),若点D 的坐标为(﹣1,0),点F (m ,n )为线段DE 上一点,且△ACF 的面积大于12,求m 的取值范围;(3)如图(2),若DE 与y 轴的交点G 在B 点上方,点P 为y 轴上一动点,请直接写出∠EBO ,∠BPD ,∠PDA 之间的数量关系.11、在平面直角坐标系中,A (a ,0),B (1,b ),a ,b 满足|a +b ﹣1|+√2a −b +10=0,连接AB 交y 轴于C .(1)直接写出a = ,b = ;(2)如图1,点P 是y 轴上一点,且三角形ABP 的面积为12,求点P 的坐标;(3)如图2,直线BD 交x 轴于D (4,0),将直线BD 平移经过点A ,交y 轴于E ,点Q (x ,y )在直线AE 上,且三角形ABQ 的面积不超过三角形ABD 面积的13,求点Q 横坐标x 的取值范围.12、已知,AB ∥DE ,点C 是直线AB ,DE 下方一点,连接BC ,DC .(1)如图1,求证:∠B +∠D ﹣∠C =180°;(2)如图2,若BF ,DG 分别平分∠ABC 和∠CDE ,BF 、DG 所在的直线相交于点H ,若∠H =α°,求∠C 的度数;(用含α的式子表示)(3)如图3,若BF ,DG 分∠ABC 和∠CDE 为两部分,且∠ABF =n ∠FBC ,∠EDG =n ∠CDG ,直线BF ,DG 相交于点H ,则∠H = .(用含n 和∠C 的式子表示)13、已知,在平面直角坐标系中,点A 在y 轴上,OA =a ,点B (b ,b ),且a 、b 满足√a +b −8+(a −b −4)2=0.(1)则a = ;b = ;(2)如图1,在x 轴上是否存在点C ,使三角形ABC 的面积等于三角形ABO 面积的一半?若存在,请求出点C 的坐标;若不存在,请说明理由;(3)如图2,将线段AB 向左平移m 个单位(m >0),得到线段A 'B ',其中点A ,点B 的对应点分别为点A ',点B '.若点N (﹣1,n )在射线A 'B '上,连接ON ,BN 得到三角形BON ,若三角形BON 的面积大于三角形ABO 面积的12并且小于三角形ABO 面积,则m 的取值范围是 .14、如图1,已知点A (﹣2,0),B (0,﹣4),C (﹣4,﹣6),过点C 作x 轴的平行线m ,一动点P 从C 点出发,在直线m 上以1个单位长度/秒的速度向右运动,与此同时,直线m 以2个单位长度/秒的速度竖直向上运动.(1)直接写出:运动1秒时,点P 的坐标为 ;运动t 秒时,点P 的坐标为 ;(用含t 的式子表示)(2)若点P 在第三象限,且S △ABP =8,求点P 的坐标;(3)如图2,如果将直线AB 沿y 轴负半轴向下平移n 个单位长度,恰好经过点C ,求n 的值.15、已知BE 平分∠ABD ,DE 平分∠BDC ,且∠BED =∠ABE +∠EDC .(1)如图1,求证:AB ∥CD ;(2)如图2,若∠ABE =3∠ABF ,且∠BFD =30°时,试求∠CDF ∠FDE 的值;(3)如图3,若H 是直线CD 上一动点(不与D 重合),BI 平分∠HBD ,画出图形,并探究出∠EBI 与∠BHD 的数量关系.问题探究:(1)如图1,∠CFP +∠EPF =∠AEP ,证明:AB ∥CD ;问题拓展:(2)如图2,AB ∥CD ,∠AEP 的角平分线EK 所在的直线和∠DFP 的角平分线FR 所在的直线交于Q 点,请写出∠EPF 和∠EQF 之间的数量关系,并证明.问题迁移:(3)如图3,AB ∥CD ,直线MN 分别交AB ,CD 于点M ,N ,若点H 在线段MN 上,且∠MEF =α,请直接写出∠HFE ,∠MEH 和∠EHF 之间满足的数量关系(用含α的式子表示).16、当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等例如:在图①、图②中,都有∠1=∠2,∠3=∠4.设镜子AB 与BC 的夹角∠ABC =α.(1)如图①,若α=90°,判断入射光线EF 与反射光线GH 的位置关系,并说明理由.(2)如图②,若90°<α<180°,入射光线EF 与反射光线GH 的夹角∠FMH =β.探索α与β的数量关系,并说明理由.(3)如图③,若α=120°,设镜子CD 与BC 的夹角∠BCD =γ(90°<γ<180°),入射光线EF 与镜面AB 的夹角∠1=m (0°<m <90°),已知入射光线EF 从镜面AB 开始反射,经过n (n 为正整数,且n ≤3)次反射,当第n 次反射光线与入射光线EF 平行时,请直接写出γ的度数.(可用含有m 的代数式表示)17、在平面直角坐标系中,点A ,C 均在x 轴上,点B 在第一象限,直线AB 上所有点的坐标(x ,y )都是二元一次方程x ﹣y =﹣2的解,直线BC 上所有点的坐标(x ,y )都是二元一次方程2x +y =8的解.(1)求B 点的坐标时,小明是这样想的:先设B 点坐标为(m ,n ),因为B 点在直线AB 上,所以(m ,n )是方程x ﹣y =﹣2的解;又因为B 点在直线BC 上,所以(m ,n )也是方程2x +y =8的解,从而m ,n 满足{m −n =−22m +n =8.据此可求出B 点坐标为 ,再求出A 点坐标为 ;C 点坐标为 .(均直接写出结果)(2)若线段BC 上存在一点D ,使S △OCD =12S △ABC (O 为原点),求D 点坐标;(3)点E (a ,﹣3)是坐标平面内的动点,若满足S △ABE ≤13S △ABC ,求a 的取值范围.18、已知:点E 在直线AB 上,点F 在直线CD 上,AB ∥CD .(1)如图1,连EF ,EP 平分∠AEF ,FP 平分∠CFE ,求∠P 的度数.(2)如图2,若∠EGF =160°,射线EH ,FH 分别在∠AEG ,∠CFG 的内部,且∠EHF =40°,当∠AEG =4∠AEH 时,求∠GFH ∠CFG 的值.(3)如图3,在(1)的条件下,在直线CD 上有一动点M (点M 不与点F 重合),EN 平分∠MEF ,若∠PEN =α(0°<α<90°),请直接写出∠EMF = (结果用含α的式子表示).19、在平面直角坐标系中,A (a ,0),B (b ,b ),C (0,c ).(其中a ,b ,c 均为正数),且a ,b ,c 满足{3a −b +2c =8a −2b −c =−9,若√b 的算术平方根为√2. (1)求a ,b ,c 的值.(2)如图1,在第二象限内有一点P (m ,12),若四边形ACPO 的面积与△ABC 的面积相等,求不等式:x−32≥2x−m 3的解集.(3)如图2,BO 平分∠AOC ,过点C 作CD ∥AB 交BO 的延长线于点D ,AE 平分∠BAX ,AE 的反向延长线交BO 的延长线于点F ,设∠CDB =α,∠F =β(其中α,β均为锐角),请直接写出:α+2β3= .23.(10分)如图1,已知直线l1∥l2,点A、B在直线l1上,点C、D在l2上,线段AD交线段BC于点E,且∠BED=60°.(1)求证:∠ABE+∠EDC=60°;(2)如图2,当F、G分别在线段AE、EC上,且∠ABF=2∠FBE,∠EDG=2∠GDC,标记∠BFE为∠1,∠BGD为∠2.①若∠1﹣∠2=16°,求∠ADC的度数;②当k=时,(k∠1+∠2)为定值,此时定值为.24.(12分)如图1,在平面直角坐标系中,已知A(a,1),B(0,b),且实数a,b满足√a+b−2+|a+2b|=0.(1)直接写出两点坐标:A(),B();(2)如图2,将线段AB沿着横坐标均为m的点组成的直线l对折,A与C对应,B与D 对应,若凸四边形ABDC的面积为18,求m的值;(3)如图3,点P在第二、四象限的角平分线上,设P点坐标为(h,﹣h),其中h≠0.①当P在线段AB上时,求h的值;②若S△ABP≥2+32S△OBP.直接写出h的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3题
填空完成推理过程:
1、 如图,∵AB ∥EF (已知)
∴∠A + =1800( ) ∵DE ∥BC ( 已知 )
∴∠DEF= ( ) ∠ADE= ( ) 2、已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.
《
3、已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.
《
4、已知AB ∥CD ,∠1=70°则∠2=_______,∠3=______,∠4=______
_
43
2
1A C
D
B
5、已知:如图4, AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数
~
6、直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD =1:4,求∠EOB 的度数.
[
A
C
D E F
B
D
E
B C
A
H G
2
1
F
%
D
C B
A
7、如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
¥
;
8、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37º,求∠D 的度数.
@
9、如图,已知:21∠∠=, 50=D ∠,求B ∠的度数。
~
;
A
B
C
D
E
!
第19题
2
1
F
E
D
B
A
C
10、已知:如图,AB∥CD,∠B=400,∠E=300
,求∠D的度数
《
11、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
b
a
341
2
12、已知等腰三角形的周长是16cm .
(1)若其中一边长为4cm ,求另外两边的长; (2)若其中一边长为6cm ,求另外两边长; (3)若三边长都是整数,求三角形各边的长.
^
·
14、如图,AB ∠2的度数.
15、如图所示,把一张长方形纸片ABCD 沿EF 折叠,若∠EFG=50°,求∠DEG 的度数.
~
E D
C
B
A
-
16、如图所示,已知AB ∥CD,分别探索下列四个图形中∠P 与∠A,∠C 的关系,请你从所得的四个关系中任选一个加以说明.
P
D
C
B
A P D
C
B
A P D
C
B A P
D
C
B A
(1) (2) (3) (4)
)
17、如图,AB ∥CD ,BF ∥CE ,则∠B 与∠C 有什么关系请说明理由.
*
18、如图,已知:DE ∥BC ,CD 是∠ACB 的平分线,∠B =70°,∠ACB =50°,求∠EDC 和∠BDC 的度数.
N
M
G F E D
C
B
A
第17题图
A
B C
D
E
.
19、如图AB∥CD,∠NCM =90°,∠NCB =30°,CM 平分∠BCE ,求∠B 的大小.
】
20、如图5-24,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;
(2)BE 与DE 平行吗为什么
N
M
F
E D
C
B
A
21、如图5-25,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . "
(1)AE 与FC 会平行吗说明理由.
(2)AD 与BC 的位置关系如何为什么
(3)BC 平分∠DBE 吗为什么.
F E
2
1
D
C
B
A
,
22、如图5-26,已知:CE =DF ,AC =BD ,∠1=∠2.求证:∠A =∠B .
第18题图
E N
M C
D B
A
第19题图
图5-24
图5-25
B
C
23、如图5-27,已知:AB ∥CD ,AB =CD ,求证:AC 与BD 互相平分.
;
B
24、如图5-27,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .
2
A
B
E
C
F
D H G
1
'
25、如图5-28,已知:在∆A B C 中,∠=︒C 90,AC=BC ,BD 平分∠CBA ,D EA B
⊥于E ,求证:AD +DE =BE .
26、如图5-29,已知:AB ∥CD ,求证:∠B +∠D +∠BED =360︒(至少用三种方法)
E
A
B
C
D
图5-26
图5-26
A
B C
D E
'
27、直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.
'
28、如图,EF ∥AD ,∠1 =∠2,∠BAC = 70°.将求∠AGD 的过程填写完整.
因为EF ∥AD ,所以 ∠2 = . 又因为 ∠1 = ∠2,所以 ∠1 = ∠3. %
所以AB ∥ .
所以∠BAC + = 180°. 又因为∠BAC = 70°,
所以∠AGD = .
!
29、如图,已知:DE ∥BC ,CD 是∠ACB 的平分线,∠B =70°, ∠ACB =50°,求∠EDC 和∠BDC 的度数.
-
30、AD ∥BC ,AB ∥DC ,∠1=100º,求∠2,∠3的度数
|
A
B
C D
3
21
G
F
E
D
B
A C
F
E D
B
A
C
31、∠ECF =900,线段AB 的端点分别在CE 和CF 上,BD 平分∠CBA ,并与∠CBA 的外角平分线AG 所在的直线交于一点D ,
(1)∠D 与∠C 有怎样的数量关系(直接写出关系及大小) (2)点A 在射线CE 上运动,(不与点C 重合)时,其它条件不变,(1)中结论还成立吗说说你的理由。
#
32、阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等。
”简称“等角对等边”,如图,在ABC
中,已知∠ABC 和∠ACB 的平分线上交于点F ,过点F 作BC 的平行线分别交AB 、AC 于点D 、E,请你用“等角对等边”的知识说明DE=BD+CE.
.
33、已知如图8,∠BAC=90°,AB=AC ,BD ⊥DE ,CE ⊥DE ,求证:DE = BD + CE.
/
34、在△ABC 中,已知∠ABC=66°,∠ACB=54°,BE 是AC 上的高,CF 是AB 上的高,H 是BE 和CF 的交点,求∠ABE 、∠ACF 和∠BHC 的度数.
…
35、已知:AD 为△ABC 中BC 边上的中线,CE ∥AB 交AD 的延长线于E 。
求证:(1)AB =CE ;(2)AD
2
1
(AB + AC )
|
36、如图,已知ΔABC 中,AB=AC ,E 是AB 的中点,延长AB 到D ,使BD = BA ,求证 :CD = 2CE
%
37、如图,在Rt △ABC 中,AB=AC,∠BAC=90°,O 为BC 的中点.
(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的关系(不证明);
(2)如果点M 、N 分别在线段AB 、AC 上移动,在移动中保持AN = BM,请判断△OMN 的形状,并证明你的结论.
N
M
C
B
O
A
:
38、如图,在ΔABC 中,AD 平分∠BAC ,DE ∥AC,EF ⊥AD 交BC 延长线于F 。
求证: ∠FAC=∠B
)
$
39、如图,ΔABC 中,过A 分别作∠ABC, ∠ ACB 的外角的平分线的垂线AD,AE,D,E 为垂足; 求证(1).ED ∥BC
(2).ED = 1
2 (AB+AC+BC );
(3).若过A 分别作∠ABC ,∠ACB 的平分线的垂线AD ,AE ,垂足分别为D ,E ,结论有无变化请加以说明。
'
40、图11所示,求∠A +∠B +∠C +∠D +∠E +∠F 的度数. '
【
;
41、如图,△ABC 中,AD 是高,AE 、BF 是角平分线,它们相交于点O ,∠A=500,∠C=600,求∠DAC 及∠BOA
F
E
D
C
B
A 图 11。
