卧式容器液体体积计算
卧式容器中液体体积的计算

卧式容器中液体体积的计算丁浩,刘辉,刘勇营,陈先进(浙江化工院科技有限公司,浙江绍兴312369)摘要:以数学分析的方法推导出卧式容器内不同液位高度下对应的液体体积计算公式,进而根据比重确定容器内的工况质量。
同时通过实验对推导出的计算公式和常见的几种计算公式进行误差对比分析,并给出了它们的液体体积与液面高度的关系曲线图。
关键词:卧式容器;椭圆封头;液体体积;误差分析文章编号:1006-4184(2019)05-0035-04收稿日期:2019-01-03作者简介:丁浩(1991-),男,浙江杭州人,硕士,助理工程师,主要从事中试及工程放大研究。
E-mail :dinghao01@ 。
卧式容器由于安装和使用方便等诸多因素,被广泛应用于化工、石油、冶金等行业中。
在生产和贮运过程中,经常需要根据液位来计算出容器中的液体体积,以方便计量和操作。
卧式圆筒容器内液体体积的计算是与其封头形式有关系的,因封头形式不同计算公式有所不同,封头形式主要有平封头、椭圆封头蝶形封头、球形封头等几种类型,但应用最广泛的主要为椭圆型封头卧式容器。
本文以数学分析的方法详细推导出椭圆型封头卧式容器内液体体积的计算公式,以便准确地计算出容器的介质质量。
1椭圆型封头卧式容器液体体积计算椭圆型封头卧式容器[1]由直筒和椭圆型封头两部分组成,如图1所示。
图1卧式容器结构示意图图1中卧式容器直筒部分的长度为L ,半径为R ,椭圆型封头曲面高度为b 。
整个容器内物料的体积为直筒部分物料体积和两个椭圆型封头物料体积之和,即,式中V 为卧式容器总体积,V 1为直筒部分体积,V 2为单个椭圆型封头体积。
1.1直筒部分液体体积直筒内装有高度为h 的液体体积等于液体淹没直筒横截面的弓形面积乘以直筒部分长度。
直筒部分横截面结构(h <R )如图2所示。
图2直筒横截面结构示意图(h<R )横截面中弓形面积为:b2RROABh则直筒部分液体体积当液位高度h=R 时,当液位高度h>R 时,横截面结构如图3所示。
卧罐体积计算公式

卧罐体积计算公式设卧式储罐内部为椭圆柱,椭圆的两半轴为a(宽度方向),b(高度方向),长度为L,内部介质的高度为h,则内部介质体积V1的计算公式与h的关系推导如下:V1=2L∫(b—h,b)√(b^2-x^2)dx=(2aL/b)[(x/2)√(b^2-x^2)+(b^2/2)arcsin(x/b)]|(b—h,b)=(2aL/b)[πb^2/4-(b—h)√(2bh-h^2)/2—(b^2/2)arcsin(1-h/b)]以上计算是假设卧式储罐为平封头时的情况,当卧式储罐带有两个半椭球封头时,内部介质体积计算公式需要修正:设椭球封头的三个半轴为a(宽度方向),b(高度方向),c(长度方向),内部介质的高度为h,则椭球封头处内部介质体积V2的计算公式与h的关系推导如下:V2=4∫(b-h,b)∫(0,a√(1—x^2/b^2))c√(1-x^2/b^2—y^2/a^2)dydx =(4c/a)∫(b—h,b)∫(0,a√(1—x^2/b^2))√(a^2—a^2x^2/b^2—y^2)dydx=(4c/a)∫(b—h,b)y√(a^2—a^2x^2/b^2—y^2)/2+ arcsin(y/√(a^2-a^2x^2/b^2 ))(a^2-a^2x^2/b^2)/2 |(0,a√(1-x^2/b^2))dx =(4c/a)∫(b—h,b)π(a^2-a^2x^2/b^2)/4dx=πac∫(b—h,b) (1—x^2/b^2)dx=(πac/3)(3x- x^3/b^2)| (b-h,b)=(πac/3)[3h—b+(b-h)^3/b^2)]故在有两个半椭球封头时,内部介质体积V的计算公式与h的关系如下:V=V1+V2=(2aL/b)[πb^2/4—(b-h)√(2bh-h^2)/2-(b^2/2)arcsin(1-h/b)]+(πac/3)[3h-b+(b-h)^3/b^2)]。
2卧式容器液位高度与体积的计算方法

以 D = 1 000 mm 、L = 3 000 mm 的标准椭圆封 头卧式容器为例进行计算 ,在软件程序中依次输入 100 mm ,200 mm , ……,1 000 mm 等高度 , 计算结
果见表 1 。
表 1 不同液位高度时的介质体积
液位高度
介质体积
液位高度
介质体积
/ mm 100 200 300 400 500
Public Functio n LBase (ByVal r A s Single ,By2 Val x A s Single) A s Single
LBase = PI/ 4 3 (r^2 3 x - x^3/ 3) End Functio n Public Functio n LBowArea (ByVal r A s Sin2 gle ,ByVal h A s Single) A s Single LBowArea = LBow (r , - r + h) - LBow (r , r) End Functio n Public Functio n LBow (ByVal r A s Single ,By2 Val x A s Single) A s Single LBow = 2 3 ( x/ 2 3 Sqr ( r^2 - x^2) + r^2/ 2 3 Arcsin ( x/ r) ) End Functio n Public Functio n Arcsin (ByVal x A s Single) If x = 1 ThenArcsin = PI/ 2 End If If x = - 1 ThenArcsin = - PI/ 2 End If If x < > 1 And x < > - 1 Then Arcsin = At n ( x/ Sqr ( - x 3 x + 1) ) End If End Functio n
储液存量体积计算

卧式储罐储液存量计算对于lng的计量我们采用静态计量的方法,就是通过测量储罐的液位等数据后确定其体积,再测量温度和压强的数据计算密度,然后根据体积密度与质量的关系得出储罐中储液的存量。
一、储罐中储液体积计算在计算储液体积时我们可以把储罐分成封头部分和筒体部分分别计算求和1、筒体储液体积计算要计算筒体储液体积只需计算筒体横截面(如图2)储液面积再乘以筒体计算长度即可。
(1)、筒体的横截面为一个圆形,其中储液平面为圆形水平截出的一个圆弓形(如图2)把截面置于平面直角坐标系中可得圆的方程为:S扇形=R3603°三角形ABC面积:S三角形=2√h(D−h)(R−h)2化简:S三角形=√h(D−h)(R−h 所求弓形面积为:S弓形=2arcsin√h(D−h)RπR²360−√h(D−h)(R−h)所求储液体积: V 筒= L [2arcsin√h (D−h )RπR²360−2如图3可拼成一个椭圆球体。
求液位从0到H 点的体积。
1°如图6(x−R )²R²+y²b²+z²R²=12°过x 其方程为:y²b²+z²R²=1- -(x−R )²R²整理得:y²b²(1− −(x−R )²R²)+z²R²(1− −(x−R )²R²)=1由椭圆面积公式:S = πab可得:S(x)= π√b²(1− −(x−R)²R²)*√R²(1− −(x−R)²R²)=πbR(2Rx−x²)根据积分法则求椭圆球体体积:V 封=∫S(x)dx H=πb R ∫(2Rx−x²)dx H=πb R [RH²- -13H³]3、对筒体部分储液体积和封头部分储液体积求和得出储罐储液总体积:V 总=L[2arcsin√h(D−h)RπR²360−√h(D−h)(R−h)] + πbR[RH²- -13H³]二、储罐中储液密度计算。
卧式椭圆封头容器不同液位的体积计算

符号
L(m)R t(m)h(m)hi(m)(E3-D3)/D3Vt(m3)Vf(m3)V(m 3)数值2100.0001000.0001000.000500.0000.0003298672230.000523598766.6673822270996.667卧式椭圆形封头容器不同液位的体积计算
Dt ——筒体内径,m Rt——筒体或球形封头内半径,m h ——液面高度,m V——卧式容器体积,m3hi ——封头曲面深度,m (标准型:hi=1/2Rt ) Vt——筒体部分体积,m3
L ——筒体长度(含封头直边高度),m Vf——封头部分体积,m3
1、 筒体内液体体积计算(如上图):
筒体的截面积方程:X 2+Y 2=Rt 2 故:X=(Rt 2-Y 2)1/2
因此:液面高度为h 时筒体内液体的体积:
2、椭圆封头内液体体积计算(如上图):
椭圆封头的椭球面方程:
]2
arcsin 2)^(1[2^2^2^2π+-+--∙-∙=-=⎰--Rt Rt h Rt Rt h Rt Rt h Rt L dy
y Rt L Vt Rt
h Rt 2^2^2^)/(12
^2^2^2^2^y x Rt Rt hi z hi z Rt y x --=∴=++
因此:当容器内的液面高度为h 时,封头内液体的体积:
]33^233)^()(2^[22^2^2^22^2^0Rt Rt h Rt h Rt Rt hi dx y x Rt dy Rt hi zdxdy
Vf y Rt Rt h Rt
f ----=--==⎰⎰⎰⎰---π。
卧式储罐体积容积计算(带公式)
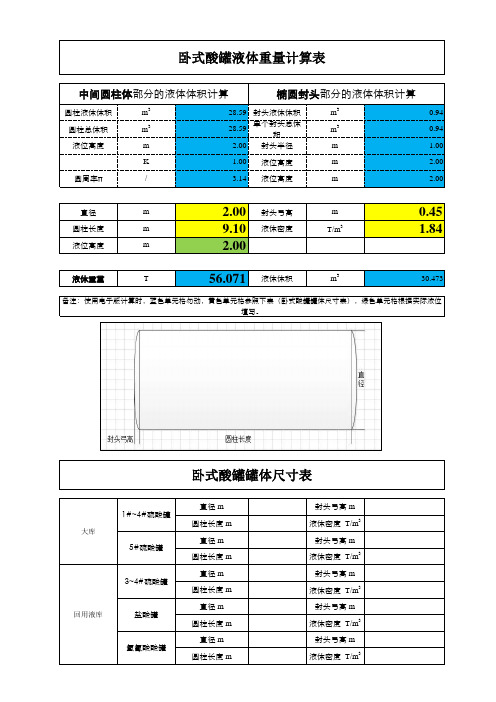
圆柱液体体积m 328.59封头液体体积
m 30.94圆柱总体积m
3
28.59
单个封头总体
积
m
3
0.94液位高度
m 2.00封头半径m 1.00K
1.00液位高度m
2.00圆周率π/
3.14
液位高度
m
2.00
直径m 2.00封头弓高m 0.45圆柱长度m 9.10液体密度
T/m
3
1.84
液位高度
m
2.00液体重量T 56.071
液体体积m
3
30.473
直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3
直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3直径 m 封头弓高 m 圆柱长度 m
液体密度 T/m 3
大库
回用液库
1#~4#硫酸罐
5#硫酸罐
3~4#硫酸罐
盐酸罐
氢氟酸酸罐
卧式酸罐液体重量计算表
中间圆柱体部分的液体体积计算
椭圆封头部分的液体体积计算
备注:使用电子版计算时,蓝色单元格勿动,黄色单元格参照下表(卧式酸罐罐体尺寸表),绿色单元格根据实际液位
填写。
卧式酸罐罐体尺寸表。
卧式容器液位体积计算

卧式容器液位体积计算
液位的测量方式有很多种,常用的液位传感器包括浮子式液位计、压力式液位计、雷达液位计、超声波液位计等。
这些液位传感器可以精确地测量液位并将其转换为相应的电信号。
液位体积计算的原理是根据容器的几何形状和液位的高度来计算液体的体积。
在卧式容器中,通常采用水平切面积乘以液位高度的方法进行计算。
卧式圆柱形容器的液位体积计算可以使用以下公式:
V=π*R^2*H
如果容器的底部是平的,液体的高度可以通过测量液体表面到容器底部的垂直距离来确定。
对于容器的底部是圆锥形的情况,液位体积计算的公式略有不同。
在这种情况下,可以使用以下公式进行计算:
V=(1/3)*π*(R1^2+R2^2+R1*R2)*H
其中,V表示液体的体积,π表示圆周率,R1表示底部较小半径(圆锥顶部半径),R2表示底部较大半径(圆锥底部半径),H表示液位的高度。
卧式容器的液位体积计算涉及到容器的几何形状和液体的液位测量,因此在进行计算时需要准确地测量液位和容器的尺寸。
此外,还需要注意单位的一致性,在计算中使用相同的单位。
液位体积计算在工业生产中非常重要,可以帮助企业准确掌握液体的储存量、流量和消耗情况,从而进行生产计划和资源调配。
此外,液位体
积计算还可以用于监测液体储罐的安全性能,确保液位不超过容器的额定容积,避免溢出和泄露。
总之,卧式容器液位体积计算是一项重要的工程计算,涉及到液位测量和容器几何形状分析。
通过准确地测量液位和应用相应的公式,可以计算出容器中液体的体积,为工业生产提供准确的数据支持。
卧式容器任意液位高度下液体体积的计算

卧式容器任意液位高度下液体体积的计算卧式容器是一种常见的储存和运输液体的设备,它具有较大的容量和较小的高度,广泛应用于石油、化学、食品、医药等工业领域。
在实际工程中,经常需要计算卧式容器在不同液位高度下的液体体积,以方便控制和管理。
液体体积的计算是通过确定液位高度来实现的。
在卧式容器中,一般将壁厚忽略,将容器看作一个圆柱体。
液体体积的计算与液位高度的测量方式有关,常见的液位测量方式包括玻璃水尺、压力变送器、超声波液位计等。
以玻璃水尺测量液位高度为例,液体体积的计算可以按照以下步骤进行:1.确定容器的内径和长度,分别记为D和L。
2.安装玻璃水尺,将液位高度读数记为h。
3.根据液位高度h计算液位高度所对应的弧长,记为S。
弧长S=πD×h÷360。
4.根据弧长S计算液体体积V。
若0 ≤ h ≤ D/2,液体体积V = L × (D² × arcsin(1 - 2h/D) - (D - 2h) × √(2hD - h²)) ÷ 4;若D/2 < h ≤ D,液体体积V = L × (D² × arcsin(1 - 2h/D) + (2h - D) × √(2hD - h²)) ÷ 4上述计算公式是基于假设液体的表面是平坦的,并且容器的形状是圆柱体。
除了基于几何结构的计算方法,还可以利用浸没法进行液体体积的计算。
浸没法是通过将卧式容器完全浸没在另一个容器中,并记录液位的变化来实现的。
根据液位的变化,可以计算出容器内的液体体积。
根据浸没法的原理,还可以使用更精确的方法进行液体体积的计算,例如基于三维模型的计算方法。
这种计算方法是利用计算机辅助设计软件,根据卧式容器的三维模型和液体表面的三维形状,通过积分计算等数值分析方法,实现更精确的液体体积计算。
总之,在工程应用中,液体体积的计算是卧式容器设计和运输过程中非常重要的一部分。
卧式容器任意液位高度下液体体积的计算
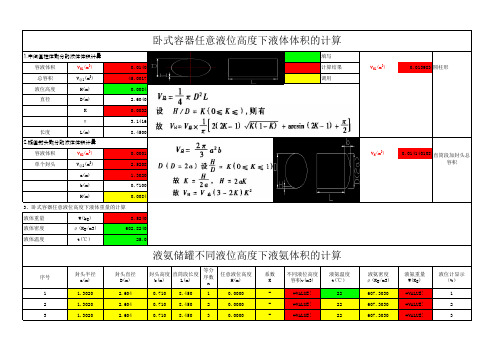
填写容液体积V H1(m 3)0.0140计算结果V H1(m 3)
0.013983
总容积V 总1(m 3)45.0017调用
液位高度H(m)0.0084直径
D(m) 2.6040K 0.0032π
3.1416长度
L(m)
8.4500
容液体积V H2(m 3)0.0001V H (m 3)
0.014140108
单个封头
V 总2(m 3) 2.5208a(m) 1.3020b(m)0.7100H(m)
0.0084
液体重量W(kg)8.5240液体密度ρ(Kg/m3)602.8240
液体温度
t(℃)
25.01 1.3020 2.6040.7108.45010.0000-#VALUE!22607.3030#VALUE!2 1.3020 2.6040.7108.45020.0000-#VALUE!22607.3030#VALUE!3
1.3020
2.604
0.710
8.450
3
0.0000
-#VALUE!
22
607.3030
#VALUE!
1.中间圆柱体部分的液体体积计算
2.椭圆封头部分的液体体积计算
序号卧式容器任意液位高度下液体体积的计算
液氨温度t (℃)
液氨密度ρ(Kg/m3)液氨重量W(Kg)封头直径D(m)封头高度b(m)直筒段长度L(m)系数K 不同液位高度容积v(m3)封头半径a(m)液氨储罐不同液位高度下液氨体积的计算
3、卧式容器任意液位高度下液体重量的计算等分序
数
n 任意液位高度H(m)。
卧式储罐不同液位下的容积(质量)计算精选全文

可编辑修改精选全文完整版卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部份长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐整体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及双侧封头组焊而成,去掉直段筒体,双侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液整体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导进程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及双侧封头组焊而成,去掉直段筒体,双侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部份该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,那么有222221x y z a c++= 垂直于y 轴分成无穷小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部份:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 那么筒体部份容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液整体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液整体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h假设液位高度h 以卧罐底部为起点,如以下图那么卧式储罐内储液整体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=其它方式如下:第一种方式卧式储罐不同液位下的容积简化计算公卧式储罐内储液整体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式圆柱罐体实际盛液的体积计算

卧式圆柱罐体实际盛液的体积计算
接下来,我们需要计算卧式圆柱罐体的高度。
卧式圆柱罐体通常有一个弓形的顶部,同时还有一个底部(通常为平面或球面)。
我们需要测量从底部到弓形顶部的垂直高度,即是罐体的高度。
最后,根据圆柱体的总体积公式:V=A*h,其中V为体积,A为底面积,h为高度,就可以得到卧式圆柱罐体的实际盛液体积。
举个例子来说明:
假设我们要计算一个卧式圆柱罐体的实际盛液体积,已知该罐体的底面直径为10米,高度为5米。
首先,根据半径计算底面积:
半径r=直径/2=10/2=5米
接下来,根据公式V=A*h,计算总体积:
V=78.54*5=392.7立方米
所以,该卧式圆柱罐体的实际盛液体积为392.7立方米。
需要注意的是,在实际运用中,我们可能会遇到一些额外的因素,比如罐体底部有凹陷或突出的结构,这样会影响到底面积的计算;另外,罐体内部可能有支撑物或导管等,也会对容积产生影响。
因此,在实际计算中需要根据具体情况进行调整。
除了通过计算卧式圆柱罐体的底面积和高度来求解体积,我们还可以通过其他方法来计算,比如浸没法、称重法等。
这些方法都是根据液体浸
没罐体的量或罐体的质量来计算容积。
不同的方法适用于不同的应用场景,具体选择哪种方法取决于具体情况和可行性。
总之,卧式圆柱罐体实际盛液的体积计算是一个基本的几何计算问题,在实际应用中需要考虑到具体情况和因素,选择合适的计算方法。
卧式圆形封头储罐液位体积计算程序

卧式圆形封头储罐液位体积计算程序下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
此文下载后可定制随意修改,请根据实际需要进行相应的调整和使用。
并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Downloaded tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The documents can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!随着工业化的发展,储罐的使用越来越广泛,而储罐液位的准确计量对生产的安全和经济是至关重要的。
