浙教版八年级上册图形的轴对称与翻折专题培优(附答案)

合集下载

浙教版八年级数学上2.1《图形的轴对称》同步练习题含答案

浙教版八年级数学上第二章特殊三角形2.1《图形的轴对称》同步练习题一、选择题1．下列图形中是轴对称图形的是(C)2．有下列图形：角，线段，直角三角形，等边三角形，长方形．其中一定是轴对称图形的有(C) A．2个B．3个C．4个D．5个3．如图，把长方形纸片折叠，使CD边落在EF处，折痕为GH，则与梯形CDGH成轴对称的图形是(C)A．梯形ABHG B．梯形A BKGC．梯形EFGH D．梯形EFKH4．如图，请在已知图案上再添加一个小正方形，使其成为轴对称图形，则不同的添法有(C)A. 1种B. 2种C. 3种D. 4种5．一只小狗正在平面镜前欣赏自己的全身像(如图所示)，此时，它所看到的全身像是(A)6．如图，△ABC的周长为30 cm，把△ABC的边AC对折，使顶点C和顶点A重合，折痕交边BC 于点D，交边AC于点E，连结AD.若AE＝4 cm，则△ABD的周长是(A)A. 22 cmB. 20 cmC. 18 cmD. 15 cm7．如图所示是由大小一样的小正方形组成的网格，△ABC的三个顶点均落在小正方形的顶点上，在网格上能画出三个顶点都落在小正方形的顶点上，且与△ABC成轴对称的三角形共有(A)A. 5个B. 4个C. 3个D.2个8．已知两条互不平行的线段AB和A′B′关于直线l对称，AB和A′B′所在的直线交于点P，有下列结论：①AB＝A′B′；②点P在直线l上；③若A，A′是对应点，则直线l垂直平分线段AA′；④若B，B′是对应点，则PB＝PB′.其中正确的是(D)A．①③④B．②④C．①②D．①②③④二填空题9．点A和点A′关于直线l成轴对称，则直线l与线段AA′的位置关系是直线l垂直平分线段AA′．10．线段AB与线段A′B′关于直线a成轴对称，那么线段AB和线段A′B′的数量关系是AB＝A′B′．11．一般长方形有2条对称轴，正方形有4条对称轴，等腰三角形有1或3条对称轴．12. 一枚图章上刻有，那么印在纸上的图案可能是__15__．13．数的运算中有一些有趣的对称式，如12×231＝132×21.请你仿照这个等式填空：24×462＝264×42．三、解答题14．如图，已知点A是锐角∠MON内的一点，试分别在OM，ON上确定点B，C，使△ABC的周长最小(要求画出图形，写出主要作图步骤)，并说明理由．（【解】分别作点A关于OM，ON的对称点A′，A″，连结A′A″，分别交OM，ON于点B，C，则点B，C即为题目所求．理由如下：∵点A关于OM，ON的对称点分别为A′，A″，∴OM，ON分别是线段AA′和线段AA″的垂直平分线，∴A′B＝AB，AC＝A″C.∴AB＋A C＋BC＝A′B＋BC＋A″C＝A′A″.若点B，C不在A′A″上，因为两点之间线段最短，则AB＋AC＋BC＝A′B＋BC＋A″C>A′A″.因此，照上述作法所求得的△ABC的周长最小．15．如图，正方形ABCD的周长为8，点E是线段B C的中点，点P是对角线AC上的一个动点，则PE＋PB的最小值是多少？(第15题)(第15题解)【解】∵四边形ABC D为正方形，∴点D为点B关于AC的对称点．连结ED，交AC于点P，如解图．由轴对称的性质，得PB＝PD，则PB＋PE＝PD＋PE＝DE，此时PE＋PB的值最小(两点之间线段最短)．在Rt△DCE中，∠DCE＝90°，DC＝2，EC＝1，由勾股定理，得DE＝DC2＋EC2＝22＋12＝5，即PE＋PB的最小值为 5.。

第13章轴对称(单元测试培优卷)(学生版) 2024-2025学年八年级数学上册基础知识专项突破

第13章轴对称（单元测试·培优卷）一、单选题（本大题共10小题，每小题3分，共30分）1．下列图形中是轴对称图形的是（）A ．B ．C ．D ．2．如图，点A 在直线l 上，△ABC 与AB C '' 关于直线l 对称，连接BB '，分别交AC ，AC '于点D ，D ¢，连接CC '，下列结论不一定正确的是（）A ．BACB AC ∠=∠''B ．CC BB '' C ．BD B D =''D ．AD DD ='3．我们知道光的反射是一种常见的物理现象.如图，某V 型路口放置如图所示的两个平面镜1l ，2l ，两个平面镜所成的夹角为1∠，位于点D 处的甲同学在平面镜2l 中看到位于点A 处的乙同学的像，其中光的路径为入射光线AB 经过平面镜1l 反射后，又沿BC 射向平面镜2l ，在点C 处再次反射，反射光线为CD ，已知入射光线2AB l ∥，反射光线1CD l ∥，则1∠等于（）A ．40︒B ．50︒C ．60︒D ．70︒4．如图，已知a b ∥，直线l 与直线a ，b 分别交于点A ，B ，分别以点A ，B 为圆心，大于12AB 长为半径画弧，两弧相交于点M ，N ，作直线MN 分别交直线a ，b 于点D 、C ，连接AC ，若135∠=︒，则BAD ∠的度数是（）A ．35︒B ．55︒C ．65︒D ．70︒5．如图，在等腰Rt ABC △，90BAC ∠=︒，AB AC =，BD 为ABC V 的角平分线，过点C 作CE BD ⊥交BD 的延长线与点E ，若2CE =，则BD 的长为（）A ．3B ．4C ．5D ．66．如图，90ACB AED ∠=∠=︒，CAE BAD ∠=∠，BC DE =，若BD AC ∥，则ABC ∠与CAE ∠间的数量关系为（）A ．2ABC CAE∠=∠B ．ABC CAE ∠=∠C ．290ABC CAE ∠+∠=︒D ．2180ABC CAE ∠+∠=︒7．某平板电脑支架如图所示，其中AB CD =，EA ED =，为了使用的舒适性，可调整AEC ∠的大小．若AEC ∠增大16︒，则BDE ∠的变化情况是（）A ．增大16︒B ．减小16︒C ．增大8︒D ．减小8︒8．如图，在ABC V 中，80BAC ∠=︒，边A 的垂直平分线交BC 于点E ，边AC 的垂直平分线交AC 于点F ，连接AE ，AG ．则EAG ∠的度数为（）A ．35︒B ．30︒C ．25︒D ．20︒9．如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，AD 是△ABC 的角平分线，若P ，Q 分别是AD 和AC 边上的动点，则PC +PQ 的最小值是（）A ．65B ．2C ．125D ．5210．如图，在ABC V 中，90BAC ∠=︒，A 是高，BE 是中线，C 是角平分线，C 交A 于G ，交BE 于H ，下面说法：①ACF BCF S S = ；②AFG AGF ∠=∠；③2FAG ACF ∠=∠；④BH CH =．其中正确的是()A ．①②③④B ．①③C ．②③D ．①③④二、填空题（本大题共8小题，每小题4分，共32分）11．如图，在ABC V 中，分别以点B 和点C 为圆心，大于12BC 的长为半径画弧，两弧相交于点M 、N ，作直线MN ，交AB 于点D ，连接CD ，若ABC V 的周长为24，9BC =，则ADC △的周长为．12．如图，直线m n ∥，点A 是直线m 上一点，点B 是直线n 上一点，AB 与直线m ，n 均不垂直，点P为线段AB 的中点，直线l 分别与m ，n 相交于点C ，D ，若90,CPD CD ∠=︒=m ，n 之间的距离为2，则PC PD ⋅的值为．13．如图，A EGF ∠=∠，F 为BE CG ，的中点，58DB DE ==，，则AD 的长为．14．如图所示，在平面直角坐标系中，ABC V 满足45,90BAC CBA ∠=︒∠=︒，点A ，C 的坐标分别是()()2,0,3,5--，点B 在y 轴上，在坐标平面内存在一点D （不与点C 重合），使ABC ABD △≌△，且AC 与AD 是对应边，请写出点D 的坐标．15．如图，60AOB ∠=︒，C 是BO 延长线上一点，12cm OC =，动点M 从点C 出发沿射线CB 以2cm /s 的速度移动，动点N 从点O 出发沿射线OA 以1cm /s 的速度移动，如果点M 、N 同时出发，设运动的时间为s t ，那么当t =s 时，MON △是等腰三角形．16．如图，锐角ABC 中，30A ∠=︒，72BC =，ABC 的面积是6，D ，E ，F 分别是三边上的动点，则DEF 周长的最小值是．17．如图，在平面直角坐标系中，点1A ，2A ，3A ，4A ，…在x 轴正半轴上，点1B ，2B ，3B ，…在直线()0y x =≥上，若()11,0A ，且112A B A △，223A B A △，334A B A △，…均为等边三角形，则线段20212022A A 的长度为．18．如图，将长方形纸片ABCD 沿EF 折叠（折线EF 交AD 于E ，交BC 于F ），点C D 、的对应点分别是1C 、1D ，1ED 交BC 于G ，再将四边形11C D GF 沿FG 折叠，点1C 、1D 的对应点分别是2C 、2D ，2GD 交EF 于H ，给出下列结论：①2EGD EFG∠=∠②2180EFC EGC ∠=∠+︒③若26FEG ∠=︒，则2102EFC ∠=︒④23FHD EFB∠=∠上述正确的结论是．三、解答题（本大题共6小题，共58分）19．（8分）在ABC V 中，90ACB ∠=︒，AC BC BE ==，AD EC ⊥，交EC 延长线于点D ．求证：2CE AD =．20．（8分）如图，点P 是AOB ∠外的一点，点E 与点P 关于OA 对称，点F 与点P 关于OB 对称，直线FE 分别交OA OB 、于C 、D 两点，连接PC PD PE PF 、、、．（1）若20OCP F ∠=∠=︒，求CPD ∠的度数；（2）若求=CP DP ，13CF =，3DE =，求CP 的长．21．（10分）如图，在ABC V 中，AD 平分BAC ∠，点E 为AC 中点，AD 与BE 相交于点F ．（1）若38,82ABC ACB ∠=︒∠=︒，求ADB ∠的度数；（2）过点B 作BH AD ⊥交AD 延长线于点H ，作ABH 关于AH 对称的AGH ，设BFH △，AEF △的面积分别为12,S S ，若6BCG S V =，试求12S S -的值．22．（10分）已知：OP 平分MON ∠，点A ，B 分别在边OM ，ON 上，且180OAP OBP ∠+∠=︒．（1）如图1，当BP OM ∥时，求证：OB PB =．（2）如图2，当90OAP ∠<︒时，作PC OM ⊥于点C ．求证：2OA OB AC -=．23．（10分）已知，在ABC V 中，90CAB ∠=︒，AD BC ⊥于点D ，点E 在线段BD 上，且CD DE =，点F 在线段AB 上，且45BEF ∠=︒（1）如图1，求证：DAE B∠=∠（2）如图1，若2AC =，且2AF BF =，求ABC V 的面积（3）如图2，若点F 是AB 的中点，求AEF ABCS S的值．24．（12分）如图，在ABC V 中，90ACB ∠=︒，30ABC ∠=︒，CDE 是等边三角形，点D 在边AB 上．（1）如图1，当点E 在边BC 上时，求证DE EB=（2）如图2，当点E 在ABC V 内部时，猜想ED 和EB 数量关系，并加以证明；（3）如图3，当点E 在ABC V 外部时，EH AB ⊥于点H ，过点E 作GE AB ，交线段AC 的延长线于点G ，5AG CG =，3BH =，求CG 的长．。

浙教版八年级数学培优试卷专题24 图形的折叠与剪拼

专题24 图形的折叠与剪拼阅读与思考图形的折叠是指把某个图形或部分沿某直线翻折，这条直线为对称轴，在折叠过程中，线短的长度、角的度数保持不变.图形的剪拼是指对某个图形通过有限次的剪裁后重新接成另外一个新的几何图形，在剪拼过程中，原图形与新图形的面积一般保持不变.解答图形的折叠与剪拼问题，要抓住折叠与剪拼过程中一些量的不变性，将计算、推理与合情想象结合起来，常用到全等三角形、勾股定理、面积等知识与方法.折叠问题的实质是对称问题，“遇到折叠用对称”就是运用对称的性质： ① 关于一条直线对称的两个图形全等； ② 对称轴是对应点连线的中垂线. 例题与求解【例1】如图，矩形ABCD 中，AB ＝8，BC ＝4，将矩形沿AC 折叠，点D 落在D '处，则重叠部分△AFC 的面积为＿＿＿＿＿.（山东省竞赛试题）A例1题图例2题图解题思路：△AFC 的高为BC ，只需求出AF ，注意到D '∠＝090，AF ＝FC【例2】如图，直线26y x =-+ 与x 轴，y 轴分别交于P ，Q 两点，把△POQ 沿PQ 翻折，点O 落在R 处，则点R 的坐标是（）A.2412(,)55B.（2,1）C.（6,3）D.（7，3.5）解题思路：过点R 作x 轴，y 轴的垂线，再利用相似三角形的性质可得垂线段的长度即求得点R 的坐标.解剪拼问题时先利用剪拼后的图形所需关键线段的长度，然后，从剪拼前的图形中寻找这些长度进行剪拼.【例3】如图，将边长为12cm 的正方形ABCD 折叠，使得A 点落在CD 边上点E 处，然后压平折痕FG ，若FG ＝13cm ，求CE 长.（北京市竞赛试题）解题思路：由折叠可得A 与E 关于FG 对称，则FG ⊥AE ，可证明FG ＝AE ，这是解本例的关键.【例4】将一矩形纸片OABC 放在平面直角坐标系中，(00)O ，，(60)A ，，(03)C ，．动点Q 从点出发以每秒1个单位长的速度沿OC 向终点C 运动，运动23秒时，动点从点出发以相等的速度沿AO 向终点O 运动．当其中一点到达终点时，另一点也停止运动．设点的运动时间为（秒）．（1）用含的代数式表示OP OQ ，；（2）当1t 时，如图1，将OPQ △沿PQ 翻折，点O 恰好落在CB 边上的点处，求点的坐标；（3）连结AC ，将O P Q △沿PQ 翻折，得到EPQ △，如图2．问：PQ 与AC 能否平行？PE 与AC能否垂直？若能，求出相应的值；若不能，说明理由．（绍兴市中考试题）图1解题思路：对于（3），假设能，由比例线段求出t的值，关键是看相应t的值是否在t的取值范围.折纸、剪纸是最富于自然情趣而又形象生动的实验，同时说明了存在的事实是怎样被发现的，现象又是怎样获得证实的，在平面几何的一些主要学习环节发挥重要作用.【例5】用10个边长分别为3，5，6，11，17，19，22，23，24，25的正方形，可以拼接一个长方形.（1）求这个长方形的长和宽；（2）请画出拼接图.（“华杯赛”决赛试题）解题思路：运用剪拼前后图形面积不变求长方形的长和宽；利用长方形对边相等的性质画拼接图.【例6】将正方形纸片ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB 折叠后与BC交于点G.（1）如果M为CD边的中点，求证：DE：DM：EM＝3：4：5；（2）如果M为CD边上的任意一点，设AB＝2a，问△CMG的周长是否有与点M的位置关系？若有关，请把△CMG的周长用含CM的长x的代数式表示；若无关，请说明理由．解题思路：折痕EF两旁部分图形是关于EF成对称的，对于（2），通过相似三角形性质，把△CMG的周长用相关代数式表示，解题的关键是将几何问题代数化.对于例6，如图，当M 为CD 边上的中点，则有3BCBG，即G 为BC 的三等分点，这一结果是由日本筑波大学的生物学教授芳贺和夫发现的，被称为芳贺第一定理.作深入思考，进一步挖掘还能得到如下重要结论：（1）无论怎样折叠，若点M 落在CD 上，则MG ＝DM ＋BG ；（2）无论怎样折叠，若点M 落在CD 上，连MA ，GA ，则∠MAG ＝450.能力训练1、如图，在矩形ABCD 中，AB ＝6cm ，BC ＝8cm ，若将矩形折叠，使B 点与D 点重合，则折痕EF 的长为＿＿＿cm.(宁夏回族自治区中考试题)2、如图，矩形ABCD 中，AB ＝12，AD ＝10，将此矩形折叠使B 点落在AD 边上的中点E 处，则折痕FG 的长为_________.第1题图第2题图第3题图(淮阴市中考试题)3、如图是用12个全等的等腰梯形镶嵌成的图形，这个等腰梯形的上底与下底长的比是_____.(陕西省中考试题)4、如图，EF 为正方形纸ABCD 的对折线，将∠A 沿DK 折叠，使它的顶点A 落在EF 上的G 点，则∠DKG ＝_______度.5、如图，已知等边△ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′，EB′分别交边AC于点F，G，若∠ADF＝080，则∠EGC的度数为________.第4题图第5题图第6题图(台州市中考试题)6、将一张长为70cm的长方形纸片ABCD沿对称轴EF折叠成如图的形状，若折叠后，AB与CD间的距离为60cm，则原纸片的宽AB是______cm.(广东省中考试题) 7、如图，在矩形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B落在F处，折痕为AE，且EF＝3，则AB的长为( )A.3B.4C.5D.6(宜宾市中考试题)8、如图，在△ABC中，∠C＝900，BC＝6，D，E分别在AB，AC上，将△ABC沿DE折叠，使点A落在点A′处，若A′为CE的中点，则折痕DE的长为 ( )A.12B、2C、3D、4(河北省中考试题)EA第7题图第8题图第9题图9、如图，有一块菱形的草地，要在其上面修筑两条笔直的道路，道路把这块草地分成面积相等的四部分，如果道路的宽度可以忽略不计，请你设计三种不同的方案.(广西赛区选拔赛试题)10、如图，折叠矩形纸片ABCD，先折出折痕(对角线)BD，再折叠使AD边与对角线BD重合，得折线DG，若AB＝2，BC＝1，求AG.(安徽省中考试题)11、如图，折叠矩形ABCD的一边AD，使点D落在BC边上的点F处，已知折痕3.4ECAEFC==，求矩形ABCD的周长.(厦门市中考试题)12、如图1，一张矩形纸片ABCD，其中AD＝8cm，AB＝6cm，先沿对角线BD对折，点C落在点C′处的位置，BC′交AD于点G.(1) 求证：AG＝GC'；(2) 如图2，再折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M，求EM的长.(深圳市中考试题)B级1、如图，一张宽为3，长为4的矩形纸片ABCD，先沿对角线BD对折，点C落在C′的位置，BC′交AD于G，再折叠一次使D点与A点重合，得折痕EN，EN交AD于点M，则ME的长为__________.2、如图，矩形纸片ABCD中，AB＝3cm，BC＝4cm，现将A，C重合，使纸片折叠压平，设折痕为EF，则重叠部分△AFE的面积为_________.第1题图第2题图第3题图3、如图，矩形ABCD沿直线BD折叠，使点C落在C′处，BC′交AD于点E，若AD＝8，AB＝4，则DE的长为________.4、如图，把矩形纸片OABC放入平面直角坐标系中，使OA，OC分别落在x轴上，y轴上，连结AC，将矩形纸片OABC沿AC折叠，使点B落在点D的位置，若B(1，2)，则点D的横坐标是______.5、如图，在平面直角坐标系中，已知直线334y x=-+与x轴，y轴分别交于A，B两点，点C(0，n)是y 轴上一点，把坐标平面沿直线AC折叠，使点B刚好落在x轴上B′处，则点C的坐标是_________.第4题图第5题图第6题图6、如图，矩形纸片ABCD，AB＝5cm，BC＝10cm，CD上有一点E，ED＝2cm，AD上有一点P，PD＝3cm，过P 作PF⊥AD交BC于F，将纸片折叠，使P点与E点重合，折痕与PF交于Q点，则PQ的长是_____cm.7、在三角形纸片ABC中，已知∠ABC＝900，AB＝6，BC＝8，过点A作直线l平行于BC，折叠三角形纸片ABC，使直角顶点B落在直线上的T处，折痕为MN，当点T在直线l上移动时，折痕的端点M，N也随之移动，若限定端点M，N分别在AB，BC边上移动，则线段AT长度的最大值与最小值之和为__________(计算结果不取近似值)8、如图，矩形纸片ABCD中，AB＝8，将纸片折叠，使顶点B落在边AD上的E点处，BG＝10.（1）当折痕的另一端F在AB边上时，如图．求△EFG的面积；（2）当折痕的另一端F在AD边上时，如图．证明四边形BGEF为菱形，并求出折痕GF的长.9、如图，已知三角形纸片ABC的面积为25，BC的长为10，∠B，∠C都为锐角，M是AB边上的一动点(M 与A，B不重合)，过点M作MN∥BC交AC于点N，设MN＝.(1）用x表示△AMN的面积；（2）△AMN沿MN折叠，使△AMN紧贴四边形BCNM（边AM、AN落在四边形BCNM所在的平面内），设点A落在平面BCNM内的点A′，△A′MN与四边形BCNM重叠部分的面积为y．①用含x的代数式表示y，并写出x的取值范围．②当x为何值时，重叠部分的面积y最大，最大为多少？10、如图：一正方形纸片，根据要求进行多次分割，把它分割成若干个直角三角形．具体操作过程如下：第一次分割：将正方形纸片分成4个全等的直角三角形；第二次分割：将上次得到的直角三角形中的一个再分成4个全等的直角三角形；以后按第二次分割的方法重复进行．（1）请你设计出两种符合题意的分割方案（分割3次）；（2）设正方形的边长为a，请你通过对其中一种方案的操作和观察，将第二、第三次分割后所得的最小的直角三角形的面积S填入下表：（3）在条件（2）下，请你猜想：分割所得的最小直角三角形面积S与分割次数n有什么关系？用数学表达式表示出来．11、如图1，将边长为4cm的正方形纸片ABCD沿EF折叠(点E，F分别在边AB，CD上)，使点B落在AD边上的点M处，点C落在点N处，MN与CD交于点P，连结EP.(1)如图②，若M为AD边的中点，①△AEM的周长＝_________cm；②求证：EP＝AE＋DP；（2）随着落点M在AD边上取遍所有的位置（点M不与A、D重合），△PDM的周长是否发生变化？请说明理由.12、如图1，在矩形ABCD 中，AB ＝3，AD ＝1，点P 在线段AB 上运动，设AP ＝x ，现将纸片折叠，使点D 与点P 重合，得折痕EF(点E ，F 为折痕与矩形边的交点)，再将纸片还原.（1）当0 x 时，折痕EF 的长为________；（2）写出使四边形EPFD 为菱形的x 的取值范围，并求出当x ＝2时菱形的边长；（3）令2EF ＝y ，当点E 在AD 上、点F 在BC 上时，写出y 与x 的函数关系式（写出x 的取值范围），当取最大值时，判断△EAP 与△PBF 是否相似．若相似，求出的值；若不相似，请说明理由.。

浙教版2022-2023学年八年级上数学期中培优测试卷2(解析版)

浙教版2022-2023学年八年级上数学期中培优测试卷2（解析版）一、选择题（本大题有10小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的.1．下列垃圾分类的图标（不含文字与字母部分）中，是轴对称图形的是（）A ．B ．C ．D ．【答案】B【解析】A 、不是轴对称图形，故本选项不合题意； B 、是轴对称图形，故本选项符合题意； C 、不是轴对称图形，故本选项不合题意； D 、不是轴对称图形，故本选项不合题意．故答案为：B ．2．下列长度的三条线段，能组成三角形的是（） A ．3，4，8 B ．5，6，10 C ．5，5，11 D ．5，6，11【答案】B【解析】A.∵3+4＜8，故不能组成三角形，A 不符合题意； B.∵5+6＞10，故能组成三角形，B 符合题意； C.∵5+5＜11，故不能组成三角形，C 不符合题意； D.∵5+6=11，故不能组成三角形，D 不符合题意；故答案为：B.3．如图是作△ABC 的作图痕迹，则此作图的已知条件是（）A ．已知两边及夹角B ．已知三边C ．已知两角及夹边D ．已知两边及一边对角【答案】C【解析】观察图象可知：已知线段AB ，∠CAB ＝α，∠CBA ＝β. 故答案为：C.4．已知关于x 的不等式组{3x −m <0x >−4的所有整数解的和为-5，则m 的取值范围为（）A ．−6<m ≤−3或3<m ≤6B ．−6≤m <−3或3≤m <6C ．−6≤m <−3D ．−6<m ≤−3 【答案】A【解析】由3x −m <0，得：x <m3，又x >−4，且不等式组所有整数解的和为−5， ∴不等式组的整数解为-3、-2或-3、-2、-1、0、1，∴−2<m 3≤−1或1<m3≤2，解得−6<m ≤−3或3<m ≤6. 故答案为：A. 5．如图，在△ABC 中，∠ABC 的平分线与AC 的垂直平分线相交于点D ，过点D 作DF ⊥BC ，DG ⊥AB ，垂足分别为F 、G ．若BG ＝4，AC ＝5，则△ABC 的周长是（）A．12B．13C．14D．15【答案】B【解析】连接AD、DC．∵BD平分∠ABC，DG⊥AB，DF⊥BC，∴DG=DF．∵D在AC的中垂线上，∴DA=DC．在Rt△DGA与Rt△DFC中，∵DG=DF，DA=DC，∴Rt△DGA≌Rt△DFC（HL）．∴AG=CF，∵DG=DF，BD=BD，∴Rt△BDG≌Rt△BDF（HL）．∴BG=BF．又∵AG=CF，∴△ABC的周长=AB+BC+AC=BG-AG+BF+FC+AC=2BG+AC=2×4+5=13.故答案为：B.6．如图，已知等边△ABC中，在射线BA上有一点D，连接CD，以CD为边向上作等边△CDE，连接BE和AE，下列结论：①AE=BD；②直线AE与直线AB所夹的锐角为60°；③当D在线段AB或BA延长线上时，总有∠BED−∠AED=2∠BDC；④∠BCD=90°时，CE2+AD2=AC2+DE2，正确的结论序号有（）A．①②B．①②③C．①②④D．①②③④【答案】C【解析】∵△ABC，△CDE都是等边三角形∴CB=CA，CD=CE，∠BCA=∠DCE= 60°∴∠BCD=∠ACE∴△BCD≅△ACE(SAS)∴BD=AE，∠BDC=∠AEC，故①正确；∵∠EOC=∠DOA∴∠OAD=∠OCE= 60°∴AE与AB的夹角为60°，故②正确；∵∠BED-∠AED=∠AEB<∠AEC∠AEC=∠BDC∴∠BED-∠AED <∠BDC，故③错误；当∠BCD= 90°时，易证AC=AD∵CE=DE∴CE2+AD2=AC2+DE2，故④正确.故答案为：C.7．如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，AB＝AC＝4，O为AC中点，若点D在直线BC上运动，连接OE，则在点D运动过程中，则OE的最小值是（）A．√22B．1C．√2D．2【答案】C【解析】设Q为AB的中点，连接DQ，如图所示：∵∠BAC=∠DAE=90°，∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，∵AB=AC=4，点O为AC的中点，∴AQ=AO，∵AD=AE，∴△AQD≌△AOE（SAS），∴QD=OE，∵点D在直线BC上运动，∴当QD⊥BC时，QD最小，∵△ABC是等腰直角三角形，∴∠B=45°，∴△QBD是等腰直角三角形，∴QD=√22QB，∵QB=12AB=2，∴QD=√2，∴线段OE的最小值为√2；故答案为：C.8．如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG⊥CE于点G，CD＝AE.若BD ＝6，CD＝5，则△DCG的面积是（）A．10B．5C．103D．53【答案】B【解析】∵CE是AB边上的中线，∴AE＝BE，∵CD＝AE＝5，∴AB＝10，根据勾股定理得：AD＝√AB2−BD2＝8，∴△ABC的面积为12BC·AD=12×11×8=44，∵CE 是△ABC 的中线， ∴S △BCE ＝S △ACE ＝22，∵BD ＝6，AD ＝8，AD ⊥BC ，∴S △ABD =12·BD ·AD =12×6×8=24 ， ∵DE 是△ABD 的中线， ∴S △BDE ＝12，∴S △DCE ＝S △BCE ﹣S △BDE ＝10，∵DE ＝AE ＝ 12 AB ，DC ＝AE ， ∴DC ＝DE ， ∵DG ⊥CE ，∴S △DCG =12S △DCE =12×10=5 . 故答案为：B.9．已知关于x 的不等式组的 {x −a ≥b2x −a <2b +1解集为3≤x ＜5，则 b a 的值为（） A ．﹣2 B ．−12 C ．﹣4 D ．﹣ 14【答案】A【解析】{x −a ≥b①2x −a <2b +1②由①得：x≥a+b ；由②得：x <a+2b+12；∵不等式组的解集为：a +b ≤x ＜a+2b+12即3≤x ＜5∴{a +b =3a+2b+12=5 解之：{a =−3b =6∴b a =6−3=−2. 故答案为：A.10．如图，在Rt △ABC 中，∠ACB ＝90°，点D 是斜边AB 边上的中点，连接CD ，延长BC 至点E ，使得CE ＝AD ，连接DE ，过点C 作CM ⊥DE 于点M ，其中BC ＝6，AD ＝5，则S △ABC ：S △MCE 等于（）A ．11：1B ．44：3C ．24：5D ．44：5【答案】C【解析】∵点D 是斜边AB 边上的中点，AD ＝5， ∴AB ＝10， ∵∠ACB ＝90°，BC ＝6，∴AC ＝ √AB 2−BC 2 ＝8，CD ＝AD ＝BD ＝ 12 AB ＝5， ∵CE ＝AD ， ∴CE ＝CD ， ∵CM ⊥DE ， ∴DM ＝EM ，∵BC ＝6，CE ＝5，∴S △BCD ：S △DCE ＝BC ：CE ＝6：5，∵S △ABC ＝2S △BCD ，S △CEM ＝ 12 S △CDE ， ∴S △ABC ：S △MCE ＝2×6： 12 ×5＝24：5. 故答案为：C.二、填空题（本大题有6小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案.11．如图，已知△ABD ≌△ACE ，∠A ＝53°，∠B ＝22°，则∠BEC ＝ °.【答案】75【解析】∵△ABD ≌△ACE ， ∴∠B=∠C=22°，∴∠BEC=∠A+∠C=53°+22°=75°. 故答案为：75.12．如图，直线 l 上有三个正方形A 、B 、C ，若正方形A 、C 的边长分别为5和7，则正方形 B 的面积为．【答案】74 【解析】如图，∵ 正方形 A ， C 的边长分别为5和7， ∴EF =5 ， MH =7 ，由正方形的性质得： ∠EFG =∠EGH =∠GMH =90° ， EG =GH ， ∵∠FEG +∠EGF =90° ， ∠EGF +∠MGH =90° ， ∴∠FEG =∠MGH ，在 ΔEFG 和 ΔGMH 中， {∠EFG =∠GMH ∠FEG =∠MGH EG =GH，∴ΔEFG ≅ΔGMH(AAS) ，∴FG =MH =7 ， GM =EF =5 ， ∴EF 2=52=25 ， HM 2=72=49 ，∴ 正方形B 的面积为 EG 2=EF 2+FG 2=EF 2+HM 2=25+49=74 ，故答案为：74.13．如图，在△ABC 中，AB=AC ，AD ⊥BC 于D 点，点E 、F 分别是AD 的三等分点，若△ABC 的面积为18cm 2，则图中阴影部分面积为 cm 2．【答案】9【解析】∵S △ABC =18cm 2，∴阴影部分面积= 12 ×18=9cm 2．故答案为：9． 14．如图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，在Rt △ABC 中，若直角边AC =6，BC =5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长（图乙中的实线）是．【答案】76【解析】依题意，设“数学风车”中的四个直角三角形的斜边长为x，则x2=122+52=169，解得：x=13，∴“数学风车”的外围周长(13+6)×4=76．故答案为：76.15．如图，将一张三角形纸片ABC的一角折叠，使得点A落在四边形BCDE的外部A'的位置，且A'与点C在直线AB的异侧，折痕为DE，已知∠C＝90°，∠A＝30°．若保持△A′DE的一边与BC平行，则∠ADE 的度数．【答案】45°或30°【解析】当DA'∥BC时，如图，∠A'DA=∠ACB=90°，∵△ADE沿DE折叠到A'DE，∴∠ADE=∠A'DE= 12∠ADA′＝45°，当EA'∥BC时，如图，在△ABC中，∠B=180°-∠C-∠A=60°，∴∠2=∠ABC=60°，由折叠可知，∠A′=∠A=30°，在△A′EF中，∠A′+∠2+∠A′FE=180°，∴∠2=180°-∠A′-∠A′FE=150°-∠A′FE，在四边形BCDF中，∠1+∠C+∠B+∠BFD=360°，∴∠1=360°-∠C-∠B-∠BFD=210°-∠BFD，∵∠BFD=∠A′FE，∴∠1-∠2=210°-150°=60°，∴∠1=∠2+60°=120°，∵△ADE 沿DE 折叠到A'DE ，∴∠ADE=∠A'DE= 12 ∠ADA′= 12 （180°-∠1）=30°，综上所述，∠ADE 的度数为：45°或30°. 故答案为：45°或30°.16．如图，已知△ABC 中，∠ACB=90°，O 为AB 的中点，点E 在BC 上，且CE=AC ，∠BAE=15°，则∠COE= 度．【答案】75【解析】∵∠ACB=90°，CE=AC ， ∴∠CAE=∠AEC=45°， ∵∠BAE=15°， ∴∠CAB=60°， ∴∠B=30°， ∵∠ACB=90°，O 为AB 的中点，∴CO=BO=AO= 12 AB ，∴△AOC 是等边三角形，∠OCB=∠B=30°， ∴AC=OC=CE ，∴∠COE=∠CEO= 12 ×（180°-30°）=75°. 故答案为：75.三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）解答应写出文字说明，证明过程或推演步骤.17．如图，△ABC 和△DCE 都是等腰直角三角形，CA ＝CB ，CD ＝CE ，且点D 在△ABC 的斜边AB 上．（1）连结AE ，求证：△ACE ≌△BCD ．（2）若BD ＝2，CD ＝6，求AD 的长．【答案】（1）证明：∵ΔABC 和ΔDCE 都是等腰直角三角形，CA =CB ，CD =CE ， ∴∠ACB =∠DCE =90°， ∴∠BCD =∠ACE ，在ΔBCD 和ΔACE 中，{CB =CA∠BCD =∠ACE CD =CE，∴ΔBCD ≅ΔACE(SAS)．（2）解：∵ΔACE ≅ΔBCD ，∴CE =CD =6，BD =AE =2，∠B =∠CAE =45°， ∴DE =6√2，∠DAE =90°，∴AD =√DE 2−AE 2=√(6√2)2−22=2√17．18．如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“奇妙三角形”．（1）如图，在△ABC 中，AB ＝AC ＝2√5，BC ＝4，求证：△ABC 是“奇妙三角形”；（2）在Rt △ABC 中，∠C ＝90°，AC ＝2√3，若△ABC 是“奇妙三角形”，求BC 的长．【答案】（1）证明：过点A 作AD ⊥BC 于D ，∵AB ＝AC ，AD ⊥BC ，∴BD ＝12BC ＝2，由勾股定理得，AD ＝√AB 2−BD 2＝4， ∴AD ＝BC ，即△ABC 是“奇妙三角形”；（2）解：∵直角三角形斜边的中线等于斜边的一半， ∴该中线不可能是斜边的中线．当AC 边上的中线BD 等于AC 时， BC ＝√BD 2−CD 2＝3，当BC 边上的中线AE 等于BC 时，AC 2＝AE 2﹣CE 2，即BC 2﹣(12BC)2＝(2√3)2，解得BC ＝4．综上所述，BC 的长是3或4．19．如图，在△ABC 中，AB =AC ，AD =AE ．（1）若∠BAD =40°，求∠EDC 的度数．（2）判断∠BAD 与∠EDC 之间的数量关系，并说明理由．【答案】（1）解：∵∠AED=∠EDC+∠C ， ∠ADC=∠B+∠BAD ，又∵AD=AE ，∴∠AED=∠ADE ， ∵AB=AC ， ∴∠B=∠C ，∴∠B+∠BAD=∠EDC+∠C+∠EDC ，即∠BAD=2∠EDC ， ∵∠BAD=40°， ∴∠EDC=20°．（2）解：∠BAD ＝2∠EDC(或∠EDC ＝12∠BAD )． ∵AD ＝AE ，∴∠ADE ＝∠AED ， ∴∠BAD ＋∠B ＝∠ADC ＝∠ADE ＋∠EDC＝∠AED ＋∠EDC＝(∠EDC ＋∠C)＋∠EDC ＝2∠EDC ＋∠C ，又∵AB ＝AC ， ∴∠B ＝∠C ，∴∠BAD ＝2∠EDC ，∴∠EDC ＝12∠BAD ．20．如图，已知在△ABC 中，∠B =90°，AC =10，BC =6，若动点P 从点B 开始，按B →A →C →B 的路径运动，且速度为每秒2个单位长度，设出发的时间为t 秒．（1）出发2秒后，求CP 的长．（2）出发几秒钟后，CP 恰好平分△ABC 的周长．（3）当t 为何值时，△BCP 为等腰三角形？【答案】（1）解：由∠B ＝90°，AC ＝10，BC ＝6，∴AB ＝8，∵P 从点B 开始，按B→A→C→B ，且速度为2， ∴出发2秒后，则BP ＝4，AP ＝6， ∵∠B ＝90°，∴在Rt △BCP 中，由勾股定理得PC ＝√BP 2+BC 2=√62+42=√52 ；（2）解：∵P 点不可能位于线段BC 和AC 上，即对P 点在线段AB 上进行探究，根据题意可得，6＋2t ＝10＋8－2t ；解得t ＝3∴出发3秒钟后，CP 恰好平分△ABC 的周长（3）解：①当P 在AB 上时，若BP ＝BC 时，得到2t ＝6；则t ＝3，②当P 在AC 上时，若BP ＝BC 时，过点B 作BD ⊥AC ，则BD =AB×BC AB=6×810=4.8在Rt △BDP 中，PD =√PD 2−BD 2=√62−4.82=3.6 在Rt △ADB 中，AD =√AB 2−BD 2=√82−4.82=6.4∴BA +AP =BA +AD −PD =8+6.4−3.6=10.8即2t =10.8 解得t =5.4③当P 在AC 上时，若CB ＝CP 时，BA +PA =BA +AC −PC =8+10−6=12即2t =12 解得t =6④当P 在AC 上时，若PC ＝PB 时，PA =12AB =5∴BA +AP =8+5=13得到2t ＝6；则t ＝6.5．综上可得t ＝3或5.4或6或6.5时，△BCP 为等腰三角形．21．某文具店准备购进甲，乙两种钢笔，若购进甲种钢笔100支，乙种钢笔50支，需要1000元，若购进甲种钢笔50支，乙种钢笔30支，需要550元．（1）求购进甲，乙两种钢笔每支各需多少元？（2）若购进了甲种钢笔80支，乙种钢笔60支，求需要多少元？（3）若该文具店准备拿出1000元全部用来购进这两种钢笔，考虑顾客需求，要求购进甲种钢笔的数量不少于乙种钢笔数量的6倍，且不超过乙种钢笔数量的8倍，那么该文具店共有几种购进方案．【答案】（1）解：设购进甲种钢笔每支需x 元，购进乙种钢笔每支需y 元，依题意得：{100x +50y =100050x +30y =550，解得：{x =5y =10．答：购进甲种钢笔每支需5元，购进乙种钢笔每支需10元．（2）解：5×80+10×60=400+600=1000（元)．答：需要1000元．（3）解：设购进甲种钢笔m 支，则购进乙种钢笔1000−5m 10=(100−12m)支，依题意得：{m ⩾6(100−12m)m ⩽8(100−12m)，解得：150⩽m ⩽160．又∵m ，(100−12m)均为正整数，∴m 可以为150，152，154，156，158，160， ∴该文具店共有6种购进方案．22．如图，在△ABC 中，AB ＝AC ，点D 在△ABC 内，BD ＝BC ，∠DBC ＝60°，点E 在△ABC 外，∠BCE ＝150°，∠ABE ＝60°．（1）求∠ADB 的度数；（2）判断△ABE 的形状并证明；（3）连接DE ，若DE ⊥BD ，DE ＝6，求AD 的长．【答案】（1）解：∵BD ＝BC ，∠DBC ＝60°，∴△DBC 是等边三角形，∴DB ＝DC ，∠BDC ＝∠DBC ＝∠DCB ＝60°，在△ADB 和△ADC 中，{AB =AC AD =AD DB =DC ，∴△ADB ≌△ADC （SSS ），∴∠ADB ＝∠ADC ，∴∠ADB ＝12（360°﹣60°）＝150°．（2）解：结论：△ABE 是等边三角形．理由：∵∠ABE ＝∠DBC ＝60°，∴∠ABD ＝∠CBE ，在△ABD 和△EBC 中，{∠ADB =∠BCE =150°BD =BC ∠ABD =∠CBE ， ∴△ABD ≌△EBC （ASA ），∴AB ＝BE ，∵∠ABE ＝60°，∴△ABE 是等边三角形．（3）解：连接DE ．∵∠BCE ＝150°，∠DCB ＝60°，∴∠DCE ＝90°，∵∠EDB ＝90°，∠BDC ＝60°，∴∠EDC ＝30°，∴EC ＝12DE ＝3，∵△ABD ≌△EBC ，∴AD ＝EC ＝3．23．在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，点D 为AB 边上一点，过点D 作DE ⊥AB ，交BC 于点E ，连接AE ，取AE 的中点P ，连接DP ，CP.（1）观察猜想：如图（1），DP与CP之间的数量关系是，DP与CP之间的位置关系是.（2）类比探究：将图（1）中的△BDE绕点B逆时针旋转45°，（1）中的结论是否仍然成立？若成立，请就图（2）的情形给出证明；若不成立，请说明理由.（3）问题解决：若BC＝3BD＝3√2，将图（1）中的△BDE绕点B在平面内自由旋转，当BE⊥AB 时，请直接写出线段CP的长.【答案】（1）PD＝PC；PD⊥PC（2）解：结论成立.理由如下：过点P作PT⊥AB交BC的延长线于T，交AC于点O.则∠APO=∠BPT=∠OCT=90°∴∠A=∠AOP=45°，∠COT=∠AOP=45°∴PA=PO，OC=CT，∠CTO=45°由勾股定理可得：OT=√2CT∴∠PBT=∠CTO=45°∴PB=PT∴PE+BE=OP+OT∵点P为AE的中点，∴PA=PE=PO∴BE=OT在Rt△BDE中，BD=DE，∴BE=√2BD，∠DBE=∠T=45°∴√2CT=√2BD∴CT=BD∴△DBP≌△CTP(SAS)，∴PD=PC，∠BPD=∠CPT，∴∠DPC=∠BPT=90°，∴PD⊥PC.（3）解：PC的长为4或2.【解析】（1）∵∠ACB＝90°，AC＝BC，∴∠BAC=∠ABC=45°，∵DE⊥AB，∴∠ADE=∠BDE=∠ACB=90°，∵点P为AE的中点，∴DP=12AE=CP=AP，∴∠PDA=∠PAD，∠PAC=∠PCA，∴∠DPC=∠DPE+∠CPE=2∠DAP+2∠CAP=2∠DAC=90°，∴PD⊥PC故答案为：PD=PC，PD⊥PC；解：（3）如图3﹣1中，当点E在BC的上方时，过点P作PQ⊥BC于Q.则DE∥PQ∥AC，PE=PA∴DQ=CQ∵BC=3BD=3√2∴CD=4√2由（2）可得，PD⊥PC，PD=PC，∴△PCD为等腰直角三角形∴PQ=12CD∴PQ=12CD=DQ=2√2由勾股定理得，PC=PD=4如图3﹣2中，当点E在BC的下方时，同法可得PC＝PD＝2.综上所述，PC的长为4或2.24．如图1，在Rt△ABC中，∠BAC＝90°，AB＝4，以AB为边在AB上方作等边△ABD，以BC为边在BC右侧作等边△CBE，连结DE．（1）当AC＝5时，求BE的长．（2）求证：BD⊥DE．（3）如图2，点C′与点C关于直线AD对称，连结C′E．①求C′E的长．②连结C′D，当△C′DE是以C′E为腰的等腰三角形时，写出所有满足条件的AC长：▲ ．（直接写出答案）【答案】（1）解：∵△ABD，△CBE都是等边三角形，∴∠ABD＝∠CBE＝60°，AB＝DB，BC＝BE，∴∠ABC+∠CBD＝∠DBE+∠CBD，∴∠ABC＝∠DBE，∴△BAC≌△BDE（SAS），∴∠BAC＝∠BDE＝90°，BE＝BC．在Rt△ABC中，AB＝4，AC＝5，∴BC=√AB2+AC2=√42+52=√41，∴BE=√41；（2）证明：∵△ABD，△CBE都是等边三角形，∴∠ABD＝∠CBE＝60°，AB＝DB，BC＝BE，∴∠ABC+∠CBD＝∠DBE+∠CBD，∴∠ABC＝∠DBE，∴△BAC≌△BDE（SAS），∴∠BAC＝∠BDE＝90°，∴BD⊥DE；（3）解：①连接AC′，由（2）知△BAC≌△BDE（SAS），∴AC＝DE，∠BAC＝∠BDE＝90°，∴∠ADE＝60°+90°＝150°，∵∠CAD＝∠BAC﹣∠BAD＝90°﹣60°＝30°，由对称的性质得∠DAC′＝∠DAC＝30°，AC＝DE＝AC′，∴∠ADE+∠DAC′＝180°，∴DE∥AC′，∴四边形AC′ED是平行四边形，∴C′E＝AD＝AB＝4；②4或4√3【解析】（3）②分两种情况：C′E＝DE时，∵C′E＝4，四边形AC′ED是平行四边形，∴C′E＝DE＝AC′＝4，由对称的性质得AC＝AC′＝4，C′E＝C′D时，作C′F⊥DE于F，∵C′E＝C′D，C′F⊥DE，∴DF＝EF，∠C′FE＝90°，∵四边形AC′ED是平行四边形，∴∠C′EF＝∠DAC′＝30°，C′E=2，EF=DF=2√3，∴C′F=12∴DE=AC′=AC=4√3，综上，AC长为4或4√3．故答案为：4或4√3．。

八年级初二数学图形的对称-翻折变换(折叠问题) 含答案

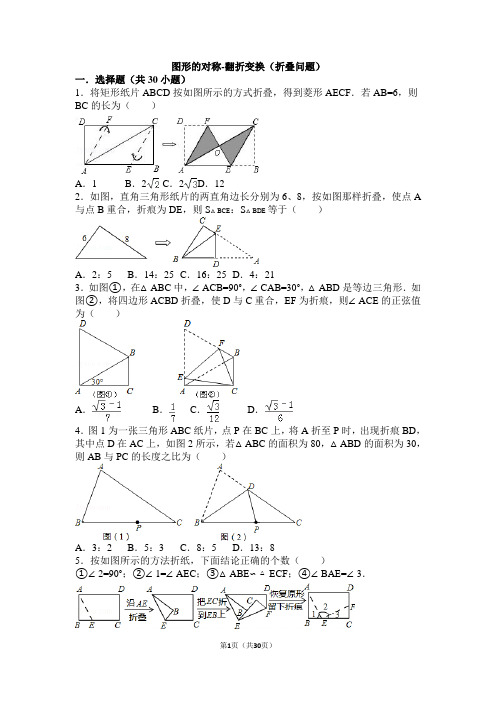
图形的对称-翻折变换（折叠问题）一．选择题（共30小题）1．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=6，则BC的长为（）A．1 B．2 C．2D．122．如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A 与点B重合，折痕为DE，则S△BCE：S△BDE等于（）A．2：5 B．14：25 C．16：25 D．4：213．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为（）A．B．C．D．4．图1为一张三角形ABC纸片，点P在BC上，将A折至P时，出现折痕BD，其中点D在AC上，如图2所示，若△ABC的面积为80，△ABD的面积为30，则AB与PC的长度之比为（）A．3：2 B．5：3 C．8：5 D．13：85．按如图所示的方法折纸，下面结论正确的个数（）①∠2=90°；②∠1=∠AEC；③△ABE∽△ECF；④∠BAE=∠3．A．1个B．2个C．3个D．4个6．如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠AED′=40°，则∠EFB等于（）A．70°B．65°C．80°D．35°7．如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=60°，且DE=1，则边BC的长（）A．3 B．4 C．3.5 D．68．如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B 落在点E处，AE交CD于点F．连接DE，则DF的长是（）A．B．C．D．9．张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形，两人作法如下：张萌：如图1，将纸片对折得到折痕EF，沿点B翻折纸片，使点A落在EF上的点M处，连接CM，△BCM即为所求；小平：如图2，将纸片对折得到折痕EF，沿点B翻折纸片，使点C落在EF上的点M处，连接BM，△BCM 即为所求，对于两人的作法，下列判断正确的是（）A．小平的作法正确，张萌的作法不正确B．两人的作法都不正确C．张萌的作法正确，小平的作法不正确D．两人的作法都正确10．如图，折叠矩形纸片ABCD的一边AD，使点D落在BC边上的点F处，若AB=8，BC=10，则△CEF的周长为（）A．12 B．16 C．18 D．2411．如图，在矩形ABCD中，AB=3，BC=5，点E在边CD上，连接BE，将△BCE 沿BE折叠，若点C恰好落在AD边上的点F处，则CE的长为（）A．B．C．D．12．如图，在△ABC中，∠C=90°，AB=5cm，AC=4cm，点D在AC上，将△BCD 沿着BD所在直线翻折，使点C落在斜边AB上的点E处，则DC的长为（）A．cm B．cm C．2cm D．cm13．如图，在平面直角坐标系中，点A（0，4）、B（3，0），连接AB，将△AOB 沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为（）A．y=﹣B．y=﹣x+C．y=﹣D．y=﹣2x+14．如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，点O落在BC边上的点E处．则直线DE的解析式为（）A．y=x+5 B．y=x+5 C．y=x+5 D．y=x+515．如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，当DE=2时，BC的长为（）A．3 B．4 C．5 D．616．如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（）A．AF=B．四边形ACDE是矩形C．图中与△ABC全等的三角形有4个D．图中有4个等腰三角形17．如图，有一张直角三角形纸片ABC，边AB=6，AC=10，∠ABC=90°，将该直角三角形纸片沿DE折叠，使点C与点B重合，则四边形ABDE的周长为（）A．16 B．17 C．18 D．1918．如图，梯形ABCD中，AD∥BC，AB=DC，∠DBC=45°，点E在BC上，点F在AB上，将梯形ABCD沿直线EF翻折，使得点B与点D重合．如果，那么的值是（）A．B．C．D．19．如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（）A．5 B．4 C．3 D．220．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣1，0），B（﹣2，3），C（﹣3，1）．将△ABC沿y轴翻折得到△A′B′C′，则点B′的坐标为（）A．（2，1）B．（2，3）C．（4，1）D．（0，2）21．如图，△ABC周长为36cm，把其边AC对折，使点C、A重合，折痕交BC 边于点D，交AC边于点E，连结AD，若AE=6cm，则△ABD的周长是（）A．24cm B．26cm C．28cm D．30cm22．如图，矩形ABCD中，AB=8，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F，若AF=，则AD的长为（）A．3 B．4 C．5 D．623．如图的实线部分是由Rt△ABC经过两次折叠得到的，首先将Rt△ABC沿BD折叠，使点C落在斜边上的点C′处，再沿DE折叠使点A落在DC′延长线上的点A′处，若图中，∠A=30°，BC=5cm，则折痕DE的长为（）A．B．2C．2D．24．如图一直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（）A．2cm B．3cm C．4cm D．5cm25．如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（）A．6 B．8 C．10 D．1226．如图，矩形ABCD中，AB=3，AD=9，将此矩形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A．6 B．8 C．10 D．1227．如图所示，有一块直角三角形纸片，∠C=90°，AC=2，BC=，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为（）A．B．C．1 D．28．如图所示，折叠平行四边形的一边AD，使点A落在DC边上的点E处，已知AB=6，BC=4，则EC的长为（）A．1 B．2 C．3 D．1.529．如图，正方形ABCD中，AB=12，点E在边BC上，BE=EC，将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连接DG、BF，给出以下结论：①△DAG≌△DFG；②BG=2AG；③S△DGF=120；④S△BEF=．其中所有正确结论的个数是（）A．4 B．3 C．2 D．130．如图，将矩形纸片ABCD沿EF折叠，使D点与BC边的中点D重合，若BC=8，CD=6，则CF的长为（）A．B．C．2 D．1图形的对称-翻折变换（折叠问题）参考答案与试题解析一．选择题（共30小题）1．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=6，则BC的长为（）A．1 B．2C．2D．12【考点】翻折变换（折叠问题）；勾股定理的应用；菱形的性质；矩形的性质．【分析】根据菱形AECF，得∠FCO=∠ECO，再利用∠ECO=∠ECB，可通过折叠的性质，结合直角三角形勾股定理求解．【解答】解：∵菱形AECF，AB=6，∴假设BE=x，∴AE=6﹣x，∴CE=6﹣x，∵四边形AECF是菱形，∴∠FCO=∠ECO，∵∠ECO=∠ECB，∴∠ECO=∠ECB=∠FCO=30°，2BE=CE，∴CE=2x，∴2x=6﹣x，解得：x=2，∴CE=4，利用勾股定理得出：BC2+BE2=EC2，BC===2，故选：C．【点评】此题主要考查了折叠问题以及勾股定理等知识，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．2．如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A 与点B重合，折痕为DE，则S△BCE：S△BDE等于（）A．2：5 B．14：25 C．16：25 D．4：21【考点】翻折变换（折叠问题）．【分析】在Rt△BEC中利用勾股定理计算出AB=10，根据折叠的性质得到AD=BD=5，EA=EB，设AE=x，则BE=x，EC=8﹣x，在Rt△BEC中根据勾股定理计算出x=，则EC=8﹣=，利用三角形面积公式计算出S△BCE=BC•CE=×6×=，在Rt△BED中利用勾股定理计算出ED==，利用三角形面积公式计算出S△BDE=BD•DE=×5×=，然后求出两面积的比．【解答】解：在Rt△BAC中，BC=6，AC=8，∴AB==10，∵把△ABC沿DE使A与B重合，∴AD=BD，EA=EB，∴BD=AB=5，设AE=x，则BE=x，EC=8﹣x，在Rt△BEC中，∵BE2=EC2+BC2，即x2=（8﹣x）2+62，∴x=，∴EC=8﹣x=8﹣=，∴S△BCE=BC•CE=×6×=，在Rt△BED中，∵BE2=ED2+BD2，∴ED==，∴S△BDE=BD•DE=×5×=，∴S△BCE：S△BDE=：=14：25．故选B．【点评】本题考查了折叠问题：折叠前后两图形全等，即对应线段相等，对应角相等．也考查了勾股定理．3．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】在Rt△ABC中，设AB=2a，已知∠ACB=90°，∠CAB=30°，即可求得AB、AC的值，由折叠的性质知：DE=CE，可设出DE、CE的长，然后表示出AE的长，进而可在Rt△AEC中，由勾股定理求得AE、CE的值，即可求∠ACE 的正弦值．【解答】解：∵△ABC中，∠ACB=90°，∠BAC=30°，设AB=2a，∴AC=a，BC=a；∵△ABD是等边三角形，∴AD=AB=2a；设DE=EC=x，则AE=2a﹣x；在Rt△AEC中，由勾股定理，得：（2a﹣x）2+3a2=x2，解得x=；∴AE=，EC=，∴sin∠ACE==．故选：B．【点评】本题考查的是翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．4．图1为一张三角形ABC纸片，点P在BC上，将A折至P时，出现折痕BD，其中点D在AC上，如图2所示，若△ABC的面积为80，△ABD的面积为30，则AB与PC的长度之比为（）A．3：2 B．5：3 C．8：5 D．13：8【考点】翻折变换（折叠问题）．【分析】如图，作辅助线；首先求出△BDP的面积，进而求出△DPC的面积；借助三角形的面积公式求出的值；由旋转变换的性质得到AB=PB，即可解决问题．【解答】解：如图，过点D作DE⊥BC于点E；由题意得：S△ABD=S△PBD=30，∴S△DPC=80﹣30﹣30=20，∴=，由题意得：AB=BP，∴AB：PC=3：2，故选A．【点评】该题主要考查了翻折变换的性质及其应用问题；解题的方法是作高线，表示出三角形的面积；解题的关键是灵活运用翻折变换的性质来分析、判断、推理或解答．5．按如图所示的方法折纸，下面结论正确的个数（）①∠2=90°；②∠1=∠AEC；③△ABE∽△ECF；④∠BAE=∠3．A．1个B．2个C．3个D．4个【考点】翻折变换（折叠问题）；相似三角形的判定与性质．【分析】根据翻折变换的性质、相似三角形的判定定理解答即可．【解答】解：由翻折变换的性质可知，∠AEB+∠FEC=×180°=90°，则∠AEF=90°，即∠2=90°，①正确；由图形可知，∠1＜∠AEC，②错误；∵∠2=90°，∴∠1+∠3=90°，又∠1+∠BAE=90°，∴∠BAE=∠3，④正确；∵∠BAE=∠3，∠B=∠C=90°，∴△ABE∽△ECF，③正确．故选：C．【点评】本题考查的是翻折变换的性质，翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．6．如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠AED′=40°，则∠EFB等于（）A．70°B．65°C．80°D．35°【考点】翻折变换（折叠问题）．【分析】根据平角的知识可求出∠DED′的度数，再由折叠的性质可得出∠D′EF=∠DEF=∠DED′，从而根据平行线的性质可得出∠EFB的度数．【解答】解：∵∠AED′=40°，∴∠DED′=180°﹣40°=140°，又由折叠的性质可得，∠D′EF=∠DEF=∠DED′，∴∠DEF=70°，又∵AD∥BC，∴∠EFB=70°．故选：A．【点评】此题考查了翻折变换的知识，解答本题的关键是根据折叠的性质得出∠D′EF=∠DEF=∠DED′，难度一般．7．如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=60°，且DE=1，则边BC的长（）A．3 B．4 C．3.5 D．6【考点】翻折变换（折叠问题）．【分析】由矩形的性质得到∠1=∠CFE=60°，由折叠可得∠2=60°，从而求得∠4的度数，得到AE=EC，在Rt△CDE中利用勾股定理可求得EC的长度，即可得到答案．【解答】解：∵矩形ABCD，∴BC∥AD，∴∠1=∠CFE=60°，∵EF为折痕，∴∠2=∠1=60°，AE=EC，∴∠3=180°﹣60°﹣60°=60°，Rt△CDE中，∠4=90°﹣60°=30°，∴EC=2×DE=2×1=2，∴BC=AE+ED=EC+ED=2+1=3．故选：A．【点评】本题考查了翻折问题；由折叠得到角相等，得到AE=EC利用勾股定理求解是正确解答本题的关键．8．如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B 落在点E处，AE交CD于点F．连接DE，则DF的长是（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】由四边形ABCD是矩形与△AEC由△ABC翻折得到，AD=CE，∠ADF=∠CEF，由AAS证得△ADF≌△CEF，的长FA=FC，设DF=x，则FA=4﹣x，由勾股定理得：DA2+DF2=AF2，即可求出DF的长．【解答】解：∵四边形ABCD是矩形，∴AD=BC，AB=DC=4，∠ADF=90°，∵△AEC由△ABC翻折得到，∴BC=EC，∠CEF=∠ABC=90°，∴AD=CE，∠ADF=∠CEF，在△ADF与△CEF中，，∴△ADF≌△CEF（AAS），∴FA=FC，设DF=x，则FA=FC=DC﹣DF=4﹣x，在Rt△DFA中，由勾股定理得：DA2+DF2=AF2，即32+x2=（4﹣x）2，解得：x=，即DF的长是．故选C．【点评】本题主要考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识；熟练掌握折叠的性质，得到相等的线段与角是解决问题的关键．9．张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形，两人作法如下：张萌：如图1，将纸片对折得到折痕EF，沿点B翻折纸片，使点A落在EF上的点M处，连接CM，△BCM即为所求；小平：如图2，将纸片对折得到折痕EF，沿点B翻折纸片，使点C落在EF上的点M处，连接BM，△BCM 即为所求，对于两人的作法，下列判断正确的是（）A．小平的作法正确，张萌的作法不正确B．两人的作法都不正确C．张萌的作法正确，小平的作法不正确D．两人的作法都正确【考点】翻折变换（折叠问题）．【分析】在图1中，由BM=2BF推出∠BMF=30°，所以∠MBF=60°，再根据等边三角形的判定方法即可证明．在图2中，证明方法类似．【解答】解：图1中，∵四边形ABCD是正方形，∴AB=AD=BC∵AE=ED=BF=FC，AB=BM，∴BM=2BF，∵∠MFB=90°，∴∠BMF=30°，∴∠MBF=90°﹣∠BMF=60°，∵MB=MC，∴△MBC是等边三角形，∴张萌的作法正确．在图2中，∵BM=BC=2BF，∠MFB=90°，∴∠BMF=30°，∴∠MBF=90°﹣∠BMF=60°，∵MB=MC∴△MBC是等边三角形，∴小平的作法正确．故选D．【点评】本题考查正方形的性质、翻折不变性、直角三角形的性质，解题的关键是在一个直角三角形中如果斜边是直角边的两倍那么这条直角边所对的锐角是30度．10．如图，折叠矩形纸片ABCD的一边AD，使点D落在BC边上的点F处，若AB=8，BC=10，则△CEF的周长为（）A．12 B．16 C．18 D．24【考点】翻折变换（折叠问题）．【分析】先根据矩形的性质得AD=BC=10，AB=CD=8，再根据折叠的性质得AF=AD=10，EF=DE，在Rt△ABF中，利用勾股定理计算出BF=6，则CF=BC ﹣BF=4，易得△CEF的周长．【解答】解：∵四边形ABCD为矩形，∴AD=BC=10，AB=CD=8，∵矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的F处，∴AF=AD=10，EF=DE，在Rt△ABF中，∵BF==6，∴CF=BC﹣BF=10﹣6=4，∴△CEF的周长为：CE+EF+CF=CE+DE+CF=CD+CF=8+4=12．故选A．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质和勾股定理，利用勾股定理得CF的长是解答此题的关键．11．如图，在矩形ABCD中，AB=3，BC=5，点E在边CD上，连接BE，将△BCE 沿BE折叠，若点C恰好落在AD边上的点F处，则CE的长为（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】设CE=x，由矩形的性质得出AD=BC=5，CD=AB=3，∠A=∠D=90°．由折叠的性质得出BF=BC=5，EF=CE=x，DE=CD﹣CE=3﹣x．在Rt△ABF中利用勾股定理求出AF的长度，进而求出DF的长度；然后在Rt△DEF中根据勾股定理列出关于x的方程，即可解决问题．【解答】解：设CE=x．∵四边形ABCD是矩形，∴AD=BC=5，CD=AB=3，∠A=∠D=90°．∵将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，∴BF=BC=5，EF=CE=x，DE=CD﹣CE=3﹣x．在Rt△ABF中，由勾股定理得：AF2=52﹣32=16，∴AF=4，DF=5﹣4=1．在Rt△DEF中，由勾股定理得：EF2=DE2+DF2，即x2=（3﹣x）2+12，解得：x=．故选B．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理、矩形的性质、方程思想等知识，关键是熟练掌握勾股定理，找准对应边．12．如图，在△ABC中，∠C=90°，AB=5cm，AC=4cm，点D在AC上，将△BCD 沿着BD所在直线翻折，使点C落在斜边AB上的点E处，则DC的长为（）A．cm B．cm C．2cm D．cm【考点】翻折变换（折叠问题）．【分析】首先由勾股定理求出BC，由折叠的性质可得∠BED=∠C=90°，BE=BC=3cm，得出AE=AB﹣BE=2cm，设DC=xcm，则DE=xcm，AD=（4﹣x）cm，由勾股定理得出方程，解方程即可．【解答】解：∵∠C=90°，AB=5cm，AC=4cm，∴BC==3cm，∵将△BCD沿着直线BD翻折，使点C落在斜边AB上的点E处，∴△BED≌△BCD，∴∠BED=∠C=90°，BE=BC=3cm，∴AE=AB﹣BE=2cm，设DC=xcm，则DE=xcm，AD=（4﹣x）cm，由勾股定理得：AE2+DE2=AD2，即22+x2=（4﹣x）2，解得：x=．故选：B．【点评】本题主要考查翻折变换的性质，全等三角形的性质，勾股定理；熟练掌握翻折变换的性质，由勾股定理得出方程是解决问题的关键．13．如图，在平面直角坐标系中，点A（0，4）、B（3，0），连接AB，将△AOB 沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为（）A．y=﹣B．y=﹣x+C．y=﹣D．y=﹣2x+【考点】翻折变换（折叠问题）；待定系数法求一次函数解析式．【分析】由点A（0，4）、B（3，0），可求得AB的长，然后由折叠的性质，求得OA′的长，且△A′OC∽△AOB，再由相似三角形的性质，求得OC的长，继而利用待定系数法求得直线BC的解析式．【解答】解：∵点A（0，4）、B（3，0），∴OA=4，OB=3，∴AB==5，由折叠的性质可得：A′B=AB=5，∠OA′C=∠OAB，∴OA′=A′B﹣OB=2，∵∠A′OC=∠AOB=90°，∴△A′OC∽△AOB，∴，即，解得：OC=，∴点C的坐标为：（0，），设直线BC的解析式为：y=kx+b，则，解得：，∴直线BC的解析式为：y=﹣x+．故选C．【点评】此题考查了折叠的性质、勾股定理、相似三角形的判定与性质以及待定系数法求一次函数的解析式．注意求得点C的坐标是解此题的关键．14．如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，点O落在BC边上的点E处．则直线DE的解析式为（）A．y=x+5 B．y=x+5 C．y=x+5 D．y=x+5【考点】翻折变换（折叠问题）；待定系数法求一次函数解析式．【分析】首先在RT△ABE中，求出EB，再在RT△CDE中利用勾股定理即可解决问题．【解答】解：∵△ADE是由△ADO翻折，∴DE=DO，AO=AE=10，∵四边形OABC是矩形，∴OC=AB=8，AO=BC=10，∠B=∠BCO=∠BAO=90°，在RT△ABE中，∵AE=10，AB=8，∴EB===6，∴EC=4，设DO=DE=x，在RT△DCE中，∵CD2+CE2=DE2，∴（8﹣a）2+42=a2，∴a=5，∴点D（0，5），点E（4，8），设直线DE为y=kx+b，∴解得，∴直线DE为：y=+5．故选A．【点评】本题考查翻折变换、待定系数法确定一次函数的解析式，解题的关键是巧妙利用勾股定理，用方程的思想去思考问题，属于中考常考题型．15．如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，当DE=2时，BC的长为（）A．3 B．4 C．5 D．6【考点】翻折变换（折叠问题）．【分析】首先由DE∥BC与折叠的性质，可证得DE是△ABC的中位线，继而求得答案．【解答】解：∵DE∥BC，∴∠ADE=∠B，∠EDF=∠BFD，由折叠的性质可得：∠ADE=∠EDF，AD=DF，∴∠B=∠BFD，∴BD=DF，∴AD=BD，同理：AE=EC，∴DE=BC，即BC=2DE=4．故选B．【点评】此题考查了折叠的性质以及三角形中位线的性质．注意证得DE是△ABC的中位线是关键．16．如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（）A．AF=B．四边形ACDE是矩形C．图中与△ABC全等的三角形有4个D．图中有4个等腰三角形【考点】翻折变换（折叠问题）；平行四边形的性质．【分析】由四边形ABCD是平行四边形，得到AB=CD，AB∥CD，AD=BC，由折叠的性质得到AB=AE，BC=CE，等量代换得到AE=CD，AD=CE，推出四边形ACDE是平行四边形，于是得到AF=BC，四边形ACDE是矩形，故A，B 正确；根据平行四边形和矩形的性质得到△ACD≌△ACE≌△CDE≌△ADE≌△ABC，于是得到图中与△ABC全等的三角形有4个，故C正确；推出△BCE是等腰三角形，△AEF，△ACF，△CDF，△DEF是等腰三角形，于是得到图中有5个等腰三角形，故D错误．【解答】解：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，AD=BC，由折叠的性质得到AB=AE，BC=CE，∴AE=CD，AD=CE，∵点B、A、E在同一条直线上，∴AE∥CD，∴四边形ACDE是平行四边形，∴AF=BC，四边形ACDE是矩形，故A，B正确；∵四边形ABCD是平行四边形，四边形ACDE是矩形，∴△ACD≌△ACE≌△CDE≌△ADE≌△ABC，∴图中与△ABC全等的三角形有4个，故C正确；∵BC=CE，∴△BCE是等腰三角形，∵四边形ACDE是矩形，∴AF=EF=CF=DF，∴△AEF，△ACF，△CDF，△DEF是等腰三角形，∴图中有5个等腰三角形，故D错误；故选D．【点评】本题考查了平行四边形的性质、折叠的性质以及等腰三角形的判定和性质，解题的关键是熟记等腰三角形和矩形的判定方法．17．如图，有一张直角三角形纸片ABC，边AB=6，AC=10，∠ABC=90°，将该直角三角形纸片沿DE折叠，使点C与点B重合，则四边形ABDE的周长为（）A．16 B．17 C．18 D．19【考点】翻折变换（折叠问题）．【分析】根据勾股定理得到BC=8，由折叠的性质得到BD=CD=BC=4，DE⊥BC，根据三角形的中位线的性质得到DE=AB=3，AE=AC=5，于是得到结论．【解答】解：∵AB=6，AC=10，∠ABC=90°，∴BC=8，∵将该直角三角形纸片沿DE折叠，使点C与点B重合，∴BD=CD=BC=4，DE⊥BC，∵∠ABC=90°，∴DE∥AB，∴DE=AB=3，AE=AC=5，∴四边形ABDE的周长=AB+AE+DE+BD=6+5+3+4=18，故选C．【点评】此题考查了折叠的性质，勾股定理，三角形的中位线的性质，注意掌握折叠前后图形的对应关系．18．如图，梯形ABCD中，AD∥BC，AB=DC，∠DBC=45°，点E在BC上，点F在AB上，将梯形ABCD沿直线EF翻折，使得点B与点D重合．如果，那么的值是（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】根据对称的性质得到△BFE≌△DFE，得到DE=BE．根据已知条件得到∠DEB=90°，设AD=1，BC=4，过A作AG⊥BC于G，根据矩形的性质得到GE=AD=1，根据全等三角形的性质得到BG=EC=1.5，根据勾股定理得到AB=CD==5，通过△BDC∽△DEF，得到，求出BF=，于是得到结论．【解答】解：∵EF是点B、D的对称轴，∴△BFE≌△DFE，∴DE=BE．∵在△BDE中，DE=BE，∠DBE=45°，∴∠BDE=∠DBE=45°．∴∠DEB=90°，∴DE⊥BC．在等腰梯形ABCD中，∵，∴设AD=1，BC=4，过A作AG⊥BC于G，∴四边形AGED是矩形．∴GE=AD=1，∵Rt△ABG≌Rt△DCE，∴BG=EC=1.5，∴AG=DE=BE=2.5∴AB=CD==5，∵∠ABC=∠C=∠FDE，∵∠CDE+∠C=90°，∴∠FDE+∠CDE=90°∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°，∴∠BDC=∠DFE，∵∠DEF=∠DBC=45°，∴△BDC∽△DEF，∴，∴DF=，∴BF=，∴AF=AB﹣BF=，∴=．故选B．【点评】此题考查等腰梯形的性质，翻折的性质，三角形全等的判定与性质，等腰直角三角形的性质，相似三角形的判定和性质等知识，注意结合图形，作出常用辅助线解决问题．19．如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（）A．5 B．4 C．3 D．2【考点】翻折变换（折叠问题）．【分析】利用翻折变换对应边关系得出AB=AF，∠B=∠AFG=90°，利用HL定理得出△ABG≌△AFG即可；利用勾股定理得出GE2=CG2+CE2，进而求出BG 即可；【解答】解：在正方形ABCD中，AD=AB=BC=CD，∠D=∠B=∠BCD=90°，∵将△ADE沿AE对折至△AFE，∴AD=AF，DE=EF，∠D=∠AFE=90°，∴AB=AF，∠B=∠AFG=90°，又∵AG=AG，在Rt△ABG和Rt△AFG中，，∴Rt△ABG≌Rt△AFG（HL），∴BG=GF，∵E是边CD的中点，∴DE=CE=6，设BG=x，则CG=12﹣x，GE=x+6，∵GE2=CG2+CE2∴（x+6）2=（12﹣x）2+62，解得x=4∴BG=4．故选B．【点评】此题主要考查了全等三角形的判定和性质，勾股定理的综合应用以及翻折变换的性质，根据翻折变换的性质得出对应线段相等是解题关键．20．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣1，0），B（﹣2，3），C（﹣3，1）．将△ABC沿y轴翻折得到△A′B′C′，则点B′的坐标为（）A．（2，1）B．（2，3）C．（4，1）D．（0，2）【考点】翻折变换（折叠问题）；坐标与图形性质．【分析】根据关于y轴对称的点的特点找到B'，结合直角坐标系可得出点B′的坐标．【解答】解：∵将△ABC沿y轴翻折得到△A′B′C′，∴点B与点B′关于y轴对称，∴B′（2，3），故选B．【点评】本题考查了翻折变换﹣折叠问题，坐标与图形的关系，熟记关于y轴对称的点的特点是解答本题的关键．21．如图，△ABC周长为36cm，把其边AC对折，使点C、A重合，折痕交BC 边于点D，交AC边于点E，连结AD，若AE=6cm，则△ABD的周长是（）A．24cm B．26cm C．28cm D．30cm【考点】翻折变换（折叠问题）．【分析】根据翻折变换的性质可得AE=EC，AD=CD，然后求出△ABD的周长=AB+BC，代入数据计算即可得解．【解答】解：∵△ABC的边AC对折顶点C和点A重合，∴AE=EC，AD=CD，∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC，∵AE=6cm，∴AC=AE+EC=6+6=12，∵△ABC的周长为36cm，∴AB+BC=36﹣12=24cm，∴△ABD的周长是24cm．故选A．【点评】本题考查了翻折变换的性质，熟记翻折前后的两个图形能够完全重合得到相等的边是解题的关键．22．如图，矩形ABCD中，AB=8，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F，若AF=，则AD的长为（）A．3 B．4 C．5 D．6【考点】翻折变换（折叠问题）．【分析】根据平行线的性质和翻转变换的性质得到FD=FE，FA=FC，根据勾股定理计算即可．【解答】解：∵DC∥AB，∴∠FCA=∠CAB，又∠FAC=∠CAB，∴∠FAC=∠FCA，∴FA=FC=，∴FD=FE，∵DC=AB=8，AF=，∴FD=FE=8﹣=，∴AD=BC=EC==6，故选：D．【点评】本题考查的是翻转变换的性质，翻转变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．23．如图的实线部分是由Rt△ABC经过两次折叠得到的，首先将Rt△ABC沿BD折叠，使点C落在斜边上的点C′处，再沿DE折叠使点A落在DC′延长线上的点A′处，若图中，∠A=30°，BC=5cm，则折痕DE的长为（）A．B．2C．2D．【考点】翻折变换（折叠问题）．【分析】根据直角三角形两锐角互余求出∠ABC=60°，翻折前后两个图形能够互相重合可得∠BDC=∠BDC′，∠CBD=∠ABD=30°，∠ADE=∠A′DE，然后求出∠BDE=90°，再解直角三角形求出BD，然后求出DE即可．【解答】解：∵△ABC是直角三角形，∠A=30°，∴∠ABC=90°﹣30°=60°，∵将Rt△ABC沿BD折叠，使点C落在斜边上的点C′处，∴∠BDC=∠BDC′，∠CBD=∠ABD=∠ABC=30°，∵沿DE折叠点A落在DC′的延长线上的点A′处，∴∠ADE=∠A′DE，∴∠BDE=∠ABD+∠A′DE=×180°=90°，在Rt△BCD中，BD=BC÷cos30°=5÷=cm，在Rt△BDE中，DE=BD•tan30°=×=cm．故选：D．【点评】本题考查了翻折变换的性质，解直角三角形，熟记性质并分别求出有一个角是30°角的直角三角形是解题的关键．24．如图一直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（）A．2cm B．3cm C．4cm D．5cm【考点】翻折变换（折叠问题）．【分析】首先根据题意得到：△AED≌△ACD；进而得到AE=AC=6，DE=CD；根据勾股定理求出AB=10；再次利用勾股定理列出关于线段CD的方程，问题即可解决．【解答】解：由勾股定理得：==10，由题意得：△AED≌△ACD，∴AE=AC=6，DE=CD（设为x）；∠AED=∠C=90°，∴BE=10﹣6=4，BD=8﹣x；由勾股定理得：（8﹣x）2=42+x2，解得：x=3（cm），故选B．【点评】该命题主要考查了翻折变换及其应用问题；解题的关键是借助翻折变换的性质，灵活运用勾股定理、全等三角形的性质等几何知识来分析、判断、推理或解答．25．如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（）A．6 B．8 C．10 D．12【考点】翻折变换（折叠问题）．【分析】因为BC为AF边上的高，要求△AFC的面积，求得AF即可，求证△AFD′≌△CFB，得BF=D′F，设D′F=x，则在Rt△AFD′中，根据勾股定理求x，于是得到AF=AB﹣BF，即可得到结果．【解答】解：易证△AFD′≌△CFB，∴D′F=BF，设D′F=x，则AF=8﹣x，在Rt△AFD′中，（8﹣x）2=x2+42，解之得：x=3，∴AF=AB﹣FB=8﹣3=5，∴S△AFC=•AF•BC=10．故选C．【点评】本题考查了翻折变换﹣折叠问题，勾股定理的正确运用，本题中设D′F=x，根据直角三角形AFD′中运用勾股定理求x是解题的关键．26．如图，矩形ABCD中，AB=3，AD=9，将此矩形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A．6 B．8 C．10 D．12【考点】翻折变换（折叠问题）．【分析】根据折叠的条件可得：BE=DE，在直角△ABE中，利用勾股定理就可以求解．【解答】解：将此长方形折叠，使点B与点D重合，∴BE=ED．∵AD=AE+DE=AE+BE=9．∴BE=9﹣AE，根据勾股定理可知AB2+AE2=BE2．解得AE=4．∴△ABE的面积为3×4÷2=6．故选：A．【点评】本题考查了利用勾股定理解直角三角形的能力，即：直角三角形两直角边的平方和等于斜边的平方．27．如图所示，有一块直角三角形纸片，∠C=90°，AC=2，BC=，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为（）A．B．C．1 D．【考点】翻折变换（折叠问题）．【分析】由有一块直角三角形纸片，∠C=90°，AC=2，BC=，利用勾股定理即可求得AB的长，然后由折叠的性质，求得AE的长，继而求得答案．【解答】解：∵∠C=90°，AC=2，BC=，∴AB==，由折叠的性质可得：AE=AB=，∴CE=AE﹣AC=．故选A．【点评】此题考查了折叠的性质以及勾股定理．注意掌握折叠前后图形的对应关系是解此题的关键．28．如图所示，折叠平行四边形的一边AD，使点A落在DC边上的点E处，已知AB=6，BC=4，则EC的长为（）A．1 B．2 C．3 D．1.5【考点】翻折变换（折叠问题）．【分析】利用平行四边形的对边相等得到AD=BC=4，DC=AB=6，再由折叠的性质得到DE=AD，由DC﹣DE求出EC的长即可．【解答】解：由折叠及平行四边形的性质得：AE=AD=BC=4，DC=AB=6，则EC=DC﹣DE=6﹣4=2，故选B．【点评】此题考查了翻折变换（折叠问题），以及平行四边形的性质，熟练掌握折叠的性质是解本题的关键．29．如图，正方形ABCD中，AB=12，点E在边BC上，BE=EC，将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连接DG、BF，给出以下结论：。

2019年课时同步练习(浙教版)八年级上2.1图形的轴对称【含答案及解析】

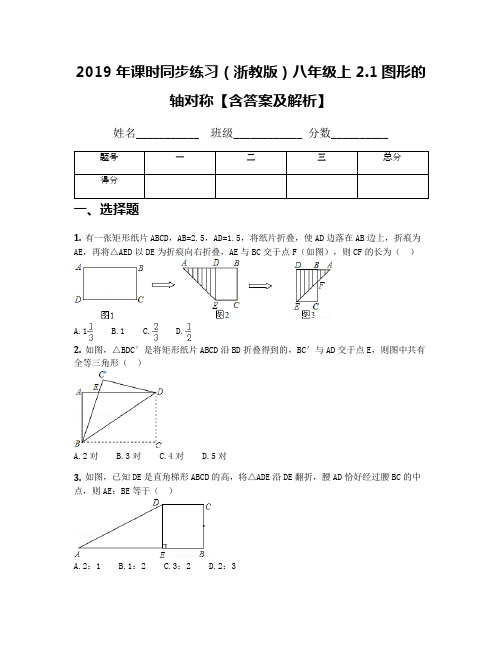
2019年课时同步练习（浙教版）八年级上2.1图形的轴对称【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 有一张矩形纸片ABCD，AB=2.5，AD=1.5，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F（如图），则CF的长为（）A.1B.1C.D.2. 如图，△BDC′是将矩形纸片ABCD沿BD折叠得到的，BC′与AD交于点E，则图中共有全等三角形（）A.2对B.3对C.4对D.5对3. 如图，已知DE是直角梯形ABCD的高，将△ADE沿DE翻折，腰AD恰好经过腰BC的中点，则AE：BE等于（）A.2：1B.1：2C.3：2D.2：34. 将一张长方形纸片按如图所示的方式折叠，EM，MF为折痕（如图所示），则∠EMF的度数为（）A.95°B.90°C.75°D.60°5. 在Rt△ABC中，∠C=90°，∠B=15°，AC=2，如果将这个三角形折叠，使得点B与点A重合，折痕交AB于点M，交BC于点N，那么BN等于（）A.2B.4C.6D.86. 如图，点D为△ABC边AB的中点，将△ABC沿经过点D的直线折叠，使点A刚好落在BC边上的点F处，若∠B=46°，则∠BDF的度数为（）A.88°B.86°C.84°D.82°7. 在三角形纸片ABC中，∠A=65°，∠B=75°．将纸片的一角对折，使点C落在△ABC内，若∠1=20°，则∠2的度数为（）A.50°B.60°C.70°D.80°8. 平面内点A（﹣1，2）和点B（﹣1，6）的对称轴是（）A.x轴B.y轴C.直线y=4D.直线x=﹣19. 如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）A.9cmB.13cmC.16cmD.10cm10. 将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，并使BA′、BC′在同一直线上，若∠ABE=ɑ，则∠DBC为（）A.2ɑB.3ɑC.90﹣ɑD.180﹣2ɑ11. 用一条宽相等的足够长的纸条，打一个结，如图1所示，然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE，则S△ABC：S四边形ACDE的值为（）A.1：2B.1：3C.（）：2D.（）：212. 如图，等腰直角△ABC中AB=AC，将其按下图所示的方式折叠两次，若DA’=1，给出下列说法：①DC’平分∠BDA’；②BA’长为；③△BC’D是等腰三角形；④△CA’D的周长等于BC的长．其中正确的有（）A.1个B.2个C.3个D.4个13. 如图，将长方形纸片ABCD折叠，使点B落在CD的中点E处，折痕为AF，CD=6，则△AEF的面积是（）A. B.4 C. D.8二、填空题14. 如图，将长方形纸片的一角折叠，使顶点A落在点A′处，BC为折痕，若BE是∠A′BD的平分线，则∠CBE的度数是度．15. 图1长方形纸带，∠CEF=25°，将纸带沿EF折叠成图2再沿AF折叠成图3，图3中的∠DFE的度数是．16. 已知：如图，把一张矩形纸片ABCD沿BD对折，使C点落在E处，BE与AD相交于点O．写出二组相等的线段（不包括AB=CD和AD=BC）．17. 一个直角梯形，两底边长为4和6，垂直于两底的腰长为2，折叠此梯形，使梯形相对的顶点重合，那么折痕长为．18. 同学们都喜欢老师给他的作业打“红勾”，我们将一张长10cm，宽1cm的矩形红纸条（如左图）进行翻折，便可得到一个漂亮的“红勾”（如右图）．如果“红勾”所成的锐角为60°，则这个“红勾”的面积为 cm2（结果保留根号）．19. 如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD 于F，连接EF，则∠BEF= 度．20. 如图，△A BC中，∠A=30°，∠A沿DE折叠后，A点落在△ABC的内部A′的位置，则∠1+∠2= ．21. 将边长为6的正方形纸片ABCD的顶点A沿折痕EF（E在AB上，F在CD上）折叠，A 恰好与BC的一个三等分点G（靠近B侧）重合，则EF= ．22. 已知A点的坐标为（﹣4，2），A与A′关于直线y=2对称，那么点A′的坐标为．23. 将一长方形纸条按如图所示折叠，∠2=54°，则∠1= ．24. 将一张长方形纸条ABCD沿EF折叠后，ED与BF交于G点，若∠EFG=54°，则∠BGE 的度数为．25. 如图所示，将△ABC沿着DE翻折，若∠AEB+∠BDC=80°，则∠B= ．三、解答题26. 如图所示，矩形AOBC在直角坐标系中，O为原点，A在x轴上，B在y轴上，直线AB 的函数关系式为，M是OB上的一点，若将梯形AMBC沿AM折叠，点B恰好落在x轴上的点B′处，C的对应点为C′．（1）求出B′点和M点的坐标；（2）求直线A C′的函数关系式；（3）设一动点P从A点出发，以每秒1个单位速度沿射线AB方向运动，过P作PQ⊥AB，交射线AM于Q；①求运动t秒时，Q点的坐标；（用含t的代数式表示）②以Q为圆心，以PQ的长为半径作圆，当t为何值时，⊙Q与y轴相切？27. （1）点（0，3）关于y=x对称的点的坐标；（2）求直线l1：y=﹣3x+3关于y=x对称的直线l2的解析式；（3）直线l1与x、y轴的交点为A、B，直线l2与y、x轴的交点为A′、B′，则△AOB 与△A′OB′重合部分的面积．28. 如图，△ABC是等腰三角形，AB=AC，（1）把△ABC沿底边BC折叠，得到△DBC，则四边形ABDC是什么四边形，为什么？（2）把△ABC沿腰AB折叠，得到△AEB，对于四边形CAEB，（1）中结论成立吗？29. 如图，在Rt△ABC中，∠ACB=90°，点D是 AB边的中点，AB=10．将△ACD沿着CD 折叠，CA的所对应的线段CP恰好与AB垂直，连接PD．试求BC的长度．30. 如图，把长方形ABCD的两角折叠，折痕为EF、HG，使HD与BF在同一直线上，已知长方形的两组对边分别平行，试说明两条折痕也相互平行．参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】第26题【答案】第27题【答案】第28题【答案】第29题【答案】第30题【答案】。

轴对称的性质—折叠问题(专项培优训练)2023-2024学年八年级数学上册(人教版)(解析版)

轴对称的性质—折叠问题（专项培优训练）试卷满分：100分考试时间：120分钟试卷难度：较难试卷说明：本套试卷结合人教版数学八年级上册同步章节知识点，精选易错，常考，压轴类问题进行专题汇编！题目经典，题型全面，解题模型主要选取热点难点类型！同步复习，考前强化必备！适合成绩中等及偏上的学生拔高冲刺。

一、选择题：本大题共10小题，每小题2分，共20分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．（本题2分）（2022秋·天津津南·八年级校考期中）如图，把一张长方形纸片ABCD ，沿对角线AC 折叠，点B 的对应点为B '，AB '与DC 相交于点E ，则下列结论正确的有（）①ABC AB C ≅'；②AE CE =；③ADE CB E ≅'；④B CE EAB ∠'=∠．A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】由折叠的性质可得ABC AB C ≅',,BAC CAB '∠=∠,AD BC B C =='由平行线的性质和等腰三角形的性质可得 ,ECA EAC AE CE ∠=∠=，由“HL ”可证()Rt ADE Rt CB E HL '≅，可得 ED EB =' ，即可进行判断；【详解】∵矩形纸片 ABCD 沿对角线 AC 折叠，点B 的对应点为 B '∴ABC AB C '≅，故①正确；,BAC CAB '∴∠=∠,AD BC B C =='∵AB CD ∥,BAC ACD ∴∠=∠,ACD CAB ∴∠=∠',ECA EAC ∴∠=∠∴AE CE =，故②正确；,,AE CE AD BC B C ==='在Rt ADE △ 和 Rt CB E '中，AE CE AD CB =⎧⎨=⎩∴()Rt ADE Rt CB E HL '≅故③正确；,DEA B CE '∴∠=∠,DEA EAB ∠≠∠,B CE EAB ∴∠'≠∠故④不正确；∴结论正确的有①②③共3个故选：C【点睛】本题考查了翻折变换，矩形的性质，全等三角形的性质，证明 AE EC = 是本题的关键.A ．①②B ．①②③C ．①③④D ．①②③④【答案】D 【分析】先求出点A ，点B 坐标，由勾股定理可求AB 的长，可判断①；由折叠的性质可得6OB BD ==，OC CD =，90BOC BDC ∠=∠=︒，由勾股定理可求OC 的长，可得点C 坐标，利用待定系数法可求BC 解析式，可判断②；由面积公式可求DH 的长，代入解析式可求点D 坐标，可判断③；分别讨论P 点在C 、B 点的情况，比较AP DP +值的情况，得出当P 点在C 点时，使得AP DP +的值最小可判断④，即可求解．【详解】解：直线3=+64y x −分别与x 、y 轴交于点A 、B ，∴点()8,0A ，点()0,6B ，8OA ∴=，6OB =，10AB ∴=，故①正确；线段OB 沿BC 翻折，点O 落在AB 边上的点D 处，6OB BD ∴==，OC CD =，90BOC BDC ∠=∠=︒，4AD AB BD ∴=−=，222AC AD CD =+，()22816OC OC ∴−=+，3OC ∴=，∴点()3,0C ，设直线BC 解析式为：6y kx =+，036k ∴=+，2k ∴=−，∴直线BC 解析式为：26y x =−+，故②正确；如图，过点D 作DH AC ⊥于H ，3CD OC ==，5CA ∴=，1122ACD S AC DH CD AD =⋅=⋅△， 341255DH ⨯∴==，∴当125y =时，123654x =−+， 245x ∴=，∴点2412,55D ⎛⎫ ⎪⎝⎭，故③正确；直线BC 上存在一点P ，当P 点在C 点时，()OC DC P =，∴AP DP AC OC OA +=+=，当P 点在B 点时，AP DP AD DB AB +=+=，在Rt OAB 中，AB OA >∴当P 点在C 点时，使得AP DP +的值最小，则点P 的坐标是()3,0，故④正确；综上分析可知，正确的结论为①②③④，故D 正确．故选：D ．【点睛】本题是一次函数综合题，考查了利用待定系数法求解析式，折叠的性质，面积法，勾股定理等知识，灵活运用这些性质解决问题是本题的关键． 3．（本题2分）（2023春·福建厦门·八年级厦门市湖滨中学校考期末）如图，在ABC 中，D 是AC 边上的中点，连接BD ，把BDC 沿BD 翻折，得到BDC '，DC '与AB 交于点E ，连接AC '，若2AD AC '==，3BD =，则C 到BD 的距离为（）【答案】B【分析】连接CC '，交BD 于点M ，由翻折知，BDC BDC '≌，BD 垂直平分CC '，证ADC '为等边三角形，利用含30度的直角三角形性质及勾股定理求出1DM =，CM =【详解】解：如图，连接CC '，交BD 于点M ，∵2AD AC ='=，D 是AC 边上的中点，∴2DC AD ==，由翻折知，BDC BDC '≌，BD 垂直平分CC '，∴2DC DC '==，BC BC '=，CM C M '=，∴2AD AC DC ''===，∴ADC '为等边三角形，∴60ADC AC D C AC ∠'=∠'=∠'=︒，∵DC DC ='， ∴160302DCC DC C ∠'=∠'=⨯︒=︒，在Rt CDM △中，30DCC ∠'=︒，2DC =，∴1DM =，CM C M '∴=∴C 到BD故选B ．【点睛】本题考查了等边三角形的判定及性质、含30度角的直角三角形的性质、勾股定理、折叠的性质、全等三角形的性质，熟练掌握性质定理是解题的关键． 4．（本题2分）（2020秋·广东广州·八年级校考期中）如图1，长方形ABCD 中，E 点在AD 上，且30ABE ∠︒=．分别以BE 、CE 为折线，将A 、D 向BC 的方向折过去，如图2，若图2中15AED ∠=︒，则BCE ∠度数为（）A ．30︒B ．32.5︒C ．35︒D ．37.5︒【答案】D 【分析】根据长方形的性质与三角形内角和定理，得到60AEB ∠=︒，再根据折叠的性质，得到A EB AEB '∠=，DEC D EC '∠=∠，由105AED '∠=︒，进而得到37.5DEC ∠=︒，最后根据平行线的性质，即可求出BCE ∠度数．【详解】解：四边形ABCD 是长方形，AD BC ∴∥，90A ∠=︒，30ABE ∠︒=，18060AEB A ABE ∴∠=︒−∠−∠=︒，由折叠的性质可知，60A EB AEB ∠=∠='︒，DEC D EC '∠=∠，15A ED ''∠=︒，606015105AED AEB A EB A ED ''''∴∠=∠+∠−∠=︒+︒−︒=︒，18075DED AED ''∴∠=︒−∠=︒，137.52DEC D EC DED ''∴∠=∠=∠=︒，AD BC ∥，37.5BCE DEC ∴∠=∠=︒，故选：D ．【点睛】本题考查了折叠的性质，三角形内角和定理，平行线的性质，熟练掌握折叠的性质是解题关键．5．（本题2分）（2023春·陕西榆林·八年级校考期末）如图，在等腰ABC 中，AB AC =，50BAC ∠=︒，BAC ∠的平分线与AB 的垂直平分线交于点O ，点C 沿EF 折叠后与点O 重合，则CEF ∠的度数是（）A ．55︒B ．50︒C ．45︒D ．40︒【答案】B 【分析】连接OB ，OC ，先求出25BAO ∠=︒，进而求出40OBC ∠=︒，求出40COE OCB ∠=∠=︒，由三角形内角和定理和12CEF OEF CEO ∠=∠=∠即可求得答案．【详解】解：如图，连接OB ，50BAC ∠=︒，AO 为BAC ∠的平分线，11502522BAO BAC ∴∠=∠=⨯︒=︒．又AB AC =，()1180652ABC ACB BAC ∴∠=∠=︒−∠=︒．DO 是AB 的垂直平分线，OA OB ∴=，25ABO BAO ∴∠=∠=︒，652540OBC ABC ABO ∴∠=∠−∠=︒−︒=︒．AO 为BAC ∠的平分线，AB AC =，∴直线AO 垂直平分BC ，OB OC ∴=，40OCB OBC ∴∠=∠=︒，点C 沿EF 折叠后与点O 重合，OE CE ∴=，12CEF OEF CEO ∠=∠=∠，40COE OCB ∴∠=∠=︒；在OCE △中，1801804040100CEO COE OCB ∠=︒−∠−∠=︒−︒−︒=︒，1502CEF CEO ∴∠=∠=︒．故选：B ．【点睛】本题主要考查了等腰三角形的性质以及翻折变换及其应用，解题的关键是根据翻折变换的性质，找出图中隐含的等量关系，灵活运用有关知识来分析、判断．．将AFG 沿AG A ．1B ．32 【答案】C 【分析】由正方形的性质可得AD AB =，设BF CF a ==，则2CD a =，24DG CD CG a =−=−，由题意知，90ADE ABF ∠=∠=︒，由折叠的性质可得HG EF ⊥，AE AF =，GE GF =，证明()Rt Rt HL ADE ABF ≌，则DE BF a ==，2434GF GE a a a ==+−=−，由勾股定理得222GF CF DG −=，即()222344a a −−=，解得3a =，0a =（舍去），则3CF =，5EG =，9EC =，由勾股定理得EF ，根据1122CEF S EG CF EF HG =⨯=⨯，即115322HG ⨯⨯=⨯，计算求解即可．【详解】解：由正方形的性质可得AD AB =，设BF CF a ==，则2CD a =，24DG CD CG a =−=−，由题意知，90ADE ABF ∠=∠=︒，由折叠的性质可得HG EF ⊥，AE AF =，GE GF =，∵AE AF =，AD AB =，∴()Rt Rt HL ADE ABF ≌，∴DE BF a ==，2434GF GE a a a ==+−=−，由勾股定理得222GF CF CG −=，即()222344a a −−=，解得3a =，0a =（舍去），∴3CF =，5EG =，9EC =，由勾股定理得EF ∵1122GEF S EG CF EF HG =⨯=⨯，∴115322HG ⨯⨯=⨯，解得HG =，故选：C ．【点睛】本题考查了正方形的性质，全等三角形的判定与性质，折叠的性质，勾股定理等知识．解题的关键在于对知识的熟练掌握与灵活运用．A ．65︒B ．62.5︒C ．55︒D ．52.5︒【答案】B 【分析】根据折叠得出90OB C B ''∠=∠=︒，求出55OB G '∠=︒，根据平行线的性质得出18055125B OB '∠=︒−︒=︒．根据折叠得出162.52BOG B OB '∠=∠=︒．【详解】解：根据折叠可知，90OB C B ''∠=∠=︒，∵35GB C ''∠=︒，∴55OB G '∠=︒，∵AB CD ∥，∴18055125B OB '∠=︒−︒=︒．由折叠可知，162.52BOG B OB '∠=∠=︒，故B 正确．故选：B ．【点睛】本题主要考查了折叠的性质，平行线的性质，解题的关键是熟练掌握两直线平行，同旁内角互补． 8．（本题2分）（2023·浙江·八年级假期作业）如图，现有一块三角板ABC ，其中90ABC ︒∠=，60CAB ︒∠=，8AB =，将该三角板沿BC 边翻转得到A BC '△，再将A BC '△沿A C '边翻转得到A B C ''△，则A 与B '两点之间的距离为（）【答案】C 【分析】连接AB '，作B D AA ''⊥，交AA '延长线于点D ，在Rt A B D ''中求得B D '、A D '的长度，在Rt AB D '中，即可求得AB '．【详解】解：连接AB '，作B D AA ''⊥，交AA '延长线于点D ，如下图：由折叠的性质可得：8AB A B A B '''===，60CAB CA B CA B '''∠=∠=∠=︒∴60B A D ''∠=︒∵B D AA ''⊥，∴90D Ð=°，∴30A B D ''∠=︒， ∴142A D A B '''==，∴B D '==，20AD =，∴AB '=故选：C【点睛】此题考查了勾股定理，折叠的性质，含30︒直角三角形的性质，解题的关键是熟练利用相关性质进行求解．A ．①②④B ．①②③C ．①③④D ．①②③④【答案】D 【分析】作FM BC ⊥于M （见详解图），①根据翻折变换的性质和正方形的性质可证ABG AFG △△≌；②设BG GF x ==，在Rt EGC △中，根据勾股定理可证3BG GC ==；③通过tan 2AB AGB BG ∠==，tan 2FM FCM CM ∠==，证明AGB FCM ∠=∠，由平行线的判定定理可得AG CF ∥；④由②得到3GC =，由③得到125FM =，根据12FCG S GC FM =△即可计算面积．【详解】解：作FM BC ⊥于M ，四边形ABCD 是正方形，∴6AB BC CD DA ====，90B D BCD ∠=∠=∠=︒，AFE △是由ADE V 翻折，∴AD AF AB ==，90ADE AFE AFG ∠=∠=∠=︒，在Rt AGF 和Rt AGB 中，AG AG AF AB =⎧⎨=⎩，∴ABG AFG △△≌．故①正确．∴BG GF =，设BG GF x ==，在Rt EGC △中，90ECG ∠=︒，2DE =，6CD =，4EC =，2EG x =+，6GC x =−，∴()()222246x x +=+−，∴3x =，∴3BG GC ==,故②正确．FM BC ⊥，CD BC ⊥∴FM EC ∥ ∴GF FM GM GE ECGC ==，3GF =，5GE =，4EC =，3GC =∴125FM =，95GM =，65CM GC GM =−=， ∴6tan 23AGB ∠==， tan 2FM FCM CM ∠==，∴AGB FCM ∠=∠，∴AG CF ∥，故③正确． ∴112183255FCG S ==△，故④正确．综上，选项D 符合题意．故选：D ．【点睛】本题考查了正方形的性质、全等三角形的判定和性质、翻折变换、勾股定理的应用等知识，熟练掌握正方形的性质，并能进行推理论证与计算是解决问题的关键．为对称轴将CDE 折叠得到CHE ，使得点 A ．90CEF ∠=︒ B ．CE 【答案】D 【分析】A.由折叠的性质可以知道EF 和CE 分别是AEG ∠和DEG ∠的平分线，同时AED ∠是平角，所以可知90CEF ∠=︒，故选项A 正确；B.由题意和折叠的性质可以知道EF AG ⊥、EF CE ⊥，就可以得到CE AG ∥，选项B 正确；C 和D.过点C 作C M A B ⊥于点M ，120CBA ∠=︒，可得2BM =，CM =BF a =，可以得到4FG AF a ==−，2FM BF BM a =+=+．根据折叠的性质可得4CG CD ==，根据勾股定理，求得2.4a =，即可得到 1.6FG =， 5.6CF =，所以5.6745CF AB ==．故选项C 正确，选项D 错误．【详解】解：A.由折叠可知EF 和CE 分别是AEG ∠和DEG ∠的平分线．又180AED ∠=︒，111809022CEF CEG FEG AED ∴∠=∠+∠=∠=⨯︒=︒，故选项A 正确．B.又点A 与点G 关于EF 对称，∴EF AG ⊥，又EF CE ⊥，∴CE AG ∥，故选项B 正确．C 和D.如答图，过点C 作C M A B ⊥于点M ．120CBA ∠=︒，∴60CBM ∠=︒，4BC =，∴易知2BM =，CM =设BF a =，∴4FG AF a ==−，2FM BF BM a =+=+，点E 是AD 的中点，折叠后点H 落到EG 上，∴点G 与点H 重合，4CG CD ==．易知点C G F ,,共线，∴448CF FG CG a a =+=−+=−．222FM CM CF +=，()(()22228a a ∴+=−+，解得 2.4a =． ∴4 2.4 1.6FG =−=，88 2.4 5.6CF a =−=−=，5.6745CF AB ∴==，故选项C 正确，选项D 错误．综上，故选：D ．【点睛】本题考查翻折变换（折叠问题）、菱形的性质、勾股定理，熟练掌握翻折的性质是解答本题的关键．二、填空题：本大题共10小题，每小题2分，共20分. 11．（本题2分）（2023春·河北承德·八年级统考期末）如图，小宇将一张平行四边形纸片折叠，使点A 落在长边CD 上的点1A 处，并得到折痕DE ，小宇测得长边6CD =，则四边形1A EBC 的周长为．【答案】12【分析】根据折叠的性质，得到DA DA '=，EA EA '=，结合平行四边形的性质，得到DA DA BC '==，代入计算即可．【详解】根据折叠的性质，得到DA DA '=，EA EA '=，∵四边形ABCD 是平行四边形，∴DA DA BC '==，6AB CD ==，∴四边形1A EBC 的周长为1111212BC BE A E AC A D AC AE BE AB CD CD +++=+++=+==．故答案为：12．【点睛】本题考查了折叠的性质，平行四边形的性质，熟练掌握性质是解题的关键．12．（本题2分）（2023春·上海浦东新·八年级统考期末）如图，在ABC 中，90A ∠=︒，28BC AC ==，点M 在边BC 上，过点M 作MN BC ⊥，垂足为点M ，交边AB 于点N ，将ABC 沿直线MN 翻折，点A 、C 分别与点D 、E 对应，如果四边形ADBE 是平行四边形，那么CM 的长是．【答案】3【分析】当点E 在线段BC 上时，连接DE 交AB 于点O ，过点O 作OH BC ⊥于点H ，则90BHO ∠=︒，求出AB =30ABC ∠=︒，由轴对称可得4DE AC ==，得OB =2OD OE ==，OH =，求出6CE =，由折叠可知，3CM =；假设点E 在线段CB 的延长线上，得到)4AN AF x ==−，与)2AN x =−矛盾，故点E 不可能在线段CB 的延长线上，即可确定CM 的长．【详解】解：当点E 在线段BC 上时，如图，连接DE 交AB 于点O ，过点O 作OH BC ⊥于点H ，则90BHO ∠=︒，∵90BAC ∠=︒，28BC AC ==，∴AB ==30ABC ∠=︒，∵将ABC 沿直线MN 翻折，点A 、C 分别与点D 、E 对应，∴4DE AC ==，∵四边形ADBE 是平行四边形，∴1122OB AB ==⨯=122OD OE DE ===，∴12OH OB ==∴3BH ==，∴1EH ==，∴312BE BH EH =−=−=，∴826CE BC BE =−=−=，由折叠可知，132CM EM CE ===，假设点E 在线段CB 的延长线上，延长MN 交AD 于点F ，则AD FM ⊥，12AF DF AD ==，∵90BAC ∠=︒，28BC AC ==，∴AB ==30ABC ∠=︒，设CM EM x ==，则8BM x =−，∴()828BE x x x AD=−−=−=， ∴142AF DF AD x ===−，在Rt BMN △中，30ABC ∠=︒，90BMN ∠=︒， ∴1MN BN 2=，∴222BM MN BN +=,即22212BM BN BN ⎛⎫+= ⎪⎝⎭，则)8BN x ==−，))82AN BN x x ==−==−，在Rt ANF △中，142AF DF AD x ===−，30NAF ABC ∠=∠=︒，90AFN ∠=︒， ∴12FN AN =，∴222AF FN AN +=,即22212AF AN AN ⎛⎫+= ⎪⎝⎭，)4AN AF x ==−，与)2AN x =−矛盾，故点E 不可能在线段CB 的延长线上，综上可知，3CM =，故答案为：3【点睛】此题考查了勾股定理、平行四边形的性质、含30︒角的直角三角形的性质等知识，分类讨论是解题的关键． 13．（本题2分）（2023春·北京丰台·八年级统考期末）如图，在Rt ABC △中，90B Ð=°，3AB =，4BC =，将ABC 折叠，使点B 恰好落在边AC 上，与点B '重合，AE 为折痕，则BE 的长等于．【答案】1.5【分析】根据折叠得到BE EB '=，AB AB 3'==，设BE EB x '==，则4EC x =−，根据勾股定理求得AC 的值，再由勾股定理可列方程求解即可．【详解】解：根据折叠可得BE EB '=，AB AB 3'==，设BE EB x '==，则4EC x =−，在Rt ABC △中，90B Ð=°，3AB =，4BC =5AC ∴=532B C AC AB ''∴=−=−=在Rt B EC '△中，由勾股定理得，()222x 24x +=− 解得 1.5x =故答案为：1.5【点睛】本题考查的是翻折变换的性质，解题的关键是掌握折叠前后图形的形状和大小不变，对应边和对应角相等，能熟练运用勾股定理列方程解决问题．14．（本题2分）（2023春·四川达州·八年级统考期末）如图，在ABC 和DCB △中，90A D ∠=∠=︒，AC ，BD 相交于点E ，AE DE =．将CDE 沿CE 折叠，点D 落在点D ¢处，若40BED '∠=︒，则BCD '∠的大小为．【答案】15︒/15度【分析】根据全等三角形的判定和性质得出BE CE =，再由等边对等角确定EBC ECB ∠∠=，利用折叠的性质及三角形内角和定理求解即可．【详解】解：在AEB 和DEC 中，90A D AE DE AEB DEC ∠∠∠∠==︒⎧⎪=⎨⎪=⎩，∴(ASA)AEB DEC ≌，∴BE CE =，∴EBC ECB ∠∠=，∵40BED '∠=︒，CDE 沿CE 折叠，点D 落在点D ¢处，∴70D EC DEC ︒'∠=∠=，∴180110BEC DEC ∠=︒−∠=︒，790200DCE ︒−︒=︒∠=，∴180110352EBC ECB ︒−∠︒=∠==︒，20DCE D CE ︒'∠=∠=，∴15BCD ECB D CE ''∠=∠−∠=︒，故答案为：15︒．【点睛】题目主要考查折叠的性质及全等三角形的判定和性质，三角形内角和定理及等腰三角形的判定和性质，理解题意，综合运用这些知识点是解题关键．15．（本题2分）（2023·浙江·八年级假期作业）折纸是一项有趣的活动，如图所示，一张长方形纸片()90ABCD A B C ∠=∠=∠=︒，先将纸片沿EF 折叠，再将折叠后的纸片沿GH 折叠，使得GD '与A B ''重合，展开纸片后若62BFE ∠=︒，则DGH ∠= ︒．【答案】17【分析】由平行线的性质得到62GEF BFE ∠=∠=︒，由平角定义得到180118AEF GEF ∠=︒−∠=︒，由轴对称的性质得到：90A A '∠=∠=︒，118A EF AEF '∠=∠=︒，DGH D GH '∠=∠，求出A EG '∠，由直角三角形的性质求出'∠A GE ，由对顶角的性质得到DGD A GE ''∠=∠，即可求出12DGH DGD '∠=．【详解】解：四边形ABCD 是矩形， AD BC ∴∥，90A ∠=︒，62GEF BFE ∴∠=∠=︒，180118AEF GEF ∴∠=︒−∠=︒，由题意得：90A A '∠=∠=︒，118A EF AEF '∠=∠=︒，DGH D GH '∠=∠，1186256A EG A EF GEF ''∴∠=∠−∠=︒−︒=︒，9034A GE A EG ''∴∠=︒−∠=︒，34DGD A GE ''∴∠=∠=︒，1172DGH DGD '∴∠==︒．故答案为：17．【点睛】本题考查轴对称的性质，平行线的性质，余角的计算，对顶角的性质，解题的关键是掌握轴对称的性质．16．（本题2分）（2023·浙江·八年级假期作业）如图，在△ABC 中，AB AC =，30C ∠=︒，将纸片沿DE 折叠，使点B 落到点A 处，若6BC =，则DE = ．【答案】1【分析】利用等腰三角形的性质得到30B C ∠=∠=︒，则120BAC ∠=︒，再由折叠性质得BD AD =，30BAD B ∠=∠=︒，90AED ∠=︒，进而得到90DAC ∠=︒，再根据含30度角的直角三角形的性质求解即可．【详解】解：∵AB AC =，30C ∠=︒∴30B C ∠=∠=︒，则3018030120BAC ∠=−︒−︒=︒，由折叠性质得BD AD =，30BAD B ∠=∠=︒，90AED ∠=︒，∴1309020DAC ︒−︒=∠=︒，12DE AD =，∴2CD AD =，又6BC =，∴236BC BD CD AD AD AD =+=+==，∴2AD =， ∴112DE AD ==，故答案为：1．【点睛】本题考查等腰三角形的性质、折叠性质、三角形的内角和定理、含30度角的直角三角形的性质，熟练掌握折叠性质和直角三角形的性质是解答的关键．上一动点，把CDE 沿直线，若D BC '为等边三角形，【答案】1或4/4或1【分析】依据折叠的性质、菱形的性质以及等边三角形的性质，分两种情况得到DE 的长即可．【详解】解：由折叠及菱形的性质可得CD CD CB '==，故D BC '是以BD '底的等腰三角形，故当60D BC '∠=︒，D BC '为等边三角形，分以下两种情况讨论，1）如图（1），当点D ¢点A 重合时，60D BC '∠=︒，此时点E 为AD 的中点，故1DE =，2）如图（2），当点D ¢与点A 关于直线BC 对称时，D ¢，C ，D 三点共线，EC DC ⊥，故24DE DC ==，综上所述，1DE =或4，故答案为：1或4．【点睛】本题考查了菱形的性质，折叠问题及等边三角形的性质等知识的综合运用，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．如图，ABC 中，【答案】108【分析】连接OB 、OC ，根据角平分线的定义求出BAO ∠，根据等腰三角形两底角相等求出ABC ∠，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA OB =，根据等边对等角可得ABO BAO ∠=∠，再求出OBC ∠，证明 OB OC =，再根据等边对等角求出OCB OBC ∠=∠，根据翻折的性质可得OE CE =，然后根据等边对等角求出COE ∠，再利用三角形的内角和定理列式计算即可．【详解】解：如图，连接OB 、OC ，54BAC ∠=︒Q ，AO 为BAC ∠的平分线，11542722BAO BAC ∴∠=∠=⨯︒=︒，又AB AC =，11(180)(18054)6322ABC BAC ∴∠=︒−∠=︒−︒=︒， DO 是AB 的垂直平分线，OA OB ∴=，27ABO BAO ∴∠=∠=︒，632736OBC ABC ABO ∴∠=∠−∠=︒−︒=︒， AO 为BAC ∠的平分线，AB AC =，∴点O 在BC 的垂直平分线上，∴OB OC =，36OCB OBC ∴∠=∠=︒，将C ∠沿(EF E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，OE CE ∴=，36COE OCB ∴∠=∠=︒，在OCE △中，1801803636108OEC COE OCB ∠=︒−∠−∠=︒−︒−︒=︒，故答案为：108．【点睛】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等腰三角形三线合一的性质，等边对等角的性质，以及翻折变换的性质，三角形内角和定理等等，熟知相关知识是解题的关键．19．（本题2分）（2023春·辽宁沈阳·八年级统考期末）如图，在ABC ∆中，90A ∠=︒，30C ∠=︒，3AB =，点D 为AC 的中点，点E 是BC 边上一个动点，将CDE ∆沿着DE 翻折，使得点C 落在点F 处，当FE AC ⊥时，EF 的长为．【答案】32或92【分析】根据题意，分两种情况：①当E 在D 的右侧时；②当E 在D 的左侧时，由翻折性质，结合含30︒的直角三角形边的关系列方程求解即可得到答案．【详解】解：在ABC 中，90A ∠=︒，30C ∠=︒，3AB =，点D 为AC 的中点，AC ∴=12CD AB =，当E 在D 的右侧时，延长FE 交AC 于H ，如图所示：FE AC ⊥，90EHC ∴∠=︒，由翻折的性质知，CD DF ==，30C DFH∠=∠=︒，设EF x =，则CE EF x ==，1122EH EC x ==， 32FH x ∴=，在直角三角形DFH 中，30DFH ∠=︒，则FH =，∴32x =，32x ∴=；当E 在D 的左侧时，如图所示：由翻折性质知，CD DF ==，30C EFD ∠=∠=︒，CE EF x ==，EF AC ⊥，90FHD ∴∠=︒，1122EH EC x ∴==，1122FH x x x =−=，在直角三角形FHD 中，HF =，∴12x =，解得92x =，故答案为：32或92．【点睛】本题考查翻折性质，充分利用翻折性质及含30︒的直角三角形边的关系分情况讨论是解决问题的关键． 20．（本题2分）（2023春·重庆忠县·八年级统考期末）如图，在正方形ABCD 中，点E 是BC 上一点，连接DE ，将BDE 沿DE 翻折得到GDE ，连接CG ．若CG BD ∥，则CEG ∠= ．【答案】60︒/60度【分析】根据直角三角形斜边中线的性质得出CH DH HB ==,1=2CH DB ，由折叠的性质得DB DG =，∠=∠BDE GDE ，利用辅助线构造矩形并由其性质得出CH GK =，再由等量代换得出12GK DG =，最后由特殊直角三角形的性质得出30GDK ∠=︒，利用折叠的性质及正方形的性质即可求解．【详解】解：如图，过点C 作直线CH DB ⊥于点H ，过点G 作直线GK DB ⊥于点K ，正方形ABCD 中，DC CB =，90452CDB ︒∠==︒，CH DH HB ∴==,1=2CH DB ． GDE △由BDE 沿DE 翻折得到，GDE BDE ∴≌△△， DB DG ∴=，∠=∠BDE GDE ，CH DB ⊥，GK DB ⊥，CG BD ∥，CH GK ∴∥,90CHK ∠=︒，∴四边形CHKG 是矩形．CH GK ∴=， ∴11=22GK CH DB DG ==，90GKD ∠=︒，∴30GDK ∠=︒．11=30=1522BDE GDK ∴∠=∠⨯︒︒．∵正方形ABCD ，∴45DBE ∠=︒，∴1804515120BED ∠=︒−︒−︒=︒，60CED ∠=︒，∵BDE 沿DE 翻折得到GDE ，∴120BED DEG ∠=∠=︒，∴12060CEG DEC ∠=︒−∠=︒，故答案为：60︒．【点睛】本题考查正方形—翻折问题．具体考查正方形的性质，折叠的性质，全等三角形的性质，特殊直角三角形的性质，矩形的判定和性质等的综合运用能力．灵活添加辅助线是解本题的关键．三、解答题：本大题共7小题，21-25题每小题8分，26-27题每小题10分，共60分．若将DAB 沿直线 (1)求点A B 、的坐标．(2)求三角形ACE 的面积．(3)求直线CD 的解析式．【答案】(1)()3,0A ，()0,4B(2)6(3)364y x =−【分析】（1）当0x =，4043y =−⨯+，解得4y =，则()0,4B ，当0y =，4043x =−+，解得3x =，则()3,0A ；（2）由折叠的性质可知AB AC =，OBA ECA ∠=∠，证明()AAS ABO ACE ≌，根据12ACE ABO S S OA OB ==⨯，计算求解即可；（3）由勾股定理得，5AB ，则8OC OA AC =+=，()80C ，，待定系数法求直线CD 的解析式即可．【详解】（1）解：当0x =，4043y =−⨯+，解得4y =，则()0,4B ，当0y =，4043x =−+，解得3x =，则()3,0A ，∴()3,0A ，()0,4B ；（2）解：由折叠的性质可知AB AC =，OBA ECA ∠=∠，∵OBA ECA ∠=∠，OAB EAC ∠=∠，AB AC =，∴()AAS ABO ACE ≌， ∴1134622ACE ABO S S OA OB ==⨯=⨯⨯=，∴三角形ACE 的面积为6；（3）解：由勾股定理得，5AB ==，由（2）可知5AC AB ==，8OC OA AC =+=，∴()80C ，，设直线CD 的解析式为y kx b =+，将()0,6D −，()80C ，，代入y kx b =+得，680b k b =−⎧⎨+=⎩，解得346k b ⎧=⎪⎨⎪=−⎩，∴直线CD 的解析式为364y x =−．【点睛】本题考查了一次函数的解析式，勾股定理，折叠的性质，全等三角形的判定与性质，一次函数的图象坐标轴的交点．解题的关键在于对知识的熟练掌握与灵活运用． 22．（本题8分）（2023春·吉林长春·八年级统考期末）将边长为2的正方形纸片ABCD 按如下操作：【操作一】如图①，将正方形纸片ABCD 对折，使点A 与点B 重合，点D 与点C 重合，再将正方形纸片ABCD 展开，得到折痕EF ．则点B 、点F 之间的距离为_____________．【操作二】如图②，G 为正方形ABCD 边BC 上一点，连接AG ，将图①的正方形纸片沿AG 翻折，使点B 的对称点H 落在折痕EF 上．连接BH ．（1）求证：ABH 是等边三角形．（2）求四边形CFGH 的周长．（1）证明见解析；（2）5【分析】操作一：由题知，4BC =，122CF DF CD ===，利用勾股定理可得BF =操作二：（1）由翻折得EF 是AB 的垂直平分线，故BH AH =，又AB AH =，即AB BH AH ==，即得ABH 是等边三角形；（2）由ABH 是等边三角形，可得2AH AB ==，1AE =．HE ==可得2FH EF HE =−=即可得出四边形ABGH 的周长．【详解】解：操作一：如图，连接BF ，由题知2BC CD ==，由翻折，知112CF DF CD ===，由勾股定理，得BF操作二：（1）由翻折知EF 是AB 的垂直平分线，BH AH ∴=，又AB AH =，AB BH AH ∴==，ABH ∴是等边三角形；（2）∵ABH 是等边三角形．∴2AH AB ==，1AE =．∴HE =∴2FH EF HE =−=∴四边形CFHG 的周长CF HF HG CG CF HF CB +++=++122=+5=【点睛】本题主要考查四边形的综合题，涉及勾股定理，等边三角形的判定和性质，正方形的性质等知识点，熟练掌握轴对称的性质与勾股定理的应用是解题的关键． (1)试判断重叠部分BED 的形状，并证明你的结论；(2)若BE 平分ABD ∠，12BC =，求BED 的面积．【答案】(1)BED 是等腰三角形，证明见解析(2)BED 的面积【分析】（1）根据折叠性质得出EBD DBC ∠=∠，进而得出EDB EBD ∠=∠，可得EB ED =，根据等角对等边即可得证；（2）根据含30度角的直角三角形的性质，勾股定理得出DE ，进而根据三角形的面积公式即可求解．【详解】（1）BED 是等腰三角形，证明：四边形ABCD 是长方形，AD BC ∴∥，EDB DBC ∴∠=∠，由折叠可知：EBD DBC ∠=∠，EDB EBD ∴∠=∠，EB ED ∴=，BED ∴是等腰三角形；（2）四边形ABCD 是长方形，AB DC ∴=，12AD BC ==，90A ABC C ∠=∠=∠=︒， BE 平分ABD ∠，ABE EBD ∴∠=∠，30ABE EBD DBC ∴∠=∠=∠=︒，2,BC CD BC ∴==，DC BC ∴==AB ∴=EB ED =，12AE AD DE DE ∴=−=−，在Rt ABE △中，根据勾股定理，得222AE AB BE +=，222(12)DE DE ∴−+=，解得8DE =，BED ∴的面积11822DE AB =⨯⋅=⨯⨯=【点睛】本题考查了勾股定理，折叠问题，含30度角的直角三角形的性质，熟练掌握勾股定理与折叠的性质是解题的关键． 24．（本题8分）（2023春·山西阳泉·八年级统考期末）综合与实践问题情境：在综合实践活动课上，同学们以“平行四边形纸片的折叠”为主题开展数学活动．在平行四边形纸片ABCD 中，E 为CD 边上任意一点，将ADE V 沿AE 折叠，点D 的对应点为D ¢．分析探究：（1）如图1，当点D ¢恰好落在AB 边上时，四边形D BCE '的形状为．问题解决：（2）如图2，当E ，F 为CD 边的三等分点时，连接FD '并延长，交AB 边于点G ．试判断线段AG 与BG 的数量关系，并说明理由．（3）如图3，当60ABC ∠=︒，45DAE =︒∠时，连接DD '并延长，交BC 边于点H ．若ABCD Y 的面积为24，4=AD ，请直接写出线段D H '的长．【答案】（1）平行四边形；（2）2BG AG =，理由见解析；（3）D H '=【分析】（1）利用平行四边形的性质及折叠的性质可得ABCD ，AD DE AD '==，可得四边形ADED '是菱形，可知DE AD ='，继而可知BD CE '=，即可求解；（2）利用折叠的性质可得AED AED '∠=∠，ED ED ¢=，结合三等分点可知ED ED EF '==，进而可得ED F EFD ''∠=∠，利用三角形外角性质可得AED ED F ''∠=∠，进而可知AE FG ∥，可得四边形AEFG 是平行四边形，再结合平行四边形的性质即可得AG 与BG 的数量关系；（3）由折叠可知：45DAE D AE '∠=∠=︒，AD AD ='，易知DAD '△为等腰直角三角形，延长AD '交BC 于M ，可知45MD H AD D ''∠=∠=︒，由平行四边形的性质可得，45BHM ADH MD H '∠=∠=︒=∠，AM AD ⊥，进而可知MD MH '=由ABCD Y 的面积为24，4=AD ，得24AD AM ⋅=，求得6AM =，可得2MD AM AD ''=−=，再利用勾股定理即可求解．【详解】解：（1）∵四边形ABCD 是平行四边形，∴AB CD ，AB CD =则D AE AED '∠=∠由折叠可知：AD AD ='，DAE D AE '∠=∠，∴DAE AED ∠=∠，∴AD DE AD '==，∴四边形ADED '是平行四边形，又∵AD AD ='，∴四边形ADED '是菱形，∴DE AD ='，∴BD CE '=，∴四边形D BCE '是平行四边形，故答案为：平行四边形；（2）2BG AG =，理由如下：∵四边形ABCD 是平行四边形，∴AB CD ，AB CD =，又∵E ，F 为CD 边的三等分点， ∴13DE EF CF DC ===，由折叠可知：ED ED ¢=，AED AED '∠=∠，则ED ED EF '==，∴ED F EFD ''∠=∠，由三角形外角可知：DED ED F EFD AED AED ''''∠=∠+∠=∠+∠，∴AED ED F ''∠=∠，∴AE FG ∥，∴四边形AEFG 是平行四边形，∴EF AG =， ∵13EF DC =，AB CD =， ∴13AG AB =，则23BG AB =，∴2BG AG =；（3）由折叠可知：45DAE D AE '∠=∠=︒，AD AD ='，∴90DAD '∠=︒，则DAD '△为等腰直角三角形，∴45ADH AD D '∠=∠=︒，延长AD '交BC 于M ，则45MD H AD D ''∠=∠=︒∵四边形ABCD 是平行四边形，∴AD BC ∥，∴45DHM ADH MD H ∠=∠=∠'︒=，90AMH DAD '∠=∠=︒，即AM AD ⊥，∴MD MH '=∵ABCD Y 的面积为24，4=AD ，即：24AD AM ⋅=，∴6AM =，则2MD AM AD AM AD ''=−=−=，∴D H '【点睛】本题考查平行四边形的判定及性质，菱形的判定，翻折的性质，等腰直角三角形的判定及性质，勾股定理等知识点，熟练掌握相关性质定理是解决问题的关键．轴的负半轴上，若将DAB 沿直线(1)求线段AB 的长(2)求直线CD 的函数表达式；(3)点P 在直线CD 上，使得2PAC OAB SS =，求点【答案】(1)5AB =(2)364y x =− (3)7224,55⎛⎫ ⎪⎝⎭或824,55⎛⎫− ⎪⎝⎭【分析】（1）先根据点,A B 的坐标可得3,4OA OB ==，再利用勾股定理可得5AB =；（2）设点D 的坐标为()0,D m ，则4,BD m OD m =−=−，先根据折叠的性质可得4CD BD m ==−，再在Rt COD 中，利用勾股定理可得6m =−，从而可得()0,6D −，然后利用待定系数法即可得；（3）设点P 的坐标为3,64P n n ⎛⎫− ⎪⎝⎭，根据2PAC OAB S S =建立方程，解方程可得n 的值，由此即可得出答案．【详解】（1）解：()3,0A ，()0,4B ， 3,4OA OB ∴==， x 轴y ⊥轴，5AB ∴=．（2）解：设点D 的坐标为()0,D m ，则4,BD m OD m =−=−，由折叠的性质得：4CD BD m ==−，5AC AB ==，8OC OA AC ∴=+=，∴点C 的坐标为()8,0，在Rt COD 中，222OD OC CD +=，即()()22284m m −+=−，解得：6m =−，()0,6D ∴−，设直线CD 的函数表达式为y kx b =+，将点()()8,0,0,6C D −代入得：806k b b +=⎧⎨=−⎩，解得346k b ⎧=⎪⎨⎪=−⎩，则直线CD 的函数表达式为364y x =−．（3）解：由题意，设点P 的坐标为3,64P n n ⎛⎫− ⎪⎝⎭， 3,4OA OB ==，162OAB S OA OB ∴=⋅=，2PAC OAB S S =，61562342n −∴⨯=⨯，解得725n =或85n =，当725n =时，732364424655n −=−=⨯，即此时7224,55P ⎛⎫ ⎪⎝⎭，当85n =时，83246534564n =−=−−⨯，即此时824,55P ⎛⎫− ⎪⎝⎭，综上，点P 的坐标为7224,55⎛⎫ ⎪⎝⎭或824,55⎛⎫− ⎪⎝⎭．【点睛】本题考查了勾股定理、折叠的性质、求一次函数的解析式、一次函数的几何应用，熟练掌握折叠的性质和待定系数法是解题关键． 26．（本题10分）（2023春·江苏苏州·八年级星海实验中学校考期中）如图1，四边形ABCD 中，AD BC ∥，90ADC ∠=︒，8AD =，6BC =，点M 从点D 出发，以每秒2个单位长度的速度向点A 运动，同时，点N 从点B 出发，以每秒1个单位长度的速度向点C 运动．其中一个动点到达终点时，另一个动点也随之停止运动，过点N 作NP AD ⊥于点P ，连接AC 交NP 于点Q ，连接MQ ．设运动时间为t 秒．(1)AM =______，AP =______．（用含t 的代数式表示）(2)当四边形ANCP 为平行四边形时，求t 的值；(3)如图2，将AQM 沿AD 翻折，得AKM ，是否存在某时刻t ，使四边形AQMK 为为菱形，若存在，求出t 的值；若不存在，请说明理由．【答案】(1)82t −，2t +(2)2t =(3)存在，1t =【分析】（1）由2DM t =，根据AM AD DM =−即可求出82AM t =−；先证明四边形CNPD 为矩形，得出6DP CN t ==−，则2AP AD DP t =−=+；（2）根据四边形ANCP 为平行四边形时，可得68(6)t t −=−−，解方程即可；（3）由NP AD ⊥，QP PK =，可得当PM PA =时有四边形AQMK 为菱形，列出方程628()6t t t −−=−−，求解即可．【详解】（1）解：如图1．2DM t =，82AM AD DM t ∴=−=−．在直角梯形ABCD 中，AD BC ∥，90ADC ∠=︒，NP AD ⊥于点P ，∴四边形CNPD 为矩形，6DP CN BC BN t ∴==−=−，8(6)2AP AD DP t t ∴=−=−−=+；故答案为：82t −，2t +．（2）四边形ANCP 为平行四边形时，CN AP =，68(6)t t ∴−=−−，解得：2t =；（3）存在时刻1t =，使四边形AQMK 为菱形．理由如下：NP AD ⊥，QP PK =，∴当PM PA =时有四边形AQMK 为菱形，628(6)t t t ∴−−=−−，解得1t =．【点睛】本题主要考查了四边形综合题，其中涉及到直角梯形的性质，矩形的判定与性质，等腰直角三角形的性质，轴对称的性质，等腰三角形的性质，正方形的性质等知识，综合性较强，难度适中．运用数形结合、方程思想是解题的关键．(1)BQ = ______ (含t 的代数式表示)；(2)如图2，连接AD ，PF ，PQ ，当AD PQ ∥时，求PQF △的面积；(3)如图3，连接PF ，PQ ，D 点关于直线PF 的对称点为D '点，若'D 落在PQB △的内部则t 的取值范围为______.【答案】(1)4(02)t t −<≤(2)PQFS = (3)4453t <<【分析】（1）根据几何动点的速度和时间可得结论；（2）根据四边形BPDQ 是平行四边形，证明四边形APQD 是平行四边形，可得1t =，再证明EFD ≌△CFQ ，最后利用三角形的面积公式可解答；（3）先证明DF FQ =，再计算两个边界点时点t 的值；①如图3，点D '与Q 重合，②如图4，D '在斜边AB 上，由此可得结论.【详解】（1）解：在Rt ABC △中，90830C AB A ∠∠=︒==︒，，，142BC AB AC ∴===，由题意，CQ t =，()402BQ t t ∴=−<≤. 故答案为：()402t t −<≤；（2）如图2中，四边形BPDQ 是平行四边形，∴DQ AB ∥，BP DQ BQ PD ==，，。

专题2.2轴对称的性质-2021-2022学年八年级数学上册尖子生同步培优题典(解析版)【浙教版】

2021-2022学年八年级数学上册尖子生同步培优题典【浙教版】专题2.2轴对称的性质姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2019秋•无为县期末）在4×4的正方形网格中，以格点为顶点的三角形称为格点三角形，在图中画出与△ABC关于某条直线对称的格点三角形，最多能画（）个．A．5B．6C．7D．8【分析】根据网格结构分别确定出不同的对称轴，然后作出轴对称三角形即可得解；【解析】如图，最多能画出7个格点三角形与△ABC成轴对称．故选：C．2．（2020•天河区一模）如图，将△ABC沿过边上两点D，E的直线折叠后，使得点B与点A重合．若已知BE＝4cm，DE＝3cm，则△ABC的周长与△ADC的周长的差为（）A．4cm B．5cm C．8cm D．10cm【分析】由折叠的性质得AD＝BD，BE＝AE＝4，△ABC的周长﹣△ADC的周长＝AB+BC+AC﹣AC﹣CD ﹣AD＝AB，即可得出结果．【解析】∵将△ABC沿直线DE折叠后，使得点B与点A重合，∴AD＝BD，BE＝AE＝4，∴AB＝BE+AE＝4+4＝8，∴△ABC的周长﹣△ADC的周长＝AB+BC+AC﹣AC﹣CD﹣AD＝AB+BD﹣AD＝AB＝8（cm），故选：C．3．（2021•南京一模）如图，在△ABC中，∠C＝90°，沿DE翻折使得A与B重合，若∠CBD＝26°，则∠ADE的度数是（）A．57°B．58°C．59°D．60°【分析】由折叠的性质可得出∠ADE＝∠BDE=12∠ADB，利用三角形的外角性质可求出∠ADB的度数，进而可求出∠ADE的度数．【解析】由题意可知：∠ADE＝∠BDE=12∠ADB．∵∠ADB＝∠C+∠CBD＝90°+26°＝116°，∴∠ADE=12×116°＝58°．故选：B．4．（2020秋•玄武区期中）如图，△ABC和△AB'C'关于直线l对称，l交CC'于点D，若AB＝4，B'C'＝2，CD＝0.5，则五边形ABCC′B'的周长为（）A．14B．13C．12D．11【分析】直接利用轴对称的性质得出AB＝AB′，BC＝B′C′，DC＝DC′，再用周长公式即可得出答案．【解析】∵△ABC和△AB'C'关于直线l对称，l交CC'于点D，∴AB＝AB′，BC＝B′C′，DC＝DC′，∵AB＝4，B'C'＝2，CD＝0.5，∴AB′＝4，BC＝2，DC′＝0.5，∴五边形ABCC′B'的周长为：4+2+0.5+0.5+2+4＝13．故选：B．5．（2021•南通一模）如图，在Rt△ACB中，∠BAC＝90°，AD⊥BC，垂足为D，△ABD与△ADB′关于直线AD对称，点B的对称点是点B′，若∠B′AC＝14°，则∠B的度数为（）A．38°B．48°C．50°D．52°【分析】通过折叠角相等，∠BAD+∠B’AD+∠B’AC＝90°计算得∠BAD，进而用余角进行计算．【解析】∵∠BAD+∠B’AD+∠B’AC＝90°，且∠BAD＝∠B’AD，∠B′AC＝14°，∴∠BAD＝38°∴∠B＝90°﹣38°＝52°故选：D．6．（2020•宿州模拟）黄帅拿一张正方形的纸按如图所示沿虚线连续对折后剪去带直角的部分，然后打开后的形状是（）A．B．C．D．【分析】本题主要考查学生的动手能力及空间想象能力．【解析】严格按照图中的顺序向右下对折，向左下对折，从直角顶点处剪去一个直角三角形，展开得到结论．故选C．7．（2020春•郫都区期末）如图，△ABC与△A′B′C′关于直线l对称，若∠A＝50°，∠C＝20°，则∠B'度数为（）A．110°B．70°C．90°D．30°【分析】利用三角形内角和定理求出∠B，再利用轴对称的性质解决问题即可．【解析】∵△ABC与△A′B′C′关于直线l对称，∴∠B′＝∠B，∵∠B＝180°﹣∠A﹣∠C＝180°﹣50°﹣20°＝110°，∴∠B′＝110°，故选：A．8．（2020春•双阳区期末）如图，正方形的边长为2，则图中阴影部分的面积为（）A．2B．4C．8D．无法确定【分析】正方形是轴对称图形，根据对称性可以将图形中带阴影的图形面积等于正方形面积的一半，进而得出答案．【解析】如图所示：图中阴影部分的面积为正方形面积一半：12×22＝2．故选：A．9．（2020秋•苏州期中）如图，在三角形纸片中，AB＝8cm，BC＝5cm，AC＝6cm，沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）A．7cm B．8cm C．9cm D．10cm【分析】根据翻折的性质和题目中的条件，可以得到AD+DE的长和AE的长，从而可以得到△ADE的周长．【解析】由题意可得，BC＝BE，CD＝DE，∵AB＝8cm，BC＝5cm，AC＝6cm，∴AD+DE＝AD+CD＝AC＝6cm，AE＝AB﹣BE＝AB﹣BC＝8﹣5＝3cm，∴AD+DE+AE＝9cm，即△AED的周长为9cm，故选：C．10．（2020春•丹阳市期末）△ABC中，∠BAC＞∠B，∠C＝50°，将∠B折叠，使得点B与点A重合，折痕PD分别交AB、BC于点D、P，当△APC中有两个角相等时，∠B的度数为（）A．40°或25°B．25°或32.5°C．40°或25°或32.5°D．65°或80°或50°【分析】分三种情形分别求解即可．【解析】当∠APC＝∠C＝50°时，∵∠B＝∠PAB，∠APC＝∠B+∠PAB＝50°，∴∠B＝25°，当∠PAC＝∠C＝50°时，∠APC＝180°﹣50°﹣50°＝80°，∴∠B=12∠APC＝40°，当∠CAP＝∠CPA=12（180°﹣50°）＝65°时，∠B=12∠CPA＝32.5°，故选：C．二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2020秋•盐都区期末）如图，△ABC与△A′B′C′关于直线l对称，则∠B的度数为　100　度．【分析】根据轴对称的性质先求出∠C等于∠C′，再利用三角形内角和定理即可求出∠B．【解析】∵△ABC与△A′B′C′关于直线l对称，∴∠C＝∠C′＝20°，∴∠B＝180°﹣∠A﹣∠C＝180°﹣50°﹣20°＝110°．故答案为：110．12．（2020秋•宝应县期中）如图，△ABC和△A′B′C′关于直线l对称，其中∠A＝36°，∠C′＝24°，则∠B＝　120　°．【分析】由△ABC和△A′B′C′关于直线l对称，推出△ABC≌△A′B′C′，推出∠C＝∠C′＝24°，即可解决问题．【解析】∵△ABC和△A′B′C′关于直线l对称，∴△ABC≌△A′B′C′，∴∠C＝∠C′＝24°，∴∠B＝180°﹣36°﹣24°＝120°，故答案为：120．13．（2019秋•涡阳县期末）如图，△ABC和△A'B'C'关于直线MN对称，并且AB＝6，BC＝3，则A'C'的取值范围是　3＜A′C′＜9　．【分析】据△ABC和△A′B′C′关于MN对称，得出△ABC≌△A′B′C′，即可得出AC＝A′C′，再利用三角形三边关系得出A′C′的取值范围．【解析】∵△ABC和△A′B′C′关于MN对称，∴得出△ABC≌△A′B′C′，∴AC＝A′C′，∵AB﹣BC＜AC＜AB+BC，∴6﹣3＜AC＜6+3∴A′C′的取值范围是：3＜A′C′＜9．故答案为：3＜A′C′＜9．14．（2020秋•南岗区校级月考）如图，点P关于OA、OB的对称点分别为H、G，直线HG交OA、OB于点C、D，若∠HOG＝80°，则∠HPG＝　140　°．【分析】根据轴对称的性质和等腰三角形的性质找出与∠CPD的关系，利用已知可得∠AOB＝40°可求出∠CPD，进而得出∠HPG．【解析】∵P关于OA、OB的对称点是H、G，∴OA垂直平分PH于R，OB垂直平分PG于T，∴CP＝CH，DG＝DP，∴∠PCD＝2∠CHP，∠PDC＝2∠DGP，∵∠PRC＝∠PTD＝90°，∴在四边形OTPR中，∴∠RPT+∠AOB＝180°，∵∠POC＝∠COH，∠POD＝∠DOG，∠HOG＝80°，∴∠AOB＝40°，∴∠RPT＝180°﹣40°＝140°，∴∠CHP+∠PGD＝40°，∴∠PCD+∠PDC＝80°，∴∠CPD＝180°﹣80°＝100°．或∠CPD＝∠CPO+∠DPO＝∠OHG+∠OGH＝180°﹣∠GOH＝100°，∴∠HPG＝100°+40°＝140°，故答案为：140．15．（2020秋•淮南期末）如图，已知△ABC中，∠BAC＝140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，则∠DAE的度数为　100°　．【分析】如图，由三角形内角和定理求出∠B+∠C＝40°；证明∠ADE+∠AED＝2（α+β）＝80°，即可解决问题．【解析】如图，∵∠BAC＝140°，∴∠B+∠C＝180°﹣140°＝40°；由题意得：∠B＝∠DAB（设为α），∠C＝∠EAC（设为β），∴∠ADE＝2α，∠AED＝2β，∴∠DAE＝180°﹣2（α+β）＝180°﹣80°＝100°，故答案为100°．16．（2020秋•李沧区期末）如图，△AOB与△COB关于边OB所在的直线成轴对称，AO的延长线交BC于点D．若∠BOD＝46°，∠C＝22°，则∠ADC＝　70　°．【分析】根据∠ADC＝∠A+∠ABD，求出∠A，∠ABD即可．【解析】∵△AOB与△COB关于边OB所在的直线成轴对称，∴△AOB≌△COB，∴∠A＝∠C＝22°，∠ABO＝∠CBO，∵∠BOD＝∠A+∠ABO，∴∠ABO＝46°﹣22°＝24°，∴∠ABD＝2∠ABO＝48°，∴∠ADC＝∠A+∠ABD＝22°+48°＝70°，故答案为：70．17．（2020秋•靖江市期中）如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM＝3cm，PN ＝4cm，MN＝5.5cm，则线段QR的长为　6.5cm　．【分析】根据轴对称的性质得到OA垂直平分PQ，OB垂直平分PR，则利用线段垂直平分线的性质得QM＝PM＝3cm，RN＝PN＝4cm，然后计算QN，再计算QN+RN即可．【解析】∵点P关于OA的对称点Q恰好落在线段MN上，∴OA垂直平分PQ，∴QM＝PM＝3cm，∴QN＝MN﹣QM＝5.5﹣3＝2.5（cm），∵点P关于OB的对称点R落在MN的延长线上，∴OB垂直平分PR，∴RN＝PN＝4cm，∴QR＝QN+RN＝2.5+4＝6.5（cm）．故答案为：6.5cm．18．（2020秋•惠山区校级月考）如图（1）为某四边形ABCD纸片，其中∠B＝70°，∠C＝80°，若将CD 叠合在AB上，出现折线MN，再将纸片展开后，M、N两点分别在AD、BC上，如图（2）所示，则∠MNB的度数为　95　°．【分析】由折叠的性质可得∠C＝∠AC'N＝80°，∠MNC＝∠MNC'，由外角的性质可求∠BNC'＝10°，即可求解．【解析】∵将CD叠合在AB上，∴∠C＝∠AC'N＝80°，∠MNC＝∠MNC'，∵∠B+∠BNC'＝∠AC'N＝80°，∴∠BNC'＝80°﹣70°＝10°，∴∠MNC=180°10°2=85°，∴∠MNB＝180°﹣85°＝95°，故答案为：95．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．（2020春•凌海市期末）如图，点P是∠AOB外的一点，点Q与P关于OA对称，点R与P关于OB对称，直线QR分别交OA、OB于点M、N，若PM＝PN＝4，MN＝5．（1）求线段QM、QN的长；（2）求线段QR的长．【分析】（1）利用轴对称的性质求出MQ即可解决问题．（2）利用轴对称的性质求出NR即可解决问题．【解析】（1）∵P，Q关于OA对称，∴OA垂直平分线段PQ，∴MQ＝MP＝4，∵MN＝5，∴QN＝MN﹣MQ＝5﹣4＝1．（2）∵P，R关于OB对称，∴OB垂直平分线段PR，∴NR＝NP＝4，∴QR＝QN+NR＝1+4＝5．20．（2020春•竞秀区期末）如图，点P在∠AOB的内部，点C和点P关于OA对称，点P关于OB对称点是D，连接CD交OA于M，交OB于N．（1）①若∠AOB＝60°，则∠COD＝　120　°；②若∠AOB＝α，求∠COD的度数．（2）若CD＝4，则△PMN的周长为　4　．【分析】（1）根据轴对称的性质，可知∠AOC＝∠AOP，∠BOD＝∠BOP，可以求出∠COD的度数；（2）根据轴对称的性质，可知CM＝PM，DN＝PN，根据周长定义可以求出△PMN的周长；【解析】（1）①∵点C和点P关于OA对称，∴∠AOC＝∠AOP，∵点P关于OB对称点是D，∴∠BOD＝∠BOP，∴∠COD＝∠AOC+∠AOP+∠BOP+∠BOD＝2（∠AOP+∠BOP）＝2∠AOB＝2×60°＝120°，故答案为：120°．②∵点C和点P关于OA对称．∴∠AOC＝∠AOP，∵点P关于OB对称点是D，∴∠BOD＝∠BOP，∴∠COD＝∠AOC+∠AOP+∠BOP+∠BOD＝2（∠AOP+∠BOP）＝2∠AOB＝2α．（2）根据轴对称的性质，可知CM＝PM，DN＝PN，所以△PMN的周长为：PM+PN+MN＝CM+DN+MN＝CD＝4，故答案为：421．（2020秋•宝应县期末）图1、图2、图3都是3×3的正方形网格，每个小正方形的顶点称为格点，A、B、C均为格点．在给定的网格中，按下列要求画图：（1）在图1中，画一条不与AB重合的线段MN，使MN与AB关于某条直线对称，且M、N为格点；（2）在图2中，画一条不与AC重合的线段PQ，使PQ与AC关于某条直线对称，且P、Q为格点；（3）在图3中，画一个△DEF，使△DEF与△ABC关于某条直线对称，且D、E、F为格点，符合条件的三角形共有　4　个．【分析】根据要求利用轴对称的性质作出图形即可（答案不唯一）．【解析】（1）如图，线段MN即为所求作（答案不唯一）．（2）如图，线段PQ即为所求作（答案不唯一）．（3）如图，△DEF即为所求作（答案不唯一），符合条件的三角形有4个．故答案为：4．22．（2019秋•赵县期末）如图，已知点O是∠APB内的一点，M，N分别是点O关于PA、PB的对称点，连接MN，与PA、PB分别相交于点E、F，已知MN＝6cm．（1）求△OEF的周长；（2）连接PM、PN，若∠APB＝a，求∠MPN（用含a的代数式表示）；（3）当∠a＝30°，判定△PMN的形状，并说明理由．【分析】（1）根据轴对称的性质得到EM＝EO，FN＝FO，根据三角形的周长公式计算即可；（2）根据轴对称的性质得到∠MPA＝∠OPA，∠NPB＝∠OPB，根据角的和差关系解答；（3）根据等边三角形的判定定理证明．【解析】（1）∵M，N分别是点O关于PA、PB的对称点，∴EM＝EO，FN＝FO，∴△OEF的周长＝OE+OF+EF＝ME+EF+FN＝MN＝6cm；（2）连接OP，∵M，N分别是点O关于PA、PB的对称点，∴∠MPA＝∠OPA，∠NPB＝∠OPB，∴∠MPN＝2∠APB＝2a；（3）∵∠a＝30°，∴∠MPN＝60°，∵M，N分别是点O关于PA、PB的对称点，∴PM＝PO，PN＝PO，∴PM＝PN，∴△PMN是等边三角形．23．（2019秋•江都区校级月考）如图，已知∠AOB＝a外有一点P，画点P关于直线OA的对称点P′，再作点P′关于直线OB的对称点P″．（1）试猜想∠POP″与a的大小关系，并说出你的理由．（2）当P为∠AOB内一点或∠AOB边上一点时，上述结论是否成立？【分析】（1）根据轴对称的性质画出图形，再由HL定理得出△DOP′≌△DOP，△EOP″≌△EOP′根据全等三角形的性质即可得出结论；（2）根据题意画出图形，同（1）可得出结论．【解析】（1）猜想：∠POP″＝2α．理由：如图1，在△DOP′与△DOP中∵OP=OP' OD=OD，∴△DOP′≌△DOP．同理可得，△EOP″≌△EOP′∴∠POP″＝2α；（2）成立．如图2，当点P在∠AOB内时，∵同（1）可得，△DOP′≌△DOP，EOP″≌△EOP′，∴∠POD＝∠P′OD，∠EOP″＝∠EOP′，∴∠POP″＝∠P′OP″﹣∠POP′＝3α﹣α＝2α．如图3，当点P在∠AOB的边上时，∵同（1）可得△EOP″≌△EOP，∴∠POP″＝2α．24．（2020秋•朝阳区校级期中）如图，△ABC中，∠ABC＝45°，点A关于直线BC的对称点为P，连接PB并延长．过点C作CD⊥AC，交射线PB于点D．（1）如图①，∠ACB为钝角时，补全图形，判断AC与CD的数量关系：　AC＝CD　；（2）如图②，∠ACB为锐角时，（1）中结论是否仍成立，并说明理由．【分析】（1）结论：AC＝CD．想办法证明，AC＝CP，CD＝CP即可．（2）结论不变，证明方法类似（1）．【解析】（1）结论：AC＝CD．理由：如图①中，设AB交CD于O，∵A，P关于BC对称，CA＝CP，∴∠A＝∠P，∠ABC＝∠CBP＝45°，∴∠ABP＝∠ABD＝90°，∵AC⊥CD，∴∠ACO＝∠DBO＝90°，∵∠AOC＝∠DOB，∴∠D＝∠A，∴∠D＝∠P，∴CD＝CP，∴AC＝CD．故答案为：AC＝CD．（2）结论不变．。

浙教版八年级数学上册2.1图形的轴对称同步练习含答案

2.1 图形的轴对称（巩固练习）姓名班级第一部分1、图中所示的几个图形是国际通用的交通标志，其中不是轴对称图形的是()2、如图，用数学的眼光欣赏这个蝴蝶图案，它的一种数学美体现在蝴蝶图案的()A．轴对称性；B．用字母表示数；C．随机性D．数形结合3、如图，∠A＝30°，∠C′＝60°，△ABC与△A′B′C′关于直线l对称，则∠B＝_______________.4、如图，在△ABC中，∠C＝90°，点D在AC上，将△BCD沿着直线BD翻折，使点C落在斜边AB上的点E处，DC＝5 cm，则点D到斜边AB的距离是______．5、在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有种.第二部分1、如图，由大小相同的小正方形组成的L形图中，请你用三种方法分别在下图中添画一个小正方形使它成为轴对称图形．2、如图是一个轴对称图形，请再画上一个圆，使它还是一个轴对称图形．3、如图，要在河边修建一个水泵站，分别向张村A和李庄B送水．水泵应建在什么地方，可使所用的水管最短？请在图中设计出水泵站的位置。

5、如图所示，∠ABC内有一点P，在BA、BC边上各取一点P1、P2，使△PP1P2的周长最小．参考答案第一部分4、如图，在△ABC中，∠C＝90°，点D在AC上，将△BCD沿着直线BD翻折，使点C落在斜边AB上的点E处，DC＝5 cm，则点D到斜边AB的距离是______．答案 5解析∵BD是折痕，∴△BCD≌△BED，∴∠CBD＝∠ABD，∠BED＝∠C＝90°.∴点D到BC、BA边的距离相等，即DE＝DC＝5.5、在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有种.【解析】13 如图所示：一共有13种做法.第二部分1、如图，由大小相同的小正方形组成的L形图中，请你用三种方法分别在下图中添画一个小正方形使它成为轴对称图形．解：如图所示：2、如图是一个轴对称图形，请再画上一个圆，使它还是一个轴对称图形．解：如下图：3、如图，要在河边修建一个水泵站，分别向张村A和李庄B送水．水泵应建在什么地方，可使所用的水管最短？请在图中设计出水泵站的位置。

初二数学培优专题(5)——折叠问题(答案详解)

折叠问题(一)正方形内的十字架结构结论1：在正方形ABCD中，E、F、G、H分别为AB、CD、BC、AD边上的点，若EF⊥GH，则GH=EF【例1】如图，将边长为4的正方形纸片ABCD折叠，使得点A落在CD的中点E处，折痕为FG，点F 在AD边，求折痕FG的长；【变式2】如图,将边长为的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.(1)求线段CN的长;(2)求以线段MN为边长的正方形的面积;(3)求线段AM的长度.（二）折痕垂直于对称点的连线结论：折痕上的点到对应点距离相等【例2】如图，在矩形ABCD 中，AB=4，AD=3，将矩形折叠使得点D 与BC 上的点E 重合，折痕分别交AB 、CD 于点G 、F ，若BE=1，求AG 的长．【变式1】如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B'处,点A 对应点为A',且,则AM 的长是______________．【变式2】（2016年山东威海中考题）如图,在矩形ABCD 中,4AB = ,6BC = ,点E 为BC 的中点,将ABE ∆沿AE 折叠,使点B 落在矩形内点F 处,连接CF ,则CF 的长为( )A.95 B.125 C.165 D.185(三) 折叠中动点轨迹与最值【例3】(2015四川自贡)如图，在矩形ABCD 中，4AB = ，6AD = ，E 是AB 边的中点，F 是线段BC 上的动点，将EBF ∆沿EF 所在直线折叠得到'EB F ∆，连接'B D ，则'B D 的最小值是（）。

A. 2B. 6C. 2-D.4【变式】（2014成都）如图，在边长为2的菱形ABCD 中，60A ∠=︒ ，M 是AD 边的中点，N 是AB 边上的一动点，将AMN ∆ 沿MN 所在直线翻折得到'A MN ∆，连接'A C ，则'A C 长度的最小值是_____ 。

浙教版八年级数学上册《2.1轴对称图形》同步练习题-带答案

浙教版八年级数学上册《2.1轴对称图形》同步练习题-带答案一、选择题1．如图，正八边形是轴对称图形，对称轴可以是直线（）A．a B．b C．c D．d2．下列轴对称图形中，对称轴条数最多的是（）A．等边三角形B．菱形C．等腰梯形D．圆3．苏州的景色非常优美，其中以苏州园林最具代表性.苏州园林溯源于春秋，发展于晋唐，繁荣于两宋，全胜于明清，现存五十多处.如图是苏州园林中的一种窗格，下面从窗格图案中提取的几何图形，不一定是轴对称图形的是（）A．矩形B．正八边形C．平行四边形D．等腰三角形4．小颖的爸爸要在某条街道l上修建一个奶站P，向居民区A，B提供牛奶，要使点P到A，B的距离之和最短，则下列作法正确的是（）A．B．C．D．5．我们在观看台球比赛时，发现选手们常常会用反弹的技巧击打目标球．在此过程中，撞击路线与桌边的夹角等于反射路线与桌边的夹角，如图1，∠1=∠2如图2，建立平面直角坐标系xOy，已知A球位于点(1，2)处，B球位于点(6，1)处．现击打A球，使A球向桌边的整点位置（横纵坐标均为整数，球洞位置不可反弹）撞击，若A球最多在台球桌边反弹两次后击中B球，则满足条件的桌边整点有（）A．1个B．2个C．3个D．4个6．如图，在△ABC中∠ABC=60°，BD平分∠ABC，点E是BC的中点，点P是BD上一动点，连接PC，PE若BC=6，AB=10，S△ABC=15√3，则PC+PE的最小值是（）A．3√3B．6C．5√3D．107．如图，在3×3的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的△ABC为格点三角形，在图中最多能画出（）个格点三角形与△ABC成轴对称.A ．6B ．5C ．4D ．38．如图，在△ABC 中，AB ＝AC ．在AB 、AC 上分别截取AP 、AQ ，使AP ＝AQ ．再分别以点P ，Q 为圆心，以大于12PQ 的长为半径作弧，两弧在∠BAC 内交于点R ，作射线AR ，交BC 于点D ．已知BC ＝5，AD=6．若点M 、N 分别是线段AD 和线段AC 上的动点，则CM+MN 的最小值为（）A ．4B ．5C ．6013D ．2√69．如图，∠AOB=20°，点M 、N 分别是边OA 、OB 上的定点，点P 、Q 分别是边OB 、OA 上的动点，记∠MPQ= α ，∠PQN= β ，当MP+PQ+QN 最小时，则 β−α 的值为（）A ．10°B ．20°C ．40°D ．60°10．如图，在 Rt ΔABC 中∠ACB =90°，AC =3，BC =4，AB =5，AD 平分 ∠CAB 交 BC 于点D ，E ，F 分别是 AD ， AC 边上的动点，则 CE +EF 的最小值为（）A ．245B ．125C ．65D ．185二、填空题11．如图，桌球的桌面上有M ，N 两个球，若要将M 球射向桌面的一边，反弹一次后击中N 球，则A ，B ，C ，D ，4个点中，可以反弹击中N 球的是点.12．如图，点P 为∠AOB 内一点，分别作出P 点关于OB 、OA 的对称点P 1，P 2，连接P 1P 2交OB 于M ，交OA 于N ，若∠AOB =40°，则∠MPN 的度数是．13．如图，在△ABC 中AB =4，AC =6，BC =7，EF 垂直平分BC ，点D 为直线EF 上的一个动点，则△ABD 周长的最小值是。

八年级数学《轴对称图形》培优专题训练(含答案)

八年级数学《轴对称图形》培优专题训练(含答案)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN《轴对称图形》培优专题训练1 运用线段的垂直平分线性质解题我们知道，线段的垂直平分线上的点，到线段两端的距离相等;反过来，到线段两端的距离相等的点，在线段的垂直平分线上.运用线段的垂直平分线的性质，我们可以解决一些计算题和证明题.经典例题如图，P 为AOB ∠的平分线OC 上任意一点，PE OA ⊥于E ，PF OB ⊥于F ，求证:OP 是EF 的垂直平分线.解题策略因为OP 为AOB ∠的平分线，PE OA ⊥，PF OB ⊥，所以PE PF =(角平分线上的点，到角两边的距离相等)，因此P 在EF 的垂直平分线上(到线段两端距离相等的点，在线段的垂直平分线上). 在Rt OEP ∆和Rt OFP ∆中，,PE PF OP OP ==，所以OEP OFP ≅∆且OE OF =，所以O 在EF 的垂直平分线上(到线段两端距离相等的点，在线段的垂直平分线上).所以OP 是EF 的垂直平分线.画龙点睛因为线段是轴对称图形，而且线段的垂直平分线是线段的对称轴.我们常利用线段的轴对称性质来证明线段的相等，也利用线段轴对称的判定方法来确定线段的垂直平分线.举一反三1. 如图，等腰ABC ∆中，,20AB AC A =∠=︒.线段AB 的垂直平分线交AB 于D ，交AC 于E ，连结BE ，则CBE ∠等于( ).(A) 80° (B)70° (C)60° (D ) 50°2.如图，在ABCAE=cm，ABD∆中，DE是AC的垂直平分线，6∆的周长为20cm，求△ABC∆的周长.3.如图，在ABC∠=︒，AD是BAC∠的平分线，EF垂直平ABC∆中，45分AD，交BC的延长线于F，试求CAF∠的大小.融会贯通4.如图，Rt ABC∠=︒，A B∆中，90ACB∠<∠，CM是斜边AB的中线，将ACM∆沿直线CM折叠，点A落在点D处，如果CD恰好与AB垂直，求A∠的大小.2 与轴对称有关的作图本节包含两种类型的问题:一类是作出一个图形的关于一条直线的轴对称图形，此类问题比较简单;另外一类问题是用作轴对称图形的方法来解题，这类问题就比较复杂了.经典例题如图1，有一张矩形纸片ABCD，上面画有一个角的两边m、n，但是这个角的顶点P在纸片的外部，试在纸片上作出P∠的平分线来.解题策略作法:(1)在纸片上作直线h m⊥;作n关于h的对称直线'n，'n与m交于'P;(2)作'P∠的平分线'p(3)作'p关于h的对称直线p.则p所在的直线也是P∠的平分线所在的直线.画龙点睛我们将例题这种类型的题称为不可及点作图问题，这个利用轴对称变换来解答的作法是解决不可及点作图问题的一般方法.举一反三1.如图，已知AOB∠与线段CD，求作一点P，使点P到CD的两端点距离相等，且到AOB∠两边的距离也相等.2.如图①，在网格中有两个全等的图形(阴影部分)，用这两个图形拼成轴对称图形，试分别在图②、③中画出两种不同的拼法.3.如图所示，把一个正方形三次对折后沿虚线剪下，则得到的图形是( ).融会贯通4. 如图，已知三点,,A B C 不在同一直线上，求作:(1)直线1l ，使A B 、两点关于直线1l 对称;(2)直线2l ，使A C 、两点关于直线2l 对称;(3)直线3l ，使B C 、两点关于直线3l 对称.观察1l 、 2l 、 3l ，你从中可以发现什么规律?3 运用轴对称方法求最值有一类几何极值问题，可以运用轴对称的方法来解决，本节我们就来介绍这种方法.经典例题如图1，已知线段AB 和直线EF (线段AB 和直线EF 不相交)，在直线上求一点C ，使ABC 周长最短.图 1解题策略如图2，作点A 关于EF 的对称点'A ，连结'A B 交EF 于点C ，则点C 为所求的点，此时，ABC ∆的周长最短.事实上，如'C 是EF 上异于C 的另外一点，如图3，连结'AC 、''A C ，由轴对称的性质有''AC A C =，'''AC A C =，于是'AC CB A C CB +=+''''A B A C C B =<+ ''AC BC =+，显然有ABC ∆的周长<'ABC ∆的周长.也就是说ABC ∆的周长最短.画龙点睛1. 利用轴对称的方法，常可以化折线段为直线段，再结合“两点之间线段最短”的性质，就可以解决一类几何最值问题了.2. 我们容易证得，当AC BC +最短时，ACE BCF ∠=∠.这是一种最短线的等角性质，有一类台球问题也可以仿此解答.举一反三1.如图，已知直线MN和在MN异侧的两点A、B，在MN上求作一点-最大.P，使线段PA PB2.如图，已知AOB∠内一定点P.试在OA、OB上各找一点M、N.使∆周长最短.PMN3.如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是 .融会贯通4.在一平直河岸l同侧有A、B两个村庄，A、B到l的距离分别是3km和2km，AB aa>.现计划在河岸l上建一抽水站P，用输水管向两=km(1)个村庄供水.方案设计某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图，设该方案中管道长度为1d ，且1d PB BA =+(其中BP l ⊥于点P );图2是方案二的示意图，设该方案中管道长度为2d ，且2d PA PB =+ (其中点'A 与点A 关于l 对称，'A B 与l 交于点P ).观察计算(1)在方案一中，1d = km(用含a 的式子表示); (2)在方案二中，组长小宇为了计算2d 的长，作了如图3所示的辅助线，请你按小宇同学的思路计算，2d = km(用含a 的式子表示). 探索归纳 (1)①当4a =时，比较大小:1d 2d (填“>”、“=”或“<”); ②当6a =时，比较大小: 1d 2d (填“>”、“=”或“<”); (2)请你参考下面方框中的方法指导，就a (当1a >时)的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案一还是方案二? 方法指导当不易直接比较两个正数m 与n 的大小时可以对它们的平方进行比较: 因为，22()()m n m n m n -=+-，0m n +> 所以22()m n -与()m n -的符号相同. 当220m n ->时，0m n ->，即m n >；当220m n -=时，0m n -=，即，m n -；当220m n -<时，0m n -<，即m n <4 等腰三角形的性质与判定经典例题如图所示，若,,AB AC BG BH AK KG ===，则BAC ∠的度数为( )(A)30° (B)32° (C)36° (D)40°解题策略设BAC x ∠=︒.则由AB AC =可得ABC ACB ∠=∠，所以1802x ABC ︒-︒∠=.由BG BH =可得G H ∠=∠，又2ABC G H G ∠=∠+∠=∠，所以1804x G ︒-︒∠=.由AK KG =得A G ∠=∠，即1804x x ︒-︒︒=.解得36x =，即36BAC ∠=︒，应选C. 画龙点睛图中的几个与等腰三角形相关的角都可以用BAC ∠的代数式来表示，因此可以建立关于BAC ∠的方程，来解决此类问题. 举一反三1. 如图，ABC ∆'中，AB AC =，36A ∠=︒，BD 、CE 分别是角平分线，且相交于F ，则图中的等腰三角形有( )个.(A) 6 (B)7 (C)8 (D)92. 如图，在ABC ∆中，点E 在AB 上，点D 在BC 上，BD BE =，BAD BCE ∠=∠，AD 与CE 相交于点F ，试判断AFC ∆的形状，并说明理由.3. 如图钢架中，焊上等长的13根钢条来加固钢架，若11223AP PP P P ===…1314P P = 14P A =，求A ∠的度数.融会贯通4. 如图，ABC ∆中，AB AC =，36A ∠=︒.仿照图1，请你再设计两种不同的分法，将ABC ∆分割成3个三角形，使得每个三角形都是等腰三角形(图2、图3供画图用，作图工具不限，不要求写出画法，不要求证明;要求标出所分得的每个等腰三角形三个内角的度数).5 等腰三角形中的辅助线我们知道，等腰三角形是以底边上的高所在直线为对称轴的轴对称图形，故在解与等腰三角形有关的问题时，常要利用这个性质. 经典例题如图1，从等腰直角ABC ∆的直角顶点C 向中线BD 引垂线，交BD 于F ，交AB 于E ，连结DE .求证: CDF ADE ∠=∠.图 1解题策略注意到CDF ∠在BCD ∆中，ADE ∠在ADE ∆中，且CD AD =，可设法在BCD ∆中构造一个与ADE ∆全等的三角形，因45A ∠=︒，可作BCA ∠的平分线CG (即AB 边上的高).如图2，作BCA ∠的平分线交BD 于G ，因为,45BC AC BCG A =∠=∠=︒又90CBG CDF ACE ∠=︒-∠=∠ 所以BCG CAE ∆≅∆ 所以CG AE =在CDG ∆和ADE ∆中，因为,45,CD AD DCG A CG AE =∠=∠=︒=所以CDG ADE ∆≅∆，因此CDF ADE ∠=∠. 画龙点睛等腰三角形是轴对称图形，作出它的对称轴即底边上的高来解题，是一种常见的作辅助线的方法. 举一反三1. 如图，在ABC ∆中，若AB AC =，AD 为BC 边上的高，E 为AC 边上的一点，且有AE AD =，已知12EDC ∠=︒，则有B ∠= .2. 如图，已知点C 、D 在ABE ∆的边BE 上，BC ED =，AB AE =，求证:AC AD =.3. 如图，在等腰Rt ABC ∆，90C ∠=︒，8AC =，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且保持AD CE =.连结DE 、DF 、EF .在此运动变化的过程中，下列结论: ①DFE ∆是等腰直角三角形;c. ②四边形CDFE 的面积保持不变; ③AD BE DE +>. 其中正确的结论是( ).(A)①②③ (B)① (C)② (D) ①②融会贯通4.如图，在ABC∆内一点，且=，O为ABC∠=︒，AB ACBAC∆中，80∠=︒，求BAO∠的度数.OCA10OBC∠=︒，206 运用等腰三角形的性质解题当一个几何问题中出现了等腰三角形时，要充分利用等腰三角形的性质或者构造一个等腰三角形来解题.经典例题如图，过ABC∆的顶点A，作直线AE与B∠的内角平分线垂直相交于点∠的内角平分线相交于点P.过P作直线与底边E，与BC相交于点N，且与C=+. BC平行，且与AB交于Q，与BE交于M，与AC交于R，求证:QR AQ CR解题策略因为//∠=∠=∠，于是∠的平分线，所以RCP NCP RPC RP BC，CP是ACB∠=∠.PR CR=.同理QMB ABE因BE AN ⊥，90EAB ABE ∠=︒-∠，90EPQ EMP ∠=︒-∠.但ABE QMB ∠=∠EMP =∠，于是EAB EPQ ∠=∠，故AQ PQ =.所以QR QP PR AQ CR =+=+. 画龙点睛在题目中出现了过角平分线上一点而又和角的一边平行的直线这样的基本图形时，就一定要注意到图形中出现了等腰三角形，利用这个等腰三角形进行计算或者证明，是解答此类问题的关键. 举一反三1. 如图，在ABC ∆中，B ∠与C ∠的平分线相交于点D ，过点D 作//EF BC ，分别交AB 、AC 于点E 、F ，14AB =，20BC =，16AC =，那么，AEF ∆的周长为( ) (A) 34 (B)38 (C)30 (D)252. 如图AB AC =，CD AB ⊥于D ，BE AC ⊥于E ，BE 与CD 相交于点O .(1)求证:AD AE =; (2) 连结OA 、BC ，试判断直线OA 、BC 的关系并说明理由.3. 如图，在凸五边形ABCDE 中，B E ∠=∠，C D ∠=∠，BC DE =，M 为CD 的中点.求证: AM CD ⊥.融会贯通4. 如图，在ABC ∆，100A ∠=︒，AB AC =，BE 是ABC ∠的平分线.求证:AE BE BC +=.7 等边三角形我们知道，等边三角形是最特殊的等腰三角形，它的三角相等，三边相等，有三条对称轴.常用“有一个角是60°的等腰三角形是等边三角形”来判定一个三角形是等边三角形.经典例题如图1所示，已知ABC∆为等边三角形，D是BC线上一点，再延长BA到=.=，求证:CE DEE，使AE BD解题策略如图2，延长BD到F，使DF AB=，连结EF.因为ABC∆为等边三角形，所以==AB BC AC∠=∠=∠=︒B BAC ACB60又因为BA AE BD DF+=+，即BE BF=所以△BEF是等边三角形.因此∠=︒=∠，EF BE60F B=从而有EDF ECB∆≅∆所以CE DE=画龙点睛当题目中出现了含有60°的三角形时，常可构造一个等边三角形，然后从等边三角形中寻找新的结论.在本题中，是通过补图，把原图形补成一个等边三角形，得出有关三角形全等，从而证明线段的相等.举一反三1.如图，在等边ABC∆中，D是AC的中点，延长BC到点E，使AB=cm.求BE的长.=，10CE CD2.如图，ABC∆是等边三角形，点D、E、F分别是线段AB、BC、CD 上的点.(1)若AD BE CF==，问DEF∆是等边三角形吗?试证明你的结论;(2)若DEF==成立吗?试证明你的结论.∆是等边三角形，问AD BE CF3. 如图，在等边ABC ∆的边AC 的延长线上取一点E ，以CE 为边作等边CDE ∆，使它与ABC ∆位于直线AE 的同一侧，点M 为线段AD 的中点，点N 为线段BE 的中点，求证: CNM ∆为等边三角形.融会贯通4. 数学课上，李老师出示了如下框中的题目.小敏与同桌小聪讨论后，进行了如下解答: (1)特殊情况，探索结论.当点E为AB的中点时，如图1，确定线段AE与DB的大小关系.请你直接写出结论:AE DB (填“>”、“<”或“=”).(2)特例启发，解答题目.解:题目中，AE与DB的大小关系是: AE DB (填“>”、“<”或“=”).理由如下:如图2，过点E作//EF BC，交AC于点F，(请你完成以下解答过程)(3)拓展结论，设计新题.在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED EC=.若ABC∆的边长为1，2AE=，求CD的长(请你直接写出结果).8 含30°角的直角三角形含30°角的直角三角形可以看作是一个等边三角形的一半，我们可以证明，在这种三角形中，30°角所对的直角边是斜边的一半.经典例题如图，在ABC∠=︒，AC的垂直平分线EF交ACBAC∆中，AB AC=，120于点E，交BC于F.求证:2=.BF CF解题策略如图，连结AF .因为EF 为AC 的垂直平分线，所以AF FC =(线段垂直平分线上的点到线段两端的距离相等)，从而有C FAC ∠=∠又AB AC =，120BAC ∠=︒，所以1(180120)302B C ∠=∠=︒-︒=︒ /因此30BAC ∠=︒，90BAF ∠=︒，于是2BF AF =(直角三角形中30°角的对边等于斜边的一半)，所以2BF CF =. 画龙点睛在题目条件中发现有含30°角的直角三角形时，要注意利用30°角所对的直角边是斜边的一半的性质来解题. 举一反三1. 如图，在Rt ABC ∆中，90ACB ∠=︒，AB 的垂直平分线DE 交于BC 的延长线于F .若30F ∠=︒，1DE =，则EF 的长是( )2.如图所示，30∠=︒，OC平分AOB∠，P为OC上任意一点，AOBOD= cm，求PE的长.⊥于E.若4PD OA交OB于D，PE OA//3.月如图，在ABC=，过线段BC(不包括端点)上一点D作∆中，AB ACBC的垂线，交BA延长线于P，交AC于Q.(1)判断APQ∆的形状，并证明你的结论;(2)若60=，求y与x之间的函数=，BP y==，设CD xAB ACB∠=︒，2关系式，并写出x的取值范围.融会贯通4.已知MAN∠∠，AC平分MAN(1)如图1，若120+=;∠=∠=︒，请说明AB AD ACMAN∠=︒，90ABC ADC(2)如图2，若120∠+∠=︒，则(1)中的结论是否仍ABC ADCMAN∠=︒，180然成立?若成立，请说明理由.参考答案1 运用线段的垂直平分线性质解题1. C2. 因为DE是AC的垂直平分线，6AE=cm以212AC AE==cm，AD DC=因为ABD∆的周长为20cm所以20AB BD AD++=(cm)所以20AB BD CD++=(cm)所以ABC∆的周长是201232AB BC AC AB BD CD AC++=+++=+=(cm) 3. 因为AD是BAC∠的平分线所以12∠=∠因为EF垂直平分AD所以FA FD=，FAD FDA∠=∠即21CAF B∠+∠=∠+∠所以45CAF B∠=∠=︒4. 因为CM为Rt ABC∆斜边AB的中线所以CM AM=，A ACM∠=∠ (等边对等角)又由折叠知A D ∠=∠，MCD MCA ∠=∠ 因为CD AB ⊥，即90A MCD MCA ∠+∠+∠=︒ 所以30A ∠=︒2 与轴对称有关的作图1. 如图，作线段CD 的垂直平分线MN ，作AOB ∠的平分线OE ，OE 交MN 于点P ，由作法知点P 既在CD 的垂直平分线上，又在AOB ∠的角平分线上，所以点P 为所求.2. 如图3. C4. 作图略：1l 、 2l 、 3l 交于一点3 运用轴对称方法求最值1. 作点A 关于直线MN 的对称点'A ，连结'A B 并延长交MN 于P ，P 就是所求作的点.证明略.2. 作P 关于OA 的对称点1P ，P 关于OB 的对称点2P ，连结12P P ，与OA 、OB交于M 、N .在OA 、OB 上任取两点'M 、'N ，连结1'PM 、2'P N ，则''PM N ∆的周长1212''''''''PM M N PN PM M N P N PP =++=++>PMN =∆的周长，所以M 、N 为所求的点.3. 如图，球最后落入①球洞.4. 观察计算(1)2a +探索归纳(1)①< ②>(2)222212(2)420d d a a -=+-=-①当4200a ->，即5a >时，22120d d ->，即120d d ->，所以12d d >②当4200a -=，即5a =时，22120d d -=，即120d d -=，所以12d d =③当4200a -<，即5a <时，22120d d -<，即120d d -<，所以12d d <综上可知：当5a >时，选第二方案；当5a =时，选第一方案或第二方案；当15a <<时，选方案一4 等腰三角形的性质与判定1. C2. AFC ∆为等腰三角形，理由如下：在ABD ∆和CBE ∆中，因为BD BE =，BAD BCE ∠=∠，ABD CBE ∠=∠ 所以ABD CBE ∆≅∆ 所以BA BC = 所以BAC BCA ∠=∠ 又因为BAD BCE ∠=∠ 所以DAC ECA ∠=∠ 所以FA FC = 即AFC ∆为等腰三角形3. 设A x ∠=，因为11223AP PP P P ===…14P A = 所以211314A AP P AP P x ∠=∠=∠= 所以2131314122P PP P P P x ∠=∠= 所以3241213113P P P P P P x ∠=∠=……7688977P P P P P P x ∠=∠=所以787AP P x ∠=，877AP P x ∠=在78AP P ∆中，7887180A AP P AP P ∠+∠+∠=︒ 即77180x x x ++=︒ 解得12x =︒，即12A ∠=︒ 4. 作法：5 等腰三角形中的辅助线1. 66°2. 如图，作AH BE ⊥于H .因为AB AE =所以H 为BE 中点(等腰三角形“三线合一”). 又BC ED = 所以CH HD = 又AH CD ⊥ 所以AC AD =(垂直平分线上的点到线段两端点距离相等). 3. A4. 不难算得50ABC ACB ∠=∠=︒，40ABO ABC OBC ∠=∠-∠=︒，30BCO ACB OCA ∠=∠-∠=︒作AE BC ⊥于E ，延长CO 交AE 于D ，连结BD ，则40BAE CAE ∠=∠=︒ 在ADB ∆和ADC ∆中， AB AC =，BAE CAE ∠=∠，AD AD = 所以ADB ADC ∆≅∆ 所以20ABD ACD ∠=∠=︒ 于是20DBO ABO ABD ∠=∠-∠=︒又9030120ADO DEC DCE ∠=∠+∠=︒+︒=︒，120ADB ADO ∠=∠=︒ 于是360120120120CDB ∠=︒-︒-︒=︒在ADB ∆和ODB ∆中，120ABD DBO ∠=∠=︒，120ADB ODB ∠=∠=︒，BD BD =所以ADB ODB ∆≅∆从而AD OD =，30OAD DOA ∠=∠=︒ 所以403070BAO BAE DAO ∠=∠+∠=︒+︒=︒6 运用等腰三角形的性质解题1. C2. (1)在ACD ∆和ABE ∆中，因为A A ∠=∠，90ADC AEB ∠=∠=︒，AB AC = 所以()ACD ABE AAS ∆≅∆所以AD AE =(2)在Rt ADO ∆和Rt AEO ∆中，因为,OA OA AD AE == 所以()ADO AEO HL ∆≅∆ 所以DAO EAO ∠=∠ 即OA 是BAC ∠的平分线又因为AB AC = 所以OA BC ⊥3. 延长BC 、ED 交于F ，连结BE 、AC 、AD 因为BCD EDC ∠=∠ 所以FCD FDC ∠=∠ 从而FC FD = 因为BC DE =所以BC FC DE FD +=+，即FB FE = 于是FBE FEB ∠=∠ 因为ABC AED ∠=∠所以ABC FBE AED FEB ∠-∠=∠-∠ 即ABE AE ∠=∠ 所以AB AE =在ABC ∆和AED ∆中，AB AE =，ABC AED ∠=∠，BC DE = 所以ABC AED ∆≅∆ 所以AC AD =又因为AM 是等腰三角形底边上的中线，于是AM CD ⊥4. 容易求得40C ABC ∠=∠=︒，20ABE CBE ∠=∠=︒ 在BC 上截取BF BE =，连结EF ，则80BEF BFE ∠=∠=︒ 于是40CEF BFE C C ∠=∠-∠=︒=∠所以EF FC =过E 作//EG CB 交AB 于G ，则40AEG AGE ∠=∠=︒于是AE AG =从而BG AB AG AC AE EC =-=-=又GEB EBC ABE ∠=∠=∠故GE GB =于是GE EC =在AGE ∆和FCE ∆中，AGE CEF ∠=∠，GE EC =，AEG C ∠=∠ 所以AGE FCE ∆≅∆所以AE FC =所以AE BE FC BF BC +=+=7等边三角形1. 因为ABC ∆是等边三角形所以10AB AC BC ===cm.又D 是AC 的中点所以152CD AC ==cm ，又CD CE =所以5CE =cm所以15BE BC CE =+=cm.2. (1) DEF ∆是等边三角形，证明如下:因为ABC ∆是等边三角形所以A B C ∠=∠=∠，AB BC CA ==因为AD BE CF ==所以DB EC FA ==因此ADF BED CFE ∆≅∆≅∆所以DF DE EF ==，即DEF ∆是等边三角形(2) AD BE CF ==成立，证明如下:因为DEF ∆是等边三角形所以DF DE EF ==，60FDE DEF EFD ∠=∠=∠=︒因此12120∠+∠=︒因为ABC∆是等边三角形所以60∠=∠=∠=︒A B C因此23120∠+∠=︒所以13∠=∠同理34∠=∠所以ADF BED CFE∆≅∆≅∆因此AD BE CF==3.先证ACD BCE∆≅∆，得CAM CBN∠=∠，BE AD=所以BN AM=，又得ACM BCN∆≅∆所以CM CN∠=∠=，ACM BCN故60∠=∠=︒NCM BCA所以CMN∆为等边三角形.4.(1) =(2) =在等边ABC==∠=∠=∠=︒，AB BC AC ∆中，60ABC ACB BAC因为//EF BC所以AEF ABC∠=∠∠=∠，AFE ACB所以60∠=∠=∠=︒AEF AFE BAC所以AE AF EF==所以AB AE AC AF-=-，即BE CF=因为ABC EDB BED∠=∠+∠∠=∠+∠，ACB ECB FCE 又因为ED EC=所以EDB ECB ∠=∠，BED FCE ∠=∠在DBE ∆和EFC ∆中，ED EC =，DEB ECF ∠=∠，EB FC = 所以()DBE EFC SAS ∆≅∆所以DB EF =所以AE BD =(3)分为四种情况:如图1，因为1,2AB AC AE ===，所以B 是AE 的中点，因为ABC ∆是等边三角形所以1AB AC BC ===，ACE ∆是直角三角形(根据直角三角形斜边的中线等于斜边的一半)所以90ACE ∠=︒，30AEC ∠=︒所以30D ECB BEC ∠=∠=∠=︒，60DBE ABC ∠=∠=︒ 所以180306090DEB ∠=︒-︒-︒=︒，即DEB ∆是直角三角形所以22BD BE ==(30°所对的直角边等于斜边的一半)，即123CD =+= 如图2，过A 作AN BC ⊥于N ，过E 作EM CD ⊥于M . 因为ABC ∆是等边三角形，EC ED = 所以1122BN CN BC ===，12CM MD CD ==，//AN EM 所以BAN BEM ∆≅∆ 所以AB BN AE MN= 因为ABC ∆边长是1，2AE =所以1MN = 所以11122CM MN CN =-=-=所以21==CD CM如图3，因为(120)∠>∠∠=︒ECD EBC EBC而ECD∆不符合三角形内角和定理∠不能大于120︒，否则EDC所以此时不存在EC ED=如图4.因为EDC ABC∠<∠∠<∠，ECB ACB又因为60∠=∠=︒ABC ACB所以ECD EDC≠，所以此时情况不存在，故CD的长∠>∠，即此时ED EC是3或1.8 含30°角的直角三角形1.连结AF，AB的垂直平分线DE交于BC的延长线于F所以AF BF=因为FD AB⊥所以30∠=∠=︒-︒=︒AFD BFDB FAB∠=∠=︒，903060因为90∠=︒ACB所以30∠=︒-︒=︒FACBAC∠=︒，603030因为1DE=所以22==AE DE因为30∠=∠=︒FAE AFD所以2==，故选B.EF AE2.如图，过点P作PF OB⊥于F因OC平分AOB⊥∠，PE OA⊥，PF OB所以PE PF=(角平分线上的点到角两边距离相等) 因OC平分AOB∠所以AOC BOC∠=∠又因//PD OA所以DPO AOC∠=∠(两直线平行内错角相等) 因此DOP DPO∠=∠ (等量代换)所以OD PD =(等角对等边)因//PD OA所以PDF AOB ∠=∠ (两直线平行，同位角相等)，即30PDF ∠=︒ 在Rt PDF ∆中，30PDF ∠=︒ 所以12PF PD =(直角三角形中，30︒角所对的直角边等于斜边的一半) 因此11222PF PD OD ===cm 从而2PE PF ==cm.3. (1)等腰三角形.证明如下:因为PD BC ⊥所以90B P ∠+∠=︒，90C DQC ∠+∠=︒因为AB AC =所以B C ∠=∠因此P DQC ∠=∠因为DQC AQP ∠=∠所以P AQP ∠=∠因此AP AQ =(2)42(01)y x x =-<<4. (1)因为AC 平分MAN ∠，120MAN ∠=︒所以60CAB CAD∠=∠=︒因为90ABC ADC∠=∠=︒所以30ACB ACD∠=∠=︒所以12 AB AD AC ==所以AB AD AC+=(2)成立.过点C作CE AM⊥，CF AN⊥，垂足分别为点E、F 因为AC平分MAN∠所以CE CF=所以180ABC ADC∠+∠=︒，180CDE ADC∠+∠=︒所以CDE ABC∠=∠因为90CED CFB∠=∠=︒所以CED CFD∆≅∆所以ED FB=所以AB AD AF BF AE ED AF AE+=++-=+由(1)知AF AE AC+=所以AB AD AC+=。

八年级数学上册轴对称解答题(培优篇)(Word版含解析)

八年级数学上册轴对称解答题（培优篇）（Word版含解析）一、八年级数学轴对称解答题压轴题（难）1.如图1, ZiABC 中，AB=AC・ ZBAC = 905, D、E 分别在BC、AC 边上，连接AD、BE 相交于点F,且ZCAD =丄ZABE.2⑵如图2,连接CF,若EF = EC,求ZCFD的度数：(3)如图3,在⑵的条件下,若AE = 3,求BF的长.【答案】(1)答案见详解：(2)45。

，(3)4.【解析】【分析】(1)设ZCAD二x,则ZABE=2x, ZBAF二90° -x, ZAFB=180° -2x-(90° -x)= 90° -x,进而得到ZBAF二ZAFB,即可得到结论：(2)由ZAEB=90°-2x t进而得到ZEFC= (90°-2x) +2=45。

-x,由BF=AB,可得：ZEFD=ZBFA=90° 根据ZCFD=ZEFD-ZEFC> 即可求解；⑶设EF=EC二x,则AOAE+EC二3+x・可得BE二BF+EF=3+x+x=3+2x,根据勾股左理列出方程，即可求解.【详解】(1)设ZCAD二x,1VZCAD=-ZABE, ZBAC=90S2AZABE=2x, ZBAF=90° -x,V ZABE+ZBAF+ZAFB=180° ,A ZAFB=180° -2x-(90° ・x)= 90° %AZBAF=ZAFB t•••BF = AB；VAB=AC,ABF = AC：(2)由(1)可知：ZCAD二x, ZABE二2x, ZBAC=90^,•••ZAEB=90°-2x,VEF = EC,AZEFC=ZECF,•/ Z EFC+ Z ECF= ZAEB=90°-2x,AZEFC= (90°-2x) -2=45° -x,VBF=AB,AZBFA=ZBAF=(180a -ZABE)-s-2=(180° -2x)-s-2=90° -x,AZEFD=ZBFA=90° ・x,A ZCFD=ZEFD-ZEFC=(90° -x) -(45。

专题21图形的轴对称-2021-2022学年八年级数学上(解析版)【浙教版】

2021-2022学年八年级数学上册尖子生同步培优题典【浙教版】专题2.1图形的轴对称姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2021•拱墅区二模）在下列运动图形的简笔画中，可以看作轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念求解．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．【解析】A．不是轴对称图形，不合题意；B．不是轴对称图形，不合题意；C．不是轴对称图形，不合题意；D．是轴对称图形，符合题意；故选：D．2．（2021•西湖区校级二模）美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（）A．B．C．D．【分析】利用轴对称图形的定义进行解答即可．【解析】A、不是轴对称图形，故此选项不合题意；B、不是轴对称图形，故此选项不合题意；D、不是轴对称图形，故此选项不合题意；故选：C．3．（2021•上城区一模）下列图片属于轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解析】A、不是轴对称图形，故此选项不合题意；B、是轴对称图形，故此选项符合题意；C、不是轴对称图形，故此选项不合题意；D、不是轴对称图形，故此选项不合题意；故选：B．4．（2020秋•南浔区期末）自2019年10月1日起，湖州正式施行“垃圾分类”，下面是垃圾分类指引标志图片，图片上有图案和文字说明．其中的图案是轴对称图形的是（）A．B．C．D．【分析】利用轴对称图形定义进行解答即可．【解析】A、不是轴对称图形，故此选项不合题意；C、是轴对称图形，故此选项符合题意；D、不是轴对称图形，故此选项不合题意；故选：C．5．（2020秋•鼓楼区校级期中）小明从镜中看到电子钟示数，则此时时间是（）A．12：01B．10：51C．11：59D．10：21【分析】根据镜面对称的性质，在平面镜中的像与现实中的事物恰好顺序颠倒，且关于镜面对称即可得出答案．【解析】此时实际时间是10：21．故选：D．6．（2020春•常德期末）如图是小明在镜子中看到的钟表的图象，此时的真实时间是（）A．4：40B．4：20C．7：40D．7：20【分析】根据镜面实质上是无数对对应点的对称，连接对应点的线段与镜面垂直并且被镜面平分解答即可．【解析】根据镜面对称的性质可得，真实时间是4：40，故选：A．7．（2019秋•涞水县期末）如图，在△ABC中，∠B＝33°，将△ABC沿直线m翻折，点B落在点D的位置，则∠1﹣∠2的度数是（）A．33°B．56°C．65°D．66°【分析】由折叠的性质得到∠D＝∠B，再利用外角性质即可求出所求角的度数．【解析】如图，由折叠的性质得：∠D＝∠B＝33°，根据外角性质得：∠1＝∠3+∠B，∠3＝∠2+∠D，∴∠1＝∠2+∠D+∠B＝∠2+2∠B＝∠2+66°，∴∠1﹣∠2＝66°．故选：D．8．（2020•天河区一模）如图，将△ABC沿过边上两点D，E的直线折叠后，使得点B与点A重合．若已知BE＝4cm，DE＝3cm，则△ABC的周长与△ADC的周长的差为（）A．4cm B．5cm C．8cm D．10cm【分析】由折叠的性质得AD＝BD，BE＝AE＝4，△ABC的周长﹣△ADC的周长＝AB+BC+AC﹣AC﹣CD ﹣AD＝AB，即可得出结果．【解析】∵将△ABC沿直线DE折叠后，使得点B与点A重合，∴AD＝BD，BE＝AE＝4，∴AB＝BE+AE＝4+4＝8，∴△ABC的周长﹣△ADC的周长＝AB+BC+AC﹣AC﹣CD﹣AD＝AB+BD﹣AD＝AB＝8（cm），故选：C．9．（2019秋•润州区校级月考）如图是一个经过改造的规格为4×7的台球桌面示意图，图中四个角上的阴影部分分别表示四个入球孔，如果一个球按图中所示的方向被击出（球可以经过台球边缘多次反弹），那么球最后将落入的球袋是（）A．1号袋B．2号袋C．3号袋D．4号袋【分析】根据题意，画出图形，由轴对称的性质判定正确选项．【解析】根据轴对称的性质可知，台球走过的路径为：所以球最后将落入的球袋是4号袋，故选：D．10．（2019秋•锡山区期中）如图，四边形ABCD中，AB＝AD，点B关于AC的对称点B′恰好落在CD上，若∠BAD＝110°，则∠ACB的度数为（）A．40°B．35°C．60°D．70°【分析】连接AB'，BB'，过A作AE⊥CD于E，依据∠BAC＝∠B'AC，∠DAE＝∠B'AE，即可得出∠CAE=12∠BAD，再根据四边形内角和以及三角形外角性质，即可得到∠ACB＝∠ACB'＝90°−12∠BAD．【解析】如图，连接AB'，BB'，过A作AE⊥CD于E，∵点B关于AC的对称点B'恰好落在CD上，∴AC垂直平分BB'，∴AB＝AB'，∴∠BAC＝∠B'AC，∵AB＝AD，∴AD＝AB'，又∵AE⊥CD，∴∠DAE＝∠B'AE，∴∠CAE=12∠BAD＝55°，又∵∠AEC＝90°，∴∠ACB＝∠ACB'＝35°，故选：B．二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2020秋•沂源县期中）等边三角形是一个轴对称图形，它有3条对称轴．【分析】根据轴对称图形和对称轴的概念求解．【解析】等边三角形是一个轴对称图形，它有3条对称轴．故答案为：3．12．（2020秋•姜堰区期中）小华从镜子中看到身后电子钟的示数如图所示，则此时的时间应是21：05．【分析】平面镜成像的特点：像与物关于平面镜对称，根据这一特点可解答出电子钟示数的像对应的时间．【解析】方法一：将显示的像数字依次左右互换并将每一个数字左右反转，得到时间为21：05；方法二：将显示的像后面正常读数为21：05就是此时的时间．故答案为：21：05．13．（2020秋•鼓楼区校级月考）把一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形是轴对称图形．【分析】如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．【解析】把一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形是轴对称图形．故答案为：折叠．14．（2019秋•阳新县期末）如图，一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔，如果一个球按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入1号球袋．【分析】由已知条件，按照反射的原理画图即可得出结论．【解析】如图，该球最后将落入1号球袋．15．（2021•连云港二模）如图，将矩形纸片的两只直角分别沿EF、DF翻折，点B恰好落在AD边上的点B′处，点C恰好落在边B′F上．若AE＝3，BE＝5，则FC＝4．【分析】由折叠的性质得到B′E＝BE＝5，BF＝B′F，∠BFE═∠EFB′，∠C′FD＝∠DFC，连接BB′，根据线段垂直平分线的性质得到EF⊥BB′，通过三角形全等可证得CF＝AB′＝4．【解析】由题意得：B′E＝BE＝5，BF＝B′F，∠BFE═∠EFB′，∠C′FD＝∠DFC，∴∠EFD＝90°，∴∠3+∠2＝90°，连接BB′，∴EF⊥BB′，∴∠1+∠3＝90°，∴∠1＝∠2，∵AE ＝3，四边形ABCD 是矩形，∴∠A ＝∠C ＝90°，AD ∥BC ，∴∠AB ′B ＝∠1，AB ′=√B′E 2−AE 2=4，∴∠AB ′B ＝∠2，∵CD ＝AB ＝8，在△ABB ′与△CDF 中，{∠A =∠C∠AB′B =∠2AB =CD，∴△ABB ′≌△CDF （AAS ），∴CF ＝AB ′＝4．16．（2019秋•盐都区期中）如图所示，有一个英语单词，四个字母都关于直线l 对称，请依据轴对称的知识，写出这个单词所指的物品书．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，解答即可．【解析】根据轴对称的知识，这个单词是book ，这个单词所指的物品是书，故答案为：书17．（2020秋•句容市期中）如图，桌面上有M 、N 两球，若要将M 球射向桌面的任意一边，使一次反弹后击中N 球，则4个点中，可以瞄准的是 D 点．【分析】利用对称的性质得出M经过的路径，进而得出答案．【解析】如图所示：要将M球射向桌面的任意一边，使一次反弹后击中N球，则4个点中，可以瞄准的是：D．故答案为：D．18．“又是一年三月三，风筝飞满天”．如图是一个燕子形风筝的图案，已知它是轴对称图形，对称轴为AF，则∠AFC的度数为90°，CF与CD的数量关系为CF=12CD．【分析】由已知条件，根据轴对称图形的性质解答．【解析】∵对称轴为AF，C与D的一对对应点，∴AF是CD的垂直平分线，∴∠AFC＝90°，CF=12 CD．∴∠AFC的度数为90°，CF与CD的数量关系为CF=12 CD．故答案为：90°；CF=12 CD．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．找出下列图形中的轴对称图形，并指出它们的对称轴：【分析】根据轴对称图形、对称轴的概念解答．【解析】（1）不是轴对称图形；（2）是轴对称图形，对称轴是六角形对角顶点连线所在的直线．（3）不是轴对称图形，（4）不是轴对称图形，（5）是轴对称图形，对称轴是各边的垂直平分线和对角线所在的直线．20．（2020秋•宝应县月考）在下列各图中分别补一个小正方形，使其成为不同的轴对称图形．【分析】直接利用轴对称图形的性质得出符合题意的答案．【解析】如图所示：21．（2019春•滕州市期末）在下列各图中分别补一个小正方形，使其成为不同的轴对称图形．【分析】直接利用轴对称图形的性质得出符合题意的答案．【解析】如图所示：．22．（2019秋•江城区期中）已知如下图，求作△ABC关于对称轴l的轴对称图形△A′B′C′．【分析】分别作出点B与点C关于直线l的对称点，然后连接AB′，AC′，B′C′．即可得到△ABC 关于对称轴l的轴对称图形△A′B′C′．【解析】23．如图，台球运动中母球P击中桌边的点A，经桌边反弹后击中相邻的另一桌边的点B，再次反弹经过点C（提示：∠P AD＝∠BAE，∠ABE＝∠CBF）．（1）若∠P AD＝32°，求∠P AB的度数；（2）已知∠BAE+∠ABE＝90°，母球P经过的路线BC与P A一定平行吗？请说明理由．【分析】（1）由∠P AD＝∠BAE、∠P AD+∠P AB+∠BAE＝180°结合∠P AD＝32°，即可求出∠P AB的度数；（2）由∠P AD＝∠BAE、∠P AD+∠P AB+∠BAE＝180°可得出∠ABC＝180°﹣2∠ABE，同理可得出∠ABC＝180°﹣2∠ABE，二者相加结合∠BAE、∠ABE互余，即可得出∠P AB+∠ABC＝180°，由“同旁内角互补，两直线平行”即可得出BC∥P A．【解析】（1）∵∠P AD＝32°，∠P AD＝∠BAE，∠P AD+∠P AB+∠BAE＝180°，∴∠P AB＝180°﹣32°﹣32°＝116°．（2）BC∥P A，理由如下：∵∠P AD＝∠BAE，∠P AB＝180°﹣∠P AD﹣∠BAE，∴∠P AB＝180°﹣2∠BAE．同理：∠ABC＝180°﹣2∠ABE．∵∠BAE+∠ABE＝90°，∴∠P AB+∠ABC＝360°﹣2（∠BAE+∠ABE）＝180°．∴BC∥P A．24．（2020秋•宝应县期末）图1、图2、图3都是3×3的正方形网格，每个小正方形的顶点称为格点，A、B、C均为格点．在给定的网格中，按下列要求画图：（1）在图1中，画一条不与AB重合的线段MN，使MN与AB关于某条直线对称，且M、N为格点；（2）在图2中，画一条不与AC重合的线段PQ，使PQ与AC关于某条直线对称，且P、Q为格点；（3）在图3中，画一个△DEF，使△DEF与△ABC关于某条直线对称，且D、E、F为格点，符合条件的三角形共有4个．【分析】根据要求利用轴对称的性质作出图形即可（答案不唯一）．【解析】（1）如图，线段MN即为所求作（答案不唯一）．（2）如图，线段PQ即为所求作（答案不唯一）．（3）如图，△DEF即为所求作（答案不唯一），符合条件的三角形有4个．故答案为：4．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020-2021学年浙教版八年级上册图形的轴对称与翻折专题培优
基础巩固
1.如图是一张长方形纸片ABCD，M为AD边的中点，将纸片沿BM，CM折叠，使
点A落在A处，点D落在D，处.若∠1 = 40°，则∠BMC的度数为（）.
A.135°
B.120°
C.100°
D.110°
第1题第2题第3题
2.如图，△ABC的内部有一点P，且点D，E，F是点P分别以AB，BC，AC为对
称轴的对称点.若△ABC的内角∠BAC = 70°，∠ABC = 60°，∠ACB = 50°，则∠ADB + ∠BEC + ∠CFA = （）.
A.180°
B.270°
C.360°
D.480°
3.如图，在长方形ABCD中，M为CD的中点，将△MBC沿BM翻折至△MBE，若
∠AME = a，∠ABE = β，则α与β之间的数量关系为（）.
A.a + 3β = 180°
B.β - α = 20°
C.α + β = 80°
D.3β - 2α = 90°
4.如图，点D，E在△ABC边上，沿DE将△ADE翻折，点A的对应点为点A′，
∠A′EC = α，∠A′DB = β，且α < β，则∠A = _________ （用含a，β的式子表示）.（用含α，β的式子表示）.
第4题第5题
5.如图，设镜面L1和L2，是平行且镜面相对的两面镜子，把一个小球A放在L1，L2之间，小球在镜L1中的像为A′，A′在镜L中的像为A″，若L1，L2的距离为7，
则AA″ = _________ .
6.生活中，有人喜欢把传送的便条折成形状，折叠过程如图1～4所示（阴影
部分表示纸条的反面）:如果由信纸折成的长方形纸条（图1）长为26 cm，宽为x （cm），分别回答下列问题:
（1）为了保证能折成图④的形状（即纸条两端均超出点P），试求x的取值范围.（2）如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点P的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点M与点A的距离（用x 表示）
7.（1）如图1，直线同侧有两点A，B，在直线上求一点C，使它到A，B两点的距
离之和最小（保留作图痕迹不写作法）.
（2）知识拓展:如图2，点P在∠AOB内部，试在OA，OB上分别找出两点E，F，使△PEF周长最短（保留作图痕迹不写作法）.
（3）解决问题:
①如图3，在五边形ABCDE中，在BC，DE上分别找一点M，N，使得△AMN周长最小（保留作图痕迹不写作法）.
②若∠BAE = 125°，∠B = ∠E = 90°，AB = BC，AE = DE，∠AMN + ∠ANM的度数为 _________ .
拓展提优
1.如图，将一个三角形纸片ABC沿过点B的直线折叠，使点C落在AB边上的点E 处，折痕为BD，则下列结论一定正确的是（）.
A.AD = BD
B.AE = AC
C.ED + EB = DB
D.AE + CB = AB
第1题
2.如图，在△ABC中，AB= AC，∠C= 70°，△AB′C′与△ABC关于直线EF对称，∠CAF = 10°，连结BB′，则∠ABB′的度数是（）.
A.30°
B.35°
C.40°
D.45°
3.如图，在Rt△ABC中，∠ACB= 90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处.若∠A = 26°，则∠CDE = _________ .
4.如图，∠AOB= 41°，点P为∠AOB内的一点，分别作出点P关于OA，OB的对称点P1，P2，连结P1P2，交OA于点M，交OB于点N，P1P2 = 15，则△PMN的周长为 _________ ，∠MPN = _________ °.
5.如图，△ABC与△ADE关于直线MN对称，BC与DE的交点F在直线MN上.若ED = 4 cm，FC = 1 cm，∠BAC = 76°，∠EAC = 58°.
（1）求出BF的长度.
（2）求∠CAD的度数.
（3）连结EC，线段EC与直线MN有什么关系?
6.如图1，在四边形OABC中，OA = a，OC = 8，∠AOC = ∠BCO = 90°，经过点O的直线l将四边形分成两部分，直线l与0C所成的角设为θ，将四边形OABC 的直角∠OCB沿直线l折叠，点C落在点D处（如图1）.
（1）若点D与点A重合，则θ = _________ ，a = _________ .
（2）若折叠后点D恰为AB的中点（如图2），求θ的度数.
冲刺重高
1.如图，在四边形ABCD中，∠BAD = 120°，∠B = ∠D = 90°，在BC，CD上分
别找一点M，N，使△AMN周长最小时，则∠AMN + ∠ANM的度数为（）.
A.130°
B.120°
C.110°
D.100°
2.如图，△ABC的BC边上有一小球P，将小球沿着与AB平行的方向击出，撞到点
M后反弹，撞击到点N又反弹撞击到点D，若∠ADN= 105°，则∠A= _________ 度.
3.如图，已知∠MON= 50°，P为∠MON内一定点，点A为OM上的点，点B为
ON上的点，当△PAB的周长取最小值时，则∠APB度数是 _________ .
4.如图1是长方形纸带，∠DEF= 26°，将纸带沿EF折叠成图2，再沿BF折叠成
图3，则图3中的∠CFE的度数是 _________ .
5.在△ABC中，∠CAB = 2a，且0° < α < 30°，AP平分∠CAB.
（1）如图1，若α= 21°，∠ABC = 32°，且AP交BC于点P，试探究线段AB，AC与PB之间的数量关系，并对你的结论加以证明.
（2）如图2，若∠ABC= 60°－α，点P在△ABC的内部，且使∠CBP= 30°，求∠APC的度数（用含α的代数式表示）.
2 3 4 5 6
7。