几何之五大模型

合集下载

小升初奥赛几何五大模型

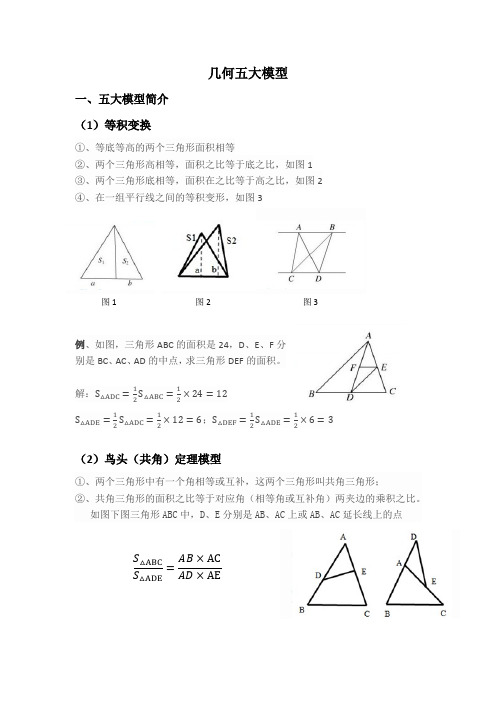
几何五大模型一、五大模型简介（1）等积变换①、等底等高的两个三角形面积相等②、两个三角形高相等，面积之比等于底之比，如图1③、两个三角形底相等，面积在之比等于高之比，如图2④、在一组平行线之间的等积变形，如图3图1 图2 图3例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。

解：S△ADC=12S△ABC=12×24=12S△ADE=12S△ADC=12×12=6；S△DEF=12S△ADE=12×6=3（2）鸟头（共角）定理模型①、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；②、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。

如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点S△ABC S△ADE =AB×AC AD×AE例、如图在ΔABC中，D在BA的延长线上，E在AC上，且AB：AD=5:2，AE：EC=3:2，△ADE的面积为12平方厘米，求ΔABC 的面积。

解：由题意知：S△ABCS△ADE =AB×ACAD×AE=52×53=256∴S△ABC=256×S△ADE=256×12=50(平方厘米)（3）蝴蝶模型1、梯形中比例关系(“梯形蝴蝶定理”)①S2=S4(梯形两翼相等)②S1:S3:S2:S4=a2:b2:ab:ab③梯形S对应的分数为（a+b)2例、如图，梯形ABCD，AB与CD平行，对角线AC、BD交于点O，已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米，求梯形ABCD的面积。

解：S△AOB:S△BOC=25:35=5:7S△AOB:S△DOC=AB2:DC2=52:72=25：49∴S△DOC=49又S△AOD=S△BOC=35∴S ABCD=25+35+35+49=144(平方厘米)2、任意四边形中的比例关系(“蝴蝶定理”)：①S1:S2=S4:S3或S1×S3=S2×S4②AO:OC=S1:S4=S2:S3=(S1+S2):(S4+S3)例、如图，四边形ABCD的对角线AC、BD交于点O，如果三角形ABD的面积等于三角形BCD面积的1/3，且AO=2，求OC解：AO:OC=S△ABD:S△BCD=1:3OC=2×3=6（4）相似模型1、相似三角形：形状相同,大小不相等的两个三角形相似；2、寻找相似模型的大前提是平行线：平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似。

小学数学五大几何模型

小学数学五大几何模型知识框架一、等积模型DC BA①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；③夹在一组平行线之间的等积变形，如右图ACDBCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、共角定理（鸟头定理）两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．:():()ABC ADE S S AB AC AD AE =⨯⨯△△(1)(2)(3)(4)三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”)： ①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．S 4S 3S 2S 1O DC BA梯形中比例关系(“梯形蝴蝶定理”)：①2213::S S a b =②221324::::::S S S S a b ab ab =； ③S 的对应份数为()2a b +．A BC DO baS 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCD ABCDEF G①AD AE DE AFAB AC BC AG ===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方； ⑶连接三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半．相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具．在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形．五、共边定理（燕尾定理）有一条公共边的三角形叫做共边三角形。

几何之五大模型

几何之五大模型在小学奥数知识体系中，几何五大模型是几何专题中非常重要的一块知识点，方法性很强，掌握了几何的五大模型，对于我们解决组合型直图形或者非规则图形是非常有帮助的，所以几何五大模型在小学几何体系中的重中之重！几何五大模型的难点在于我们要在掌握各个模型适用的题型、相应的方法、公式的基础上学会灵活运用，还有就是有时要根据题意同时运用多种模型，从而更好的解决问题！PS:对于不同题型均会有例题讲解分析以及精选练习题，以供大家有针对性学习巩固，相信大家对于应用题的攻克将不在话下！一、五大模型简介（1）等积变换模型1、等底等高的两个三角形面积相等；2、两个三角形高相等，面积之比等于底之比，如图①所示，S1：S2=a:b；3、两个三角形底相等，面积在之比等于高之比，如图②所示，S1：S2=a:b；4、在一组平行线之间的等积变形，如图③所示，S△ACD=S△BCD；反之，如果S△ACD=S△BCD，则可知直线AB平行于CD。

例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。

（2）鸟头（共角）定理模型1、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；2、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。

如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点则有：S△ABC：S△ADE=（AB×AC）：（AD×AE）我们现在以互补为例来简单证明一下共角定理！如图连接BE，根据等积变化模型知S△ADE：S△ABE=AD：ABS△ABE：S△CBE=AE：CE所以S△ABE：S△ABC=S△ABE：（S△ABE+S△CBE）=AE：AC因此S△ADE：S△ABC =（S△ADE：S△ABE）×（S△ABE：S△ABC）=（AD：AB）×（AE：AC）。

例、如图在ΔABC中，D在BA的延长线上，E在AC上，且AB：AD=5:2，AE：EC=3:2，△ADE的面积为12平方厘米，求ΔABC的面积。

小升初复习重难点一几何五大模型

几何五大模型一、五大模型简介（1）等积变换模型1、等底等高的两个三角形面积相等；2、两个三角形高相等，面积之比等于底之比，如图①所示，S[sub]1[/sub]：S[sub]2[/sub]=a:b；3、两个三角形底相等，面积在之比等于高之比，如图②所示，S[sub]1[/sub]：S[sub]2[/sub]=a:b；4、在一组平行线之间的等积变形，如图③所示，S[sub]△ACD[/sub]=S[sub]△BCD[/sub]；反之，如果S[sub]△ACD[/sub]=S[sub]△BCD[/sub]，则可知直线AB平行于CD。

例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。

如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点则有：S[sub]△ABC[/sub]：S[sub]△ADE[/sub]=（AB×AC）：（AD×AE）我们现在以互补为例来简单证明一下共角定理！如图连接BE，根据等积变化模型知，S[sub]△ADE[/sub]：S[sub]△ABE[/sub]=AD：AB、S[sub]△ABE[/sub]：S[sub]△CBE[/sub]=AE：CE，所以S[sub]△ABE[/sub]：S[sub]△ABC[/sub]=S[sub]△ABE[/sub]：（S[sub]△ABE[/sub]+S[sub]△CBE[/sub]）=AE：AC，因此S[sub]△ADE[/sub]：S[sub]△ABC[/sub]=（S[sub]△ADE[/sub]：S[sub]△ABE[/sub]）×（S[sub]△ABE[/sub]：S[sub]△ABC[/sub]）=（AD：AB）×（AE：AC）。

小升初复习重难点一几何五大模型

几何五大模型一、五大模型简介(1)等积变换模型1 、等底等高的两个三角形面积相等；2 、两个三角形高相等，面积之比等于底之比，如图①所示，S[sub]1[/sub] : S[sub]2[/sub]=a:b ；3 、两个三角形底相等，面积在之比等于高之比，如图②所示,S[sub]1[/sub] : S[sub]2[/sub]=a:b ；4 、在一组平行线之间的等积变形，如图③所示，S[sub] △ ACD[/sub]=S[sub] △ BCD[/sub];反之，如果S[sub] △ ACD[/sub]=S[sub] △ BCD[/sub]，则可知直线AB平行于CD点，求三角形DEF的面积。

例、如图，三角形ABC的面积是24，D、E、F分别是BC AC AD的中【详解】根据等积变换知，5^=15^ = 1x24=12,]$丄攻=斥卅1匚=6 • EggF = Q6 - 3（2）鸟头（共角）定理模型1 、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；2 、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。

如图下图三角形ABC中，D、E分别是AB AC上或AB AC延长线上的点A D则有：S[sub] △ ABC[/sub] : S[sub] △ ADE[/sub]= (ABX AC (ADX AE我们现在以互补为例来简单证明一下共角定理!p _AB AC . 亨尹Z （平方厘料如图连接BE 根据等积变化模型知，S[sub] △ ADE[/sub]:S[sub] △ ABE[/sub] =AD AB S[sub] △ ABE[/sub]:S[sub] △ CBE[/sub]=AE : CE 所以 S[sub] △ ABE[/sub]:S[sub] △ ABC[/sub]=S[sub] △ ABE[/sub]:(S[sub] △ ABE[/sub]+S[sub] △ CBE[/sub] ) =AE AC,因此 S[sub] △ ADE[/sub] : S[sub] △ ABC[/sub]= (S[sub] △ ADE[/sub]: S[sub] △ ABE[/sub] ) x( S[sub] △ ABE[/sub] : S[sub] △ ABC[/sub])= (AD AB x ( AE AC 。

小学数学几何必考五大模型

∵在正方形ABCD中，S△ABG=×AB × AB边上的高，
∴ S△ABG= S□ABCD（三角形面积等于与它等底等高的平行四边形面积的一半）
同理，S△ABG=

S
□EFGB
∴ 正方形ABCD与长方形EFGB面积相等。长方形的宽=8 ×8÷10=6.4（厘米）
【例2】长方形ABCD的面积为36cm2，E 、F、G为各边中点，H为AD边上
任意一点，问阴影部分面积是多少？
【解析】解法一：寻找可利用的条件，连接BH ,HC ，如下图：
解法二：特殊点法．找H的特殊点，把H点与D点重合，那么图形就可变成右图：
这样阴影部分的面积就是△DEF的面积，
根据鸟头定理，则有：
【巩固】
a
如右图
③夹在一组平行线之间的等积变形，如右图
反之，如果
，则可知直线
平行于
等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；
⑤三角形面积等于与它等底等高的平行四边形面积的一半；
⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于
它们的高之比．
二、鸟头定理
两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．
D
A
A
D
E
E
B
C
图 ⑴
如图在
上，E在AC上)，则
B
图 (2)
C
中，D、E分别是AB、AC上的点如图 ⑴(或D在BA的延长线
三、蝴蝶定理
任意四边形中的比例关系(“蝴蝶定理”)：
梯形中比例关系(“梯形蝴蝶定理”)：

平面几何五种模型

② AO : OC S1 S2 : S4 S3
【上下比】
=
=
=
【上上比】
=
=
=
由上述比例可以按数学运算原则推出很多规则：如
面积交叉相乘的乘积相等
=
= S1 S3 S2 S4
梯形蝴蝶定理（梯蝴蝶）
① S1 : S3 a2 : b2 →上：下 = a2 : b2
② S1 : S3 : S2 : S4 a2 : b2 : ab : ab →上：下：左：右 = a2 : b2 : ab : ab
+
+
=1
2
③ S 的对应份数为 a b →a2+2ab+b2=a2+b2+ab+ab 有木有↑
4 相似三角形形状相同，大小不同的三角形，只要形状不变，无论大小怎么改变，他们都相似。 1 相似三角形的一切对应线段的长度成比例，并且 =它们的相似比 2 相似三角形的面积比 =相似比的平方
3 连接三角形两边中点的线段叫做三角形的中位线三角形中位线定理：三角形的中位线长 =它所对应的底边长的一半就是三角形任 2 边中点连出来的中位线就是第三边长的一半！出题几率：多产生于 2 条平行线造成的相似三角形
等于浅紫色三角形是“嵌入”在大三角形 ABC里面，注意，鸟头定理用的是乘积比！不是
单独的线段比 ~
记忆上用夹角 2 边
最好记，这里等于
E
D
A 对顶角
D E
A
B
C
B
C
D 互补角 A
E
D
A
E
B
CB
C
鸟头定理的证明，写出来是因为很多题目的解题过程，都需要补这么一条辅助线来过度连

几何五大模型定理

几何五大模型定理
几何学是一个古老的学科，并在数学领域发挥着不可替代的作用。

过去2000多年来，一些极具影响力的几何学家们有力地推动了几何学研究的发展，创造了许多引人注目的几何模型定理。

以下将介绍五大几何模型定理，它们是几何学的代表性研究成果。

第一个几何模型定理是欧几里得定理，也称为“欧几里得尺规定理”，这是古希腊数学家欧几里得著名的定理。

它声明：“三角形内角之和等于180度”。

它是数学基本概念的基础，借此可以证明各种几何图形的构成关系。

第二个几何模型定理是埃及人定理，也称为“埃及三角形定理”。

这是一个基本定理，它宣称：“正三角形的高等于它的底乘以三角形的高”。

第三个几何模型定理是勾股定理，这是古希腊数学家勾股第六世纪首次提出的定理。

它表明：“三角形的斜边的平方等于两常规边的平方之和”。

第四个几何模型定理是朱丽叶定理，由十八世纪法国数学家朱丽叶蒙德拉克提出。

它宣称：“在平面内，给定一个三角形与
它的外接圆，三角形内角周长和半径之比等于外角角度和圆周长的比之和”。

第五个几何模型定理是莱布尼茨定理，由德国数学家马克斯·莱布尼茨于1794年提出的定理。

它声明：“存在唯一的平行四边形，其面积等于任何给定四边形的面积之和”。

以上就是几何学五大模型定理的主要内容，它们的发现和推导象征着几何学的成熟，也为更深入研究几何学提供了基础。

几何的五大模型

5、想想？正方形ABCD中，还有哪些没有包块进去，及与份数之间旳关系
6、SΔADE =S2+S3，S ΔBCF =S4+S3 想想？为何，用了什么模型
7、∴正方形ABCD被提成了24份 S阴影=S2+S4=6÷24×12=3cm2
例题：相同模型
例题4：如图，长方形ABCD中，E为AD旳中点，AF与BE、BD分别交于
例题：二分之一模型
例题3：如图ABFE和CDEF都是矩形，AB旳长是4厘米，BC旳长是3厘米，那么图中阴影部分旳面积是多少平方厘米。
分析：阴影部分是一种个三角形，矩形CDEF中阴影 A
B
部分旳三角形底边长度为矩形旳长，高与矩 E
F
形宽相等，根据面积公式可知S阴影=SEDCF÷2
D
C
思索：二分之一模型是什么意思？
分析：SΔ黄+SΔ绿=S长方形÷2（=宽×长÷2）
黄色三角形面积21cm2，占长方形面积百分比
黄
50%-15%=35% 所以，长方形面积=21÷35%=60cm2
红
红
绿
例题：等积变换
例题2：图中ABCD是个直角梯形，以AD为一边向外作长方形ADEF，其面积为6.36平方厘米，连接BE交AD于P，再连接PC，则图中阴影部分旳面积是多少平方厘米？
AB
S1 S2
a
b
图1
CD 图2
概念
2、鸟头定理（共角定理）模型
1）两个三角形中有一种角相等或互补，这两个三角形叫做共角三角形
2）共角三角形旳面积比等于相应交（相等或互补角）两夹边旳乘积之比
D
E
A
D
A
A
E D
BC

1数学几何五大模型

数学几何五大模型一、等积变换模型⑴等底等高的两个三角形面积相等；其它常见的面积相等的情况⑵两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比。

如上图12::S S a b =⑶夹在一组平行线之间的等积变形，如下图ACD BCD S S =△△；反之，如果ACDBCD S S =△△，则可知直线AB 平行于CD 。

⑷正方形的面积等于对角线长度平方的一半；⑸三角形面积等于与它等底等高的平行四边形面积的一半；二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图，在ABC △中，,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上，E 在AC 上(如图2)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S 1S 2S ab图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：（1） 1243::S S S S =或者1324S S S S ⨯=⨯（2）()()1243::AO OC S S S S =++ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。

梯形中比例关系(“梯形蝴蝶定理”)（1）2213::S S a b =（2）221324::::::S S S S a b ab ab =；（3）梯形S 的对应份数为()2a b +。

四、相似模型相似三角形性质：金字塔模型沙漏模型（1）AD AE DE AFAB AC BC AG===；（2）22::ADE ABCS S AF AG =△△。

所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；⑵相似三角形的面积比等于它们相似比的平方。

小学奥数之几何五大模型

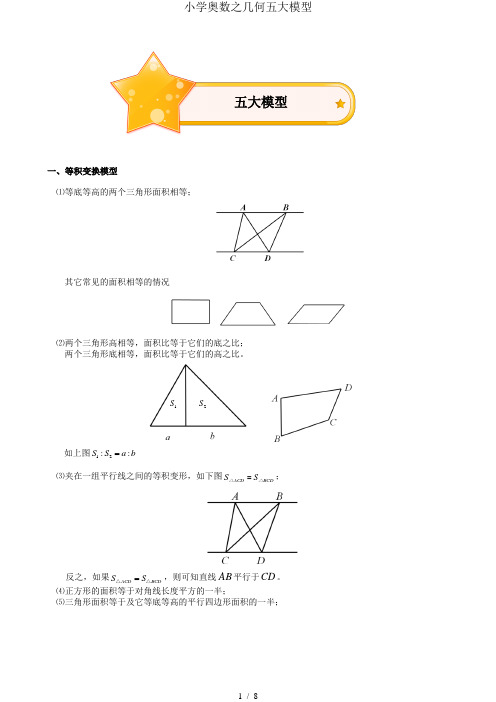
一、等积变换模型⑴等底等高的两个三角形面积相等；其它常见的面积相等的情况⑵两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比。

如上图12::S S a b =⑶夹在一组平行线之间的等积变形，如下图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD 。

⑷正方形的面积等于对角线长度平方的一半；⑸三角形面积等于及它等底等高的平行四边形面积的一半；五大模型1S 2S二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图，在ABC △中，,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上，E 在AC 上(如图2)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系及四边形内的三角形相联系；另一方面，也可以得到及面积对应的对角线的比例关系。

梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =； ③梯形S 的对应份数为()2a b +。

四、相似模型相似三角形性质：金字塔模型沙漏模型 ①AD AE DE AFAB AC BC AG===； ②22::ADE ABC S S AF AG =△△。

所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，及相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方。

几何的五大模型

解析：
利用燕尾定理，连接FC，BFD面积/BFC面积=DE/EC=1/2，如果BFD面积为1份的话，BFC为2份；又DF=FG，所以BFG面积与BFD面积相等也是1份，故FGC面积是2-1=1份，那么BG=GC；再利用燕尾定理，DFC的面积与DFB相等也是1份，BDC的面积是4份=6，故一份面积是6/4=1.5，阴影部分是1+2/3=5/3份，面积是1.5×5/3=2关系是一样的。）
四、相似三角形模型
相似三角形：是形状相同，但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型
解析：
因为阴影部分比三角形EFG的面积大10厘米2，都加上梯形FGCB后，根据差不变性质，所得的两个新图形的面积差不变，即平行四边行ABCD比直角三角形ECB的面积大10厘米2，所以平行四边形ABCD的面积等于10×8÷2+10=50厘米2。
几何的五大模型
一、等积变换模型
1、等底等高的两个三角形面积相等。
2、两个三角形高相等，面积比等于它们的底之比。
3、两个三角形底相等，面积比等于它的的高之比。
二、共角定理模型
两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。
三、蝴蝶定理模型
显然，最大的三角形的面积为21公顷．
解析：
如图所示，设上底为a，则下底为2a，梯形的高为h，则EF= （a+2a）= ，所以，
。所以
阴影部分
= 即，梯形 ABCD的面积=
如下图所示，为了方便叙述，将某些点标上字母．

小升初-数学-几何-五大几何模型

12
小升初数学-几何是
平方厘米．
A E D
B M
F
N C
【作业 4】一个等腰直角三角形和一个正方形如图摆放，①、②、③这三块的面积比依次为 1: 4 : 41．那么，④、⑤这两块的面积比是______．
① ①
①
①
①
【作业 5】下图中，四边形 ABCD 都是边长为 1 的正方形，E、F、G、H 分别是
1
小升初数学-几何
S△△ABC : S ADE ( AB AC) : ( AD AE)
(1)
(2)
(3)
(4)
三、蝴蝶定理
任意四边形中的比例关系(“蝴蝶定理”)：
① S1 : S2 S4 : S3 或者 S1 S3 S2 S4 ② AO : OC S1 S2 : S4 S3
D
A
4 O E3
C
F
B
【巩固】 ABCD 是平行四边形，面积为 72 平方厘米， E 、 F 分别为 AB 、 BC 的中点，则图中
阴影部分的面积为
平方厘米．
A
D
O E
M
B
F
C
二、蝴蝶模型【例 4】如图所示，长方形 ABCD 内的阴影部分的面积之和为 70，AB=8,AD=15 四边形
6
小升初数学-几何 EFGO 的面积为______．
AB、BC、CD、DA 的重点，如果左图中阴影部分与右图中阴影部分的面积之比
是最简分数 m ，那么，m＋n 的值等于__________。
n
H A
DA
H D
E
GE
G
B
F
CB
F
C

几何图形的五大模型

几何图形的五大模型一、等积变换模型1、等底等高的两个三角形面积相等。

2、两个三角形高相等，面积比等于它们的底之比。

3、两个三角形底相等，面积比等于它的的高之比。

二、共角定理模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。

三、蝴蝶定理模型（说明：任意四边形与四边形、长方形、梯形，连接对角线所成四部的比例关系是一样的。

）四、相似三角形模型相似三角形：是形状相同，但大小不同的三角形叫相似三角形。

相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比。

相似三角形的面积比等于它们相似比的平方。

五、燕尾定理模型1. 甲、乙、丙三人在A、B两块地植树，A地要植900棵，B地要植1250棵.已知甲、乙、丙每天分别能植树24，30，32棵，甲在A地植树，丙在B地植树，乙先在A地植树，然后转到B地植树.两块地同时开始同时结束，乙应在开始后第几天从A地转到B地？总棵数是900＋1250＝2150棵，每天可以植树24＋30＋32＝86棵需要种的天数是2150÷86＝25天甲25天完成24×25＝600棵那么乙就要完成900-600=300棵之后，才去帮丙即做了300÷30＝10天之后即第11天从A地转到B地。

2. 有三块草地，面积分别是5，15，24亩.草地上的草一样厚，而且长得一样快.第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天，问第三块地可供多少头牛吃80天？这是一道牛吃草问题，是比较复杂的牛吃草问题。

把每头牛每天吃的草看作1份。

因为第一块草地5亩面积原有草量＋5亩面积30天长的草＝10×30＝300份所以每亩面积原有草量和每亩面积30天长的草是300÷5＝60份因为第二块草地15亩面积原有草量＋15亩面积45天长的草＝28×45＝1260份所以每亩面积原有草量和每亩面积45天长的草是1260÷15＝84份所以45－30＝15天，每亩面积长84－60＝24份所以，每亩面积每天长24÷15＝1.6份所以，每亩原有草量60－30×1.6＝12份第三块地面积是24亩，所以每天要长1.6×24＝38.4份，原有草就有24×12＝288份新生长的每天就要用38.4头牛去吃，其余的牛每天去吃原有的草，那么原有的草就要够吃80天，因此288÷80＝3.6头牛所以，一共需要38.4＋3.6＝42头牛来吃。

小升初平面几何常考五大模型知识分享

一、等积变换模型1、等底等高的两个三角形面积相等。

2、两个三角形高相等，面积比等于它们的底之比。

3、两个三角形底相等，面积比等于它的的高之比。

二、共角定理模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。

三、蝴蝶定理模型（说明：任意四边形与四边形、长方形、梯形，连接对角线所成四部的比例关系是一样的。

）四、相似三角形模型相似三角形：是形状相同，但大小不同的三角形叫相似三角形。

相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比。

相似三角形的面积比等于它们相似比的平方。

五、燕尾定理模型正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为由题知DC/GP=GC/PK，即DC/(DC-4)=(4+PK)/PK，令DC=a，PK=c，则a=4+c，则S△DEK=a^2+16+c*(4-c)/2+c^2-ac-a(4+a)/2=a^2/2+c^2/2-ac-2a+2c+16=(c+4)^2/2+c^2/2 -c(c+4)-2(c+4)+2c+16=16。

1、图17是一个正方形地板砖示意图，在大正方形ABCD中AA1=AA2=BB1=BB2=CC1=CC2=DD1=D D2，中间小正方形 EFGH的面积是16平方厘米，四块蓝色的三角形的面积总和是72平方厘米，那么大正方形ABCD的面积是多少平方厘米？分析与解连AC和BD两条大正方形的对角线，它们相交于O，然后将三角形AOB放在D PC处（如图18和图19）。

已知小正方形EFGH的面积是16平方厘米，所以小正方形EFGH的边长是4厘米。

又知道四个蓝色的三角形的面积总和是72平方厘米，所以两个蓝色三角形的面积是72÷2=36平方厘米，即图19的正方形OCPD中的小正方形的面积是36平方厘米，那么这个正方形的边长就是6厘米。

几何之五大模型(加梅涅劳斯及赛瓦定理)

• 如图：G、H是AC的三等分点，D是 BC的四等分点，求AF：FE：ED= （）：（）：（）
思考：《塞瓦定理》
• 设M是三角形ABC内的任意一点，直线AM、 BM、CM分别交对边于点D、E、F，则
BD DC
•
CE EA •
AF FB
＝1
当三角形的顶点向对边连线并交于一点时，从三角形任一顶点出发，沿顺（或逆）时针围着三角形的外周，按“部、部、部、部、部、部”的顺序，一笔画并回到起点。
s2 O S4 S3
•（S1+S2）︰（S4+SB3）=AO︰OC
C
• 练习4.如图，某公园的外轮廓是四边形ABCD，被对角线AC、BD分成四个部分， △AOB面积为1平方千米， △BOC面积为2平方千米， △COD的面积为3平方千米，公园陆地的面积是6.92平方千米，求人工湖的面积是多少平方千米？
S1 S3 S2 S4
• 设AO︰OC= S1︰S4= S2︰S3=a:b
• S1=ax, S4=bx,S2=ay, S3=by
• 则（S1+S2）︰（S4+S3）
• =（ax+ay）：（bx+by）
• =a（x+y）：b（x+y）
D
• =a:b
A s1
• = AO︰OC
蝴蝶定理：
若每个小方格面积均为1，则：格点多边形面积=外周格点数÷2+内部格点数-1
练习：图中每个小正方形的面积都是1平方厘米,求图中阴影部分的面积.(每个小正方形的面积为2平方厘米呢？)
• 4、右图中每个小正方形的面积为1平方分米，那么阴影部分的面积是多少平方分米？
阴影面积：大三角形面积（2 1）：（3 4） 1: 6

几何五大模型-汇总

几何五大模型-汇总小学平面几何五大模型一、共角定理两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角（相等角或互补角）两夹边的乘积之比. 如图在AABC中，DE分别是AB.AQ 上的点如图⑴（或D在朋的延长线上，£在AC 上），贝!J S“c : S“E =⑷ x AC）: （AD x AE）证明：由三角形面积公式S=1/2*a*b*sinC可推导出若AABC 和ZXADE 中，ZBAC=ZDAE 或ZBAC+ZDAET80。

，S A/IBC AB X ACS MDE AD X AE二、等积模型①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如下图£:二=“"③夹在一组平行线之间的等积变形，如右图S^CD二Sg 反之，如果SycD=Sg则可知直线A3平行于CD・④等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四边形）；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比.三、蝶形定理1、任意四边形中的比例关系（“蝶形定理”）:①S, :S2=S4:S3或者S|XS严S’xSj®/IO:OC = （S1+5j：（S.+S,）速记：上X下二左X右蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系.2、梯形中比例关系（“梯形蝶形定理”）：①S,:53=fl2:/>2②S : S；'.S2:S i=a~:b:iab: ab ;③S的对应份数为仗+疔.四、相似模型（二）沙漏模型（一）金字塔模型②S'DE：=虫尸：MG?・相似三角形，就是形状相同，大小不同的三角形（只要其形状不改变，不论大小怎样改变它们都相似），与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；⑵相似三角形的面积比等于它们相似比的平方；⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理（燕尾模型和风筝模型）在AABC 中，AD9 BE, CF 相交于同一点O,那么5^ : =BD.DC.上述定理给出了一个新的转化面积比与线段比的手段，因为和A4CO的形状很象燕子的尾巴，所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用，它的特殊性在于，它可以存在于任何一个三角形之中，为三角形中的三角形面积对应底边之间提供互相联系的途径.附件1:鸟头模型例题及习题:逵扶方廠积$g=l,三角形$2= £, ,3少=2设AB F , EC 二丄；aBS=-x2-a = —,那么 C5=l- —=—；6 3a a 3a 3aCF = -x2^—=—；5 3a 5 那么Mm-®# 那么$5=卜善¥ = £：所以S'如=】-卜卜卜知即：S T =证明:如有图.连接BE 。