八年级下数学第八周周测题

合集下载

八年级最新数学下册单元测试题初二数学下册章节练习题带图文答案解析全部100篇下学期期中复习同步练习

八年级数学下学期期中复习同步练习（答题时间：60分钟）一、选择题1. 如果三角形的两边分别为3和5，那么连接这个三角形三边中点所得三角形的周长可能是（）A. 5.5B. 5C. 4.5D. 42. 如图，平行四边形ABCD的对角线AC、BD相交于点O，下列结论正确的是（）A. S平行四边形ABCD=4S△AOBB. AC=BDC. AC⊥BDD. 平行四边形ABCD是轴对称图形3. 如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合，若AB=2，则C′D的长为（）A. 1B. 2C. 3D. 44. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（）A. 48B. 60C. 76D. 80*5. 如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为（）A. 4B. 3C. 52D. 2*6. 如图，等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD，则下列结论：①AD=BC；②BD、AC互相平分；③四边形ACED是菱形；其中正确的个数是（）A. 0B. 1C. 2D. 3*7. 如图，已知菱形ABCD 的对角线AC 、BD 的长分别为6cm 、8cm ，AE ⊥BC 于点E ，则AE 的长是（）A. 53cmB. 25 cmC. 485 cmD. 245cm *8.如图，在矩形ABCD 中，AB=2，BC=4，对角线AC 的垂直平分线分别交AD 、AC 于点E 、O ，连接CE ，则CE 的长为（）A. 3B. 3.5C. 2.5D. 2.8**9. 如图，△ABC 中，AC 的垂直平分线分别交AC 、AB 于点D 、F ，BE ⊥DF 交DF 的延长线于点E ，已知∠A=30°，BC=2，AF=BF ，则四边形BCDE 的面积是（）A. 32B. 33C. 4D. 34**10. 如图，在Rt △ABC 中，∠B=90°，AB=3，BC=4，点D 在BC 上，以AC 为对角线的所有平行四边形ADCE 中，DE 最小的值是（）A. 2B. 3C. 4D. 5二、填空题11. 5082。

八年级数学测试题及答案

八年级数学测试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是等腰三角形的性质？A. 三条边相等B. 两条边相等C. 三个角相等D. 两个角相等答案：B2. 一个数的平方根是4，那么这个数是：A. 16B. 8C. 4D. 2答案：A3. 一个圆的半径是5，那么它的周长是：A. 10πB. 20πC. 25πD. 50π答案：B4. 下列哪个选项表示的是一次函数？A. y = 2x + 3B. y = x^2 + 1C. y = 3x^3D. y = 1/x答案：A5. 一个等差数列的首项是2，公差是3，那么第5项是：A. 14B. 17C. 20D. 23答案：A6. 如果一个三角形的两边长分别是3和4，那么第三边的长x满足：A. 1 < x < 7B. 0 < x < 7C. 1 < x < 7D. 0 < x < 7答案：A7. 一个正数的倒数是1/4，那么这个数是：A. 4B. 1/4C. 1/2D. 2答案：A8. 一个数的绝对值是5，那么这个数可能是：A. 5B. -5C. 5或-5D. 0答案：C9. 下列哪个选项是二次函数的图像？A. 一条直线B. 一个点C. 一个抛物线D. 一个圆答案：C10. 一个数的立方根是2，那么这个数是：A. 8B. 6C. 2D. 4答案：A二、填空题（每题4分，共20分）1. 一个数的平方是25，那么这个数是____。

答案：±52. 一个等腰三角形的底边长是6，两腰长是5，那么它的周长是____。

答案：163. 一个圆的直径是10，那么它的半径是____。

答案：54. 一个数列的前三项是2，4，8，那么第四项是____。

答案：165. 如果一个三角形的两边长分别是5和12，那么第三边的长x满足的条件是____。

答案：7 < x < 17三、解答题（每题10分，共50分）1. 已知一个等差数列的前三项分别是2，5，8，求第10项的值。

第十五章周测(15.2.2～15.2.3)【习题课件】八年级上册人教版数学

＋
.
−
－2
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
周测(15.2.2～15.2.3)
一、选择题
二、填空题
三、解答题
14. 【教材第147页习题15.2第12题改编】我国是一个水资源贫乏的国
家，每一个公民都应自觉养成节约用水的意识和习惯.为提高水资源的
利用率，某住宅小区安装了循环用水装置. 经测算，原来 a 天用水 b
三、解答题
10. (2023·沧州模拟预测)小敏在做数学作业时，不小心将式子中除号后
边的代数式污染，即
−
−
被污染的代数式█为(
C
+
A.
+
+
B.
−
−
C.
+
+
D.
−
1
2
3
4
5
6
−

÷█，通过查看答案，答案为
，则
−
)
7
8
9
10
11
12
13
14
三、解答题
−+
÷
，其中 x ＝4.
−
+

−+
− (+)(−)
−
解：原式＝(
－
)÷
＝
·
＝
.

+
+
−
+
(−)
−
−

当 x ＝4时，原式＝
＝ .
−

1

人教版数学八年级上册周周测(含解析)第8周

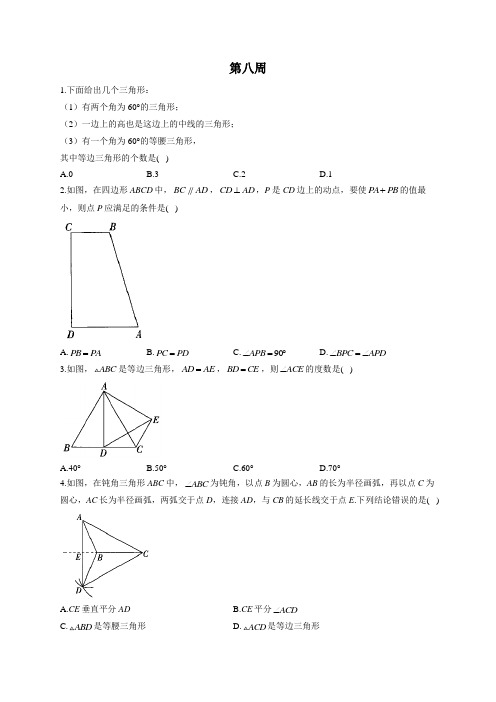
第八周1.下面给出几个三角形：（1）有两个角为60°的三角形；（2）一边上的高也是这边上的中线的三角形；（3）有一个角为60°的等腰三角形，其中等边三角形的个数是( )A.0B.3C.2D.12.如图，在四边形ABCD中，BC AD，CD AD+的值最⊥，P是CD边上的动点，要使PA PB小，则点P应满足的条件是( )A.PB PA= B.PC PD∠=∠∠=︒ D.BPC APD= C.90APB3.如图，ABC是等边三角形，AD AE=，BD CE=，则ACE∠的度数是( )A.40°B.50°C.60°D.70°4.如图，在钝角三角形ABC中，ABC∠为钝角，以点B为圆心，AB的长为半径画弧，再以点C为圆心，AC长为半径画弧，两弧交于点D，连接AD，与CB的延长线交于点E.下列结论错误的是( )A.CE垂直平分ADB.CE平分ACD∠C.ABD是等腰三角形D.ACD是等边三角形5.如图，牧童在A 处放牛，其家在B 处，A 、B 到河岸的距离分别为AC 的长和BD 的长，且AC BD =，若点A 到河岸CD 的中点的距离为500米，则牧童从A 处把牛牵到河边饮水再回家，最短距离是( )A.750米B.1000米C.1500米D.2000米 6.如图，在等边ABC 中，BD 平分ABC ∠交AC 于点D ，过点D 作DE BC ⊥于点E ，且1.5CE =，则AB 的长为( )A.3B.4.5C.6D.7.57.如图，CD 是ABC 的角平分线，ABC 的面积为12，BC 的长为6，点E ，F 分别是CD ，AC 上的动点，则AE EF +的最小值是( )A.6B.4C.3D.28.如图，等边三角形ABC 的边长为4，AD 是BC 边上的中线，F 是AD 上的动点，E 是AC 边上一点.若2AE =，则EF CF +取得最小值时，ECF ∠的度数为( )A.15°B.22.5°C.30°D.45°9.如图，在等边ABC 中，BD 为AC 边上的中线，CE 为ACB ∠的平分线，BD 、CE 交于点M ，则BME ∠=___________°.10.如图，在等边ABC中，9AO=，点P是AB上一动点，连接AC=，点O在AC上，且3OP，将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上，则AP的长是____________.11.如图，直线m是ABC中BC边的垂直平分线，点P是直线m上的动点.若6AC=，AB=，4 BC=，则APC的周长的最小值是_____________.712.如图，A,B,C是平面内三点.（1）按要求作图：①作射线BC，过点B作直线l，使A,C两点在直线l两旁；②点P为直线l上任意一点，点Q为射线BC上任意一点，连接线段AP,PQ.（2）在（1）所作图形中，若点A到直线l的距离为2，点A到直线BC的距离为5，点A,B之间的距离为8，点A,C之间的距离为6，求AP PQ+的最小值，并写出其依据.答案以及解析1.答案：C解析：易知（1）有两个角为60°的三角形的三个内角都是60°，（3）有一个角是60°的等腰三角形是等边三角形，所以（1）（3）为等边三角形，故等边三角形的个数是2.2.答案：D解析：如图所示，作点A 关于CD 的对称点A '，连接A B '，交CD 于点P ，连接AP ，则PA PB +的最小值为A B '的长，点P 即为所求.点A '与点A 关于CD 对称，APD A PD '∴∠=∠，BPC A PD '∠=∠，BPC APD ∴∠=∠，故D 符合题意.由图可知，选项A 和选项B 不成立，而C 只有在PC BC =时才成立，故选项C 不一定成立.故选D.3.答案：C解析：ABC 是等边三角形，AB AC BC ∴==，60B ∠=︒，在ABD 和ACE 中，AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩，ABD ACE ∴≌，60ACE B ∴∠=∠=︒，故选C.4.答案：D解析：由题意可得CA CD =，BA BD =，∴直线CB 是AD 的垂直平分线，即CE 垂直平分AD ，故A 选项结论正确；CE 垂直平分AD ，CAD CDA ∴∠=∠，CEA CED ∠=∠，ACE DCE ∴∠=∠，即CE 平分ACD ∠，故B 选项结论正确；DB AB =，ABD ∴是等腰三角形，故C 选项结论正确；AD 与AC 不一定相等，ACD ∴不一定是等边三角形，故D 选项结论错误.故选D.5.答案：B解析：作A 关于CD 的对称点A '，连接A B '交CD 于P ，则AC A C BD '==，90A CD ACD '∠=∠=︒，A P AP '=，在A CP '和BDP 中，A CP BDP A PC BPD A C BD '∠=∠⎧⎪'∠=∠⎨⎪'=⎩，A CP BDP '∴≅，CP PD ∴=，A P PB '=，∴P 为CD 的中点，500AP A P PB '∴===米，1000A B AP PB '∴=+=米.6.答案：C解析：ABC 是等边三角形，60ABC C ∴∠=∠=︒，AB BC AC ==，DE BC ⊥，30CDE ∴∠=︒， 1.5EC =，23CD EC ∴==，BD 平分ABC ∠，3AD CD ∴==，6AB AC AD CD ∴==+=.7.答案：B解析：如图，作点A 关于CD 的对称点H .CD 是ABC 的角平分线，∴点H 一定在BC 上.过H 作HF AC ⊥于F ，交CD 于E ，此时AE EF +的值最小，AE EF +的最小值HF =.过A 作AG BC ⊥于G .ABC 的面积为12，BC 的长为6，4AG ∴=，CD 垂直平分AH ，AC CH ∴=，1122ACH S AC HF CH AG ∴=-⋅=⋅，4HF AG ∴==，AE EF ∴+的最小值是4，故选B. 8.答案：C解析：如图,连接BE 交AD 于点.F AD 是等边三角形ABC 的中线,,, ,AD BC BD CD FC FB CF EF BF EF BE ∴⊥=∴=∴+=+=,此时CF EF +的值最小.4,2,AC AE E ==∴是AC 的中点.ABC 是等边三角形,,BE AC BE ∴⊥平分,60ABC ABC ACB ∠∠=∠=︒,30FBC ∴∠=︒.,30FC FB FCB FBC =∴∠=∠=︒,603030ECF ACB FCB ∴∠=∠-∠=︒-︒=︒.故选C.9.答案：60解析：ABC 是等边三角形，60ABC ∴∠=︒，BD 为AC 边上的中线，CE 为ACB ∠的平分线，11603022EBD ABC ∴∠=∠=⨯︒=︒，90BEC ∠=︒，180180309060BME EBD BEC ∴∠=︒-∠-∠=︒-︒-︒=︒.10.答案：6解析：A APO POC POD COD ∠+∠=∠=∠+∠，60A POD ∠=∠=︒，APO COD ∴∠=∠.在APO 和COD 中，,,,A C APO COD OP DO ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)APO COD ∴≅，AP CO ∴=，6CO AC AO =-=，6AP ∴=.11.答案：10 解析：直线m 垂直平分BC ，∴B 、C 两点关于直线m 对称，如图，设直线m 交AB 于D ，连接CD ，则BD CD =.当P 和D 重合时，AP CP +的值最小，最小值等于AB 的长，APC ∴的周长的最小值是6410+=.12.答案：（1）（作法不唯一）如图所示，射线BC ，直线l ，线段AP ,PQ 即为所求.（2）如图，过点A 作AQ BC ⊥于点Q ，交直线l 于点P ，此时AP PQ +的值最小.因为点A 到直线BC 的距离为5，所以AP PQ +的最小值为5，依据是垂线段最短.。

八年级数学下册(北师版) 周周清检测内容：1

检测内容：1.1－1.2得分________卷后分________评价________一、选择题(每小题5分，共35分)1．如图，a∥b，点A在直线a上，点C在直线b上，∠BAC＝90°，AB＝AC，若∠1＝20°，则∠2的度数为(B)A．25°B．65°C．70°D．75°第1题图第3题图2．在△ABC中，a，b，c分别是∠A，∠B，∠C的对边．若(a－2)2＋b－2＋|c－22 |＝0，则此三角形是(A)A．等腰直角三角形B．直角三角形C．等腰三角形D．钝角三角形3．如图，在△ABC中，AB＝AC，∠A＝36°，BD，CE分别是△ABC，△BCD的角平分线，则图中的等腰三角形有(A)A．5个B．4个C．3个D．2个4．某市在旧城改造中，计划在一块如图所示的△ABC空地上种植一草皮以美化环境，已知∠A＝150°，这种草皮每平方米售价a元，则购买这种草皮至少需要(B)A.300a元B．150a元C．450a元D．225a元5．等腰三角形一腰上的高与另一腰的夹角为20°，则顶角的度数是(C)A．70°B．110°C．70°或110°D．20°或160°6．如图，点A，B，C在同一条直线上，△ABD，△BCE均为等边三角形，连接AE 和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM, 则∠DMA的度数为(B)A．45°B．60°C．75°D．90°第6题图第7题图7．如图，∠AOB ＝120°，OP 平分∠AOB ，且OP ＝2.若点M ，N 分别在OA ，OB 上，且△PMN 为等边三角形，则满足上述条件的△PMN 有(D)A ．1个B ．2个C ．3个D ．3个以上二、填空题(每小题5分，共20分)8．命题“两条直线相交只有一个交点”的逆命题是__只有一个交点的两条直线一定相交__，它是__真__命题．9．如图，在△ABC 中，AB ＝AC ，AD ，CE 是三角形的高，垂足为D ，E ，若∠CAD ＝20°，则∠BCE ＝__20°__．第9题图第10题图10．如图，在Rt △ABC 中，∠C ＝90°，点D 在线段BC 上，且∠B ＝30°，∠ADC ＝60°，BC ＝3，则BD 的长度为__2__．11．在△ABC 中，AB ＝22 ，BC ＝1，∠ABC ＝45°，以AB 为边作等腰直角三角形ABD ，使∠ABD ＝90°，连接CD ，则线段CD 的长为．三、解答题(共45分)12．(8分)如图，AC ⊥BC ，BD ⊥AD ，AC ，BD 相交于点O ，AC ＝BD .(1)求证：BC ＝AD ；(2)求证：△OAB 是等腰三角形．证明：(1)∵AC ⊥BC ，BD ⊥AD ，∴∠D ＝∠C ＝90°，在Rt △ADB 与Rt △BCA 中，⎩⎪⎨⎪⎧AB ＝BA ，AC ＝BD ， ∴Rt △ABD ≌Rt △BAC (HL)，∴BC ＝AD (2)由(1)得，∠DBA ＝∠CAB ，∴OA ＝OB ，即△OAB 是等腰三角形13．(12分)如图，△ABC 为等边三角形，∠1＝∠2＝∠3.(1)求∠BEC 的度数；(2)△DEF 是等边三角形吗？请说明理由．解：(1)∠BEC＝∠ADE＋∠DFE＝∠ABD＋∠2＋∠CAF＋∠1＝∠ABC＋∠BAC＝60°＋60°＝120°(2)是等边三角形．理由：由(1)知∠DEF＝180°－120°＝60°.同理∠EDF＝∠DFE＝60°，∴△DEF是等边三角形14．(12分)如图，把长方形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处．(1)求证：B′E＝BF；(2)设AE＝a，AB＝b，BF＝c，试猜想a，b，c之间的一种关系，并给予证明．解：(1)证明：由题意得B′F＝BF，∠B′FE＝∠BFE.又∵AD∥BC，∴∠B′EF＝∠BFE，∴∠B′FE＝∠B′EF，∴B′F＝B′E，∴B′E＝BF(2)a，b，c的关系为a2＋b2＝c2，连接BE，则BE＝B′E，由(1)知B′E＝BF＝c，∴BE＝c.∵AE2＋AB2＝BE2，又∵AE＝a，AB＝b，∴a2＋b2＝c2(若写a＋b>c也可以)15．(13分)(1)操作发现：如图①，D是等边三角形ABC边BA上一动点(点D与点B 不重合)，连接DC，以DC为边在BC上方作等边三角形DCF，连接AF.你能发现AF与BD之间的数量关系吗？并证明你发现的结论；(2)类比猜想：如图②，当动点D运动至等边三角形ABC边BA的延长线上时，其他作法与(1)相同，猜想AF与BD在(1)中的结论是否仍然成立？(3)深入探究：如图③，当动点D在等边三角形ABC边BA上运动时(点D与点B不重合)，连接DC，以DC为边在BC上方，下方分别作等边三角形DCF和等边三角形DCF′，连接AF，BF′，探究AF，BF′与AB有何数量关系？并证明你探究的结论．解：(1)AF＝BD，证明△ACF≌△BCD(SAS)(2)仍成立(3)AF＋BF′＝AB，证明：由(1)知，AF＝BD，易证△ACD≌△BCF′(SAS)，∴BF′＝AD，∴AF＋BF′＝BD＋AD＝AB。

八年级(上)第8周周测数学试卷

八年级上期数学周测（八）考试时间：120分钟班级姓名学号考点：A 卷（共100分）一、选择题（本大题共10个小题，每小题3分，共30分）3.（2015•余姚市模拟）函数y=中，自变量x 的取值范围是（）A ．x>-1 B.x>-1且x ≠1 C ．x ≥-1 D. x ≥-1且x ≠1图8-14.已知点P 的坐标为，且点P 到两坐标轴的距离相等，则点P 的坐标是（） A ．（3，3） B ．（3，－3） C ．（6，－6） D ．（3， 3）或（6，－6） 5.如图8-2，直线AB 对应的函数表达式是（）A ．3y x 32=-+B ．3y x 32=+ C ．2y x 33=-+ D ．2y x 33=+6.（2014•黔南州）正比例函数y=kx （k≠0）的图象在第二、四象限，则一次函数y=x+k 的所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y（km）与已用时间图8-3 图8-4 图8-5二．填空题（本大题共4个小题，每小题4分，共16分）11.在一次函数y=kx+2中，若y随x的增大而增大，则它的图象不经过第象限．12.（2012•淮安）如图8-4，射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中s、t分别表示行驶距离和时间，则这两人骑自行车的速度相差km/h．13.如图8-5所示中的折线ABC为甲地向乙地打长途电话需付的电话费y（元）与通话时间t（分钟）之间的函数关系，则通话8分钟应付电话费元．14.（2014•成都）在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1y2．（填“＞”“＜”或“=”）三．解答题（本大题共6个小题，共54分）15．（本小题满分8分，每题4分）（1（2）解方程()221(2)x-=-16．（本小题满分10分，每小题5分）（1）（2010•密云县）已知一次函数y=kx﹣3的图象经过点M（﹣2，1），求此图象与x、y 轴的交点坐标．（2）如图8-6所示，已知正比例函数y=kx经过点P（2，3），将该直线向上平移3个单位，求平移后所得直线的解析式．图8-6 17．（本小题满分8分）已知函数y=﹣2x+6与函数y=3x﹣4．（1）在同一平面直角坐标系内，画出这两个函数的图象；（2）求这两个函数图象的交点坐标；（3）根据图象回答，当x在什么范围内取值时，函数y=﹣2x+6的图象在函数y=3x﹣4的图象的上方？18．（本小题满分8分）（2014•珠海）为庆祝商都正式营业，商都推出了两种购物方案．方案一：非会员购物所有商品价格可获九五折优惠，方案二：如交纳300元会费成为该商都会员，则所有商品价格可获九折优惠．（1）以x（元）表示商品价格，y（元）表示支出金额，分别写出两种购物方案中y关于x 的函数解析式；（2）若某人计划在商都购买价格为5880元的电视机一台，请分析选择哪种方案更省钱？19．（本小题满分10分）将正面分别标有数字1，2，3，4，6，背面花色相同的五张卡片洗匀后，背面朝上放在桌面上，从中随机抽取两张．（1）写出所有机会均等的结果，并求抽出的两张卡片上的数字之和为偶数的概率；（2）记抽得的两张卡片的数字为（a，b），求点P（a，b）在直线y=x﹣2上的概率．20.（本小题满分10分）（2014•绍兴）已知甲、乙两地相距90km，A，B两人沿同一公路从甲地出发到乙地，A骑摩托车，B骑电动车，图中DE，OC分别表示A，B离开甲地的路程s（km）与时间t（h）的函数关系的图象，根据图象解答下列问题．（1）A比B后出发几个小时？B的速度是多少？（2）在B出发后几小时，两人相遇？B 卷(50分)一．填空题：(每题4分,共20分)21.（2015•丹东模拟）函数中，自变量x 的取值范围是．22.已知一次函数5)12(232+-=-mx m y 的图象过第一、二、四象限，则m =___23.一次函数y=kx+b （k ，b 为常数，且k ≠0）的图象如图8-7所示，根据图象信息可求得关于x 的方程kx+b=0的解为．图8-7 图8-824.如图8-8，一次函数y=kx+b 的图象与正比例函数y=2x 的图象平行，且经过点A （1，﹣2），则kb= ．25.已知A （4，0），AB=5，点B 坐标轴上，则B 点的坐标为二、解答题（本小题共三个小题，共30分） 26. （本小题满分8分）若x =,y =，求(1)xy y x 和+的值；（2）求223y xy x +-的值27. （本小题满分10分）（2015•未央区二模）小东从A 地出发以某一速度向B 地走去，同时小明从B 地出发以另一速度向A 地而行，如图所示，图中的线段y 1，y 2分别表示小东、小明离B 地的距离（千米）与所用时间（小时）的关系．（1）试用文字说明：交点P 所表示的实际意义．（2）试求出A ，B 两地之间的距离．28. （本小题满分12分）（2015•建邺区二模）小林家、小华家与图书馆依次在一条直线上．小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书，已知小林到达图书馆花了20分钟．设两人出发x（分钟）后，小林离小华家的距离为y（米），y与x的函数关系如图所示．（1）小林的速度为米/分钟，a=，小林家离图书馆的距离为米；（2）已知小华的步行速度是40米/分钟，设小华步行时与家的距离为y1（米），请在图中画出y1（米）与x（分钟）的函数图象；（3）小华出发几分钟后两人在途中相遇？。

2022年八年级数学下册周周卷二特殊的平行四边形习题课件新版新人教版

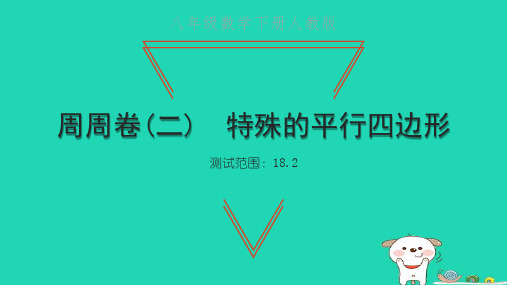
(2)若AE＝6，BF＝8，CE＝3，求四边形 A解：B过C点DF作的FG面⊥B积C于点. G.
∵四边形ABEF是菱形，AE＝6，BF＝8，AE⊥BF，
∴OE＝ 1 AE＝3，OB＝ 1 BF＝4，
2
2
∴BE＝ OB2 + OE2 ＝5，∴BC＝BE＋CE＝8.
∵S菱形ABEF＝
1 2
AE·BF＝BE·FG，即 1
– C.75°
– D.80°
7.如图，已知O是矩形ABCD的对角线的交点，∠AOB＝60°，DE∥AC，CE∥BD， DE，CE相交于点E.若四边形OCED的周长
B
是–2A0.5，则BC的长是 ( – B.5 )
3
– C.10
– D.10
3
8.如图，在四边形ABCD中，E是AB上的一点，△ADE和△BCE都是等边三角形，CP， Q–，A.M等腰，梯N形分别为AB，BC，CD，DA的中点，则–四B.矩边形形MNPQ是( )
13.如图，O是矩形ABCD的对角线AC的中点，菱形2 3ABEO的边长为2，则BC的长为
________.
14.如图，在正方形ABCD中，点P在边AB
上，AE⊥DP于点E，3 CF⊥DP于点F.若AE ＝4，CF＝7，则EF＝________.
15.如图，将两条宽度都为3的纸片重叠在一起，使∠6A3BC＝60°，则四边形ABCD 的面积为________.
附加题(20分)
如图，在矩形ABCD中，AD＝6，DC＝7，菱形EFGH的
三个顶点E，G，H分别在矩形ABCD的边AB，CD，AD上
，AH＝2，连接CF.
2
(1)当四边形EFGH为正方形时，6 DG的长为________；

人教版八年级数学下册-第十九章一次函数周周测1(19.1)

第十九章一次函数周周测1一选择题1.对圆的周长公式2c r π=的说法正确的是（）A. π.r 是变量，2是常量B.C.r 是变量，π.2是常量 C. r 是变量，2.π.C 是常量D. C 是变量，2.π.r 是常量2.当圆的半径发生变化时，圆的面积也发生变化，圆的面积S 与半径r 的关系为S =2rπ下列说法正确的是（）.A.S .π.r 都是变量B. 只有r 是变量C. S .r 是变量， π是常量D. S .π.r 都是常量 3.函数y =的自变量的取值范围是（）A .x ≥-2B .x ＜ -2C .x ＞-2D .x ≤ -24.下列各点：①（0，0）；②（1，-1）；③（-1，-1）；④（-1，1），其中在函数2xy x =+的图像上的点（） A .1个 B .2个 C .3个 D .4个5.下列给出的四个点中，在函数y =3x +1的图像上的是（） A ．（1，4） B.（0，-1） C.（2，-7） D.（-1，2）6.一家校办工厂2013年的年产值是15万元，计划从2014年开始，每年增加2万元，则年产值（从2013年开始）y （万元）与年数x 的函数关系式是（）. A.215y x =- （0x ≥的整数） B. 215y x =+（0x ≥的整数） C.152y x =+ （0x ≥的整数） D.152y x =-（0x ≥的整数）7.下列四个图象中，表示某一函数图象的是（）8.下列图形中的曲线不表示y 是x 的函数的是（）.9.小明骑自行车上学，一开始以某一恒定的速度行驶，但行驶至途中自行车发生了故障，只好停下来修车，车修好后，因怕耽误了上课，他比修车前加快了骑车的速度，下面四BACD幅图中最能反映小明这段行程的是（）OtsOtsOtsstOCDBA10.当圆的半径变化时，它的面积也相应的发生变化.圆面积S 与半径r 之间的关系式为S =πr 2，下列说法正确的是（）A.S .π.r 都是自变量B.S 是自变量，r 是因变量C.S 是因变量，r 是自变量D.以上都不对11.下列关系式：①x 2-3x =4；②S =3.5t ；③y =32x ；④y =5x -3；⑤C=2πR ；⑥S =v 0t+21at 2；（v 0和a 均为常数值）⑦2y +y 2=0，其中不是函数关系的是（） A.①⑦ B.①②③④ C.④⑥ D.①②⑦ 12.下列各种图象中，y 不是x 的函数的是（）13.甲.乙两同学骑自行车从A 地沿同一条路到B 地,已知乙比甲先出发,他们离出发地的距离S (km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.根据图象信息,以上说法正确的有（） A.1个B.2个C.3个D.4个14.某蓄水池的横断面示意图如图，分深水区和浅水区，如果这个注满水的蓄水池以固定的流量把水全部放出．下面的图象能大致表示水的深度h 和放水时间t 之间的关系的是（）x yO A xyO x yO x yO B C D15.三军受命，我解放军各部奋力抗战在救灾一线.现有甲.乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到该小镇只有唯一通道,且路程为24km .如图是他们行走的路程关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是（）A.1B.2C.3D.4二填空题16.函数的三种表示方法是_________.___________. . 17.下列变量间的关系是函数关系的有___ __（填序号）①正方形的周长与边长； ②圆的面积与半径；③y x = ④商场中某种商品的单价为a 元，销售总额与销售数量18.某物体从上午7时至下午4时的温度M （℃）是时间t(h)的函数：35100m t t =-+ (其中t=0表示中午12时，t=-1表示上午11时，t=1表示13时)，则上午10时此物体的温度为 ℃19..如图是甲.乙两个施工队修建某段高速公路的工程进展图，从图中可见施工队的工作效率更高.h tO A ．ht O B ．h t Oht OD ．h20.如图所示的函数图象反映的过程是：小红从家去书店，又去学校取封信后马上回家，其中x 表示时间，y 表示小红离她家的距离，则小红从学校回家的平均速度为 _____ 千米/小时.三解答题21.在等腰△ABC 中，底角x 为（单位：度），顶角y （单位：度）（1）写出y 与x 的函数解析式;（2）求自变量x 的取值范围.22.下面是小林画出函数1021+-=x y 的一部分图象，利用图象回答：（1）自变量x 的取值范围.（2）当x 取什么值时，y 的最小值.最大值各是多少？（3）在图中，当x 增大时，y 的值是怎样变化？x10y5O第十九章一次函数周周测1试题答案1. B2. C3. A4. B5. A6. A7. A8. C9. C 10. C 11. A 12. B 13. B 14. D 15. D16.图像法，列表法，公式法 17. ①②④ 18. 102 19. 甲 20. 6 21.解（1）y=180-2x （2）0＜x ＜9022.解（1）0＜x ＜10（2）由图象得，当x=0时，y 最大，此时y=10；当x=10时，y 最小，此时y=5. （3）当x 增大时，y 减小.第十九章一次函数周周测6一选择题 1．如图，函数和的图象相交于点，则不等式的解集为（）A. B. C. D.2．一次函数y=kx+b的图象如图所示，不等式kx+b＞0的解集是（）A. x＞2B. x＞4C. x＜2D. x＜43．一次函数y1=kx+b与y2=mx+n的部分自变量和对应函数值如下表：x …0 1 2 3 …y1… 2 32112…x …0 1 2 3 …y2…﹣3 ﹣1 1 3 …则关于x的不等式kx+b＞mx+n的解集是（）A. x＞2B. x＜2C. x＞1D. x＜14．观察函数y1和y2的图象，当x=0，两个函数值的大小为（）A. y1＞y2B. y1＜y2C. y1=y2D. y1≥y25.6月份以来，猪肉价格一路上涨．为平抑猪肉价格，某省积极组织货源，计划由A、B、C三市分别组织10辆、10辆和8辆运输车向D、E两市运送猪肉，现决定派往D、E 两地的运输车分别是18辆、10辆，已知一辆运输车从A市到D、E两市的运费分别是200元和800元，从B市到D、E两市的运费分别是300元和700元，从C市到D、E 两市的运费分别是400元和500元．若设从A、B两市都派x辆车到D市，则当这28辆运输车全部派出时，总运费W（元）的最小值和最大值分别是（）A．8000，13200 B．9000，10000 C．10000，13200 D．13200，154006．如图，是一对变量满足的函数关系的图象．有下列3个不同的问题情境：①小明骑车以400米/分的速度匀速骑了5分钟，在原地休息了4分钟，然后以500米/分的速度匀速骑回出发地，设时间为x分钟，离出发地的距离为y千米；②有一个容积为6升的开口空桶，小亮以1.2升/分的速度匀速向这个桶注水，注5分钟后停止，等4分钟后，再以2升/分的速度匀速倒空桶中的水，设时间为x分钟，桶内的水量为y升；③矩形ABCD中，AB=4，BC=3，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，当点P与点A不重合时，y=S△ABP；当点P与点A重合时，y=0，其中，符合图中所示函数关系的问题情境的个数为（）A．0 B．1 C．2 D．3 7.．甲、乙二人从学校出发去科技馆，甲步行一段时间后，乙骑自行车沿相同路线行进，两人均匀速前行，他们的路程差s（米）与甲出发时间t（分）之间的函数关系如图所示．下列说法：①乙先到达青少年宫；②乙的速度是甲速度的2.5倍；③b=480；④a=24．其中正确的是（）A．①②③B．①②④C．①③④D．①②③④二填空题8．如图，平面直角坐标系中，经过点B（﹣4，0）的直线y=kx+b与直线y=mx+2相交于点A(-32,-1)，则不等式mx+2＜kx+b＜0的解集为_____．9．函数y=kx+b 的图象如图所示，则方程kx+b=0的解为________，不等式kx+b>0的解集为_________，不等式kx+b －3>0的解集为________．10．一次函数y=kx+b 的图象经过A(-1，1）和B(- ，0），则不等式组的解为________________.11．已知一次函数的图象过点()35，与()49--，，那么这个函数的解析式是__________，则该函数的图象与y 轴交点的坐标为__________________. 12．如图，直线y ＝kx ＋b 上有一点P (－1，3)，回答下列问题：(1)关于x 的方程kx ＋b ＝3的解是_______． (2)关于x 的不等式kx ＋b >3的解是________． (3)关于x 的不等式kx ＋b －3<0的解是______． (4)求不等式－3x ≥kx ＋b 的解． (5)求不等式(k+3)x ＋b >0的解．三解答题13．画出函数y ＝2x －4的图象，并回答下列问题： (1)当x 取何值时，y ＞0?(2)若函数值满足－6≤y ≤6，求相应的x 的取值范围．14．已知：直线与轴交于点，与轴交于点，坐标原点为．（）求点，点的坐标．（）求直线与轴、轴围成的三角形的面积．（）求原点到直线的距离．15．在平面直角坐标系xoy 中，已知一次函数()10y mx m =≠与()20y kx b k =+≠相交于点()12A ，，且()20y kx b k =+≠与y 轴交于点()03B ，．（1）求一次函数1y 和2y 的解析式；（2）当120y y >>时，求出x 的取值范围．16．已知直线y=kx+5交x 轴于A ，交y 轴于B 且A 坐标为（5，0），直线y=2x ﹣4与x 轴于D ，与直线AB 相交于点C ．（1）求点C 的坐标；（2）根据图象，写出关于x 的不等式2x ﹣4＞kx+5的解集；（3）求△ADC 的面积．17．水果商贩小李去水果批发市场采购被誉为“果中之王”的泰顺猕猴桃，他了解到猕猴桃有精品盒与普通盒两种包装，精品盒的批发价格每盒60元，普通盒的批发价格每盒40元，现小李购得精品盒与普通盒共60盒，费用共为3100元。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级数学第八周周测题
初二（）班学号姓名成绩
一选择题（每题4分，共20分）
1、下列分式中是最简分式是（）
A 、2222n m n m +-
B 、9322-+m m m
C 、22
2)
(y x y x +- D 、222)(n m n m -- 2、57000000-用科学记数表示为( )
Ａ、61057⨯- Ｂ、6107.5⨯- Ｃ、7107.5⨯ Ｄ、7107.5⨯-
3、选择:以下各组数为边长,不能组成直角三角形的是( )
A 、5,4,3.
B 、8,10,6.
C 、7,25,24
D 、13,12,5
4、反比例函数x
k y 2
=的图象在（）。

A 、第一、二象限 B 、第一、三象限 C 、第二、四象限 D 、第三、四象限
5、函数y=kx+1与函数y=
k x
在同一坐标系中的大致图象是（• ）．
二填空题（每题4分，共20分）
6、
12+-=x y 的图象经过象限，y 随x 的增大而。

7、当x_________时，分式242--x x 的值为0。

8、22
+-=a x
y 是反比例函数，则a= 。

9、如右上图，反比例函数在第二象限的图象，点A 是图象上一点，A B ⊥x 轴，垂足为B ，0是原点，若△AOB 的面积为3，则这个反比例函数的解析式为。

10、“两直线平行,内错角相等”的逆命题是: ,它是命题。

三解答题（每题10分，共60分）
11、已知反比例函数y=k x
的图象与一次函数y=kx+m 的图象相交于点（2，1）。

（1）求反比例函数的解析式； 2）求一次函数的解析式。

D C
B A
12、计算
2
2
21
1
x x
x
-+
-
÷
2
1
x
x x
-
+
13、解方程4
2
3
5
3
2
=
-
-
-x
x
x
14、做一批机器零件，小明做120个与小婷做90个所用的时间相同，已知小明每天比小婷多做10个，问小明、小婷每天分别做多少个？
15、若等腰三角形的腰长为10cm,底边长为16cm,求底边上的高。

16、在△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于D点,求CD的长。