03_06_晶格热容的量子理论
合集下载
固体物理：3-6晶格热容的量子理论
固体热容主要来自两部分贡献
一是来源于晶格热振动，称为晶格热容； 是固体热容的主要贡献，是本节的主要讨 论内容；
一是来源于电子热运动，称电子热容； 一般贡献很小，除非在很低温度情况下。
求解CV的一般方法
固体中的热容一般指定容比热容CV， 在热力学中，
CV
(
E T
)V
其中，E是指固体的平均内能。
第一步：写出 E 的表达式； 第二步：代入公式计算CV。
j
j
e j / kBT
1
j
(
j )2 e kBT
CVj
(
dE j (T dT
)
)V
kB
kBT
j
(e kBT 1)2
（3）晶格总热容
设晶体中包括N个原子，共有3N个简谐振动模式，则
E(T )
3N
j 3N
E j (T )
CV CV j
j
其中E
j
(T
)
1 2
j
e j
j
1
CVj
(
(1 z)2 n0
讨论： 因为x ,则 D ;
kBT
T
令z
e
x
,
则
x (e x
4e x 1) 2
x 4e x (1 ex )2
x 4e x (n 1)e nx
n0
x4e x
(e x 1)2
x 4 (n 1)e (n1) x
n0
x 4 ne nx
n1
(二)Debye模型的讨论--- 低温情况
gD(
)
gl
(
)
2gt (
)
V 2 2 2
(
3.8-晶格热容的量子理论
得到在用频率表示的，在频率范围ω到ω＋dω内
的纵波数目为
V 4 q2dq (2 )3
V 2d 2 2Cl3
类似地可写出横波的数目为
2
V
2 2Ct3
2d
加起来得到ω到ω＋dω内的总格波的模式数
V
2 2
(
1 Cl3
2 Ct3
)
2
d
V
2 2
3 C
2d
g() d
g ( )
3V
2 2 C3
2
g(ω) 称为振动的频率分布函数或振动模的态密度函数
CV
(T
/
D
)
9R
T D
3
D /T 0
4e
e 1
2 d
ΘD: Debye 温度
所以按照 Debye 理论, 一种晶体的热容量完全由它的 Debye 温度确定
ΘD 可以根据实验的热容量值来确定, 使理论的 CV 和实验值尽可能符合的好
Debye 理论与实验比较 (镱)
低温测量技术的发展暴露出 Debye 理论与实际间仍存 在显著的偏离。一个常用的比较理论与实验的办法是 在各不同温度令理论函数 CV(T/ ΘD) 与实验值相等
根据周期性边界条件, 允许的 q 值在 q 空间形成均匀 分布的点, 在体积元 dk = dkxdkydkz 中数目为
V
(2 )3 dk
V 表示所考虑的晶体的体积， V/(2π)³是均匀分布 q 值的“密度”
q 虽然不能取任意值, 但由于 V 是一个宏观的体积, 允许的 q 值在 q 空间是十分密集的, 可以看成是准 连续的, 纵波、横波频率的取值也同样是准连续的
格波的个数[(q)取值数]=晶体的自由度数
3.5 晶格热容的量子理论
2
将系数用ωm 表示
ℏω ℏω / kBT 3ω e m 1 k BT CV (T ) = 9 R ω 2 dω ∫ ωm 0 ( e ℏω / kBT − 1)2
2
kT = 9R ℏωm
3 ℏω / kT m
∫
0
(e
ξ 4 eξ
低温极限有特别意义, 在一定的温度 T, ħω >> kBT 的振动对热容几乎没有贡献, 热容主要来自
ɶ ℏω < k BT
的振动模。所以在低温极限, 热容决定于最低频率 的振动, 这些正是波长最长的弹性波 前面已经指出, 当波长远远大于微观尺 度时, Debye 的宏观近似是成立的。因此, Debye 理论在低温的极限是严格正确的
− β ℏω j
1 E j (T ) = ℏω j + − β ℏω j 2 1− e
ℏω j e
ℏω j 1 = ℏω j + β ℏω j 2 e −1
前一项为零点能，后一项代表平均热能 求内能对 T 的微商得到晶格热容
ℏω j ℏω j / kBT e d E j (T ) k BT = kB 2 ℏω j / k B T dT e −1
0
显然将发散
换句话说, 振动模的数目是无限的 这是因为理想的连续介质包含无限的自由度 然而实际晶体是由原子组成的, 如果晶体包含 N 个原子, 自由度只有 3N 个 表现出德拜模型的局限性
波长远大于微观尺度时, Debye 的 宏观处理方法应当是适用的 但当波长已短到和微观尺度可比, 以至更短时, 宏观模型必然会导致很大的偏差以致完全错误 Debye 的解决办法: 假设 ω大于某一ωm 的短波实际 上不存在, 而对ωm 以下的振动都应用弹性波的近似 ωm 则根据自由度确定
将系数用ωm 表示
ℏω ℏω / kBT 3ω e m 1 k BT CV (T ) = 9 R ω 2 dω ∫ ωm 0 ( e ℏω / kBT − 1)2
2
kT = 9R ℏωm
3 ℏω / kT m
∫
0
(e
ξ 4 eξ
低温极限有特别意义, 在一定的温度 T, ħω >> kBT 的振动对热容几乎没有贡献, 热容主要来自
ɶ ℏω < k BT
的振动模。所以在低温极限, 热容决定于最低频率 的振动, 这些正是波长最长的弹性波 前面已经指出, 当波长远远大于微观尺 度时, Debye 的宏观近似是成立的。因此, Debye 理论在低温的极限是严格正确的
− β ℏω j
1 E j (T ) = ℏω j + − β ℏω j 2 1− e
ℏω j e
ℏω j 1 = ℏω j + β ℏω j 2 e −1
前一项为零点能，后一项代表平均热能 求内能对 T 的微商得到晶格热容
ℏω j ℏω j / kBT e d E j (T ) k BT = kB 2 ℏω j / k B T dT e −1
0
显然将发散
换句话说, 振动模的数目是无限的 这是因为理想的连续介质包含无限的自由度 然而实际晶体是由原子组成的, 如果晶体包含 N 个原子, 自由度只有 3N 个 表现出德拜模型的局限性
波长远大于微观尺度时, Debye 的 宏观处理方法应当是适用的 但当波长已短到和微观尺度可比, 以至更短时, 宏观模型必然会导致很大的偏差以致完全错误 Debye 的解决办法: 假设 ω大于某一ωm 的短波实际 上不存在, 而对ωm 以下的振动都应用弹性波的近似 ωm 则根据自由度确定
固体物理-第三章 晶格振动及晶体的热学性质-8(新疆大学李强老师课件)
)
2
1 e
i / kBT
T 0, CVi 0
--- 与实验结果相符
低温时，固体热容趋向于0是一种量子效应。
Xinjiang University
Solid State Physics, Dr. Q. Li
2015-4-2
§3.8 晶体热容的量子理论
晶格热容的量子理论
2 2 1 i exp( i / kBT ) 1
解决的思路
格波波矢在波矢空间 ( 倒格子空间 ) 是均匀分布的，即 振动波矢分布函数g(q)是常数；
(2 )3 对三维晶体, 波矢空间中每 大小的区域中存在一个格波; V V 所以，振动波矢分布函数 g (q) (2 )3
利用色散关系, 可将波矢分布函数 g (q)转化为频率分布函数 g ( )
德拜Debye模型
e i / kBT 晶格热容 CV kB ( ) i / kBT 2 k T ( e 1) i B
3N
i
2
求和可化为积分 频率是准连续的
格波频率取决于波矢q (色散关系) 格波波矢q的取分立值 q 格波波矢q取值间隔 q
2
2 Na
2 h Na
保持体积不变 W 0
Solid State Physics, Dr. Q. Li
2015-4-2
§3.8 晶体热容的量子理论
热容 Heat Capacity
U U (V ) EL (V , T ) Ee (V , T )
晶体内能
晶体内聚能(势能) 晶格振动能
电子能量
U EL Ee 晶体定容热容 CV T T T V V V
3.6 晶格振动热容理论
e
E
T
2
1
E
T
2
(1
E
)
1 (1
E)2ຫໍສະໝຸດ 2T2T
E
T
2
E
eT
E
eT
e
E
2T
eE
2T
2
ex 1 x x2 x3 2! 3!
E
2
T E
1
E
2
x 4dx
CV
3 NkB
f
D
T
f D ---德拜热容函数
T
其中：
f
D
T
3
T
D
3
D
T
0
ex ex 1
2
x 4dx
3.高低温极限情况讨论
(1)当T较高时，x<<1，
f
D
T
dn2
2
V
(2 )3
4q2dq
2V
(2 )3
4 2
C2 t
d
Ct
V 42d 2V 42d
总的振动模式为：dn
(2 )3
C3 t
(2 )3
C3 t
所以模式密度为：
g
V 2
2π2
1 Cl3
2 Ct3
令
3 C3
1 Cl3
2 Ct3
所以
g
E
T
2
1
E
T
2
(1
E
)
1 (1
E)2ຫໍສະໝຸດ 2T2T
E
T
2
E
eT
E
eT
e
E
2T
eE
2T
2
ex 1 x x2 x3 2! 3!
E
2
T E
1
E
2
x 4dx
CV
3 NkB
f
D
T
f D ---德拜热容函数
T
其中：
f
D
T
3
T
D
3
D
T
0
ex ex 1
2
x 4dx
3.高低温极限情况讨论
(1)当T较高时，x<<1，
f
D
T
dn2
2
V
(2 )3
4q2dq
2V
(2 )3
4 2
C2 t
d
Ct
V 42d 2V 42d
总的振动模式为：dn
(2 )3
C3 t
(2 )3
C3 t
所以模式密度为：
g
V 2
2π2
1 Cl3
2 Ct3
令
3 C3
1 Cl3
2 Ct3
所以
g
固体物理学之晶格热容
hω0 2 hω0 / kBT ( ) e k BT CV = 3 Nk B hω0 / kBT (e − 1) 2
及其简单的 一个假定
上式为爱因斯坦热容函数。在与实际实验比 较中，可以尽量选取ω0使理论值和实验值尽 可能吻合。
晶格热容计算的简化模型 －－－爱因斯坦模型
爱因斯坦温度ΘE：
k B Θ E = hω
晶格热容计算的简化模型 －－－爱因斯坦模型
分析讨论：
按照上式可以作出格波振动能与频 率的关系曲线。可以看出，格波频 率越高，其热振动能越小。爱因斯 坦模型考虑的格波频率很高，热振 动能很小，对热容量贡献不大，当 温度很低时，就微不足道了。爱因 斯坦把所有格波都视为光学波，没 有考虑长声学波在甚低温下对热容 的主要贡献，导致理论热容合实验 热容在甚低温下的偏差很大。
E
0
ω
晶格热容计算的简化模型 －－－德拜模型
德拜模型：把格波当成弹性波考虑，而且考虑了频率分布。
ω = vq
德拜模型具体分析的是各向同性的弹性介质，对 于一定的波数矢量q，有一个纵波( ω = Cl q )和 两个独立的横波( ω = Ct q )。德拜模型中各种 不同的波矢q的纵波和横波，构成了晶体的全部 振动模。 传播方向垂直－－横波 传播方向平行－－纵波
2 hω j / k B T
C = kB
j V
1、量子理论值与频率和温度有关，温度趋于0时，晶体热容将趋于0 2、在高温极限情况下( k BT >> h ω j ⇒ h ω j / k B T << 1 )，把量子理论值表达式中 的指数按的级数展开，得到与经典理论值相同的结果。
dE j (T ) dT
∫
ωm
0
高二物理竞赛课件：晶体热容的量子理论
得到 Cv
定义德拜温度
有
9R
m3
m
0
(
k BT
)2
e
(e
/ k BT
/ k BT
1)
2
d
2
ΘD m / k B ，并令 m / k B
T 3 ΘD / T 4e
Cv 9R( )
d
2
0
Θ
(e 1)
R Nk B
晶体热容的量子理论
爱因斯坦模型忽略了各格波的频率差别
金刚石
11
晶体热容的量子理论
德拜模型
• 德拜模型的晶格振动假设方案：
• 以各向同性连续介质的弹性波来代表格波，非单一频率，
即 ω∝ q
• 格波包含有1个纵波和2个独立的横波
• 三种格波的波矢 q 在倒易空间均匀（准连续）分布
• 假设晶体中只存在小于某一ωm的长波以保证结果收敛
• 与实验结果相符合
j
Cv k B
k BT
/ k T
e j B
/ k T
j
B
1) 2
(e
2
2
1
/ k T 0
j
B
e
量子理论表明，晶体热容与晶格振动频率和温度有关系
晶体热容的量子理论
爱因斯坦模型
• 爱因斯坦模型的晶格振动假设方案：
2
j
B
1)
(e
2
与经典理论符合：振子的能量远远大于能量的量子
ℏ时，量子化效应可忽略，即
CV k B
与杜隆－ 珀替定律相符
晶体热容的量子理论
定义德拜温度
有
9R
m3
m
0
(
k BT
)2
e
(e
/ k BT
/ k BT
1)
2
d
2
ΘD m / k B ，并令 m / k B
T 3 ΘD / T 4e
Cv 9R( )
d
2
0
Θ
(e 1)
R Nk B
晶体热容的量子理论
爱因斯坦模型忽略了各格波的频率差别
金刚石
11
晶体热容的量子理论
德拜模型
• 德拜模型的晶格振动假设方案：
• 以各向同性连续介质的弹性波来代表格波，非单一频率，
即 ω∝ q
• 格波包含有1个纵波和2个独立的横波
• 三种格波的波矢 q 在倒易空间均匀（准连续）分布
• 假设晶体中只存在小于某一ωm的长波以保证结果收敛
• 与实验结果相符合
j
Cv k B
k BT
/ k T
e j B
/ k T
j
B
1) 2
(e
2
2
1
/ k T 0
j
B
e
量子理论表明，晶体热容与晶格振动频率和温度有关系
晶体热容的量子理论
爱因斯坦模型
• 爱因斯坦模型的晶格振动假设方案：
2
j
B
1)
(e
2
与经典理论符合：振子的能量远远大于能量的量子
ℏ时，量子化效应可忽略，即
CV k B
与杜隆－ 珀替定律相符
晶体热容的量子理论
热容的量子理论
27
德拜模型
德拜模型认为：
热容的量子理论
晶体对热容的贡献主要是弹性波的振动，即 较长的声频支在低温下的振动 由于声频支的波长远大于晶格常数，故可将 晶体当成是连续介质，声频支也是连续的， 频率具有0～ωmax 高于ωmax的频率在光频支范围，对热容贡献 很小，可忽略
28
德拜模型
热容的量子理论
当温度较高时，T >> θD，Cv = 3Nk 当温度稳低时，T << θD，有：
25
爱因斯坦模型
当 T >> θE 时
热容的量子理论
故有
当T << θE时，有
26
爱因斯坦模型的缺陷
爱因斯坦模型中：
热容的量子理论
1 ）低温时， Cv 与温度按指数律随温度 而变化，与实验得出的按 T 的立方变化 规律仍有偏差。
2 ）问题主要在于基本假设：各个振子 频率相同有问题，各振子的频率可以不 同，原子振动间有耦合作用 。
＝元素 i 的摩尔热容。
经典热容理论的解释
按经典理论，能量按自由度均分。 每个原子三个振动自由度； 每个振动自由度的平均动能、平均位能均为
则一个原子的总能量为3kT。
1 kT ，即一个振动自由度能量为kT。 2
14
1mol 固体中有
个原子，总能量为
= 6.023×1023 / mol ＝阿佛加德罗常数， = R/N = 1.381×10-23 J/K ＝ 玻尔茨曼常数， = 8.314 J/ (k· mol)，T＝热力学温度（K）。
这就是按照量子理论求得的热容表达式。但要计算CV 必须知道谐振子的频谱——非常困难（very difficult）。
德拜模型
德拜模型认为：
热容的量子理论
晶体对热容的贡献主要是弹性波的振动，即 较长的声频支在低温下的振动 由于声频支的波长远大于晶格常数，故可将 晶体当成是连续介质，声频支也是连续的， 频率具有0～ωmax 高于ωmax的频率在光频支范围，对热容贡献 很小，可忽略
28
德拜模型
热容的量子理论
当温度较高时，T >> θD，Cv = 3Nk 当温度稳低时，T << θD，有：
25
爱因斯坦模型
当 T >> θE 时
热容的量子理论
故有
当T << θE时，有
26
爱因斯坦模型的缺陷
爱因斯坦模型中：
热容的量子理论
1 ）低温时， Cv 与温度按指数律随温度 而变化，与实验得出的按 T 的立方变化 规律仍有偏差。
2 ）问题主要在于基本假设：各个振子 频率相同有问题，各振子的频率可以不 同，原子振动间有耦合作用 。
＝元素 i 的摩尔热容。
经典热容理论的解释
按经典理论，能量按自由度均分。 每个原子三个振动自由度； 每个振动自由度的平均动能、平均位能均为
则一个原子的总能量为3kT。
1 kT ，即一个振动自由度能量为kT。 2
14
1mol 固体中有
个原子，总能量为
= 6.023×1023 / mol ＝阿佛加德罗常数， = R/N = 1.381×10-23 J/K ＝ 玻尔茨曼常数， = 8.314 J/ (k· mol)，T＝热力学温度（K）。
这就是按照量子理论求得的热容表达式。但要计算CV 必须知道谐振子的频谱——非常困难（very difficult）。
3.6 晶格振动的热容理论
vpq
—— 频率也近似于连续取值
频率在 d 之间振动模式的数目 dn D( )d
D( ) ——模式密度函数
i 2 e i / kBT 一个振动模的热容 Ci k B ( ) i / kBT 2 1) k BT ( e
晶体总的热容 CV
m
3N
e
i / k BT
i 1
) 3N
e 0 / k B T 1
0 / k BT
0
0 2 e E 热容 CV ( ) 0 / k BT )V 3Nk B ( 2 k BT ( e 1) T
0 CV 3 Nk B f E ( ) k BT
D
V 3 2 2 v p
3
0
2 e / k B T 2 kB ( ) / k B T d 2 k BT ( e 1)
机动 目录 上页 下页 返回 结束
V 3 晶体总的热容 CV 2 2 v p
令 x k BT D D xD k BT T
德拜温度
3
D
2 e / kBT 2 kB ( ) / kBT d 2 kBT (e 1) 0
D D kB
N 1/ 3 D v p [6 ( )] V
2
xD 4 x
T T 3 xe CV ( ) 3R [3( ) x dx] 2 D D 0 (e 1)
机动 目录 上页 下页 返回 结束
0 0 2 e 0 / kBT —— 爱因斯坦热容函数 )( ) 0 / kBT fE ( 2 1) k BT k BT ( e
爱因斯坦温度
0 k B E
0 E kB
热容的量子理论
二、热传导的微观机理 三、影响热导率的因素 四、某些无机材料的热导率
51
一、材料的热传导 1.热导率（导热系数）的定义：
当固体材料一端 的温度比另一端高时，热量会从热端自动地传向冷 端，这个现象就是热传导。
T1 T2 Q S L
：热能Q从高温端T1传递到低温端T2所需 要的时间 ：热导率（导热系数）
44
式中第一项为常数，第二项为零，则
式中，
则，
；
；如果只考虑上式的前两项，
即点阵能曲线是抛物线。原子间的引力为： 式中β是微观弹性系数，为线性简谐振动，平衡位置仍在
r0处，上式只适用于热容CV的分析。
但对于热膨胀问题，如果还只考虑前两项，就会 得出所有固体物质均无热膨胀。因此必须再考虑第三 项。此时点阵能曲线为三次抛物线，即固体的热振动 是非线性振动。用波尔兹曼统计法，可算出平均位移
6
光频支振动：格波中频率甚高的振动波， 质点彼此之间的位相差很大，邻近质点 的运动几乎相反时，频率往往在红外光 区，称为“光频支振动”。
特点： 1）频率较高，类似光波频率。 2）可认为相邻原子振动方向相反。
7
第一节 材料的热容
一、基本概念
热容：是物体温度升高1K所需要增加的能量。
（J/K）
显然，质量不同热容不同，温度不同热容也不同。
各种热容
比热容单位 — ,
摩尔热容单位—
平均热容 恒压热容 恒容热容 ，
。
范围愈大，精度愈差。
10
对于固体材料CP与CV差异很小，见图3.2。
二、晶态固体热容的经验定律（experience law）
1、杜隆一珀替定律：（元素的热容定律） 恒压下元素的原子热容为
51
一、材料的热传导 1.热导率（导热系数）的定义：
当固体材料一端 的温度比另一端高时，热量会从热端自动地传向冷 端，这个现象就是热传导。
T1 T2 Q S L
：热能Q从高温端T1传递到低温端T2所需 要的时间 ：热导率（导热系数）
44
式中第一项为常数，第二项为零，则
式中，
则，
；
；如果只考虑上式的前两项，
即点阵能曲线是抛物线。原子间的引力为： 式中β是微观弹性系数，为线性简谐振动，平衡位置仍在
r0处，上式只适用于热容CV的分析。
但对于热膨胀问题，如果还只考虑前两项，就会 得出所有固体物质均无热膨胀。因此必须再考虑第三 项。此时点阵能曲线为三次抛物线，即固体的热振动 是非线性振动。用波尔兹曼统计法，可算出平均位移
6
光频支振动：格波中频率甚高的振动波， 质点彼此之间的位相差很大，邻近质点 的运动几乎相反时，频率往往在红外光 区，称为“光频支振动”。
特点： 1）频率较高，类似光波频率。 2）可认为相邻原子振动方向相反。
7
第一节 材料的热容
一、基本概念
热容：是物体温度升高1K所需要增加的能量。
（J/K）
显然，质量不同热容不同，温度不同热容也不同。
各种热容
比热容单位 — ,
摩尔热容单位—
平均热容 恒压热容 恒容热容 ，
。
范围愈大，精度愈差。
10
对于固体材料CP与CV差异很小，见图3.2。
二、晶态固体热容的经验定律（experience law）
1、杜隆一珀替定律：（元素的热容定律） 恒压下元素的原子热容为
4-7 晶格热容的量子理论
E CV T V
E CP T P
其中 E 是固体的平均内能，它包括晶格振动能量和电子运动能量，
这两种运动能量对固体的热容都有贡献，分别称为晶格热容（lattice heat capacity) 和电子热容(electronic heat capacity)。 当温度不太低时，电子热容<<晶格热容,因此在温度不太低时，电子 的热容可以略去，因此我们在这只讨论晶格热容.另外，由于CV与CP 相差甚微，我们也只讨论定容热容。
Department of Physics, Northwest University
Solid State Physics
一、热容( heat capacity ) 1、晶格热容和电子热容 （lattice heat capacity and electronic heat capacity) 在热力学里，固体的定容热容和定压热容分别定义为
与经典值一致。
(
) (1
2
j
)
（6）
上式在量子理论的基础上说明了在较高温度时杜隆－珀替定律成立的 原因。实际上，当振子的能量远大于其能量量子时，量子化效应就可 以忽略。
Department of Physics, Northwest University
Solid State Physics
j 1
总热容为
CV
C
j 1
3N
j
V
j 1
3N
d E j (T ) dT
（9）
因此，对于晶格的热容，只要知道晶格的各简正振动的频率，就可以由上式直 接写出。对于具体的晶体，3N 个正则频率的计算是相当复杂的，常采用简化模型。
E CP T P
其中 E 是固体的平均内能，它包括晶格振动能量和电子运动能量，
这两种运动能量对固体的热容都有贡献，分别称为晶格热容（lattice heat capacity) 和电子热容(electronic heat capacity)。 当温度不太低时，电子热容<<晶格热容,因此在温度不太低时，电子 的热容可以略去，因此我们在这只讨论晶格热容.另外，由于CV与CP 相差甚微，我们也只讨论定容热容。
Department of Physics, Northwest University
Solid State Physics
一、热容( heat capacity ) 1、晶格热容和电子热容 （lattice heat capacity and electronic heat capacity) 在热力学里，固体的定容热容和定压热容分别定义为
与经典值一致。
(
) (1
2
j
)
（6）
上式在量子理论的基础上说明了在较高温度时杜隆－珀替定律成立的 原因。实际上，当振子的能量远大于其能量量子时，量子化效应就可 以忽略。
Department of Physics, Northwest University
Solid State Physics
j 1
总热容为
CV
C
j 1
3N
j
V
j 1
3N
d E j (T ) dT
（9）
因此，对于晶格的热容，只要知道晶格的各简正振动的频率，就可以由上式直 接写出。对于具体的晶体，3N 个正则频率的计算是相当复杂的，常采用简化模型。
热容的量子理论教学手段及教具：多媒体
课后作业
1． 举出在工程应用中你可能选用下列两类材料的例子： （1）低比热容材料；（2）高比热容材料。
2． 试比较在 973K 时 NaCl 及 MgO 的摩尔比热。 3.相变对热容、热焓如何影响
参考资料
1.《材料性能学》 王从曾编著 ，北京工业大学出版社，2001
2.《材料性能学》 张帆 周伟敏编著，上海交通大学出版社， 2009 3.《材料物理性能》 陈树川编著，上海交通大学出版社，1999
一、晶格振动
晶体内的原子并不是在各自的平衡位置上固定不动的。由于热运动，各原子离开了 它们的平衡位置，由于原子间的相互作用，有回到平衡位置的趋势。这两个矛盾相互作 用的结果，使每个原子在平衡附近作微振动。
图 9.1 晶体内原子振动实际平衡位置
第2 页
河北科技大学教案用纸
图 9.2 原子简谐振动示意图
第1 页
河北科技大学教案用纸
第九章
材料的热学性能 5-6 学时
本章内容：
9.1 热学性能的物理基础
0.5 学时
9.2 材料的热容
2 学时
9.3 材料的热膨胀
2 学时
9.4 材料的热传导
1 学时
重点：材料的热容、热膨胀、热传导的表征、物理本质及影响因素和应用
难点：材料的热容、热膨胀、热传导的机理
9.1 热学性能的物理基础
C=pC1+qC2
式中， p 、 q 各组元的原子百分比，C1、C2 各组元的摩尔热容。
该定律适用于金属化合物、中间相、固溶体和多相合金。
3.陶瓷材料的热容
主要由离子键和共价键组成，室温下几乎无自由电子，热容与温度关系更符合德拜模
型。在德拜温度附近趋近 25J/mol.K，
固体物理06-晶格振动的量子化理论
声子：
1. 声子是晶格格波的量子，它的能量等于 q 。一个格
波（一种振动模）称为一种声子。当这种振动模处于
1 nq q 本征态时，称为有 2
nq 个声子。
Байду номын сангаас
2. 电子或光子与晶格相互作用，交换能量以 q 为单位。 若电子从晶格获得 q 能量称为吸收一个声子，反之 称为放出一个声子。声子与声子相互作用，或声子与其 他粒子（电子或光子）相互作用时，声子数目并不守恒。 声子可以产生，也可以湮灭。其作用过程遵从能量守恒 和准动量守恒。
2
金刚石的热容 （TE=1320K） 高温下（T>>TE）CV 趋向经典 结果 温度下降时，CV 减 小 低温下（T<<TE）CV 趋向于0。
e TE / T TE CV 3 Nk 2 T e TE / T 1
2
1. 高温下
T TE , kT 0
这里的简正模式就是我们前面得到的本征模式，是全体晶格都 参与得振动模式。
量子化方程：
1 2 2 2 2 q Qq Q1 , Q2 , , Q N E Q1 , Q2 , , Q N Q q 2 q
3. 声子具有能量，也具有准动量，它的行为类似于电子或光 子，具有粒子的性质。但声子与电子或光子是有本质区别 的，声子只是反映晶体原子集体运动状态的激发单元，它 不能脱离固体而单独存在，它并不是一种真实的粒子。我 们将这种具有粒子性质，但又不是真实物理实体的概念称 为准粒子。声子是一种准粒子。 引入声子的概念不仅能简化对晶格振动的描述，更能反映 晶格集体运动的量子本质。
以上方程实际上是N个独立振子的方程
晶格比热容
������ Ω∗ 0
=
������ 2������
3
න ������ ������ Ԧ
������ Ω∗
由于s=1,2,…,3n，Ω∗ = 2������ 3 /Ω，������ = ������Ω
∞
න ������ ������ ������������ = 3������������
0
声子态密度
• 在q空间频率相等的所有模式处于一系列连续的曲面������������ ， 称为等频率面 • 由于������ 3 ������ = ������������������ ������������⊥ ，������������ = ������������ ������������ ������ ∙ ������������⊥
一、声子态密度
• 在温度下，晶格的平均热能是 ������ ������ ������, ������ = ������������������
������,������
−1
1 ������ + ℏ������������ ������ Ԧ 2
其中������������������ = ������ ℏ������ /������������ ������ − 1
• 热容是固体原子热运动在宏观性质上的最直接体现， 因而对固体原子热运动的认识实际上首先是从固体 热容研究开始的，并得出了原子热运动能量是量子 化的这个无可争辩的结论。我们讨论固体热容仍是 以揭示原子热运动特征为目的，而完整地介绍热容 统计理论应是统计物理的内容。 • 固体热容由两部分组成：一部分来自晶格振动的贡 献，称为晶格热容；另一部分来自电子运动的贡献， 称为电子热容。除非在极低温度下，电子热容是很 小的（常温下只有晶格热容的1%）。这里我们只讨 论晶格热容。
=
������ 2������
3
න ������ ������ Ԧ
������ Ω∗
由于s=1,2,…,3n，Ω∗ = 2������ 3 /Ω，������ = ������Ω
∞
න ������ ������ ������������ = 3������������
0
声子态密度
• 在q空间频率相等的所有模式处于一系列连续的曲面������������ ， 称为等频率面 • 由于������ 3 ������ = ������������������ ������������⊥ ，������������ = ������������ ������������ ������ ∙ ������������⊥
一、声子态密度
• 在温度下，晶格的平均热能是 ������ ������ ������, ������ = ������������������
������,������
−1
1 ������ + ℏ������������ ������ Ԧ 2
其中������������������ = ������ ℏ������ /������������ ������ − 1
• 热容是固体原子热运动在宏观性质上的最直接体现， 因而对固体原子热运动的认识实际上首先是从固体 热容研究开始的，并得出了原子热运动能量是量子 化的这个无可争辩的结论。我们讨论固体热容仍是 以揭示原子热运动特征为目的，而完整地介绍热容 统计理论应是统计物理的内容。 • 固体热容由两部分组成：一部分来自晶格振动的贡 献，称为晶格热容；另一部分来自电子运动的贡献， 称为电子热容。除非在极低温度下，电子热容是很 小的（常温下只有晶格热容的1%）。这里我们只讨 论晶格热容。
孙会元固体物理基础第四章晶格振动和晶体的热性质4.4 晶格比热
e e
s ( q )
k BT
FBZ
s ( q )
k BT
第一布里渊区是多面体,所以很难精确计算.需要 做近似处理.常用近似有德拜(Debye)近似或叫德 拜模型和爱因斯坦模型(Einstein model).
上述积分既要考虑所有的 s (q ) ,又要考虑到
2 s (q ) q 2 dq 2 k T B 1
kBT 3 kBT cs (q )( x) V dxd cs (q ) cs (q ) x 3 T s e 1 8 3 2 3 4 3 (k T ) 1 d Vx dx 2 c
B
T
3
c (q )
s s
3
8
3
0
e 1
x
二、晶格比热的量子理论 晶体可以看成是一个热力学系统,在简谐近似下,晶格 中原子的热振动可以看成是相互独立的简谐振动.每个 谐振子的能量都是量子化的。 第s个谐振子的能量为：
1 s nqs s (q) 2
nqs 是频率为s的谐振子的平均声子数，满足波色统 计：
nqs (T ) e 1
1
e
s ( q )
s (q )
k BT
1
kBT
k B 3pNk B
qs 3 pN
e 1 pN为晶体中原子总数，所以每个原子对比热的贡献为3kB
k BT
CV qs T
3 pN
s ( q )
s (q )
这就是杜隆—贝蒂定律(Dulong-Petit law) 如果在展开式中取温度的更高次项,就可给出对 该定律的高温量子力学修正,我们这里不再讨论.
晶格比热容的量子理论
§3-5 晶格比热容的量子理论研究固体的比热容是探索固体微观结构与运动机理和重要手段。
固体物理学中的比热容一般是指定容比热容，即()()V VE T C T T ⎛⎫∂= ⎪∂⎝⎭…………………………………………………………(3-5-1)其中()E T 为固体在温度T 时的热力学平均能量。
()V C T 主要是由两部分组成，即()()()V Vc Ve C T C T C T =+………………………………………………………(3-5-2)其中()Vc C T 是晶格（离子）热运动的结果，称晶格比热容；()Ve C T 是电子热运动的结果，称为电子比热容。
电子比热容仅在低温下才起作用。
本节仅涉及晶格比热容。
3. 5. 1 经典理论的困难如果不考虑量子效应，用经典的能量均分定理求N 个原子三维运动的总能量E 。
设晶体有N 个原子，则自由度数为3N ，根据经典统计的能量均分定理，每个简谐振动的平均能量为j B E k T =，因而晶体的总能量为3B E Nk T =，比热容为() 3V B C T Nk =，摩尔比热容为V 0B C (T) =3N k =3R （大约为-125J K mol ⋅⋅），是一个与材料性质和温度无关的常数，此即为杜隆—珀替定律。
该定律在高温下成立，但在低温下不成立。
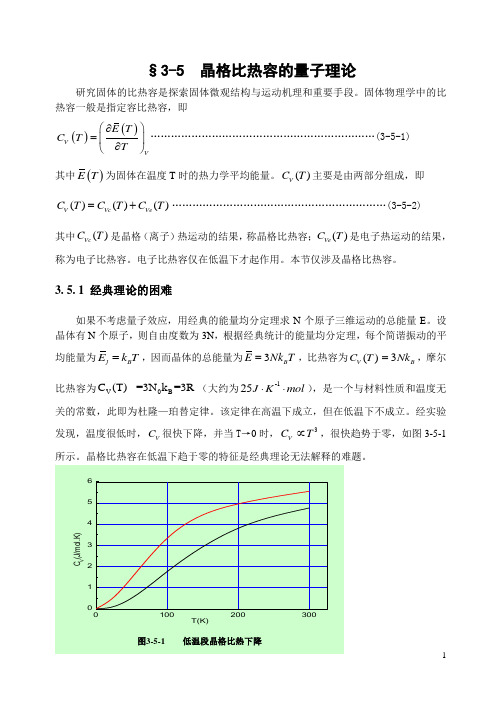
经实验发现，温度很低时，V C 很快下降，并当T →0时，3V C T ∝，很快趋势于零，如图3-5-13. 5. 2 晶格比热的一般公式我们知道，晶体中原子的热振动可归结为3N 个相互独立的简谐振动模。
每个谐振子的能量均是量子化的。
由于量子化，使得每个振动平均热运动能量不再是B k T ，如果忽略零点能，而成为()() j j n ω q q ，则由式（3-3-14）可得：()B ()1j j j k T E T eωω=- ……………………………………………………………(3-5-3)晶体的总的能量为：()B 3()11j Nj k T j E T eωω==-∑…………………………………………………………(3-5-4)晶体的总热容：()()()()3311N N j j V V Vj j VdE T E T C T C T C T dT ==⎛⎫∂=== ⎪∂⎝⎭∑∑或……………………(3-5-5) 但在具体计算过程中碰到了求和的困难，计算出成果N 个简正振动频率往往是十分复杂的。
材料物理读书笔记
读书笔记第四章 晶格振动Ⅱ—热学性质晶态固体的热学性质来源于固体中原子的振动（晶格振动）和电子运动两方面的贡献，本章主要讨论与晶格振动密切相关的热学性质（热容、热导及热膨胀等），或者说晶格振动对热学性质的贡献。
4.1固体的热容4.1.1 晶体热容的基本物理意义热容是物体温度升高1K 所需要增加的能量。
热容是分子热运动的能量随温度而变化的一个物理量。
单位是J/K 。
不同温度下，物体的热容不一定相同，所以在温度T 时物体的热容为TT Q C ⎪⎭⎫ ⎝⎛∂∂=。
物体的热容还与它的热过程有关，假如加热过程是恒压条件下进行的，所测定的热容称为恒压热容，常用字母C P 表示。
假如加热过程保持物体容积不变，所测定的热容称为恒容热容。
常用字母C V 表示。
即⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T H T Q C P P ，⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T H T Q C P P 由于恒压加热过程中，物体除温度升高外，还要对外界做功，所以温度每提高1K 需要吸收更多的热量，即C P ＞C V 。
C P 的测定比较简单，但C V 更有理论意义，因为它可以直接从系统的能量增量计算。
根据热力学第二定律可以导出C P 和C V 的关系，即κβT V C C V P 02=- 式中VdTdV =β 是体膨胀系数，1-=K κ是压缩系数，m2/N ；V 0是摩尔容积，m 3/mol 。
4.1.2 固体的热容理论固态晶体的热容理论是依据固体中原子热振动的特点，从理论上阐明热容的物理本质，并建立热容随温度变化的定量关系。
由于固体的内能一般包括晶格振动能量和电子运动的能量，因此固体的热容主要有两部分贡献：一是来源于晶格振动，称为晶格热容；一是来源于电子运动，称为电子热容。
晶格热容理论的发展过程经历了经典的杜隆-珀替（Dulong-Petit ）定律和量子热容理论（包括爱因斯坦（Einstein ）热容理论和德拜（Debye ）热容理论）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实际晶体 态密度：
金属铝
• 总态密度是两 支横波(T1,T2) 和一支纵波 （L) 的叠加。 • 低频部分都近 似为抛物线。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
习题3.1
• 固体物理教程--王矜奉 习题 3.10
V ds g (w ) (2 )3 qw ( q)
假设1：N个原子构成的晶体，原子以相同频率 w0 振动；
假设2：谐振子能量是量子化的
温度T下，平衡后谐振子平均能量：
总能量
热容
w0 CV 3NkB f B ( ) —— 爱因斯坦热容函数 k BT
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
—— 爱因斯坦热容函数
爱因斯坦温度
定容比热
在较高温下，该理论与实验符合很好； 但在低温下，与实验结果差别很大，低温下测量有 Cv~ T 3
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
实验表明 —— 在低温时热容量随温度迅速趋于零 。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
2. 爱因斯坦模型
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
上面推导使用积分公式
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
T T 3 CV ( ) 9 NkB ( ) D D
D /T
0
x 4e x dx x 2 (e 1)
徳拜公式的比热容曲线
金属镱实验结果与 徳拜模型比较。
2
为简化，做变量代换，令
T T 3 CV ( ) 9 NkB ( ) D D
D /T
0
x 4e x dx x 2 (e 1)
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
晶体总热容 C ( T ) 9 Nk ( T )3 V B
D /T
D
D
0
xe dx x 2 (e 1)
其中Vc 为晶体体积
间振动模式的数目
因此，波矢空间单位体积中 的波矢数目，即波矢密度： 是一个定值。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
利用q 空间中的波矢密度： 先求出
模式密度/态密度 的计算
两个等频率面所包体积内的模式数：
两个等频面 和 之间一个小体积 dsdq 内的振动模式数 等于 “ 波矢密度×体积元的体积 ”
1. 经典理论
—— 杜隆－珀替定律
• Dulong－Petit 1819 年发现大多数固体常温下的摩尔热容量 差不多都等于一个与材料和温度无关的常数值: ~25 J/mol-1K-1, 这个结果就称为Dulong－Petit定律。 • 解释： 类比于理想气体的能量均分定理，原子振动看做 是谐振子，谐振子三个自由度能量均分(kBT)，一摩尔固 体中有NA个原子，所以每摩尔固体晶格振动能量为：
§3.6 A
晶格振动的态密度/模式密度
• 讨论晶格振动的热力学函数，如热容、自由能时，需 要对晶体中所有原子求和，这对于N值是十分困难的。 实际上，通过近似处理，可以把求和变为对频率ω w+Dw （或能量E）的积分，为此需要引入态密度 (模式密度) w 的概念。
D n个 q
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
01/36
晶格振动的模式密度/态密度 ： q空间中，波矢q是准连续的，对应w也是准连续分布的， 单位频率区间内的振动模式的数目称 Dn dn g (w ) lim 为晶格振动模式密度/态密度 g(w) Dw 0 Dw dw
-- 频率在
-- 对某一支格波(3D)： 已知，在倒空间(q空间)，每个波矢所占体积：
1D
L 1 g (w ) 2 2 qw (q)
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
几种简单情况下振动模式密度的表示 例1：计算一维单原子链的振动模式密度。
— 最大频率
一维情况下 单位长度里的波矢密度：
每个波矢占据宽度
dq长度里的波矢数：
振动模式密度定义：
D /T
0
x 4e x dx x 2 (e 1)
积分为常数
晶体热容
T 12 4 T 3 CV ( ) Nk B ( ) D 5 D
— T3成正比
德拜 T3 定律 —— 温度愈低时，德拜模型近似计算结果愈好； —— 低温下，只有长声学模式（低ω）被热激发，高能量的
被冻结，弹性波近似恰好符合低温时的情况。
w / k B T
由 振动频率分布函数
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
3V 3 1 2 2 频率分布函数 g (w ) w , 3+ 3 2 3 3 2 v p vp vL vT
格波总的数目
N 1/3 wD v p [6 ( )] V
2
晶体总的热容, 带入 g (w)
3D
V ds g (w ) (2 )3 qw ( q)
即w曲线对q梯度为0的 平坦处，会有奇异性出 现 — 范霍夫奇点。
dn g (w ) dw
范霍夫奇点是与晶体对称性相联系的，常常出现 在布里渊区的某些高对称点上。 2D
g (w )
S (2 ) 2
dl qw ( q )
弹性波态密 度呈现抛物 线形。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
10/36
方法2.
V ds 直接利用公式： g (w ) (2 )3 qw ( q)
由于波速(色散关系)与传播方向q无关，故在q空间等频 面为球面，ds 积分即该球面面积：
于是：
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
3V 2 g (w ) 2 3 w , 2 v p
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
一个振动模的热容
零点能
温度T下激发声子数
晶体总的热容
CV
wD
0
w 2 e kB ( ) w / k B T g (w )d w 2 k BT ( e 1)
和wD的决定。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
§3.6 晶体热容的量子理论
固体的定容热容 (比热)
E CV ( )V T
经典理论 爱因斯坦模型 (1907) 德拜模型 (Debye 1912) 实际晶体 (非简谐近似)
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
3 德拜模型 Debye 1912年
(1). 修正了全同谐振子假设，将布喇菲晶格看作是各向同 性的连续介质，以连续介质的弹性波来代表格波 (2). 每个弹性波等价于一个谐振子，能量是量子化的，并 规定了弹性波频率上限 wD，即徳拜频率。
等频率面为球面
g (w )
V 2 v
2
2 w 3
见例2
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
三支格波态密度： 频率在 之间，纵波数目
频率在
之间，横波数目
频率在 三支格波总态密度：
之间，格波数目
1 2 V 2 ( 3 + 3) 2w vL vT 2
3 1 2 3+ 3 3 vp vL vT
有1个纵波和2个独立的横波
w Cl q 色散关系 w Ct q
For Longitudinal Wave For Transverse Wave
—— 不同q的纵波和横波，构成了晶格的全部振动模 —— 不同的振动模，能量不同。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
德拜近似下的振动模式密度 (弹性波近似) 振动频率与波矢成正比
之间振动模式数目:
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
之间振动模式数目
频率是q的准连续函数，故有：
Dn g (w ) lim dn g (w ) D w0 Dw dw
V ds g (w ) 3 (2 ) qw ( q)
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
4
x
在高温极限下
kB D wD
积分内只保留 x 最低阶小量
CV 3NkB —— 与杜隆-珀替定律一致，与
爱因斯坦模型也一致。
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
相当于全部弹性波模式都被激发，可以忽视量子效应的经典情形。
晶体热容 C ( T ) 9 Nk ( T )3 V B D D 低温极限
• 1907年 Einstein 用量子论解释了固体热容随温度下 降的事实，这是1905 年 Einstein 首次用量子论解释 光电效应后，量子论的又一巨大成功；对于人们从经 典理论的思想束缚中解放出来起了巨大作用。该理论 在科学历史上的意义远远超过了其解释固体热容本身 的价值。
• Einstein 模型假设过于简单，只适于描写格波中的光 学支，因为光学支一般频率宽度很窄，可以近似的用 一个固定频率来描述。Einstein模型忽略了频率较低 的声学波对热容的贡献，而在低温时声学波对热容的 贡献恰恰是主要的，因此模型中热容随温度下降要比 实验结果更快。 Debye, Born等人之后在晶格振动基础上提出了新的模型。
类似的， 一维双原子链的振动模式密度
03_06_晶体热容的量子理论 —— 晶格振动与晶体的热学性质
几种简单情况下振动模式密度的表示 例2：计算三维长声学波在弹性波近似下的振动模式密度。