2018年专升本招生考试试题A卷-高等数学
2018年浙江数学专升本真题答案

2018年浙江专升本高数考试真题ㆊṾ一、选择题)45(⨯1.C 解析:0lim )(lim 0==→→x x f x x ,1sin lim)(lim )(lim 00===→→→xxx f x f x x x 因为)(lim )(lim 0x f x f x x →→≠,但是又存在,所以0=x 是跳跃间断点2.D 解析:02sin lim 2sin cos cos lim cos sin lim0020==+-=-→→→x x xx x x xx x x x x x 3.A解析:因为0)(lim00=-→x x x f x x ,所以,0)()(lim )('0000=--=→x x x f x f x f x x 则其0)(,0)('00==x f x f ,又因为0)(''0<x f ,所以0x x =是极大值点。
4.B 解析:)()2(2)(2x f x f dx x f dxd xx -=⎰5.C解析:,9cos 13∑∞=+n n n 因为9cos 3+n n<233191nn <+,所以∑∞+1231n n是收敛的.所以根据比较审敛法;,9cos 13∑∞=+n n n是收敛的,所以,9cos 13∑∞=+n n n是绝对收敛。
6.ae解析:axxa x xx a x a x xx e ex a x a ==+=+→→→sin 01sin sin 101lim )sin 1(lim )sin 1(lim 7.,3sin )23()3(lim0=--→x x f f x 则)3('f =23解析:3)3('222)3()23(lim sin )23()3(lim 00==---=--→→f x f x f xx f f x x 8.‐9解析:0lim →x a e x x -2sin =-)(cos b x 0lim→x a e b x x x --2)(cos =5,所以根据洛必达法则可知:1,01==-a a 0lim →x x b x x 2)(cos -=212cos bb x -=-=5b=‐99.3解析:2221)1)(2(11111t t t tt dxdy +++=+++=31==t dx dy 10.322y x y -解析:方程两边同时求导:得:yxy y y x ==⋅-',0'22=-==32221''y x x y dx y d 322y x y -11.(‐1,1)解析:4224222)1(1)1(21'x x x x x y +-=+-+=令0'=y ,则11,12<<-<x x 浙江中浙专升本12.1-e 解析:⎰∑-=+==-=∞→'0101)()()(1lim 2e c e dx xf n k f n x n k n 13.解析:=⎰+∞dx x x e2)(ln 11ln 1ln )(ln 12=∞+-=⎰∞+e x x d x e14.解析:3412)31()1(3212=-=-=⎰x x dx x A 15.解析:特征方程:0122=+-r r ,特征根:121==r r 通解为:2,121()(C C e x C C y x+=为任意常数)二、计算题16.解析:2sin 2lim )sin 1ln(1lim )sin 1ln(lim 02100==--=+-→-→-→x x x e ex e e x x x x x x 17.两边同时求导得x xx x y x cos sin 11)sin 1ln(1+=+=,所以⎥⎦⎤⎢⎣⎡+++=x x x x dy cos sin 11)sin 1ln(dx x x )sin 1(+π=x 代入得在此处的微分为118.10sin sin sin sin sin sin cos 10232435450502=+-+-==-⎰⎰⎰⎰⎰⎰⎰πππππππππππxdx xdx xdx xdx xdx dx x xdx 19.令tdtdx t x x t 2,,2===原式=dt ttt t tdt tdt t tdt t 222211arctan arctan arctan 22arctan +-===⎰⎰⎰⎰=dt tt t 111(arctan 22⎰+--=dt t dt t t 22111arctan +--⎰⎰=c t t t t ++-arctan arctan 2=cx x x x ++-arctan arctan 20.解析:令tdx t x x t 21,45,452-=-=-=原式=6113)315(81)5(81)21(1453312132=-=-=-⋅-⎰⎰t t dt t dt t t t 21.解析:因为)(x f 在0=x 处可导,所以在0=x 处连续)1ln(lim )2(lim 0ax b x x x +=+→→所以0=b 22lim )1ln(lim00==+→→x xxax x x ,所以2=a 浙江中浙专升本22.解析:直线过两点)1,2,1(-A 因为直线平行于平面,所以→→⊥n S ,)1,3,2(-=→n 设两条直线的交点)12,3,1(-+-t t t p ,所以)12,1,(-+==→→t t t P A S 4,012332==-+--t t t t 所以)7,5,4(P ,所以直线方程;715241-=-=+z y x 23.(1)解析:34)('2+-=x x x f 令0)('=x f ,则3,1==x x 列表如下x)1,(-∞1)3,1(3),3(+∞)('x f +0‐+)(x f ↑极大值↓极小值↑(2)42)(''-=x x f 令0)(''=x f ,则2=x 列表如下;x)2,(-∞2),2(+∞)('x f ‐0+)(x f 凸拐点凹浙江中浙专升本。
2018年专升本高数真题

2018年河南省普通高等学校选拔优秀专科毕业生进入本科阶段学习考试高等数学注意事项:答题前,考生务必将自己的姓名、考场号、座位号、考生号填写在答题卡上.本卷的试题答案必须答在答题卡上,答在卷上无效.一、选择题(每小题2分,共60分) 1.函数()f x =的定义域是( )A.[)2,2- B.(2,2)- C.(]2,2- D.[]2,2-2.函数()()sin x x f x e e x -=-是A.偶函数B.奇函数C.非奇非偶函数D.无法判断奇偶性3. 221lim 21x x x x →∞+=-+( )A.0B.12C.1D.24.当0x →时,()211kx +-与1cos x -为等价无穷小,则k 的值为( ) A.1B. 12-C.12D.1-5.函数22132x y x x -=-+在1x =处间断点类型为( )A.连续点B. 可去间断点C.跳跃间断点D.第二类间断点6.设()f x 在x a =的某个邻域内有定义,则()f x 在x a =处可导的一个充要条件为()A. ()()02limh f a h a h h →+-+存在 B. ()()0lim 2h f a h a h h→+--存在C. ()()limh f a a h h →--存在D. ()1lim h h f a f a h →+∞⎡⎤⎛⎫+- ⎪⎢⎥⎝⎭⎣⎦存在 7.极限01arctan lim arctan x x x x x →⎛⎫-= ⎪⎝⎭( ) A.1- B.1 C.0 D.28.已知ln y x x =,则y ''=( )。
A.1xB.21x C. 1x-D. 21x -9.已知二元函数()21xz y =+,则zy∂=∂( ) A.()121x x y -+ B. ()1221x x y -+ C.()()21ln 21xy y ++ D.()()221ln 21x y y ++10.曲线222x y x x =+-的水平渐近线为:( )。
2018年河南专升本高数真题+答案解析

2018年河南省普通高等学校选拔专科优秀毕业生进入本科学校学习考试高等数学试卷一、选择题(每小题2分,共60分) 1.函数()f x = )A .[)2,2-B .()2,2-C .(]2,2-D .[]2,2-【答案】B【解析】()2402,2x x ->⇒∈-,故选B .2.函数()()sin x x f x e e x -=-是( ) A .偶函数 B .奇函数C .非奇非偶函数D .无法判断奇偶性【答案】A【解析】sin x ,x x e e --都是奇函数,两个奇函数的乘积为偶函数,故选A .3.极限221lim 21x x x x →∞+=-+( )A .0B .12C .1D .2【答案】B【解析】根据有理分式函数求无穷大时的极限结论知,所求极限值为最高次项系数之比,故选B .4.当0x →时,2(1)1k x +-与1cos x -为等价无穷小,则k 的值为( )A .1B .12-C .12D .1-【答案】C【解析】0x →时,22(1)1~k x kx +-,211cos ~2x x -,根据等价无穷小传递性,有12k =.5.函数22132x y x x -=-+在1x =处间断点的类型为( )A .连续点B .可去间断点C .跳跃间断点D .第二类间断点【答案】B【解析】()()()()221111111lim lim lim 232122x x x x x x x x x x x x →→→+--+===--+---,且函数在1x =处无定义,故为可去间断点.6.设()f x 在x a =的某个领域内有定义,则()f x 在x a =处可导的一个充要条件是( )A .0(2)()limh f a h f a h h →+-+存在B .0()(-)limh f a h f a h h→+-存在C .0()(-)limh f a f a h h→-存在D .01lim ()()h h f a f a h →⎡⎤+-⎢⎥⎣⎦存在 【答案】C【解析】()f x 在x a =处可导时,四个选项的极限都存在,且都等于()f a ',00()()()()limlim h h f a f a h f a h f a h h→-→----=-就是导数的定义,即有()f x 在x a =处可导,故选C .7.极限01arctan lim arctan x x x x x →⎛⎫-= ⎪⎝⎭( ) A .1- B .1 C .0 D .2【答案】A【解析】0001arctan 1arctan lim arctan lim arctan lim 011x x x x x x x x x x x →→→⎛⎫-=-=-=- ⎪⎝⎭.8.已知ln y x x =,则y '''=( )A .1xB .21x C .1x-D .21x -【答案】D【解析】ln 1y x '=+,1y x''=,21y x '''=-.9.已知二元函数(21)xz y =+,则zy∂=∂( )A .1(21)x x y -+B .12(21)x x y -+C .(21)ln(21)x y y ++D .2(21)ln(21)x y y ++【答案】B 【解析】()1221x z x y y-∂=+∂,故选B .10.曲线22xy x x =+-的水平渐近线为( )A .1y =B .0y =C .2x =-D .1x =【答案】A 【解析】2lim 12x xx x →∞=+-,所以水平渐近线为1y =.11下列等式正确的是( ) A .()()d df x f x C '=+⎰ B .()()d df x f x C =+⎰C .()()f x dx f x C '=+⎰D .()()ddf x f x dx =⎰【答案】C【解析】根据不定积分的性质,()()f x dx f x C '=+⎰,故选C .12.已知2()f x dx x C =+⎰,则2(1)xf x dx -=⎰( )A .23(1)x C -+B .231(1)2x -C .231(1)2x C -+D .231(1)2x C --+【答案】D【解析】2222311(1)(1)(1)(1)22xf x dx f x d x x C -=---=--+⎰⎰,故选D .13.导数20(1)xe d t dt dx +=⎰( )A .2(1)x x e e +B .2(1)x x e e +C .22(1)x x e e +D .22(1)x x e e +【答案】A【解析】()()()2220(1)11x e x x x xd t dte e e e dx'+=+=+⎰,故选A .14.下列不等式成立的是( ) A .1120xdx x dx >⎰⎰B .22211xdx x dx >⎰⎰C .1120xdx x dx <⎰⎰D .22311xdx x dx >⎰⎰【答案】A【解析】[]0,1x ∈,2x x >,所以1120xdx x dx >⎰⎰,故选A .15.下列广义积分收敛的是( )A .1+∞⎰B .e+∞⎰C .11dx x+∞⎰D .1ln edx x x+∞⎰【答案】B【解析】四个广义积分都是p 广义积分,只有B 中312p =>是收敛的,故选B .16.已知向量{}2,3,1=-a ,{}1,1,3=-b ,则a 与b 夹角的余弦为( ) AB C D .0【答案】C 【解析】cos θ⋅===⋅a b a b ,故选C .17.曲线20z y x ⎧=⎨=⎩绕z 轴旋转所得旋转曲面的方程为( )A .22z x y =+B .22z x y =-C .22z y x =-D .2()z x y =+【答案】A【解析】绕z 轴旋转,z 不动,y 用代替,即(222z x y ==+,故选A .18.极限222222(,)(0,0)1cos()lim ()xy x y x y x y e +→-+=+( )A .12B .2C .1D .0【答案】D 【解析】222222222(,)(0,0)0001cos()1cos lim lim lim lim 022()x y tt t t xy x y t t t x y t t tte te ex y e +=+→→→→-+-−−−−→===+,故选D . 19.关于二元函数(,)z f x y =在点00(,)x y 处,下列说法正确的是( ) A .可微则偏导数一定存在 B .连续一定可微C .偏导数存在一定可微D .偏导数存在一定连续【答案】A【解析】由可微的必要条件和充分条件可知,选A .20.将二次积分2330(,)xxdx f x y dy ⎰⎰改写为另一种次序的积分是( )A .2330(,)xxdy f x y dx ⎰⎰B .233(,)x xdx f x y dy ⎰⎰C .233(,)x xdx f x y dy ⎰⎰D .93(,)dy f x y dx ⎰⎰【答案】D【解析】将X 型区域转化为Y 型区域(,)09,3y x y y x ⎧≤≤≤≤⎨⎩,则可化为93(,)y dy f x y dx ⎰⎰,故选D .21.设L 为抛物线2y x =介于(0,0)和之间的一段弧,则曲线积分=⎰( )A .136B .136-C .613-D .613【答案】A【解析】2:(0y x L x x x ⎧=≤≤⎨=⎩, 1222011)(41)8x d x ===++⎰3221213(41)836x =⋅+=,故选A .22.关于级数21sin()n na n ∞=⎡⎢⎣∑,下列说法正确的是( ) A .绝对收敛 B .发散C .条件收敛D .敛散性与a 有关【答案】B【解析】级数21sin()n na n ∞=∑收敛,级数n ∞=由级数的性质知,级数21sin()n na n ∞=⎡⎢⎣∑发散,故选B .23.设幂级数0(1)nn n a x ∞=-∑在1x =-处条件收敛,则它在2x =处( )A .绝对收敛B .条件收敛C .发散D .不能确定【答案】A【解析】令1x t -=,级数化为0nn n a t ∞=∑,在1x =-处原级数条件收敛,即级数0nn n a t ∞=∑在2t =-处条件收敛,2x =处,1t =,根据阿贝尔定理知,1t =时,级数0nn n a t ∞=∑绝对收敛,即2x =时原级数绝对收敛,故选A .24.设1y ,2y ,3y 是非齐次线性微分方程()()()y p x y q x y x ϕ'''++=三个线性无关的特解,则该方程的通解为( ) A .112233C y C y C y ++ B .1122123()C y C y C C y +-+C .1122123(1)C y C y C C y +---D .1132233()()C y y C y y y -+-+【答案】D【解析】1y ,2y ,3y 是非齐次线性微分方程()()()y p x y q x y x ϕ'''++=三个线性无关的特解,则13y y -,23y y -为对应齐次方程的两个无关特解,而3y 为非齐次线性微分方程的特解,故非齐次线性微分方程通解为1132233()()C y y C y y y -+-+,故选D .25.微分方程43()2()0y x y xy '''+-=的阶数是( )A .1B .2C .3D .4【答案】B【解析】导数的最高阶为2,故方程的阶数为2,故选B .26.平面230x y z π+-=:与直线111123x y z l ---==-:的位置关系是( )A .平行但不在平面内B .在平面内C .垂直D .相交但不垂直【答案】C【解析】平面的法向量与直线方向向量相等,故直线与平面垂直,故选C .27.用待定系数法求微分方程232x y y y xe '''-+=的特解y *时,下列y *设法正确的是( )A .2()x y x AxB e *=+ B .2()x y Ax B e *=+C .22x y Ax e *=D .2x y Axe *=【答案】A【解析】特征方程有两个根为11r =,22r =,2λ=是特征方程的单根,所以1k =,故特解y *设为2()x y x Ax B e *=+,故选A .28.若曲线积分2232(3)(812)yL x y axy dx x x y ye dy ++++⎰在整个xOy 面内与路径无关,则常数a =( )A .8-B .18-C .18D .8【答案】D【解析】2(,)32P x y x axy y ∂=+∂,2(,)316Q x y x xy x ∂=+∂,因曲线积分在整个xOy 面内与路径无关,则(,)(,)P x y Q x y y x∂∂=∂∂,即2232316x axy x xy +=+,从而8a =,故选D .29.下列微分方程中,通解为2312x x y C e C e =+的二阶常系数齐次线性微分方程是( ) A .560y y y '''-+= B .560y y y '''++=C .650y y y '''-+=D .650y y y '''++=【答案】A【解析】特征方程的两个根为12r =,23r =,由根与系数之间的关系知,5p =-,6q =,故对应的二阶常系数齐次线性微分方程是560y y y '''-+=,故选A .30.对函数()1f x =在闭区间[]1,4上应用拉格朗日中值定理时,结论中的ξ=( )A .32B .23C .49D .94【答案】D 【解析】(4)(1)1()413f f f ξ-'===-,解得94ξ=,故选D .二、填空题(每小题2分,共20分)31.已知()x f x e =且[]()12(0)f x x x ϕ=+>,则()x ϕ=________. 【答案】ln(12)(0)x x +>【解析】由()x f x e =得[]()()x f x e ϕϕ=,所以()12x e x ϕ=+,故()ln(12)(0)x x x ϕ=+>.32.极限23lim 2xx x x →∞+⎛⎫= ⎪+⎝⎭________.【答案】2e 【解析】12(2)222lim2231lim lim 122x xx x xxxx x x ee x x →∞+⋅⋅++→∞→∞+⎛⎫⎛⎫=+== ⎪ ⎪++⎝⎭⎝⎭.33.20()20x ae x f x x x ⎧+<=⎨+≥⎩,,在0x =处连续,则a =________.【答案】1【解析】函数在0x =处连续,则该点处左右极限存在且相等,还等于该点处的函数值,而lim ()lim(1)1x x x f x ae a --→→=+=+,00lim ()lim(2)2x x f x x ++→→=+=,所以12a +=,即1a =.34.已知函数sin y x x =,则dy =________. 【答案】(sin cos )x x x dx +【解析】(sin )(sin cos )dy x x dx x x x dx '==+.35.曲线23x t y t z t=⎧⎪=⎨⎪=⎩在1t =对应的点处的法平面方程为________.【答案】236x y z ++=【解析】在1t =对应的点为(1,1,1),该点处曲线的切向量,即平面的法向量为{}{}211,2,31,2,3t t t ===n ,故该点处的法平面方程为1(1)2(1)3(1)0x y z ⋅-+-+-=,即236x y z ++=.36.极限ln(1)lim x x e x→+∞+=________.【答案】1【解析】ln(1)limlim 11x xx x x e e xe →+∞→+∞+==+.37.不定积分21dx x =⎰________. 【答案】1C x-+【解析】211dx C x x=-+⎰.38.定积分121(cos )x x x dx -+=⎰________.【答案】23【解析】111122231011122(cos )cos 233x x x dx x dx x xdx x dx x ---+=+===⎰⎰⎰⎰.39.已知函数(,,)f x y z =(1,1,1)grad =________. 【答案】111,,333⎧⎫⎨⎬⎩⎭【解析】(,,)f x y z =则222x x f x y z '=++,222y y f x y z '=++,222zzf x y z '=++, 故(1,1,1)222222222111(1,1,1),,,,333x y zgrad x y z x y z x y z ⎧⎫⎧⎫==⎨⎬⎨⎬++++++⎩⎭⎩⎭.40.级数1023n nn ∞-==∑________.【答案】9 【解析】10021233392313nn nn n ∞∞-==⎛⎫==⋅= ⎪⎝⎭-∑∑.三、计算题(每小题5分,共50分) 41.求极限20tan lim (1)x x x xx e →--.【答案】13【解析】2222222200000tan tan sec 1tan 1lim lim lim lim lim (1)3333x x x x x x x x x x x x x x e x x x x x →→→→→---=====-⋅.42.已知2(sin )2(1cos )x t t y t =-⎧⎨=-⎩,02t π≤≤,则22d ydx .【答案】212(1cos )t --【解析】sin 1cos t t y dy t dx x t'=='-,22221sin 1cos (1cos )sin 11cos 2(1cos )(1cos )2(1cos )t d y d dy t t t t dx dt dx x t t t t '--⎛⎫⎛⎫=⋅=⋅=⋅ ⎪ ⎪'----⎝⎭⎝⎭ 212(1cos )t =--.43.求不定积分⎰.【答案】352235C ++【解析】t =,则21x t =+,2dx tdt =,故22435352222(1)22()3535t t tdt t t dt t t C C =+⋅=+=++=++⎰⎰⎰.44.求定积分21e ⎰.【答案】1)【解析】22211(1ln )1)e e x =+==⎰⎰.45.求微分方程690y y y '''-+=的通解. 【答案】312()x y C C x e =+【解析】对应特征方程为2690r r -+=,特征根为123r r ==,故所求微分方程的通解为312()x y C C x e =+.46.求函数22(,)22f x y x y y x =++-的极值.【答案】【解析】令220220fx xf y y∂⎧=-=⎪∂⎪⎨∂⎪=+=⎪∂⎩,得唯一驻点(1,1)-.在驻点(1,1)-处有:2xx A f ==,0xy B f ==,2yy C f ==,且20B AC -<,0A >, 故点(1,1)-为(,)f x y 的极小值点,且极小值(1,1)2f -=-,无极大值.47.将函数()ln(2)f x x =+展开为1x -的幂级数. 【答案】11(1)ln 3(1)(24)3(1)n nn n x x n +∞+=-+--<≤+∑ 【解析】令1x t -=,则1x t =+,所以()ln(3)ln 3ln 13t f t t ⎛⎫=+=++ ⎪⎝⎭,而10ln(1)(1)(11)1n n n x x x n +∞=+=--<≤+∑,故 11100(1)3ln(2)ln 3(1)ln 3(1)(24)13(1)n n n n n n n t x x x n n ++∞∞+==⎛⎫ ⎪-⎝⎭+=+-=+--<≤++∑∑.48.设D 是由直线y x =、2y x =及1x =所围成的闭区域,求二重积分Dydxdy ⎰⎰.【答案】12【解析】把D 看作X 型区域,则可表示为{}(,)01,2D x y x x y x =≤≤≤≤,故2121310311222xxDx ydxdy dx ydy dx x ====⎰⎰⎰⎰⎰.49.求函数43342y x x =-+的凹凸区间和拐点.【答案】凸区间为20,3⎛⎫ ⎪⎝⎭,凹区间为(,0)-∞和2,3⎛⎫+∞ ⎪⎝⎭;拐点为(0,2)和238,327⎛⎫⎪⎝⎭【解析】函数定义域为(,)-∞+∞,321212y x x '=-,2362412(32)y x x x x ''=-=-, 令0y ''=,得0x =,23x =, 列表如下故所求函数的凸区间为20,3⎛⎫ ⎪⎝⎭,凹区间为(,0)-∞和2,3⎛⎫+∞ ⎪⎝⎭;拐点为(0,2)和238,327⎛⎫⎪⎝⎭.50.已知函数cos()xy z e x y =++,求全微分dz .【答案】sin()sin()xy xyye x y dx xe x y dy ⎡⎤⎡⎤-++-+⎣⎦⎣⎦【解析】sin()xy z ye x y x∂=-+∂,sin()xyz xe x y y ∂=-+∂,在定义域内为连续函数,由全微分存在的充分条件可知dz 存在,且sin()sin()xy xyz z dz dx dy ye x y dx xe x y dy x y∂∂⎡⎤⎡⎤=+=-++-+⎣⎦⎣⎦∂∂.四、应用题(每小题7分,共14分) 51.设平面图形D 由曲线1y x=、直线y x =及3x =所围成的部分,求D 绕x 轴旋转形成的旋转体的体积. 【答案】8π【解析】把区域D 看作X 型区域,取x 为积分变量,且[]1,3x ∈, 平面图形D 绕x 轴旋转一周所得旋转体的体积为323312111183x V x dx x x x πππ⎛⎫⎛⎫=-=+= ⎪ ⎪⎝⎭⎝⎭⎰.52.某车间靠墙壁要盖一间长方形的小屋,现有存砖只够砌20米长的墙壁,应围城怎样的长方形才能使这间小屋的面积最大?【答案】长方形小屋的长为10米,宽为5米时小屋面积最大【解析】设长方形的正面长为x ,侧面长为y 时,面积为S ,则S xy =且220y x +=,即 (202)S y y =-,令2040S y '=-=,则唯一可能的极值点5y =,而此时40S ''=-<,所以5y =是极大值点,即为最大值点,此时10x =, 故长方形小屋的长为10米,宽为5米时小屋面积最大.五、证明题(6分)53.设()f x 在区间[]0,1内连续,(0,1)内可导,且(0)0f =,1(1)2f =,证明:存在不同两个点,12,(0,1)ξξ∈,使得12()()1f f ξξ''+=成立.【解析】函数()f x 在区间10,2⎡⎤⎢⎥⎣⎦,1,12⎡⎤⎢⎥⎣⎦都满足拉格朗日中值定理,所以110,2ξ⎛⎫∃∈ ⎪⎝⎭,21,12ξ⎛⎫∃∈ ⎪⎝⎭,使得11(0)12()21202f f f fξ⎛⎫- ⎪⎛⎫⎝⎭'== ⎪⎝⎭-,21(1)12()121212f f f f ξ⎛⎫- ⎪⎛⎫⎝⎭'==- ⎪⎝⎭-,两式相加,即可得 存在不同两个点,12,(0,1)ξξ∈,使得12()()1f f ξξ''+=成立.。
江苏省2018年专转本高等数学试卷及解答培训讲学

5.下列反常积分中发散的是( D ).
∫ A . 0 exdx −∞
+∞ 1
∫ B . 1
x3 dx
+∞ 1
∫ C . −∞ 1 + x2 dx
+∞ 1
D . ∫0
dx 1+ x
∫ ∫ ∫ 解
0 e= xdx
−∞
e= x 0 −∞
1,
+∞ 1
1 x3
dx
= − 1 +∞ 2x2 1
= 1 , +∞
解 ln y = x ln x , = 1 y′ ln x = + 1 ln x + 2 ⋅ x x y 2x x 2x
9.设 z = z(x, y) 是由方程 z2 + xyz = 1所确定的函数,则 ∂z =
▲
. − yz
∂x
2z + xy
解 2z ∂z + yz + xy ∂z = 0 , ∂z = − yz
7.设 lim(1 +
1
ax) x
= lim x sin
2
,则常数 a
=
▲
. ln 2
x→0
x→∞
x
解
1
由 lim(1 + ax) x
= lim x sin 2 ,得 ea
= 2 ,所以 a = ln 2
x→0
x→∞
x
8.设 y = x x ( x > 0 ),则 y′ =
▲
. ln x + 2 ⋅ x x 2x
2
−∞
1
1 + x2
dx
=
π
2018年成人高考专升本《高等数学(一)》考试及参考答案(共三套)

2018年成人高等学校专升本招生全国统一考试高等数学(一)。
答案必须答在答题卡上指定的位置,答在试卷上无效.......(共三套及参考答案)第Ⅰ卷(选择题,共40分)一、选择题:1~10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.A.0B.1C.2D.不存在2.().A.单调增加且为凹B.单调增加且为凸c.单调减少且为凹D.单调减少且为凸3.A.较高阶的无穷小量B.等价无穷小量C.同阶但不等价无穷小量D.较低阶的无穷小量4.A.B.0C.D.15.A.3B.5C.1D.A.-sinxB.cos xC.D.A.B.x2C.2xD.28.A.B.C.D.9.设有直线当直线l1与l2平行时,λ等于().A.1B.0C.D.一110.下列命题中正确的有().A.B.C.D.第Ⅱ卷(非选择题,共110分)二、填空题:11~20小题,每小题4分,共40分.11.12.13.14.15.16.17.18.19.20.三、解答题.21~28小题,共70分.解答应写出推理、演算步骤.21.(本题满分8分)22.(本题满分8分)设y=x+arctanx,求y'.23.(本题满分8分)24.(本题满分8分)计算25.(本题满分8分)26.(本题满分10分)27.(本题满分10分)28.(本题满分10分)求由曲线y=x,y=lnx及y=0,y=1围成的平面图形的面积S及此平面图形绕y轴旋转一周所得旋转体体积.模拟试题参考答案一、选择题1.【答案】C.【解析】本题考查的知识点为左极限、右极限与极限的关系.2.【答案】B.【解析】本题考查的知识点为利用一阶导数符号判定函数的单调性和利用二阶导数符号判定曲线的凹凸性.3.【答案】C.【解析】本题考查的知识点为无穷小量阶的比较.4.【答案】D.【解析】本题考查的知识点为拉格朗日中值定理的条件与结论.可知应选D.5.【答案】A.【解析】本题考查的知识点为判定极值的必要条件.故应选A.6.【答案】C.【解析】本题考查的知识点为基本导数公式.可知应选C.7.【答案】D.【解析】本题考查的知识点为原函数的概念.可知应选D.8.【答案】D.【解析】本题考查的知识点为牛顿一莱布尼茨公式和定积分的换元法.因此选D.9.【答案】C.【解析】本题考查的知识点为直线间的关系.10.【答案】B.【解析】本题考查的知识点为级数的性质.可知应选B.通常可以将其作为判定级数发散的充分条件使用.二、填空题11.【参考答案】e.【解析】本题考查的知识点为极限的运算.12.【参考答案】1.【解析】本题考查的知识点为导数的计算.13.【参考答案】x—arctan x+C.【解析】本题考查的知识点为不定积分的运算.14.【参考答案】【解析】本题考查的知识点为定积分运算.15.【参考答案】【解析】本题考查的知识点为隐函数的微分.解法1将所给表达式两端关于x求导,可得从而解法2将所给表达式两端微分,16.【参考答案】【解析】本题考查的知识点为二阶常系数线性齐次微分方程的求解.17.【参考答案】1.【解析】本题考查的知识点为二元函数的极值.可知点(0,0)为z的极小值点,极小值为1.18.【参考答案】【解析】本题考查的知识点为二元函数的偏导数.19.【参考答案】【解析】本题考查的知识点为二重积分的计算.20.【参考答案】【解析】本题考查的知识点为幂级数的收敛半径.所给级数为缺项情形,三、解答题21.【解析】本题考查的知识点为极限运算.解法1解法2【解题指导】在极限运算中,先进行等价无穷小代换,这是首要问题.应引起注意.22.【解析】23.【解析】本题考查的知识点为定积分的换元积分法.【解题指导】比较典型的错误是利用换元计算时,一些考生忘记将积分限也随之变化. 24.【解析】本题考查的知识点为计算反常积分.计算反常积分应依反常积分收敛性定义,将其转化为定积分与极限两种运算.25.【解析】26.【解析】27.【解析】本题考查的知识点为二重积分运算和选择二次积分次序.28.【解析】所给曲线围成的图形如图8—1所示.2018年成人高等学校专升本招生全国统一考试高等数学(一)。
(完整版)2018年江苏省普通高校“专转本”统一考试《高等数学》试卷

2018年江苏省普通高校“专转本”统一考试一、 选择题(本大题共6小题,每小题4分,满分24分)1、当0x →时,下列无穷小与()2sin f x x x =同阶的是 ( )A.2cos 1x -1 C. 31x - D 。
()3211x +- 2、设函数2()x a f x x x b-=++,若1x =为其可去间断点,则常数a ,b 的值分别为 ( ) A 。
1,2- B 。
1,2- C 。
1,2-- D. 1,23、设1()1x f x x ϕ-⎛⎫= ⎪+⎝⎭,其中()x ϕ为可导函数,且()13ϕ'=,则()0f '等于 ( ) A.6- B 。
6 C.3- D. 34、设()2x F x e =是函数()f x 的一个原函数,则()xf x dx '=⎰ ( ) A. 2112x e x C ⎛⎫-+ ⎪⎝⎭ B. ()221x e x C -+ C. 2112x e x C ⎛⎫++ ⎪⎝⎭D. ()221x e x C ++ 5、下列反常积分发散的是( )A 。
0x e dx -∞⎰B 。
311dx x +∞⎰C 。
211dx x +∞-∞+⎰D 。
011dx x+∞+⎰ 6、下列级数中绝对收敛的是( )A. 1n n ∞=∑()1121nn n ∞=+-∑ C. 21sin n n n ∞=∑ D 。
31(3)n n n ∞=-∑ 二、填空题(本大题共6小题,每小题4分,共24分)7设()102lim 1lim sin x x x ax x x→→∞+=,则常数a =_________. 8、设函数()0y x =>,则y '=____________.9、设(),z z x y =是由方程21z xyz +=所确定的函数,则z x ∂=∂___________. 10、曲线43234612y x x x x =+--的凸区间为___________.11、已知空间三点()1,1,1M ,()1,1,0A ,()2,1,2B ,则AMB ∠的大小为__________.12、幂级数1(4)5nn n x n ∞=+∑的收敛域为____________.三、计算题(本大题共8小题,每小题8分,共64分)13、求极限()22011lim ln 1x x x →⎡⎤⎢⎥-+⎢⎥⎣⎦. 14、设函数)(x y y =由参数方程323101x xt t y t t ⎧-+-=⎪⎨=++⎪⎩所确定,求0t dy dx =. 15、求不定积分. 16、计算定积分()2121ln x xdx +⎰ .17、求通过点()1,2,3M 及直线131415x t y t z t =+⎧⎪=+⎨⎪=+⎩的平面方程.18、求微分方程()323220y x y dx x dy -+=的通解. 19、设,x z xf y y ⎛⎫= ⎪⎝⎭,其中函数具有一阶连续偏导数,求全微分dz .20、计算二重积分D xydxdy ⎰⎰,其中()(){}22,11,0D x y x y y x =-+≤≤≤. 四、证明题(本大题共2小题,每小题9分,共18分)21、证明:当0x >时,ln x ≤ 22、设0()0()00x f t dt x F x x x⎧⎪≠=⎨⎪⎩⎰ =,其中函数()f x 在),(+∞-∞上连续,且0()lim 1x f x x →=,证明:()F x '在点0=x 处连续.五、综合题(本大题共2小题,每小题10分,共20分)23、设D 是由曲线弧cos 42y x x ππ⎛⎫=≤≤ ⎪⎝⎭与sin 4y x x ππ⎛⎫=≤≤ ⎪⎝⎭及x 轴所围成的平面图形,试求: (1)D 的面积;(2)D 绕x 轴旋转一周所形成的旋转体的体积.24、设函数()f x 满足方程()()()320f x f x f x '''-+=,且在0x =处取得极值1,试求:(1)函数)(x f 的表达式;(2)曲线()()f x y f x '=的渐近线.。
2018年专升本高数真题答案解析
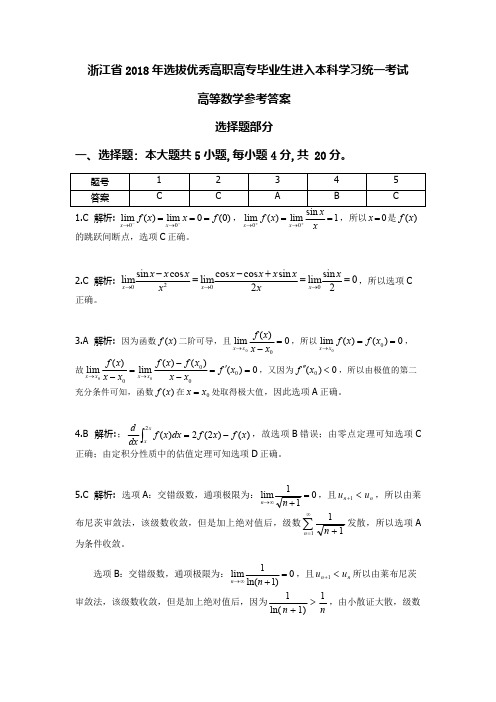
浙江省2018年选拔优秀高职高专毕业生进入本科学习统一考试高等数学参考答案选择题部分一、选择题:本大题共5小题,每小题4分,共20分。
题号12345答案CCABC1.C 解析:)0(0lim )(lim 0f x x f x x ===--→→,1sin lim )(lim 0==++→→xxx f x x ,所以0=x 是)(x f 的跳跃间断点,选项C 正确。
2.C 解析:02sin lim 2sin cos cos lim cos sin lim 0020==+-=-→→→xx x x x x x x x x x x x ,所以选项C 正确。
3.A 解析:因为函数)(x f 二阶可导,且0)(lim=-→x x x f x x ,所以0)()(lim 00==→x f x f x x ,故0)()()(lim )(lim000000='=--=-→→x f x x x f x f x x x f x x x x ,又因为0)(0<''x f ,所以由极值的第二充分条件可知,函数)(x f 在0x x =处取得极大值,因此选项A 正确。
4.B 解析:;⎰-=xxx f x f dx x f dx d 2)()2(2)(,故选项B 错误;由零点定理可知选项C 正确;由定积分性质中的估值定理可知选项D 正确。
5.C 解析:选项A :交错级数,通项极限为:011lim =+∞→n n ,且n n u u <+1,所以由莱布尼茨审敛法,该级数收敛,但是加上绝对值后,级数∑∞=+111n n 发散,所以选项A为条件收敛。
选项B :交错级数,通项极限为:0)1ln(1lim=+∞→n n ,且n n u u <+1所以由莱布尼茨审敛法,该级数收敛,但是加上绝对值后,因为nn 1)1ln(1>+,由小散证大散,级数∑∞=+1)1ln(1n n 发散,所以选项B 为条件收敛。
2018年成人高等学校招生全国统一考试专升本《高等数学(二)》试题及答案解析

2018年成人高等学校招生全国统一考试专升本高等数学(二)本试卷分第Ⅰ卷(选择题)和第卷(非选择题)两部分,满分150分,考试时间120分.第Ⅰ卷(选择题,共40分)一、选择题(1~10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. lim x→0xcosx =( )A. eB.2C. 1D. 02. 若y =1+cosx ,则dy = ( )A. (1+ sinx)dxB. (1−sinx)dxC. sinxdxD.−sinxdx3. 若函数f(x)=5x ,则f′(x)= ( )A. 5x−1B. x5x−1C. 5x ln5D.5x4. 曲线y =x 3+2x 在点(1,3)处的法线方程是 ( )A. 5x +y −8=0B. 5x −y −2=0C. x +5y −16=0D. x −5y +14=05. ∫12−xdx =( )A. ln |2−x|+CB. −ln |2−x|+CC.−1(2−x)2+C D. 1(2−x )2+C6. ∫f′(2x)dx = ( )A. 12f(2x)+CB. f(2x)+CC. 2f(2x)+CD. 12f(x)+C7. 若f(x)为连续的奇函数,则∫f(x)1−1dx = ( )A. 0B. 2C. 2f(−1)D. 2f(1)8. 若二元函数z =x 2y +3x +2y ,则ðz ðx=( )A. 2xy +3+2yB. xy +3+2yC. 2xy +3D. xy +39. 设区域D ={(x ,y)|0≤y ≤x 2,0≤x ≤1},则D 绕x 轴旋转一周所得旋转体的体积为 ( )A. π5B. π3C. π2D. π10. 设A ,B 为两个随机事件,且相互独立,P(A)=0.6,P(B)=0.4,则P(A −B )=( )A. 0.24B. 0.36C. 0.4D. 0.6第Ⅱ卷(非选择题,共110分)二、填空题(11~20小题,每小题4分,共40分)11. 曲线y =x 3−6x 2+3x +4的拐点为 . 12. lim x→0(1−3x )1x = .13.若函数f(x)=x −arctanx ,则f′(x)= . 14. 若y =e 2x 则dy = . 15. 设f(x)=x 2x ,则f′(x)= . 16. ∫(2x +3)dx = . 17. ∫(x 5+x 2)1−1dx = . 18. ∫sin x 2π0dx = . 19. ∫e−x +∞0dx = .20. 若二元函数:z =x 2y 2,则ð2z ðxðy= .三、解答题(21~28题,共70分。
山东省2018年普通高等教育专升本统一考试高等数学真题+答案

山东省 2018 年专升本真题试卷高等数学(一)一、单项选择题(本大题共五小题,每小题3分共15分。
在每小题列出的四个备选项中只有一个符合题目要求)1. 函数y =arcsin (1−x )+12lg 1+x 1−x 的定义域是A. (0,1)B.[0,1)C.(0,1]D.[0,1]2.如果函数y ={x 2−16x−4,x ≠4a ,x =4在(−∞,+∞)内连续,则a = A.6 B.7 C.8 D.9 3.曲线y =e 1x arctan x 2+x+1(x−1)(x+2)的渐近线的条数为 A.0 B.1 C.3 D.2 4.如果lim x→∞(1+x x )ax=∫te t dt a−∞,则a = A.0 B.1 C.2 D.35.微分方程x ln xdy +(y −ln x )=0满足y|x=e =1的特解为A.12(ln x +1ln x )B.12(x +1ln x) C.12(ln x +1x ) D.12(x +1x)二、填空题(本大题共5小题,每小题3分,共15分)6.函数f(x)=xa x −1a x +1的图像关于_______________对称. 7.lim n→∞√1+2+⋯+n −√1+2+⋯+(n −1)=_______________________.8.f(x)=1x −1x+11x−1−1x 的第二类间断点为__________________.9. 设a ⃗ ={1,2,3}, b ⃗ ={0,1,−2},则(a ⃗ +b ⃗ )×(a ⃗ −b⃗ )=_____________. 10.直线{x +y +z −4=0x −y −z +2=0与直线{x −2y −z −1=0x −y −2z =0的位置关系为__________.三、解答题(本大题共7小题,每小题6分,共42分)11.设lim x→1x 3+ax−2x −1=2,求a 的值12.当x →1时,f(x)=1−x 1+x 与g(x)=1−√x 3比较,会得到什么样的结论?13.求由方程x2+2xy−y2−2x=0确定的隐函数y=y(x)的导数14.设函数f(x)=limn→∞ddx(∫1+t1+tdtx−1),求f(x)的间断点15.设z =z(x,y)是由F (x +mz,y +nz )=0确定的函数,求ðz ðy16.改变积分∫dx 10∫f (x,y )dy +∫dx 21∫f (x,y )dy 2−x 0x 20的积分次序17.求幂级数∑n √n ∞n=1的收敛域18.求y=x2上(2,4)处切线与y=−x2+4x+1所围成的图形面积19.求z=6−x2−y2,z=√x2+y2所围立体体积20.证明方程x5−2x2+x+1=0在(−1,1)内至少有一个实根21.证明等式arcsinx+arccos=π2。
2018年专升本数学真题

2018年天津市高等院校“高职升本科”招生统一考试高等数学一、单选题:共6题,每小题6分,共36分1.当0→x 时,与x 等价的无穷小量是()A、xtan B、xsin 2C、12-x e D、)1ln(x -2.函数x y 2sin =在点2π=x 处的导数是()A、-1B、1C、-2D、23.已知函数)(u f y =可导,若)(2x f y -=,则微分=dy ()A、)(22'x xf --B、dx x xf )(22'--C、)(2'x f -D、dxx f )(2'-4.下列等式正确的是()A、⎰=)()('x f dx x f B、Cx f dx x f +=⎰)())(('C、⎰=)()(x f dx x f d D、dxx f dx x f d ⎰=)()(5.定积分=⎰dx x sin 20π()A、xdxxdx sin sin 20⎰⎰+πππB、dxx xdx )(-sin sin 20⎰⎰+πππB、dxx dx x )(-sin )(-sin 20⎰⎰+πππD、xdxdx x sin )(-sin 20⎰⎰+πππ6.直线311221:1-=+=-z y x l 和直线⎪⎩⎪⎨⎧-=+=-=33232:2t z t y t x l (t 为参数)的位置关系为()A、平行B、相交C、异面D、重合二、填空题:共6题,每小题6分,共36分7.极限=+⋅→)1ln(sin cos lim0x xx x 8.函数723+--=x x x y 的单调递减区间为9.已知)(x f 的一个原函数为1+x ,则⎰=dx x f )(10.=⎰dt e dxd t x211.函数y x e z -=2的全微分=dz12.设平面区域}1,10|),{(e y x y x D ≤≤≤≤=,则二重积分⎰⎰Dydxdy x ln 的值为三、解答题:共5题,共78分13.(本题14分)已知⎪⎪⎩⎪⎪⎨⎧+=,)1ln(,,2sin )(x bx a x xx f 000>=<x x x 在点0=x 处连续,求常数b a ,的值.14.(本题14分)设直线0,2,===y x x y 与曲线)0(1>=x xy 所围成的平面区域为D .(1)求D 的面积S ;(2)求D 绕x 轴旋转一周所得的旋转体的体积V .15.(本题16分)(1)求微分方程0cos '=-x y y 的通解;(2)求微分方程086'''=+-y y y 满足初始条件6)0(,2)0('==y y 的特解.16.(本题16分)求二元函数xy y x y x f 6),(33-+=所有的极值点和极值.17.(本题18分)求过直线⎪⎩⎪⎨⎧-=+=-=322312:1t z t y t x l (t 为参数)和直线213123:2-=+=-z y x l 的平面π的方程.。
2018年山东专升本(数学)真题试卷(题后含答案及解析)

2018年山东专升本(数学)真题试卷(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题 4. 综合题 5. 证明题一、选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.函数y=arcsin(1一x)+的定义域是A.(0,1)B.[0,1)C.(0,1]D.[0,1]正确答案:B解析:要使函数有意义,须即D=[0,1).故选B.2.如果函数在(一∞,+∞)内连续,则a=A.6B.7C.8D.9正确答案:C解析:由函y=在(-∞,+∞)内连续可知该函数x=4处连续,于是f(x)=f(4),因为(x+4)=8,f(4)=8,所以a=8,故选C.3.曲线y=的渐进线的条数为A.0B.1C.3D.2正确答案:D解析:因为=e0·arctan1=1·,所y=为其水平渐近线;又因为=+∞·arctan=一∞,于x=0为其垂直渐近线,故应选D.4.如果=∫-∞atetdt,则a=A.0B.1C.2D.3正确答案:C解析:=ea,∫-∞atetdt?-∞a-∫-∞aetdt=(t-1)et?-∞a=(a一1)ea-(t一1)et=(a一1)ea一=(a一1)ea一=(a一1)ea+=(a一1)et,∴ea=(a一1)ea,则a=2,故选C.5.微分方程xlnxdy+(y一lnx)dx=0满足y?x=e=1的特解为A.B.C.D.正确答案:A解析:原方程变形为:(x≠1)其中P(x)=.于是通解为y=将y?x=0=1代入得C=,得特解:y=.故选A.二、填空题6.函数f(x)=的图像关于________对称.正确答案:x=0解析:D=(一∞,+∞),且f(一x)=(一x)=f(x)∴f(x)是偶函数,图像关于y轴对称.故填x=0.7.=________.正确答案:解析:8.f(x)=的第二类间断点为_________.正确答案:x=0,x=1解析:f(x)=的间断点为x=0,x=1,x=一1,分别求这三个点处的函数极限其中,极限存在的为第一类间断点,极限不存在的为第二类间断点.由此可得第一类间断点为x=0,x=1.故应填x=0,x=1.9.设=_________.正确答案:{14,一4,一2}解析:=({l,2,3}+{0,1,一2})×({1,2,3}一{0,1,一2})={1,3,1)×{1,1,5}=={14,一4,一2),故填{14,一4,一2}.10.直线的位置关系为__________.正确答案:垂直解析:直线的方向向量为:={1,1,1}×{1,一1,一1)=:{0,2,-2},直线的方向向量为:={1,一2,一1)×{1,一1,一2}=={3,1,1},∵={0,2,—2}·{3,1,1}=0×3+2×1+(一2)×1=0,∴.∴两直线垂直,故填垂直.三、解答题解答时应写出推理、演算步骤。
2018年成人高考专升本《高等数学(二)》试题及参考答案(共三套)

2018年成人高等学校专升本招生全国统一考试高等数学(二)(模拟试题)答案必须答在答题卡上指定的位置,答在试卷上无效。
.......(共三套及参考答案)第Ⅰ卷(选择题,共40分)一、选择题:1~10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内.1.当x→2时,下列函数中不是无穷小量的是().A.B.C.D.2.A.-3B.一1C.0D.不存在3.A.B.C.D.4.A.B.C.D.5.A.0B.2x3C.6x2D.3x26.设ƒ(x)的一个原函数为Inx,则ƒ(x)等于().A.B.C.D.7.A.y=x+1B.y=x-1C.D.8.A.0B.e一1C.2(e-1)D.9.A.y4cos(xy2)B.- y4cos(xy2)C.y4sin(xy2)D.- y4sin(xy2)10.设100件产品中有次品4件,从中任取5件的不可能事件是().A.“5件都是正品”B.“5件都是次品”C.“至少有1件是次品”D.“至少有1件是正品”第Ⅱ部分(非选择题,共110分)二、填空题:11~20小题,每小题4分,共40分.把答案填在题中横线上.11.12.13.14.15.16.17.18.19.20.三、解答题:21~28题,共70分.解答应写出推理、演算步骤.21.22.23.24.25.(本题满分8分)设事件A与B相互独立,且P(A)=0.6,P(B)=0.7,求P(A+B). 26.27.28.(本题满分10分)求由曲线y=2-x2,),=2x-1及X≥0围成的平面图形的面积S以及此平面图形绕X轴旋转一周所得旋转体的体积Vx.模拟试题参考答案一、选择题1.【答案】应选C.2.【答案】应选D.【解析】本题考查的知识点是分段函数在分段点处的极限计算.分段点处的极限一定要分别计算其左、右极限后,再进行判定.3.【答案】应选A.【提示】本题考查的知识点是基本初等函数的导数公式.只需注意e3是常数即可.4.【答案】应选D.5.【答案】应选C.【解析】本题考查的知识点是函数在任意一点x的导数定义.注意导数定义的结构式为6.【答案】应选A.【提示】本题考查的知识点是原函数的概念,因此有所以选A.7.【答案】应选B.【解析】本题考查的知识点是:函数y=ƒ(x)在点(x,ƒ(x))处导数的几何意义是表示该函数对应曲线过点(x,ƒ(x)))的切线的斜率.由可知,切线过点(1,0),则切线方程为y=x-1,所以选B.8.【答案】应选C.【解析】本题考查的知识点是奇、偶函数在对称区间上的定积分计算.注意到被积函数是偶函数的特性,可知所以选C.9.【答案】应选D.【提示】z对x求偏导时应将y视为常数,则有所以选D.10.【答案】应选B.【解析】本题考查的知识点是不可能事件的概念.不可能事件是指在一次试验中不可能发生的事件.由于只有4件次品,一次取出5件都是次品是根本不可能的,所以选B.二、填空题11.【答案】应填2.12.13.【答案】应填一2sin 2x.【提示】用复合函数求导公式计算即可.14.【答案】应填4.15.【答案】应填1.16.【提示】凑微分后用积分公式.17.【答案】应填2In 2.【解析】本题考查的知识点是定积分的换元积分法.换元时,积分的上、下限一定要一起换.18.19.【答案】20.【答案】应填0.【解析】本题考查的知识点是二元函数的二阶混合偏导数的求法.三、解答题21.【解析】型不定式极限的一般求法是提取分子与分母中的最高次因子,也可用洛必达法则求解.解法1解法2洛必达法则.22.本题考查的知识点是函数乘积的导数计算.23.本题考查的知识点是凑微分积分法.24.本题考查的知识点是定积分的凑微分法和分部积分法.【解析】本题的关键是用凑微分法将ƒ(x)dx写成udυ的形式,然后再分部积分.25.本题考查事件相互独立的概念及加法公式.【解析】若事件A与B相互独立,则P(AB)=P(A)P(B).P(A+B)=P(A)+P(B)-p(AB)=P(A)+P(B)-p(A)P(日)=0.6+0.7-0.6×0.7=0.88.26.本题考查的知识点是利用导数的图像来判定函数的单调区间和极值点,并以此确定函数的表达式.编者希望通过本题达到培养考生数形结合的能力.【解析】(1)(2)因为由上面三式解得α=2,b=-9,c=12.27.本题考查的知识点是二元隐函数全微分的求法.利用公式法求导的关键是需构造辅助函数然后将等式两边分别对x(或y或z)求导.读者一定要注意:对x求导时,y,z均视为常数,而对y或z求导时,另外两个变量同样也视为常数.也即用公式法时,辅助函数F(x,y,z)中的三个变量均视为自变量.求全微分的第三种解法是直接对等式两边求微分,最后解出出,这种方法也十分简捷有效,建议考生能熟练掌握.解法1等式两边对x求导得解法2解法328.本题考查的知识点有平面图形面积的计算及旋转体体积的计算.【解析】本题的难点是根据所给的已知曲线画出封闭的平面图形,然后再求其面积S.求面积的关键是确定对x积分还是对Y积分.确定平面图形的最简单方法是:题中给的曲线是三条,则该平面图形的边界也必须是三条,多一条或少一条都不是题中所要求的.确定对x积分还是对y积分的一般原则是:尽可能用一个定积分而不是几个定积分之和来表示.本题如改为对y积分,则有计算量显然比对x积分的计算量要大,所以选择积分变量的次序是能否快而准地求出积分的关键.在求旋转体的体积时,一定要注意题目中的旋转轴是戈轴还是y轴.由于本题在x轴下面的图形绕x轴旋转成的体积与x轴上面的图形绕x轴旋转的旋转体的体积重合了,所以只要计算x轴上面的图形绕戈轴旋转的旋转体体积即可.如果将旋转体的体积写成上面的这种错误是考生比较容易出现的,所以审题时一定要注意.解由已知曲线画出平面图形为如图2—1—2所示的阴影区域.2018年成人高等学校专升本招生全国统一考试高等数学(二)。
2018年成人高考高数真题及答案解析

2018年成人高等学校专升本招生全国统一考试高等数学(一)一、选择题:每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求。
1.=→xxx cos lim0( ) A.e B.2 C.1 D.0 2.设x y cos 1+=,则dy=( )A.()dx x sin 1+B.()dx x sin 1-C.xdx sinD.xdx sin - 3.若函数()x x f 5=,则()='x f ( ) A.15-x B.15-x x C.5ln 5x D.x 5 4.=-⎰dx x21( ) A.C x +-2ln B.C x +--2ln C.()C x +--221D.()C x +-2215.()='⎰dx x f 2( ) A.()Cx f +221B.()C x f +2C.()C x f +22D.()C x f +216.若()x f 为连续的奇函数,则()=⎰-dx x f 11 A.0 B.2 C.()12-f D.()12f 7.若二元函数y x y x z 232++=,则=∂∂xz( ) A.y xy 232++ B.y xy 23++ C.32+xy D.3+xy 8.方程0222=-+z y x 表示的二次曲面是( ) A.柱面 B.球面 C.旋转抛物面 D.椭球面9.已知区域(){}11,11,≤≤-≤≤-=y x y x D ,则=⎰⎰Dxdxdy ( )A.0B.1C.2D.410.微分方程1='y y 的通解为( ) A.C x y +=2 B.Cx y +=221C.Cx y =2D.C x y +=22 二、填空题:11~20小题,每小题4分,共40分 11.曲线43623++-=x x x y 的拐点为___________ 12.()=-→xx x 1031lim ___________13.若函数()x x x f arctan -=,则()='x f ___________ 14.若x e y 2=,则=dy ___________ 15.()=+⎰dx x 32___________ 16.()=+⎰-dx x x 1125___________17.=⎰dx x π02sin ___________ 18.=∑∞=031n n___________ 19.=⎰+∞-dx e x 0___________20.若二元函数22y x z =,则=∂∂∂yx z2___________ 三、解答题:21~28题,共70分.解答应写出推理、演算步骤21.设函数()⎪⎩⎪⎨⎧≥+=0a,30<,sin 3x x x x xx f ,在0=x 处连续,求a22.求()1sin 123lim 2231---→x x x x23.设函数()()23ln 2++=x x x f ,求()0f '' 24.求23sin lim x tdt x x ⎰→25.求⎰xdx x cos26.求函数()5213123+-=x x x f 的极值27.求微方程x y xy ln 21=-'的通解28.设区域(){}0,9,22≥≤+=y y x y x D ,计算()d xdy y x D⎰⎰+222018年成人高等学校专升本招生全国统一考试高等数学(一)试题答案解析1.【答案】D【解析】01cos lim lim cos lim00===→→→x x x x x x 2.【答案】D【解析】()x x y sin cos 1-='+=',故xdx dy sin -= 3.【答案】C【解析】()()5ln 55x x x f ='=' 4.【答案】B 【解析】C x dx x+--=-⎰2ln 215.【答案】A 【解析】()()()()C x f x d x f dx x f +='='⎰⎰22122212 6.【答案】A【解析】因为()x f 为连续的奇函数,故()011=⎰-dx x f 7.【答案】C【解析】y x y x z 232++=,故32+=∂∂xy xz8.【答案】C【解析】0222=-+z y x 可化为z y x =+2222,故表示的是旋转抛物面9.【答案】A【解析】02111111===⎰⎰⎰⎰⎰---xdx dy xdx xdxdy D10.【答案】B【解析】原方程分离变量得dx ydy =,两边同时积分得C x y +=221,故方程的通解为C x y +=221 11.【答案】(2,-6)【解析】31232+-='x x y ,126-=''x y ,令0=''y ,则6,2-==y x ,故拐点为(2,-6) 12.【答案】3-e【解析】()()[]()33310131lim 31lim --⋅-→→=-+=-e x x xx xx13.【答案】221x x +【解析】()x x x f arctan -=,则()2221111xx x x f +=+-=' 14.【答案】dx e x 22【解析】()x x e e y 222='=',则dx e dy x 22= 15.【答案】C x x ++32 【解析】()C x x dx x ++=+⎰3322 16.【答案】32【解析】()32316111361125=⎪⎭⎫ ⎝⎛+=+--⎰x x dx x x17.【答案】2【解析】22cos222sin 22sin 000=-=⎪⎭⎫ ⎝⎛=⎰⎰πππxx d x dx x18.【答案】23【解析】2331123lim 3113111lim 31000=⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-⋅=→→∞=∑n x n x n n19.【答案】1 【解析】100=-=∞+-+∞-⎰x x e dx e20.【答案】xy 4【解析】22y x z =,22xy xz =∂∂,xy y x z 42=∂∂∂ 21.【答案】()3sin 3limlim 00==--→→xxx f x x()()a a x x f x x =+=++→→3lim lim 0且()a f =0因为()0=x x f 在处连续 所以()()()0lim lim 00f x f x f x x ==+-→→3=a22.【答案】()1123lim 1sin 123lim 22312231---=---→→x x x x x x x x ()()()()25113lim11113lim2121=+++=+--++=→→x x x x x x x x x x23.【答案】()()()22392332+-=''++='x x f x x f故()490-=''f24.【答案】2002003cos 31lim 3sin lim xt x tdtx x xx -=→→⎰()2329lim 313cos 131lim 22020==-=→→x xx x x x25.【答案】⎰⎰-=xdx x x xdx x sin sin cos C x x x ++=cos sin26.【答案】()x x x f -='2,令()0='x f ,得01=x ,12=x , 当1>0<x x 或时,()0>x f ',此时()x f 为单调增加函数 当1<x <0时,()0<x f ',此时()x f 为单调减少函数 故当0=x 时,()x f 取极大值,极大值()50=f 当1=x 时,,()x f 取极小值,极小值()6291=f 27.【答案】这是个一阶线性非齐次微分方程()xx P 1-=,()x x Q ln 2=故通解为⎪⎪⎭⎫ ⎝⎛+⎰⎰=⎰-C dx xe e y dx x dx x 11ln 2()[]Cx x C dx x x x +=⎪⎭⎫ ⎝⎛+⋅=⎰2ln ln 228.【答案】D 在极坐标系里可表示为30,0≤≤≤≤r πθ,故()πθπ48132022=⋅=+⎰⎰⎰⎰rdr r d dxdy y xD。
2018福建专升本高等数学真题

2018年福建省专升本高等数学真题【2018】1.已知单调函数()y f x =其的定义域为(0,1]值域为[1,2),则()y f x =反函数的的定义域为()A.(0,1]B.[1,2)C.[0,1)D.(1,2]【2018】2.函数[]0002lim ()2,lim ()1,lim ()()x x x x x x f x g x f x g x →→→==+=则【2018】3.已知函数()()()()()2115x x f x x x +-=--的所有间断点的是().2,1,5A x x x =-==.1,5B x x ==.5C x =.2D x =-【2018】4.下列各式中正确的是【】1.lim 1x x A e x →∞⎛⎫-= ⎪⎝⎭01.lim 1x x B e x →⎛⎫+= ⎪⎝⎭0sin .lim 1x x C x →=01.lim sin 1x D x x→=【2018】5.已知函数()f x 在[0,1]上连续,任意的(0,1),x '∈有f (x)>0,则必有【】().00A f <().10B f >().1(0)C f f <()().10D f f >【2018】6.若函数f (x)在点0x 具有二阶导数()0f x ''<且()00f x '=,则()0f x 是A.极大值B.极小值C.最大值D.最小值【2018】7.已知()(),F x G x 都是f(x)的原函数,则必有()()().A F x G x =()().B F x CG x =()().C F x G x C =+()().D CF x G x =【2018】8.设()()x f dt t x f x '⎰=则,cos 20是()2.cos A x 2.cos B x 2.2cos C x x 2.sin cos D x x-【2018】9.在空间直角坐标系中,点(1,0,-1)和点(1,0,1)关于下列哪个选项对称是()A.原点B.y 轴C.z 轴D.xy 坐标面【2018】10.下列微分方程中,属于一阶可分离变量微分方程的是()2.0A y dx xdy +=.()0B dx x y dy ++=.dy C x y dx =+22.d y D x y dx=+【2018】11.若()()()==e f f x x f 则ln 【2018】12.当时x →,函数1()1f x x =-为无穷小【2018】13.已知()()()22f x x x '=+-则函数f (x)的单调递减区间是【2018】14.()2212f x ax x c x =++=在点处取得极值,则a =,c =【2018】15.求定积分1dx ⎰【2018】16.若向量{k ,1,0},垂直于xz坐标平面,则k=【2018】17.求极限20sin lim x x x x →-【2018】18.已知220y y x ++=求(1)y ';(2)在点(0,0)处的切线方程【2018】19.求定积分()221x dx +⎰【2018】20.(1)已知()ln f x x x x =-求dy(2)定积分1ln exdx⎰【2018】21.设向量a ={3,0,-1},b ={2,-1,1},(1)计算向量n =2a -b ;积(2)求以向量n 作为法向量且过点(1,-2,-1)的平面方程【2018】22.求微分方程y x dx dy =满足初始条件2|1==x y 的特解【2018】23.()()21x f x x +=(1)讨论曲线y =f (x )的几何性质(定义域、单调性、凹凸性),并作出其图形(2)判断曲线y =f (x )与直线y =x +2有几个交点?〈直接写出答案不必写理由)【2018】24.设曲线y =e x ,与直线x =0,x =1和x 轴围成的平面图形为D(如图).(1)求D 的面枳。
2018年专升本高数真题答案

2018年专升本高数真题答案1、下列有关《红楼梦》的说明,正确的一项是( ) [单选题] *A.《红楼梦》中长着“两弯似蹙非蹙罥烟眉,一双似喜非喜含情目”的是王熙凤,该人最擅弄权术,例如毒设相思局、弄权铁槛寺、逼死尤二姐、破坏宝黛婚姻,最后落了个“机关算尽太聪明,反误了卿卿性命”的悲剧下场。
B.《红楼梦》中贾府的“四春”分别是:孤独的贾元春、精明的贾迎春、懦弱的贾探春、孤僻的贾惜春,取“原应叹息”之意。
C.“花谢花飞飞满天,红消香断有谁怜?……一朝春尽红颜老,花落人亡两不知!”这首诗出自《红楼梦》中人物林黛玉之手。
(正确答案)D.《红楼梦》中表明贾府收入主要书回的情节在第二十五回“乌庄头交租”一事上,表明贾府“排场费用,又不肯讲究省俭”的主要情节是“可卿丧仪”和“元春省亲”两件事。
2、1《边城》是沈从文创作的一部中篇小说。
[判断题] *对错(正确答案)3、14.下面各组词语中加点字的注音,完全正确的一项是()[单选题] *A.渲染(xuàn)抽噎(yè)逞能(chěnɡ)自惭形秽(huì)B.迸溅(bènɡ)荣膺(yīnɡ)褶皱(zhě)气冲斗牛(dǒu)(正确答案)C.殷红(yīn)阔绰(chuò)惩戒(chéng)戛然而止(jiá)D.缄默(jiān)追溯(sù)栈桥(zhàn)鲜为人知(xiān)4、下列各句中加点词的解释,全部正确的一项是()[单选题] *A.虞常果引张胜引:招出会论虞常论:判罪(正确答案)B.欲信大义于天下信:通“伸”,伸张子为父死,亡所恨恨:怨恨C.自分己死久矣分:职责恐前语发发:暴露,泄露D.又非亲属,何谓相坐坐:定罪,治罪汉使张胜谋杀单于近臣,当死当:应当5、关联词选用:()怎么样,()让你觉得它们是泰山的天然的主人,好像少了谁都不应该似的。
[单选题] *只有才不仅还不但而且不管都(正确答案)6、下列关于名著的表述,不正确的一项是;( ) [单选题] *A.凤姐发现贾琏偷娶尤二姐,待贾琏外出办事,把尤二姐骗到家中,百般羞辱二姐,后又利用贾琏新妾秋桐羞辱折磨尤二姐,最后逼得尤二姐吞金自杀。
2018年贵州省专升本高等数学试卷

2018年贵州省专升本招生统一考试高 等 数 学 试 卷注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
3.选择题部分必须使用 2B. 铅笔填涂,如需改动,用橡皮擦干净之后,再选涂其他答案标号;非选择题部分必须使用 0.5 毫米的黑字签字笔书写,字体工整、笔记清楚。
4.请按照题号顺序在各个题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
5.保持卷面清洁,不要折叠、不要弄破,禁用涂改液、涂改胶条。
第Ⅰ卷 选择题一、选择题(本大题共10小题,每题5分,共50分)1.函数()ln 1y x =+ ). A .[—1,3] B .(—1,3] C .[—1,3) D .()1,3-2.已知函数2sin 1y x =+,则其周期T =( ).A .2πB .3πC .2π3D .6π3.已知函数()1f x x =-,则x 1为()f x 的( ).A .极大值点B .极小值点C .非极值点D .间断点 4.当0x →时,tan x 是x 的( )无穷小A .高阶B .低阶C .同阶D .等阶 5.()()00lim lim x x x x f x f x -+→→=是()0lim x x f x →存在的( )条件. A .充分不必要 B .必要不充分 C .充要 D .无关6.已知()f x x =,则()()02lim x f a x f a x∆→+∆-=∆( ). A . 1 B .1 C .2 D . 27.已知函数()()()()3 00 020 x x x f x x x ⎧-<⎪==⎨⎪>⎩,则()0lim x f x →=( ). A .3- B .1 C .0 D .不存在8.下列式子中不正确的一项是( ).A .()()d d f x x f x =⎰B . ∫f(x)dx f(x)dxC .()()d d d f x x f x x =⎰D .()()d f x x f x C '=+⎰ 9.已知函数x y xe =,则()n y =( ).A .x e n x )(+B . n xe x +C . x ne x +D . x e n x )-(10.下列书法正确的是( ).A .可导不一定可微B .可导一定连续C .连续一定可导D .可导不一定连续第Ⅱ卷 非选择题二、填空题(本大题共10小题,每题5分,共50分)11.已知极限0sin 1lim 22x ax x →=,则a =______. 12.已知()2241f x x =+,则()f x =______.13.函数()2ln 1y x =+在区间[]2,1-上的最大值与最小值为______.14.已知y sinx cosx ,则d y =______. 15.极限221lim 31x x x x x →∞+-=-+______. 16.已知函数2x y e =,则y '=______.17.参数方程1sin x t y t =⎧⎨=+⎩,在πt =处切线方程为:______. 18.定积分()1211d 23x x -=+⎰______. 19.定积分2π0cos d x x =⎰______.20.函数ln y k x =在3x =的斜率为3,则k =______.三、计算题(本大题共4小题,21小题6分,22小题、23小题、24小题各8分,共30分)21.已知函数()()()3 1 1 x x f x ax b x ⎧<⎪=⎨+≥⎪⎩,()f x 在1x =处连续且可导,求a ,b .22.已知由方程23250y xy y -++=所确定的函数()y y x =,求d d y x .23.计算不定积分sind 2x x x ⎛ ⎝⎰.24.求由曲线()0x y e x =≥,y e =所围成封闭图形的面积.四、应用题(本题共1小题,共12分)25.已知某提车厂有50个停车位出租,当租金为2000时,可全部租出.然而每当租金增加100时,就会有一个车位租不出去,且租出去的每个车位需要花费100维护费.问当租金为多少时,可获得最大收入?五、证明题(本大题共1小题,共8分)26.证明:当1x >时,()22x x xex e -->-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南昌工学院2018年专升本招生考试试题
高等数学 A 卷
注意事项:
1.答题前,将姓名和准考证号用黑色字迹的签字笔或钢笔填写在试题左上角和答题纸规定的位置上;
2.每小题作出答案后,用黑色字迹的签字笔或钢笔将答案书写在答题纸规定处,不能作答在试题卷上;
3.本科目满分100分,考试时间为120分钟。
――――――――――――――――――――――――――――――――――――――――
一、选择题。
(共10题,每题2分,共20分)
1.函数)1()1ln()(-++=x x x x f 的定义域是( ) A. 1}{->x x B. }01{≤<-x x C. }101{≥≤<-x x x 或 D. 1}{≥x x
2. 如果)(lim 0x f x x +→与)(lim 0
x f x x -→都存在,则 ( ) A. )(lim 0x f x x →存在且)()(lim 00x f x f x x =→ B. )(lim 0
x f x x →不一定存在 C. )(lim 0x f x x →存在,但不一定有)()(lim 00x f x f x x =→ D. )(lim 0
x f x x →一定不存在 3. 按给定的x 的变化趋势,下列函数为无穷小量的是( ) A. )(12112∞→-+x x x )( B. )0(214→--x x C.)(1
43+∞→+-x x x x D. )0(3sin 3→x x x 4. =-→x x x 10
)21(lim ( ) A. 2e B. 2
e - C. e D. 1
5. 已知函数)(x f 在区间],[b a 上连续,则( )
A. )(x f 在],[b a 上有界
B. )(x f 在],[b a 上无界
C. )(x f 在],[b a 上有最大值,无最小值
D. )(x f 在],[b a 上有最小值,无最大值
6. 已知2ln cos )(+=x x f ,则=')(x f ( ) A. 21sin +
x B. 2
1sin +-x C. x sin D. x sin - 7. 设函数()f x 在0x 处可导,则=∆-∆-→∆x x f x x f x )()(lim 000( ) A. '()f x B. )(0x f '- C. 0 D. 不存在
8. 函数)
1(cos )(2-=x x x x f 的间断点个数为( ) A. 0 B. 1 C. 2 D. 3
9. 设函数)(x f 连续,dx x f I b
a ⎰=)(,则I 的值( )
A. 只依赖于a 和b
B. 依赖于a 和b 及x
C. 依赖于a 和b 及)(x f
D. 依赖于a ,不依赖b
10. 下列等式中正确的是( )
A. ⎰=)()(x f x df
B. ⎰=)()(x f dx x f d
C. ⎰=')()(x f dx x f
D. ⎰=)()(x f dx x f dx
d 二、填空题。
(共10题,每题3分,共30分)
11. 已知12
3lim 22=-+-→x k x x x ,则=k . 12. =→x
x x 1sin lim 20 . 13. 已知2)(lim 1
=→x f x ,则=-+→)]()23[(lim 2
1x f x x x . 14. 设5
3)(2
x x x f -=,则=')2(f . 15. 设)1ln()(2x x f += ,则=')(x f
. 16. 设函数()y y x =由方程2334y x x y +=所确定,则'()y 0= .
17. 设函数x x y ln =,则dy = .
18. 定积分=-⎰dx x 2
0)2cos( .
19. 不定积分=⎰
dx xe x . 20. 定积分31
21cos =1x x dx x -+⎰ . 三、计算题。
(共8题,其中第21-26题每题6分,27-28题每题7分,共50分)
21. 已知⎪⎩
⎪⎨⎧>-=<+=1,11,
1,2)(x x x b x a x x f ,若)(x f 在1=x 处连续,求a 和b 的值. 22. 求参数方程⎩⎨⎧+=+=232322t
t y t t x 的二阶导数22d y dx . 23. 求函数32
232)(x x x f -=的极值. 24. 讨论函数⎪⎩⎪⎨⎧=≠=0,
00,41sin 3)(x x x x x f 在0=x 处的连续性与可导性.
25. 求不定积分dx x ⎰-21.
26. 设⎩
⎨⎧≤<≤≤-+=10,02,cos )(x e x x x x f x ,求⎰-12)(dx x f . 27. 求函数dt t t t x f x ⎰
+--=02112)(在区间]1,0[上的最大值与最小值. 28. 求由曲线22-=x y 和12+=x y 所围成图形的面积.。
