高斯光束的聚焦和准直
第8章高斯光束

l2 f 2
f
2
1
l f
(3) F 1 R(l) 1 (l f 2 )时,
2
2l
(4)F
时,
w0 w0
1
lim w0 lim
F
w F 0
F (l F )2 f 2
lim F
1
1
(l
- F)2 F
f F
2 2
w0 1 w0
w0 w0
1
l f
2
1
RR
2
F
25
结论
只有 F 1 R(l) ,才有聚焦作用
F15 q
五、透镜对高斯光束的变换规律
q=l+if q=-l+if
q Fq Fq
q、q:透镜处物、像高斯光束q参数
l、l :物、像高斯光束腰到透镜距离
f、f :物像高斯光束焦参数
q q
f(w0)
O
f(w0) Z
O
l F l
16
例1 某高斯光束焦参数为f=1m,将焦距F=1m 的凸透镜置於其腰右方l=2m处,求经透镜变换 后的像光束的焦参数f及其腰距透镜的距离l
解 (1)
0
f
f
02
3.14 106 3.14 106
1m
z=0.5m
q(z) பைடு நூலகம் if 0.5 i(m)
(2)
w(z) w0
1
z2 f2
w0
1
0.52 12
1.12mm
f2
12
R(z) z 0.5 2.5m
z
0.5
8
例8-2 高斯光束在某处的光斑半径为w=1mm, 等相
高斯光束的聚焦和准直课件

高斯光束的参数如束腰半径、波长等 也会影响准直效果。
光学元件质量
透镜、反射镜等光学元件的质量对准 直效果有重要影响,如光学元件的加 工精度、表面质量等。
04
高斯光束聚焦和准直的应用
光学通信
总结词
高斯光束的聚焦和准直技术在光学通信领域具有广泛应用,能够实现高速、高效 、远距离的光信号传输。
详细描述
实时处理能力
对于动态变化的光束,需要具备实 时处理能力,以便快速响应和调整 。
研究方向
新型光学元件研究
研究新型的光学元件,以提高光 束的聚焦和准直精度。
光束质量提升技术
研究提高光束质量的方法和技术 ,以满足各种应用需求。
实时控制系统
研究实时的光学控制系统,以快 速响应和调整光束。
发展前景
应用领域拓展
比较不同聚焦透镜和不同输入光束参 数对聚焦效果的影响,得出结论和建 议。
06
高斯光束聚焦和准直的未来 发展
技术挑战
高精度控制
高斯光束的聚焦和准直需要高精 度的光学元件和控制系统,以实
现光束的稳定和精确控制。
光束质量提高
目前的高斯光束聚焦和准直技术受 到光束质量的限制,如何提高光束 质量是未来的一个重要挑战。
减小。
高斯光束的应用
1 2
3
激光加工
高斯光束可被用于激光切割、打标和焊接等加工领域。
光学测量
高斯光束可被用于光学测量领域,如干涉仪、光谱仪和全息 术等。
光学通信
高斯光束在光纤通信中用作信号传输的光源,具有传输损耗 低、信号稳定等优点。
02
高斯光束的聚焦
聚焦原理
高斯光束的聚焦是指将发散的高 斯光束通过透镜或反射镜系统, 使其在空间上形成一个能量集中
第7讲 高斯光束的聚焦和准直[优质PPT]
![第7讲 高斯光束的聚焦和准直[优质PPT]](https://img.taocdn.com/s3/m/0b8981bb02d276a200292ef0.png)
例题
出射高斯光束束腰位置位于
空气中z=z’处,此处q参数
为q0’
q0
'
i
0
'2
该高斯光束经过距离l’=l2-z’的自由空间传输到达z=l2处的q参数为:
q2 ' q0 ' l2 z '
q2 ' q2
0 '2 02
0 ' 0
0
'
qC
lC
F
l(F l) (F l)2
2 0
2 0
2 2
i
(F
F
2
2 0
l
)2
2 0
L
0
0'
A BC
l
lC
q(0) q(A) q(B) q(C)
•当C面取在像方束腰处,此时 的方程联立可以求出:
1 1 1 l' l F
几何光学薄透 镜成像公式
束腰半径
1
'
2 0
1
2 0
1
l F
2
1 0 2 F 2
'0 F l ' k 0 l F l
几何光学薄透 镜成像垂轴放
大率公式
7.1 高斯光束通过薄透镜的变换
•
7.1 高斯光束通过薄透镜的变换
F
)2
2 0
/
激光原理与技术 第7讲 高斯光束的聚焦和准直

第七讲 高斯光束的聚焦、准直
7.1 高斯光束通过薄透镜的变换
已知入射高斯光束束腰半径为0,束腰位置与透镜的距离为l,
透镜的焦距为F,各参数相互关系如下图,则有:
z
0处:q 0
q0
i
02
在B面处: q
1
B
q
1
A
1 F
在A面处:q A q0 l 在C面处:q C q B lC
研究其规律:
1
02
1
02
1
l F
2
f2
F
2
d dl
2 0
02
2 F2
l
F
d0
dl
03 02 F
2
F
l
7
7.2 高斯光束的聚焦
A、l F:
d0
dl
03 02 F
2
F
l
0
0 将随着l的减小而减小,
因此当l 0时有最小值:
此时像方高斯光束束腰位置:l
lC
F
F2 0 F 0 F 2 f 2
4
7.1 高斯光束通过薄透镜的变换
当不满足以上条件时,则不能套用几何光学的结论。
当l F时,可以求出l F,此时物方、像方高斯光束的束腰都位于 焦点处,这与几何光学中平行光成像于无穷远处的结论不相符。
当l F时,l仍可解出大于零的解。 例如当时l 0,即入射的物方高斯光束的束腰位于透镜上,可以得到:
2
0 F l k 0 l F l
几何光学薄透 镜成像垂轴
放大率公式
束腰半径是高斯光束所有光斑半径的最小值,可以将其类比为几何光学中
光束的焦点,在满足假设条件的情况下,物方、像方高斯光束经过薄透镜
11-12讲 高斯光束

+ z0 )
与上式相比,位相之差一常数。 与上式相比,位相之差一常数。 Z>0处波阵面是球面,曲率半径 处波阵面是球面, 处波阵面是球面
πW02 2 R ( z 0 ) = z 0 1 + ( ) > z0 > 0 zλ
x R(z) z W0 W(z0) y W(z) z
为有限大小的高斯光束,无论F 对w01为有限大小的高斯光束,无论 和z1如何取都不可能使 w02→∞,也不可能使 2→0,说明单个透镜不能将 高斯光束变换 ,也不可能使θ , 成平行光束。 成平行光束。
方向性,提高准直性, 单透镜可以改善高斯光束的 方向性,提高准直性, 就有θ 尽可能使w 当w01 > w02,就有 2 <θ1,尽可能使 02达到极大值 尽可能使
x θ R(z) z W0 W(z0) y W(z) z
在z=0处,发散角为 ,光斑最小 0称为腰斑,远离腰束光斑逐 处 发散角为0,光斑最小W 称为腰斑, 渐增大, 增大而增大。 渐增大,W(z) 随z增大而增大。 增大而增大
dW ( z ) 2 zλ 2θ = 2 = πW0 dz
当z=0时,2θ=0,平面波 时 ,
平面波
A0 E(x, y,0) = A(x, y, z = 0) = e W0
r2 − 2 W0
表明和 , 坐标相关的相位部分消失了 坐标相关的相位部分消失了, 的平面是等相位面, 表明和x,y坐标相关的相位部分消失了,即z=0的平面是等相位面, 的平面是等相位面 和平面光波一样, 和平面光波一样,振幅部分是高斯函数
W01 W02 = = 2 f W01 2 1 + ( )2 1+ ( ) F λF
W01
现代光学系统

第八章 现代光学系统随着激光技术、光纤技术和光电技术的不断发展,各种不同的用途的新型光学系统相继出现,例如激光光学系统、付里叶光学系统、扫描光学系统等。
为能全面地了解这些光学系统的成像特性和设计要求,本章就上述几种新型光学系统作一简要介绍。
§8-1 激光光学系统一、高斯光束的特性激光作为一种光源,其光束截面内的光强分布式不均匀的,激光束波面上各点的振幅是不相等的,其振幅A 与光束截面半径r 的函数关系为:220r A A e ω-=其中A 0为光束截面中心的振幅;ω为一个与光束截面半径有关的参数;r 为光束截面半径。
由上式可以看出光束波面的振幅A 呈高斯型函数分布,如图8-1所示,所以激光光束又称为高斯光束。
图8-1 高斯光束截面当r =ω时,0A A e=,说明高斯光束的名义截面半径ω是当振幅A 下降到中心振幅0A 的1/e 时所对应的光束截面半径。
二、高斯光束的传播高斯光束的截面半径、波面曲率半径和位相因子是高斯光束传播中的三个重要参数。
1、高斯光束的截面半径高斯光束截面半径()z ω的表达式为:()1220201z z λωωπω⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦ 从图8-2中可以看出,高斯光束在均匀的透明介质中传播时,其光束截面半径()z ω与z 不成线性关系,而是一种非线性关系,这与同心光束在均匀介质中的传播完全不同。
图8-2高斯光束传播2、高斯光束的波面曲率半径高斯光束的波面曲率半径表达式为:()2201R z z z πωλ⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦高斯光束在传播过程中,光束波面的的曲率半径由无穷逐渐变小,达到最小后又开始变大,直至达到无限远时变成无穷大。
3、高斯光束的位相因子高斯光束的位相因子表达式为:()20zz arctg λπωΦ=高斯光束的截面半径轨迹为一对双曲线,双曲线的渐近线可以表示高斯光束的远场发散程度,如图8-3所示。
图8-3 高斯光束的发散角高斯光束的孔径角为:tg λθπω= 4、高斯光束传播的复参数表示假设有一个复参数()q z ,并令()()()211i q z R z z λπω=-当z =0时,得()()()211000i q R λπω=-因为()0R =∞,()00ωω=所以()2000q q i πωλ==- 把()2201R z z z πωλ⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦和()2220201z z λωωπω⎡⎤⎛⎫⎢⎥=+ ⎪⎢⎥⎝⎭⎣⎦代入式()()()211i q z R z z λπω=-得()0q z q z =+这与同心球面光束沿z 轴传播时,其表达式为0R R z =+有相同的表达形式。
高斯光束-聚焦与准直

高斯光束的聚焦
F f
ω0 ' ω0
(2)F< f
ω0 ' ω0
1 F f
1
f 1+ ( F ) 2
2
1
有:
ω0' =1 ω0
ω0
0
F− F − f2
F
F+ F2 −f 2
l
结论: ①若F< f,总有聚焦作用 ②若F > f,只有
l < F − F2 − f 2
1
f 1+( F) 2
证:令 ω
'
(2)
① ②
+ z2 =1 f
1 1 1 1− i 1 1 1 λ (= )= = = − i (= − ) q z + if 1+ i 2 2 2 R πω 2 2λ 1 λ 1 1 ω= = = π πω 2 2 R 2
R = 2m
=
2 × 3 .14 × 10 − 6 = 1 .414 mm 3 .14
ω0' 有极大值 ω0
ω0' = ω0
1 1 + ( )2 f
F =l+
f2 l
高斯光束的聚焦 将 F =l+
代入
ω0' = ω0
ω0' = ω0
f 2 l2 + f 2 = l l F (l − F ) 2 + f 2
2 2
(3) F = R(l ) = (l + (4)F →∞时,
l + f l f4 + f l2
λ z2 (f + ) π f
2 2
R( z ) = z +
3.14 高斯光束的聚焦与准直资料

1
02
0
R(l ) / 2
R (l )
F
一、高斯光束的聚焦
2. l一定时,ω0’随F 的变化情况 表明,当l一定时,透镜的焦距只有小于光束 在透镜处波阵面曲率半径的一半时,透镜对高斯 光束才有聚焦作用。
一、高斯光束的聚焦
例题1:波长为3.14微米的高斯光束,束腰半径1 毫米,使用焦距F=0.1m的透镜对它进行聚焦, 分别将透镜置于束腰处、距离束腰2m处,求:聚 焦后的束腰半径及位置。
1 03 F2 f1 2 F2 f1 2 M ' 1 ( ) 1 ( ) 2 3 01 01 F1 f1 F1
F2 F1 2 F2 1 ( ) M F1 f1 F1 F2 M (几何压缩比) F1
二、高斯光束的准直
3. l1>>F1时,利用望l一定时,ω0’随F 的变化情况
1 2 0'
1
02
0
R(l ) / 2
R (l )
F
一、高斯光束的聚焦
2. l一定时,ω0’随F 的变化情况
令式中0 0' F 2 (l F ) 2 f 2 l 2 F 2 2lF f 2 1 f2 1 F (l ) R(l ) 2 l 2 R(l )为透镜处波阵面的曲率半径, 1 1 1 当F R (l )时, 2 2 , 即0 ' 0 2 0 ' 0
一、高斯光束的聚焦
② 当 l >>F 时,有:
02 F 02 F F 0 ' 2 2 2 f (l ) 0 (l ) l 2 l f (l ) f 0 1 ( ) f
高斯光束的聚焦和准直

八、高斯光束的自再现变换与稳定球面腔
• 利用透镜实现自再现变换
当透镜的焦距等于高斯光束入射在透镜表面上的波 面曲率半径的一半时,透镜对该高斯光束作自再现 变换。
• 球面反射镜对高斯光束的自再现变换
当球面镜的曲率半径与高斯光束入射在球面镜表面 上的波前曲率半径相等时,球面镜对该高斯光束作 自再现变换。
基模高斯光束的特征参数 用参数0(或f)及束腰位置表征高斯光束 用参数(z)和R(z)表征高斯光束 高斯光束的q参数 • 高阶高斯光束(厄米特-高斯光束和拉盖尔高 斯光束,存在于什么腔型中?)
六、高斯光束q参数变换规律
• 高斯光束的q参数与点光源发出光波的等 相位面半径R在光学系统中的变换规律相 A B 同。当高斯光束经过一个变换矩阵为 C D 的光学系统时,若入射及出射的q参数分 别为q1和q2,则遵循以下变换规律
主要内容: • 概述-光腔理论的一般问题 • 共轴球面腔的稳定性条件 • 开腔模式和衍射理论分析方法 • 稳定球面腔中的模结构 • 高斯光束的基本性质及特征参数 • 高斯光束q参数变换规律 • 高斯光束的聚焦和准直 • 高斯光束的自再现变换与稳定球面腔 • 光束衍射倍率因子M2 • 非稳腔
本章总结
2
2 0 (F l) ( )2 2
2 F 2 0
(1)若F一定, 当l<F时, 0随l的减小而减小; 当l=0时, 0达到最小值;当l>F时, 0随l的 增大而减小; 当l时, 00, l F ;当 l= F时, 0达到极大值, 0=(F/0)。
d1 d2
R1=∞
F
R2=∞
第二章作业(二) • 基本题:书本98-100页10、15、17、23、 27 • 附加题: 26、24(主镜口径改为10cm)
10第二章-5 高斯光束的基本性质及特征参数

c r2 r2 z 00 ( x, y, z ) exp[ 2 ] exp{ i[k ( z ) arctg ]} ( z) ( z) 2R f
其中,c为常数,r2=x2+y2,k=2/,
二、高斯光束的准直
• 单透镜对高斯光束发散角的影响 对0为有限大小的高斯光束,无论F、l取什 么值,都不可能使0 ,也就不可能使0 0。 结论:用单个透镜将高斯光束转换成平面波, 从原则上说是不可能的。 l=F 时, 0 达到极大值, 0 达到极小值, 0/ 0=f/F,此时,F愈大, 0 愈小。当 f/F=02/F<<1时,有较好的准直效果。与F 和0关联。
解 (1)
z=1m f=1m
0 f
3.14 106 1 1mm 3.14
腰位置为在该处左方1m处
(2)
1 1 1 i 1 1 i q 1 i 2 2 2
1 1 R 2
R 2m
1 2 2
2
2 3.14 106 1.414mm 3.14
复曲率半径q
三、用q参数分析高斯光束的传输问题
• 已知:入射高斯光束腰斑半径为0 ,束腰与透 镜的距离为l,透镜的焦距为F。 • 求:通过透镜L后在与透镜相距lC处的高斯光束 参数C和RC。
• • • •
在z=0处 q(0)=i02/ 在A处(紧靠透镜的左方)qA=q(0)+l 在B处(紧靠透镜的右方)1/qB=1/qA-1/F 在C处 qC=qB+lC qC C、RC
2 0 q0 i if
用q0=q(0)表示z=0处 的参数值,得出
第7讲 高斯光束的聚焦和准直(PPT文档)

f F2
0 F
2
C
0
F
7.2 高斯光束的聚焦
– 高斯光束的聚焦,指的是通过适当的光学系统 减小像方高斯光束的束腰半径,从而达到对其 进行聚焦的目的。
– 1、F一定时,ω’0随着l变化的情况 我们将通过前面得到的高斯光束通过薄透镜变 换时束腰半径变换规律研究其规律:
激光原理与技术·原理部分
第7讲 高斯光束的聚焦、准直
7.1 高斯光束通过薄透镜的变换
– 已知入射高斯光束束腰半径为ω0,束腰位置
与透镜的距离为l,透镜的焦距为F,各参数相
互关系如下图,则有:
L
–
z=0处,q(0)
q0
i
2 0
/
0
0 ' C
– 在A面处:q(A) q0 l
–
在B面处:q(1B)
0
2
1 F2
0
2
1
l
2 0
2
2 F 2
2
2(l
)
'0
(l)
F
此时
l'
F
(l
(l F)2
F )F 2
2 0
/ 2
lF F
0
F
7.2 高斯光束的聚焦
若同时满足
l
f
2
a ib
其中:
f
2 0
F 2(F l)
a
(F
激光物理第1.3章 高斯光束

1 1 i 2 q( z ) ( z ) ( z )
z = 0 ,ρ(0)→∞,
(0) 0
1 1 1 i q0 q( 0 ) ( 0 ) 2 ( 0 )
02 q0 i iz0
可将高斯光束表示为
0 E ( x , y , z ) E0 e z
(1.3.30)
注意到类透镜介质中传播距离z时的变换矩阵为
A B cos z C D sin z sin z cos z 1
Aq0 B qz Cq0 D
1.4 基横模高斯光束变换的ABCD定律
证明
Aq1 B q2 Cq1 D
2 02
( f l1 )
(1.3.8)
得:
dP z 2 dQ z Q z r 2iQz 2k kr k 2 2r 2 0 dz dz
2 2
上式要对任意r值均成立,必然要求r2项的系数与其余 项分别为0,即
dQz 2 2 Q z k k 0 dz dPz iQz k 0 dz
(二)远场发散角
定义在基模高斯光束强度的1/e2点的远场发散角 (半角)为
0 lim
z
( z )
z
0
(1.3.22)
由此式可见,腰斑越小,发散角越大。 高斯光束在傍轴近似条件下,可以将它看成是一 种曲率中心与曲率半径都随传播过程而不断改变的 非均匀球面波,这是因为它的等相位面是球形,但
dy1
令 则
y2 v , B
1 2
s
2
1 A i q B 1
2.7 高斯光束聚焦和准直
2
b、z处光斑半径
x方向: m 2 z 2m 1 z 2 M x 2 z 2
n 2 z 2n 1z 2 z 2 y方向:
远场发散角
2 m z 2 2 m lim 2m 1 2m 1 0 M x 0 z z 0
1 R l 2
时,才具有聚焦作用,F越
(2) 让物光束腰斑远离透镜焦点,满足
l f
(3) 取
l F
和
l0
,并设法满足条件
f F 。
二、高斯光束的准直 1、核心问题:减小发散角,提高方向性。 2 z 01 e2 lim 2 02 F 2 2 z z 0 '0 2 2 0 2 途径:提高光束束腰半径 F l
选择 0 F、l 取值
2、单透镜法
选取大F 使l=F
2、双透镜法(倒置望远镜准直)
' 01 ,同时使 使用第一个短焦透镜缩小束腰半径为
束腰位于另一大焦距透镜物方焦平面上,经第二透镜 后光束准直
20
, 20 , 20,
l
'
2 0
f
2
2 2 0 1 2
0 f1 l
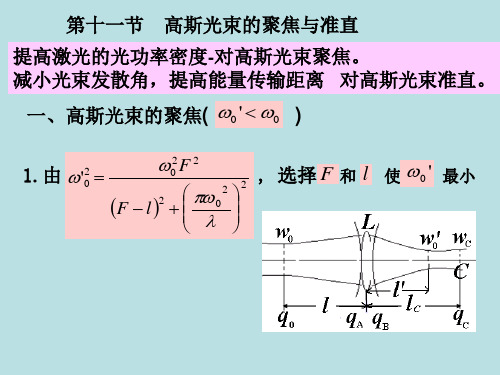
第十一节
高斯光束的聚焦与准直
提高激光的光功率密度-对高斯光束聚焦。 减小光束发散角,提高能量传输距离 对高斯光束准直。 一、高斯光束的聚焦( 0 ' 0 )
2 1.由 '0 2 0 F 2
F l
2
0
2
2
, 选择 F 和 l 使 0 ' 最小
'0
第7讲 高斯光束的聚焦和准直

F2 F 此时像方高斯光束束腰位置: 此时像方高斯光束束腰位置:l ' = F 1 − = F 2 + (πω 20 / λ ) 2 1 + ( F / f ) 2 < F
而垂轴放大率: 而垂轴放大率: k =
(l − F ) F λ 此时 l ' = F + → ω '0 ≈ F 2 F + 0 ≈ F 2 l >> F 2 (l − F ) + (πω 0 / λ ) πω (l )
2
7.2 ;> = f λ
则
F ω '0 = ω 0 l
1 1 πω 0 2 l 2 f 2 1 l 2 l 2 = 2 1 + ≈ 2 2 2 = 2 Fω 0 ω'0 F λ f F ω 0 f
•
7.1 高斯光束通过薄透镜的变换
• 如果令 lC = F ,即像方高斯光束束腰位于透镜前焦面,可以利用前面的公式求出束腰 即像方高斯光束束腰位于透镜前焦面, 的半径: 的半径: πω 20 f = λ 2 2 F (F − l) F f F 2( F − l ) qC = +i = a + ib 其中: a = 其中: 2 2 2 2 ( F − l )2 + f 2 (F − l) + f (F − l) + f F2 f b = ( F − l )2 + f 2 1 a b 1 λ
更进一步的,如果满足 l 更进一步的,
第17讲 高斯光束的聚集、准直与模匹配

M1
M2
M 2
M1
l
l´
17.4 高斯光束的匹配
两谐振腔的间距不固定的情形
解:
f w02 , f w02
17.4 高斯光束的匹配
q l if , q l if
1 11 q q F
因此, l F w0 F 2 ff , l F w0
f 2
17.2 单透镜对高斯光束的聚焦
w0
F
l F 2
f
2
w0
F l2
f
2
w0
F w(l)
17.2 单透镜对高斯光束的聚焦
w0 max
F w0
相应地, l F
17.2 单透镜对高斯光束的聚焦
17.2 单透镜对高斯光束的聚焦
w0
w0
l = 0.5f
w0
F2 f
w0
F2 w0
F2 F1
w(l)
F2 F1
w0
l 2
1
f
根据准直倍率的定义,
M w0 F2 w0 F1
1
l f
2
17.3 实现高斯光束的准直与扩束
总结:倒望远镜系统两种情形的准直倍率:
l 0 l F1
M F2 F1
l(l F1) (l F1)2
f2 f2
F1
F1
F1 F12
f
2
w0
17.3 实现高斯光束的准直与扩束
w0
F2 f
第7讲 高斯光束的聚焦和准直

0 ' 0
高斯光束经过均匀介质块后,光束发散角 不发生变化。
例题
入射高斯光束在介质块左侧界面处q参 数为q1:
0 2 q1 i l1
经过平面介质界面折射的传输矩阵为:
1 0 则进入介质块左侧界面的q 参数q2为: 2 1 0 q2 q1 i 0 l1
例题
入射高斯光束束腰位置处 q参数为q0,经过自由空间 l1后的q参数为q1,经过介 质块后出射的q参数为q2。
q1 q0 l1
故:
l 1 折射率为n的介质块的光纤传输矩阵为: 0 1
q2 q1
L
q0 l1
l2 l1
0 2 l2 l1 i l1
0 '2 02 i i z 1 l 1
高斯光束入射到均匀介质中,其束腰半径不发生变化,束腰位置向右移动。
7.1 高斯光束通过薄透镜的变换
– 已知入射高斯光束束腰半径为ω0,束腰位置与透 镜的距离为l,透镜的焦距为F,各参数相互关系如 下图。
高斯光束束腰的变换关系式
7.1 高斯光束通过薄透镜的变换
束腰位置
(l F ) F 2 l' F 2 (l F )2 20 /
束腰半径
1 1 l 2 1 0 2 2 1 2 2 ' 0 0 F F
0
L
0 '
C
l
q(0)
A
B
lC
C q(C)
q(A) q(B)
7.1 高斯光束通过薄透镜的变换
方法一:分步计算
高斯光束-聚焦与准直

透镜对高斯光束的变换公式
l2 + f 2 )ω0 F 2l ∴ω0'= ω0 = 2 2 2 2 (l − F) + f l +f 2 2 [l − ( )] + f 2l l2 + f 2 l2 + f 2 2 2 ( )ω 0 ( )ω0 ( l + f )ω 2l 0 2l = 2l = = = ω0 (l 2 − f 2 )2 2 l2 + f 2 ( l 2 + f 2 )2 + f 4l 2 2l 4l 2 (
l
l′
0.1( 2 + i ) 0.1(2 + i )(-1.9 + i ) = −0.104 + 0.00217 i = 0.1 − 2 − i (-1.9 − i )(-1.9 + i )
l ′ = 0 .099 m
l ′ = 0.104m
ω0 ' =
3.14 × 10 −6 × 0.00217 λf ' = = 0.0466mm 3.14 π
ω0' 有极大值 ω0
ω0' = ω0
1 1 + ( )2 f
F =l+
f2 l
高斯光束的聚焦 将 F =l+
代入
ω0' = ω0
ω0' = ω0
f 2 l2 + f 2 = l l F (l − F ) 2 + f 2
2 2
(3) F = R(l ) = (l + (4)F →∞时,
l + f l f4 + f l2
透镜对高斯光束的变换规律I—q参数变换 q =l+if q′=-l′+if ′
10第二章-5高斯光束的基本性质及特征参数

z f
]}
重新整理r
00 (x, y, z)
c exp{ik
(z)
r2 2
[
1 R(z
)
i
2(
z
)
]}
exp[
i(k
z
arctg
z )] f
引入一个新的参数q(z), 定义为
1 q(z)
1 R(z)
i
2 (z)
• 参数q将(z)和R(z)统一在一个表达式中,知
道了高斯光束在某位置处的q参数值,可由下
对称共焦腔/一般稳定球面腔
二、高斯光束在自由空间的传输规律
振幅因子光斑半径(z)
基模高斯光束在横截面内的场振幅分布按高斯
函数所描述的规律从中心向外平滑地降落。由 振幅降落到中心值的1/e处的点所定义的光斑半
径为(z);光斑半径随坐标z按双曲线规律扩展
远场发散角0(定义在基模高斯光束强度的
1/e2点的远场发散角)
解
f
02
3.14 106 3.14 106
1m
(z) 0
1
z2 f2
w0
1
0.52 12
1.12mm
R(z) z f 2 0.5 12 2.5m
z
0.5
例2 高斯光束在某处的光斑半径为w=1mm, 等相位
面曲率半径为R=0.5m, 求此高斯光束(1)该处的q参
数 (2)腰斑半径w0及腰位置(光波长为=3.14m)
(
2 0
)
2
令
0
0
l l
F
1 2
l 1
2 0
l
2
0、
1 R(l) 2
3.14 高斯光束的聚焦与准直

3.14 高斯光束的聚焦与准直
高斯光束的聚焦与准直
聚焦: 经过光学系统(透镜)使高斯光束的腰斑变小, (需要研究ω0’、l、F的变化规律) 准直: 利用光学系统改善光束的方向性(压缩束散
F
一、高斯光束的聚焦
2. l一定时,ω0’随F 的变化情况
令式中0 0' F 2 (l F ) 2 f 2 l 2 F 2 2lF f 2 1 f2 1 F (l ) R(l ) 2 l 2 R(l )为透镜处波阵面的曲率半径, 1 1 1 当F R (l )时, 2 2 , 即0 ' 0 2 0 ' 0
F1 02 , l1 ' F1 F1 2 f1 2 1 ( ) 1 ( ) f1 F1
01
(短焦距)
l2=F2时,
F2 F2 F2 03 02 1 f2 02 01
f1 2 F1
二、高斯光束的准直
2. l1=0情况下,利用望远镜准直高斯光束 望远镜对高斯光束的准直倍率为:
二、高斯光束的准直
当0'达到极大值时, '达到极小。 什么条件下,0'达到极大值? l F时,0'极大, F 此时,0 ' 0 F , 代入上式得: f 0
' 0 02 ,可见: 0 ' F ()在 1 l F 条件下,0 ' 极小,因而 ' 可达到极大;
角),这个问题通常称为高斯光束的准直问题。
一、高斯光束的聚焦
第7讲 高斯光束的聚焦和准直

f2 F2 l F F 1 2 F 2 2 2 2 2 F f F f 0 F f
这与几何光学中当l F 时不能成实像的情况不同。
F 2 0 F
0 l F
F 2 l F l lC F 2 l F f2 2 1 1 f2 l 1 2 Im q 2 1 F F 2 0 c 0
0
F
根据高斯光 束参数定义
F 2 l F l lC F 2 l F f2 2 1 1 f2 l 1 2 Im q 2 1 F F 2 0 c 0
激光原理与技术
第七讲 高斯光束的聚焦、准直
7.1 高斯光束通过薄透镜的变换
已知入射高斯光束束腰半径为0,束腰位置与透镜的距离为l, 透镜的焦距为F,各参数相互关系如下图,则有:
1 1 1 在B面处: q B q A F
02 z 0处:q 0 q0 i
1 当C 面取在像方束腰处,此时RC , Re 0,可以得到 qc
F l
2
f
2
i
F2 f
F l
2
f2
得到的式子是高斯光束束腰的变换关系式。
02 f
3
7.1 高斯光束通过薄透镜的变换
l 2 f 当满足 l F 或 1 条件时,由束腰位置关系公式: F F
l f 1 1 F F
2 2
随F的变化规律如图所示:从结果 当 0 和l一定时, 0 Rl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、高斯光束的基本性质及特征参数
• 基模高斯光束 • 基模高斯光束在自由空间的传输规律
基模高斯光束的光斑半径 基模高斯光束的相移特性 基模高斯光束的远场发散角
高斯光束在其传输轴线附近可近似看作是一 种非均匀球面波,其曲率中心随着传输过程 而不断改变,但其振幅和强度在横截面内始 终保持高斯分布特性,且其等相位面始终保 持为球面。
Aq1 B q2 Cq1 D
七、高斯光束的聚焦和准直
•高斯光束的聚焦
若出射高斯光束的腰斑半径小于入射高斯光束的腰 斑半径,则称之为聚焦。 采用焦距为F的单透镜对高斯光束进行聚焦时,
l F (l F ) F 2
2 0 2 (l F ) ( )2
0
一般地, vmn(x,y)应为复函数,它的模 vmn(x,y)描述镜面上场的振幅分布,而其辐角 arg vmn(x,y) 描述镜面上场的相位分布。 复常数mn的模量度自再现模的单程损耗(对称 开腔),它的辐角量度自再现模的单程相移, 2 从而也决定模的谐振频率。 1
d 1 e 2 1
主要内容: • 概述-光腔理论的一般问题 • 共轴球面腔的稳定性条件 • 开腔模式和衍射理论分析方法 • 稳定球面腔中的模结构 • 高斯光束的基本性质及特征参数 • 高斯光束q参数变换规律 • 高斯光束的聚焦和准直 • 高斯光束的自再现变换与稳定球面腔 • 光束衍射倍率因子M2 • 非稳腔
本章总结
• 光腔的损耗
损耗类型:选择性损耗(?)与非选择损耗(?) 损耗参数:平均单程损耗因子、光子在无源腔内的 平均寿命、线宽、无源谐振腔的品质因数
二、共轴球面腔的稳定性条件
• 腔内光线往返传播的矩阵表示:
腔内任一傍轴光线在某一给定的横截面内都可以由 两个坐标参数来表征:光线离轴线的距离r、光线与 轴线的夹角。 光线在自由空间行进距离L时所引起的坐标变换为TL 球面镜对傍轴光线的变换矩阵为TR
d1 d2
R1=∞
F
R2=∞
第二章作业(二) • 基本题:书本98-100页10、15、17、23、 27 • 附加题: 26、24(主镜口径改为10cm)
end
• 稳定腔模式理论是以共焦腔模的解析理论为基 础的。对方形镜共焦腔,镜面上场的分布可用 厄米特--高斯函数表示,对圆形镜共焦腔,镜 面上场的分布可用拉盖尔--高斯函数描述,并 且整个腔内(以及腔外)空间中的场都可以表 示为厄米特--高斯光束或拉盖尔--高斯光束的 形式。共焦腔振荡模的一系列基本特征都可以 解析地表示出来。在高斯光束传输规律的基础 上,建立了一般(非共焦的)稳定球面腔与共 焦腔之间的等价性,从而将共焦腔解析理论的 结果推广到一般稳定球面腔,解决了应用最广 的这一大类谐振腔的模式问题。
模的基本特征: (1)电磁场空间分布 (2)模的谐振频率; (3)在腔内往返一次经受的相对功率损耗; (4)与该模相对应的激光束的发散角 纵模:通常将由整数q所表征的腔内纵向光场的分 布称为腔的纵模,不同的q相应于不同的纵模;达到 谐振时,腔的光学长度应为半波长的整数倍,腔的 谐振频率是分立的,纵模间隔与q无关
第二章作业(一) • 书本97-98页:1、2、3(指对称共焦腔)、 4(求双凹、凹凸腔情况) • 第5题: 在稳区图中,标出以下特殊腔型:对称共焦 腔、半共焦腔、对称共心腔、半共心腔、平 行平面腔。
附加题: • 第6题:书本98页5题 • 第7题:如图所示谐振腔,给出该腔的稳定性 条件。(提示:先求出光线通过镜面反射的 变换矩阵,然后选定一个起始平面,求出光 线在腔内往返一周的变换矩阵)
本章内容提要
一、光腔理论的一般问题
• 光腔的作用:模式选择、提供轴向光波模的反馈
构成、分类:开放式光腔和波导腔;稳定腔、非稳 腔和临界腔
• 模式的概念
模式:通常将光学谐振腔内可能存在的电磁波的 本征态称为腔的模式。腔的模式也就是腔内可区分 的光子的状态。一旦给定了腔的具体结构,则其中 振荡模的特征也就随之确定下来了。
• 自再现模应满足的积分方程:
寻求开腔振荡模的问题归结为求解菲涅耳—基尔霍 夫衍射积分方程这样一个数学问题(积分本征值问 题) 通过解析解或数值解可求出积分方程的本征值(m、 n)与本征函数(vm(x) 、 vn(y) ),从;从而得到开腔 自再现模的全部特征(包括场分布及传输特性)
mn ( x, y) m ( x) n ( y) mn m n
• 高斯光束的自再现变换与稳定球面腔
九、光束衍射倍率因子M2
• M2定义为实际光束的腰斑半径与远场发散角 的乘积与基模高斯光束的腰斑半径与远场发 散角的乘积之比 • M2值可以表征实际光束偏离衍射极限的程度, 称为衍射倍率因子 • M2因子也是表征激光束空间相干性好坏的本 质参量 • K=1/M2称作光束传输因子,国际上公认的一 个描述光束空域传输特性的量。 十、非稳腔(非稳腔的构成)
• 主要讨论了光腔模式问题。它是理解激光的相干性、 方向性、单色性等一系列重要特性、进行激光器件 的设计和装调的基础,也是研究和掌握激光基本技 术和应用的基础。 • 开放式光腔根据几何偏折损耗的高低,可以分为稳 定腔、非稳腔和临界腔。稳定腔的几何偏折损耗很 低,绝大多数中、小功率器件都采用稳定腔。其模 式理论是腔模理论中比较成熟的部分。由于稳定腔 应用广泛,其模式理论具有最广泛、最重要的实践 意义。
• 一般稳定球面腔的模式特征
共焦腔模式理论可以推广到一般两镜稳定球面腔。 基于:任意一个共焦腔与无穷多个稳定球面腔等价; 任一满足稳定性条件的球面腔唯一地等价于某一共 焦腔。 “等价”指具有相同的行波场 一般稳定球面腔的两个镜面与其等价共焦腔高斯光 束过轴线上z1、z2两点的等相位面重合(坐标原点在 共焦腔中心)。如果已知稳定球面腔镜面曲率半径 R1、R2和腔长L,则这一关系可描述为
0 F1 f
八、高斯光束的自再现变换与稳定球面腔
• 利用透镜实现自再现变换
当透镜的焦距等于高斯光束入射在透镜表面上的波 面曲率半径的一半时,透镜对该高斯光束作自再现 变换。
• 球面反射镜对高斯光束的自再现变换
当球面镜的曲率半径与高斯光束入射在球面镜表面 上的波前曲率半径相等时,球面镜对该高斯光束作 自再现变换。
基模高斯光束的特征参数 用参数0(或f)及束腰位置表征高斯光束 用参数(z)和R(z)表征高斯光束 高斯光束的q参数 • 高阶高斯光束(厄米特-高斯光束和拉盖尔高 斯光束,存在于什么腔型中?)
六、高斯光束q参数变换规律
• 高斯光束的q参数与点光源发出光波的等 相位面半径R在光学系统中的变换规律相 A B 同。当高斯光束经过一个变换矩阵为 C D 的光学系统时,若入射及出射的q参数分 别为q1和q2,则遵循以下变换规律
• 共轴球面腔的稳定性条件:
1
对于复杂开腔,稳定性条件为: 对简单共轴球面腔,稳定性条件为:
1 ( A D) 1 2
0 (1
• 稳区图
L L )(1 ) 1 R1 R2
g1=g2=0
三、稳定开腔中模式的衍射理论分析方法
• 开腔模的物理概念:
开腔镜面上的经过一次往返能再现的稳态场分布称 为开腔的自再现模或横模。自再现模一次往返所经 受的能量损耗称为模的往返损耗,所发生的相移称 为往返相移,该相移等于2的整数倍。
R1 R( z1 ) ( z1 f z1 ) 2 R2 R( z2 ) ( z2 f z2 ) L R R 2 1
2
可求出其等价共焦 腔的共焦参数f及其 和一般稳定球面镜 腔的相对位置
L( R2 L) z 1 ( L R1 ) ( L R2 ) L( R1 L) z 2 ( L R1 ) ( L R2 ) 2 L( R1 L)( R2 L)( R1 R2 L) f [( L R1 ) ( L R2 )]2
2 2 arg 1
对称开腔:
q 2
四、稳定球面腔中的模结构
• 方形镜共焦腔与圆形镜共焦腔的自再现模
镜面上场的振幅和相位分布
共焦腔基模在镜面上的分布 高阶横模(强度花样) 相位分布 单程损耗 单程相移和谐振频率
共焦腔行波场(共焦场)的特征
振幅分布和光斑尺寸 模体积 等相位面的分布 远场发散角
• 采用稳定球面腔的激光器所发出的激光,以 高斯光束的形式在空间传播。研究高斯光束 在空间的传输规律,以及光学系统对高斯光 束的变换规律,成为激光的理论和实际应用 中的重要问题。讨论了最简单和最基本的情 形,即高斯光束在自由空间中的传输和简单 透镜(或球面反射镜)系统对高斯光束的变 换,以及它的聚焦和准直问题。
第二章 开放式光腔与高斯光束
• 讨论光腔模式问题;只讨论无源腔 • 开放式光腔可以分为稳定腔、非稳腔和临界腔 • 稳定腔模式理论是以对称共焦腔模的解析理论为基 础的,推广到一般稳定球面腔 • 采用稳定腔的激光器所发出的激光,将以高斯光束 的形式在空间传播。研究高斯光束在空间的传播规 律以及光学系统对高斯光束的变换规律 • 稳定腔不适用于某些高功率激光器,非稳腔却能同 时满足高输出功率和良好光束质量这两个要求
(2)若l一定,当F<R(l)/2时,透镜才能对高斯光束起聚 焦作用。F愈小,聚集效果愈好 结论:为获得良好聚集,采用 用短焦距透镜;使高斯光束远离透镜焦点,从而满足 l>>f、l>>F;取l=0,并使f>>F。
•பைடு நூலகம்斯光束的准直
单透镜对高斯光束发散角的影响
l=F时,0达到极大值,0达到极小值,0/0=f/F; 用单个透镜将高斯光束转换成平面波,从原则上说是 不可能的。 利用倒装望远镜将高斯光束准直 M 0 F2 1 ( l )2
2
2 0 (F l) ( )2 2
