勾股定理11
勾股定理的证明与应用

勾股定理的证明与应用勾股定理是数学中的一条重要定理,它表明在直角三角形中,直角边的平方和等于斜边的平方。
本文将对勾股定理的证明方法进行探讨,并结合实际应用场景进行具体分析。
一、勾股定理的证明勾股定理最早可以追溯到中国古代。
相传,公元前11世纪的周朝时期,中国古代数学家祖冲之发现了勾股定理,并给出了一种证明方法。
他的证明方法基于图形的几何性质,被称为“割弦法”。
具体来说,首先假设有一个直角三角形,三边分别为a、b、c。
利用割弦法,我们可以得到如下等式:sin A = a / ccos A = b / c根据三角函数的定义,我们可以将上述两个等式相加:sin^2 A + cos^2 A = (a^2 / c^2) + (b^2 / c^2) = (a^2 + b^2) / c^2由于在直角三角形中,sin A 和 cos A 的平方和等于1,即 sin^2 A + cos^2 A = 1,因此可以得到:1 = (a^2 + b^2) / c^2进一步变换得:c^2 = a^2 + b^2因此,勾股定理得证。
二、勾股定理的应用勾股定理在数学和实际生活中都有广泛的应用。
下面将以几个实际场景为例,介绍勾股定理的应用。
1. 测量直角三角形的边长勾股定理可以用于测量一个直角三角形的边长。
假设我们已知一个直角三角形的两个直角边的长度分别为3和4,我们可以利用勾股定理计算出斜边的长度:c^2 = 3^2 + 4^2= 9 + 16= 25因此,斜边的长度为5。
2. 解决几何问题勾股定理在解决几何问题中有重要作用。
例如,我们可以利用勾股定理来判断一个三角形是否为直角三角形。
如果三条边的长度满足勾股定理的条件,即c^2 = a^2 + b^2,那么该三角形就是直角三角形。
3. 工程应用勾股定理在工程中也有广泛的应用。
例如,在建筑设计中,我们需要确保房间的角度为直角。
通过测量房间的两个边长,可以利用勾股定理来判断是否满足直角条件。
勾股定理常用11个公式

勾股定理常用11个公式勾股定理也叫毕达哥拉斯定理,指的是直角三角形中,任意一条直角边的平方等于另外两条边的平方之和。
勾股定理是数学中非常重要的一条定理,广泛应用于各个领域。
以下是勾股定理常用的11个公式:1. 勾股定理的一般形式在直角三角形 ABC 中,设 AB、AC 为直角边,BC 为斜边,则有:BC² = AB² + AC²2. 勾股定理的两个常见形式a. 已知直角边和斜边设直角边 AB = a,AC = b,BC = c,则有:c² = a² + b²b. 已知两条直角边设直角边 AB = a,BC = b,AC = c,则有:c² = a² + b²3. 勾股定理的逆定理如果在一个三角形中,某一边的平方等于另外两边的平方之和,那么这个三角形肯定是直角三角形,即有:若 c² = a² + b²,则三角形 ABC 是直角三角形。
4. 勾股数指满足勾股定理的整数三元组 (a, b, c),其中 a、b、c 都是正整数,称为勾股数。
例如:(3, 4, 5)、(5, 12, 13)。
5. 勾股数的生成公式生成勾股数的公式称为勾股数生成公式。
其中,m 和 n 是正整数,且 m > n,gcd(m, n) = 1,k 是任意正整数,则有:a = k × (m² - n²),b = k × (2mn),c = k × (m² + n²)6. 勾股数的性质a. 勾股数只存在于原始勾股数列中。
b. 勾股数之间不存在公因数。
c. 每个奇数都可以表示为两个勾股数之和。
d. 每个正整数都可以表示为不超过四个勾股数之和。
7. 勾股数的应用a. 构造直角三角形。
b. 计算斜线长度。
c. 解决一些证明问题。
d. 在几何光学中,勾股数用于计算光路长度。
勾股定理20种证明方法

勾股定理20种证明方法1. 最常见的勾股定理证明是基于三角形面积公式的。
利用三角形的底边与高的关系,可以将直角三角形分成两个三角形,然后应用面积公式进行计算得出勾股定理。
2. 通过向直角三角形内部引入一个圆形,利用圆的性质可以得到勾股定理。
3. 将直角三角形中的一条直角边平移到非直角边上,形成一个平行四边形,再利用平行四边形对角线的关系即可得到勾股定理。
4. 利用正弦定理和余弦定理进行推导,可以得出勾股定理。
5. 通过三角形内部的相似三角形进行推导得出勾股定理。
将直角三角形分成两个相似三角形,利用相似三角形的性质进行推导得出勾股定理。
6. 通过归纳法进行证明,即证明勾股定理对于所有自然数n都成立。
7. 利用勾股定理推导其他几何定理,例如正弦定理、余弦定理等,进而证明勾股定理。
8. 利用数学归纳法,可证勾股定理对于所有正整数n都成立。
9. 利用勾股定理证明勾股三角形的存在性,也就是存在一组自然数a、b、c,使得a²+b²=c²。
这可以通过暴力算法或递推算法来实现。
10. 利用反证法证明勾股定理。
假设勾股定理不成立,即假设存在一个直角三角形,其两条直角边的平方和不等于斜边的平方。
通过假设的前提,推导出矛盾的结论,从而证明勾股定理成立。
11. 利用勾股定理证明三角形的周长和面积公式。
将直角三角形分成两个直角三角形,利用勾股定理计算出直角边的长度,然后应用周长和面积公式。
12. 利用勾股定理证明三角形的内心与垂心之间的关系。
将直角三角形分成两个相似三角形,利用勾股定理计算出内心与垂心之间的距离。
13. 利用勾股定理证明三角形的外心与垂心之间的关系。
通过三角形的外接圆,证明外心与垂心之间的距离等于直角边之间距离的一半。
14. 利用圆的性质证明勾股定理。
将三角形中的一条直角边作为直径,表示成圆上的弦长,利用圆的定理得到勾股定理。
15. 通过三角形的相似性质,证明勾股定理。
将直角三角形分成两个与之相似的三角形,利用相似三角形的性质得到勾股定理。
勾股定理常用个公式

勾股定理常用个公式勾股定理是数学中一个非常重要的定理,它是平面几何中的基础定理,常用来求解直角三角形的边长和角度。
根据勾股定理,我们可以推导出多个相关的公式来解决各种问题。
在本篇文章中,我将介绍11个常用的勾股定理公式,每个公式都会附带一个解析和一个示例。
1.三角形斜边的长度(已知两边长度):c=√(a²+b²),其中a和b分别是直角三角形的两条直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的两条直角边的长度分别为3和4,求斜边的长度。
解析:根据公式,c=√(3²+4²)=√(9+16)=√25=5、因此,斜边的长度为52.直角三角形的直角边长度(已知斜边长度和另一直角边长度):a=√(c²-b²),其中b是已知直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的斜边长度为5,另一直角边的长度为4,求第二个直角边的长度。
解析:根据公式,a=√(5²-4²)=√(25-16)=√9=3、因此,第二个直角边的长度为33.直角三角形的直角边长度(已知斜边长度和另一直角边长度):b=√(c²-a²),其中a是已知直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的斜边长度为5,另一直角边的长度为3,求第二个直角边的长度。
解析:根据公式,b=√(5²-3²)=√(25-9)=√16=4、因此,第二个直角边的长度为44.直角三角形的面积(已知两个直角边的长度):A=1/2*a*b,其中a和b为直角三角形的两个直角边的长度。
示例:已知一个直角三角形的两个直角边的长度分别为3和4,求其面积。
解析:根据公式,A=1/2*3*4=6、因此,直角三角形的面积为65.直角三角形的周长(已知两个直角边的长度):P=a+b+c,其中a和b分别为直角三角形的两个直角边的长度,c为斜边的长度。
勾股定理

勾 股 定 理1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c += 勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方 2.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 3.勾股定理的应用 ①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a c b =- ②知道直角三角形一边,可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题 4.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边 ①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边 ③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形题型一:直接考查勾股定理 例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长 ⑵已知17AB =,15AC =,求BC 的长题型二:应用勾股定理建立方程 例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD = ⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为 分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21EDCBA例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mABCD E题型四:利用勾股定理求线段长度——例题6 如图4,已知长方形ABCD 中AB=8cm,BC=10cm,在边CD 上取一点E ,将△ADE 折叠使点D 恰好落在BC 边上的点F ,求CE 的长.BAC7.关于翻折问题例7、如图,矩形纸片ABCD 的边AB=10cm ,BC=6cm ,E 为BC 上一点,将矩形纸片沿AE 折叠,点B 恰好落在CD 边上的点G 处,求BE 的长.变式:如图,AD 是△ABC 的中线,∠ADC=45°,把△ADC 沿直线AD 翻折,点C 落在点C ’的位置,BC=4,求BC ’的长.课后训练: 一、填空题1.如图(1),在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需________米.图(1)2.种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做 ㎝。
勾股定理16种经典证明方法
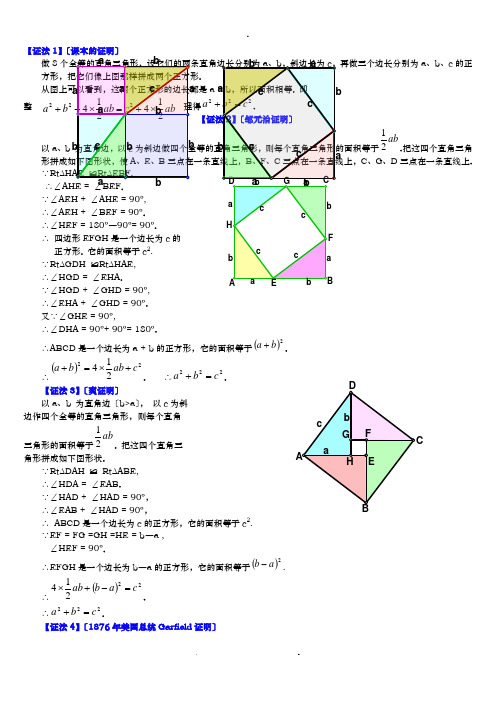
b a22+【证法1】〔课本的证明〕做8a 、b 、c 的正.2a 整以a 、b ab21.把这四个直角三角C 、G、D 三点在一条直线上.∵Rt Δ∴∠AHE = ∠BEF . ∵∠AEH + ∠AHE = 90º, ∴∠AEH + ∠BEF = 90º. ∴∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵Rt ΔGDH ≌Rt ΔHAE, ∴∠HGD = ∠EHA .∵∠HGD + ∠GHD = 90º, ∴∠EHA + ∠GHD = 90º. 又∵∠GHE = 90º,∴∠DHA = 90º+ 90º= 180º.∴ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴222c b a =+.【证法3】〔爽证明〕以a 、b 为直角边〔b>a 〕, 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如下图形状.∵Rt ΔDAH ≌ Rt ΔABE, ∴∠HDA = ∠EAB .∵∠HAD + ∠HAD = 90º, ∴∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴()22214c a b ab =-+⨯.∴222c b a =+. 【证法4】〔1876年美国总统Garfield 证明〕以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如下图形状,使A 、E 、B 三点在一条直线上. ∵Rt ΔEAD ≌Rt ΔCBE, ∴∠ADE = ∠BEC .∵∠AED + ∠ADE = 90º, ∴∠AED + ∠BEC = 90º. ∴∠DEC = 180º―90º= 90º. ∴ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ABCD 是一个直角梯形,它的面积等于()221b a +.∴()222121221c ab b a +⨯=+. ∴222c b a =+.【证法5】〔梅文鼎证明〕 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵D 、E 、F 在一条直线上,且Rt ΔGEF ≌Rt ΔEBD, ∴∠EGF = ∠BED ,∵∠EGF + ∠GEF = 90°,∴∠BED + ∠GEF = 90°,∴∠BEG =180º―90º= 90º.又∵AB = BE = EG = GA = c ,∴ABEG 是一个边长为c 的正方形.∴∠ABC + ∠CBE = 90º. ∵Rt ΔABC ≌Rt ΔEBD, ∴∠ABC = ∠EBD .∴∠EBD + ∠CBE = 90º.即∠CBD= 90º.又∵∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴222c b a =+. 【证法6】〔项明达证明〕做两个全等的直角三角形,设它们的两条直角边长分别为a 、b 〔b>a 〕 ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如下图的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P .过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N .∵∠BCA = 90º,QP ∥BC , ∴∠MPC = 90º, ∵BM ⊥PQ ,∴∠BMP = 90º,∴BCPM 是一个矩形,即∠MBC = 90º. ∵∠QBM + ∠MBA = ∠QBA = 90º, ∠ABC + ∠MBA = ∠MBC = 90º, ∴∠QBM = ∠ABC ,又∵∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴Rt ΔBMQ ≌Rt ΔBCA .同理可证Rt ΔQNF ≌Rt ΔAEF . 从而将问题转化为【证法4】〔梅文鼎证明〕. 【证法7】〔欧几里得证明〕做三个边长分别为a 、b 、c 的正方形,把它们拼成如下图形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L .∵AF = AC ,AB = AD ,∠FAB = ∠GAD , ∴ΔFAB ≌ΔGAD , ∵ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形∴222b ac += ,即 222c b a =+. 【证法8】〔利用相似三角形性质证明〕如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵∠ADC = ∠ACB = 90º, ∠CAD = ∠BAC , ∴ΔADC ∽ΔACB .AD ∶AC = AC ∶AB ,即AB AD AC •=2.同理可证,ΔCDB ∽ΔACB ,从而有AB BD BC •=2.∴()222AB AB DB AD BC AC =•+=+,即 222c b a =+.【证法9】〔作玫证明〕做两个全等的直角三角形,设它们的两条直角边长分别为a 、b 〔b>a 〕,斜边长为c . 再做一个边长为c 的正方形.把它们拼成如下图的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵∠BAD = 90º,∠PAC = 90º, ∴∠DAH = ∠BAC . 又∵∠DHA = 90º,∠BCA = 90º,AD = AB = c ,∴Rt ΔDHA ≌Rt ΔBCA . ∴DH = BC = a ,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵Rt ΔDGT ≌Rt ΔBCA ,Rt ΔDHA ≌Rt ΔBCA .∴Rt ΔDGT ≌Rt ΔDHA .∴DH = DG = a ,∠GDT = ∠HDA . 又∵∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴DGFH 是一个边长为a 的正方形.∴GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +〔b ―a 〕. 用数字表示面积的编号〔如图〕,则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+•-+=++21438=ab b 212-, 985S S S +=,∴824321S ab b S S --=+=812SS b --.② 把②代入①,得=922S S b ++ = 22a b +. ∴222c b a =+. 【证法10】〔锐证明〕设直角三角形两直角边的长分别为a 、b 〔b>a 〕,斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如下图形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号〔如图〕.∵∠TBE = ∠ABH = 90º, ∴∠TBH = ∠ABE .又∵∠BTH = ∠BEA = 90º,BT = BE = b ,∴Rt ΔHBT ≌Rt ΔABE . ∴HT = AE = a . ∴GH = GT ―HT = b ―a .又∵∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90∴∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ,∠HGF = ∠BDC = 90º,∴Rt ΔHGF ≌Rt ΔBDC . 即27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌Rt ΔQAM .即58S S =.由Rt ΔABE ≌Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴∠FQM = ∠CAR .又∵∠QMF = ∠ARC = 90º,QM = AR = a ,∴Rt ΔQMF ≌Rt ΔARC . 即64S S =.∵543212S S S S S c ++++=,612S S a +=,8732S S S b ++=, 又∵27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++ =2c ,即 222c b a =+. 【证法11】〔利用切割线定理证明〕在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得=()()BD AB BE AB -+ =()()a c a c -+ = 22a c -, 即222a c b -=,∴222c b a =+. 【证法12】〔利用多列米定理证明〕在Rt ΔABC 中,设直角边BC = a ,AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 接于一个圆. 根据多列米定理,圆接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴222AC BC AB +=,即 222b a c +=,∴222c b a =+.【证法13】〔作直角三角形的切圆证明〕在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边O ,切点分别为D 、E 、F 〔如图〕,设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即r c b a 2=-+,∴c r b a +=+2. ∴()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵abS ABC 21=∆, ∴ABC S ab ∆=42, 又∵AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴()ab rc r242=+,∴22222c ab ab b a +=++, ∴222c b a =+. 【证法14】〔利用反证法证明〕如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中, ∵∠A = ∠A , ∴假设 AD :AC ≠AC :AB ,则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵∠B = ∠B ,∴假设BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵∠ACB = 90º,∴∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴222c b a =+.【证法15】〔辛卜松证明〕ABCD . 把正方形ABCD 划分ABCD 划分成上方右图 ()2b a +∴2a +2c =.【证法〔b>a 〕a 、b 的正方形〔b>a 〕,把它. . D D在EH = b 上截取ED = a ,连结DA 、DC , 则 AD = c .∵EM = EH + HM = b + a , ED = a ,∴DM = EM ―ED = ()a b +―a = b .又∵∠CMD = 90º,CM = a ,∠AED = 90º, AE = b , ∴Rt ΔAED ≌Rt ΔDMC .∴∠EAD = ∠MDC ,DC = AD = c . ∵∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º,∴∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ΔABF ≌ΔADE .∴∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵AB = BC = c ,BF = CG = a , ∴Rt ΔABF ≌Rt ΔBCG .∵54322S S S S c +++=, 6212S S S b ++=,732S S a +=, 76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++ =5432S S S S +++ =2c∴222c b a =+.。
11_勾股定理_

2
图2-1
3 1
2
图2-2
正方形2的面积是 9 个单位面积。 正方形3的面积是 18 个单位面积。
(图中每个小方格代表一个单位面积)
一、阅读课本 回答问题
3 1
(2)在图2-2中,正 方形1,2,3中各含 有多少个小方格?它 们的面积各是多少?
2
(3)你能发现两图
3
中三个正方形1,2,
CaB
a 2+b 2= 169cm2 c 2= 169cm2
a2+b2=c2
勾股定理:(gou-gu theorem)
直角三角形两直角边的平方和 等于斜边的平方.
弦c 股b
┏
勾a
a2+b2=c2
人类最伟大的十个科学发现之一 .
三、应用定理 巩固新知
例:如图,为得到池塘两岸A点和B点间的距离,
观测者在C点设桩,使△ABC为直角三角形,并测得
AC为100米,BC为80米.求A、B两点间的距离是多少?
B
C 解:如图,根据题意 得
Rt △ABC中,∠B=90°
AC=100米, BC=80米, 由勾股定理 得
A
∵AB2+BC2 =AC2
∴AB2 =AC2-BC2 =1002 - 802=602
∴AB=60(米)
答:A、B两点间的距离是60米.
27
• (4)若∠A=60º,AC=3,则AB=__4t△ABC中,AC=3,AB=5,则BC 的长为____________.
• 3、Rt△ABC中,∠C=901º3,AC=12, BC=10,则BC边上的中线AD的长为 _______.
重要的 思想方 法及数 学思想
《勾股定理》数学教学PPT课件(10篇)

=BD·
CD.
D
B
E
C
课堂小
结
利用勾股定理解
决实际问题
勾股定理
的应用
构造直角三角形
解决实际问题
第十七章 勾股定理
17.1 勾股定理
第3课时
利用勾股定理作图和计算
知识要点
1.勾股定理与数轴、坐标系
2.勾股定理与网格
3.勾股定理与几何图形
新知导入
想一想:
我们知道数轴上的点有的表示有理数,有的表示无理数,你
能在数轴上画出表示 13 的点吗?
如果能画出长为 13 的线段,就能在数轴上画出表示 13 的
2
点.容易知道,长为
的线段是两条直角边的长都为1的直角三
角形的斜边.
长为 13 的线段能是直角边的长为正整数的直角三角形的
斜边吗?
新知导入
想一想:
利用勾股定理,可以发现,直角边的长为正整数2, 3
知识
的直角三角形的斜边长为
AC2+BC2=AB2
由上面的例子,我们猜想:
命题1 如果直角三角形的两条直角边长分别为a,b,斜边
长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
a
c
b
课程讲授
1
勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c
证明:∵S大正方形=c2,
S小正方形=(b-a)2,
b
a
b-a
例 如图是由4个边长为1的正方形构成的“田字格”,只用没有刻
度的直尺在这个“田字格”中最多可以作出长度为
8
_____条.
勾股定理的所有证明方法

勾股定理的所有证明方法勾股定理是数学中的经典定理,也是最为著名的几何定理之一。
它指出,对于一个直角三角形,其斜边的平方等于两腰的平方和。
这个定理的证明方法有很多种,本文将介绍其中的一些。
1. 几何证明法几何证明法是最为直观的证明方法,它通过图形的构造和几何关系的推导来证明定理的正确性。
具体来说,我们可以通过以下步骤来进行证明:(1)画出一个直角三角形ABC,其中∠B为直角,边长分别为a、b、c。
(2)以AB为直角边,画出一个正方形ACDE,使得AE=AB=c。
(3)以BC为直角边,画出一个正方形BFGH,使得BG=BC=a。
(4)连接DG、EF两条线段,交于点I。
(5)由于正方形的对角线相等,因此DI=AF=c,EI=BF=a。
(6)根据正方形的性质可知,DG=GH=EF=EI=a。
(7)因此,三角形ADI、BFI、DGH都是等腰直角三角形,且它们的底边分别为a、b、c。
(8)根据勾股定理可知,ADI和BFI的斜边分别为c和a,因此它们的底边分别为b。
(9)由此可得,b=c-a和b=a-c,即勾股定理成立。
2. 代数证明法代数证明法是通过代数运算来证明定理的正确性。
具体来说,我们可以通过以下步骤来进行证明:(1)假设有一个直角三角形ABC,其中∠B为直角,边长分别为a、b、c。
(2)根据勾股定理可知,c=a+b。
(3)将上式移项得到a=c-b。
(4)同理可得b=c-a。
(5)因此,勾股定理成立。
3. 平面几何证明法平面几何证明法是通过平面几何中的相关定理和性质来证明定理的正确性。
具体来说,我们可以通过以下步骤来进行证明:(1)假设有一个直角三角形ABC,其中∠B为直角,边长分别为a、b、c。
(2)作AC的垂线BD,交于点E。
(3)根据勾股定理可知,c=a+b。
(4)根据相似三角形的性质可知,BDE和ABC相似。
(5)因此,BD/AB=DE/AC,即BD/c=DE/a。
(6)移项得到BD=c/a。
专题11 勾股定理的实际应用模型(原卷版)

专题11勾股定理的实际应用模型勾股定理将图形与数量关系有机结合起来,在解决实际问题和几何应用中有着广泛的应用。
运用勾股定理解决实际问题的一般步骤:(1)从实际问题中抽象出几何图形(建模);(2)确定要求的线段所在的直角三角形;(3)确定三边,找准直角边和斜边:①若已知两边,则根据勾股定理直接计算第3边;②若已知一边,则根据勾股定理列方程间接求解。
(挖掘两个未知边之间的数量关系,设出一边为未知数,把另一边用含有未知数的式子表示出来)。
模型1、梯子滑动模型相关模型背景:梯子滑动、绳子移动等。
解题关键:梯子的长度为不变量、墙与地面垂直。
梯子滑动模型解题步骤:1)运用勾股定理求出梯子滑动之前在墙上或者地面上的距离;2)运用勾股定理求出梯子滑动之后在墙上或者地面上的距离;3)两者相减即可求出梯子在墙上或者地面上滑动的距离。
例1.(2023春·安徽亳州·八年级校考期中)风华中学八年级(2班)小明同学和他的好朋友小亮一起利用所学知识完成下面的操作,如图,梯子AB斜靠在墙角MON处,4mAB=,梯子底端离墙角的距离 2.4mBO=.(1)求这个梯子顶端A距地面有多高;(2)上下移动梯子的过程中,小明发现梯子上总有一个定点到墙角O的距离始终是不变,你能说出这个点并说明其中的道理吗?(3)若梯子顶端A下滑的距离为m a,底端B向左滑b,小亮认为a与b的值始终相等,小明认为b可能比a的值大,也可能比a的值小,也有可动的距离为m能相等.你认为他们两个谁说的正确,请说明理由.A.2m B.2.5m例3.(2023秋·河南郑州·八年级校考期末)图中的两个滑块平的滑道上滑动.开始时,滑块A时,滑块B滑动了厘米.例4.(2023春·重庆·八年级专题练习)位于沈阳周边的红河峡谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A子拉船移动,开始时绳子AC的长为D的位置,问此时游船移动的距离模型2、轮船航行模型相关模型背景:轮船航行等。
勾股定理优秀教学设计模板(精选11篇)

勾股定理优秀教学设计模板(精选11篇)勾股定理优秀教学设计模板(精选11篇)作为一位不辞辛劳的人民教师,通常需要用到教学设计来辅助教学,教学设计是连接基础理论与实践的桥梁,对于教学理论与实践的紧密结合具有沟通作用。
我们应该怎么写教学设计呢?以下是小编精心整理的勾股定理优秀教学设计模板,欢迎阅读与收藏。
勾股定理优秀教学设计篇1一、教案背景概述:教材分析:勾股定理是直角三角形的重要性质,它把三角形有一个直角的"形"的特点,转化为三边之间的"数"的关系,它是数形结合的典范。
它可以解决许多直角三角形中的计算问题,它是直角三角形特有的性质,是初中数学教学内容重点之一。
本节课的重点是发现勾股定理,难点是说明勾股定理的正确性。
学生分析:1、考虑到三角尺学生天天在用,较为熟悉,但真正能仔细研究过三角尺的同学并不多,通过这样的情景设计,能非常简单地将学生的注意力引向本节课的本质。
2、以与勾股定理有关的人文历史知识为背景展开对直角三角形三边关系的讨论,能激发学生的学习兴趣。
设计理念:本教案以学生手中舞动的三角尺为知识背景展开,以勾股定理在古今中外的发展史为主线贯穿课堂始终,让学生对勾股定理的发展过程有所了解,让他们感受勾股定理的丰富文化内涵,体验勾股定理的探索和运用过程,激发学生学习数学的兴趣,特别是通过向学生介绍我国古代在勾股定理研究和运用方面的成就,激发学生热爱祖国,热爱祖国悠久文化的思想感情,培养他们的民族自豪感和探究创新的精神。
教学目标:1、经历用面积割、补法探索勾股定理的过程,培养学生主动探究意识,发展合理推理能力,体现数形结合思想。
2、经历用多种割、补图形的方法验证勾股定理的过程,发展用数学的眼光观察现实世界和有条理地思考能力以及语言表达能力等,感受勾股定理的文化价值。
3、培养学生学习数学的兴趣和爱国热情。
4、欣赏设计图形美。
二、教案运行描述:教学准备阶段:学生准备:正方形网格纸若干,全等的直角三角形纸片若干,彩笔、直角三角尺、铅笔等。
勾股定理的应用

详细描述
在计算机图形学中,勾股定理被用于计算两点之间的距 离,以实现图形的测量和比较。同时,勾股定理还可以 用于计算角度和面积,以实现图形的旋转、缩放和平移 等变换。此外,勾股定理在三维图形学中也被用于计算 深度和阴影等效果,以提高图形的真实感和立体感。
案例三:利用勾股定理解决物理学中的问题
总结词
THANK YOU
风险管理
在衡量投资组合的风险时,利用勾股定理可以计算投资组合的波动率, 从而更好地评估和降低投资风险。
03
估值模型
基于勾股定理的估值模型可以更准确地评估公司的价值,尤其是在考虑
公司未来的增长率和折现率时。
利用勾股定理在环境科学中的应用
地理信息系统(GIS)
在环境科学领域,勾股定理被广泛应用于地理信息系统中,以帮助 研究人员更好地了解地球表面形态、地形地貌以及植被分布等信息 。
利用勾股定理解决实际问题
01
02
03
建筑学
在建筑设计中,勾股定理 被用来确定角度、长度等 参数,以确保建筑物的稳 定性和美观。
航空航天
在航空航天领域,勾股定 理被用来计算飞行器的路 径、高度等,以确保飞行 器的安全和高效。
地理学
在地理学中,勾股定理被 用来确定两点之间的距离 、高度差等,以便更好地 了解地球的形状和大小。
空间计量经济学
空间计量经济学是研究空间自相关和空间异质性的学科,利用勾股定理可以更好地理解和 分析空间数据的结构和特征。
人类行为研究
在研究人类行为和社会现象时,利用勾股定理可以帮助解释人类行为和决策的背后逻辑, 例如人类的迁移、聚集和社会分层等现象。
05
勾股定理的应用前景 与挑战
勾股定理的应用前景
第11讲勾股定理折叠问题

第十一讲勾股定理折叠问题一、知识梳理初中数学中,有关折叠的问题也是相对比较难的问题,主要涉及求角的度数、求线段的长度、求周长、面积等,其中求线段的长度的问题必然用到勾股定理.图形折叠问题核心实质是轴对称性质,即先找出对称轴,再观察元素不变量与变量,然后运用所学知识合理、有序、全面解决问题。
图形折叠对象主要是三角形、矩形、梯形等,考查问题涉及点坐标、角度、线段、周长、面积、图形规律、最值、三角函数、比例、解析式等等,折叠问题中,“折”是过程,“叠”是结果,此题型灵活多变,能考查学生的自主探索能力与空间想象能力以及推理能力,解决折叠问题,首先要对图形折叠有一定准确定位,把握折叠实质,从点、线、面三个方面发现图形中的位置关系和数量关系,抓住图形的变量和不变量,其次探索折叠变化规律,充分挖掘图形隐含的几何性质,运用所学知识合理、有序、全面解决问题。
折叠性质:①对应线段相等(能够重合的线段)②对应角相等(能够重合的角)性质记忆:折叠必有角相等、边相等。
处理策略:求什么设什么,找直角三角形,用勾股定理二、典型例题(1)折叠与角度问题例1、如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=25°,则∠CDE=__________.解:∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,∴∠BCD=∠ECD=45°,∠B=∠CED,∵∠A=25°,∴∠B=90°-25°=65°,∴∠CED=65°,∴∠CDE=180°-45°-65°=70°,故答案为:70°.例2、如图,在△ABC 中,∠ACB=90°,将∠A 折叠,使点A 落在边CB 上的点A′处,折痕为CD ;若∠A′DC=84°,则∠B=________°.解:∵△CDA′与△CDA 关于CD 成轴对称,∴∠ADC=∠A′DC=84°,∵∠ACB=90°,∴∠DCA=∠DCB=45°,∵∠CDA=∠B+∠DCB ,∴∠B=84°-45°=39°故答案为:39.(2)折叠与线段长度例3、如图,有一张直角三角形纸片,90ACB ∠=︒,5cm AB =,3cm AC =,现将ABC ∆折叠,使边AC 与AB 重合,折痕为AE ,则CE 的长为()A .1cmB .2cmC .3cm2D .5cm 2【解析】∵90ACB ∠=︒,5cm AB =,3cm AC =∴4BC ===由折叠可知CE=DE,AC=AD ,90ADE ACE ∠=∠=︒设CE x =,则4,2,BE x BD AB AD =-=-=在Rt BDE 中∵222DE BD BE +=∴2222(4)x x +=-解得32x =故选C例4、如图,在矩形ABCD 中,6,8AB AD ==,点E 是边A D 上一动点,将ABE △沿直线BE 对折,点A 的落点为A ',当A DE ' 为直角三角形时,线段AE 的长为()A .3B .4C .6或3D .3或4【答案】C 【分析】当A DE ' 为直角三角形时,有两种情况:①当点A '在矩形内部时,如图1所示,先利用勾股定理求出BD =10,根据折叠的性质得90BA E DA E ''∠=∠=︒,设AE =x ,则A E x '=,DE =8-x ,然后在Rt A DE ' 中运用勾股定理计算出x 的值即可;②当点A '落在边BC 上时,如图2所示,此时四边形ABA E '是正方形,得出AE =AB =6.【详解】解:∵四边形ABCD 是矩形∴∠A =∠C =90°,AB =6,AD =8∴10BD ===当A DE ' 为直角三角形时,有两种情况:①当点A '在矩形内部时,如图1所示,由折叠的性质得,AE A E '=,6A B AB '==设AE x =,则A E x '=,8DE x =-∴1064DA BD A B ''=-=-=在Rt A DE ' 中,222A E DA DE ''+=∴2224(8)x x +=-解得,x =3∴AE =3;②当点A '落在边BC 上时,如图2所示,此时四边形ABA E '是正方形,∴AE =AB =6故选:C .例5、如图,在Rt ABC 的纸片中,90C ∠=︒,5AC =,13AB =.点D 在边BC 上,以A D 为折痕将ADB △折叠得到AD B ' ,A B '与边BC 交于点E .若D EB ' 为直角三角形,则BD 的长是_______.【答案】7或263【分析】由勾股定理可以求出BC 的长,由折叠可知对应边相等,对应角相等,当△DEB′为直角三角形时,可以分为两种情况进行考虑,分别利用勾股定理可求出BD 的长.【详解】解:在Rt ABC 中,12BC ===,(1)当90ED B ∠'=︒时,如图1,过点B ′作B F AC '⊥,交AC 的延长线于点F ,由折叠得:13AB AB ='=,BD B D C F ='=,设BD x =,则B D CF x '==,12B F CD x '==-,在Rt AFB' 中,由勾股定理得:222(5)(12)13x x ++-=,即:270x x -=,解得:10x =(舍去),27x =,因此,7BD =.(2)当90D EB ∠'=︒时,如图2,此时点E 与点C 重合,由折叠得:13AB AB ='=,则1358B C '=-=,设BD x =,则B D x '=,12CD x =-,在Rt △B CD ¢中,由勾股定理得:222(12)8x x -+=,解得:263x =,因此263BD =.故答案为:7或263.例6、如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,将边AC A 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B'处,两条折痕与斜边AB 分别交于点E 、F ,则△B'FC 的面积为______________.【答案】9625【分析】由题意可得AB=10,根据面积可得CE=4.8,根据勾股定理可求BE=6.4,由折叠可求∠ECF=45°,可得EC=EF=4.8,即可求BF 的长,可求面积.【详解】解:∵Rt △ABC 中,∠ACB=90°,AC=6,BC=8,∴BA==10,∵将边AC 沿CE 翻折,使点A 落在AB 上的点D 处,∴∠AEC=∠CED ,∠ACE=∠DCE ,∵∠AED=180°,∴∠CED=90°,即CE ⊥AB ,∵S △ABC =12AB×EC=12AC×BC ,∴EC=4.8,在Rt △BCE 中,=6.4,∵将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B′处,∴BF=B'F ,∠BCF=∠B'CF ,∵∠BCF+∠B'CF+∠ACE+∠DCE=∠ACB=90°,∴ECF=45°,又CE ⊥AB ,∴∠EFC=∠ECF=45°,∴CE=EF=4.8,∵BF=BE-EF=6.4-4.8=1.6,∴△BFC 的面积为:12FB×EC=18249625525⨯⨯=,由翻折可知,△B'FC 的面积=△BFC 的面积=9625故答案为9625.【点睛】本题考查了折叠问题,勾股定理,根据折叠的性质求∠ECF=45°是本题的关键.(2)折叠与最值问题例7、如图,在ABC 中,,904C AC ︒∠==cm ,3BC =cm ,点D 、E 分别在AC 、BC上,现将DCE 沿DE 翻折,使点C 落在点'C 处,连接AC ',则AC '长度的最小值()A .不存在B .等于1cmC .等于2cmD .等于2.5cm【解析】当C′落在AB 上,点B 与E 重合时,AC'长度的值最小,∵∠C=90°,AC=4cm ,BC=3cm ,∴AB=5cm ,由折叠的性质知,BC′=BC=3cm ,∴AC′=AB-BC′=2cm .故选:C .例8、如图,矩形纸片ABCD,3AD=,折叠纸片,使点A落在BC边上的E处,AB=,5折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动,若限定点P、Q分别在AB、A D边上移动,则点E在BC边上可移动的最大距离为()A.1B.2C.4D.5【答案】B【分析】根据翻折变换,当点Q与点D重合时,点E到达最左边,当点P与点B重合时,点E到达最右边,所以点E就在这两个点之间移动,分别求出这两个位置时EB的长度,然后两数相减就是最大距离.【详解】解:如图1,当点D与点Q重合时,根据翻折对称性可得ED=AD=5,在Rt△ECD中,ED2=EC2+CD2,即52=(5-EB)2+32,解得EB=1,例9、如图2,当点P与点B重合时,根据翻折对称性可得EB=AB=3,∵3-1=2,∴点E在BC边上可移动的最大距离为2.故选:B .例10、如图,在矩形ABCD 中,10AB =,12AD =,点E 是AB 的中点,点F 是A D 边上的动点,将AEF ∆沿EF 翻折,得到A EF '∆,则A C '的最小值是()A .6B .7C .8D .9【答案】C 【分析】求A C '的最小值,先求出EC 的大小,再根据EA A C EC ''+≥,求出A C '的范围即可.【详解】解析:连接E C 在△A CE '中,可得EA A C EC ''+≥.在Rt EBC ∆中,由勾股定理,得13EC ==.由折叠可知,5EA EA '==,∴8A C '≥故选C .【点睛】本题主要考查了三角形三边的大小关系及勾股定理,正确掌握三角形三边的大小关系及勾股定理是解题的关键.例11、如图在三角形纸片ABC 中,已知∠ABC =90º,AC =5,BC=4,过点A 作直线l 平行于BC ,折叠三角形纸片ABC ,使直角顶点B 落在直线l 上的点P 处,折痕为MN ,当点P 在直线l 上移动时,折痕的端点M 、N 也随之移动,若限定端点M 、N 分别在AB 、BC 边上(包括端点)移动,则线段AP 长度的最大值与最小值的差为________________.【答案】1【分析】分别找到两个极端,当M 与A 重合时,AP 取最大值,当点N 与C 重合时,AP 取最小,即可求出线段AP 长度的最大值与最小值之差【详解】如图所示,当M 与A 重合时,AP 取最大值,此时标记为P 1,由折叠的性质易得四边形AP 1NB是正方形,在Rt △ABC 中,,∴AP 的最大值为A P 1=AB=3如图所示,当点N 与C 重合时,AP 取最小,过C 点作CD ⊥直线l 于点D ,可得矩形ABCD ,∴CD=AB=3,AD=BC=4,由折叠的性质有PC=BC=4,在Rt △PCD 中,∴AP 的最小值为AD PD=4-线段AP 长度的最大值与最小值之差为(1AP AP=341----故答案为1例12、如图,在△ABC 中,∠C =90°,∠ABC =45°,D 是BC 边上的一点,BD =2,将△ACD 沿直线AD 翻折,点C 刚好落在AB 边上的点E 处.若P 是直线AD 上的动点,则△PEB 的周长的最小值是________.【答案】2【分析】连接CE,交AD于M,根据折叠和等腰三角形性质得出当P和D重合时,PE+BP的值最小,此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,先求出BC和BE 长,代入求出即可.【详解】如图,连接CE,交AD于M,∵沿AD折叠C和E重合,∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,∴AD垂直平分CE,即C和E关于AD对称,BD=2,∴,∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,∵∠DEA=90°,∴∠DEB=90°,∵∠ABC=45°,∴∠B=45°,∵,∴,即,∴△PEB 的周长的最小值是.故答案为.【点睛】本题考查了折叠性质,等腰三角形性质,轴对称-最短路线问题,勾股定理,含30度角的直角三角形性质的应用,关键是求出P 点的位置.三、课堂练习1.如图所示,将长方形ABCD 沿DE 折叠,使点C 恰好落在BA 边上,得到点C′,若∠C′EB=40°,求∠EDC′的度数.2.在Rt △ACB 中,∠ACB =90°,点D 在边AB 上,连接CD ,将△ADC 沿直线CD 翻折,点A 恰好落在BC 边上的点E 处,若AC =3,BE =1,则DE 的长是_____.【答案】157【分析】过点D 作DHAC ⊥于H ,DF BC ⊥于F ,由折叠的性质可得3AC CE ==,45ACD BCD ∠=∠=︒,由勾股定理可求5AB =,由面积法可求D F 的长,由勾股定理可求D E 的长.【详解】解:如图,过点D 作DHAC ⊥于H ,DF BC ⊥于F ,将ADC ∆沿直线CD 翻折,3AC CE ∴==,45ACD BCD ∠=∠=︒,4BC ∴=,D H AC ⊥ ,DF BC ⊥,45ACD BCD ∠=∠=︒,DF DH ∴=,45DCF FDC ∠=∠=︒,DF CF ∴=,22291625AB AC BC =+=+= ,5AB ∴=,111222ABC S AC BC AC DH BC DF ∆=⨯⨯=⨯⨯+⨯⨯ ,127DF ∴=,127DF ∴=,127DF CF ∴==,97EF =,157DE ∴===,故答案为:157.3.如图,矩形ABCD 中,AB=8,BC=4,把矩形ABCD 沿过点A 的直线AE 折叠,点D 落在矩形ABCD 内部的点D′处,则CD′的最小值是()A .4B .C .4-D .4+【答案】C 【解析】【分析】根据翻折的性质和当点D'在对角线AC 上时CD′最小解答即可.【详解】解:当点D'在对角线AC 上时CD′最小,∵矩形ABCD中,AB=4,BC=2,把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处,∴AD=AD'=BC=2,在Rt△ABC中,=4∴,故选:C.4.如图,在长方形ABCD的边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.已知AB=6cm,△ABF的面积是24cm2.(1)求BF的长;(2)求AD的长;(3)求点E与点C的距离.【答案】(1)8cm;(2)10cm;(3)83 cm【分析】(1)由在长方形ABCD中,AB=6cm,△ABF的面积是24cm2,即可求得BF的长;(2)由(1),易得AD=AF,DE=EF,即可求得AF的长,然后得出AD的长;(3)首先设EC=xcm,则EF=DE=(6﹣x)cm.由勾股定理得:CE2+CF2=EF2求出x 的值即可得出答案.【详解】(1)∵ABCD是长方形,∴△ABF是直角三角形,∵△ABF面积是24cm2,∴12AB•BF=24.∵AB=6cm,∴BF=8cm;(2)由题意知,△ADE和△AFE重合,则△ADE≌△AFE,则AD=AF,DE=EF.在Rt△ABF中,由勾股定理得10AF===(cm).则AD=10cm;(3)∵BC=AD=10cm,∴CF=BC﹣BF=2cm.设EC =xcm ,则EF =DE =(6﹣x )cm .由勾股定理得:CE 2+CF 2=EF 2,∴x 2+22=(6﹣x )2,解得:83x =,∴点E 与点C 间的距离是83cm.【点睛】此题考查长方形的性质、勾股定理、折叠的性质,(3)是此题的难点,根据(2)求出CF ,由折叠得到EF =DE ,设EC =xcm ,因此利用勾股定理列得关于x 的关系式解出x 的值,由此解答此题.5.在矩形纸片ABCD 中,3AB =,5AD =.如图所示,折叠纸片,使点A 落在BC 边上的'A 处,折痕为PQ ,当点'A 在BC 边上移动时,折痕的端点P ,Q 也随之移动,若限定点P 、Q 分别在线段AB 、A D 边上移动,则点'A 在BC 边上可移动的最大距离为()A .1B .2C .3D .4【答案】B 【分析】根据翻折变换,当点Q 与点D 重合时,点A′到达最左边,当点P 与点B 重合时,点A′到达最右边,所以点A′就在这两个点之间移动,分别求出这两个位置时A′B 的长度,然后两数相减就是最大距离.【详解】解:如图1,当点D 与点Q 重合时,根据翻折对称性可得A’D=AD=5,在Rt △A’CD 中,A’D 2=A’C 2+CD 2,即52=(5-A’B)2+32,解得A’B=1;如图2,当点P与点B重合时,根据翻折对称性可得A’B=AB=3,∵3-1=2,∴点A’在BC边上可移动的最大距离为2.故选B.6.矩形ABCD中,AB=4,BC=6,点E是AB的中点,点F是BC上任意一点,把△EBF沿直线EF翻折,点B落在点P处,则PC的最小值是_______________.【答案】2【详解】连接CE,当点P在CE上时,CP的值最小.CE===∴=-=.CP CE EP2故答案为:2.7.如图,在长方形纸片ABCD 中,3AB =,9AD =,折叠纸片ABCD ,使顶点C 落在边A D 的点G 处,折痕分别交边A D 、BC 于点E 、F .(1)求证:GEF △是等腰三角形(2)求GEF △面积的最大值.【答案】(1)见解析;(2)152【分析】(1)根据翻折的性质得到EFC EFG ∠=∠,根据//AD BC 得到EFC GEF ∠=∠,从而得到EFG GEF ∠=∠,问题得证;(2)根据GEF △高为AB=3,得到当点G 与点A 重合时,GEF △的面积最大.根据勾股定理求出AF=5,进而得到GE=5,即可求出GEF △的面积.【详解】(1)由翻折得:EFC EFG ∠=∠.∵//AD BC ,∴EFC GEF ∠=∠,∴EFG GEF ∠=∠,∴GE=GF ,∴GEF △是等腰三角形.(2)如图,∵GEF △高为AB=3,∴当GE 最大时GEF △的面积最大,∴当点G 与点A 重合时,GEF △的面积最大.在Rt ABF 中,222AF AB BF =+,∴()22239AF AF =+-,解得:5AF =,∴5GE AF ==,∴GEF △的面积最大值=1155322=⨯⨯=.四、举一反三1.如图,EF 是正方形两对边中点的连线段,将∠A 沿DK 折叠,使它的顶点A落在EF 上的G 点,求∠DKG 的度数.2.如图,在Rt ABC 中,90,A AB AC ∠=︒==,点,E F 分别是边,AB BC 上的动点,沿EF 所在直线折叠B Ð,使点B 的对应点B ′始终落在边AC 上,若FB C ' 为直角三角形,则BF 的长为__________.【解析】90,A AB AC ∠=︒==,∴∠C=45°,2BC ==,折叠后,要使FB C ' 为直角三角形,则有:FB C ' 也为等腰直角三角形,①当90B FC '∠=︒时,∴45C FB C '∠=∠=︒,此时点B '与点C 重合,∴E 、F 分别是AB 、BC 的中点,∴112BF BC ==,②当90FB C'∠=︒时,∴45C B FC '∠=∠=︒,∴BF FB B C ''==,在Rt B FC '△中,FC F '=,BC=BF+FC ,∴)12BC BF BF =+=+=,解得:2BF =-;故答案为2-或1.3.如图,Rt △ABC 中,AB =18,BC =12,∠B =90°,将△ABC 折叠,使点A 与BC 的中点D 重合,折痕为MN ,则线段BN 的长为()A .8B .6C .4D .104.如图,长方形纸片ABCD ,10AB =,8BC =,点P 在BC 边上,将CDP 沿DP 折叠,点C 落在E 处,PE ,D E 分别交AB 于点O ,F ,且OP OF =,则A F 长为______.【答案】103【分析】根据折叠的性质可得出DC=DE 、CP=EP ,由“AAS”可证△OEF ≌△OBP ,可得出OE=OB 、EF=BP ,设EF=x ,则BP=x 、DF=10-x 、BF=PC=8-x ,进而可得出AF=2+x ,在Rt △DAF 中,利用勾股定理可求出x 的值,即可得AF 的长.【详解】解:∵将△CDP 沿DP 折叠,点C 落在点E 处,∴DC=DE=10,CP=EP .在△OEF 和△OBP 中,90EOF BOP E B OF OP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△OEF ≌△OBP (AAS ),∴OE=OB ,EF=BP .设EF=x ,则BP=x ,DF=DE -EF=10-x ,又∵BF=OB+OF=OE+OP=PE=PC ,PC=BC-BP=8-x ,∴AF=AB -BF=2+x .在Rt △DAF 中,AF 2+AD 2=DF 2,∴(2+x )2+82=(10-x )2,∴43x =;∴410233AF =+=.故答案为:103.5.如图,在矩形ABCD 中,AB=3,AD=4,点E 是AD 边上一动点,将△ABE 沿BE 折叠,使点A 的对应点A′恰好落在矩形ABCD 的对角线上,则AE 的长为_______.答案:3924or 6.如图,已知等腰△ABC 中,AB =AC =5,BC =8,E 是BC 上的一个动点,将△ABE 沿着AE 折叠到△ADE 处,再将边AC 折叠到与AD 重合,折痕为AF ,当△DEF 是等腰三角形时,BE 的长是___________.【答案】52或258或74.【分析】分三种情况讨论:DE=DF ,DE=EF ,EF=DF .利用等腰三角形的性质和全等三角形解题.【详解】解:由折叠可知,BE=DE ,DF=CF ,AD=AB=AC=5,当DE=DF 时,如图1,此时DE=DF=BE=CF ,∵AB=AC ,∴∠B=∠C ,在△ABE 和△ACF 中,AB AC B C BE CF =⎧⎪=⎨⎪=⎩∠∠∴△ABE ≌△ACF ,∴AE=AF ,∴AD 垂直平分EF ,∴EH=FH ,142BH CH BC ===,∴3AH ===,∴532HD =-=,设BE DE x ==,则4EH x =-,则在直角△DHE 中,()22242x x -+=,解得52x =,当DE=EF 时,如图2,作AH ⊥BC 于H ,连接BD ,延长AE 交BD 于N ,可知BE=DE=EF ,∵AH ⊥BC ,AB=AC ,BC=8∴BH=CH=4,∴3AH ===,设EH m =,则4BE EF m ==-,∴()8242CF m m =--=,即2DF m=∵AB=AD ,∠BAN=∠DAN ,∴AN ⊥BD ,BN=DN ,∴12EN DF m ==,∴EN EH=在△AHE 和△BNE 中,90AHE BNE EH ENAEH BEN ==︒⎧⎪=⎨⎪=⎩∠∠∠∠∴△AHE ≌△BNE ,∴AE=BE ,设BE AE x ==,则4EH x =-,在直角△AEH 中,()22243x x -+=,解得258x =,当DF=EF 时,如图3,过A 作AH ⊥BC 于H ,延长AF 交DC 于M,同理258 EF CF==∴252578884 BE=--=故答案为:52或258或74.【点睛】本题考查了折叠问题,全等三角形的判定和性质,等腰三角形的性质,注意分类讨论是解题的关键.7.如图,等腰△ABC中,AB=AC=10,BC=12,AD平分B A C∠,且AD=8,P,Q分别是AB、AD上的动点,连接BP,PQ,则BP+PQ的最小值为___.【答案】9.6【分析】过C作CQ⊥AB于Q,交AD于P,得到CQ=BP+PQ的最小值,由勾股定理不求得AD=8,再利用等面积法即可求得其值.【详解】∵AB=AC,AD是角平分线,∴AD⊥BC,BD=CD,∴B点,C点关于AD对称,如图,过C作CQ⊥AB于Q,交AD于P,则CQ=BP+PQ的最小值,根据勾股定理得,AD=8,利用等面积法得:AB•CQ=BC•AD,∴CQ=12310BC ADAB⨯==9.6故答案为:9.6.8.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,联结CE.(1)求证:AD∥CE;(2)求CE的长.【答案】(1)见解析;(2)75【分析】(1)由折叠的性质可得DE=BD ,AE=AB ,可证EF=BF ,AD ⊥BE ,由等腰三角形的性质可求∠DBE =∠DEB ,∠DEC =∠DCE ,由三角形的内角和定理可求CE ⊥BE ,可得结论;(2)由三角形的面积公式可求BF 的长,由勾股定理可求CE 的长.【详解】证明:(1)∵∠BAC =90°,AB =3,AC =4,∴BC 5==,∵点D 是BC 的中点,∴AD =BD =DE =52,∵将△ABD 沿AD 翻折得到△AED ,∴DE =BD ,AE =AB ,∴AD 垂直平分BE ,∴EF =BF ,AD ⊥BE ,∵DE =DB =CD ,∴∠DBE =∠DEB ,∠DEC =∠DCE ,∵∠DBE +∠DEB +∠DEC +∠DCE =180°,∴∠DEB +∠DEC =90°,∴∠BEC =90°,∴CE ⊥BE ,∴AD ∥CE ;(2)∵S △ABC =12×AC ×AB =12×3×4=6,且CD =BD ,∴S △ADB =12S △ABC =3,∴12AD ×FB =3,∴FB =125,∴BE =245,∴CE 75==.【点睛】本题考查了翻折变换,直角三角形的性质,平行线的判定,三角形的面积公式,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.五、课后练习一、选择题1.如图,在△ABC 中,AB =10,AC =6,BC =8,将△ABC 折叠,使点C 落在AB 边上的点E 处,AD 是折痕,则△BDE 的周长为()A .6B .8C .12D .14【解析】在Rt △ABC 中,∵AC =6,BC =8,∠C =90°,∴AB ==10,由翻折的性质可知:AE =AC =6,CD =DE ,∴BE =4,∴△BDE 的周长=DE +BD +BE =CD +BD +E =BC +BE =8+4=12.故选:C .2.如图,将等腰直角三角形ABC (90ABC ∠=︒)沿EF 折叠,使点A 落在BC 边的中点1A 处,6BC =,那么线段AE 的长度为()A .5B .4C .4.25D .154【解析】由折叠的性质可得AE=A 1E ,∵△ABC 为等腰直角三角形,BC=6,∴AB=6,∵A 1为BC 的中点,∴A 1B=3,设AE=A 1E=x ,则BE=6-x ,在Rt △A 1BE 中,由勾股定理可得32+(6-x )2=x 2,解得x=154,故选:D .3.如图,矩形ABCD ,AB =3,BC =4,点E 是AD 上一点,连接BE ,将△ABE 沿BE 折叠,点A 恰好落在BD 上的点G 处,则AE 的长为()A .2B .52C .32D .3【解析】在Rt △ABD 中,AB=3,AD=BC=4,∴BD=5由折叠得,∠BGE=∠A=90°,BG=AB=3,EG=AE ,∴DG=BD-BG=2,DE=AD-AE=4-AE ,在Rt △DEG 中,EG 2+DG 2=DE 2,∴AE 2+4=(4-AE )2,∴AE=32.故选:C .4.如图,在四边形ABCD 中,∠A =∠B =90°,∠C =60°,BC =CD =8,将四边形ABCD 折叠,使点C 与点A 重合,折痕为EF ,则BE 的长为()A .1B .2CD .2【解析】作DG ⊥BC ,连接AE ,在Rt △CDG ,∠DCG=60°,得出CG=4,∴DG=4AB=,设BE=x ,则CE=8-x ,根据折叠得AE=CE=8-x ,在Rt △ABE 中,AE 2=AB 2+BE 2,即(8-x)2)2+x 2解得x=1,故选A.5.如图,有一块直角三角形纸片,两直角边6AC cm =,8BC cm =,现将直角边AC 沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm【解析】在RT△ABC中,∵AC=6,BC=8,∴AB=10,△ADE是由△ACD翻折,∴AC=AE=6,EB=AB−AE=10−6=4,设CD=DE=x,在RT△DEB中,∵DE2+EB2=DB2,∴x2+42=(8−x)2∴x=3,∴CD=3.故选:B.6.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC =9,则BF的长为()A.4B.C.4.5D.5【解析】∵点C′是AB边的中点,AB=6,∴BC′=3,由图形折叠特性知,C′F=CF=BC﹣BF=9﹣BF,在Rt△C′BF中,BF2+BC′2=C′F2,∴BF2+9=(9﹣BF)2,解得,BF=4,故选:A.二、填空题7.如图,在矩形ABCD 中,AB =5,BC =6,P 为AD 上一动点,把△ABP 沿BP 翻折,使点A 落在点F 处,连接CF ,若BF =CF ,则AP 的长为_____.【答案】53【分析】过点F 作EN ∥DC 交BC 于点N ,交AD 于点E ,设AP =x ,则PF =x ,得出(3﹣x )2+12=x 2,解方程即可得解.【详解】解:过点F 作EN ∥DC 交BC 于点N ,交AD 于点E ,∵四边形ABCD 是矩形,∴∠A =∠D =∠DCB =90°,∴FN ⊥BC ,FE ⊥AD ,∵BF =CF ,BC =6,∴CN =BN =3,由折叠的性质可知,AB =BF =5,AP =PF ,∴4FN ==,∴EF =EN ﹣FN =5﹣4=1,设AP =x ,则PF =x ,∵PE 2+EF 2=PF 2,∴(3﹣x )2+12=x 2,解得,53x =,故答案为:53.【点睛】本题主要考查了折叠变换的性质、等腰三角形的性质、矩形的性质、勾股定理的综合运用;熟练掌握折叠变换的性质、勾股定理是关键.8.如图,三角形纸片ABC 中,∠ACB =90 ,BC =6,AB =10.在AC 边上取一点E ,以BE 为折痕,使AB 的一部分与BC 重合,A 与BC 延长线上的点D 重合,则CE 的长为________.【答案】3【分析】根据折叠得,BD=AB=10,EA=ED,求出CD=4,在直角三角形CDE中,设未知数,利用勾股定理列方程求解即可.【详解】∵∠ACB=90 ,BC=6,AB=10∴8=由折叠得,BD=AB=10,EA=ED,设CE=x,则EA=ED=8−x,在Rt△DCE中,CD=10−6=4,由勾股定理得,x2+42=(8−x)2,解得,x=3故填:3.9.如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在射线BC上运动,AD=AB=1,则△ADE的周长最小值为______.【答案】1+【分析】作D点关于BC的对称点D’,连接AD’与BC的交点即为E点,此时△ADE的周长为AD+AE+DE=AD+AD’,故可求解.【详解】作D点关于BC的对称点D’,连接AD’与BC的交点即为E点,此时△ADE的周长最小,即△ADE的周长AD+AE+DE=AD+AD’,∵在四边形ABCD中,AD∥BC,AB⊥BC,AD=AB=1∴四边形ABFD为正方形,∴AD+AD’=1+1+1+.10.如图,矩形ABCD中,AB=1,BC=2,点E是BC边上一点,连接AE,把∠B沿AE 折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为___________.【答案】12-或1.【分析】当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=1,可计算出-1,设BE=x,则EB′=x,CE=2-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.【详解】解:当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如图1所示.连结AC,在Rt△ABC中,AB=1,BC=2,∴=∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△CEB′为直角三角形时,只能得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,∴EB=EB′,AB=AB′=1,∴CB′=1-,设BE=x,则EB′=x,CE=2-x,在Rt△CEB′中,∵EB′2+CB′2=CE2,∴x2+1-)2=(2-x)2,解得x=51 2-,∴BE=1 2;②当点B′落在AD边上时,如图2所示.此时ABEB′为正方形,∴BE=AB=1.故答案为:12-或1.11.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,AB=18,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则BP+EP的最小值是____.【答案】9【分析】根据翻折变换的性质可得点C、E关于AD对称,再根据轴对称确定最短路线问题,BC与AD的交点D即为使PB+PE的最小值的点P的位置,然后根据直角三角形两锐角互余求出∠BAC=60°,再求出∠CAD=30°,然后解直角三角形求解即可.【详解】∵将△ACD沿直线AD翻折,点C落在AB边上的点E处,∴点C、E关于AD对称,∴点D即为使PB+PE的最小值的点P的位置,PB+PE=BC,∵∠C=90°,∠BAC=30°,∴BC=12AB,∴BC=9.∴PB+PE的最小值为9.故答案为9.12.如图,在Rt△ABC中,∠C=90°,AC=6,∠A=60°,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_________.【答案】.【分析】延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小.运用勾股定理求解.【详解】解:如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小.∵AC=6,CF=2,∴AF=AC-CF=4,∵∠A=60°,∠AMF=90°,∴∠AFM=30°,∴AM=12AF=2,∴,∵FP=FC=2,∴-2,∴点P到边AB距离的最小值是-2.故答案为:.【点睛】本题考查了翻折变换,涉及到的知识点有直角三角形两锐角互余、勾股定理等,解题的关键是确定出点P 的位置.12.如图,折叠矩形纸片ABCD ,使B 点落在A D 上一点E 处,折痕FG 的两端点分别在AB BC 、上(含端点),且6,10AB BC ==.则AE 的最大值是_____,最小值是_______.【答案】6;2.【分析】点G 在AB 边上,点F 在BC 边上.分别利用当点F 与点C 重合时,以及当点G 与点A 重合时,求出AE 的极值进而得出答案:【详解】解:如图,设AE 的长度为,x 当点F 与点C 重合时,根据翻折对称性可得10,EC BC ==在Rt CDE ∆中,222,CE CD ED =+即()22210106AE =-+,解得2,AE =即2,x =如图,当点G 与点A 重合时,根据翻折对称性可得6,AE AB ==即6x =;所以AE 的最大值是6,最小值为2.故答案是:6,2.三、解答题13.如图,在矩形ABCD 中,AB=8,BC=10,E 为CD 边上一点,将△ADE 沿AE 折叠,使点D 落在BC 边上的点F 处.(1)求BF 的长;(2)求CE的长.【答案】(1)BF长为6;(2)CE长为3,详细过程见解析.【分析】(1)由矩形的性质及翻折可知,∠B=90°,AF=AD=10,且AB=8,在Rt△ABF中,可由勾股定理求出BF的长;(2)设CE=x,根据翻折可知,EF=DE=8-x,由(1)可知BF=6,则CF=4,在Rt△CEF中,可由勾股定理求出CE的长.【详解】解:(1)∵四边形ABCD为矩形,∴∠B=90°,且AD=BC=10,又∵ AFE是由 ADE沿AE翻折得到的,∴AF=AD=10,又∵AB=8,在Rt△ABF中,由勾股定理得:,故BF的长为6.(2)设CE=x,∵四边形ABCD为矩形,∴CD=AB=8,∠C=90°,DE=CD-CE=8-x,又∵△AFE是由△ADE沿AE翻折得到的,∴FE=DE=8-x,由(1)知:BF=6,故CF=BC-BF=10-6=4,CF+CE=EF,在Rt△CEF中,由勾股定理得:2224+x=(8-x),解得:x=3,∴222故CE的长为3.14.如图,在△ABC中,∠C=90°,把△ABC沿直线DE折叠,使△ADE与△BDE重合.(1)若∠A=35°,则∠CBD的度数为________;(2)若AC=8,BC=6,求AD的长;(3)当AB=m(m>0),△ABC的面积为m+1时,求△BCD的周长.(用含m的代数式表示)【答案】(1)∠CBD=20°;(2)AD=164;(3)△BCD 的周长为m+2【分析】(1)根据折叠可得∠1=∠A=35°,根据三角形内角和定理可以计算出∠ABC=55°,进而得到∠CBD=20°;(2)根据折叠可得AD=DB ,设CD=x ,则AD=BD=8-x ,再在Rt △CDB 中利用勾股定理可得x 2+62=(8-x )2,再解方程可得x 的值,进而得到AD 的长;(3)根据三角形ACB 的面积可得112AC CB m =+ ,进而得到AC•BC=2m+2,再在Rt △CAB 中,CA 2+CB 2=BA 2,再把左边配成完全平方可得CA+CB 的长,进而得到△BCD 的周长.【详解】(1)∵把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合,∴∠1=∠A=35°,∵∠C=90°,∴∠ABC=180°-90°-35°=55°,∴∠2=55°-35°=20°,即∠CBD=20°;(2)∵把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合,∴AD=DB ,设CD=x ,则AD=BD=8-x ,在Rt △CDB 中,CD 2+CB 2=BD 2,x 2+62=(8-x )2,解得:x=74,AD=8-74=164;(3)∵△ABC的面积为m+1,∴12AC•BC=m+1,∴AC•BC=2m+2,∵在Rt△CAB中,CA2+CB2=BA2,∴CA2+CB2+2AC•BC=BA2+2AC•BC,∴(CA+BC)2=m2+4m+4=(m+2)2,∴CA+CB=m+2,∵AD=DB,∴CD+DB+BC=m+2.即△BCD的周长为m+2.15.如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处(1)求CE的长;(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.【答案】(1)3;(2.【分析】(1)先判断出AF=AD=8,进而利用勾股定理求出BF=6,最后在Rt△ECF,利用勾股定理,即可得出结论;(2)先作出点E关于BC的对称点E,进而求出DE',再利用勾股定理即可得出结论.【详解】解:(1)长方形ABCD中,AB=8,BC=10,∴∠B=∠BCD=90°,CD=AB=8,AD=BC=10,由折叠知,EF=DE,AF=AD=8,在Rt△ABF中,根据勾股定理得,BF6,∴CF=BC﹣BF=4,设CE=x,则EF=DE=CD﹣CE=8﹣x,在Rt△ECF中,根据勾股定理得,CF2+CE2=EF2,∴16+x2=(8﹣x)2,∴x=3,∴CE=3;(2)如图,延长EC 至E '使CE '=CE =3,连接AE '交BC 于P ,此时,PA +PE 最小,最小值为AE ',∵CD =8,∴DE '=CD +CE '=8+3=11,在Rt △ADE '中,根据勾股定理得,AE '.16.如图,在矩形ABCD 中,2,AB AD m ==,动点P 从点D 出发,沿射线DA 以每秒1个单位的速度向点A 方向运动,连接CP ,把PDC △沿PC 翻折,得到PEC V .设点P 的运动时间为()t s .(1)若3m =,当P E B 、、三点在同一直线上时,求t 的值;(2)若点E 到直线BC 的距离等于1,求t 的值;(3)若AE 的最小值为1,直接写出m 的值.【答案】(1)t=3(2)t=;(3)m=【分析】(1)如图1中,设PD=t .则PA=3-t .首先证明BP=BC=6,在Rt △ABP 中利用勾股定理即可解决问题;(2)通过添加辅助线,构造直角三角形再解决问题;(3)当点A,点E ,点C 在同一条直线上时,AE 最短,利用勾股定理求值即可.【详解】解:(1)如图1中,设PD=t .则PA=3-t∵P 、B 、E 共线,∴∠BPC=∠DPC ,∵AD ∥BC ,∴∠DPC=∠PCB ,∴∠BPC=∠PCB ,∴BP=BC=3,在Rt △ABP 中,∵AB 2+AP 2=BP 2,∴22+(3-t )2=32,∴t=3(舍去)或∴当t=3P E B 、、三点在同一直线上.(2)过点E 作MN ⊥BC ,交AD 于点M∵四边形ABCD 是矩形,MN ⊥BC∴MN ⊥AD∵点E 到直线BC 的距离等于1∴EN=1∵MN=AB=2,EC=CD=2,∴EN=MN-EN=2-1=1∴在Rt △ENC 中,∴MD=∵由题意得:-t,ME=MN-EN=2-1=1,EP=PD=t∴在Rt △MPE 中,222=ME MP PE +即:)2221=t +,解得:(3)如图,当点A,点E ,点C 在同一条直线上时,AE 最短.由题意得:AE=1,EC=CD=AB=2∴在Rt△ABC中,BC=∴.【点睛】本题考查四边形综合题、矩形的性质、勾股定理,学会构造图形思考问题是解答此题的关键,属于中考压轴题.。
八上数学勾股定理知识点

勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方。
勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2.勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:①有一个角为90°的三角形是直角三角形。
②有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:①确定最大边(不妨设为c);②若c2=a2+b2,则△ABC是以∠C为直角的三角形;若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)4.注意:①直角三角形斜边上的中线等于斜边的一半②在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
③在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:①已知直角三角形的两边求第三边;②已知直角三角形的一边,求另两边的关系;③用于证明线段平方关系的问题; ④利用勾股定理,作出长为n 的线段。
二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
(也称为二次方根),也就是说如果x 2=a ,那么x 就叫做a 的平方根。
2、平方根的性质:①一个正数有两个平方根,它们互为相反数;一个正数a 的正的平方根,记作“a ”,又叫做算术平方根,它负的平方根,记作“—a ”,这两个平方根合起来记作“±a ”。
勾股定理16种证明方法

【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即a²+b²+4x1/2ab=c²+4x1/2ab,整理得a²+b²=c²。
1. 2【证法2】(邹元治证明)以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角1ab2形的面积等于. 把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上. ∵RtΔHAE ≌RtΔEBF, ∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90o, ∴∠AEH + ∠BEF = 90o. ∴∠HEF = 180o―90o= 90o.∴四边形EFGH是一个边长为c的正方形. 它的面积等于c2. ∵ RtΔGDH ≌ RtΔHAE,∴∠HGD = ∠EHA. ∵∠HGD + ∠GHD = 90o,∴∠EHA + ∠GHD = 90o.又∵∠GHE = 90o,∴∠DHA = 90o+ 90o= 180o.∴ ABCD是一个边长为a + b的正方形,它的面积等于(a+b)².∴(a+b)²=4x1/2ab+c²∴ a²+b²=c²。
2. 3【证法3】(赵爽证明)以a、b 为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角 1ab2三角形的面积等于. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴∠HDA = ∠EAB.∵∠HAD + ∠HAD = 90o,∴∠EAB + ∠HAD = 90o, 2∴ ABCD是一个边长为c的正方形,它的面积等于c.∵ EF = FG =GH =HE = b―a ,∠HEF = 90o.∴ EFGH是一个边长为b―a的正方形,它的面积等于(b-a)².∴(b-a)²=4x1/2ab+c²∴ a²+b²=c²。
勾股定理的十六种证明方法

勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF ,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE , ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE ,∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠D EC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD , ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD , ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+abS c 2122⨯+=, ∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P .过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L .∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a , ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a . 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积 = 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+.【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中, ∵ ∠ADC = ∠ACB = 90º, ∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB ,即 AB AD AC •=2. 同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC •=2.∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠P AC = 90º, ∴ ∠DAH = ∠BAC . 又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ,AH = AC = b .由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA ,Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . T F ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为 543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º,BT = BE = b ,∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ,∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE= ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a , ∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ,即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC •=2=()()BD AB BE AB -+ =()()a c a c -+= 22a c -,即222a c b -=, ∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•, ∵ AB = DC = c ,AD = BC = a ,AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ ab S ABC 21=∆,∴ ABC S ab ∆=42,又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+. 【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中, ∵ ∠A = ∠A , ∴ 若 AD :AC ≠AC :AB ,则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B ,∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC ,则 AD = c .∵ EM = EH + HM = b + a , ED = a ,∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b ,∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º, ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º,∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中, ∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,D D76451S S S S S +===, ∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【学习目标】 1. 通过数格子或割、补等方法探索勾股定理,能正确说出勾股定理。
2. 能运用勾股定理进行简单的计算,解决求直角三角形三边之间的
数量关系的问题。
【学习重点】勾股定理的探索。
【学习难点】运用勾股定理,进行简单的计算。
【自学指导】自学课本2-3页,完成做一做。
完成下列问题:
1. 请你任意画一个直角三角形,分别测量它的三条边,看看三边长的平方之间有怎样的关系?与小组同学交流。
图中每个小方格代表一个单位面积
(1)观察图1,
正方形A中含有个小方格,
即它的面积是个单位面积。
正方形B的面积是个单位面积。
正方形C的面积是个单位面积。
(2)在图2中,正方形A、B、C中各含
几个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形
A、B、C的面积之间有什么关系吗?
(4)图3,正方形A的面积是个
单位面积,正方形B的面积是个
单位面积,正方形C的面积是个
单位面积。
问题:如何求正方形C的面积?有哪
些方法?正方形 A、B、C的面积之间
有什么关系吗?
3. 勾股定理:
如果用a,b和c分别表示直角三角形的两直角边和斜边,那么
【自学检测】
1. 求下列图中字母所代表的正方形的面积。
2.
4,5,则第三边长的平方为 3. 求下列图中表示边的未知数x 、
【达标检测】
1. 求出下列直角三角形中未知边的长度。
2. 求斜边长为17cm 、一条直角边长为15cm 的直角三角形的面积。
3. 如图,求等腰三角形ABC 的面积。
4. 判断正误并说明理由:
若直角三角形的两条边长为6cm 、8cm ,则第三边长一定为10cm.
5. 直角三角形的两边长为4,5,则第三边长的平方为
【课时小结】 通过本节课学习,你学会了哪些知识?你心中还存在什么疑惑? 【作业】 课本P5习题1.1 【反思】
5
3
z
6
8 5
y
A
B。
