2019年北师大版七年级下册数学《第四章三角形》单元测试题(含答案)
北师大七级下第四章三角形单元测试题(一)含答案

北师大版七年级下册三角形单元测试题(一)一、选择题1.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为( )A.10B.12C.14D.162.满足下列条件的△ABC中,不是直角三角形的是()A、∠B+∠A=∠CB、∠A:∠B:∠C=2:3:5C、∠A=2∠B=3∠CD、一个外角等于和它相邻的一个内角3.一个三角形的三个内角中,锐角的个数最少为 ( )A.0B.1C.2 D.34.三角形的一个外角是锐角,则此三角形的形状是()A、锐角三角形B、钝角三角形C、直角三角形D、无法确定5.能将一个三角形分成面积相等的两个三角形的一条线段是 ( )A.中线B.角平分线C.高线D.三角形的角平分线6.如图5—12,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是 ( )A.∠1B.∠2C.∠B D.∠1、∠2和∠B7.下列命题中的真命题是()A、锐角大于它的余角B、锐角大于它的补角C、钝角大于它的补角D、锐角与钝角之和等于平角8.已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么( )A.M>0 B. M=0C.M<0 D.不能确定9.锐角三角形中,最大角α的取值范围是()A、00<α<900ºB、600<α<900ºC、600<α<1800D、600º≤α<900º10.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )A.5个B.4个C.3个D.2个二、填空题1.直角三角形中两个锐角的差为20º,则两个锐角的度数分别为.2.在△ABC 中,AB =6,AC =10,那么BC 边的取值范围是________,周长的取值范围是___________.3.把下列命题“对顶角相等”改写成:如果 ,那么 .4.一个等腰三角形两边的长分别是15cm 和7cm 则它的周长是__________. 5.在△ABC 中,三边长分别为正整数a 、b 、c ,且c≥b≥a>0,如果b =4,则这样的三角形共有_________个.6.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________. 7.如下图左,DH ∥GE ∥BC ,AC ∥EF ,那么与∠HDC 相等的角有 .8.如图5—13,在△ABC 中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D 、C 、F 、E ,则_______是△ABC 中BC 边上的高,_________是△ABC 中AB 边上的高,_________是△ABC 中AC 边上的高,CF 是△ABC 的高,也是△_______、△_______、△_______、△_________的高.9.如图5—14,△ABC 的两个外角的平分线相交于点D ,如果∠A=50°,那么∠D=_____.10.如图5—15,△ABC 中,∠A=60°,∠ABC、∠ACB 的平分线BD 、CD 交于点D ,则∠BDC=_____.MHGFED CBA11.如图5—16,该五角星中,∠A+∠B+∠C+∠D+∠E=________度.12.等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是________.三、解答题1.如图5—17,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形?说明理由.2.如图5—18,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.3.一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?4.如图:(1) 画△ABC 的外角∠BCD ,再画∠BCD 的平分线CE. (2) 若∠A=∠B ,请完成下面的证明:已知:△ABC 中,∠A=∠B ,CE 是外角∠BCD 的平分线 求证:CE ∥AB5.如图5—21,△ABC 中,∠B=34°,∠ACB=104°,AD 是BC 边上的高,AE 是∠BAC 的平分线,求∠DAE 的度数.6.如图5—22,在△ABC 中,∠ACB=90°,CD 是AB 边上的高,AB =13cm ,BC =12cm ,AC =5cm ,求:(1)△ABC 的面积;(2)CD 的长.7.看图填空:(1) 如下图左,∠A +∠D =180º(已知)∴∥( )CBA∴∠1= ( ) ∵∠1=65º(已知)∴∠C =65º( )(2) 如上图右,已知,∠ADC =∠ABC ,BE 、DF 分别平分∠ABC 、∠ADC ,且∠1=∠2,求证:∠A=∠C.证明:∵BE 、DF 分别平分∠ABC 、∠ADC (已知)∴ ∠1=21∠ABC ,∠3=21∠ADC ( ) ∵∠ABC =∠ADC (已知) ∴21∠ABC =21∠ADC ( ) ∴∠1=∠3( ) ∵∠1=∠2(已知)∴∠2=∠3( )∴( )∥( )( ) ∴∠A +∠=180º ,∠C +∠=180º( ) ∴∠A =∠C ( )8.已知:如图5—24,P 是△ABC 内任一点,求证:AB +AC >BP +PC .1DCB A答案:一、1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C二、1.3; 2.; 3.锐角(等腰锐角); 4.;5.10; 6.和; 7.; 8.;9.; 10.; 11.; 12.. 三、1.可以确定6个三角形.理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,所以图中可以确定6个三角形.2.错误.因为AD 虽然是线段,但不符合三角形角平分线定义,这里射线AD 是的平分线.3.假设此零件合格,连接BD ,则;可知.这与上面的结果不一致,从而知这个零件不合格.4.∵ AD 是BC 边上的中线, ∴ D 为BC 的中点,. ∵的周长-的周长=5cm . ∴. 又∵, ∴.5.由三角形内角和定理,得32周长20,164<<<<BC cm 37︒65︒25︒100GAC FAC FGC BFC BE CF AD ∆∆∆∆,,,,,,︒65︒120︒180126<<x BAC ∠︒=︒-︒=∠+∠37143180CBD CDB ()︒=︒+︒-︒=∠+∠40203090CBD CDB BD CD =ADC ∆ABD ∆cm AB AC 5=-cm AB AC 11=+cm AC 8=. ∴. 又∵ AE 平分∠BAC . ∴. ∴. 又∵,∴.6.(1)∵在△ABC 中,,,,(2)∵ CD 是AB 边上的高, ∴. 即. ∴. 7.如图,延长BP 交AC 于D , ∵, ∴. 8.∵, ∴, ∴. 又∵,∴. ∴,∵, ∴.︒=∠+∠+∠180BAC ACB B ︒=︒-︒-︒=∠4210434180BAC ︒=︒⨯=∠=∠21422121BAC BAE ︒=︒+︒=∠+∠=∠552134BAE B AED ︒=∠+∠90DAE AED ︒=︒-︒=∠-︒=∠35559090AED DAE ︒=∠90ACB cm AC 5=cm BC 12=().3012521212cm BC AC S ABC =⨯⨯=⋅=∴∆CD AB S ABC ⋅=∆21CD ⨯⨯=132130()cm CD 1360=A PDC PDC BPC ∠>∠∠>∠,A BPC ∠>∠A C ∠=∠74C A ∠=∠74C B C ∠<∠<∠74︒=∠+∠+∠180C B A ︒=∠+∠+∠18074C B C C B ∠-︒=∠711180C C C ∠<∠-︒<∠71118074︒<∠<︒8470C又∵为整数, ∴∠C 的度数为7的倍数. ∴,∴. 9.如图,延长BP 交AC 于点D .在△BAD 中,, 即:. 在△PDC 中,. ①+②得, 即.C A ∠=∠74︒=∠77C ︒=∠=∠4474C A BD AD AB >+PD BP AD AB +>+PC DC PD >+PC PD BP DC PD AD AB ++>+++PC BP AC AB +>+。
北师大版七年级数学下册第4单元《三角形》单元测试题(含答案)

北师大版七年级数学下册第4单元《三角形》单元测试题(含答案)1.下列各组长度的三条线段能组成三角形的是()A.1,2,3B.1,1,2C.1,2,2D.1,5,72.在△ABC中作AB边上的高,下图中不正确的是()A.B.C.D.3.若AD是△ABC的中线,则下列结论正确的是()A.AD⊥BC B.BD=CD C.∠BAD=∠CAD D.AD=BC 4.下列说法正确的是()A.一个钝角三角形一定不是等腰三角形,也不是等边三角形B.一个等腰三角形一定是锐角三角形,或直角三角形C.一个直角三角形一定不是等腰三角形,也不是等边三角形D.一个等边三角形一定不是钝角三角形,也不是直角三角形5.如图,用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的判别方法是()A.SAS B.ASA C.AAS D.SSS6.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是()A.SAS B.ASA C.AAS D.SSS7.如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,DH⊥BC于H,交BE于G,有下列结论:①BH=DH;②BD=CD;③AD+CF=BD;④CE=BF.其中正确的是()A.①②B.①③C.①②③D.①②③④8.如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=2cm2,则S△ABC为()A.4 cm2B.6 cm2C.8 cm2D.10 cm29.如图所示,BE=3EC,D是线段AC的中点,BD和AE交于点F,已知△ABC的面积是7,求四边形DCEF的面积()A.1B.C.D.210.如图将一副三角板拼成如图所示的图形(∠D=30°,∠ABC=90°,∠DCE=90°,∠A=45°),BC交DE于点F,则∠DFC的度数是()A.75°B.105°C.135°D.125°11.下列说法中正确的是()A.两个面积相等的图形,一定是全等图形B.两个等边三角形是全等图形C.两个全等图形的面积一定相等D.若两个图形周长相等,则它们一定是全等图形12.如图,已知:在△AFD和△CEB,点A、E、F、C在同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④DF∥BE,选出三个条件可以证明△AFD ≌△CEB的有()组.A.4B.3C.2D.113.如图,△ABC的两条中线AD、CE交于点G,联结BG并延长,交边AC于点F,那么下列结论不正确的是()A.AF=FC B.GF=BG C.AG=2GD D.EG=CE 14.如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=30°,则∠2的度数为()A.140°B.130°C.120°D.110°15.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,添加下列条件,不能判定△EAB≌△BCD的是()A.EB=BD B.∠E+∠D=90°C.AC=AE+CD D.∠EBD=60°16.在下列各组条件中,不能说明△ABC≌△DEF的是()A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠DC.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF17.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=8,则四边形ABCD的面积为()A.32B.24C.40D.3618.如图,△ABC的中线BD、CE相交于点O,OF⊥BC,垂足为F,且AB=6,BC=5,AC=3,OF=2,则四边形ADOE的面积是()A.9B.6C.5D.319.要想使一个六边形活动支架ABCDEF稳固且不变形,至少需要增加根木条才能固定.20.(1)线段AD是△ABC的角平分线,那么∠BAD=∠=∠.(2)线段AE是△ABC的中线,那么BE==BC.21.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE ⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是.22.如图,BE平分∠ABC,CE平分∠ACD,∠A=60°,则∠E=.23.如图,已知∠1=∠2、AD=AB,若再增加一个条件不一定能使结论△ADE≌△ABC成立,则这个条件是.24.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.这种做法是利用了全等三角形对应角相等,图中判断三角形全等的依据是.25.如图,要测量河两岸相对两点A、B间的距离,先在过点B的AB的垂线上取两点C、D,使CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC 的理由是.26.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:(1)Rt△ABF≌Rt△DCE;(2)OE=OF.27.如图,点B、F、C、E在同一条直线上,∠B=∠E,∠A=∠D,BF=CE.求证:△ABC≌△DEF.28.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:(1)△AEH≌△BEC.(2)AH=2BD.29.如图,△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,∠A=60°,∠BDC =100°.求∠BDE的度数.30.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB ∥DE,∠A=∠D,测得AB=DE.(1)求证:△ABC≌△DEF;(2)若BE=10m,BF=3m,求FC的长度.31.如图所示,已知△ABC中,∠B=∠C,AB=4厘米,BC=3厘米,点D为AB的中点.如果点P在线段BC上以每秒1厘米的速度由点B向点C运动,同时,点Q在线段CA上以每秒a厘米的速度由点C向点A运动,设运动时间为t(秒)(0≤t≤3).(1)用含t的式子表示PC的长度是;(2)若点P,Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(3)若点P,Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?参考答案1.解:A.1+2=3,不能构成三角形,不合题意;B.1+1=2,不能构成三角形,不合题意;C..1+2>2,能构成三角形,符合题意;D.1+5<7,不能构成三角形,不合题意.故选:C.2.解:由题可得,过点C作AB的垂线段,垂足为H,则CH是BC边上的高,∴A、B、D选项正确,C选项错误.故选:C.3.解:∵AD是△ABC的中线,∴BD=DC,故选:B.4.解:A、一个钝角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;B、一个等腰三角形不一定是锐角三角形,或直角三角形,故本选项错误;C、一个直角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;D、一个等边三角形一定不是钝角三角形,也不是直角三角形,故本选项正确;故选:D.5.解:由画法得OC=OD,PC=PD,而OP=OP,所以△OCP≌△ODP(SSS),所以∠COP=∠DOP,即OP平分∠AOB.故选:D.6.解:如图,∠A、AB、∠B都可以测量,即他的依据是ASA.故选:B.7.解:∵DH⊥BC,∠ABC=45°,∴△BDH为等腰直角三角形,∴BH=DH,故①正确,∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.故②正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC(ASA).∴BF=AC;DF=AD.∵CD=CF+DF,∴AD+CF=BD;故③正确;在Rt△BEA和Rt△BEC中∵BE平分∠ABC,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt△BEA≌Rt△BEC(ASA).∴CE=AE=AC.又由(1)可知:BF=AC,∴CE=AC=BF;故④正确;故选:D.8.解:∵点E是AD的中点,∴S△ABE=S△ABD,S△ACE=S△ADC,∴S△ABE+S△ACE=S△ABC,∴S△BCE=S△ABC,∵点F是CE的中点,∴S△BEF=S△BCE.∴S△ABC=8cm2故选:C.9.解:∵AD=DC,BE=3EC,∴可以假设S△ADF=S△DFC=x,S△EFC=y,则S△EFB=3y,则有,解得,∴四边形DCEF的面积=x+y=,故选:B.10.解:由题意得,∠ACB=45°,∠DEC=60°,∵∠DFC是△CFE的一个外角,∴∠DFC=∠ACB+∠DEC=105°,故选:B.11.解:全等的两个图形的面积、周长均相等,但是周长、面积相等的两个图形不一定全等.故选:C.12.解:∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,∵DF∥BE,∴∠DF A=∠BEC,∴若①②③为条件,不能证明△AFD≌△CEB,若①②④为条件,能证明△AFD≌△CEB(AAS),若①③④为条件,不能证明△AFD≌△CEB,若②③④为条件,能证明△AFD≌△CEB(AAS),故选:C.13.解:如图连接DE.∵△ABC的两条中线AD、CE交于点G,∴点G是△ABC的重心,∴DF也是△ABC的中线,∴AF=FC,故A不符合题意,∵BE=AE,BD=CD,∴DE∥AC,DE=AC,∴===,∴AG=2DG,EG=CE,故C,D不符合题意,故选:B.14.解:如图:∵m∥n,∠1=30°,∴∠3=∠1=30°.∵∠ACB=90°,∴∠4=∠ACB﹣∠3=90°﹣30°=60°,∴∠2=180°﹣∠4=180°﹣60°=120°.故选:C.15.解:∵∠A=∠C=90°,AB=CD,∴当添加EB=BD时,则可根据“HL”判定△EAB≌△BCD;当添加AE=BC,即AC=AE+CD,则可根据“SAS”判定△EAB≌△BCD;当添加∠ABE=∠D时,此时∠D+∠E=90°,∠EBD=90°,则可根据“SAS”判定△EAB≌△BCD,故选:D.16.解:A、AB=DE,∠B=∠E,∠C=∠F,可以利用AAS定理证明△ABC≌△DEF,故此选项不合题意;B、AC=DF,BC=EF,∠A=∠D不能证明△ABC≌△DEF,故此选项符合题意;C、AB=DE,∠A=∠D,∠B=∠E,可以利用ASA定理证明△ABC≌△DEF,故此选项不合题意;D、AB=DE,BC=EF,AC=DF可以利用SSS定理证明△ABC≌△DEF,故此选项不合题意;故选:B.17.解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N;∵∠BAD=∠BCD=90°∴四边形AMCN为矩形,∠MAN=90°,∵∠BAD=90°,∴∠BAM=∠DAN,在△ABM与△ADN中,,∴△ABM≌△ADN(AAS),∴AM=AN;∴△ABM与△ADN的面积相等;∴四边形ABCD的面积=正方形AMCN的面积;设AM=a,由勾股定理得:AC2=AM2+MC2,而AC=8;∴2a2=64,a2=32,故选:A.18.解:∵BD、CE均是△ABC的中线,∴S△BCD=S△ACE=S△ABC,∴S四边形ADOE+S△COD=S△BOC+S△COD,∴S四边形ADOE=S△BOC=5×2÷2=5.故选:C.19.解:如图,,要想使一个六边形活动支架ABCDEF稳固且不变形,至少需要增加3根木条才能固定.故答案为:3.20.解:(1)线段AD是△ABC的角平分线,那么∠BAD=∠CAD=∠BAC.故答案为:CAD,BAC;(2)线段AE是△ABC的中线,那么BE=CE=BC.故答案为:CE,.21.解:∵AD平分∠CAB,∠CAD=20°,∴∠CAB=2∠CAD=40°,∵∠ACB=90°,∴∠B=90°﹣40°=50°,∵DE⊥AB,∴∠DEB=90°,∴∠EDB=90°﹣50°=40°,故答案为:40°.22.解:∵∠ACD=∠A+∠ABC,∴∠ECD=(∠A+∠ABC).又∵∠ECD=∠E+∠EBC,∴∠E+∠EBC=(∠A+∠ABC).∵BE平分∠ABC,∴∠EBC=∠ABC,∴∠ABC+∠E=(∠A+∠ABC),∴∠E=∠A,∵∠A=60°,∴∠E=30°.故答案为30°.23.解:增加的条件为DE=BC,理由:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,∴∠DAE=∠BAC,∵AD=AB,DE=BC,∴△ADE≌△ABC不一定成立,故答案为:DE=BC.24.解:由图可知,CM=CN,又OM=ON,∵在△MCO和△NCO中,∴△COM≌△CON(SSS),∴∠AOC=∠BOC,即OC是∠AOB的平分线.故答案为:SSS.25.解:∵AB⊥BD,ED⊥BD,∴∠ABD=∠EDC=90°,在△EDC和△ABC中,,∴△EDC≌△ABC(ASA).故答案为:ASA.26.证明:(1)∵BE=CF,∴BE+EF=CF+EF,即BF=CE,∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形,在Rt△ABF和Rt△DCE中,,∴Rt△ABF≌Rt△DCE(HL);(2)∵Rt△ABF≌Rt△DCE(已证),∴∠AFB=∠DEC,∴OE=OF.27.证明:∵BF=EC∴BF+CF=EC+CF,∴BC=EF,∵∠B=∠E,∠A=∠D,∴180°﹣∠B﹣∠A=180°﹣∠E﹣∠D,即∠ACB=∠DFE,在△ABC和△DEF中,,∴△ABC≌△DEF(ASA).28.解:(1)∵AD⊥BC,∴∠DAC+∠C=90°,∵BE⊥AC,∴∠EBC+∠C=90°,∴∠DAC=∠EBC,在△AEH与△BEC中,,∴△AEH≌△BEC(ASA);(2)∵△AEH≌△BEC,∴AH=BC,∵AB=AC,AD⊥BC,∴BC=2BD,∴AH=2BD.29.解:如图,∵∠BDC=∠A+∠ABD,∴∠ABD=∠BDC﹣∠A=100°﹣60°=40°∵BD平分∠ABC,∴∠DBC=∠ABD=40°,又∵DE∥BC,∴∠BDE=∠DBC=40°.30.(1)证明:∵AB∥DE,∴∠ABC=∠DEF,在△ABC与△DEF中,∴△ABC≌△DEF;(2)∵△ABC≌△DEF,∴BC=EF,∴BF+FC=EC+FC,∴BF=EC,∵BE=10m,BF=3m,∴FC=10﹣3﹣3=4m.31.解:(1)PC=3﹣t.(2)△CPQ≌△BDP,理由如下:∵P、Q的运动速度相等,∴1秒后,CQ=BP=1,CP=BC﹣BP=3﹣1=2,∵D为AB的中点,∴BD=,∴CP=BD,在△CPQ和△BDP中,,∴△CPQ≌△BDP(SAS).(3)解:由(1)知,PC=3﹣t,BP=t,CQ=at,BD=2,∵∠C=∠B∵△BPD与△CQP全等,①当△CPQ≌△BDP时,BP=CQ,t=at,∵t≠0,∴a=1与P、Q的运动速度不相等矛盾,故舍去.②当△CPQ≌△BPD时,BP=CP,CQ=BD,∴t=3﹣t,at=2,t=a=.即点P、Q的运动速度不相等时,点Q的运动速度a为时,能够使△BPD与△CQP 全等。
北师大版数学七年级下册第4章《三角形》单元测试试题 附答案解析
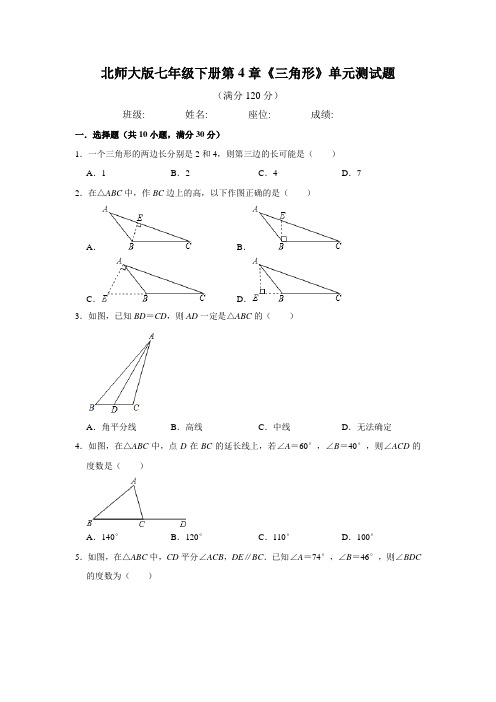
北师大版七年级下册第4章《三角形》单元测试题(满分120分)班级:________姓名:________座位:________成绩:________一.选择题(共10小题,满分30分)1.一个三角形的两边长分别是2和4,则第三边的长可能是()A.1B.2C.4D.72.在△ABC中,作BC边上的高,以下作图正确的是()A.B.C.D.3.如图,已知BD=CD,则AD一定是△ABC的()A.角平分线B.高线C.中线D.无法确定4.如图,在△ABC中,点D在BC的延长线上,若∠A=60°,∠B=40°,则∠ACD的度数是()A.140°B.120°C.110°D.100°5.如图,在△ABC中,CD平分∠ACB,DE∥BC.已知∠A=74°,∠B=46°,则∠BDC 的度数为()A.104°B.106°C.134°D.136°6.如图,AB=AC,若要使△ABE≌△ACD.则添加的一个条件不能是()A.∠B=∠C B.∠ADC=∠AEB C.BD=CE D.BE=CD7.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的()A.SSS B.ASA C.AAS D.SAS8.小明学习了全等三角形后总结了以下结论:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;③面积相等的两个三角形是全等图形;④全等三角形的周长相等.其中正确的结论个数是()A.1B.2C.3D.49.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD =42°,则∠BFD=()A.45°B.54°C.56°D.66°10.如图,△ABC的三边长均为整数,且周长为22,AM是边BC上的中线,△ABM的周长比△ACM的周长大2,则BC长的可能值有()个.A.4B.5C.6D.7二.填空题(共6小题,满分24分)11.下列4个图形中,属于全等的2个图形是.(填序号)12.如图,某人将一块三角形玻璃打碎成两块,带块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是.13.如图,Rt△ABC中,∠C=90°,∠B=25°,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD,则∠CAD 的度数是.14.如图,在△ABC中,AC=BC,过点A,B分别作过点C的直线的垂线AE,BF.若AE =CF=3,BF=4.5,则EF=.15.边长为整数、周长为20的三角形的个数为.16.如图,Rt△ABC中,∠BAC=90°,AB=6,AC=3,G是△ABC重心,则S△AGC=.三.解答题(共8小题,满分66分)17.如图,在一个三角形的一条边上取四个点,把这些点与这条边所对的顶点连接起来.问图中共有多少个三角形.请你通过与数线段或数角的问题进行类比来思考.18.如图,AB=DE,AC=DF,BE=CF,求证:△ABC≌△DEF.19.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.(1)求证:△ADC≌△CEB;(2)求两堵木墙之间的距离.20.如图,已知B,D在线段AC上,且AD=CB,BF=DE,∠AED=∠CFB=90°求证:(1)△AED≌△CFB;(2)BE∥DF.21.如图,已知锐角△ABC,AB>BC.(1)尺规作图:求作△ABC的角平分线BD;(保留作图痕迹,不写作法)(2)点E在AB边上,当BE满足什么条件时?∠BED=∠C.并说明理由.22.如图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB垂线,交AC于E,交BC的延长线于F.(1)∠1与∠B有什么关系?说明理由.(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由.23.如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO 和∠ABO的角平分线,BC延长线交OM于点G.(1)若∠MON=60°,则∠ACG=°;若∠MON=90°,则∠ACG=°;(2)若∠MON=n°.请求出∠ACG的度数;(用含n的代数式表示)(3)如图2,若∠MON=n°,过C作直线与AB交F.若CF∥OA时,求∠BGO﹣∠ACF的度数.(用含n的代数式表示)24.如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB,点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.(1)若∠AEF=20°,∠ADE=50°,BC=2,求AB的长度;(2)求证:AE=AF+BC;(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明你的结论.参考答案一.选择题(共10小题)1.【解答】解:设第三边的长为x,由题意得:4﹣2<x<4+2,2<x<6,故选:C.2.【解答】解:BC边上的高应从点A向BC引垂线,只有选项D符合条件,故选:D.3.【解答】解:由于BD=CD,则点D是边BC的中点,所以AD一定是△ABC的一条中线.故选:C.4.【解答】解:∠ACD是△ABC的一个外角,∴∠ACD=∠A+∠B=100°,故选:D.5.【解答】解:∵∠A=74°,∠B=46°,∴∠ACB=60°,CD平分∠ACB,∴∠BCD=∠ACD=∠ACB=×60°=30°,∴∠BDC=180°﹣∠B﹣∠BCD=104°,故选:A.6.【解答】解:A、添加∠B=∠C可利用ASA定理判定△ABE≌△ACD,故此选项不合题意;B、添加∠ADC=∠AEB可利用AAS定理判定△ABE≌△ACD,故此选项不合题意;C、添加BD=CE可得AD=AE,可利用利用SAS定理判定△ABE≌△ACD,故此选项不合题意;D、添加BE=CD不能判定△ABE≌△ACD,故此选项符合题意;故选:D.7.【解答】解:观察图形发现:AC=DC,BC=BC,∠ACB=∠DCB,所以利用了三角形全等中的SAS,故选:D.8.【解答】解:①全等三角形的形状相同、大小相等,正确;②全等三角形的对应边相等、对应角相等,正确;③面积相等的两个三角形是全等图形,错误;④全等三角形的周长相等,正确.故选:C.9.【解答】解:∵AD是△ABC的高,∴∠ADB=90°,∵∠BAD=42°,∴∠ABD=180°﹣∠ADB﹣∠BAD=48°,∵BE是△ABC的角平分线,∴∠ABF=∠ABD=24°,∴∠BFD=∠BAD+∠ABF=42°+24°=66°,故选:D.10.【解答】解:∵△ABC的周长为22,△ABM的周长比△ACM的周长大2,∴2<BC<22﹣BC,解得2<BC<11,又∵△ABC的三边长均为整数,△ABM的周长比△ACM的周长大2,∴AC=为整数,∴BC边长为偶数,∴BC=4,6,8,10,故选:A.二.填空题(共6小题)11.【解答】解:根据全等三角形的判定(SAS)可知属于全等的2个图形是①③,故答案为:①③.12.【解答】解:第①块只保留了原三角形的一个角和部分边,根据这两块中的任一块不能配一块与原来完全一样的;第②块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带②去.故答案为:②,ASA.13.【解答】解:∵Rt△ABC中,∠C=90°,∠B=25°,∴∠CAB=90°﹣∠B=90°﹣25°=65°,由作图过程可知:MN是AB的垂直平分线,∴DA=DB,∴∠DAB=∠B=25°,∴∠CAD=∠CAB﹣∠DAB=65°﹣25°=40°.答:∠CAD的度数是40°.故答案为:40°.14.【解答】解:∵过点A,B分别作过点C的直线的垂线AE,BF,∴∠AEC=∠CFB=90°,在Rt△AEC和Rt△CFB中,,∴Rt△AEC≌Rt△CFB(HL),∴EC=BF=4.5,∴EF=EC+CF=4.5+3=7.5,故答案为:7.5.15.【解答】解:边长为整数、周长为20的三角形分别是:(9,9,2)(8,8,4)(7,7,6)(6,6,8)(9,6,5)(9,7,4)(9,8,3)(8,7,5),共8个.故答案为:8.16.【解答】解:延长AG交BC于E.∵∠BAC=90°,AB=6,AC=3,∴S△ABC=•AB•AC=9,∵G是△ABC的重心,∴AG=2GE,BE=EC,∴S△AEC=×9=4.5,∴S△AGC=×S△AEC=3,故答案为3三.解答题(共8小题)17.【解答】解:如图所示,图中三角形的个数有△ABC,△ACD,△ADE,△AEF,△AFG,△ABD,△ABE,△ABF,△ABG,△ACE,△ACF,△ACG,△ADF,△ADG,△AEG.18.【解答】解:∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,∵,∴△ABC≌△DEF(SSS).19.【解答】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC在△ADC和△CEB中,∴△ADC≌△CEB(AAS);(2)解:由题意得:AD=2×3=6cm,BE=7×2=14cm,∵△ADC≌△CEB,∴EC=AD=6cm,DC=BE=14cm,∴DE=DC+CE=20(cm),答:两堵木墙之间的距离为20cm.20.【解答】证明(1)∵∠AED=∠CFB=90°,在Rt△AED和Rt△CFB中,∴Rt△AED≌Rt△CFB(HL).(2)∵△AED≌△CFB,∴∠BDE=∠DBF,在△DBE和△BDF中,∴△DBE≌△BDF(SAS),∴∠DBE=∠BDF,∴BE∥DF.21.【解答】解:(1)如图,线段BD即为所求.(2)结论:BE=BC.理由:∵BD平分∠ABC,∵BE=BC,BD=BD,∴△BDE≌△BDC(SAS),∴∠BED=∠C.22.【解答】解:(1))∠1与∠B相等,理由:∵,△ABC中,∠ACB=90°,∴∠1+∠F=90°,∵FD⊥AB,∴∠B+∠F=90°,∴∠1=∠B;(2)若BC=BD,AB与FB相等,理由:∵△ABC中,∠ACB=90°,DF⊥AB,∴∠ACB=∠FDB=90°,在△ACB和△FDB中,,∴△ACB≌△FDB(AAS),∴AB=FB.23.【解答】解:(1)∵∠MON=60°,∴∠OBA+∠OAB=120°,∵∠OBA、∠OAB的平分线交于点C,∴∠ABC+∠BAC=×120°=60°,∴∠ACB=180°﹣60°=120°,∴∠ACG=60°;∵∠MON=90°,∴∠OBA+∠OAB=90°,∵∠OBA、∠OAB的平分线交于点C,∴∠ABC+∠BAC=×90°=45°,∴∠ACB=180°﹣45°=135°;故答案为:60,45;(2)在△AOB中,∠OBA+∠OAB=180°﹣∠AOB=180°﹣n°,∵∠OBA、∠OAB的平分线交于点C,∴∠ABC+∠BAC=(∠OBA+∠OAB)=(180°﹣n°),即∠ABC+∠BAC=90°﹣n°,∴∠ACB=180°﹣(∠ABC+∠BAC)=180°﹣(90°﹣n°)=90°+n°,∴∠ACG=180°﹣(90°+n°)=90°﹣n°;(3)∵AC、BC分别是∠BAO和∠ABO的角平分线,∴∠ABC=ABO,∠BAC=∠OAC=,∵CF∥AO,∴∠ACF=∠CAG,∵∠BGO=∠BAG+∠ABG,∴∠BGO﹣∠ACF=∠BAG+∠ABG﹣∠ACF=2∠BAC+∠ABG﹣∠BAC=∠ABG+∠BAC=90°﹣n°.24.【解答】解:(1)在等腰直角三角形DEF中,∠DEF=90°,∵∠1=20°,∴∠2=∠DEF﹣∠1=70°,∵∠EDA+∠2+∠3=180°,∴∠3=60°,∵EA⊥AB,∴∠EAB=90°,∵∠3+∠EAB+∠A=180°,∴∠4=30°,∵∠C=90°,∴AB=2BC=4;(2)如图1,过D作DM⊥AE于M,在△DEM中,∠2+∠5=90°,∵∠2+∠1=90°,∵DE=FE,在△DEM与△EF A中,,∴△DEM≌△EF A,∴AF=EM,∵∠4+∠B=90°,∵∠3+∠EAB+∠4=180°,∴∠3+∠4=90°,∴∠3=∠B,在△DAM与△ABC中,,∴△DAM≌△ABC,∴BC=AM,∴AE=EM+AM=AF+BC;(3)如图2,过D作DM⊥AE交AE的延长线于M,∵∠C=90°,∴∠1+∠B=90°,∵∠2+∠MAB+∠1=180°,∠MAB=90°,∴∠2+∠1=90°,∠2=∠B,在△ADM与△BAC中,,∴△ADM≌△BAC,∵EF=DE,∠DEF=90°,∵∠3+∠DEF+∠4=180°,∴∠3+∠4=90°,∵∠3+∠5=90°,∴∠4=∠5,在△MED与△AFE中,,∴△MED≌△AFE,∴ME=AF,∴AE+AF=AE+ME=AM=BC,即AE+AF=BC.。
北师大版七年级数学下册第4单元《三角形》单元测试题(含答案)

北师大版七年级数学下册第4单元《三角形》单元测试题(含答案)1.如果∠A=∠B﹣∠C,那么△ABC是()A.锐角三角形B.钝角三角形C.直角三角形D.无法确定2.下列各组线段能组成一个三角形的是()A.2cm,3cm,6cm B.6cm,8cm,10cmC.5cm,5cm,10cm D.4cm,6cm,10cm3.画△ABC的边BC上的高,正确的是()A.B.C.D.4.已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是()A.BC=B'C' B.∠A=∠A′C.∠C=∠C′D.∠B=∠B′=90°5.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是()A.20B.24C.26D.286.如图,∠1=140°,∠2=100°,则∠3=()A.100°B.120°C.130°D.140°7.如图,点F,C在BE上,AC=DF,BF=EC,AB=DE,AC与DF相交于点G,则与2∠DFE相等的是()A.∠A+∠D B.3∠B C.180°﹣∠FGC D.∠ACE+∠B 8.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为()A.60°B.100°C.120°D.130°9.如图,点C,F,B,E在同一直线上,∠C=∠DFE=90°,添加下列条件,仍不能判定△ACB与△DFE全等的是()A.∠A=∠D,AB=DE B.AC=DF,CF=BEC.AB=DE,BC=EF D.∠A=∠D,∠ABC=∠E10.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠A的度数为()A.56°B.34°C.36°D.24°11.如图,点A,F,C,D在同一条直线上,BC∥EF,AC=FD,请你添加一个条件,使得△ABC≌△DEF.12.如图,在△ABC中,已知点D、点E分别为BC、AD的中点,且△BDE的面积为3,则△ABC的面积是.13.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D=.14.如图,∠ABC与∠ACB的平分线交于I点,若∠ABC+∠ACB=100°,则∠BIC =;若∠A=50°,则∠BIC=.15.如图,△ABC的两条高BD,CE相交于点O,若∠A=75°,则∠ABD=,∠ACE=,∠BOC=.16.如图,三角形ABC的面积为1,分别延长AB、BC、CA至M、N、P,使得BM=2AB,CN=3BC,AP=4CA,则三角形MNP面积是.17.将一副三角板如图所示摆放,若∠BAE=125°,则∠CAD的度数是.18.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P=°.19.设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|b﹣c﹣a|=.20.如图所示,在△ABC中,AD平分∠BAC,BE是高线,∠BAC=50°,∠EBC=20°,则∠ADC的度数为.21.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论正确的是.A.∠1=∠2;B.BE=CF;C.△CAN≌△ABM;D.CD=DN.22.如图,在△ABC中,点E为边BC的中点,连接AE,点D为线段AE上的一点(不与A,E重合),连接BD、CD,若BD=CD,求证:∠ADB=∠ADC.23.已知:如图,在△ABC和△DEF中,点B、E、C、F四点在一条直线上,且BE=CF,AB=DE,∠B=∠DEF.求证:△ABC≌△DEF.24.如图,△ABC中,点D、E在边BC上,∠ADC=∠AEB,CD=BE.求证:∠BAD=∠CAE.25.风筝起源于中国,至今已有2300多年的历史,如图,在小明设计的“风筝”图案中,已知AB=AD.∠B=∠D,∠BAE=∠DAC.求证:AC=AE.26.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD =BE.(1)求证:△ABD≌△ECB.(2)若∠BDC=70°.求∠ADB的度数.27.如图,点A,B,C,D在同一条直线上,AB=CD,∠A=∠D,AE=DF.(1)求证:△ACE≌△DBF.(2)若BF⊥CE于点H,求∠HBC的度数.28.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A 之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.参考答案1.解:因为∠A+∠B+C=180°,且∠A=∠B﹣∠C,所以∠B﹣∠C+∠B+C=180°,所以∠B=90°,所以△ABC是直角三角形.故选:C.2.解:A、2+3<6,不能组成三角形,不符合题意;B、6+8=14>10,能组成三角形,符合题意;C、5+5=10,不能组成三角形,不符合题意;D、4+6=10,不能组成三角形,不符合题意;故选:B.3.解:A.此图形中AD是BC边上的高,符合题意;B.此图形中CD不是BC边上的高,不符合题意;C.此图形中CD是AB边上的高,不符合题意;D.此图形中AD是AB边上的高,不符合题意;故选:A.4.解:A、由AB=A′B′,AC=A′C′,BC=B'C'可以判定△ABC≌△A′B′C′(SSS),不符合题意.B、由AB=A′B′,AC=A′C′,∠A=∠A′可以判定△ABC≌△A′B′C′(SAS),不符合题意.C、由AB=A′B′,AC=A′C′,∠C=∠C′不可以判定△ABC≌△A′B′C′(SSA),符合题意.D、由AB=A′B′,AC=A′C′,∠B=∠B′=90°可以判定Rt△ABC≌Rt△A′B′C′(HL),不符合题意.故选:C.5.解:∵BD是AC边上的中线,∴AD=CD.∵△ABD的周长为30,∴AB+BD+AD=30.∴BD+AD=30﹣AB=30﹣15=15.∴△BCD的周长为BC+CD+BD=BC+AD+BD=9+15=24.故选:B.6.解:∵∠1=140°,∠2=100°,∴∠3=360°﹣140°﹣100°=120°,故选:B.7.解:∵BF=EC,∴BF+FC=EC+FC,∴BC=EF,在△ABC与△DEF中,,∴△ABC≌△DEF(SSS),∴∠ACB=∠DFE,∴2∠DFE=180°﹣∠FGC,故选:C.8.解:如图,∵CD、BE均为△ABC的高,∴∠BEC=∠ADC=90°,∵∠A=60°,∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,则∠BOC=∠BEC+∠OCE=90°+30°=120°.故选:C.9.解:A、∵∠A=∠D,AB=DE,∠C=∠DFE=90°,根据AAS判定△ACB与△DFE 全等,不符合题意;B、∵CF=BE,可得,BC=EF,AC=DF,BC=EF,∠C=∠DFE=90°,根据SAS判定△ACB与△DFE全等,不符合题意;C、∵AB=DE,BC=EF,∠C=∠DFE=90°,根据HL判断Rt△ACB与Rt△DFE全等,不符合题意;D、∵∠A=∠D,∠ABC=∠E,∠C=∠DFE=90°,由AAA不能判定△ACB与△DFE全等,符合题意;故选:D.10.解:如图,∵∠1=54°,a∥b,∴∠3=∠1=58°.∵∠2=24°,∠A=∠3﹣∠2,∴∠A=58°﹣24°=34°.故选:B.11.解:∵BC∥EF,∴∠BCA=∠EFD,若添加BC=EF,且AC=FD,由“SAS”可证△ABC≌△DEF;若添加∠B=∠E,且AC=FD,由“AAS”可证△ABC≌△DEF;若添加∠A=∠D,且AC=FD,由“ASA”可证△ABC≌△DEF;故答案为:BC=EF或∠B=∠E或∠A=∠D(答案不唯一).12.解:∵点E为AD的中点,△BDE的面积为3,∴△ABD的面积为3×2=6,∵点D为BC的中点,∴△ABC的面积为6×2=12.故答案为:12.13.解:∵∠B=46°,∠C=30°,∴∠DAC=∠B+∠C=76°,∵∠EFC=70°,∴∠AFD=70°,∴∠D=180°﹣∠DAC﹣∠AFD=34°,故答案为:34°.14.解:∵BI平分∠ABC,CI平分∠ACB,∴∠IBC=∠ABC,∠ICB=∠ACB,∴∠IBC+∠ICB=(∠ABC+∠ACB)=50°,∴∠BIC=180°﹣(∠IBC+∠ICB)=130°;当∠A=50°时,∠ABC+∠ACB=180°﹣∠A=130°,∴∠IBC+∠ICB=(∠ABC+∠ACB)=65°,∴∠BIC=180°﹣(∠IBC+∠ICB)=115°.故答案为:130°;115°.15.解:∵△ABC的两条高BD,CE相交于点O,∴∠AEC=∠ADB=90°,∵∠A=75°,∴∠ABD=180°﹣∠A﹣∠ADB=180°﹣75°﹣90°=15°,∠ACE=180°﹣∠A﹣∠AEC=180°﹣75°﹣90°=15°,在△ABC中,∠DBC+∠ECB=180°﹣∠A﹣∠ABD﹣∠ACE=180°﹣75°﹣15°﹣15°=75°,在△BOC中,∠BOC=180°﹣(∠DBC+∠ECB)=180°﹣75°=105°.故答案为:15°,15°,105°.16.解:连接MC,AN∵2AB=BM,∴S△BCM=2S△ABC,∴S△BCM=2×1=2,∵3BC=CN,∴S△MNC=3S△BCM,S△ACN=3S△ABC,∴S△MNC=3×2=6,S△ACN=3×1=3,∵4CA=AP,∴S△ANP=4S△ACN,S△AMP=4S△AMC,∴S△ANP=4×3=12,S△AMP=4×(2+1)=12,∵S△MNP=S△ABC+S△BCM+S△MNC+S△ACN+S△ANP+S△AMP,∴S△MNP=1+2+6+3+12+12=36.故答案为:36.17.解:∵∠BAE=125°,∴∠DAE=∠BAE﹣∠BAD=125°﹣90°=35°,∴∠CAD=∠CAE﹣∠DAE=90°﹣35°=55°,故答案为:55°.18.解:∵BP是△ABC中∠ABC的平分线,∠ABP=15°,∴∠CBP=∠ABP=15°,∵CP是∠ACB的外角的平分线,∠ACP=50°,∴∠PCM=∠ACP=50°,∴∠P=∠PCM﹣∠CBP=50°﹣15°=35°,故答案为:35.19.解:∵a、b、c分别为△ABC的三边长,∴a+b﹣c>0,b﹣c﹣a<0,∴|a+b﹣c|﹣|b﹣c﹣a|=a+b﹣c+b﹣c﹣a=2b﹣2c,故答案为:2b﹣2c.20.解:∵AD平分∠BAC,BE是高,∠BAC=50°,∴∠BAD=∠BAC=25°,∠ABE=40°.∵∠EBC=20°,∴∠ADC=∠ABD+∠BAD=∠ABE+∠EBC+∠BAD=40°+20°+25°=85°.故答案为:85°.21.解:如图,∵∠E=∠F=90°,∠B=∠C,AE=AF,∴Rt△ABE≌Rt△ACF(AAS),∴∠F AC=∠EAB,BE=CF,AB=AC,∴∠1=∠2,故A,B正确;又∠B=∠C,∠CAN=∠BAM,∴△ACN≌△ABM(ASA),故C错误;∵△ACN≌△ABM(ASA),∴AN=AM,∴MC=BN,而∠B=∠C,∠CDM=∠BDN,∴△DMC≌△DMB(AAS),∴DC=DB,∴DC≠DN,故D错误.故答案为:A,B;22.证明:∵点E为边BC的中点,∴BE=CE,在△BDE和△CDE中,,∴△BDE≌△CDE(SSS),∴∠BDE=∠CDE,∠DBE=∠DCE,∴∠ADB=∠ADC,在△ABD和△ACD中,,∴△ABD≌△ACD(SAS),∴∠ADB=∠ADC.23.证明:∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC与△DEF中,,∴△ABC≌△DEF(SAS).24.证明:∵∠ADC=∠AEB,∴AD=AE,在△ADC和△AEB中,,∴△ADC≌△AEB(SAS),∴∠BAE=∠DAC,∴∠BAD=∠CAE.25.证明:∵∠BAE=∠DAC,∴∠BAE+∠EAC=∠DAC+∠EAC,即∠BAC=∠DAE,在△BAC和△DAE中,,∴△BAC≌△DAE(ASA),∴AC=AE.26.证明:(1)∵AD∥BC,∴∠ADB=∠CBE,在△ABD和△ECB中,,∴△ABD≌△ECB(AAS);(2)∵△ABD≌△ECB,∴BD=BC,∴∠BDC=∠BCD=70°,∴∠DBC=40°,∴∠ADB=∠CBD=40°.27.(1)证明:∵AB=CD,∴AB+BC=CD+BC.∴AC=BD.在△ABC和△EDF中,,∴△ACE≌△DBF(SAS);(2)解:由(1)知△ACE≌△DBF,∴∠ACE=∠DBF.∵BF⊥CE,∴∠BHC=90°,∴∠HBC+∠HCB=90°,∴∠HBC=∠HCB=45°.28.(1)解:∵∠A=80°.∴∠ABC+∠ACB=100°,∵点P是∠ABC和∠ACB的平分线的交点,∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,(2)∵外角∠MBC,∠NCB的角平分线交于点Q,∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°﹣∠ABC﹣∠ACB)=(180°+∠A)=90°+∠A∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;(3)延长BC至F,∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠ECF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠ABC+2∠E,又∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=∠A;∵∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°.如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.综上所述,∠A的度数是90°或60°或120°.。
北师大版七年级数学下册 第四章 三角形 单元测试训练卷(word版 含解析)

北师大版七年级数学下册第四章 三角形单元测试训练卷一、单选题(共10小题,每小题4分,共40分)1.下列各组数为边,能构成三角形的是( )A .1,2,3B .2,3,4C .4,4,8D .3,5,9 2.如图,65A ∠=︒,45B ∠=︒,则ACD ∠=( )A .65°B .60°C .45°D .110° 3.如图,12,AC AD ∠=∠=,要使ABC AED ≌△△,还需添加一个条件,那么在以下条件中不能选择的是( )A .AB AE = B .BC ED = C .C D ∠=∠ D .BE ∠=∠ 4.若△ABC 的一个外角等于其中一个内角,则( )A .必有一个内角等于30°B .必有一个内角等于45°C .必有一个内角等于60°D .必有一个内角等于90° 5.如果一个三角形的两边长分别为3和7,则第三边长可能是( ). A .3 B .4 C .7 D .10 6.如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带( )去最省事.A.△B.△C.△D.△△7.已知:如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连接DE,点P 以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒()秒时.△ABP和△DCE全等.A.1B.1或3C.1或7D.3或78.如图,△CAB=△DBA,再添加一个条件,不一定能判定△ABC△△BAD的是()A.AC=BD B.△1=△2C.△C=△D D.AD=BC 9.如图,在△ABC中,△BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD△AD于D,CE△AD于E,交AB于点F,CE=10,BD=4,则DE的长为()A.6B.5C.4D.810.如图,在ABC中,△ACB=45°,AD△BC,BE△AC,AD与BE相交下点F,连接并延长CF交AB于点G,△AEB的平分线交CG的延长线于点H,连接AH.则下列结论:△△EBD=45°;△AH=HF;△ABD△CFD;△CH=AB+AH;△BD=CD﹣AF.其中正确的有()个.A .5B .4C .3D .2二、填空题(共6小题,每小题4分,共24分)11.用木棒钉成一个三角架,两根小棒长分别是7cm 和10cm,第三根小棒长为x cm,则x 的取值范围是___.12.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带________去玻璃店.13.如图,AB =AC ,D ,E 分别是AB ,AC 上的点,添加一个条件能判断△ABE △△ACD 的是____.14.如图,A E ∠=∠,AC BE ⊥,AB EF =,25BE =,8=CF ,则AC =_______.15.在△ABC 中,D 、E 分别是BC 、AD 的中点,S △ABC =4cm 2,则S △ABE =_____.16.如图,ABC 和ADE 均为等边三角形,D ,E 分别在边AB ,AC 上,连接BE ,CD ,若15ACD =︒∠,则CBE =∠__________.三、解答题(共6小题, 56分)17.如图,在ABC ∆中,AD BC ⊥,垂足为D ,BE AC ⊥,垂足为E ,AE BE =,AD 与BE 相交于点F .(1)请说明AEF BEC ∆∆≌的理由.(2)如果2AF BD =,试说明AD 平分BAC ∠的理由.18.如图,△ABC中,D为BC上一点,△C=△BAD,△ABC的角平分线BE交AD于点F.(1)求证:△AEF=△AFE;(2)G为BC上一点且FE平分△AFG.求证:AB=GB19.如图,已知AE△AB,AF△AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC△BF.20.探索归纳:(1)如图1,已知ABC 为直角三角形,90A ∠=︒,若沿图中虚线剪去A ∠,则12∠+∠=________︒.(2)如图2,已知ABC 中,40A ∠=︒,剪去A ∠后成四边形,则12∠+∠=__________︒.(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想12∠+∠与A ∠的关系是___________.(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究12∠+∠与A ∠的关系并说明理由.21.在△BAC中,△BAC=90°,AB=AC,AE是过A的一条直线,BD△AE于点D,CE△AE于E.(1)如图(1)所示,若B,C在AE的异侧,易得BD与DE,CE的关系是DE=;(2)若直线AE绕点A旋转到图(2)位置时,(BD<CE),其余条件不变,问BD与DE,CE 的关系如何?请予以证明;(3)若直线AE绕点A旋转,(BD>CE),问BD与DE,CE的关系如何?请直接写出结果,不需证明.22.如图,AB=12cm,AC△AB,BD△AB,AC=BD=9cm,点P在线段AB上以3cm/s的速度,由A向B运动,同时点Q在线段BD上由B向D运动;设点P的运动时间为t秒.(1) PB=________ cm.(用含t的代数式表示)(2)如图1,若点Q的运动速度与点P的运动速度相等,当运动时间t=1秒时,△ACP与△BPQ是否全等?并说明理由.(3)如图2,将“AC△AB,BD△AB”改为“△CAB=△DBA”,其余条件不变;设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.参考答案:1.B【解析】【分析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,逐项分析判断即可.【详解】解:A. 1+2=3 ,不能构成三角形,故该选项不符合题意;B. 2+3>4,能构成三角形,故该选项符合题意;C. 4+4=8,不能构成三角形,故该选项不符合题意;D. 3+5<9,不能构成三角形,故该选项不符合题意;故选B【点睛】本题考查了构成三角形的条件,掌握三角形三边关系是解题的关键.2.D【解析】【分析】根据三角形外角的性质求解即可.【详解】解:△65A ∠=︒,45B ∠=︒,△110ACD A B ∠=∠+∠=︒,故选:D .【点睛】本题考查了三角形外角的性质,熟练掌握三角形外角的性质是解题的关键.3.B【解析】【分析】由△1=△2,可得∠BAC=∠EAD ,又AC=AD ,可知在△ABC 和△AED 中,已知一角及其临边对应相等,要证两三角形全等,任意再找一对角对应相等,或者找已知角的另一边对应相等,由此可得答案.解:△△1=△2,△∠BAC=∠EAD ,当AB=AE 时,根据SAS 可得ABC AED ≌△△;当C D ∠=∠时,根据ASA 可得ABC AED ≌△△;当B E ∠=∠时,根据AAS 可得ABC AED ≌△△;当BC=ED 时,SSA 不能判定两个三角形全等,故答案为:B【点睛】本题考查三角形全等的判定,角的和差是常考的判定已知角相等的方法,熟知三角形全等的判定定理是解题的关键.4.D【解析】【分析】根据三角形的外角性质、邻补角的概念计算即可.【详解】解:△三角形的一个外角大于和它不相邻的任何一个内角,△△ABC 的一个外角等于其中一个内角时,这个外角等于它的邻补角,△这个三角形必有一个内角等于90°,故选:D .【点睛】本题考查的是三角形的外角性质,掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键.5.C【解析】【分析】根据三角形三边之间的关系即可判定.【详解】解:设第三边长为x ,则4<x <10,所以选项中符合条件的整数只有7.故选:C .本题考查了三角形三边关系,三角形中,任意两边之差小于第三边,任意两边之和大于第三边.6.C【解析】【分析】根据全等三角形的判定方法“角边角”可以判定应当带△去.【详解】解:由图形可知,△有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形, 所以,最省事的做法是带△去.故选:C.【点睛】本题考查了全等三角形的判定方法,正确理解“角边角”的内容是解题的关键.7.C【解析】【分析】分P点在线段BC上和P点在线段AD上两种情况讨论,当P点在线段BC上时得到△ABP=△DCE=90°,BP=CE=2进而求解;当P点在线段AD上时得到△BAP=△DCE=90°,AP=CE=2进而求解.【详解】解:由题意可知:AB=CD,当P点在线段BC上时:△ABP=△DCE=90°,BP=CE=2,此时△ABP△△DCE(SAS),由题意得:BP=2t=2,△t=1;当P点在线段AD上时:△BAP=△DCE=90°,AP=CE=2,此时△BAP△△DCE(SAS),由题意得:AP=16-2t=2,△t=7.△当t的值为1或7秒时.△ABP和△DCE全等.故答案为:C.【点睛】本题考查了三角形全等的判定方法,注意要分类讨论,熟练掌握三角形全等判定方法是解题的关键.8.D【解析】【分析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)判断即可.【详解】解答:解:A.△AC=BD,△CAB=△DBA,AB=AB,△根据SAS能推出△ABC△△BAD,故本选项错误;B.△△CAB=△DBA,AB=AB,△1=△2,△根据ASA能推出△ABC△△BAD,故本选项错误;C.△△C=△D,△CAB=△DBA,AB=AB,△根据AAS能推出△ABC△△BAD,故本选项错误;D.根据AD=BC和已知不能推出△ABC△△BAD,故本选项正确;故选:D.【点睛】本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.9.A【解析】【分析】根据△BAC=90°得到△BAD+△CAD=90°,由于CE△AD于E,于是得到△ACE+△CAE=90°,根据余角的性质得到△BAD=△ACE,推出△ABD△△CAE,根据全等三角形的性质即可得到结论.【详解】解:△△BAC=90°,△△BAD+△CAD=90°,△CE△AD于E,△△ACE+△CAE=90°,△△BAD=△ACE,在△ABD 与△CAE 中,90D AEC BAD ACE AB AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, △△ABD △△CAE (AAS ),△AE =BD =4,AD =CE =10,△DE =AD ﹣AE =6.故选:A .【点睛】本题考查全等三角形的判定与性质,解题的关键是利用余角的性质得到△BAD =△ACE . 10.A【解析】【分析】△利用三角形内角和定理即可说明其正确;△利用垂直平分线的性质即可说明其正确;△利用SAS 判定全等即可;△利用△中的结论结合等量代换和等式的性质即可得出结论;△利用△中的结论结合等量代换和等式的性质即可得出结论.【详解】如图所示,设EH 与AD 交于点M ,△△ACB =45°,BE △AC ,△△EBD =90°﹣△ACD =45°,故△正确;△AD △BC ,△EBD =45°,△△BFD =45°,△△AFE =△BFD =45°,△BE △AC ,△△F AE =△AFE =45°,△△AEF 为等腰直角三角形,△EM 是△AEF 的平分线,△EM △AF ,AM =MF ,即EH 为AF 的垂直平分线,△AH =HF ,△△正确;△AD △BC ,△ACD =45°,△△ADC 是等腰直角三角形,△AD =CD ,同理,BD =DF ,在△ABD 和△CFD 中,90AD CD ADB CDF BD FD =⎧⎪∠=∠=︒⎨⎪=⎩, △△ABD △△CFD (SAS ),△△正确;△△ABD △△CFD ,△CF =AB ,△CH =CF +HF ,由△知:HF =AH ,△CH =AB +AH ,△△正确;△BD =DF ,CD =AD ,又△DF =AD ﹣AF ,△BD =CD ﹣AF ,△△正确,综上,正确结论的个数为5个.故选:A .【点睛】本题考查了直角三角形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,垂直平分线的判定与性质等相关知识,综合性较强,难度较大,做题时要分清角的关系与边的关系.11.3<x<17【解析】【分析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,确定出第三边的取值范围即可得出答案.【详解】解:设第三根小棒的长为x cm,根据三角形的三边关系可得:10-7<x<10+7,即3<x<17,故答案为3<x<17.【点睛】本题考查了三角形的三边关系.三角形的三边关系:第三边大于两边之差而小于两边之和.12.△【解析】【分析】观察每块玻璃形状特征,利用ASA判定三角形全等可得出答案.【详解】第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA 来配一块一样的玻璃.应带△去.故答案为:△.【点睛】本题属于利用ASA判定三角形全等的实际应用,难度不大,但形式较颖,要善于将所学知识与实际问题相结合.13.AD=AE(答案不唯一)【解析】【分析】根据全等三角形的判定定理添加条件可以,添加AD =AE ,根据SAS 证明△ABE △△ACD 即可.【详解】解:添加的条件是AD =AE ,理由是:在△ABE 和△ACD 中,AE AD A A AB AC =⎧⎪∠=∠⎨⎪=⎩,△△ABE △△ACD (SAS ),故答案为:AD =AE (答案不唯一).【点睛】本题考查了全等三角形的判定定理,熟练掌握全等三角形的判定定理是解题的关键. 14.17【解析】【分析】由“AAS ”可证ABC EFC ∆≅∆,可得AC CE =,9BC CF ==,即可求解.【详解】解:AC BE ⊥,90ACB ECF ∴∠=∠=︒,在ABC ∆和EFC ∆中,A E ACB ECF AB EF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ABC EFC AAS ∴∆≅∆,AC CE ∴=,8BC CF ==,25817AC CE BE BC ∴==-=-=,故答案为:17.【点睛】本题考查了全等三角形的判定和性质,解题的关键是证明三角形全等.15.1cm 2【解析】【分析】根据三角形的中线把三角形分成两个面积相等的三角形的性质分析,即可得到答案.【详解】∵D 是BC 的中点,S △ABC =4cm 2∴S △ABD =12S △ABC =12×4=2cm 2∵E 是AD 的中点,∴S △ABE =12S △ABD =12×2=1cm 2故答案为:1cm 2.【点睛】本题考查了三角形中线的知识;解题的关键是熟练掌握三角形中线的性质,从而完成求解. 16.45︒##45度【解析】【分析】根据题意利用全等三角形的判定与性质得出()BD C S ED E SA ≅和15EBD ACD ︒∠=∠=,进而依据CBE =∠ABC EBD ∠-∠进行计算即可.【详解】解:△ABC 和ADE 均为等边三角形,△,,AB AC AE AD EC DB ===,△60,120,AED ADE ABC DEC EDB ︒︒∠=∠=∠=∠=∠=在CED 和BDE 中, EC DB DEC EDB ED ED =⎧⎪∠=∠⎨⎪=⎩, △()BD C S ED E SA ≅,△15EBD ACD ︒∠=∠=,△CBE =∠601545ABC EBD ︒︒︒∠-∠=-=.故答案为:45︒.【点睛】本题考查全等三角形的判定与性质以及等边三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.17.(1)见解析(2)见解析【解析】【分析】(1)由余角的性质可证DAC EBC ∠=∠,根据“ASA”可证结论成立;(2)由AEF BEC ∆∆≌可得AF BC =,结合2AF BD =可知BD CD =,然后根据“SAS”证明△ABD △△ACD 可证结论成立.(1)证明:AD BC ⊥,BE AC ⊥,90ADC ∴∠=,△AEB =△CEB =90°,90DAC C +∠=∴∠,△EBC +△C =90°,DAC EBC =∠∴∠,在AEF ∆与BEC ∆中,EAF EBC AEF BEC AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ΔΔASA AEF BEC ∴≌.(2)解:由(1)知,AF BC =,2AF BD =,2BC BD ∴=,D ∴是BC 的中点,BD CD ∴=,在△ABD 和△ACD 中AD AD ADB ADC BD CD =⎧⎪∠=∠⎨⎪=⎩, △△ABD △△ACD ,△BAD CAD ∠=∠,AD ∴平分BAC ∠.【点睛】本题考查了全等三角形的判定和性质,余角的性质,角平分线的定义,熟练掌握全等三角形的判定和性质是解题的关键.18.(1)证明见解析(2)证明见解析【解析】【分析】(1)先根据角平分线的定义得到△1=△2,再由三角形外角的性质得到△AEF=△2+△C,△AFE=△1+△BAD,由△C=△BAD,即可推出△AEF=△AFE;(2)根据角平分线的定义得到△AFE=△GFE,再由△AFB+△AFE=180°,△BFG+△GFE=180°,得到△AFB=△BFG,然后证明△ABF△△GBF即可得到AB=GB.(1)解:△BE是△ABC的角平分线,△△1=△2,△△AEF、△AFE分别是△BCE、△ABF的外角,△△AEF=△2+△C,△AFE=△1+△BAD,又△△C=△BAD,△△AEF=△AFE;(2)解:△FE平分△AFG,△△AFE=△GFE,△△AFB+△AFE=180°,△BFG+△GFE=180°,△△AFB=△BFG,在△ABF和△GBF中12AFB BFG BF BF∠=∠⎧⎪=⎨⎪∠=∠⎩, △△ABF △△GBF (ASA )△AB =GB .【点睛】本题主要考查了角平分线的定义,全等三角形的性质与判定,三角形外角的性质,熟知相关知识是解题的关键.19.(1)见解析(2)见解析【解析】【分析】(1)先求出△EAC =△BAF ,然后利用“边角边”证明△ABF 和△AEC 全等,根据全等三角形对应边相等即可证明;(2)根据全等三角形对应角相等可得△AEC =△ABF ,设AB 、CE 相交于点D ,根据△AEC +△ADE =90°可得△ABF +△ADM =90°,再根据三角形内角和定理推出△BMD =90°,从而得证.(1)△AE △AB ,AF △AC ,△△BAE =△CAF =90°,△△BAE +△BAC =△CAF +△BAC ,即△EAC =△BAF ,在△ABF 和△AEC 中,AE AB EAC BAF AF AC =⎧⎪∠=∠⎨⎪=⎩, △△ABF △△AEC (SAS ),△EC =BF ;(2)如图,设AB 交CE 于D根据(1),△ABF△△AEC,△△AEC=△ABF,△AE△AB,△△BAE=90°,△△AEC+△ADE=90°,△△ADE=△BDM(对顶角相等),△△ABF+△BDM=90°,在△BDM中,△BMD=180°-△ABF-△BDM=180°-90°=90°,所以EC△BF.【点睛】本题考查等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用“8字型”证明角相等.20.(1)270(2)220∠+∠=︒+∠(3)12180A(4)122A∠+∠=∠,理由见解析【解析】【分析】(1)利用三角形的外角定理及直角三角形的性质求解;(2)利用三角形的外角等于与它不相邻的两个内角和求解;(3)根据(1)、(2)中思路即可求解;∠=︒-∠, (4)根据折叠对应角相等,得到AFE PFE∠=∠,AEF PEF∠=∠,进而求出11802AFE∠+∠=︒-∠即可求解.AFE AEF A∠=︒-∠,最后利用18021802AEF(1)解:如下图所示:在△AEF中,由外角性质可知:△1=△A+△EF A=90°+△EF A,△2=△A+△AEF=90°+△AEF,△△1+△2=(90°+△EF A)+( 90°+△AEF)=180°+△EF A+△AEF,△△ABC为直角三角形,△△A=90°,△EF A+△AEF=180°-△A=90°,△△1+△2=180°+90°=270°.(2)解:如下图所示:在△AEF中,由外角性质可知:△1=△A+△EF A,△2=△A+△AEF,△△1+△2=(△A+△EF A)+( △A+△AEF)=(△A +△EF A+△AEF)+∠A=180°+40°=220°.(3)解:由(1)、(2)中思路,由三角形外角性质可知:△1=△A +△EF A ,△2=△A +△AEF ,△△1+△2=(△A +△EF A )+( △A +△AEF )=(△A +△EF A +△AEF)+∠A =180°+∠A ,△12∠+∠与A ∠的关系是:△1+△2=180°+∠A .(4)解:12∠+∠与A ∠的关系为:122A ∠+∠=∠,理由如下:如图,△EFP △是由EFA △折叠得到的,△AFE PFE ∠=∠,AEF PEF ∠=∠,△11802AFE ∠=︒-∠,21802AEF ∠=︒-∠,△()12(1802)(1802)3602AFE AEF AFE AEF ∠+∠=︒-∠+︒-∠=︒-∠+∠,又△180AFE AEF A ∠+∠=︒-∠,△()1236021802A A ∠+∠=︒-︒-∠=∠,△12∠+∠与A ∠的关系122A ∠+∠=∠.【点睛】主要考查了折叠的性质及三角形的内角和外角之间的关系:三角形的外角等于与它不相邻的两个内角和、三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.21.(1)BD ﹣EC(2)BD =DE ﹣CE .见解析(3)当B ,C 在AE 的同侧时,BD =DE ﹣CE ;当B ,C 在AE 的异侧时,BD =DE +CE .【解析】【分析】(1)通过互余关系可得△ABD =△CAE ,进而证明△ABD △△ACE (AAS ),即可求得BD =AE ,AD =EC ,进而即可求得关系式;(2)方法同(1)证明△ABD △△CAE (AAS ),进而得出结论;(3)综合(1)(2)结论,分当B ,C 在AE 的同侧或异侧时,写出结论即可.(1)结论:DE =BD ﹣EC .理由:如图1中,△BD △AE ,CE △AE ,△△ADB =△CEA =90°,△△ABD +△BAD =90°,又△△BAC =90°,△△EAC +△BAD =90°,△△ABD =△CAE ,在△ABD 与△ACE 中,ADB CEA ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩, △△BAD △△ACE (AAS ),△BD =AE ,AD =EC ,△BD =DE +CE ,即DE =BD ﹣EC .故答案为:BD ﹣EC ;(2)结论:BD =DE ﹣CE .理由:如图2中,△BD △AE ,CE △AE ,△△ADB =△CEA =90°,△△ABD +△BAD =90°,又△△BAC =90°,△△EAC +△BAD =90°,△△ABD =△CAE ,在△ABD 与△CAE 中,ADB CEA ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩, △△ABD △△CAE (AAS ),△BD =AE ,AD =EC ,△BD =DE ﹣CE ;(3)归纳:由(1)(2)可知:当B ,C 在AE 的同侧时,BD =DE ﹣CE ;当B ,C 在AE 的异侧时,BD =DE +CE .【点睛】本题考查了全等三角形的性质与判定,掌握全等三角形的性质与判定是解题的关键. 22.(1)(12-3t )(2)△CAP △△PBQ ,理由见解析(3)满足条件的点Q 的速度为3或92cm /s . 【解析】【分析】(1)求出AP ,再根据题意写出PB 的值即可;(2)求出AP ,PB ,BQ 的值,根据SAS 证明△CAP △△PBQ (SAS )即可;(3)分两种情形分别求解:△由(1)可知,Q 的速度为3cm /s 时,△ACP △△BPQ ,这种情形符合题意.△当P A =PB ,AC =BQ 时,△APC △△BPQ (SAS ),首先确定运动时间,再求出点Q 的运动速度即可.(1)解:由题意:P A =3t (cm ),△AB =12cm ,△PB =AB -AP =12-3t (cm ),故答案为:(12-3t );(2)解:△CAP△△PBQ,理由如下:由题意:t=1(s)时,P A=BQ=3(cm),△AB=12cm,△PB=AB-AP=12-3=9(cm),△AC=9cm,△AC=BP,△△CAP=△PBQ=90°,P A=BQ,△△CAP△△PBQ(SAS);(3)解:△由(2)可知,Q的速度为3cm/s时,△ACP△△BPQ,这种情形符合题意.△当P A=PB,AC=BQ时,△APC△△BPQ(SAS),△t=63=2(s),△点Q的运动速度为92cm/s.△满足条件的点Q的速度为3或92cm/s.【点睛】本题考查的是全等三角形的判定与性质,掌握全等三角形的判定定理和性质定理、注意分类讨论思想的灵活运用是解题的关键.。
北师大版七年级数学下册第4单元《三角形》单元测试题(含答案)

北师大版七年级数学下册第4单元《三角形》单元测试题(含答案)一.选择题1.下列各组中的两个图形属于全等图形的是()A.B.C.D.2.画△ABC的边BC上的高,正确的是()A.B.C.D.3.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能()A.都是锐角三角形B.都是直角三角形C.都是钝角三角形D.是一个锐角三角形和一个钝角三角形4.如图,已知在△ABC中,∠A=90°,∠1+∠2的度数是()A.180°B.270°C.360°D.无法确定5.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是()A.带①②去B.带②③去C.带③④去D.带②④去6.如图,点A,D在线段BC的同一侧,AC与BD相交于点E,连接AB,CD,已知∠1=∠2,现添加以下哪个条件仍不能判定△ABC≌△DCB的是()A.∠A=∠D B.AC=DB C.∠ABC=∠DCB D.AB=DC7.如图,在△ABC中,∠A=45°,△ABC的外角∠CBD=75°,则∠C的度数是()A.30°B.45°C.60°D.75°8.如图,已知AB=AC,AD是△ABC的高,下列结论不一定正确的是()A.∠B=60°B.∠B=∠C C.∠BAD=∠CAD D.BD=CD二.填空题9.如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是.10.如图,点A,F,C,D在同一条直线上,BC∥EF,AC=FD,请你添加一个条件,使得△ABC≌△DEF.11.如图所示,要测量河两岸相对的两点A、B的距离,在AB的垂线段BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为20米,则河宽AB长为米.12.在△ABC中,∠A:∠B:∠C=4:5:9,若按角分类,△ABC是三角形.13.如图,∠1=115°,∠2=50°,那么∠3=.14.如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是.三.解答题15.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).16.如图,已知△EFG,利用尺规作FG边上的高EH.(不写作法,保留作图痕迹)17.某中学八年级同学到野外开展数学综合实践活动,在营地看到一池塘,同学们想知道池塘两端的距离.某同学设计了如下测量方案:先取一个可直接到达池塘的两端的点A,B 的点E,连接AE,BE,分别延长AE至点D,BE至点C,使得ED=AE,EC=BE.再测出CD的长度即可知道AB之间的距离.他的方案可行吗?请说明理由.18.已知:如图,在△ABC中,∠DAE=10°,AD⊥BC于点D,AE平分∠BAC,∠B=60°,求∠C的度数.19.如图,在四边形ABCD中,∠B=∠D=90°,点B,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.20.如图,在△ABC中,CD是AB边上的高,AE平分∠BAC,AE、CD相交于点F,若∠BAC=∠DCB.求证:∠CFE=∠CEF.21.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD =BE.(1)求证:△ABD≌△ECB.(2)若∠BDC=70°.求∠ADB的度数.22.直线MN与直线PQ垂直相交于点O,点A在射线OP上运动(点A不与点O重合),点B在射线OM上运动(点B不与点O重合).(1)如图1,MN⊥PQ,若∠BAO=30°,∠BAO与∠ABO的角平分线相交于点E,∠AEB的度数为,(2)如图2,MN⊥PQ,∠BAP与∠ABM的角平分线相交于点E,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;(3)如图3,若∠MOQ<90°,∠BAO与∠BOQ的角平分线相交于点E,延长BA至点G,∠OAG的角平分线与射线EO相交于点F,点A、B在运动的过程中,试探索∠F与∠ABO之间的等量关系,并证明你的结论.参考答案一.选择题1.解:A、两个图形不能完全重合,故本选项错误;B、两个图形能够完全重合,故本选项正确;C、两个图形不能完全重合,故本选项错误;D、两个图形不能完全重合,故本选项错误;故选:B.2.解:A.此图形中AD是BC边上的高,符合题意;B.此图形中CD不是BC边上的高,不符合题意;C.此图形中CD是AB边上的高,不符合题意;D.此图形中AD是AB边上的高,不符合题意;故选:A.3.解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.如图,锐角三角形沿虚线剪开即可得到一个锐角三角形和一个钝角三角形.因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.故选:A.4.解:在△ABC中,∠A=90°,所以∠ACB+∠ABC=90°,又因为∠1+∠ACB=180°,∠2+∠ABC=180°,所以∠1+∠2=270°,故选:B.5.解:A、带①②去,符合ASA判定,选项符合题意;B、带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;C、带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;D、带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;故选:A.6.解:∵BC=CB,∠1=∠2,A、如添加∠A=∠D,利用AAS即可证明△ABC≌△DCB;B、如添加AC=BD,利用SAS即可证明△ABC≌△DCB.C、如添加∠ABC=∠DCB,利用ASA即可证明△ABC≌△DCB;D、如添加AB=DC,因为SSA,不能证明△ABC≌△DCB,所以此选项不能作为添加的条件;故选:D.7.解:∵∠A=45°,△ABC的外角∠CBD=75°,∴∠C=∠CBD﹣∠A=75°﹣45°=30°,故选:A.8.解:∵AB=AC,∴∠B=∠C,∵AD是△ABC的高,∴AD平分∠BAC,BC=2BD=2CD,∴∠BAD=∠CAD,BD=CD,∴B、C、D都是正确的,故选:A.二.填空题9.解:给凳子加了两根木条之后形成了三角形,所以“这样凳子就比较牢固了”的数学原理是:三角形的稳定性,故答案为:三角形的稳定性.10.解:∵BC∥EF,∴∠BCA=∠EFD,若添加BC=EF,且AC=FD,由“SAS”可证△ABC≌△DEF;若添加∠B=∠E,且AC=FD,由“AAS”可证△ABC≌△DEF;若添加∠A=∠D,且AC=FD,由“ASA”可证△ABC≌△DEF;故答案为:BC=EF或∠B=∠E或∠A=∠D(答案不唯一).11.解:在△ABC和△EDC中,,∴△ABC≌△EDC(ASA),∴AB=DE=20米.故答案为:20.12.解:∵∠A:∠B:∠C=4:5:9,且∠A+∠B+∠C=180°,∴∠C=180°×=90°,∴△ABC是直角三角形,故答案为:直角.13.解:∵∠1=115°,∠2=50°,∴∠3=∠1+∠2=165°,故答案为:165°.14.解:连接BE,∵∠C=90°,DE⊥AB于D,∴∠C=∠BDE=90°,在Rt△BCE与Rt△BDE中,,∴Rt△BCE≌Rt△BDE(HL),∴DE=CE,∵AB=10cm,BC=8cm,AC=6cm,∴△ADE的周长=DE+AE+AD=CE+AE+AB﹣BD=AC+AB﹣BC=6+10﹣8=8(cm),故答案为:8cm.三.解答题15.解:如图所示:.16.解:如图,EH为所作.17.解:在△AEB和△DEC中,,∴△AEB≌△DEC(SAS);∴AB=CD.18.解:∵AD⊥BC,∠B=60°,∴在△ABD中,∠BAD=90°﹣60°=30°,又∵∠DAE=10°,∴∠BAE=∠BAD+∠DAE=30°+10°=40°,又∵AE平分∠BAC,∴∠BAC=2∠BAE=80°,∴在△ABC中,∠C=180°﹣∠BAC﹣∠B=180°﹣80°﹣60°=40°.答:∠C的度数是40°.19.证明:如图,连接AC,在△ACE和△ACF中,,∴△ACE≌△ACF(SSS),∴∠EAC=∠F AC,在△ACB和△ACD中,,∴△ACB≌△ACD(AAS),∴CB=CD.20.证明:在△ABC中,CD是高,∠BAC=∠DCB,∴∠CDA=90°,∠BAC+∠ACD=90°,∴∠DCB+∠ACD=90°,∴∠ACB=90°;∵AE是角平分线,∴∠CAE=∠BAE,∵∠FDA=90°,∠ACE=90°,∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,∴∠AFD=∠CEA,∵∠AFD=∠CFE,∴∠CFE=∠CEA,即∠CFE=∠CEF.21.证明:(1)∵AD∥BC,∴∠ADB=∠CBE,在△ABD和△ECB中,,∴△ABD≌△ECB(AAS);(2)∵△ABD≌△ECB,∴BD=BC,∴∠BDC=∠BCD=70°,∴∠DBC=40°,∴∠ADB=∠CBD=40°.22.解:(1)∵MN⊥PQ,∴∠AOB=90°,∵∠BAO=30°,∴∠ABO=60°,∵AE、BE分别是∠BAO和∠ABO的角平分线,∴∠ABE=∠ABO=30°,∠BAE=∠BAO=15°,∴∠AEB=180°﹣∠ABE﹣∠BAE=135°.故答案为:135°.(2)不会发生变化.∵∠BAP与∠ABM的角平分线相交于点E,∴∠EAB=∠P AB,∠EBA=∠MBA,∵MN⊥PQ,∴∠AOB=90°,∵∠P AB=∠ABO+∠AOB=90°+∠ABO,∠MBA=∠BAO+∠AOB=90°+∠BAO,∴∠EAB+∠EBA=(90°+∠ABO+90°+∠BAO)=90°+(∠ABO+∠BAO),∵∠ABO+∠BAO=90°,∴∠EAB+∠EBA=90°+45°=135°,∴∠AEB=180°﹣135°=45°.(3)∠ABO+∠F=90°.如图:∵∠BAO与∠BOQ的角平分线相交于点E,∴∠1=∠BAO,∠2=∠BOQ,由外角的性质可得:∠ABO=∠BOQ﹣∠BAO,∠E=∠2﹣∠1,∴∠E=∠ABO.∵AE平分∠BAO,AF平分∠GAO,∴∠EAF=90°,∴∠E+∠F=90°,即∠ABO+∠F=90°。
北师大版七年级数学下学期《第4章三角形》单元练习题含答案
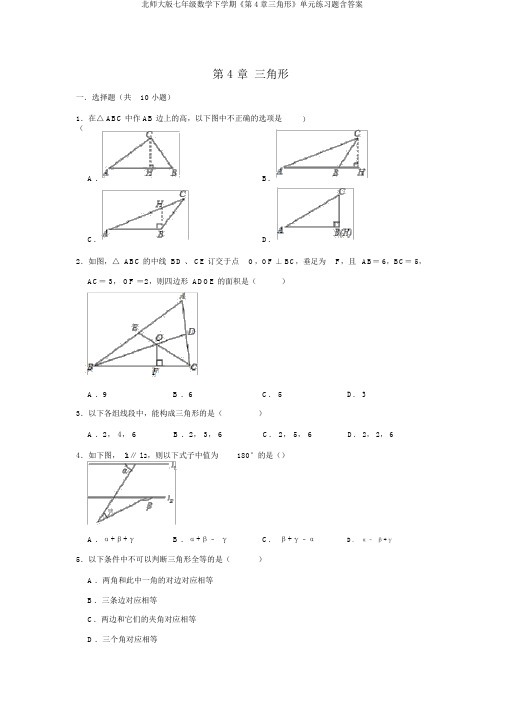
第 4 章三角形一.选择题(共10 小题)1.在△ ABC 中作 AB 边上的高,以下图中不正确的选项是)(A .B.C.D.F,且AB= 6,BC= 5,2.如图,△ ABC 的中线 BD 、 CE 订交于点O,OF ⊥ BC,垂足为AC= 3, OF =2,则四边形ADOE 的面积是()A .9B .6C. 5D. 33.以下各组线段中,能构成三角形的是()A .2, 4, 6B .2, 3, 6C. 2, 5, 6D. 2, 2, 64.如下图, l1∥ l 2,则以下式子中值为180°的是()A .α+β+γB .α+β﹣γC.β+γ﹣αD.α﹣β+γ5.以下条件中不可以判断三角形全等的是()A.两角和此中一角的对边对应相等B.三条边对应相等C.两边和它们的夹角对应相等D.三个角对应相等6.如图, C 为线段 AE 上一动点(不与点A、 E 重合),在 AE 同侧分别作正三角形ABC 和正三角形 CDE ,AD 与 BE 交于点 O,AD 与 BC 交于点 P,BE 与 CD 交于点 Q,连结 PQ,以下七个结论:①AD = BE;② PQ∥AE ;③ AP =BQ;④ DE= DP;⑤∠AOB= 60°;⑥ △ PCQ 是等边三角形;⑦ 点C在∠ AOE的均分线上,此中正确的有()A .3 个B .4 个C. 5 个D. 6 个7.如图,已知点A、D、C、F 在同向来线上,AB= DE ,AD=CF ,且∠ B=∠ E= 90°,判定△ ABC≌△ DEF 的依照是()A .SASB .ASA C. AAS D. HL8.如图,在△ OAB 和△ OCD 中, OA=OB,OC= OD ,OA> OC,∠ AOB=∠ COD =40°,连结 AC, BD 交于点 M,连结 OM.以下结论:① AC= BD ;②∠ AMB= 40°;③ OM 均分∠ BOC ;④ MO 均分∠ BMC .此中正确的个数为()A .4B .3C. 2D. 19.如图, AB ∥ FC ,E 是 DF 的中点,若AB= 20, CF= 12,则 BD 等于()A .12B .8C. 6D. 1010.如图,工人师傅常用“卡钳”这类工具测定工件内槽的宽.卡钳由两根钢条AA′、BB′构成, O 为 AA′、 BB′的中点.只需量出A′B′的长度,由三角形全等就能够知道工件内槽 AB 的长度.那么判断△OAB≌△ OA′ B′的原因是()A .SASB .ASA C. SSS D. AAS二.填空题(共 5 小题)11.一个三角形的三边长分别为x,4, 6,那么 x 的取值范围.12.如图,自行车的主框架采纳了三角形构造,这样设计的依照是三角形拥有.13.如图,在△ ABC 中, AD⊥ BC,AE 均分∠ BAC,若∠ BAE= 30°,∠ CAD = 20°,则∠B=.14.如图, AB= 6cm, AC= BD = 4cm.∠ CAB=∠ DBA,点 P 在线段 AB 上以 2cm/s 的速度由点 A 向点 B 运动,同时,点Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为t ( s).设点 Q 的运动速度为xcm/s,若使得△ ACP 与△ BPQ 全等,则 x 的值为.15.如图,已知A D 和 BC 订交于点O 且 AD =BC,分别连结AC,AB,BD,已知 AC= BD,∠ ABC=20°,则∠ AOB 的度数为.三.解答题(共 5 小题)16.如图,∠ BAD =∠ CAE= 90°, AB= AD , AE= AC, AF⊥ CB,垂足为F.(1)求证:△ ABC≌△ ADE;(2)求∠ FAE 的度数;(3)求证: CD =2BF+DE .17.把下边的推理过程增补完好,并在括号内注明原因.如图,点B、D 在线段 AE 上, BC∥EF, AD = BE, BC=EF ,试说明:( 1)∠ C=∠ F;( 2) AC∥DF .解:( 1)∵ AD= BE(已知)∴ AD+DB =DB +BE()即 AB= DE∵ BC∥ EF(已知)∴∠ ABC=∠()又∵ BC= EF(已知)∴△ ABC≌△ DEF ()∴∠ C=∠ F,∠ A=∠ FDE ()∴ AC∥ DF ()18.已知:如图,点A, F,C,D 在同向来线上,AF =DC,AB∥ DE ,AB= DE ,求证: BC∥EF.19.如图,在△A BC 中,∠ ACB= 45°,过点A 作 AD ⊥ BC 于点 D ,点 E 为 AD 上一点,且ED = BD.(1)求证:△ ABD ≌△ CED;(2)若 CE 为∠ ACD 的角均分线,求∠ BAC 的度数.20.如图,△ ABC 和△ EBD 中,∠ ABC =∠ DBE = 90°, AB= CB,BE= BD ,连结 AE,CD , AE 与 CD 交于点 M, AE 与 BC 交于点 N.(1)求证: AE= CD;(2)求证: AE⊥ CD;( 3)连结 BM ,有以下两个结论:① BM均分∠ CBE;② MB均分∠ AMD.此中正确的有(请写序号,少选、错选均不得分).参照答案一.选择题(共10 小题)1.C.2.C.3.C.4. B.5.D.6.D.7.D.8.:B.9.B.10.A.二.填空题(共 5 小题)11.:2< x< 1012.稳固性.13.50°.14.2 或.15.140°三.解答题(共 5 小题)16.证明:( 1)∵∠ BAD =∠ CAE= 90°,∴∠ BAC+∠ CAD =90°,∠ CAD +∠DAE = 90°,∴∠ BAC=∠ DAE ,在△ BAC 和△ DAE 中,,∴△ BAC≌△ DAE (SAS);(2)∵∠ CAE= 90°, AC= AE,∴∠ E= 45°,由( 1)知△ BAC≌△ DAE ,∴∠ BCA=∠ E= 45°,∵AF⊥ BC,∴∠CFA=90°,∴∠ CAF= 45°,∴∠ FAE=∠ FAC+∠CAE= 45°+90 °= 135°;(3)延伸 BF 到 G,使得 FG= FB,∵ AF⊥ BG,∴∠ AFG=∠ AFB = 90°,在△ AFB 和△ AFG 中,,∴△ AFB ≌△ AFG ( SAS),∴AB=AG,∠ABF =∠G,∵△ BAC≌△ DAE ,∴AB= AD ,∠ CBA=∠ EDA, CB= ED,∴AG= AD,∠ ABF =∠ CDA,∴∠ G=∠ CDA ,∵∠ GCA=∠ DCA= 45°,在△ CGA 和△ CDA 中,,∴△ CGA≌△ CDA( AAS),∴CG= CD,∵CG=CB+BF+FG=CB+2BF =DE+2BF ,∴ CD = 2BF +DE .17.解:( 1)∵ AD = BE(已知)∴AD+DB =DB +BE(等式的性质)即 AB= DE∵ BC∥ EF(已知)∴∠ ABC=∠ E(两直线平行,同位角相等)又∵ BC= EF(已知)∴△ ABC≌△ DEF ( SAS)∴∠ C=∠ F,∠ A=∠ FDE (全等三角形的对应角相等);故答案为:等式的性质; E;两直线平行,同位角相等; SAS;全等三角形的对应角相等;( 2)∵∠ A=∠ FDE ,∴ AC∥ DF (同位角相等,两直线平行).故答案为:同位角相等,两直线平行.18.证明:∵ AB∥ DE,∴∠ A=∠ D,∵AF= CD ,∴ AC= DF ,在△ ABC 和△ DEF 中,∴△ ABC≌△ DEF (SAS),∴∠ BCA=∠ EFD ,∴BC∥ EF.19.( 1)证明:∵ AD⊥BC,∠ ACB= 45°,∴∠ ADB=∠ CDE= 90°,△ ADC 是等腰直角三角形,∴AD= CD,∠ CAD =∠ ACD = 45°,在△ ABD 与△ CED 中,,∴△ ABD≌△ CED( SAS);(2)解:∵ CE 为∠ ACD 的角均分线,∴∠ ECD=∠ ACD = 22.5°,由( 1)得:△ ABD ≌△ CED,∴∠ BAD=∠ ECD= 22.5°,∴∠ BAC=∠ BAD +∠ CAD =22.5° +45°= 67.5°.20.( 1)证明:∵∠ ABC=∠ DBE,∴∠ ABC+∠ CBE=∠ DBE +∠ CBE,即∠ ABE=∠ CBD ,在△ ABE 和△ CBD 中,,∴△ ABE≌△ CBD ,∴AE= CD .(2)∵△ ABE≌△ CBD ,∴∠ BAE=∠ BCD ,∵∠ NMC = 180°﹣∠ BCD ﹣∠ CNM ,∠ ABC= 180°﹣∠ BAE﹣∠ ANB,又∠ CNM =∠ ABC,∵∠ABC=90°,∴∠ NMC = 90°,∴ AE⊥ CD .(3)结论:②原因:作BK⊥ AE 于 K, BJ⊥ CD 于 J.∵△ ABE≌△ CBD ,∴AE= CD , S△ABE= S△CDB,∴?AE?BK = ?CD?BJ,∴BK= BJ,∵作 BK⊥AE 于 K , BJ⊥ CD 于 J,∴BM 均分∠ AMD .不如设①建立,则△ ABM ≌△ DBM ,则 AB= BD ,明显可不可以,故① 错误.故答案为② .。
北师大版七年级数学下册《第4章 三角形》 单元同步练习 包含答案

第4章三角形一.选择题(共10小题)1.下列长度的三条线段,能组成三角形的是()A.4cm,5cm,9cm B.8cm,8cm,15cmC.5cm,5cm,10cm D.6cm,7cm,14cm2.一副三角板有两个三角形,如图叠放在一起,则∠α的度数是()A.120°B.135°C.150°D.165°3.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是()A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC4.如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP,交CD 于点M.若∠CMA=25°,则∠C的度数为()A.100°B.110°C.120°D.130°5.如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为()A.40°B.45°C.50°D.55°6.如图所示,△ABC中AC边上的高线是()A.线段DA B.线段BA C.线段BC D.线段BD7.如图,点O是△ABC的重心,连接BO、CO并延长分别交AC、AB于点E、点F,则下列说法中一定正确的是()A.∠ABE=∠CBE B.BO=CO C.∠AEB=90°D.AF=BF8.如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=2cm2,则S△ABC为()A.4 cm2B.6 cm2C.8 cm2D.10 cm29.如图,在△ABC中,∠ABC=45°,AC=9cm,F是高AD和BE的交点,则BF的长是()A.4cm B.6cm C.8cm D.9cm10.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是()A.0.5B.1C.1.5D.2二.填空题(共5小题)11.如图,已知△ABC为等边三角形,点D,E分别在边BC,AB上,且CD=BE,若CE =5cm,则AD的长度为cm.12.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD 的周长是.13.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E 处.若∠A=22°,则∠ADE=°.14.一副直角三角板如上图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,则∠DBC=°.15.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=.三.解答题(共5小题)16.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.17.已知:如图,E,F,为AC上两点,AD∥BC,∠1=∠2,AE=CF,求证:△ADF≌△CBE.18.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB ∥DE,∠A=∠D,测得AB=DE.(1)求证:△ABC≌△DEF;(2)若BE=10m,BF=3m,求FC的长度.19.探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC 边上,且∠ADE=∠AED,连接DE.(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC(点B、C除外)边上运动时,试猜想∠BAD与∠CDE的数量关系,并说明理由.(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试探究∠BAD与∠CDE的数量关系.20.如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB 的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.(1)直接写出:①BD=厘米;②BP=厘米;③CP=厘米;④CQ=厘米;(可用含t、a的代数式表示)(2)若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,试求a、t的值.参考答案一.选择题(共10小题)1.B.2.D.3.B.4.D.5.A.6.D.7.D.8.C.9.D.10.B.二.填空题(共5小题)11.5.12.9.13.46.14.15.15.50°.三.解答题(共5小题)16.解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,理由如下:∵AB=AC,AE=AB,AF=AC,∴AE=AF,在△AOE与△AOF中,,∴△AOE≌△AOF(SSS),∴∠BAD=∠CAD.17.证明:∵AD∥BC,∴∠A=∠C,∵AE=CF∴AE+EF=CF+EF即:AF=CE在△ADF和△CBE中∴△ADF≌△CBE(ASA).18.(1)证明:∵AB∥DE,∴∠ABC=∠DEF,在△ABC与△DEF中,∴△ABC≌△DEF;(2)∵△ABC≌△DEF,∴BC=EF,∴BF+FC=EC+FC,∴BF=EC,∵BE=10m,BF=3m,∴FC=10﹣3﹣3=4m.19.解:(1)∵∠ADC是△ABD的外角,∴∠ADC=∠BAD+∠B=105°,∠DAE=∠BAC﹣∠BAD=30°,∴∠ADE=∠AED=75°,∴∠CDE=105°﹣75°=30°;(2)∠BAD=2∠CDE,理由如下:设∠BAD=x,∴∠ADC=∠BAD+∠B=45°+x,∠DAE=∠BAC﹣∠BAD=90°﹣x,∴∠ADE=∠AED=,∴∠CDE=45°+x﹣=x,∴∠BAD=2∠CDE;(3)设∠BAD=x,∴∠ADC=∠BAD+∠B=∠B+x,∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,∴∠ADE=∠AED=∠C+x,∴∠CDE=∠B+x﹣(∠C+x)=x,∴∠BAD=2∠CDE.20.解(1)由题意得:①BD=12,②BP=4t;③CP=16﹣4t,④CQ=at,(2)∵BP=4t,BD=12,CP=16﹣4t,CQ=at,∵∠B=∠C,∴分两种情况:①若△DBP≌△QCP,则,∴,∴,②若△DBP≌△PCQ,则,∴,∴.,综上所述,a的值为6、t的值为2或a的值为4、t的值为1.故答案为:12,4t,(16﹣4t),at.。
北师大版七年级数学下册第四章单元测试题(含答案)

第四章三角形一.选择题(共10小题,每小题4分,满分40分.每小题只有一个正确的选项.)1.在下列图形中,最具有稳定性的是()2.如面是个网球场地,在A、B、C、D、E、F六个图形中,其中全等图形有()A.1对B.2对C.3对D.4对第2题图第3题图第4题图3.在课堂上,老师把教学用的两块三角板叠放在一起,得到如图所示的图形,其中三角形有()A.2个B.3个C.5个D.6个4.已知:∠AOB.作法:(1)作射线O'A';(2)以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D;(3)以点O'为圆心,以OC长为半径作弧,交O’A'于C';(4)以点C'为圆心,以CD长为半径作弧,交前弧于D';(5)经过点D'作射线O'B'.∠A'D'B'就是所求的角.这个作图是() A.平分已知角 B.作一个角等于已知角C.作一个三角形等于已知三角形D.作一个角的平分线5.下列各三角形中,能正确画出AC边长的高的是()A B C D6.下列各组线段的长度,能构成三角形的是()A.3、4、8B.5、6、10C.5、6、11D.2、3、6 7.若一个三角形三个内角的度数之比为2∶3∶7,则此三角形一定是()A.钝角三角形B.直角三角形C.锐角三角形D.等腰三角形8.如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依此规律,则第n个图形中有全等三角形的对数是()A.n B.2n﹣1C.(1)2n nD.3(n+1)9.如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,关于∠A,∠1与∠2的数量关系,下列结论正确的是()A.∠1=∠2+∠A B.∠1=2∠A+∠2C.∠1=2∠2+2∠A D.2∠1=∠2+∠A第9题图第12题图第13题图10.若三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|的结果为()A.2a-10B.10-2a C.4D.-4二.填空题(每空4分,共24分)11.已知在直角△ABC中,有一个锐角等于50°,则另一个锐角的度数是°.12.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有性.13.如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,若∠BOC=132°,则∠A=°.14.一个缺角的三角形ABC残片如图,若量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C=°.第14题图第15题图第16题图15.如图,AD是△ABC的角平分线,BE是△ABC的高,若∠BAC=40°,则∠AFE=_°.16.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADC的面积为S1,△ACE的面积为S2,若S△ABC=6,则S1﹣S2的值为.三.解答题(满分86分)17.在我市19年春季田径运动会上,某校七年级(1)班的全体同学荣幸成为拉拉队队员,为了在明天的比赛中给同学加油助威,提前每人制作了一面同一规格的直角三角形彩旗.队员小明放学回家后,发现自己的彩旗破损了一角,他想用如下图所示的长方形彩纸重新制作一面彩旗.请你帮助小明,用直尺与圆规在彩纸上作出一个与破损前完全一样的三角形(保留作图痕迹,不写作法).18.如图,在△ABC 中,AE 是角平分线,AD 是高,∠BAC =80°,∠EAD =10°,求∠B 的度数.19.如图,A ,B 两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B 出发沿河岸画一条射线BF ,在BF 上截取BC =CD ,过D 作DE ∥AB ,使E ,C ,A 在同一条直线上,则DE 的长就等于A ,B 之间的距离,请你说明道理.第17题图第18题图第19题图20.已知,a ,b ,c 为△ABC 的三边长,b ,c 满足(b -2)2+|c -3|=0,且a 为方程|a -4|=2的解,求△ABC 的周长,并判断△ABC 的形状.21.如图,在△ABC 中,∠ACB =90°,AE 是角平分线,CD 是高,AE ,CD 相交于点F ,试说明:∠CEF =∠CFE .22.如图,在△ABC 和△DAE 中,D 是AC 边上一点,AD =AB ,DE ∥AB ,DE =AC .求证:AE =BC .23.如图,有一块直角三角板XYZ 放置在△ABC 中,三角板的两条直角边XY 和XZ 恰好分别经过点B 和点C .(1)若∠A =30°,则∠ABX +∠ACX 的大小是多少?(2)若改变三角板的位置,但仍使点B ,C 分别在三角板的边XY 和第21题图第22题图边XZ 上,此时∠ABX +∠ACX 的大小有变化吗?请说明你的理由.24.如图1,已知线段AB 、CD 相交于点O ,连接AC 、BD ,则我们把形如这样的图形称为“8字型”.(1)试说明:∠A +∠C =∠B +D ;(2)如图2,若∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,且与CD 、AB 分别相交于点M 、N .①以线段AC 为边的“8字型”有个,以点O 为交点的“8字型”有个;②若∠B =100°,∠C =120°,求∠P 的度数;③若角平分线中角的关系改为“∠CAP =∠CAB ,∠CDP =∠CDB ”,试探究∠P 与∠B 、∠C之间存在的数量关系,并证明理由.第23题图第24题图25.“如图1,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm,求BE的长.”(1)请你也独立完成这道题;(2)待同学们完成这道题后,张老师又出示了一道题:在课本原题其它条件不变的前提下,将CE所在直线旋转到△ABC的外部(如图2),请你猜想AD,DE,BE三者之间的数量关系,直接写出结论,不需说理.(3)如图3,将(1)中的条件改为:在△ABC中,AC=BC,D,C,E三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=α,其中α为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由.第25题图参考答案一.选择题(共10小题,每小题4分,满分40分.每小题只有一个正确的选项,请将正确选项填入相应的表格内)题号12345678910答案D C C B D B A C B C二、填空题(共6小题,每小题4分,满分24分)11.4012.稳定13.8414.4515.7016.1.三.解答题(满分86分)17.解:18.解:∵AD是高,∴∠ADC=90°,∵AE是角平分线,∠BAC=80°,∴∠CAE=BAC=40°,∵∠EAD=10°,∴∠CAD=30°,∴∠C=60°,∴∠B=180°﹣∠BAC﹣∠C=40°.19.解:∵AB∥DE,∴∠A=∠E或∠ABC=∠EDC,在ΔABC与ΔEDC中,∴ΔABC≌ΔEDC(AAS),∴AB=ED,即测出ED的长后即可知道A,B之间的距离.20.解:∵(b-2)2+|c-3|=0,∴b-2=0,c-3=0,解得b=2,c=3,∵a为方程|a-4|=2的解,解得a=6或2,∵a,b,c为△ABC的三边长,b+c<6,∴a=6不合题意,舍去,∴a=2,∴△ABC的周长为:2+2+3=7.∵a=b,∴△ABC是等腰三角形.21.解:∵∠ACB=90°,CD是高,∴∠ACD+∠CAB=90°,∠B+∠CAB=90°,∴∠ACD=∠B.∵AE是角平分线,∴∠CAE=∠BAE.∵∠CEF=∠BAE+∠B,∠CFE=∠CAE+∠ACD,∴∠CEF=∠CFE.22.证明:∵DE∥AB,∴∠ADE=∠BAC.在△ADE和△BAC中,=BA,ADE=∠BAC,=AC,∴△ADE≌△BAC(SAS).∴AE=BC.23.解:(1)∵∠A=30°,∴∠ABC+∠ACB=180°-∠A=180°-30°=150°,∵∠YXZ=90°,∴∠XBC+∠XCB=90°,∴∠ABX+∠ACX=150°-90°=60°.(2)∠ABX+∠ACX的大小没有变化,理由:∵∠ABC+∠ACB=180°-∠A,∠YXZ=90°,∴∠XBC+∠XCB=90°,∴∠ABX+∠ACX=180°-∠A-90°=90°-∠A,即∠ABX+∠ACX的大小没有变化.24.(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;(2)解:①3;4;②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,∵AP、DP分别平分∠CAB和∠BDC,∴∠BAP=∠CAP,∠CDP=∠BDP,∴2∠P=∠B+∠C,∵∠B=100°,∠C=120°,∴∠P=(∠B+∠C)=(100°+120°)=110°;③3∠P=∠B+2∠C,其理由是:∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠CAB,∠BDP=∠CDB,以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).∴2(∠C﹣∠P)=∠P﹣∠B,∴3∠P=∠B+2∠C.25.解:(1)∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.∵∠BCE+∠ACD=90°,∴∠EBC=∠DCA.∵AC=BC,∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5.∵DC=CE﹣DE,DE=1.7cm,∴DC=2.5﹣1.7=0.8cm,∴BE=0.8cm;(2)AD+BE=DE,证明:∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.∵∠BCE+∠ACD=90°,∴∠EBC=∠DCA.∵AC=BC,∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD,∴DE=CE+DE=AD+BE;(3)、(2)中的猜想还成立,证明:∵∠BCE+∠ACB+∠ACD=180°,∠DAC+∠ACB+∠ACD=180°,∠ADC=∠BCA,∴∠BCE=∠CAD,∵AC=BC,∴△CEB≌△ADC,∴BE=CD,EC=AD,∴DE=EC+CD=AD+BE.。
北师大版数学七年级下册数学第4章《三角形》单元测试题(含答案)

北师大版2019-2020学年七年级下册第4章《三角形》单元测试题(满分120分)姓名:___________班级:___________成绩:___________一.选择题(共10小题,满分30分)1.以下列各组线段长为边,不能组成三角形的是()A.8cm,7cm,13cm B.6cm,6cm,12cmC.5cm,5cm,2cm D.10cm,15cm,17cm2.下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是()A.B.C.D.3.若三角形三边长分别为2,x,3,且x为正整数,则这样的三角形个数为()A.2 B.3 C.4 D.54.如图,已知△ABC,下面甲、乙、丙、丁四个三角形中,与△ABC全等的是()A.甲B.乙C.丙D.丁5.如图,若AB=AC,则添加下列一个条件后,仍无法判定△ABE≌△ACD的是()A.∠B=∠C B.AE=AD C.BE=CD D.∠AEB=ADC 6.若线段AD、AE分别是△ABC的BC边上的中线和高线,则()A.AD≥AE B.AD>AE C.AD≤AE D.AD<AE7.如图,在△ABC中,CD平分∠ACB,DE∥AB.已知∠A=74°,∠B=46°,则∠BDC的度数为()A.104°B.106°C.134°D.136°8.如图,在△P AB中,∠A=∠B,M,N,K分别是P A,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为()A.44°B.66°C.88°D.92°9.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD 于点G,交BE于点H,下面说法正确的是()①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠F AG=2∠ACF;④BH=CH.A.①②③④B.①②③C.②④D.①③10.如图,有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ改变位置,但始终满足经过B、C两点.如果△ABC中∠A=52°,则∠ABX+∠ACX=()A.38°B.48°C.28°D.58°二.填空题(共8小题,满分24分)11.在△ABC中,∠A=50°,若∠B比∠A的2倍小30°,则△ABC是三角形.12.如图,已知AB=DC,∠A=∠D,则补充条件可使△ACE≌△DBF(填写你认为合理的一个条件).13.如图,在△ABC中,D在AC上,连结BD,且∠ABC=∠C=∠BDC,∠A=∠ABD,则∠A的度数为.14.如图,在△ABC中,∠C=78°,沿图中虚线截去∠C,则∠1+∠2.15.在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC,则∠DAE 的度数是.16.如图,已知△ABC的周长为21cm,AB=6cm,BC边上中线AD=5cm,△ABD的周长为15cm,则AC长为.17.已知一个三角形的两边长分别为2cm和3cm,它的第三边长是偶数,且其长度也是整数.则这个三角形的周长是cm.18.AD,BE是△ABC的高,这两条高所在的直线相交于点O,若BO=AC,则∠ABC =.三.解答题(共8小题,满分66分)19.点C是AE的中点,∠A=∠ECD,AB=CD,求证:△ABC≌△CDE.20.如图,AD是△ABC的高,BE平分∠ABC交AD于点E.若∠C=76°,∠BED=64°.求∠BAC的度数.21.已知,如图,在△ABC中,D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,且BE =CF.求证:AB=AC.完成下面的证明过程证明:∵DE⊥AB,DF⊥AC∴∠BED=∠CFD=Rt∠∵D是BC的中点∴BD=又∵BE=CF∴Rt△BDE≌Rt△CDF∴∠B=∠C∴AB=AC22.如图,已知∠ABC,求作:(1)∠ABC的平分线BD(写出作法,并保留作图痕迹);(2)在BD上任取一点P,作直线PQ,使PQ⊥AB(不写作法,保留作图痕迹).23.如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F.(1)如图1,直接写出AB与CE的位置关系;(2)如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB 于K,求证:HK=BK.24.如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.25.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下问题:①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=°.②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.26.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=.(2)设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.参考答案一.选择题(共10小题)1.【解答】解:根据三角形的三边关系,得A、8+7>13,能组成三角形;B、6+6=12,不能组成三角形;C、2+5>5,能组成三角形;D、10+15>17,能组成三角形.故选:B.2.【解答】解:观察图象可知:选项B,D的三角形是钝角三角形,选项C中的三角形是锐角三角形,选项A中的三角形无法判定三角形的类型,故选:A.3.【解答】解:由题意可得,4﹣2<x<4+2,解得2<x<6,∵x为整数,∴x为4、5、3,∴这样的三角形个数为3.故选:B.4.【解答】解:A.△ABC和甲所示三角形根据SA无法判定它们全等,故本选项错误;B.△ABC和乙所示三角形根据SAS可判定它们全等,故本选项正确;C.△ABC和丙所示三角形根据SA无法判定它们全等,故本选项错误;D.△ABC和丁所示三角形根据AA无法判定它们全等,故本选项错误;故选:B.5.【解答】解:A、根据ASA(∠A=∠A,∠C=∠B,AB=AC)能推出△ABE≌△ACD,正确,故本选项错误;B、根据SAS(∠A=∠A,AB=AC,AE=AD)能推出△ABE≌△ACD,正确,故本选项错误;C、两边和一角对应相等的两三角形不一定全等,错误,故本选项正确;D、根据AAS(∠A=∠A,AB=AC,∠AEB=∠ADC)能推出△ABE≌△ACD,正确,故本选项错误;故选:C.6.【解答】解:如图所示:故选:A.7.【解答】解:∵∠A=74°,∠B=46°,∴∠ACB=60°,CD平分∠ACB,∴∠BCD=∠ACD=∠ACB=×60°=30°,∴∠BDC=180°﹣∠B﹣∠BCD=104°,故选:A.8.【解答】解:∵P A=PB,∴∠A=∠B,在△AMK和△BKN中,,∴△AMK≌△BKN,∴∠AMK=∠BKN,∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,∴∠A=∠MKN=44°,∴∠P=180°﹣∠A﹣∠B=92°,故选:D.9.【解答】解:∵BE是中线,∴AE=CE,∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;∵CF是角平分线,∴∠ACF=∠BCF,∵AD为高,∴∠ADC=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,∴∠ABC=∠CAD,∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,∴∠AFG=∠AGF,故②正确;∵AD为高,∴∠ADB=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,∴∠ACB=∠BAD,∵CF是∠ACB的平分线,∴∠ACB=2∠ACF,∴∠BAD=2∠ACF,即∠F AG=2∠ACF,故③正确;根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;故选:B.10.【解答】解:连接AX,∵∠BXC=90°,∴∠AXB+∠AXC=360°﹣∠BXC=270°,∵∠A=52°,∴∠BAX+∠CAX=52°,∵∠ABX+∠BAX+∠AXB=180°,∠ACX+∠CAX+∠AXC=180°,∴∠ABX+∠ACX=360°﹣270°﹣52°=38°,故选:A.二.填空题(共8小题)11.【解答】解:∵∠B比∠A的2倍小30°,∴∠B=2×50°﹣30°=70°,∴∠C=180°﹣∠A﹣∠B=180°﹣50°﹣70°=60°,∴△ABC是锐角三角形,故答案为:锐角.12.【解答】解:添加条件∠ECA=∠FBD,理由如下:∵AB=DC,∴AB+BC=CD+BC,即AC=BD,在△EAC和△FDB中,∴△EAC≌△FDB(ASA).故答案为:∠ECA=∠FBD(答案不唯一).13.【解答】解:设∠A=∠ABD=x,则∠BDC=∠A+∠ABD=2x,∴∠ABC=∠C=∠BDC=2x,∵∠A+∠ABC+∠C=180°,∴5x=180°,∴∠A=36°,故答案为36°.14.【解答】解:如图,∵∠1=∠C+∠4,∠2=∠C+∠3,∴∠1+∠2=∠C+(∠3+∠4+∠C)=78°+180°=258°,故答案为=258°.15.【解答】解:∵在△ABC中,∠B=50°,∠C=60°,∴∠BAC=180°﹣50°﹣60°=70°.∵AD平分∠BAC,∴∠CAD=∠BAC=35°.∵AE⊥BC于E,∴∠CAE=90°﹣60°=30°,∴∠DAE=∠CAD﹣∠CAE=35°﹣30°=5°.故答案为:5°.16.【解答】解:∵AB=6cm,AD=5cm,△ABD周长为15cm,∴BD=15﹣6﹣5=4cm,∵AD是BC边上的中线,∴BC=8cm,∵△ABC的周长为21cm,∴AC=21﹣6﹣8=7cm.故AC长为7cm,故答案为:7cm.17.【解答】解:设第三边长为x,则3﹣2<x<2+3,即1<x<5.又x为偶数,因此x=2或4,故这个三角形的周长是:2+2+3=7(cm)或2+3+4=9(cm).故答案为:7或9.18.【解答】解:如图1,∵AD、BE是锐角△ABC的高,∴∠AEO=∠BDO=90°,∵∠AOE=∠BOD,∴∠DBO=∠DAC,∵BO=AC,∠BDO=∠ADC=90°∴△BDO≌△ADC(ASA),∴∠ABC=∠BAD=45°,如图2,同理证得△BDO≌△ADC(ASA),∴BD=AD,∴∠ABD=∠BAD=45°,∴∠ABC=135°,故答案为:45°或135°.三.解答题(共8小题)19.【解答】证明:∵点C是AE的中点,∴AC=CE,在△ACB与△CED中,∴△ABC≌△CDE(SAS).20.【解答】解:∵AD是△ABC的高,∠C=76°,∴∠DAC=14°,∵BE平分∠ABC交AD于E,∴∠ABE=∠EBD,∵∠BED=64°,∴∠ABE+∠BAE=64°,∴∠EBD+64°=90°,∴∠EBD=∠ABE=26°,∴∠BAE=38°,∴∠BAC=∠BAE+∠CAD=38°+14°=52°.21.【解答】解:∵DE⊥AB,DF⊥AC(已知)∴∠BED=∠CFD=Rt∠(垂直的定义)∵D是BC的中点,∴BD=CD,又∵BE=CF,∴在Rt△BDE和Rt△CDF中,,∴Rt△BDE≌Rt△CDF(HL)∴∠B=∠C(全等三角形的对应角相等)∴AB=AC(在同一个三角形中,等角对等边).故答案:已知;CD;HL;全等三角形的对应角相等;在同一个三角形中,等角对等边.22.【解答】解:(1)作法:①以B点为圆心,任意长为半径画弧分别交BA、BC于M、N 点;②再以M、N为圆心,以大于它们之间的距离的二分之一为半径画弧,两弧在∠ABC内相交于E,则BD为所作;(2)如图,PQ为所作.23.【解答】解:(1)AB与CE的位置关系是垂直,AB⊥CE(2)证明:∵Rt△ABC≌Rt△CED∴AC=CD,BC=ED,∠E=∠B又∵∠ACB=90°∴∠ADC=45°又∵∠CDE=90°∴∠EDG=∠HDG=45°∵CH=DB∴CH+CD=DB+CH即HD=CB∴HD=ED在△HGD和△EGD中∴△HGD≌△EGD(SAS)∴∠H=∠E又∵∠E=∠B∴∠H=∠B∴HK=BK24.【解答】解:(1)△ACP≌△BPQ,∵AC⊥AB,BD⊥AB∴∠A=∠B=90°∵AP=BQ=2,∴BP=5,∴BP=AC,在△ACP和△BPQ中,,∴△ACP≌△BPQ;∴∠C=∠BPQ,∵∠C+∠APC=90°,∴∠APC+∠BPQ=90°,∴∠CPQ=90°,∴PC⊥PQ;(2)存在x的值,使得△ACP与△BPQ全等,①若△ACP≌△BPQ,则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt解得:x=2,t=1;②若△ACP≌△BQP,则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t解得:x=,t=.25.【解答】解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:过点A、D作射线AF,∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,即∠BDC=∠BAC+∠B+∠C;(2)①∵∠X=90°,由(1)知:∠A+∠ABX+∠ACX=∠X=90°,∵∠A=40°,∴∠ABX+∠ACX=50°,故答案为:50;②如图(3),∵∠A=40°,∠DBE=130°,∴∠ADE+∠AEB=130°﹣40°=90°,∵DC平分∠ADB,EC平分∠AEB,∴∠ADC=∠ADB,∠AEC=∠AEB,∴∠ADC+∠AEC==45°,∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.26.【解答】(1)解:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中∵,∴△BAD≌△CAE(SAS),∴∠B=∠ACE,∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE,∵∠BAC=25°,∴∠DCE=25°,故答案为:25°;(2)解:当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由是:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中∵,∴△BAD≌△CAE(SAS),∴∠B=∠ACE,∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠,北师大版∵∠BAC=α,∠DCE=β,∴α=β;(3)解:当D在线段BC上时,α+β=180°,当点D在线段BC延长线或反向延长线上时,α=β.。
北师大数学七年级下《第四章三角形》章节检测题含答案

北师大版数学七年级下册第四章三角形章节检测题一、选择题1.在下列长度的四根木棒中,能与长为4 cm,9 cm的两根木棒钉成一个三角形的是( )A.4 cm B.5 cm C.9 cm D.13 cm2.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形3.下列说法中正确的是( )A.面积相等的两个图形是全等图形B.周长相等的两个图形是全等图形C.所有正方形都是全等图形D.能够完全重合的两个图形是全等图形4.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于( )A.8 B.7 C.6 D.55.如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么需要测量________才能测得A,B之间的距离( )A.AB B.AC C.BM D.CM6.如图,∠A=∠B,∠C=α,DE⊥AC,FD⊥AB,则∠EDF等于( )A.α B.90°-12α C.90°-α D.180°-2α7.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为( )A.95° B.85° C.90° D.100°二、填空题8.如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=_______.9.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连接AD,CD.若∠B=65°,则∠ADC的大小为________.10.如图是一副三角板叠放的示意图,则∠α=________.11.如图,在△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD=____°.12.一角为80°的三角形中,另两角的角平分线相交所成的锐角是________.13.如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为____.三、解答题14.如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)15.(·河北)如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB =DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)指出图中所有平行的线段,并说明理由.16.如图,在△ABC中,BE,CF分别是AC,AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG.求证:AG=AD.17.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20步有一棵树C,继续前行20步到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长就是河宽AB.请你证明他们做法的正确性.18.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.(2)延长AC 至点E ,使CE =AC ,求证:DA =DE.答案:一、1---7 CDDBC BB二、8. 70°9. 65°10. 75°11. 19 °12. 50°13. 8三、14. 解:答案不唯一,如添加AC =DF ,证明:∵BF =EC ,∴BF -CF =EC -CF ,即BC =EF ,在△ABC 和△DEF 中,⎩⎪⎨⎪⎧AC =DF ,∠1=∠2,BC =EF ,∴△ABC ≌△DEF15. 解:(1)∵BF =CE ,∴BF +CF =CE +CF ,即BC =EF ,又∵AB =DE ,AC =DF ,∴△ABC ≌△DEF(SSS) (2)AB ∥DE ,AC ∥DF.理由:∵△ABC ≌△DEF ,∴∠ABC =∠DEF ,∠ACF =∠DFE ,∴AB ∥DE ,AC16. 解:∵BE ,CF 分别是AC ,AB 两条边上的高,∴∠ABD +∠BAC =90°,∠GCA +∠BAC =90°,∴∠GCA =∠ABD ,在△GCA 和△ABD 中,∵GC =AB ,∠GCA =∠ABD ,CA =BD ,∴△GCA ≌△ABD ,∴AG =AD17. 解:做法正确.证明:在△ABC 和△EDC 中,∴△ABC ≌△EDC(ASA),∴AB =DE18. 解:(1)∵在Rt △ABC 中,∠ACB =90°,∠B =30°,∴∠CAB =60°.又∵AD 平分∠CAB ,∴∠CAD =12∠CAB =30° (2)∵∠ACD +∠ECD =180°,且∠ACD =90°,∴∠ECD =90°,∴∠ACD =∠ECD.在△ACD 与△ECD 中,⎩⎪⎨⎪⎧AC =EC ,∠ACD =∠ECD ,CD =CD ,∴△ACD ≌△ECD(SAS),∴DA =DE。
北师大版七年级下册数学 第四章 三角形 单元测试卷(含答案)

第四章三角形单元测试卷一.选择题1.三角形三条中线的交点叫做三角形的()A.内心 B.外心C.中心D.重心2. 如图, 在∠AOB的两边上截取AO = BO, CO = DO, 连结AD、BC交于点P. 则下列结论正确的是( )①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上A. 只有①B. 只有②C. 只有①②D. ①②③3. 如图,三角形的角平分线、中线、高的画法错误的个数是()A.0B.1C.2D.34.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为()A. 1B. 2C. 5D. 无法确定5. 利用尺规作图不能唯一作出三角形的是()A. 已知三边B. 已知两边及夹角C. 已知两角及夹边D. 已知两边及其中一边的对角6. 如图,AB⊥BC于B,BE⊥AC于E,∠1=∠2,D为AC上一点,AD=AB,则().A.∠1=∠EFD B. FD∥BC C.BF=DF=CD D.BE=EC7. 如图,已知AB=AC,PB=PC,且点A、P、D、E在同一条直线上.下面的结论:①EB=EC;②AD⊥BC;③EA平分∠BEC;④∠PBC=∠PCB.其中正确的有()A.1个B. 2个C.3个D. 4个8. 如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=()A.330° B.315° C.310° D.320°二.填空题9.各边长度都是整数、最大边长为8的三角形共有个.10. 如图,已知点C是∠AOB平分线上的点,点P、P′分别在OA、OB上,如果要得到OP=OP′,需要添加以下条件中的某一个即可:①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.请你写出所有可能的结果的序号:.11. 如图,已知△ABC是等边三角形,点O是BC上任意一点,OE、OF分别与两边垂直,等边三角形的高为1,则OE+OF的值为.12.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC= .13. 一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是_________.14. 如图所示,AD,AE是三角形ABC的高和角平分线,∠B=36°,∠C=76°,则∠DAE的度数.15.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是 .16. 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。
2019年北师大版七下数学《第4章三角形》单元测试卷(解析版)

2019年北师大版七下数学《第4章三角形》单元测试卷一.选择题(共10小题)1.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为()A.2cm B.3cm C.4cm D.5cm2.下面四个图形中,线段BD是△ABC的高的是()A.B.C.D.3.如图△ABC中,已知D、E、F分别是BC、AD、CE的中点,且S=4,那么阴影部分的面△ABC积等于()A.2B.1C.D.4.下列图形中有稳定性的是()A.正方形B.长方形C.直角三角形D.平行四边形5.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的()A.三边高的交点B.三条角平分线的交点C.三边垂直平分线的交点D.三边中线的交点6.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.7.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.SAS B.AAS C.ASA D.SSS8.用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;③作射线OC.则射线OC为∠AOB的平分线.由上述作法可得△OCD≌△OCE的依据是()A.SAS B.ASA C.AAS D.SSS9.如图,已知∠AOB,按照以下步骤画图:(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.(2)分别以点M、N为圆心,大于MN的长半径画弧,两弧在∠AOB内部相交于点C.(3)作射线OC.则判断△OMC≌△ONC的依据是()A.SAS B.SSS C.ASA D.AAS10.如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是()A.SAS B.SSS C.AAS D.ASA二.填空题(共5小题)11.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有对.12.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE 交于H,则∠CHD=.13.若a、b、c是△ABC的三边,且a=3cm,b=4cm,c=5cm,则△ABC最大边上的高是cm.14.如图:作∠AOB的角平分线OP的依据是.(填全等三角形的一种判定方法)15.如图,用直尺和圆规画∠AOB的平分线OE,其理论依据是.三.解答题(共6小题)16.观察以下图形,回答问题:(1)图②有个三角形;图③有个三角形;图④有个三角形;…猜测第七个图形中共有个三角形.(2)按上面的方法继续下去,第n个图形中有个三角形(用n的代数式表示结论).17.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.18.如图,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少.19.如图,在方格纸中,直线m与n相交于点C,(1)请过点A画直线AB,使AB⊥m,垂足为点B;(2)请过点A画直线AD,使AD∥m;交直线n于点D;(3)若方格纸中每个小正方形的边长为1,求四边形ABCD的面积.20.如图,直线CD与直线AB相交于C,根据下列语句画图(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.21.按要求用尺规作图(要求:不写作法,但要保留作图痕迹,并写出结论)已知:线段AB求作:线段AB的垂直平分线MN.2019年北师大版七下数学《第4章三角形》单元测试卷参考答案与试题解析一.选择题(共10小题)1.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为()A.2cm B.3cm C.4cm D.5cm【分析】设大小处于中间的边长是xcm,则最大的边是(x+1)cm,最小的边长是(x﹣1)cm,根据三角形的周长即可求得x,进而求解.【解答】解:设大小处于中间的边长是xcm,则最大的边是(x+1)cm,最小的边长是(x﹣1)cm.则(x+1)+x+(x﹣1)=12,解得:x=4,则最短的边长是:4﹣1=3cm.故选:B.【点评】本题考查了三角形的周长,理解三边长的设法是关键.2.下面四个图形中,线段BD是△ABC的高的是()A.B.C.D.【分析】根据高的画法知,过点B作AC边上的高,垂足为E,其中线段BD是△ABC的高.【解答】解:由图可得,线段BD是△ABC的高的图是D选项.故选:D.【点评】本题主要考查了三角形的高,三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.3.如图△ABC中,已知D、E、F分别是BC、AD、CE的中点,且S=4,那么阴影部分的面△ABC积等于()A .2B .1C .D .【分析】如图,因为点F 是CE 的中点,所以△BEF 的底是△BEC 的底的一半,△BEF 高等于△BEC 的高;同理,D 、E 、分别是BC 、AD 的中点,△EBC 与△ABC 同底,△EBC 的高是△ABC 高的一半;利用三角形的等积变换可解答.【解答】解:如图,点F 是CE 的中点,∴△BEF 的底是EF ,△BEC 的底是EC ,即EF =EC ,高相等;∴S △BEF =S △BEC ,D 、E 、分别是BC 、AD 的中点,同理得,S △EBC =S △ABC ,∴S △BEF =S △ABC ,且S △ABC =4,∴S △BEF =1,即阴影部分的面积为1.故选:B .【点评】本题主要考查了三角形面积的等积变换:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.结合图形直观解答.4.下列图形中有稳定性的是( )A .正方形B .长方形C .直角三角形D .平行四边形【分析】稳定性是三角形的特性.【解答】解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.故选:C .【点评】稳定性是三角形的特性,这一点需要记忆.5.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )A.三边高的交点B.三条角平分线的交点C.三边垂直平分线的交点D.三边中线的交点【分析】根据题意得:支撑点应是三角形的重心.根据三角形的重心是三角形三边中线的交点.【解答】解:∵支撑点应是三角形的重心,∴三角形的重心是三角形三边中线的交点,故选:D.【点评】考查了三角形的重心的概念和性质.注意数学知识在实际生活中的运用.6.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答【解答】解:∵四个选项中只有AD⊥BC,∴C正确.故选:C.【点评】本题考查的是作图﹣基本作图,熟记三角形高线的定义是解题的关键.7.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.SAS B.AAS C.ASA D.SSS【分析】利用作法得到OD=OC=OC′=OD′,CD=C′D′,于是可根据“SSS”判定△OCD ≌△OC′D′,然后根据全等三角形的性质得到∠A′O′B′=∠AOB.【解答】解:由作法得OD=OC=OC′=OD′,CD=C′D′,则可根据“SSS”可判定△OCD≌△OC′D′,所以∠A′O′B′=∠AOB.故选:D.【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).8.用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;③作射线OC.则射线OC为∠AOB的平分线.由上述作法可得△OCD≌△OCE的依据是()A.SAS B.ASA C.AAS D.SSS【分析】根据作图得出符合全等三角形的判定定理SSS,即可得出答案.【解答】解:在△OEC和△ODC中,∵,∴△OEC≌△ODC(SSS),故选:D.【点评】本题考查的是作图﹣基本作图及全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.9.如图,已知∠AOB,按照以下步骤画图:(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.(2)分别以点M、N为圆心,大于MN的长半径画弧,两弧在∠AOB内部相交于点C.(3)作射线OC.则判断△OMC≌△ONC的依据是()A.SAS B.SSS C.ASA D.AAS【分析】根据角平分线的作图方法解答.【解答】解:根据角平分线的作法可知,OM=ON,CM=CN,又∵OC是公共边,∴△OMC≌△ONC的根据是“SSS”.故选:B.【点评】本题考查了全等三角形的判定,熟悉角平分线的作法,找出相等的条件是解题的关键.10.如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是()A.SAS B.SSS C.AAS D.ASA【分析】由作法易得OD=O′D′,OC=O′C′,CD=C′D′,根据SSS可得到三角形全等.【解答】解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD ≌△C'O'D',故选:B.【点评】本题主要考查了全等三角形的判定,关键是掌握全等三角形的判定定理.二.填空题(共5小题)11.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有3对.【分析】以BC为公共边的“共边三角形”有:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC三对.【解答】解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.故答案为:3.【点评】本题考查了三角形的定义,学生全面准确的识图能力,正确的识别图形是解题的关键.12.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE 交于H,则∠CHD=45°.【分析】在三角形中,三内角之和等于180°,锐角三角形三个高交于一点.【解答】解:在△ABC中,三边的高交于一点,所以CF⊥AB,∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,∵∠ACB=60°,∴∠BCF=45°在△CDH中,三内角之和为180°,∴∠CHD=45°,故答案为∠CHD=45°.【点评】考查三角形中,三条边的高交于一点,且内角和为180°.13.若a、b、c是△ABC的三边,且a=3cm,b=4cm,c=5cm,则△ABC最大边上的高是 2.4cm.【分析】根据勾股定理的逆定理,得△ABC是直角三角形,根据三角形的面积公式,求得斜边上的高即可.【解答】解:∵a=3cm,b=4cm,c=5cm,∴△ABC是直角三角形,∵S△ABC =3×4÷2=6cm2,∴S△ABC=5×最大边上的高=12,∴△ABC最大边上的高是2.4cm.【点评】本题考查了勾股定理的逆定理及三角形面积的计算.14.如图:作∠AOB的角平分线OP的依据是SSS.(填全等三角形的一种判定方法)【分析】根据作法可知OC=OD,PC=PD,OP=OP,故可得出△OPC≌△OPD,进而可得出结论.【解答】解:在△OPC与△OPD中,∵,∴△OPC≌△OPD(SSS),∴OP是∠AOB的平分线.故答案为:SSS.【点评】本题考查的是作图﹣基本作图,熟知角平分线的作法是解答此题的关键.15.如图,用直尺和圆规画∠AOB的平分线OE,其理论依据是全等三角形,对应角相等.【分析】首先连接CE、DE,然后证明△OCE≌△ODE,根据全等三角形的性质可得∠AOE=∠BOE.【解答】解:连接CE、DE,在△OCE和△ODE中,,∴△OCE≌△ODE(SSS),∴∠AOE=∠BOE.因此画∠AOB的平分线OE,其理论依据是:全等三角形,对应角相等.【点评】此题主要考查了全等三角形的判定与性质,关键是掌握证明三角形全等的方法.三.解答题(共6小题)16.观察以下图形,回答问题:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.(2)按上面的方法继续下去,第n个图形中有(2n﹣1)个三角形(用n的代数式表示结论).【分析】(1)根据观察可得:图②有3个三角形;图③有5个三角形;图④有7个三角形;由此可以猜测第七个图形中共有13个三角形(2)按照(1)中规律如此画下去,三角形的个数等于图形序号的2倍减去1,据此求得第n个图形中的三角形的个数.【解答】解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.(2)∵图②有3个三角形,3=2×2﹣1;图③有5个三角形,5=2×3﹣1;图④有7个三角形,7=2×4﹣1;∴第n个图形中有(2n﹣1)个三角形.故答案为3,5,7,13,(2n﹣1).【点评】本题考查了图形的变化类﹣规律型,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.17.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.【分析】先利用三角形内角和定理可求∠ABC,在直角三角形ACD中,易求∠DAC;再根据角平分线定义可求∠CBF、∠EAF,可得∠DAE的度数;然后利用三角形外角性质,可先求∠AFB,再次利用三角形外角性质,容易求出∠BOA.【解答】解:∵∠CAB=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,又∵AD是高,∴∠ADC=90°,∴∠DAC=180°﹣90°﹣∠C=30°,∵AE、BF是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°,∴∠DAE=∠DAC﹣∠EAF=5°,∠AFB=∠C+∠CBF=60°+35°=95°,∴∠BOA=∠EAF+∠AFB=25°+95°=120°,∴∠DAC=30°,∠BOA=120°.故∠DAE=5°,∠BOA=120°.【点评】本题考查了三角形内角和定理、角平分线定义、三角形外角性质.关键是利用角平分线的性质解出∠EAF、∠CBF,再运用三角形外角性质求出∠AFB.18.如图,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少.【分析】(1)根据三角形内角与外角的性质解答即可;(2)过E作BC边的垂线即可得:E到BC边的距离为EF的长,然后过A作BC边的垂线AG,再根据三角形中位线定理求解即可.【解答】解:(1)∵∠BED是△ABE的外角,∴∠BED=∠ABE+∠BAD=15°+40°=55°;(2)过E作BC边的垂线,F为垂足,则EF为所求的E到BC边的距离,过A作BC边的垂线AG,∴AD为△ABC的中线,BD=5,∴BC=2BD=2×5=10,∵△ABC的面积为40,∴BC•AG=40,即×10•AG=40,解得AG=8,∵EF⊥BC于F,∴EF∥AG,∵E为AD的中点,∴EF是△AGD的中位线,∴EF=AG=×8=4.∴E到BC边的距离为4.【点评】本题考查了三角形外角的性质、三角形中位线定理及三角形的面积公式,涉及面较广,但难度适中.添加适当的辅助线是解题的关键.19.如图,在方格纸中,直线m与n相交于点C,(1)请过点A画直线AB,使AB⊥m,垂足为点B;(2)请过点A画直线AD,使AD∥m;交直线n于点D;(3)若方格纸中每个小正方形的边长为1,求四边形ABCD的面积.【分析】(1)(2)根据网格结构作出AB⊥m,AD∥m即可;(2)首先利用勾股定理计算出AB2,再根据正方形的面积公式可直接得到答案.【解答】解:(1)(2)如图所示:(3)AB2=12+32=10,四边形ABCD的面积为10.【点评】本题考查了垂线的定义,垂线的性质,以及网格结构,勾股定理,是基础题.20.如图,直线CD与直线AB相交于C,根据下列语句画图(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.【分析】(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)利用两直线平行,同旁内角互补即可解决问题.【解答】解:(1)如图所示:PQ即为所求;(2)如图所示:PR即为所求;(3)∠PQC=60°理由:∵PQ∥CD,∴∠DCB+∠PQC=180°,∵∠DCB=120°,∴∠PQC=180°﹣120°=60°.【点评】本题主要考查了基本作图,熟练掌握基本作图,并能利用平行线的性质来解决问题是解题关键.21.按要求用尺规作图(要求:不写作法,但要保留作图痕迹,并写出结论)已知:线段AB求作:线段AB的垂直平分线MN.【分析】分别以A,B点为圆心,以大于的长为半径作弧,两弧相交于M,N两点;作直线MN,MN即为线段AB的垂直平分线.【解答】解:作法:(1)分别以A,B点为圆心,以大于的长为半径作弧,两弧相交于M,N两点;(2)作直线MN,MN即为线段AB的垂直平分线.【点评】本题考查的是基本作图,熟知线段垂直平分线的作法是解答此题的关键.。
北师大版七年级数学下册 第四章《三角形》单元测试卷(含答案)

七年级下第4章《三角形》单元测试卷一、选择题(每题3分,共30分) 1.图中三角形的个数是( ) A .8 B .9 C .10 D .11 2.下面四个图形中,线段BE 是⊿ABC 的高的图是( )A B C D3.以下各组线段为边,能组成三角形的是( )A .1cm ,2cm ,4cmB .8cm ,6cm ,4cmC .12cm ,5cm ,6cmD .2cm ,3cm ,6cm 4.三角形一个外角小于与它相邻的内角,这个三角形是( )A .直角三角形B .锐角三角形C .钝角三角形D .属于哪一类不能确定 5.如图,在直角三角形ABC 中,AC ≠AB ,AD 是斜边上的高, DE ⊥AC ,DF ⊥AB ,垂足分别为E 、F ,则图中与∠C (∠C 除外)相等的角的个数是( )A 、3个B 、4个C 、5个D 、6个6.下面说法正确的个数有( )①如果三角形三个内角的比是1∶2∶3,那么这个三角形是直角三角形;②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;④如果∠A=∠B=21∠C ,那么△ABC 是直角三角形;⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;⑥在∆ABC 中,若∠A +∠B=∠C ,则此三角形是直角三角形。
A 、3个 B 、4个 C 、5个 D 、6个7.在∆ABC 中,C B ∠∠,的平分线相交于点P ,设,︒=∠x A 用x 的代数式表示BPC ∠的度数,正确的是( ) (A )x 2190+(B )x 2190- (C )x 290+ (D )x +90 8.如图,将一副三角板叠放在一起,使直角的顶点重合于O ,则∠AOC+∠DOB=( ) A 、900 B 、1200 C 、1600 D 、1800 9.以长为13cm 、10cm 、5cm 、7cm 的四条线段中的三条线段为边,可以画出三角形的个数是( )(A)1个 (B)2个 (C)3个 (D)4个10.给出下列命题:①三条线段组成的图形叫三角形 ②三角形相邻两边组成的角叫三角形的内角 ③三角形的角平分线是射线 ④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外 ⑤任何一个三角形都有三条高、三条中线、三条角平分线⑥三角形的三条角平分线交于一点,且这点在三角形内。
北师大版数学七年级下册第四章 三角形 单元测试题(附答案)
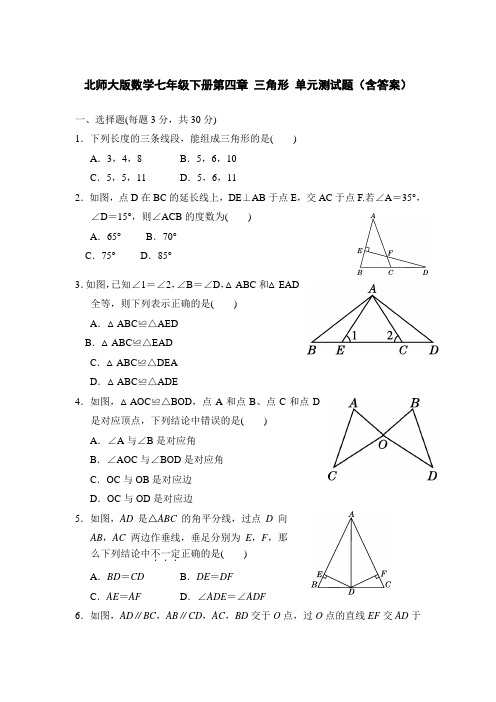
北师大版数学七年级下册第四章三角形单元测试题(含答案)一、选择题(每题3分,共30分)1.下列长度的三条线段,能组成三角形的是()A.3,4,8 B.5,6,10C.5,5,11 D.5,6,112.如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为()A.65°B.70°C.75°D.85°3.如图,已知∠1=∠2,∠B=∠D,△ABC和△EAD全等,则下列表示正确的是()A.△ABC≌△AEDB.△ABC≌△EADC.△ABC≌△DEAD.△ABC≌△ADE4.如图,△AOC≌△BOD,点A和点B、点C和点D是对应顶点,下列结论中错误的是()A.∠A与∠B是对应角B.∠AOC与∠BOD是对应角C.OC与OB是对应边D.OC与OD是对应边5.如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定...正确的是()A.BD=CD B.DE=DFC.AE=AF D.∠ADE=∠ADF6.如图,AD∥BC,AB∥CD,AC,BD交于O点,过O点的直线EF交AD于E点,交BC于F点,且BF=DE,则图中的全等三角形共有()A.6对B.5对C.3对D.2对7.将一副三角尺按下列方式进行摆放,∠1,∠2不一定...互补的是()8.如图,这是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为()A.45 cm B.48 cm C.51 cm D.54 cm9.根据下列已知条件,能画出唯一一个....△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=610.如图,在△ABC中,AC⊥CB,CD平分∠ACB,点E在AC上,且CE=CB,则下列结论:①DC平分∠BDE;②BD=DE;③∠B=∠CED;④∠A+∠CED=90°.其中正确的有()A.1个B.2个C.3个D.4个二、填空题(每题3分,共30分)11.如图,照相机的底部用三脚架支撑着,请你说说这样做的依据是____________________.12.如图,点B,C,E,F在同一直线上,AB∥DC,DE∥GF,∠B=∠F=72°,则∠D=________.13.已知三角形的两边长分别为2 和7,第三边长为偶数,则三角形的周长为__________.14.如图,点C,F在线段BE上,BF=EC,∠1=∠2.请你添加一个条件,使△ABC≌△DEF,这个条件可以是____________(不再添加辅助线和字母).15.如图,在△ABC中,BC=8 cm,AB>BC,BD是AC边上的中线,△ABD 与△BDC的周长的差是2 cm,则AB=__________.16.设a,b,c是△ABC的三边长,化简|a+b-c|+|b-c-a|+|c-a-b|=__________.17.如图,D,E,F分别为AB,AC,BC上的点,且DE∥BC,△ABC沿线段DE折叠,使点A落在点F处.若∠B=50°,则∠BDF=________.18.如图,已知边长为1的正方形ABCD,AC,BD交于点O,过点O任作一条直线分别交AD,BC于点E,F,则阴影部分的面积是________.19.如图,AD,AE分别是△ABC的角平分线、高线,且∠B=50°,∠C=70°,则∠EAD=________.20.如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=12(AB+AD),若∠D=115°,则∠B=________.三、解答题(21~24题每题9分,其余每题12分,共60分)21.如图,点B,F,C,E在一条直线上,FB=CE,AB∥ED,AC∥FD.试说明:AC=DF.22.如图,在△ABC中,AD是角平分线,∠B=54°,∠C=76°.(1)求∠ADB和∠ADC的度数;(2)若DE⊥AC于E,求∠EDC的度数.23.如图,在正方形ABCD中,点E,F分别在边AB,BC上,AE=BF,AF和DE相交于点G.(1)观察图形,写出图中所有与∠AED相等的角;(2)选择图中与∠AED相等的任意一个角,并加以说明.24.如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.试说明:BD=AE.25.如图,小明和小月两家位于A,B两处,要测得两家之间的距离,小明设计方案如下:①从点A出发沿河岸画一条射线AM;②在射线AM上截取AF=FE;③过点E作EC∥AB,使B,F,C在一条直线上;④CE的长就是A,B间的距离.(1)请你说明小明设计的原理.(2)如果不借助测量仪,小明的设计中哪一步难以实现?(3)你能设计出其他的方案吗?26.如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A 旋转,BD⊥l于D,CE⊥l于E.(1)试说明:DE=BD+CE.(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.答案一、1.B 2.B 3.D 4.C 5.A 6.A 7.D8.A9.C10.D二、11.三角形具有稳定性12.36°13.15或1714.CA=FD(答案不唯一)15.10 cm16.3a+b-c17.80°18.1 419.10°20.65°三、21.解:因为AB∥ED,AC∥FD,所以∠B=∠E,∠ACB=∠DFE.因为FB=CE,所以BF+FC=CE+FC,即BC=EF.所以△ABC≌△DEF(ASA).所以AC=DF.22.解:(1)因为∠B=54°,∠C=76°,所以∠BAC=180°-54°-76°=50°.因为AD平分∠BAC,所以∠BAD=∠CAD=25°.所以∠ADB=180°-54°-25°=101°,∠ADC=180°-101°=79°.(2)因为DE⊥AC,所以∠DEC=90°.所以∠EDC=180°-90°-76°=14°.23.解:(1)由题可知∠DAG,∠AFB,∠CDE与∠AED相等.(2)(答案不唯一)选择∠DAG=∠AED.说明如下:因为四边形ABCD是正方形,所以∠DAB=∠B=90°,AD=AB.在△DAE 和△ABF 中,⎩⎨⎧AD =BA ,∠DAE =∠B =90°,AE =BF ,所以△DAE ≌△ABF (SAS). 所以∠ADE =∠BAF .因为∠DAG +∠BAF =90°,∠GDA +∠AED =90°, 所以∠DAG =∠AED .24.解:因为△ABC 和△ECD 都是等腰直角三角形,且∠ACB =∠DCE =90°,所以AC =BC ,CD =CE , ∠ACE +∠ACD =∠BCD +∠ACD . 所以∠ACE =∠BCD .在△ACE 和△BCD 中,⎩⎨⎧AC =BC ,∠ACE =∠BCD ,CE =CD ,所以△ACE ≌△BCD (SAS). 所以BD =AE .25.解:(1)全等三角形的对应边相等. (2)③难以实现.(3)略(答案不唯一,只要设计合理即可). 26.解:(1)因为BD ⊥l ,CE ⊥l ,所以∠ADB =∠AEC =90°.所以∠DBA +∠BAD =90°. 又因为∠BAC =90°,所以∠BAD +∠CAE =90°.所以∠DBA =∠CAE . 因为AB =AC ,∠ADB =∠CEA =90°,所以△ABD ≌△CAE (AAS).所以AD =CE ,BD =AE . 则AD +AE =BD +CE ,即DE =BD +CE . (2)(1)中结论不成立.DE =BD -CE .同(1)说明△ABD ≌△CAE , 所以BD =AE ,AD =CE .又因为AE-AD=DE,所以DE=BD-CE.。
北师大版七年级数学下册单元测试卷第四章 三角形附答案

第四章三角形一、选择题(共18小题;共54分)1. 如图,,,,,则的取值范围是A. 大于B. 小于C. 大于且小于D. 无法确定2. 若线段,分别是边上的高线和中线,则A. B. C. D.3. 给出下列关于三角形的条件:已知三边;已知两边及其夹角;已知两角及其夹边;已知两边及其一边的对角,利用尺规作图,能作出唯一的三角形的条件分别是A. B. C. D.4. 用下列长度的三条线段首尾顺次连接,能构成等腰三角形的是A. ,,B. ,,C. ,,D. ,,5. 如图所示,已知正方形网格中每个小方格都是边长为的正方形,,两点在小方格的顶点上,点也在小方格的顶点上,且以,,为顶点的三角形的面积为个平方单位,则点的个数为A. 个B. 个C. 个D. 个6. 已知某三角形第一条边长为,第二条边比第一条边长,第三条边比第一条边的倍少,则这个三角形的周长为A. B. C. D.7. 长为的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边的取值范围为8. 在中,如果,那么是A. 直角三角形B. 锐角三角形C. 钝角三角形D. 无法确定9. 三角形的重心是三角形的A. 三条中线的交点B. 三条角平分线的交点C. 三边垂直平分线的交点D. 三条高所在直线的交点10. 下列各组条件中,能判定的是A. ,,B. ,,C. ,,D. ,,的周长的周长11. 如图,在中,于,于,,交于,且,那么下列结论中正确的是A. B.C. D.12. 某同学不小心把一块玻璃打碎了,变成了如图所示的三块,现在要到玻璃店配一块完全一样的玻璃,那么应带哪块去才能配好A. B. C. D. 任意一块13. 如图,在中,于,于,,是的平分线,则图中与相等的角(不包含)的个数为A. B. C. D.14. 如图,已知,,与相交于点,则图中全等三角形的对数为A. B. C. D.15. 已知的内角,,满足,,则这个三角形是A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定16. 已知三角形的两边长分别为和,则下列长度的四条线段中能作为第三边的是A.17. 已知实数,满足,则以,的值为两边长的等腰三角形的周长是A. 或B.C. D. 以上答案均不对18. 如图,,,,给出下列结论:①;②;③;④,其中一定成立的结论是A. ①②③B. ①②④C. ①③④D. ①②③④二、填空题(共8小题;共36分)19. 如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片即可.20. 已知中,周长为,,则.21. 已知中,是的重心,则.22. 如图,方格纸中的三个顶点分别在小正方形的顶点(格点)上,请你在图中再画一个顶点都在格点上的,且使.23. 已知点,,在同一直线上,厘米,厘米,则厘米.24. 如图所示,已知线段,用尺规作出,使,.作法:()作一条线段;()分别以,为圆心,以为半径画弧,两弧交于点;()连接,,则就是所求作的三角形.25. 如图,已知,要得到结论,小明添加的条件:,你认为小明添加的条件能得出吗? (填“能”与“不能”).26. 当三角形中一个内角是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中称为“特征角”.如果一个“特征三角形”的“特征角”为,那么这个“特征三角形”的最小内角的度数为.三、解答题(共5小题;共60分)27. 一个等腰三角形的三边长分别为,,,求的值,并求这个等腰三角形三边的长.28. 已知为锐角三角形,那么图中一共有多少个三角形?锐角三角形、直角三角形、钝角三角形各有多少个?用符号表示这些三角形.29. 如图,把大小为的正方形方格图形分割成两个全等图形,如图.请在下图中,沿着虚线画出四种不同的分法,把的正方形方格图形分割成两个全等图形.30. 如图,已知是的边上的中线,,.垂足分别为点,,请说明的理由.31. 中,是最小角,是最大角,且,求的取值范围(提示:三角形内角和为).。
北师大版七年级下数学《第四章三角形》单元测试(含答案)

列说法中正确的个数是(①作出AD 的依据是SAS ② / ADC=60、选择题1. 下列长度的三条线段能组成三角形的是( )A. 5cm 2cm 3cmB. 5cm 2 cm 2cmC. 5cm 2cm 4cmD. 5cm 12cm 6cm2. 某同学把一块三角形的玻璃打碎成了 3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法 是( )4•一个角的平分线的尺规作图的理论依据是( )5.三角形两条边分别为 3和7,则第三边可以为( )8. 如图,在△ ABC 中,/ C=90° / B=30°以A 为圆心,任意长为半径画弧分别交 AB 、AC 于点M 和N , 再分别以M 、N 为圆心,大于 MN 的长为半径画弧,两弧交于点 P,连结AP 并延长交BC 于点D ,则下第四章三角形A.带①去 B 带②去3.不能判定两个三角形全等的条件是() A.三条边对应相等B.两角及一边对应相等 C 带③去C.两边及夹角对应相等D ①②③都带去 D.两边及一边的对角相等 A. SAS B. SSS C. ASAD. AAS A. 2 B. 3 C. 9 D. 106.下图所示的五角星是用螺栓将两端打有孔的 5根木条连接构成的图形,它的形状不稳定。
如果在木条交 叉点打孔加装螺栓的办法使其形状稳定,那么至少需要添加 ( )个螺栓。
B. 2C. 3 7.全等图形是指两个图形() A.能够重合 B 形状相C 大小相同13.一个三角形的两边长分别是 2和6,第三边长为奇数,则其周长为9. 有5根小木棒,长度分别为 2cm 、3cm 、4cm 、5cm 、6cm ,任意取其中的3根小木棒首尾相接搭三角形, 可搭出不同的三角形的个数为() 、填空题11. _______________________ 任意一个三角形被一条中线分成两个三角形,则这两个三角形:①形状相同;②面积相等;③全等.上 述说法中,正确的是 .12. 如图,以Rt A ABC 的斜边AB 为一边在厶ABC 同侧作正方形 ABEF.点O 为AE 与BF 的交点,连接CO.若③点D 在AB 的中垂线上; ④S △DAC : S A ABD =1 : 2.A. 1C. 3D. 4 A. 5个B.个C.个D.个 10•如图,将△ ABC 沿DE,EF 翻折,顶点A,B 均落在点 O 处,且EA 与EB 重合于线段 EO,若/ CDO+Z CFO=98°, A. 40C. 42D. 43B. 2 则/C 的度数为(B. 41 E14•用尺规作图作已知角/ AOB的平分线0C,其根据是构造两个三角形全等,用到的三角形全等的判定方法是. 15. ____________________________________________________________________ 在厶ABC中,/ A=80° / ABC与/ ACB的平分线交于点0,则/ B0C= _________________________________ .16. __________________________________________________________ 如图,ADABC中线,点G为重心,若AD=6,贝U AG= _______________________________________________18. ________________________________________________________________________________________ 如图,已知△ ABC的周长为27cm, AC=9cm, BC边上中线AD=6cm, △ ABD周长为19cm, AB= _____________19. 如图,-.1皿一x」n i•'分别平分—is;|.的外角「「、内角•、外角LACF•以下结论:①②ZJC5 = 2Z_!05;③AQ平分LADC\④G1DC = 90° —£ ABD;⑤其中正确的结论是_____________________________________ .三、解答题20. 陆老师布置了一道题目:过直线I外一点A作I的垂线.(用尺规作图)小淇同学作法如下:(1) 在直线I上任意取一点C,连接AC;(2) 作AC的中点0;(3) 以0为圆心,0A长为半径画弧交直线I于点B,如图所示;(4) 作直线AB.则直线AB就是所要作图形.你认为小淇的作法正确吗?如果不正确,请画出一个反例;如果正确,请给出证明.21. 如图,AD平分/ BAC, AB=AC,试判断△ ABD^A ACD.并说明理由.22•如图,在五边形ABCDE和五边形A i BiGD i E i中,如果AB=A i Bi , BC=BG , CD=GD iDE=DiE i , EA=EiA i .请添加尽可能少的条件,使它们全等(写出添加的条件,不需要说明理由)23.如图,线段AD、BE相交与点。
北师大版七年级数学下册第四章 三角形 章节测试(含答案)
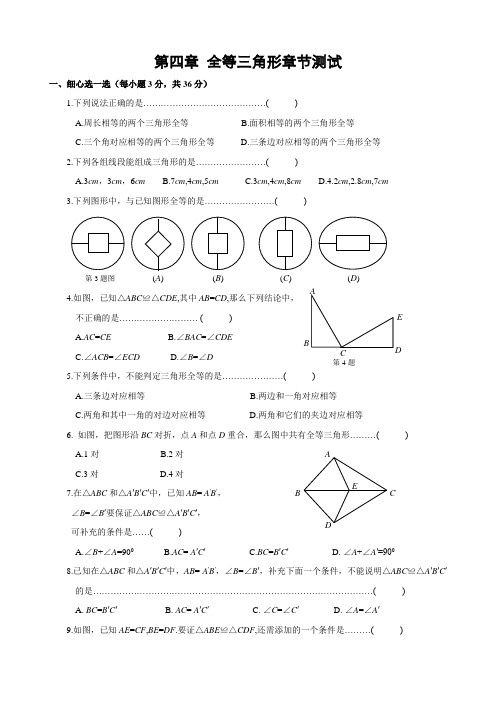
第四章 全等三角形章节测试一、细心选一选(每小题3分,共36分)1.下列说法正确的是……………………………………( )A.周长相等的两个三角形全等B.面积相等的两个三角形全等C.三个角对应相等的两个三角形全等D.三条边对应相等的两个三角形全等 2.下列各组线段能组成三角形的是……………………( )A.3cm ,3cm ,6cmB.7cm ,4cm ,5cmC.3cm ,4cm ,8cmD.4.2cm ,2.8cm ,7cm 3.下列图形中,与已知图形全等的是……………………( )4.如图,已知△ABC ≌△CDE,其中AB =CD ,那么下列结论中, 不正确的是……………………… ( ) A.AC =CEB.∠BAC =∠CDEC.∠ACB =∠ECDD.∠B =∠D5.下列条件中,不能判定三角形全等的是…………………( ) A.三条边对应相等 B.两边和一角对应相等 C.两角和其中一角的对边对应相等 D.两角和它们的夹边对应相等6. 如图,把图形沿BC 对折,点A 和点D 重合,那么图中共有全等三角形………( ) A.1对 B.2对 C.3对 D.4对7.在△ABC 和△A ′B ′C ′中,已知AB = A ′B ′, ∠B =∠B ′要保证△ABC ≌△A ′B ′C ′, 可补充的条件是……( )A.∠B +∠A =900B.AC = A ′C ′C.BC =B ′C ′D. ∠A +∠A ′=9008.已知在△ABC 和△A ′B ′C ′中,AB = A ′B ′,∠B =∠B ′,补充下面一个条件,不能说明△ABC ≌△A ′B ′C ′的是……………………………………………………………………………………( ) A. BC =B ′C ′ B. AC = A ′C ′ C. ∠C =∠C ′ D. ∠A =∠A ′ 9.如图,已知AE =CF ,BE =DF .要证△ABE ≌△CDF ,还需添加的一个条件是………( )(A ) (B ) (C )(D )第3题图B DE第4题ABDCEA.∠BAC =∠ACDB.∠ABE =∠CDFC.∠DAC =∠BCAD.∠AEB =∠CFD10.如图AD 是△ABC 的角平分线,DE 是△ABD 的高,EF 是△ACD 的高,则…( ) A.∠B =∠C B.∠EDB =∠FDC C.∠ADE =∠ADF D. ∠ADB =∠ADC 11.如图AC 与BD 相交于点O ,已知AB =CD ,AD =BC ,则图中全等三角形有………( ) A.1对 B.2对 C.3对 D.4对 12.如图,D 、E 分别是AB ,AC 上一点,若∠B =∠C ,则在下列条件中,无法判定△ABE ≌△ACD 是………………………………( ) A.AD =AE B.AB =ACC.BE =CDD.∠AEB =∠ADC 二、专心填一填:(每小题3分,共24分)13.如图,△ABC ≌△DEF ,点B 和点E , 点A 和点D 是对应顶点, 则AB = ,CB = , ∠C = ,∠CAB = . 14.若已知两个三角形有两条边对应,则要视这两个三角形全等, 还需增加的条件可以是 或 .15.如图已知AC 与BD 相交于点O ,AO =CO ,BO =DO ,则AB =CD 请说明理由. 解:在△AOB 和△COD 中(BO DO(AO CO ==⎧⎪⎨⎪⎩已知)(对顶角相等已知) ∴△AOB ≌△COD ( )∴AB =DC ( )16.如图,已知AO =OB ,OC =OD ,AD 和BC 相交于点E , 则图中全等三角形有 对.17.在△ABC 和△DEF 中,AB =4, ∠A =350, ∠B =700,DE =4, ∠D = , ∠E 根据 判定△ABC ≌△DEF .ABC D F E 第9题AA AAA 第10题A BCDO第11题ABCE第12题D第13题ABC DEFABD CO第15题OABD第16题CE第18题A D18.如图,在△ABC和△DEF中AB=DC( BC=DA(=⎧⎪⎨⎪⎩已知)已知)()∴△ABC≌△DEF( )19.如图∠B=∠DEF,AB=DE,要证明△ABC≌△DEF,(1)若以“ASA”为依据,需添加的条件是;(2)若以“SAS”为依据,需添加的条件是.20.如图,△ABC中,AB=AC=13cm,AB的垂直平分线交AB于D,交AC于E,若△EBC的周长为21cm,则BC= cm.三、耐心答一答:(本题有6小题,共40分)21.(本题4分)已知∠α、∠β和线段a, 如图,用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,BC=a.22.(本题6分)已知AD平分∠CAB,且DC⊥AC, DB⊥AB,那么AB和AC相等吗?请说明理由.第19题B CAE CDAB CED第20题DCAB23.(本题6分)如图,已知BD =CD ,∠1=∠2. 说出△ABD ≌△ACD 的理由.24.(本题8分)如图,已知AB =DC ,AD =BC ,说出下列判断成立的理由: (1) △ABC ≌△CDA (2) ∠B =∠D25.(本题8分) 如图,把大小为4×4的正方形方格图形分别分割成两个全等图形,例如图①,请在下图中,沿着须先画出四种不同的分法,把4×4的正方形分割成两个全等图形ABC12DB D图①画法1画法2画法3画法426.(本题8分)如图,△ABC 中,AD 垂直平分BC ,H 是AD 上一点,连接BH ,CH .(1)AD 平分∠BAC 吗?为什么?(2)你能找出几堆相等的角?请把他么写出来(不需写理由)ACBH D参考答案一、细心选一选:(每小题3分,共36分)题号 1 2 3 4 5 6 7 8 9 10 11 12答案D B B C D C C B D C D D二、专心填一填(每小题3分,共24分)13.DE,FE,∠F, ∠FE D. 14.3第三边相等,这两边的夹角相等15. ∠AOB=∠COD,SAS,全等三角形的对应边相等16.4 17.350, AAS18.AC,CA,公共边,SSS19.∠A=∠D20.8三、耐心答一答(本题有六小题,共40分)21.图略22.AB=AC23.略24.略25.画法1 画法2 画法3 画法426.(1)由△ADB≌△ADC(SAS)得∠BAD=∠CAD(4)4对,∠BHD=∠CHD, ∠ABD=∠ACD,∠HBD=∠HCD, ∠BDA=∠CDA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章三角形
一、选择题
1.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是()
A. 带①去
B. 带②去
C. 带③去
D. ①②③都带去
2.下列长度的三条线段能组成三角形的是()
A. 5cm 2cm 3cm
B. 5cm 2cm 2cm
C. 5cm 2cm 4cm
D. 5cm 12cm 6cm
3.不能判定两个三角形全等的条件是()
A. 三条边对应相等
B. 两角及一边对应相等
C. 两边及夹角对应相等
D. 两边及一边的对角相等
4.一个角的平分线的尺规作图的理论依据是()
A. SAS
B. SSS
C. ASA
D. AAS
5.三角形两条边分别为3和7,则第三边可以为()
A. 2
B. 3
C. 9
D. 10
6.下图所示的五角星是用螺栓将两端打有孔的5根木条连接构成的图形,它的形状不稳定。
如果在木条交叉点打孔加装螺栓的办法使其形状稳定,那么至少需要添加( )个螺栓。
A. 1
B. 2
C. 3
D. 4
7.全等图形是指两个图形()
A. 能够重合
B. 形状相同
C. 大小相同
D. 相等
8.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是()
①作出AD的依据是SAS;②∠ADC=60°
③点D在AB的中垂线上;④S△DAC:S△ABD=1:2.
A. 1
B. 2
C. 3
D. 4
9.有5根小木棒,长度分别为2cm、3cm、4cm、5cm、6cm,任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为()
A. 5个
B. 6个
C. 7个
D. 8个
10.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为()
A. 40°
B. 41°
C. 42°
D. 43°
二、填空题
11.任意一个三角形被一条中线分成两个三角形,则这两个三角形:①形状相同;②面积相等;③全等.上述说法中,正确的是________ .
12.如图,以Rt△ABC的斜边AB为一边在△ABC同侧作正方形ABEF.点O为AE与BF的交点,连接CO.若CA=2,CO=,那么CB的长为________.
13.一个三角形的两边长分别是2和6,第三边长为奇数,则其周长为________.
14.用尺规作图作已知角∠AOB的平分线OC,其根据是构造两个三角形全等,用到的三角形全等的判定方法是________ .
15.在△ABC中,∠A=80°,∠ABC与∠ACB的平分线交于点O,则∠BOC=________度.
16.如图,AD为△ABC中线,点G为重心,若AD=6,则AG=________ .
17.用尺规做一个角等于已知角的依据是________ .
18.如图,已知△ABC的周长为27cm,AC=9cm,BC边上中线AD=6cm,△ABD周长为19cm,AB=________.
19.如图,分别平分的外角、内角、外角
.
以下结论: ① ;② ;③ 平分;④
; ⑤ 其中正确的结论是________.
三、解答题
20.陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)
小淇同学作法如下:
(1)在直线l上任意取一点C,连接AC;
(2)作AC的中点O;
(3)以O为圆心,OA长为半径画弧交直线l于点B,如图所示;
(4)作直线AB.
则直线AB就是所要作图形.
你认为小淇的作法正确吗?如果不正确,请画出一个反例;如果正确,请给出证明.
21.如图,AD平分∠BAC,AB=AC,试判断△ABD≌△ACD.并说明理由.
22.如图,在五边形ABCDE和五边形A1B1C1D1E1中,如果AB=A1B1,BC=B1C1,CD=C1D1,
DE=D1E1,EA=E1A1.请添加尽可能少的条件,使它们全等(写出添加的条件,不需要说明理由)
23.如图,线段AD、BE相交与点C,且△ABC≌△DEC,点M、N分别为线段AC、CD的中点.求证:
(1)ME=BN;
(2)ME∥BN.
参考答案
一、选择题
C C
D B C A A C C B
二、填空题
11.②
12.+2
13.13或15
14.SSS
15.130
16.4
17.SSS
18 .8cm
19.①②④⑤
三、解答题
20.解:小淇同学作法正确.
理由如下:连接OB.
∵O为AC中点,以O为圆心,OA长为半径画弧交直线l于点B,∴OA=OC=OB.
∴∠CAB=∠ABO,∠ACB=∠CBO,
又∵∠CAB+∠ABO+∠ABC+∠CBO=180°,
∴∠ABO+∠CBO=90°.
∴∠ABC=90°,
21.解:△ABD≌△ACD,理由是:∵AD平分∠BAC,∴∠BAD=∠CAD,在△BAD和△CAD中,
,
∴△BAD≌△CAD(SAS)
22.解:如图:
连接AC,AD,A′C′,A′D′,
AC=A′C′,AD=A′D′,五边形ABCDE≌五边形A1B1C1D1E1.
23.(1)证明:∵△ABC≌△DEC,
∴AC=DC,BC=CE.
∵点M、N分别为线段AC、CD的中点,
∴CM=CN.
在△BCN和△ECM中
∵MC=NC, ∠BCN=∠ECM,BC=CE
∴△BCN≌△ECM(SAS)
∴ME=BN.
(2)证明:由(1)知△BCN≌△ECM,
∴∠CBN=∠CEM,。
