六方晶系的晶面间距公式为
合集下载
晶体几何学基础
体心立方
体心立方晶格的晶胞中, 原子位置 体心立方晶格的晶胞中, 八个原子处于立方体的角上, 八个原子处于立方体的角上,一个原 子处于立方体的中心, 子处于立方体的中心, 角上八个原子 与中心原子紧靠。 与中心原子紧靠。 具有体心立方晶格的金属有钼 (Mo)、 (W)、 (V)、 (α(Mo)、钨(W)、钒(V)、α-铁(α-Fe, <912℃)等 <912℃)等。 体心立方晶胞特征： 体心立方晶胞特征： 晶格常数： α=β=γ=90° 晶格常数：a=b=c, α=β=γ=90°
体心立方
原子位置 立方体的八个顶角和体心
体心立方中原子排列
面心立方
原子位置：立方体的八个顶角和每个侧面中心 原子位置：立方体的八个顶角和每个侧面中心
具有这种晶格的金属有铝(Al)、铜(Cu)、镍 、 具有这种晶格的金属有铝 、 (Ni)、金(Au)、银(Ag)、γ- 铁(γ-Fe, 912 ℃～ 、 、 、 1394 ℃)等 等
晶面间距 晶面间距(d)公式： 晶面间距(d)公式： 公式 立方晶系： 四方晶系：
1 d hkl
2
h2 + k 2 + l 2 = a2
1
2
d hkl 1 h2 k 2 l 2 正交晶系： = 2+ 2+ 2 2 a b c d hkl
h +k l = + 2 2 a c
2 2 2
晶面夹角的计算公式
倒易点阵的作法
首先求基矢，然后利用基矢绘图。 首先求基矢，然后利用基矢绘图。 进而求倒易点阵. 由a,b,c,α,β,γ求a*,b*,c*,α*,β*,γ*进而求倒易点阵 求 进而求倒易点阵 同样可求 得b*,c*。 。
v v v v b ×c c ×a v* v v v v v* v v v v ⋅ a ⋅b (b ⋅ c )(c ⋅ a ) − (c ⋅ c )(b ⋅ a ) V V cos γ * = v * v * = = abc 2 sin α sin β | a b | bc sin α ca sin β V V cos α cos β − cos γ = 同样可求 得α *, β *。 。 sin α sin β
六方晶系的晶面间距公式为
二、 晶面
通过空间点阵任意三结点的 平面是一个晶面，而且同时 还有一系列等间距的晶面与 之平行，组成一组晶面。例 如，图2－2中的晶面，在三 轴上截距长为1、2、3时； 系数的倒数为：1、1/2、 1/3；将三个倒数乘以最小 公倍数6，得三整数为：6、 3、2，则此晶面的晶面指数 为（632）。
当泛指某一晶面指数时，一般用（hkl）代表。如果晶面 与某坐标轴的负方向相交 时，则在相应的指数上加一负 号来表示。例如，（ hk l ）即表示晶面与z轴的负方向相 交。当某晶面与某坐标轴平行时，则认为晶面与该轴的截 距为∞，其倒数为0。
七个晶系
Crystal systems
Cubic Tetragonal Hexagonal Rhomboedric Orthorhombic Monoclinic Triclinic
Lattice Paramater
a = b = c , = = = 90° a = b c , = = = 90° a = b c , = = 90° , = 120° a = b = c , = = 90° a b c , = = = 90° a b c , = = 90°, 90° a b c , °
五、十四种布拉菲（Bravais）点阵
在晶体结构理论中，按照对称的特点将自然界的晶体物质 分成七个晶系，每个晶系都有互相对应的空间点阵，布拉 菲于1848年用布拉菲晶胞证实了七种晶系共仅有十四种可 能的点阵，后人为了纪念他的这一重要论断，称为布拉菲 点阵。
六、 晶体的32种点群及符号
任何一种晶体结构都可能同时具有多种对称元素。在有限 对称图形中由宏观对称元素组合成的对称元素群称为点群。 之所以称为点群，是因为构成它的对称元素必须至少相交 于一点，此点称为点群中心。利用数学方法推导出，点群 只可能有32种。
晶面指数六方晶系的晶面指数标定82523
1
1°确定交点坐标，X轴：1/3、 Y轴：1、 Z轴：1/2
2°取倒数 3、1、2 3°消除分数 3、1、2 4°晶面指数（312）
0,0,1
练习
1,0,0
0,1,0 晶面指数（233）
2
常见的晶面指数
(001)
(110)
(100)
(010)
(111)
晶面指数的几点说明：
1°h,k,l 三个数分别对应于a,b,c三晶轴方向。
19
ቤተ መጻሕፍቲ ባይዱ
六方晶系一些晶面的指数
20
六方晶系晶向指数标定
采用4轴坐标时，晶向指数的确定原则仍同前述 晶向指数可用｛u v t w｝来表示，这里 u + v = - t。
六方晶系晶向指数的表示方法(c轴与图面垂直) 21
六方晶系中，三轴指数和四轴指数 的相互转化
三轴晶向指数(U V W) 四轴晶向指数(u v t w)
线表示。
4°用[ ] 括起来，记为[uvw]
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
O
Y
●
X
4
Z
练习
●
O X
晶向符号 [221]
Y
[001] [111]
●
●
常见的晶向指数
O
●
●
[100]
[010]
5
1°确定交点坐标，X轴：1/3、 Y轴：1、 Z轴：1/2
[001]晶带包含的晶面有： （100）、（010）、（110）、 （110）、（120）等晶面
[001]
晶带定律：凡是属于[uvw]晶
带的晶面，它的晶面指数必须
1°确定交点坐标，X轴：1/3、 Y轴：1、 Z轴：1/2
2°取倒数 3、1、2 3°消除分数 3、1、2 4°晶面指数（312）
0,0,1
练习
1,0,0
0,1,0 晶面指数（233）
2
常见的晶面指数
(001)
(110)
(100)
(010)
(111)
晶面指数的几点说明：
1°h,k,l 三个数分别对应于a,b,c三晶轴方向。
19
ቤተ መጻሕፍቲ ባይዱ
六方晶系一些晶面的指数
20
六方晶系晶向指数标定
采用4轴坐标时，晶向指数的确定原则仍同前述 晶向指数可用｛u v t w｝来表示，这里 u + v = - t。
六方晶系晶向指数的表示方法(c轴与图面垂直) 21
六方晶系中，三轴指数和四轴指数 的相互转化
三轴晶向指数(U V W) 四轴晶向指数(u v t w)
线表示。
4°用[ ] 括起来，记为[uvw]
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
O
Y
●
X
4
Z
练习
●
O X
晶向符号 [221]
Y
[001] [111]
●
●
常见的晶向指数
O
●
●
[100]
[010]
5
1°确定交点坐标，X轴：1/3、 Y轴：1、 Z轴：1/2
[001]晶带包含的晶面有： （100）、（010）、（110）、 （110）、（120）等晶面
[001]
晶带定律：凡是属于[uvw]晶
带的晶面，它的晶面指数必须
材料科学导论-第一章 晶体学基础3
3、六方晶系晶面指数标定
根据六方晶系的对称特点，对六方晶系采用a1，a2，a3 及c四个晶轴，a1，a2，a3之间的夹角均为120度，这样， 其晶面指数就以(h k i l）四个指数来表示。 根据几何学可知，三维空间独立的坐标轴最多不超过三 个。前三个指数中只有两个是独立的，它们之间存在以 下关系：i ＝－ ( h + k ) 。
三轴晶面指数(h k l) 四轴晶面指数(h k i l) i=- ( h + k )
立方晶系：
d hkl
a h k l
2 2 2
§ 1.6 晶面指数及晶面间距 范例:
m/l
c
a
m/k
b
m/h
画出晶面 （100），（110），（111），（201），（211），（321）
பைடு நூலகம்
c a
（100）
b
画出晶面 （100），（110），（111），（201），（211），（321）
d V [h b c sin k a c sin l a b sin
2 2 2 2 2 2 2 2 2 2 2 2
2hkabc (cos cos cos )
2
2kla bc(cos cos cos )
2
2hlab c(cos cos cos )]
2
2 2 2
1
2
1 2
V abc(1 cos cos cos 2cos cos cos )
单斜晶系：d＝sinβ(h2/a2＋k2sin2β/b2＋l2/c2－2hlcosβ/ac)-1/2 正交晶系：d＝[h2/a2＋k2/b2＋l2/c2]-1/2 四方晶系：d＝[(h2＋k2)/a2＋l2/c2]-1/2 六方晶系：d＝[4(h2＋hk＋k2)/3a2＋l2/c2]-1/2
晶体学基础(晶向指数与晶面指数)
图 1 晶向指数的确定方法
图 2 不同的晶向及其指数 当然，在确定晶向指数时，坐标原点不一定非选取在晶向上不可。若原点不在待标晶向 上， 那就需要选取该晶向上两点的坐标 P(x1， y1， z1)和 Q(x2， y2， z2)， 然后将(x1-x2)， (y1-y2)，
(z1-z2)三个数化成最小的简单整数 u， v， w， 并使之满足 u∶v∶w=(x1-x2)∶(y1-y2)∶(z1-z2)。 则[uvw]为该晶向的指数。 显然，晶向指数表示了所有相互平行、方向一致的晶向。若所指的方向相反，则晶向指 数的数字相同，但符号相反，如图 3 中[0 1 0 ]与[010]。 说明： a 指数意义：代表相互平行、方向一致的所有晶向。 b 负值：标于数字上方，表示同一晶向的相反方向。 c 晶向族：晶体中原子排列情况相同但空间位向不同的一组晶向。用<uvw>表示，数字 相同，但排列顺序不同或正负号不同的晶向属于同一晶向族。晶体结构中那些原子密 度相同的等同晶向称为晶向轴，用<UVW>表示。 <100>：[100] [010] [001] [ 1 00 ] [ 0 1 0 ] [ 00 1 ] <111>：[111] [ 1 1 1 ] [ 1 1 1 ] [ 1 11 ] [ 1 1 1 ] [ 1 1 1 ] [ 1 1 1 ] [ 11 1 ]
图 11 六方晶体中常见的晶面 （2）六方晶系晶向指数的标定 采用四轴坐标，六方晶系晶向指数的标定方法如下：当晶向通过原点时，把晶向沿四个 轴分解成四个分量，晶向 OP 可表示为：OP=ua1+va2+ta3+wC，晶向指数用[uvtw]表示，其中 t=-(u+v)。原子排列相同的晶向为同一晶向族，图 12 中 a1 轴为[ 2 1 1 0 ]，a2 轴[ 1 2 1 0 ]， a3 轴[ 1 1 20 ]均属〈 2 1 1 0 〉 ，其缺点是标定较麻烦。可先用三轴制确定晶向指数[UVW]， 再利用公式转换为[uvtw]。采用三轴坐标系时。C 轴垂直底面，a1、a2 轴在底面上，其夹角 o 为 120 ，如图 12，确定晶向指数的方法同前。采用三轴制虽然指数标定简单，但原子排列 相同的晶向本应属于同一晶向族，其晶向指数的数字却不尽相同，例如 [100] ， [010] ， [ 1 1 0 2 晶面指数的确定 国际上通用的是密勒指数，即用三个数字来表示晶面指数（h k l）。图 4 中的红色晶 面为待确定的晶面，其确定方法如下。
02晶面位向
r* rhkl = 1 d hkl
3、晶体几何计算公式
c×a a×b b .c . sin α c .a . sin β a .b . sin γ = ; b* = = ; c* = = ; a* = V V V V V V v a * h h r v r r r 1 v (h k l ) b * a * b * c * k = (h k l )G * k = rhkl .rhkl = 2 v d c * l l b×c
＊
* * * * * a r*001 * * * * * * *c * β * *
＊
＊
202 ＊ ＊ r*001 ＊ ＊
a* = r*200 = 1/d200 = 2/(a.cos[β-90])= 2/(a.sinβ) b* = r*002 = 1/d002 = 2/b c* = r*001 = 1/d001 = 1/(c.cos[β-90])= 1/(c.sinβ) ＊
r*200 ＊ ＊ β∗
＊
＊
（二）、倒易点阵与正点阵的关系
4、体心点阵
r c
r a
( 200 )
r c (111 )
r r ba r b
r a
r c
(110)
r b
对于体心型，指数和为偶数的晶面才出现；
（二）、倒易点阵与正点阵的关系
5、对于面心型，指数同为偶数或奇数的晶面才出现；
(200)
(111)
400
422
立方系指数表 （续）
25 26 27 29 30 32 33 34 35 36 37 38 40 41 42 43 44 45 46 48 430, 500 431, 501 333, 511 432, 520 521 440 441, 522 433, 530 531 442, 600 610 532, 611 620 443, 540, 541, 621 533 622 542, 630 631 444 430, 500 431, 501 333, 511 432, 520 521 440 441, 522 433, 530 531 442, 600 610 532, 611 620 443, 540, 621 541 533 622 542, 630 631 444 431, 501 333, 511 521 440 433, 530 442, 600 532, 611 620 541 622 631 444 533 622 531 442, 600
晶面指数_六方晶系的晶面指数标定讲解
如：立方晶系，晶面间距公式为
1 d
2
h2 a2
k2 b2
l2 c2
＝ h2 ＋ k2 ＋ l2 a2
d＝/（2sin）
2（ h2 ＋ k2 ＋ l2 ）
∴ sin2 ＝
4a2
已知晶胞参数的（hkl）晶面，当已知波长，可确定衍射方向；
反之，通过测定衍射方向，可以确定晶胞参数，即可确定晶胞的
1 d2
hkl
h2 a2
k2 b2
l2 c2
a、b、c为晶胞参数
单斜
[ 了解 ]
1 d2
hkl
h2 a 2 sin 2
k2 b2
l2 c2 sin 2
2hl cos ac sin 2
三斜
1
1
d
2 hkl
(1 2 cos cos
cos
cos2
cos2
cos2 )
h2 sin 2
[ a2
k 2 sin 2 b2
l 2 sin 2
c2
2hk ab
(cos
cos
cos )
2kl (cos cos cos ) 2hl (cos cos cos )]
bc
ac
例 : 某 斜 方 晶 体 的 a=0.742nm, b=0.494nm,
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点，确定其坐标 3°消除分数，把它们化为互质的最小整数。负数用上划
晶面指数-六方晶系的晶面指数标定
Y
●
X
常见的晶向指数
Z
●
O X
练习
晶向符号 [221]
Y
[001] [111]
●
●
O
●
[100]
●
[010]
1°确定交点坐标，X轴：1/3、 Y轴：1、 Z轴：1/2
2°取倒数 3、1、2 3°消除分数 3、1、2 4°晶面指数（312）
0,0,1
练习
0,1,0 晶面指数（233）
常见的晶面指数
晶面指数的确定方 法
1°确定平面与晶胞三个坐标轴的交点坐标（平面不能通过原点） 2°取在三个坐标轴上截距的倒数。 3°消除分数，把它们化为互质的最小整数h、k、l。负数用上划线
表示。 4°用（）括起来，记为（hkl ）
0,0,1
1°确定交点坐标，X轴：1/2、 Y轴：1、 Z轴：1
2°取倒数 2、1、1 3°消除分数 2、1、1 0,1,0 4°晶面指数（211）
(001)
(110)
(100)
(010)
晶面指数的几点说明：
(111)
1°h,k,l 三个数分别对应于a,b,c三晶轴方向。 2°指数中某一数为“0”，表示晶面与相应的晶轴平行，例如(hk0) 晶面平行于c轴。因交点为，倒数为零。 3° (hkl）中括号代表一组互相平行、面间距相等的晶面。
晶向指数的确定方法
b、c为晶胞参数
1 dh2kl
ah22kb22源自cl22d1 h 2k la2sh2i2nk b2 2c2sl2i2n2 ahsc cli2o ns
01
02
1 dh2k
单斜
l (12c
osc
osc
1
晶体学习题与答案
一、 名词解释（1）阵点;(2）(空间）点阵；（3）晶体结构；（4）晶胞；（5）晶带轴；二、填空（1）晶体中共有 种空间点阵，属于立方晶系的空间点阵有 三种。
（2）对于立方晶系,晶面间距的计算公式为 。
（3）{110}晶面族包括 等晶面。
(4）｛h 1k 1l 1｝和{h 2k 2l 2}两晶面的晶带轴指数[u v w]为 。
(5)(110）和（11-0)晶面的交线是 ;包括有[112]和［123］晶向的晶面是 。
三、计算及简答（1）原子间的结合键共有几种?各自有何特点？(2)在立方晶系的晶胞中，画出（111）、（112）、(011）、（123）晶面和［111］、［101］、[111-]晶向.(3）列出六方晶系{101-2｝ 晶面族中所有晶面的密勒指数，并绘出（101-0）、（112-0）晶面和〔112-0〕晶向。
（4）试证明立方晶系的〔111〕晶向垂直于(111）晶面。
(5）绘图指出面心立方和体心立方晶体的（100)、(110）、及（111)晶面，并求其面间距；试分别指出两种晶体中,哪一种晶面的面间距最大?(6)在立方晶系中，（1-10）、（3-11）、（1-3-2)晶面是否属于同一晶带？如果是，请指出其晶带轴；并指出属于该晶带的任一其他晶面.（7）写出立方晶系的｛111}、{123｝晶面族和〈112>晶向族中的全部等价晶面和晶向的具体指数。
(8）计算立方晶系中（111）和〔111-〕两晶面间的夹角。
(9）若采用四轴坐标系标定六方晶体的晶向指数,应该有什么约束条件？为什么？答 案二、填空（1)14 简单、体心、面心（2）222hkl d h k l =++(3) (110)、（101）、（011）、（1-10）、(1-01） 、(01-1)（4)1122k l u k l =；1122l h v l h =；1122h k w h k = （5）〔001〕 （111-）三、简答及计算（1）略（2）（3）｛101-2｝晶面的密勒指数为（101-2)、(1-012)、(01-12)、（011-2)、（1-102）、(11-02）。
晶面指数六方晶系的晶面指数标定
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点，确定其坐标 3°消除分数，把它们化为互质的最小整数。负数用上划
线表示。
4°用[ ] 括起来，记为[uvw]
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
2hk(c ab
osc
osc
os)
2kl(coscoscos)2hl(coscoscos)]
bc
ac
例 : 某 斜 方 晶 体 的 a=0.742nm, b=0.494nm,
c=0.255nm, 计算d110和d200。
1 d2
hkl
h2 a2
kb22
cl22
1
[001]
晶带定律：凡是属于[uvw]晶
带的晶面，它的晶面指数必须
O
符合hu＋kv＋lw＝0
晶面间距：是两个相邻的平行晶面间的垂直距离，通常 用dhkl 或 d 表示。
晶面间距是现代测试中一个重要的参数。在简单点阵中， 通过晶面指数（hkl）可以方便地计算出相互平行的一组 晶面之间的距离d。
正交（立方、四方、 斜方晶系）
晶面指数的确定方法
1°确定平面与晶胞三个坐标轴的交点坐标（平面不能通过原点） 2°取在三个坐标轴上截距的倒数。
3°消除分数，把它们化为互质的最小整数h、k、l。负数用上划
线表示。 4°用（）括起来，记为（hkl ）
0,0,1 1,0,0
1°确定交点坐标，X轴：1/2、 Y轴：1、 Z轴：1
2°取倒数 2、1、1 3°消除分数 2、1、1 0,1,0 4°晶面指数（211）
• 但是，用三指数表示六方晶系的晶面和晶向 有一个很大的缺点，即晶体学上等价的晶面 和晶向不具有类似的指数。这一点可以从上 图看出。图中六棱柱的两个相邻表面（红面 和绿面）是晶体学上等价的晶面，但其密勒 指数（Miller Indices）却分别是 (110 ) 和(100)。 图中夹角为 60°的两个密排方向 D1 和 D2 是 晶体学上的等价方向，但其晶向指数却分别 是[100]和[110]。
晶体学基础(晶向指数与晶面指数)
1。
4 晶向指数和晶面指数一晶向和晶面1 晶向晶向：空间点阵中各阵点列的方向（连接点阵中任意结点列的直线方向）。
晶体中的某些方向，涉及到晶体中原子的位置，原子列方向，表示的是一组相互平行、方向一致的直线的指向。
2 晶面晶面：通过空间点阵中任意一组阵点的平面（在点阵中由结点构成的平面)。
晶体中原子所构成的平面.不同的晶面和晶向具有不同的原子排列和不同的取向。
材料的许多性质和行为（如各种物理性质、力学行为、相变、X光和电子衍射特性等）都和晶面、晶向有密切的关系。
所以，为了研究和描述材料的性质和行为，首先就要设法表征晶面和晶向.为了便于确定和区别晶体中不同方位的晶向和晶面，国际上通用密勒（Miller)指数来统一标定晶向指数与晶面指数.二晶向指数和晶面指数的确定1 晶向指数的确定方法三指数表示晶向指数[uvw]的步骤如图1所示。
(1)建立以晶轴a，b，c为坐标轴的坐标系，各轴上的坐标长度单位分别是晶胞边长a，b,c,坐标原点在待标晶向上。
(2)选取该晶向上原点以外的任一点P（xa,yb，zc）。
（3)将xa，yb，zc化成最小的简单整数比u，v,w，且u∶v∶w = xa∶yb∶zc.(4）将u，v，w三数置于方括号内就得到晶向指数[uvw］。
图1 晶向指数的确定方法图2 不同的晶向及其指数当然，在确定晶向指数时，坐标原点不一定非选取在晶向上不可.若原点不在待标晶向上，那就需要选取该晶向上两点的坐标P（x1,y1，z1)和Q(x2，y2,z2)，然后将（x1—x2)，（y1-y2)，(z 1-z 2)三个数化成最小的简单整数u ,v ，w ，并使之满足u ∶v ∶w =（x 1-x 2)∶（y 1—y 2)∶（z 1-z 2）.则［uvw ]为该晶向的指数。
显然，晶向指数表示了所有相互平行、方向一致的晶向。
若所指的方向相反，则晶向指数的数字相同，但符号相反,如图3中［001］与[010］。
说明： a 指数意义:代表相互平行、方向一致的所有晶向。
晶面指数六方晶系的晶面指数标定
六方晶系晶面指数标定
根据六方晶系的对称特点，对六方晶系采用a1， a2，a3及c四个晶轴，a1，a2，a3之间的夹角均 为120度，这样，其晶面指数就以(h k i l）四个 指数来表示。
根据几何学可知，三维空间独立的坐标轴最多 不超过三个。前三个指数中只有两个是独立的， 它们之间存在以下关系：i ＝－ ( h + k ) 。
2°指数中某一数为“0”，表示晶面与相应的晶轴平行，例 如(hk0)晶面平行于c轴。因交点为，倒数为零。
3° (hkl）中括号代表一组互相平行、面间距相等的晶面。
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点，确定其坐标 3°消除分数，把它们化为互质的最小整数。负数用上划 线表示。 4°用[ ] 括起来，记为[uvw]
2
得出： d110 =0.41nm, d200=0.37nm
（4）衍射方向（衍射角θ）的确定
将布拉格方程和晶面间距公式联系起来，可得到不同晶系 的衍射方向。
如：立方晶系，晶面间距公式为
h2 ＋ k2 ＋ l2 1 h2 k 2 l 2 ＝ 2 2 2 2 a2 d a b c d＝/（2sin） 4a2 已知晶胞参数的（hkl）晶面，当已知波长，可确定衍射方向； 反之，通过测定衍射方向，可以确定晶胞参数，即可确定晶胞的 大小、形状。【物相分析】 ∴ sin2 ＝ 2（ h2 ＋ k2 ＋ l2 ）
O
●
Y
X
Z
练习
●
O X
Y
晶向符号 [221] [001] [111]
● ●
常见的晶向指数
●
O
●
[010]
[100]
厦门大学材料学院考研 材料测试习题
1、1、X射线衍射在材料分析测试方面有哪些具体的应用？2、X射线的本质是什么？获得X射线的方法有哪些？3、简述X射线管的基本原理。
4、滤波片的作用是什么？应该怎样选择？5、写出求解公式：I）已知同一晶带的两晶面指数，求晶带轴；II）已知两晶带轴平行于同一晶面，求此晶面指数。
6、在立方点阵中画出下面的点阵面和结点方向。
（010）（0-11）（113）[1-10] [201][101]7、将下面几个干涉晶面（属立方晶系）按面间距的大小排列。
（123）（100）（-200）（31-1）（1-21）（210）（110）（-221）（030）（130）8、证明在六方晶系中h+k＝-i。
9、晶面（110）（311）（132）是否属于同一晶带？晶带轴是什么？再指出属于这个晶带的其它几个晶面。
10、试求六方晶系的面间距公式。
（自由选作）2、1、试推导劳厄方程并解释其物理意义。
2、推导布拉格定律。
该定律有何应用？3、试述影响X射线的衍射线束强度的主要因素。
4、什么是结构因子？对衍射强度结果有何影响？5、X射线照射在单晶Au薄膜样品上，表面是（111）晶面，入射波波长为0.1542nm，点阵常数为0.4078nm，求最低角衍射束的衍射角2θ。
6、上题中单晶Au薄膜样品，如果是电子束垂直薄膜表面入射，电子波波长为0.002nm，求晶面（20-2）反射束的衍射角。
7、写出三个立方晶体中与晶面（11-1）和（011）都垂直的晶面。
8、假设薄晶体只有一层晶胞，现有单色平面波垂直该晶体表面入射，试分析该晶体产生的衍射现象。
（选做）9、对于晶粒直径分别为100，75，50，25nm的粉末衍射图形，请计算由于晶粒细化引起的衍射线条宽化幅度（设θ＝45°，λ＝0.15nm）。
又对于晶粒直径为25nm的粉末，试计算θ＝10°、45°、80°时的B值。
10、试计算出金刚石晶体的系统消光规律（F2表达式）。
晶面指数-六方晶系的晶面指数标定
O
Y
●
X
Z
练习
●
O X
晶向符号 [221]
Y
[001] [111]
●
●
常见的晶向指数
O
●
●
[100]
[010]
1°确定交点坐标，X轴：1/3、 Y轴：1、 Z轴：1/2
2°取倒数 3、1、2 3°消除分数 3、1、2 4°晶面指数（312）
0,0,1
练习
1,0,0
0,1,0 晶面指数（233）
常见的晶面指数
O X
晶向符号 [221]
Y
[001] [111]
●
●
常见的晶向指数
O
●
●
[100]
[010]
4、晶带、晶面间距和晶面夹角
晶带：在晶体结构和空间点阵中平行于某一轴向的所有
晶面属于同一晶带。
• 同一晶带中包含不同的晶面，这些晶面的交线互相平行。
• 晶带由所平行的轴向的晶向指数表示。
[001]晶带包含的晶面有： （100）、（010）、（110）、 （110）、（120）等晶面
1 d2
hkl
h2 a2
k2 b2
l2 c2
a、b、c为晶胞参数
单斜
[ 了解 ]
1 d2
hkl
h2 a 2 sin 2
k2 b2
l2 c2 sin 2
2hl cos ac sin 2
三斜
1
1
d
2 hkl
(1 2 cos cos
cos
cos2
cos2
晶面间距(1)
多晶型性或同素异构转变
结构： 体心四方 → 金刚石结构 单位体积：增加 27％ 密度：7.30 g/cm3 → 5.77 g/cm3
原子半径
1、温度与压力的影响 2、结合键的影响 3、配位数的影响 4、原子核外层电子结构的影响
结构：fcc → bcc 致密度： 0.74 → 0.68 体积变化： 0.8％ （而不是 8.8％）
1
h a
2
k b
2
l c
2
(3-7)
d.
dhkl
六方晶系：
1
4 3
h2
hk a2
k
2
2
l c
2
2010年9月
复旦大学材料科学系
12
晶面间距：一组平行晶面中，相邻两个平行晶面之间的距离。
计算公式（简单立方）：
d=a/(h2+k2+l2)1/2
注意： 只适用于简单晶胞；
0.414
近邻配位数与间距
fcc 近邻序号 近邻间距 近邻数
1
12
2
6
hcp 近邻间距 近邻数
12
6
bcc 近邻间距 近邻数
8
6
3
24
2
12
4
12
18
24
5
12
8
6
6
a. 立方晶系：
dhkl
a h2 k2 l2
b.
正方晶系：
dhkl
1
(h2 k a22)l c Nhomakorabea2
c. 正交晶系： dhkl
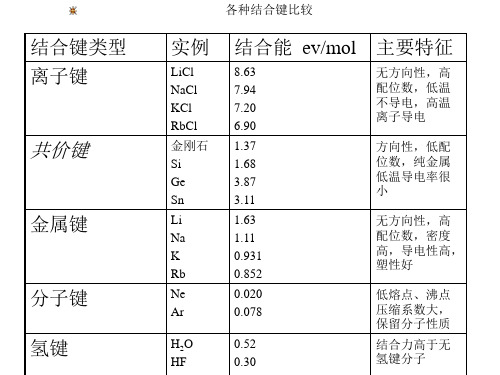
结合键类型 离子键
共价键
金属键
分子键 氢键
各种结合键比较
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
五、十四种布拉菲（Bravais）点阵
在晶体结构理论中，按照对称的特点将自然界的晶体物质 分成七个晶系，每个晶系都有互相对应的空间点阵，布拉 菲于1848年用布拉菲晶胞证实了七种晶系共仅有十四种可 能的点阵，后人为了纪念他的这一重要论断，称为布拉菲 点阵。
六、 晶体的32种点群及符号
任何一种晶体结构都可能同时具有多种对称元素。在有限 对称图形中由宏观对称元素组合成的对称元素群称为点群。 之所以称为点群，是因为构成它的对称元素必须至少相交 于一点，此点称为点群中心。利用数学方法推导出，点群 只可能有32种。
二、 晶面
通过空间点阵任意三结点的 平面是一个晶面，而且同时 还有一系列等间距的晶面与 之平行，组成一组晶面。例 如，图2－2中的晶面，在三 轴上截距长为1、2、3时； 系数的倒数为：1、1/2、 1/3；将三个倒数乘以最小 公倍数6，得三整数为：6、 3、2，则此晶面的晶面指数 为（632）。
当泛指某一晶面指数时，一般用（hkl）代表。如果晶面 与某坐标轴的负方向相交 时，则在相应的指数上加一负 号来表示。例如，（ hk l ）即表示晶面与z轴的负方向相 交。当某晶面与某坐标轴平行时，则认为晶面与该轴的截 距为∞，其倒数为0。
空间点阵研究表明，晶体结构中晶体结构周期性与对称性，原 子排列的规律分属七个晶系。
四、 四种晶胞类型
1、简单晶胞（P）：这类晶胞仅在阵胞的八个顶点上有结 点，用符号P表示。 2、 底心晶胞（C）：这类晶胞除在阵胞的八个顶点上有 结点外，上下两个面的面心上还有结点，用符号C表示。 3、体心晶胞（I）：这类晶胞除在阵胞的八个顶点上有结 点外，在体心有一个结点，用符号I表示。 4、面心晶胞（F）：这类晶胞除在阵胞的八个顶点上有结 点外，每个面心上都有一个结点，用符号F表示。
§2.4 晶面间距、晶面夹角
一、 晶面间距的计算
晶面间距是指两个相邻的平行晶面间的垂直距离。通常用 dhkl或简写为d来表示。
立方晶系的晶面间距公式为：
d
a h2 k 2 l 2
1 h2 k 2 l 2 2 2 a c
四方晶系的晶面间距公式为：
d
三、 晶胞
结点在三维空间形成的最 小单位 (引出: 晶胞参数： a, b, c; α,β,γ ,也称为轴长 与轴角） 可以把点阵按平行六面体 划分为许多大小、形状相 同的格（称为晶格）。最 简单的格子只有顶角有阵 点。晶体学取能反映对称 性的最小晶格来构成空间 格子。这样的重复单元称 为晶胞（布拉菲晶胞或单 位晶胞）。
b
a
c
• 单位晶胞选取的原则是：见图2－1， 基本矢量a、b、c长 度相等的数目最多，其夹角α、β、γ为直角的数目最多， 且晶胞体积最小为条件。一般称a、b、c及α、β、γ 为 点阵参数或晶胞参数，其中a、b、c又称为点阵常数。晶体分为七个晶系（或 六个晶系，菱方用六方晶系表示时）：①立方晶系（C）； ②四方晶系（T）；③六方晶系（H）；④菱方晶系（R）； ⑤正交晶系（O）；⑥单斜晶系（M）；⑦三斜晶系（A）。
§2. 晶体学基础知识
§2.1 §2.2 §2.3 §2.4 晶体的特征 晶体结构的周期性和空间点阵 晶体的定向和 晶面符号 晶面间距、晶面夹角
§2.1 晶体的特征
在自然界的固态物质一般分晶体和非晶体两大类， 绝大多数是晶体，非晶体在一定条件下也可以转 变成晶体。两者的主要差别就在于它们是否具有 周期排列的内部结构。 晶体是由原子、分子或离子等在空间周期地排列 构成的固体物质。在晶体中，原子、分子或离子 等按照一定的方式在空间作周期性规律的排列， 隔一定的距离重复出现，具有三维空间的周期性。
§2.2 晶体结构的周期性和空间点阵
一、 晶体结构的周期性
自从1912年劳厄等人用X射线衍射实验证实了晶体结构具 有周期性后，几十年来，大量的研究探明了成千上万个晶 体结构，充分肯定了晶体的周期性质。
二、 点阵和结构
点阵定义为在空间中由相同的点排列成的无限阵列，每一 点周围都有相同的环境。 把空间点阵想象为晶体的结构框架，点阵中每一阵点所代 表的周期重复的内容（原子、分子或离子）称为晶体的结 构基元，所以晶体结构可表述为： 晶体结构＝点阵＋结构基元
七个晶系
Crystal systems
Cubic Tetragonal Hexagonal Rhomboedric Orthorhombic Monoclinic Triclinic
Lattice Paramater
a = b = c , = = = 90° a = b c , = = = 90° a = b c , = = 90° , = 120° a = b = c , = = 90° a b c , = = = 90° a b c , = = 90°, 90° a b c , °
七、 晶体的230种空间群
在晶体结构内部的无限对称图形中，由宏观对称元素和微 观对称元素共同组合成的对称群，称为空间群。了解和识 别空间群十分重要。空间群能提供晶体的全部对称性资料。 一旦知道空间群和每个晶胞中含有几个化学式单位，常常 可推测出原子在晶胞中的位置，这就是晶体结构测定要完 成的工作。 根据俄国晶体学家费多罗夫的精确分析，空间群共有230 种。
§2.3 晶体的定向和 晶面符号
空间点阵中的结点平面相当于晶体结构中的晶面。在晶体 学中结点平面的空间取向用晶面指数（或称密勒Miller， W.H.指数）来表示。
一、晶向
晶体的定向就是确定晶面在空间的位置。它包括两个方面 的内容，即选择坐标轴（晶轴）和确定单位或其相对比例 （轴率）。 1、晶轴的选择：优先选择对称轴为晶轴；在缺少对称轴 时，可以选择对称面法线。 2、轴单位的确定：轴单位是指在结晶轴上度量距离时， 用作计量单位的那段长度，它等于该行列上的结点间距。