2018年(专业学位)硕士研究生入学考试科目《数学教育学》
2018考研数学试题题型及分值多少介绍

2018考研数学试题题型及分值多少介绍前面整理了考研英语的题型及分值,怎么能少得了数学呢?数学也是考研中一个科目之一。
下面就是店铺给大家整理的2018考研数学试题题型及分值,希望对你有用!2018考研数学题型及分值1. 试卷结构选择题:8题(每题4分);填空题:6题(每题4分);解答题:9题(每题10分左右);满分150分,考试时间3小时。
2. 考试科目及分值高等数学:84分,占56%(4道选择题,4道填空题,5道大题);线性代数:33分,占22%(2道选择题,1道填空题,2道大题);概率论与数理统计:33分,占22%(2道选择题,1道填空题,2道大题)。
注意:数学二不考概率论与数理统计,这一科的分值和试题全加到高等数学中。
3. 考试特点①总分150分,在公共课中所占分值大,全国平均分在70左右,分数之间差距较大;②注重基础,遵循考试大纲出题,考查公式定理,知识点固定;③注重高质量的考点训练与题型总结。
考研数学各个题型答题方法一、选择题对于选择题来说,只有一个正确选项,其余三个都是干扰项,做题的时候只需给出正确选项的字母即可,不用给出推导过程,选对得满分,选错或者不选均得0分,不倒扣分。
在做选择题的时候大家还是有很多方法可选的,常用的方法有:代入法、排除法、图示法、逆推法、反例法等。
如果考试的时候大家发现哪种方法都不奏效的话,大家还可以选择猜测法,至少有25%的正确性。
选择题属于客观题,答案是唯一的,并且考研数学考试中的多选题也是以单选的形式出现的,最终的答案只有一个,评分是不偏不倚的。
选择题的难度一般都是适中的,均为中等难度,没有特别难的,也没有一眼就能看出选项的题目。
选择题主要考查的是考生对基本的数学概念、性质的理解,要求考生能进行简单的推理、判断、计算和比较即可。
所以选择题对于考生来说,要么依靠扎实的知识得分,要么靠自身的运气得分,这32分要想稳拿需要考生在复习的时候深入思考,不能主观臆想,要思考与动手相结合才行。
温州大学2018年专业学位硕士研究生入学考试参考书目_温州大学考研网

温州大学2018年专业学位硕士研究生入学考试参考书目333《教育综合》由我校统一命题,参考书目:1.教育学原理《教育学》王道俊、郭文安主编,人民教育出版社,2001年2.中国教育史《中国教育史》孙培青主编,华东师范大学出版社,2009年3、外国教育史《外国教育史》张斌贤主编,王晨副主编,教育科学出版社,2008年4、教育心理学《教育心理学》张大均主编,人民教育出版社,2005年045101教育管理《教育管理学》罗双凤、叶安珊主编,中国人民大学出版社,2010年2月版,ISBN:9787300116273复试参考书《学校管理学》(第四版)萧宗六主编,人民教育出版社,2011年1月版,ISBN:9787107210495同等学力加试参考书:1.《中国教育史》(第三版)孙培青主编,华东师范大学出版社,2009年6月版,ISBN:97875617645272.《外国教育史》贺国庆、于洪波、朱文富主编,高等教育出版社,2009年8月版,ISBN:9787040266931045102学科教学(思政)《现代思想政治教育学》,张耀灿等著,人民出版社,2006年复试或同等学力加试参考书:1.《思想政治学科教学论》,刘强著,高等教育出版社,2000年2月2.《政治学原理》,王惠岩主编,高等教育出版社,1999年3.《伦理学引论》,章海山主编,高等教育出版社,1999年045103学科教学(语文)《中学语文课程与教学论》,朱绍禹主编,高等教育出版社;复试或同等学力加试参考书:1.《义务教育:语文课程标准(2011年版)》,北京师范大学出版社;2.《普通高中语文课程标准(实验)》,人民教育出版社。
045104学科教学(数学)《数学教育概论》(第二版),张奠宙宋乃庆,高等教育出版社,2009年复试或同等学力及跨专业加试参考书:1.《数学分析》(第三版),华东师大数学系,高等教育出版社,2001年2.《高等代数》(第三版),北京大学数学系,高等教育出版社,1997年3.《常微分方程》第二版),东北师大,高等教育出版社4.《复变函数》(第三版),钟玉泉著,高等教育出版社,2002年045105学科教学(物理)1.《普通物理学教程:力学》(第二版),漆安慎,高等教育出版社,2005年2.《电磁学》(上、下册)(第二版),赵凯华,高等教育出版社,1985年复试或同等学力加试参考书:1.《物理课程与教学论》,朱铁成等主编,浙江大学出版社,2010年12月2.《理论力学》,周衍珀,高等教育出版社,2004年3.《热学》(第二版),李春,高等教育出版社,2008年045106学科教学(化学)《无机及分析化学》,钟国清编,科学出版社,2006年复试或同等学力加试参考书:1.《化学课程与教学论》,陈迪妹编著,科学出版社,2013年1月2.《中学化学实验教学与创新研究》,陈迪妹编著,科学出版社,2014年7月3、《普通化学》,王延安、梅冬、原健安等编,科学出版社,2010年5月045107学科教学(生物)《普通生物学》(第三版),吴相钰陈守良葛明德编著,高等教育出版社,2009复试参考书:《中学生物学教学论》,刘恩山主编,高等教育出版社,2009年同等学力加试参考书:1.《普通动物学》(第3版),刘凌云、郑光美主编,高等教育出版社,1997年2.《植物学》(上册,第2版),陆时万等编,高等教育出版社,1992年3.《植物学》(下册,第2版),吴国芳等编,高等教育出版社,1992年045108学科教学(英语)1、王蔷主编.2006.《英语教学法教程》(第二版),高等教育出版社.2、Stern,H.H.1997.Fundamental Concepts of Language Teaching(10th edition),上海外语教育出版社.045109学科教学(历史)仝晰纲主编:《历史学基础》(中国史部分),山东人民出版社(最新版本);复试或同等学力加试参考书:1.于友西主编:《中学历史教学法》,高等教育出版社(第三版),2009年版。
2018年全国硕士研究生招生考试数学考试大纲(数学一)

2018年全国硕士研究生招生考试数学考试大纲(数学一)高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数函数关系的建立数列极限与函数极限的定义及其性质 函数的左极限和右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:0sin 1lim 1,lim 11xx x x e x →→∞⎛⎫=+= ⎪⎝⎭ 函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质 考试要求1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性 微分中值定理 洛必达(L’Hospital)法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线 函数图形的描绘函数的最大值与最小值 弧微分 曲率的概念 曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy)中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间()b a ,内,设函数()x f 具有二阶导数.当()0>''x f 时,()x f 的图形是凹的;当()0<''x f 时,()x f 的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿-莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值.四、向量代数和空间解析几何考试内容向量的概念向量的线性运算向量的数量积和向量积向量的混合积两向量垂直、平行的条件两向量的夹角向量的坐标表达式及其运算单位向量方向数与方向余弦曲面方程和空间曲线方程的概念平面方程直线方程平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件点到平面和点到直线的距离球面柱面旋转曲面常用的二次曲面方程及其图形空间曲线的参数方程和一般方程空间曲线在坐标面上的投影曲线方程考试要求1.理解空间直角坐标系,理解向量的概念及其表示.2.掌握向量的运算(线性运算、数量积、向量积、混合积),了解两个向量垂直、平行的条件.3.理解单位向量、方向数与方向余弦、向量的坐标表达式,掌握用坐标表达式进行向量运算的方法.4.掌握平面方程和直线方程及其求法.5.会求平面与平面、平面与直线、直线与直线之间的夹角,并会利用平面、直线的相互关系(平行、垂直、相交等))解决有关问题.6.会求点到直线以及点到平面的距离.7.了解曲面方程和空间曲线方程的概念.8.了解常用二次曲面的方程及其图形,会求简单的柱面和旋转曲面的方程.9.了解空间曲线的参数方程和一般方程.了解空间曲线在坐标平面上的投影,并会求该投影曲线的方程.五、多元函数微分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上多元连续函数的性质多元函数的偏导数和全微分全微分存在的必要条件和充分条件多元复合函数、隐函数的求导法二阶偏导数方向导数和梯度空间曲线的切线和法平面曲面的切平面和法线二元函数的二阶泰勒公式多元函数的极值和条件极值多元函数的最大值、最小值及其简单应用考试要求1.理解多元函数的概念,理解二元函数的几何意义.2.了解二元函数的极限与连续的概念以及有界闭区域上连续函数的性质.3.理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和充分条件,了解全微分形式的不变性.4.理解方向导数与梯度的概念,并掌握其计算方法.5.掌握多元复合函数一阶、二阶偏导数的求法.6.了解隐函数存在定理,会求多元隐函数的偏导数.7.了解空间曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程.8.了解二元函数的二阶泰勒公式.9.理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.六、多元函数积分学考试内容二重积分与三重积分的概念、性质、计算和应用两类曲线积分的概念、性质及计算两类曲线积分的关系格林(Green)公式平面曲线积分与路径无关的条件二元函数全微分的原函数两类曲面积分的概念、性质及计算两类曲面积分的关系高斯(Gauss)公式斯托克斯(Stokes)公式散度、旋度的概念及计算曲线积分和曲面积分的应用考试要求1.理解二重积分、三重积分的概念,了解重积分的性质,了解二重积分的中值定理.2.掌握二重积分的计算方法(直角坐标、极坐标),会计算三重积分(直角坐标、柱面坐标、球面坐标).3.理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系.4.掌握计算两类曲线积分的方法.5.掌握格林公式并会运用平面曲线积分与路径无关的条件,会求二元函数全微分的原函数.6.了解两类曲面积分的概念、性质及两类曲面积分的关系,掌握计算两类曲面积分的方法,掌握用高斯公式计算曲面积分的方法,并会用斯托克斯公式计算曲线积分.7.了解散度与旋度的概念,并会计算.8.会用重积分、曲线积分及曲面积分求一些几何量与物理量(平面图形的面积、体积、曲面面积、弧长、质量、质心、形心、转动惯量、引力、功及流量等).七、无穷级数考试内容常数项级数的收敛与发散的概念收敛级数的和的概念级数的基本性质与收敛的必要条件几何级数与级数及其收敛性正项级数收敛性的判别法交错级数与莱布尼茨定理任意项级数的绝对收敛与条件收敛函数项级数的收敛域与和函数的概念幂级数及其收敛半径、收敛区间(指开区间)和收敛域幂级数的和函数幂级数在其收敛区间内的基本性质简单幂级数的和函数的求法初等函数的幂级数展开式函数的傅里叶(Fourier)系数与傅里叶级数狄利克雷(Dirichlet)定理函数在[]l l ,-上的傅里叶级数函数在[]l ,0上的正弦级数和余弦级数考试要求1.理解常数项级数收敛、发散以及收敛级数的和的概念,掌握级数的基本性质及收敛的必要条件.2.掌握几何级数与级数的收敛与发散的条件.3.掌握正项级数收敛性的比较判别法和比值判别法,会用根值判别法.4.掌握交错级数的莱布尼茨判别法.5.了解任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系.6.了解函数项级数的收敛域及和函数的概念.7.理解幂级数收敛半径的概念,并掌握幂级数的收敛半径、收敛区间及收敛域的求法.8.了解幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分),会求一些幂级数在收敛区间内的和函数,并会由此求出某些数项级数的和.9.了解函数展开为泰勒级数的充分必要条件.10.掌握()()αx x x x e x ++1,1ln ,cos ,sin ,的麦克劳林(Maclaurin)展开式,会用它们将一些简单函数间接展开为幂级数.11.了解傅里叶级数的概念和狄利克雷收敛定理,会将定义在[]l l ,-上的函数展开为傅里叶级数,会将定义在[]l ,0上的函数展开为正弦级数与余弦级数,会写出傅里叶级数的和函数的表达式.八、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程伯努利(Bernoulli)方程全微分方程可用简单的变量代换求解的某些微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程欧拉(Euler)方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法.3.会解齐次微分方程、伯努利方程和全微分方程,会用简单的变量代换解某些微分方程.4.会用降阶法解下列形式的微分方程:()()()()y y f y y x f y x f y n '='''=''=,,,和5.理解线性微分方程解的性质及解的结构.6.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.7.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.8.会解欧拉方程.9.会用微分方程解决一些简单的应用问题.线性代数一、行列式考试内容行列式的概念和基本性质行列式按行(列)展开定理考试要求1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵考试内容矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件,理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.理解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量考试内容向量的概念向量的线性组合与线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量空间及其相关概念维向量空间的基变换和坐标变换过渡矩阵向量的内积线性无关向量组的正交规范化方法规范正交基正交矩阵及其性质考试要求1.理解n维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.理解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.理解向量组等价的概念,理解矩阵的秩与其行(列)向量组的秩之间的关系.5.了解n维向量空间、子空间、基底、维数、坐标等概念.6.了解基变换和坐标变换公式,会求过渡矩阵.7.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.8.了解规范正交基、正交矩阵的概念以及它们的性质.四、线性方程组考试内容线性方程组的克拉默(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解解空间非齐次线性方程组的通解考试要求l.会用克拉默法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系、通解及解空间的概念,掌握齐次线性方程组的基础解系和通解的求法.4.理解非齐次线性方程组解的结构及通解的概念.5.掌握用初等行变换求解线性方程组的方法.五、矩阵的特征值和特征向量考试内容矩阵的特征值和特征向量的概念、性质相似变换、相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵的特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,掌握将矩阵化为相似对角矩阵的方法.3.掌握实对称矩阵的特征值和特征向量的性质.六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1.掌握二次型及其矩阵表示,了解二次型秩的概念,了解合同变换与合同矩阵的概念,了解二次型的标准形、规范形的概念以及惯性定理.2.掌握用正交变换化二次型为标准形的方法,会用配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.概率论与数理统计一、随机事件和概率考试内容随机事件与样本空间事件的关系与运算完备事件组概率的概念概率的基本性质古典型概率几何型概率条件概率概率的基本公式事件的独立性独立重复试验考试要求1.了解样本空间(基本事件空间)的概念,理解随机事件的概念,掌握事件的关系及运算.2.理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率和几何型概率,掌握概率的加法公式、减法公式、乘法公式、全概率公式以及贝叶斯(Bayes)公式.3.理解事件独立性的概念,掌握用事件独立性进行概率计算;理解独立重复试验的概念,掌握计算有关事件概率的方法.二、随机变量及其分布考试内容随机变量随机变量分布函数的概念及其性质离散型随机变量的概率分布连续型随机变量的概率密度常见随机变量的分布随机变量函数的分布考试要求1.理解随机变量的概念,理解分布函数{}()()F x P x x x =≤-∞<<+∞的概念及性质,会计算与随机变量相联系的事件的概率.2.理解离散型随机变量及其概率分布的概念,掌握0-1分布、二项分布(,)B n p 、几何分布、超几何分布、泊松(Poisson)分布()P λ及其应用.3.了解泊松定理的结论和应用条件,会用泊松分布近似表示二项分布.4.理解连续型随机变量及其概率密度的概念,掌握均匀分布(,)U a b 、正态分布2(,)N μσ、指数分布及其应用,其中参数为(0)λλ>的指数分布()λE 的概率密度为()⎩⎨⎧≤>=-0,00,x x e f x 若若λλλ 5.会求随机变量函数的分布.三、多维随机变量及其分布考试内容多维随机变量及其分布二维离散型随机变量的概率分布、边缘分布和条件分布二维连续型随机变量的概率密度、边缘概率密度和条件密度随机变量的独立性和不相关性常用二维随机变量的分布两个及两个以上随机变量简单函数的分布考试要求1.理解多维随机变量的概念,理解多维随机变量的分布的概念和性质,理解二维离散型随机变量的概率分布、边缘分布和条件分布,理解二维连续型随机变量的概率密度、边缘密度和条件密度,会求与二维随机变量相关事件的概率.2.理解随机变量的独立性及不相关性的概念,掌握随机变量相互独立的条件.3.掌握二维均匀分布,了解二维正态分布221212(,,,;)N p μμσσ的概率密度,理解其中参数的概率意义.4.会求两个随机变量简单函数的分布,会求多个相互独立随机变量简单函数的分布.四、随机变量的数字特征考试内容随机变量的数学期望(均值)、方差、标准差及其性质随机变量函数的数学期望矩、协方差、相关系数及其性质考试要求1.理解随机变量数字特征(数学期望、方差、标准差、矩、协方差、相关系数)的概念,会运用数字特征的基本性质,并掌握常用分布的数字特征.2.会求随机变量函数的数学期望.五、大数定律和中心极限定理考试内容切比雪夫(Chebyshev)不等式切比雪夫大数定律伯努利(Bernoulli)大数定律辛钦(Khinchine)大数定律棣莫弗-拉普拉斯(DeMoivre-Laplace)定理列维-林德伯格(Levy-Lindberg)定理 考试要求1.了解切比雪夫不等式.2.了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律(独立同分布随机变量序列的大数定律).3.了解棣莫弗-拉普拉斯定理(二项分布以正态分布为极限分布)和列维-林德伯格定理(独立同分布随机变量序列的中心极限定理).六、数理统计的基本概念考试内容总体个体简单随机样本统计量样本均值样本方差和样本矩2χ分布 t 分布 F 分布 分位数 正态总体的常用抽样分布考试要求1.理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念,其中样本方差定义为 ()21211∑=--=n i i X X n S 2.了解2χ分布、t 分布和F 分布的概念及性质,了解上侧分位数的概念并会查表计算.3.了解正态总体的常用抽样分布.七、参数估计考试内容点估计的概念估计量与估计值矩估计法最大似然估计法估计量的评选标准区间估计的概念单个正态总体的均值和方差的区间估计两个正态总体的均值差和方差比的区间估计 考试要求1.理解参数的点估计、估计量与估计值的概念.2.掌握矩估计法(一阶矩、二阶矩)和最大似然估计法.3.了解估计量的无偏性、有效性(最小方差性)和一致性(相合性)的概念,并会验证估计量的无偏性.4、理解区间估计的概念,会求单个正态总体的均值和方差的置信区间,会求两个正态总体的均值差和方差比的置信区间.八、假设检验考试内容显著性检验假设检验的两类错误单个及两个正态总体的均值和方差的假设检验考试要求1.理解显著性检验的基本思想,掌握假设检验的基本步骤,了解假设检验可能产生的两类错误.2.掌握单个及两个正态总体的均值和方差的假设检验.。
赣南师范大学2018年《915数学教学论》考研专业课真题试卷

二 、 辨 析 题 (共
2题 ,每 题 15分 ,合 计 sO分 ) 1.义 务教育数 学课程标准 (⒛ 11版 )指 出:有 效的教学活动是学生学与
教师教 的统一 ,学 生是学习的主体 ,教 师是学习的组织者 、引导者与合 作者 。因此有人认为 :数 学教师只要做好组织、引导并适当参与学生学 习就行 。请对这 一说法进行评判 ,并 说明理由。
2.有 人提出:在 数学教学中运用信息技术 ,主 要是帮助数学教师把教学
中难 以呈现的数学过程以动态 、色彩 、声音等多种媒体组合的方式加 以 呈现 ,至 于其他方面没有更多的用处 。请对这一说法进行评判 ,并 说明 理由。 三、论述题 (共 2题 ,每 题 zO分 ,合 计 40分 ) 1.新 教师入 职初期 ,往 往充满热情 ,对 各项工作 :备 课 、上课 、课外作 业、第 二课堂等 ,全 心投入 。不过 ,在 教学中却常常陷入困境 :精 心准 备的学习内容 ,学 生却不感兴趣 。请论述造成这一状况的原因。 ” “ 2.《 义务教育数学课程标准 (⒛ 11版 )》 对 课程 内容 的描述中,提 出 ” ” “ “ 了应当注重发展学生的 运算能力 。请简要论述 运算能力 ,并 概要 ” “ 说明如何发展学生的 运算能力 。 四、案例分析题 (共 2题 ,每 题 ⒛ 分 ,合 计 00分 ) 1.案 例 1:《 电脑基础知识 》课堂实录 (片 段 ) 许老师在学校 里教 电脑课 ,这 是一门必修课 。她所教的班大概 M 个学生,学 生能力差异很大 。今天 ,她 要讲授微机系统的组成要素,为 “ 今天的课是上一次课 什 必须掌握的文字处理做铺垫。 学生即将要学的、 ” “ ” 么是电脑 的后续课程 ,也 是前一个学习单元 电脑如何 工作 的后续 单元 。开学的第二周 ,我 们旁听了许老师 当天的第一 堂课程 。 许老师:(上 课铃响 了)好 ,安 静。把电脑关掉 。我们还需要花几节 课讲电脑基础知识 。之后 ,你 们就能使用电脑 了,孩 子们 ,耐 心 点。 上个星期 ,我 们讲 了什么是电脑 。我们所具有 的选择、记忆 、处理 信息的能力与电脑类似 。电脑容纳信息的过程 ,有 点类似于人工整理柜 子;电 脑处理统计信息的过程 ,有 点类似于算盘 ;电 脑创建符号和编码 有点类似于创作音乐或绘制图画。这些是 电脑的各种若 气 +饥
大学考研数学(2018.11.13)

显然 g'(x) 1 1 x 0 ,当x 0时 1 x 1 x
又∵ g(0) 0
g(x) 0, 当x 0时
令x 1 n
可得g(1 ) 0 即 ln(1 1 ) 1
n
nn
19
返璞归真
考研数学概览
20
(I
)
(II) 根据(I )
证明:对任意的正1 整数ln(nn, 1都) 有ln
考前一周
速览自己总结的重难点,公式、定理,延续应试感觉. 考场踩点,租酒店……
26
• 课本
– 自己的课本为最佳 – 微积分:同济各种版本 – 线性代数:同济版 – 概率论与数理统计:浙大盛骤版
如何备考
27
• 参考书
– 历年真题集 – 李正元版复习全书 – 王式安、李永乐版复习全书
28
Sina微博:新东方张伟
23
n
2
n 1
an
1
1 2
....
1 n
ln
n
所以
0
1 n
an
1
即an
有界
而an1
an
ln n ln(n 1)
1 n 1
0
可见an
单减
数列an 收敛
21
若x1 x2 ;显然(x1 ) f (x1 ) g(x1) 0; 又(a) f (a) g(a) 0 (b) f (b) g(b) 0
11~12月
数学基础巩固(课本、讲义)过n?遍 专业课学习,英语开始单词。
强化第一阶段 数学知识点归类,考研真题的分知识点练习。
复习全书争取做完第一遍。
强化第二阶段,做套题(真题,套/周),开始复习政治。 复习全书第二遍。
2018年硕士研究生招生考试大纲 .doc

2018年硕士研究生招生考试大纲002 信息科学与工程学院目录初试考试大纲 1610高等数学 1638 量子力学 1953 声学基础 3806 普通物理 5807数据结构7808地理信息系统8810数字电子技术10341农业知识综合三11910高级程序设计12911软件工程14912数据结构和软件工程16930程序设计基础19940 计算机网络与安全 21946 信号与系统23954计算机基础综合24复试考试大纲28现代物理基础28科技英语(光学、凝聚态物理) 30现代光学基础31电子技术基础33科技英语(光学工程专业(学术型080300和专业型085202)34 电子技术A 35通信原理36计算机系统结构38面向对象的程序设计40数据库系统41程序设计实践43保密概论45安全程序设计实践47农业信息化概论50数字信号处理52C++语言编程54科技英语(地图学与地理信息系统、测绘工程)56 光学电磁学57信号与系统59数字电子技术61科技英语(海洋探测技术、摄影测量与遥感)62同等学力加试科目考试大纲63数据结构63软件工程65初试考试大纲610高等数学一、考试性质高等数学是理、工科专业硕士研究生入学考试的专业基础课程。
高等数学入学考试是为招收理、工科专业硕士研究生而实施的具有选拔功能的水平考试,它的指导思想是既要为国家选拔具有较强分析问题与解决问题能力的高层次人才,又要有利于促进高等学校高等数学课程教学质量的提高。
二、考察目标要求考生能系统理解高等数学的基本概念和基本原理,掌握高等数学的基本思想与方法,具有较好的逻辑推理能力、空间想象能力、计算能力以及运用所学知识分析问题和解决问题的能力。
三、考试形式本考试为闭卷考试,满分为150分,考试时间为180分钟。
试卷结构:高等数据75%,线性代数25%。
四、考试内容(一)高等数学(75%)考试内容:函数的极限与连续,一元函数微积分及其应用,向量代数与空间解析几何,多元函数微积分及其应用,场论,含参变量积分,无穷级数,常微分方程及其应用。
2018年教育部最新硕士研究生指导专业目录

2018年教育部最新硕士研究生指导专业目录注:二级学科名称仅作参考专业名称后加★表示专业硕士01哲学010101马克思主义哲学010102中国哲学010103外国哲学010104逻辑学010105伦理学010106美学010107宗教学010108科学技术哲学02 经济学0201理论经济学020101政治经济学020102经济思想020103经济史020104西方经济学020105世界经济020106人口、资源与环境经济学0202应用经济学020201国民经济学020202区域经济学020203财政学020204金融学020205产业经济学020206国际贸易学020207劳动经济学020208统计学020209数量经济学020210国防经济0251金融★0252应用统计★0253税务★0254国际商务★0255保险★0256资产评估★0257审计★03 法学0301法学030101法学理论030102法律史030103宪法学与行政法学030104刑法学030105民商法学030106诉讼法学030107经济法学030108环境与资源保护法学030109国际法学030110军事法学0302政治学030201政治学理论030202中外政治制度030203科学社会主义与国际共产主义运动030204中共党史030206国际政治030207国际关系030208外交学0303社会学030301社会学030302人口学030303人类学030304民俗学0304民族学030401民族学030402马克思主义民族理论与政策030403中国少数民族经济030404中国少数民族史030405中国少数民族艺术0305马克思主义理论030501马克思主义基本原理030502马克思主义发展史030503马克思主义中国化研究030504国外马克思主义研究030505思想政治教育030506中国近现代史基本问题研究0306 公安学0351法律★035101法律硕士(非法学)035102法律硕士(法学)0352社会工作★0353警务★04 教育学0401教育学040101教育学原理040102课程与教学论040103教育史040104比较教育学040105学前教育学040106高等教育学040107成人教育学040108职业技术教育学040109特殊教育学040110教育技术学0402心理学040201基础心理学040202发展与教育心理学040203应用心理学0403体育学040301体育人文社会学040302运动人体科学040303体育教育训练学040304民族传统体育学0451教育★045101教育管理045102学科教学(思政)045103学科教学(语文)045104学科教学(数学)045105学科教学(物理)045106学科教学(化学)045107学科教学(生物)045108学科教学(英语)045109学科教学(历史)045110学科教学(地理)045111学科教学(音乐)045112学科教学(体育)045113学科教学(美术)045114现代教育技术045115小学教育045116心理健康教育045117科学与技术教育045118学前教育045119特殊教育0452体育★045201体育教学045202运动训练045203竞赛组织045204社会体育指导0453汉语国际教育★0454应用心理★05 文学0501中国语言文学050101文艺学050102语言学及应用语言学050103汉语言文字学050104中国古典文献学050105中国古代文学050106中国现当代文学050107中国少数民族语言文学050108比较文学与世界文学0502外国语言文学050201英语语言文学050202俄语语言文学050203法语语言文学050204德语语言文学050205日语语言文学050206印度语语言文学050207西班牙度语语言文学050208阿拉伯语语言文学050209欧洲语言文学050210亚非语言文学050211外国语言学及应用语言学0503新闻传播学050301新闻学050302传播学0551翻译★055101英语笔译055102英语口译055103俄语笔译055104俄语口译055105日语笔译055106日语口译055107法语笔译055108法语口译055109德语笔译055110德语口译055111朝鲜语笔译055112朝鲜语口译0552 新闻与传播★0553 出版★06 历史学0601 考古学0602 中国史0603 世界史0601历史学060101 史学理论及史学史060102 考古学及博物馆学060103 历史地理学060104 历史文献学(含∶敦煌学、古文字学)060105 专门史060106 中国古代史060107 中国近现代史060108 世界史0651文物与博物馆★07 理学0701数学070101基础数学070102计算数学070103概率论与数理统计070104应用数学070105运筹学与控制论0702物理学070201理论物理070202粒子物理与原子核物理070203原子与分子物理070204等离子体物理070205凝聚态物理070206声学070207光学070208无线电物理0703化学070301无机化学070302分析化学070303有机化学070304物理化学070305高分子化学与物理0704天文学070401天体物理070402天体测量与天体力学0705地理学070501自然地理学070502人文地理学070503地图学与地理信息系统0706大气科学070601气象学070602大气物理学与大气环境0707海洋科学070701物理海洋学070702海洋化学070703海洋生物学070704海洋地质0708地球物理学070801固体地球物理学070802空间物理学0709地质学070901矿物学、岩石学、矿床学070902地球化学070903古生物学与地层学070904构造地质学070905第四纪地质学0710生物学071001植物学071002动物学071003生理学071004水生生物学071005微生物学071006神经生物学071007遗传学071008发育生物学071009细胞生物学071010生物化学与分子生物学071011生物物理学071012生态学0711系统科学071101系统理论071102系统分析与集成0712科学技术史0713 生态学0714 统计学(可授理学、经济学学位)08 工学0801力学080101一般力学与力学基础080102固体力学080103流体力学080104工程力学0802机械工程080201机械制造及其自动化080202机械电子工程080203机械设计及理论080204车辆工程0803光学工程0804仪器科学与技术080401精密仪器及机械080402测试计量技术及仪器0805材料科学与工程080501材料物理与化学080502材料学080503材料加工工程0806冶金工程080601冶金物理化学080602钢铁冶金080603有色金属冶金0807动力工程及工程热物理080701工程热物理080702热能工程080703动力机械及工程080704流体机械及工程080705制冷及低温工程080706化工过程机械0808电气工程080801电机与电器080802电力系统及其自动化080803高电压与绝缘技术080804电力电子与电力传动080805电工理论与新技术0809电子科学与技术080901物理电子学080902电路与系统080903微电子学与固体电子学080904电磁场与微波技术0810信息与通信工程081001通信与信息系统081002信号与信息处理0811控制科学与工程081101控制理论与控制工程081102检测技术与自动化装置081103系统工程081104模式识别与智能系统081105导航、制导与控制0812计算机科学与技术081201计算机系统结构081202计算机软件与理论081203计算机应用技术0813建筑学081301建筑历史与理论081302建筑设计及其理论081303城市规划与设计081304 建筑技术科学0814土木工程081401岩土工程081402结构工程081403市政工程081404供热、供燃气、通风及空调工程081405防灾减灾工程及防护工程081406桥梁与隧道工程0815水利工程081501水文学及水资源081502水力学及河流动力学081503水工结构工程081504水利水电工程081505港口、海岸及近海工程0816测绘科学与技术081601大地测量学与测量工程081602摄影测量与遥感081603地图制图学与地理信息工程0817化学工程与技术081701化学工程081702化学工艺081703生物化工081704应用化学081705工业催化0818地质资源与地质工程081801矿产普查与勘探081802地球探测与信息技术081803地质工程0819矿业工程081901采矿工程081902矿物加工工程081903安全技术及工程0820石油与天然气工程082001油气井工程082002油气田开发工程082003油气储运工程0821纺织科学与工程082101纺织工程082102纺织材料与纺织品设计082103纺织化学与染整工程082104服装设计与工程0822轻工技术与工程082201制浆造纸工程082202制糖工程082203发酵工程082204皮革化学与工程0823交通运输工程082301道路与铁道工程082302交通信息工程及控制082303交通运输规划与管理082304载运工具运用工程0824船舶与海洋工程082401船舶与海洋结构物设计制造082402轮机工程082403水声工程0825航空宇航科学与技术082501飞行器设计082502航空宇航推进理论与工程082503航空宇航制造工程082504人机与环境工程0826兵器科学与技术082601武器系统与运用工程082602兵器发射理论与技术082603火炮、自动武器与弹药工程082604军事化学与烟火技术0827核科学与技术082701核能科学与工程082702核燃料循环与材料082703核技术及应用082704辐射防护及环境保护0828农业工程082801农业机械化工程082802农业水土工程082803农业生物环境与能源工程082804农业电气化与自动化0829林业工程082901森林工程082902木材科学与技术082903林产化学加工工程0830环境科学与工程083001环境科学083002环境工程0831生物医学工程0832食品科学与工程083201食品科学083202粮食、油脂及植物蛋白工程083203农产品加工及贮藏工程083204水产品加工及贮藏工程0833 城乡规划学0834 风景园林学(可授工学、农学学位)0835 软件工程0836 生物工程0837 安全科学与工程0838 公安技术0839 网络空间安全0851建筑学★0853城市规划★0854 电子信息★0855 机械★0856 材料与化工★0857 资源与环境★0858 能源动力★0859 土木水利★0860 生物与医药★0861 交通运输★09 农学0901作物学090101作物栽培学与耕作学090102作物遗传育种0902园艺学090201果树学090202蔬菜学090203茶学0903农业资源与环境090301土壤学090302植物营养学0904植物保护090401植物病理学090402农业昆明与害虫防治090403农药学0905畜牧学090501动物遗传育种与繁殖090502动物营养与饲料科学090504特种经济动物饲养0906兽医学090601基础兽医学090602预防兽医学090603临床兽医学0907林学090701林木遗传育种090702森林培育090703森林保护学090704森林经理学090705野生动植物保护与利用090706园林植物与观赏园艺090707水土保持与荒漠化防治0908水产090801水产养殖090802捕捞学090803渔业资源0909草学0951农业★095101作物095102园艺095103农业资源利用095104植物保护095105养殖095106草业095107林业095108渔业095109农业机械化095110农村与区域发展095111农业科技组织与服务095112农业信息化095113食品加工与安全095114设施农业095115种业0952兽医★0953风景园林★0954林业★10 医学1001基础医学100101人体解剖与组织胚胎学100102免疫学100103病原生物学100104病理学与病理生理学100105法医学100106放射医学100107航空、航天与航海医学1002临床医学100201内科学100202儿科学100203老年医学100204神经病学100205精神病与精神卫生学100206皮肤病与性病学100207影像医学与核医学100208临床检验诊断学100209护理学100210外科学100211妇产科学100212眼科学100213耳鼻咽喉科学100214肿瘤学100215康复医学与理疗学100216运动医学100217麻醉学100218急诊医学1003口腔医学100301口腔基础医学100202口腔临床医学1004公共卫生与预防医学100401流行病与卫生统计学100402劳动卫生与环境卫生学100403营养与食品卫生学100404儿少卫生与妇幼保健学100405卫生毒理学100406军事预防医学1005中医学100501中医基础理论100502中医临床基础100503中医医史文献100504方剂学100505中医诊断学100506中医内科学100507中医外科学100508中医骨伤科学100509中医妇科学100510中医儿科学100511中医五官科学100512针灸推拿学100513民族医学1006中西医结合100601中西医结合基础100602中西医结合临床1007药学100701药物化学100702药剂学100703生药学100704药物分析学100705微生物与生化药学100706药理学1008中药学1009特种医学1011护理学1051临床医学★105101内科学105102儿科学105103老年医学105104神经病学105105精神病与精神卫生学105106皮肤病与性病学105107影像医学与核医学105108临床检验诊断学105109外科学105110妇产科学105111眼科学105112耳鼻喉科学105113肿瘤学105114康复医学与理疗学105115运动医学105116麻醉学105117急诊医学105118中医内科学105119中医外科学105120中医骨伤科学105121中医妇科学105122中医儿科学105123中医五官科学105124针灸推拿学105125民族医学105126中西医结合临床105127全科医学105128临床病理学1052口腔医学★1053公共卫生★1054护理★1055药学★1056中药学★1057中医★11 军事学1101军事思想及军事历史110101军事思想110102军事历史1102战略学110201军事战略学110202战争动员学110203国防动员学1103战役学110301联合战役学110302军种战役学1104战术学110401合同战术学110402兵种战术学1105军队指挥学110501作战指挥学110502军事运筹学110503军事通信学110504军事情报学110505密码学1106军制学110601军事组织编制学110602军队管理学110603军事法制学110604军事管理学1107军队政治工作学1108军事后勤学110801军事后勤建设学110802后方专业勤务110804军事物流学1109军事装备学110902军事装备保障学110903军事装备管理学1110军事训练学1151军事★115101军事指挥115102军队政治工作115103军事后勤115104军事装备12 管理学1201管理科学与工程1202工商管理120201会计学120202企业管理120203旅游管理120204技术经济及管理1203农林经济管理120301农业经济管理120302林业经济管理1204公共管理120401行政管理120402社会医学与卫生事业管理120403教育经济与管理120404社会保障120405土地资源管理1205图书情报与档案管理120501图书馆学120502情报学120503档案学1251工商管理★1252公共管理★1253会计★1254旅游管理★1255图书情报★1256工程管理★13 艺术学1301 艺术学理论1302 音乐与舞蹈学1303 戏剧与影视学1304 美术学1305设计学(可授艺术学、工学学位)1351艺术★135101音乐135102戏剧135103戏曲135104电影135105广播电视135106舞蹈135107美术135108艺术设计。
2018硕士研究生入学考试大纲

2018硕士研究生入学考试大纲考试科目名称:高等代数一、考试要求:1.一元多项式理论:①掌握多项式的整除理论;② 会求最大公因式与最小公倍式;③ 掌握复系数、实系数与有理系数多项式的因式分解理论。
2.行列式理论:①理解行列式的定义、熟悉行列式的性质;②掌握有特殊结构的n阶行列式的计算;③会用Laplace展开定理。
3.线性方程组理论:①会用Cramer法则进行方程组求解;②掌握向量的线性相关与线性无关的定义及判别;③掌握线性方程组有解的判别法;④掌握线性方程组解的结构。
4.矩阵理论:①熟悉矩阵的各种运算与运算律;②会求矩阵的逆;③理解矩阵分块与分块矩阵;④掌握初等矩阵的性质与基本用法;5. 二次型理论:①掌握二次型的化简与标准型;②掌握正定、半正定矩阵的定义与基本性质;③熟悉惯性定理。
6. 线性空间理论:①掌握线性空间的基底和维数的定义与性质;②掌握线性空间基变换与坐标变换;③掌握子空间以及它们的交与直和的性质;④理解线性空间的同构。
7. 线性变换理论:①掌握线性变换的运算及其矩阵表示;②会求线性变换与矩阵的特征值与特征向量;③掌握相似矩阵与某些矩阵的对角化;④掌握线性变换的值域与核及其性质;⑤理解不变子空间;8. 欧式空间理论:①掌握内积空间与欧式空间的定义与性质;②掌握正交变换与正交矩阵的性质;③理解对称变换;④掌握实对称矩阵及其对角化理论。
二、考试内容:1) 一元多项式理论a: 多项式的整除,b: 最大公因式与最小公倍式,c: 复系数、实系数与有理系数多项式的因式分解理论。
2) 行列式a: 行列式的定义、性质与计算,b: Laplace展开定理。
3) 线性方程组理论a: Cramer法则,b: 线性相关与线性无关,c: 线性方程组有解的判别,d: 线性方程组解的结构。
4) 矩阵a: 矩阵的各种运算与运算律,b: 矩阵的逆,c: 分块矩阵,d: 初等矩阵,5) 二次型a: 二次型的化简与标准型,b: 正定二次型与正定矩阵,半定阵。
广西师范大学2018年学科数学864答案

⼴西师范⼤学2018年学科数学864答案⼴西师范⼤学2018年研究⽣⼊学考试试题科⽬名称:数学教育学科⽬代码:864适⽤专业代码及名称:045104学科教学(数学)(答案必须站在考试专⽤答题纸上。
否则造成错批、漏批等后果⾃负)⼀、说明题:(共4⼩题,每⼩题15分,共60分)1.什么是数学核⼼素养?为什么要加强对学⽣数学核⼼素养的培育?参考:⾼中数学课程标准(2017年版)PP4学科核⼼素养是育⼈价值的集中体现,是学⽣通过学科学习⽽逐步形成的正确价值观、必备品格和关键能⼒。
数学学科核⼼素养是数学课程⽬标的集中体现,是具有数学基本特征的思维品质、关键能⼒以及情感、态度与价值观的综合体现,是在数学学习和应⽤的过程中逐步形成和发展的。
数学学科核⼼素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。
这些数学学科核⼼素养既相对独⽴、⼜相互交融,是⼀个有机的整体。
1.数学抽象数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养。
主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出⼀般规律和结构,并⽤数学语⾔予以表征。
数学抽象是数学的基本思想,是形成理性思维的重要基础,反映了数学的本质特征,贯穿在数学产⽣、发展、应⽤的过程中。
数学抽象使得数学成为⾼度概括、表达准确、结论⼀般、有序多级的系统。
数学抽象主要表现为:获得数学概念和规则,提出数学命题和模型,形成数学⽅法与思想,认识数学结构与体系。
通过⾼中数学课程的学习,学⽣能在情境中抽象出数学概念、命题、⽅法和体系,积累从具体到抽象的活动经验;养成在⽇常⽣活和实践中⼀般性思考问题的习惯,把握事物的本质,以简驭繁;运⽤数学抽象的思维⽅式思考并解决问题。
2.逻辑推理逻辑推理是指从⼀些事实和命题出发,依据规则推出其他命题的素养。
主要包括两类:⼀类是从特殊到⼀般的推理,推理形式主要有归纳、类⽐;--类是从⼀般到特殊的推理,推理形式主要有演绎。
2018杭州师范大学硕士研究生考研真题841数学教育学

杭州师范大学
2018年招收攻读硕士研究生入学考试题
考试科目代码:841
考试科目名称:数学教育学
说明:考生答题时一律写在答题纸上,否则漏批责任自负。
一、简答题(每题10分,共60分)
1.简述数学概念及其分类。
2.简述信息技术在数学课堂教学中的应用。
3.简述现代数学教学的基本特征。
4.简述数学语言的特征及分类。
5.简述“空间观念”包括的主要内容。
6.简述数学命题教学的一般模式。
二、计算题(每题10分,共20分)
1.求011lim()sin x x x
→-2.m 取什么值时,方程22(32)120x m x -++=与24(92)360x m x --+=有一个相同的根?
三、论述题(每题15分,共30分)
1.谈谈你对验证型数学实验的认识,并举例说明。
2.谈谈你对数学教学中估算与精算的理解。
四、案例设计(共40分)
附件是初中“等腰三角形”的教材内容。
请依据该内容设计一个详细的教案。
要求包括以下内容:学情分析,教材分析,教学目标,重点、难点,教学方法,教学过程(反映出教学指导思想和师生的活动情况。
)(不低于1000字)。
全国硕士研究报告生入学统一考试数学考试大纲数学

2018全国硕士研究生入学统一考试数学考试大纲数学三考试科目微积分、线性代数、概率论与数理统计试卷结构一、总分试卷满分为150分,考试时间180分钟二、内容比例微积分约56 %线性代数约22 %概率论与数理统计约22 %三、题型结构单项选择题 8小题,每小题4分,共32分填空题 6小题,每小题4分,共24分解答题<包括证明题) 9小题,共94分微积分一、函数、极限、连续考试内容函数的概念及表示法,函数的有界性、单调性、周期性和奇偶性,复合函数、反函数、分段函数和隐函数,基本初等函数的性质及其图形,初等函数,函数关系的建立数列极限与函数极限的定义及其性质,函数的左极限和右极限,无穷小量和无穷大量的概念及其关系,无穷小量的性质及无穷小量的比较,极限的四则运算,极限存在的两个准则:单调有界准则和夹逼准则,两个重要极限:,函数连续的概念,函数间断点的类型,初等函数的连续性,闭区间上连续函数的性质。
考试要求1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系。
2.了解函数的有界性、单调性、周期性和奇偶性。
3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。
4.掌握基本初等函数的性质及其图形,了解初等函数的概念。
5.了解数列极限和函数极限<包括左极限和右极限)的概念。
6.了解极限的性质与极限存在的两个准则,掌握极限的四则运算法则,掌握利用两个重要极限求极限的方法。
7.理解无穷小量的概念和基本性质,掌握无穷小量的比较方法,了解无穷大量的概念及其无穷小量的关系。
8.理解函数连续性的概念<含左连续和右连续),会判断函数间断点的类型。
9.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质<有界性、最大值和最小值定理、介值定理),并会应用这些性质。
二、一元函数微分学考试内容导数和微分的概念,导数的几何意义和经济意义,函数的可导性与连续性之间的关系,平面曲线的切线与法线,导数和微分的四则运算,基本初等函数的导数,复合函数、反函数和隐函数的微分法,高阶导数,一阶微分形式的不变性,微分中值定理,洛必达<L’Hospital)法则,函数单调性的判别,函数的极值,函数图形的凹凸性、拐点及渐近线,函数图形的描绘,函数的最大值与最小值考试要求1.理解导数的概念及可导性与连续性之间的关系,了解导数的几何意义与经济意义<含边际与弹性的概念),会求平面曲线的切线方程和法线方程。
2018年硕士研究生招生考试大纲

2018年硕士研究生招生考试大纲考试科目名称:数学综合(线性代数、数学分析共占50%,数学教育概论占50%)考试科目代码:[812]线性代数部分一、考试内容1、行列式逆序数;对换;n阶行列式的概念;行列式的性质;余子式;代数余子式;行列式按行(列)展开定理;克莱姆法则。
2、矩阵矩阵概念;矩阵的线性运算、乘法运算、转置以及方阵的幂等运算规律;逆矩阵的概念及性质;伴随矩阵的概念及应用方法;分块矩阵及其运算;矩阵的初等变换与初等矩阵;矩阵秩的概念及其性质。
3、线性方程组线性方程组有解的判别定理;n维向量概念;向量组的线性组合;向量的线性表示;向量组的线性相关与线性无关;向量组的极大无关组;向量组的秩;两向量组的等价;极大无关组;线性方程组解的性质与结构。
4、二次型与矩阵对角化矩阵的特征值与特征向量;相似矩阵与矩阵对角化;二次型及其标准型;正定性。
二、考试要求1、行列式(1)了解排列的逆序及逆序数的概念,了解逆序数在行列式定义中的作用,了解逆序和排列的奇偶性,了解对换改变奇偶性。
(2)理解n阶行列式的定义。
(3)熟练掌握行列式的性质,并能熟练地运用它们进行行列式的计算。
(4)掌握用递推的方法计算n阶行列式。
(5)理解代数余子式的概念,熟练掌握行列式按行(列)展开从而降阶的方法。
(6)理解克莱姆法则,会用克拉默法则求解相应的线性方程组。
2、矩阵(1)理解矩阵的概念(包括矩阵的元素、阶数),掌握矩阵的表示法。
(2)了解一些常用的特殊矩阵,如行(列)矩阵、零矩阵、方阵、上(下)三角阵、主(次)对角阵、数量阵、单位阵、对称矩阵和反对称矩阵等。
(3)熟练掌握矩阵的加法、数乘、乘法、转置以及方阵的幂、方阵的行列式等概念及相应的运算规律。
(4)理解可逆矩阵的概念,熟练掌握逆矩阵的性质,以及矩阵可逆的充要条件,了解伴随矩阵的概念,会用伴随矩阵求逆矩阵,能利用逆矩阵解简单的矩阵方程。
(5)了解分块矩阵的概念,会进行分块矩阵的加法、数乘等运算,会用分块矩阵解题。
2018考研数学

2018考研数学一、绪论1.1 考研概述考研,即研究生入学考试,是中国高等教育体系中的一项重要考试。
作为考研的一部分,数学是综合素质考试中的一门必修科目。
本文将以2018年考研数学为主题,探讨考研数学的考试形式、考点以及备考技巧等内容。
1.2 考试形式2018年考研数学分为两个科目:高数和线性代数。
高数科目包括数列、极限、连续性、微分和积分等内容;线性代数科目包括向量、矩阵、行列式、特征值和特征向量等内容。
考试形式主要为选择题和解答题。
选择题是考察考生的基本理解能力,解答题是考察考生的问题解决能力和计算能力。
二、高数2.1 基础知识高数作为数学的一门基础学科,是考研数学中的重点和难点。
考生需要掌握数列的概念、极限的计算方法、连续性的判断条件、微分和积分的相关公式和运算规则等基础知识。
2.2 考点分析在2018年高数考研中,重点考察的考点包括但不限于:一致收敛、导数的性质、微分中值定理、泰勒公式、定积分的计算方法等。
考生需要根据以往的考试情况和教材重点来有针对性地备考。
2.3 备考技巧高数的备考主要需要从两个方面入手:理论与实践。
理论方面,考生需要系统地学习教材,掌握基础知识和考点。
实践方面,考生需要多做题,在不同难度的题目中寻找规律和方法,提高解题能力和速度。
此外,考生还需要注意总结经验,及时复习和整理错题,不断提高复习效果。
三、线性代数3.1 基础知识线性代数是数学的一个分支,是考研数学中的另一个重要学科。
考生需要掌握向量的运算、矩阵的基本概念、行列式的性质、特征值和特征向量的求解方法等基础知识。
3.2 考点分析2018年线性代数考研中的考点包括但不限于:向量组的线性相关性、矩阵的秩、矩阵的特征值和特征向量的求解、对角化、相似矩阵等。
考生需要针对这些考点进行重点复习和练习。
3.3 备考技巧线性代数的备考主要需要从两个方面入手:理论与实践。
理论方面,考生需要对线性代数的基本概念和定理有深入理解,掌握基础知识和考点。
宁波大学2018年《835数学教学论》考研专业课真题试卷

(答案必须写在考点提供的答题纸上)
科目代码:
835
总分值:
150
科目名称:
数学教学论
一、概念题(5 分×3=15 分)
1.化归方法 2.符号意识 3.合情推理
二、简答题(10 分×6=60 分)
1.数学教育有哪些基本功能?简述思维训练功能。 2.建构主义指导下的课堂教学基于怎样的假设? 3.简析数学概念学习的 APOS 理论。 4.简述中国双基教学的四个特征。 5.简述三个基本的数学教学模式。 6.简述弗赖登塔尔(Hans Freude述题(25 分×2=50 分)
1.述评建构主义的数学教育理论。 2.数学课堂上教师如何与学生沟通交流,进行教学对话?
四、教学设计题(25 分×1=25 分)
围绕“代数式概念”的教学做一个教学设计。
第 1 页 共 1 页
2018年学术学位硕士研究生入学考试初试科目设置及试题选用一览表
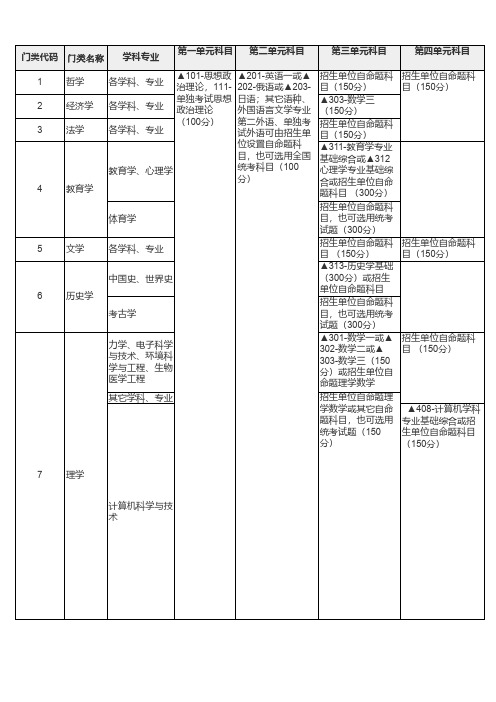
科,都应使用其所在一级学科的统考试题;
2.加“▲”者为全国统考或全国联考科目。
加“★”者为全国统一规定代码的招生单位联合命题或自命题科目。
3.第二单元招生单位自命题科目代码一律使用240-289
4.第三单元招生单位自命题科目代码使用6××或7××(其中,601-609仅供招生单位自命题理学数学使用,其它自命题科目不得使用)。
5.第四单元招生单位自命题科目,考试时间为3小时的科目代码使用8××或9××,考试时间为三小时以上六小时以下的科目代码使用5××。
6.招生单位自命题科目均可选用相应单元、相同分值的统考科目试题。
7.括号内所注分值为该栏考试科目的满分值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考试大纲
参考书
《数学教育概论》(张奠宙,宋乃庆主编,第3版),高等教育出版社,2016.
考试内容
与时俱进的数学教育;数学教育的基本理论;数学教育的核心内容;学习心理学与数学教育;数学课程的制定与改革;数学问题与数学考试;数学教学设计;数学课堂教学的基本技能;数学思维与数学基本能力。
试卷内容结构
指定参考书中的相应章节
试卷难易结构
难易பைடு நூலகம்例为3:7
试卷题型结构
简答题、计算(证明)题、论述题、教学设计(撰写教案)
试卷分值结构
简答题40%、计算(证明)题15%、论述题20%、教学设计(撰写教案)25%
评分标准和要求
按照评分标准分步给分
备注
一级学科硕士点召集人签名:(学院盖章)学院分管院长签名:
