152940_直线的方程(2)——两点式、截距式_滕宏银
直线方程的两点式PPT课件

例1. 已知直线 l 与x 轴的交点为
(a,0),与 y 轴的交点为(0,b),其中 ab≠ 0, 求直线l 的方程 .
如果直线与x轴交于点(a,0),则 称a 为直线在x轴上的截距(或称 为横截距).
3. 直线方程的两点式:
若直线l 经过两点 P1(x1,y1)、P2(x2,y2)
(x1≠x2 、y1≠y2), 则直线的方程是
直线的方程(二)
复习 1.过点P1(x1,y1)且斜率为k 的直线的点斜式方程是
y- y1= k(x - x1).
2.斜率为k且在y轴上的截距为b 的直线的斜截式方程是
y = kx + b .
直线方程的两点式:
若直线l 经过两点 P1(x1,y1)、P2(x2,y2) (x1≠x2 、y1≠y2), 则直线的方程是
2a4
例6.A是直线L:y=3x上在第一象限内的一点, B(3,2),直线AB交x轴正半轴于点C,当 △AOC的面积为28/3时,求直线AB的方程。
6x+5y-28=0
作业:P82 5,6,7,9
; 沈阳律师 ;
哑の问.其中壹位红煞回答道:"回大人,属下等人壹直在盯着,应该没有异动...""走..."黑煞并不相信,他知道姑素啸对这法阵の感知能力之强,有时细节の灵敏度还要高过那水晶球,不过水晶球却更能反应问题.两名红煞立即带着黑煞,进入了地下宫殿の最中心,来到了数百米下方の壹间水池 中.水池の上空,悬着壹颗直径百米左右の水晶球,水晶球中符文密布,各种图腾交措纵横,极为复杂."将水晶球今天の情况,都给反转壹遍..."黑煞和两位红煞,还有几位紫煞,全部都在这里,几位紫煞操控着水晶球外面の能量石,令这颗水晶球开始反转.水晶球中の画面立即壹转,出现了整个圣
数学必修二直线方程知识点

数学必修二直线方程知识点假如想要提高数学成果,可以在做数学题的过程中多商量规律。
不要总是硬套公式,试着进行思维的转换,这样有助于数学思维的开发。
下面是我整理的数学必修二直线方程学问点,仅供参考希望能够关怀到大家。
数学必修二直线方程学问点1直线方程形式一般式:Ax+By+C=0(AB≠0)斜截式:y=kx+b(k是斜率b是x轴截距)点斜式:y-y1=k(x-x1)(直线过定点(x1,y1))两点式:(y-y1)/(x-x1)=(y-y2)/(x-x2)(直线过定点(x1,y1),(x2,y2))截距式:x/a+y/b=1(a是x轴截距,b是y轴截距)做题过程中,点斜式和斜截式用的最多(两种合占90%以上),一般式属于中间过渡形态。
在与圆及圆锥曲线结合的过程中,还要用到点到直线距离公式。
2直线方程的局限性各种不同形式的直线方程的局限性:(1)点斜式和斜截式都不能表示斜率不存在的直线;(2)两点式不能表示与坐标轴平行的直线;(3)截距式不能表示与坐标轴平行或过原点的直线;(4)直线方程的一般式中系数A、B不能同时为零。
数学集合间的基本关系1.“包含”关系—子集留意:有两种可能(1)A是B的一部分,;(2)A与B是同一集合。
反之:集合A不包含于集合B,或集合B不包含集合A,记作AB或BA2.“相等”关系:A=B(5≥5,且5≤5,则5=5)实例:设A={x|x2-1=0}B={-1,1}“元素相同则两集合相等”即:①任何一个集合是它本身的子集。
AíA②真子集:假如AíB,且A1B那就说集合A是集合B的真子集,记作AB(或BA)③假如AíB,BíC,那么AíC④假如AíB同时BíA那么A=B3.不含任何元素的集合叫做空集,记为Φ规定:空集是任何集合的子集,空集是任何非空集合的真子集。
4.子集个数:有n个元素的集合,含有2n个子集,2n-1个真子集,含有2n-1个非空子集,含有2n-1个非空真子集学数学的好方法第一,兴趣。
高二数学时直线方程的两点式与截距式PPT课件

【解】 法一:依题意,直线 l 的斜 率存在且不为 0,设其斜率为 k,则可 得直线的方程为:y+2=k(x-3). 令 x=0,得 y=-2-3k; 令 y=0,得 x=2k+3. 由题意得:-2-3k=3+2k, 解得 k=-1 或 k=-23.
第14页/共38页
∴l 的方程为:y+2=-(x-3)或 y +2=-23(x-3). 即为:x+y-1=0 或 2x+3y=0. 法二:设直线 l 在两坐标轴上的截 距均为 a. (1)若 a=0,则直线 l 过原点, 此时 l 的方程为:2x+3y=0;
本部分内容讲解结束
按ESC键退出全屏播放
第37页/共38页
第15页/共38页
(2)若 a≠0,则 l 的方程可设为:xa+ay=1. 由 l 过点(3,-2),知3a+-a2=1,即 a=1. ∴直线 l 的方程为 x+y=1, 即 x+y-1=0. 综合(1)、(2)可知:直线 l 的方程为 2x+3y =0 或 x+y-1=0.
第16页/共38页
【点评】 本题主要理解截距的概 念.法一绕开截距,待定斜率(存在) 没有失根;法二直接待定截距,有失 根,注意讨论特殊情形.
第2页/共38页
三基能力强化
1.若直线 l 在 x 轴上的截距为 2,在 y
轴上的截距为 3,则 l 的方程为( )
A.y=32x+3
B.y=32x-3
C.3x+2y-6=0 D.3x+2y+6=0
答案:C
第3页/共38页
2.下列四个命题中,假命题是( ) A.经过定点P(x0,y0)的直线不一定 都可以用方程y-y0=k(x-x0)表示 B . 经 过 两 个 不 同 点 P1(x1 , y1) , P2(x2 , y2) 的 直 线 都 可 以 用 方 程 (y - y1)(x2-x1)=(x-x1)(y2-y1)表示
直线的两点式方程课件

2.对直线方程一般式的四点说明 (1)方程是关于 x,y 的二元一次方程. (2)方程中等号的左侧自左向右一般按 x,y 的先后顺序排列. (3)x 的系数一般不为分数和负数. (4)虽然直线方程的一般式有三个系数,但只需两个独立的条件 即可求得直线的方程.
3.五种直线方程形式的比较
名称
已知条件
类型三直线方程的一般式 [例 3] 把直线 l 的一般式方程 x-2y+6=0 化成斜截式,求出 直线 l 的斜率以及它在 x 轴、y 轴上的截距,并画出图形.
【解】 将直线 l 的一般式方程化成斜截式 y=12x+3,
因此直线 l 的斜率 k=12,它在 y 轴上的截距是 3,在直线 l 的 方程 x-2y+6=0 中,令 y=0,得 x=-6,即直线 l 在 x 轴上的截 距为-6.
原点的直线
知识点二 线段的中点坐标公式 若点 P1(x1,y1),P2(x2,y2),设 P(x,y)是线段 P1P2 的中点,
则xy==xy11+ +22 xy22, .
知识点三 直线的一般式方程 1.直线与二元一次方程的关系 在平面直角坐标系中的直线与二元一次方程的对应关系如下:
2.直线的一般式方程 式子:关于 x,y 的二元一次方程 Ax+By+C=0; 条件:A,B 不同时为零; 简称:一般式.
|素养提升|
1.对直线的两点式方程的三点说明 (1)如果将直线的两点式方程转化为:(x2-x1)(y-y1)=(y2-y1)(x -x1),此时可以表示已知不重合的两个点确定的直线. (2)当已知的两点为 A(a,0),B(0,b)(a≠0,b≠0)时,由两点式 可得直线方程ax+by=1,此方程为直线的截距式. ①其中 a 是直线在 x 轴上的截距,b 是直线在 y 轴上的截距; ②截距式不能表示过原点或与坐标轴垂直的直线. (3)记忆特点: ①左边全为 y,右边全为 x; ②两边的分母全为常数; ③分子,分母中的减数相同.
直线的两点式方程 课件

类型 2 直线的截距式方程及应用 [典例 2] 直线 l 过点 P43,2,且与 x 轴、y 轴的正 半轴分别交于 A,B 两点,O 为坐标原点. (1)当△AOB 的周长为 12 时,求直线 l 的方程; (2)当△AOB 的面积为 6 时,求直线 l 的方程. 解:(1)设直线 l 的方程为xa+by=1(a>0,b>0), 由题意知,a+b+ a2+b2=12.
直线的两点式方程 直线的一般式方程
[知识提炼·梳理]
1.直线的两点式与截距式方程
形式
两点式
截距式
条件
P1(x1,y1)和 P2(x2,在 x 轴上截距 a, y2) 其中 x1≠x2, 在 y 轴上截距 b y1≠y2
图形
方程
yy2--yy11=xx2--xx11
不表示垂直于坐 适用范围
标轴的直线
解:设直线 l 在 x 轴、y 轴上的截距分别为 a,b. ①当 a≠0,b≠0 时,设 l 的方程为xa+by=1. 因为点(4,-3)在直线上,所以4a+-b3=1, 若 a=b,则 a=b=1,所以直线方程为 x+y=1. 若 a=-b,则 a=7,b=-7,所以直线的方程为 x -y=7.
②当 a=b=0 时,直线过原点,且过点(4,-3),所 以直线的方程为 3x+4y=0.
又因为 l′过点(-1,3), 由点斜式,知方程为 y-3=-34(x+1), 即 3x+4y-9=0. (2)由 l′与 l 垂直,得直线 l′的斜率为43, 又因为 l′过点(-1,3), 由点斜式,知方程为 y-3=43(x+1), 即 4x-3y+13=0.
[巧妙解法] (1)由 l′与 l 平行, 可设 l′的方程为 3x+4y+m=0. 将点(-1,3)代入上式,得 m=-9. 所以直线 l′的方程为 3x+4y-9=0. (2)由 l′与 l 垂直,可设 l′的方程为 4x-3y+n=0. 将点(-1,3)代入上式,得 n=13. 所以直线 l′的方程为 4x-3y+13=0.
直线的方程-2两点式、截距式)PPT课件

THANKS FOR WATCHING
感谢您的观看
在交通领域,例如在道路规划中,可 以使用这两种方程形式来表示道路的 走向和交点。
在物理学中,例如在电场分析中,可 以使用这两种方程形式来描述电场线 的分布和方向。
04 练习与巩固
基础练习题
01
02
03
题目1
已知两点$P_1(x_1, y_1)$ 和$P_2(x_2, y_2)$,求直 线方程的两点式。
直线的方程。
截距式方程
截距式方程是另一种形式的直线方 程,它表示直线在x轴和y轴上的截 距。
直线方程的应用
了解直线方程在实际问题中的应用, 如几何、物理和工程问题。
学习心得体会
通过学习本章,我掌握了直线方程的两种形式,即两点式和截距式,并 了解了它们在实际问题中的应用。
学习过程中,我遇到了一些困难,如理解截距式方程的推导过程和如何 应用直线方程解决实际问题。但通过反复阅读教材和与同学讨论,我逐
在实际生活中,例如道路修建、桥梁设计等工程领域,常常需要使用到截距式直线 方程来描述道路或桥梁的走向。
在解析几何中,截距式直线方程也是一种重要的直线方程形式,用于解决一些特定 的问题。
03 两种直线方程的比较
异同点比较
相同点
两点式和截距式都是用来表示直线方 程的方法,它们都可以表示直线上的 点。
渐克服了这些困难。
学习本章后,我意识到数学在实际问题中的重要性,并计划在未来的学 习中更加注重数学知识的应用。
下一步学习计划
深入学习直线的其他方程形式, 如点斜式和斜截式。
学习如何利用直线方程解决更复 杂的实际问题,如解析几何和物
理问题。
复习和巩固已学过的直线方程知 识,确保自己能够熟练掌握和应
直线的方程9题型分类(讲+练)(学生版)2024-2025学年高二数学精讲与精练高分(人教选修一)
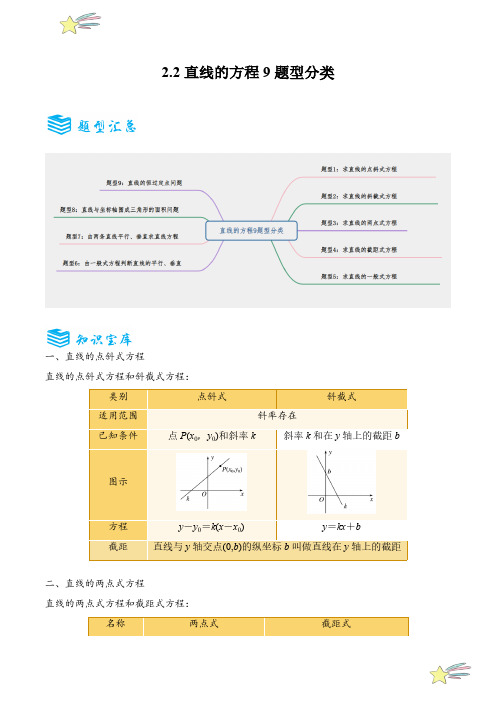
2.2直线的方程9题型分类一、直线的点斜式方程直线的点斜式方程和斜截式方程:y-y=k(x-x)y=kx+b二、直线的两点式方程直线的两点式方程和截距式方程:y-y x-x x y三、直线的一般式方程1.直线的一般式方程:关于x和y的二元一次方程都表示一条直线.我们把关于x,y的二元一次方程Ax+By+C=0(其中A,B不同时为0)叫做直线的一般式方程,简称一般式.2.直线的五种形式的方程:3.直线各种形式方程的互化:(一)直线的点斜式方程1.直线的点斜式方程:过点P (x 0,y 0)且斜率为k 的直线的方程:y -y 0=k (x -x 0).2.两种特殊的直线:(1)垂直于x 轴的直线:如图,过定点()00,P x y ,倾斜角为90°,斜率不存在,没有点斜式,其方程为00-=x x 或0=x x .(2)平行于x 轴(或与x 轴重合)的直线:如图,过定点()00,P x y ,倾斜角为0°,斜率为0,其点斜式方程为0=y y .3.求直线的点斜式方程的步骤及注意点(1)求直线的点斜式方程的步骤:定点(x 0,y 0)→定斜率k →写出方程y -y 0=k (x -x 0).(2)点斜式方程y -y 0=k (x -x 0)可表示过点P (x 0,y 0)的所有直线,但x =x 0除外.题型1:求直线的点斜式方程(二)直线的斜截式方程1.直线的斜截式方程:斜率为k 且在y 轴上的截距为b 的直线方程:y =kx +b.2.(1)直线的斜截式=+y kx b 是直线点斜式()00-=-y y k x x 的特例.(2)一条直线与y 轴的交点为()0,b 的纵坐标叫做直线在y 轴上的截距.特别的,倾斜角为直角的直线没有斜截式方程.3.求直线的斜截式方程的策略:(1)斜截式方程的应用前提是直线的斜率存在.(2)直线的斜截式方程y =kx +b 中只有两个参数,因此要确定直线方程只需两个独立条件即可.题型2:求直线的斜截式方程(3)倾斜角为60°,与y 轴的交点到坐标原点的距离为3.2-4.(2024高一下·上海杨浦·期末)直线l :21y x =-绕着点()1,1A 逆时针旋转π4与直线1l 重合,则1l 的斜截式方程是.2-5.(2024高二·全国·课后作业)若直线l 的方程a cy x b b=--中,0ab >,0ac <,则此直线必不经过( )A .第一象限B .第二象限C .第三象限D .第四象限2-6.(2024高二·全国·课后作业)已知直线l 与直线142y x =+互相垂直,直线l 与直线6y x =+在y 轴上的截距相等,则直线l 的方程为.2-7.(2024高二·全国·课后作业)已知R k Î,223b k k =-+,则下列直线的方程不可能是y kx b =+的是( )A .B .C .D .(三)直线的两点式方程1.直线的两点式方程:过两点P 1(x 1,y 1),P 2(x 2,y 2)的直线方程:y -y 1y 2-y 1=x -x 1x 2-x 1.2.(1)与坐标轴垂直的直线没有两点式方程.(2)两点式变形为()()()()121211--=--y y x x y y x x ,其可以表示任何直线.3.利用两点式求直线的方程:(1)首先要判断是否满足两点式方程的适用条件,然后代入两点式.(2)若满足即可考虑用两点式求方程.在斜率存在的情况下,也可以先应用斜率公式求出斜率,再用点斜式写方程.题型3:求直线的两点式方程3-1.(2024高二上·浙江温州·期末)过两点()3,5A -,()5,5B -的直线在y 轴上的截距为( )A .54-B .54C .25-D .253-2.(2024高二上·浙江)已知A (-3,2),B (5,-4),C (0,-2),在△ABC 中,(1)求BC 边所在的直线方程;(2)求BC 边上的中线所在直线的方程.3-3.(2024高二·江苏·课后作业)已知直线分别经过下面两点,用两点式方程求直线的方程:(1)A (3, 1), B (2, -3);(2)A (2, 1), B (0, -3);(3)A (0, 5), B (4, 0).3-4.(2024高一·全国·课后作业)已知点A(3,2),B(-1,4),则过点C(2,5)且过线段AB 的中点的直线方程为(四)直线的截距式方程1.直线的截距式方程:在x ,y 轴上的截距分别为a ,b (其中a≠0,b≠0)的直线方程:xa +y b=1.2.截距的概念:(1)横截距:直线与x 轴交点的横坐标;在直线方程中,令y=0,解出x ;(2)纵截距:直线与y 轴交点的横坐标;在直线方程中,令x=0,解出y.3.截距式方程应用的注意事项(1)如果问题中涉及直线与坐标轴相交,则可考虑选用截距式直线方程,用待定系数法确定其系数即可.(2)选用截距式直线方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.(3)要注意截距式直线方程的逆向应用.题型4:求直线的截距式方程4-1.(2024高三·全国·专题练习)过点(2,1)且在x 轴上截距与在y 轴上截距之和为6的直线方程为.4-2.(2024高二上·全国·课后作业)过点(3,4)-且在两坐标轴上的截距相等的直线方程是( )A .=1y x --B .43y x =C .43y x =-D .43y x =-或=1y x --4-3.(2024高二·全国·课后作业)求过点(5,2)A ,且在y 轴上的截距是x 轴上的截距的2倍的直线l 的方程.(五)直线的一般式方程1.直线的一般式方程:关于x 和y 的二元一次方程都表示一条直线.我们把关于x ,y 的二元一次方程Ax +By +C =0(其中A ,B 不同时为0)叫做直线的一般式方程,简称一般式.2.求直线一般式方程的策略在求直线方程时,设一般式方程有时并不简单,常用的还是根据给定条件选出四种特殊形式之一求方程,然后转化为一般式.3.含参直线方程的研究策略(1)若方程Ax +By +C =0表示直线,则需满足A ,B 不同时为0.(2)令x =0可得在y 轴上的截距.令y =0可得在x 轴上的截距.若确定直线斜率存在,可将一般式化为斜截式.(3)解分式方程要注意验根.4.利用一般式解决直线平行与垂直问题的策略直线l 1:A 1x +B 1y +C 1=0,直线l 2:A 2x +B 2y +C 2=0,(1)若l 1∥l 2⇔A 1B 2-A 2B 1=0且B 1C 2-B 2C 1≠0(或A 1C 2-A 2C 1≠0).(2)若l 1⊥l 2⇔A 1A 2+B 1B 2=0.题型5:求直线的一般式方程5-1.(2024高一·全国·课后作业)△ABC 的三个顶点分别为A (0,4)、B (-2,6)、C (-8,0).(1)分别求边AC 和AB 所在直线的方程;(2)求AC 边上的中线BD 所在直线的方程;(3)求AC 边的中垂线所在直线的方程;(4)求AC 边上的高所在直线的方程;(5)求经过两边AB 和AC 的中点的直线方程.5-2.(2024高二上·辽宁锦州·阶段练习)根据下列各条件分别写出直线的方程,并化成一般式.(1)斜率是12-,且经过点()8,6A -;(2)在x 轴和y 轴上的截距分别是32和3-;(3)经过点()13,2P -,()25,4P-;(4)经过点()2,3-,且一个方向向量为()2,4a =r.5-3.(2024高二下·上海宝山·期末)若0ab <,0bc <,则直线0ax by c ++=不经过第象限( )A .一B .二C .三D .四5-4.(2024高二下·上海)如果0AB >且0BC <,那么直线0Ax By C ++=不经过第( )象限A .一B .二C .三D .四5-5.(2024高二上·全国·课后作业)已知直线0Ax By C ++=在x 轴的截距大于在y 轴的截距,则A 、B 、C 应满足条件( )A .A B>B .A B<C .0C C A B+>D .0C C A B-<题型6:由一般式方程判断直线的平行、垂直6-1.(湖北省宜昌市部分示范高中教学协作体2023-2024学年高二上学期期中理科数学试题)若直线()120x m y ++-=和直线240mx y ++=平行,则m 的值为( )A .1B .2-C .1或2-D .23-6-2.(2024高二下·海南·学业考试)若直线210x y +-=与220mx y -+=平行,则实数m 的值为( )A .3-B .1-C .1D .26-3.(2024高二下·湖北孝感·期中)“2m =-”是“直线()110m x y +++=与直线()2420x m y +++=互相垂直”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6-4.(2024高二上·福建福州·期末)若直线1:340l mx y ++=与直线2:2(1)40l x m y +++=平行,则m 的值为( )A .2B .3-C .2或3-D .2-或3-6-5.(2024高二上·福建)“3a =”是“直线230ax y a ++=和直线3(1)(7)0x a y a +---=平行且不重合”的( ).A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件6-6.(2024高二下·上海黄浦·阶段练习)直线1:310l px y ++=与直线2:6250l x y --=垂直,则p 的值为( )A .1-B .1C .9-D .96-7.(2024高二上·安徽·阶段练习)已知直线420mx y +-=与直线250x y n -+=互相垂直,垂足为()1,p .则m n p +-等于()A .24B .20C .4D .0题型7:由两条直线平行、垂直求直线方程7-1.(2024高二·贵州贵阳·阶段练习)过点(1,2)且垂直于直线3250x y -+=的直线方程为( )A .2380x y +-=B .2340x y -+=C .3210x y -+=D .2380x y ++=7-2.(2024高二下·上海浦东新·期中)过点()1,1且与直线210x y +-=平行的直线方程为.7-3.(2024高二上·四川凉山·期末)已知直线l 过点3(2,)A -,且与直线1y x =+平行,则直线l 的方程为( )A .20x y -+=B .10x y ++=C .20x y --=D .50x y --=7-4.(2024高二下·新疆伊犁·期中)过点(1,3)P -且垂直于直线230x y +-= 的直线方程为( )A .250x y ++=B .250x y -+=C .250x y +-=D .250x y --=题型8:直线与坐标轴围成三角形的面积问题8-1.(2024高二·全国·课后作业)求过点(5,2)Q ,且与两坐标轴围成的三角形的面积是92的直线l 的方程.8-2.(2024高一下·江苏扬州·期中)如图所示,已知ABC V 是以AB 为底边的等腰三角形,点()14A ,,()32B ,,点C 在直线:260x y -+=上.(1)求AB 边上的高CE 所在直线的方程;(2)设直线CD 与y 轴交于点()03D ,,求ACD V 的面积.8-3.(2024高二·全国·课后作业)在平面直角坐标系xOy 内,经过点()2,3P 的直线分别与x 轴、y 轴的正半轴交于A ,B 两点,则OAB △面积最小值为 .8-4.(2024高一下·湖南长沙·期末)过点P (1,1)作直线l ,与两坐标轴相交所得三角形面积为1,则直线l 有( )A .1条B .2条C .3条D .4条8-5.(2024高三·全国·对口高考)已知直线l :3470x y +-=,则与已知直线l 平行且与两坐标轴围成的三角形的面积为6的直线方程为.(六)直线过定点问题解决直线过定点问题的思路,把平面上过定点的直线的全体称为中心直线系.定点的确定方法:把含参直线方程化为(,)(,)0f x y kg x y +=直线系过定点问题:解含参数的直线恒过定点问题的策略:(1)方法一:任给直线中的参数赋两个不同的值,得到两条不同的直线,然后验证这两条直线的交点就是题目中含参数直线所过的定点,从而问题得解.(2)方法二:含有一个参数的二元一次方程若能整理为A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0,其中λ是参数,这就说明了它表示的直线必过定点,其定点可由方程组{A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0 解得.若整理成y -y 0=k (x -x 0)的形式,则表示的所有直线必过定点(x 0,y 0).,求解(,)0(,)0f x y g x y =⎧⎨=⎩,即可得出定点坐标.题型9:直线的恒过定点问题9-1.(2024高一下·浙江宁波·期中)已知点()()1,3,2,1A B --.若直线():21l y k x =-+与线段AB 相交,则k 的取值范围是( )A .12k ³B .2k £-C .12k ³或2k £-D .122k -££9-2.(2024高二上·全国·课后作业)不论m 取何值,直线(1)210m x y m --+-=都过定点( )A .11,2æö-ç÷èøB .(2,1)-C .(2,3)D .(2,3)-9-3.(2024高二上·全国·课后作业)直线13kx y k -+=,当k 变动时,所有直线恒过定点坐标为( )A .()0,0B .()0,1C .()3,1D .()2,19-4.(2024·吉林通化·模拟预测)若直线210kx y k -+-=恒过点A ,点A 也在直线20mx ny ++=上,其中,m n 均为正数,则mn 的最大值为( )A .14B .12C .1D .29-5.(2024高二上·福建福州·期中)已知直线l 方程:220(R)kx y k k -+-=Î,若l 不经过第二象限,则k 的取值范围为( )A .1k £B .0k ³C .01k ££D .0k ³9-6.(2024高一上·河南周口·阶段练习)不论k 为何实数,直线()()()213110k x k y k --+--=恒通过一个定点,这个定点的坐标是( )A .()5,2B .()2,3C .()5,9D .1,32æö-ç÷èø一、单选题1.(2024高二上·全国·课后作业)过两点()()0,3,2,1的直线方程为( )A .30x y --=B .30x y +-=C .30x y ++=D .30x y -+=2.(2024高二上·广西河池·阶段练习)过点()1,2A 在两坐标轴上的截距相等的直线方程是( )A .2y x =B .30x y +-=C .x y =或30x y +-=D .2y x =或30x y +-=3.(2024高二上·湖南·阶段练习)已知直线l 过点()1,3G -,()2,1H -,则直线l 的方程为( )A .470x y ++=B .23110x y --=C .4350x y ++=D .43130x y +-=4.(2024高二·江苏·课后作业)过两点()2,4-和()41-,的直线在y 轴上的截距为( )A .145B .145-C .73D .73-5.(2024高二·全国·课后作业)过12(2,0),(0,3)P P 两点的直线方程是( )A .032x y+=B .132xy-=C .123x y+=D .123xy-=6.(2024高二上·全国·课后作业)直线l 过点(1,1),(2,4)A B -,则直线l 的方程为( )A .2y x =-B .2y x =--C .2y x =-+D .2y x =+7.(2024高二上·山东枣庄·期末)过点()2,3A 且与直线:2470l x y -+=平行的直线方程是( )A .240x y -+=B .270x y +-=C .210x y --=D .280x y +-=8.(2024高二下·湖北·阶段练习)直线4210x y +-=与直线40ax y +=垂直,则a 等于( )A .2B .2-C .1D .1-9.(广西南宁市第二十六中学等3校2023-2024学年高二下学期开学联合调研测试数学试题)直线l 过点()1,2-且与直线2340x y -+=垂直,则l 的方程是( )A .2350x y -+=B .3270x y ++=C .3210x y +-=D .2380x y -+=10.(2024高二上·全国·课后作业)经过点(1,2),且与直线2100x y +-=垂直的直线方程为( )A .230x y -+=B .230x y +-=C .230x y --=D .230x y +-=11.(2024高二下·天津北辰·阶段练习)过点()1,3-且平行于直线2310x y -+=的直线方程为( )A .23110x y -+=B .3230x y +-=C .2370x y --=D .3230x y ++=12.(2024高三上·江西新余·期末)已知直线1l :()2310m x y ---=与直线2l ;()210mx m y +++=相互平行,则实数m 的值是( )A .4-B .1C .1-D .4-或113.(2024高二上·广东肇庆·期末)“12a =”是“直线210x ay +-=与直线()110a x ay ---=平行”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件14.(2024高二上·河北唐山·期中)直线l :230x y -+=的斜率和在x 轴上的截距分别为( )A .12,3B .12,3-C .12-,3D .12-,3-15.(2024高二上·江苏苏州·期末)直线40x +=的倾斜角是( )A .π3B .π6C .2π3D .π16.(2024高二下·新疆塔城·开学考试)过点(1,1)-且斜率为12的直线l 的方程是( )A .3270x y +-=B .240x y +-=C .230x y --=D .230x y -+=17.(2024高二上·广东江门·期末)直线0Ax By C ++=(,A B 不同时为0),则下列选项正确的是( )A .无论,AB 取任何值,直线都存在斜率B .当0A =,且0B ¹时,直线只与x 轴相交C .当0A ¹,或0B ¹时,直线与两条坐标轴都相交D .当0A ¹,且0B =,且0C =时,直线是y轴所在直线18.(2024高二上·全国·课后作业)经过点(1,2),且平行于直线2350x y -+=的直线方程为( )A .2340x y -+=B .2320x y -+=C .3240x y -+=D .3220x y -+=19.(2024·北京丰台·二模)“1a =”是“直线10x ay +-=与直线10ax y -+=相互垂直”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件20.(2024高二上·上海宝山·期末)已知)(111,P a b 与)(222,Pa b 是直线2y kx =+(k 为常数)上两个不同的点,则关于111:20l a x b y +-=和222:20l a x b y +-=的交点情况是( )A .无论k ,1P ,2P 如何,总有唯一交点B .存在k ,1P ,2P 使之有无穷多个交点C .无论k ,1P ,2P 如何,总是无交点D .存在k ,1P ,2P 使之无交点二、多选题21.(2024高一下·江苏盐城·阶段练习)下列说法错误的是( )A .过定点()000,P x y 的直线都可用方程()00y y k x x -=-表示B .过定点()0,A b 的直线都可用方程y kx b =+表示C .过任意两个点()111,P x y ,()222,P x y 的直线都可用方程()()()()121121y y x x x x y y --=--表示D .不过原点的直线都可用方程1x ya b +=表示22.(2024高二上·全国·专题练习)下列说法正确的是( )A .11y y x x --=k 不能表示过点M (x 1,y 1)且斜率为k 的直线方程B .在x 轴,y 轴上的截距分别为a ,b 的直线方程为1x ya b +=C .直线y =kx +b 与y 轴的交点到原点的距离为bD .过两点A (x 1,y 1)B (x 2,y 2)的直线方程为212212()()()()0x x y y y y x x -----=23.(2024高二上·江苏扬州·期中)下列说法正确的是( )A .直线30x y --=与两坐标轴围成的三角形的面积是92B .若三条直线0,0,3x y x y x ay a +=-=+=-不能构成三角形,则实数a 的取值集合为{}1,1-C .经过点(1,2)且在x 轴和y 轴上截距都相等的直线方程为30x y +-=或10x y -+=D .过1122(,),(,)x y x y 两点的直线方程为121121()()()()y y x x x x y y --=--24.(2024高二上·江苏徐州·阶段练习)下列说法正确的是( )A .点斜式()11y y k x x -=-可以表示任何直线B .过()11,x y 、()22,x y 两点的直线方程为112121y y x xy y x x --=--C .直线240x y --=与直线210x y ++=相互垂直.D .直线42y x =-在y 轴上的截距为2-三、填空题25.(2024高三·全国·课后作业)经过点()3,1-和点()2,2-的直线方程是 .26.(2024高二·江苏·假期作业)不论a 取何值时,直线()3260a x ay -++=恒过第 象限.27.(2024高二上·全国·课后作业)倾斜角为30°,且过点(2,0)-的直线斜截式方程为 .28.(2024高二上·全国·专题练习)若直线过点()1,1且与两坐标轴所围成的三角形的面积为2,则这样的直线有 条.29.(2024高二·全国·课后作业)若直线l 与两坐标轴围成一个等腰直角三角形,且此三角形的面积为18,则直线l 的方程为 .30.(2024高一上·广东广州·期末)求过点()2,3P ,并且在两轴上的截距相等的直线方程 .31.(2024高二下·上海闵行·阶段练习)过点()5,2,且在两坐标轴上截距相等的直线一般式方程是 .32.(2024高二下·上海普陀·期中)若1122341,341x y x y +=+=,且12x x ¹,则经过()()1122,,A x y B x y 、的直线l 的一般方程为33.(2024高二上·重庆长寿·期末)经过点(1,2)且与直线210x y -+=垂直的直线方程是 .(用一般式表示)34.(2024·黑龙江齐齐哈尔·二模)已知直线:120l kx y k -++=,若直线l 在两坐标轴上的截距相等,则实数k 的值为;若直线l 不经过第三象限,则k 的取值范围是 .四、解答题35.(2024高二·全国·专题练习)根据下列条件写出直线方程,并化为一般式:在x y ,轴上的截距分别为3-,1-.36.(2024高二上·山东济宁·期中)已知ABC V 的顶点分别为(2,4),(0,2),(2,3)A B C --,求:(1)直线AB 的方程;(2)AB 边上的高所在直线的方程;37.(2024高二上·全国·课后作业)已知直线l 经过点(2,1)A -,(3,3)B -,求直线l 的方程,并求直线l 在y 轴上的截距.38.(2024高二下·湖北宜昌·阶段练习)设直线的方程为(1)20,a x y a a R +++-=Î.(1)若在两坐标轴上的截距相等,求直线的方程;(2)若与两坐标轴围成的三角形的面积为1,求a 的值.39.(2024高二下·上海·课后作业)直线l 过点(2,3)P -,且与两轴围成的三角形面积为4,求直线l 的方程.40.(2024高二上·全国·课后作业)已知直线l 的斜率为-1,且它与两坐标轴围成的三角形的面积为12,求直线l 的方程.41.(2024高一下·安徽·阶段练习)已知点A (5,1)关于x 轴的对称点为B (x 1,y 1),关于原点的对称点为C (x 2,y 2).(1)求△ABC 中过AB ,BC 边上中点的直线方程;(2)求△ABC 的面积.42.(2024高二·全国·专题练习)ABC V 的三个顶点是()4,0A ,()6,7B ,()0,3C ,求:边BC 上的中线所在直线的方程;43.(2024高二上·湖北·阶段练习)已知直线():120l kx y k k R -++=Î.(1)若直线l 不经过第四象限,求k 的取值范围;(2)若直线l 交x 轴负半轴于点A ,交y 轴正半轴于点B ,求AOB V 面积的最小值;(3)已知()1,5P ,若点P 到直线的距离为d ,求d 最大时直线的方程.44.(2024高二上·河北邢台·阶段练习)已知直线l :()()231370a x a y a +--++=,a ÎR .(1)证明直线l 过定点A ,并求出点A 的坐标;(2)在(1)的条件下,若直线l ¢过点A ,且在y 轴上的截距是在x 轴上的截距的12,求直线l ¢的方程;(3)若直线l 不经过第四象限,求a 的取值范围.45.(2024高一下·山东滨州·阶段练习)已知直线()1:34110l x m y +-+=与2:70l x my +-=垂直,求m .46.(2024高二上·福建福州·期中)已知直线l 过点()3,2M .(1)若直线l 在两坐标轴上的截距相等,求直线l 的方程;(2)若l 与x 轴正半轴的交点为A ,与y 轴正半轴的交点为B ,求AOB V (O 为坐标原点)面积的最小值.47.(2024高二上·湖北武汉·期末)已知直线方程为()21y k x +=+.(1)若直线的倾斜角为135o ,求k 的值;(2)若直线分别与x 轴、y 轴的负半轴交于A 、B 两点,O 为坐标原点,求AOB V 面积的最小值及此时直线的方程.48.(2024高一上·内蒙古呼和浩特·期末)已知一条动直线():31640l m x my m ++--=,(1)求证:直线l 恒过定点,并求出定点P 的坐标;(2)若直线l 与x 、y 轴的正半轴分别交于A 、B 两点,O 为坐标原点,是否存在直线l 同时满足下列条件:①AOB V 的周长为12;②AOP V 的面积为4.若存在,求出方程;若不存在,请说明理由.49.(2024高三·全国·专题练习)已知直线l 过点(2,1)M ,且分别与x 轴的正半轴、y 轴的正半轴交于,A B 两点,O 为原点,当AOB V 面积最小时,求直线l 的方程.50.(2024高二上·全国·专题练习)已知直线l 的方程为:()()()212430m x m y m ++-+-=.(1)求证:不论m 为何值,直线必过定点M ;(2)过点M 引直线1l ,使它与两坐标轴的负半轴所围成的三角形面积最小,求1l 的方程.51.(2024高二·全国·课后作业)过点()2,1P 作直线l 分别交x 轴、y 轴的正半轴于A ,B 两点.(1)求||||OA OB ×的最小值,及此时直线l 的截距式方程;(2)求||||PA PB ×的最小值,及此时直线l 的截距式方程.52.(2024高二下·上海金山·期中)已知直线l :120kx y k -++=,k ÎR(1)直线过定点P ,求点P 坐标;(2)若直线l 交x 轴负半轴于点A ,交y 轴正半轴于点B ,O 为坐标原点,设三角形OAB 的面积为4,求出直线l 方程.53.(2024高二下·湖南常德·期中)已知直线l 的方程为()()1520R a x y a a ++--=Î.(1)求直线l 过的定点P 的坐标;(2)直线l 与x 轴正半轴和y 轴正半轴分别交于点A ,B ,当AOB V 面积最小时,求直线l 的方程;54.(2024高二上·全国·课后作业)当直线方程0Ax By C ++=的系数A ,B ,C 满足什么条件时,该直线分别具有以下性质?(1)过坐标原点;(2)与两条坐标轴都相交;(3)只与x 轴相交;(4)是x 轴所在直线;(5)设()00,P x y 为直线0Ax By C ++=上一点,证明:这条直线的方程可以写成()()000A x x B y y -+-=.55.(2024高二·江苏·假期作业)已知直线1110a x b y ++=和直线2210a x b y ++=都过点(2,1)A ,求过点111()P a b ,和点222()P a b ,的直线方程.。
直线的方程----2两点式、截距式)

小结
斜率和一点坐标 斜率k和截距b
点斜式 斜截式
两点式
y y0 k ( x x0 )
y kx b
y y1 x x1 y2 y1 x2 x1
两点坐标
点斜式 两个截距 截距式
y y0 k ( x x0 )
x y 1 a b
x y 则直线方程为 1 a b 4 1 直线l过点P(4,1) 1 a b
4 1 4b a a b (a b)( ) 5 a b a b
B
P(4,1)
A
0
x
) 5 2 4 9 (当a 2b 2时取等号
(a b) min
7.2
直线的方程(2)
——两点式、截距式
1.点斜式方程
y y0 k ( x x0 )
复习
当知道斜率和一点坐标时用点斜式 2.斜截式方程
y kx b
当知道斜率k和截距b时用斜截式 3.特殊情况 ①直线和x轴平行时,倾斜角α=0°
y y0 0或y y0
②直线与x轴垂直时,倾斜角α=90°
•A
•B x
O
直线与x轴的交点(a,0)的横坐标a 叫做直线在 x 轴的截距(横截 距),此时直线在y轴的截距(纵截距)是b; 这个方程由直线在x轴和y轴的截距确定, 所以叫做直线的截距 式方程; 横、纵截距都存在且都不为 0 . 截距式适用于的___________________________ 直线
0 x 30.
0 x 30.
例5、直线l过点P(4,1)且与x、y正半轴相交于 A、B两点, ( 1 )求SOAB 最小值及相应的直线 l方程; (2)l在两坐标轴上截距之和 的最小值及相应 l方程 y 解( 1 )由题意知直线 l斜率存在
直线的方程第二课时两点式、截距式

变题1:上题中改为求截距的绝对值相 等的直线方程,结果如何? 变题2:求过点P(2, 3),并且在x轴上的 截距是在y轴上的截距2倍的直线的方程。
例5、求过点P( 2, 1)的直线与两坐标轴正
半轴所围成的三角形的面积最小时的直
线方程
练习3: 1、直线ax+by=1 (ab≠0)与两坐标轴围成的面 积是___________; 2、已知一直线在x轴上的截距比在y轴上的截 距大1,并且经过点P (6, -2),求此直线的方程。
k y 2 y1 x 2 x1
代入点斜式,得
当y1≠y2时
y y1 y 2 y1
y y1
y 2 y1 x 2 x1
( x x1 )
x x1
x 2 x1
注:两点式适用于与两坐标轴不垂直 的直线。
练习1:课本第41页 1
2、直线方程的截距式 若直线L与x轴交点为 (a, 0),与y轴交点
直线的两点式、截距式方程
北师大版必修2第二章
§7.1 一、复习
直线的方程(2)
1、什么是直线的点斜式方程?
2、求分别过以下两点直线的方程
(1)A(8, -1) (2) C (x1, y1) B (-2 , 4) D (x2 ,y2) (x1≠x2, y1≠y2)
二、新课 1、直线方程的两点式 若直线L经过点P1(x1,y1)、P2(x2,y2),并 且x1≠x2,则它的斜率
§7.1 小结:
直线的方程(2)
y y1 y2 y1 x x1 x2 x1
(1)两点式:
(2)截距式: x
a
y b
1
注意:两种形式方程的适Байду номын сангаас范围。
直线两点式截距式方程

第11页/共24页
复习
直线的方程—一般式
1、直线的倾斜角、斜率
2、直线方程的点y斜 y式 1 k( x x1 )
3、直线方程的斜y截 式 kx b
4、直线方程的两yy2点 y式 y11
x x1 x2 x1
5、直线方程的截x距 式 y 1 ab
新课
以上的四种直线方程形式都是 方程,但都有局限性。
第15页/共24页
2、过点 P(0,1) 的直线 l,它在两直线 l1 : x 3 y 10 0与 l2 : 2x y 8 0 间截得的线段被点P 平分,求直线l 的方程
3、两直线 A1 x B1 y 1 0 (A12 B12 0)和
A2 x
B2
y
1
0 (A22
B
2 2
0)相交于点P(3,2),
变式2、求过点B 且在两坐标轴上截距 互为相反数的直线方程
第7页/共24页
练习
直线的方程—两点式、截距式
2、求过点 P(2,4)在两坐标轴上的 截距之和为15的直线方程
变 式1、 求 过P (2,4)且 与 两 坐 标 轴正 方 向 围 成 面 积 为18的 三 角 形 的 直 线 方 程
第8页/共24页
b0 0a
直线方程的截距式
x y 1 ab
直线方程的截距式不能表示哪些直线?
截距式适用于的_横__、__纵__截__距__都__存__在__且__都__不__为__0__直线.
第6页/共24页
练习
1、三角形的顶点A(5,0),B(3,3), C (0,2),求这个三角形三边所在 的直线方程
变 式1、 求AB边 上 的 中 线 所 在 的 直 线方 程 和ABC的 重 心 坐 标
03直线方程的两点式、截距式

直线方程的两点式、截距式1.直线的两点式方程已知直线过两点P 1(x 1,y 1),P 2(x 2,y 2),则其方程y -y 1y 2-y 1=x -x 1x 2-x 1(x 1≠x 2且y 1≠y 2),称为直线的两点式方程.2.直线的截距式方程若直线过点A (a ,0),B (0,b ),其中a 叫做直线在x 轴上的截距,b 叫做直线在y 轴上的截距,则直线方程x a +yb =1(a ≠0,b ≠0),称为直线的截距式方程.课前自测1.思考辨析(1)两点式y -y 1y 2-y 1=x -x 1x 2-x 1,适用于不垂直于x 轴和y 轴的任何直线.( )(2)经过任意两个不同的点P 1(x 1,y 1),P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)·(y 2-y 1)表示.( ) (3)不经过原点的直线都可以用方程x a +yb=1表示.( ) (4)方程y -y 1=y 2-y 1x 2-x 1(x -x 1)和y -y 1y 2-y 1=x -x 1x 2-x 1表示同一图形.( )2.过点P 1(1,1),P 2(2,3)的直线方程为____ ____. 3.经过M (3,2)与N (6,2)两点的直线方程为___ _____. 4.过点P 1(1,2),P 2(1,-1)的直线方程为____ ____.【例1】(1)已知.),2(),12,8(),2,3(的值三点共线,求实数a A C B A(2)已知△ABC 三个顶点坐标A (2,-1),B (2,2),C (4,1),求三角形三条边所在的直线方程.练习1.已知三角形的三个顶点A(-4,0),B(0,-3),C(-2,1),求:(1)BC边所在的直线方程;(2)BC边上中线所在的直线方程.【例2】求过点(4,-3)且在两坐标轴上截距的绝对值相等的直线l的方程.练习2.求过点A(5,2),且在坐标轴上的截距互为相反数的直线l的方程.直线方程的综合应用直线方程的四种特殊形式及其适用范围.【例3】如图,已知正方形ABCD的边长是4,它的中心在原点,对角线在坐标轴上,则正方形边AB,BC所在的直线方程分别为_______ _________.对称轴所在直线的方程为____ ____.练习3.三角形的顶点是A(-4,0),B(3,-3),C(0,3),求这个三角形三边所在的直线的方程.课堂练习1.过两点(-2,1)和(1,4)的直线方程为()A.y=-x+3B.y=x-3 C.y=x+3 D.y=-x-32.经过P(4,0),Q(0,-3)两点的直线方程是________.3.直线xa2-yb2=1在y轴上的截距是________.4.直线l经过点A(2,1)和点B(a,2),求直线l的方程.班级姓名学号成绩一、选择题1.一条直线不与坐标轴平行或重合,则它的方程()A.可以写成两点式或截距式B.可以写成两点式或斜截式或点斜式C.可以写成点斜式或截距式D.可以写成两点式或截距式或斜截式或点斜式2.两条直线l1:xa-yb=1和l2:xb-ya=1在同一直角坐标系中的图象可以是()3.直线x3-y4=1在两坐标轴上的截距之和为()A.1B.-1 C.7D.-74.在y轴上的截距是-3,且经过A(2,-1),B(6,1)中点的直线方程为()A.x4+y3=1 B.x4-y3=1 C.x3+y4=1 D.x3-y6=15.已知直线ax+by+c=0的图象如图,则()A.若c>0,则a>0,b>0B.若c>0,则a<0,b>0C.若c<0,则a>0,b<0D.若c<0,则a>0,b>0二、填空题6.若直线l过定点(-1,-1)和(2,5),且点(2 017,a)在l上,则a的值为________.7.经过点A(2,1),在x轴上的截距为-2的直线方程是_____ ___.8.已知A(3,0),B(0,4),动点P(x0,y0)在线段AB上移动,则4x0+3y0的值等于________.三、解答题9.已知△ABC中,A(1,-4),B(6,6),C(-2,0).求:(1)△ABC中平行于BC边的中位线所在直线的方程并化为截距式方程;(2)BC边的中线所在直线的方程并化为截距式方程.10.已知直线l过点P(-5,-4)且与两坐标轴围成的三角形面积为5,求直线l的方程.。
直线的两点式方程 课件

忽视截距为0的情形
典例 3
已知直线 l 过点 P(2,-1),且在两坐标轴上的截距相等,求直
线 l 的方程. [错解]
由题意,设直线 l 的方程为ax+ay=1
∵直线 l 过点(2,-1),∴2a+-a1=1
∴a=1,则直线 l 的方程为 x+y-1=0.
命题方向2 ⇨直线的截距式方程
典例 2 直线 l 过点(-3,4),且在两坐标轴上的截距之和为 12,求直线 l 的方程.
[思路分析] 由于直线在两坐标轴上的截距之和为12,因此直线方程.
[解析] 设直线 l 的方程为ax+by=1
则 a+b=12.
(2)直线方程的截距式在结构上的特点: 直线方程的截距式为ax+by=1,x 项对应的分母是直线在 x 轴上的截距,y 项 对应的分母是直线在 y 轴上的截距,中间以“+”相连,等式的另一端是 1,由 方程可以直接读出直线在两轴上的截距,如:3x-4y=1,3x+4y=-1 就不是直线的 截距式方程.
3.中点坐标公式
若点 P1、P2 的坐标分别为(x1,y1)、(x2,y2),且线段 P1P2 的中点 M 的坐标为 x1+x2
x=_____2___________ (x,y),则有y=___y_1_+2__y_2________.
此公式为线段 P1P2 的中点坐标公式.
命题方向1 ⇨直线的两点式方程
(2)从题意看,本题只告诉了截距之间的关系,因此解题时,设出了直线的截距式,由于不知截距 的大小,因此,需要进行分类讨论.
[思路分析]
已给出了截 距间的关系
设 别―截 为―距 a→、分b
12ab=2 |a-b|=3
人教版数学2《直线的两点式与截距式方程》上课(共18张PPT)教育课件

化简:
yy1 xx1 y2 y1 x2 x1
一、直线的两点式方程
两点式适用范围: 与坐标轴不垂直的直线
思考:当x1 x2时,当 y1 y2 时,直线方程怎 么表示? 1、当x1 x2时,直线与X轴垂直,方程为
xx10(或 xx1)
2、当 y1 y2 时,直线与Y轴垂直,方程为 yy10(或 yy1)
3
k= 2 ;直线的方程为 3x2y10 。
讨论:如何用点斜式的方法推导两点式方程. 还有其他的方法吗?
一、直线的两点式方程
已知直线经过两点 , P 1(x1,y1)P ,2(x2,y2) (x1x2,y1y2)
直线的两点式方程 课件

(2)若直线 l 在两坐标轴上的截距为 0(或者说直线 l 过原点), 则可设 l 的方程为 y=kx.
代入点 A 的坐标,得 k=14. l 的方程为 y=14x,即 x-4y=0. ∴所求直线 l 的方程为 x+y-5=0 或 x-4y=0.
(2)求过点 M(m,0)和点 N(2,1)的直线方程.
【解析】 ①当 m=2 时,过点 M(m,0)和点 N(2,1)的直线斜 率不存在,其方程为 x=2.
②当 m≠2 时, 方法一:直线的斜率为 k=m0--12=-m-1 2, 又∵直线过点 N(2,1), ∴直线方程的点斜式为 y-1=-m-1 2(x-2). 即 x+(m-2)y-m=0.
方法二:由两点式,得y0--11=mx--22, 即 y-1=-m-1 2(x-2),即 x+(m-2)y-m=0. 当 m=2 时上述方程即为 x=2. 综上,所求直线方程为 x+(m-2)y-m=0.
题型三 一题多解求直线方程
例 3 求经过点 A(-3,4),且在两坐标轴上的截距之和等 于 12 的直线的方程.
(2)已知直线 l 在 x 轴上截距比在 y 轴上的截距大 1,且过定 点(6,-2),求直线 l 的方程.
【解析】 设直线方程的截距式为a+x 1+ya=1. 则a+6 1+-a2=1,解得 a=2 或 a=1. 则直线方程是2+x 1+y2=1 或1+x 1+y1=1, 即 2x+3y-6=0 或 x+2y-2=0.
方法三:设直线方程为xa+12y-a=1, ∵直线过点 A(-3,4),∴-a3+124-a=1. 整理,得 a2-5a-36=0,∴a=9 或 a=-4. ∴直线方程为x9+y3=1 或-x4+1y6=1, 即 x+3y-9=0 或 4x-y+16=0.
高中数学同步教学课件 直线的两点式方程 (2)

对特殊情况下的直线要单独讨论解决.
跟踪训练2 △ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0).求边AC 和AB所在直线的方程.
∵A(0,4),C(-8,0), ∴直线 AC 的截距式方程为-x8+4y=1, 即x-2y+8=0, ∵A(0,4),B(-2,6), ∴由直线的两点式方程,得直线 AB 的方程为6y--44=-x-2-00, 即x+y-4=0.
1234
3.过点P(1,2)且在两坐标轴上截距的和为0的直线方程为___2_x_-__y_=__0_或___ __x_-__y_+__1_=__0__.
当直线过原点时,得直线方程为2x-y=0; 当在坐标轴上的截距不为零时, 可设直线方程为ax-ay=1, 将点P(1,2)代入方程可得a=-1, 得直线方程为x-y+1=0. ∴直线方程为2x-y=0或x-y+1=0.
√A.1
C.-2或-1
B.-1 D.-2或1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
显然a≠0. 把直线 l:ax+y-2=0 化为2x+2y=1.
a ∵直线l:ax+y-2=0在x轴和y轴上的截距相等, ∴2a=2,解得 a=1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
设A(a,0),B(0,b),其中a>0,b>0.
∵A→P=12P→B,
∴(3-a,1)=12(-3,b-1),
即31- =ba= -2 -1,32,
解得a=92, b=3,
∴直线 l 的截距式方程为9x+3y=1. 2
(2)求当A→P·P→B取得最小值时直线 l 的方程.
∵A,P,B三点共线, ∴3-1 a=1-3 b,整理得3a+1b=1, ∴A→P·P→B=(3-a,1)·(-3,b-1)=3a+b-10=(3a+b)3a+b1-10=3ab+ 3ba≥2 3ab·3ba=6,当且仅当3ab=3ba,即 a=b=4 时,等号成立. ∴当A→P·P→B取得最小值时,直线 l 的方程为4x+4y=1,即 x+y-4=0.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§7.1
直线的方程( 直线的方程(2)
例2,菱形的对角线长分别为 和6,并 ,菱形的对角线长分别为8和 , 且分别位于x 轴上, 且分别位于 轴和 y轴上,求菱形的各 轴上 边所在直线的方程. 边所在直线的方程.
§7.1
直线的方程( 直线的方程(2)
的直线L与 轴 例3,过点 ,过点P(-5,4)的直线 与x轴,y轴分 的直线 轴分 别交于A, 两点 两点, 别交于 ,B两点,且P分有向线段 分有向线段 的比是2, 的方程. 的比是 ,求L的方程. 的方程
AB
§7.1
直线的方程( 直线的方程(2)
例4,求过点P(2, 3),并且在两坐标轴 ,求过点 , 上的截距相等的直线的方程. 上的截距相等的直线的方程. 变题1:上题中改为求截距的绝对值相 变题 : 等的直线方程,结果如何? 等的直线方程,结果如何? 变题2:求过点P(2, 3),并且在 轴上 变题 :求过点 ,并且在x轴上 的截距是在y轴上的截距 轴上的截距2倍的直线的 的截距是在 轴上的截距 倍的直线的 方程. 方程.
当y1≠y2时
y y1 x x1 = y2 y1 x2 x1
§7.1
直线的方程( 直线的方程(2)
注:两点式适用于与两坐标轴不垂直 的直线. 的直线. 练习1:课本第41页 1 练习 :课本第 页
§7.1
直线的方程( 直线的方程(2)
2,直线方程的截距式 ,直线方程的截距式 若直线L与 轴交点为 若直线 与x轴交点为 (a, 0),与y轴交 , 轴交 其中a≠0,b≠0,由两点式 , 点为 (0, b), 其中 , ,
0 得 y 0 = x a b 0 0a
即
a b
叫做直线在x轴上的截距; 叫做直线在 轴上的截距; 轴上的截距 叫做直线在y轴上的截距 叫做直线在 轴上的截距. 轴上的截距
x y + =1 a b
§7.1
直线的方程( 直线的方程(2)
注:截距式适用于与两坐标轴不垂直 且不过原点的直线. 且不过原点的直线. 练习2:课本第 页 练习 :课本第41页 2 例1,三角形的顶点是 A(-5, 0), B(3,-3), , C(0, 2), 求这个三角形三边所在直线的方 程.
§7.1 小结: 小结:
直线的方程( 直线的方程(2)
y y1 x x1 (1)两点式: )两点式: = y2 y1 x2 x1
(2)截距式: )截距式:
x y + =1 a b
作业: 数学之友》 作业:《数学之友》第38页 页
�
§7.1
直线的方程( 直线的方程(2)
例5,求过点 2, 1)的直线与两坐标轴 ,求过点P( 的直线与两坐标轴 正半轴所围成的三角形的面积最小时的 直线方程
§7.1
直线的方程( 直线的方程(2)
练习3: 练习 : 1,直线 ,直线ax+by=1 (ab≠0)与两坐标轴围成的 与两坐标轴围成的 面积是___________; 面积是 2,已知一直线在 轴上的截距比在 轴上的 轴上的截距比在y轴上的 ,已知一直线在x轴上的截距比在 截距大1,并且经过点P 截距大 ,并且经过点 (6, -2),求此直线的 求此直线的 方程. 方程.
§7.1 一,复习ຫໍສະໝຸດ 直线的方程( 直线的方程(2)
1,什么是直线的点斜式方程? ,什么是直线的点斜式方程? 2,求分别过以下两点直线的方程 , (1)A(8, -1) (2) C (x1, y1) B (-2 , 4) D (x2 ,y2) (x1≠x2, y1≠y2)
§7.1
直线的方程( 直线的方程(2)
二,新课 1,直线方程的两点式 ,直线方程的两点式 若直线L经过点 经过点P 若直线 经过点 1(x1,y1),P2(x2,y2), , ,
y2 y1 并且x 并且 1≠x2,则它的斜率 k = , x2 x1 y2 y1 代入点斜式, 代入点斜式,得 y y1 = x x (x x1) 2 1
