传热学 第8章辐射换热计算例题
传热学辐射传热课后习题及答案.doc

Q.2第八章黑体辐射基本定律8-1、一电炉的电功率为1KW,炉丝温度为847°C,直径为Immo 电炉的效率为0.96。
试确 定所需炉丝.的最短长度。
<273 + 847丫 〃 八* 前------------ jvdL = 0.96 x 10解:5.67x1 1°° 7 得 L=3.61m8-5、在一空间飞行物的外壳上有一块向阳的漫射面板。
板背面可以认为是绝热的,向阳面 得到的太阳投入辐射GT300W 〃疟。
该表面的光谱发射率为:时£(") = 0.5; 人>2彻时£(人)二°・2。
试确定当该板表而温度处于稳态时的温度值。
为简化计算,设太 阳的辐射能均集中在0〜2即刀之内。
解:由 UOOJ 得 T=463K8-6、人工黑体腔上的辐射小孔是一个直径为20mm 的圆,辐射力场=3.72 x " W /帚。
一个辐射热流计置于该黑体小孔的正前方l=0.5m,处,该热流计吸收热量的面积为 1.6'10一5 "己问该热流计所得到的黑体投入辐射是多少?L. =^ = 1.185xlO 5W/m 2 解: 人 AO = T = 6.4x10-5rL h .A = 312W所得投入辐射能量为37.2X6.4X10-5 = 2.38x IO” w8-15、已知材料AB 的光谱发射率林久)与波K 的关系如附图所示,试估计这两种材料的发射 那£随温度变化的特性,并说明理由。
解:A 随稳定的降低而降低;B 随温度的降低而•升高。
理由:温度升高,热辐射中的短波比例增加。
8-16、一•选择性吸收表面的光谱吸收比随人变化的特性如附图所示,试计算当太阳投入辐射 为G=8()0W//H 2时,该表面单位面积上所吸收的太阳能量及对太阳辐射的总吸收比。
1-4QF -------------- + % -----------o o解:二°・9氏(()~|.4)+ °・2丹(].4~8)查表代入数据得 a = 0.7 x 86.0792% = 0.80268-23、已知一表面的光谱吸收比与波长关系如附图所示,在某一瞬间,测得表面温度为lOOOKo投入辐射G/按波长分布的情形示于附图b。
2020年高中物理竞赛—传热学基础08辐射换热的计算:多表面系统辐射换热的计算(共35张PPT) 课

dL , x L , x
K dx
式中,负号表示吸收,K为光谱衰减系数,m-1, 它取决于其体的种类、密度和波长。对上式进行积
分可得
dL L,s ,x
L L ,0 ,x
s
0 Kdx
即
L,s L,0eKs
Beer 定律
式中,s 是辐射通过的路程长度,常称之为射 线程长。从上式可知,热辐射在气体内呈指数规 律衰减。
(4)按公式
i
Ebi确 定Ji 每一个表
1 i
i Ai
面的净辐射换热量。
2.网络法的应用举例
以图(a)所示的三表面的辐射换热问题为例画出图(b) 的等效网络图
(a)由三个表面组成的封闭系统
(b)三表面封闭腔的等效网络图
3. 两个重要特例
a 有一个表面为黑体。黑体的表面热阻为 零。其网络图见图8-14a。 b 有一个表面绝热,即该表面的净换热 量为零。其网络图见图8-14b 和8-14c,
1 1 A11
J1
J2
1 A1,2 X1,2
Eb2
12 A2 2
两表面封闭系统辐射换热等效网络图
这种把辐射热阻比拟成等效的电阻从 而通过等校的网络图来求解辐射换热的方 法成为辐射换热的网络法。
应用网络法求解多表面封闭系统辐射换热 问题的步骤: (1)画出等效的网络图。 (2)列出节点的电流方程
(3)求解上述代数方程得出节点电势。
)
Tg Tw
0.65
* H 2O
* H 2O
Tw , pH2Os(Tw
Tg
)
Tg Tw
0.45
Tw
在其体发射率和吸收比确定后,气体 与黑体外壳之间的辐射换热公式为:
新大《传热学》习题及解答第8章 热辐射基本定律和辐射特性

第8章 热辐射基本定律和辐射特性(题解)【习题8-3】 把太阳表面近似地看成是K 5800=T 的黑体,试确定太阳发出的辐射能中可见光所占的百分数。
解:K μm 220458003801⋅=⨯=.T λ,K μm 440858007602⋅=⨯=.T λ ()%.F b 191010=-λ,()%.F b 045520=-λ()()()%.%.%.F F F b b b 854419100455122100=-=-=---λλλλ【习题8-4】 一炉膛内火焰的平均温度为500K 1,炉墙上有一看火孔。
试计算当看火孔打开时从孔(单位面积)向外辐射的功率。
该辐射能中波长为μm 2的光谱辐射力是多少?哪一种波长下的能量最多? 解:小孔辐射看成黑体辐射:25484m W 10872150010675⨯=⨯⨯==-..T E b σ对μm 2=λ的辐射:()()()31015001021043881561651m W 107449110210741931622⨯=-⨯⨯⨯=-=⨯⨯⨯------.e .e c E .T c b λλλ最大辐射能对应波长m λ:31092-⨯=.T m λ,m 109331150010921092633---⨯=⨯=⨯=..T .m λ【习题8-6】 一人工黑体腔上的辐射小孔是一个直径为0mm 2的圆。
辐射力25m W 1072.3⨯=b E 。
一个辐射热流计置于该黑体小孔的正前方m 5.0=l 处,该热流计吸收热量的面积为25m 106.1-⨯。
问该热流计所得到的黑体投入辐射是多少?解:2422m 10141634020141634d -⨯=⨯==...d A π sr 1046501061d d 5252--⨯=⨯==...l S Ω ()()545104610141631416310723d d d d d --⨯⨯⨯⨯⨯=⎪⎭⎫⎝⎛==....A E A I b ΩπΩθθΦW 103823-⨯=.【习题8-17】 一漫射表面在某一温度下的光谱辐射强度与波长的关系可以近似地用附图表示,试:(1)计算此时的辐射力;(2)计算此时法线方向的定向辐射强度,及与法向成o 60角处的定向辐射强度。
传热学 第8章辐射换热计算例题教材

解:设加热室及被燃烧物的温度分别为T2, T1,被燃烧物单位面积、单位时间吸收 的辐射热量为:
Qw
=h辐[(
T2 100
)
4
-(
T1 100
)4
]
(1)
T2
T1
H辐—辐射换热系数
2Qw
=h
辐[(
T'2 100
)4
-(
T1 100
)4
]
(2)
2020/4/15
联立(1),(2)式:
17
联立(1),(2)式:
2[( T2 )4 -( T1 )4 ]=[( T'2 )4 -( T1 )4 ] 100 100 100 100
T2=1000 ℃ ,T1=400 ℃
T’2=1226 ℃ 。即炉温的温度升高了226 ℃
2020/4/15
18
【例6】将一根长1m、直径为2cm经一般研磨的钢 棒投入1000 ℃的加热炉中,钢棒的最初温度为20 ℃ ,求当钢棒加热到500 ℃大约需要多少时间。 钢的密度为7.86×103kg/m3,质量热容为 0.640kJ/(kgk)
• 解:钢棒近似为灰体, 根据四次方定律,
Qw
=Cb
ε[(
T2 100
)4
-(
T1 100
)4
]A
A=π 0.021 2π (0.02)2 0.0635m2 2
从附录8可以查出钢棒的黑度为0.32。钢棒投入炉内 时的热辐射量为:
2020/4/15
19
2020/4/15
20
2020/4/15
2020/4/15
4
【例2】如图所示的三个非凹表面组成
的封闭系统,三个表面面积分别为A1、 A2、 A3 , 在垂直于纸面方向无限长,试求所有相 关角系数。
辐射传热的计算

Q12
A(Eb1Eb2)A T14T24
1112 1
21
在两块平壁之间加一块大小一样、表面发射率相同的遮热板 (忽略导热热阻)
辐射换热量减少为原来的 1/2,即:
112
1 2
12
A 3X 3,1A 3X 3,2A 3
根据角系数的相对性有:
A1X1,2A2X2,1
A1X1,3A3X3,1 A2X2,3A3X3,2
三个非凹表面组成的封闭辐射系统
X1
2
A1
A2 A3 2A1
X1,3
A1
A3 A2 2A1
X2,3
A2
A3 A1 2A2
黑体间的辐射换热及角系数例题讲解:
[例] 试用代数法确定如图所示
的辐射和吸收是在整个气体容积中进行的,属 于体积辐射。
(4) 气体的反射率为零
气体辐射的特点1:
在工业上常见的温度范围内,单原子气体 及空气、H2、O2、N2等结构对称的双原 子气体,无发射和吸收辐射的能力可认为 是透明体。 CO2、H2O、SO2、CH4和CO等气体都具 有辐射的本领。
例:煤和天然气的燃烧产物中常有一定浓度的CO2和
例:大气中的臭氧层能保护人类免受紫外线的伤害
气体辐射的特点3:
热射线穿过气体层时,辐射能沿途被气体 分子吸收而逐渐减弱。其减弱程度取决于 沿途碰到的气体分子数目,碰到的分子数 目越多,被吸收的辐射能也越多。因此气 体的吸收能力αg与热射线经历的行程长 度L,气体分压力p和气体温度Tg等因素有 关。
9.5 辐射传热的控制(强化与削弱)
遮热板的应用:
在现代隔热保温技术中,遮热板的应用 比较广泛。例如:
2020年高中物理竞赛—传热学基础08辐射换热的计算:角系数的定义、性质和计算(共42张PPT) 课

一. 角系数的定义 角系数是进行辐射换热计算时空间热组的 主要组成部分。 定义:把表面1发出的辐射能中落到表面2 上的百分数称为表面1对表面2的角系数,
记为X1,2。
同理,表面1发出的辐射能中落到表面 2上的百分数称为表面1对表面2的角系数,
记为X 2, 1
二. 角系数的性质
❖ 研究角系数的性质是用代数法(代数分析法) 求解角系数的前提:
考察表面温度均匀、表面辐射特性为常数的表面 1(如图8-8所示)。根据有效辐射的定义,表面1 的有效辐射有如下表达式:
J1 E1 1G1 1Eb1 (1 1)G1
在表面外能感受到的表面辐射就是有效辐射, 它也是用辐射探测仪能测量到的单位表面积上的辐 射功率 W / m2。
从表面1外部来观察,其能量收支差额应 等于有效辐射 J与1 投入辐射 之G1 差,即
二、两漫灰表面组成的封闭系统的辐
射换热计算
1、有效辐射 (1)投入辐射:单位时间内投射到单位面积上的 总辐射能,记为G。
(2)有效辐射:单位时间内离开单位面积的总辐 射能为该表面的有效辐射,记为J。
有效辐射包括
自身射辐射E
投入辐射 G 被反射辐射的部分 G
表面的反射比,可表示成 1 1
图8-8 有效辐射示意图
n
X 1,2
X 1,2i
i 1
(6)
图8-4 角系数的可加性
注意,利用角系数可加性时,只有对角 系数符号中第二个角码是可加的,对角系数 符号中的第一个角码则不存在类似的关系。
从表面2上发出而落到表面1上的辐射能,等于从 表面2的各部分发出而落到表面1上的辐射能之和, 于是有
A2 Eb2 X 2,1 A2 Eb2 X 2a,1 A2 Eb2 X 2b,1
传热学68-第八章 辐射换热的计算

解方程组得
( bc ad ) ( ac bd ) 2 ab
X
a b ,c d
交叉线之和 -不交叉线之和 2 表 面 A 1的 断 面 长 度
该方法又被称为交叉线法。
第八章 辐射换热的计算
17
§8-2 被透明介质隔开的两固体 表面间的辐射换热
采用“净热量 ”法。
1.
黑体表面
图8-7
1
X 1, 2 1
A1 A2 1
(2)表面积 A 和 A 2 相差很小,
(3)表面积 A 2 比 A 大得多,
1
A1 A2
0
第八章 辐射换热的计算
27
§8-3 多表面系统辐射换热的计算
(1)
热网络法的原理:
是用电学中的电流、电位差和电阻比 拟热辐射中的热流、热势差与热阻,用电 路来比拟辐射热流的传递路径。
X 1, 2 1 A1
A A
1
cos 1 cos 2 d A1 d A 2
2
r
2
1 A1
A A
1
X d 1, d 2 d A1
2
(8-4a)
X 2 ,1
1 A2
A A
1
cos 1 cos 2 d A1 d A 2
2
r
2
d 1d A2
黑体系统的辐射换热
第八章 辐射换热的计算 18
如图8-7所示,表面1和2之间的辐射换热量为
1 , 2 A1 E b 1 X 1 , 2 A 2 E b 2 X 2 ,1 A1 X 1 , 2 ( E b 1 E b 2 ) 表面 1发出 的热辐射 表面 2 投入 的热辐射
第八章-辐射换热的计算-2

J2 J1 A1
Q2→1 = A J2 X2,1 2
两个表面之间交换的热流量为 :
Q ,2 = A J1 X1,2 − A2 J2 X2,1 1 1
Q ,2 = A J1 X1,2 − A2 J2 X2,1 1 1
A2
由角系数的互换性有
A X1,2 = A2 X2,1 1
q = J −G
εEb
ρG
J
从表面内部观察, 从表面内部观察 , 该表面与外界的辐 射换热量应为: 射换热量应为: q = E −αG 从上两式消去G得到: 从上两式消去 得到: 得到
G
αG
Eb − J q= 1−ε
或
ε
Eb − J Q= 1−ε Aε
Eb − J Q= 1−ε Aε
A为物体表面的面积。Q表示物体表 为物体表面的面积。 表示物体表 为物体表面的面积 面实际向空间辐射出去的辐射能 (热流量),单位为W。 热流量),单位为 。 ),单位为
J2 J1 A1
J1 − J2 J1 − J2 Q ,2 = = 1 1 1 A X1,2 A2 X2,1 1
我们称Q , 为两表面交换的的热流量; 我们称 1,2为两表面交换的的热流量; J1-J2为两表面间的空间辐射势差; J1 为两表面间的空间辐射势差 空间辐射势差; 1/(A1X1,2)或1/(A2X2,1)为两表面之间的 或 为两表面之间的 空间辐射热阻。
2 两个灰体表面间的辐射换热
当两个灰表面的有效辐射和角系数确定之后, 当两个灰表面的有效辐射和角系数确定之后,我们 就可以计算它们之间的辐射换热量。 就可以计算它们之间的辐射换热量。 表面1投射到表面2上的辐射能流为: 表面1投射到表面2上的辐射能流为:
传热学第八章-辐射换热的计算-3

(4)每个表面的温度、辐射特性及投入辐射分布均匀。
(一)封闭空腔中诸灰表面间的辐射换热
对于多个表面组成的封闭空腔,采用网络法计算不方 便,可以从能量平衡法入手进行分析。
考察如图所示的封闭空腔内诸表面间的换热:
(a)从包括i在内的所有表面
第八章 辐射换热计算
本节内容:
(1)封闭空腔中诸灰表面间的辐射换热; (2)辐射换热的强化与削弱; (3)气体辐射; (4) 火焰辐射
假设:
(1)把参与辐射换热的有关表面视作一个封闭腔,表面 间的开口设想为具有黑表面的假想面;
(2)进行辐射换热的物体表面之间是不参与辐射的透明 介质(如单原子或具有对称分子结构的双原子气体、空 气)或真空;
f (T , P, S)
3-2:气体吸收定律 设x=0处的单色辐射强度为I, 在经过x距离后,发生在 厚度为 dx的无限小薄层的衰减量为
dI (x) K I,xdx
分离变量并在整个辐射(吸收)层内积分,有
即,
dI I,s ,x
I I ,0 ,x
s
K dx
I,S
I eKS ,0
此为Beer定律,为描述气体吸收的基本定律,反 映气体穿透辐射的指数衰减规律。
tw t3
d t1 s
(三)气体辐射
3-1:气体辐射的特点 (a) 固体表面的辐射和吸收光谱具有连续性,但气体的 辐射和吸收具有明显选择性;只能辐射和吸收某一定 波长范围内的能量。利用这一性质可制成谱带分析仪 ,分析物质的成份; (b) 对于某一投射辐射,只存在吸收和透射;+=1 (c) 气体的吸收和辐射在整个气体空间中进行,而固体 的辐射和吸收则仅在很薄的表面层中进行。气体对辐 射的吸收与气体的温度、气体分压和辐射层厚度S有关
新大《传热学》复习题及解答第8章 热辐射基本定律和辐射特性

第8章热辐射基本定律和辐射特性(复习题解答)【复习题8-1】什么叫黑体?在热辐射理论中为什么要引入这一概念?答:吸收比α=l的物体叫做黑体。
黑体完全吸收投入辐射,从黑体表面发出的辐射都为自身辐射,没有反射,因而黑体辐射的特性反映了物体辐射的规律,这为研究实际物体的辐射提供了理论依据和简化分析的基础。
【复习题8-2]温度均匀的空腔壁面上的小孔具有黑体辐射的特性,那么空腔内部壁面的辐射是否也是黑体辐射?答:空腔内部壁面不一定是黑体辐射。
小孔之所以呈现黑体特性,是因为辐射在空腔内经历了多次的吸收和反射,辐射能基本基本都被内壁面吸收,从小孔射出的辐射能基本为零。
【复习题8-3]试说明,为什么在定义物体的辐射力时要加上“半球空间”及“全部波长”的说明?答:因为辐射表面会向半球空间各个方向辐射能量,且辐射能中包含各种波长的电磁波,而辐射力必须包括辐射面辐射出去的所有能量,所以要加上“半球空间”和“全部波长”的说明。
【复习题8-4】黑体的辐射能按波长是怎样分布的?光谱辐射力E根的单位中分母的“n?”代表什么意义?答:黑体辐射能按波长的分布服从普朗克定律。
光谱辐射力单位中的分母“n?”代表了单位辐射面积“n?”和辐射的电磁波单位波长范围“m”的意思。
【复习题8-5]黑体的辐射能按空间方向是怎样分布的?定向辐射强度与空间方向无关是否意味着黑体的辐射能在半球空间各方向上是均匀分布的?答:黑体辐射能按空间方向分布服从拦贝特定律。
定向辐射强度与空间方向无关并不意味着黑体的辐射能在半球空间是均匀分布的。
因为定向辐射强度是指单位可见辐射面积,而在空间不同方向可见辐射面积是不同的,辐射能在各个方向也不同。
【复习题8-6】什么叫光谱吸收比?在不同光源的照耀下,物体常呈现不同的颜色,如何解释?答:光谱吸收比是指物体对某一特定波长的投入辐射所吸收的百分比。
在光源照射下,物体会吸收一部分辐射,并反射一部分辐射,物体呈现的是反射光的颜色,因而光源不同,反射光也会不同,物体也会呈现不同的颜色。
传热学第八章例题
可见发光效率很低。
例8-7:一火床炉墙内表面温度为500K,其光谱发射
率可近似地表示为:1.5m时, () = 0.1; =1.510m时, () = 0.5; > 10m时, () = 0.8。(
非灰体);炉墙内壁接受来自燃烧着的煤层的辐射,
煤层温度为2000K。设煤层的辐射可作为黑体辐射, 炉墙为漫射表面,试计算炉墙发射率及其对煤层辐射
2T2 10m 2000K 20000m K
F( 02 ) 0.9856
所以: 0.1 0.2736 0.5 (0.9856 0.2736) 0.8 (1 0.9856)
0.395
这里(T1) = 0.61,而(T1, T2)=0.395, ) (2 ) Fb ( ) (3 ) Fb ( )
其中的辐射函数是2000K下的值:
1T2 1.5m 2000K 3000m K
查表8-1得: F( 0 ) 0.2736 1
而 查得:
则,可见光范围的辐射能为:
W 2500K E (0.0523 0.0003) 0.45 5.67 2 4 m K 100 5.18 10 4 W/m 2
4
发光效率为:
E 5.18 104 W/m 2 7.27% 5 2 E 7.13 10 W/m
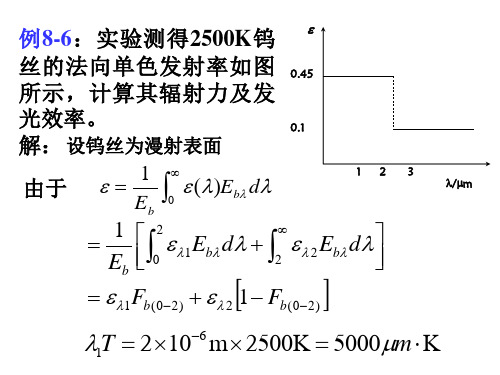
例8-6:实验测得2500K钨 丝的法向单色发射率如图 所示,计算其辐射力及发 光效率。 解: 设钨丝为漫射表面
由于
1 Eb
0.45
0.1
0
( )Eb d
1
2
3
/m
1 2 1 Eb d 2 Eb d 0 2 Eb
第四版传热学第六,七八章习题解答

第五章复习题1、试用简明的语言说明热边界层的概念。
答:在壁面附近的一个薄层内,流体温度在壁面的法线方向上发生剧烈变化,而在此薄层之外,流体的温度梯度几乎为零,固体表面附近流体温度发生剧烈变化的这一薄层称为温度边界层或热边界层。
2、与完全的能量方程相比,边界层能量方程最重要的特点是什么?答:与完全的能量方程相比,它忽略了主流方向温度的次变化率σα22x A,因此仅适用于边界层内,不适用整个流体。
3、式(5—4)与导热问题的第三类边界条件式(2—17)有什么区别?答:=∂∆∂-=yyt th λ(5—4))()(f w t t h h t-=∂∂-λ (2—11)式(5—4)中的h 是未知量,而式(2—17)中的h 是作为已知的边界条件给出,此外(2—17)中的λ为固体导热系数而此式为流体导热系数,式(5—4)将用来导出一个包括h 的无量纲数,只是局部表面传热系数,而整个换热表面的表面系数应该把牛顿冷却公式应用到整个表面而得出。
4、式(5—4)表面,在边界上垂直壁面的热量传递完全依靠导热,那么在对流换热中,流体的流动起什么作用?答:固体表面所形成的边界层的厚度除了与流体的粘性有关外还与主流区的速度有关,流动速度越大,边界层越薄,因此导热的热阻也就越小,因此起到影响传热大小5、对流换热问题完整的数字描述应包括什么内容?既然对大多数实际对流传热问题尚无法求得其精确解,那么建立对流换热问题的数字描述有什么意义?答:对流换热问题完整的数字描述应包括:对流换热微分方程组及定解条件,定解条件包括,(1)初始条件 (2)边界条件 (速度、压力及温度)建立对流换热问题的数字描述目的在于找出影响对流换热中各物理量之间的相互制约关系,每一种关系都必须满足动量,能量和质量守恒关系,避免在研究遗漏某种物理因素。
基本概念与定性分析5-1 、对于流体外标平板的流动,试用数量级分析的方法,从动量方程引出边界层厚度的如下变化关系式:x xRe 1~δ解:对于流体外标平板的流动,其动量方程为:221xy u v dx d y u v xy u ∂+-=∂∂+∂∂ρρ 根据数量级的关系,主流方的数量级为1,y 方线的数量级为δ则有2211111111δρδδv +⨯-=⨯+⨯ 从上式可以看出等式左侧的数量级为1级,那么,等式右侧也是数量级为1级, 为使等式是数量级为1,则v 必须是2δ量级。
传热学第8章-辐射换热的计算

传热学第8章-辐射换热的计算第⼋章辐射换热的计算重点内容:辐射空间热阻及⿊体表⾯间的辐射传热计算分析⽅法。
影响辐射换热的因素:物体表⾯的温度,表⾯形状及尺⼨,表⾯间相对位置,表⾯的辐射及吸收特性。
分析中的假定:物体表⾯⑴为恒温表⾯;⑵为漫-灰表⾯;⑶之间⽓体为透明体。
任何换热均有阻⼒,辐射换热也不例外,但其热阻形式与导热和对流换热有所不同,它包括仅与表⾯间⼏何因素有关的空间热阻和仅与表⾯辐射及吸收特性有关的表⾯热阻两⼤类。
因此,辐射换热计算中最有效、应⽤最普遍的⽅法是封闭空腔⽹络法。
这⾥将分析⿊体表⾯间的辐射换热并引出空间热阻,并讨论如何应⽤封闭空腔⽹络法进⾏⿊体表⾯间辐射换热的分析计算。
§ 8-1 ⾓系数的定义、性质及计算前⾯讲过,热辐射的发射和吸收均具有空间⽅向特性,因此,表⾯间的辐射换热与表⾯⼏何形状、⼤⼩和各表⾯的相对位置等⼏个因素均有关系,这种因素常⽤⾓系数来考虑。
⾓系数的概念是随着固体表⾯辐射换热计算的出现与发展,于 20 世纪 20 年代提出的,它有很多名称,如,形状因⼦、可视因⼦、交换系数等等。
但叫得最多的是⾓系数。
值得注意的是,⾓系数只对漫射⾯ ( 既漫辐射⼜漫发射 ) 、表⾯的发射辐射和投射辐射均匀的情况下适⽤。
1. ⾓系数的定义在介绍⾓系数概念前,要先温习两个概念. (1)投⼊辐射:单位时间内投射到单位⾯积上的总辐射能,记为 G 。
(2) 有效辐射:单位时间内离开单位⾯积的总辐射能为该表⾯的有效辐射,参见图 8-1 。
包括了⾃⾝的发射辐射 E 和反射辐射 r G 。
G 为投射辐射。
下⾯介绍⾓系数的概念及表达式。
(1) ⾓系数:有两个表⾯,编号为 1 和 2 ,其间充满透明介质,则表⾯ 1 对表⾯ 2 的⾓系数 X 1,2 是:表⾯ 1 直接投射到表⾯2(8—1)同理,也可以定义表⾯ 2 对表⾯ 1 的⾓系数。
从这个概念我们可以得出⾓系数的应⽤是有⼀定限制条件的,即漫射⾯、等温、物性均匀(2) 微元⾯对微元⾯的⾓系数如图8-2所⽰,⿊体微元⾯d A1对微元⾯d A2的⾓系数记图8-1为(8—2b )(3) 微元⾯对⾯的⾓系数(8—3a )微元⾯dA2对⾯(8—3b )(4) ⾯对⾯的⾓系数⾯A 1(8—4a )(8—4b )2. ⾓系数性质根据⾓系数的定义和诸解析式,可导出⾓系数的代数性质。
第8章-辐射换热的计算

d
dAc dA2 cos 2 2 r r2
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
1
两微元面间的辐射
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
同理:
整理得:
dA1 cos 1 cos 2 X dA2 ,dA1 r2
同理 X 2,4 X 2, 34) X 2,3 (
A(12) X (12), 34) A(34) X 34) 2) ( ( ,(1
A(12) X (12),3 A3 X 3,(12)
A2 X 2,(34) A(34) X (34),2
A2 X 2,3 A3 X 3,2
上述方法又被称为交叉线法。注意:这里所 谓的交叉线和不交叉线都是指虚拟面断面的线, 或者说是辅助线。
【例】求下列图形中的角系数
解:
A1 X1, A2 X 2, 2 1
A2 X1, X 2, 2 1 A1
X1, 2
X 2, 1 1
X1,2 4 1 3 3 2 R 4 2R
8.1.2.
角系数的性质
1、角系数的相对性
一个微元表面到另一个微元表面的角系数
由dA1发出的落到dA2上的辐射能 Ib1 d A1 cos 1 d X dA1 ,dA2 由dA1发出的辐射能 Eb1 d A1
E b1 I b1 Eb1 : 辐射力 I b1:定向辐射强度
(2)任意两个非凹表面间的角系数 如图所示表面和假定在垂直于纸面的方向上表面的长 度是无限延伸的,只有封闭系统才能应用角系数的完整性, 为此作辅助线ac和bd,与ab、cd一起构成封闭腔。
A1 两个非凹表面及假想面组 成的封闭系统
传热学第八章-辐射换热的计算-3

12
1
1
2 F2
X 1,2 A1 X 2,3 A2
其中 J3 Eb3 T34 459W / m2
Eb2 T24 7348W / m2
查图8-7求得 X 1,2 0.39
则 于是
X 2,1
A1 * X1,2 2
10 0.39 0.26 15
X 1,3 1 X 1,2 0.61
各个表面进行辐射换热的各个净辐射热流分量Qi,j之
和。
于是,节点i的有效辐射通用表达式可写为
图解表示为
Ebi Ji
1i
n Ji J j j1 (Fi X i, j )1
i Fi
对于已知表面的净辐射 热流而温度未知的情况
Qi
n Ji J j j1 (Fi X i, j ) 1
(二)辐射换热的强化与削弱-防辐射屏
(3)用于超级隔热油管 间隔材料
外管
石油在地层下数千米,粘度
大,开采时需注射高温高压 蒸汽使其粘度降低。为减少
内管 注蒸汽
蒸汽散热损失,可采用类似
低温保温容器的多层遮热板
并抽真空。
(4)用于提高温度测量的准确度
如果使用裸露热电偶测量高温气流的温度,高温 气流以对流方式把热量传给热电偶,同时热电偶又 以辐射方式把热量传给温度较低的容器壁。
定义气体的透过率为 则对于气体,有
I,S I ,0
eK S
1 eK S
若认为对于气体,基尔霍夫定律仍然有效,则有
1 eK S
此即为介质的光谱发射率。
如果按气体发射辐射的定义来确定气体发射率,则
有
g
Eg
bTg 4
Eb d
(1 eK S )Eb d
0
《传热学》习题课(辐射换热)

第八章 热辐射基本定律及物体的 辐射特性—复习题
• 6. 什么叫光谱吸收比?在不同光源的照耀 下,物体常呈现不同的颜色,如何解释? 答:光谱吸收比:物体对某一特定波长的辐 射能所吸收的百分数。 是因为物体的光谱吸收具有选择性,而造成 的。如果只反射了一种波长的可见光,而几 乎全部吸收了其他可见光,它就呈现被反射 的这种辐射线的颜色。
第九章 辐射换热的计算—复习题
• 6. 对于温度已知的多表面系统,试总结求解 每一表面净辐射换热量的基本步骤。 答:温度已知时,发射率、辐射能可求出。 可采用网络法或数值方法求解。 但首先应计算出每个面的辐射能Ebi发射率εi, 解系数Xi,j。然后再计算各表面的有效辐射Ji, 最后由 Ebi J i 确定每个表面的净辐射换热 i 1 i 量。
《传热学》习题课(辐射换热)
课件制作:尹华杰
第八章 热辐射基本定律及物体的 辐射特性—复习题
• 1. 什么叫黑体?在热辐射理论中为什么要引 入这一概念? 答:黑体:吸收比等于1的物体。 因吸收比等于1,反射比和透射比等于零,黑 体的辐射能力最大。引入这一概念可使物体 辐射的研究简化,方便充分地研究物体辐射 的各种性质、规律。在研究了黑体辐射的基 础上,处理其他物体辐射时,与黑体相比较, 找出其与黑体辐射的偏离,然后确定修正系 数。把黑体的研究结果运用于实际。
dAc H=1m 传感器 θ θ dA
x1
热试件
d dA cos dL
第八章 热辐射基本定律及物体的 辐射特性—习题
dAc 直上下时 : d0 dA 2 L cos 0 dAdAc L 1 dAc cos 1 斜方向时 : d dA L cos cos 2 1 x1 1 x12 d dA
传热学教学课件第八章 第三节 多表面间辐射换热的计算

辐射换热计算的重点
• 工程计算的主要目的是获得一个表面的净辐射 换热量。因此,要计算一个表面的净辐射换热 量就必须计算该表面与其他表面间的辐射换热 量。
• 多表面系统中,任意两个表面间的辐射换热量 的计算可按如下的公式计算
i, j Ai Ji X i, j Aj J j X j,i
• 因此,计算的重点是获得各个表面的有效辐射。
间的辐射换热量。
画等效网络图应注意的问题
• 每一个参与辐射的表面(净换热量不为零的表 面)都应该有一段相应的电路,它包括源电势、 与表面热阻相应的电阻及节点电势;
• 各表面之间的链接,由节点电势出发通过空间 热阻进行链接。每一个节点电势都应该与其他 节点电势链接起来。
列节点方程的方法
• 画出等效网络图后,可按电学中的基尔霍夫定 律列出各节点的“电流”方程,即从各个方向 流入同一节点的电流之和为零。
25
273
4
13
273
4
100 100 291W
0.233
• 天花板的净辐射换热量
2
Eb2 J 2 R2
1
291W
• 这里负号表示得到热量
• 地面与天花板之间的辐射换热量
1,2
J1 J2 R2
439 .0 387 .4 0.436
118 .3W
1
Eb1 J1 1 1
1,2
Eb1
Eb2 Rt
1
1 1
A1 X1,2
12
A11
A2 2
Eb1
J1 J3 Eb3 J 2
Eb2
11
A1 X1,3 A2 X 2,3
总热阻的计算
1
1 1
A1 X1,2
传热学-辐射传热的计算

这一章讨论物体间辐射换热的计算方法 重点是固体表面间辐射换热的计算 首先讨论辐射换热计算中的一个重要几何因子——角系数的
定义、性质及其计算实例 接着介绍由两个表面及多个表面所组成系统的辐射传热计算
方法,然后简要介绍气体热辐射的特点 在此基础上总结辐射换热的强化及削弱的方法 最后是本章的小结与应用举例
Φ1,2 = A1 J1 X 1,2 − A2 J 2 X 2,1
(a)
J1 A1
=
A1 E b1
−
⎛ ⎜ ⎝
1 ε1
⎞ − 1⎟ Φ1,2
⎠
(b)
J 2 A2
=
A2 Eb 2
−
⎛ ⎜ ⎝
1 ε2
⎞ − 1⎟ Φ 2,1
⎠
(c)
根据上式及能量守恒有 Φ1,2 = −Φ2,1
(d)
Φ 1,2
=
1 − ε1
J1 A1
=
A1 E b1
−
⎛ ⎜ ⎝
1 ε1
⎞ − 1⎟ Φ1,2
⎠
(b)
J 2 A2
=
A2 Eb 2
−
⎛ ⎜ ⎝
1 ε2
⎞ − 1⎟ Φ 2,1
⎠
(c)
9.2.2 有效辐射
有效辐射与辐射传热量的关系
从表面1外部来观察,其能量收支差额
应等于有效辐射 J1 与投入辐射 G1之
差,即
q = J1 − G1
从表面1发出的总辐射能中直接投射到表面2 上份额称为表面1对表面2的角系数,用符号X1,2 表示。
基本原则:角系数是纯几何因子,与表面温度、发射率无关 研究角系数时把物体当做黑体来处理
9.1 辐射传热的角系数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辐射换热量的变化率为
' Q1,2 -Q1,2
Q1,2
-0.5+0.25 = =50% -0.5
【讨论】插入遮热板后辐射换热量
减少了50%。需要注意的是对筒状的遮热
板,随其直径的变化遮热效果会改变,而
对于平行平板间插入的遮热板,遮热效果
并不因板的靠近哪一方而发生改变。
2013-11-19
2013-11-19
1,2 1,3
A1 A 2 A 3 A 2 A1 A 3 2,1 2A 2 2A1 A1 A 3 A 2 A 3 A1 A 2 3,1 2A 3 2A
1
2,3
A2 A3 A1 3,2 A 3 A 2 A1 2A 3 2A2
• 解:钢棒近似为灰体, 根据四次方定律,
T2 4 T1 4 ) -( ) ]A 100 100
Q w =Cb ε[(
0.02 2 A=π 0.02 1 2π ( ) 0.0635m 2 2
从附录8可以查出钢棒的黑度为0.32。钢棒投入炉内时的热辐
2013-11-19 19来自2013-11-19 773 4 573 4 0.03 5.67 100 100 1 3 1 1 0.3 5 0.6
=356.6 W/m
2013-11-19 10
【例4】低温流体在直径D1=20mm 的长管 内流动,管外表面是灰体表面,黑度ε1=0.02, 温度T1=77K。此管与直径D2=50mm的外套管同 心,外套管的内表面黑度ε2= 0.05,温度 T2=300K,也为灰体表面,两表面之间是真空状 态。如图所示。试计算 (1)单位管长低温流体所得热量; (2)在内外表面的中间布置一直径D3= 35mm,两侧表面黑度为ε3=0.02的薄遮板,计算 单位管长低温流体所得热量的变化。
第8章 辐射换热例题
2013-11-19
1
【例1】求图中所示表面间的角系数。(a) 内包壳;(b)在垂直纸面方向无限长的矩 形槽1(高H,宽L)与环境2。
2013-11-19
2
解: (1) A1为非凹面,根据角系数
的定义,图中离开表面 A1的辐射能全部落
在表面A2上,因而 φ 1,2=1, φ2,1 =
D2 D3 D1
2013-11-19 11
解:(1)无遮热板时,系统辐射换
热的网络图如图6-10(b)所示,因此所
求的辐射换热量为
代入数据,求得单位管长的辐射热流为:
2013-11-19 12
Q1,2
T1 4 T2 4 πD1Lc0 - 100 100 1 πD1L 1 1 1 πD 2 L 2
T2=1000 ℃ ,T1=400 ℃ T’2=1226 ℃ 。即炉温的温度升高了226 ℃
2013-11-19
18
【例6】将一根长1m、直径为2cm经一般研磨的钢 棒投入1000 ℃的加热炉中,钢棒的最初温度为20 ℃ ,求当钢棒加热到500 ℃大约需要多少时间。 钢的密度为7.86×103kg/m3,质量热容为 0.640kJ/(kgk)
2013-11-19
=
4
【例2】如图所示的三个非凹表面组成 的封闭系统,三个表面面积分别为A1、 A2、 A3 , 在垂直于纸面方向无限长,试求所有相 关角系数。
2013-11-19
5
解:根据角系数的完整性和相互性:
A1 φ1,2=A2 φ 2,1
A2 φ 2,3=A3 φ 3,2 A1 φ 1,3=A3 φ 3,1 φ 1,2+ φ 1,3=1 φ 2,1+ φ 2,3=1 φ 3,1+ φ 3,2=1
返回
16
【例5】某燃烧加热室内的火焰平均温度为1000℃.计算为使 火焰的辐射传热增加一倍,应当使火焰燃烧温度升高到多少? 假定被燃烧的物体的平均温度为400 ℃,火焰及被燃烧物表 面的辐射率均为定值。 T2
解:设加热室及被燃烧物的温度分别为T2, T1,被燃烧物单位面积、单位时间吸收 的辐射热量为:
' 1, 2
77 4 300 4 3.14 0.02 5.67 100 100 1 0.02 1 0.02 0.02 1 2 1 1 0.02 0.035 0.02 0.035 0.05 0.05 0.25W / m
套筒端部辐射热损失为零,试计算套筒之
间单位长度的辐射换热量。
2013-11-19
8
解:本题为两灰体表面间的辐射换热 问题,代入式 (6-12b)有
T1 4 T2 4 Q1,2 =C导[( ) -( ) ]A12 = 100 100 Cb T1 4 T2 4 [( ) -( ) ]A12 1 1 100 ( -1)12 1 ( -1)21 100
1
2
其中 A1=πDL, A2=πd L, T1=500+273=773 K, T2=300+273=573K 代入上式: 2013-11-19
9
T1 4 T2 4 πdLc0 - 100 100 Q1,2 = 1 πdL 1 + -1 ε 2 πDL ε1
T1
T2 4 T1 4 Q w =h 辐 [( ) -( ) ] 100 100
H辐—辐射换热系数
(1)
T'2 4 T1 4 (2) 2Q w =h 辐[( ) -( ) ] 100 100
2013-11-19
联立(1),(2)式:
17
联立(1),(2)式:
T2 4 T1 4 T'2 4 T1 4 2[( ) -( ) ]=[( ) -( ) ] 100 100 100 100
2013-11-19
3
2
2
(b)在垂直纸面方向无限长的矩 形槽1(高H,宽L)与环境2。
H
1
L
(b)作一个辅助表面2 ,离开表面1的辐 射能必然通过假想面2 而辐射出去,因此考 虑表面 2 与表面1之间的角系数。离开表面2 的辐射能全部落在表面1上,因而有φ 2 ,1 = 1 ,
φ 1,2 = φ 1,2=
20
2013-11-19
21
2013-11-19
22
2013-11-19
23
2013-11-19
24
2013-11-19
25
6
若L1、L2和L3为表面A1、A2和A3分别与 纸面交线的长度,上面的角系数还可表示 为
L1 +L 2 -L3 φ1,2 = 2L1
2013-11-19
7
【例3】有一同心圆套筒,外筒内径
为D=50mm,表面温度T1=500℃,表面
黑度ε1为 0.6;内筒外径为d=30mm,表面
温度T2=300 ℃,表面黑度ε2=0.3,假定
77 4 300 4 3.14 0.02 5.67 100 100 0.5W / m 1 0.02 1 1 0.02 0.05 0.05
2013-11-19
13
(2)当插入遮热板后,辐射换热量为
1 Q13 = Q32 = Q12 2
因为φ
1,3 =
φ
3,2
= 1,
2013-11-19
14
代入数据
T1 4 T2 4 D1 Lc0 100 100 1 D1 L 1 D1 L D1 L 1 1 2 D L D L 1 1 D3 L 3 3 2 2
