(完整版)初中数学经典相似三角形练习题(附参考答案)
相似三角形练习题及答案

相似三角形练习题及答案在初中数学中,相似三角形是一个很重要的概念。
相似三角形具有相同的形状,但是尺寸不同。
理解相似三角形的性质对于解决几何问题和计算三角形的边长和角度非常有帮助。
下面是一些相似三角形的练习题,帮助你巩固对该概念的理解,并附有答案供参考。
练习题一:已知△ABC和△DEF相似,且AB = 6cm,AC = 8cm,BC = 12cm。
若DE = 9cm,求DF和EF的长度。
练习题二:△ABC和△PQR中,∠B = ∠Q,AB = 5cm,BC = 8cm,PQ = 6cm,若AC = 10cm,求PR的长度。
练习题三:已知△ABC和△DEF相似,DE = 4.5cm,EF = 6cm,BC = 12cm,若AC = 8cm,求△ABC和△DEF的周长比。
练习题四:在△ABC中,∠B = 90°,AB = 9cm,BC = 12cm。
点D是BC的中点,于BC上作DE ⊥ BC,DE = 3cm。
求△ADE和△ABC的周长比。
练习题五:已知△ABC和△DEF相似,AB = 10cm,BC = 12cm,AC = 15cm,EF = 6cm,若△DEF的面积为18平方厘米,求△ABC的面积。
答案及解析如下:练习题一:由相似三角形的性质可知,相似三角形的边长之比相等。
设DF = x,EF = y。
根据题意可写出比例:AB/DE = AC/EF = BC/DF代入已知值,得到:6/9 = 8/y = 12/x解得:x = 16cm,y = 12cm因此,DF = 16cm,EF = 12cm。
练习题二:由相似三角形的性质可知,相似三角形的边长之比相等。
设PR = x。
根据题意可写出比例:AB/PQ = AC/PR = BC/QR代入已知值,得到:5/6 = 10/x = 8/(6 + x)解得:x = 15cm因此,PR = 15cm。
练习题三:由相似三角形的性质可知,相似三角形的边长之比相等。
完整版)九年级数学相似三角形综合练习题及答案

完整版)九年级数学相似三角形综合练习题及答案1.填空题:1) 若$a=8$cm,$b=6$cm,$c=4$cm,则$a$、$b$、$c$的第四比例项$d=\underline{12}$;$a$、$c$的比例中项$x=\underline{5}$。
2) $(2-x):x=x:(1-x)$。
则$x=\underline{1}$。
3) 在比例尺为1:的地图上,距离为3cm的两地实际距离为\underline{30}公里。
4) 圆的周长与其直径的比为\underline{$\pi$}。
5) $\frac{a^5-ab}{b^3}=\frac{a^4}{b^2}$,则$\frac{a}{b}=\underline{a^2}$。
6) 若$a:b:c=1:2:3$,且$a-b+c=6$,则$a=\underline{2}$,$b=\underline{1}$,$c=\underline{3}$。
7) 如图1,则$\frac{AB}{AC}=\frac{BC}{CE}=\underline{\frac{3}{2}}$;若$BD=10$cm,则$AD=\underline{6}$cm;若$\triangle ADE$的周长为16cm,则$\triangle ABC$的周长为\underline{24}cm。
8) 若点$c$是线段$AB$的黄金分割点,且$AC>CB$,则$\frac{AC}{AB}=\underline{\frac{1+\sqrt{5}}{2}}$,$\frac{CB}{AB}=\underline{\frac{\sqrt{5}-1}{2}}$。
2.选择题:1) 根据$ab=cd$,共可写出以$a$为第四比例项的比例式的个数是()A.$1$,B.$2$,C.$3$,D.$4$。
答案:B。
2) 若线段$a$、$b$、$c$、$d$成比例,则下列各式中一定能成立的是()A.$abcd=1$,B.$a+b=c+d$,C.$\frac{a}{b}=\frac{c}{d}$,D.$a^2+b^2=c^2+d^2$。
九年级数学相似三角形经典题(含答案)
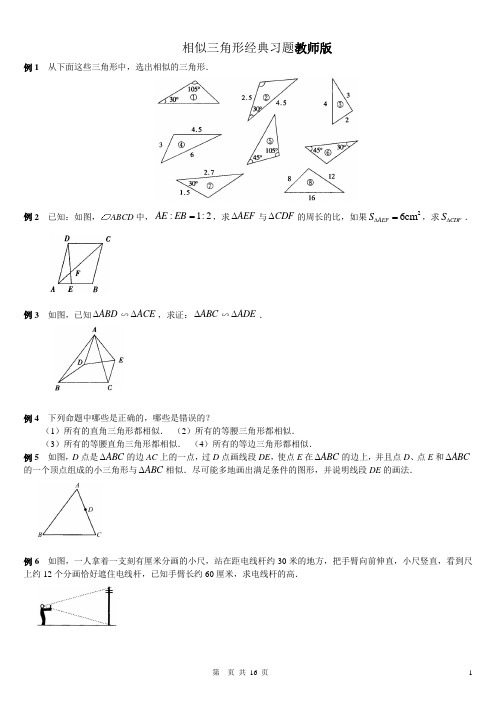
相似三角形经典习题教师版例1 从下面这些三角形中,选出相似的三角形.例2 已知:如图,ABCD 中,2:1:=EB AE ,求AEF ∆与CDF ∆的周长的比,如果2cm 6=∆AEF S ,求CDF S ∆.例3 如图,已知ABD ∆∽ACE ∆,求证:ABC ∆∽ADE ∆.例4 下列命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似. (2)所有的等腰三角形都相似. (3)所有的等腰直角三角形都相似. (4)所有的等边三角形都相似.例5 如图,D 点是ABC ∆的边AC 上的一点,过D 点画线段DE ,使点E 在ABC ∆的边上,并且点D 、点E 和ABC ∆的一个顶点组成的小三角形与ABC ∆相似.尽可能多地画出满足条件的图形,并说明线段DE 的画法.例6 如图,一人拿着一支刻有厘米分画的小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.例7 如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,若5.1=AC m ,小明的眼睛离地面的高度为1.6m ,请你帮助小明计算一下楼房的高度(精确到0.1m ).例8 格点图中的两个三角形是否是相似三角形,说明理由.例9 根据下列各组条件,判定ABC ∆和C B A '''∆是否相似,并说明理由:(1),cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A . (2)︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A .(3)︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB .例10 如图,下列每个图形中,存不存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.例11 已知:如图,在ABC ∆中,BD A AC AB ,36,︒=∠=是角平分线,试利用三角形相似的关系说明AC DC AD ⋅=2.例12 已知ABC ∆的三边长分别为5、12、13,与其相似的C B A '''∆的最大边长为26,求C B A '''∆的面积S .例13 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C 处(如图),然后沿BC 方向走到D 处,这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上,又测得C 、D 两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.例14.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确定BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗?例15.如图,为了求出海岛上的山峰AB 的高度,在D 和F 处树立标杆DC 和FE ,标杆的高都是3丈,相隔1000步(1步等于5尺),并且AB 、CD 和EF 在同一平面内,从标杆DC 退后123步的G 处,可看到山峰A 和标杆顶端C 在一直线上,从标杆FE 退后127步的H 处,可看到山峰A 和标杆顶端E 在一直线上.求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少?(古代问题)例16 如图,已知△ABC 的边AB =32,AC =2,BC 边上的高AD =3.(1)求BC 的长;(2)如果有一个正方形的边在AB 上,另外两个顶点分别在AC ,BC 上,求这个正方形的面积.相似三角形经典习题答案例1. 解 ①、⑤、⑥相似,②、⑦相似,③、④、⑧相似例2. 解 ABCD 是平行四边形,∴CD AB CD AB =,//,∴AEF ∆∽CDF ∆,又2:1:=EB AE ,∴3:1:=CD AE ,∴AEF ∆与CDF ∆的周长的比是1:3. 又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ,∴)cm (542=∆CD F S . 例3 分析 由于ABD ∆∽ACE ∆,则CAE BAD ∠=∠,因此DAE BAC ∠=∠,如果再进一步证明AECAAD BA =,则问题得证.证明 ∵ABD ∆∽ACE ∆,∴CAE BAD ∠=∠.又DAC BAD BAC ∠+∠=∠ ,∴CAE DAC DAE ∠+∠=∠, ∴DAE BAC ∠=∠.∵ABD ∆∽ACE ∆,∴AEACAD AB =. 在ABC ∆和ADE ∆中,∵AEACAD AB ADE BAC =∠=∠,,∴ABC ∆∽ADE ∆ 例4.分析 (1)不正确,因为在直角三角形中,两个锐角的大小不确定,因此直角三角形的形状不同.(2)也不正确,等腰三角形的顶角大小不确定,因此等腰三角形的形状也不同. (3)正确.设有等腰直角三角形ABC 和C B A ''',其中︒='∠=∠90C C ,则︒='∠=∠︒='∠=∠45,45B B A A ,设ABC ∆的三边为a 、b 、c ,C B A '''∆的边为c b a '''、、, 则a c b a a c b a '=''='==2,,2,,∴a ac c b b a a '=''=',,∴ABC ∆∽C B A '''∆. (4)也正确,如ABC ∆与C B A '''∆都是等边三角形,对应角相等,对应边都成比例,因此ABC ∆∽C B A '''∆.答:(1)、(2)不正确.(3)、(4)正确. 例5.解:画法略.例6.分析 本题所叙述的内容可以画出如下图那样的几何图形,即60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=CE 米,求BC .由于ADF ∆∽ACAF EC DF AEC =∆,,又ACF ∆∽ABC ∆,∴BC GFEC DF =,从而可以求出BC 的长.解 EC DF EC AE //,⊥ ,∴EAC DAF AEC ADF ∠=∠∠=∠,,∴ADF ∆∽AEC ∆.∴ACAFEC DF =. 又EC BC EC GF ⊥⊥,,∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//, ∴AGF ∆∽ABC ∆,∴BC GF AC AF =,∴BCGFEC DF =.又60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=EC 米,∴6=BC 米.即电线杆的高为6米. 例7.分析 根据物理学定律:光线的入射角等于反射角,这样,BCA ∆与MNA ∆的相似关系就明确了.解 因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,,所以BCA ∆∽MNA ∆.所以AC AN BC MN ::=,即5.1:206.1:=MN .所以3.215.1206.1≈÷⨯=MN (m ). 说明 这是一个实际应用问题,方法看似简单,其实很巧妙,省却了使用仪器测量的麻烦.例8.分析 这两个图如果不是画在格点中,那是无法判断的.实际上格点无形中给图形增添了条件——长度和角度.解 在格点中BC AB EF DE ⊥⊥,,所以︒=∠=∠90B E , 又4,2,2,1====AB BC DE EF .所以21==BC EF AB DE .所以DEF ∆∽ABC ∆. 说明 遇到格点的题目一定要充分发现其中的各种条件,勿使遗漏.例9.解 (1)因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ,所以ABC ∆∽C B A '''∆; (2)因为︒=∠-∠-︒=∠41180B A C ,两个三角形中只有A A '∠=∠,另外两个角都不相等,所以ABC ∆与C B A '''∆不相似;(3)因为12,=''='''∠=∠C B BC B A AB B B ,所以ABC ∆相似于C B A '''∆. 例10.解 (1)ADE ∆∽ABC ∆ 两角相等; (2)ADE ∆∽ACB ∆ 两角相等;(3)CDE ∆∽CAB ∆ 两角相等; (4)EAB ∆∽ECD ∆ 两边成比例夹角相等; (5)ABD ∆∽ACB ∆ 两边成比例夹角相等; (6)ABD ∆∽ACB ∆ 两边成比例夹角相等.例11.分析 有一个角是65°的等腰三角形,它的底角是72°,而BD 是底角的平分线,∴︒=∠36CBD ,则可推出ABC ∆∽BCD ∆,进而由相似三角形对应边成比例推出线段之间的比例关系.证明 AC AB A =︒=∠,36 ,∴︒=∠=∠72C ABC . 又BD 平分ABC ∠,∴︒=∠=∠36CBD ABD .∴BC BD AD ==,且ABC ∆∽BCD ∆,∴BC CD AB BC ::=,∴CD AB BC ⋅=2,∴CD AC AD ⋅=2.说明 (1)有两个角对应相等,那么这两个三角形相似,这是判断两个三角形相似最常用的方法,并且根据相等的角的位置,可以确定哪些边是对应边.(2)要说明线段的乘积式cd ab =,或平方式bc a =2,一般都是证明比例式,b dc a =,或caa b =,再根据比例的基本性质推出乘积式或平方式.例12分析 由ABC ∆的三边长可以判断出ABC ∆为直角三角形,又因为ABC ∆∽C B A '''∆,所以C B A '''∆也是直角三角形,那么由C B A '''∆的最大边长为26,可以求出相似比,从而求出C B A '''∆的两条直角边长,再求得C B A '''∆的面积.解 设ABC ∆的三边依次为,13,12,5===AB AC BC ,则222AC BC AB += ,∴︒=∠90C .又∵ABC ∆∽C B A '''∆,∴︒=∠='∠90C C .212613==''=''=''B A AB C A AC C B BC , 又12,5==AC BC ,∴24,10=''=''C A C B . ∴12010242121=⨯⨯=''⨯''=C B C A S .例13.分析 判断方法是否可行,应考虑利用这种方法加之我们现有的知识能否求出旗杆的高.按这种测量方法,过F作AB FG ⊥于G ,交CE 于H ,可知AGF ∆∽EHF ∆,且GF 、HF 、EH 可求,这样可求得AG ,故旗杆AB 可求.解 这种测量方法可行.理由如下:设旗杆高x AB =.过F 作AB FG ⊥于G ,交CE 于H (如图).所以AGF ∆∽EHF ∆.因为3,30327,5.1==+==HF GF FD ,所以5.1,25.15.3-==-=x AG EH .由AGF ∆∽EHF ∆,得HF GF EH AG =,即33025.1=-x ,所以205.1=-x ,解得5.21=x (米) 所以旗杆的高为21.5米.说明 在具体测量时,方法要现实、切实可行. 例14. 解:︒=∠=∠∠=∠90,ECD ABC EDC ADB ,∴ABD ∆∽ECD ∆,1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB (米),答:两岸间AB 大致相距100米. 例15. 答案:1506=AB 米,30750=BD 步,(注意:AK FEFHKE AK CD DG KC ⋅=⋅=,.) 例16. 分析:要求BC 的长,需画图来解,因AB 、AC 都大于高AD ,那么有两种情况存在,即点D 在BC 上或点D 在BC 的延长线上,所以求BC 的长时要分两种情况讨论.求正方形的面积,关键是求正方形的边长. 解:(1)如上图,由AD ⊥BC ,由勾股定理得BD =3,DC =1,所以BC =BD +DC =3+1=4. 如下图,同理可求BD =3,DC =1,所以BC =BD -CD =3-1=2.(2)如下图,由题目中的图知BC =4,且162)32(2222=+=+AC AB ,162=BC ,∴222BC AC AB =+.所以△ABC 是直角三角形.由AE G F 是正方形,设G F =x ,则FC =2-x , ∵G F ∥AB ,∴AC FC AB GF =,即2232xx -=. ∴33-=x ,∴3612)33(2-=-=AEG F S 正方形. 如下图,当BC =2,AC =2,△ABC 是等腰三角形,作CP ⊥AB 于P ,∴AP =321=AB ,在Rt △APC 中,由勾股定理得CP =1, ∵GH ∥AB ,∴△C GH ∽△CBA ,∵x x x -=132,32132+=x ∴121348156)32132(2-=+=GFEH S 正方形 因此,正方形的面积为3612-或121348156-.相似三角形 一,比例线段 1, 成比例线段对于四条线段a ,b ,c ,d ,如果其中两条线段的长度的比等于另外两条线段的比,如b a =dc(或a :b=c :d ),那么,这四条线段叫做成比例线段,简称比例线段。
初三数学相似三角形典例及练习题含答案

初三数学相似三角形典例及练习题含答案典例典例1已知三角形ABC中,∠B=90°,AC=6cm,BD垂直AC于D点,BD=3cm,求BC的长度。
解析:根据勾股定理可得:BC^2 = AB^2 + AC^2 = BD^2 + AD^2 + AC^2因为∆ABC与∆ABD相似,所以可以得到:\frac{AD}{AB}=\frac{AB}{AC}即:AD = \frac{AB^2}{AC}将公式代入原式中,得到:BC^2 = BD^2 + \frac{AB^4}{AC^2} + AC^2因为AC=6,BD=3,所以代入可得:BC^2 = 3^2 + \frac{AB^4}{6^2} + 6^2化简得:BC^2 = AB^4 \cdot \frac{1}{36} + 45AB^4 = 36(BC^2 - 45)因此,我们可以得到:AB = \sqrt[4]{36(BC^2 - 45)}典例2已知两个三角形ABC和DEF,且它们相似,已知AC=20cm,EF=12cm,AB=15cm,计算DE的长度。
解析:由于两个三角形相似,所以可以得到:\frac{AB}{DE}=\frac{AC}{EF}将已知条件带入即可得到:\frac{15}{DE}=\frac{20}{12}解得:DE = \frac{36}{4} = 9因此,DE的长度为9cm。
典例3已知三角形ABC和DEF相似,且AB=5cm,DE=2.5cm,BC=6cm,计算EF的长度。
解析:由于两个三角形相似,所以可以得到:\frac{AB}{DE}=\frac{BC}{EF}将已知条件带入即可得到:\frac{5}{2.5}=\frac{6}{EF}解得:EF = 12因此,EF的长度为12cm。
练习题练习题1已知三角形ABC中,∠B=90°,AB=3cm,AC=4cm,D、E、F分别是BC、AC、AB上的点,且∆DEF与∆ABC相似。
初中数学经典相似三角形练习题(附参考答案)

经典练习题相似三角形一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=_________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD 面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s 的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s 的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC 相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q 为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q 沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太阳光线NH 与⊙O 相切于点M .请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG 的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m 宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m ,窗口高AB=1.8m ,求窗口底边离地面的高BC .26.如图,李华晚上在路灯下散步.已知李华的身高AB=h ,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m. (1)若李华距灯柱OP 的水平距离OA=a ,求他影子AC 的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC )是否是定值请说明理由; (3)若李华在点A 朝着影子(如图箭头)的方向以v 1匀速行走,试求他影子的顶端在地面上移动的速度v 2.27.如图①,分别以直角三角形ABC 三边为直径向外作三个半圆,其面积分别用S 1,S 2,S 3表示,则不难证明S 1=S 2+S 3.(1)如图②,分别以直角三角形ABC 三边为边向外作三个正方形,其面积分别用S 1,S 2,S 3表示,那么S 1,S 2,S 3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC 三边为边向外作三个正三角形,其面积分别用S 1、S 2、S 3表示,请你确定S 1,S 2,S 3之间的关系并加以证明;(3)若分别以直角三角形ABC 三边为边向外作三个一般三角形,其面积分别用S 1,S 2,S 3表示,为使S 1,S 2,S 3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论; (4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE .29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E 是▱ABCD 的边BA 延长线上一点,连接EC ,交AD 于点F .在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上. (1)填空:∠ABC= 135° °,BC=;(2)判断△ABC 与△DEC 是否相似,并证明你的结论.BC==22、,可得BC=∵BC==;∴;∴8.如图,已知矩形ABCD 的边长AB=3cm ,BC=6cm .某一时刻,动点M 从A 点出发沿AB 方向以1cm/s 的速度向B 点匀速运动;同时,动点N 从D 点出发沿DA 方向以2cm/s 的速度向A 点匀速运动,问: (1)经过多少时间,△AMN 的面积等于矩形ABCD 面积的?(2)是否存在时刻t ,使以A ,M ,N 为顶点的三角形与△ACD 相似?若存在,求t 的值;若不存在,请说明理由.面积的面积的则有:×3×6,即面积的因此有①,或②(t=t=(或t=都符合题意,同时出发后,经过秒或秒时,以9.如图,在梯形ABCD 中,若AB∥DC,AD=BC ,对角线BD 、AC 把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.(,即相似三角形的证明.还考查了相似三角形的判定.10.附加题:如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.CE=.AE=∴sin∠AEF=,∴AF=AE•sin∠AEF=∴.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.AB=12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.AD∴PC=BC=AD=∴.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s 的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.(×(∴tan∠ADP=tan∠C==∴=,∴t=∴tan∠APD=tan∠C==,∴=t=或t=时,△PAD∴PD=∵CE=t QE=t∴QH=BE=8﹣t t∴PH=t﹣t=t∴PQ=,t=t=,,>14.已知矩形ABCD ,长BC=12cm ,宽AB=8cm ,P 、Q 分别是AB 、BC 上运动的两点.若P 自点A 出发,以1cm/s的速度沿AB 方向运动,同时,Q 自点B 出发以2cm/s 的速度沿BC 方向运动,问经过几秒,以P 、B 、Q 为顶点的三角形与△BDC 相似?时,有:,;时,有:,∴经过15.如图,在△ABC 中,AB=10cm ,BC=20cm ,点P 从点A 开始沿AB 边向B 点以2cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以4cm/s 的速度移动,如果P 、Q 分别从A 、B 同时出发,问经过几秒钟,△PBQ 与△ABC 相似.=,即=,解得=,即=16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.解:∵AC=∴CD==.要使这两个直角三角形相似,有两种情况:时,有=,∴AB==3时,有=,∴AB==3.时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.AN=a=aAN=18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q 为顶点的三角形与△CBA相似?或)当,∴x=;)当,∴x=.所以,经过秒或秒后,两三角形相似.19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.∴=,∴=,∴=,∴=,∴=,∴AP=.AP=BP=∴=,、20.△ABC 和△DEF 是两个等腰直角三角形,∠A=∠D=90°,△DEF 的顶点E 位于边BC 的中点上. (1)如图1,设DE 与AB 交于点M ,EF 与AC 交于点N ,求证:△BEM∽△CNE;(2)如图2,将△DEF 绕点E 旋转,使得DE 与BA 的延长线交于点M ,EF 与AC 交于点N ,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.∴∴中有21.如图,在矩形ABCD 中,AB=15cm ,BC=10cm ,点P 沿AB 边从点A 开始向B 以2cm/s 的速度移动;点Q沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P 、Q 同时出发,用t (秒)表示移动的时间,那么当t 为何值时,以点Q 、A 、P 为顶点的三角形与△ABC 相似.所以所以;=,即=,;=,即=,t=22.如图,路灯(P 点)距地面8米,身高1.6米的小明从距路灯的底部(O 点)20米的A 点,沿OA 所在的直线行走14米到B 点时,身影的长度是变长了还是变短了?变长或变短了多少米?∴23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是: ;(2)请在下图中画出测量示意图;(3)设树高AB 的长度为x ,请用所测数据(用小写字母表示)求出x .∴∴∴24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm 的竹竿的影长为60cm .乙组:如图2,测得学校旗杆的影长为900cm .丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)∴,即与①类似得:∴∴与①类似得:∴∴MN=r(25.(2007•白银)阳光通过窗口照射到室内,在地面上留下2.7m 宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m ,窗口高AB=1.8m ,求窗口底边离地面的高BC .,从而算出∴∴26.如图,李华晚上在路灯下散步.已知李华的身高AB=h ,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m. (1)若李华距灯柱OP 的水平距离OA=a ,求他影子AC 的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC )是否是定值请说明理由; (3)若李华在点A 朝着影子(如图箭头)的方向以v 1匀速行走,试求他影子的顶端在地面上移动的速度v 2.∵∴∴解得:∴,,即∴同理可得:,∴=)可知,即,同理可得:∴由等比性质得:∴所以人影顶端在地面上移动的速度为27.如图①,分别以直角三角形ABC 三边为直径向外作三个半圆,其面积分别用S 1,S 2,S 3表示,则不难证明S 1=S 2+S 3.(1)如图②,分别以直角三角形ABC 三边为边向外作三个正方形,其面积分别用S 1,S 2,S 3表示,那么S 1,S 2,S 3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC 三边为边向外作三个正三角形,其面积分别用S 1、S 2、S 3表示,请你确定S 1,S 2,S 3之间的关系并加以证明;(3)若分别以直角三角形ABC 三边为边向外作三个一般三角形,其面积分别用S 1,S 2,S 3表示,为使S 1,S 2,S 3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论; (4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.==∴∴28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE .29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4. (1)求BD 、CD 的长;(2)过B 作BE⊥DC 于E ,求BE 的长.∴==,==,CD=;BE•CD=BD•BC,∴BE==30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.)设=k。
相似三角形经典练习题(4套)附带答案

练习(一)一、填空题:1. 已知a ba b+-=2295,则a b:=__________2. 若三角形三边之比为3:5:7,与它相似的三角形的最长边是21cm,则其余两边之和是__________cm3. 如图,△ABC中,D、E分别是AB、AC的中点,BC=6,则DE=__________;△ADE与△ABC的面积之比为:__________。
题3 题7 题84. 已知线段a=4cm,b=9cm,则线段a、b的比例中项c为__________cm。
5. 在△ABC中,点D、E分别在边AB、AC上,DE∥BC,如果AD=8,DB=6,EC=9,那么AE=__________6. 已知三个数1,2,3,请你添上一个数,使它能构成一个比例式,则这个数是__________7. 如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=18cm,AE:EB=2:3,则EF=__________8. 如图,在梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD,AD=6,BC=10,则梯形的面积为:__________二、选择题:1. 如果两个相似三角形对应边的比是3:4,那么它们的对应高的比是__________A. 9:16B. 3:2C. 3:4D. 3:72. 在比例尺为1:m的某市地图上,规划出长a厘米,宽b厘米的矩形工业园区,该园区的实际面积是__________米2A. 104mabB.1042mabC.abm104D.abm24103. 已知,如图,DE∥BC,EF∥AB,则下列结论:题3 题4 题5①AEECBEFC=②ADBFABBC=③EFABDEBC=④CECFEABF=其中正确的比例式的个数是__________A. 4个B. 3个C. 2个D. 1个4. 如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点为顶点组成的三角形与△ABC相似,则AE的长是__________A. 16B. 14C. 16或14D. 16或95. 如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,AE⊥AD,交CB的延长线于点E,则下列结论正确的是__________A. △AED∽△ACBB. △AEB∽△ACDC. △BAE∽△ACED. △AEC∽△DAC三、解答题:1. 如图,AD∥EG∥BC,AD=6,BC=9,AE:AB=2:3,求GF的长。
九年级数学相似三角形经典题(含答案)

相似三角形经典习题教师版例1 从下面这些三角形中,选出相似的三角形.例2 已知:如图,ABCD 中,2:1:=EB AE ,求AEF ∆与CDF ∆的周长的比,如果2cm 6=∆AEF S ,求CDF S ∆.例3 如图,已知ABD ∆∽ACE ∆,求证:ABC ∆∽ADE ∆.例4 下列命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似. (2)所有的等腰三角形都相似. (3)所有的等腰直角三角形都相似. (4)所有的等边三角形都相似.例5 如图,D 点是ABC ∆的边AC 上的一点,过D 点画线段DE ,使点E 在ABC ∆的边上,并且点D 、点E 和ABC ∆的一个顶点组成的小三角形与ABC ∆相似.尽可能多地画出满足条件的图形,并说明线段DE 的画法.例6 如图,一人拿着一支刻有厘米分画的小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.例7 如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,若5.1=AC m ,小明的眼睛离地面的高度为1.6m ,请你帮助小明计算一下楼房的高度(精确到0.1m ).例8 格点图中的两个三角形是否是相似三角形,说明理由.例9 根据下列各组条件,判定ABC ∆和C B A '''∆是否相似,并说明理由:(1),cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A . (2)︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A .(3)︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB .例10 如图,下列每个图形中,存不存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.例11 已知:如图,在ABC ∆中,BD A AC AB ,36,︒=∠=是角平分线,试利用三角形相似的关系说明AC DC AD ⋅=2.例12 已知ABC ∆的三边长分别为5、12、13,与其相似的C B A '''∆的最大边长为26,求C B A '''∆的面积S .例13 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C 处(如图),然后沿BC 方向走到D 处,这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上,又测得C 、D 两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.例14.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确定BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗?例15.如图,为了求出海岛上的山峰AB 的高度,在D 和F 处树立标杆DC 和FE ,标杆的高都是3丈,相隔1000步(1步等于5尺),并且AB 、CD 和EF 在同一平面内,从标杆DC 退后123步的G 处,可看到山峰A 和标杆顶端C 在一直线上,从标杆FE 退后127步的H 处,可看到山峰A 和标杆顶端E 在一直线上.求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少?(古代问题)例16 如图,已知△ABC 的边AB =32,AC =2,BC 边上的高AD =3.(1)求BC 的长;(2)如果有一个正方形的边在AB 上,另外两个顶点分别在AC ,BC 上,求这个正方形的面积.相似三角形经典习题答案例1. 解 ①、⑤、⑥相似,②、⑦相似,③、④、⑧相似例2. 解 ABCD 是平行四边形,∴CD AB CD AB =,//,∴AEF ∆∽CDF ∆,又2:1:=EB AE ,∴3:1:=CD AE ,∴AEF ∆与CDF ∆的周长的比是1:3. 又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ,∴)cm (542=∆CD F S . 例3 分析 由于ABD ∆∽ACE ∆,则CAE BAD ∠=∠,因此DAE BAC ∠=∠,如果再进一步证明AECAAD BA =,则问题得证.证明 ∵ABD ∆∽ACE ∆,∴CAE BAD ∠=∠.又DAC BAD BAC ∠+∠=∠ ,∴CAE DAC DAE ∠+∠=∠, ∴DAE BAC ∠=∠.∵ABD ∆∽ACE ∆,∴AEACAD AB =. 在ABC ∆和ADE ∆中,∵AEACAD AB ADE BAC =∠=∠,,∴ABC ∆∽ADE ∆ 例4.分析 (1)不正确,因为在直角三角形中,两个锐角的大小不确定,因此直角三角形的形状不同.(2)也不正确,等腰三角形的顶角大小不确定,因此等腰三角形的形状也不同. (3)正确.设有等腰直角三角形ABC 和C B A ''',其中︒='∠=∠90C C ,则︒='∠=∠︒='∠=∠45,45B B A A ,设ABC ∆的三边为a 、b 、c ,C B A '''∆的边为c b a '''、、, 则a c b a a c b a '=''='==2,,2,,∴a ac c b b a a '=''=',,∴ABC ∆∽C B A '''∆. (4)也正确,如ABC ∆与C B A '''∆都是等边三角形,对应角相等,对应边都成比例,因此ABC ∆∽C B A '''∆.答:(1)、(2)不正确.(3)、(4)正确. 例5.解:画法略.例6.分析 本题所叙述的内容可以画出如下图那样的几何图形,即60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=CE 米,求BC .由于ADF ∆∽ACAF EC DF AEC =∆,,又ACF ∆∽ABC ∆,∴BC GFEC DF =,从而可以求出BC 的长.解 EC DF EC AE //,⊥ ,∴EAC DAF AEC ADF ∠=∠∠=∠,,∴ADF ∆∽AEC ∆.∴ACAFEC DF =. 又EC BC EC GF ⊥⊥,,∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//, ∴AGF ∆∽ABC ∆,∴BC GF AC AF =,∴BCGFEC DF =.又60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=EC 米,∴6=BC 米.即电线杆的高为6米. 例7.分析 根据物理学定律:光线的入射角等于反射角,这样,BCA ∆与MNA ∆的相似关系就明确了.解 因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,,所以BCA ∆∽MNA ∆.所以AC AN BC MN ::=,即5.1:206.1:=MN .所以3.215.1206.1≈÷⨯=MN (m ). 说明 这是一个实际应用问题,方法看似简单,其实很巧妙,省却了使用仪器测量的麻烦.例8.分析 这两个图如果不是画在格点中,那是无法判断的.实际上格点无形中给图形增添了条件——长度和角度.解 在格点中BC AB EF DE ⊥⊥,,所以︒=∠=∠90B E , 又4,2,2,1====AB BC DE EF .所以21==BC EF AB DE .所以DEF ∆∽ABC ∆. 说明 遇到格点的题目一定要充分发现其中的各种条件,勿使遗漏.例9.解 (1)因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ,所以ABC ∆∽C B A '''∆; (2)因为︒=∠-∠-︒=∠41180B A C ,两个三角形中只有A A '∠=∠,另外两个角都不相等,所以ABC ∆与C B A '''∆不相似;(3)因为12,=''='''∠=∠C B BC B A AB B B ,所以ABC ∆相似于C B A '''∆. 例10.解 (1)ADE ∆∽ABC ∆ 两角相等; (2)ADE ∆∽ACB ∆ 两角相等;(3)CDE ∆∽CAB ∆ 两角相等; (4)EAB ∆∽ECD ∆ 两边成比例夹角相等; (5)ABD ∆∽ACB ∆ 两边成比例夹角相等; (6)ABD ∆∽ACB ∆ 两边成比例夹角相等.例11.分析 有一个角是65°的等腰三角形,它的底角是72°,而BD 是底角的平分线,∴︒=∠36CBD ,则可推出ABC ∆∽BCD ∆,进而由相似三角形对应边成比例推出线段之间的比例关系.证明 AC AB A =︒=∠,36 ,∴︒=∠=∠72C ABC . 又BD 平分ABC ∠,∴︒=∠=∠36CBD ABD .∴BC BD AD ==,且ABC ∆∽BCD ∆,∴BC CD AB BC ::=,∴CD AB BC ⋅=2,∴CD AC AD ⋅=2.说明 (1)有两个角对应相等,那么这两个三角形相似,这是判断两个三角形相似最常用的方法,并且根据相等的角的位置,可以确定哪些边是对应边.(2)要说明线段的乘积式cd ab =,或平方式bc a =2,一般都是证明比例式,b dc a =,或caa b =,再根据比例的基本性质推出乘积式或平方式.例12分析 由ABC ∆的三边长可以判断出ABC ∆为直角三角形,又因为ABC ∆∽C B A '''∆,所以C B A '''∆也是直角三角形,那么由C B A '''∆的最大边长为26,可以求出相似比,从而求出C B A '''∆的两条直角边长,再求得C B A '''∆的面积.解 设ABC ∆的三边依次为,13,12,5===AB AC BC ,则222AC BC AB += ,∴︒=∠90C .又∵ABC ∆∽C B A '''∆,∴︒=∠='∠90C C .212613==''=''=''B A AB C A AC C B BC , 又12,5==AC BC ,∴24,10=''=''C A C B . ∴12010242121=⨯⨯=''⨯''=C B C A S .例13.分析 判断方法是否可行,应考虑利用这种方法加之我们现有的知识能否求出旗杆的高.按这种测量方法,过F作AB FG ⊥于G ,交CE 于H ,可知AGF ∆∽EHF ∆,且GF 、HF 、EH 可求,这样可求得AG ,故旗杆AB 可求.解 这种测量方法可行.理由如下:设旗杆高x AB =.过F 作AB FG ⊥于G ,交CE 于H (如图).所以AGF ∆∽EHF ∆.因为3,30327,5.1==+==HF GF FD ,所以5.1,25.15.3-==-=x AG EH .由AGF ∆∽EHF ∆,得HF GF EH AG =,即33025.1=-x ,所以205.1=-x ,解得5.21=x (米) 所以旗杆的高为21.5米.说明 在具体测量时,方法要现实、切实可行. 例14. 解:︒=∠=∠∠=∠90,ECD ABC EDC ADB ,∴ABD ∆∽ECD ∆,1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB (米),答:两岸间AB 大致相距100米. 例15. 答案:1506=AB 米,30750=BD 步,(注意:AK FEFHKE AK CD DG KC ⋅=⋅=,.) 例16. 分析:要求BC 的长,需画图来解,因AB 、AC 都大于高AD ,那么有两种情况存在,即点D 在BC 上或点D 在BC 的延长线上,所以求BC 的长时要分两种情况讨论.求正方形的面积,关键是求正方形的边长. 解:(1)如上图,由AD ⊥BC ,由勾股定理得BD =3,DC =1,所以BC =BD +DC =3+1=4. 如下图,同理可求BD =3,DC =1,所以BC =BD -CD =3-1=2.(2)如下图,由题目中的图知BC =4,且162)32(2222=+=+AC AB ,162=BC ,∴222BC AC AB =+.所以△ABC 是直角三角形.由AE G F 是正方形,设G F =x ,则FC =2-x , ∵G F ∥AB ,∴AC FC AB GF =,即2232xx -=. ∴33-=x ,∴3612)33(2-=-=AEG F S 正方形. 如下图,当BC =2,AC =2,△ABC 是等腰三角形,作CP ⊥AB 于P ,∴AP =321=AB ,在Rt △APC 中,由勾股定理得CP =1, ∵GH ∥AB ,∴△C GH ∽△CBA ,∵x x x -=132,32132+=x ∴121348156)32132(2-=+=GFEH S 正方形 因此,正方形的面积为3612-或121348156-.相似三角形 一,比例线段 1, 成比例线段对于四条线段a ,b ,c ,d ,如果其中两条线段的长度的比等于另外两条线段的比,如b a =dc(或a :b=c :d ),那么,这四条线段叫做成比例线段,简称比例线段。
相似三角形练习题及答案
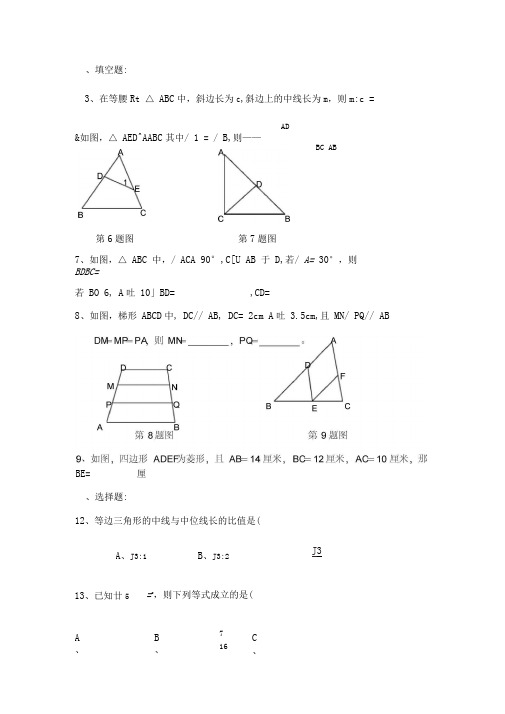
、填空题:3、在等腰Rt △ ABC中,斜边长为c,斜边上的中线长为m,则m:c =AD&如图,△ AED^AABC其中/ 1 = / B,则——7、如图,△ ABC 中,/ ACA 90°,C[U AB 于D,若/ A= 30°,则BDBC=、选择题:12、等边三角形的中线与中位线长的比值是(A、J3:1B、J3:2 J 313、已知廿5 =z,则下列等式成立的是(A 、B、716C、BC AB若BO 6, A吐10」BD= ,CD=第6题图第7题图8、如图,梯形ABCD中, DC// AB, DC= 2cm A吐3.5cm,且MN/ PQ// AB厘BE=14、已知直角三角形三边分别为a,a+b,a+2b , (a>0,b>0),则a:b=()15、AABC 中, A 吐12, BCh 18,CAh24,另一个和它相似的三角形最长的一边 是36,则最短的一边是()16、已知a,b,c 是^ABC 的三条边,对应高分别为h a ,h b ,h c ,且a:b:c = 4:5:6 ,那么h a : h b : h c 等于()17、一个三角形三边长之比为4:5:6,三边中点连线组成的三角形的周长为 30cm 则原三角形最大边长为( )A 1: 3B 、1: 4C 、2: 1D 3: 1A 27B 、12C 、18D 20A 4: 5: 615B 、 6: 5: 4C 、15: 12: 10D 10: 12:A 、44厘米B 、40厘米C 36厘米D 24厘个20、如图,在平行四边形 ABCC 中,E 为BC 边上的点,若BE ECh4: 5, AE 交 BD于F ,则BF: FD 等于()A 4: 5B 、3: 5 21、C 、4: 9D 3: 8解答题:已知(X —y ) y =2:3, 求 3x —2y 如图,在Rt △ ABC 中, CD 为斜边AB 上的高,且 AO6厘米,AD= 4厘米, 22、求AB 与BC 的长24、如图,Rt A ABC 中斜边 AB 上一点 M MNL AB交AC 于N,若AMh 3厘米,AB AO5: 4,求MN 的长。
初中数学经典相似三角形练习题(附参考答案)

5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s 的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t 的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.50、(2013年广东省)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,4.将这副直角三角板按如题25图(1)所示位置摆放,点B与点F重合,直角边BA ∠FDE=90°,DF=4,DE=3与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如题25图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC=______度;(2)如题25图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围.51、(2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.。
初中数学经典相似三角形专题(附参考答案)

经典练习题相似三角形(附答案)一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD 于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF 的顶点都在边长为1的小正方形的顶点上.(1)填空:∠A BC= _________ °,BC=_________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N 从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD 面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC 上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A 运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A 出发,以1cm/s的速度沿AB方向运动,同时,Q 自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA 的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m 宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=135°°,BC= ;(2)判断△ABC与△DEC是否相似,并证明你的结论.BC==22、,可得BC=∵BC=EC=;∴,∴8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.面积的面积的则有:(×3×6,即面积的因此有①,或t=(t=t=都符合题意,同时出发后,经过秒或9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.P=,即相似三角形的证明.还考查了相似三角形的判定.10.附加题:如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.CE=.AE=∴sin∠AEF=,∴AF=AE•sin∠AEF=∴.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC 于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.∴QM=PM=AB=12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.∴CM=MD=∴PC=BC=AD=∴.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.(AB=∴tan∠ADP=tan∠C==∴=,∴t=∴tan∠APD=tan∠C==,∴=∴t=∴t=t=时,△PAD∴PD=∵CE=t QE=t∴QH=BE=8﹣t t∴PH=t﹣t=t∴PQ=,,,>∴t=t=14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?时,有:;时,有:∴经过15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.=,即=,解得对应时,有=,即=16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.解:∵AC=∴CD==.要使这两个直角三角形相似,有两种情况:时,有=,∴AB==3时,有=,∴AB=.317.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.a①若△CDM∽△MAN,则=∴AN=②若△CDM∽△NAM,则AN=18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?或)当,∴x=;)当,∴x=.所以,经过秒或19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.∴=,∴=,∴=,∴=,∴=,∴AP=.AP=时,由BP=,∴=,、20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.∴∴中有21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.所以所以;=,即=,;=,即=,t=时,以点22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?∴,23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.∴∴,∴.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)∴,即与①类似得:∴∴,与①类似得:,∴,∴MN=r(25.(2007•白银)阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.AE∥BD,所以△ECA∽△DCB,则有∴∴26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.∵∴∴解得:.∴,,即.∴同理可得:,∴=)可知,即,同理可得:∴,由等比性质得:∴,所以人影顶端在地面上移动的速度为27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.===∴∴28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.BC=∴==,==,∴BD=CD=;=BE•CD=∴BE==30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.)设=k,。
(完整版)初中数学经典相似三角形练习题(附参考答案)

1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=_________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC 于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度:(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点:相似三角形的判定;平行线的性质。
初中数学经典相似三角形练习题(附参考答案)

经典练习题相似三角形(附答案)一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠A BC= _________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC 于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.通过窗口照射到室,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,华晚上在路灯下散步.已知华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点:相似三角形的判定;平行线的性质。
(完整word版)九年级下数学相似三角形经典习题(含答案)

九年级下数学相似三角形经典习题例1 从下面这些三角形中,选出相似的三角形.例2 已知:如图,ABCD 中,2:1:=EB AE ,求AEF ∆与CDF ∆的周长的比,如果2cm 6=∆AEF S ,求CDF S ∆.例3 如图,已知ABD ∆∽ACE ∆,求证:ABC ∆∽ADE ∆.例4 下列命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似. (2)所有的等腰三角形都相似. (3)所有的等腰直角三角形都相似. (4)所有的等边三角形都相似.例5 如图,D 点是ABC ∆的边AC 上的一点,过D 点画线段DE ,使点E 在ABC ∆的边上,并且点D 、点E 和ABC ∆的一个顶点组成的小三角形与ABC ∆相似.尽可能多地画出满足条件的图形,并说明线段DE 的画法.例6 如图,一人拿着一支刻有厘米分画的小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.例7 如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,若5.1=AC m ,小明的眼睛离地面的高度为1.6m ,请你帮助小明计算一下楼房的高度(精确到0.1m ).例8 格点图中的两个三角形是否是相似三角形,说明理由.例9 根据下列各组条件,判定ABC ∆和C B A '''∆是否相似,并说明理由:(1),cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A . (2)︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A .(3)︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB .例10 如图,下列每个图形中,存不存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.例11 已知:如图,在ABC ∆中,BD A AC AB ,36,︒=∠=是角平分线,试利用三角形相似的关系说明AC DC AD ⋅=2.例12 已知ABC ∆的三边长分别为5、12、13,与其相似的C B A '''∆的最大边长为26,求C B A '''∆的面积S .例13 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C 处(如图),然后沿BC 方向走到D 处,这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上,又测得C 、D 两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.例14.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确定BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗?例15.如图,为了求出海岛上的山峰AB 的高度,在D 和F 处树立标杆DC 和FE ,标杆的高都是3丈,相隔1000步(1步等于5尺),并且AB 、CD 和EF 在同一平面内,从标杆DC 退后123步的G 处,可看到山峰A 和标杆顶端C 在一直线上,从标杆FE 退后127步的H 处,可看到山峰A 和标杆顶端E 在一直线上.求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少?(古代问题)例16 如图,已知△ABC 的边AB =32,AC =2,BC 边上的高AD =3.(1)求BC 的长;(2)如果有一个正方形的边在AB 上,另外两个顶点分别在AC ,BC 上,求这个正方形的面积.相似三角形经典习题答案例1. 解 ①、⑤、⑥相似,②、⑦相似,③、④、⑧相似例2. 解 ABCD 是平行四边形,∴CD AB CD AB =,//,∴AEF ∆∽CDF ∆,又2:1:=EB AE ,∴3:1:=CD AE ,∴AEF ∆与CDF ∆的周长的比是1:3. 又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ,∴)cm (542=∆CDF S . 例3 分析 由于ABD ∆∽ACE ∆,则CAE BAD ∠=∠,因此DAE BAC ∠=∠,如果再进一步证明AECAAD BA =,则问题得证.证明 ∵ABD ∆∽ACE ∆,∴CAE BAD ∠=∠.又DAC BAD BAC ∠+∠=∠ ,∴CAE DAC DAE ∠+∠=∠, ∴DAE BAC ∠=∠.∵ABD ∆∽ACE ∆,∴AEACAD AB =. 在ABC ∆和ADE ∆中,∵AEACAD AB ADE BAC =∠=∠,,∴ABC ∆∽ADE ∆ 例4.分析 (1)不正确,因为在直角三角形中,两个锐角的大小不确定,因此直角三角形的形状不同.(2)也不正确,等腰三角形的顶角大小不确定,因此等腰三角形的形状也不同. (3)正确.设有等腰直角三角形ABC 和C B A ''',其中︒='∠=∠90C C ,则︒='∠=∠︒='∠=∠45,45B B A A ,设ABC ∆的三边为a 、b 、c ,C B A '''∆的边为c b a '''、、, 则a c b a a c b a '=''='==2,,2,,∴a ac c b b a a '=''=',,∴ABC ∆∽C B A '''∆. (4)也正确,如ABC ∆与C B A '''∆都是等边三角形,对应角相等,对应边都成比例,因此ABC ∆∽C B A '''∆.答:(1)、(2)不正确.(3)、(4)正确. 例5.解:画法略.例6.分析 本题所叙述的内容可以画出如下图那样的几何图形,即60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=CE 米,求BC .由于ADF ∆∽ACAF EC DF AEC =∆,,又ACF ∆∽ABC ∆,∴BC GFEC DF =,从而可以求出BC 的长. 解 EC DF EC AE //,⊥ ,∴EAC DAF AEC ADF ∠=∠∠=∠,,∴ADF ∆∽AEC ∆.∴ACAFEC DF =. 又EC BC EC GF ⊥⊥,,∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//, ∴AGF ∆∽ABC ∆,∴BC GF AC AF =,∴BCGFEC DF =.又60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=EC 米,∴6=BC 米.即电线杆的高为6米. 例7.分析 根据物理学定律:光线的入射角等于反射角,这样,BCA ∆与MNA ∆的相似关系就明确了.解 因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,,所以BCA ∆∽MNA ∆.所以AC AN BC MN ::=,即5.1:206.1:=MN .所以3.215.1206.1≈÷⨯=MN (m ). 说明 这是一个实际应用问题,方法看似简单,其实很巧妙,省却了使用仪器测量的麻烦.例8.分析 这两个图如果不是画在格点中,那是无法判断的.实际上格点无形中给图形增添了条件——长度和角度.解 在格点中BC AB EF DE ⊥⊥,,所以︒=∠=∠90B E , 又4,2,2,1====AB BC DE EF .所以21==BC EF AB DE .所以DEF ∆∽ABC ∆. 说明 遇到格点的题目一定要充分发现其中的各种条件,勿使遗漏.例9.解 (1)因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ,所以ABC ∆∽C B A '''∆; (2)因为︒=∠-∠-︒=∠41180B A C ,两个三角形中只有A A '∠=∠,另外两个角都不相等,所以ABC ∆与C B A '''∆不相似;(3)因为12,=''='''∠=∠C B BC B A AB B B ,所以ABC ∆相似于C B A '''∆.例10.解 (1)ADE ∆∽ABC ∆ 两角相等; (2)ADE ∆∽ACB ∆ 两角相等;(3)CDE ∆∽CAB ∆ 两角相等; (4)EAB ∆∽ECD ∆ 两边成比例夹角相等; (5)ABD ∆∽ACB ∆ 两边成比例夹角相等; (6)ABD ∆∽ACB ∆ 两边成比例夹角相等.例11.分析 有一个角是65°的等腰三角形,它的底角是72°,而BD 是底角的平分线,∴︒=∠36CBD ,则可推出ABC ∆∽BCD ∆,进而由相似三角形对应边成比例推出线段之间的比例关系.证明 AC AB A =︒=∠,36 ,∴︒=∠=∠72C ABC . 又BD 平分ABC ∠,∴︒=∠=∠36CBD ABD .∴BC BD AD ==,且ABC ∆∽BCD ∆,∴BC CD AB BC ::=,∴CD AB BC ⋅=2,∴CD AC AD ⋅=2. 说明 (1)有两个角对应相等,那么这两个三角形相似,这是判断两个三角形相似最常用的方法,并且根据相等的角的位置,可以确定哪些边是对应边.(2)要说明线段的乘积式cd ab =,或平方式bc a =2,一般都是证明比例式,b dc a =,或caa b =,再根据比例的基本性质推出乘积式或平方式.例12分析 由ABC ∆的三边长可以判断出ABC ∆为直角三角形,又因为ABC ∆∽C B A '''∆,所以C B A '''∆也是直角三角形,那么由C B A '''∆的最大边长为26,可以求出相似比,从而求出C B A '''∆的两条直角边长,再求得C B A '''∆的面积.解 设ABC ∆的三边依次为,13,12,5===AB AC BC ,则222AC BC AB += ,∴︒=∠90C .又∵ABC ∆∽C B A '''∆,∴︒=∠='∠90C C .212613==''=''=''B A AB C A AC C B BC , 又12,5==AC BC ,∴24,10=''=''C A C B . ∴12010242121=⨯⨯=''⨯''=C B C A S .例13.分析 判断方法是否可行,应考虑利用这种方法加之我们现有的知识能否求出旗杆的高.按这种测量方法,过F作AB FG ⊥于G ,交CE 于H ,可知AGF ∆∽EHF ∆,且GF 、HF 、EH 可求,这样可求得AG ,故旗杆AB 可求.解 这种测量方法可行.理由如下:设旗杆高x AB =.过F 作AB FG ⊥于G ,交CE 于H (如图).所以AGF ∆∽EHF ∆.因为3,30327,5.1==+==HF GF FD ,所以5.1,25.15.3-==-=x AG EH .由AGF ∆∽EHF ∆,得HF GF EH AG =,即33025.1=-x ,所以205.1=-x ,解得5.21=x (米) 所以旗杆的高为21.5米.说明 在具体测量时,方法要现实、切实可行. 例14. 解:︒=∠=∠∠=∠90,ECD ABC EDC ADB ,∴ABD ∆∽ECD ∆,1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB (米),答:两岸间AB 大致相距100米. 例15. 答案:1506=AB 米,30750=BD 步,(注意:AK FEFHKE AK CD DG KC ⋅=⋅=,.) 例16. 分析:要求BC 的长,需画图来解,因AB 、AC 都大于高AD ,那么有两种情况存在,即点D 在BC 上或点D 在BC 的延长线上,所以求BC 的长时要分两种情况讨论.求正方形的面积,关键是求正方形的边长. 解:(1)如上图,由AD ⊥BC ,由勾股定理得BD =3,DC =1,所以BC =BD +DC =3+1=4. 如下图,同理可求BD =3,DC =1,所以BC =BD -CD =3-1=2.(2)如下图,由题目中的图知BC =4,且162)32(2222=+=+AC AB ,162=BC ,∴222BC AC AB =+.所以△ABC 是直角三角形.由AE G F 是正方形,设G F =x ,则FC =2-x , ∵G F ∥AB ,∴AC FCAB GF =,即2232x x -=. ∴33-=x ,∴3612)33(2-=-=AEGF S 正方形. 如下图,当BC =2,AC =2,△ABC 是等腰三角形,作CP ⊥AB 于P ,∴AP =321=AB ,在Rt △APC 中,由勾股定理得CP =1, ∵GH ∥AB ,∴△C GH ∽△CBA ,∵x x x -=132,32132+=x ∴121348156)32132(2-=+=GFEH S 正方形 因此,正方形的面积为3612-或121348156-.。
初中数学经典相似三角形练习题附参考答案

1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.2 / 58(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是?ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC= _________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.3 / 58某一时刻,动点M从A点出发沿AB方向以1cm/s 8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm..的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.4 / 5811.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B?A?D?C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C?D?A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:5 / 58①当点P在B?A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A 出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.6 / 5816.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.7 / 5820.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA 所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?8 / 5823.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm..乙组:如图2,测得学校旗杆的影长为900cm..9 / 58丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度:(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.10 / 5827.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.11 / 5830.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点相似三角形的判定;平行线的性质专题证明题分析根据平行线的性质可知∠AED=∠C,∠A=∠FEC,根据相似三角形的判定定理可知△ADE∽△EFC 解答证明:∵DE∥BC∴DE∥FC,∴∠AED=∠C.又∵EF∥AB,∴EF∥AD,∴∠A=∠FEC.∴△ADE∽△EFC.点评:本题考查的是平行线的性质及相似三角形的判定定理.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.13 / 58(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.考点相似三角形的判定;三角形中位线定理;梯形专题几何综合题分析)利用平行线的性质可证明△CDF∽△BGF)根据B的中点这一已知条件,可得△CDF≌△BGF,CD=B,只要求B的长即解题解答)证明:∵梯ABC,AB∥CD∴∠CDF=∠FGB,∠DCF=∠GBF分∴△CDF∽△BGF分(2)解:由(1)△CDF∽△BGF,又F是BC的中点,BF=FC,∴△CDF≌△BGF,∴DF=GF,CD=BG,(6分)∵AB∥DC∥EF,F为BC中点,14 / 58∴A中点∴E是△DA的中位线∴2EF=AG=AB+BG∴BG=2EF﹣AB=2×46=,∴CD=BG=2cm.(8分)点评:本题主要考查了相似三角形的判定定理及性质,全等三角形的判定及线段的等量代换,比较复杂.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.考点:相似三角形的判定。
相似三角形经典练习题及答案

相似三角形经典练习题及答案一、选择题1、若两个相似三角形的面积之比为 1∶4,则它们的周长之比为()A 1∶2B 1∶4C 1∶5D 1∶16答案:A解析:相似三角形面积的比等于相似比的平方,相似三角形周长的比等于相似比。
因为两个相似三角形的面积之比为 1∶4,所以相似比为 1∶2,那么它们的周长之比为 1∶2。
2、如图,在△ABC 中,点 D、E 分别在边 AB、AC 上,DE∥BC,若 AD∶DB = 1∶2,则下列结论中正确的是()A AE∶EC = 1∶2B AE∶EC = 1∶3 C DE∶BC = 1∶2 DDE∶BC = 1∶3答案:B解析:因为 DE∥BC,所以△ADE∽△ABC。
因为 AD∶DB =1∶2,所以 AD∶AB = 1∶3。
因为相似三角形对应边成比例,所以AE∶AC = AD∶AB = 1∶3,所以 AE∶EC = 1∶2。
3、已知△ABC∽△A'B'C',相似比为 3∶4,△ABC 的周长为 6,则△A'B'C'的周长为()A 8B 7C 9D 10答案:A解析:因为相似三角形周长的比等于相似比,所以△ABC 与△A'B'C'的周长之比为3∶4。
设△A'B'C'的周长为x,则6∶x =3∶4,解得 x = 8。
4、如图,在△ABC 中,D、E 分别是 AB、AC 上的点,且DE∥BC,如果 AD = 2cm,DB = 1cm,AE = 15cm,则 EC =()A 05cmB 1cmC 15cmD 3cm答案:B解析:因为 DE∥BC,所以△ADE∽△ABC,所以 AD∶AB =AE∶AC。
因为 AD = 2cm,DB = 1cm,所以 AB = 3cm。
所以 2∶3= 15∶(15 + EC),解得 EC = 1cm。
5、下列各组图形一定相似的是()A 两个直角三角形B 两个等边三角形C 两个菱形D 两个矩形答案:B解析:等边三角形的三个角都相等,都是 60°,所以两个等边三角形一定相似。
初中数学经典相似三角形练习题(附参考答案)

经典练习题相似三角形30小题)一.解答题(共1.如图,在△A中BC,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连D F与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边C D上一点,BF⊥A于EF,试说明:△ABF∽△EAD.5.已知:如图①所示,在△和△ABCADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△A是MN等腰三角形;转180°,其他条件不变,得到图②所示的图形.请向旋(2)在图①的基础上,将△绕点A D A E按顺时针方直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段B C于点P.求证:△PBD∽△AMN.6.如图,E是?ABCD的边B A延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写.明出图中所有的相似三角形,并任选一对相似三角形给予证27.如图,在4×3的正方形方格中,△和A△BCDE的F顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=_________°,BC=_________;(2)判断△AB与C△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△的AM面N积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△相A似CD?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.3(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△AB中C,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE于⊥EB,D连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BE与C△BEA的面积之比.4A B、AC的平行线交AC边BC上的任意一点,过点M分别作11.如图,在△A中B,CAB=AC=a,M为底于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);.论(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.513.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B?A?D?C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C?D?A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B?A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△相C似Q?E若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.614.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△相B似DC?15.如图,在△A中B,CAB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90A°C,=,AD=2.问当AB的长为多少时,这两个直角三角形相似.7A B上找一点N(不含A、B),17.已知,如图,在边a的正方形ABCD中,M是AD的中点,能否在边为长由.使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理18.如图在△A中BC,∠C=90°B,C=8cm,AC=6cm,点Q从B出发,沿B C方向以2cm/s的速度移动,,点P从C出发,沿C A方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后以点C、P、Q为顶点的三角形与△相C似B?A19.如图所示,梯形ABCD中,AD∥BC,∠A=90°AB,=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DE是F两个等腰直角三角形,∠A=∠D=90°的,顶△点E D E位F于边B C的中点上.(1)如图1,设D E与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;8(2)如图2,将△DE绕F点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△相A似BC.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?923.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;10(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=两l灯,柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.1127.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面S1,S2,S3表示,则不难积分别用证明S1=S2+S3.S1,S2,S3表示,那么(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3之间有什么关系;(不必证明)S1、S2、S3表示,请(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用你确定S1,S2,S3之间的关系并加以证明;S1,S1,S2,S3表示,为使(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△AA B D=1E5,,AC=9,BD=5.求AE.1229.已知:如图R t△ABC∽Rt△BDC,AB若=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;为3:10,且这两个三角形的周长差为560cm,求它们的周长.(2)已知:两相似三角形对应高的比13参考答案与试题解析30小题)一.解答题(共1.如图,在△A中BC,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点:相似三角形的判定;平行线的性质。
初中数学经典相似三角形练习题附答案(供参考)

1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=_________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC 于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度:(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=,窗口高AB=,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点:相似三角形的判定;平行线的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
康桥国际天虹教育谢相似三角形一.解答题(共30小题)中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.1.如图,在△ABC2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;的长.(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD 面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.的中点,试说明:△ADM∽△MCP.5.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD6.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?7.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.8.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?9.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.10.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.11.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所点时,身影的长度是变长了还是变短了?变长或变短了多少米?在的直线行走14米到B12.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离.EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC13.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.14.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.15.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.相似三角形一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.s i n t h e i rb d f o r s o 2.如图,梯形ABCD 中,AB∥CD,点F 在BC 上,连DF 与AB 的延长线交于点G .(1)求证:△CDF∽△BGF;(2)当点F 是BC 的中点时,过F 作EF∥CD 交AD 于点E ,若AB=6cm ,EF=4cm ,求CD 的长.分析:(1)利用平行线的性质可证明△CDF∽△BGF.(2)根据点F 是BC 的中点这一已知条件,可得△CDF≌△BGF,则CD=BG ,只要求出BG 的长即可解题.3.如图,点D ,E 在BC 上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.点评:本题很简单,考查的是相似三角形的判定定理:(1)如果两个三角形的两个角对应相等,那么这两个三角形相似;b e i n g a r e g o o d f o r s o 角形相似;(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.4.如图,已知矩形ABCD 的边长AB=3cm ,BC=6cm .某一时刻,动点M 从A 点出发沿AB 方向以1cm/s 的速度向B 点匀速运动;同时,动点N 从D 点出发沿DA 方向以2cm/s 的速度向A 点匀速运动,问:(1)经过多少时间,△AMN 的面积等于矩形ABCD 面积的?(2)是否存在时刻t ,使以A ,M ,N 为顶点的三角形与△ACD 相似?若存在,求t 的值;若不存在,请说明理由.分析:(1)关于动点问题,可设时间为x ,根据速度表示出所涉及到的线段的长度,找到相等关系,列方程求解即可,如本题中利用,△AMN 的面积等于矩形ABCD 面积的作为相等关系;(2)先假设相似,利用相似中的比例线段列出方程,有解的且符合题意的t 值即可说明存在,反之则不存在.解答:(1)设经过x 秒后,(6﹣2x)x=×3×6,得x 1=1,x 2=2,(2)假设经过t 秒时,以A ,M ,N 为顶点的三角形与△ACD 相似,由矩形ABCD ,可得∠CDA=∠MAN=90°,e anth ei r br s o 因此有或即①,或②解①,得t=;解②,得t=经检验,t=或t=都符合题意12.已知:P 是正方形ABCD 的边BC 上的点,且BP=3PC ,M 是CD 的中点,试说明:△ADM∽△MCP .分析:欲证△ADM∽△MCP,通过观察发现两个三角形已经具备一组角对应相等,即∠D=∠C,此时,再求夹此对应角的两边对应成比例即可.6.已知矩形ABCD ,长BC=12cm ,宽AB=8cm ,P 、Q 分别是AB 、BC 上运动的两点.若P 自点A 出发,以1cm/s 的速度沿AB 方向运动,同时,Q 自点B 出发以2cm/s 的速度沿BC 方向运动,问经过几秒,以P 、B 、Q 为顶点的三角形与△BDC 相似?分析:要使以P 、B 、Q 为顶点的三角形与△BDC 相似,则要分两两种情况进行分析.分别是△PBQ∽△BDChingsiningaregoodf 或△QBP∽△BDC,从而解得所需的时间.解答:解:设经x秒后,△PBQ∽△BCD,由于∠PBQ=∠BCD=90°,(1)当∠1=∠2时,有:,即;(2)当∠1=∠3时,有:,即,∴经过秒或2秒,△PBQ∽△BCD.7.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.解答:解:∵AC=,AD=2,∴CD==.要使这两个直角三角形相似,有两种情况:(1)当Rt△ABC∽Rt△ACD时,有=,∴AB==3;(2)当Rt△ACB∽Rt△CDA时,有=,∴AB==3.8.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?meandAllthinngaregoodforso 解答:解:设经过x秒后,两三角形相似,则CQ=(8﹣2x)cm,CP=xcm,∵∠C=∠C=90°,当或时,两三角形相似.(1)当时,,∴x=;(2)当时,,∴x=.19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.解答:解:(1)若点A,P,D分别与点B,C,P对应,即△APD∽△BCP,∴=,=,AP2﹣7AP+6=0,AP=1或AP=6,检测:当AP=1时,由BC=3,AD=2,BP=6,∴=,又∵∠A=∠B=90°,∴△APD∽△BCP.当AP=6时,由BC=3,AD=2,BP=1,又∵∠A=∠B=90°,△APD∽△BCP.(2)若点A,P,D分别与点B,P,C对应,即△APD∽△BPC.ntheirbeingaregoo ∴=,∴=,∴AP=.检验:当AP=时,由BP=,AD=2,BC=3,=,∵∠A=∠B=90°,∴△APD∽△BPC.此,点P的位置有三处,即在线段AB距离点A的1、、6处.10.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.分析:若以点Q、A、P为顶点的三角形与△ABC相似,有四种情况:①△APQ∽△BAC,此时得AQ:BC=AP:AB;②△APQ∽△BCA,此时得AQ:AB=AP:BC;③△AQP∽△BAC,此时得AQ:BA=AP:BC;④△AQP∽△BCA,此时得AQ:BC=AP:BA.可根据上述四种情况所得到的不同的对应成比例线段求出t的值.11.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?ti m ei n th e i r 分析:如图,由于AC∥BD∥OP,故有△MAC∽△MOP,△NBD∽△NOP 即可由相似三角形的性质求解.12.阳光通过窗口照射到室内,在地面上留下2.7m 宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m ,窗口高AB=1.8m ,求窗口底边离地面的高BC .分析:因为光线AE 、BD 是一组平行光线,即AE∥BD,所以△ECA∽△DCB,则有,从而算出BC 的长.(BC=4米)13.如图,李华晚上在路灯下散步.已知李华的身高AB=h ,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP 的水平距离OA=a ,求他影子AC 的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC )是否是定值请说明理由;(3)若李华在点A 朝着影子(如图箭头)的方向以v 1匀速行走,试求他影子的顶端在地面上移动的速度v 2.a n d A l l thi n gs in t h e i r be i n g a r e g o o df or 解答:解:(1)由已知:AB∥OP,∴△ABC∽△OPC.∵,∵OP=l,AB=h ,OA=a ,∴,∴解得:.(2)∵AB∥OP,∴△ABC∽△OPC,∴,即,即.∴.同理可得:,∴=是定值.(3)根据题意设李华由A 到A',身高为A'B',A'C'代表其影长(如图).由(1)可知,即,∴,同理可得:,∴,由等比性质得:,当李华从A 走到A'的时候,他的影子也从C 移到C',因此速度与路程成正比∴,所以人影顶端在地面上移动的速度为.mt h i n g s i 14.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE .解答:解:∵△ABC∽△ADE,∴AE:AC=AD :AB .∵AE:AC=(AB+BD ):AB ,∴AE:9=(15+5):15.AE=12.15.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD 、CD 的长;(2)过B 作BE⊥DC 于E ,求BE 的长.。
