机械工程测试技术基础第三版课后答案全集
机械工程测试技术基础第三版课后习题答案

机械工程测试技术基础习题解答教材:机械工程测试技术基础,熊诗波 黄长艺主编,机械工业出版社,2006年9月第3版第二次印刷。
绪 论0-1 叙述我国法定计量单位的基本内容。
解答:教材P4~5,二、法定计量单位。
0-2 如何保证量值的准确和一致? 解答:(参考教材P4~6,二、法定计量单位~五、量值的传递和计量器具检定) 1、对计量单位做出严格的定义; 2、有保存、复现和传递单位的一整套制度和设备; 3、必须保存有基准计量器具,包括国家基准、副基准、工作基准等。
3、必须按检定规程对计量器具实施检定或校准,将国家级准所复现的计量单位量值经过各级计算标准传递到工作计量器具。
0-3 何谓测量误差?通常测量误差是如何分类表示的? 解答:(教材P8~10,八、测量误差)0-4 请将下列诸测量结果中的绝对误差改写为相对误差。
①1.0182544V±7.8μV ②(25.04894±0.00003)g ③(5.482±0.026)g/cm 2 解答: ①-667.810/1.01825447.6601682/10±⨯≈±②60.00003/25.04894 1.197655/10±≈±③0.026/5.482 4.743±≈‰ 0-5 何谓测量不确定度?国际计量局于1980年提出的建议《实验不确定度的规定建议书INC-1(1980)》的要点是什么? 解答: (1)测量不确定度是表征被测量值的真值在所处量值范围的一个估计,亦即由于测量误差的存在而对被测量值不能肯定的程度。
(2)要点:见教材P11。
0-6为什么选用电表时,不但要考虑它的准确度,而且要考虑它的量程?为什么是用电表时应尽可能地在电表量程上限的三分之二以上使用?用量程为150V 的0.5级电压表和量程为30V 的1.5级电压表分别测量25V 电压,请问哪一个测量准确度高? 解答: (1)因为多数的电工仪表、热工仪表和部分无线电测量仪器是按引用误差分级的(例如,精度等级为0.2级的电表,其引用误差为0.2%),而 引用误差=绝对误差/引用值其中的引用值一般是仪表的满度值(或量程),所以用电表测量的结果的绝对误差大小与量程有关。
机械工程测试技术基础第三版熊诗波课后答案(打印版)

机械工程测试技术基础第三版熊诗波课后答案(打印版)如何表达测量结果?对某量进行8次测量,测得值分别为:802、40,802、50,802、38,802、48,802、42,802、46,802、45,802、43。
求其测量结果。
解答:(1)测量结果=样本平均值不确定度或(2)所以测量结果=802、44+0、0-8 用米尺逐段丈量一段10m的距离,设丈量1m距离的标准差为0、2mm。
如何表示此项间接测量的函数式?求测此10m距离的标准差。
解答:(1)(2)第一章信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|cn|–ω和φn–ω图,并与表1-1对比。
解答:在一个周期的表达式为积分区间取(-T/2,T/2)所以复指数函数形式的傅里叶级数为,。
没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号的绝对均值和均方根值。
解答:1-5 求被截断的余弦函数(见图1-26)的傅里叶变换。
解:w(t)为矩形脉冲信号所以根据频移特性和叠加性得:可见被截断余弦函数的频谱等于将矩形脉冲的频谱一分为二,各向左右移动f0,同时谱线高度减小一半。
也说明,单一频率的简谐信号由于截断导致频谱变得无限宽。
1-7 设有一时间函数f(t)及其频谱如图1-27所示。
现乘以余弦型振荡。
在这个关系中,函数f(t)叫做调制信号,余弦振荡叫做载波。
试求调幅信号的傅里叶变换,示意画出调幅信号及其频谱。
又问:若时将会出现什么情况?解:所以根据频移特性和叠加性得:可见调幅信号的频谱等于将调制信号的频谱一分为二,各向左右移动载频ω0,同时谱线高度减小一半。
若将发生混叠。
第二章测试装置的基本特性2-1 进行某动态压力测量时,所采用的压电式力传感器的灵敏度为90、9nC/MPa,将它与增益为0、005V/nC的电荷放大器相连,而电荷放大器的输出接到一台笔式记录仪上,记录仪的灵敏度为20mm/V。
试计算这个测量系统的总灵敏度。
机械工程测试技术基础第三版课后题答案

1.1求周期方波(图1-4)的傅立叶级数(复指数函数形式)。
画出频谱图|C n |—ω ;φn —ω 图并与表1-1对比。
解:傅立叶级数的复指数形式表达式:⋅⋅⋅±±±==∑+∞-∞=,3,2,1,0;)(0n eC t x n tjn nω式中:所以:幅值频谱:相位频谱:傅立叶级数的复指数形式的幅值频谱图和相位频谱都是双边频谱图。
1.2求正弦信号 x (t )=x 0sin ωt 的绝对均值μ|x |和均方根值x rms解:1.3求指数函数 的频谱。
解:1.4求符号函数(题图1-1a )和单位阶跃函数(题图1-1b )的频谱.解:1) 符号函数的频谱: []()⎪⎩⎪⎨⎧⋅⋅⋅±±±=⋅⋅⋅±±±=-=--=+⨯+-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=⎥⎦⎤+⎢⎣⎡-==---------⎰⎰⎰,6,4,2;0,5,3,1;2cos 12111)(1)(1200002002002022000000000000n n n A j n n Aj e e n jA n jA e jn A T e jn A T dt Ae dt e A T dt e t x T C jn jn T t jn T t jn T t jn T t jn T T t jn n πππππωωππωωωωω⋅⋅⋅±±±±=⎪⎭⎫ ⎝⎛-=∑+∞-∞=,7,5,3,1;2)(0n en A j t x t jn n ωπ⋅⋅⋅±±±==+=,5,3,1;222n n A C C C nI nR n π⎪⎩⎪⎨⎧⋅⋅⋅---=⋅⋅⋅=-=⎪⎪⎪⎪⎭⎫⎝⎛-==,5,3,1;2,5,3,1;202n n n A arctg C C arctg nR nI n πππϕωππωμ2;2sin 1)(lim 0000000====⎰⎰∞→T x tdt x T dt t x T T T x 式中:()2sin 1)(10020002000x dt dt x T dt t x T x T T rms ===⎰⎰ω)0;0(;)(≥>=-t Ae t x t ααfj Adt eAe dt e t x f X ftj t ft j παπαπ2)()(022+=⋅==⎰⎰∞+--∞+∞--令:2)单位阶跃函数的频谱:1.5求被截断的余弦函数cos ω0t (题图1-2)的傅立叶变换。
机械工程测试技术基础(第三版)课后答案全集
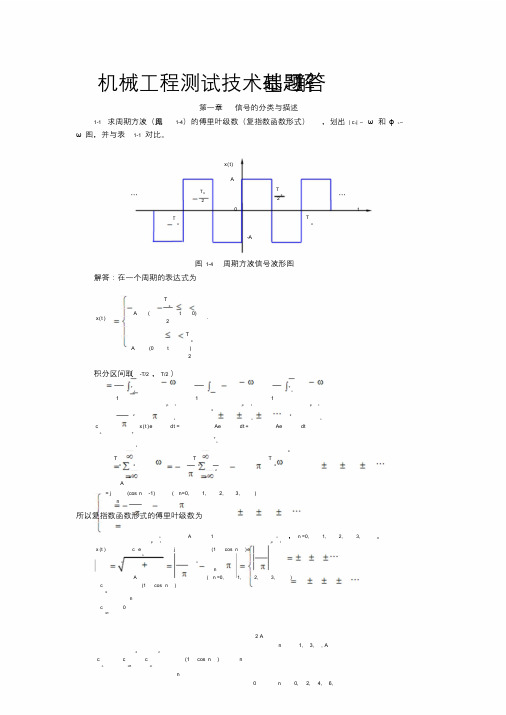
机械工程测试技术基础习题解答第一章信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出| c n| –ω和φn –ω图,并与表1-1 对比。
x(t)A⋯T0T0 ⋯22T 00 tT-A图1-4 周期方波信号波形图解答:在一个周期的表达式为x(t )TA ( t 0)2TA (0 t )2.积分区间取(-T/2 ,T/2 )T T0 01 1 1jn t jn t jn t2 20 0 0c x(t)e dt = Ae dt +Ae dtn TTT T T0 2 0 02A= j (cos n -1) ( n=0, 1, 2, 3, )n所以复指数函数形式的傅里叶级数为0 A 1 0jn t jn t x (t ) c e j (1 cos n ) enn nn ,n =0, 1, 2, 3, 。
Ac (1 cos n ) nIn (n =0, 1, 2, 3, )cnR2 An 1, 3, , A2 2c c c (1 cos n ) nn nR nIn0 n 0, 2, 4, 6,π2n 1, 3, 5,c πnIφarctan n 1, 3, 5,nc 2nR0 n 0, 2, 4, 6,没有偶次谐波。
其频谱图如下图所示。
|c n|φn2A/π2A/ππ/22A/ 3π2A/ 3π2A/ 5π-5ω0 -3ω0 -ω0ω03ω0 5ω02A/ 5πω-π/2-5ω0 -3ω0 -ω0 ω0 3ω0 5ω0ω幅频图相频图周期方波复指数函数形式频谱图1-2 求正弦信号x (t) x sin ωt 的绝对均值0 μ和均方根值x rm s 。
x解答:T T1 12 x x x x 2T T0 2 2 0 μx(t )dt x sin ωt dt sin ωtdt cos ωtx 0 0T T T TωTωπ0 021 T 1 T x T 1 cos 2ωt x2 2 2 0 0x x (t )d t x sin ωtdt dtrms 0T T T 2 20 0 0at1-3 求指数函数( ) ( 0, 0)x t Ae a t 的频谱。
机械工程测试技术基础第三版课后习题答案汇总

5-2假定有一个信号x(t),它由两个频率、相角均不相等的余弦函数叠加而成,其数学表达式为
x(t)=A1cos(1t+1)+A2cos(2t+2)
求该信号的自相关函数。
解:设x1(t)=A1cos(1t+1);x2(t)=A2cos(2t+2),则
因为12,所以 , 。
又因为x1(t)和x2(t)为周期信号,所以
解:
所以
根据频移特性和叠加性得:
可见调幅信号的频谱等于将调制信号的频谱一分为二,各向左右移动载频ω0,同时谱线高度减小一半。
若 将发生混叠。
2-2用一个时间常数为的一阶装置去测量周期分别为1s、2s和5s的正弦信号,问稳态响应幅值误差将是多少?
解:设一阶系统 ,
,T是输入的正弦信号的周期
稳态响应相对幅值误差 ,将已知周期代入得
解:设 ,则
, ,即
,
将fn= 800Hz,= ,f= 400Hz,代入上面的式子得到
A(400),(400)−
如果= ,则A(400),(400)−
2-11对一个可视为二阶系统的装置输入一单位阶跃函数后,测得其响应的第一个超调量峰值为,振荡周期为。设已知该装置的静态增益为3,求该装置的传递函数和该装置在无阻尼固有频率处的频率响应。
幅频图为
4-5已知调幅波xa(t)=(100+30cost+20cos3t)cosct,其中fc=10kHz,f=500Hz。试求:
1)xa(t)所包含的各分量的频率及幅值;
2)绘出调制信号与调幅波的频谱。
解:1)xa(t)=100cosct+15cos(c-)t+15cos(c+)t+10cos(c-3)t+10cos(c+3)t
测试技术基础(第三版)课后答案全集 (2)

将fn = 800Hz, = 0.14,f = 400Hz,代入上面的式子得到 A(400) 1.31,(400) −10.57 如果 = 0.7,则A(400) 0.975,(400) −43.03 2-11 对一个可视为二阶系统的装置输入一单位阶跃函数后,测得其 响应的第一个超调量峰值为1.5,振荡周期为6.28s。设已知该装置的静 态增益为3,求该装置的传递函数和该装置在无阻尼固有频率处的频率 响应。 解: 因为d = 6.28s,所以 d = 2/d = 1rad/s 所以 当 = n时,
机械工程测试技术基础习题解答
第一章 信号的分类与描述 1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划 出|cn|–ω和φn–ω图,并与表1-1对比。
图1-4 周期方波信号波形图 0 t x(t) … … A -A
解答:在一个周期的表达式为 . 积分区间取(-T/2,T/2) 所以复指数函数形式的傅里叶级数为 ,。 没有偶次谐波。其频谱图如下图所示。 |cn| φn π/2 -π/2 ω ω ω0 ω0 3ω0 5ω0
程的微安表,则量程不够,无法测量12.5mA的电流;如果采用毫安表, 无法分辨0.025mA的电流变化。一般需要电桥来测量,将无应变时的灵 位电流平衡掉,只取有应变时的微小输出量,并可根据需要采用放大器 放大。
3-5 电感传感器(自感型)的灵敏度与哪些因素有关?要提高灵敏度可 采取哪些措施?采取这些措施会带来什么样后果? 解答:以气隙变化式为例进行分析。 又因为线圈阻抗Z=L,所以灵敏度又可写成
解:设该一阶系统的频响函数为 ,是时间常数 则 稳态响应相对幅值误差 令≤5%,f=100Hz,解得≤523s。 如果f=50Hz,则 相对幅值误差: 相角差: 2-6 试说明二阶装置阻尼比多采用0.6~0.8的原因。 解答:从不失真条件出发分析。在0.707左右时,幅频特性近似常数 的频率范围最宽,而相频特性曲线最接近直线。 2-7 将信号cost输入一个传递函数为H(s)=1/(s+1)的一阶装置后, 试求其包括瞬态过程在内的输出y(t)的表达式。 解答:令x(t)=cost,则,所以 利用部分分式法可得到 利用逆拉普拉斯变换得到 2-8 求频率响应函数为3155072 / (1 + 0.01j)(1577536 + 1760j 2)的系统对正弦输入x(t)=10sin(62.8t)的稳态响应的均值显示。 解:该系统可以看成是一个一阶线性定常系统和一个二阶线性定常 系统的串联,串联后仍然为线性定常系统。根据线性定常系统的频率保 持性可知,当输入为正弦信号时,其稳态响应仍然为同频率的正弦信 号,而正弦信号的平均值为0,所以稳态响应的均值显示为0。 2-9 试求传递函数分别为1.5/(3.5s + 0.5)和的系统的总灵敏度(不考虑负载效应)。 解: ,即静态灵敏度K1=3 ,即静态灵敏度K2=41 因为两者串联无负载效应,所以 总静态灵敏度K = K1 K2 = 3 41 = 123 2-10 设某力传感器可作为二阶振荡系统处理。已知传感器的固有频 率为800Hz,阻尼比=0.14,问使用该传感器作频率为400Hz的正弦力测 试时,其幅值比A()和相角差()各为多少?若该装置的阻尼比改为 =0.7,问A()和()又将如何变化? 解:设,则 ,,即 ,
《机械工程测试技术基础》(第三版,熊诗波等主编)课后答案

《机械工程测试技术基础》(第三版,熊诗波等主编)课后答案机械工程测试技术基础第三版课后题答案1.1求周期方波(图1-4)的傅立叶级数(复指数函数形式)。
画出频谱图|Cn|―ω ;φn―ω 图并与表1-1对比。
解:傅立叶级数的复指数形式表达式:x(t)nCenjn 0t;n 0, 1, 2, 3,式中:T0T00 11 jn t jn t jn 0t0022 Cn x(t)edt ( A)edt AedtTT0 0T0 20T0 2T021 A jn 0t 1 A jn 0t ee T jn T jn T0 00 0 0 02jAjA1 jn Ajn1 cosn e e jn n 2n2A j;n 1, 3, 5,n n 2, 4, 6, 0;所以:2A jn 0tx(t) ;n 1, 3, 5, 7, j en n幅值频谱:2A22Cn nR CnI ;n 1, 3, 5,n相位频谱:2A;n 1,3,5, CnI 2 n arctg arctgCnR0 ;n 1, 3, 5, 2傅立叶级数的复指数形式的幅值频谱图和相位频谱都是双边频谱图。
1.2求正弦信号x(t)=x0sinωt的绝对均值μ|x |和均方根值x rms解:T 1T02x2x limx(t)dt x0sin tdt 0;式中:T0T 0 T001T021T0x02x x(t)dt xsin dtdt rms0 T00T0021.3求指数函数x ( Ae t; ( 0 ; t 0 ) 的频谱。
t) 解:j2 ft t j2 ftX(f) x(t)edtAe eAdtj2 f1.4求符号函数(题图1-1a)和单位阶跃函数(题图1-1b)的频谱. 解:1) 符号函数的频谱:令:x1(t) limetx(t);X1(f) x1(t)e j2 ftdt0 t tj2 ft lim e( 1)edt ee j2 ftdt 0 01 j f2)单位阶跃函数的频谱:2x(t) limetx(t)j2 ft;t1 j2 ft dt lim eedt 0 0 j2 f22-------------------------------------------------------------------------------------------------------------- ------------------------------------------------------------------------------------------------------------- 1.5求被截断的余弦函数cosω0t(题图1-2)的傅立叶变换。
[工学]机械工程测试技术基础第三版课后答案全集
![[工学]机械工程测试技术基础第三版课后答案全集](https://img.taocdn.com/s3/m/f115b4a73968011ca30091bf.png)
机械工程测试技术基础习题解答第一章信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c|–ω和φ–nnω图,并与表1-1对比。
x(t)ATT00 … … ,22t 0 T ,T00-A图1-4 周期方波信号波形图解答:在一个周期的表达式为T,0,,,,At (0),,2xt(),. ,T0, (0)At,,,,2积分区间取(-T/2,T/2)TT000111,,,jntjntjnt,,,22000cxtetAetAet,,()d=d+dTTn0,,,0,0,TTT20002A,jnn,,, =(cos-1) (=0, 1, 2, 3, )n,所以复指数函数形式的傅里叶级数为,,A1jntjnt,,00 ,。
,,,,,n=0, 1, 2,3, ,,,xtcejne()(1cos),,n,nnn,,,,,,A,(1cos),cn,,,,nI (=0, 1, 2, 3, )n,,, n,,,0c,nR,,2A n ,,,,1,3,,A,22,cccn ,,,,,(1cos) ,n,nnRnIn,,00,2,4,6, n,,,,,π,,,,,,n1,3,5,,2,cπ,nI arctan1,3,5,φ,,,,,,n,nc2nR,00,2,4,6,n,,,,,,,没有偶次谐波。
其频谱图如下图所示。
| |cnφn2A/π 2A/ππ/2ω 5ω 3ω0002A/3π 2A/3π 2A/5π 2A/5π -5ω -3ω ω -ω000-π/2 ω -5ω -3ω -ω ω 3ω 5ω 000000幅频图相频图周期方波复指数函数形式频谱图1-2 求正弦信号的绝对均值和均方根值。
xtx()sin,ωtμx0rmsx解答:TTTT2242xxxx11000022μ,,,,,,,xttx()dsindsindcosωttωttωt0x,,,0000TTTTωTωπ2TTTxx111cos2,ωt22200 xxttx,,,,()dsinddωtttrms0,,,000TTT22,at 1-3 求指数函数的频谱。
机械工程测试技术基础(第三版)课后答案全集

A x(t ) A
(
T0 t 0) 2 . T0 (0 t ) 2
积分区间取(-T/2,T/2)
1 cn T0 =j
T0 2 T 0 2
x(t )e
jn0t
1 dt = T0
0 T0 2
Ae
jn0t
1 dt + T0
T0
0
x0 sin(ωt φ)dt 0 ,式中 T0
2π —正弦信号周期 ω
1 T 2 1 x (t )dt T T 0 T0
T0
0
x0 2 sin 2 (ωt φ)dt
x0 2 T0
T0
0
x2 1 cos 2(ωt φ) dt 0 2 2
(3)在一个周期内
1 T 2 1 T 2 2 x (t )dt x0 sin ωtdt T 0 T 0
0
x 1 cos 2ωt dt 0 2 2
1-3 求指数函数 x(t ) Ae at (a 0, t 0) 的频谱。 解答:
X ( f ) x(t )e j 2 f t dt Ae at e j 2 f t dt A
Δt Δt
x(t)
x+2-1 进行某动态压力测量时,所采用的压电式力传感器的灵敏度为 90.9nC/MPa,将它 与增益为 0.005V/nC 的电荷放大器相连, 而电荷放大器的输出接到一台笔式记录仪上, 记录 仪的灵敏度为 20mm/V。试计算这个测量系统的总灵敏度。当压力变化为 3.5MPa 时,记录笔 在记录纸上的偏移量是多少? 解:若不考虑负载效应,则各装置串联后总的灵敏度等于各装置灵敏度相乘,即 S=90.9(nC/MPa)0.005(V/nC)20(mm/V)=9.09mm/MPa。 偏移量:y=S3.5=9.093.5=31.815mm。 2-2 用一个时间常数为 0.35s 的一阶装置去测量周期分别为 1s、2s 和 5s 的正弦信号, 问稳态响应幅值误差将是多少? 解:设一阶系统 H ( s )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解答:
1-3求指数函数 的频谱。
解答:
1-4求符号函数(见图1-25a)和单位阶跃函数(见图1-25b)的频谱。
a)符号函数的频谱
t=0处可不予定义,或规定sgn(0)=0。
该信号不满足绝对可积条件,不能直接求解,但傅里叶变换存在。
可以借助于双边指数衰减信号与符号函数相乘,这样便满足傅里叶变换的条件。先求此乘积信号x1(t)的频谱,然后取极限得出符号函数x(t)的频谱。
相角差:
2-6试说明二阶装置阻尼比多采用0.6~0.8的原因。
解答:从不失真条件出发分析。在0.707左右时,幅频特性近似常数的频率范围最宽,而相频特性曲线最接近直线。
2-7将信号cost输入一个传递函数为H(s)=1/(s+1)的一阶装置后,试求其包括瞬态过程在内的输出y(t)的表达式。
解答:令x(t)=cost,则 ,所以
解:
因为d= 6.28s,所以
d= 2/d= 1rad/s
所以
当=n时,
第三章常用传感器与敏感元件
3-1在机械式传感器中,影响线性度的主要因素是什么?可举例说明。
解答:主要因素是弹性敏感元件的蠕变、弹性后效等。
3-2试举出你所熟悉的五种机械式传感器,并说明它们的变换原理。
解答:气压表、弹簧秤、双金属片温度传感器、液体温度传感器、毛发湿度计等。
选用时要根据测量精度要求、现场条件、灵敏度要求等来选择。
3-4有一电阻应变片(见图3-84),其灵敏度Sg=2,R=120。设工作时其应变为1000,问R=?设将此应变片接成如图所示的电路,试求:1)无应变时电流表示值;2)有应变时电流表示值;3)电流表指示值相对变化量;4)试分析这个变量能否从表中读出?
不同点:电阻应变式传感器可以使用直流电桥电路,而电容式、电感式则不能。另外电容式、电感式传感器测量电路种类繁多。
3-7一个电容测微仪,其传感器的圆形极板半径r=4mm,工作初始间隙=0.3mm,问:1)工作时,如果传感器与工件的间隙变化量=1m时,电容变化量是多少?2)如果测量电路的灵敏度S1=100mV/pF,读数仪表的灵敏度S2=5格/mV,在=1m时,读数仪表的指示值变化多少格?
,输出电阻与输入位移成线性关系。
,输出电压与输入位移成非线性关系。
由上式可见,只有当Rp/RL0时,才有 。所以要求后续测量仪表的输入阻抗RL要远大于变阻器式传感器的电阻Rp,只有这样才能使输出电压和输入位移有较好的线性关系。
3-9试按接触式与非接触式区分传感器,列出它们的名称、变换原理,用在何处?
解:若不考虑负载效应,则各装置串联后总的灵敏度等于各装置灵敏度相乘,即
S=90.9(nC/MPa)0.005(V/nC)20(mm/V)=9.09mm/MPa。
偏移量:y=S3.5=9.093.5=31.815mm。
2-2用一个时间常数为0.35s的一阶装置去测量周期分别为1s、2s和5s的正弦信号,问稳态响应幅值误差将是多少?
y(t)=y01cos(10t+1)+y02cos(100t−45+2)
其中 ,
,
所以稳态响应为
2-4气象气球携带一种时间常数为15s的一阶温度计,以5m/s的上升速度通过大气层。设温度按每升高30m下降0.15℃的规律而变化,气球将温度和高度的数据用无线电送回地面。在3000m处所记录的温度为−l℃。试问实际出现−l℃的真实高度是多少?
加大磁路横截面积A0、线圈匝数N会增大传感器尺寸,重量增加,并影响到动态特性;减小气隙会增大非线性。
3-6电容式、电感式、电阻应变式传感器的测量电路有何Байду номын сангаас同?举例说明。
解答:电容式传感器的测量电路
自感型变磁阻式电感传感器的测量电路:
电阻应变式传感器的测量电路:电桥电路(直流电桥和交流电桥)。
相同点:都可使用电桥电路,都可输出调幅波。电容、电感式传感器都可使用调幅电路、调频电路等。
解答:接触式:变阻器式、电阻应变式、电感式(涡流式除外)、电容式、磁电式、压电式、热电式、广线式、热敏电阻、气敏、湿敏等传感器。
非接触式:涡电流式、光电式、热释电式、霍尔式、固态图像传感器等。
可以实现非接触测量的是:电容式、光纤式等传感器。
3-10欲测量液体压力,拟采用电容式、电感式、电阻应变式和压电式传感器,请绘出可行方案原理图,并作比较。
3-11一压电式压力传感器的灵敏度S=90pC/MPa,把它和一台灵敏度调到0.005V/pC的电荷放大器连接,放大器的输出又接到一灵敏度已调到20mm/V的光线示波器上记录,试绘出这个测试系统的框图,并计算其总的灵敏度。
解:框图如下
各装置串联,如果忽略负载效应,则总灵敏度S等于各装置灵敏度相乘,即
解:1)
2)B=S1S2C=1005(4.9410-3)2.47格
答:
3-8把一个变阻器式传感器按图3-85接线。它的输人量是什么?输出量是什么?在什么样条件下它的输出量与输人量之间有较好的线性关系?
解答:输入量是电刷相对电阻元件的位移x,输出量为电刷到端点电阻Rx。如果接入分压式测量电路,则输出量可以认为是电压uo。
S=x/P=900.00520=9mm/MPa。
3-12光电传感器包含哪儿种类型?各有何特点?用光电式传感器可以测量哪些物理量?
解答:包括利用外光电效应工作的光电传感器、利用内光电效应工作的光电传感器、利用光生伏特效应工作的光电传感器三种。
外光电效应(亦称光电子发射效应)—光线照射物体,使物体的电子逸出表面的现象,包括光电管和光电倍增管。
解法2:利用冲激函数
根据傅里叶变换的积分特性
1-5求被截断的余弦函数 (见图1-26)的傅里叶变换。
解:
w(t)为矩形脉冲信号
所以
根据频移特性和叠加性得:
可见被截断余弦函数的频谱等于将矩形脉冲的频谱一分为二,各向左右移动f0,同时谱线高度减小一半。也说明,单一频率的简谐信号由于截断导致频谱变得无限宽。
解:设 ,则
, ,即
,
将fn= 800Hz,= 0.14,f= 400Hz,代入上面的式子得到
A(400)1.31,(400)−10.57
如果= 0.7,则A(400)0.975,(400)−43.03
2-11对一个可视为二阶系统的装置输入一单位阶跃函数后,测得其响应的第一个超调量峰值为1.5,振荡周期为6.28s。设已知该装置的静态增益为3,求该装置的传递函数和该装置在无阻尼固有频率处的频率响应。
3-5电感传感器(自感型)的灵敏度与哪些因素有关?要提高灵敏度可采取哪些措施?采取这些措施会带来什么样后果?
解答:以气隙变化式为例进行分析。
又因为线圈阻抗Z=L,所以灵敏度又可写成
由上式可见,灵敏度与磁路横截面积A0、线圈匝数N、电源角频率、铁芯磁导率0,气隙等有关。
如果加大磁路横截面积A0、线圈匝数N、电源角频率、铁芯磁导率0,减小气隙,都可提高灵敏度。
内光电效应(亦称光导效应)—物体受到光线照射时,物体的电子吸收光能是其导电性增加,电阻率下降的现象,有光敏电阻和由其制成的光导管。
1-6求指数衰减信号 的频谱
解答:
所以
单边指数衰减信号 的频谱密度函数为
根据频移特性和叠加性得:
1-7设有一时间函数f(t)及其频谱如图1-27所示。现乘以余弦型振荡 。在这个关系中,函数f(t)叫做调制信号,余弦振荡 叫做载波。试求调幅信号 的傅里叶变换,示意画出调幅信号及其频谱。又问:若 时将会出现什么情况?
解:
所以
根据频移特性和叠加性得:
可见调幅信号的频谱等于将调制信号的频谱一分为二,各向左右移动载频ω0,同时谱线高度减小一半。
若 将发生混叠。
1-8求正弦信号 的均值 、均方值 和概率密度函数p(x)。
解答:
(1) ,式中 —正弦信号周期
(2)
(3)在一个周期内
第二章测试装置的基本特性
2-1进行某动态压力测量时,所采用的压电式力传感器的灵敏度为90.9nC/MPa,将它与增益为0.005V/nC的电荷放大器相连,而电荷放大器的输出接到一台笔式记录仪上,记录仪的灵敏度为20mm/V。试计算这个测量系统的总灵敏度。当压力变化为3.5MPa时,记录笔在记录纸上的偏移量是多少?
3-3电阻丝应变片与半导体应变片在工作原理上有何区别?各有何优缺点?应如何针对具体情况来选用?
解答:电阻丝应变片主要利用形变效应,而半导体应变片主要利用压阻效应。
电阻丝应变片主要优点是性能稳定,现行较好;主要缺点是灵敏度低,横向效应大。
半导体应变片主要优点是灵敏度高、机械滞后小、横向效应小;主要缺点是温度稳定性差、灵敏度离散度大、非线性大。
2-5想用一个一阶系统做100Hz正弦信号的测量,如要求限制振幅误差在5%以内,那么时间常数应取多少?若用该系统测量50Hz正弦信号,问此时的振幅误差和相角差是多少?
解:设该一阶系统的频响函数为
,是时间常数
则
稳态响应相对幅值误差
令≤5%,f=100Hz,解得≤523s。
如果f=50Hz,则
相对幅值误差:
机械工程测试技术基础第三版课后答案全集
机械工程测试技术基础习题解答
第一章信号的分类与描述
1-1求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|cn|–ω和φn–ω图,并与表1-1对比。
解答:在一个周期的表达式为
.
积分区间取(-T/2,T/2)
所以复指数函数形式的傅里叶级数为
, 。
没有偶次谐波。其频谱图如下图所示。
解:根据应变效应表达式R/R=Sg得
R=SgR=2100010-6120=0.24
1)I1=1.5/R=1.5/120=0.0125A=12.5mA
2)I2=1.5/(R+R)=1.5/(120+0.24)0.012475A=12.475mA
