计算水力学--第四章(3)
工程流体水力学第四章习题答案
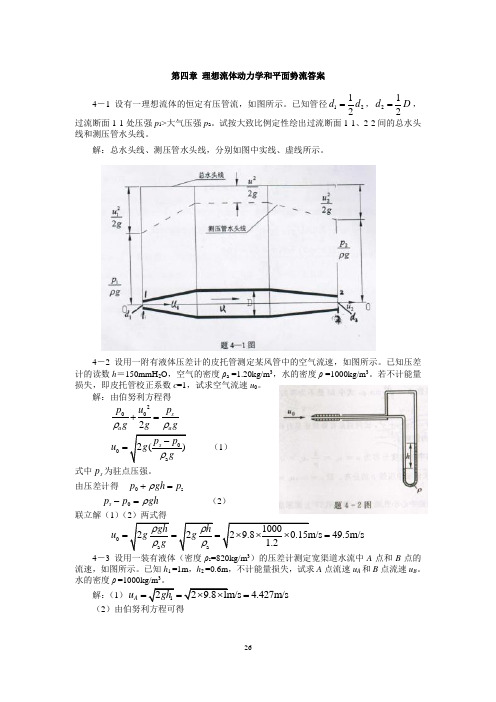
第四章 理想流体动力学和平面势流答案4-1 设有一理想流体的恒定有压管流,如图所示。
已知管径1212d d =,212d D =,过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解:总水头线、测压管水头线,分别如图中实线、虚线所示。
4-2 设用一附有液体压差计的皮托管测定某风管中的空气流速,如图所示。
已知压差计的读数h =150mmH 2O ,空气的密度ρa =1.20kg/m 3,水的密度ρ =1000kg/m 3。
若不计能量损失,即皮托管校正系数c =1,试求空气流速u 0。
解:由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=(1) 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= (2)联立解(1)(2)两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4-3 设用一装有液体(密度ρs =820kg/m 3)的压差计测定宽渠道水流中A 点和B 点的流速,如图所示。
已知h 1 =1m ,h 2 =0.6m ,不计能量损失,试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解:(1)1229.81m/s 4.427m/s A u gh ==⨯⨯= (2)由伯努利方程可得22A AA u p h g gρ+= (1)22B BB u p h g gρ+= (2)式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由(1)、(2)式可得2222A B A BA B p p u u h h g g gρ-=+-- (3) 由压差计得,22ρρρρ--++=A A s B B p gh gh gh gh p ,所以220.82A BA B p p h h h h gρ-=+-- (4) 由(3)式、(4)式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
北航水力学 第四章理想流体动力学和恒定平面势流解读

z1
p1
u12 2g
z2
p2
u22 2g
4.2.2 由动能定理推导理想流体的伯努利方程
推导过程同学们自学
z1
p1
u12 2g
z2
p2
u22 2g
本公式是由动能定理推导而得,它使伯努利方程有更加明确的 物理意义,说明伯努利方程是一能量方程。
第三节 元流伯努利方程的意义和应用
4.3.1 沿流线的伯努利方程的水力学意义
可见,在同一流线上各点的流函数为一常数,故等流函数线就是流线。
2、平面内任意两点流函数值的差等于通过这两点连线的流量。
y ABdrBnA x
d r dxi dy j
n cos i sin j dy i dx j
dr dr V ui v j
dq V
ndr
u
dy dr
v
dx dr
等 线和等Ψ线,这两族曲线互相垂直,构
成流网。
两族曲线所构成的正交网络,称为流网
流网的特征:
流网
等 线和速度矢量垂直,或者说, 等 线与等Ψ线(流线)垂直,
【例题】
已知90度角域内无粘流动,速度分布
ux kx uy ky
(k 0, x 0, y 0)
求:(1)判断该流场是否存在速度势函数, 若存在请给出并画出等势线;
流动。但粘滞性对流动 的影响很微小时,影响可以忽略。 --机械能守恒
引入势流的意义:使问题简化。
波浪运动,无分离的边界层外部的流动,多孔介质的流动(渗流) 等等可以看为势流。
4.4.1 流速势函数
以二维流动为例,根据流体运动学,它与无旋流动等价
由 ux 0 无旋流的条件→涡量 z 0
《水力学》第四章 有压管中的恒定流.

4-1 简单管道水力计算的基本公式
简单管道:指管道直径不变且无分支的管道。
简单管道的水力计算可分为自由出流和淹没出流。
一、自由出流
对1-1断面和2-2断面 建立能量方程
v0 称为行近流速
H
1v02
2g
2v2
2g
hw12
令 H 1v02
2g
H0
且因
hw12 hf hj
流的粗糙区或过渡粗糙区。可近似认为当v<1.2m/s时,
管流属于过渡粗糙区,hf约与流速v的1.8次方成正比。故
当按常用的经验公式计算谢齐系数C求hf应在右端乘以修
正系数k,即
H
hf
k
Q2 K2
l
管道的流量模数K,以及修正系数k可根据相关手册资料
得到。
11
12
13
例4-1 一简单管道,如图4-3所示。长为800m,管径 为0.1m,水头为20m,管道中间有二个弯头,每个弯头的 局部水头损失系数为0.3,已知沿程阻力系数λ=0.025,试 求通过管道的流量。
Z
l d
淹
注:1 自=淹 8
以上是按短管计算的情况。如按长管的情况,忽略
局部水头损失及流速水头损失。有
H
hf
l
d
v2 2g
水利工程的有压输水管道水流一般属于紊流的水力粗糙
区,其水头损失可直接按谢齐公式计算,用 8g 则
C2
H
8g C2
l d
v2 2g
8gl C 2 4R
Q 0.0703 3.14 0.12 19.6 20 0.01093 m2 / s
水力学第4章

γJ 2 u r0 r 2 4μ
γJ 2 r0 4μ
断面平均速度:
V
udA u 2πrdr
A
r0
A
0
πr02
umax 2
二.沿程损失系数:
umax γJ 2 γh f 2 V r0 r0 2 8μ 8 μl
第四章
流态和水头损失
§4-1
水头损失及其分类
流体从1-1断面运移到2-2断面,机械能减少:
p1 V12 p2 V22 z1 α1 z2 α2 hw γ 2g γ 2g
h w为水头损失。
hw分为两类:沿程水头损失hf和局部水头损失hj。
一.圆管流动:
hf的计算公式:
l V hf λ d 2g
u*r0 V Vd u* 2.5 ln 1.75 2.5 ln 1.75 u* ν ν 2V
又因为:
V 8 u λ
故:
1 λ 8 1.75 2.5 ln Re 2 8 λ 1 (2.5 ln 10) log Re λ 1.75 2 8
2
二.液体的非圆管流动:
A 水力半径:R χ
上式中:为过流断面上液体与固壁接触的周线长,称为湿周。
例如:
1).矩形断面管道:χ (b h) 2 A bh R χ 2(b h)
2).矩形断面排水沟:χ b 2h R A bh χ b 2h
π 2 d A 4 d 3).对于液体在圆管中的流动:R 。即:d 4 R。 χ πd 4
u um
平均速度:
第四章 水流型态与水头损失.

水力学
解:(1)先求弯管内的流速:
QV
A tA
水
A
100
0.28
0.052
4
1.43m s
Δh B
水力学
(2)再求沿程水头损失,由达西公式得:
hf
l 2
d 2g
0.0264 10 1.43 2 0.55m 0.05 2 9.8
1.雷诺实验
1883年英国科学家雷诺,通过实验发现液体 在流动中存在两种内部结构完全不同的流态: 层流和紊流。
(1)层流 当流速较小时,各流层质点互不混杂,
这种型态的流动叫层流。
水力学
(2)紊流 当流速较大时,各流层质点形成涡体
互相混掺,这种型态的流动叫做紊流。
水力学
同时发现,层流的沿程水头损失hf与流速一 次方成正比,紊流的hf与流速的1.75~2.0次方 成正比;在层流与紊流之间存在过渡区,hf与
2.83 3 0.0101
840.592000层流
水力学
五. 圆管层流运动和沿程水头损失
圆管层流运动可以应用牛顿内摩擦定律表达 式和均匀流内切应力表达式,通过积分求出过 水断面上的流速分布为抛物型分布。
J
u
4
r02 r 2
最大流速在管轴线处 u J r 2
max 4 0
(3)紊流过渡区 :λ既与Re有关,也与Δ有 关,hf 1.75~2。0 。
七. 沿程水头损失经验公式
谢才公式
C RJ
水力学
C是反映边界对液体运动影响的综合系 数,称为舍齐系数,单位:m1/2/s 。
水力学第四章层流、紊流,液流阻力和水头损失

3.7d
结论2:
•紊流光滑区水流沿程水头损失系数只取决于雷诺数,粗糙度不 起作用。容易得出光滑区紊流沿程损失与流速的1.75次方成正 比。 •紊流粗糙区水流沿程水头损失系数只取决于粗糙度,由于粗糙 高度进入流速对数区,阻力大大增加,这是不难理解的。容易 得出粗糙区紊流沿程损失与流速的2.0次方成正比。 •在紊流光滑区与粗糙区之间存在紊流过渡粗糙区,此时沿 程损失系数与雷诺数和粗糙度都有关。 •尼古拉兹试验反映了圆管流动的全部情况,在其试验结果图上 能划分出层流区,过渡区、紊流光滑区、紊流过渡粗糙区,紊 流粗糙区。紊流粗糙区通常也叫做‘阻力平方区’。
ro gJ 2 2 gJ 4 1 4 gJ 4 Q (ro r )2 rdr (ro ro ) d 0 4v 4v 2 128v
上式为哈根——泊肃叶定律:圆管均匀层流的流量Q与管径d 的四次方成比例。 3、断面平均流速: V
Q gJ 2 1 ro umax A 8 2
1 1 1 1 1 , , , , 及 30 61 .2 120 252 507 1
1 1 1 1 1 1 , , , , 及 30 61 .2 120 252 507 10
层流时,
64 Re
f (Re)
1 1 1 1 1 1 , , , , 及 30 61.2 120 252 507 1014
1 u u x x dt 0 T0
2、紊流的切应力 由相邻两流层间时均流速相对运动
所产生的粘滞切应力
紊流产生附加切应力
du l t v Re
t v Re 2
纯粹由脉动流速所产生 的附加切应力
dy ( du 2 ) dy
普朗特 混合长 Re 与 du 有关,根据质点脉动引起动量交换(传递),又称为动量传递理论 dy 理论
第四章.液流形态及水头损失

水头损失分类
(依据边界条件以及作用范围) 依据边界条件以及作用范围) hw 沿程损失 hf 局部损失 hj
沿程水头损失hf
水道中, 在平直的固体边界水道中,单位重量的液 体从一个断面流至另一个断面的机械能损失。 体从一个断面流至另一个断面的机械能损失。 这种 并随沿程长度增加而增加, 水头损失沿程都有并随沿程长度增加而增加,称 作沿程水头损失。 作沿程水头损失。
k
lg v
紊流:质点混掺, h ∝v 紊流:质点混掺,
f
1.75 ~ 2.0
3.液流流态的判断 3.液流流态的判断
雷诺发现, 雷诺发现,判断层流和紊流的临界流速 与液体密度、动力粘性系数、管径关系密切, 与液体密度、动力粘性系数、管径关系密切, 判断: 提出液流型态可用下列无量纲数判断:
ρvd Re = µ
对于圆管, 对于圆管,则
l v hf = λ d 2g
l v2 hf = λ 4R 2g
2
对于明渠均匀流, 对于明渠均匀流,则
可见,欲求出水头损失, 可见,欲求出水头损失,必须研究沿程阻力系数 的变化规律。 的变化规律。
沿程阻力系数λ包含的影响因素: 沿程阻力系数 包含的影响因素: 包含的影响因素
液流产生水头损失必须具备两个条件: 液流产生水头损失必须具备两个条件: 1)液体具有粘滞性;(决定作用) 液体具有粘滞性;(决定作用) ;(决定作用 2)由于固体边界的影响,液流内部质 由于固体边界的影响, 点间产生相对运动。 点间产生相对运动。
水力学上能量损失用单位重量液体 表示。 的能量损失 hw 表示。
H = H 0 + ∑ hw
水头损失在工程上的意义: 水头损失在工程上的意义:
水头损失的数值大小直接关系到动力设备容量 的确定,因而关系到工程的可靠和经济性。 的确定,因而关系到工程的可靠和经济性。 如图为水泵供水示意图,据供水要求, 如图为水泵供水示意图,据供水要求,水泵将 水池中水从断面1 提升到断面2 水池中水从断面1-1提升到断面2-2。 静扬高:断面1 的高程差H 静扬高:断面1和2的高程差H0 扬程H:静扬高加水头损失, H:静扬高加水头损失 扬程H:静扬高加水头损失, 即:
【重庆大学出版社·肖明葵】版【水力学习题评讲】第四章解析

Hale Waihona Puke v v1 v2 Q 1 2 d 4
h
7.7 4 27.23cm / s 2 0.6
题4.11图
2 p1 1v12 p2 2v2 0 0 h f 12 g 2g g 2g
p1 p2 汞 g 油 g 9.8 13600 9.8 843 h 0.15 2.222m g g 油 g 9.8 843
已知液体的运动粘滞系数ν为0.015cm2/s。试求Q为5000cm3/s、
4000cm3/s、2000cm3/s时,管道的沿程阻力系数λ各为若干? 解:由于 Re vd 4Q
d
2000 Re1 105
4 5000 Re1 21221.29, 3.1415 20 0.015
H
选取1-1、2-2两渐变流过水 断面分别在两水池液面上, 并取2-2断面为基准面0-0, 则写1-2的伯诺里方程有:
题4.25图
l v2 v2 H 00 000 (进 3弯 阀 出 ) d 2g 2g
l v2 v2 H (进 3弯 阀 出 ) d 2g 2g
v1d1 4v2 d 2 / 2 v2 d 2 Re1 2 2 Re 2 v v v Re1 2 所以小管径对应的断面雷诺数大, Re 2
4.4
圆管内径d =6 mm,有重油通过,密度
ρ=870.0kg/m3,运动粘性系数为ν=2.2×10–6 m2/s,管中 流量Q=0.02×10-3m3/s。试判别其流态。
o A l1 d1 B d2 o 1 h1 1 2 h2 H 2
伯诺里方程,
C
题4.27图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5 . 内边界的处理—堰闸过流
自由出流
堰闸过流
Q ? mbh 2gh0
h0 = Zi- Zd 为上游水深 b 是闸孔净宽; h 为计算过流水深 ; 孔流 h=a ; 堰流 h=h0 ; m 为综合流量系数。计算方法同关闸情况。
Leila for 水文09 版权所有
水文09级计算水力学教学课件
第四章 河道水流计算
§5 . 内边界的处理
Qf
Qi
Q i+1
Δx i=0 集中入流
断
面
Qi
Qi+1 突
变
情
i
i+1
况
面积 A
i
i+1
河道与贮水池汇合
过闸示意
Leila for 水文09 版权所有
§5 . 内边界的处理
? 在河道水流计算中,除了外部边界条件外,还 可能遇到内部边界条件 。
? 比较可得
Leila for 水文09 版权所有
§5 . 内边界的处理—过水断面突然放大
三、河道与贮水池汇合
? 相容条件
Qi
Q i+1
令
i
i+1
断面突变情况
Leila for 水文09 版权所有
§5 . 内边界的处理—过水断面突然放大
? 上边界为水位边界条件
? 同追赶方程
? 比较可得
Leila for 水文09 版权所有
As ?t
Vi
? ?Ti ? 1 ? ?
?
? 1?
1
As ?t
Vi
? ? ? Pi?1 ?? ?
?
Vi
As ?t
1?
Zi0 ?
As ?t
Vi
Pi
? ?Vi?1 ? ?
?
1?
Vi As ?t
Vi
Leila for 水文09 版权所有
§5 . 内边界的处理—河道与贮水池汇合
?上边界是 流量边界条件 ? 同追赶方程
§5 . 内边界的处理—集中旁侧入流
一、集中旁侧入流
? 对于集中旁侧入流,可设一虚拟河段,这时 基本的连接方程为
Qf
Qi
Q i+1
Δx i=0 集中入流
Leila for 水文09 版权所有
§5 . 内边界的处理—集中旁侧入流
? 当上边界为 水位边界条件
用上式计算虚拟河段的追赶系数,可同正常 河道一样递推求解。
堰闸过流
关闸
Qi ? Qi?1 ? 0
自由出流
堰闸过流
Q ? mbh 2gh0
淹没出流
堰闸过流
Q ? ?bh 2g ?Zi ? ? Zi?1
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
? 三种情况:关闸、自由出流、淹没出流 ? 关闸:
闸上、闸下可以作为两条单一河道来处理,对上游 河道来说,为下边界流量已知条件,可单独求解。 对于下游河道,可按流量已知边界条件单独求解 。
§5 . 内边界的处理—堰闸过流
? 上游边界为水位边界条件,过闸后仍然以水位边界 计算,当流量为零的情况会引起较大的误差。当接 近关闸时,有α=β=0,计算无法进行。
?最好的改进办法是 把下游河道计算改用流量边界条 件,可连续进行求解。
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
§5 . 内边界的处理—过水断面突然放大
? 上边界为流量边界条件
? 同追赶方程
? 比较可得
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
四、过闸
Zi Zi+1
i
i+1
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
? 三种情况:关闸、自由出流、淹没出流
i
i+1
河道与贮水池汇合
ห้องสมุดไป่ตู้
过闸示意
Leila for 水文09 版权所有
本章要点
? 内边界处理 用相容方程替换圣维南方程,单独计 算特殊河段的追赶系数,其它同正常 河道一样计算。
Leila for 水文09 版权所有
?上边界为水位边界条件
相容方程 联立解得
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
同追赶方程
比较可得
这样必须在上游河道与下游河道分别用不同的关系求解。先 以水位边界条件计算上游河道的追赶系数,在下游河道i+1 处的边界处,以流量边界条件计算下游河道的追赶系数。
Leila for 水文09 版权所有
§5 . 内边界的处理
?对于内边界的处理归结于特殊河段的追赶系 数计算。计算依据的是特殊河段的相容方程 (水量守恒与动量守恒,这些方程与非恒定流 的基本方程无关),对相容方程进行必要的处 理,单独计算特殊河段的追赶系数,可同正 常河段一样求解。
Leila for 水文09 版权所有
本章要点
? Preissmann 四点隐格式
Leila for 水文09 版权所有
§5 . 内边界的处理—河道与贮水池汇合
?上边界是 水位边界条件
? 同追赶方程
? 比较可得
??Qi ? Si?1 ? Ti?1Qi?1 ? ?? Zi?1 ? Pi?1 ? Vi ?1Qi ?1
? ? ?
? ?Si?1 ? ?? ?
As ?t
Pi ? Zi0
1?
? 内部边界条件是指:河道的几何形状的不连续或水 力特性的不连续点。例如,集中入流,过水断面突 然放大,堰闸过流等等。
? 内边界处,圣维南方程组不再适用,必须根据其水 力特性作特殊处理。内部边界条件通常包含 两个相 容条件,即流量的连续性条件和能量守恒条件 (或动 量守恒条件 )。
Leila for 水文09 版权所有
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
同追赶方程 比较可得
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
?上边界为水位边界条件
相容方程 联立解得
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
同追赶方程 比较可得
Leila for 水文09 版权所有
Leila for 水文09 版权所有
§5 . 内边界的处理—集中旁侧入流
? 当上边界为 流量条件
用上式计算虚拟河段的追赶系数,可同正常 河道一样递推求解。
Leila for 水文09 版权所有
§5 . 内边界的处理—河道与贮水池汇合
二、河道与贮水池汇合
面积 A
Qs
? 贮水池的连续方程
i
i+1
河道与贮水池汇合
§5 . 内边界的处理—堰闸过流
淹没出流
堰闸过流
Q ? ?bh 2g ?Zi ? ? Zi?1
线性化处理
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
差分代替微分
相容方程
Leila for 水文09 版权所有
§5 . 内边界的处理—堰闸过流
?上边界为流量边界条件
相容方程 联立解得
Leila for 水文09 版权所有
本章要点
? 四点线性隐格式
Leila for 水文09 版权所有
本章要点
? 差分方程
? 计算方法:追赶法
? 水位边界
? 流量边界
Leila for 水文09 版权所有
本章要点
Qf
Qi
Q i+1
Δx i=0 集中入流
断
面
Qi
Qi+1 突
变
情
i
i+1
况
面积 A
