负载转矩的计算公式
电机负载扭矩计算

一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:9.8*μ·W·P BT L=2π·R·η(N·M)式P B:滚珠丝杆螺距(m)μ:摩擦系数η:传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:9.8*(W-W C)P BT L=2π·R·η(N·M)式W C:配重块重量(KG)3、旋转轴运动:T1TL=R·η(N·M)式T1:负载转矩(N·M)二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量D(cm)L(cm)由下式计算有中心轴的圆柱体的惯量。
如滚珠丝杆,齿轮等。
4L(kg·cm·sec2)或πγ·L·D4(KG·M2)πγDJ K=32*980JK=32式γ:密度(KG/CM3)铁:γ〧7.87*10 -3KG/CM3=7.87*103KG/M3铝:γ〧2.70*10 -3KG/CM3=2.70*103KG/M3 JK:惯量(KG·CM·SEC2)(KG·M2)D:圆柱体直径(CM)·(M)L:圆柱体长度(CM)·(M)2、运动体的惯量用下式计算诸如工作台、工件等部件的惯量WPB2J L1=9802π(KG·CM·SEC2)PB22=W2π(KG·M)式中:W:直线运动体的重量(KG)PB:以直线方向电机每转移动量(cm)或(m)3、有变速机构时折算到电机轴上的惯量1、Z2JJO电机Z1KG·CN:齿轮齿数2Z122JL1=Z2*J0(KG·CM·SEC)(KG·M)三、运转功率及加速功率计算在电机选用中,除惯量、转矩之外,另一个注意事项即是电机功率计算。
伺服电机负载转矩计算公式

伺服电机负载转矩计算公式伺服电机在工业自动化领域中可是个相当重要的角色,而要搞清楚它的负载转矩计算公式,咱们得一步步来。
先来说说啥是负载转矩。
想象一下,你正在费力地推动一个大箱子,这个让你感到费劲的“力”,在电机的世界里,就可以理解为负载转矩。
那伺服电机的负载转矩到底咋算呢?一般来说,它可以通过下面这个公式来计算:负载转矩 = (摩擦力×半径) + (惯性转矩)这里面的摩擦力和半径比较好理解。
就比如说,一辆自行车的轮子,轮子和地面之间的摩擦力,还有轮子的半径,就能算出一部分转矩。
惯性转矩就稍微复杂点啦。
这就好像你要让一个静止的大转盘转起来,一开始得费很大的劲儿,这就是因为有惯性的存在。
给大家讲个我自己的经历。
有一次,我在工厂里看到一台机器出了故障,师傅们在那着急忙慌地找问题。
我凑过去一看,发现就是伺服电机的负载转矩出了差错。
他们按照以前的经验来设置,结果机器运行得磕磕绊绊的。
我就跟他们说,得重新算一下负载转矩。
我们先仔细检查了机器各个部件之间的摩擦力,测量了相关部件的半径。
然后,对于惯性转矩,我们得搞清楚转动部件的质量、形状还有转动速度的变化。
这可真是个细致活儿,一点都不能马虎。
经过一番努力,终于算出了新的负载转矩值。
调整之后,那台机器就像被施了魔法一样,顺畅地运行起来啦!在实际应用中,还有很多因素会影响负载转矩的计算。
比如工作环境的温度变化,会导致部件的摩擦系数改变;还有机器的运行速度不稳定,也会让惯性转矩的计算变得更复杂。
所以啊,要准确计算伺服电机的负载转矩,不仅要熟悉公式,还得对具体的工作场景有深入的了解。
每一个参数都得仔细琢磨,不能有一点儿马虎。
总之,搞清楚伺服电机负载转矩的计算公式,对于让机器高效稳定地运行,那可是至关重要的。
希望大家在实际操作中都能算得准准的,让机器乖乖听话,为我们好好干活!。
圆盘负载转矩公式

圆盘负载转矩公式
计算有以下三个公式:
1,M=N/ω(扭矩等于功率除以角速度)
2,M=Jα(扭矩等于转动惯量乘以角加速度)
3,M=FL (扭矩等于力乘以力距)
额定转矩表示额定条件下电机轴端输出转矩。
转矩等于力与力臂或力偶臂的乘积,在国际单位制(SI)中,转矩的计量单位为牛顿・米(N・m)。
工程技术中也曾用过公斤力・米等作为转矩的计量单位。
电机轴端输出转矩等于转子输出的机械功率除以转子的机械角速度。
直流电动机堵转转矩计算公式TK=9.55KeIK 。
机械元件在转矩作用下都会产生一定程度的扭转变形,故转矩有时又称为扭矩。
转矩是各种工作机械传动轴的基本载荷形式,与动力机械的工作能力、能源消耗、效率、运转寿命及安全性能等因素紧密联系。
转矩的测量对传动轴载荷的确定与控制、传动系统工作零件的强度设计以及原动机容量的选择等都具有重要的意义。
此外,转矩与功率的关系
T=9549P/n或T=P/Ω(Ω为角速度,单位为rad/s)。
=T*W,输出轴功率=扭矩*角速度,输出功率不变时角速度(转速)越小,输出扭矩就越大,就能带动越重的负荷。
转矩M=Ja; J-转动惯量;a-角加速度。
J=mr²; m=80kg(质量);
a=2πn/60/t;其中t是加速度时间,n是每分钟转数(即转速),t可以取0.1秒或你实际加速时间。
其实质量m可以用材料密度算出,即体积乘密度。
m=ρπr²L。
扭矩M知道后,扭力P=M/r,其中r是转动体的半径。
单位都用公斤米
计算。
电机负载扭矩计算

电机负载扭矩计算 Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:*μ·W·P BT L= 2π·R·η(N·M)式P B:滚珠丝杆螺距(m)μ:摩擦系数η:传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:*(W-W C)P BT L= 2π·R·η(N·M)式 W C:配重块重量(KG)3、旋转轴运动:T1= R·η(N·M)TL式 T1:负载转矩(N·M)二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量D(cm)L(cm)由下式计算有中心轴的圆柱体的惯量。
如滚珠丝杆,齿轮等。
πγD4L (kg·cm·sec2)或πγ·L·D4(KG·M2)J K= 32*980 J K= 32式γ:密度(KG/CM3)铁:γ〧*10-3KG/CM3=*103KG/M3铝:γ〧*10-3KG/CM3=*103KG/M3JK:惯量(KG·CM·SEC2)(KG·M2)D:圆柱体直径(CM)·(M)L:圆柱体长度(CM )·(M)2、运动体的惯量用下式计算诸如工作台、工件等部件的惯量2W PBJ= 980 2π(KG·CM·SEC2)L12PB=W 2π(KG·M2)式中:W:直线运动体的重量(KG)PB:以直线方向电机每转移动量(cm)或(m)3、有变速机构时折算到电机轴上的惯量1、JL1= Z2 *J(KG·CM·SEC2)(KG·M2)三、运转功率及加速功率计算在电机选用中,除惯量、转矩之外,另一个注意事项即是电机功率计算。
电机负载扭矩计算

一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:9.8*μ·W·P BT L=2π·R·η(N·M)式P B:滚珠丝杆螺距(m)μ:摩擦系数η:传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:9.8*(W-W C)P BT L=2π·R·η(N·M)式W C:配重块重量(KG)3、旋转轴运动:T1T L=R·η(N·M)式T1:负载转矩(N·M)二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量D(cm)L(cm)由下式计算有中心轴的圆柱体的惯量。
如滚珠丝杆,齿轮等。
πγD4L(kg·cm·sec2)或πγ·L·D4(KG·M2)J K=32*980J K=32式γ:密度(KG/CM3)铁:γ〧7.87*10-3KG/CM3=7.87*103KG/M3铝:γ〧2.70*10-3KG/CM3=2.70*103KG/M3JK:惯量(KG·CM·SEC2)(KG·M2)D:圆柱体直径(CM)·(M)L:圆柱体长度(CM)·(M)2、运动体的惯量用下式计算诸如工作台、工件等部件的惯量WP B2J L1=9802π(KG·CM·SEC2)P B2=W2π(KG·M2)式中:W:直线运动体的重量(KG)PB:以直线方向电机每转移动量(cm)或(m)3、有变速机构时折算到电机轴上的惯量1、JJOZ1KG ·CN :齿轮齿数 Z 12 JL1=Z 2*J 0(KG ·CM ·SEC 2)(KG ·M 2) 三、运转功率及加速功率计算在电机选用中,除惯量、转矩之外,另一个注意事项即是电机功率计算。
电机负载扭矩计算

一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:9. 8* 卩• W • P BT L=2n • R • n ( N • M) 式P B:滚珠丝杆螺距(m)U :摩擦系数n :传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:9.8* (W-Wc) P BT2 JI ■—L=式%配重块重量(KG)3、旋转轴运动:T1TL=R • q ( N • M)式T1:负载转矩(N・M)二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量't-'t'kg' • cm • sec2)或皿Y • L • D (KG • M)JT丫DJ K二32*980J式Y:密度(KG/CM3)铁:丫±7.87*10 _3KG/CM3=7. 87*103KG/M3铝:丫±2. 70*10「'KG/CM'二2. TO^IOWM3JK:惯量(KG • CM • SEC2) (KG • M)圆柱体直径(CM) • (M)L :圆柱体长度(CM ) • (W 2、运动体的惯量用下式计算诸如工作台、工件等部件的惯量式中:W 直线运动体的重量(KG )PB :以直线方向电机每转移动量(cm )或(ni )3、有变速机构时折算到电机轴上的惯量1、JL1 二Z2*J° ( KG • CM • SEC) (KG • M 三、运转功率及加速功率计算在电机选用中,除惯量、转矩之外,另一个注意事项即是电机功率计算。
一般可按下式求得。
1、转功 -------------2 兀• Nm • T LPo=6O (W )式中:PO :运转功率(酚Nm :电机运行速度(rpm )TL :何载转矩(N ・F2、速功率计算 ___________2兀• NnJLKG • CN :齿轮齿数222)Z1式Pd:加速功率(妙Nm:电机运行速度(rpm)2J1:负载惯性(KG-M)Ta:加速时间常数(sec)电机扭矩计算公式旋转物体的扭矩计算公式T=9550P/nP是功率,单位是kW, n是转速,单位是转/分,r/min扭矩单位为Nm功率二力*速度p 二F*v—-公式1转矩(T)二扭力(F)*作用半径(R) ----------- 推出F二T/R-一公式2线速度(V)二2 Ji R*每秒转速(n秒)二2 n R*每分转速(n分)/60= n R*n分/30---公式3将公式2、3代入公式1得:P二F*V二T/R* Ji R*n分/30二肌/30*T*n分- P二功率单位W, T二转矩单位Nm, n分二每分钟转速单位转/分钟如果将P的单位换成KW,那么就是如下公式:P*1000二Ji /30*T*n30000/ Ji *P=T*n30000/3. 1415926*P=T*n9549.297*P=T*n伺服电机扭矩计算公式:伺服五機扭矩計畀公式:F*R •(減速比戶T(扭矩)比如:偌動IOOKG的物惴・R-5OMM・減速比為I: 50計算為:100*9.8 (逼力加速度)*0.05*0.02=0.98 (N.M)。
电机负载扭矩计算精选文档

电机负载扭矩计算精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:*μ·W·PBTL= 2π·R·η(N·M)式 PB:滚珠丝杆螺距(m)μ:摩擦系数η:传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:*(W-WC )PBTL=2π·R·η(N·M)式 WC:配重块重量(KG)3、旋转轴运动:T1= R·η(N·M)TL式 T:负载转矩(N·M)1二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量)L(cm)由下式计算有中心轴的圆柱体的惯量。
如滚珠丝杆,齿轮等。
πγD 4L (kg ·cm ·sec2)或 πγ·L ·D4(KG ·M 2)J K = 32*980 J K = 32式 γ:密度(KG/CM3) 铁:γ〧*10-3KG/CM 3=*103KG/M 3 铝:γ〧*10-3KG/CM 3=*103KG/M 3JK :惯量(KG ·CM ·SEC 2) (KG ·M 2)D : 圆柱体直径(CM )·(M )L :圆柱体长度(CM )·(M )2、 运动体的惯量用下式计算诸如工作台、工件等部件的惯量 W P B 2J L1= 980 2π (KG ·CM ·SEC 2)P B 2=W 2π (KG ·M 2)式中:W:直线运动体的重量(KG)PB:以直线方向电机每转移动量(cm)或(m)3、有变速机构时折算到电机轴上的惯量1、J JOZ1KG·CN:齿轮齿数Z12JL1= Z2 *J(KG·CM·SEC2)(KG·M2)三、运转功率及加速功率计算在电机选用中,除惯量、转矩之外,另一个注意事项即是电机功率计算。
直线模组负载转矩计算公式

直线模组的负载转矩计算公式是转矩=施加力×施加力与旋转中心的距离。
其中,施加力的大小和方向会直接决定转矩的大小和方向。
在直线模组中,特别是当涉及到同步带传动或滚珠丝杠传动时,负载转矩的计算会涉及更多的因素。
对于同步带传动,假设已知重物重量和主动轮的直径,以及传送带的摩擦系数,可以通过计算得到摩擦力,然后乘以主动轮的半径得到扭矩。
对于滚珠丝杠传动,负载转矩的计算公式为T=F×P/(2π×n),其中T为扭矩,F为轴向力,P为导程,n为效率。
这个公式可以帮助我们计算电机所需的扭矩。
请注意,以上信息仅供参考,实际应用中可能还需要考虑其他因素,如步进电机转动后力矩的下降以及机械部分传动效率的可能降低等。
因此,在计算得到的理论结果基础上,可能需要进行适当的调整或放大。
电机负载转矩计算公式

电机负载转矩计算公式电机负载转矩的计算公式如下:SR2,M=CU12 公式,R22+(S X20)2,其中C为常数同电机本身的特性有关;U1输入电压;R2为转子电阻;X20为转子漏感抗;S为转差率。
可以知道M∝U12 转矩与电源电压的平方成正比,设正常输入电压时负载转矩为M2 ,电压下降使电磁转矩M下降很多;由于M2不变,所以M小于M2平衡关系受到破坏,导致电动机转速的下降,转差率S上升;又引起转子电压平衡方程式的变化,使转子电流I2上升。
也就是定子电流I1随之增加(由变压器关系可以知道);同时I2增加也是电动机轴上送出的转矩M又回升,直到与M2相等为止。
这时电动机转速又趋于新的稳定值。
注:负载转矩是用途的名称负载转矩占全负载驱动转矩的百分数起步加速峰值运转。
扩展资料:负载转矩的折算:负载转矩作用在生产机械轴上,如果把它等效到电机轴上为TL,则就相当于电机拖动一个具有等效负载转矩TL的负载在运动,而等效负载消耗的功率与实际负载所消耗的功率应相等,即以功率守恒原则进行折算。
对于如所示的旋转运动,当系统匀速运动时生产机械的负载功率为式中,——生产机械的负载转矩;——生产机械的旋转角速度。
设折算到电动机轴上的负载转矩为,则电动机轴上的负载功率为式中,——电动机转轴的角速度。
由于传动机构在传递功率的过程中有损耗,这个损耗可以用传动效率来表示。
即可得折算到电动机轴上的负载转式中,——电动机拖动生产机械时的传动效率;——传动机构的速比对于的直线传动,如齿轮齿条机构传动,若生产机械直线运动部件的负载力为F,运动速度为v。
则所需的机械功率为它反映在电动机轴上的机械功率为式中,——负载力F在电动机轴上产生的负载转矩。
同样考虑到由于摩擦阻力等因数,电动机拖动生产机械移动,传动机构中存在着能量损耗。
负载转矩的计算公式

负载转矩的计算公式负载转矩是机械工程中一个重要的概念,用于描述物体受到的扭转力矩。
在工程设计和分析中,准确计算和理解负载转矩是至关重要的。
本文将介绍负载转矩的计算公式,并阐述其在实际应用中的意义和作用。
在机械系统中,负载转矩是由外部施加的力矩或扭矩所引起的。
这种力矩可以是静态的,也可以是动态的。
负载转矩的计算通常涉及多个因素,包括力的大小、施加力的位置以及物体的几何形状和材料性质等。
根据牛顿第二定律和力矩的定义,我们可以得到负载转矩的计算公式。
负载转矩的计算公式可以用以下方式表示:M = F * d其中,M表示负载转矩,F表示施加力的大小,d表示施加力的作用点到物体转轴的距离。
这个公式适用于力矩是纯扭转力矩的情况,即施加力与物体转轴之间的距离保持不变。
在实际应用中,负载转矩的计算可以更加复杂。
例如,当施加力矩不是纯扭转力矩时,我们需要考虑力矩的方向和施加点的位置。
此外,当物体的几何形状复杂或材料的性质不均匀时,负载转矩的计算也会更加复杂。
负载转矩的计算在工程设计和分析中具有重要的意义。
首先,通过准确计算负载转矩,我们可以评估物体的承载能力和结构强度。
这对于设计和优化机械系统非常重要。
其次,负载转矩的计算可以帮助我们选择合适的材料和尺寸,以确保系统的安全性和可靠性。
最后,负载转矩的计算还可以用于预测和分析系统的运行性能,从而指导实际操作和维护。
在实际应用中,我们经常遇到需要计算负载转矩的情况。
例如,在设计机械传动系统时,我们需要计算传动轴的承载能力,以确保系统能够正常工作。
此外,在设计起重设备或机械臂时,我们也需要计算负载转矩,以确保设备能够承受预期的工作负载。
负载转矩的计算是机械工程中一个重要且常见的任务。
准确计算负载转矩可以帮助我们评估结构强度、选择合适的材料和尺寸,并预测系统的运行性能。
通过理解负载转矩的计算公式和应用意义,我们可以更好地进行工程设计和分析,提高机械系统的性能和可靠性。
计算折合到电机上的负载转矩的方法如下

一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:9.8*µ·W·P BT L= 2π·R·η(N·M)式P B:滚珠丝杆螺距(m)µ:摩擦系数η:传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:9.8*(W-W C)P BT L= 2π·R·η(N·M)式 W C:配重块重量(KG)3、旋转轴运动:T1T L= R·η(N·M)式 T1:负载转矩(N·M)二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量)由下式计算有中心轴的援助体的惯量。
如滚珠丝杆,齿轮等。
πγD4L (kg·cm·sec2)或πγ·L·D4(KG·M2)J K= 32*980 J K= 32式γ:密度(KG/CM3)铁:γ〧7.87*10-3KG/CM3=7.87*103KG/M3铝:γ〧2.70*10-3KG/CM3=2.70*103KG/M3 JK:惯量(KG·CM·SEC2)(KG·M2)D:圆柱体直径(CM)·(M)L:圆柱体长度(CM )·(M)2、运动体的惯量用下式计算诸如工作台、工件等部件的惯量 W P BJ L1= 980 2π(KG·CM·SEC2)P B 2=W2π(KG·M2)式中:W:直线运动体的重量(KG)PB:以直线方向电机每转移动量(cm)或(m)3、有变速机构时折算到电机轴上的惯量1、KG·CN:齿轮齿数Z12JL1= Z2 *J0 (KG·CM·SEC2)(KG·M2)三、运转功率及加速功率计算在电机选用中,除惯量、转矩之外,另一个注意事项即是电机功率计算。
负载转矩的计算公式

负载转矩的计算公式负载转矩是工程力学中常用的一个概念,它用来描述物体受到外力作用时所产生的力矩。
在工程设计和结构分析中,负载转矩的计算是一项重要的任务,它能够帮助工程师确定结构的稳定性和安全性。
负载转矩的计算公式是根据物体受到的外力和力臂的大小来确定的。
通常情况下,负载转矩的计算可以通过以下公式来进行:M = F × d其中,M表示负载转矩,F表示外力的大小,d表示力臂的长度。
根据这个公式,我们可以计算出物体受到的负载转矩的大小。
在实际工程中,负载转矩的计算是一个复杂而繁琐的过程。
首先,我们需要确定物体受到的外力的大小和方向。
外力可以是静力或动力,可以是集中力或分布力,可以是恒定力或变化力。
根据实际情况,我们需要选择合适的计算方法和公式来计算负载转矩。
我们需要确定力臂的长度。
力臂是指力作用点到负载转矩中心的垂直距离。
在实际工程中,力臂的长度可以通过测量或计算来确定。
对于简单的结构,力臂的长度可以直接测量得到;对于复杂的结构,我们需要使用几何和数学方法来计算力臂的长度。
我们可以使用负载转矩的计算公式来计算出物体受到的负载转矩的大小。
根据实际情况,我们可以选择将力和力臂的大小代入公式进行计算,也可以选择通过图形分析或数值计算来确定负载转矩的大小。
除了负载转矩的计算公式,工程师还需要考虑其他因素来确定结构的稳定性和安全性。
例如,我们需要考虑物体的材料特性、结构形式、支撑条件等因素。
在实际工程中,我们还需要进行一系列的实验和测试来验证计算结果的准确性和可靠性。
负载转矩的计算是工程设计和结构分析中的重要内容。
通过合理选择计算方法和公式,我们可以准确地计算出物体受到的负载转矩的大小。
这有助于工程师确定结构的稳定性和安全性,从而保证工程项目的顺利进行。
负载转矩的计算公式

负载转矩的计算公式负载转矩的计算公式是工程力学中的重要概念,它用于计算物体在受力作用下的扭转效应。
在工程设计和结构分析领域,负载转矩的计算是必不可少的一项工作。
本文将介绍负载转矩的计算公式及其应用。
负载转矩的计算公式是根据力的定义和扭转力矩的计算原理推导得出的。
根据牛顿第二定律,力的定义是质量乘以加速度。
扭转力矩是力矩的一种,它描述的是力的扭转效应。
负载转矩是指物体受到外力作用时,由于力的扭转效应产生的转矩。
负载转矩的计算公式可以分为静力学和动力学两种情况。
静力学是指物体处于静止状态下的转矩计算,动力学是指物体处于运动状态下的转矩计算。
静力学的负载转矩计算公式为:M = F × d其中,M表示负载转矩,F表示作用在物体上的力,d表示力的作用点到物体旋转轴的距离。
这个公式是根据力矩的定义和转动定律推导得出的。
根据转动定律,负载转矩等于力乘以力臂的长度。
动力学的负载转矩计算公式为:M = I × α其中,M表示负载转矩,I表示物体的转动惯量,α表示物体的角加速度。
这个公式是根据牛顿第二定律和角动量定理推导得出的。
根据角动量定理,负载转矩等于转动惯量乘以角加速度。
负载转矩的计算公式可以应用于各种工程设计和结构分析中。
例如,在建筑设计中,可以使用负载转矩的计算公式来确定梁柱的尺寸和材料强度。
在机械设计中,可以使用负载转矩的计算公式来确定机械零件的强度和耐久性。
在电气工程中,可以使用负载转矩的计算公式来确定电机的扭矩输出和传动系统的设计。
负载转矩的计算公式在实际工程中有广泛的应用。
它可以帮助工程师们进行合理的设计和分析,确保工程项目的安全性和可靠性。
同时,负载转矩的计算公式也可以用于优化设计和提高工程效率。
总结起来,负载转矩的计算公式是工程力学中的重要工具,它可以用于计算物体在受力作用下的扭转效应。
在静力学和动力学两种情况下,负载转矩的计算公式均为力乘以力臂的长度或转动惯量乘以角加速度。
电机负载扭矩计算(借鉴内容)
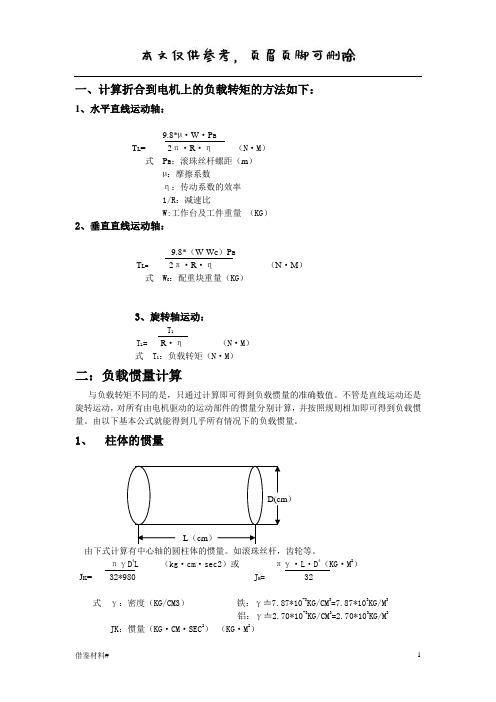
一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:9.8*µ·W·P BT L= 2π·R·η(N·M)式P B:滚珠丝杆螺距(m)µ:摩擦系数η:传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:9.8*(W-W C)P BT L= 2π·R·η(N·M)式 W C:配重块重量(KG)3、旋转轴运动:T1T L= R·η(N·M)式 T1:负载转矩(N·M)二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量D(cm)L(cm)由下式计算有中心轴的圆柱体的惯量。
如滚珠丝杆,齿轮等。
πγD4L (kg·cm·sec2)或πγ·L·D4(KG·M2)J K= 32*980 J K= 32式γ:密度(KG/CM3)铁:γ〧7.87*10-3KG/CM3=7.87*103KG/M3铝:γ〧2.70*10-3KG/CM3=2.70*103KG/M3 JK:惯量(KG·CM·SEC2)(KG·M2)D:圆柱体直径(CM)·(M)L:圆柱体长度(CM )·(M)2、运动体的惯量用下式计算诸如工作台、工件等部件的惯量W P BJ L1= 980 2π(KG·CM·SEC2)P B 2=W2π(KG·M2)式中:W:直线运动体的重量(KG)PB:以直线方向电机每转移动量(cm)或(m)3、有变速机构时折算到电机轴上的惯量1、Z2J JO电机Z1KG·CN:齿轮齿数2Z1JL1= Z2 *J0 (KG·CM·SEC2)(KG·M2)三、运转功率及加速功率计算在电机选用中,除惯量、转矩之外,另一个注意事项即是电机功率计算。
负载转矩计算公式

负载转矩计算公式
负载转矩计算公式是用于计算物体在旋转运动中所受到的力矩的数学公式。
力矩是描述物体旋转运动的力的产生和作用效果的物理量。
我们可以通过计算负载转矩来确定物体的平衡性和稳定性。
负载转矩计算公式的一般形式是:
负载转矩 = 负载力 ×转动半径
其中,负载力是施加在物体上的力,转动半径是绕某一轴旋转时负载力作用点离该轴的距离。
在实际应用中,负载转矩的计算可以根据具体情况进行修正和扩展。
例如,如果负载力不是指向轴的方向,我们需要将其分解为垂直和平行于轴的分量,并根据具体的力方向和转动半径的关系来进行计算。
此外,还需要考虑到物体的形状和负载力的分布情况,进一步修正负载转矩的计算公式。
需要注意的是,负载转矩的单位通常是牛顿·米(N·m)。
负载转矩的计算对于各种工程领域和物体的设计、运动分析等具有重要意义。
通过合理计算和评估负载转矩,我们可以确保物体在运动过程中的平衡性和稳定性,从而保证其安全运行。
总之,负载转矩计算公式是物体旋转运动中力矩的数学表示。
通过计算负载转矩,我们可以了解物体所受力矩的大小和方向,从而评估物体的平衡性和稳定性,确保其安全运行。
这对于工程设计和运动分析等领域具有重要的应用价值。
负载转矩的计算公式

负载转矩的计算公式负载转矩是指在机械系统中由于外部作用力引起的转动效应。
它是机械运动过程中非常重要的参数,对于机械设计和系统运行的安全性和可靠性具有至关重要的影响。
下面我们将介绍负载转矩的计算公式以及如何应用这些公式来进行工程设计和分析。
首先,我们来看负载转矩的定义。
负载转矩是指作用在旋转部件上的力矩,它与施加力的大小和施加力与旋转中心的距离有关。
当外部力矩作用于旋转部件时,将产生一个使旋转部件发生转动的力矩。
负载转矩的大小可以通过以下公式计算:转矩=施加力×施加力与旋转中心的距离这个公式表达了负载转矩与施加力和力臂(即施加力与旋转中心的距离)之间的关系。
施加力的大小和方向会直接决定转矩的大小和方向。
因此,在机械设计中,我们需要准确计算负载转矩,以确保机械系统的正常运行和结构的安全性。
在实际应用中,我们通常需要考虑多个外部力矩对机械系统的影响。
这些力矩可以来自于各种不同的元件,例如电机、齿轮、传动带等。
为了综合考虑这些力矩,我们可以使用以下公式计算总转矩:总转矩=负载转矩1+负载转矩2+...+负载转矩n通过将所有负载转矩相加,我们可以得到机械系统受到的总转矩。
这对于设计和分析机械系统的强度和承载能力非常有帮助。
另一方面,从机械系统中传递的转矩也会引起变形和应力。
这会影响到机械系统的稳定性和寿命。
因此,在设计机械系统时,我们还需要考虑转矩对结构的影响,并采取相应的措施来保证结构的安全性和可靠性。
除了负载转矩的计算,我们还需要了解负载转矩的测量方法。
常见的测量方法包括使用力矩传感器或测力仪等专业设备进行测量。
这些设备可以精确地测量外部力矩的大小和方向,并提供数据用于分析和验证设计的正确性。
总之,负载转矩是机械系统设计和分析中不可忽视的重要参数。
通过合理计算和测量负载转矩,我们可以更好地理解机械系统的工作原理和性能,并采取相应的措施来确保机械系统的安全性和可靠性。
通过不断学习和实践,我们可以不断提高对负载转矩的认识,为机械工程领域的发展和进步做出贡献。
电机负载转矩与负载惯量计算方法

电机负载转矩与负载惯量计算方法一、计算折合到电机上的负载转矩的方法如下:1、水平直线运动轴:9.8*μ·W·PBTL= 2π·R·η (N·M)式PB:滚珠丝杆螺距(m)μ:摩擦系数η:传动系数的效率1/R:减速比W:工作台及工件重量(KG)2、垂直直线运动轴:9.8*(W-WC)PBTL= 2π·R·η (N·M)式WC:配重块重量(KG)3、旋转轴运动:T1TL= R·η (N·M)式T1:负载转矩(N·M)二:负载惯量计算与负载转矩不同的是,只通过计算即可得到负载惯量的准确数值。
不管是直线运动还是旋转运动,对所有由电机驱动的运动部件的惯量分别计算,并按照规则相加即可得到负载惯量。
由以下基本公式就能得到几乎所有情况下的负载惯量。
1、柱体的惯量D(cm)L(cm)由下式计算有中心轴的援助体的惯量。
如滚珠丝杆,齿轮等。
πγD4L (kg·cm·sec2)或πγ·L·D4(KG·M2)JK= 32*980 JK= 32式γ:密度(KG/CM3)铁:γ〧7.87*10-3KG/CM3=7.87*103KG/M3铝:γ〧2.70*10-3KG/CM3=2.70*103KG/M3JK:惯量(KG·CM·SEC2)(KG·M2)D:圆柱体直径(CM)·(M)L:圆柱体长度(CM )·(M)2、运动体的惯量用下式计算诸如工作台、工件等部件的惯量W PB 2JL1= 980 2π (KG·CM·SEC2)PB 2=W 2π (KG·M2)式中:W:直线运动体的重量(KG)PB:以直线方向电机每转移动量(cm)或(m)3、有变速机构时折算到电机轴上的惯量1、电机Z2J JOZ1KG·CN:齿轮齿数Z1 2JL1= Z2 *J0 (KG·CM·SEC2)(KG·M2)。
负载转矩的计算公式

负载转矩的计算公式负载转矩是工程力学中的一个重要概念,用于描述物体或结构所受到的扭矩大小。
在工程设计和分析中,准确计算负载转矩是非常重要的。
本文将介绍负载转矩的计算公式及其应用。
负载转矩可以定义为物体或结构所受到的外部力矩和内部力矩之和。
外部力矩是由外部施加的力所产生的扭矩,而内部力矩则是物体或结构内部产生的扭矩。
负载转矩的计算需要考虑物体或结构的几何形状、材料特性以及施加在物体上的外部力。
在工程设计中,负载转矩的计算是非常常见的。
例如,在机械工程中,当设计齿轮、轴和传动装置时,需要计算负载转矩以确保它们的可靠性和安全性。
在土木工程中,当设计桥梁、建筑物和其他结构时,也需要考虑负载转矩以确定结构的强度和稳定性。
对于简单的情况,负载转矩的计算可以使用基本的力矩公式进行。
当物体或结构处于平衡状态时,负载转矩的总和为零。
根据力矩的定义,负载转矩可以用以下公式表示:负载转矩 = 外部力矩 + 内部力矩其中,外部力矩是施加在物体上的外部力所产生的扭矩,内部力矩是物体或结构内部产生的扭矩。
对于简单的力矩场合,外部力矩可以通过计算施加在物体上的力与力臂的乘积来获得。
力臂是力矩的杠杆臂长,是力矩垂直于力的作用线的距离。
当外部力矩是一个向量时,可以将其分解为水平和垂直方向上的分量,并分别计算它们的力矩。
然后将这些力矩进行矢量相加即可得到总的外部力矩。
而内部力矩则取决于物体或结构的几何形状和材料特性。
在实际工程中,内部力矩可以通过应力和截面积之间的关系来计算。
根据材料的弹性性质,应力可以通过外部力和物体或结构的截面积之间的关系来计算。
然后,通过将应力与截面积相乘,可以得到内部力矩。
需要注意的是,负载转矩的计算通常是一个复杂的过程,需要综合考虑多种因素。
例如,在考虑外部力矩时,需要考虑力的大小、方向和作用点的位置。
在考虑内部力矩时,需要考虑材料的弹性性质、几何形状和截面特性。
此外,还需要考虑到物体或结构的边界条件和约束条件。
三相电机设计常用公式

三相电机设计常用公式三相电机是一种常见的电动机类型,广泛应用于各个领域中。
在进行三相电机设计时,需要考虑多个参数和公式,以确保电机的性能和效率。
下面是三相电机设计常用的公式的整理。
1. 输入功率(Pinput)的计算公式:Pinput = √3 × V × I × cosφ其中,√3 是一个常数,V 是线电压(单位为伏特),I 是输入电流(单位为安培),cosφ 是功率因数。
2. 输出功率(Poutput)的计算公式:Poutput = Pinput × η其中,η是电机的效率(以百分比表示)。
3. 负载转矩(Tload)的计算公式:Tload = Poutput / ω其中,Poutput 是输出功率,ω 是电机的转速(单位为弧度/秒)。
4.转矩与电机转速的关系:Tload = Kt × (Nf - N)其中,Kt是电机的转矩常数,Nf是电机的额定转速,N是电机实际转速。
5. 额定转矩(Trated)的计算公式:Trated = Poutput / ωrated其中,ωrated 是电机的额定转速(单位为弧度/秒)。
6.转速与电源频率的关系:N=K×f/p其中,N是电机的转速,K是一个常数,f是电源的频率(单位为赫兹),p是电机的极数。
7.线电流与相电流的关系:Iline = Iphase / √3其中,Iline 是线电流,Iphase 是相电流。
8.电机效率(ηm)的计算公式:ηm = Pout / Pin其中,Pout 是输出功率,Pin 是输入功率。
9.电机滑差(S)的计算公式:S = (Nsync - N) / Nsync其中,Nsync 是同步速度,N 是电机实际转速。
10.频率(f)与电机转矩的关系:f = (PolePairs × N) / (120 × p)其中,PolePairs 是极对数目,N 是电机的转速,p 是电机的极数。
