二次函数的图象与性质(第3课时)最新版
九年级数学上册《二次函数的图象和性质3》课件
y 1 x2 2
列表:
y 1 x 22
2
y 1 x 22
2
x
-5
y 1 x2 . . .
2
y 1 x 22
2
4.
y 1 x 22 ·5·· 2
-4 -3 -2 -1 0 1 2 3 4 5
8 4.5 2 0.5 0 0.5 2 4.5 8 . . .
2 0.5 0 0.5 2 4.5
y = -3(x1)2
y=5(x+4)
2
向上 向下 向上 向下
y = -4(x-
直线x=-3 直线x=1 直线x=-4 直线x=3
顶点坐 标
( -3 , 0 )
(1,0)
( -4 , 0 )
( 3, 0)
3、抛物线的平移:
y 2x2 2.5
2.5
y 2(x 5)2 5 y 2x2 3 y 2(x 3)2
···
4.5 2 0.5 0 0.5 2 4.5
在同一坐标系中作出下列二次函数:
y 1 x 2 y 1 (x 2)2
2
2
观察三条抛物线的 y 1 x 22 相互关系,并分别指 2
y
1
6
(x
2)2
25
4
3
y 1 x2 2
出它们的开口方向,
2
对称轴及顶点.
1
y 1 x 22
2
-8
-6
-4
-2 B
2
4
6
y
1 2
(x
2)2
向左平移 2个单位
y 1 x2 2
向右平-1 移 2个单位
-2
y 1 (x 2)2 2
顶点(-2,0)
2 二次函数的图象与性质2.二次函数y=ax2+bx+c的图象与性质第3课时PPT课件(华师大版)

减”的平移规律,确定平移后的抛物线对应的函数关系式.
第3课时
二次函数y=a(x-h)2+k的图象与性质
目标三 理解二次函数y=a(x-h)2+k的性质
例 3 [高频考题]
已知函数 y=3 - +9.
(1)确定此函数图象的开口方向、对称轴和顶点坐标;
第3课时
二次函数y=a(x-h)2+k的图象与性质
知识点二 二次函数y=a(x-h)2+k的图象与性质
二次
a的
图象的开 图象的 图象的顶
函数值的
图象
函数
符号
最值
口方向
对称轴 点坐标
变化情况
当x>h时,y随x的
y=
a(x-
a>0
向上
直线
( h , 增大而 增大 ;
图象有最 低点,
当x=h时,y有最
x=h
2
称轴分别为 y 轴,直线 x=1,直线 x=1;顶点坐标分别为
(0,0),(1,0),(1,-2).
第3课时
二次函数y=a(x-h)2+k的图象与性质
【归纳总结】画二次函数 y=a(x-h)2+k 的图象的技巧:
(1)找到对称轴直线 x=h(即顶点的横坐标 h);
(2)列表时选取的 x 值中把 h 放在中间,比 h 小和比 h 大的数各取若干个
k
)
当x<h时,y随x的
h)2+k
增大而
增大
大值
k
第3课时
二次函数y=a(x-h)2+k的图象与性质
反思
二次函数图像和性质(第3课时)ppt课件

图象
1
画出二次函数 对称轴和顶点.
y1x12,y的图 象1 ,并x考 虑1 它2 们的开口方向、
2
2
x
··· -3 -2 -1
0
1
2
3
···
y 1x12 ··· -2
1
0
1
-2 -4.5 -8
···
2
2
2
y 1x12 ··· -8 -4.5 -2
1
2
2
(1)当a>0时, 开口向上,当a<0时,开口向下;
(2)对称轴是y轴;
(3)顶点是(0,k).
抛物线y=a(x-h)2有如下特点: (1)当a>0时, 开口向上,当a<0时,开口向上;
(2)对称轴是x=h;
(3)顶点是(h,0).
19
–2
–3
–4
y 1 x2 2
12345
x
12
二次函数y=a(x±h)2的图象和性质.
h>0
y=ax2
当向右平移h时 当向左平移h时
y=a(x-h)2 y=a(x+h)2
y=a(x+h)2的图象
a>0时,开口_____, 最 ____ 点向是上顶点;
低
a<0时,开口_____, 最 ____ 点是顶点;
的
开口向_________,对称轴是________________,顶点是_________________.
y 1x12
下
2
x=1
(1,0)
7
指出下列函数图象的开口方向,对称轴和顶点坐标. 开口 对称轴 顶点坐标
1y2x32
2.2 二次函数的图象与性质 第3课时 教案

一、情境导入二次函数y =ax 2+c (a ≠0)的图象可以由y =ax 2(a ≠0)的图象平移得到: 当c >0时,向上平移c 个单位长度; 当c <0时,向下平移-c 个单位长度.问题:函数y = (x -2)2的图象,能否也可以由函数y = x 2平移得到?本节课我们就一起讨论. 二、合作探究探究点:二次函数y =a (x -h )2的图象与性质 【类型一】 二次函数y =a (x -h )2的图象顶点为(-2,0),开口方向、形状与函数y =-12x 2的图象相同的抛物线的解析式为( )A .y =12(x -2)2B .y =12(x +2)2C .y =-12(x +2)2D .y =-12(x -2)2解析:因为抛物线的顶点在x 轴上,所以可设该抛物线的解析式为y =a (x -h )2(a ≠0),而二次函数y =a (x -h )2(a ≠0)与y =-12x 2的图象相同,所以a =-12,而抛物线的顶点为(-2,0),所以h =2,把a=-12,h =2代入y =a (x -h )2得y =-12(x +2)2.故选C.方法总结:决定抛物线形状的是二次项的系数,二次项系数相同的抛物线的形状完全相同. 变式训练:见《学练优》本课时练习“课堂达标训练” 第5题 【类型二】 二次函数y =a (x -h )2的性质若抛物线y =3(x +2)2的图象上的三个点,A (-32,y 1),B (-1,y 2),C (0,y 3),则y 1,y 2,y 3的大小关系为________________.解析:∵抛物线y =3(x +2)2的对称轴为x =-2,a =3>0,∴x <-2时,y 随x 的增大而减小;x >-2时,y 随x 的增大而增大.∵点A 的坐标为(-32,y 1),∴点A 在抛物线上的对称点A ′的坐标为(2,y 1).∵-1<0<2,∴y 2<y 3<y 1.故答案为y 2<y 3<y 1.方法总结:函数图象上点的坐标满足解析式,即点在抛物线上.解决本题可采用代入求值方法,也可以利用二次函数的增减性解决.变式训练:见《学练优》本课时练习“课后巩固提升” 第4题 【类型三】 二次函数y =a (x -h )2的图象与y =ax 2的图象的关系将二次函数y =-2x 2的图象平移后,可得到二次函数y =-2(x +1)2的图象,平移的方法是( )A .向上平移1个单位B .向下平移1个单位C .向左平移1个单位D .向右平移1个单位解析:抛物线y =-2x 2的顶点坐标是(0,0),抛物线y =-2(x +1)2的顶点坐标是(-1,0).则由二次函数y =-2x 2的图象向左平移1个单位即可得到二次函数y =-2(x +1)2的图象.故选C.方法总结:解决本题要熟练掌握二次函数的平移规律.变式训练:见《学练优》本课时练习“课堂达标训练”第6题 【类型四】 二次函数y =a (x -h )2与三角形的综合如图,已知抛物线y =(x -2)2的顶点为C ,直线y =2x +4与抛物线交于A 、B 两点,试求S △ABC .解析:根据抛物线的解析式,易求得点C 的坐标;联立两函数的解析式,可求得A 、B 的坐标.画出草图后,发现△ABC 的面积无法直接求出,因此可将其转换为其他规则图形的面积求解.解:抛物线y =(x -2)2的顶点C 的坐标为(2,0),联立两函数的解析式,得⎩⎪⎨⎪⎧y =2x +4,y =(x -2)2,解得⎩⎪⎨⎪⎧x 1=0,y 1=4,⎩⎪⎨⎪⎧x 2=6,y 2=16.所以点A 的坐标为(6,16),点B 的坐标为(0,4).如图,过A 作AD ⊥x 轴,垂足为D ,则S △ABC =S 梯形ABOD -S △ACD -S △BOC =12(OB +AD )·OD -12OC ·OB-12CD ·AD =12(4+16)×6-12×2×4-12×4×16=24. 方法总结:解决本题要明确以下两点:(1)函数图象交点坐标为两函数解析式组成的方程组的解;(2)不规则图形的面积通常转化为规则图形的面积的和差.变式训练:见《学练优》本课时练习“课后巩固提升”第10题 【类型五】 二次函数y =a (x -h )2的探究性问题某抛物线是由抛物线y =-2x 2向左平移2个单位得到. (1)求抛物线的解析式,并画出此抛物线的大致图象; (2)设抛物线的顶点为A ,与y 轴的交点为B . ①求线段AB 的长及直线AB 的解析式;②在此抛物线的对称轴上是否存在点C ,使△ABC 为等腰三角形?若存在,求出这样的点C 的坐标;若不存在,请说明理由.解析:(1)抛物线y =-2x 2向左平移2个单位所得的抛物线的解析式是y =-2(x +2)2;(2)①根据(1)得出的抛物线的解析式,即可得出其顶点A 和B 点的坐标,然后根据A ,B 两点的坐标即可求出直线AB 的解析式;②本题要分三种情况进行讨论解答.解:(1)y =-2(x +2)2,图略;(2)①根据(1)得出的抛物线的解析式y =-2(x +2)2,可得A 点的坐标为(-2,0),B 点的坐标为(0,-8).因此在Rt △ABO 中,根据勾股定理可得AB =217.设直线AB 的解析式为y =kx -8,已知直线AB 过A 点,则有0=-2k -8,k =-4,因此直线AB 的解析式为y =-4x -8;②本题要分三种情况进行讨论:当AB =AC 时,此时C 点的纵坐标的绝对值即为AB 的长,因此C 点的坐标为C 1(-2,217),C 2(-2,-217);当AB =BC 时,B 点位于AC 的垂直平分线上,所以C 点的纵坐标为B 点的纵坐标的2倍,因此C 点的坐标为C 3(-2,-16);当AC =BC 时,此时C 为AB 垂直平分线与抛物线对称轴的交点.过B 作BD 垂直于抛物线的对称轴于D ,那么在直角三角形BDC 中,BD =2(A 点横坐标的绝对值),CD =8-AC ,而BC =AC ,由此可根据勾股定理求出AC =174,因此这个C 点的坐标为C 4(-2,174). 综上所述,存在四个点,C 1(-2,217),C 2(-2,-217 ),C 3(-2,-16),C 4(-2,-174).方法总结:本题主要考查了二次函数图象的平移及等腰三角形的构成情况,主要涉及分类讨论、数形结合的数学思想方法的运用.变式训练:见《学练优》本课时练习“课后巩固提升”第10题 三、板书设计二次函数y =a (x -h )2的图象与性质。
1.2 第3课时 二次函数的图象与性质-2024-2025学年九年级数学下册课件(湘教版)
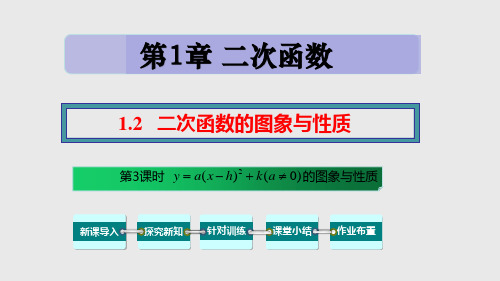
(h,k)
当x=h时,y最小值=k
当x<h时,y随x的 增大而减小;x>h 时,y随x的增大而 增大.
a<0
向下 直线x=h
(h,k)
当x=h时,y最大值=k 当x>h时,y随x的 增大而减小;x<h 时,y随x的增大而 增大.
练一练
1点.坐标抛是物_线(_0_,-y_6_)_,12它x可2 以 看6 作的是开由口抛__向物__上线__,对y 称 轴12 是x2___y向_轴____下__,平顶
横坐标
a a
纵坐标
1 a-12
2
1 a-12 3
2
观察上表你 发现了什么?
从上表看出: 对于每一个相同的x 值, 函数
y
1 2
(
x
1)2
3的值都要比函数
y
1 2
(
x
1)2
的值大3,
y
8
y
1 2
(
x
1)2
3
76Leabharlann 5 4y1 2
(x
1)2
3
2
1
-4
-3
-2
y
1 2
(
x
1)2
-1
O1
2
3
4
5
6x
向上平移3个单位
y
1 2
(
x
1)2
3
探究三、 将二次函数
y
1 2
(x
1)2
的图象向下平移 7 个单位,
得到的是哪个函数的图象?
y
1 2
(
x
1)2
7
探究四、二次函数 y a( x h)2 与 y a(x h)2 k
22.1.3 第3课时 二次函数y=a(x-h)2+k的图象和性质说课稿

22.1.3 第3课时二次函数y=a(x-h)2+k的图象和性质教学设计【典型例题】例1对二次函数y=-5(x+2)2-6的说法错误的是(C)A.开口向下B.最大值为-6C.顶点(2,-6) D.x<-2时,y随x的增大而增大例2如何平移二次函数y=4(x+3)2-7的图象,可得到二次函数y=4x2的图象?解:二次函数y=4(x+3)2-7的图象向右平移3个单位长度,向上平移7个单位长度即可得到二次函数y=4x2的图象.例3要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处离池中心3 m,如图所示,水管应多长?解:水管应长2.25 m.教师为学生理解问题、顺利解答问题,进行分层次设问:(1)分析该题的突破口是什么?(2)如何建立平面直角坐标系?(3)你能求出该抛物线的函数解析式吗?(4)根据解析式你能求出水管的长度吗?学生思考讨论,小组合作探究,教师进行点拨指导,进行板书过程. 【变式训练】1.抛物线y=a(x+k)2+k(k≠0),当k取不同的值时,抛物线的顶点恒在(B)A.直线y=x上B.直线y=-x上C.x轴上 D.y轴上2.对于抛物线y=-(x+2)2+3,下列结论中正确的有(A)【课堂检测】1.二次函数y =2(x -2)2-1的图象大致是(A)A B C D2.在平面直角坐标系中,对于二次函数y =(x -2)2+1,下列说法中错误的是(C) A.y 的最小值为1B.图象顶点坐标为(2,1),对称轴为直线x =2C.当x <2时,y 的值随x 值的增大而增大,当x ≥2时,y 的值随x 值的增大而减小D.当x <2时,y 的值随x 值的增大而减小,当x ≥2时,y 的值随x 值的增大而增大3.把二次函数y =a(x -h)2+k 的图象先向左平移2个单位长度,再向上平移4个单位长度后,得到二次函数y =12(x +1)2-1的图象.(1)试确定a ,h ,k 的值.(2)指出二次函数y =a(x -h)2+k 的图象的开口方向、对称轴和顶点坐标.解:(1)a =12,h =1,k =-5.(2)开口向上,对称轴为直线x =1,顶点坐标为(1,-5). 学生进行当堂检测,完成后,教师进行批阅、点评、讲解.。
2,2二次函数的图象与性质 第三课时-九年级数学下册课件(北师大版)

第3课时
复习回顾:
二次函数 y =ax ²的性质
函数y= ax 2
图象
开口 方向
a>0
向上
顶点坐标 对称轴
(0,0)
y 轴(直线 x=0)
a<0
向下
(0,0)
y 轴(直线 x=0)
续表:
函数y =ax 2
增减性
最值
a>0
当x>0时,y 随x 的增大而增大 当x=0时, 当x<0时,y 随x 的增大而减小 y最小值=0
总结
函数 y=ax 2+c (a≠0)与函数y=ax 2(a≠0)图象特征:
只有顶点坐标不同,其他都相同.
1 抛物线 y=ax 2+(a-2)的顶点在x 轴的下方,则a 的取 值范围是_a_<__2__且__a_≠__0_.
2 在平面直角坐标系中,下列函数的图象经过原点的是( D )
A.y= 1 x
数的表达式为y=x 2-1.
总结
平移的方向决定是加还是减,平移的距离决定加 或减的数值.
例4 抛物线 y=ax 2+c 与抛物线 y=-5x 2的形状相同,
开口方向一样,且顶点坐标为(0,3),则其所对应的
函数表达式是什么?它是由抛物线y=-5x 2怎样平移
得到的?
导引:由两抛物线的形状、开口方向相同,可确定a 的值; 再由顶点坐标为(0,3)可确定c 的值,从而可确定
<-1,∴y3<y2<y1.
总结
对于在抛物线的对称轴两侧的函数值的大小比较,运用 转化思想.先根据对称性将不在对称轴同侧的点转化为在对 称轴同侧的点,再运用二次函数的增减性比较大小.
1 对于二次函数 y=3x 2+2,下列说法错误的是( C )
数学人教版九年级上册22.1 二次函数的图象和性质(第3课时)PPT课件

2.类比探究二次函数 y = ax2 + k 的图象和性质
你能说出二次函数 y = ax2 + k (a<0)的图象特征 和性质吗?
2.类比探究二次函数 y = ax2 + k 的图象和性质
归纳: 一般地, 当 a<0 时, 抛物线 y = ax2 + k 的对称轴是 y 轴, 顶点是(0, k), 开口向下, 顶点是抛物线的最高点, a 越小, 抛物线的开口越小.当 x<0 时, y 随 x 的增大而 增大, 当 x>0 时, y 随 x 的增大而减小.
九年级 上册
22.1 二次函数的图象和性质 (第3课时)
课件说明
• 本课是在学生已经学习了二次函数 y = ax2 的基础上, 继续进行二次函数的学习, 这是对二次函数图象和性 质研究的延续.
课件说明
• 学习目标: 1.会用描点法画出二次函数 y = ax2+k 的图象; 2.通过图象了解二次函数的图象特征和性质.
学习重点: 观察图象, 得出图象特征和性质.
1.复习 y = ax2 的图象和性质
问题1 (1)二次函数 y = ax2 的图象是什么? (2)它具有怎样的图象特征和性质? (3)你是怎么研究的?
2.类比探究二次函数 y = ax2 + k 的图象和性质
问题2 类比 y = ax2 的研究内容和研究方法, 画出二次函数 y = 2x 2 + 1, y = 2x 2 - 1 的图象, 并探究它们的图象特征 和性质.
3.运用性质, 巩固练习
在同一直角坐标系中, 画出下列二次函数的图象:
(1)y 1 x2; (2) y 1 x2 2; (3) y 1 x2 .2
2
2
2
1.2 第3课时 二次函数y=a(x-h)2的图象与性质

第3课时 二次函数y =a (x -h )2的图象与性质1.会用描点法画出y =a (x -h )2的图象;2.掌握形如y =a (x -h )2的二次函数图象的性质,并会应用;(重点)3.理解二次函数y =a (x -h )2与y =ax 2之间的联系.(难点)一、情境导入涵洞是指在公路工程建设中,为了使公路顺利通过水渠不妨碍交通,修筑于路面以下的排水孔道(过水通道),通过这种结构可以让水从公路的下面流过.如图建立直角坐标系,你能得到函数图象解析式吗?二、合作探究探究点一:二次函数y =a (x -h )2的图象与性质【类型一】 y =a (x -h )2的顶点坐标已知抛物线y =a (x -h )2(a ≠0)的顶点坐标是(-2,0),且图象经过点(-4,2),求a ,h 的值.解:∵抛物线y =a (x -h )2(a ≠0)的顶点坐标为(-2,0),∴h =-2.又∵抛物线y =a (x +2)2经过点(-4,2),∴a (-4+2)2=2.∴a =12.方法总结:二次函数y =a (x -h )2的顶点坐标为(h ,0).变式训练:见《学练优》本课时练习“课堂达标训练”第2题【类型二】 二次函数y =a (x -h )2图象的形状顶点为(-2,0),开口方向、形状与函数y =-12x 2的图象相同的抛物线的解析式为( )A .y =12(x -2)2B .y =12(x +2)2C .y =-12(x +2)2D .y =-12(x -2)2解析:因为抛物线的顶点在x 轴上,所以可设该抛物线的解析式为y =a (x -h )2(a ≠0),而二次函数y =a (x -h )2(a ≠0)与y =-12x 2的图象相同,所以a =-12,而抛物线的顶点为(-2,0),所以h =-2,把a =-12,h =-2代入y =a (x -h )2得y =-12(x +2)2.故选C. 方法总结:决定抛物线形状的是二次项的系数,二次项系数相同的抛物线的形状完全相同.变式训练:见《学练优》本课时练习“课后巩固提升”第1题【类型三】 二次函数y =a (x -h )2的增减性及最值对于二次函数y =9(x -1)2,下列结论正确的是( )A .y 随x 的增大而增大B .当x >0时,y 随x 的增大而增大C .当x =-1时,y 有最小值0D .当x >1时,y 随x 的增大而增大 解析:因为a =9>0,所以抛物线开口向上,且h =1,顶点坐标为(1,0),所以当x >1时,y 随x 的增大而增大.故选D.变式训练:见《学练优》本课时练习“课堂达标训练”第3题探究点二:二次函数y =a (x -h )2图象的平移【类型一】 利用平移确定y =a (x -h )2的解析式抛物线y =ax 2向右平移3个单位后经过点(-1,4),求a 的值和平移后的函数关系式.解析:y =ax 2向右平移3个单位后的关系式可表示为y =a (x -3)2,把点(-1,4)的坐标代入即可求得a 的值.解:二次函数y =ax 2的图象向右平移3个单位后的二次函数关系式可表示为y =a (x -3)2,把x =-1,y =4代入,得4=a (-1-3)2,a =14,∴平移后二次函数关系式为y =14(x -3)2. 方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a 不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.变式训练:见《学练优》本课时练习“课堂达标训练”第6题【类型二】 确定y =a (x -h )2与y =ax 2的关系向左或向右平移函数y =-12x 2的图象,能使得到的新的图象过点(-9,-8)吗?若能,请求出平移的方向和距离;若不能,请说明理由.解:能,理由如下:设平移后的函数为y =-12(x -h )2,将x =-9,y =-8代入得-8=-12(-9-h )2,所以h =-5或h =-13,所以平移后的函数为y =-12(x +5)2或y=-12(x +13)2.即抛物线的顶点坐标为(-5,0)或(-13,0),所以应向左平移5或13个单位.变式训练:见《学练优》本课时练习“课后巩固提升”第6题探究点三:二次函数y =a (x -h )2与几何图形的综合把函数y =12x 2的图象向右平移4个单位后,其顶点为C ,并与直线y =x 分别相交于A 、B 两点(点A 在点B 的左边),求△ABC 的面积.解析:利用二次函数平移规律先确定平移后的抛物线解析式,确定C 点坐标,再解由所得到的二次函数解析式与y =x 组成的方程组,确定A 、B 两点坐标,最后求△ABC 的面积.解:平移后的函数为y =12(x -4)2,顶点C 的坐标为(4,0),OC =4.解方程组⎩⎪⎨⎪⎧y =12(x -4)2,y =x ,得⎩⎪⎨⎪⎧x =2,y =2,或⎩⎪⎨⎪⎧x =8,y =8. ∵点A 在点B 的左边,∴A (2,2),B (8,8),∴S △ABC =S △OBC -S △OAC =12×4×8-12×4×2=12.方法总结:两个函数交点的横、纵坐标与两个解析式组成的方程组的解是一致的.变式训练:见《学练优》本课时练习“课后巩固提升”第8题三、板书设计通过本节学习使学生认识到y =a (x -h )2的图象是由y =ax 2的图象左右平移得到的,初步认识到a ,h 对y =a (x -h )2位置的影响,a 的符号决定抛物线方向,|a |决定抛物线开口的大小,h 决定向左、向右平移,从中领会数形结合的数学思想.。
《二次函数的图象与性质(第3课时)》优秀课件

小结:
本节课主要运用了数形结合的思想方法,通过对
函数图象的讨论,分析归纳出 y a(x h)2 k
的性质:(1)a的符号决定抛物线的开口方向 (2)对称轴是直线x=h
(3)顶点坐标是(h,k)
抛物线
开口方向 对称轴 顶点坐标
y ax2 (a 0)
y ax 2 k(a 0) y a(x h)2 (a 0)
开口向上 开口向上 开口向上
直线X=0 直线X=0 直线X=h
(0,0) (0,k)
(h,0)
y a(x h)2 k(a 0) 开口向上 直线X=h (h,k)
2
直线x=-1
(- 1, 0)4,y2)(
1 4
,y3)为二次函数
y=(x-2)2图象上的三点,则y1 ,y2 ,y3的大小关系为
___y_3_<__y_2_<__y1____.
典例精析
例1 抛物线y=ax2向右平移3个单位后经过点(-1,4), 求a的值和平移后的函数关系式.
解:设平移后的函数关系式为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴
1 a=
4
∴平移后二次函数关系式为y= 1 (x-3)2.
4
小结
比较y=ax2 , y=ax²+k , y=a(x-h)²的图像的不同
y=ax2 y=ax²+k
对称轴 Y轴
Y轴
(直线x=0) (直线x=0)
2) 如何将抛物线y=2(x-1) 2+3经过平移得到 抛物线y=2x2
3) 将抛 物线y=2(x -1)2+3经过怎样的平移得 到抛物线y=2(x+2)2-1
4) 若抛物线y=2(x-1)2+3沿x轴方向平移后,经 过(3,5),求平移后的抛物线的解析式_______
人教版数学九年级上册 22.1.3《二次函数的图象和性质》第三课时(共17张PPT)

2 1个单位 2
-5 -4 -3 -2 -1-1 o 1 2 3 4 5 x
-2
-3 -4
y 1 (x 1)2 2
-5
-6
-7
y 1 (x 1)2 2
-8
-9 -10
y 1 x2
2
例如:
二次函数左右平移 的口决
左加右减
y
= 2(x+1)2向1个左单平位移 y
= 2x2
向右平移 1个单位
(2)对称轴是y轴;
(3)顶点是(0,k).
抛物线y=a(x-h)2有如下特点:
(1)当a>0时, 开口向上,当a<0时,开口向上;
(2)对称轴是x=h; (3)顶点是(h,0).
课堂小结
复习y=ax2
探索y=ax2+c
的图象及性质
图象的画法
描点法 平移法
平移关系
图象的特征
开口方向
a>0,开口向上 a<0,开口向下对称轴
y=
2(x-1)2
y = ax2 y = ax2
当向右平移h个单位时 y = a(x-h)2 h>0 当向左平移h个单位时y = a(x+h)2 h>0
y = a(x-h)2 对称轴 是直线 x=h , 顶点坐标 (h ,0) h>0 y = a(x+h)2 对称轴 是直线 x=-h , 顶点 坐标(-h,0) h>0
2、抛物线y=4(x-3)2的开口方向 向上 , 对称轴是 直线x=3,顶点坐标 是 (3,0) ,抛物线是最 低 点, 当x= 3 时,y有最 小 值,其值为 0 。 抛物线与x轴交点坐标 (3,0) ,与y轴交 点坐标 (0,36)。
22.1.3 第3课时 二次函数y=a(x-h)2+k的图象和性质

坐标及增减性等;
2.掌握二次函数 y=a(x-h)2+k 的图象的平移规律. 课堂导入
一个运动员打高尔夫球,如果球的飞行高度 y(m)与水平距离 x(m)之间的函数
解析式为 y=-510(x-25)2+12,那么高尔夫球飞行过程中的最大高度是多少?
课件目录
首页
末页
第3课时 二次函数y=a(x-h)2+k的图象和性质
首页
末页
第3课时 二次函数y=a(x-h)2+k的图象和性质
(3)当 y=1.5 时,1.5=-34(x-1)2+3, 解得 x1=1+ 2,x2=1- 2, 故当 0<m<1+ 2时,才不会淋湿衣裳.
课件目录
首页
末页
第3课时 二次函数y=a(x-h)2+k的图象和性质
8.[2018·湘潭]如图 22-1-16,点 P 为抛物线 y=14x2 上的一动点.
后的铅球沿一段抛物线轨迹运行,当运行到最高 3 m 时,水平距离为 4 m.
(1)求这个二次函数的解析式. (2)该同学把铅球推出去多远? 图 22-1-14
课件目录
首页
末页
第3课时 二次函数y=a(x-h)2+k的图象和性质
解:(1)设二次函数的解析式为 y=a(x-4)2+3, 把(0,0.6)代入,得 0.6=a(0-4)2+3,a=-230, ∴y=-230(x-4)2+3. (2)当 y=0 时,0=-230(x-4)2+3, 解得 x1=4+2 5,x2=4-2 5(舍去). 答:该同学把铅球推出去(4+2 5) m.
2.[2017·金华]对于二次函数 y=-(x-1)2+2 的图象与性质,下列说法正确的 是( B )
A.对称轴是直线 x=1,最小值是 2 B.对称轴是直线 x=1,最大值是 2 C.对称轴是直线 x=-1,最小值是 2 D.对称轴是直线 x=-1,最大值是 2
二次函数的图像和性质 第三课时-九年级数学下册课件(冀教版)

解:(1)在 y=(x+2)2中,令y=0,得x=-2;令x=0,得y =4. ∴点A,点B 的坐标分别为(-2,0),(0,4).
(2)∵点A,点B 的坐标分别为(-2,0),(0,4), ∴OA=2,OB=4.
∴S△AOB=
1 2
OA·OB= 1 ×2×4=4.
2
(3)抛物线的对称轴为x=-2.
y
2
1(x 2
1)2 与 y
1 ( x 1)2 2
的图像的形状和位置有什么关系?
2
形状相同,位置不同.
1 抛物线 y=-5(x-2)2的顶点坐标是( B )
A.(-2,0)
B.(2,0)
C.(0,-2)
D.(0,2)
2 在下列二次函数中,其图象的对称轴为直线x=-2的是( A )
A.y=(x+2)2
易错点:函数y=ax 2+c 与y=a (x-h)2的图象与性质
区别不清
二次函数 y=3x 2+1的图象开口向上,对称轴是 y 轴,顶 点坐标是(0,1),当x >0时,y 随x 的增大而增大;二次 函数y=3(x-1)2的图象开口向上,对称轴是直线x=1,顶 点坐标是(1,0),当x >1时,y 随x 的增大而增大;二次 函数 y=3x 2+1和y=3(x-1)2的图象的开口大小一样.因
x_>__5时,y 随x 的增大而减小.
导引:
y =-1 (x-5)2的图象与抛物线y =-1 x 2的形状相
4
同,但位置不同,y
=-1
4
(x-5)2的图象由抛物线
y
=-1
x
4 2向右平移5个单位得到.
4
1 把抛物线 y =x 2平移得到抛物线 y =(x+2)2,则这
人教版九年级数学上册《二次函数的图象和性质(第3课时)》示范教学课件

向上
观看动图,思考抛物线 y=ax²+k(a>0)与抛物线 y=ax²(a>0)有什么关系?
归纳
开口方向
顶点坐标
最大(小)值
对称轴
增减性
二次函数 y=ax2+k(a>0)的图象性质
向上
(0,k)
当 x=0 时,y最小值=k
y 轴
当 x>0 时,பைடு நூலகம் 随 x 的增大而增大;当 x<0 时,y 随 x 的增大而减小
4
-4
x
y
x
y
O
y=-2x2-1
y=-2x2+1
2
-2
-4
-6
-8
-10
-2
2
4
-4
思考
(1)抛物线 y=-2x²+1,y=-2x²-1 的开口方向、对称轴和顶点各是什么?
函数
y=-2x²+1
y=-2x²-1
开口方向
对称轴
顶点坐标
向下
y 轴
x
y
y=-2x2+1
O
y=-2x2-1
2
-2
-4
-6
例2 在同一直角坐标系中,画出二次函数 y=-2x²+1, y=-2x²-1 的图象.
解:先列表,然后描点,再分别画出它们的图象.
x
···
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
···
y=-2x2+1
y=-2x2-1
O
2
-2
-4
-6
-8
-10
-2
2
4
-4
2
-2
-4
-6
最新人教版九年级数学上册《22.1.3(第3课时)》优质教学课件

22.1 二次函数的图象和性质
22.1.3 二次函数y=a(x-h)2+k的图象和性质 第3课时
导入新知
说出平移方式,并指出其顶点与对称轴.
y=ax2
k>0 上移 y=ax2+k
k<0 下移
顶点
对称轴
在y轴上(0,k) y轴
y=ax2
左加 右减
y=a(x-h)2
顶点 对称轴 在x轴上(h,0) x=h
2
探究新知 二次函数y=a(x-h)2+k的几种图象:
这些图象与抛 物线y=ax2有什 么关系?
? 平移关系
y=ax2
y=a(x-h)2+k
探究新知
方法点拨
一般地,抛物线y=a(x-h) ²+k与y=ax²形状相同,位 置不同.把抛物线y=ax²向上(下)向右(左)平移,可以得到 抛物线y=a(x-h) ²+k.平移的方向、距离要根据h、k的 值来决定.
链接中考
1.抛物线y=3(x﹣1)2+1的顶点坐标是( A )
A.(1,1)
B.(﹣1,1)
C.(﹣1,﹣1)
D.(1,﹣1)
2.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下
平移2个单位长度,所得到的抛物线为( A )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3
解:由函数顶点坐标是(1,-2), 设二次函数的关系式为y=a(x-1)2-2. 因为图象过点(0,0),则0=a(0-1)2-2, 解得a=2. 所以这个二次函数的关系式为y=2(x-1)2-2.
课堂检测
22.1.4二次函数y=ax2+bx+c的图象和性质(第三课时)

解得k≤1,
即k的取值范围是k≤1
(3)解:设方程的两个根分别是x1,x2,
根据题意,得(x1 -3)(x2 -3)< 0, 即 x1 x2 -3(x1 + x2 )+9 < 0, ∵ x1 + x2 = 5-k, x1 x2 =1-k ∴ 1-k-3(5-k)+9<0 解得k< ,
则k的最大整数值为2.
16.(2017•荆州调考)已知关于x的方程 (m-1)x2+(m-2)x-1=0. (1)求证:无论m为何实数,方程总有实数根; (2)m为何整数时,方程有两个不相等的整数根; (3)m 取不同的实数(m ≠1),就对应不同的抛物线 y=(m-1)x2+(m-2)x-1,请证明当m(m ≠1) 变化时,所有这些不同的抛物线 y=(m-1)x2+(m-2)x-1有公共点,并求出它们 的公共点. (1)证明:当m=1时,方程为-x-1=0有唯一实数根x=1 当m ≠1时 △=(m﹣2)2+4(m﹣2) =m2 ≥0 ∴无论m为何实数,方程总有实数根.
y
O A x
y O B
y
y x O x
-1 0
x
x
O
C
D
7. 小明从左边的二次函数y=ax2+bx+c的图象观察得出 下面的五条信息:① a<0;② c=0;③ 函数的最小 值为-3; ④当x<0时,y>0; ⑤当0<x1<x2<2时, y1>y2 你认为其中正确的个数有( C ) A.2 B .3 C.4 D.5 y y
看作是抛物线y=-
x2+bx+c的一部分,其中出球点B离地面O
点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物 线的解析式是 ( B ) A. C. B. D.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
它的顶点坐标是 (d,0).当a0 抛物线的开口向上;当 a 0
由于我们已经知道了函数 ya(xd)2的图象的性质,因此今后在画
y a(xd)2的图象,只要先画出对称轴以及图象在对称轴右边的部分,
然后利用对称性,画出左边的部分,在画图象的右边部分时,只需要“列 表,描点,连线”三个步骤就可以了.
顶点坐标(5,0)
(2)y3(x2)2 对称轴 x=-2
顶点坐标(-2,0)
现代人每天生活在纷繁、复杂的社会当中,紧张、高速的节奏让人难得有休闲和放松的时光。人们在奋斗事业的搏斗中深感身心的疲惫。然而,如果你细心观察,你会发现作 为现代人,其实人们每天都在尽可能的放松自己,调整生活节奏,追求充实快乐的人生。看似纷繁的社会里,人们的生活方式其实也不复杂。大家在忙忙碌碌中体味着平凡的 人生乐趣。由此我悟出一个道理,那就是----生活简单就是幸福。生活简单就是幸福。一首优美的音乐、一支喜爱的歌曲,会让你心境开朗。你可以静静地欣赏你喜爱的音乐, 可以在流荡的旋律中回忆些什么,或者什么都不去想;你可以一个人在房间里大声的放着摇滚,也可以在网上用耳麦与远方的朋友静静地共享;你还可以一边放送着音乐,一 边做着家务....生活简单就是幸福。一杯清茶,或一杯咖啡,放在你的桌边,你的心情格外的怡然。你可以浏览当天的报纸,了解最新的国内外动态,哪怕是街头趣闻;或者捧 一本自己喜欢的杂志、小说,从字里行间获得那种特别的轻松和愉悦....生活简单就是幸福。经过精心的烹制,一桌可心的菜肴就在你的面前,你招呼家人快来品尝,再备上最 喜欢的美酒,这是多么难得的享受!生活简单就是幸福。春暖花开的季节,或是清风送爽的金秋,你和家人一起,或是朋友结伴,走出户外,来一次假日的郊游,享受大自然 带给你的美丽、芬芳。吸一口新鲜的空气,忘却都市的喧嚣,身心仿佛受到一番洗涤,这是一种什么样的轻松感受!生活简单就是幸福。你参加朋友们的一次聚会,那久违的 感觉带给你温馨和激动,在觥酬交错之间你享受与回味真挚的友情。朋友,是那样的弥足珍贵....生活简单就是幸福。周末的夜晚,一家老小围坐在电视机旁,尽享团圆的欢乐 现代人越来越会生活,越来越会用各种不同的方式来放松自己。垂钓、上网、打牌、玩球、唱卡拉OK、下棋.....不一而足。人们根据自己的兴趣爱好寻找放松身心的最佳方式, 在相对固定的社交圈子里怡然的生活,而且不断的扩大交往的圈子,结交新的朋友有时,你会为新添置的一套漂亮时装而快乐无比;有时,你会为孩子的一次小考成绩优异而 倍感欣慰;有时,你会为刚参加的一项比赛拿了名次而喜不自胜;有时,你会为完成了上司交给的一个任务而信心大增生活简单就是幸福!生活简单就是幸福,不意味着我们 放弃了对目标的追逐,是在忙碌中的停歇,是身心的恢复和调整,是下一步冲刺的前奏,是以饱满的精力和旺盛的热情去投入新的“战斗”的一个“驿站”;生活简单就是幸 福,不意味着我们放弃了对生活的热爱,是于点点滴滴中去积累人生,在平平淡淡中寻求充实和快乐。放下沉重的负累,敞开明丽的心扉,去过好你的每一天。生活简单就是 幸福!我的心徜徉于春风又绿的江南岸,纯粹,清透,雀跃,欣喜。原来,真正的愉悦感莫过于触摸到一颗不染的初心。人到中年,初心依然,纯真依然,情怀依然,幸甚至 哉。生而为人,芳华刹那,真的不必太多要求,一盏茶,一本书,一颗笃静的心,三两心灵知己,兴趣爱好一二,足矣。亦舒说:“什么叫做理想生活?不用吃得太好穿得太 好住得太好,但必需自由自在,不感到任何压力,不做工作的奴隶,不受名利的支配,有志同道合的伴侣,活泼可爱的孩子,丰衣足食,已经算是理想。”时间如此猝不及防, 生命如此仓促,忠于自己的内心才是真正的勇敢,以不张扬的姿态,将自己活成一道独一无二的风景,才是最大的成功。试问,你有多久没有靠在门槛上看月亮了,你有多久 没有在家门口的那棵大树下乘凉了,你有多久没有因为一个人一件事而心生感动了,你又有多久没有审视自己的内心了?与命运的较量中,我们被迫前行,却忘记了来时的方
原象
象
抛物线E:
y 1 x2 2
图形F也是抛物线
E的顶点O(0,0) 点O'(-1,0)是F的顶点
E有对称轴l(与y轴重
合)
直线l`(过点O'与y轴平行)是F的对称轴
E开口向上
F也开口向上
抛物线F是哪个函数的图象呢?
在抛物线 y 1 x 2
2
上任取一点
p(a, 1 2
a2)
,它在向
左平移1个单位后,P的象点Q的坐标是什么?
这样我们证明了:函数 y 1 ( x 1)2 的图象是抛物线F它的 2
顶点是O'(-1,0),它的对称轴是过点O'(-1,0)且平行与y轴 的直线l ' ,直线l'是有横坐标为-1的所有点组成的,我们把直线l '记 做直线x =-1,抛物线 y 1 (x 1)2 的开口向上.
2
类似地,我们可以证明下述结论:
义务教育课程标准实验教科书 SHUXUE 九年级下
第2章 二 次2函.2数二次函数的图象与 性质(第3课时)
湖南教育出版社
抽
象把二次函数
y 1 x2 2
的图象E向左平移1个单位,得到图形F,如图.
y
5 4 3 2 1
FE
-3 -2 -1O' o 1 2 3 4 x
由于平移不改变图形的形状和大小,因此在向左平移1个单位后;
把点P的横坐标A减去1,纵坐标 1 a 2
不变,即象点Q的坐标为
(a
1,
1
2
a2
)
2
证 明: 记 ba1,则 ab1从而点Q的坐标为 (b, 1 (b 1)2 )
2
这表明:点Q在函数 y 1 ( x 1)2 的图象上,由此得出,
抛物线F是函数
y
1
2
(x
1) 2
的图象,
2
y
8
6
4
这样我们得到了函数 y (x2)2
的图象 .
2
-4 -3 -2 -1
o
1 2 3 4x
练习
1.画二次函数 y (x1)2 的图象x1 1.5 2 3 3.5
y (x1)2 0 -0.25 -1 -4 -6.25
y
O
-4 -2
2
4
x
-2
-4
2.说出下列二次函数的图象的对称轴和顶点坐标; (1)y 1 (x 5)2 3 对称轴 x=5
例 画函数 y (x2)2 的图象. 3解 抛物线 y (x2)2 的对称轴是 x=2,顶点坐标是(2,0)
列表:自变量x从顶点的横坐标2开始取值.
x
2 2.5 3 4 5
y (x2)2 0 0.25 1 4 9
描点和连线:画出图象在对称轴右边的部分.
利用对称性画出图象在对称轴左边的部分:
