用混合遗传算法解决单机调度问题c语言程序
基于混合遗传算法的作业车间调度问题的研究与仿真

种 基 于遗 传 和 模 拟 退 火 的 混合 算 法 , 算 法将 模 拟 退 火 算 法 赋 予 搜 索 过 程 时 变性 融 入 其 中 , 有 明 显 的 概 率 跳 跃 性 , 选 该 具 并 取 了典 型 问题 进 行 分析 和 仿 真 研 究 。仿 真 结 果 表 明 , 与传 统 的遗 传 算 法 相 比 该 方 法是 行 之 有 效 的。 关 键 词 : 业 车 间调 度 , 传 算 法 , 拟 退 火 算 法 作 遗 模
ห้องสมุดไป่ตู้
s o h loi m t re rb bl -u . a whl,y a ay ig tpc lpo lmste ag rh s su i ho g h w te ag rh wi a mak d p o a iy jmpMe n i b n lzn y ia rbe , lo i m i tde tru h t h i t e h t d
的 NP问题 _。 目前 , 究 作 业 车 间调 度 问题 的方 法 主 要 有 启 发 1 ] 研
r x = n ax m≤ ax cr i ) mim T
, , ≤ 《
L , n 《 J
() 1
S t设 备 h先 于 设 备 k加 工工 件 i ・: :
c 一 ≥c , , ・ 几 k , 。 m m 『 2,・ ,=72,・ =7 ’ () 2
《 工业 控 制 计 算 机 } o 第 2 2l 2年 5卷 第 1 O期
7 1
基于混合遗传算法的作业车间调度问题的研究与仿真
J b- h p c e u ig r lm s d on Hy r Ge e i Alo i m o s o S h d l P obe Ba e b i n d n t g rh c t
基于遗传算法的混合Flow—shop调度方法

J l 2 0 uy 0 2
基于遗传算 法 的混合 Fo .h p调度 方法 lw so
王 万 良 姚 明海 吴 云 高 , , ,吴 启迪
( 浙江 工 业大 学 信息 工 程学 院,杭州 30 1; 同济 大学 电子 与信 息 工程 学 院,上 海 2 0 9 ) 10 4 0 02
Th s p r t r a a i e p t e f a i i t f o u i n Th y c lo s t f eso h si e n fg n t l o i m e e o e a o sc n e s l k e h e b ly o l t , e a a s a i yt t c a tcd ma d o e e i a g r h y s i s o n s h c t b tef F n l , n e a l f r d c i n s h d l g p o lm rme a wo k n r s o n a c r n i e p a t sg v n y i l. i a l a x mp e o o u t c e u i r b e f t l r i g wo k h p i a g n ln ie , s y p o n o e i
Matlab/Visual C++混合编程求解单件车间调度问题

m e n ta r
y
,
o
f
the
he d u lin g
the
y , bu t
tc
ha
c
gre
a
in f l
.
m o
r
de
r n
iz
a
g
e m e n s c
t in
e n
te
p is
it h
a n c o m v e
in g le
it e
tin
m
v a r
ie ty
p
r o
du d
c
ts
o n
,
,
则 约束条件为 :
,
工
任 务 所 需 的 各 种 约 束 ( 加 工 次 序 所 需 机 器 ) 使所 有 的
、
,
( 1 ) 每 个 工 件 的 各 道 工 序 的 加 工 顺 序 预 先 确 定 且 保持 有
任 务 能尽 量 如期 完 成 就 成 为 十 分 现 实 和 迫 切 的 问 题 这
, ,
s m a e
ll ba
n c
h p r o du
n c
t io
to
u
m o
s o
de
e
T his p a p e
p
r e s e n
ts
a n n
im p r
the the
e
d
he du lin g
s w e r e
lg o r it hm
o
d
dj u
e
s
g
a
lg o r ith m
用混合遗传算法解决单机调度问题c语言程序

用混合遗传算法解决单机调度问题c语言程序#include#include#include#include#include#include "ceshi.h"void main(){s_individual *temp=NULL;long run_start,run_finish,run_sum=0;float run_avg=0;int sum_k=0;srand((unsigned)time(NULL));/*将当前时间设置成随机函数的种子,所以每次产生的数都不一样*///printf("%d\n",time(NULL));//srand((unsigned)1398759277);if((outfp = fopen("newfile1","w")) == NULL){fprintf(stderr,"Cannot open output file %s\n","file1");exit(-1);}init_parameter();//初始化工件参数print_parameter();//打印工件参数for(run=1; run<=maxruns; run++){run_start=clock();initialize();//初始化包括初始参数设置initmalloc();//分配全局空间gererate_pop();//产生初始种群statistics(oldpop);//统计种群数据,得到最优个体init_temperature=(min-max)/log(preceive); temperature_k=init_temperature;while(k{generation();//交叉select_better(oldpop,newpop);//保留最佳个体newpop popsize_copy(oldpop,newpop);gen_mu(newpop);//变异保留最佳个体select_better(oldpop,newpop);popsize_copy(oldpop,newpop);CSA(newpop);//模拟退火操作定步长抽样select_better(oldpop,newpop);statistics(newpop);run_finish=clock();if (last_fitness==bestfit.fitness){last_maxgen++;}else{last_maxgen=0;last_runtime=run_finish;}last_fitness=bestfit.fitness;k++;//退温temperature_k=temperature_k*ptemper;temp=oldpop;oldpop=newpop;newpop=temp;}sum_k=sum_k+k;run_time=last_runtime-run_start;run_sum=run_sum+run_time;print_popsize();ceshi_popstatic();freeall();}run_avg=(float)run_sum/float(maxruns);fprintf(outfp,"\nmax=%d min=%d avg=%d run_sum=%f avg_k=%d\n",pop_max,pop_min,pop_sum/maxruns,run_avg,su m_k);fclose(outfp);}。
遗传算法优化调度问题研究

遗传算法优化调度问题研究随着现代生产和工程技术的不断发展,人们对于生产和物流方面的效率要求也越来越高。
然而,如何更好地调度设备和人力资源以及如何优化配送方案等问题,一直是企业所面临的难题。
近年来,遗传算法被广泛运用于各个领域的优化问题中,并取得了良好的效果。
本文将从遗传算法在调度问题中的应用入手,探讨其原理和优点,同时介绍一些相关优化调度算法的研究。
一、遗传算法遗传算法是一种启发式算法,其基本思想源自生物的进化和遗传原理。
遗传算法通过模拟自然界中生物进化的过程来寻找最优解,也就是通过代际交换来进行优化搜索。
遗传算法的主要操作包括:选择、交叉和变异。
首先,从群体中选择一定数量的个体进行交叉和变异,生成新的个体。
然后计算新个体的适应度,根据适应度进行选择,保留适应度高的个体,淘汰适应度低的个体。
不断重复这个过程,直到满足停止准则。
遗传算法解决问题的关键在于如何度量个体的适应度,也就是如何对问题进行建模。
在调度问题中,我们可以以每个方案的成本、时间和效率等指标为衡量标准,这就是优化调度问题中所使用的适应度函数。
二、基于遗传算法的调度优化方法1. 遗传算法调度优化模型基于遗传算法的调度优化模型需要考虑两个因素:资源调度和任务分配。
资源调度包括车辆、机器、人员等资源的分配;任务分配则需要根据任务的紧急程度、持续时间等信息进行优化,以满足最终目标,使资源得到最大的利用。
2. 基于遗传算法的车辆调度问题基于遗传算法的车辆调度问题是指为满足顾客的要求,在最短时间内对配送车辆进行优化分配。
在解决这类问题时,遗传算法可以将车辆的速度、容量和行驶路线等因素整合起来,以得到最优的配送方案。
3. 基于遗传算法的生产调度问题基于遗传算法的生产调度问题是指为了最大化设备利用率和生产优化,对生产计划进行优化调度。
通过分析每个设备的运行时间和生产能力,遗传算法可以将不同任务之间的先后顺序进行优化匹配,以达到更高效的生产目标。
4. 基于遗传算法的作业车间调度问题基于遗传算法的作业车间调度问题是指如何最大化设备利用率,通过合理的装配和分散装配工序来完成任务目标。
(完整版)遗传算法c语言代码

}
}
}
//拷贝种群
for(i=0;i<num;i++)
{
grouptemp[i].adapt=group[i].adapt;
grouptemp[i].p=group[i].p;
for(j=0;j<cities;j++)
grouptemp[i].city[j]=group[i].city[j];
{
group[i].p=1-(double)group[i].adapt/(double)biggestsum;
biggestp+=group[i].p;
}
for(i=0;i<num;i++)
group[i].p=group[i].p/biggestp;
//求最佳路劲
bestsolution=0;
for(i=0;i<num;i++)
printf("\n******************是否想再一次计算(y or n)***********************\n");
fflush(stdin);
scanf("%c",&choice);
}while(choice=='y');
return 0;
}
遗传算法代码
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define cities 10 //城市的个数
改进遗传算法求解混合流水装配作业调度问题

p r o b l e m. T he r e s u l t s o f i t s c o mp a r s i o n wi t h o t h e r me t h o d s s h o w t h a t t h e g e n e t i c a l g o i r t h ms wi t h e l i t i s t s t r a t e g y a n d g r e e d y d e c o d e
0 引言
在汽车 、 液 晶面板等产品装 配生产过程 中, 其生产线通 常是混合流水式生产,特 点是多 品种 ,小批量,产 品类型和 尺寸 不断变换 。在这 一类混合流 水装配生产线 的运 作过程 中 ,最 关键 的 问 题 是 装 配 生 产 线 的平 衡 问题 以及 相 关 的 作业 调度 问题 。本 文只研究混合流 水装配生产线 的调度 问
Mi c r o c o mp u t e r Ap p l i c a t i o n s V o 1 . 2 9 , N o . 9 , 2 0 1 3
文章编号:1 0 0 7 - 7 5 7 X( 2 0 1 3 ) 9 — 0 0 5 8 — 0 4
技 术交 流
微 型 电脑应 用
关键 词:装配作 业调 度;液 晶面板 ;遗传 算法 ;精 英保 留 中图分类号:T H1 6 ,T P 3 1 2 文献标志码 :A
遗传算法在任务调度中的解决方案

遗传算法在任务调度中的解决方案在现代社会中,任务调度是一项非常重要的工作,它涉及到资源的分配和时间的合理安排。
然而,由于任务的多样性和复杂性,传统的调度方法往往无法满足需求。
这时候,遗传算法作为一种智能优化方法,可以提供一种有效的解决方案。
遗传算法是一种模拟自然进化过程的优化算法。
它通过模拟进化的过程,利用选择、交叉和变异等操作,逐步优化解空间中的解。
在任务调度中,遗传算法可以被用来解决资源分配和时间安排的问题。
首先,遗传算法可以用来解决资源分配的问题。
在一个任务调度系统中,有多个任务需要被分配给不同的资源进行处理。
而资源的数量和性能各不相同,因此如何将任务合理地分配给资源是一个复杂的问题。
遗传算法可以通过优化目标函数,找到最佳的资源分配方案。
它可以根据任务的属性和资源的性能,通过选择和交叉操作,逐步优化解空间中的解,找到最佳的资源分配方案。
其次,遗传算法可以用来解决时间安排的问题。
在任务调度中,任务的执行时间是一个关键因素。
不同的任务可能有不同的执行时间要求,而资源的可用时间也是有限的。
因此,如何合理地安排任务的执行时间是一个重要的问题。
遗传算法可以通过优化目标函数,找到最佳的时间安排方案。
它可以根据任务的执行时间要求和资源的可用时间,通过选择和变异操作,逐步优化解空间中的解,找到最佳的时间安排方案。
此外,遗传算法还可以用来解决任务调度中的多目标优化问题。
在实际应用中,任务调度往往涉及到多个目标的优化,例如最小化任务的执行时间和最大化资源利用率等。
传统的优化方法往往只能解决单目标优化问题,而遗传算法可以通过适应度函数的设计,同时考虑多个目标,找到最优的综合解。
总之,遗传算法作为一种智能优化方法,可以提供一种有效的解决方案来解决任务调度中的问题。
它可以通过模拟自然进化的过程,利用选择、交叉和变异等操作,逐步优化解空间中的解,找到最佳的资源分配和时间安排方案。
此外,遗传算法还可以解决多目标优化问题,提供综合的解决方案。
车间调度问题的一种基于遗传算法的混合调度算法
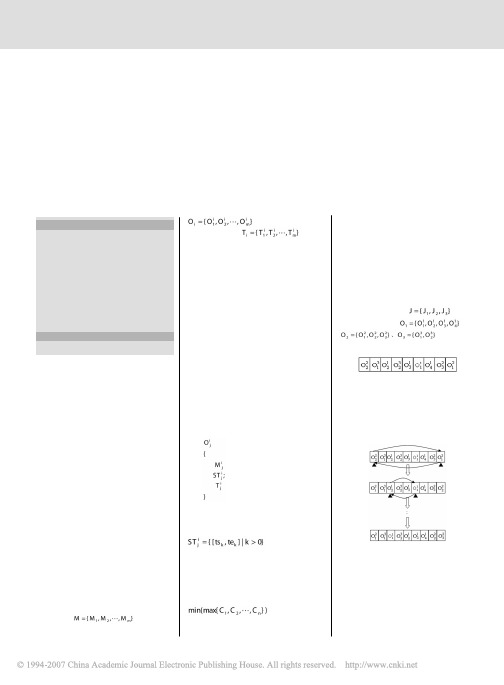
针对一个6台机器 6个工件的基准车间 调度问题 FT06[3]运行本文提出的算法,获 得了较优的调度结果,目标值为 53,优于
图 3 工件操作序列图
图 2 交叉过程示意图
该问题提出者获得的目标值 55。所有工件 的操作加工时间如图 3 所示。(FT06 作,
因此这两个基因位交换基因值。依次进行,
最后即可得到一合理操作顺序,即合理个
体。基因调整过程如图 1 所示。
图1 基因调整过程示意图 3.2 适应度函数 适应度函数就采用目标函数。 3.3 选择算子 选择是遗传算法实现优胜劣汰的关键 过程,为了保证当前种群中的最优解被选 择,同时不失种群的多样性,本文采取最 佳个体保存法和适应度比例法两种方法结合
3.4 交叉算子 采用 Watanabe[6]提出的一种交叉算子, 类似于双点交叉。如果直接采用双点交叉, 存在一个问题就是:交叉后的新个体中某个 或某些工件可能存在两个相同的操作。而 Watanabe 提出的交叉算子巧妙的避免了这 一点,其操作过程为: Step 1、按照交叉概率从种群中选择两 个个体,称为父个体;然后产生两个新的空 个体,即任何基因位上还不存在基因值的个 体,称为子个体。 Step 2、随机在两个父个体中确定两个 交叉点,两个交叉点外的基因值直接取出置 于两个子个体对应的基因位中。 Step 3、对于两个父个体中两个交叉点 中间的基因值操作如下: Step3.1、在每个父个体中,确定出与另 一个父个体不相同的基因值,并取出置于一 旁,此时该基因值对应的基因位上为空; Step3.2、将两个父个体中的基因值互相 替换后,分别置于相应子个体中; Step3.3、再将置于一旁的基因值按照原 来顺序分别置于对应子个体的空基因位。 Step4、对不合理的子个体进行基因调 整。 整个交叉过程如图 2 所示。 3.5 变异算子 采用基因块倒置变异算子,首先按照 变异概率随机选择一个需要变异的父个体, 然后再随机确定两个变异位置,最后对这 两个点之间的基因块顺序倒置,生成一新 的个体。若新个体在操作顺序上不合理, 则对该新个体进行基因调整。 3.6 终止条件
混合遗传算法在车间调度中的应用的开题报告

混合遗传算法在车间调度中的应用的开题报告1.研究背景车间调度是制造企业不可或缺的一个环节。
在制造企业中,车间调度涉及到车间机器设备的配置和修理,以及工人和生产线的协调和管理等复杂问题。
车间调度的目标通常是通过合理的调度方案来实现最优化的生产效益,从而提高生产效率,降低成本,增加企业盈利。
传统的车间调度方法往往是基于人工经验和试错的方式来制定调度规划,这种方法的缺点是耗时、耗力,且往往不能达到最优化的效果。
因此,在车间调度中引入智能优化算法来求解最优调度方案成为一种趋势,其中混合遗传算法近年来成为研究热点。
2.研究目的本文旨在研究混合遗传算法在车间调度中的应用,探究其优势和不足,并尝试提出一种改进的混合遗传算法,以提高车间调度方案的优化效果和实际可行性。
3.研究内容3.1 混合遗传算法的基本原理和步骤本文首先介绍混合遗传算法的基本原理和步骤,包括遗传算法和局部优化算法的结合、个体表达、适应度函数、选择、交叉、变异等。
3.2 车间调度问题的描述和建模本文进一步探讨车间调度问题的描述和建模方法,包括车间任务、车间机器设备、优先级、作业时间等的定义和表示。
3.3 混合遗传算法在车间调度中的应用本文探究混合遗传算法在车间调度中的应用,包括求解车间调度问题的具体步骤和方法,以及基于混合遗传算法的车间调度方案的评估和优化。
3.4 算法改进本文基于对混合遗传算法在车间调度中的应用实践的总结,尝试提出一种改进的混合遗传算法。
改进的主要方向包括增加不同的适应度函数、调整遗传算法的参数和优化交叉和变异的方式等。
4.研究意义本文研究混合遗传算法在车间调度中的应用,可以帮助制造企业更加高效地进行生产调度和任务分配,提高产品的质量和企业的盈利能力,同时也可以为智能优化算法的研究和应用提供一定的参考和借鉴价值。
5.研究方案本文的研究方案包括以下几个步骤:5.1 文献综述对混合遗传算法、车间调度问题及其求解算法进行文献综述,包括分别从理论角度和实践应用角度进行分析,总结已有研究的成果和不足。
遗传算法解决人员调度问题的最佳实践与技巧

遗传算法解决人员调度问题的最佳实践与技巧遗传算法(Genetic Algorithm)是一种基于生物进化理论的优化算法,通过模拟遗传和进化的过程,寻找问题的最优解。
在实际应用中,遗传算法被广泛用于解决人员调度问题,如员工排班、任务分配等。
本文将介绍遗传算法解决人员调度问题的最佳实践与技巧。
1. 问题定义与编码方式选择在使用遗传算法解决人员调度问题之前,首先需要明确问题的定义,并选择适合的编码方式。
例如,对于员工排班问题,可以将每个员工表示为一个基因,将一周的排班作为一个染色体,每个基因对应染色体上的一天。
这样,问题就被转化为寻找最优染色体的过程。
2. 适应度函数设计适应度函数是遗传算法中评价染色体优劣的标准。
在人员调度问题中,适应度函数应该能够综合考虑多个指标,如员工的工作时间、工作负荷均衡度、员工之间的协作关系等。
通过合理设计适应度函数,可以将问题的约束条件和优化目标有效地转化为数值化的评价指标。
3. 选择操作选择操作是遗传算法中的一个重要环节,它决定了哪些个体能够进入下一代。
在人员调度问题中,选择操作应该根据个体的适应度值进行选择,适应度值越高的个体越有可能被选中。
常用的选择算法有轮盘赌选择、锦标赛选择等,可以根据具体问题的特点选择合适的算法。
4. 交叉操作交叉操作是遗传算法中的一个关键步骤,它模拟了生物进化中的基因交换过程。
在人员调度问题中,交叉操作可以通过交换染色体上的基因片段来生成新的个体。
交叉操作的目的是增加种群的多样性,从而有助于避免陷入局部最优解。
5. 变异操作变异操作是遗传算法中的另一个重要步骤,它模拟了生物进化中的基因突变过程。
在人员调度问题中,变异操作可以通过随机改变染色体上的基因值来生成新的个体。
变异操作的目的是引入新的基因组合,从而有机会跳出当前搜索空间,寻找更优的解。
6. 算法参数调优遗传算法中的一些参数,如种群大小、交叉概率、变异概率等,都会对算法的性能产生影响。
在解决人员调度问题时,需要根据具体情况对这些参数进行调优。
混合遗传算法求解车间作业调度问题

混合遗传算法求解车间作业调度问题
李钢;李金勇
【期刊名称】《天津大学学报》
【年(卷),期】2003(036)002
【摘要】分析了生产调度问题,提出一种更为有效的动态混合遗传算法,成功地解决了复杂的FT10×10问题.研究过程中引入自适应遗传算法思想,结合一种能够很好解决调度问题的编码规则和适应度值函数,对该算法进行了详细分析.为防止在遗传操作过程中非法染色体导致程序运行失败,给出了非法染色体合法化的规则.仿真结果表明,该算法和编码规则非常适合调度问题,且所提出的动态混合算法优于其它算法.
【总页数】4页(P239-242)
【作者】李钢;李金勇
【作者单位】天津大学管理学院,天津,300072;天津大学管理学院,天津,300072【正文语种】中文
【中图分类】F406.3
【相关文献】
1.一种求解车间作业调度问题的改进遗传算法 [J], 赵杰;刘战强;周军
2.求解车间作业调度问题的混合遗传算法 [J], 刘胜辉;王丽红
3.一种求解车间作业调度的自适应混合遗传算法 [J], 陶思南;傅鹂;蔡斌
4.求解车间作业调度问题的一种改进遗传算法 [J], 光熠;刘心报;程浩
5.混合遗传算法求解车间作业调度问题 [J], 周海峰
因版权原因,仅展示原文概要,查看原文内容请购买。
遗传算法 c语言代码

以下是一个简单的遗传算法的C语言代码示例:c#include <stdio.h>#include <stdlib.h>#include <time.h>#include <math.h>#define POPULATION_SIZE 100#define GENE_LENGTH 10#define MAX_GENERATIONS 1000#define MUTATION_RATE 0.01#define CROSSOVER_RATE 0.8typedef struct Individual {char genes[GENE_LENGTH];double fitness;} Individual;double calculate_fitness(Individual* individual) {// 计算适应度函数,这里使用简单的二进制字符串中1的个数作为适应度 int count = 0;for (int i = 0; i < GENE_LENGTH; i++) {if (individual->genes[i] == '1') {count++;}}return count;}void initialize_population(Individual* population) {// 初始化种群for (int i = 0; i < POPULATION_SIZE; i++) {for (int j = 0; j < GENE_LENGTH; j++) {population[i].genes[j] = rand() % 2 ? '0' : '1';}population[i].fitness = calculate_fitness(&population[i]); }}void selection(Individual* population, Individual* parents) {// 选择操作,采用轮盘赌算法选择两个父代个体double total_fitness = 0;for (int i = 0; i < POPULATION_SIZE; i++) {total_fitness += population[i].fitness;}double rand1 = rand() / (double)RAND_MAX * total_fitness;double rand2 = rand() / (double)RAND_MAX * total_fitness;double cumulative_fitness = 0;int parent1_index = -1, parent2_index = -1;for (int i = 0; i < POPULATION_SIZE; i++) {cumulative_fitness += population[i].fitness;if (rand1 < cumulative_fitness && parent1_index == -1) {parent1_index = i;}if (rand2 < cumulative_fitness && parent2_index == -1) {parent2_index = i;}}parents[0] = population[parent1_index];parents[1] = population[parent2_index];}void crossover(Individual* parents, Individual* offspring) {// 交叉操作,采用单点交叉算法生成两个子代个体int crossover_point = rand() % GENE_LENGTH;for (int i = 0; i < crossover_point; i++) {offspring[0].genes[i] = parents[0].genes[i];offspring[1].genes[i] = parents[1].genes[i];}for (int i = crossover_point; i < GENE_LENGTH; i++) {offspring[0].genes[i] = parents[1].genes[i];offspring[1].genes[i] = parents[0].genes[i];}offspring[0].fitness = calculate_fitness(&offspring[0]);offspring[1].fitness = calculate_fitness(&offspring[1]);}void mutation(Individual* individual) {// 变异操作,以一定概率翻转基因位上的值for (int i = 0; i < GENE_LENGTH; i++) {if (rand() / (double)RAND_MAX < MUTATION_RATE) {individual->genes[i] = individual->genes[i] == '0' ? '1' : '0'; }}individual->fitness = calculate_fitness(individual);}void replace(Individual* population, Individual* offspring) {// 替换操作,将两个子代个体中适应度更高的一个替换掉种群中适应度最低的一个个体int worst_index = -1;double worst_fitness = INFINITY;for (int i = 0; i < POPULATION_SIZE; i++) {if (population[i].fitness < worst_fitness) {worst_index = i;worst_fitness = population[i].fitness;}}if (offspring[0].fitness > worst_fitness || offspring[1].fitness > worst_fitness) {if (offspring[0].fitness > offspring[1].fitness) {population[worst_index] = offspring[0];} else {population[worst_index] = offspring[1];}}}。
混合遗传算法求解车间作业调度问题

色体进行编码为设备序列袁以该序列为基码袁编码
的具体实现为院
工件编号为 1,2,3,噎n曰各工件的对应的工序编
号为 1,2,3,噎k曰对应的机床编号为 1,2,3,噎m.从而
符号 1.1.1 则代表工件 1 的 1 工序在机床 1 上完
成袁以 3渊 工件冤 × 3渊 机床冤 为例院假如工件的加工工
序最多为 4袁机床所对应不存在的加工工序则定义
-1 8-
第五袁每个工件每道加工工序的开工时间必须大于 或者等于零袁即 STiKi≥ 0曰第六袁所有的要件要在预 定交期前全部完工袁设 Ti 为加工工件 Pi 的总时间袁 即∑ TiKi=Ti. 2 混合遗传算法
本文所提出的混合遗传算法的应用为院将启发 式算法融入遗传算法中袁再利用该混合算法求解车 间生产调度排序的问题.遗传算法为一种群体优化 算法袁其通过选择和变异及交叉等不同操作袁不断 的进化解集性能袁从而可以使搜索的速度得到进一 步提高.不过遗传算法也存在不足袁即难以控制早 熟及收敛性等问题.作为传统的启发式算法袁有着 搜索速度快且结构简单的优点袁但是其也存在搜索 能力差且容易陷入局部最优等不足.基于二者的优 势与不足袁将其进行结合袁将启发式算法融入遗传 算法中袁 重新构造出的混合遗传算法能力更强袁对 于求解比较复杂的优化问题有着积极的意义.该混 合方法融合了遗传算法的记忆功能和并行性袁并将 其与启发式算法的快速搜索优势相结合袁使得求解 质量得到了进一步的提高.具体来讲对遗传算法进 行改进的方法始解群袁且该初始解群要 具备良好的适应性能袁这种方法可以使混合遗传算 法优于启发式算法曰第二袁把启发式融入评估函数 中袁将染色体进行解码转换为生产调度曰第三袁对个 体变异及交叉率进行自适应设计. 上述几点中袁在 进行个体中全局搜索时主要采用遗传算法曰而对染 色体部分搜索则利用启发式算法.由于启发式与遗 传算法二者存在相应的互补性袁所以二者相混合的 算法更优于两种单独算法. 3 利用混合遗传算法进行车间作业调度的求解
求解Hadoop作业调度问题的混合遗传算法

求解Hadoop作业调度问题的混合遗传算法
王丽红;夏魁良;金丹
【期刊名称】《齐齐哈尔大学学报(自然科学版)》
【年(卷),期】2018(034)003
【摘要】将自适应遗传算法和改进的蚁群算法融合用以求解Hadoop作业调度问题.首先利用自适应遗传算法的全局搜素能力产生任务所分配的资源列表,在遗传算法的搜索速度逐渐降低时,适时切换到蚁群算法,由自遗传算法求解的最优解生成蚁群算法的初始信息素分布.改进蚁群算法的目标节点选择策略,考虑节点完成任务的成功率,加快蚁群算法求解最优解的速度.仿真结果表明,与遗传算法和蚁群算法相比,混合遗传算法用时较少,并且任务数越多,优势越明显.
【总页数】5页(P6-10)
【作者】王丽红;夏魁良;金丹
【作者单位】黑河学院计算机与信息工程学院,黑龙江黑河 164399;黑河学院计算机与信息工程学院,黑龙江黑河 164399;黑河学院美术学院,黑龙江黑河164399
【正文语种】中文
【中图分类】TP391
【相关文献】
1.混合遗传算法求解包含柔性工艺的作业车间调度问题 [J], 马雪丽;曹德弼;刘晓冰;刘巍巍
2.双种群混合遗传算法求解柔性作业车间调度问题 [J], 程子安;童鹰;申丽娟;于帅帅;李明
3.混合遗传算法求解作业车间调度问题 [J], 阳光灿;熊禾根
4.求解并行JSP作业车间调度问题的一种混合遗传算法 [J], 方霞;俞宏图;熊齐
5.基于混合果蝇-遗传算法求解柔性作业车间调度问题 [J], 刘晶晶;刘业峰;黎虹因版权原因,仅展示原文概要,查看原文内容请购买。
混合遗传算法及在多处理机调度问题中的应用

mo o s o h r o ii n n r sc s c at c o d n O ce t nt lg o p h v lt n r l o i m o i t n f te eg d ct a d i t n i t h s c a c r ig t r a ii a r u ,te e o ui ay a r h f r y i o i e i o g t i r n es ae y ma et ec r m s r e i o ui c d fee c t tg , k h h o o ot s n s lt ns a emo ee fci es ac p i l ou o . ia l, h s y rd r 3 o p r fe t r ho t v e ma l t n F n y t i h b i s i l
l oi ag rtm i he ce c o eo tmi a o c lb te p mi ai nr s l h i hg f i n yf rt pi z t n, al etro t z to e u ̄. s i h i i Ke wo d : e e cag rt m ; h os d fee ta v l t n m ut r c so c e ui g y r s g n t l o h i i ca ; i r n il o u o ; lp o e s rs h e i d ln
一种基于混合遗传算法的车间调度算法

我们 主要 通过 以下 方式 实现 遗传 算法 的改进 : ① 把启 发式嵌入 到初 始化 中, 产生一 个适 应性好 的初始解群 。按这 种方 式 , 混合 式遗传算 法能够优于启 发式 算法 。 ② 将 启发 式嵌入 到评估 函数 中 , 将染 色体解 码为 作 业调 度 。 ③ 自适应设 计个体 的交叉 率与变异 率 。 其 中, 遗传 算法 被用 于个 体 中 的全 局搜 索 , 而启 发 式算 法在 染色 体 中施行 局 部探 寻 。 由于遗 传算 法和 启 发式 算法 的互 补性 能 , 混合 遗 传算 法将 优 于 两种 单 独
资源分配 问题 , 是最 困难的组合优 化 问题 之一【 , ¨ 由于该 问题 计算 复杂性 过高 , 因此在 工程 实践 中 , 多 采用启 大
结合 , 高 了求解 质量 。 提
2 混 合 遗 传 算 法
本文将 传统 的启 发 式算法和遗 传算法 结合起 来 , 应 用该 混 合遗 传算 法解 决作 业 计划 排序 问题 。针对 遗传 算法 的早熟和 收敛性 的问题 , 加入启 发式算法 的一些规 则, 同时对遗传 算法 的一 些关键参 数 ( 如交叉概 率 、变
控 ¥1 论 与 应 用 1 理
Co t o eo y an pl a i s nrl Th r d Ap i t c on
Байду номын сангаас
《 自动化技术与应用 》2 0 0 8年第 2 7卷第 1 期 1
一
种 基 于 混 合 遗 传算 法 的车 间调 度算 法
顾晓芬 , 永平 。 郝 唐 健
Ke r s g n t loi m;o h psh d l g h u i i ag r h ywo d : e ei ag r h jbs o c e ui ; e r t loi m c t n sc t
基于遗传算法的单机调度优化研究

基于遗传算法的单机调度优化研究单机调度优化是一项重要的研究领域,它通过优化调度策略来提高单机系统的性能和效率。
遗传算法作为一种经典的优化算法,在单机调度优化中发挥着重要的作用。
本文将基于遗传算法,对单机调度优化进行研究。
首先,我们需要了解单机调度优化的背景和目标。
单机调度是指在一个处理器上调度多个任务的过程。
在实际应用中,我们常常面临着多个任务同时到达,这就给单机调度带来了挑战。
如何合理地安排任务的执行顺序和时间,以最大化系统的性能和效率,是单机调度优化研究的核心问题。
在遗传算法中,我们将任务调度问题看作是一个优化问题。
通过设计适应度函数,我们可以评估不同调度方案的好坏程度。
遗传算法通过不断地演化和迭代,搜索到最优的调度方案。
具体而言,遗传算法通过模拟自然界中的进化过程,通过选择、交叉和变异等操作,逐渐优化现有的调度方案,找到最优方案。
在单机调度优化的研究中,我们需要考虑以下几个方面的内容:一、任务的建模和表示在使用遗传算法进行单机调度优化之前,我们首先需要将任务的相关信息进行建模和表示。
常用的任务表示方法有任务图和任务链。
任务图是一种以节点表示任务,边表示任务之间的依赖关系的图结构。
任务链则是将任务按照执行先后顺序形成链表结构。
通过合适的任务建模和表示,我们可以更好地描述任务之间的依赖关系和执行顺序。
二、适应度函数的设计适应度函数是遗传算法中的一个关键部分,它用于评估不同调度方案的好坏。
在单机调度优化中,我们可以使用多种指标来评估调度方案,例如任务完成时间、资源利用率、能耗等。
根据实际需求,设计合适的适应度函数,能够更好地评估调度方案的优劣程度。
三、遗传算法的运算子设计遗传算法中的运算子包括选择、交叉和变异。
选择操作通过评估个体适应度,选择出适应度较高的个体作为繁殖的父代。
交叉操作通过将不同父代的基因进行交换,生成新的个体。
变异操作则是在新个体中随机改变某些基因值。
通过合理地设计这些运算子,能够促使种群不断进化,逼近最优解。
采用混合策略遗传算法求解一类资源约束最短时间调度问题

采用混合策略遗传算法求解一类资源约束最短时间调度问题刘昆;颜钢锋
【期刊名称】《系统工程》
【年(卷),期】2000(18)6
【摘要】资源约束最短时间调度问题是一类 NP完全问题 ,求解难度相当大 ,本文提出一种采用混合策略的遗传算法求解该类问题 ,混合策略中包含启发式的调度规则。
理论分析表明本文提出的混合策略的遗传算法是全局收敛的 ,实际应用表明该算法快速有效优于传统算法。
【总页数】5页(P33-37)
【关键词】资源约束;遗传算法;启发式调度规则;混合策略
【作者】刘昆;颜钢锋
【作者单位】浙江大学
【正文语种】中文
【中图分类】O224
【相关文献】
1.改进遗传算法求解低碳约束的柔性车间调度问题 [J], 张国辉;张海军;张理涛;王永成
2.混合遗传算法求解一类多资源生产调度问题 [J], 徐建国;左春荣;李凯
3.一种求解多模式资源约束下项目调度问题的遗传算法 [J], 向来生;刘楠;刘希玉
4.改进遗传算法求解多时间约束的柔性作业车间调度问题 [J], 张国辉; 胡一凡; 孙
靖贺
5.一类含时间窗口的多资源动态调度问题的建模与求解方法 [J], 刘洋;陈英武;谭跃进
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
if((outfp = fopen("newfile1","w")) == NULL)
{
fprintf(stderr,"Cannot open output file %s\n","file1");
exit(-1);
{
generation();//交叉
select_better(oldpop,newpop);//保留最佳个体newpop
popsize_copy(oldpop,newpop);
gen_mu(newpop);//变异 保留最佳个体
select_better(oldpop,newpop);
}
init_parameter();//初始化工件参数
print_parameter();//打印工件参数
for(run=1; run<=maxruns; run++)
{
run_start=clock();
initialize();//初始化 包括初始参数设置
initmalloc();//分配全局空间
fclose(outfp);
}
#include<stdlib.h>
#include<stdio.h>
#include<time.h>
#include<math.h>
#include <string.h>
#include "ceshi.h"
void main()
{
s_individual *temp=NULL;
gererate_pop();//产生初始种群
statistics(oldpop);//统计种群数据,得到最优个体
init_temperature=(min-max)/log(preceive);
temperature_k=init_temperature;
while(k<maxgen && last_maxgen<70)//收敛准则
ceshi_popstatic();
freeall();
}
run_avg=(float)run_sum/float(maxruns);
fprintf(outfp,"\nmax=%d min=%d avg=%d run_sum=%f avg_k=%d\n",pop_max,pop_min,pop_sum/maxruns,run_avg,sum_k);
long run_start,run_finish,run_sum=0;
float run_avgned)time(NULL));/*将当前时间设置成随机函数的种子,所以每次产生的数都不一样*/
//printf("%d\n",time(NULL));
popsize_copy(oldpop,newpop);
CSA(newpop);//模拟退火操作 定步长抽样
select_better(oldpop,newpop);
statistics(newpop);
run_finish=clock();
if (last_fitness==bestfit.fitness)
{
last_maxgen++;
}
else{
last_maxgen=0;
last_runtime=run_finish;
}
last_fitness=bestfit.fitness;
k++;//退温
temperature_k=temperature_k*ptemper;
temp=oldpop;
oldpop=newpop;
newpop=temp;
}
sum_k=sum_k+k;
run_time=last_runtime-run_start;
run_sum=run_sum+run_time;
print_popsize();
