高斯小学奥数四年级上册含答案第12讲_乘法原理进阶
【详解】四年级上第12讲_乘法原理进阶

第十二讲乘法原理进阶1.例题1答案:96详解:分步,分别给E、B、C、A、D染色,分别有4、3、2、2、2种染法,所以一共有4322296⨯⨯⨯⨯=种染色方法.2.例题2答案:48;32方法;(2)分步,先染易拉罐垃圾桶,再分别给废纸、塑料、电池、其他这四个垃圾桶染色,五个垃圾桶分别有2、2、2、2、2种染法,所以一共有2222232⨯⨯⨯⨯=种染色方法.3.例题3答案:24;6;12;18种;⨯⨯=种;(2)分别确定班长、学委、生活委员的人选,分别有1、3、2种选法,所以共有1326(3)分别确定生活委员、学委、班长的人选,分别有2、3、2种选法,所以共有23212⨯⨯=种;⨯⨯=种.(4)分别确定学委、班长、生活委员的人选,分别有3、3、2种选法,所以共有332184.例题4答案:4种选法.5.例题5答案:18;24详解:(1)先考虑甲,后考虑乙,再考虑其他三个人,分别有1、3、3、2、1种可能,共有⨯⨯⨯⨯=种;1332118(2)先考虑A,后考虑E,再考虑其他三辆车,分别有2、2、3、2、1种可能,所以共有⨯⨯⨯⨯=种.22321246.例题6答案:16详解:一共要选5个格子放棋子,一行一行选,每行1个,而且不能在同一列,从上往下,5行⨯⨯⨯⨯=种选法.分别有2、2、2、2、1种选法,所以一共有22221167.练习1答案:48详解:分步,分别给B、C、A、D染色,分别有4、3、2、2种染法,所以一共有⨯⨯⨯=种染色方法.4322488.练习2答案:6详解:先让麦兜点,只有鱼丸油面1种可选,然后让其他3位同学依次点,分别有3、2、1种选法,共分四步,乘法原理,所以共有13216⨯⨯⨯=中不同的选法.9.练习3答案:120;72;72⨯⨯⨯=种;(2)先确定副班长,再依次确定其他,共有343272(3)先确定卫生委员,再依次确定其他,共有343272⨯⨯⨯=种.10.练习4答案:8种选法.11.作业1答案:96.简答:可以按照萱萱、小高、墨莫、阿呆、阿瓜的顺序安排座位,有4432196⨯⨯⨯⨯=种.安排座位的顺序不唯一.12.作业2答案:24简答:可以按照A、B、C的顺序染色,43224⨯⨯=种.染色顺序不唯一.13.作业3答案:96简答:可以按照A、B、C、D、E的顺序染色,有4322296⨯⨯⨯⨯=种.染色顺序不唯一.14.作业4答案:8简答:按照乙、甲、丙、丁的顺序安排,有22218⨯⨯⨯=种排法.15.作业5答案:12简答:一行一行选位置,第一行有4个格子可选,即4种选法;第二行还有3个格子可选,即有3种选法.因此有4312⨯=种不同的放法.。
小学数学奥数基础教程(四年级)目录.doc

小学数学奥数基础教程(四年级)目录(含答案).word文档下载地址.文档贡献者:与你的缘.第1讲速算与巧算(一)练习1第2讲速算与巧算(二)练习2第3讲高斯求和练习3第4讲数的整除性(一)练习4第5讲弃九法练习5第6讲数的整除性练习6第7讲找规律(一)练习7第8讲找规律(二)练习8第九讲数字迷(一)练习9第10讲数字迷(二)练习10第11讲归一问题与归总问题练习11第12讲年龄问题练习12第13讲鸡兔同笼问题与假设法练习13第14讲盈亏问题与比较法(一)练习14第15讲盈亏问题与比较法(二)练习15第16讲数阵图(一)练习16第17讲数阵图(二)练习17第18讲数阵图(三)练习18第19讲乘法原理练习19第20讲加法原理(一)练习20第21讲加法原理(二)练习21第22讲还原问题(一)练习22第23讲还原问题(二)练习23第24讲页码问题练习24第25讲智取火柴练习25第26讲逻辑问题(一)练习26第27讲逻辑问题(二)练习27第28讲逻辑问题(二)练习28第29讲抽屉原理(一)练习29第30讲抽屉原理(二)练习30情感语录1.爱情合适就好,不要委屈将就,只要随意,彼此之间不要太大压力2.时间会把最正确的人带到你身边,在此之前,你要做的,是好好的照顾自己3.女人的眼泪是最无用的液体,但你让女人流泪说明你很无用4.总有一天,你会遇上那个人,陪你看日出,直到你的人生落幕5.最美的感动是我以为人去楼空的时候你依然在6.我莫名其妙的地笑了,原来只因为想到了你7.会离开的都是废品,能抢走的都是垃圾8.其实你不知道,如果可以,我愿意把整颗心都刻满你的名字9.女人谁不愿意青春永驻,但我愿意用来换一个疼我的你10.我们和好吧,我想和你拌嘴吵架,想闹小脾气,想为了你哭鼻子,我想你了11.如此情深,却难以启齿。
其实你若真爱一个人,内心酸涩,反而会说不出话来12.生命中有一些人与我们擦肩了,却来不及遇见;遇见了,却来不及相识;相识了,却来不及熟悉,却还要是再见13.对自己好点,因为一辈子不长;对身边的人好点,因为下辈子不一定能遇见14.世上总有一颗心在期待、呼唤着另一颗心15.离开之后,我想你不要忘记一件事:不要忘记想念我。
四年级奥数培优《乘法原理》

乘法原理一、知识梳理我们在完成一件事时往往要分为多个步骤,每个步骤又有多种方法,当计算一共有多少种完成方法时就要用到乘法原理。
乘法原理:一般地,如果完成一件事需要n 个步骤,其中,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法 ,…,做第n 步有m n 种不同的方法,则完成这件事一共有N=m 1×m 2×…×m n 种不同的方法。
乘法原理运用的范围:这件事要分几个彼此互不影响....的独立步骤....来完成,这几步是完成这件任务缺一不可的.....,这样的问题可以使用乘法原理解决.我们可以简记为:“乘法分步,步步相关”。
二、例题精讲例1. 在下图中,一只甲虫要从A 点沿着线段爬到B 点,要求任何点不得重复经过,问这只甲虫最多各有几种不同走法?例 2. 要从五年级六个班中评选出学习,体育、卫生先进集体各一个,有多少种不同的评选结果(同一个班级只能得到一个先进集体?)例3. 5种不同颜色的笔来写“智康教育”这几个字,相邻的字颜色不同,共有多少种写法?例4. 如下图,A ,B ,C ,D ,E 五个区域分别用红、黄、蓝、白、黑五种颜色中的某一种染色,要使相邻的区域染不同的颜色,共有多少种不同的染色方法?B例5. 北京到上海之间一共有6站,车站应该准备多少种不同的车票?(往返车票算不同的两种)三、课堂小测7. 邮递员投递邮件由A村去B村的道路有3条,由B村去C村的道路有2条,那么邮递员从A村经B村去C村,共有多少种不同的走法?8.将四封不同的信投入3个不同的信箱中,有多少种不同的投法。
9. “IMO”是国际数学奥林匹克的缩写,把这3个字母写成三种不同颜色.现在有五种不同颜色的笔,按上述要求能写出多少种不同颜色搭配的“IMO”?10.用四种颜色给右图的五块区域染色,要求每块区域染一种颜色,相邻的区域染不同的颜色.问:共有多少种不同的染色方法?11. 北京到广州之间有10个站,其中有四个站是大站(包括北京、广州),从大站出发的车辆可以配卧铺,那么铁路局要准备多少种不同的卧铺车票。
高斯小学奥数四年级上册含答案第12讲_乘法原理进阶

第十二讲乘法原理进阶在之前我们学习了“加法原理与乘法原理”一讲,即分类相加与分步相乘的思想.如果完成一件事分为几个步骤,在每一个步骤中又有不同的方法,那么把每步的方法数相乘就得到所有的方法数——这就是乘法原理.要想把过程分成几个步骤从而应用乘法原理,必须保证各步骤之间满足下面两个要求:1.2.那么是不是只要分步骤完成整件事情就可以直接用乘法原理呢?如下图,把A、B、C三部分用三种不同的颜色染色,要求相邻两部分不能同色,那么一共有多少种不同的染法呢?A B C其实,整个染色过程是需要分为三步的,即分别给其中一块染色:当染色顺序为A→B→C时,那么A有3种染法,B不能和A一样,有2种染法,同样C有2种,那么一共就有“322⨯⨯”种染法;(C→B→A同理)当染色顺序为B→A→C时,那么B有3种染法,A不能和B一样,有2种染法,同样C有2种,那么一共就有“322⨯⨯”种染法;(B→C→A同理)当染色顺序为A→C→B时,那么A有3种染法,第二步C没有限制,也有3种染法,但是最后的B就出问题了,我们没法确定它有2种还是1种染法——如果C和A同色,则B有2种染法;如果C和A不同色,则B只有1种染法——此时,根据分步相乘的思想计算整个过程的染色方法“33?⨯⨯”就不再适用了.(C→A→B同理)因此,并不是只要分步完成整件事情就一定可以应用乘法原理,要想应用乘法原理,还必须满足第三个要求:3.——简称“前不影响后.....原则”染色问题,是应用乘法原理最常见的一类题型,其实,从上面对A、B、C 三部分的染色分析我们应该可以发现,染色的时候,要尽量避免“隔”着染,一定不要“跳”着染,而且,第一步要尽量去染“接触最多”的那一部分,这样,才能够使得后面的染色过程尽量避开“前影响后”.例题1如图,把A 、B 、C 、D 、E 这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?「分析」分五步染色,先染哪一块呢?能否按照A 、B 、C 、D 、E 的顺序染呢? 练习1如图,把A 、B 、C 、D 这四部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?例题2某市实行垃圾分类处理.每个地方放置五个垃圾桶,从左向右依次标明:电池、塑料、废纸、易拉罐、其它.现在准备把五个垃圾桶染成红、绿、蓝这3种颜色之一.(1)要求相邻两个垃圾桶颜色不同,一共有多少种染色方法? (2)要求相邻两个垃圾桶颜色不同且回收易拉罐的垃圾桶不能染成红色,一共有多少种染色方法?「分析」如果我们先染废纸垃圾桶:当它染红色时,回收易拉罐的垃圾桶可以染绿、蓝两种颜色;而当它染绿色(蓝色)时,回收废纸的垃圾桶只能染蓝色(绿色).因此先染废纸垃圾桶时,会影响易拉罐垃圾桶的染色方法数,就不能直接用乘法原理计算了.那么我们应该先给哪个垃圾桶染色呢?练习2麦兜很挑食,只吃带有鱼丸或粗面的搭配.一天它和3位同学来餐厅吃东西,一开口就要鱼丸粗面,结果老板说没有.这个时候,由于时间太晚,餐厅快打烊了,只能做牛肚河粉,鱼丸油面,猪肉米线和牛肉拉面各一份,请问它们四只猪各点一份,有几种点法?在例题2中,有一个垃圾桶是有特殊要求的——易拉罐垃圾桶不能染成红色,我们通过尝试可知:如果一开始先染其他的垃圾桶,那么前面垃圾桶的染色方法就会影响到易拉罐垃圾桶的染色方法数,即不能满足“前不影响后”原则,而如果首先染易拉罐垃圾桶,则不会出现该问题,所以一般而言,如果题目中有些对象是有特殊要求的,那么我们分步..分析计算的时候,首先要考虑这些特殊的对象.例题3卡莉娅、墨莫、小高和大头4名同学竞选班委.有班长、学习委员、生活委员三个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任.(1)有多少种可能的选举结果?(2)如果班长必须由卡莉娅来担任,有多少种可能的选举结果?(3)如果生活委员只能在墨莫和大头之中选,有多少种可能的选举结果?(4)如果学习委员不能由小高担任,有多少种可能的选举结果?「分析」可以按照职位一一确定,第(2)问中,班长只能由卡莉娅来担任,那么先确定哪一个职位的人选呢?其他小问呢?练习3甲、乙、丙、丁、戊5个人竞选班委.有班长、副班长、纪律委员、卫生委员四个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任:请问:(1)一共有多少种可能的选举结果?(2)如果副班长只能在甲、丁和戊中选,有多少种可能的选举结果?(3)如果卫生委员不能由乙、丙担任,有多少种可能的选举结果?例题4甲、乙、丙、丁四个人要住进A、B、C、D四间房间,每个房间住一个人.其中甲不住A房间,丙只住D房间.请问:这四个人住进四个房间有多少种住法?「分析」本题中甲和丙有特殊要求,我们应该先考虑甲还是丙呢?练习4甲、乙、丙、丁四个人要住进A 、B 、C 、D 四间房间,每个房间住一个人.其中甲只住A 或B 房间,丙只住A 、B 或C 房间.请问:这四个人住进四个房间有多少种住法?例题5甲、乙、丙、丁、戊五人要驾驶A 、B 、C 、D 、E 这五辆不同型号的汽车,请计算在下列情况下,分别共有多少种不同的安排方案: (1)只有甲能开汽车A ,乙不会开汽车B ;(2)会开A 的只有甲和乙,会开E 的只有甲、乙、丙.「分析」第(1)问中,甲和丙两人有特殊要求,我们应该先考虑哪一个人呢?第(2)问中,A 和E 两车有特殊要求,我们应该先考虑哪辆车呢?接下来我们分析一下“放相同棋子”的问题.如右图,将2枚相同的棋子放入2×2的方格内,每个格子只能放1枚,且要求每行每列最多只能放1枚,那么一共会有几种方法呢?其实,要把两枚相同的棋子放进格子内,只需要选出两个格子即可,然后每个格子里放一枚棋子.一共有两行,所以必定会是每行一枚,所以我们完全可以分行选格子,第一行有两种选法,第一行选好后,第二行就只有一种选法了,所以一共有2×1=2种.例题6右图是一个阶梯形方格表,在方格中放入五枚相同的棋子,使得每行、每列中都只有一枚棋子,这样的放法共有多少种?「分析」容易看出,每行只能有1枚棋子,每列也只能由一枚棋子,我们可以把放五枚棋子的过程分成五步:一行一行或一列一列的放.课堂内外四色定理四色定理与费马大定理、哥德巴赫猜想并称为近代数学三大难题.四色定理的内容是:对于任何一张地图,只用四种颜色,就可以把有相邻边界的国家染上不同的颜色.四色问题的提出来自英国.1852年,在大学读书的格斯里向他的老师——著名数学家摩根提出了这个问题,摩根没有能找到解决这个问题的途径.“四色问题”提出以后,最初并没有引起广泛的重视,许多数学家低估了它的难度.就连素以谦虚著称的德国数论专家闵可夫斯基在大学上拓扑课时也说:四色问题之所以一直没有获得解决,那仅仅是由于没有一流的数学家来解决它.说罢,他拿起粉笔,竟要当堂给学生推导出来,结果没有成功.下一节课他又去试,还是没有成功.过了几个星期,仍无进展.有一天,他刚跨进教室,适逢天上雷声大作,震耳欲聋.他马上对学生说:“上天在责备我自大,我也无法解决四色问题.”这样,四色问题就成了世界最著名的问题之一.l00多年中,“四色问题”使数学家们深为困扰.没有人能证明它,也没有人推翻它.电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了四色猜想的证明进程.就在1976年6月,哈肯与阿佩尔在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿次判断,终于完成了四色定理的证明,轰动了世界.作业1. 五个座位排成一排,小高、墨莫、萱萱、阿呆、阿瓜每人选一个座位坐下,其中每个座位只能坐一个人,且萱萱不坐在中间的位置.这五个人有多少种坐法?2. 如图,把A 、B 、C 这三部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问,这幅图共有多少种不同的染色方法?3. 把A 、B 、C 、D 、E 这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.这幅图共有多少种不同的染色方法?4. 甲、乙、丙、丁四个人排成一队,甲不当排头,乙不当排头也不当排尾,共有多少种不同的排法?5. 在的方格中放入两枚相同的棋子,要求两枚棋子既不在同一行也不在同一列,共有多少种放法?24 ABCD E第十二讲乘法原理进阶1.例题1答案:96详解:分步,分别给E、B、C、A、D染色,分别有4、3、2、2、2种染法,所以一共有4322296⨯⨯⨯⨯=种染色方法.2.例题2答案:48;32方法;(2)分步,先染易拉罐垃圾桶,再分别给废纸、塑料、电池、其他这四个垃圾桶染色,五个垃圾桶分别有2、2、2、2、2种染法,所以一共有2222232⨯⨯⨯⨯=种染色方法.3.例题3答案:24;6;12;18种;(2)分别确定班长、学委、生活委员的人选,分别有1、3、2种选法,所以共有1326⨯⨯=种;(3)分别确定生活委员、学委、班长的人选,分别有2、3、2种选法,所以共有23212⨯⨯=种;(4)分别确定学委、班长、生活委员的人选,分别有3、3、2种选法,所以共有33218⨯⨯=种.4.例题4答案:4种选法.5.例题5答案:18;24详解:(1)先考虑甲,后考虑乙,再考虑其他三个人,分别有1、3、3、2、1种可能,共有⨯⨯⨯⨯=种;1332118(2)先考虑A,后考虑E,再考虑其他三辆车,分别有2、2、3、2、1种可能,所以共有⨯⨯⨯⨯=种.22321246.例题6答案:16详解:一共要选5个格子放棋子,一行一行选,每行1个,而且不能在同一列,从上往下,5行分别有2、2、2、2、1种选法,所以一共有2222116⨯⨯⨯⨯=种选法.7.练习1答案:48详解:分步,分别给B、C、A、D染色,分别有4、3、2、2种染法,所以一共有⨯⨯⨯=种染色方法.4322488.练习2答案:6详解:先让麦兜点,只有鱼丸油面1种可选,然后让其他3位同学依次点,分别有3、2、1种选法,共分四步,乘法原理,所以共有13216⨯⨯⨯=中不同的选法.9.练习3答案:120;72;72⨯⨯⨯=5432120(2)先确定副班长,再依次确定其他,共有343272⨯⨯⨯=种;(3)先确定卫生委员,再依次确定其他,共有343272⨯⨯⨯=种.10.练习4答案:8种选法.11.作业1答案:96.简答:可以按照萱萱、小高、墨莫、阿呆、阿瓜的顺序安排座位,有4432196⨯⨯⨯⨯=种.安排座位的顺序不唯一.12.作业2答案:24简答:可以按照A、B、C的顺序染色,43224⨯⨯=种.染色顺序不唯一.13.作业3答案:96简答:可以按照A、B、C、D、E的顺序染色,有4322296⨯⨯⨯⨯=种.染色顺序不唯一.14.作业4答案:8简答:按照乙、甲、丙、丁的顺序安排,有22218⨯⨯⨯=种排法.15.作业5答案:12简答:一行一行选位置,第一行有4个格子可选,即4种选法;第二行还有3个格子可选,即有3种选法.因此有4312⨯=种不同的放法.。
【精品奥数】四年级上册数学思维训练讲义-第十二讲 速算与巧算(一) 人教版(含答案)

第十二讲速算与巧算(一)第一部分:趣味数学蜗牛爬啊爬一只蜗牛不小心掉进了一只枯井里,它趴在井底上哭起来,一只癞蛤蟆过来,翁声翁气的对蜗牛说:“别哭了,小兄弟,哭也没用,这井壁又高又滑,掉到这里只能在这里生活了。
我已经在这里生活了许多年了。
”蜗牛望着又老又丑的癞蛤蟆,心里想:“井外的世界多美呀!我决不能像它那样生活在又黑又冷的井底里。
”蜗牛对癞蛤蟆说:“癞大叔,我不能生活在这里,我一定要爬出去,请问这口井有多深?”“哈哈哈……,真是笑话,这井有10米深,你小小年纪。
又背负着这么重的壳,怎么能爬出去呢?”“我不怕苦不怕累,每天爬一段,总能爬出去!”第二天,蜗牛吃得饱饱的,开始顺着井壁往上爬了,它不停的爬呀爬,到了傍晚,终于爬了5米,蜗牛特别高兴,心想:“照这样的速度,明天傍晚我就可以爬出去了。
”想着想着不知不觉睡着了,早上,蜗牛被一阵呼噜声吵醒了,一看,原来是癞大叔还以睡觉,他心里一惊:“我怎么离井底这么近?”原来,蜗牛睡着以后,从井壁上滑下来4米,蜗牛叹了一口气,咬咬牙,又开始往上爬,到傍晚又往上爬了5米,可晚上,蜗牛又滑下来4米,就这样,爬呀爬,滑呀滑,最后坚强的蜗牛终于爬上了井台。
聪明的小朋友你能猜出来蜗牛用了多少天才爬上井台的吗?第二部分:奥数小练速算与巧算是计算中的一个重要组成部分,掌握一些速算与巧算的方法,有助于提高我们的计算能力和思维能力。
这一周我们学习加、减法的巧算方法,这些方法主要根据加、减法的运算定律和运算性质,通过对算式适当变形从而使计算简便。
在巧算方法里,蕴含着一种重要的解决问题的策略。
转化问题法即把所给的算式,根据运算定律和运算性质,或改变它的运算顺序,或减整从而变成一个易于算出结果的算式。
【例题1】计算9+99+999+9999【思路导航】这四个加数分别接近10、100、1000、10000。
在计算这类题目时,常使用减整法,例如将99转化为100-1。
这是小学数学计算中常用的一种技巧。
小学奥数——乘法原理与加法原理

乘法原理与加法原理在日常生活中常常会遇到这样一些问题,就是在做一件事时,要分几步才能完成,而在完成每一步时,又有几种不同的方法,要知道完成这件事一共有多少种方法,就用我们将讨论的乘法原理来解决.例如某人要从北京到大连拿一份资料,之后再到天津开会.其中,他从北京到大连可以乘长途汽车、火车或飞机,而他从大连到天津却只想乘船.那么,他从北京经大连到天津共有多少种不同的走法?分析这个问题发现,某人从北京到天津要分两步走.第一步是从北京到大连,可以有三种走法,即:第二步是从大连到天津,只选择乘船这一种走法,所以他从北京到天津共有下面的三种走法:3×1=3.如果此人到大连后,可以乘船或飞机到天津,那么他从北京到天津则有以下的走法:共有六种走法,注意到3×2=6.在上面讨论问题的过程中,我们把所有可能的办法一一列举出来.这种方法叫穷举法.穷举法对于讨论方法数不太多的问题是很有效的.在上面的例子中,完成一件事要分两个步骤.由穷举法得到的结论看到,用第一步所有的可能方法数乘以第二步所有的可能方法数,就是完成这件事所有的方法数.一般地,如果完成一件事需要个步骤,其中,做第一步有种不同的方法,做第二步有种不同的方法,…,做第步有种不同的方法,那么,完成这件事一共有种不同的方法.这就是乘法原理.例1.某人到食堂去买饭,主食有三种,副食有五种,他主食和副食各买一种,共有多少种不同的买法?补充说明:由例题可以看出,乘法原理运用的范围是:①这件事要分几个彼此互不影响的独立步骤来完成;②每个步骤各有若干种不同的方法来完成.这样的问题就可以使用乘法原理解决问题.例2.右图中有7个点和十条线段,一只甲虫要从A点沿着线段爬到B点,要求任何线段和点不得重复经过.问:这只甲虫最多有几种不同的走法?例3.书架上有6本不同的外语书,4本不同的语文书,从中任取外语、语文书各一本,有多少种不同的取法?例4.王英、赵明、李刚三人约好每人报名参加学校运动会的跳远、跳高、100米跑、200米跑四项中的一项比赛,问:报名的结果会出现多少种不同的情形?例5.由数字0、1、2、3组成三位数,问:①可组成多少个不相等的三位数?②可组成多少个没有重复数字的三位数?分析在确定由0、1、2、3组成的三位数的过程中,应该一位一位地去确定.所以,每个问题都可以看成是分三个步骤来完成.①要求组成不相等的三位数.所以,数字可以重复使用,百位上,不能取0,故有3种不同的取法;十位上,可以在四个数字中任取一个,有4种不同的取法;个位上,也有4种不同的取法.②要求组成的三位数中没有重复数字,百位上,不能取0,有3种不同的取法;十位上,由于百位已在1、2、3中取走一个,故只剩下0和其余两个数字,故有3种取法;个位上,由于百位和十位已各取走一个数字,故只能在剩下的两个数字中取,有2种取法.例6.由数字1、2、3、4、5、6共可组成多少个没有重复数字的四位奇数?分析要组成四位数,需一位一位地确定各个数位上的数字,即分四步完成,由于要求组成的数是奇数,故个位上只有能取1、3、5中的一个,有3种不同的取法;十位上,可以从余下的五个数字中取一个,有5种取法;百位上有4种取法;千位上有3种取法,故可由乘法原理解决.例7.右图中共有16个方格,要把A、B、C、D四个不同的棋子放在方格里,并使每行每列只能出现一个棋子.问:共有多少种不同的放法?分析由于四个棋子要一个一个地放入方格内.故可看成是分四步完成这件事.第一步放棋子A,A可以放在16个方格中的任意一个中,故有16种不同的放法;第二步放棋子B,由于A已放定,那么放A的那一行和一列中的其他方格内也不能放B,故还剩下9个方格可以放B,B有9种放法;第三步放C,再去掉B所在的行和列的方格,还剩下四个方格可以放C,C有4种放法;最后一步放D,再去掉C所在的行和列的方格,只剩下一个方格可以放D,D有1种放法,本题要由乘法原理解决.例8.现有一角的人民币4张,贰角的人民币2张,壹元的人民币3张,如果从中至少取一张,至多取9张,那么,共可以配成多少种不同的钱数?分析要从三种面值的人民币中任取几张,构成一个钱数,需一步一步地来做.如先取一角的,再取贰角的,最后取壹元的.但注意到,取2张一角的人民币和取1张贰角的人民币,得到的钱数是相同的.这就会产生重复,如何解决这一问题呢?我们可以把壹角的人民币4张和贰角的人民币2张统一起来考虑.即从中取出几张组成一种面值,看共可以组成多少种.分析知,共可以组成从壹角到捌角间的任何一种面值,共8种情况.(即取两张壹角的人民币与取一张贰角的人民币是一种情况;取4张壹角的人民币与取2张贰角的人民币是一种情况.)这样一来,可以把它们看成是8张壹角的人民币.整个问题就变成了从8张壹角的人民币和3张壹元的人民币中分别取钱.这样,第一步,从8张壹角的人民币中取;第二步,从3张壹元的人民币中取共4种取法,即0、1、2、3.但要注意,要求“至少取一张"。
四年级奥数详解答案乘法原理

四年级奥数详解答案第九讲乘法原理一、知识概要如果要完成一件任务需要分成几个步骤进行做,第一步有m1种方法,做第二步有m2种方法……,做第n步有m n种方法,即么,按这样的步骤完成这件任务共有N= m1×m2×…×m n种不同的方法。
这就是乘法原理。
乘法原理和加法原理的区别是:加法原理是指完成一件工作的方法有几类,之间不相关系,每类都能独立完成一件工作任务;而乘法原理是指完成一件工作的方法是一类中的几个不同步骤,互相关联,缺一不可,共同才能完成一件工作任务。
二、典型例题精讲1. 从甲地到乙地有两条路可走,从乙地到丙地有三条路可走,试问:从甲地经乙地到丙地共有多少种不同的走法?分析:如图,很明显,这是个乘法原理的题目。
要完成“从甲到丙的行走任务”必须分两步完成。
第一步:甲分别通过乙的三条路线到达丙,故有3种走法。
第二步:甲从第二条路线出发又分别通过乙的三条路线到达丙,故又有3种走法。
这两种走法相类似,共同完成“从甲到丙”的任务。
解:3×2=6(种) 答:共有6种不同的走法。
2. 右图中共有16个方格,要把A、B、C、D四个不同的棋子放在方格里,并使每行、每列只能出现一个棋子,共有多少种不同的放法?分析:(如图二)摆放四个棋子分四步来完成。
第一步放棋子A,A可任意摆放,有16种摆放;第二步摆B,由于A所在的位置那一行,那一列都不能放,故只有9种放法;第三步摆C子,也由A、B所在的那一行,那一到都不能,只有四格可任意放,故有4种放法;第四步,只剩一格放D子,当然只有一种放法。
解:16×9×4×1=576(种) 答:共有576种不同的放法。
3. 有五张卡片,分别写有数字1,2,4,5,8。
现从中取出3张片排在一起,组成一个三位数,如□1□5□2,可以组成个不同的偶数。
分析:分三步取出卡片:1.个位,个位只能放2、4、8;故有3种放法;2.百位,因个位用去1张,所以百位上还有四张可选,故有4种放法;3.十位,因个位和百位共放了两张,所以还有3张可选放,有3种放法。
高思数学_4年级上-第17讲-乘法原理进阶(彩色)

101在上一讲中,我们学习了加法原理及较简单的乘法原理.要想把过程分成几个步骤从而应用乘法原理,必须保证各步骤之间满足下面三个要求:1.每步都只是整件事情的一个部分,必须全部完成才能做完这件事;2.步骤之间要有先后顺序,先确定好一步,再做下一步,直到最后.3.做完一步时,这一步的结果很可能会影响后面步骤的结果,但一定不能影响后面步骤的方法数.如果这一步的不同结果会导致后面某一步的方法数不同,就不能直接用乘法原理计算.102分析以染绿、蓝两种颜色;而当它染绿色(蓝色)时,回收废纸的垃圾桶只能染蓝色(绿色).因此先染回收塑料的垃圾桶时,会影响染回收废纸的垃圾桶的染色方法数,就不能直接用乘法原理计算了.那么我们应该先给哪个垃圾桶染色呢?练习1.把1分、2分、5分、1角的硬币各一枚排成一排,其中1分硬币不在两边,共有多少种排硬币的方法?分析 我们应该把这五部分按照什么顺序染色呢?如果我们按照A 、E 、C 、B 、D 的顺序染色,能直接用乘法原理计算染色的方法吗?练习2.把A 、B 、C 、D 这四部分用四种不同的颜色染色,且相邻的部分不能使用同一种颜色,向右依次标明:染成红、绿、蓝这纸的垃圾桶不能染成红色,一共有多少种染色方法?种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:例题2不相邻的部分可以使用同一种颜色.请问:这幅图共有多少种不同的染色方法?在上面的染色问题中,我们只要能保证前面步骤的染色结果不会影响到后面步骤染色的方法数,就是合理的分步方法.大家试着多找出几种合理的分步方法,看看有没有什么规律可循. 四色定理 四色定理的内容是:“对于任何一张地图,只用四种颜色,就可以把有相邻边界的国家染上不同的颜色.”四色问题的提出来自英国.1852年,在大学读书的格斯里向他的老师、著名数学家摩根提出了这个问题,摩根没有能找到解决这个问题的途径.“四色问题”提出以后,最初并没有引起广泛的重视,许多数学家低估了它的难度.就连素以谦虚著称的德国数论专家闵可夫斯基在大学上拓扑课时也说:四色问题之所以一直没有获得解决,那仅仅是由于没有一流的数学家来解决它.说罢,他拿起粉笔,竟要当堂给学生推导出来,结果没有成功.下一节课他又去试,还是没有成功.过了几个星期,仍无进展.有一天,他刚跨进教室,适逢天上雷声大作,震耳欲聋.他马上对学生说:“上天在责备我自大,我也无法解决四色问题.”这样,四色问题就成了世界最著名的问题之一.100多年中,“四色问题”使数学家们深为困扰.没有人能证明它,也没有人推翻它.电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了四色猜想的证明进程.就在1976年6月,哈肯与阿佩尔在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿次判断,终于完成了四色定理的证明,轰动了世界.AD CB 的小圆圈染色,每个小圆圈只能染一种颜色.请问:种不同的染法?称,一共有多少种不同的染法?104分析 染色过程应该分成几步?练习3.如图,用红、蓝两种颜色来给图中的小圆圈染色,每个小圆圈只能染一种颜色.请问:如果要求染色结果关于中间那条竖线左右对称,一共有多少种不同的染法?分析 本题中汽车A 和汽车E 有特殊要求,我们应该优先考虑有特殊要求的位置.应该按照什么顺序给这五辆车分配司机呢?练习4.甲、乙、丙、丁四个人要住进A 、B 、C 、D 四间房间,每个房间住一个人,其中甲不住A 房间,丙只住D 房间.请问:这四个人住进四个房间有多少种住法?分析 容易看出,每行只能有一枚棋子,每列也只能有一枚棋子.我们可以把不同型号的汽车.会驾驶汽车三人中的某一人驾驶,一共有多少种不同的安排方案?例题4内,每个方格只能放一枚,任何两枚棋子都不能在同一行或同一列.一共有多少种不同的放法?例题5105放四枚棋子的过程分成四步,每一步放一枚棋子.你知道每一步分别有多少种放棋子的方法吗?练习5.将一枚白子和一枚黑子放在棋盘线的交叉点上,但不能在同一条横线或竖线上(下图是一个可能的方法).问:共有多少种不同的放法?在做数字谜问题时,我们总是希望寻找合适的突破口,这样能尽可能多地填出确定的数字.即使在没有更多突破口时,也要从可能情况较少的地方入手分析.对于较复杂的乘法原理问题,我们在分步时也要优先考虑可选择情况较少的步骤,尽可能地让前面步骤的结果不影响后面步骤选择的方法数.本讲知识点汇总一、应用乘法原理时,某一步的结果可以影响后面步骤的结果,但一定不能影响后面步骤的方法数.二、对于染色问题等较复杂的乘法原理问题,在分步时要优先考虑可选择情况较少的步骤,必须让前面步骤的结果不影响后面步骤选择的方法数.中都只有一枚棋子,这样的放法共有多少种?106作业1.五个座位排成一排,小高、墨莫、萱萱、阿呆、阿瓜每人选一个座位坐下,其中每个座位只能坐一个人,且萱萱不坐在中间的位置.请问:这五个人有多少种坐法?2.把A 、B 、C 、D 、E 这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?3.如图,用红、黄、蓝三种颜色来给图中的小圆圈染色,每个小圆圈只能染一种颜色,而且要求角上的四个圆圈必须染相同的颜色.请问:一共有多少种不同的染法?4.甲、乙、丙、丁四个人排成一队,甲不能当排头,乙不当排头也不当排尾,共有多少种不同的排法?5.在44×的方格中放黑棋子和白棋子各一枚,要求两枚棋子既不在同一行也不在同一列,问:共有多少种放法?A B C DE。
高斯小学奥数四年级上册含答案第12讲_乘法原理进阶

第十二讲乘法原理进阶在之前我们学习了 “加法原理与乘法原理” 一讲,即分类相加与分步相乘的 思想. 如果完成一件事分为几个步骤,在每一个步骤中又有不同的方法,那么把每 步的方法数相乘就得到所有的方法数一一这就是乘法原理.要想把过程分成几个步骤从而应用乘法原理,必须保证各步骤之间满足下面 两个要求:1. 每步都只是整件事情的一个部分,必须全部完成才算做完这件事;2. 步骤之间要有先后顺序,先确定好一步,再做下一步, 直到最后.那么是不是只要分步骤完成整件事情就可以直接用乘法原理呢?沽你来当服装 设讣人师.给小高 挑迭帽子、上衣" 棘了、柱了.如采 这四件衣物械不 可.但只能甸种选 -件'有多少种不 同的搭配?如下图,把A、B、C三部分用三种不同的颜色染色,要求相邻两部分不能同色,那么一共有多少种不同的染法呢?其实,整个染色过程是需要分为三步的,即分别给其中一块染色:当染色顺序为A-B-C时,那么A有3种染法,B不能和A 一样,有2种染法,同样C 有2种,那么一共就有“ 3 2 2 ”种染法;(C-B-A同理)当染色顺序为B-A-C时,那么B有3种染法,A不能和B 一样,有2种染法,同样C 有2种,那么一共就有“ 3 2 2 ”种染法;(B-C-A同理)当染色顺序为A-C-B时,那么A有3种染法,第二步C没有限制,也有3种染法,但是最后的B就出问题了,我们没法确定它有2种还是1种染法一一如果C和A同色,则B 有2种染法;如果C和A不同色,则B只有1种染法一—此时,根据分步相乘的思想计算整个过程的染色方法“ 3 3 ? ”就不再适用了. (C-A- B 同理)因此,并不是只要分步完成整件事情就一定可以应用乘法原理,要想应用乘法原理,还必须满足第三个要求:3.做完一步时,这一步的结果很可能会影响后面步骤的结果,但一定不能影响后面步骤的方法数.如果这一步的不同结果会导致后面某一步的方法数发—变化,就不能直接用乘法原理计算—--- 简称“前不影响后原则”染色问题,是应用乘法原理最常见的一类题型,其实,从上面对A、B、C三部分的染色分析我们应该可以发现,染色的时候,要尽量避免“隔”着染,一定不要“跳”着染,而且,第一步要尽量去染“接触最多”的那一部分,这样,才能够使得后面的染色过程尽量避开“前影响后”.例题1如图,把A、B、C、D、E这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?「分析」分五步染色,先染哪一块呢?能否按照A、B、C、D、E的顺序染呢?练习1如图,把A、B、C、D这四部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问: 这幅图共有多少种不同的染色方法?例题2某市实行垃圾分类处理.每个地方放置五个垃圾桶,从左向右依次标明:电池、塑料、废纸、易拉罐、其它.现在准备把五个垃圾桶染成红、绿、蓝这3种颜色之一.(1)要求相邻两个垃圾桶颜色不同,一共有多少种染色方法?(2)要求相邻两个垃圾桶颜色不同且回收易拉罐的垃圾桶不能染成红色,一共有多少种染色方法?「分析」如果我们先染废纸垃圾桶:当它染红色时,回收易拉罐的垃圾桶可以染绿、蓝两种颜色;而当它染绿色(蓝色)时,回收废纸的垃圾桶只能染蓝色(绿色).因此先染废纸垃圾桶时,会影响易拉罐垃圾桶的染色方法数,就不能直接用乘法原理计算了.那么我们应该先给哪个垃圾桶染色呢?练习2麦兜很挑食,只吃带有鱼丸或粗面的搭配.一天它和3位同学来餐厅吃东西, 一开口就要鱼丸粗面,结果老板说没有.这个时候,由于时间太晚,餐厅快打烊了,只能做牛肚河粉,鱼丸油面,猪肉米线和牛肉拉面各一份,请问它们四只猪各点一份,有几种点法?在例题2中,有一个垃圾桶是有特殊要求的一一易拉罐垃圾桶不能染成红色,我们通过尝试可知:如果一开始先染其他的垃圾桶,那么前面垃圾桶的染色方法就会影响到易拉罐垃圾桶的染色方法数,即不能满足“前不影响后”原则,而如果首先染易拉罐垃圾桶,则不会出现该问题,所以一般而言,如果题目中有些对象是有特殊要求的,那么我们分步分析计算的时候,首先要考虑这些特殊的对象.卡莉娅、墨莫、小高和大头4名同学竞选班委.有班长、学习委员、生活委员三个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任.(1)有多少种可能的选举结果?(2)如果班长必须由卡莉娅来担任,有多少种可能的选举结果?(3)如果生活委员只能在墨莫和大头之中选,有多少种可能的选举结果?(4)如果学习委员不能由小高担任,有多少种可能的选举结果?「分析」可以按照职位一一确定,第(2)问中,班长只能由卡莉娅来担任,那么先确定哪一个职位的人选呢?其他小问呢?甲、乙、丙、丁、戊5个人竞选班委.有班长、副班长、纪律委员、卫生委员四个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任:请问:(1) 一共有多少种可能的选举结果?( 2)如果副班长只能在甲、丁和戊中选,有多少种可能的选举结果? ( 3)如果卫生委员不能由乙、丙担任,有多少种可能的选举结果?甲、乙、丙、丁四个人要住进A、B、C、D四间房间,每个房间住一个人.其中甲不住A房间,丙只住D房间.请问:这四个人住进四个房间有多少种住法?「分析」本题中甲和丙有特殊要求,我们应该先考虑甲还是丙呢?练习4甲、乙、丙、丁四个人要住进A、B、C、D四间房间,每个房间住一个人.其中甲只住A或B房间,丙只住A、B或C房间.请问:这四个人住进四个房间有多少种住法?例题5甲、乙、丙、丁、戊五人要驾驶A、B、C、D、E这五辆不同型号的汽车,请计算在下列情况下,分别共有多少种不同的安排方案:(1)只有甲能开汽车A,乙不会开汽车B;(2)会开A的只有甲和乙,会开E的只有甲、乙、丙.「分析」第(1)问中,甲和丙两人有特殊要求,我们应该先考虑哪一个人呢?第(2)问中,A和E两车有特殊要求,我们应该先考虑哪辆车呢?接下来我们分析一下“放相同棋子”的问题.如右图,将2枚相同的棋子放入2X2的方格内,每个格子只能放1枚,且要求每行每列最多只能放1枚,那么一共会有几种方法呢?其实,要把两枚相同的棋子放进格子内,只需要选出两个格子即可,然后每个格子里放一枚棋子.一共有两行,所以必定会是每行一枚,所以我们完全可以分行选格子,第行有两种选法,第一行选好后,第二行就只有一种选法了,所以一共有2X1=2 种.例题6右图是一个阶梯形方格表,在方格中放入五枚相同的棋子,使得每行、每列中都只有一枚棋子,这样的放法共有多少种?「分析」容易看出,每行只能有1枚棋子,每列也只能由一枚棋子, 我们可以把放五枚棋子的过程分成五步:一行一行或一列一列的放.课堂内外四色定理读书的格斯里向他的老师一一著名数学家摩根提出了这个问题,摩根没有能找到解决这个问题的途径.“四色问题”提出以后,最初并没有引起广泛的重视,许多数学家低估了它的难度.就连素以谦虚著称的德国数论专家闵可夫斯基在大学上拓扑课时也说:四色问题之所以一直没有获得解决,那仅仅是由于没有一流的数学家来解决它.说罢,他拿起粉笔,竟要当堂给学生推导出来,结果没有成功.下一节课他又去试,还是没有成功.过了几个星期,仍无进展.有一天,他刚跨进教室,适逢天上雷声大作,震耳欲聋.他马上对学生说:“上天在责备我自大,我也无法解决四色问题.”这样,四色问题就成了世界最著名的问题之一. 100多年中, “四色问题”使数学家们深为困扰.没有人能证明它,也没有人推翻它.电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了四色猜想的证明进程.就在1976年6月,哈肯与阿佩尔在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿次判断,终于完成了四色定理的证明,轰动了世界.作业1.五个座位排成一排,小高、墨莫、萱萱、阿呆、阿瓜每人选一个座位坐下,其中每个座位只能坐一个人,且萱萱不坐在中间的位置•这五个人有多少种坐法?2.如图,把A、B、C这三部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色•请问,这幅图共有多少种不同的染色方法?3.把A、B、C、D、E这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.这幅图共有多少种不同的染色方法?AL D亠4.甲、乙、丙、丁四个人排成一队,甲不当排头,乙不当排头也不当排尾,共有多少种不同的排法?5.在2 4的方格中放入两枚相同的棋子,要求两枚棋子既不在同一行也不在同一列,共有多少种放法?第十二讲乘法原理进阶1. 例题1答案:96详解:分步,分别给E、B、C、A、D染色,分别有4、3、2、2、2种染法,所以一共有4 3 2 2 2 96 种染色方法.2. 例题2答案:48; 32详解:(1)从左往右依次染色,分别有3、2、2、2、2种染法,共有3 2 2 2 2 48种染色方法;(2)分步,先染易拉罐垃圾桶,再分别给废纸、塑料、电池、其他这四个垃圾桶染色,五个垃圾桶分别有2、2、2、2、2种染法,所以一共有 2 2 2 2 2 32种染色方法.3. 例题3答案:24; 6; 12; 18详解:(1 )分别确定班长、学委、生活委员的人选,分别有4、3、2种选法,所以共有4 3 2 24种;(2)分别确定班长、学委、生活委员的人选,分别有1、3、2种选法,所以共有1 3 2 6种;(3)分别确定生活委员、学委、班长的人选,分别有2、3、2种选法,所以共有2 3 2 12种;(4)分别确定学委、班长、生活委员的人选,分别有3、3、2种选法,所以共有3 3 2 18种.4. 例题4答案:4详解:分步,分别安排丙、甲、乙、丁,分别有1、2、2、1种选法,所以一共有12 2 14 种选法.5. 例题5答案:18;24详解:(1 )先考虑甲,后考虑乙,再考虑其他三个人,分别有1、3、3、2、1种可能,共有1 3 32 1 18 种;(2)先考虑A,后考虑E,再考虑其他三辆车,分别有2、2、3、2、1种可能,所以共有2 23 2 1 24 种.6. 例题6答案:16详解:一共要选5个格子放棋子,一行一行选,每行1个,而且不能在同一列,从上往下,5行分别有2、2、2、2、1种选法,所以一共有2 2 2 2 1 16种选法.7. 练习1答案:48详解:分步,分别给B、C、A、D染色,分别有4、3、2、2种染法,所以一共有4 3 2 2 48种染色方法.8. 练习2答案:6详解:先让麦兜点,只有鱼丸油面1种可选,然后让其他3位同学依次点,分别有3、2、1种选法,共分四步,乘法原理,所以共有13 2 1 6中不同的选法.9. 练习3答案:120; 72; 72简答:(1) 5 4 3 2 120 种;(2)先确定副班长,再依次确定其他,共有 3 4 3 2 72种;(3)先确定卫生委员,再依次确定其他,共有 3 4 3 2 72种.10. 练习4答案:8简答:分步,分别安排甲、丙、乙、丁,分别有2、2、2、1种选法,所以一共有2 2 2 1 8种选法.11. 作业1答案:96.简答:可以按照萱萱、小高、墨莫、阿呆、阿瓜的顺序安排座位,有 4 4 3 2 1 96种•安排座位的顺序不唯一.12. 作业2答案:24简答:可以按照A、B、C的顺序染色,4 3 2 24种.染色顺序不唯一.13. 作业3答案:96简答:可以按照A、B、C、D、E的顺序染色,有4 3 2 2 2 96种.染色顺序不唯一.14. 作业4答案:8简答:按照乙、甲、丙、丁的顺序安排,有 2 2 2 1 8种排法.15. 作业5答案:12简答:一行一行选位置,第一行有4个格子可选,即4种选法;第二行还有3个格子可选,即有 3 种选法. 因此有 4 3 12 种不同的放法.。
四年级上册奥数乘法原理共张

丈夫志不大,何以佐乾坤。
海纳百川有容乃大壁立千仞无欲则刚
第二步确定十位,除了百位上已使用的数字不能用,所以有( )种方法;
作 业 回 顾 海纳百川有容乃大壁立千仞无欲则刚
第二步,确定百位上的数字,有( )种. 【变式】
由数字0、1、2组成三位数,问:
得意时应善待他人,因为你失意时会需要他们。
第三步确定个位,除了百位和十位上已使用过的数字,还有( )种选择.
有志始知蓬莱近,无为总觉咫尺远。
第一步,确定百位上的数字,有( )种.
请问有一农夫养了10头 牛,为什么只有19只角 ?
答案:有一头犀牛
乘法原理6 数字问题
对没志气的人,路程显得远;对没有银钱的人,城镇显得远。
雄鹰必须比鸟飞得高,因为它的猎物就是鸟。
第二步,确定百位上的数字,有( )种.
根据乘法原理,可以组成
个没有重复数字的三位数.
01 海纳百川有容乃大壁立千仞无欲则刚
一位数: 5个 二位数: 4×4=16 三位数: 4×4×3=48
【5】
由数字0,3,6组成的所有三位数的和是多少?
306 + 603 + 360 + 630 = 1899
THANKS
根据乘法原理,可以组成 3×3×3=27
个
⑵ 也分三步完成.
第一步,百位上有( 3)种选择;
第二步确定十位,除了百位上已使用的数字不能用,所以有( 2 )种方法; 第三步确定个位,除了百位和十位上已使用过的数字,还有( 1 )种选择.
高思奥数导引小学四年级含详解答案第12讲 复杂竖式
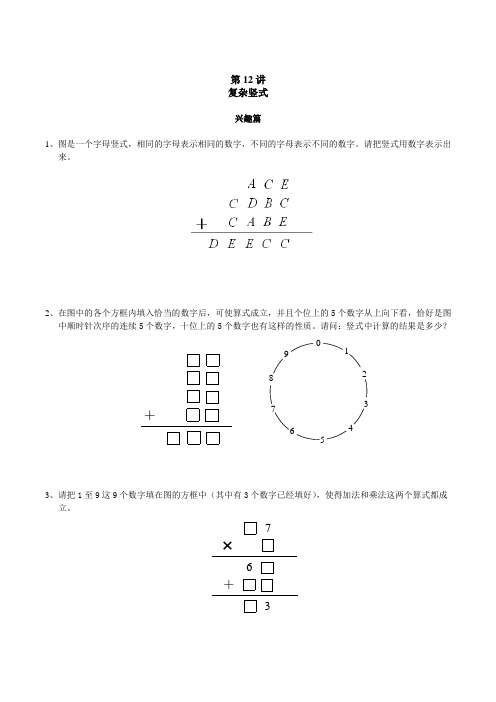
第12讲 复杂竖式兴趣篇1、图是一个字母竖式,相同的字母表示相同的数字,不同的字母表示不同的数字。
请把竖式用数字表示出 来。
2、在图中的各个方框内填入恰当的数字后,可使算式成立,并且个位上的5个数字从上向下看,恰好是图 中顺时针次序的连续5个数字,十位上的5个数字也有这样的性质。
请问:竖式中计算的结果是多少?+80123456793、请把1至9这9个数字填在图的方框中(其中有3个数字已经填好),使得加法和乘法这两个算式都成 立。
367×+4、图是一个乘法竖式,请在其中的10个方框内分别填入0至9这10个数字,使得竖式成立。
84227543×835、如图,在乘法竖式的每个方框中填入一个数字,使其成为正确的竖式,那么所得的乘积应该是多少?×116、如图,在乘法竖式的每个方框中填入一个数字,使其成为正确的竖式,那么所得的乘积应该是多少?551×7、在图的方框内填入恰当的数字,可以得到一个正确的乘法竖式。
已知这样的填法有两种,这两种填法所得到的两个不同的乘积相差多少?×153248、在图的方框内填上适当的数字,使得竖式成立,请写出所有的答案。
2112672029、请把图中的除法竖式补充完整。
22290410、请把图中的除法竖式补充完整。
这个算式的被除数、除数以及商的总和是多少?668592拓展篇1、在图的字母竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字。
已知个位向十位的进位为2,且E 是奇数,则A 、B 、C 、D 分别代表什么数字?A AB D E +A B E ECC D A C2、在图中,相同的字母代表相同的数字,不同的字母代表不同的数字。
请给出两种使竖式成立的填法。
E S V YN E T E T E NF F II F F N Y E F T +O R T E3、在图所示的乘法竖式中,每个方框和字母都代表一个数字,相同的字母代表相同的数字,不同的字母代表不同的数字。
高斯小学奥数四年级上册含答案第12讲_乘法原理进阶

第十二讲乘法原理进阶在之前我们学习了“加法原理与乘法原理”一讲,即分类相加与分步相乘的思想.如果完成一件事分为几个步骤,在每一个步骤中又有不同的方法,那么把每步的方法数相乘就得到所有的方法数——这就是乘法原理.要想把过程分成几个步骤从而应用乘法原理,必须保证各步骤之间满足下面两个要求:1.2.那么是不是只要分步骤完成整件事情就可以直接用乘法原理呢?如下图,把A、B、C三部分用三种不同的颜色染色,要求相邻两部分不能同色,那么一共有多少种不同的染法呢?A B C其实,整个染色过程是需要分为三步的,即分别给其中一块染色:当染色顺序为A→B→C时,那么A有3种染法,B不能和A一样,有2种染法,同样C有2种,那么一共就有“322⨯⨯”种染法;(C→B→A同理)当染色顺序为B→A→C时,那么B有3种染法,A不能和B一样,有2种染法,同样C有2种,那么一共就有“322⨯⨯”种染法;(B→C→A同理)当染色顺序为A→C→B时,那么A有3种染法,第二步C没有限制,也有3种染法,但是最后的B就出问题了,我们没法确定它有2种还是1种染法——如果C和A同色,则B有2种染法;如果C和A不同色,则B只有1种染法——此时,根据分步相乘的思想计算整个过程的染色方法“33?⨯⨯”就不再适用了.(C→A→B同理)因此,并不是只要分步完成整件事情就一定可以应用乘法原理,要想应用乘法原理,还必须满足第三个要求:3.——简称“前不影响后.....原则”染色问题,是应用乘法原理最常见的一类题型,其实,从上面对A、B、C 三部分的染色分析我们应该可以发现,染色的时候,要尽量避免“隔”着染,一定不要“跳”着染,而且,第一步要尽量去染“接触最多”的那一部分,这样,才能够使得后面的染色过程尽量避开“前影响后”.例题1如图,把A 、B 、C 、D 、E 这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?「分析」分五步染色,先染哪一块呢?能否按照A 、B 、C 、D 、E 的顺序染呢? 练习1如图,把A 、B 、C 、D 这四部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问:这幅图共有多少种不同的染色方法?例题2某市实行垃圾分类处理.每个地方放置五个垃圾桶,从左向右依次标明:电池、塑料、废纸、易拉罐、其它.现在准备把五个垃圾桶染成红、绿、蓝这3种颜色之一.(1)要求相邻两个垃圾桶颜色不同,一共有多少种染色方法? (2)要求相邻两个垃圾桶颜色不同且回收易拉罐的垃圾桶不能染成红色,一共有多少种染色方法?「分析」如果我们先染废纸垃圾桶:当它染红色时,回收易拉罐的垃圾桶可以染绿、蓝两种颜色;而当它染绿色(蓝色)时,回收废纸的垃圾桶只能染蓝色(绿色).因此先染废纸垃圾桶时,会影响易拉罐垃圾桶的染色方法数,就不能直接用乘法原理计算了.那么我们应该先给哪个垃圾桶染色呢?练习2麦兜很挑食,只吃带有鱼丸或粗面的搭配.一天它和3位同学来餐厅吃东西,一开口就要鱼丸粗面,结果老板说没有.这个时候,由于时间太晚,餐厅快打烊了,只能做牛肚河粉,鱼丸油面,猪肉米线和牛肉拉面各一份,请问它们四只猪各点一份,有几种点法?在例题2中,有一个垃圾桶是有特殊要求的——易拉罐垃圾桶不能染成红色,我们通过尝试可知:如果一开始先染其他的垃圾桶,那么前面垃圾桶的染色方法就会影响到易拉罐垃圾桶的染色方法数,即不能满足“前不影响后”原则,而如果首先染易拉罐垃圾桶,则不会出现该问题,所以一般而言,如果题目中有些对象是有特殊要求的,那么我们分步..分析计算的时候,首先要考虑这些特殊的对象.例题3卡莉娅、墨莫、小高和大头4名同学竞选班委.有班长、学习委员、生活委员三个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任.(1)有多少种可能的选举结果?(2)如果班长必须由卡莉娅来担任,有多少种可能的选举结果?(3)如果生活委员只能在墨莫和大头之中选,有多少种可能的选举结果?(4)如果学习委员不能由小高担任,有多少种可能的选举结果?「分析」可以按照职位一一确定,第(2)问中,班长只能由卡莉娅来担任,那么先确定哪一个职位的人选呢?其他小问呢?练习3甲、乙、丙、丁、戊5个人竞选班委.有班长、副班长、纪律委员、卫生委员四个职位,每个人只能担任一个职位,并且每个职位只能由一个人担任:请问:(1)一共有多少种可能的选举结果?(2)如果副班长只能在甲、丁和戊中选,有多少种可能的选举结果?(3)如果卫生委员不能由乙、丙担任,有多少种可能的选举结果?例题4甲、乙、丙、丁四个人要住进A、B、C、D四间房间,每个房间住一个人.其中甲不住A房间,丙只住D房间.请问:这四个人住进四个房间有多少种住法?「分析」本题中甲和丙有特殊要求,我们应该先考虑甲还是丙呢?练习4甲、乙、丙、丁四个人要住进A 、B 、C 、D 四间房间,每个房间住一个人.其中甲只住A 或B 房间,丙只住A 、B 或C 房间.请问:这四个人住进四个房间有多少种住法?例题5甲、乙、丙、丁、戊五人要驾驶A 、B 、C 、D 、E 这五辆不同型号的汽车,请计算在下列情况下,分别共有多少种不同的安排方案: (1)只有甲能开汽车A ,乙不会开汽车B ;(2)会开A 的只有甲和乙,会开E 的只有甲、乙、丙.「分析」第(1)问中,甲和丙两人有特殊要求,我们应该先考虑哪一个人呢?第(2)问中,A 和E 两车有特殊要求,我们应该先考虑哪辆车呢?接下来我们分析一下“放相同棋子”的问题.如右图,将2枚相同的棋子放入2×2的方格内,每个格子只能放1枚,且要求每行每列最多只能放1枚,那么一共会有几种方法呢?其实,要把两枚相同的棋子放进格子内,只需要选出两个格子即可,然后每个格子里放一枚棋子.一共有两行,所以必定会是每行一枚,所以我们完全可以分行选格子,第一行有两种选法,第一行选好后,第二行就只有一种选法了,所以一共有2×1=2种.例题6右图是一个阶梯形方格表,在方格中放入五枚相同的棋子,使得每行、每列中都只有一枚棋子,这样的放法共有多少种?「分析」容易看出,每行只能有1枚棋子,每列也只能由一枚棋子,我们可以把放五枚棋子的过程分成五步:一行一行或一列一列的放.课堂内外四色定理四色定理与费马大定理、哥德巴赫猜想并称为近代数学三大难题.四色定理的内容是:对于任何一张地图,只用四种颜色,就可以把有相邻边界的国家染上不同的颜色.四色问题的提出来自英国.1852年,在大学读书的格斯里向他的老师——著名数学家摩根提出了这个问题,摩根没有能找到解决这个问题的途径.“四色问题”提出以后,最初并没有引起广泛的重视,许多数学家低估了它的难度.就连素以谦虚著称的德国数论专家闵可夫斯基在大学上拓扑课时也说:四色问题之所以一直没有获得解决,那仅仅是由于没有一流的数学家来解决它.说罢,他拿起粉笔,竟要当堂给学生推导出来,结果没有成功.下一节课他又去试,还是没有成功.过了几个星期,仍无进展.有一天,他刚跨进教室,适逢天上雷声大作,震耳欲聋.他马上对学生说:“上天在责备我自大,我也无法解决四色问题.”这样,四色问题就成了世界最著名的问题之一.l00多年中,“四色问题”使数学家们深为困扰.没有人能证明它,也没有人推翻它.电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了四色猜想的证明进程.就在1976年6月,哈肯与阿佩尔在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿次判断,终于完成了四色定理的证明,轰动了世界.作业1. 五个座位排成一排,小高、墨莫、萱萱、阿呆、阿瓜每人选一个座位坐下,其中每个座位只能坐一个人,且萱萱不坐在中间的位置.这五个人有多少种坐法?2. 如图,把A 、B 、C 这三部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.请问,这幅图共有多少种不同的染色方法?3. 把A 、B 、C 、D 、E 这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色.这幅图共有多少种不同的染色方法?4. 甲、乙、丙、丁四个人排成一队,甲不当排头,乙不当排头也不当排尾,共有多少种不同的排法?5. 在的方格中放入两枚相同的棋子,要求两枚棋子既不在同一行也不在同一列,共有多少种放法?24 ABCD E第十二讲乘法原理进阶1.例题1答案:96详解:分步,分别给E、B、C、A、D染色,分别有4、3、2、2、2种染法,所以一共有4322296⨯⨯⨯⨯=种染色方法.2.例题2答案:48;32方法;(2)分步,先染易拉罐垃圾桶,再分别给废纸、塑料、电池、其他这四个垃圾桶染色,五个垃圾桶分别有2、2、2、2、2种染法,所以一共有2222232⨯⨯⨯⨯=种染色方法.3.例题3答案:24;6;12;18种;(2)分别确定班长、学委、生活委员的人选,分别有1、3、2种选法,所以共有1326⨯⨯=种;(3)分别确定生活委员、学委、班长的人选,分别有2、3、2种选法,所以共有23212⨯⨯=种;(4)分别确定学委、班长、生活委员的人选,分别有3、3、2种选法,所以共有33218⨯⨯=种.4.例题4答案:4种选法.5.例题5答案:18;24详解:(1)先考虑甲,后考虑乙,再考虑其他三个人,分别有1、3、3、2、1种可能,共有⨯⨯⨯⨯=种;1332118(2)先考虑A,后考虑E,再考虑其他三辆车,分别有2、2、3、2、1种可能,所以共有⨯⨯⨯⨯=种.22321246.例题6答案:16详解:一共要选5个格子放棋子,一行一行选,每行1个,而且不能在同一列,从上往下,5行分别有2、2、2、2、1种选法,所以一共有2222116⨯⨯⨯⨯=种选法.7.练习1答案:48详解:分步,分别给B、C、A、D染色,分别有4、3、2、2种染法,所以一共有⨯⨯⨯=种染色方法.4322488.练习2答案:6详解:先让麦兜点,只有鱼丸油面1种可选,然后让其他3位同学依次点,分别有3、2、1种选法,共分四步,乘法原理,所以共有13216⨯⨯⨯=中不同的选法.9.练习3答案:120;72;72⨯⨯⨯=5432120(2)先确定副班长,再依次确定其他,共有343272⨯⨯⨯=种;(3)先确定卫生委员,再依次确定其他,共有343272⨯⨯⨯=种.10.练习4答案:8种选法.11.作业1答案:96.简答:可以按照萱萱、小高、墨莫、阿呆、阿瓜的顺序安排座位,有4432196⨯⨯⨯⨯=种.安排座位的顺序不唯一.12.作业2答案:24简答:可以按照A、B、C的顺序染色,43224⨯⨯=种.染色顺序不唯一.13.作业3答案:96简答:可以按照A、B、C、D、E的顺序染色,有4322296⨯⨯⨯⨯=种.染色顺序不唯一.14.作业4答案:8简答:按照乙、甲、丙、丁的顺序安排,有22218⨯⨯⨯=种排法.15.作业5答案:12简答:一行一行选位置,第一行有4个格子可选,即4种选法;第二行还有3个格子可选,即有3种选法.因此有4312⨯=种不同的放法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 例题 1 答案: 96
第十二讲 乘法原理进阶
详解:分步,分别给 E 、B 、C、A、D 染色,分别有 4、3、2、2、2 种染法,所以一共有 4 3 2 2 2 96
种染色方法.
2. 例题 2 答案: 48; 32 详解:(1)从左往右依次染色,分别有 3、2、 2、 2、2 种染法,共有 3 2 2 2 2 48 种染色 方法; ( 2)分步,先染易拉罐垃圾桶,再分别给废纸、塑料、电池、其他这四个垃圾桶染色,五个垃 圾桶分别有 2、2、2、 2、2 种染法,所以一共有 2 2 2 2 2 32 种染色方法.
接下来我们分析一下“放相同棋子”的问题.
如右图,将 2 枚相同的棋子放入 2×2 的方格内,每个格子
只能放 1 枚,且要求每行每列最多只能放 1 枚,那么一共会有
几种方法呢?
其实,要把两枚相同的棋子放进格子内,只需要选出两个
格子即可,然后每个格子里放一枚棋子.
一共有两行, 所以必定会是每行一枚, 所以我们完全可以分行选格子, 第一
1. 每步都只是整件事情的一个部分,必须全部完成才算做完这件事;
2. 步骤之间要有先后顺序,先确定好一步,再做下一步,……直到最后. 那么是不是只要分步骤完成整件事情就可以直接用乘法原理呢? 如下图,把 A、B、C 三部分用三种不同的颜色染色,要求相邻两部分不能 同色,那么一共有多少种不同的染法呢?
“四色问题”提出以后,最初并没有引起广泛的重视,许多数学家低估了它 的难度.就连素以谦虚著称的德国数论专家闵可夫斯基在大学上拓扑课时也说: 四色问题之所以一直没有获得解决,那仅仅是由于没有一流的数学家来解决 它.说罢,他拿起粉笔,竟要当堂给学生推导出来,结果没有成功.下一节课他 又去试,还是没有成功.过了几个星期,仍无进展.有一天,他刚跨进教室,适 逢天上雷声大作,震耳欲聋.他马上对学生说: “上天在责备我自大,我也无法 解决四色问题.”这样,四色问题就成了世界最著名的问题之一. l00 多年中, “四色问题”使数学家们深为困扰.没有人能证明它,也没有人推翻它.
( 2)先考虑 A ,后考虑 E ,再考虑其他三辆车,分别有 2、 2、 3、 2 、1 种可能,所以共有
2 2 3 2 1 24 种.
6. 例题 6 答案: 16 详解: 一共要选 5 个格子放棋子,一行一行选,每行 1 个,而且不能在同一列,从上往下, 5 行 分别有 2、2、2、 2、1 种选法,所以一共有 2 2 2 2 1 16 种选法.来自3 3 ? ”就不再适用
了.( C→ A→B 同理)
因此,并不是只要分步完成整件事情就一定可以应用乘法原理, 要想应用乘
法原理,还必须满足第三个要求:
3. 做完一步时,这一步的结果很可能会影响后面步骤的结果,但一定不能
影响后面步骤的方法数. 如果这一步的不同结果会导致后面某一步的方法数发生
变化,就不能直接用乘法原理计算.
2. 如图,把 A、B、 C 这三部分用 4 种不同的颜色染色,且相邻的部分不能使用同一种颜 色.请问,这幅图共有多少种不同的染色方法?
AB C
3. 把 A、B、C、 D、E 这五部分用 4 种不同的颜色染色,且相邻的部分不能使用同一种颜 色.这幅图共有多少种不同的染色方法? A D BC E
4. 甲、乙、丙、丁四个人排成一队,甲不当排头,乙不当排头也不当排尾,共有多少种不 同的排法?
4. 例题 4 答案: 4 详解: 分步,分别安排丙、甲、乙、丁,分别有 种选法.
1、2、2、1 种选法,所以一共有 1 2 2 1 4
5. 例题 5 答案: 18; 24 详解:(1 )先考虑甲,后考虑乙,再考虑其他三个人,分别有
1、 3、 3、2 、 1 种可能,共有
1 3 3 2 1 18 种;
「分析」 可以按照职位一一确定,第( 2)问中,班长只能由卡莉娅来担任,那么 先确定哪一个职位的人选呢?其他小问呢?
练习 3
甲、乙、丙、丁、戊 5 个人竞选班委.有班长、副班长、纪律委员、卫生委 员四个职位, 每个人只能担任一个职位, 并且每个职位只能由一个人担任: 请问: ( 1)一共有多少种可能的选举结果?( 2)如果副班长只能在甲、丁和戊中选, 有多少种可能的选举结果?( 3)如果卫生委员不能由乙、丙担任,有多少种可 能的选举结果?
第十二讲 乘法原理进阶
在之前我们学习了 “加法原理与乘法原理” 一讲, 即分类相加与分步相乘的 思想.
如果完成一件事分为几个步骤, 在每一个步骤中又有不同的方法, 那么把每 步的方法数相乘就得到所有的方法数——这就是乘法原理.
要想把过程分成几个步骤从而应用乘法原理, 必须保证各步骤之间满足下面 两个要求:
电子计算机问世以后,由于演算速度迅速提高,加 之人机对话的出现,大大加快了四色猜想的证明进程.
就在 1976 年 6 月,哈肯与阿佩尔在美国伊利诺斯大 学 的两台不同的电子计算机上,用了 1200 个小时,作了 100 亿次判断,终于完成了四色定理的证明, 轰动了世界.
作业
1. 五个座位排成一排,小高、墨莫、萱萱、阿呆、阿瓜每人选一个座位坐下,其中每个座 位只能坐一个人,且萱萱不坐在中间的位置.这五个人有多少种坐法?
「分析」 如果我们先染废纸垃圾桶:当它染红色时,回收易拉罐的垃圾桶可以染 绿、蓝两种颜色;而当它染绿色(蓝色)时,回收废纸的垃圾桶只能染蓝色(绿 色).因此先染废纸垃圾桶时,会影响易拉罐垃圾桶的染色方法数,就不能直接 用乘法原理计算了.那么我们应该先给哪个垃圾桶染色呢?
练习 2
麦兜很挑食,只吃带有鱼丸或粗面的搭配. 一天它和 3 位同学来餐厅吃东西, 一开口就要鱼丸粗面,结果老板说没有.这个时候,由于时间太晚,餐厅快打烊 了,只能做牛肚河粉,鱼丸油面,猪肉米线和牛肉拉面各一份,请问它们四只猪 各点一份,有几种点法?
9. 练习 3 答案: 120;72;72 简答:(1) 5 4 3 2 120 种; (2)先确定副班长,再依次确定其他,共有 3 4 3 2 72 种; (3)先确定卫生委员,再依次确定其他,共有 3 4 3 2 72 种.
10. 练习 4 答案: 8 简答: 分步,分别安排甲、丙、乙、丁,分别有 种选法.
——简称“前.不.影.响.后.原则” 染色问题,是应用乘法原理最常见的一类题型,其实,从上面对
A、 B、 C
三部分的染色分析我们应该可以发现,染色的时候,要尽量避免“隔”着染,一
定不要“跳”着染,而且,第一步要尽量去染“接触最多”的那一部分,这样,
才能够使得后面的染色过程尽量避开“前影响后” .
例题 1
如图,把 A、B、C、D、E 这五部分用 4 种不同的颜色
A
染色,且相邻的部分不能使用同一种颜色.请问:这
B
幅图共有多少种不同的染色方法?
E
「分析」 分五步染色,先染哪一块呢?能否按照 A、 B、 C、D、
E 的顺序染呢?
C
D
练习 1
如图,把 A、B、C、D 这四部分用 4 种不同的
B
颜色染色,且相邻的部分不能使用同一种颜色. 请问: A
3. 例题 3 答案: 24; 6; 12; 18 详解:(1)分别确定班长、 学委、生活委员的人选, 分别有 4、3、2 种选法, 所以共有 4 3 2 24 种; (2)分别确定班长、 学委、 生活委员的人选, 分别有 1、3、2 种选法, 所以共有 1 3 2 6 种; (3)分别确定生活委员、 学委、 班长的人选, 分别有 2、3、2 种选法, 所以共有 2 3 2 12 种; (4)分别确定学委、 班长、 生活委员的人选, 分别有 3、3、2 种选法, 所以共有 3 3 2 18 种.
例题 3
卡莉娅、墨莫、小高和大头 4 名同学竞选班委.有班长、学习委员、 生活委员三个职位, 每个人只能担任一个职位, 并且每个职位只能由 一个人担任. ( 1)有多少种可能的选举结果? ( 2)如果班长必须由卡莉娅来担任,有多少种可能的选举结果? ( 3)如果生活委员只能在墨莫和大头之中选,有多少种可能的选举 结果? ( 4)如果学习委员不能由小高担任,有多少种可能的选举结果?
A
B
C
其实,整个染色过程是需要分为三步的,即分别给其中一块染色:
当染色顺序为 A→B→C 时,那么 A 有 3 种染法, B 不能和 A 一样,有 2 种 染法,同样 C 有 2 种,那么一共就有“ 3 2 2 ”种染法;(C→B→A 同理)
当染色顺序为 B→A→C 时,那么 B 有 3 种染法, A 不能和 B 一样,有 2 种 染法,同样 C 有 2 种,那么一共就有“ 3 2 2 ”种染法;(B→C→A 同理)
行有两种选法,第一行选好后,第二行就只有一种选法了,所以一共有
2×1=2
种.
例题 6
右图是一个阶梯形方格表,在方格中放入五枚相同的棋 子,使得每行、每列中都只有一枚棋子,这样的放法共 有多少种?
「分析」容易看出,每行只能有 1 枚棋子,每列也只能由一枚棋子, 我们可以把放五枚棋子的过程分成五步:一行一行或一列一列的 放.
在例题 2 中,有一个垃圾桶是有特殊要求的——易拉罐垃圾桶不能染成红色, 我们通过尝试可知: 如果一开始先染其他的垃圾桶, 那么前面垃圾桶的染色方法 就会影响到易拉罐垃圾桶的染色方法数,即不能满足“前不影响后”原则,而如 果首先染易拉罐垃圾桶, 则不会出现该问题, 所以一般而言, 如果题目中有些对 象是有特殊要求的, 那么我们 分.步.分析计算的时候, 首先要考虑这些特殊的对象.
D
这幅图共有多少种不同的染色方法?
C
例题 2
某市实行垃圾分类处理. 每个地方放置五个垃圾桶, 从左向右依次标 明:电池、塑料、废纸、易拉罐、其它.现在准备把五个垃圾桶染成 红、绿、蓝这 3 种颜色之一. ( 1)要求相邻两个垃圾桶颜色不同,一共有多少种染色方法? ( 2)要求相邻两个垃圾桶颜色不同且回收易拉罐的垃圾桶不能染成 红色,一共有多少种染色方法?
