圆的有关计算练习题1
《圆的周长、面积》练习题加答案(完整版)

《圆的周长、面积》练习题一.选择题(共10题,共20分)1.把一个圆的半径按n:1的比放大,放大后与放大前圆的面积比是()。
A.n:1B.2n:1C.:1 D.:22.圆的面积与它半径成()比例。
A.正B.反C.不成3.强强要在方格纸上画一个圆,要求点(1,4)、(3,2)、(3,6)恰好在圆周上(如图),这个圆的圆心应该在()上。
A.(3,5)B.(4,4)C.(3,4)D.(5,4)4.圆的周长是它的半径的()倍。
A.πB.2πC.3.14D.6.285.画圆时,圆的周长为15.7cm,那么圆规两脚间的距离为()。
A.2.5cmB.5cmC.15.7cm6.一个圆的直径与一个正方形的边长相等,比较它们的面积()。
A.相等B.圆面积大C.正方形面积大D.不能确定7.如图。
以大圆的半径为直径画一小圆。
大圆的周长是小圆周长的()倍。
A.2B.4C.68.一个直径为2厘米的半圆面,它的周长是()厘米。
A.6.28B.3.14C.4.14D.5.149.在同圆或等圆中,扇形的大小和()有关。
A.直径B.半径C.圆心角10.一个圆的半径扩大2倍,那么面积和周长()。
A.面积和周长扩大2倍B.面积扩大4倍,周长扩大2倍 C.周长扩大4倍,面积扩大2倍二.判断题(共10题,共20分)1.如果圆的半径扩大2倍,那么它的周长扩大6倍,它的面积扩大9倍。
()2.把一张圆形纸片从不同方向折叠,折痕都经过圆心。
()3.任何一个圆的周长都是它直径长度的π倍。
()4.圆周率π=3.14。
()5.有两个面积相等的圆,他们的周长也一定相等。
()6.通过圆心的线段是半径。
()7.在一个圆内,剪去一个扇形后,剩下的部分仍是扇形。
()8.半圆的面积是圆面积的一半,半圆的周长也是圆周长的一半。
()9.量角器是把半圆分成180份制成的。
()10.周长相等的长方形正方形和圆,正方形的面积最大。
()三.填空题(共10题,共17分)1.把一个圆平均分成若干(偶数)等份,剪开后可以拼成一个近似的(),这个长方形的长相当于圆的(),宽相当于圆的()。
2023年数学中考真题:圆的有关计算及证明精选(一)

圆的有关计算及证明2023年数学中考试题精选(一)1.(2023.营口23题)如图,在△ABC中,AB=BC,以BC为直径作圆O与AC将于点D,过点D作DE⊥AB,交CB延长线于点F,垂足为点E.(1)求证:DF为圆O的切线;,求BF的长。
(2)若BE=3,cosC=452.(2023.本溪铁岭辽阳24题)如图,AB是圆O的直径,点C,E在圆O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.(1)求证:EF与圆O相切;,求BC的长。
(2)若BF=1,sin∠AFE=453.(2023.沈阳22题)如图,BE是圆O的直径,点A和点D是圆O上的两点,过点A作圆O的切线交BE延长线于点C.(1)若∠ADE=25°,求∠C的度数;(2)若AB=AC,CE=2,求圆O半径的长.4.(2023.大连市23题)如图1,在圆O中,AB为圆O的直径,点C为圆O上一点,AD为∠CAB的平分线交圆O于点D,连接OD交BC于点E.(1)求∠BED的度数;(2)如图2,过点A作圆O的切线BC延长线于点F,过点D作DG ∥AF交AB于点G.若AD=2√35,DE=4,求DG的长。
5.(2023.湖北省恩施州23题)如图,△ABC是等腰直角三角形,∠ACB=90°,点O为AB的中点,连接CO交圆O于点E,圆O与AC 相切于点D.(1)求证:BC是圆O的切线;(2)延长CO交圆O于点G,连接AC交圆O于点F,若AC=4√(2),求FG的长.6.(2023.贵州省23题)如图,已知圆O是等边三角形ABC的外接圆,连接CO并延长交AB于点D,交圆O于点E,连接EA,EB.(1)写出图中一个度数为30°的角;____,图中与△ACD全等的三角形是______;(2)求证:△AED∽△CEB;(3)连接OA,OB,判断四边形OAEB的形状,并说明理由。
7.(2023.江苏省24题)如图,在△ABC中,AB=AC,以AB为直径的圆O交边AC于点D,连接BD,过点C作CE∥AB.(1)请用无刻度的直尺和圆规作图:过点B作圆O的切线,交CE 于点F;(不写作法,保留作图痕迹,标明字母)(2)在(1)的条件下,求证:BD=BF.8.(2023.江西省20题)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的圆O与AC相交于点D,E为优弧ABD上一点,且∠ADE=40°.(1)求BE的长;(2)若∠EAD=76°,求证:CB为圆O的切线.9.(2023.沈阳22题)如图,AB是圆O的直径,点C是圆O上的一点(点C不与点A,B重合),连接AC,BC,点D是AB上的一点,AC=AD,BE交CD的延长线于点E,且BE=BC.(1)求证:BE是圆O的切线;(2)若圆O的半径为5,tanE=1,则BE的长为_____.210.(2023.扬州市25题)如图,在△ABC中,∠ACB=90°,点D是AB∠A,点O在BC上,以点O为圆心的圆经过C、上一点,且∠BCD=12D两点.(1)试判断直线AB与圆O的位置关系,并说明理由;,圆O的半径为3,求AC的长.(2)若sinB=3511.(2023.广西壮族自治区23题)如图,PO平分∠APD,PA与圆O相切于点A,延长AO交PD于点C,过点O作OB⊥PD,垂足为B.(1)求证:PB是圆O的切线;(2)若圆O的半径为4,OC=5,求PA的长.12.(2023.广东省22题)如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A`,连接AA`交BD于点E,连接CA`.(1)求证:AA`⊥CA`;(2)以点O为圆心,OE为半径作圆.①如图2,圆O与CD相切,求证:AA`=√3CA`;②如图3,圆O与CA`相切,AD=1,求圆O的面积.13.(2023.安徽省20题)已知四边形ABCD内接于圆O,对角线BD是圆O的直径.(1)如图1,连接OA,CA,若OA⊥BD,求证:CA平分⊥BCD; (2)如图2,E为圆O内一点,满足AE⊥BC,CE⊥AB,若BD=3√3,AE=3.求弦BC的长.14.(2023.湖北黄冈市20题)如图,⊥ABC 中,以AB 为直径的圆O 交BC 于点D ,DE 是圆O 的切线 ,且DE⊥AC ,垂足为E ,延长CA 交圆O 于点F.(1)求证:AB=AC ;(2)若AE=3,ED=6,求AF 的长。
圆的周长和面积练习题

圆的周长和⾯积练习题圆的周长和⾯积练习题(1)⼀.填空题1.圆是平⾯上的()线图形。
()决定圆的位置,⽤字母()表⽰;()决定圆的⼤⼩,⽤字母()表⽰。
2.画圆时,圆规两脚间的距离就是圆的()。
3.两端都在圆上的线段,()最长。
4.圆⽆论⼤⼩,它的周长总是直径的()倍多⼀些,我们叫它做(),⽤字母()表⽰。
5.有⼀个圆形鱼池的半径是10⽶,如果绕其周围⾛⼀圈,要⾛()⽶。
6.⼀个挂钟的时针长5厘⽶,⼀昼夜这根时针的尖端⾛了()厘⽶。
7.把圆分成16等份,剪开后,⽤这些近似等腰三⾓形的⼩纸⽚拼成近似的长⽅形,这个长⽅形的长相当于圆的(),即(),长⽅形的宽是圆的(),长⽅形的⾯积=(),所以圆的⾯积=()。
8.在同⼀个圆⾥,所有的()相等,所有的()也相等,且()等于()的2倍。
⼆.选择题。
1.从圆⼼到圆上任意⼀点的线段叫做()A.直径 B。
半径 C直线2.周长相等的长⽅形、正⽅形、圆,()⾯积最⼤。
A正⽅形 B长⽅形 C.圆3.⼤圆直径是⼩圆直径的3倍,⼤圆的⾯积是⼩圆⾯积的()倍。
A .3 B.6 C .9 D.124.圆的半径由6厘⽶增加到9厘⽶,圆的⾯积增加了()平⽅厘⽶。
A.9B.45C.45π三.填表。
四.计算1、⼀种汽车轮胎的外直径是1.02⽶,每分钟转50周,车轮每分钟前进多少⽶?2⼀种⼿榴弹爆炸后,有效杀伤范围的半径是8⽶,有效杀伤⾯积是多少平⽅⽶?3在⼀个直径是16⽶的圆⼼花坛周围,有⼀条宽为2⽶的⼩路围绕,⼩路的⾯积是多少平⽅⽶?4.⼀个圆环的外圆直径是8分⽶,内圆半径是40厘⽶.求这个圆环的⾯积?圆的周长和⾯积练习题(2)1、⼀辆⾃⾏车车轮外直径为0.6⽶,⼩华骑⾃⾏车从家到学校,如果每分钟转动100周,他从家到学校出发10分钟到达学校,⼩华家距学校多少⽶?2、⽕车轮的外直径长0.9⽶,如果它分钟转400周,那么这列⽕车每⼩时前进多少千⽶?3、⼀辆⾃⾏车轮胎的外直径是70厘⽶,如果车轮平均每分钟转100圈,半⼩时可以⾏多少⽶?4、⼀个圆形花圃直径8⽶,⽤四分之三种兰花,兰花的种植⾯积是多少?5、在⼀张边长10厘⽶的正⽅形纸上剪⼀个最⼤的圆后,这个圆周长和⾯积各是多少?6、在⼀张周长为4厘⽶的正⽅形硬纸板上,剪⼀个最⼤的圆,剩下部分的⾯积是多少平⽅厘⽶?7、⽤两根长12.56厘⽶的铁丝分别围成⼀个正⽅形和⼀个圆,哪个⾯积⼤?⼤多少?8、在⼀个长8分⽶,宽5分⽶的⽩铁⽪上剪下⼀个最⼤的圆,剪去的边⾓料的⾯积是多少平⽅分⽶?9、⼀种零件的横截⾯是⼀个圆环,外圈半径是0.5⽶,内圈半径是0.4⽶.这种零件横截⾯的⾯积是多少平⽅⽶?10、⼀个环形,外圆直径是30厘⽶,内圆直径是10厘⽶,这个环形的⾯积是多少平⽅厘⽶?11、⼀个⽊盆的底⾯是圆形。
圆练习题1

一、填空:1、当圆规两脚尖间的距离为3厘米时,画出的圆的周长是()厘米2、圆的直径扩大3倍,周长就()倍,圆的周长缩小4倍,半径就().3、有一个圆形鱼池的半径是10米,如果绕其周围走一圈,要走()米,5、圆中最长的线段是6厘米,这个圆的周长是()厘米8、要在底面半径是14厘米的圆柱形水桶外面打上一个铁丝箍,接头部分是6厘米,需用铁丝()厘米。
9、圆的周长是直径的()倍,是半径的()。
10、在从边长是6厘米的正方形纸片中剪出一个最大的圆,圆的直径是(),它的周长是()。
11、在一个周长是16厘米的正方形纸上剪下一个最大的圆,这个圆的周长是(),12、在长10厘米、宽8厘米的长方形中剪下一个最大的圆,这个圆的半径是()厘米,周长是()厘米13、在长5厘米,宽3厘米的长方形中剪下一个最大的半圆,这个半圆的周长是()13、用铜丝绕线圈,线圈半径1.5cm,绕100 圈需用( )铜丝。
14、台钟的分针长6cm,时针长5cm,从星期一上午8 点到星期二上午8点,分针走了()厘米,时针走了()厘米15、一个半圆形的鱼池周长是51.4米,它的半径是()米。
16、大圆直径是小圆直径的3倍,大圆周长是小圆周长的()倍。
小圆的半径是大圆半径的1/3,则小圆的周长是大圆周长的()17、用一根18.84米长的铁丝围成一个正方形,它的边长是()米,如果围成一个圆,圆的周长是()米。
18、把一个圆形纸片,截成两个相同的半圆,它的周长增加了10厘米,这个圆的周长是()19、一根铁丝正好围成一个直径2米的圆,这根铁丝长()米;如果改围成一个正方形,正方形的边长是()米,20、用一根长12.56米的绳子围成一个圆,这个圆的直径是()。
21、将一个圆沿直径剪开,如果这个圆的直径为4.6米,那么现在它的周长比原来的周长长(),变化后的长度为()22、把一个周长是15.7厘米的圆平均分成两份,这个半圆的周长是()厘米。
23、在一张长60厘米、宽40厘米的长方形纸片中,最多能剪()个直径为4厘米的圆。
中考数学《圆(一)》专题练习含答案解析

圆(一)一、选择题1.如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是()A.30°B.45°C.60°D.75°2.如图,在⊙O中,=,∠AOB=50°,则∠ADC的度数是()A.50°B.40°C.30°D.25°3.如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是()A.55°B.60°C.65°D.70°4.如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是()A.∠A=∠D B.=C.∠ACB=90°D.∠COB=3∠D5.如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为()A.50°B.20°C.60°D.70°6.如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于()A.32°B.38°C.52°D.66°7.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°8.如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为()A.15°B.18°C.20°D.28°9.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是()A.30°B.45°C.60°D.70°10.如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=()A.80°B.90°C.100° D.无法确定11.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是()A.80°B.160°C.100° D.80°或100°12.如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是()A.2 B.3 C.4 D.513.如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是()A.30°B.40°C.50°D.60°14.如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是()A.22°B.26°C.32°D.68°15.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=()A.20°B.30°C.40°D.70°16.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()A.50°B.80°C.100° D.130°17.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°18.如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于()A.50°B.80°C.100° D.130°二、填空题19.如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC,其中正确的序号是.20.将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A、B的读数分别为100°、150°,则∠ACB的大小为度.21.如图所示,A、B、C三点均在⊙O上,若∠AOB=80°,则∠ACB=°.22.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是4,sinB=,则线段AC的长为.23.如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=48°,则∠C的度数为.24.如图,点O为所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=.25.如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=度.三、解答题(共5小题)26.已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;(2)求图中阴影部分的面积.27.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;(2)求证:∠1=∠2.28.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.29.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF 并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2.(1)求AC的长度;(2)求图中阴影部分的面积.(计算结果保留根号)30.如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.(1)求的长.(2)求弦BD的长.圆(一)参考答案与试题解析一、选择题1.如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是()A.30°B.45°C.60°D.75°【考点】圆周角定理;含30度角的直角三角形.【专题】几何图形问题.【分析】由⊙O的直径是AB,得到∠ACB=90°,根据特殊三角函数值可以求得∠B的值,继而求得∠A和∠D的值.【解答】解:∵⊙O的直径是AB,∴∠ACB=90°,又∵AB=2,弦AC=1,∴sin∠CBA=,∴∠CBA=30°,∴∠A=∠D=60°,故选:C.【点评】本题考查的是圆周角定理及直角三角形的性质,比较简单,但在解答时要注意特殊三角函数的取值.2.如图,在⊙O中,=,∠AOB=50°,则∠ADC的度数是()A.50°B.40°C.30°D.25°【考点】圆周角定理;垂径定理.【分析】先求出∠AOC=∠AOB=50°,再由圆周角定理即可得出结论.【解答】解:∵在⊙O中,=,∴∠AOC=∠AOB,∵∠AOB=50°,∴∠AOC=50°,∴∠ADC=∠AOC=25°,故选D.【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.3.如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是()A.55°B.60°C.65°D.70°【考点】圆周角定理.【分析】连接OB,要求∠BAO的度数,只要在等腰三角形OAB中求得一个角的度数即可得到答案,利用同弧所对的圆周角是圆心角的一半可得∠AOB=50°,然后根据等腰三角形两底角相等和三角形内角和定理即可求得.【解答】解:连接OB,∵∠ACB=25°,∴∠AOB=2×25°=50°,由OA=OB,∴∠BAO=∠ABO,∴∠BAO=(180°﹣50°)=65°.故选C.【点评】本题考查了圆周角定理;作出辅助线,构建等腰三角形是正确解答本题的关键.4.如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是()A.∠A=∠D B.=C.∠ACB=90°D.∠COB=3∠D【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.【分析】根据垂径定理、圆周角定理,进行判断即可解答.【解答】解:A、∠A=∠D,正确;B、,正确;C、∠ACB=90°,正确;D、∠COB=2∠CDB,故错误;故选:D.【点评】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧,也考查了圆周角定理,解集本题的关键是熟记垂径定理和圆周角定理.5.如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为()A.50°B.20°C.60°D.70°【考点】圆周角定理.【专题】计算题.【分析】先根据半圆(或直径)所对的圆周角是直角得到∠ACB=90°,再利用互余得∠ACD=90°﹣∠DCB=70°,然后根据同弧或等弧所对的圆周角相等求解.【解答】解:∵AB为⊙O直径,∴∠ACB=90°,∴∠ACD=90°﹣∠DCB=90°﹣20°=70°,∴∠DBA=∠ACD=70°.故选D.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.6.如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于()A.32°B.38°C.52°D.66°【考点】圆周角定理.【分析】由AB是⊙O的直径,根据直径所对的圆周角是直角,即可求得∠ADB的度数,继而求得∠A的度数,又由圆周角定理,即可求得答案.【解答】解:∵AB是⊙O的直径,∴∠ADB=90°,∵∠ABD=52°,∴∠A=90°﹣∠ABD=38°;∴∠BCD=∠A=38°.故选:B.【点评】此题考查了圆周角定理以及直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.7.如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠BOD的度数是()A.25°B.30°C.40°D.50°【考点】圆周角定理;垂径定理.【专题】压轴题.【分析】由“等弧所对的圆周角是所对的圆心角的一半”推知∠DOB=2∠C,得到答案.【解答】解:∵在⊙O中,直径CD垂直于弦AB,∴=,∴∠DOB=2∠C=50°.故选:D.【点评】本题考查了圆周角定理、垂径定理.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.8.如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为()A.15°B.18°C.20°D.28°【考点】圆周角定理.【专题】计算题.【分析】连结OB,如图,先根据圆周角定理得到∠BOC=2∠A=144°,然后根据等腰三角形的性质和三角形内角和定理计算∠BCO的度数.【解答】解:连结OB,如图,∠BOC=2∠A=2×72°=144°,∵OB=OC,∴∠CBO=∠BCO,∴∠BCO=(180°﹣∠BOC)=×(180°﹣144°)=18°.故选B.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的性质.9.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是()A.30°B.45°C.60°D.70°【考点】圆周角定理.【专题】计算题.【分析】先根据圆周角定理得到∠ABC=∠AOC,由于∠ABC+∠AOC=90°,所以∠AOC+∠AOC=90°,然后解方程即可.【解答】解:∵∠ABC=∠AOC,而∠ABC+∠AOC=90°,∴∠AOC+∠AOC=90°,∴∠AOC=60°.故选:C.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.10.如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=()A.80°B.90°C.100° D.无法确定【考点】圆周角定理;坐标与图形性质.【分析】由∠AOB与∠ACB是优弧AB所对的圆周角,根据圆周角定理,即可求得∠ACB=∠AOB=90°.【解答】解:∵∠AOB与∠ACB是优弧AB所对的圆周角,∴∠AOB=∠ACB,∵∠AOB=90°,∴∠ACB=90°.故选B.【点评】此题考查了圆周角定理.此题比较简单,解题的关键是观察图形,得到∠AOB 与∠ACB是优弧AB所对的圆周角.11.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是()A.80°B.160°C.100° D.80°或100°【考点】圆周角定理.【分析】首先根据题意画出图形,由圆周角定理即可求得答案∠ABC的度数,又由圆的内接四边形的性质,即可求得∠ABC的度数.【解答】解:如图,∵∠AOC=160°,∴∠ABC=∠AOC=×160°=80°,∵∠ABC+∠AB′C=180°,∴∠AB′C=180°﹣∠ABC=180°﹣80°=100°.∴∠ABC的度数是:80°或100°.故选D.【点评】此题考查了圆周角定理与圆的内接四边形的性质.此题难度不大,注意数形结合思想与分类讨论思想的应用,注意别漏解.12.如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.其中正确结论的个数是()A.2 B.3 C.4 D.5【考点】圆周角定理;垂径定理.【专题】压轴题.【分析】根据AB⊥MN,垂径定理得出①③正确,利用MN是直径得出②正确,==,得出④正确,结合②④得出⑤正确即可.【解答】解:∵MN是⊙O的直径,AB⊥MN,∴AD=BD,=,∠MAN=90°(①②③正确)∵=,∴==,∴∠ACM+∠ANM=∠MOB(④正确)∵∠MAE=∠AME,∴AE=ME,∠EAF=∠AFM,∴AE=EF,∴AE=MF(⑤正确).正确的结论共5个.故选:D.【点评】此题考查圆周角定理,垂径定理,以及直角三角形斜边上的中线等于斜边的一半等知识.13.如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是()A.30°B.40°C.50°D.60°【考点】圆周角定理.【专题】计算题;压轴题.【分析】根据图形,利用圆周角定理求出所求角度数即可.【解答】解:∵∠AOB与∠ACB都对,且∠AOB=100°,∴∠ACB=∠AOB=50°,故选C【点评】此题考查了圆周角定理,熟练掌握圆周角定理是解本题的关键.14.如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是()A.22°B.26°C.32°D.68°【考点】圆周角定理.【分析】先根据圆周角定理求出∠BOC的度数,再根据等腰三角形的性质即可得出结论.【解答】解:∵∠A与∠BOC是同弧所对的圆周角与圆心角,∠A=68°,∴∠BOC=2∠A=136°.∵OB=OC,∴∠OBC==22°.故选A.【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.15.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=()A.20°B.30°C.40°D.70°【考点】圆周角定理.【分析】根据∠DOB=140°,求出∠AOD的度数,根据圆周角定理求出∠ACD的度数.【解答】解:∵∠DOB=140°,∴∠AOD=40°,∴∠ACD=∠AOD=20°,故选:A.【点评】本题考查的是圆周角定理,掌握一条弧所对的圆周角是这条弧所对的圆心角的一半是解题的关键.16.如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()A.50°B.80°C.100° D.130°【考点】圆周角定理;圆内接四边形的性质.【分析】首先根据圆周角与圆心角的关系,求出∠BAD的度数;然后根据圆内接四边形的对角互补,用180°减去∠BAD的度数,求出∠BCD的度数是多少即可.【解答】解:∵∠BOD=100°,∴∠BAD=100°÷2=50°,∴∠BCD=180°﹣∠BAD=180°﹣50°=130°故选:D.【点评】(1)此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,要熟练掌握.(2)此题还考查了圆内接四边形的性质,要熟练掌握,解答此题的关键是要明确:①圆内接四边形的对角互补.②圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).17.如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为()A.30°B.35°C.40°D.45°【考点】圆周角定理.【分析】先根据OA=OC,∠ACO=45°可得出∠OAC=45°,故可得出∠AOC的度数,再由圆周角定理即可得出结论.【解答】解:∵OA=OC,∠ACO=45°,∴∠OAC=45°,∴∠AOC=180°﹣45°﹣45°=90°,∴∠B=∠AOC=45°.故选D.【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.18.如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于()A.50°B.80°C.100° D.130°【考点】圆周角定理.【分析】首先在上取点D,连接AD,CD,由圆周角定理即可求得∠D的度数,然后由圆的内接四边形的性质,求得∠ABC的度数.【解答】解:如图,在优弧上取点D,连接AD,CD,∵∠AOC=100°,∴∠ADC=∠AOC=50°,∴∠ABC=180°﹣∠ADC=130°.故选D.【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.二、填空题19.如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC,其中正确的序号是①②④.【考点】圆周角定理;等腰三角形的判定与性质;弧长的计算.【专题】压轴题.【分析】根据圆周角定理,等边对等角,等腰三角形的性质,直径对的圆周角是直角等知识,运用排除法逐条分析判断.【解答】解:连接AD,AB是直径,则AD⊥BC,又∵△ABC是等腰三角形,故点D是BC的中点,即BD=CD,故②正确;∵AD是∠BAC的平分线,由圆周角定理知,∠EBC=∠DAC=∠BAC=22.5°,故①正确;∵∠ABE=90°﹣∠EBC﹣∠BAD=45°=2∠CAD,故④正确;∵∠EBC=22.5°,2EC≠BE,AE=BE,∴AE≠2CE,③不正确;∵AE=BE,BE是直角边,BC是斜边,肯定不等,故⑤错误.综上所述,正确的结论是:①②④.故答案是:①②④.【点评】本题考查了圆周角定理,等腰三角形的判定与性质以及弧长的计算等.利用了圆周角定理,等边对等角,等腰三角形的性质,直径对的圆周角是直角求解.20.将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A、B的读数分别为100°、150°,则∠ACB的大小为25度.【考点】圆周角定理.【专题】计算题.【分析】连接OA,OB,根据题意确定出∠AOB的度数,利用圆周角定理即可求出∠ACB 的度数.【解答】解:连接OA,OB,由题意得:∠AOB=50°,∵∠ACB与∠AOB都对,∴∠ACB=∠AOB=25°,故答案为:25【点评】此题考查了圆周角定理,熟练掌握圆周角定理是解本题的关键.21.如图所示,A、B、C三点均在⊙O上,若∠AOB=80°,则∠ACB=40°.【考点】圆周角定理.【专题】计算题.【分析】直接根据圆周角定理求解.【解答】解:∠ACB=∠AOB=×80°=40°.故答案为40.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.22.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是4,sinB=,则线段AC的长为2.【考点】圆周角定理;解直角三角形.【专题】计算题.【分析】连结CD如图,根据圆周角定理得到∠ACD=90°,∠D=∠B,则sinD=sinB=,然后在Rt△ACD中利用∠D的正弦可计算出AC的长.【解答】解:连结CD,如图,∵AD是⊙O的直径,∴∠ACD=90°,∵∠D=∠B,∴sinD=sinB=,在Rt△ACD中,∵sinD==,∴AC=AD=×8=2.故答案为2.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.23.如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=48°,则∠C的度数为42°.【考点】圆周角定理.【分析】根据三角形的内角和定理求得∠AOB的度数,再进一步根据圆周角定理求解.【解答】解:∵OA=OB,∠OBA=48°,∴∠OAB=∠OBA=48°,∴∠AOB=180°﹣48°×2=84°,∴∠C=∠AOB=42°,故答案为:42°.【点评】此题综合运用了三角形的内角和定理以及圆周角定理.解决本题的关键是熟记一条弧所对的圆周角等于它所对的圆心角的一半.24.如图,点O为所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.【考点】圆周角定理;等腰三角形的性质.【分析】由AD=AC,可得∠ACD=∠ADC,由∠BAC=∠ACD+∠ADC=2∠D,可得∠BAC的度数,由∠D=∠BAC即可求解.【解答】解:∵AD=AC,∴∠ACD=∠ADC,∵∠BAC=∠ACD+∠ADC=2∠D,∴∠BAC=∠BOC=×112°=56°,∴∠D=∠BAC=28°.故答案为:28°.【点评】本题主要考查了圆周角及等腰三角形的性质,解题的关键是找出∠D与∠BOC 的关系.25.如图,点A,B,C是⊙O上的点,AO=AB,则∠ACB=150度.【考点】圆周角定理;等边三角形的判定与性质;圆内接四边形的性质.【分析】根据AO=AB,且OA=OB,得出△OAB是等边三角形,再利用圆周角和圆心角的关系得出∠BAC+∠ABC=30°,解答即可.【解答】解:∵点A,B,C是⊙O上的点,AO=AB,∴OA=OB=AB,∴△OAB是等边三角形,∴∠AOB=60°,∴∠BAC+∠ABC=30°,∴∠ACB=150°,故答案为:150【点评】此题考查了圆心角、圆周角定理问题,关键是根据AO=AB,且OA=OB,得出△OAB是等边三角形.三、解答题26.已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;(2)求图中阴影部分的面积.【考点】圆周角定理;勾股定理;扇形面积的计算.【分析】(1)由AB为⊙O的直径,得到∠ACB=90°,由勾股定理求得AB,OB=5cm.连OD,得到等腰直角三角形,根据勾股定理即可得到结论;(2)根据S阴影=S扇形﹣S△OBD即可得到结论.【解答】解:(1)∵AB为⊙O的直径,∴∠ACB=90°,∵BC=6cm,AC=8cm,∴AB=10cm.∴OB=5cm.连OD,∵OD=OB,∴∠ODB=∠ABD=45°.∴∠BOD=90°.∴BD==5cm.(2)S阴影=S扇形﹣S△OBD=π•52﹣×5×5=cm2.【点评】本题考查了圆周角定理,勾股定理,等腰直角三角形的性质,扇形的面积,三角形的面积,连接OD构造直角三角形是解题的关键.27.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;(2)求证:∠1=∠2.【考点】圆周角定理;圆心角、弧、弦的关系.【专题】计算题.【分析】(1)根据等腰三角形的性质由BC=DC得到∠CBD=∠CDB=39°,再根据圆周角定理得∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,所以∠BAD=∠BAC+∠CAD=78°;(2)根据等腰三角形的性质由EC=BC得∠CEB=∠CBE,再利用三角形外角性质得∠CEB=∠2+∠BAE,则∠2+∠BAE=∠1+∠CBD,加上∠BAE=∠CBD,所以∠1=∠2.【解答】(1)解:∵BC=DC,∴∠CBD=∠CDB=39°,∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,∴∠BAD=∠BAC+∠CAD=39°+39°=78°;(2)证明:∵EC=BC,∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,∴∠2+∠BAE=∠1+∠CBD,∵∠BAE=∠BDC=∠CBD,∴∠1=∠2.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的性质.28.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:等边三角形;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.【考点】圆周角定理;全等三角形的判定与性质;等边三角形的判定与性质;垂径定理.【分析】(1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;(2)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得;(3)过点P作PE⊥AB,垂足为E,过点C作CF⊥AB,垂足为F,把四边形的面积转化为两个三角形的面积进行计算,当点P为的中点时,PE+CF=PC从而得出最大面积.【解答】证明:(1)△ABC是等边三角形.证明如下:在⊙O中∵∠BAC与∠CPB是所对的圆周角,∠ABC与∠APC是所对的圆周角,∴∠BAC=∠CPB,∠ABC=∠APC,又∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC为等边三角形;(2)在PC上截取PD=AP,如图1,又∵∠APC=60°,∴△APD是等边三角形,∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,在△APB和△ADC中,,∴△APB≌△ADC(AAS),∴BP=CD,又∵PD=AP,∴CP=BP+AP;(3)当点P为的中点时,四边形APBC的面积最大.理由如下,如图2,过点P作PE⊥AB,垂足为E.过点C作CF⊥AB,垂足为F.=AB•PE,S△ABC=AB•CF,∵S△APB=AB•(PE+CF),∴S四边形APBC当点P为的中点时,PE+CF=PC,PC为⊙O的直径,∴此时四边形APBC的面积最大.又∵⊙O的半径为1,∴其内接正三角形的边长AB=,=×2×=.∴S四边形APBC【点评】本题考查了圆周角定理、等边三角形的判定、三角形的面积公式以及三角形的全等的判定与性质,正确作出辅助线,证明△APB≌△ADC是关键.29.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF 并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2.(1)求AC的长度;(2)求图中阴影部分的面积.(计算结果保留根号)【考点】圆周角定理;全等三角形的判定与性质;扇形面积的计算.【分析】(1)解直角三角形求出OB,求出AB,根据圆周角定理求出∠ACB,解直角三角求出AC即可;(2)求出△ACF和△AOF全等,得出阴影部分的面积=△AOD的面积,求出三角形的面积即可.【解答】解:(1)∵OF⊥AB,∴∠BOF=90°,∵∠B=30°,FO=2,∴OB=6,AB=2OB=12,又∵AB为⊙O的直径,∴∠ACB=90°,∴AC=AB=6;(2)∵由(1)可知,AB=12,∴AO=6,即AC=AO,在Rt△ACF和Rt△AOF中,∴Rt△ACF≌Rt△AOF,∴∠FAO=∠FAC=30°,∴∠DOB=60°,过点D作DG⊥AB于点G,∵OD=6,∴DG=3,∴S△ACF +S△OFD=S△AOD=×6×3=9,即阴影部分的面积是9.【点评】本题考查了三角形的面积,全等三角形的性质和判定,圆周角定理,解直角三角形的应用,能求出△AOD的面积=阴影部分的面积是解此题的关键.30.如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.(1)求的长.(2)求弦BD的长.【考点】圆周角定理;含30度角的直角三角形;等腰直角三角形;弧长的计算.【分析】(1)首先根据AB是⊙O的直径,可得∠ACB=∠ADB=90°,然后在Rt△ABC中,求出∠BAC的度数,即可求出∠BOC的度数;最后根据弧长公式,求出的长即可.(2)首先根据CD平分∠ACB,可得∠ACD=∠BCD;然后根据圆周角定理,可得∠AOD=∠BOD,所以AD=BD,∠ABD=∠BAD=45°;最后在Rt△ABD中,求出弦BD的长是多少即可.【解答】解:(1)如图,连接OC,OD,,∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,在Rt△ABC中,∵,∴∠BAC=60°,∴∠BOC=2∠BAC=2×60°=120°,∴的长=.(2)∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠AOD=∠BOD,∴AD=BD,∴∠ABD=∠BAD=45°,在Rt△ABD中,BD=AB×sin45°=10×.【点评】(1)此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,要熟练掌握.(2)此题还考查了含30度角的直角三角形,以及等腰直角三角形的性质和应用,要熟练掌握.(3)此题还考查了弧长的求法,要熟练掌握,解答此题的关键是要明确:①弧长公式:l=(弧长为l,圆心角度数为n,圆的半径为R).②在弧长的计算公式中,n是表示1°的圆心角的倍数,n和180都不要带单位.。
北师大版六年级数学上册第一单元圆练习题(常考题型)

第一单元 圆
十五、考点15:圆环的面积。
1、圆环的面积=( 大圆的面积 )-(小圆的面积 ),公式 S圆环=( πR2-πr2 )=( π(R2-r2 ) )
例题:求阴影部分的面积。(单位:厘米)
解题思路:先计算出大圆的半径和小圆 的半径,再用大圆的面积-小圆的面积。
1 1、半圆是( 轴对称 )图形,它有(
)对称轴。
判断:2、半圆的周长就是圆周长的一半
(× )
3、同一个圆中,半圆的周长大于圆周长的一半。( √ )
4、圆的周长除以2就是半圆的周长。
(×)
5、两个半圆一定可以拼成一个圆。
( ×)
6、两个相等的半圆一定可以拼成一个圆。 ( √ )
7、半圆的周长公式是( C )
1、花坛的周长是62.8米,你能算出这个圆形花坛的直径吗?
解:直径:62.8÷3.14=20米 答:直径是20米。
2、一根长12.56米的绳子正好绕一树干10周,树 干横截面的直径是多少?
解:周长:12.56÷10=1.256米 直径:1.256÷3.14=0.4米
答:直径是0.4米。
七、考点7:圆的周长公式及其应用。(四)、告诉周长,求半径。
相等,这个圆的半径是( D )米。
A、3.14 B、3 C、9. 42 D、1.5 2、一根圆木,它的横截面的周长是62.8厘米,则它的横截面 积是多少平方厘米?
解:周长:62.8÷3.14÷2=10厘米 面积:3.14×102=314平方厘米
答:它的面积是314平方厘米。
第一单元 圆
(每空13分,共100分) 十、考点10:半圆的性质、周长和面积。
2、圆是(轴对称)图形,它有( 无数)条对称轴;
圆的面积计算 练习题 (1)

圆的面积计算练习题一、填空1.一个圆形桌面的直径是 2米,它的面积是()平方米。
2.已知圆的周长,求d=(),求r=()。
3.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
4.环形面积S=()。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加,圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
10.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
11.大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为()平方厘米。
12.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是()平方厘米。
13.鼓楼中心岛是半径 10米的圆,它的占地面积是()平方米。
14.小华量得一根树干的周长是75.36厘米,这根树干的横截面大约是()平方厘米15.一只羊栓在一块草地中央的树桩上,树桩到羊颈的绳长是 3米。
这只羊可以吃到()平方米地面的草。
16.一根 2米长的铁丝,围成一个半径是30厘米的圆,(接头处不计),还多()米,围成的面积是()17.用一根 10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()18.从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是()19.大圆的半径等于小圆的直径,大圆的面积是小圆面积的()20.一个圆的周长扩大3倍,面积就扩大()倍。
21.用三根同样长的铁丝分别围成一个长方形、一个正方形、和一个圆,其中()面积最小,()面积最大。
小学6年级--圆专项练习1

第一章圆的习题一填空题:1、圆是平面上的一种()图形,围成圆的()的长叫做圆的周长。
在大大小小的圆中,它们的周长总是各自圆直径的()倍多一些,我们把这个固定的数叫做(),用字母()表示,它是一个()小数,在()和()之间,在计算时,一般只取它的近似值()。
2、一个圆的直径扩大2倍,它的半径扩大()倍,它的周长扩大()倍。
3、用铁丝在一个半径25厘米的圆柱形水桶外面加一圈箍,接头处多用5厘米,共需要()厘米长的铁丝。
4、一个圆形花坛的半径2.25米,直径是()米,周长()米。
5、一个圆的直径扩大4倍,半径扩大()倍,周长扩大()倍。
6、画一个周长12.56厘米的圆,圆规两脚间的距离是()厘米。
7、在一张长6厘米,宽4厘米的长方形纸片上画一个最大的圆,这个圆的半径是()厘米;如果画一个最大的半圆,这个圆的半径是()厘米。
8、()叫做圆的面积。
把圆沿着它的半径r分成若干等份,剪开后可以拼成一个近似的(),这个图形的长相当于圆周长的(),用字母表示是();宽相当于圆的(),用字母表示是()。
所以圆的面积S=( )×( ) =( )。
9、一个圆的半径2厘米,它的周长是();面积是()。
10、一个圆的直径6米,半径(),周长(),面积()。
11、在长6分米,宽4分米的长方形中画一个最大的圆,圆的面积()。
12、一个圆的周长总是它半径的()倍。
13、用12.56米的铁丝围成一个正方形,正方形面积是(),如果把它围成一个圆,圆的面积是()。
14、圆的半径扩大5倍,直径扩大()倍;周长扩大()倍;面积扩大()倍。
15、小圆半径2厘米,大圆半径6厘米,小于半径是大圆半径的(),小于直径是大圆直径的(),小于周长是大圆周长的(),小于面积是大圆面积的(),16、用圆规画一个周长50.24厘米的圆,圆规两脚之间的距离是()厘米,所画的圆的面积是()平方厘米。
17、圆的半径扩大3倍,直径扩大()倍,周长扩大()倍;面积扩大()倍。
圆的面积练习精1

圆的面积练习精选一、填空题。
(1)把一个圆分成若干等份,剪开拼成一个近似的长方形。
这个长方形的长相当于(),长方形的宽就是圆的()。
因为长方形的面积是(),所以圆的面积是().(2)圆的直径是6厘米,它的周长是(),面积是()。
(3)圆的周长是25.12分米,它的面积是()。
(4)甲圆半径是乙圆半径的3倍,甲圆的周长是乙圆周长的(),甲圆面积是乙圆面积的()。
(5)一个圆的半径是8厘米,这个圆面积的3/4 是()平方厘米。
(6)周长相等的长方形、正方形、圆,()面积最大。
(7)圆的半径由6厘米增加到9厘米,圆的面积增加了()平方厘米。
(8)要在一个边长为10厘米的正方形纸板里剪出一个最大的圆,剩下的面积是()。
(9)要在底面半径是12厘米的圆柱形水桶外面打上一个铁丝箍,接头部分是8厘米,需用铁丝()厘米。
(10)用圆规画一个圆,如果圆规两脚之间的距离是7厘米,画出的这个圆的周长是()厘米。
这个圆的面积是()平方厘米。
(11)有大小两个圆,大圆直径是小圆半径的4倍,小圆与大圆周长的比是(),小圆与大圆面积的比是()。
(12)一个半圆半径是r,它的周长是()。
二、应用题。
(1)有一只羊栓在草地的木桩上,绳子的长度是4米,这只羊最多可以吃到多少平方米的草?(2)一种手榴弹爆炸后,有效杀伤范围的半径是8米,有效杀伤面积是多少平方米?(3)一种铝制面盆是用直径30厘米的圆形铝板冲压而成的,要做1000个这样的面盆至少需要多少平方米的铝板?(4)一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆。
还剩下多少平方厘米的纸没用?(5)在一个圆形喷水池的周长是62.8米,绕着这个水池修一条宽2米的水泥路。
求路面的面积。
(6)一个半圆形养鱼池,直径是4米,这个养鱼池的周长是多少米?占地面积是多少平方米?(7)在一个直径是16米的圆心花坛周围,有一条宽为2米的小路围绕,小路的面积是多少平方米?(8)一个环形铁片,内圆直径是14厘米,外圆直径是18厘米,这个环形铁片的面积是多少?(9)用一根长16分米的铁丝围成一个圆,接头处长0.3分米,这个圆的面积是多少?圆柱的侧面积和表面积练习题一、填空:(1)2.6米=()厘米48分米=()米7.5平方分米=()平方厘米9300平方厘米=()平方米(2)圆柱的侧面积等于()乘以高。
初三数学圆第一部分练习题

初三数学圆第一部分练习题1. 已知直径为8cm的圆的面积为何?解答:由于直径是8cm,半径则为4cm(半径等于直径的一半)。
圆的面积公式为:面积= π * 半径²,其中π取近似值3.14。
将半径代入公式可得:面积 = 3.14 * 4² = 3.14 * 16 = 50.24 平方厘米。
因此,直径为8cm的圆的面积为50.24平方厘米。
2. 若一个半径为6cm的圆,求该圆的周长是多少?解答:圆的周长公式为:周长= 2 * π * 半径,其中π取近似值3.14。
将半径代入公式可得:周长 = 2 * 3.14 * 6 = 37.68 厘米。
因此,半径为6cm的圆的周长是37.68厘米。
3. 若一个圆的半径为12cm,求该圆的直径和面积。
解答:圆的直径等于半径的两倍,所以直径为:直径 = 2 * 半径 = 2 * 12cm = 24cm。
圆的面积公式为:面积= π * 半径²。
将半径代入公式可得:面积 = 3.14 * 12² = 3.14 * 144 = 452.16 平方厘米。
因此,半径为12cm的圆的直径为24cm,面积为452.16平方厘米。
4. 若一个圆的直径为16cm,求该圆的半径和周长。
解答:圆的半径等于直径的一半,所以半径为:半径 = 直径 / 2 =16cm / 2 = 8cm。
圆的周长公式为:周长= 2 * π * 半径,其中π取近似值3.14。
将半径代入公式可得:周长 = 2 * 3.14 * 8 = 50.24 厘米。
因此,直径为16cm的圆的半径为8cm,周长为50.24厘米。
5. 若一个圆的面积为154 平方厘米,求该圆的直径和周长。
解答:已知面积为154平方厘米,需要先求出半径,再通过半径计算直径和周长。
圆的面积公式为:面积= π * 半径²,反过来可以求出半径:半径= √(面积/ π)。
将面积代入公式可得:半径= √(154 / 3.14) ≈ √49 ≈ 7cm。
圆的周长练习题 (1)
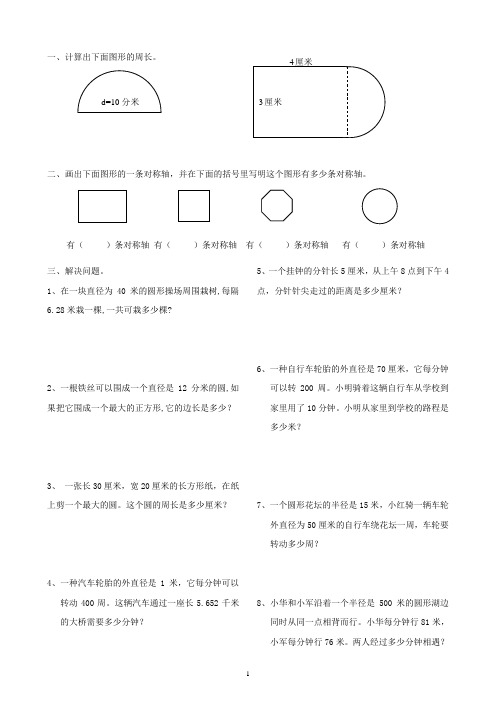
一、计算出下面图形的周长。
二、画出下面图形的一条对称轴,并在下面的括号里写明这个图形有多少条对称轴。
三、解决问题。
1、在一块直径为40米的圆形操场周围栽树,每隔6.28米栽一棵,一共可栽多少棵?2、一根铁丝可以围成一个直径是12分米的圆,如果把它围成一个最大的正方形,它的边长是多少?3、一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆。
这个圆的周长是多少厘米?4、一种汽车轮胎的外直径是1米,它每分钟可以转动400周。
这辆汽车通过一座长5.652千米的大桥需要多少分钟?5、一个挂钟的分针长5厘米,从上午8点到下午4点,分针针尖走过的距离是多少厘米?6、一种自行车轮胎的外直径是70厘米,它每分钟可以转200周。
小明骑着这辆自行车从学校到家里用了10分钟。
小明从家里到学校的路程是多少米?7、一个圆形花坛的半径是15米,小红骑一辆车轮外直径为50厘米的自行车绕花坛一周,车轮要转动多少周?8、小华和小军沿着一个半径是500米的圆形湖边同时从同一点相背而行。
小华每分钟行81米,小军每分钟行76米。
两人经过多少分钟相遇?有()条对称轴有()条对称轴有()条对称轴有()条对称轴9、一个半圆的周长是15.42分米,这个半圆的直径是多少分米?10、一个圆形舞台要扩建,原来直径是20米,现在直径要增加到50米,扩建后,周长增加了多少?11、用一根30米的长的绳子绕一棵大树的树干3周,绳子还剩下1.74米,这棵大树树干的直径是多少米?12、一个正方形的周长是96厘米,在这个正方形里面画一个最大的圆,圆的周长是多少厘米?13、一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过2512米的桥,大约需要几分钟?14、一个圆形花坛的直径是8m ,在花坛的周围摆放盆花,每隔1.57 m 放一盆,一共可以放几盆花?15、一只挂钟分针的针尖在41小时内,正好走了25.12厘米。
它的分针长多少?16、饭店的大厅内挂着一只大钟,它的分针长48厘米。
圆的周长练习题精选

圆的周长练习题精选-CAL-FENGHAI.-(YICAI)-Company One1圆的周长检测一、 填空1、通过圆心并且两端都在圆上的线段,叫做圆的( ),一般用字母( )来表示。
2、在一个圆里,有( )条半径,这些半径的长度( ),有( )条直径,这些直径的长度( )。
3、在同一个圆里,直径和半径的关系可以表示为( )或( )。
4、用( )可以画出一个精确的圆。
( )决定圆的大小,( )决定圆的位置。
5、一个圆的半径是6厘米,这个圆的周长是( )厘米,如果半径增加3厘米,直径是( )厘米,周长是( )厘米。
6、一个圆的直径是12厘米,周长是( )厘米,如果直径扩大到原来的3倍,周长是( )厘米。
如果直径缩小的原来的31,周长是( )厘米。
7、一个圆的周长是分米,这个圆的半径是( )分米。
一个圆的周长是25.12米,这个圆的直径是( )米。
8、一个半圆的半径是6分米,这个半圆的周长是( )分米,一个半圆的直径是15厘米,这个半圆的周长是( )厘米。
9、甲圆的半径是4厘米,乙圆的半径是6厘米,甲圆直径和乙圆直径的比是( ),乙圆周长和甲圆周长的比是( )。
10、一张长方形纸,长6分米,宽4分米。
如果在上面剪出一个最大的圆,这个圆的半径是( )分米,周长是( )。
二、判断题1、如果两个圆的周长相等,那个这两个圆的直径也一定相等。
( )2、甲圆直径是乙圆的半径,乙圆的周长是甲圆周长的2倍。
( )3、在一个正方形内画一个最大的圆,圆的直径等于正方形的边长。
( )4、直径越大,这个圆的周长就越大。
( )5、半圆的周长就是圆周长的一半。
( )6、圆的周长是直径的倍。
( )7、圆的直径是半径的两倍。
( )8、圆的直径就是圆的对称轴。
( )三、操作题。
1、画一个直径是4厘米的圆,计算出圆的周长。
2、计算出下面图形的周长。
五、解决问题。
1、在一块直径为40米的圆形操场周围栽树,每隔6.28米栽一棵,一共可栽多少棵3、 一张长30厘米,宽20厘米的长方形纸,在纸上剪一个最大的圆。
圆的周长练习题及答案

[标签:标题]篇一:圆的周长专项练习题圆的周长一、计算下列各题,并熟记它们的得数。
∏=3.14 2∏= 3∏= 4∏= 5∏=6∏=7∏= 8∏= 9∏= 10∏=二、填空(基础题):1、圆的周长总是直径长度的()倍多一些。
这个倍数是个固定的数,我们把它叫做(),用字母()表示。
2、用字母表示圆周长的公式是()或()。
3、自行车的车轮滚动一周,所行的路程是车轮的()。
4、要画一个半径为4厘米的圆,圆规的两脚应叉开()厘米;要画一个周长是18.84厘米的圆,圆规的两脚应叉开()厘米。
5、大圆直径是小圆直径的3倍,大圆周长是小圆周长的()倍。
6、圆的直径扩大3倍,周长就()倍,圆的周长缩小4倍,半径就()。
7、在一个长5厘米,宽3厘米的长方形中花一个最大的圆,这个圆的半径式()厘米。
8、把一块边长是10分米的正方形铁片,剪成一个最大的圆形,这个圆的周长是()。
列式:9、用铁丝把2根横截面直径都是20厘米的圆木捆在一起,如果接头处铁丝长5厘米,那么捆一周至少需要()厘米的铁丝。
10、用圆规画直径20厘米的圆,圆规两脚步间的距离是()厘米.11、圆是()图形,它有()对称轴.12、正方形有()条对称轴,长方形有()条对称轴,等腰三角形有()条对称轴,等边三角形有()条对称轴.半圆有()条对称轴,等腰梯形有()条对称轴。
13、一个圆的周长是同圆直径的()倍.14、有一圆形鱼池的半径是10米,绕其周围走一圈,要走()米。
15、挂钟的时针长5厘米,一昼夜这根时针的尖端走了()厘米。
16、画圆时,圆规两脚间的距离就是圆的()。
17、两端都在圆上的线段,()最长。
18、圆的半径是7厘米,它的周长是()厘米,19、圆的直径是13米,它的周长是()米。
20、圆的周长是75.36分米,它的半径是()分米。
21、底面半径是14厘米的圆柱形水桶外面打上一个铁丝箍,接头部分是6厘米,需用铁丝()厘米。
22、用圆规画一个圆,如果圆规两脚之间的距离是6厘米,画出的这个圆的周长是()厘米。
圆面积计算讲解和练习题---六年级数学1

圆的面积计算 讲解与练习题【基础知识】【知识点一】圆的周长的意义及测量方法1、圆的周长:围成圆的曲线的长度叫做圆的周长。
用字母C表示。
2、圆周率实验:在圆形纸片上做个记号,与直尺0刻度对齐,在直尺上滚动一周,求出圆的周长。
发现一般规律,就是圆周长与它直径的比值是一个固定数(π).【知识点二】圆周率的意义圆周率:任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率。
用字母π(pai)表示。
(1)一个圆的周长总是它直径的3倍多一些,这个比值是一个固定的数。
圆周率π是一个无限不循环小数。
在计算时,一般取π≈3.14。
(2)在判断时,圆周长与它直径的比值是π倍,而不是3。
14倍。
(3)世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
【知识点三】圆的周长计算公式圆的周长公式: C= πd d = C ÷π或C=2π r r = C ÷ 2π在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
在一个长方形里画一个最大的圆,圆的直径等于长方形的宽.区分周长的一半和半圆的周长:(1)周长的一半:等于圆的周长÷2 方法:2π r ÷ 2 即 π r (2)半圆的周长:等于圆的周长的一半加直径。
计算方法:πr+2r即 5。
14 r计算图形周长.1、一个圆的直径扩大2倍,它的半径扩大( )倍,它的周长扩大( )倍。
2、两个圆的半径的比是2:3,它们直径的比是( ),周长的比是( ).3、一个圆形花坛的半径2.25米,直径是( )米,周长( )米。
4、一个圆的直径扩大4倍,半径扩大( )倍,周长扩大( )倍.5、画一个周长12。
56厘米的圆,圆规两脚间的距离是( )厘米。
6、在一张长6厘米,宽4厘米的长方形纸片上画一个最大的圆,这个圆的半径是()厘米;如果画一个最大的半圆,这个圆的半径是( )厘米。
7、填表半径(分米)28直径(分米)312周长(分18.8462.8米)【考点题库】1、计算下面各圆的周长.(单位:分米) 1.5 6判断1)半径2厘米的圆,它的周长是6.28厘米。
圆练习题1

《圆》练习题一、选择题1、若一直角三角形的斜边长为c ,内切圆半径是r ,则内切圆的面积与三角形面积之比是( )(A )r c r 2+π(B )r c r +π(C )rc r +2π(D )22r c r +π 2、已知AB 是半圆的直径,BC 切半圆于B 点,BC=2AB =r ,AC 交半圆于D 点,DE ⊥AB 于E ,则DE 的长为( )(A )r 53(B )r 22(C )r 35(D )r 543、等腰三角形中,AB=AC ,BC=4,△ABC 的内切圆的半径为1,则AB 的长为() (A )2(B )3(C )32+(D )3104、如图,四边形ABCD 内接于半圆O ,AB 为直径,AB=4,AD=DC=1,则BC 的长为()(A )27(B )15(C )32(D )475、如果⊙O 1和⊙O 2相交于C 、D ,CB 是⊙O 1的直径,过B 作⊙O 1的切线交CE 的延长线于A ,AFD 是割线,交⊙O 2于F 、D ,BC=FD=2,CE=3,则AF 的长为( )(A )332(B )3121+(C )3321+(D )3321-6、已知⊙O 的半径为r ,AB 、CD 为⊙O 的两条直径,且弧AC=600,P 为弧BC 上的任意一点,PA 、PD 分别交CD 、AB 于E 、F ,则AE ·AP+DF ·DP 等于( )(A )23r (B )232r (C )24r (D )223r7、如图1,凸五边形ABCDE 内接于半径为1的⊙O,ABCD 是矩形,AE=ED,且BE 和CE 把AD 三等分.则此五边形ABCDE 的面积是:则弦AN 的 长为( )(A )53(B )54(C )34(D )3510、如图,A 是半径为1的圆O 外的一点,OA=2,AB 是⊙O 的切线,B 是切点,弦BC ∥OA ,连结AC ,则阴影部分的面积等于( )(A )92π(B )6π(C )836+π(D )834-π 11、如果20个点将某圆周20等分,那么顶点只能在这20个点中选取的正多边形的个数有( )(A )4个(B )8个(C )12个(D )24个12、如果边长顺次为25、39、52与60的四边形内接于一圆,那么此圆的周长为( )(A )62π(B )63π(C )64π(D )65π13、设AB 为⊙O 的一条弦,CD 为⊙O 的一条直径,且与弦AB 相交,记||DAB CAB S S M ∆∆-=,OAB S N ∆=2,则( )(A )M>N (B )M=N (C )M<N (D )M 、N 大小关系不确定14、如图,半圆O 的直径在梯形ABCD 的底边AB 上,且与其余三边BC 、CD 、DA 相切,若BC=2,DA=3,则AB 的长( )(A )等于4(B )等于5(C )等于6(D )不能确定15、如右图,P 为半⊙O 直径BA 延长线上一点,PC 切半⊙O 于C ,且PA :PC=2:3,则sin ∠ACP 的值为( )(A )32(B )13132(C )13133(D )无法确定 二、填空题16、扇形OAB 的弦AB=18,半径为6的圆C 恰与OA 、OB和弧AB 相切,圆D 又与圆C 、OA 和OB 相切,则圆D 的半径为_____________。
圆的周长与面积练习题(1)

圆的周长与面积练习题(1)条路的面积是多少平方米?圆形水池的面积是多少平方米?3、一块铁皮,长为20厘米,宽为15厘米,要制作一个直径为10厘米的圆形盘子,问这块铁皮能制作几个圆形盘子?剩下的铁皮面积是多少平方厘米?4、一家披萨店的披萨直径为30厘米,售价为20元,求每平方厘米的价格。
5、一个圆形花坛的直径为3米,围绕花坛修建一条宽1米的小路,小路的面积是多少平方米?花坛的面积是多少平方米?如果要在花坛中种植草坪,需要多少平方米的草皮?1.条石子路的面积是多少?需要知道路的长度和宽度才能计算面积。
如果已知长度和宽度,则可以将它们相乘得到面积。
如果没有提供这些信息,则无法计算面积。
2.一只钟的时针长40毫米,这根时针的尖端一天(24小时)所走过的路是多少?时针的尖端在一天中绕时钟盘转了一圈,即走过了360度。
时针的长度对应着时钟盘的半径,因此可以使用圆的周长公式来计算时针尖端走过的路程。
周长等于2πr,其中r是半径。
所以,时针尖端走过的路程等于2π乘以40毫米,即80π毫米或约251.33毫米。
3.一辆自行车的轮胎的外直径是1.12米,每分转50周,这辆自行车每小时行驶多少千米?轮胎的外直径是1.12米,因此轮胎的周长等于直径乘以π,约等于3.52米。
每分钟轮胎转50周,因此每分钟行驶的距离是3.52米乘以50,即176米。
每小时有60分钟,因此这辆自行车每小时行驶的距离是176米乘以60,即米或10.56千米。
4.一根铁箍长11.49分米,正好做成一个木桶的一道箍。
已知铁箍接头处是0.5分米。
这个木桶的外直径是多少分米?铁箍的长度等于木桶的周长,因此可以使用周长公式来计算木桶的直径。
周长等于π乘以直径,所以直径等于周长除以π。
铁箍的长度为11.49分米,减去接头处的0.5分米,得到木桶的周长为11.49分米减去0.5分米,即11分米。
因此,木桶的直径等于11分米除以π,约等于3.5分米左右。
5.一张长方形纸片,长60厘米,宽40厘米。
2020-2021初四数学圆的有关计算综合练习题1(附答案详解)
2010-2021初四数学圆的有关计算综合练习题1(附答案详解)一.选择题(共10小题)1.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为()A.B.C.D.2.如图,点P、M、N分别是边长为2的正六边形中不相邻三条边的中点,则△PMN的周长为()A.6B.6C.6D.93.若一个正多边形的一个内角是135°,则这个正多边形的中心角为()A.20°B.45°C.60°D.90°4.下列圆的内接正多边形中,中心角最大的图形是()A.正三角形B.正方形C.正五边形D.正六边形5.如图,圆上有A、B、C、D四点,其中∠BAD=80°,若弧ABC、弧ADC的长度分别为7π、11π,则弧BAD的长度是()A.4πB.8πC.l0πD.15π6.如图,四边形ABCD为⊙O的内接四边形,⊙O的半径为3,AO⊥BC,垂足为点E,若∠ADC=130°,则的长等于()A.B.C.D.7.如图,矩形ABCD的边AB=1,BC=2,以点B为圆心,BC为半径画弧,交AD于点E,则图中阴影部分的面积是()A.B.2C.D.2﹣8.已知圆锥的底面半径为5cm,侧面积为60πcm2,设圆锥的母线与高的夹角为θ,则sinθ的值为()A.B.C.D.9.如图,圆锥的底面半径为1,母线长为3,则侧面积为()A.2πB.3πC.6πD.8π10.已知圆柱的底面半径为3cm,母线长为6cm,则圆柱的侧面积是()A.36cm2B.36πcm2C.18cm2D.18πcm2二.填空题(共10小题)11.我们规定:一个正n边形(n为整数,n≥4)的最长对角线与边长的比值,叫做这个正n边形的“特征值”,记为a n,那么a6=.12.有三个大小一样的正六边形,可按下列方式进行拼接:方式1:如图1;方式2:如图2;若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是.有n个长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则n的最大值为.13.如图,ABCDE是边长为1的正五边形,则它的内切圆与外接圆所围圆环的面积为.14.如图,点O是正八边形ABCDEFGH的中心点,点M和点N分别在AB和DE上,且AM=DN,则∠MON的大小为度.15.如图,半径为6的⊙O的直径AB与弦CD垂直,且∠BAC=40°,则劣弧BD的长是(结果保留π).16.如图,已知扇形的圆心角∠AOB=120°,半径OA=2,则扇形的弧长为.17.如图,等边△ABC的边长是4,O是△ABC的中心,连接OB,OC,把△BOC绕着点CO旋转到△AO′C的位置,在这个旋转过程中,线段OB所扫过的图形的面积是.18.如图是一个圆锥形冰淇淋,已知它的母线长是13cm,高是12cm,则这个圆锥形冰淇淋的底面面积是.19.圆锥的母线长是6cm,侧面积是30πcm2,该圆锥底面圆的半径长等于cm.20.如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是.三.解答题(共8小题)21.如图,在正五边形ABCDE中,CA与DB相交于点F,若AB=1,求BF.22.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.(1)求∠F AB的度数;(2)求证:OG=OH.23.求半径为3的圆的内接正方形的边长.24.如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是的中点,连结AD、BC 若,∠DAB=30°.(1)求∠ABC的度数;(2)若AD=8,求的长度(结果保留π).25.如图,半圆O的直径AB=6,弦CD=3,的长为π,求的长.26.如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.(1)求证:BD=CD;(2)若AB=4,∠BAC=45°,求阴影部分的面积.27.已知圆锥的底面半径为3,母线长为6,求此圆锥侧面展开图的圆心角.28.一个圆柱形容器的内半径为10厘米,里面盛有一定高度的水,将一个长25厘米,宽6厘米的长方体金属块完全淹没,结果容器内的水升高了4厘米(没有溢出),问这个金属块的高是多少厘米?(π的取值3)答案详解:一.选择题(共10小题)1.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为()A.B.C.D.【解答】解:∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1且相似比为2:1,∵正六角星形AFBDCE的面积为1,∴正六角星形A1F1B1D1C1E1的面积为,同理可得,第二个六角形的面积为:=,第三个六角形的面积为:=,第四个六角形的面积为:=.故选:D.2.如图,点P、M、N分别是边长为2的正六边形中不相邻三条边的中点,则△PMN的周长为()A.6B.6C.6D.9【解答】解:分别过正六边形的顶点A,B作AE⊥MN于E,BF⊥MN于F,则∠EAM=∠NBF=30°,EF=AB=2,∵AM=BN=2=1,∴EM=FN=1=,∴MN=++2=3,∴△PMN的周长3×3=9,故选:D.3.若一个正多边形的一个内角是135°,则这个正多边形的中心角为()A.20°B.45°C.60°D.90°【解答】解:∵正多边形的一个内角是135°,∴该正多边形的一个外角为45°,∵多边形的外角之和为360°,∴边数n==8,∴该正多边形为正八边形,故这个正多边形的中心角为:=45°.故选:B.4.下列圆的内接正多边形中,中心角最大的图形是()A.正三角形B.正方形C.正五边形D.正六边形【解答】解:∵正三角形一条边所对的圆心角是360°÷3=120°,正方形一条边所对的圆心角是360°÷4=90°,正五边形一条边所对的圆心角是360°÷5=72°,正六边形一条边所对的圆心角是360°÷6=60°,∴一条边所对的圆心角最大的图形是正三角形,故选:A.5.如图,圆上有A、B、C、D四点,其中∠BAD=80°,若弧ABC、弧ADC的长度分别为7π、11π,则弧BAD的长度是()A.4πB.8πC.l0πD.15π【解答】解:∵、的长度分别为7π,11π,∴圆的周长为18π,∵∠A=80°,∴∠C=180°﹣80°=100°,故=×18π=10π.故选:C.6.如图,四边形ABCD为⊙O的内接四边形,⊙O的半径为3,AO⊥BC,垂足为点E,若∠ADC=130°,则的长等于()A.B.C.D.【解答】解:连接OB、OC,∵四边形ABCD为⊙O的内接四边形,∴∠ABC+∠ADC=180°,∴∠ABC=180°﹣∠ADC=50°,∴∠AOC=100°,∴∠EOC=80°,∵AO⊥BC,OB=OC,∴∠BOC=2∠EOC=160°,∴的长==π,故选:D.7.如图,矩形ABCD的边AB=1,BC=2,以点B为圆心,BC为半径画弧,交AD于点E,则图中阴影部分的面积是()A.B.2C.D.2﹣【解答】解:如图,连接BE,则BE=BC=2,在Rt△ABE中,∵AB=1、BE=2,∴∠AEB=∠EBC=30°,AE==,则阴影部分的面积=S矩形ABCD﹣S△ABE﹣S扇形BCE=1×2﹣×1×﹣=2﹣﹣,故选:A.8.已知圆锥的底面半径为5cm,侧面积为60πcm2,设圆锥的母线与高的夹角为θ,则sinθ的值为()A.B.C.D.【解答】解:设圆锥的母线长为R,由题意得60π=π×5×R,解得R=12.∴sinθ=,故选:C.9.如图,圆锥的底面半径为1,母线长为3,则侧面积为()A.2πB.3πC.6πD.8π【解答】解:圆锥的侧面积为:×2π×1×3=3π,故选:B.10.已知圆柱的底面半径为3cm,母线长为6cm,则圆柱的侧面积是()A.36cm2B.36πcm2C.18cm2D.18πcm2【解答】解:根据侧面积公式可得π×2×3×6=36πcm2,故选:B.二.填空题(共10小题)11.我们规定:一个正n边形(n为整数,n≥4)的最长对角线与边长的比值,叫做这个正n边形的“特征值”,记为a n,那么a6=2.【解答】解:如图,正六边形ABCDEF中,对角线BE、CF交于点O,连接EC,根据题意得:BE是正六边形最长的对角线,∵ABCDEF是正六边形,∴△OBC是等边三角形,∴∠OBC=∠OCB=∠BOC=60°,∵ABCDEF是正六边形,∴OE=OC,∴∠OEC=∠OCE,∵∠BOC=∠OEC+∠OCE,∴∠OEC=∠OCE=30°,即∠BEC=30°,∴∠BCE=90°,∴△BEC是直角三角形,∴BC=BE,∴=2,∴a6=2,故答案为2.12.有三个大小一样的正六边形,可按下列方式进行拼接:方式1:如图1;方式2:如图2;若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是7.有n个长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则n的最大值为.【解答】解:有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长为4×4+2=18;按下图拼接,图案的外轮廓的周长为18,此时正六边形的个数最多,即n的最大值为7.故答案为:18,7.13.如图,ABCDE是边长为1的正五边形,则它的内切圆与外接圆所围圆环的面积为.【解答】解:正五边形的内切圆与外接圆所围圆环的面积为:π(OA2﹣OH2)=π×AH2=.故答案为:.14.如图,点O是正八边形ABCDEFGH的中心点,点M和点N分别在AB和DE上,且AM=DN,则∠MON的大小为135度.【解答】解:连接OA、OB、OC、OD;∵正八边形是中心对称图形,∴中心角为360°÷8=45°;∴∠OAM=∠ODN=67.5°,∵OA=OD,∠OAM=∠ODN,AM=DN,∴△OAM≌△ODN(SAS),∴∠AOM=∠DON,∴∠MON=∠MOB+∠BOC+∠COD+∠NOD=3∠AOB=135°,故答案为:135.15.如图,半径为6的⊙O的直径AB与弦CD垂直,且∠BAC=40°,则劣弧BD的长是π(结果保留π).【解答】解:如图,连接OC、OD,∵∠BAC=40°,∴∠BOC=2∠BAC=80°.∵⊙O的直径AB与弦CD垂直,∴=,∴∠BOC=∠BOD=80°,∴劣弧BD的长是:=π.故答案为π.16.如图,已知扇形的圆心角∠AOB=120°,半径OA=2,则扇形的弧长为.【解答】解:由弧长公式得:扇形的弧长==;故答案为:.17.如图,等边△ABC的边长是4,O是△ABC的中心,连接OB,OC,把△BOC绕着点CO旋转到△AO′C的位置,在这个旋转过程中,线段OB所扫过的图形的面积是.【解答】解:∵等边△ABC的边长是4,O是△ABC的中心,∴OB=OC=,∴线段OB所扫过的图形的面积=S扇形OAB﹣S扇形OCO′=﹣=﹣=,故答案为:.18.如图是一个圆锥形冰淇淋,已知它的母线长是13cm,高是12cm,则这个圆锥形冰淇淋的底面面积是25πcm2.【解答】解:如图,圆锥的母线AB=13cm,圆锥的高AO=12cm,圆锥的底面半径OB =r,在Rt△AOB中,(cm),∴S=πr2=π×52=25πcm2.故答案为25πcm2.19.圆锥的母线长是6cm,侧面积是30πcm2,该圆锥底面圆的半径长等于5cm.【解答】解:根据题意得:S=πrl,即r===5,则圆锥底面圆的半径长等于5cm,故答案为:520.如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是20πcm2.【解答】解:这个圆柱的侧面积=5×2π×2=20π(cm2).故答案为20πcm2.三.解答题(共8小题)21.如图,在正五边形ABCDE中,CA与DB相交于点F,若AB=1,求BF.【解答】解:在正五边形ABCDE中,∵∠ABC=∠DCB=108°,BC=BA=CD,∴∠BAC=∠BCA=∠CDB=∠CBD=36°,∴∠ABF=72°,∴∠AFB=∠CBD+∠ACB=72°,∴∠AFB=∠ABF,∠FCB=∠FBC,∴AF=AB=1,FB=CF,设FB=FC=x,∵∠BCF=∠BCA,∠CBF=∠CAB,∴△BCF∽△ACB,∴CB2=CF•CA,∴x(x+1)=1,∴x2+x﹣1=0,∴x=或(舍去),∴BF=.22.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.(1)求∠F AB的度数;(2)求证:OG=OH.【解答】(1)解:∵六边形ABCDEF是正六边形,∴∠F AB==120°;(2)证明:连接OA、OB,∵OA=OB,∴∠OAB=∠OBA,∵∠F AB=∠CBA,∴∠OAG=∠OBH,在△AOG和△BOH中,,∴△AOG≌△BOH(SAS)∴OG=OH.23.求半径为3的圆的内接正方形的边长.【解答】解:如图,∵四边形ABCD是⊙O的内接正方形,∴∠OBE=45°;而OE⊥BC,∴BE=CE;而OB=3,∴sin45°=,cos45°=,∴OE=,BE=,∴BC=3,故半径为3的圆内接正方形的边长为3.24.如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是的中点,连结AD、BC 若,∠DAB=30°.(1)求∠ABC的度数;(2)若AD=8,求的长度(结果保留π).【解答】解:(1)如图,连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∵∠DAB=30°,∴∠ABD=90°﹣30°=60°.∵C是的中点,∴∠ABC=∠DBC=∠ABD=30°.(2)如图,连接OC,则∠AOC=2∠ABC=60°,∵∠A=30°,AD=8,.∴AB=16,∴AO=8,∴的长度==π.25.如图,半圆O的直径AB=6,弦CD=3,的长为π,求的长.【解答】解:(1)连接OD、OC,∵CD=OC=OD=3,∴△CDO是等边三角形,∴∠COD=60°,∴的长==π,又∵半圆弧的长度为:×6π=3π,∴=3π﹣π﹣=.26.如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.(1)求证:BD=CD;(2)若AB=4,∠BAC=45°,求阴影部分的面积.【解答】(1)证明:连结AD,∵AB为⊙O直径,∴AD⊥BC,又∵AB=AC,∴BD=CD;(2)解:连结OE,∵AB=4,∠BAC=45°,∴∠BOE=90°,BO=EO=2,∠AOE=90°,∴S阴=S△BOE+S扇形OAE=×2×2+=π+2.27.已知圆锥的底面半径为3,母线长为6,求此圆锥侧面展开图的圆心角.【解答】解:∵圆锥底面半径是3,∴圆锥的底面周长为6π,设圆锥的侧面展开的扇形圆心角为n°,=6π,解得n=180,答:此圆锥侧面展开图的圆心角是180°.28.一个圆柱形容器的内半径为10厘米,里面盛有一定高度的水,将一个长25厘米,宽6厘米的长方体金属块完全淹没,结果容器内的水升高了4厘米(没有溢出),问这个金属块的高是多少厘米?(π的取值3)【解答】解:设长方形的高是xcm,则利用体积公式可得25×6x=π×102×4,解得x≈8.答:这个金属块的高是8厘米。
圆的周长练习已打印

六年级数学上册第一单元《圆的周长》练习一、填空1.圆的周长是它直径的( )倍。
2.在一个周长是28厘米的正方形里画一个最大的圆,圆的周长是( )3.用一根铁丝围成一个圆,半径正好是5分米,如果把这根铁丝改围成一个正方形,它的边长是( )分米。
4.汽车轮滚动一周,所行的路程是车轮的()5.用圆规画一个圆,如果圆规两脚之间的距离是6厘米,画出的这个圆的周长是()厘米。
6.画一个周长是12.56厘米的圆,圆规两脚的距离是()。
7.一个闹钟的分针长5厘米,经过1小时分针尖端走过的路程是(),经过30分钟分针尖端走过的路程是()8.做半径是20厘米的铁拳100个,需要铁丝()米9.在一块直径是1米的圆形桌布周围缝一条花边,接头处4厘米,这条花边长()米10.一个半圆的周长是15.42米,它的半径是()米11.圆的半径扩大3倍,周长扩大()倍12.时钟的分针转动一周形成的图形是().13.从()到()任意一点的线段叫半径.14.通过()并且()都在()的线段叫做直径.15.在同一个圆里,所有的半径(),所有的()也都相等,直径等于半径的().16.用圆规画一个直径20厘米的圆,圆规两脚步间的距离是()厘米.17.圆是()图形,它有()对称轴.18.正方形有()条对称轴,长方形有()条对称轴,等腰三角形有()条对称轴,等边三角形有()条对称轴.半圆有()条对称轴,等腰梯形有()条对称轴。
19.一个圆的周长是同圆直径的()倍.20.有一个圆形鱼池的半径是10米,如果绕其周围走一圈,要走()米。
21.一个挂钟的时针长5厘米,一昼夜这根时针的尖端走了()厘米。
22.画圆时,圆规两脚间的距离就是圆的()。
23.两端都在圆上的线段,()最长。
.24圆的半径是7厘米,它的周长是()厘米,圆的直径是13米,它的周长是()米。
圆的周长是75.36分米,它的半径是()分米。
25.要在底面半径是14厘米的圆柱形水桶外面打上一个铁丝箍,接头部分是6厘米,需用铁丝()厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的有关计算练习题
一、知识点与方法:
1.弧长公式L弧=;扇形的面积公式:S扇==。
2.S弓=S扇-S△(弧为劣弧时);S弓=S扇+S△(弧为优弧时)。
3.求路线长或求阴影部分的面积时,常用转化的思想:化不规则图形为规则图形;化不好求的为容易求的;有时“割”——分割,有时“补”——补全图形。
二、练习题:
(一)填空题:
1.(2011聊城)在半径为6cm的圆中,60º圆心角所对的弧长为cm(结果保留π)。
2.(2012重庆)一个扇形的圆心角为120°,半径为3,则这个扇形的面积为_ _(保留π)。
3.(2012肇庆)扇形的半径是9 cm,弧长是3πcm,则此扇形的圆心角为度。
4.(2012巴中)已知一个圆的半径为5cm,则它的内接正六边形的边长为_______㎝。
5.(2012河南)母线长为3,底面圆的直径为2的圆锥的侧面积为。
6.(2012达州)已知圆锥的底面半径为4,母线长为6,则它的侧面积是 .(不取近似值)
7.(2012苏州)已知扇形的圆心角为45°,弧长等于,则该扇形的半径为。
8.(2012哈尔滨)一个圆锥的母线长为4,侧面积为8π,则这个圆锥的底面圆的半径是。
9.(2012遵义)如图,将边长为cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动6次后,正方形的中心O经过的路线长是cm.(结果保留π)
10.(2012德州)如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成. 已知正三角形的边长为1,则凸轮的周长等于_________.
11.(2012成都)一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为________ (结果保留π )。
12.(2012广东汕头,13,4分)如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π)。
13.(2012衡阳)如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥
AO,若∠A=30°,则劣弧的长为cm。
14. (2012日照)如图,正方形OCDE的边长为1,阴影部分的面积记作S1;如图2,最大圆半径r=1,阴影部分的面积记作S2,则S1S2(用“>”、“<”或“=”填空).
15.(2012绥化)小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径
cm.
=,则这个圆锥形漏斗的侧面积是2
OC cm
3
OB cm
=,高4
16.(2012广安)如图,Rt △ABC 的边BC 位于直线l 上,AC=3,∠ACB=90o ,∠A=30o ,若△RtABC 由现在的位置向右无滑动地翻转,当点A 第3次落在直线上l 时,点A 所经过的路线的长为________________(结果用含л的式子表示).
1.(2012嘉兴)已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为( )
A. 15π cm 2
B. 30πcm 2
C. 60πcm 2 2
(2012铜仁)小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作一个底面半径为9cm,母线长为30cm 的圆锥形生日礼帽,则这个圆锥形礼帽的侧面积为( )
A .270πcm 2
B .540πcm 2
C .135πcm 2
D .216πcm 2
(2012南充) 一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是( )A .120° B .180° C .240° D .300°
(2012莱芜)若一个圆锥的底面积为4πcm 2,圆锥的高为42cm ,则该圆锥的侧面展开图中圆心角的度数为( )A .4 0° B .80° C . 120° D .150°
(2012连云港,3,3分)用半径为2cm 的半圆围城一个圆锥的侧面,则这个圆锥的底面半径为( )A. 1cm B. 2cm C. πcm D. 2πcm
(2012兰州)如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为( )A. π B. 1 C. 2 D. 23
π (2012珠海)如果一个扇形的半径是1,弧长是3
π,那么此扇形的圆心角的大小为( ) A .30°B .45°C .60°D .90°
(2012泰安)如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连接BC ,若ABC ∠=120°,OC=3,则BC 的长为( )A.π B.2π D.3π D.5π
(2012内江)如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠CDB =30°,CD =
部分图形的面积为( )A .4π B .2π C .π D .2π3
(2012临沂市)如图,AB 是⊙O 的直径,点E 是BC 的中点,AB=4,∠BED=1200,则图中阴影部分的面积之和为( )A.1 B. 23 C. 3 D. 32
(2012衢州)用圆心角为120°,半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( ) A
B
.cm C
.D .4cm
(2012绍兴)如图,扇形DOE 的半径为3,边长为3的菱形OABC 的顶点A ,C ,B 分别在OD ,OE ,DE 上,若把扇形DOE 围成一个圆锥,则此圆锥的高为( ) A.21 B. 22 C.237 D. 2
35 (2012宁波)如图,用邻边长为a,b(a <b )的矩形硬纸板截出以a 为直径的两个半圆,再截出与矩形的较边、两个半圆均相切的两个小圆,把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a 与b 关系式是
(A )b= 3 a (B)b=5+12 (C) 52
(D) b= 2 a (2012北海)如图,在边长为1的正方形组成的网格中,△ABC 的顶点都在格点上,将△ABC 绕点C 顺时针旋转60°,则顶点A 所经过的路径长为: ( )
A .10π B
C
π D .π
(2012咸宁)如图,⊙O 的外切正六边形ABCDEF 的边长为2,则图中阴影部分的面积为
( )A .-3π2 B .-32π3 C .-32π2 D .-322π3
(2012山西)如图是某公园的一角,∠AOB=90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB 上,CD ∥OB ,则图中休闲区(阴影部分)的面积是( )
A .(10π﹣)米2
B .(π﹣)米2
C .(6π﹣)米2
D .(6π﹣)米2 (2012日照)如图,在4×4的正方形网格中,若将△ABC 绕着点A 逆时针旋转得到△AB ′C ′
,
B
A B C 第11题图
则⌒B B ′
的长为( )A.π B.2π C.7π D.6π
三、解答题:
1.(2012贵阳)如图,在⊙O 中,直径AB=2,CA 切⊙O 于A ,BC 交⊙O 于D ,若∠C=45°,则(1)BD 的长是 ;(2)求阴影部分的面积。
2.(2012义乌)如图,已知AB 是⊙O 的直径,点C 、D 在⊙O 上,点E 在⊙O 外,∠EAC =∠D =60°。
(1)求∠ABC 的度数;(2)求证:AE 是⊙O 的切线;(3)当BC =4时,求劣弧AC 的长。
3.(2012宁波)如图在△ABC 中,BE 是它的角平分线,∠C=900,D 在AB 边上,以DB 为直径的
半圆O 经过点E 交BC 于点F.
(1)求证:AC 是⊙O 的切线;(2)已知sinA=12
,⊙O 的半径为4,求图中阴影部分的面积。
A B C D E
F
(第7题)
O 第23题图 A C
E
4.(2012吉林)如图,在扇形OAB 中,∠AOB=90°,半径OA=6.将扇形OAB 沿过点B 的直线折叠.点O 恰好落在弧AB 上点D 处,折痕交OA 于点C ,求整个阴影部分的周长和面积.
5.(2010宁夏)如图,已知:⊙O 的直径AB 与弦AC 的夹角∠A=30°,过点C 作⊙O 的切线交AB 的延长线于点P .
(1)求证:AC=CP ;(2)若PC=6,求图中阴影部分的面积(结果精确到0.1). (
1.73=
3.14π=)
6.(2010宁波)如图,AB 是⊙O 的直径,弦DE 垂直平分半径OA ,C 为垂足,弦DF 与半径 OB 相交于点P ,连结EF 、EO ,若DE =23,∠DPA =45°。
(1)求⊙O 的半径;(2)求图中阴影部分的面积.
A
P E A
B
O D P C。
