倒立摆的建模与控制仿真
自动化实验-倒立摆实验-附仿真结果图

一、直线一级倒立摆的仿真(一)直线一级倒立摆的数学建模对于倒立摆系统,由于其本身是自不稳定的系统,实验建模存在一定的困难。
但是忽略掉一些次要的因素后,倒立摆系统就是一个典型的运动的刚体系统,可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。
下面我们采用其中的牛顿-欧拉方法和拉格朗日方法分别建立直线型一级倒立摆系统的数学模型.图2 直线一级倒立摆模型φ摆杆与垂直向上方向的夹角;θ摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下)。
图3 小车及摆杆受力分析分析小车水平方向所受的合力,可以得到以下方程:由摆杆水平方向的受力进行分析可以得到下面等式:把这个等式代入式1中,就得到系统的第一个运动方程:为了推出系统的第二个运动方程,我们对摆杆垂直方向上的合力进行分析,可以得到下面方程:力矩平衡方程如下:注意:此方程中力矩的方向,由于θ=π+φ,cosφ= −cosθ,sinφ= −sin θ,故等式前面有负号。
合并这两个方程,约去P 和N,得到第二个运动方程:设θ=π+φ(φ是摆杆与垂直向上方向之间的夹角),假设φ与1(单位是弧度)相比很小,即φ<〈1,则可以进行近似处理:。
用u 来代表被控对象的输入力F,线性化后两个运动方程如下:对式9进行拉普拉斯变换,得到注意:推导传递函数时假设初始条件为0。
由于输出为角度φ,求解方程组的第一个方程,可以得到:或如果令v = x,则有:把上式代入方程组的第二个方程,得到:整理后得到传递函数:其中设系统状态空间方程为:方程组对解代数方程,得到解如下:整理后得到系统状态空间方程:设则有:实际系统的模型参数如下:M 小车质量1。
096 Kgm 摆杆质量0.109 Kgb 小车摩擦系数0 。
1N/m/secl 摆杆转动轴心到杆质心的长度0。
2 5mI 摆杆惯量0。
0034 kg*m*m把上述参数代入,可以得到系统的实际模型。
摆杆角度和小车位移的传递函数:摆杆角度和小车加速度之间的传递函数为:摆杆角度和小车所受外界作用力的传递函数:以外界作用力作为输入的系统状态方程:(二)倒立摆的PID调节:经典控制理论的研究对象主要是单输入单输出的系统,控制器设计时一般需要有关被控对象的较精确模型。
一级倒立摆的建模及控制分析

直线一级倒立摆的建模及控制分析摘要:本文利用牛顿—欧拉方法,建立了直线型一级倒立摆系统的数学模型。
在分析的基础上, 采用状态反馈控制中极点配置法设计了用于直线型一级倒立摆系统的控制器。
此外,用MATLAB 仿真绘制了相应的曲线并做了分析。
一、问题描述倒立摆控制系统是机器人技术、控制理论、计算机控制等多个领域和多种技术的有机结合,其被控系统本身是一个绝对不稳定、高阶次、多变量、强耦合的非线性系统,是控制理论研究中较为理想的实验对象。
它为控制理论的教学、实验和科研构建了一个良好的实验平台,促进了控制系统新理论、新思想的发展。
倒立摆系统可以采用多种理论和方法来实现其稳定控制,如PID,自适应、状态反馈、智能控制等方法都己经在倒立摆控制系统上得到实现。
由于直线一级倒立摆的力学模型较简单,又是研究其他倒立摆的基础,所以本文利用所学的矩阵论知识对此倒立摆进行建模和控制分析。
二、方法简述本文利用牛顿—欧拉方法,建立了直线型一级倒立摆系统的数学模型。
在分析的基础上, 采用状态反馈控制中极点配置法设计了用于直线型一级倒立摆系统的控制器。
此外,用MATLAB 仿真绘制了相应的曲线并做了分析。
三、模型的建立及分析3.1 微分方程的推导在忽略了空气阻力,各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如下图1所示。
图1 直线一级倒立摆系统假设 M 为小车质量;m 为摆杆质量;b 为小车摩擦系数;l 为摆杆转动轴心到杆质心的长度;I 为摆杆惯量;F 为加在小车上的力;x 为小车位置;φ为摆杆与垂直向上方向的夹角;θ为摆杆与垂直向下方向的夹角。
图2是系统中小车和摆杆的受力分析图。
其中,N 和P 为小车与摆杆相互作用力的水平和垂直方向的分量。
值得注意的是: 在实际倒立摆系统中检测和执行装置的正负方向已确定, 因而矢量方向定义如图2所示, 图示方向为矢量正向。
(a) (b)图2 小车和摆杆的受力分析图分析小车水平方向所受的合力,可以得到以下方程:N x b F x M --= (1)由摆杆水平方向的受力进行分析可以得到下面等式:θθθθs i n c o s 2ml ml x m N -+= (2) 把这个等式代入上式中,就得到系统的第一个运动方程:()F ml ml x b x m M =-+++θθθθsin cos 2 (3)为了推出系统的第二个运动方程,我们对摆杆垂直方向上的合力进行分析,可以得到下面方程:θθθθc o s s i n 2 ml ml mg P --=- (4) 力矩平衡方程如下:θθθI Nl Pl =--cos sin (5)合并这(4)、(5)两个方程,约去P 和N ,得到第二个运动方程:()θθθc o s s i n 2x ml mgl ml I -=++ (6) 假设φ与1(单位是弧度)相比很小,即φ《1,则可以进行近似处理:0d d s i n 1c o s 2=⎪⎭⎫ ⎝⎛-=-=t θφθθ,, (7) 用u 来代表被控对象的输入力F ,线性化后两个运动方程如下:()()⎩⎨⎧=-++=-+u ml x b x m M xml mgl ml I φφφ 2 (8) 3.2 状态空间方程方程组(8)对φ,x 解代数方程,整理后的系统状态空间方程为: ()()()()()()()()u Mm l m M I m l Mm l m M I m lI x x Mm l m M I m M m gl Mm l m M I m lbMm l m M I gl m Mm l m M I b m l I x x ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++++++⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+++++-+++++-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡222222222200001000000010φφφφ u x x x y ⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=0001000001φφφ 对于质量均匀分布的摆杆有:3/2ml I =,于是可得:()x ml mgl ml ml =-+φφ223/ 化简得:xll g 4343+=φφ设}{x u x x X ==1,,,,φφ ,则有:14301004300100000000010u l x x l g x x⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡φφφφ10001000001u x x x y ⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=φφφ 3.3 实际系统模型实际系统模型参数: M =1.096 Kg ;m =0.109 Kg ;b =0.1 N/m/s ; l =0.25 m ;I =0.0034 kg ·m ·m ;采样频率 T =0.005 s 。
单级倒立摆及其控制系统的研究和图形化仿真

������
B
A
������
图 1 倒立摆的物理模型
控制倒立摆的目的是使摆杆不到,滑块不动,即 为 0 且 不随时间变化。这里,控 制量被定义为作用在滑块 A 上沿 方向的力 。
根据以上物理模型得到系统的动力学方程:
(
)
将滑块速度 和摆杆角速度 分别定义为:
若控制作用 恒为 0,则由动力学方程可知,倒立摆是非线性自治系统。该系统的状
参考文献
1. 施颂椒, 陈学中, 杜秀华. 现代控制理论基础. 北京:高等教育出版社, 2005 2. 刘崇新. 非线性电路理论及应用. 西安:西安交通大学出版社, 2007
3.2. 碰撞过程
定义:设物体 A 与物体 B 以一定相对速率碰撞,碰撞前后,撞击点切面法线方向上的速 率分量分别为 和 ,则物体 A 与物体 B 之间的碰撞分离率 被定义为:
显然,碰撞分离率 与物体 A 和 B 的材质有关,其取值范围为 [ ],当
生完全弹性碰撞,当
则发生完全非弹性碰撞。
则发
设墙壁与滑块之间的碰撞分离率为 速度 撞击墙壁后,将以速度 击地面后,将以角速度
4. 镇定控制
倒立摆接近平衡状态
时,有
(
)
,系统动力学方程线性化为
令 [] [ 其特征方程为:
⁄
]
[ ⁄ ],系统可用状态空间表示为:
(
)⁄
⁄
̇
(
)
令̅
̅
其中
̅
,原状态方程变换为能控标准型:
̅̇ ̅ ̅ ̅
⁄
⁄
[
⁄
⁄]
根据给定的极点位置,可以求得期望的特征方程,形如
能控标准型状态方程的反馈向量为:
基于MATLAB的单级旋转倒立摆建模与控制仿真
基于MATLAB的单级旋转倒立摆建模与控制仿真一、分析课题,选择数据源外文数据库多种多样,对于工程应用所研究的课题,通常选取比较常用的数据库为:IEEE Xplore(/Xplore/home.jsp)、Google学术搜索(/)以及SpringerLink(/)。
二、选取检索词单级旋转倒立摆的英文名称为:single rotational inverted pendulum,故以此为检索词进行检索。
三、构造检索式Single (and)rotational inverted pendulum四、实施检索,调整检索策略由于搜索步骤较多,此处只详细给出使用IEEE Xplore数据库的检索过程,另外两个数据库提供大概检索过程及结果截图。
由于搜索结果只有9条,数量较少,故调整检索词,过程如下:Google学术搜索:SpringerLink数据库:五、检索结果1、题目:Analysis of human gait using an Inverted Pendulum Model基于倒立摆模型的人体步态分析Zhe Tang ; Meng Joo Er ; Chien, C.-J. Fuzzy Systems, 2008. FUZZ-IEEE 2008. (IEEE World Congress on Computational Intelligence). IEEE International Conference onAbstract: IPM(Inverted Pendulum Model) has been widely used for modeling of human motion gaits. There is a common condition in most of these models, the reaction force between the floor and the humanoid must go through the CoG (Center of Gravity) of the a humanoid or human being. However, the recent bio-mechanical studies show that there are angular moments around the CoG of a human being during human motion. In other words, the reaction force does not necessarily pass through the CoG. In this paper, the motion of IPM is analyzed by taking into consideration two kinds of rotational moments, namely around the pivot and around the CoG. The human motion has been decomposed into the sagittal plane and front plane in the double support phase and single support phase. The motions of the IPM in these four different phases are derived by solving four differential equations with boundary conditions. Simulation results show that a stable human gait is synthesized by using our proposed IPM.摘要:IPM(倒立摆模型)已被广泛用于人体运动步态建模。
二级直线倒立摆系统建模、仿真与实物控制的开题报告

二级直线倒立摆系统建模、仿真与实物控制的开题报告一、选题背景及意义直线倒立摆系统是一种应用广泛的控制系统,它具有复杂的非线性特性,因此对其建模、控制和仿真都具有一定的挑战性。
直线倒立摆系统广泛应用于自动驾驶、飞行器、医疗器械等领域。
本文将研究二级直线倒立摆系统的建模、仿真与实物控制,以提高对该系统的理解和掌握。
通过实验控制实际系统,验证仿真模型的正确性并提高控制策略的可靠性与性能。
二、研究内容1.二级直线倒立摆系统的建模研究系统的动力学特性,建立数学模型,包括机械、电子等方面的模型,并给出系统的描述方程。
2.仿真系统的设计与实现通过MATLAB或Simulink等工具,根据系统的动力学模型进行仿真,分析系统的动态特性,验证模型的正确性。
3.实物系统的设计与实现根据建模结果,设计实物系统,包括硬件和软件,搭建实验环境,并选取合适的控制器,使用反馈控制算法对实验数据进行处理。
4.实物控制系统的测试与优化将实验得到的数据进行分析、处理和优化,比较实物系统和仿真系统的差异并给出改进方案,从而提高系统的动态响应特性和控制性能。
三、研究方法及预期结果本文将采用系统分析、数学建模、仿真分析、控制器设计和优化等方法,通过建模、仿真、实物控制等多个方面去了解直线倒立摆系统。
预期结果是建立二级直线倒立摆系统的模型,完成仿真和实验的设计与实现,控制系统实现稳定的控制策略,并得出实物系统和仿真系统的控制性能优化方案。
四、进度安排第一阶段:文献综述和理论研究,研究直线倒立摆控制系统的基本原理和方法。
(2周)第二阶段:根据文献进行仿真研究,建立稳定的仿真模型。
(2周)第三阶段:设计实物控制系统,搭建实验环境。
(2周)第四阶段:实现控制系统与优化,得出实验数据并进行分析和优化,提高系统的控制性能。
(2周)第五阶段:撰写论文和答辩。
(4周)五、预期成果本文通过对二级直线倒立摆系统的建模、仿真和实物控制的研究,完成了对系统的深入理解和掌握,得出了系统的优化控制方案。
一级倒立摆的可视化建模与稳定控制设计

1966年
1976年
1995年
倒立摆的应用
倒立摆的分类
直线倒立摆 一级倒立摆
基座运动
环形倒立摆
摆杆
二级倒立摆
平面倒立摆
多级倒立摆
另外根据材料分类:刚体摆杆倒立摆系统和柔性摆杆倒立摆系统 „„
根据不同的分类方法,我们可以将倒立摆进行不同的分类。
倒立摆的特点
特性:非线性、多变量、强耦合、不稳定性
倒立摆系统拥有低投入、简易的结构、直观 的形象、方便仿真等特点。
设计演示界面
保存文件,命名为 fangzhenjieguo.fig ,同时会自动生成一 个fangzhenjieguo.m 文件
将摆角、小车位 移和时间参量, 导入到工作区中 ,供GUI编程使 用。
打开之前保存演示界面是生成的fangzhenjieguo.m文件,找到 “仿真开始”按钮所对应的回调函数,在函数下方加入程序: sim('daolibaimoxing');%运行仿真模型
初始条件设为[0.1rad,0.5rad/s,0,0],仿真曲线如 图所示,上面图线为摆角,下面为小车位移。
右图为未加控制器前的系统 阶跃响应曲线,可以看出, 摆角和小车位移的曲线都是 发散的。通过与仿真结果比 较,可以看出,加了BP神经 网络控制器的倒立摆系统, 摆角和小车位移曲线趋于稳 定,说明所设计的BP神经网 络控制器能够起到有效的控 制作用。验证了控制器设计 的正确性和可行性。
四、GUI设计
图形用户界面(Graphical User Interface, 简称 GUI,又称图形用户接口)是指采用图形 方式显示的计算机操作用户界面。
GUI具有下面几个方面的基本要求:轻型、 占用资源少、高性能、高可靠性、便于移 植、可配置等特点。
直线二级倒立摆建模与matlab仿真LQR
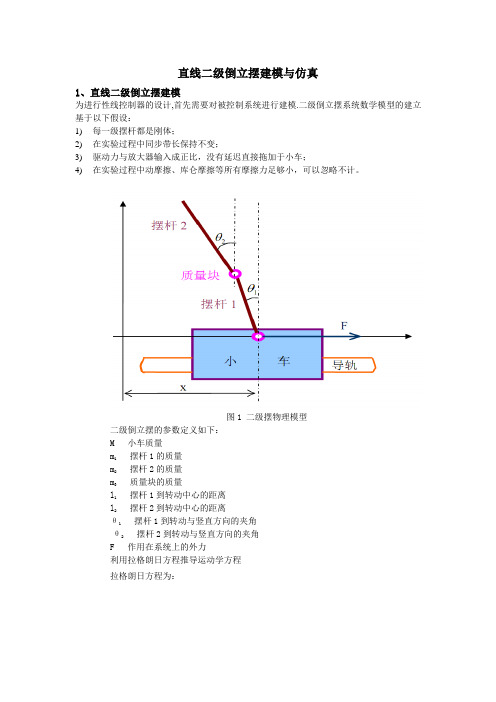
直线二级倒立摆建模与仿真1、直线二级倒立摆建模为进行性线控制器的设计,首先需要对被控制系统进行建模.二级倒立摆系统数学模型的建立基于以下假设:1)每一级摆杆都是刚体;2)在实验过程中同步带长保持不变;3)驱动力与放大器输入成正比,没有延迟直接拖加于小车;4)在实验过程中动摩擦、库仑摩擦等所有摩擦力足够小,可以忽略不计。
图1 二级摆物理模型二级倒立摆的参数定义如下:M 小车质量m1摆杆1的质量m2摆杆2的质量m3质量块的质量l1摆杆1到转动中心的距离l2摆杆2到转动中心的距离θ1摆杆1到转动与竖直方向的夹角θ2摆杆2到转动与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程拉格朗日方程为:其中L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的势能其中错误!未找到引用源。
,错误!未找到引用源。
为系统在第i 个广义坐标上的外力,在二级倒立摆系统中,系统有三个广义坐标,分别为x,θ1,θ2,θ3。
首先计算系统的动能:其中错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
分别为小车的动能,摆杆1的动能,摆杆2的动能和质量块的动能。
小车的动能:错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆1的平动动能和转动动能。
错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆2的平动动能和转动动能。
对于系统,设以下变量: xpend1摆杆1质心横坐标 xpend2摆杆2质心横坐标 yangle1摆杆1质心纵坐标 yangle2摆杆2质心纵坐标 xmass 质量块质心横坐标 ymass 质量块质心纵坐标 又有:(,)(,)(,)L q q T q q V q q =-则有:系统总动能:系统总势能:则有:求解状态方程:可解得:使用MATLAB对得到的系统进行阶跃响应分析,执行命令:A=[0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 1 01;0 0 0 0 0 0;0 86.69 -21.62 0 0 0;0 -40.31 39.45 0 0 0];B=[0;0;0;1;6.64;-0.808];C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0];sys=ss(A,B,C,D);t=0:0.001:5;step(sys,t)求取系统的单位阶跃响应曲线:图2 二级摆阶跃响应曲线由图示可知系统小车位置、摆杆1角度和摆杆2角度均发散,需要设计控制器以满足期望要求。
基于MATLAB的旋转倒立摆建模和控制仿真

倒立摆系统作为一个被控对象具有非线性、强耦合、欠驱动、不稳定等典型特点,因此一直被研究者视为研究控制理论的理想平台,其作为控制实验平台具有简单、便于操作、实验效果直观等诸多优点。
倒立摆具有很多形式,如直线倒立摆、旋转倒立摆、轮式移动倒立摆等等。
其中,旋转倒立摆本体结构仅由旋臂和摆杆组成,具有结构简单、空间布置紧凑的优点,非常适合控制方案的研究,因此得到了研究者们广泛的关注[1-2]。
文献[3]介绍了直线一级倒立摆的建模过程,并基于MATLAB 进行了仿真分析;文献[4]通过建立倒立摆的数学模型,采用MATLAB 研究了倒立摆控制算法及仿真。
在倒立摆建模、仿真和研究中大多数研究者常用理论建模方法,也可以利用SimMechanics 搭建三维可视化模型仿真;文献[5]使用SimMechanics 工具箱建立旋转倒立摆物理模型,通过极点配置、PD 控制和基于线性二次型控制实现了倒立摆的平衡控制;文献[6]通过设计的全状态观反馈控制器来实现单极旋转倒立摆SimMechanics 模型控制,表明了SimMechanics 可用于不稳定的非线性系统;文献[7]通过单级倒立摆SimMechanics 仿真,研究了Bang-Bang 控制和LQR 控制对倒立摆的自起摆和平衡控制;文献[8]基于Sim⁃Mechanics 建立了直线六级倒立摆模型,并基于LRQ 设计状态反馈器进行了仿真控制分析。
本文首先采用Lagrange 方法建立了旋转倒立摆的动力学模型,在获得了旋转倒立摆动力学微分方程后建立了s-func⁃tion 仿真模型;然后,本文采用SimMechanics 建立了旋转的可视化动力学模型。
针对两种动力学模型,采用同一个PID 控制器进行了控制,从控制结果可以看出两种模型的响应曲线完全一致,这两种模型相互印证了各自的正确性。
1旋转倒立摆系统的动力学建模旋转倒立摆是由旋臂和摆杆构成的系统,如图1所示,旋臂绕固定中心旋转(角度记为θ)带动摆杆运动,摆杆可以绕旋臂自由转动,角度记为α。
单级移动倒立摆建模及控制器设计matlab

单级移动倒立摆建模及控制器设计matlab 单级移动倒立摆是一种常见的控制系统模型,它在机器人控制、自动驾驶等领域有着广泛的应用。
本文将介绍如何使用MATLAB进行单级移动倒立摆的建模和控制器设计。
首先,我们需要了解单级移动倒立摆的基本原理。
单级移动倒立摆由一个垂直的杆和一个可以在水平方向上移动的小车组成。
小车上有一个可以旋转的杆,杆的一端连接着小车,另一端有一个质量块。
通过控制小车的位置和杆的角度,我们可以实现倒立摆的平衡。
接下来,我们开始建立单级移动倒立摆的数学模型。
首先,我们需要定义系统的状态变量。
在这个模型中,我们可以选择小车的位置x、小车的速度v、杆的角度θ和杆的角速度ω作为状态变量。
然后,我们可以根据物理原理建立系统的动力学方程。
根据牛顿第二定律和角动量守恒定律,我们可以得到如下的动力学方程:m*x'' = F - m*g*sin(θ) - m*l*θ'^2*cos(θ)m*l^2*θ'' = -m*g*l*sin(θ) + m*l*x''*cos(θ) - b*θ'其中,m是小车和质量块的总质量,l是杆的长度,F是施加在小车上的外力,g是重力加速度,b是杆的阻尼系数。
接下来,我们可以使用MATLAB进行模型的建立和仿真。
首先,我们需要定义系统的参数和初始条件。
然后,我们可以使用ode45函数来求解系统的动力学方程。
ode45函数是MATLAB中用于求解常微分方程的函数,它可以根据给定的初始条件和参数,计算出系统在一段时间内的状态变化。
在求解动力学方程之后,我们可以得到系统的状态变量随时间的变化。
通过绘制状态变量随时间的曲线,我们可以观察到系统的动态行为。
例如,我们可以绘制小车位置随时间的变化曲线,以及杆角度随时间的变化曲线。
最后,我们需要设计一个控制器来实现单级移动倒立摆的平衡。
常见的控制器设计方法包括PID控制器和模糊控制器。
三级倒立摆建模与控制器设计仿真

>> figure(2);plot(T,Y(:,2));
>> xlabel('Time/sec');ylabel('01/rad');title('下摆角度变化曲线');grid;
>> figure(3);plot(T,Y(:,3));
MATLAB中,用函数eig(A)来计算系统矩阵的特征值,经过计算,式⑵式所示的线性定常系统的特征值为:
r1 =[013.27158.39193.1656-18.2950-2.9940-8.5547-13.7810]
因此,该系统为不稳定系统,需加外部控制器形如式(2)所示的线性定常系统能控的充分必要条件是:
PA+ P-PB +Q=0⑷
可以得到状态反馈阵
此时各摆角的动态和稳态指标较为理想。初始条件为 。
仿真结果
程序:
>>A=[0,0,0,0,1,0,0,0;0,0,0,0,0,1,0,0;0,0,0,0,0,0,1,0;0,0,0,0,0,0,0,1;0,-3.6551,0.12698,0.44281,-16.809,0.016897,-0.0056447,-0.0032595;0,45.74,-80.216,-8.3647,57.098,-0.56272,0.32956,-0.072179;0,-49.782,169.9,-4.781,-62.143,0.98145,-0.65964,0.32957;0,-5.159,-114.49,72.269,6.4401,-0.53453,0.51673,-0.76437;];
基于倒立摆顺摆控制的建模与仿真研究

基于倒立摆顺摆控制的建模与仿真研究基于倒立摆顺摆控制的建模与仿真研究倒立摆是一种经典的非线性控制系统,其稳定性分析和控制方法一直是控制理论研究的热点。
本文将介绍基于倒立摆顺摆控制的建模与仿真研究。
一、倒立摆系统建模倒立摆系统由一个质量为m、长度为l的杆和一个质量为M的小车组成,杆与小车通过一根无摩擦的轴连接。
小车可以在水平方向上移动,杆可以在竖直方向上旋转。
系统的状态变量为小车的位置x、小车的速度v、杆的角度θ和杆的角速度ω。
根据牛顿第二定律和杆的运动方程,可以得到系统的动力学方程:m x'' = F - m g sinθ - m l θ'^2M x'' = F + m l θ'' cosθ - m l θ'^2 sinθl θ'' + g sinθ = x'' cosθ其中,F为小车受到的外力,g为重力加速度。
二、顺摆控制顺摆控制是一种基于状态反馈的控制方法,其目的是使倒立摆系统保持在竖直方向上。
顺摆控制器的设计需要满足系统的稳定性和性能要求。
首先,需要将系统的动力学方程转化为状态空间形式:x' = Ax + Buy = Cx其中,x为状态向量,u为控制输入,y为输出向量,A、B和C为系统的矩阵。
然后,可以设计状态反馈控制器:u = -Kx其中,K为状态反馈矩阵。
最后,可以通过极点配置法或线性二次调节法来确定状态反馈矩阵K,以满足系统的稳定性和性能要求。
三、仿真研究为了验证顺摆控制器的有效性,可以进行仿真研究。
使用MATLAB/Simulink软件,可以建立倒立摆系统的仿真模型,并进行控制器的设计和仿真。
首先,需要建立倒立摆系统的仿真模型。
可以使用Simulink中的Simscape Multibody工具箱,将倒立摆系统建模为一个多体动力学系统。
然后,可以添加控制器模块,设计顺摆控制器,并将其与倒立摆系统相连。
一级直线倒立摆的控制策略与仿真分析

一级直线倒立摆的控制策略与仿真分析一、引言倒立摆系统是研究控制理论的一种典型的实验装置,具有成本低廉,结构简单,参数和结构易于调整的优点。
然而倒立摆系统具有高阶次、不稳定、多变量、非线性和强耦合特性,是一个绝对不稳定系统。
倒立摆实物仿真实验是控制领域中用来检验某种控制理论或方法的典型方案,它对一类不稳定系统的控制以及对深入理解反馈控制理论具有重要意义。
倒立摆系统在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重要的现实意义,相关的科研成果已经应用到航天科技和机器人学等诸多领域。
二、一级直线倒立摆模型的建立图1 一级直线倒立摆物理模型图2 小车和摆杆的受力分析图2.1 传递函数模型图1、2是系统中小车和摆杆的受力分析图。
设小车质量为M,摆杆质量为m,小车摩擦系数为b,摆杆转动轴心到杆质心的长度为l,摆杆的转动惯量为I,根据牛顿第二定律,可以得到系统的两个运动方程:F ml ml x b x m M =-+++∙∙∙∙∙∙θθθθsin cos )(2(1)θθθcos sin )(2∙∙∙∙-=++x m l m gl m l I (2)设φπθ+=, 假设φ与1(单位是弧度)相比很小,即c <<1,则可以进行近似处理:1cos -=θ,φθ-=sin ,0)(2=dtd θ。
用u 来代表被控对象的输入力F ,线性化后两个运动方程如下:2()()I ml mgl ml x M m x b x ml uϕϕϕ∙∙∙∙∙∙∙∙∙+-=++-= (3)假设初始条件为0,对式(3)进行拉普拉斯变换得到:22222()()()()()()()()()I ml s s mgl s mlX s s M m X s s bX s s ml s s U s +Φ-Φ=++-Φ=(4)由于输出为角度φ,求解方程组的第一个方程,可以得到:mgl s ml I mls s X s -+=Φ222)()()((5)令∙∙=x v ,则有:mgls ml I mls V s -+=Φ22)()()((6) 把上式代入方程组的第二个方程,得到:)()()(])([)(])()[(222222s U s s ml s s sg ml ml I b s s s g ml ml I m M =Φ-Φ+++Φ-++(7)整理后得到传递函数:232()()()()mlss qb I ml M m mgl bmgl U s s s s q q qΦ=+++--(8) 其中])())([(22ml ml I m M q -++=。
倒立摆的s函数建模及仿真

倒立摆的s函数建模及仿真倒立摆是一类普遍存在于现实生活中的控制工程问题,也是机器人控制领域中的典型问题。
为了探究倒立摆的控制方法,需要进行建模和仿真研究。
本文将介绍如何对倒立摆进行s函数建模,并进行仿真研究。
一、倒立摆的建模1. 系统假设倒立摆系统假设为:(1)摆杆质量可以忽略,只考虑质点的重量;(2)摆杆的摩擦系数可以忽略;(3)摆杆的惯性可以忽略。
2. 系统模型假设摆杆长度为L,质点质量为m,摆杆与竖直方向成θ角度,摩擦系数为f,则可得到如下系统模型:mx”=mgLsinθ-fx’+uθ’=x其中,x表示质点距离垂直方向的距离,u是外部输入信号,可用来控制系统。
3. s函数模型根据系统模型,可以进行s函数建模。
将其转化为状态空间的形式,得到如下s函数模型:function [sys,x0,str,ts] = pendulum(t,x,u,flag)switch flag% Initializationcase 0sys = [0 0 1 2 0 1];x0 = [0; 0];str = [];ts = [];% Derivativescase 1sys = [x(2); (u(1)*cos(x(1))-9.8*sin(x(1)))/0.5];% Outputscase 3sys = [x(1)];% Unhandled flagscase {2, 4, 9}sys = [];otherwiseerror(['Unhandled flag = ',num2str(flag)]);end二、倒立摆的仿真倒立摆的仿真可以使用Matlab软件进行实现。
下面介绍具体的仿真过程:1. 创建仿真模型打开Matlab软件,选择“Simulink”工具栏,创建一个新的模型文件。
2. 添加控制器在模型中添加一个控制器,用于产生外部输入信号u。
具体可选择Proportional Integral Derivative(PI D)控制器或者其他控制器。
倒立摆系统建模及MATLAB仿真

倒立摆系统的建模及MATLAB仿真通过建立倒立摆系统的数学模型,应用状态反馈控制配置系统极点设计倒立摆系统的控制器,实现其状态反馈,从而使倒立摆系统稳定工作。
之后通过MA TLAB 软件中Simulink工具对倒立摆的运动进行计算机仿真,仿真结果表明,所设计方法可使系统稳定工作并具有良好的动静态性能。
倒立摆系统是1个经典的快速、多变量、非线性、绝对不稳定系统,是用来检验某种控制理论或方法的典型方案。
倒立摆控制理论产生的方法和技术在半导体及精密仪器加工、机器人技术、导弹拦截控制系统和航空器对接控制技术等方面具有广阔的开发利用前景。
因此研究倒立摆系统具有重要的实践意义,一直受到国内外学者的广泛关注。
本文就一级倒立摆系统进行分析和研究,建立倒立摆系统的数学模型,采用状态反馈极点配置的方法设计控制器,并应用MA TLAB 软件进行仿真。
1 一级倒立摆系统的建模1. 1 系统的物理模型如图1 所示,在惯性参考系下,设小车的质量为M ,摆杆的质量为m ,摆杆长度为l ,在某一瞬间时刻摆角(即摆杆与竖直线的夹角)为θ,作用在小车上的水平控制力为f 。
这样,整个倒立摆系统就受到重力,水平控制力和摩擦力的3 外力的共同作用。
图1 一级倒立摆物理模型1. 2 系统的数学模型在系统数学模型中,本文首先假设:(1) 摆杆为刚体。
(2)忽略摆杆与支点之间的摩擦。
(3)忽略小车与导轨之间的摩擦。
然后根据牛顿第二运动定律,求得系统的运动方程为:方程(1) , (2) 是非线性方程,由于控制的目的是保持倒立摆直立,在施加合适的外力条件下,假定θ很小,接近于零是合理的。
则sinθ≈θ,co sθ≈1 。
在以上假设条件下,对方程线性化处理后,得倒立摆系统的数学模型:1. 3 系统的状态方程以摆角θ,角速度θ',小车的位移x ,速度x'为状态变量,输出为y 。
即令:则一级倒立摆系统的状态方程为:2 控制器设计及MATLAB 仿真2. 1 极点配置状态反馈的基本原理图2 状态反馈闭环控制系统极点配置的方法就是通过一个适当的状态反馈增益矩阵的状态反馈方法,将闭环系统的极点配置到任意期望的位置。
直线一级倒立摆系统的建模及仿真

计算机控制技术课程设计实验:直线一级倒立摆系统的建模及仿真一、已知条件:图1倒立摆简化模型摆杆角度为输出,小车的位移为输入。
导轨中点为坐标轴的中心即零点,右向为坐标值增加的方向,杆偏移其瞬时平衡位置右侧的角度为正值。
二、任务要求:总体任务通过调节PID参数,设计PID控制器实现摆杆在受到干扰的情况下,依然能恢复平衡。
具体包括以下几部分:1. 理论推导包括倒立摆系统的动力学模型,传递函数,离散传递函数,状态空间或差分方程,稳定性分析,PID控制器设计2. 程序实现实现内容:倒立摆系统模型,控制器以及仿真结果的显示。
开发语言和工具:Matlab m 文件或C/C++ (工具:VC++或其它)3. PID控制参数设定及仿真结果。
分别列出不同杆长的仿真结果(例如:L=0.25 和L=0.5)。
4. 将理论推导、程序实现、仿真结果写成实验报告。
具体求解过程如下:一,倒立摆系统动力学模型的建立图1 摆杆的受力分析图以摆杆为研究对象,对其进行受力分析,如图1所示。
根据质点系的达朗贝尔原理得IC I 0F CP mg CP M →→⨯+⨯-= (1)式中,IC F 为杆的惯性力,表达式为()IC C P CP CP IP ICP ICP t n t nF ma m a a a F F F ==++=++,m 为杆的质量,g 为重力加速度,I M 为杆的惯性力偶。
惯性力及惯性力偶的大小分别为2222IP P ICP I c 2221,,3t d x d d F ma m F m m M J mL dt dt dt θθαα======(2)式中,α为杆的角加速度,P a 为小车的加速度,2L 为杆的长度,θ为杆偏离中心位置的角度,x 偏离轨道中心的位移。
对(2)式代入(1)式,并整理可得22224sin cos 3d d x L g dt dt θθθ-=-(3) 当摆动较小时,可以进行近似处理sin ,cos 1θθθ≈≈。
一阶倒立摆系统建模与仿真研究

一阶倒立摆系统建模与仿真研究一阶倒立摆系统是一种典型的非线性控制系统,具有多种状态和复杂的运动特性。
在实际生活中,倒立摆被广泛应用于许多领域,如机器人平衡控制、航空航天、制造业等。
因此,对一阶倒立摆系统进行建模与仿真研究具有重要的理论价值和实际意义。
ml''(t) + b*l'(t) + k*l(t) = F(t)其中,m为质量,b为阻尼系数,k为弹簧常数,l(t)为摆杆的位移,l'(t)为摆杆的加速度,l''(t)为摆杆的角加速度,F(t)为外界作用力。
在仿真过程中,需要设定摆杆的初始位置和速度。
一般而言,初始位置设为0,初始速度设为0。
边界条件则根据具体实验需求进行设定,如限制摆杆的最大位移、最大速度等。
利用MATLAB/Simulink等仿真软件进行建模和实验,可以方便地通过改变输入信号的参数(如力F)或系统参数(如质量m、阻尼系数b、弹簧常数k)来探究一阶倒立摆系统的性能和反应。
通过仿真实验,我们可以观察到一阶倒立摆系统在受到不同输入信号的作用下,会呈现出不同的运动规律。
在适当的输入信号作用下,摆杆能够达到稳定状态;而在某些特定的输入信号作用下,摆杆可能会出现共振现象。
在仿真过程中,我们可以发现一阶倒立摆系统具有一定的鲁棒性。
在一定范围内,即使输入信号发生变化或系统参数产生偏差,摆杆也能够保持稳定状态。
然而,当输入信号或系统参数超过一定范围时,摆杆可能会出现共振现象,导致系统失稳。
因此,在实际应用中,需要对输入信号和系统参数进行合理控制,以保证系统的稳定性。
为了避免共振现象的发生,可以通过优化系统参数或采用其他控制策略来实现。
例如,适当增加阻尼系数b能够减小系统的振荡幅度,有利于系统尽快达到稳定状态。
可以采用反馈控制策略,根据摆杆的实时运动状态调整输入信号,以抑制系统的共振响应。
本文对一阶倒立摆系统进行了建模与仿真研究,通过观察不同参数设置下的系统性能和反应,对其运动规律、鲁棒性及稳定性进行了分析。
倒立摆控制系统的Simulink仿真

倒立摆控制系统的Simulink 仿真本文针对一个倒立摆系统进行了系统的建模、求解、控制系统的设计,并且使用Simulink 对控制算法进行了仿真。
一、模型的描述倒立摆系统如图(1),设有一个倒立摆装在只能沿x 轴方向移动的小车上,图中1m 为小车的质量,2m 为摆球的质量,g 为重力加速度,l 为摆长,J 为摆的转动惯量。
当小车受到外力()f t 的作用时,小车产生位移()x t ,且摆产生角位移()t θ。
二、模型的建立下面针对该倒立摆系统进行建模求解。
当小车1m 在外力作用下产生位移()x t 时,摆球受力情况如图(2)所示。
图中2m g 为摆球2m 所受重力,222()d x t m dt 为x 方向的惯性力,2sin ()m g t θ为垂直于摆杆方向的重力分量。
在x 方向上,小车的惯性力矩为212()d x t m dt ,摆球产生的位移量为()sin ()x t l t θ+;在垂直于摆杆的方向上,摆球的转动惯性力为22()d t J dt θ;222()d x t m dt的分力为222()cos ()d x t m t dt θ。
图(1)装有倒立摆的小车 图(2)倒立摆受力图根据牛顿运动定律,按照力的平衡原理,可以分别列出该系统在x 方向上和垂直于摆杆方向上的的运动方程222122222()()[sin ()]()d x t d x t d l t m m m f t dt dt dt θ++=(1) 222222()()cos ()sin ()d t d x t J m l t m lg t dt dtθθθ+= (2) 三、模型的求解3.1微分方程组的求解联立式(1)、(2),经过方程组的恒等变形得2222222122222()()2[()cos ()]sin 2()2sin ()()2()d x t d t m m J m l t m l g t Jm l t dt dtJf t θθθθ+-=-++ (3) 2222222212221222()()[cos ()()]sin ()cos ()()()sin ()()d t d t m l t m m J m l t t dt dtm m m lg t m lf t θθθθθθ-+=-++ (4) 由式(3)、(4)令''121343()(),(),()(),()()x t t x x t x t x t x t x t θ====,可建立如下的微分方程组进行求解'12'2222221222222122'34'222422222122()()1()()(sin ()cos ()()()sin ()cos ()()())()()1()()(sin 2()2sin ()()2())2[()cos ()]x t x t d t x t x m l t t m m m lg t m l t m m J dt m lf t x t x t d t x t m l g t Jm l t Jf t m m J m l t dt θθθθθθθθθ⎧=⎪⎪=-+⎪-+⎪+⎨==-+++-⎪⎪⎪⎪⎩3.2控制系统的分析与设计在该模型中,对该倒立摆系统实施角度环、速度换的控制,并假设小车在运行过程中受到空气阻力,阻力大小与小车的速度成正比。
倒立摆平衡控制与仿真

0.5*(10*.NEW01.NormIPAng+2*.NEW01.IPVel+0.4*.NEW01.NormMotorAng+0.5*.NEW01.MotorVel )
六. 仿真及仿真结果
设置仿真时间为 5s,仿真步数为 1000 步,开始仿真。当仿真进行到 2.5s 时倒立摆达到平 衡,随后一直保持平衡状态。
进入结果后处理模块,绘制的 NormMotorAng,MotorVel,NormIPAng 和 IPVel 曲线,另外 再新建一个测量函数用于测量 Motordrive 的驱动力矩,得到的曲线和摆锤和摆杆的质心运动轨 迹如图 5 所示。
首先采用固定约束将基座固定在 ground 上,再添加两个旋转副分别位于基座和连杆、连 个和摆杆之间。旋转副分别命名为 REVO01 和 REVO02。
在连杆上添加驱动力矩“Motordrive”,注意设置力矩的方向与重力加速度的方向一致,设 置好的力矩标识如图 2。
Gravity
图 2 模型旋转约束和力矩
If(.NEW01.NormIPAng-0.34907:if(-0.34907-.NEW01.NormIPAng:.NEW01.LinControl,.NEW01.NonLinC ontrol,.NEW01.NonLinControl),.NEW01.NonLinControl,.NEW01.NonLinControl)
单级倒立摆的 ADAMS 仿真
一. 三维建模与导入
直接在 Adams 中建立单级倒立摆模型过程比较复杂,简单起见,单级倒立摆的三维 CAD 模型在 Pro-E 中创建,然后将模型保存成 Parasolid 格式(后缀“. x_t”)文件,最后导入 Adams 中。导入模型名称为 NEW01(或者其他名称亦可)。倒立摆模型和大致尺寸见图 1,有四个部 分组成:基座,连杆,摆杆和摆锤。其中摆杆和摆锤为一个零件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s zc s 7.0 , s z p s 26.1
( s 7.0) 1 ( s 26.1) (0.3333s 2 9.8)
Root Locus
Step Response
60 40
1.5
1
Imaginary Axis
20 0 -20 -40
Amplitude
0.5
0
系统传递函数为:
( s)
1 a( s ) g 4 Ls 2 3 x( s ) 1 a( s) s 2
设
x1 d x dt 2 X x3 x x x4 dx Y 1 x3 x dt ,
1 0
x1 0 x 0 0 0.2671 2 2.6708 F 0 0 1 x3 0 0 0 0.089 x4 0.8903 0
x1 1 0 0 0 x2 Y 0 0 1 0 x3 x4
1.2 控制系统模型 1.2.1 状态空间模型
d dx 以θ , dt ,x, dt 为系统状态变量,F 为系统输入,θ ,x 为输出:
即
x 1 d x dt 2 X x3 x x x4 dx Y 1 x3 x dt ,
8
Step Response 1.4 1.2 1
Amplitude
0.8 0.6 0.4 0.2 0
0
0.1
0.2
0.3
Fy L sin Fx L cos
,由牛顿第二定律有:
Fy L sin Fx L cos
mL2 d 2 3 dt 2
(4)
由(2) (3)可解得 Fx 和 Fy,代入(1) (4)可得
d 2x d2 L sin dx F ( m M ) m 2 2 dt dt dt 2 2 2 2 ( g d L cos ) sin ( d x L d ) cos L d 3 dt 2 dt 2 dt 2 dt 2
则系统状态空间模型为:
0 3g dX 4L dt 0 0 1 0 0 0 3 0 0 0 X 4L a 0 0 0 1 0 0 0 1
x1 1 0 0 0 x2 Y 0 0 1 0 x3 x4
s 0.3744s 0.0333s 2 11.809s 0.98
3
X ( s) 0.3333s 2 9.8 F ( s) 0.3744s 4 0.0333s 3 11.809s 2 0.98s
1.2.3 另一种不同的模型 若系统输入不是力,而是加速度,则系统满足一下线性化后的方程:
其中:
x1 d x dt 2 X x3 x x x4 dx Y 1 x3 x dt ,
传递函数:
( s)
F ( s)
F Fx
dx d 2x M 2 dt dt
(1)
对细杆重心,在水平方向上,由牛顿第二定律有:
d2 Fx m 2 x L sin dt
对细杆重心,在竖直方向上,由牛顿第二定律有:
(2)
1
Fy mg m
d2 L cos dt 2
3
(3) ,细杆所受力矩为
2 长 度 为 2L 的 细 杆 , 围 绕 重 心 旋 转 , 转 动 惯 量 为 mL
秩为 4,系统能控。
Ⅲ 经பைடு நூலகம்控制方法
3.1 根轨迹校正 由系统性能要求: 调节时间: ts 0.5s (2%) 最大超调量: % 10% 所以 % e
1 2
10% 得 0.6 ,而 ts
4
n
0.5s 得 n 13.53 ,
则 s1,2 8.1197 j10.8262 ,校正装置提供相角为 c 180(2k 1) G(s1 ) 65.36 利用 Matlab 编程,由最佳确定法,超前校正控制器为 Gc ( s) 所以校正后系统的开环传递函数为 G2 ( s) 124.92
由此知系统传递函数为:
( s)
F ( s)
(
s m 4 4 M ) Ls 3 Ls 2 (m M ) gs g 3 3 3
X ( s) F ( s)
g (
4 2 Ls 3
m 4 4 M ) Ls 4 Ls 3 (m M ) gs 2 gs 3 3 3
4
d 2x dt 2 a d2 F m ( x L ) x dt 2 Fy mg mL2 d 2 F L F L y x 3 dt 2
消去 Fx,Fy 得:
d 2x a dt 2 2 g a 4 L d 3 dt 2
3
实验系统的模型参数如下: 小车质量 M=1.096kg 摆杆质量 m=0.109kg 小车摩擦系数 =0.1N/m/s 摆杆转动轴心到杆质心的长度 L=0.25m
I 摆杆惯量 0.0034 kg*m*m
把上述参数代入,可得系统实际模型: 状态空间模型:
dx1 dt 0 dx2 dX dt 31.5397 dt dx3 0 dt 0.7132 dx 4 dt
倒立摆的建模与控制仿真
武汉大学自动化系 09 级 区金鹏
摘要 本文建立和分析一级倒立摆的数学模型,通过根轨迹校正,PID 控制,极点配置等 不同方法对系统进行控制仿真,得到不同控制器的理论性能。 关键词:一级倒立摆 建模 控制仿真
Ⅰ 数学模型
1.1 物理受力分析 质量为 m,长度为 2L 的细杆,与质量为 M 的小车通过铰链相连,通过施加在小车上 的力 F(设电机为力矩电机)能够使细杆处于θ =0 的稳定倒立状态。在忽略其他零件质 量和各种摩擦和阻尼的条件下。
0
0.5
0
-0.5
-1.5 -6
10
10 Frequency (rad/sec)
1
10
2
由于系统的阶跃响应发散和根轨迹中存在大于零的极点, 可以看出系统不能靠自身 稳定,需要校正。 2.3 系统能控性
7
系统的能控性矩阵为
0 88.2 0 3 3 0 88.2 0 n 1 Qc [ B AB A B] 0 1 0 0 0 0 1 0
x1 1 0 0 0 x2 Y 0 0 1 0 x3 x4
Ⅱ 系统初步分析
2.1 系统阶跃响应 系统开环传递函数为:
G(s)
( s)
a( s)
1 0.3333s 2 9.8
系统框图为:
阶跃响应为:
6
0 -2
x 10
26
2
dx1 dt dx 2 dt dx3 dt dx 4 dt
x2 (m M ) g 1 x1 x4 F m 4 m 4 m 4 ( M )L ( M )L ( M )L 3 3 3 3 3 3
x4 3 mg 1 4 x1 x4 F m m m M M M 4 4 4
0
1
2
3
4
5
-60 -30
-20
-10 Real Axis
0
10
Time (sec)
图 2 校正后系统的阶跃响应与根轨迹 由阶跃相应可以看到, 校正后稳态误差还是比较大, 考虑加入滞后校正, 利用 Matlab ( s 12.5) ( s 11.7) 1 自动校正功能得到 G3 ( s) 128691.3 , 能够满足系 ( s 2241.0) ( s 1.5) (0.3333s 2 9.8) 统的性能要求。
0
x1 1 0 0 0 x 2 Y 0 0 1 0 x 3 x4
1.2.2 传递函数模型 传递函数:
d 2x d 2 dx F ( m M ) mL u 2 2 dt dt dt 2 2 g d x 4 L d 3 dt 2 dt 2
带入实际参数的系统模型为: 传递函数:
5
( s)
a( s)
1 9.8 0.3333s 2
x( s ) 1 a( s) s 2
状态空间模型:
0 dX 29.4 dt 0 0
1 0 0 0 3 0 0 0 X a 0 0 0 1 0 0 0 1
Y X 图 1 倒立摆受力分析 设θ 正方向为顺时针方向,向右为 x 正方向,向上为 y 正方向,当细杆顺时针偏转 θ 时,给小车施加一个向右的力 F,铰链对杆有平行于杆的支持力,该支持力可分解为 水平方向的 Fx 与竖直方向的 Fy。 现将小车的运动与细杆的运动隔离, 并且将细杆的运动分解为水平运动和围绕重心 的转动。 对小车,支持力的 Fx 分量的反作用力方向与 F 相反,根据牛顿第二定律有:
由此可得系统状态空间模型为:
dx1 0 ( m M )g dt dx m 4 2 ( 3 3 M )L dX dt 0 dt dx 3 3 mg dt 4 dx m M 4 4 dt 1 0 0 1 0 0 m 4 x1 m 4 ( M )L ( M )L 3 3 x2 3 3 0 0 1 F x 0 3 x4 1 0 0 m m M M 4 4
