广东省历年中考数学压轴题
广东2020中考数学压轴题训练1(含答案)

广东2020中考数学压轴题训练1(含答案)1. 如图,AB 是半径O 的直径,AB=2.射线AM 、BN 为半圆O 的切线.在AM 上取一点D ,连接BD 交半圆于点C ,连接AC .过O 点作BC 的垂线OE ,垂足为点E ,与BN 相交于点F .过D 点作半圆O 的切线DP ,切点为P ,与BN 相交于点Q . (1)求证:△ABC ∽△OFB ;(2)当△ABD 与△BFO 的面枳相等时,求BQ 的长; (3)求证:当D 在AM 上移动时(A 点除外),点Q 始终是线段BF 的中点2.如图①,在平面直角坐标系中,等腰直角△AOB 的斜边OB 在x 轴上,顶点A 的坐标为(3,3),AD 为斜边上的高.抛物线y =ax 2+2x 与直线y = 12x 交于点O 、C ,点C 的横坐标为6.点P 在x 轴的正半轴上,过点P 作PE ∥y 轴,交射线OA 于点E .设点P 的横坐标为m ,以A 、B 、D 、E 为顶点的四边形的面积为S . (1)求OA 所在直线的解析式.(2)当m ≠3时,求S 与m 的函数关系式.(3)如图②,设直线PE 交射线OC 于点R ,交抛物线于点Q .以RQ 为一边,在RQ 的右侧作矩形RQMN ,其中RN = 32.直接写出矩形RQMN 与△AOB 重叠部分为轴对称图形时m 的取值范围.答案:1.(1) 设直线OA 的解析式为y=kx ,则有:3k=3,k=1; ∴直线OA 的解析式为y=x ; (2)当x=6时,y=12x=3, ∴C (6,3);将C (6,3)代入抛物线的解析式中, 得:36a+12=3,a=-14; 即a 的值为--14;根据题意,D (3,0),B (6,0).∵点P 的横坐标为m ,PE ∥y 轴交OA 于点E , ∴E (m ,m ). 当0<m<3时,如图1, S=S △OAB -S △OED =12×6×3- 12×m ×3=9- 32m当m>3时,如图2, S=S △OBE -S △ODA=12×6×m- 12×3×3=3m- 92如图3、RQ=RN 时,m- 12m=32m=3如图4、AD 所在的直线为矩形RQMN 的对称轴时,3-m=32×12m=94如图5、RQ 与AD 重合时,重叠部分为等腰直角三角形,m=3; 如图6、当点R 落在AB 上时,m=4,所以3≤m<4.。
广东省中考冲刺二次函数压轴题及答案

1、如图,在平面直角坐标系中,抛物线y =-32x 2+b x +c 经过A (0,-4)、B (x 1,0)、 C (x 2,0)三点,且x 2-x 1=5. (1)求b 、c 的值;(4分)(2)在抛物线上求一点D ,使得四边形BDCE 是以BC 为对 角线的菱形;(3分)(3)在抛物线上是否存在一点P ,使得四边形BPOH 是以OB 为对角线的菱形?若存在,求出点P 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分) 解: (08广东茂名25题解析)解:(1)解法一:∵抛物线y =-32x 2+b x +c 经过点A (0,-4),∴c =-4 ……1分又由题意可知,x 1、x 2是方程-32x 2+b x +c =0的两个根, ∴x 1+x 2=23b , x 1x 2=-23c =6 2分由已知得(x 2-x 1)2=25又(x 2-x 1)2=(x 2+x 1)2-4x 1x 2=49b 2-24 ∴ 49b 2-24=25 解得b =±3143分当b =314时,抛物线与x 轴的交点在x 轴的正半轴上,不合题意,舍去.∴b =-314.4分解法二:∵x 1、x 2是方程-32x 2+b x +c=0的两个根,即方程2x 2-3bx +12=0的两个根.(第25题图)x∴x =4969b 32-±b ,2分∴x 2-x 1=2969b 2-=5,解得 b =±3143分(以下与解法一相同.)(2)∵四边形BDCE 是以BC 为对角线的菱形,根据菱形的性质,点D 必在抛物线的对称轴上, 5分又∵y =-32x 2-314x -4=-32(x +27)2+6256分 ∴抛物线的顶点(-27,625)即为所求的点D . 7分(3)∵四边形BPOH 是以OB 为对角线的菱形,点B 的坐标为(-6,0), 根据菱形的性质,点P 必是直线x =-3与抛物线y =-32x 2-314x -4的交点, 8分∴当x =-3时,y =-32×(-3)2-314×(-3)-4=4,∴在抛物线上存在一点P (-3,4),使得四边形BPOH 为菱形. 9分四边形BPOH 不能成为正方形,因为如果四边形BPOH 为正方形,点P 的坐标只能是(-3,3),但这一点不在抛物线上. 10分2.如图,已知二次函数y =-x2+bx +c 的图象经过A(-2,-1),B(0,7)两点.(1)求该抛物线的解析式及对称轴;(2)当x 为何值时,y >0?(3)在x 轴上方作平行于x 轴的直线l ,与抛物线交于C 、D 两点(点C 在对称轴的左侧),过点C 、D 作x 轴的垂线,垂足分别为F 、E.当矩形CDEF 为正方形时,求C 点的坐标. 22.解:(1)把A(-2,-1),B(0,7)两点的坐标代入 y =-x2+bx +c ,得⎩⎪⎨⎪⎧-4-2b +c =-1c =7,解得⎩⎪⎨⎪⎧b =2c =7.所以,该抛物线的解析式为y =-x2+2x +7,又因为y =-x2+2x +7=-(x -1)2+8,所以对称轴为直线x =1. (2)当函数值y =0时,-x2+2x +7=0的解为x =1±2 2,结合图象,容易知道1-2 2<x<1+2 2时,y>0.(3)当矩形CDEF 为正方形时,设C 点的坐标为(m ,n),则n =-m2+2m +7,即CF =-m2+2m +7.因为C 、D 两点的纵坐标相等,所以C 、D 两点关于对称轴x =1对称,设点D 的横坐标为p ,则1-m =p -1,所以p =2-m ,所以CD =(2-m)-m =2-2m.因为CD =CF ,所以2-2m =-m2+2m +7,整理,得m2-4m -5=0,解得m =-1或5.因为点C 在对称轴的左侧,所以m 只能取-1.当m =-1时,n =-m2+2m +7=-(-1)2+2×(-1)+7=4.于是,点C 的坐标为(-1,4).3如图11,已知抛物线243y x x =-+与x 轴交于两点A 、B ,其顶点为C . (1)对于任意实数m ,点M (m ,-2)是否在该抛物线上?请说明理由;(2)求证:△ABC 是等腰直角三角形;(3)已知点D 在x 轴上,那么在抛物线上是否存在点P ,使得以B 、C 、D 、P 为顶点的四边形是平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.图11 22.解:(1)假如点M (m ,-2)在该抛物线上,则-2=m2-4m+3, m2-4m+5=0,由于△=(-4)2-4×1×5=-4<0,此方程无实数解, 所以点M (m ,-2)不会在该抛物线上;(2)当y=0时,x2-4x+3=0,x1=1,x2=3,由于点A 在点B 左侧,∴A(1,0),B(3,0) y= x2-4x+3=(x-2)2-1, ∴顶点C 的坐标是(2,-1), 由勾股定理得,AC=2,BC=2,AB=2,∵AC2+BC2=AB2, ∴△ABC 是等腰直角三角形; (3)存在这样的点P.根据对角线互相平分的四边形是平行四边形,因此连接点P 与点C 的线段应被x 轴平分, ∴点P 的纵坐标是1,∵点P 在抛物线y= x2-4x+3上,∴当y=1时,即x2-4x+3=1,解得x1=2-2,x2=2+2, ∴点P 的坐标是(2-2,1)或(2+2,1). 4如图,在平面直角坐标系xoy 中,已知抛物线经过点A(0,4),B(1,0),C (5,0),抛物线对称轴l 与x 轴相交于点M .(1)求抛物线的解析式和对称轴; (3分) (2)设点P 为抛物线(5>x )上的一点,若以A 、O 、M 、P 为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P 的坐标; (2分)(3)连接AC .探索:在直线AC 下方的抛物线上是否存在一点N ,使△NAC 的面积最大?若存在,请你求出点N 的坐标;若不存在,请你说明理由. (3分)25、解:(1)根据已知条件可设抛物线的解析式为)5)(1(--=x x a y ,············1分把点A (0,4)代入上式得:54=a ,∴=y 516)3(54452454)5)(1(5422--=+-=--x x x x x ,···········2分∴抛物线的对称轴是:3=x .························3分 (2)由已知,可求得P (6,4). ··················5分第25题图提示:由题意可知以A 、O 、M 、P 为顶点的四边形有两条边AO=4、OM=3,又知点P 的坐标中5>x ,所以,MP>2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt △AOM 中,5342222=+=+=OMOA AM ,因为抛物线对称轴过点M ,所以在抛物线5>x 的图象上有关于点A 的对称点与M 的距离为5,即PM=5,此时点P 横坐标为6,即AP=6;故以A 、O 、M 、P 为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立, 即P (6,4).···································5分⑶法一:在直线AC 的下方的抛物线上存在点N ,使△NAC 面积最大.设N 点的横坐标为t ,此时点N )452454,(2+-t t t ()50<<t ,过点N作NG ∥y 轴交AC 于G ;由点A (0,4)和点C (5,0)可求出直线AC的解析式为:454+-=x y ;把t x =代入得:454+-=t y ,则G )454,(+-t t ,此时:NG=454+-t -(4524542+-t t ),=tt 520542+-. ····················7分 ∴225)25(21025)52054(2121222+--=+-=⨯+-=⋅=∆t t t t t OC NG S ACN∴当25=t 时,△CAN 面积的最大值为225,由25=t ,得:34524542-=+-=t t y ,∴N (25, -3). ········ 8分5.如图9,抛物线y =(x +1)2+k 与x 轴交于A 、B 两点,与y 轴交于点C (0,-3). (1)求抛物线的对称轴及k 的值;(2)抛物线的对称轴上存在一点P ,使得PA +PC 的值最小,求此时点P 的坐标; (3)点M 是抛物线上一动点,且在第三象限.① 当M 点运动到何处时,△AMB 的面积最大?求出△AMB 的最大面积及此时点M 的坐标;② 当M 点运动到何处时,四边形AMCB 的面积最大?求出四边形AMCB 的最大面积及此时点M 的坐标.【答案】(1)抛物线的对称轴为直线x =-1, 把C (0,-3)代入y =(x +1)2+k 得 -3=1+k ∴k =-4(2)连结AC ,交对称轴于点P∵y =(x +1)2-4 令y =0 可得(x +1)2-4=0 ∴x1=1 x2=-3∴A (-3,0) B (1,0)设直线AC 的关系式为:y =m x +b把A (-3,0),C (0,-3)代入y =m x +b 得, -3m +b =0 b =-3 ∴m =-1∴线AC 的关系式为y =-x -3当x =-1时,y =1-3=-2 ∴P (-1,-2)② 当M 点运动到何处时,四边形AMCB 的面积最大?求出四边形AMCB M 的坐标. (3)① 设M 的坐标为(x, (x +1)2-4)∴S △AMB =12×AB ×|ym |=12×4×[4-(x +1)2]=8-2(x +1)2当x =-1时,S 最大,最大值为S =8 M 的坐标为(-1,-4)② 过M 作x 轴的垂线交于点E ,连接OM ,S 四边形AMCB =S △AMO +S △CMO +S △CBO =12×AB ×|ym|+12×CO ×|xm|+12×OC ×BO=6-32 (x +1)2+12×3×(-x)+12×3×1=-32x2-92 x +6=-32(x2+3x -9)=-32(x +32)2-818当x =-32 时,S 最大,最大值为818。
2024广东中考数学压轴题

2024广东中考数学压轴题一、在直角坐标系中,抛物线y = ax2 + bx + c与x轴交于点A(-3,0)和B(1,0),且与y 轴交于点C(0,3)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 抛物线的对称轴是直线x = -1(答案:D)二、已知三角形ABC的三边长为a,b,c,且满足a2 + b2 + c2 = 10a + 6b + 8c - 50。
则下列判断三角形ABC的形状中,正确的是:A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形(答案:D)三、函数y = (x - 1)/(x + 2)中,当x的值增大时,y的值会:A. 一直增大B. 一直减小C. 在某个区间内增大,在另一个区间内减小D. 保持不变(答案:C)四、已知四边形ABCD是平行四边形,且AB = 6,BC = 8,对角线AC与BD相交于点O,则下列关于O点到AB和BC的距离d1和d2的说法正确的是:A. d1 + d2 = 14B. d1 × d2 = 24C. d1/d2 = AB/BCD. d12 + d22 = AB2 + BC2(答案:B)五、圆O的半径为5,点P在圆O外,且OP = 8。
过点P作圆O的两条切线,分别与圆O 相切于点A和B。
则弦AB的长度为:A. 6B. 4√3C. 5√2D. 2√15(答案:A)六、在数轴上,点A表示的数为-2,点B表示的数为3。
若点C表示的数为x,且满足AC + BC = 8,则x的值为:A. -3或4B. -4或3C. -3或-1D. 2或-5(答案:B)七、已知二次函数y = ax2 + bx + c的图像经过点(1,0),(2,0)和(3,4)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 函数的顶点在x轴上(答案:A)八、正方形ABCD的边长为4,点E在边AB上,且AE = 1。
广州中考数学压轴题(学生版)

1.如图,以O 为原点的直角坐标系中,A 点的坐标为(0,1),直线1交x 轴于点B 。
P 为线段上一动点,作直线⊥,交直线1于点C 。
过P 点作直线平行于x 轴,交y 轴于点M ,交直线1于点N 。
(1)当点C 在第一象限时,求证:△≌△;(2)当点C 在第一象限时,设长为m ,四边形的面积为S ,请求出S 与m 间的函数关系式,并写出自变量m 的取值范围;(3)当点P 在线段上移动时,点C 也随之在直线1上移动,△是否可能成为等腰三角形?如果可能,求出所有能使△成为等腰三角形的点P 的坐标;如果不可能,请说明理由。
说明:●考查字母运算能力 ● 分类讨论思想,取值范围内解的有效性 ●2.关于x 的二次函数y =2+(k 2-4)x +22以y 轴为对称轴,且与y 轴的交点在x 轴上方.(1)求此抛物线的解析式(2)设A 是y 轴右侧抛物线上的一个动点,过点A 作垂直x 轴于点B,再过点A 作x 轴的平行线交抛物线于点D ,过D 点作垂直x 轴于点C, 得到矩形.设矩形的周长为C ,点A 的横坐标为x ,试求C 关于x 的函数关系式;(3)当点A 在y 轴右侧的抛物线上运动时,矩形能否成为正方形.若能,请求出此时正方形的周长;若不能,请说明理由.x 第1题图 第2题图说明:●考查字母运算能力●分类讨论思想,取值范围内解的有效性●方法多样化,易错点为用字母表示边长时,注意边长的非负性3.如图所示, 在平面直角坐标系中, 矩形的边长、分别为12、6, 点A、C 分别在y轴的负半轴和x轴的正半轴上, 抛物线2经过点A、B, 且18a + c = 0.(1)求抛物线的解析式.(2)如果点P由点A开始沿边以1的速度向终点B移动, 同时点Q由点B开始沿边以2的速度向终点C移动.①移动开始后第t秒时, 设△的面积为S, 试写出S与t之间的函数关系式, 并写出t的取值范围.②当S取得最大值时, 在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形如第3题图果存在, 求出R点的坐标, 如果不存在, 请说明理由.说明:●图形必须准确,存在性问题如果不会做,可通过画图判断(答存在得分的机会大得多)4.已知二次函数2++c与x轴交于A(-1,0)、B(1,0)两点.(1)求这个二次函数的关系式;(2)若有一半径为r 的⊙P ,且圆心P 在抛物线上运动,当⊙P 与两坐标轴都相切时,求半径r 的值.(3)半径为1的⊙P 在抛物线上,当点P 的纵坐标在什么范围内取值时,⊙P 与y 轴相离、相交?说明:●考查画图能力和字母运算能力 ●分类讨论思想,取值范围内解的有效性 ● 方法多样化,易错点为用字母表示边长时,注意边长的非负性5.如图示已知点M 的坐标为(4,0),以M 为圆心,以2为半径的圆交x 轴于A 、B ,抛物线c bx x y ++=261过A 、B 两点且与y 轴交于点C .(1)求点C 的坐标并画出抛物线的大致图象(2)过C 点作⊙M 的切线,求直线的解析式.说明:●图形必须准确,画切线后巧妙解法是利用两直线平行,K 相等 ●易错点为漏解(过圆外一点作圆的切线有两条) ● 两直线垂直,K 互为负倒数可以使用6.如图,在ABC ∆中,∠A 90=°,10=BC , ABC ∆的面积为25,点D 为AB 边上的任意一点(D 不与A 、B 重合),过点D 作DE ∥BC ,交AC 于点E .设x DE =以DE 为折线将△ADE 翻折,所得的DE A '∆与梯形DBCE 重叠部分的面积记为y.(1).用x 表示∆的面积;第5题图(2).求出0﹤x≤5时y与x的函数关系式;(3).求出5﹤x﹤10时y与x的函数关系式;(4).当x取何值时,y的值最大?最大值是多少?说明:●考查画图能力和字母运算能力●分类讨论思想,取值范围内解的有效性●方法多样化,在设未知数或用字母表示未知量时,要充分发挥“勾股、相似、锐角三角函数”的作用,挖掘题目中的特殊角(特殊比值)来巧妙运算7.在△中,∠A=90°,=4,3,M是上的动点(不与A、B重合),过点M作∥交于点N. 以为直径作⊙O,并在⊙O内作内接矩形,令. 当x为何值时,⊙O与直线相切?8.如图,直线334y x=+和x轴y轴分别交与点B、A,点C是的中点,过点C向左方作射线⊥y轴,点D是线段上一动点,不和B重合,⊥于点P,⊥于点E,连接。
广东省历年中考数学压轴题

广东省历年中考数学压轴题(1) 姓名:1.(2010年)阅读下列材料:)210321(3121⨯⨯-⨯⨯=⨯,)321432(3132⨯⨯-⨯⨯=⨯,)432543(3143⨯⨯-⨯⨯=⨯,由以上三个等式相加,可得2054331433221=⨯⨯=⨯+⨯+⨯.读完以上材料,请你计算下各题:(1)1110433221⨯++⨯+⨯+⨯ (写出过程); (2)=+⨯++⨯+⨯+⨯)1(433221n n ; (3)=⨯⨯++⨯⨯+⨯⨯+⨯⨯987543432321 .2.(2009年9分)小明用下面的方法求出方程032=-x 的解,请你仿照他的方法求出下面两个方程的解,并把你的解答过程填写在下面的表格,3.(2010年9分)某学校组织340名师生进行长途考察活动,带有行礼170件,计划租用甲、乙两种型号的汽车共有10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.⑴请你帮助学校设计所有可行的租车方案;⑵如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省?A 2A A 1 BB 1B 2 B 3 B 4 B 5 B 6 B 7A 3A 4A 5 A 6A 7 O广东省历年中考数学压轴题(2) 姓名:4.(2007年9分)已知等边OAB ∆的边长为a ,以AB 边上的高1OA 为边,按逆时针方向作等边11B OA ∆,11B A 与OB 相交于点2A . (1)求线段2OA 的长;(2)若再以2OA 为边按逆时针方向作等边22B OA ∆,22B A 与1OB 相交于点3A ,按此作法进行下去,得到33B OA ∆,44B OA ∆,…,n n B OA ∆ (如图)。
求66B OA ∆的周长.5.(2005年9分)如图,已知半圆O的直径AB=4,将一个三角板的直角顶点固定在圆心O上,当三角板绕点O转动时,三角板的两条直角边与半圆圆周分别交于C、D两点,连接AD、BC交于点E.(1)求证:ACE∆;∆∽BDE(2)求证:BD=DE恒成立;(3)设x∆的面积y与x的函数关系式,并写出自变量x的取值范BD=,求AEC围.广东省历年中考数学压轴题(3) 姓名:6.(2006年9分)ABCD 中,060=∠DAB ,点E ,F 分别在CD ,AB 的延长线上,且AE=AD ,CF=CB . (1)求证:四边形AFCE 是平行四边形;(2)若去掉巳知条件的“060=∠DAB ”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.7.(2007年9分)如图,正方形ABCD的边长为a3,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与BCF∆在运动过∆相对应的EGH程中始終保持EGH∆,对应边EG=BC,B、E、C、G在一直线上.∆≌BCF(1)若BE=a,求DH的长;(2)当E点在BC边上的什么位置时,DHE∆的面积取得最小值?并求该三角形广东省历年中考数学压轴题(4)姓名:8.(2009年9分)正方形ABCD的边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,(1)证明:Rt△ABM∽Rt△MCN;(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN面积最大,并求出最大面积;(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.9.(2010年)如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA 向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A 时,M、N两点同时停止运动.连结FM、MN、FN,当F、N、M不在同一条直线时,可得FMN∆三边的中点作∆PQW.设动点M、N的速∆,过FMN度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:(1)说明FMN∆∽∆QWP;(2)设0≤x≤4(即M从D到A运动的时间段).试问x为何值时,∆PQW为直角三角形?当x在何范围时,∆PQW不为直角三角形?(3)问当x为何值时,线段MN最短?求此时MN的值.广东省历年中考数学压轴题(5)姓名:10.(2008年9分)(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC,求∠AEB的大小;(2)如图2,OAB∆固定不动,保持OCD∆的形状和大小不变,将OCD∆绕着点O旋转(OAB∆和OCD∆不能重叠),求∠AEB的大小.BAODCE11.(2006年9分)如图所示,在平面直角坐标系中,四边形OABC 是等腰梯形,BC ∥OA ,7=OA ,4=AB ,060=∠COA ,点P 为x 轴上的一个动点,点P 不与点O 、点A 重合。
广州市数学中考压轴题目综合题目-8页文档资料

2019年广州市数学中考压轴题29.已知一次函数y =-x +6和反比例函数xk y =(k ≠0). (1)k 满足什么条件时,这两个函数在同一坐标系xOy 中的图象有两个公共点?(2)设(1)中的两个公共点分别为A 、B ,∠AOB 是锐角还是钝角?八、(本题满分14分)30.(1)已知:如图7,过B 、C 两点的圆与△ABC 的边AB 、AC 分别相交于点D和点E ,且DE =21BC .求证:S △ADE ∶S 四边形DBCE =31.图7(2)在△ABC 的外部取一点P (直线BC 上的点除外),分别连结PB 、PC ,∠BPC 与∠BAC 的大小关系怎样?(不要求证明)31.在车站开始检票时,有a (a >0)名旅客在候车室排队等候检票进站.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.若开放一个检票口,则需30分钟才可将排队等候检票的旅客全部检票完毕;若开放两个检票口,则只需l0分钟便可将排队等候检票的旅客全部检票完毕;如果要在5分钟内将排队等候检票的旅客全部检票完毕,以使后来到站的旅客能随到随检,至少要同时开放几个检票口?29.解:(1)依题意,得⎪⎩⎪⎨⎧≠=+-=②.①,)0(6k x k y x y 由①,②消去y ,得x 2-6x +k =0.③ △=36—4k ,由36—4k >0得k <9.∴当k <9且k ≠0时,方程③有两个不相等的非零的实数解.∴由方程①和②组成的方程组有两个解.故当k <9且k ≠0时,一次函数y =-x +6和反比例函数y =xk (k ≠0)的图象有两个公共点.(2)∵y =-x +6的图象经过第一、二、四象限,∴当0<k <9时,双曲线两分支分别在第一、三象限,由此知这两个函数图象的两个公共点A 、B 在第一象限,此时∠AOB 是锐角.当k <0时,方程③两根异号,双曲线两分支分别在第二、四象限,由此知这两个函数图象的公共点A 、B 分别在第二、四象限。
挑战压轴题解答题(真题汇编压轴特训)-2024年中考数学冲刺 挑战压轴题专题汇编(广州卷)(原卷版)

03挑战压轴题(解答题一)(1)尺规作图:将法);(2)在(1)所作的图中,连接V①求证:ABD②若tan BAC∠2.(2022·广东广州·统考中考真题)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆的AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE,CD = 1.6m,BC =5CD.(1)求BC的长;(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.条件①:CE = 1.0m;条件②:从D处看旗杆顶部A的仰角α为54.46°.注:如果选择条件①和条件②分别作答,按第一个解答计分.参考数据:sin54.46°≈0.81,cos54.46°≈0.58,tan54.46°≈1.40.(1)求A 、B 两点的坐标;(2)设PAO V 的面积为S ,求S 关于x 的函数解析式:并写出x 的取值范围;(3)作PAO V 的外接圆C e ,延长PC 交C e 于点Q ,当POQ △的面积最小时,求C e 的半径.(1)沿AC BC 、剪下ABC V ,则ABC V 是_______三角形(填“锐角______.(2)分别取半圆弧上的点E 、F 和直径AB 上的点G 、H .已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm 的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);2.(2022上·陕西西安·九年级校考期中)如图,在等边ABC V 中,点D 是AB 边上的一个动点(不与点A ,B 重合),以CD 为边作等边EDC △,AC 与DE 交于点F ,连接AE .(1)求证:ADF BCD △∽△;(2)若:5:2AB BD =,且20AB =,求ADF △的面积.3.(2022·安徽合肥·统考一模)如图,在正方形ABCD 中,9AB =,E 为AC 上一点,以AE 为直角边构造等腰直角AEF △(点F 在AB 左侧),分别延长FB ,DE 交于点H ,DH 交线段BC 于点M ,AB 与EF 交于点G ,连结BE .(1)求证:AFB AED≅V V (2)当62AE =时,求sin MBH ∠的值.(3)若BEH △与DEC V 的面积相等,记△(1)当点D 与圆心O 重合时,如图2所示,求DE 的长.(2)当CEF △与ABC V 相似时,求cos BDE ∠的值.6.(2023下·安徽蚌埠·九年级校考开学考试)如图,矩形ABCD 中,8AB =厘米,12BC =厘米,P 、Q 分别是AB 、BC 上运动的两点,若点P 从点A 出发,以1厘米/秒的速度沿AB 方向运动,同时,点Q 从点B 出发以2厘米/秒的速度沿BC 方向运动,设点P ,Q 运动的时间为x 秒.(1)设PBQ V 的面积为y ,求y 与x 之间的函数关系式及自变量x 的取值范围;(2)当x 为何值时,以P ,B ,Q 为顶点的三角形与BDC V 相似?7.(2021下·湖北随州·七年级统考期末)阅读材料:在平面直角坐标系中,二元一次方程0x y -=的一个解11x y =⎧⎨=⎩可以用一个点(1,1)表示,二元一次方程有无数个解,以方程0x y -=的解为坐标的点的全体叫作方程0x y -=的图象.一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程0x y -=的图象称为直线0x y -=.直线x -y =0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M (x 0,y 0)的坐标满足不等式x -y ≤0,那么点M (x 0,y 0)就在直线x -y =0的上方区域内。
广东中考数学压轴题
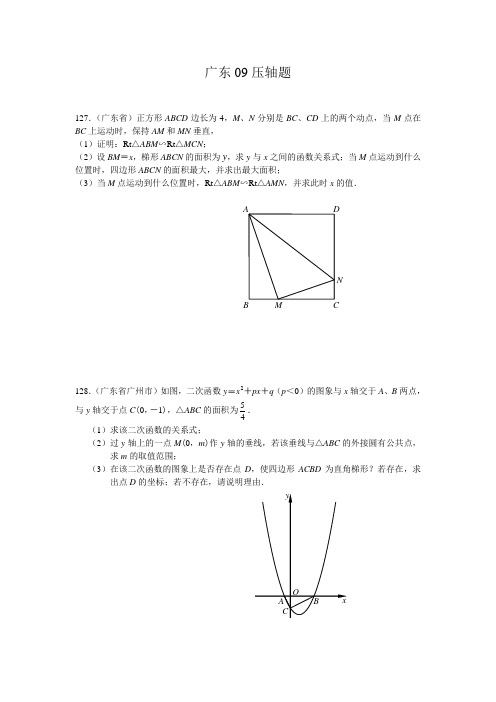
广东09压轴题127.(广东省)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt △ABM ∽Rt △MCN ;(2)设BM =x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 的面积最大,并求出最大面积;(3)当M 点运动到什么位置时,Rt △ABM ∽Rt △AMN ,并求此时x 的值.128.(广东省广州市)如图,二次函数y =x2+px +q (p <0)的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45. (1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ACBD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由.M B CND A129.(广东省深圳市)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△P AB是否有最大面积?若有,求出此时P点的坐标及△P AB的最大面积;若没有,请说明理由.130.(广东省深圳市)如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连结P A,若P A=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?备用图131.(广东省深圳市)已知:Rt △ABC 的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB 与x 轴重合(其中OA <OB ),直角顶点C 落在y 轴正半轴上(如图1).(1)求线段OA 、OB 的长和经过点A 、B 、C 的抛物线的关系式. (2)如图2,点D 的坐标为(2,0),点P (m ,n )是该抛物线上的一个动点(其中m >0,n >0),连接DP 交BC 于点E .①当△BDE 是等腰三角形时,直接写出....此时点E 的坐标. ②又连接CD 、CP (如图3),△CDP 是否有最大面积?若有,求出△CDP 的最大面积和此时点P 的坐标;若没有,请说明理由.132.(广东省珠海市)已知抛物线y =x2-32mx 与x 轴相交于点A 、B ,抛物线的顶点为C .(1)试用含m 的代数式表示AB 的长度; (2)当△ABC 为等边三角形时,求点C 的坐标; (3)在(2)的条件下,如何平移抛物线,使AC =213AB ?133.(广东省佛山市)如图1,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A 处沿着木柜表面爬到柜角C 1处. (1)请你画出蚂蚁能够最快到达目的地的可能路径;(2)当AB =4,BC =4,CC 1=5时,求蚂蚁爬过的最短路径的长; (3)求点B 1到最短路径的距离. A Bxy O 图1C A B x y O PD E图2 C A BPxy O D E 图3 C 备用图 图1134.(广东省茂名市)已知:如图,直线l :y =31x +b ,经过点M (0,41),一组抛物线的顶点B 1(1,y 1),B 2(2,y 2),B 3(3,y 3),…,B n (n ,y n )(n 为正整数)依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:A 1(x 1,0),A 2(x 2,0),A 3(x 3,0),…,A n +1(x n +1,0)(n 为正整数),设x 1=d (0<d <1). (1)求b 的值;(2)求经过点A 1、B 1、A 2的抛物线的解析式(用含d 的代数式表示)(3)定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.探究:当d (0<d <1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的d 的值.135.(广东省湛江市)已知矩形纸片OABC 的长为4,宽为3,以长OA 所在的直线为x 轴,O 为坐标原点建立平面直角坐标系;点P 是OA 边上的动点(与点OA 不重合),现将△POC 沿PC 翻折得到△PEC ,再在AB 边上选取适当的点D ,将△P AD 沿PD 翻折,得到△PFD ,使得直线PE 、PF 重合.(1)若点E 落在BC 边上,如图①,求点P 、C 、D 的坐标,并求过此三点的抛物线的函数关系式;(2)若点E 落在矩形纸片OABC 的内部,如图②,设OP =x ,AD =y ,当x 为何值时,y 取得最大值?(3)在(1)的情况下,过点P 、C 、D 三点的抛物线上是否存在点Q ,使△PDQ 是以PD为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标.136.(广东省肇庆市)如图,⊙O 的直径AB =2,AM 和BN 是它的两条切线,DE 切⊙O 于E ,交AM 于D ,交BN 于C .设AD =x ,BC =y . (1)求证:AM ∥BN ;(2)求y 关于x 的关系式;(3)求四边形ABCD 的面积S ,并证明:S≥2.137.(广东省清远市)如图,已知一个三角形纸片ABC ,BC 边的长为8,BC 边上的高为6,∠B 和∠C 都为锐角,M 为AB 上一动点(点M 与点A 、B 不重合),过点M 作MN ∥BC ,交AC 于点N ,在△AMN 中,设MN 的长为x ,MN 上的高为h . (1)请你用含x 的代数式表示h .(2)将△AMN 沿MN 折叠,使△AMN 落在四边形BCNM 所在平面,设点A 落在平面的点为A 1,△A 1MN 与四边形BCNM 重叠部分的面积为y ,当x 为何值时,y 最大,最大值为多少?138.(广东省梅州市)如图,矩形ABCD 中,AB =5,AD =3.点E 是CD 上的动点,以AE 为直径的⊙O 与AB 交于点F ,过点F 作FG ⊥BE 于点G . (1)当E 是CD 的中点时:①tan ∠EAB 的值为______________; ②证明:FG 是⊙O 的切线;(2)试探究:BE 能否与⊙O 相切?若能,求出此时DE 的长; 若不能,请说明理由.NB C N M A139.(广东省梅州市)如图,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动点,OP的垂直平分线交L于点Q,交x轴于点M.(1)直接写出直线L的解析式;(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;并求出当0<t<2时,S的最大值;(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.1。
广东省中考数学压轴题全解全析

2019年广东省中考数学压轴题全解全析2020年中考在即,备受广大师生关注的中考数学中的压轴题,因为这些试题有较强的选拔性,往往在很大的程度上决定了考试的成败,为帮助大家迎接今年的中考,特对2007年广东省各市中考数学压轴题加以整理,希望对大家有所帮助。
1.(深圳) 如图7,在平面直角坐标系中,抛物线2164y x =-与直线12y x =相交于A B ,两点. (1)求线段AB 的长.(2)若一个扇形的周长等于(1)中线段AB 的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少?(3)如图8,线段AB 的垂直平分线分别交x 轴、y 轴于C D ,两点,垂足为点M ,分别求出OM OC OD,,的长,并验证等式222111+=是否成立.(4)如图9,在Rt ABC △中,90ACB =∠,CD AB⊥,垂足为D,设BC a =,AC b=,AB c =.CD b =,试说明:222111a b h +=.解(1) ∴A (-4,-2),B (6,3) 分别过A 、B 两点作x AE ⊥轴,y BF ⊥轴,垂足分别为E 、F∴AB =OA+OB 22223624+++=55=(2)设扇形的半径为x ,则弧长为)255(x -,扇形的面积为y则)255(21x x y -=x x 5252+-=16125)455(2+--=x∵01<-=a ∴当455=x 时,函数有最大值16125=最大y (3)过点A 作AE ⊥x 轴,垂足为点E ∵CD 垂直平分AB ,点M 为垂足 ∴255225521=-=-=OA AB OM∵COM EOA OMC AEO ∠=∠∠=∠, 图7 图8图9∴△AEO ∽△CMO ∴CO AO OM OE = ∴CO52254=∴45415225=⋅⋅=CO 同理可得 25=OD∴542520)52()54(112222==+=+OD OC ∴5412=OM ∴222111OM OD OC =+(4)等式222111hb a =+成立.理由如下:∵AB CD ACB ⊥=∠,90∴2222121b a AB h AB ab +=⋅= ∴h c ab ⋅=∴ 2222h c b a ⋅= ∴22222)(h b a b a += ∴22222222222)(h b a h b a h b a b a +=∴222221b a b a h += ∴222111b a h += ∴222111h b a =+2. (梅州 11分)如图12,直角梯形ABCD 中,90643AB CD A AB AD DC ∠====∥,°,,,,动点P 从点A 出发,沿A D CB →→→方向移动,动点Q 从点A 出发,在AB 边上移动.设点P 移动的路程为x ,点Q 移动的路程为y ,线段PQ 平分梯形ABCD 的周长.(1)求y 与x 的函数关系式,并求出x y ,的取值范围;(2)当PQ AC ∥时,求x y ,的值;(3)当P 不在BC 边上时,线段PQ 能否平分梯形ABCD 的面积?若能,求出此时x 的值;若不能,说明理由. 解:(1)过C 作CE AB ⊥于E ,则34CD AE CE ===,,可得5BC =,所以梯形ABCD 的周长为18. ····················································································· 1分PQ 平分ABCD 的周长,所以9x y +=, ··································································· 2分 因为06y ≤≤,所以39x ≤≤, 所求关系式为:939y x x =-+,≤≤. ················ 3分(2)依题意,P 只能在BC 边上,79x ≤≤.126PB x BQ y =-=-,,因为PQ AC ∥,所以BPQ BCA △∽△,所以BP BQBC BA=,得 ······································ 4分12656x y --=,即6542x y -=, 解方程组96542x y x y +=⎧⎨-=⎩, 得87121111x y ==,. ······ 6分图12(3)梯形ABCD 的面积为18. ························································································ 7分 当P 不在BC 边上,则37x ≤≤(a )当34x <≤时,P 在AD 边上,12APQ S xy =△.如果线段PQ 能平分梯形ABCD 的面积,则有192xy = ······················································· 8分可得:918.x y xy +=⎧⎨=⎩,解得36x y =⎧⎨=⎩,;(63x y ==,舍去). ····················································· 9分(b )当47x ≤≤时,点P 在DC 边上,此时14(4)2ADPQ S x y =⨯-+. 如果线段PQ 能平分梯形ABCD 的面积,则有14(4)92x y ⨯-+=,可得92217.x y x y +=⎧⎨+=⎩,此方程组无解. 所以当3x =时,线段PQ 能平分梯形ABCD 的面积.11分3. (韶关 9分)如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
(完整版)广东中考数学省卷压轴题汇总
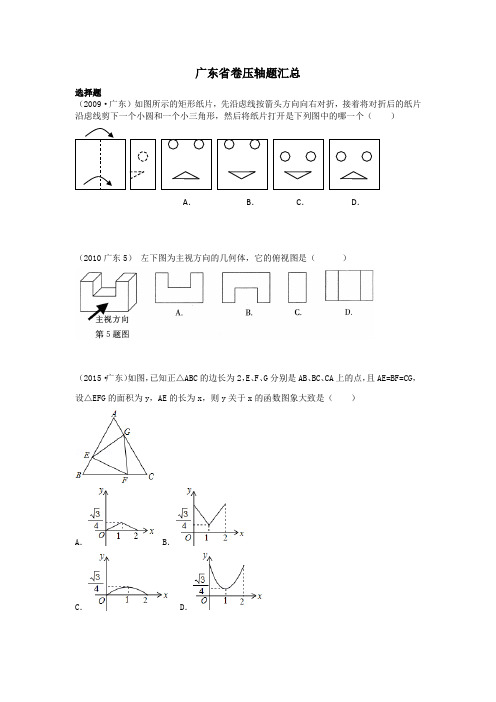
广东省卷压轴题汇总选择题(2009·广东)如图所示的矩形纸片,先沿虑线按箭头方向向右对折,接着将对折后的纸片沿虑线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个( )(2010广东5) 左下图为主视方向的几何体,它的俯视图是( )(2015·广东)如图,已知正△ABC 的边长为2,E 、F 、G 分别是AB 、BC 、CA 上的点,且AE=BF=CG ,设△EFG 的面积为y ,AE 的长为x ,则y 关于x 的函数图象大致是( )A .B .C .D .C .D . A . B .(2016·广东)如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是()A.B.C.D.(2017·广东)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是()A.①③ B.②③ C.①④ D.②④(2018·广东)如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为()A.B.C.D.填空题(2009)用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有黑色瓷砖 __________块,第n个图形中需要黑色瓷砖__________块(用含n的代数式表示).……(1)(2)(3)第10题图(2010广东10)如图(1),已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形A 1B 1C 1D 1;把正方形A 1B 1C 1D 1边长按原法延长一倍得到新正方形A 2B 2C 2D 2(如图(2));以此下去…, 则正方形A 4B 4C 4D 4的面积为 .(2011广东10)如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1;取△ABC 和△DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图(2)中阴影部分;取△A 1B 1C 1和△D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2,如图(3)中阴影部分;如此下去…,则正六角星形A 4F 4B 4D 4C 4E 4的面积为_________________.(2012•广东)如图,在▱ABCD 中,AD=2,AB=4,∠A=30°,以点A 为圆心,AD 的长为半径画弧交AB 于点E ,连接CE ,则阴影部分的面积是 _________ (结果保留π).题10图(1)A 1BCD AFEBCD A FEB CD A FEB 1C 1F 1 D 1 E 1 A 1B 1C 1F 1 D 1 E 1 A 2B 2C 2F 2 D 2E 2 题10图(2)题10图(3)(2013•广东)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是_________ (结果保留π).(2014•广东)如图,ABC∠=︒,∆绕点A顺时针旋转45︒得到△AB C'',若90BAC==,则图中阴影部分的面积等于.AB AC(2015.广东)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是.(2016·广东)如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA、PB、PC,若PA=a,则点A到PB和PC的距离之和AE+AF= .(2017·广东)如图,矩形纸片ABCD中,AB=5,BC=3,先按图(2)操作:将矩形纸片ABCD 沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF;再按图(3)操作,沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A、H两点间的距离为.(2018·广东)如图,已知等边△OA1B1,顶点A1在双曲线y=(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为.解答题(2009.广东)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点, 当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt Rt ABM MCN △∽△;(2)设BM x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积;(3)当M 点运动到什么位置时Rt Rt ABM AMN △∽△,求此时x 的值.DM AB C第22题图N(2010广东20)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.∆是等腰三角形;(1)求证:EGB∆绕点F逆时针旋转最小____度时,四边形ACDE成为以(2)若纸片DEF不动,问ABCED为底的梯形(如图(2)).求此梯形的高.(2011广东22)如图,抛物线1417452++-=x x y 与y 轴交于A 点,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C (3,0).(1)求直线AB 的函数关系式;(2)动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N . 设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;(3)设在(2)的条件下(不考虑点P 与点O ,点C 重合的情况),连接C M ,BN ,当t 为何值时,四边形BCMN 为平行四边形?问对于所求的t 值,平行四边形BCMN 是否菱形?请说明理由.(2012•广东21)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;(2)求tan∠ABG的值;(3)求EF的长.(2012•广东22)如图,抛物线y=x2﹣x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).(2013•广东24)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.(2013•广东25)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA 方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= _________ 度;(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.(2014•广东24)如图,O是ABC⊥于点D,∆的外接圆,AC是直径,过点O作OD AB延长DO交O于点P,过点P作PE AC⊥于点E,作射线DE交BC的延长线于F点,连接PF.π(1)若60AC=,求劣弧PC的长;(结果保留)POC∠=︒,12(2)求证:OD OE=;(3)求证:PF是O的切线.(2014•广东25)如图,在ABC=,8=.点AD cmBC cm⊥于点D,10∆中,AB AC=,AD BCP从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(0)t>.(1)当2t=时,连接DE、DF,求证:四边形AEDF为菱形;(2)在整个运动过程中,所形成的PEF∆的面积最大时,求∆的面积存在最大值,当PEF 线段BP的长;(3)是否存在某一时刻t,使PEF∆为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.(2015•广东24)⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.(2015•广东25)如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm(1)填空:AD= (cm),DC= (cm)(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A →D,C→B方向运动,当N点运动到B点时,M、N两点同时停止运动,连接MN,求当M、N 点运动了x秒时,点N到AD的距离(用含x的式子表示)(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.(参考数据sin75°=,sin15°=)(2016·广东24)如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.(1)求证:△ACF∽△DAE;(2)若S△AOC=,求DE的长;(3)连接EF,求证:EF是⊙O的切线.(2016·广东25)如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.(2017·广东24)如图,AB是⊙O的直径,AB=4,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(1)求证:CB是∠ECP的平分线;(2)求证:CF=CE;(3)当=时,求劣弧的长度(结果保留π)(2017·广东25)如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C 的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:点B的坐标为;(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)①求证:=;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y 的最小值.(2018·广东24)如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.(1)证明:OD∥BC;(2)若tan∠ABC=2,证明:DA与⊙O相切;(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.(2018·广东24)已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O 顺时针旋转60°,如图1,连接BC.(1)填空:∠OBC= °;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N 沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y 取得最大值?最大值为多少?。
2024年深圳中考数学压轴题

2024年深圳中考数学压轴题一、在平面直角坐标系中,点A的坐标为(3,4),以点A为圆心,半径为5的圆与x轴的位置关系是?A. 相离B. 相切C. 相交D. 无法确定(答案)C。
解析:点A到x轴的距离为其纵坐标的绝对值,即4,小于圆的半径5,所以圆与x轴相交。
二、若一个正方形的对角线长为12cm,则这个正方形的面积为?A. 36平方厘米B. 48平方厘米C. 72平方厘米D. 144平方厘米(答案)C。
解析:正方形的对角线将正方形分为两个等腰直角三角形,对角线作为斜边,长度为12cm。
根据勾股定理,正方形的边长为6√2cm,所以面积为(6√2)²=72平方厘米。
三、已知一元二次方程x²+2x-3=0的两个根为x1和x2,则x1+x2的值为?A. -1B. 1C. 2D. -2(答案)D。
解析:对于一元二次方程ax²+bx+c=0,其两个根的和为-b/a。
在此题中,a=1,b=2,所以x1+x2=-2/1=-2。
四、小明家有一个长方形花园,长为10米,宽为6米,他计划在花园的四周种上花,每米花需要5元,小明至少需要多少钱来买花?A. 160元B. 120元C. 80元D. 40元(答案)A。
解析:花园的周长为2×(10+6)=32米,每米花需要5元,所以总共需要32×5=160元。
五、若一个等腰三角形的顶角为80°,则它的一个底角为?A. 80°B. 50°C. 60°D. 40°(答案)B。
解析:等腰三角形的两个底角相等,且三角形内角和为180°,所以一个底角为(180°-80°)/2=50°。
六、小丽在做一个关于概率的实验,她抛掷一枚均匀的骰子两次,两次点数之和为7的概率是多少?A. 1/6B. 1/5C. 1/4D. 1/3(答案)A。
解析:抛掷一枚骰子两次,每次有6种可能的结果,总共有6×6=36种可能的结果。
2020年广东省中考数学压轴题专题训练(含解析)

2020年(广东)中考数学压轴题专题训练1.如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是的中点.(1)求证:PC是⊙O的切线;(2)求证:CD•DE=2OD•PD;(3)若AB=8,CD•DE=15,求P A的长.2.已知:矩形ABCD内接于⊙O,连接BD,点E在⊙O上,连接BE交AD于点F,∠BDC+45°=∠BFD,连接ED.(1)如图1,求证:∠EBD=∠EDB;(2)如图2,点G是AB上一点,过点G作AB的垂线分别交BE和BD于点H和点K,若HK=BG+AF,求证:AB=KG;(3)如图3,在(2)的条件下,⊙O上有一点N,连接CN分别交BD和AD于点M和点P,连接OP,∠APO=∠CPO,若MD=8,MC=3,求线段GB的长.3.如图,AB是⊙O的直径,CD⊥AB,交⊙O于C、D两点,交AB点E、F是弧BD上一点,过点F作一条直线,交CD的延长线于点G,交AB的延长线于点M.连结AF,交CD于点H,GF=GH.(1)求证:MG是⊙O的切线;(2)若弧AF=弧CF,求证:HC=AC;(3)在(2)的条件下,若tan G=,AE=6,求GM的值.4.如图,已知AC是半径为2的⊙O的一条弦,且AC=2,点B是⊙O上不与A、C重合的一个动点,(1)请计算△ABC的面积的最大值;(2)当点B在优弧上,∠BAC>∠ACB时,∠ABC的平分线交AC于D,且OD⊥BD,请计算AD的长;(3)在(2)条件下,请探究线段AB、BC、BD之间的数量关系.5.如图,△ABC为⊙O的内接三角形,BC为⊙O的直径,在线段OC上取点D(不与端点重合),作DG⊥BC,分别交AC、圆周于E、F,连接AG,已知AG=EG.(1)求证:AG为⊙O的切线;(2)已知AG=2,填空:①当四边形ABOF是菱形时,∠AEG=°;②若OC=2DC,△AGE为等腰直角三角形,则AB=.6.如图,△ABC内接于⊙O,AB=AC,AD是⊙O的弦,AD=BC,AD与BC相交于点E.(1)求证:CB平分∠ACD;(2)过点B作BG⊥AC于G,交AD于点F.①猜想AC、AG、CD之间的数量关系,并且说明理由;②若S△ABG=S△ACD,⊙O的半径为15,求DF的长.7.如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,交y轴于点A,以AC为直角边作等腰Rt△ACD,连接BD分别交y轴和AC于E、F两点,连接AB.(1)求证:AB=AD;(2)若BF=4,DF=6,求线段CD的长;(3)当⊙P的大小发生变化而其他条件不变时,的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.8.如图,在△ABC中,∠ACB=90°,点D在BC边上(不包括端点B,C),过A,C,D 三点的⊙O交AB于另一点E,连结AD,DE,CE,且CE⊥AD于点G,过点C作CF∥DE交AD于点F,连结EF.(1)求证:四边形DCFE是菱形;(2)当tan∠AEF=,AC=4时,求⊙O的直径长.9.如图,抛物线y=x2+mx+n与x轴交于A,B两点,与y轴交于点C,若A(﹣1,0),且OC=3OA.(1)求抛物线的解析式;(2)若点M为抛物线上第四象限内一动点,顺次连接AC,CM,MB,是否存在点M,使四边形MBAC的面积为9,若存在,求出点M的坐标,若不存在,请说明理由.(3)将直线BC沿x轴翻折交y轴于N点,过B点的直线l交y轴、抛物线分别于D、E,且D在N的上方,将A点绕O顺时针旋转90°得M,若∠NBD=∠MBO,试求E的的坐标.10.已知:如图,直线y=﹣x﹣3交坐标轴于A、C两点,抛物线y=x2+bx+c过A、C两点,(1)求抛物线的解析式;(2)若点P为抛物线位于第三象限上一动点,连接P A,PC,试问△P AC的面积是否存在最大值,若存在,请求出△APC面积的最大值,以及此时点P的坐标;若不存在,请说明理由;(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.11.如图,二次函数y=a(x2+2mx﹣3m2)(其中a,m是常数a<0,m>0)的图象与x轴分别交于A、B(点A位于点B的右侧),与y轴交于点C(0,3),点D在二次函数的图象上,CD∥AB,连结AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.(1)求a与m的关系式;(2)求证:为定值;(3)设该二次函数的图象的顶点为F.探索:在x轴的正半轴上是否存在点G,连结GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.12.如图,抛物线y=ax2+4ax+与x轴交于点A、B(A在B的左侧),过点A的直线y=kx+3k交抛物线于另一点C.(1)求抛物线的解析式;(2)连接BC,过点B作BD⊥BC,交直线AC于点D,若BC=5BD,求k的值;(3)将直线y=kx+3k向上平移4个单位,平移后的直线交抛物线于E、F两点,求△AEF的面积的最小值.13.如图1,二次函数y=﹣x2+x+3的图象交x轴于A、B两点(点A在点B的左侧),交y轴于C点,连结AC,过点C作CD⊥AC交AB于点D.(1)求点D的坐标;(2)如图2,已知点E是该二次函数图象的顶点,在线段AO上取一点F,过点F作FH ⊥CD,交该二次函数的图象于点H(点H在点E的右侧),当五边形FCEHB的面积最大时,求点H的横坐标;(3)如图3,在直线BC上取一点M(不与点B重合),在直线CD的右上方是否存在这样的点N,使得以C、M、N为顶点的三角形与△BCD全等?若存在,请求出点N的坐标;若不存在,请说明理由.14.如图,已知二次函数y=ax2﹣8ax+6(a>0)的图象与x轴分别交于A、B两点,与y 轴交于点C,点D在抛物线的对称轴上,且四边形ABDC为平行四边形.(1)求此抛物线的对称轴,并确定此二次函数的表达式;(2)点E为x轴下方抛物线上一点,若△ODE的面积为12,求点E的坐标;(3)在(2)的条件下,设抛物线的顶点为M,点P是抛物线的对称轴上一动点,连接PE、EM,过点P作PE的垂线交抛物线于点Q,当∠PQE=∠EMP时,求点Q到抛物线的对称轴的距离.15.如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+与抛物线的另一交点为D,且点D的横坐标为﹣5.(1)求抛物线的函数表达式;(2)该二次函数图象上有一点P(x,y)使得S△BCD=S△ABP,求点P的坐标;(3)设F为线段BD上一点(不含端点),连接AF,求2AF+DF的最小值.16.二次函数y=x2﹣x﹣与x轴分别交于A、B两点,与y轴交于点C,点D 为抛物线的顶点,连接BD.(1)如图1,点P为抛物线上的一点,且在线段BD的下方(包括线段的端点),连接P A,PC,AC.求△P AC的最大面积;(2)如图2,直线l1过点B、D.过点A作直线l2∥l1交y轴于点E,连接点A、E,得到△OAE,将△OAE绕着原点O顺时针旋转α°(0<α<180)得到△OA1E1,旋转过程中直线OE1与直线l1交于点M,直线A1E1与直线l1交于点N.当△E1MN为等腰三角形时,直接写出点E1的坐标并写出相应的α值.17.如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(﹣6,0).(1)求点D和点M的坐标;(2)如图①,将▱ABCD沿着x轴向右平移a个单位长度,点D的对应点D′和点M的对应点M′恰好在反比例函数y=(x>0)的图象上,请求出a的值以及这个反比例函数的表达式;(3)如图②,在(2)的条件下,过点M,M′作直线l,点P是直线l上的动点,点Q 是平面内任意一点,若以B′,C′,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.18.如图,过原点的直线y1=mx(m≠0)与反比例函数y2=(k<0)的图象交于A、B 两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为.(1)根据图象回答:当x取何值时,y1<y2;(2)求△AOD的面积;(3)若点P的坐标为(m,k),在y轴的轴上是否存在一点M,使得△OMP是直角三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.19.阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC中,∠ACB=90°,AC=BC,分别过A、B向经过点C直线作垂线,垂足分别为D、E,我们很容易发现结论:△ADC≌△CEB.(1)探究问题:如果AC≠BC,其他条件不变,如图②,可得到结论;△ADC∽△CEB.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y=x与直线CD交于点M(2,1),且两直线夹角为α,且tanα=,请你求出直线CD的解析式.(3)拓展应用:如图④,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接BE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD 外部时,连接PC,PD.若△DPC为直角三角形时,请你探究并直接写出BE的长.20.笛卡尔是法国数学家、科学家和哲学家,他的哲学与数学思想对历史的影响是深远的.1637年,笛卡尔发表了《几何学》,创立了直角坐标系.其中笛卡尔的思想核心是:把几何学的问题归结成代数形式的问题,用代数的方法进行计算、证明,从而达到最终解决几何问题的目的.某学习小组利用平面直角坐标系在研究直线上点的坐标规律时,发现直线y=kx+b(k≠0)上的任意三点A(x1,y1),B(x2,y2),C(x3,y3)(x1≠x1≠x3),满足===k,经学习小组查阅资料得知,以上发现是成立的,即直线y=kx+b(k≠0)上任意两点的坐标M(x1,y1)N(x2,y2)(x1≠x2),都有的值为k,其中k叫直线y=kx+b的斜率.如,P(1,3),Q(2,4)为直线y=x+2上两点,则k PQ==1,即直线y=x+2的斜率为1.(1)请你直接写出过E(2,3)、F(4,﹣2)两点的直线的斜率k EF=.(2)学习小组继续深入研究直线的“斜率”问题,得到如下正确结论:不与坐标轴平行的任意两条直线互相垂直时,这两条直线的斜率之积是定值.如图1,直线GH⊥GI于点G,G(1,3),H(﹣2,1),I(﹣1,6).请求出直线GH 与直线GI的斜率之积.(3)如图2,已知正方形OKRS的顶点S的坐标为(6,8),点K,R在第二象限,OR 为正方形的对角线.过顶点R作RT⊥OR于点R.求直线RT的解析式.参考答案一.解答题(共20小题)1.(1)证明:连接OC,OE,∵OC=OE,∴∠E=∠OCE,∵E是的中点,∴=,∴∠AOE=∠BOE=90°,∴∠E+∠ODE=90°,∵PC=PD,∴∠PCD=∠PDC,∵∠PDC=∠ODE,∴∠PCD=∠ODE,∴∠PCD+∠OCD=∠ODE+∠E=90°,∴OC⊥PC,∴PC是⊙O的切线;(2)证明:连接AC,BE,BC,∵∠ACD=∠DBE,∠CAD=∠DEB,∴△ACD∽△EBD,∴=,∴CD•DE=AD•BD=(AO﹣OD)(AO+OD)=AO2﹣OD2;∵AB为⊙O的直径,∴∠ACB=90°,∵∠PCO=90°,∴∠ACP+∠ACO=∠ACO+∠BCO=90°,∴∠ACP=∠BCO,∵∠BCO=∠CBO,∴∠ACP=∠PBC,∵∠P=∠P,∴△ACP∽△CBP,∴,∴PC2=PB•P A=(PD+DB)(PD﹣AD)=(PD+OD+OA)(PD+OD﹣OA)=(PD+OD)2﹣OA2=PD2+2PD•OD+OD2﹣OA2,∵PC=PD,∴PD2=PD2+2PD•OD+OD2﹣OA2,∴OA2﹣OD2=2OD•PD,∴CD•DE=2OD•PD;(3)解:∵AB=8,∴OA=4,由(2)知,CD•DE=AO2﹣OD2;∵CD•DE=15,∴15=42﹣OD2,∴OD=1(负值舍去),∴AD=3,由(2)知,CD•DE=2OD•PD,∴PD==,∴P A=PD﹣AD=.2.(1)证明:∵四边形ABCD是矩形,∴AB∥CD,∠BAD=90°,∴∠BDC=∠DBA,BD是⊙O的直径,∴∠BED=90°,∵∠BFD=∠ABF+∠BAD,∠BFD=∠BDC+45°,∴∠ABF+90°=∠DBA+45°,∴∠DBA﹣∠ABF=45°,∴∠EBD=45°,∴△BED是等腰直角三角形,∴∠EBD=∠EDB;(2)证明:过点K作KS⊥BE,垂足为R,交AB于S,如图2所示:∵KG⊥AB,∴∠BGH=∠KRH=∠SRB=∠KGS=90°,∴∠SBR=∠HKR,∵∠BED=90°,∴∠RBK=∠RKB=45°,∴BR=KR,在△SRB和△HRK中,,∴△SRB≌△HRK(ASA),∴SB=HK,∵SB=BG+SG,HK=BG+AF,∴BG+SG=BG+AF,∴SG=AF,在△ABF和△GKS中,,∴△ABF≌△GKS(AAS),∴AB=KG;(3)解:过点O分别作AD与CN的垂线,垂足分别为Q和T,连接OC,如图3所示:∵∠APO=∠CPO,∴OQ=OT,在Rt△OQD和Rt△OTC中,,∴Rt△OQD≌Rt△OTC(HL),∴DQ=CT,∴AD=CN,∵四边形ABCD是矩形,∴AD=CN=BC,连接ON,在△NOC和△BOC中,,∴△NOC≌△BOC(SSS),∴∠BCO=∠NCO,设∠OBC=∠OCB=∠NCO=α,∴∠MOC=2α,过点M作MW⊥OC于W,在OC上取一点L,使WL=OW,连接ML,∴MO=ML,∴∠MOL=∠MLO=2α,∴∠LCM=∠LMC=α,∴ML=CL,设OM=ML=LC=a,则OD=a+8=OC,∴OL=8,OW=WL=4,∴CW=4+a,由勾股定理得:OM2﹣OW2=MW2=MC2﹣CW2,即a2﹣42=(3)2﹣(4+a)2,整理得:a2+4a﹣45=0,解得:a1=﹣9(不合题意舍去),a2=5,∴OM=5,∴MW=3,WC=9,∴OB=OC=OD=13,BD=26,∵∠GKB=∠CBD=∠ADB=∠BCO=∠MCW,tan∠MCW===,∴tan∠GKB=tan∠CBD=tan∠ADB=tan∠BCO=tan∠MCW=,设AB=b,则AD=3b,由勾股定理得:b2+(3b)2=262,解得b=,∴CD=GK=AB=,在Rt△GKB中,tan∠GKB==,∴GB=GK=×=.3.(1)证明:连接OF.∴AB⊥CD,∴∠AEH=90°,∴∠EAH+∠AHE=90°,∵GF=GH,∴∠GFH=∠GHF=∠AHE,∵OA=OF,∴∠OAF=∠OF A,∴∠OF A+∠GFH=90°,∴OF⊥GM,∴MG是⊙O的切线.(2)证明:∵=,∴OF垂直平分线段AC∵OF⊥MG,∴AC∥GM,∴∠CAH=∠GFH,∵∠CHA=∠GHF,∠HGF=∠GFH,∴∠CAH=∠CHA,∴CA=CH.(3)解:∵AC∥GM,∴∠G=∠ACH,∴tan∠CAH=tan∠G==,∵AE=6,∴EC=8,AC===10,设GF=GH=x,则CG=CH+GH=AC+GH=10+x,∵CD=2EC=16,∴GD=10+x﹣16=x﹣6,∵GF2=GD•GC,∴x2=(x﹣6)(x+10),解得x=15,∴EG=CG﹣CE=25﹣8=17,∵tan∠G==,∴EM=,∴GM===.4.解:(1)如图1中,当点B在优弧AC的中点时,△ABC的面积的最大,连接AB,BC,OB,延长BO交AC于H.∵=,∴BH⊥AC,∴AH=HC=,∴OH==1,∴BH=OB+OH=2+1=3,∴△ABC的最大面积=×AC×BH=×2×3=3.(2)如图2中,延长BD交⊙O于E,连结OE交AC于F,连结OC.由BD平分∠ABC可得,E为弧AC中点,∴OE⊥AC,∴AF=CF=∴OF===1=EF,∴DF垂直平分OE,又∵OD⊥BD,∴△ODE是等腰直角三角形,∴DF=OE=1,∴AD=.(3)如图3,连结AE、CE,由已知得AE=CE,∠AEC=120〫,将△EAB绕点E顺时针旋转120〫得△ECF,∵∠BAE=∠ECF,∠BAE+∠BCE=180〫,∴∠ECF+∠BCE=180〫,∴BF=BC+CF,∵AB=CF,∴BF=AB+BC,∵BE=FE,∠BEF=∠AEC=120〫,∴BF=BE,∵OD⊥BD,∴BE=2BD,∴BF=2BD,∴BA+BC=2BD.5.(1)证明:连接OA.∵OA=OC,∴∠OAC=∠OCA,∵GA=GE,∴∠GAE=∠GEA,∵DG⊥BC,∴∠EDC=90°,∴∠OCA+∠DEC=90°,∵∠CED=∠GEA=∠GAE,∴∠OAC+∠GAE=90°,∴∠OAG=90°,∴OA⊥AG,∴AG是⊙O的切线.(2)①如图2中,连接OA,AF,OF.∵四边形ABOF是菱形,∴AB=BO=OF=AF=OA,∴△ABO是等边三角形,∴∠B=60°,∵BC是直径,∴∠BAC=90°∴∠ACB=90°﹣60°=30°,∵ED⊥BC,∴∠DEC=90°﹣∠ACB=60°,∴∠AEG=∠DEC=60°.故答案为60.②如图3中,当AB=4时,△AGE是等腰直角三角形.理由:连接OA.∵△AGE是等腰直角三角形,∴∠AEG=∠DEC=∠DCE=45°,∴△EDC,△ABC都是等腰直角三角形,∵OB=OC,∴AO⊥OC,∴∠AOD=∠ODG=∠G=90°,∴四边形AODG是矩形,∴AG=OD=2,∴OC=2OD=4,∴BC=2OC=8,∴AB=AC=4,故答案为4.6.(1)证明:如图1中,∵AD=BC,∴=,∴=,∵AB=AC,∴=,∴=,∴∠ACB=∠BCD,∴CB平分∠ACD.(2)①结论:AC﹣2AG=CD.理由:如图2中,连接BD,在GC上取一点H,使得GH=GA.∵BG⊥AH,GA=GH,∴BA=BH,∴∠BAH=∠BHA,∵∠BAH+∠BDC=180°,∠BHG+∠BHC=180°,∴∠BDC=∠BHC,∵∠BCH=∠BCD,CB=CB,∴△BCH≌△BCD(AAS),∴CD=CH,∴AC﹣2AG=AC﹣AH=CH=CD.②如图3中,过点G作GN⊥AB于G,过点D作DM⊥AC交AC的延长线于M,连接AO,延长AO交BC于J,连接OC.∵=,∴∠BAD=∠ADC,∴AB∥CD,∴S△ACD=S△BCD,∵△BCH≌△BCD,∴S△BCH=S△BCD,∵AG=GH,∴S△ABG=S△BGH,∵S△ABG=S△ACD,∴S△ABG=S△BGH=S△BCH,∴AG=GH=CH,设AG=GH=HC=a,则AB=AC=3a,BG===2a,∵BG⊥AC,∴•BG•AG=•AB•GN,∴GN==a,在Rt△BGC中,BC===2a,∵AB=AC,∴=,∴AJ⊥BC,∴BJ=JC=a,∴AJ===a,在Rt△OJC中,∵OC2=OJ2+JC2,∴152=(a﹣15)2+(a)2,∴a=,∵S△ABG=S△ACD,AB=AC,GN⊥AB,DM∠AC,∴DM=GN=a=,∵BC=AD=2a=20,∴AM===,∵FG∥DM,∴=,∴=,∴AF=6,∴DF=AD=AF=20﹣6=14. 7.(1)证明:∵OA⊥BC,且OA过圆心点P,∴OB=OC,在△AOB和△AOC中,,∴△AOB≌△AOC(SAS),∴AB=AC,∵以AC为直角边作等腰Rt△ACD,∴AD=AC,∴AB=AD;(2)如图1,过点A作AM⊥BD于M,由(1)知,AB=AD,∴DM=BD,∵BF=4,DF=6,∴BD=10,∴DM=5,∵∠AMD=90°=∠DAF,∠ADM=∠FDA,∴△ADM∽△FDA,∴,∴,∴AD=,在等腰直角三角形ADC中,CD=AD=2;(3)的值是不发生变化,理由:如图2,过点D作DH⊥y轴于H,作DQ⊥x轴于Q,∴∠AHD=90°=∠COA,∴∠ADH+∠DAH=90°,∵∠CAD=90°,∴∠CAO+∠DAH=90°,∴∠ADH=∠CAO,∵AD=AC,∴△ADH≌△ACO(AAS),∴DH=AO,AH=OC,∵∠OHD=∠QOH=∠OQD=90°,∴四边形OQDH是矩形,DH=OQ,DQ=OH,又∵HO=AH+AO=OC+DH=OB+DH=OB+OQ=BQ,∴DQ=BQ,∴△DBQ为等腰直角三角形,∴∠DBQ=45°,∴∠DEH=∠BEO=45°,∴sin∠DEH=,∴=,∴,∴.8.解:(1)证明:∵CE⊥AD,∴EG=CG,∵CF∥DE,∴∠DEG=∠FCG,∵∠FGC=∠DGE,∴△DEG≌△FCG(ASA),∴ED=FC,∴四边形DCFE为平行四边形,又∵CE⊥DF,∴四边形DCFE是菱形;(2)∵AG⊥EC,EG=CG,∴AE=AC=4,∵四边形AEDC内接于⊙O,∴∠BED=∠BCA=90°,∵四边形DCFE是菱形,∴EF∥DC,DE=DC,∴∠AEF=∠ABC,∴tan∠ABC=tan∠AEF=,在Rt△BED中,设DE=3a,则BE=4a,∴DC=3a,BD==5a,∵BC2+AC2=AB2,∴(5a+3a)2+42=(4a+4)2,解得a=或a=0(舍去),∴DE=DC=2,∴AD===2.即⊙O的直径长为2.9.解:(1)∵A(﹣1,0),∴OA=1,OC=3OA=3,∴C(0,﹣3),将A(﹣1,0)、C(0,﹣3)代入y=x2+mx+n中,得,解得,∴y=x2﹣2x﹣3;(2)存在,理由:令y=0,则x2﹣2x﹣3=0,解得x1=﹣1,x2=3,∴B(3,0),∴直线BC的解析式为y=x﹣3,设M(m,m2﹣2m﹣3),过点M作MN∥y轴交BC于N,如图1,∴N(m,m﹣3),∴MN=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,∴S四边形MBAC=S△ABC+S△BCM=AB×OC+MN×OB=×4×3×(﹣m2+3m)×3=9,解得:m=1或2,故点M的坐标为(1,﹣4)或(2,﹣3);(3)∵OB=OC=ON,∴△BON为等腰直角三角形,∵∠OBM+∠NBM=45°,∴∠NBD+∠NBM=∠DBM=45°,∴MB=MF,过点M作MF⊥BM交BE于F,过点F作FH⊥y轴于点H,如图2,∴∠HFM+∠BMO=90°,∵∠BMO+∠OMB=90°,∴∠OMB=∠HFM,∵∠BOM=∠MHF=90°,∴△BOM≌△MHF(AAS),∴FH=OM=1,MH=OB=3,故点F(1,4),由点B、F的坐标得,直线BF的解析式为y=﹣2x+6,联立,解得,∴E(﹣3,12).10.解:(1)y=﹣x﹣3交坐标轴于A、C两点,则点A、C的坐标分别为:(﹣3,0)、(0,﹣3);将点A、C的坐标代入抛物线表达式得:,解得,故抛物线的表达式为:y=x2+2x﹣3;(2)存在,理由:如图1,过点P作y轴的平行线交AC于点H,设点P(x,x2+2x﹣3),则点H(x,﹣x﹣3),△APC面积S=S△PHA+S△PHC=×PH×OA=(﹣x﹣3﹣x2﹣2x+3)×3=﹣x2﹣x,∵﹣<0,故S有最大值,当x=﹣时,S的最大值为,此时点P(﹣,﹣);(3)如图2,设点N(﹣1,s),点M(m,n),n=m2+2m﹣3,过点M作y轴的平行线交过点C与x轴的平行线于点H,交过点N与x轴的平行线于点G,∵∠GMN+∠GNM=90°,∠GMN+∠HMC=90°,∴∠HMC=∠GNM,∵∠MGN=∠CHM=90°,MN=MC,∴△MGN≌△CHM(AAS),∴GN=MH,即GN=|﹣1﹣m|=MH=|n+3|,①当﹣1﹣m=n+3时,即m+n+4=0,即m2+3m+1=0,解得:m=,故点P(,);②当﹣1﹣m=﹣(n+3)时,即m=n+2,同理可得:点P(,);故点P的坐标为:(,)或(,)或(,)或(,).11.解:(1)将点C的坐标代入抛物线表达式得:﹣3am2=3,解得:am2=﹣1;(2)对于二次函数y=a(x2+2mx﹣3m2),令y=0,则x=m或﹣3m,∴函数的对称轴为:x=﹣m,∵CD∥AB,∴点D、C的纵坐标相同,故点D(﹣2m,3),故点A、B的坐标分别为:(m,0)、(﹣3m,0),设点E(x,y),y=a(x2+2mx﹣3m2),分别过点D、E作x轴的垂线,垂足分别为M、N,∵AB平分∠DAE,∴∠DAM=∠EAN,∴RtADM△∽Rt△ANE,∴,即,解得:y=,故点E(x,),将点E的坐标代入抛物线表达式并解得:x==﹣4m,则y==﹣5,故点E(﹣4m,﹣5),故===为定值;(3)存在,理由:函数的对称轴为x=﹣m,当x=﹣m时,y=a(x2+2mx﹣3m2)=4,即点F(﹣m,4),由点F、C的坐标得,直线FC的表达式为:y=﹣x+3,令y=0,则x=3m,即点G(3m,0),GF2=(3m+m)2+42=16m2+16,同理AD2=9m2+9,AE2=25m2+25,故AE2=AD2+GF2,GF、AD、AE的长度为三边长的三角形是直角三角形,点G的横坐标为3m.12.解:(1)∵直线y=kx+3k过点A,∴y=0时,0=kx+3k,解得x=﹣3,∴A(﹣3,0),把点A的坐标代入y=ax2+4ax+,得9a﹣12a+=0,解得a=,∴抛物线解析式为y=x2+x+;(2)如图1,过点D作DF⊥x轴于F,过点C作CG⊥x轴于G,∴∠DFB=∠CGO=90°=∠DBC,∴∠DBF+∠BDF=90°,又∵∠DBF+∠CBG=90°,∴∠BDF=∠CBG,∴△BDF∽△CBG,∴,∵CB=5BD,∴CG=5BF,BG=5DF,联立方程组,解得:,(舍去),∴点C(4k﹣1,4k2+2k),∴CG=4k2+2k,OG=4k﹣1,设BF=m,则CG=5m,DF=2k﹣km,BG=5(2k﹣km),∴,解得k=﹣(舍去)或k=0(舍去)或k=1,∴k的值为1;(3)∵将直线y=kx+3k向上平移4个单位,∴平移后解析式为y=kx+3k+4,∴kx+3k+4=x2+x+,∴x E+x F=4k﹣4,x E•x F=﹣12k﹣13,∴|x F﹣x E|==,∵△AEF的面积=×4×,∴当k=﹣时,△AEF的面积的最小值为16.13.解:(1)令x=0,则y=3,∴C(0,3),∴OC=3.令y=0,则﹣x2+x+3=0,解得:x1=﹣4,x2=6,∴A(﹣4,0),B(6,0),∴OA=4,OB=6.∵CD⊥AC,∴∠ACD=90°,∵CO⊥AD,∴OC2=OA•OD,∴OD=,∴D(,0).∴E(1,).如图2,连接OE、BE,作HG⊥x轴于点G,交BE于点P.由B、E两点坐标可求得直线BE的解析式为:y=﹣x+.设H(m,﹣m2+m+3),则P(m,﹣m+).∴HG=﹣m2+m+3,HP=y H﹣y P=﹣m2+m﹣.∴S△BHE=(x B﹣x E)•HP=(﹣m2+m﹣)=﹣m2+m﹣.∵FH⊥CD,AC⊥CD,∴AC∥FH,∴∠HFG=∠CAO,∵∠AOC=∠FGH=90°,∴△ACO∼△FHG,∴==,∴FG=HG=﹣m2+m+4,∴AF=AG﹣FG=m+4+m2﹣m﹣4=m2+m,∴S△AFC=AF•OC=(m2+m)=m2+m,∵S四边形ACEB=S△ACO+S△OCE+S△OEB=×4×3+×3×1+6×=,∴S五边形FCEHB=S四边形ACEB+S△BHE﹣S△AFC=+(﹣m2+m﹣)﹣(m2+m)∴当m=时,S五边形FCEHB取得最大值.此时,H的横坐标为.(3)∵B(6,0),C(0,3),D(,0),∴CD=BD=,BC=3,∴∠DCB=∠DBC.①如图3﹣1,△CMN≌△DCB,MN交y轴于K,则CM=CN=DC=DB=,MN=BC=3,∠CMN=∠CNM=∠DBC=∠DCB,∴MN∥AB,∴MN⊥y轴,∴∠CKN=∠COB=90°,MK=NK=MN=,∴△CKN∼△COB,∴==,∴CK=,∴OK=OC+CK=,∴N(,).②如图3﹣2,△MCN≌△DBC,则CN=CB=3,∠MCN=∠DBC,∴CN∥AB,∴N(3,3).③如图3﹣3,△CMN≌△DBC,则∠CMN=∠DCB,CM=CN=DC=DB=,MN=BC=3,∴MN∥CD,作MR⊥y轴于R,则===,∴CR=,RM=,∴OR=3﹣,作MQ∥y轴,NQ⊥MQ于点Q,则∠NMQ=∠DCO,∠NQM=∠DOC=90°,∴△COD∼△MQN,∴==,∴MQ=MN=,NQ=MN=,∴NQ﹣RM=,OR+MQ=,∴N(﹣,).综上所述,满足要标的N点坐标有:(,)、(3,3)、(﹣,).14.解:(1)对称轴为直线x=﹣=4,则CD=4,∵四边形ABDC为平行四边形,∴DC∥AB,DC=AB,∴DC=AB=4,∴A(2,0),B(6,0),把点A(2,0)代入得y=ax2﹣8ax+12得4a﹣16a+6=0,解得a=,∴二次函数解析式为y=x2﹣4x+6;(2)如图1,设E(m,m2﹣4m+6),其中2<m<6,作EN⊥y轴于N,如图2,∵S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE,∴(4+m)(6﹣m2+4m﹣6)﹣×4×6﹣m(﹣m2+4m﹣6)=12,化简得:m2﹣11m+24=0,解得m1=3,m2=8(舍),∴点E的坐标为(3,﹣);(3)Ⅰ、当点Q在对称轴右侧时,如图2,过点E作EF⊥PM于F,MQ交x轴于G,∵∠PQE=∠PME,∴点E,M,Q,P四点共圆,∵PE⊥PQ,∴∠EPQ=90°,∴∠EMQ=90°,∴∠EMF+∠HMG=90°,∵∠HMG+∠HGM=90°,∴∠EMF=∠HGM,在Rt△EFM中,EF=1,FM=,tan∠EMF==2,∴tan∠HGM=2,∴,∴HG=HM=1,∴点G(5,0),∵M(4,﹣2),∴直线MG的解析式为y=2x﹣10①,∵二次函数解析式为y=x2﹣4x+6②,联立①②解得,(舍)或,∴Q(8,6),∴点Q到对称轴的距离为8﹣4=4;Ⅱ、当点Q在对称轴左侧时,如图3,过点E作EF⊥PM于F,过点Q作QD⊥PM于D,∴∠DQP+∠QPD=90°,∵∠EPQ=90°,∴∠DPQ+∠FPE=90°,∴∠DQP=∠FPE,∵∠PDQ=∠EFP,∴△PDQ∽△EFP,∴,由Ⅰ知,tan∠PQE==2,∵EF=1,∴=,∴DP=,PF=2QD,设Q(n,n2﹣4n+6),∴DQ=4﹣n,DH=n2﹣4n+6,∴PF=DH+FH﹣DP=n2﹣4n+6+﹣=n2﹣4n+7,∴n2﹣4n+7=2(4﹣n),∴n=2+(舍)或n=2﹣,∴DQ=4﹣n=2+,即点Q到对称轴的距离为4或2+.15.解:(1)抛物线y=a(x+2)(x﹣4),令y=0,解得x=﹣2或x=4,∴A(﹣2,0),B(4,0).∵直线y=﹣x+,当x=﹣5时,y=3,∴D(﹣5,3),∵点D(﹣5,3)在抛物线y=a(x+2)(x﹣4)上,∴a(﹣5+2)(﹣5﹣4)=3,∴a=.∴抛物线的函数表达式为:y=x2﹣x﹣.(2)如图1中,设直线BD交y轴于J,则J(0,).连接CD,BC.∵S△BDC=××9=10,∴S△P AB=10,∴×6×|y P|=10y P=±,当y=时,=x2﹣x﹣,解得x=1±,∴P(,)或(,),当﹣=x2﹣x﹣,方程无解,∴满足条件的点P的坐标为(,)或(,).(3)如图2中,过点D作DM平行于x轴,∵D(﹣5,3),B(4,0),∴tan∠DBA==,∴∠DBA=30°∴∠BDM=∠DBA=30°,过F作FJ⊥DM于J,则有sin30°=,∴HF=,∴2AF+DF=2(AF+)=2(AF+HF),当A、F、H三点共线时,即AH⊥DM时,2AF+DF=2(AF+HF)取最小值为=.16.解:(1)∵y=x2﹣x﹣=(x2﹣2x﹣3)=(x﹣1)2﹣2,∴顶点D的坐标为(1,﹣2),令y=0,则(x2﹣2x﹣3)=0,∴x=﹣1或x=3,∴A(﹣1,0),B(3,0),令x=0,则y=﹣,∴C(0,﹣),∴AC是定值,要△ACP的面积最大,则点P到AC的距离最大,即当点P在点B位置时,点P到AC的距离最大,∴S△ACP最大=S△ABC=AB•OC=(3+1)•=3;(2)由(1)知,B(3,0),D(1,﹣2),∴直线l1的解析式为y=x﹣3,∵l1∥l2,且l1过点A,∴直线l2的解析式为y=x+,∴E(0,),∴OE=,在Rt△AOE中,OA=1,∴tan∠AEO==,∴∠AEO=30°,∵l1∥l2,∴∠DBO=60°,由旋转知,OE1=OE=,∠A1E1O=∠AEO=30°,∴∠ME1N=30°如图,∵△E1MN为等腰三角形,∴①当E1N1=M1N1时,∴∠E1M1N1=∠A1E1O=30°,∴α=∠BOM=60°﹣30°=60°,过点E1作E1F⊥x轴于F,∴E1F=OE1=,∴OF=E1F=,∴E1(,),②当E2M2=E2N2时,∠E2N2M2=∠E2M2N2=(180°﹣30°)=75°,∴∠BOM2=75°﹣60°=15°,∴α=105°,过点E2作E2H⊥x轴,在OH上取一点Q,使OQ=E2Q,∴∠E2QH=30°,设E2H=a,则E2Q=2a,HQ=a,∴OQ=E2Q=2a,OH=(2+)a,在Rt△OHE2中,根据勾股定理得,[(2+)a]2+a2=3,∴a=(舍去负值),∴E2(,﹣).③当E3M3=M3N3时,∠E3N3M3=∠M3E3N3=30,∴∠E3M3N3=120°,∴∠BOM3=60°,∴α=150°,∵∠OBM3=60°,∠E3N3M3=30°,∴∠N3GB=90°,∴OG=,E3G=,∴E3(,﹣).17.解:(1)∵AB=6,点B的坐标为(﹣6,0),∴点A(﹣12,0),如图1,过点D作DE⊥x轴于点D,则ED=AD sin∠DAB=8×=4,同理AE=4,故点D(﹣8,4),则点C(﹣2,4),由中点公式得,点M(﹣4,2);(2)图象向右平移了a个单位,则点D′(a﹣8,4)、点M′(a﹣4,2),∵点D′M′都在函数上,∴(a﹣8)×4=(a﹣4)×2,解得:a=12,则k=(12﹣8)×4=16,故反比例函数的表达式为=;(3)由(2)知,点M′的坐标为(8,2),点B′、C′的坐标分别为(6,0)、(10,4),设点P(m,2),点Q(s,t);①当B′C′是矩形的边时,如图2,求解的矩形为矩形B′C′PQ和矩形B′C′Q′P′,过点C′作C′H⊥l交于点H,C′H=4﹣2=2,直线B′C′的倾斜角为60°,则∠M′PC′=30°,PH=C′H÷tan∠M′PC′=故点P的坐标为(16,2),由题意得:点P、Q′关于点C′对称,由中点公式得,点Q的坐标为(12,﹣4);同理点Q、Q′关于点M′对称,由中点公式得,点Q′(4,6);故点Q的坐标为:(12,﹣4)或(4,6);②当B′C′是矩形的对角线时,∵B′C′的中点即为PQ的中点,且PQ=B′C′,∴,解得:,,故点Q的坐标为(4,2)或(12,2);综上,点Q的坐标为:(12,﹣4)或(4,6)或(4,2)或(12,2).18.解:(1)∵直线y1=mx(m≠0)与反比例函数y2=(k<0)的图象交于A、B两点,且点A的横坐标为﹣1,∴点A,点B关于原点对称,∴点B的横坐标为1,∴当x取﹣1<x<0或x>1时,y1<y2;(2)连接OC,OE,由图象知,点A,点B关于原点对称,∴OA=OB,∵AC⊥CB,∴∠ACB=90°,∴OC=AB=AO,∴∠OAC=∠OCA,∵AC为∠BAD的平分线,∴∠OAC=∠DAC,∴∠OCA=∠DAC,∴AD∥OC,∴S△AEO=S△ACE=,∴AE=DE,∴S△AOD=2S△AOE=3;(3)作EF⊥x轴于F,作AH⊥x轴于H,则EF∥AH,∵AD=2DE,∴DE=EA,∵EF∥AH,∴==1,∴DF=FH,∴EF是△DHA的中位线,∴EF=AH,∵S△OEF=S△OAH=﹣,∴OF•EF=OH•HA,∴OH=OF,∴OH=HF,∴DF=FH=HO=DO,∴S△OAH=S△ADO=3=1,∴﹣=1,∴k=﹣2,∴y=﹣,∵点A在y=﹣的图象上,∴把x=﹣1代入得,y=2,∴A(﹣1,2),∵点A在直线y=mx上,∴m=﹣2,∴P(﹣2,﹣2),在y轴上找到一点M,使得△OMP是直角三角形,当∠OMP=90°时,PM⊥y轴,则OM=2,∴点M的坐标为(0.﹣2);当∠OPM=90°时,过P作PG⊥y轴于G,则△OPM是等腰直角三角形,∴OM=2PG=4,∴点M的坐标为(0.﹣4);综上所述,点M的坐标为(0.﹣2)或(0,﹣4).19.解:(1)理由:∵∠ACB=90°,∴∠ACD=∠BCE=90°,又∵∠ADC=90°,∴∠ACD+∠DAC=90°,∴∠BCE=∠DAC,且∠ADC=∠BEC=90°,∴△ADC∽△CEB;(2)如图,过点O作ON⊥OM交直线CD于点N,分别过M、N作ME⊥x轴NF⊥x轴,由(1)可得:△NFO∽△OEM,∴,∵点M(2,1),∴OE=2,ME=1,∵tanα==,∴,∴NF=3,OF=,∴点N(﹣,3),∵设直线CD表达式:y=kx+b,∴∴∴直线CD的解析式为:y=﹣x+;(3)当∠CDP=90°时,如图,过点P作PH⊥BC,交BC延长线于点H,∵∠ADC+∠CDP=180°,∴点A,点D,点P三点共线,∵∠BAP=∠B=∠H=90°,∴四边形ABHP是矩形,∴AB=PH=3,∵将线段AE绕点E顺时针旋转90°,∴AE=EP,∠AEP=90°,∴∠AEB=∠PEH=90°,且∠BAE+∠AEB=90°,∴∠BAE=∠PEH,且∠B=∠H=90°,AE=EP,∴△ABE≌△EHP(AAS),∴BE=PH=3,当∠CPD=90°时,如图,过点P作PH⊥BC,交BC延长线于点H,延长HP交AD的延长线于N,则四边形CDNH是矩形,∴CD=NH=3,DN=CH,设BE=x,则EC=5﹣x,∵将线段AE绕点E顺时针旋转90°,∴AE=EP,∠AEP=90°,∴∠AEB=∠PEH=90°,且∠BAE+∠AEB=90°,∴∠BAE=∠PEH,且∠B=∠EHP=90°,AE=EP,∴△ABE≌△EHP(AAS),∴PH=BE=x,AB=EH=3,∴PN=3﹣x,CH=3﹣(5﹣x)=x﹣2=DN,∵∠DPC=90°,∴∠DPN+∠CPH=90°,且∠CPH+∠PCH=90°,∴∠PCH=∠DPN,且∠N=∠CHP=90°,∴△CPH∽△PDH,∴,∴∴x=∵点P在矩形ABCD外部,∴x=,∴BE=,综上所述:当BE的长为3或时,△DPC为直角三角形.20.解:(1)∵E(2,3)、F(4,﹣2),∴k EF==﹣,故答案为﹣.(2)∵G(1,3),H(﹣2,1),I(﹣1,6),∴k GH==,k GI==﹣,∴k GH•k GI=﹣1.(3)如图2中,过点K作KM⊥x轴于M,过点S作SN⊥x轴于N,连接KS交OR于J.∴S(6,8),∴ON=6,SN=8,∵四边形OKRS是正方形,∴OK=OS,∠KPS=∠KMO=∠SNO=90°,KJ=JS,JR=JO,∴∠KOM+∠SON=90°,∠SON+∠OSN=90°,∴∠KOM=∠OSN,∴△OMK≌△SNO(AAS),∴KM=ON=6,OM=SN=8,∴K(﹣8,6),∵KJ=JS,∴J(﹣1,7),∵JR=OJ,∴R(﹣2,14),∵k OR==﹣7,∵RT⊥OR,∴k RT=﹣=,设直线RT的解析式为y=x+b.。
最新广东省各市中考数学压轴题目及答案

(2)设0≤x≤4(即M从D到A运动的时间段)。试问x为何值时,△PQW为直角三角形?
当x在何范围时,△PQW不为直角三角形?
(3)问当x为何值时,线段MN最短?求此时MN的值。
4.(2010广东清远)如图9,直线y=x-3于x轴、y轴分别交于B、C;两点,抛物线y=x2+bx+c同时经过B、C两点,点A是抛物线与x轴的另一个交点。
15.(2010广东佛山)新知识一般有两类:第一类是不依赖于其他知识的新知识,如“数”、“字母表示数”这样的初始性的知识;第二类是在某些就只是的基础上进行联系、拓广等方式产生的知识,大多数知识是这样的知识。
(1)多项式乘以多项式的法则,是第几类知识?
(2)在多项式乘以多项式之前,你已拥有的有关知识是哪些?(写出三条即可)
从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),
当动点N运动到点A时,M、N两点同时停止运动。连接FM、FN,当F、N、M不在同一直线时,
可得△FMN,过△FMN三边的中点作△PQW。设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒。试解答下列问题:
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小_____度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
2.(2010广东中山)阅读下列材料:
1×2 = ×(1×2×3-0×1×2),2×3 = ×(2×3×4-1×2×3),3×4 = ×(3×4×5-2×3×4),
由以上三个等式相加,可得1×2+2×3+3×4 = ×3×4×5 = 20。
9.(肇庆市2010)如图,AB是⊙O的直径,AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交A△FCA;(3)CP=AE.
广东省佛山市,2020~2021年中考数学压轴题精选解析

广东省佛山市,2020~2021年中考数学压轴题精选解析广东省佛山市中考数学压轴题精选~~第1题~~(2020台州.中考模拟) 如图,在矩形ABCD 中,CD =3cm ,BC =4cm ,连接BD ,并过点C 作CN ⊥BD ,垂足为N ,直线l 垂直BC ,分别交BD 、BC 于点P 、Q .直线l 从AB 出发,以每秒1cm 的速度沿BC 方向匀速运动到CD 为止;点M 沿线段D A 以每秒1cm 的速度由点D 向点A 匀速运动,到点A 为止,直线1与点M 同时出发,设运动时间为t 秒(t >0).(1) 线段CN =;(2) 连接PM 和QN ,当四边形MPQN 为平行四边形时,求t 的值;(3) 在整个运动过程中,当t 为何值时△PMN 的面积取得最大值,最大值是多少?~~第2题~~(2020顺德.中考模拟) 如图,直线l :y =﹣m 与y 轴交于点A ,直线a :y =x+m 与y 轴交于点B ,抛物线y =x +mx 的顶点为C ,且与x 轴左交点为D (其中m >0).(1) 当AB =12时,在抛物线的对称轴上求一点P 使得△BOP 的周长最小;(2) 当点C 在直线l 上方时,求点C 到直线l 距离的最大值;(3) 若把横坐标、纵坐标都是整数的点称为“整点”.当m =2020时,求出在抛物线和直线a 所围成的封闭图形的边界上的“整点”的个数.~~第3题~~(2019顺德.中考模拟) 如图,点O 是平面直角坐标系的原点,点A (,3),AC ⊥OA 与x 轴的交点为C .动点M 以每秒个单位长度由点A 向点O 运动.同时,动点N 以每秒3个单位长度由点O 向点C 运动,当一动点先到终点时,另一动点立即停止运动.(1) 写出∠AOC 的值;(2) 用t 表示出四边形AMNC 的面积;(3) 求点P 的坐标,使得以O 、N 、M 、P 为顶点的四边形是特殊的平行四边形?~~第4题~~2(2019禅城.中考模拟) 如图,等腰直角△OAB的斜边OA在坐标轴上,顶点B的坐标为(﹣2,2).点P从点A出发,以每秒1个单位的速度沿x轴向点O运动,点Q从点O同时出发,以相同的速度沿x轴的正方向运动,当点P到达点O时,点P、点Q同时停止运动.连接BP,过P点作∠BPC=45°,射线PC与y轴相交于点C,过点Q作平行于y轴的直线l,连接BC 并延长与直线l相交于点D,设点P运动的时间为t(s).(1)点P的坐标为(用t表示);(2)当t为何值,△PBE为等腰三角形?(3)在点P运动过程中,判断的值是否发生变化?请说明理由.~~第5题~~(2019南海.中考模拟) 如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别为O(0,0),A(3,3 )、B (9,5 ),C(14,0),动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OA﹣AB﹣BC运动,在OA、AB、BC上运动的速度分别为3,,(单位长度/秒),当P、Q中的一点到达C点时,两点同时停止运动.(1)求AB所在直线的函数表达式;(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值;(3)在P、Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.~~第6题~~(2019禅城.中考模拟) 为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵?~~第7题~~(2019佛山.中考模拟) 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.(1)求二次函数解析式;(2)连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.~~第8题~~(2018南海.中考模拟) 如图,抛物线与x轴交于点A(1,0)和B(4,0).(1)求抛物线的解析式;(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C ,且四边形OECF是平行四边形,求点C的坐标;(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.~~第9题~~(2017顺德.中考模拟) 如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.~~第10题~~(2015佛山.中考真卷) 如图,在▱ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接B E、BF,使它们分别与AO相交于点G、H.(1)(1)求EG:BG的值;(2)(2)求证:AG=OG;(3)(3)设AG=a,GH=b,HO=c,求a:b:c的值.广东省佛山市中考数学压轴题答案解析~~第1题~~答案:解析:~~第2题~~答案:解析:~~第3题~~答案:解析:~~第4题~~答案:解析:~~第5题~~答案:解析:答案:解析:答案:解析:答案:解析:~~第9题~~答案:解析:答案:解析:。
2024年中考数学压轴题型(广东专用)专题07一次函数与反比例函数综合问题(教师版)

专题07一次函数与反比例函数综合问题通用的解题思路:1.三角形面积的解题步骤:类型一:三角形有其中一边与坐标轴平行(垂直)的,以这边为底边,以该边所对的顶点的坐标的绝对值为高•底边平行于V轴,则以所对顶点的横坐标的绝对值为高,反之则以纵坐标的绝对值为高.类型二:三角形没有其中一边与坐标轴平行(垂直)的,可以用公式水平宽X铅垂高求解.2.利用图象法解不等式解集的解题步骤:①求交点:联立方程求出方程组的解;②分区间:将一次函数和反比例函数两个交点以及y轴左右两侧分层4个区间;③比大小:图象谁在上方谁就大;④:写出对应区间自变量的取值范围.3.两线段和差的最值问题利用将军饮马模型:做对称,连定点,求交点.1.(2024广东东莞•一模)如图,一次函数y=+3的图象与'轴交于点,与反比例函数日的图象在第一象限内交于点瓦点B的横坐标为1,连接。
8,过点B作BClx轴于点C.⑴求一次函数和反比例函数的解析式;.....................................~4〜.......................⑵设点。
是x轴上一点,使得S^BCD=~S^AOB,求点Q的坐标.【答案】(1)必=2x+3,J=-x⑵点。
的坐标为(-1,0)或(3,0)【分析】本题主要考查了待定系数法确定函数的解析式,一次函数图象的性质,一次函数图象上点的坐标的特征,反比例函数的性质,反比例函数图象上点的坐标的特征,利用点的坐标表示出相应线段的长度是解题的关键.(1)把点代入一次函数了=心+3中,解得m=2,进而可得点B的坐标为(1,5),再利用待定系数法解答即可;(2)根据坐标求得S△朝=可知S%co=:S△皿=5,再根据S^cd=?CD・BC,得CD=2,即可求解.【详解】(1)解:把点{―代入一次函数:Y=m+3中,,一3___——m+3=0,解得m=2,园一次函数的解析式为"2x+3.把点B的横坐标工二1代入y=2x+3中,得"5,国点B的坐标为(1,5),国点B为一次函数和反比例函数图象的交点,园把点8(1,5)代入反比例函数y=|中,得S5,园反比例函数的解析式为:y=-;(2)园jo],8(1,5),BClx轴,0OA=-,BC=5,C(l,0),S5aaob=-AO-BC=-x-x5=—,△如2224[?]Q=—V-^x—=5U*BCD3°AA(9B34,0S ABCn=-CD BC=-CD=5,园CD=2,M(l,0),回点。
2020年广东省中考数学压轴题专题训练(含解析)

2020年(广东)中考数学压轴题专题训练1.如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是的中点.(1)求证:PC是⊙O的切线;(2)求证:CD•DE=2OD•PD;(3)若AB=8,CD•DE=15,求P A的长.2.已知:矩形ABCD内接于⊙O,连接BD,点E在⊙O上,连接BE交AD于点F,∠BDC+45°=∠BFD,连接ED.(1)如图1,求证:∠EBD=∠EDB;(2)如图2,点G是AB上一点,过点G作AB的垂线分别交BE和BD于点H和点K,若HK=BG+AF,求证:AB=KG;(3)如图3,在(2)的条件下,⊙O上有一点N,连接CN分别交BD和AD于点M和点P,连接OP,∠APO=∠CPO,若MD=8,MC=3,求线段GB的长.3.如图,AB是⊙O的直径,CD⊥AB,交⊙O于C、D两点,交AB点E、F是弧BD上一点,过点F作一条直线,交CD的延长线于点G,交AB的延长线于点M.连结AF,交CD于点H,GF=GH.(1)求证:MG是⊙O的切线;(2)若弧AF=弧CF,求证:HC=AC;(3)在(2)的条件下,若tan G=,AE=6,求GM的值.4.如图,已知AC是半径为2的⊙O的一条弦,且AC=2,点B是⊙O上不与A、C重合的一个动点,(1)请计算△ABC的面积的最大值;(2)当点B在优弧上,∠BAC>∠ACB时,∠ABC的平分线交AC于D,且OD⊥BD,请计算AD的长;(3)在(2)条件下,请探究线段AB、BC、BD之间的数量关系.5.如图,△ABC为⊙O的内接三角形,BC为⊙O的直径,在线段OC上取点D(不与端点重合),作DG⊥BC,分别交AC、圆周于E、F,连接AG,已知AG=EG.(1)求证:AG为⊙O的切线;(2)已知AG=2,填空:①当四边形ABOF是菱形时,∠AEG=°;②若OC=2DC,△AGE为等腰直角三角形,则AB=.6.如图,△ABC内接于⊙O,AB=AC,AD是⊙O的弦,AD=BC,AD与BC相交于点E.(1)求证:CB平分∠ACD;(2)过点B作BG⊥AC于G,交AD于点F.①猜想AC、AG、CD之间的数量关系,并且说明理由;②若S△ABG=S△ACD,⊙O的半径为15,求DF的长.7.如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,交y轴于点A,以AC为直角边作等腰Rt△ACD,连接BD分别交y轴和AC于E、F两点,连接AB.(1)求证:AB=AD;(2)若BF=4,DF=6,求线段CD的长;(3)当⊙P的大小发生变化而其他条件不变时,的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.8.如图,在△ABC中,∠ACB=90°,点D在BC边上(不包括端点B,C),过A,C,D 三点的⊙O交AB于另一点E,连结AD,DE,CE,且CE⊥AD于点G,过点C作CF∥DE交AD于点F,连结EF.(1)求证:四边形DCFE是菱形;(2)当tan∠AEF=,AC=4时,求⊙O的直径长.9.如图,抛物线y=x2+mx+n与x轴交于A,B两点,与y轴交于点C,若A(﹣1,0),且OC=3OA.(1)求抛物线的解析式;(2)若点M为抛物线上第四象限内一动点,顺次连接AC,CM,MB,是否存在点M,使四边形MBAC的面积为9,若存在,求出点M的坐标,若不存在,请说明理由.(3)将直线BC沿x轴翻折交y轴于N点,过B点的直线l交y轴、抛物线分别于D、E,且D在N的上方,将A点绕O顺时针旋转90°得M,若∠NBD=∠MBO,试求E的的坐标.10.已知:如图,直线y=﹣x﹣3交坐标轴于A、C两点,抛物线y=x2+bx+c过A、C两点,(1)求抛物线的解析式;(2)若点P为抛物线位于第三象限上一动点,连接P A,PC,试问△P AC的面积是否存在最大值,若存在,请求出△APC面积的最大值,以及此时点P的坐标;若不存在,请说明理由;(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.11.如图,二次函数y=a(x2+2mx﹣3m2)(其中a,m是常数a<0,m>0)的图象与x轴分别交于A、B(点A位于点B的右侧),与y轴交于点C(0,3),点D在二次函数的图象上,CD∥AB,连结AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.(1)求a与m的关系式;(2)求证:为定值;(3)设该二次函数的图象的顶点为F.探索:在x轴的正半轴上是否存在点G,连结GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.12.如图,抛物线y=ax2+4ax+与x轴交于点A、B(A在B的左侧),过点A的直线y=kx+3k交抛物线于另一点C.(1)求抛物线的解析式;(2)连接BC,过点B作BD⊥BC,交直线AC于点D,若BC=5BD,求k的值;(3)将直线y=kx+3k向上平移4个单位,平移后的直线交抛物线于E、F两点,求△AEF的面积的最小值.13.如图1,二次函数y=﹣x2+x+3的图象交x轴于A、B两点(点A在点B的左侧),交y轴于C点,连结AC,过点C作CD⊥AC交AB于点D.(1)求点D的坐标;(2)如图2,已知点E是该二次函数图象的顶点,在线段AO上取一点F,过点F作FH ⊥CD,交该二次函数的图象于点H(点H在点E的右侧),当五边形FCEHB的面积最大时,求点H的横坐标;(3)如图3,在直线BC上取一点M(不与点B重合),在直线CD的右上方是否存在这样的点N,使得以C、M、N为顶点的三角形与△BCD全等?若存在,请求出点N的坐标;若不存在,请说明理由.14.如图,已知二次函数y=ax2﹣8ax+6(a>0)的图象与x轴分别交于A、B两点,与y 轴交于点C,点D在抛物线的对称轴上,且四边形ABDC为平行四边形.(1)求此抛物线的对称轴,并确定此二次函数的表达式;(2)点E为x轴下方抛物线上一点,若△ODE的面积为12,求点E的坐标;(3)在(2)的条件下,设抛物线的顶点为M,点P是抛物线的对称轴上一动点,连接PE、EM,过点P作PE的垂线交抛物线于点Q,当∠PQE=∠EMP时,求点Q到抛物线的对称轴的距离.15.如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+与抛物线的另一交点为D,且点D的横坐标为﹣5.(1)求抛物线的函数表达式;(2)该二次函数图象上有一点P(x,y)使得S△BCD=S△ABP,求点P的坐标;(3)设F为线段BD上一点(不含端点),连接AF,求2AF+DF的最小值.16.二次函数y=x2﹣x﹣与x轴分别交于A、B两点,与y轴交于点C,点D 为抛物线的顶点,连接BD.(1)如图1,点P为抛物线上的一点,且在线段BD的下方(包括线段的端点),连接P A,PC,AC.求△P AC的最大面积;(2)如图2,直线l1过点B、D.过点A作直线l2∥l1交y轴于点E,连接点A、E,得到△OAE,将△OAE绕着原点O顺时针旋转α°(0<α<180)得到△OA1E1,旋转过程中直线OE1与直线l1交于点M,直线A1E1与直线l1交于点N.当△E1MN为等腰三角形时,直接写出点E1的坐标并写出相应的α值.17.如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(﹣6,0).(1)求点D和点M的坐标;(2)如图①,将▱ABCD沿着x轴向右平移a个单位长度,点D的对应点D′和点M的对应点M′恰好在反比例函数y=(x>0)的图象上,请求出a的值以及这个反比例函数的表达式;(3)如图②,在(2)的条件下,过点M,M′作直线l,点P是直线l上的动点,点Q 是平面内任意一点,若以B′,C′,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.18.如图,过原点的直线y1=mx(m≠0)与反比例函数y2=(k<0)的图象交于A、B 两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为.(1)根据图象回答:当x取何值时,y1<y2;(2)求△AOD的面积;(3)若点P的坐标为(m,k),在y轴的轴上是否存在一点M,使得△OMP是直角三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.19.阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC中,∠ACB=90°,AC=BC,分别过A、B向经过点C直线作垂线,垂足分别为D、E,我们很容易发现结论:△ADC≌△CEB.(1)探究问题:如果AC≠BC,其他条件不变,如图②,可得到结论;△ADC∽△CEB.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y=x与直线CD交于点M(2,1),且两直线夹角为α,且tanα=,请你求出直线CD的解析式.(3)拓展应用:如图④,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接BE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD 外部时,连接PC,PD.若△DPC为直角三角形时,请你探究并直接写出BE的长.20.笛卡尔是法国数学家、科学家和哲学家,他的哲学与数学思想对历史的影响是深远的.1637年,笛卡尔发表了《几何学》,创立了直角坐标系.其中笛卡尔的思想核心是:把几何学的问题归结成代数形式的问题,用代数的方法进行计算、证明,从而达到最终解决几何问题的目的.某学习小组利用平面直角坐标系在研究直线上点的坐标规律时,发现直线y=kx+b(k≠0)上的任意三点A(x1,y1),B(x2,y2),C(x3,y3)(x1≠x1≠x3),满足===k,经学习小组查阅资料得知,以上发现是成立的,即直线y=kx+b(k≠0)上任意两点的坐标M(x1,y1)N(x2,y2)(x1≠x2),都有的值为k,其中k叫直线y=kx+b的斜率.如,P(1,3),Q(2,4)为直线y=x+2上两点,则k PQ==1,即直线y=x+2的斜率为1.(1)请你直接写出过E(2,3)、F(4,﹣2)两点的直线的斜率k EF=.(2)学习小组继续深入研究直线的“斜率”问题,得到如下正确结论:不与坐标轴平行的任意两条直线互相垂直时,这两条直线的斜率之积是定值.如图1,直线GH⊥GI于点G,G(1,3),H(﹣2,1),I(﹣1,6).请求出直线GH 与直线GI的斜率之积.(3)如图2,已知正方形OKRS的顶点S的坐标为(6,8),点K,R在第二象限,OR 为正方形的对角线.过顶点R作RT⊥OR于点R.求直线RT的解析式.参考答案一.解答题(共20小题)1.(1)证明:连接OC,OE,∵OC=OE,∴∠E=∠OCE,∵E是的中点,∴=,∴∠AOE=∠BOE=90°,∴∠E+∠ODE=90°,∵PC=PD,∴∠PCD=∠PDC,∵∠PDC=∠ODE,∴∠PCD=∠ODE,∴∠PCD+∠OCD=∠ODE+∠E=90°,∴OC⊥PC,∴PC是⊙O的切线;(2)证明:连接AC,BE,BC,∵∠ACD=∠DBE,∠CAD=∠DEB,∴△ACD∽△EBD,∴=,∴CD•DE=AD•BD=(AO﹣OD)(AO+OD)=AO2﹣OD2;∵AB为⊙O的直径,∴∠ACB=90°,∵∠PCO=90°,∴∠ACP+∠ACO=∠ACO+∠BCO=90°,∴∠ACP=∠BCO,∵∠BCO=∠CBO,∴∠ACP=∠PBC,∵∠P=∠P,∴△ACP∽△CBP,∴,∴PC2=PB•P A=(PD+DB)(PD﹣AD)=(PD+OD+OA)(PD+OD﹣OA)=(PD+OD)2﹣OA2=PD2+2PD•OD+OD2﹣OA2,∵PC=PD,∴PD2=PD2+2PD•OD+OD2﹣OA2,∴OA2﹣OD2=2OD•PD,∴CD•DE=2OD•PD;(3)解:∵AB=8,∴OA=4,由(2)知,CD•DE=AO2﹣OD2;∵CD•DE=15,∴15=42﹣OD2,∴OD=1(负值舍去),∴AD=3,由(2)知,CD•DE=2OD•PD,∴PD==,∴P A=PD﹣AD=.2.(1)证明:∵四边形ABCD是矩形,∴AB∥CD,∠BAD=90°,∴∠BDC=∠DBA,BD是⊙O的直径,∴∠BED=90°,∵∠BFD=∠ABF+∠BAD,∠BFD=∠BDC+45°,∴∠ABF+90°=∠DBA+45°,∴∠DBA﹣∠ABF=45°,∴∠EBD=45°,∴△BED是等腰直角三角形,∴∠EBD=∠EDB;(2)证明:过点K作KS⊥BE,垂足为R,交AB于S,如图2所示:∵KG⊥AB,∴∠BGH=∠KRH=∠SRB=∠KGS=90°,∴∠SBR=∠HKR,∵∠BED=90°,∴∠RBK=∠RKB=45°,∴BR=KR,在△SRB和△HRK中,,∴△SRB≌△HRK(ASA),∴SB=HK,∵SB=BG+SG,HK=BG+AF,∴BG+SG=BG+AF,∴SG=AF,在△ABF和△GKS中,,∴△ABF≌△GKS(AAS),∴AB=KG;(3)解:过点O分别作AD与CN的垂线,垂足分别为Q和T,连接OC,如图3所示:∵∠APO=∠CPO,∴OQ=OT,在Rt△OQD和Rt△OTC中,,∴Rt△OQD≌Rt△OTC(HL),∴DQ=CT,∴AD=CN,∵四边形ABCD是矩形,∴AD=CN=BC,连接ON,在△NOC和△BOC中,,∴△NOC≌△BOC(SSS),∴∠BCO=∠NCO,设∠OBC=∠OCB=∠NCO=α,∴∠MOC=2α,过点M作MW⊥OC于W,在OC上取一点L,使WL=OW,连接ML,∴MO=ML,∴∠MOL=∠MLO=2α,∴∠LCM=∠LMC=α,∴ML=CL,设OM=ML=LC=a,则OD=a+8=OC,∴OL=8,OW=WL=4,∴CW=4+a,由勾股定理得:OM2﹣OW2=MW2=MC2﹣CW2,即a2﹣42=(3)2﹣(4+a)2,整理得:a2+4a﹣45=0,解得:a1=﹣9(不合题意舍去),a2=5,∴OM=5,∴MW=3,WC=9,∴OB=OC=OD=13,BD=26,∵∠GKB=∠CBD=∠ADB=∠BCO=∠MCW,tan∠MCW===,∴tan∠GKB=tan∠CBD=tan∠ADB=tan∠BCO=tan∠MCW=,设AB=b,则AD=3b,由勾股定理得:b2+(3b)2=262,解得b=,∴CD=GK=AB=,在Rt△GKB中,tan∠GKB==,∴GB=GK=×=.3.(1)证明:连接OF.∴AB⊥CD,∴∠AEH=90°,∴∠EAH+∠AHE=90°,∵GF=GH,∴∠GFH=∠GHF=∠AHE,∵OA=OF,∴∠OAF=∠OF A,∴∠OF A+∠GFH=90°,∴OF⊥GM,∴MG是⊙O的切线.(2)证明:∵=,∴OF垂直平分线段AC∵OF⊥MG,∴AC∥GM,∴∠CAH=∠GFH,∵∠CHA=∠GHF,∠HGF=∠GFH,∴∠CAH=∠CHA,∴CA=CH.(3)解:∵AC∥GM,∴∠G=∠ACH,∴tan∠CAH=tan∠G==,∵AE=6,∴EC=8,AC===10,设GF=GH=x,则CG=CH+GH=AC+GH=10+x,∵CD=2EC=16,∴GD=10+x﹣16=x﹣6,∵GF2=GD•GC,∴x2=(x﹣6)(x+10),解得x=15,∴EG=CG﹣CE=25﹣8=17,∵tan∠G==,∴EM=,∴GM===.4.解:(1)如图1中,当点B在优弧AC的中点时,△ABC的面积的最大,连接AB,BC,OB,延长BO交AC于H.∵=,∴BH⊥AC,∴AH=HC=,∴OH==1,∴BH=OB+OH=2+1=3,∴△ABC的最大面积=×AC×BH=×2×3=3.(2)如图2中,延长BD交⊙O于E,连结OE交AC于F,连结OC.由BD平分∠ABC可得,E为弧AC中点,∴OE⊥AC,∴AF=CF=∴OF===1=EF,∴DF垂直平分OE,又∵OD⊥BD,∴△ODE是等腰直角三角形,∴DF=OE=1,∴AD=.(3)如图3,连结AE、CE,由已知得AE=CE,∠AEC=120〫,将△EAB绕点E顺时针旋转120〫得△ECF,∵∠BAE=∠ECF,∠BAE+∠BCE=180〫,∴∠ECF+∠BCE=180〫,∴BF=BC+CF,∵AB=CF,∴BF=AB+BC,∵BE=FE,∠BEF=∠AEC=120〫,∴BF=BE,∵OD⊥BD,∴BE=2BD,∴BF=2BD,∴BA+BC=2BD.5.(1)证明:连接OA.∵OA=OC,∴∠OAC=∠OCA,∵GA=GE,∴∠GAE=∠GEA,∵DG⊥BC,∴∠EDC=90°,∴∠OCA+∠DEC=90°,∵∠CED=∠GEA=∠GAE,∴∠OAC+∠GAE=90°,∴∠OAG=90°,∴OA⊥AG,∴AG是⊙O的切线.(2)①如图2中,连接OA,AF,OF.∵四边形ABOF是菱形,∴AB=BO=OF=AF=OA,∴△ABO是等边三角形,∴∠B=60°,∵BC是直径,∴∠BAC=90°∴∠ACB=90°﹣60°=30°,∵ED⊥BC,∴∠DEC=90°﹣∠ACB=60°,∴∠AEG=∠DEC=60°.故答案为60.②如图3中,当AB=4时,△AGE是等腰直角三角形.理由:连接OA.∵△AGE是等腰直角三角形,∴∠AEG=∠DEC=∠DCE=45°,∴△EDC,△ABC都是等腰直角三角形,∵OB=OC,∴AO⊥OC,∴∠AOD=∠ODG=∠G=90°,∴四边形AODG是矩形,∴AG=OD=2,∴OC=2OD=4,∴BC=2OC=8,∴AB=AC=4,故答案为4.6.(1)证明:如图1中,∵AD=BC,∴=,∴=,∵AB=AC,∴=,∴=,∴∠ACB=∠BCD,∴CB平分∠ACD.(2)①结论:AC﹣2AG=CD.理由:如图2中,连接BD,在GC上取一点H,使得GH=GA.∵BG⊥AH,GA=GH,∴BA=BH,∴∠BAH=∠BHA,∵∠BAH+∠BDC=180°,∠BHG+∠BHC=180°,∴∠BDC=∠BHC,∵∠BCH=∠BCD,CB=CB,∴△BCH≌△BCD(AAS),∴CD=CH,∴AC﹣2AG=AC﹣AH=CH=CD.②如图3中,过点G作GN⊥AB于G,过点D作DM⊥AC交AC的延长线于M,连接AO,延长AO交BC于J,连接OC.∵=,∴∠BAD=∠ADC,∴AB∥CD,∴S△ACD=S△BCD,∵△BCH≌△BCD,∴S△BCH=S△BCD,∵AG=GH,∴S△ABG=S△BGH,∵S△ABG=S△ACD,∴S△ABG=S△BGH=S△BCH,∴AG=GH=CH,设AG=GH=HC=a,则AB=AC=3a,BG===2a,∵BG⊥AC,∴•BG•AG=•AB•GN,∴GN==a,在Rt△BGC中,BC===2a,∵AB=AC,∴=,∴AJ⊥BC,∴BJ=JC=a,∴AJ===a,在Rt△OJC中,∵OC2=OJ2+JC2,∴152=(a﹣15)2+(a)2,∴a=,∵S△ABG=S△ACD,AB=AC,GN⊥AB,DM∠AC,∴DM=GN=a=,∵BC=AD=2a=20,∴AM===,∵FG∥DM,∴=,∴=,∴AF=6,∴DF=AD=AF=20﹣6=14. 7.(1)证明:∵OA⊥BC,且OA过圆心点P,∴OB=OC,在△AOB和△AOC中,,∴△AOB≌△AOC(SAS),∴AB=AC,∵以AC为直角边作等腰Rt△ACD,∴AD=AC,∴AB=AD;(2)如图1,过点A作AM⊥BD于M,由(1)知,AB=AD,∴DM=BD,∵BF=4,DF=6,∴BD=10,∴DM=5,∵∠AMD=90°=∠DAF,∠ADM=∠FDA,∴△ADM∽△FDA,∴,∴,∴AD=,在等腰直角三角形ADC中,CD=AD=2;(3)的值是不发生变化,理由:如图2,过点D作DH⊥y轴于H,作DQ⊥x轴于Q,∴∠AHD=90°=∠COA,∴∠ADH+∠DAH=90°,∵∠CAD=90°,∴∠CAO+∠DAH=90°,∴∠ADH=∠CAO,∵AD=AC,∴△ADH≌△ACO(AAS),∴DH=AO,AH=OC,∵∠OHD=∠QOH=∠OQD=90°,∴四边形OQDH是矩形,DH=OQ,DQ=OH,又∵HO=AH+AO=OC+DH=OB+DH=OB+OQ=BQ,∴DQ=BQ,∴△DBQ为等腰直角三角形,∴∠DBQ=45°,∴∠DEH=∠BEO=45°,∴sin∠DEH=,∴=,∴,∴.8.解:(1)证明:∵CE⊥AD,∴EG=CG,∵CF∥DE,∴∠DEG=∠FCG,∵∠FGC=∠DGE,∴△DEG≌△FCG(ASA),∴ED=FC,∴四边形DCFE为平行四边形,又∵CE⊥DF,∴四边形DCFE是菱形;(2)∵AG⊥EC,EG=CG,∴AE=AC=4,∵四边形AEDC内接于⊙O,∴∠BED=∠BCA=90°,∵四边形DCFE是菱形,∴EF∥DC,DE=DC,∴∠AEF=∠ABC,∴tan∠ABC=tan∠AEF=,在Rt△BED中,设DE=3a,则BE=4a,∴DC=3a,BD==5a,∵BC2+AC2=AB2,∴(5a+3a)2+42=(4a+4)2,解得a=或a=0(舍去),∴DE=DC=2,∴AD===2.即⊙O的直径长为2.9.解:(1)∵A(﹣1,0),∴OA=1,OC=3OA=3,∴C(0,﹣3),将A(﹣1,0)、C(0,﹣3)代入y=x2+mx+n中,得,解得,∴y=x2﹣2x﹣3;(2)存在,理由:令y=0,则x2﹣2x﹣3=0,解得x1=﹣1,x2=3,∴B(3,0),∴直线BC的解析式为y=x﹣3,设M(m,m2﹣2m﹣3),过点M作MN∥y轴交BC于N,如图1,∴N(m,m﹣3),∴MN=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,∴S四边形MBAC=S△ABC+S△BCM=AB×OC+MN×OB=×4×3×(﹣m2+3m)×3=9,解得:m=1或2,故点M的坐标为(1,﹣4)或(2,﹣3);(3)∵OB=OC=ON,∴△BON为等腰直角三角形,∵∠OBM+∠NBM=45°,∴∠NBD+∠NBM=∠DBM=45°,∴MB=MF,过点M作MF⊥BM交BE于F,过点F作FH⊥y轴于点H,如图2,∴∠HFM+∠BMO=90°,∵∠BMO+∠OMB=90°,∴∠OMB=∠HFM,∵∠BOM=∠MHF=90°,∴△BOM≌△MHF(AAS),∴FH=OM=1,MH=OB=3,故点F(1,4),由点B、F的坐标得,直线BF的解析式为y=﹣2x+6,联立,解得,∴E(﹣3,12).10.解:(1)y=﹣x﹣3交坐标轴于A、C两点,则点A、C的坐标分别为:(﹣3,0)、(0,﹣3);将点A、C的坐标代入抛物线表达式得:,解得,故抛物线的表达式为:y=x2+2x﹣3;(2)存在,理由:如图1,过点P作y轴的平行线交AC于点H,设点P(x,x2+2x﹣3),则点H(x,﹣x﹣3),△APC面积S=S△PHA+S△PHC=×PH×OA=(﹣x﹣3﹣x2﹣2x+3)×3=﹣x2﹣x,∵﹣<0,故S有最大值,当x=﹣时,S的最大值为,此时点P(﹣,﹣);(3)如图2,设点N(﹣1,s),点M(m,n),n=m2+2m﹣3,过点M作y轴的平行线交过点C与x轴的平行线于点H,交过点N与x轴的平行线于点G,∵∠GMN+∠GNM=90°,∠GMN+∠HMC=90°,∴∠HMC=∠GNM,∵∠MGN=∠CHM=90°,MN=MC,∴△MGN≌△CHM(AAS),∴GN=MH,即GN=|﹣1﹣m|=MH=|n+3|,①当﹣1﹣m=n+3时,即m+n+4=0,即m2+3m+1=0,解得:m=,故点P(,);②当﹣1﹣m=﹣(n+3)时,即m=n+2,同理可得:点P(,);故点P的坐标为:(,)或(,)或(,)或(,).11.解:(1)将点C的坐标代入抛物线表达式得:﹣3am2=3,解得:am2=﹣1;(2)对于二次函数y=a(x2+2mx﹣3m2),令y=0,则x=m或﹣3m,∴函数的对称轴为:x=﹣m,∵CD∥AB,∴点D、C的纵坐标相同,故点D(﹣2m,3),故点A、B的坐标分别为:(m,0)、(﹣3m,0),设点E(x,y),y=a(x2+2mx﹣3m2),分别过点D、E作x轴的垂线,垂足分别为M、N,∵AB平分∠DAE,∴∠DAM=∠EAN,∴RtADM△∽Rt△ANE,∴,即,解得:y=,故点E(x,),将点E的坐标代入抛物线表达式并解得:x==﹣4m,则y==﹣5,故点E(﹣4m,﹣5),故===为定值;(3)存在,理由:函数的对称轴为x=﹣m,当x=﹣m时,y=a(x2+2mx﹣3m2)=4,即点F(﹣m,4),由点F、C的坐标得,直线FC的表达式为:y=﹣x+3,令y=0,则x=3m,即点G(3m,0),GF2=(3m+m)2+42=16m2+16,同理AD2=9m2+9,AE2=25m2+25,故AE2=AD2+GF2,GF、AD、AE的长度为三边长的三角形是直角三角形,点G的横坐标为3m.12.解:(1)∵直线y=kx+3k过点A,∴y=0时,0=kx+3k,解得x=﹣3,∴A(﹣3,0),把点A的坐标代入y=ax2+4ax+,得9a﹣12a+=0,解得a=,∴抛物线解析式为y=x2+x+;(2)如图1,过点D作DF⊥x轴于F,过点C作CG⊥x轴于G,∴∠DFB=∠CGO=90°=∠DBC,∴∠DBF+∠BDF=90°,又∵∠DBF+∠CBG=90°,∴∠BDF=∠CBG,∴△BDF∽△CBG,∴,∵CB=5BD,∴CG=5BF,BG=5DF,联立方程组,解得:,(舍去),∴点C(4k﹣1,4k2+2k),∴CG=4k2+2k,OG=4k﹣1,设BF=m,则CG=5m,DF=2k﹣km,BG=5(2k﹣km),∴,解得k=﹣(舍去)或k=0(舍去)或k=1,∴k的值为1;(3)∵将直线y=kx+3k向上平移4个单位,∴平移后解析式为y=kx+3k+4,∴kx+3k+4=x2+x+,∴x E+x F=4k﹣4,x E•x F=﹣12k﹣13,∴|x F﹣x E|==,∵△AEF的面积=×4×,∴当k=﹣时,△AEF的面积的最小值为16.13.解:(1)令x=0,则y=3,∴C(0,3),∴OC=3.令y=0,则﹣x2+x+3=0,解得:x1=﹣4,x2=6,∴A(﹣4,0),B(6,0),∴OA=4,OB=6.∵CD⊥AC,∴∠ACD=90°,∵CO⊥AD,∴OC2=OA•OD,∴OD=,∴D(,0).∴E(1,).如图2,连接OE、BE,作HG⊥x轴于点G,交BE于点P.由B、E两点坐标可求得直线BE的解析式为:y=﹣x+.设H(m,﹣m2+m+3),则P(m,﹣m+).∴HG=﹣m2+m+3,HP=y H﹣y P=﹣m2+m﹣.∴S△BHE=(x B﹣x E)•HP=(﹣m2+m﹣)=﹣m2+m﹣.∵FH⊥CD,AC⊥CD,∴AC∥FH,∴∠HFG=∠CAO,∵∠AOC=∠FGH=90°,∴△ACO∼△FHG,∴==,∴FG=HG=﹣m2+m+4,∴AF=AG﹣FG=m+4+m2﹣m﹣4=m2+m,∴S△AFC=AF•OC=(m2+m)=m2+m,∵S四边形ACEB=S△ACO+S△OCE+S△OEB=×4×3+×3×1+6×=,∴S五边形FCEHB=S四边形ACEB+S△BHE﹣S△AFC=+(﹣m2+m﹣)﹣(m2+m)∴当m=时,S五边形FCEHB取得最大值.此时,H的横坐标为.(3)∵B(6,0),C(0,3),D(,0),∴CD=BD=,BC=3,∴∠DCB=∠DBC.①如图3﹣1,△CMN≌△DCB,MN交y轴于K,则CM=CN=DC=DB=,MN=BC=3,∠CMN=∠CNM=∠DBC=∠DCB,∴MN∥AB,∴MN⊥y轴,∴∠CKN=∠COB=90°,MK=NK=MN=,∴△CKN∼△COB,∴==,∴CK=,∴OK=OC+CK=,∴N(,).②如图3﹣2,△MCN≌△DBC,则CN=CB=3,∠MCN=∠DBC,∴CN∥AB,∴N(3,3).③如图3﹣3,△CMN≌△DBC,则∠CMN=∠DCB,CM=CN=DC=DB=,MN=BC=3,∴MN∥CD,作MR⊥y轴于R,则===,∴CR=,RM=,∴OR=3﹣,作MQ∥y轴,NQ⊥MQ于点Q,则∠NMQ=∠DCO,∠NQM=∠DOC=90°,∴△COD∼△MQN,∴==,∴MQ=MN=,NQ=MN=,∴NQ﹣RM=,OR+MQ=,∴N(﹣,).综上所述,满足要标的N点坐标有:(,)、(3,3)、(﹣,).14.解:(1)对称轴为直线x=﹣=4,则CD=4,∵四边形ABDC为平行四边形,∴DC∥AB,DC=AB,∴DC=AB=4,∴A(2,0),B(6,0),把点A(2,0)代入得y=ax2﹣8ax+12得4a﹣16a+6=0,解得a=,∴二次函数解析式为y=x2﹣4x+6;(2)如图1,设E(m,m2﹣4m+6),其中2<m<6,作EN⊥y轴于N,如图2,∵S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE,∴(4+m)(6﹣m2+4m﹣6)﹣×4×6﹣m(﹣m2+4m﹣6)=12,化简得:m2﹣11m+24=0,解得m1=3,m2=8(舍),∴点E的坐标为(3,﹣);(3)Ⅰ、当点Q在对称轴右侧时,如图2,过点E作EF⊥PM于F,MQ交x轴于G,∵∠PQE=∠PME,∴点E,M,Q,P四点共圆,∵PE⊥PQ,∴∠EPQ=90°,∴∠EMQ=90°,∴∠EMF+∠HMG=90°,∵∠HMG+∠HGM=90°,∴∠EMF=∠HGM,在Rt△EFM中,EF=1,FM=,tan∠EMF==2,∴tan∠HGM=2,∴,∴HG=HM=1,∴点G(5,0),∵M(4,﹣2),∴直线MG的解析式为y=2x﹣10①,∵二次函数解析式为y=x2﹣4x+6②,联立①②解得,(舍)或,∴Q(8,6),∴点Q到对称轴的距离为8﹣4=4;Ⅱ、当点Q在对称轴左侧时,如图3,过点E作EF⊥PM于F,过点Q作QD⊥PM于D,∴∠DQP+∠QPD=90°,∵∠EPQ=90°,∴∠DPQ+∠FPE=90°,∴∠DQP=∠FPE,∵∠PDQ=∠EFP,∴△PDQ∽△EFP,∴,由Ⅰ知,tan∠PQE==2,∵EF=1,∴=,∴DP=,PF=2QD,设Q(n,n2﹣4n+6),∴DQ=4﹣n,DH=n2﹣4n+6,∴PF=DH+FH﹣DP=n2﹣4n+6+﹣=n2﹣4n+7,∴n2﹣4n+7=2(4﹣n),∴n=2+(舍)或n=2﹣,∴DQ=4﹣n=2+,即点Q到对称轴的距离为4或2+.15.解:(1)抛物线y=a(x+2)(x﹣4),令y=0,解得x=﹣2或x=4,∴A(﹣2,0),B(4,0).∵直线y=﹣x+,当x=﹣5时,y=3,∴D(﹣5,3),∵点D(﹣5,3)在抛物线y=a(x+2)(x﹣4)上,∴a(﹣5+2)(﹣5﹣4)=3,∴a=.∴抛物线的函数表达式为:y=x2﹣x﹣.(2)如图1中,设直线BD交y轴于J,则J(0,).连接CD,BC.∵S△BDC=××9=10,∴S△P AB=10,∴×6×|y P|=10y P=±,当y=时,=x2﹣x﹣,解得x=1±,∴P(,)或(,),当﹣=x2﹣x﹣,方程无解,∴满足条件的点P的坐标为(,)或(,).(3)如图2中,过点D作DM平行于x轴,∵D(﹣5,3),B(4,0),∴tan∠DBA==,∴∠DBA=30°∴∠BDM=∠DBA=30°,过F作FJ⊥DM于J,则有sin30°=,∴HF=,∴2AF+DF=2(AF+)=2(AF+HF),当A、F、H三点共线时,即AH⊥DM时,2AF+DF=2(AF+HF)取最小值为=.16.解:(1)∵y=x2﹣x﹣=(x2﹣2x﹣3)=(x﹣1)2﹣2,∴顶点D的坐标为(1,﹣2),令y=0,则(x2﹣2x﹣3)=0,∴x=﹣1或x=3,∴A(﹣1,0),B(3,0),令x=0,则y=﹣,∴C(0,﹣),∴AC是定值,要△ACP的面积最大,则点P到AC的距离最大,即当点P在点B位置时,点P到AC的距离最大,∴S△ACP最大=S△ABC=AB•OC=(3+1)•=3;(2)由(1)知,B(3,0),D(1,﹣2),∴直线l1的解析式为y=x﹣3,∵l1∥l2,且l1过点A,∴直线l2的解析式为y=x+,∴E(0,),∴OE=,在Rt△AOE中,OA=1,∴tan∠AEO==,∴∠AEO=30°,∵l1∥l2,∴∠DBO=60°,由旋转知,OE1=OE=,∠A1E1O=∠AEO=30°,∴∠ME1N=30°如图,∵△E1MN为等腰三角形,∴①当E1N1=M1N1时,∴∠E1M1N1=∠A1E1O=30°,∴α=∠BOM=60°﹣30°=60°,过点E1作E1F⊥x轴于F,∴E1F=OE1=,∴OF=E1F=,∴E1(,),②当E2M2=E2N2时,∠E2N2M2=∠E2M2N2=(180°﹣30°)=75°,∴∠BOM2=75°﹣60°=15°,∴α=105°,过点E2作E2H⊥x轴,在OH上取一点Q,使OQ=E2Q,∴∠E2QH=30°,设E2H=a,则E2Q=2a,HQ=a,∴OQ=E2Q=2a,OH=(2+)a,在Rt△OHE2中,根据勾股定理得,[(2+)a]2+a2=3,∴a=(舍去负值),∴E2(,﹣).③当E3M3=M3N3时,∠E3N3M3=∠M3E3N3=30,∴∠E3M3N3=120°,∴∠BOM3=60°,∴α=150°,∵∠OBM3=60°,∠E3N3M3=30°,∴∠N3GB=90°,∴OG=,E3G=,∴E3(,﹣).17.解:(1)∵AB=6,点B的坐标为(﹣6,0),∴点A(﹣12,0),如图1,过点D作DE⊥x轴于点D,则ED=AD sin∠DAB=8×=4,同理AE=4,故点D(﹣8,4),则点C(﹣2,4),由中点公式得,点M(﹣4,2);(2)图象向右平移了a个单位,则点D′(a﹣8,4)、点M′(a﹣4,2),∵点D′M′都在函数上,∴(a﹣8)×4=(a﹣4)×2,解得:a=12,则k=(12﹣8)×4=16,故反比例函数的表达式为=;(3)由(2)知,点M′的坐标为(8,2),点B′、C′的坐标分别为(6,0)、(10,4),设点P(m,2),点Q(s,t);①当B′C′是矩形的边时,如图2,求解的矩形为矩形B′C′PQ和矩形B′C′Q′P′,过点C′作C′H⊥l交于点H,C′H=4﹣2=2,直线B′C′的倾斜角为60°,则∠M′PC′=30°,PH=C′H÷tan∠M′PC′=故点P的坐标为(16,2),由题意得:点P、Q′关于点C′对称,由中点公式得,点Q的坐标为(12,﹣4);同理点Q、Q′关于点M′对称,由中点公式得,点Q′(4,6);故点Q的坐标为:(12,﹣4)或(4,6);②当B′C′是矩形的对角线时,∵B′C′的中点即为PQ的中点,且PQ=B′C′,∴,解得:,,故点Q的坐标为(4,2)或(12,2);综上,点Q的坐标为:(12,﹣4)或(4,6)或(4,2)或(12,2).18.解:(1)∵直线y1=mx(m≠0)与反比例函数y2=(k<0)的图象交于A、B两点,且点A的横坐标为﹣1,∴点A,点B关于原点对称,∴点B的横坐标为1,∴当x取﹣1<x<0或x>1时,y1<y2;(2)连接OC,OE,由图象知,点A,点B关于原点对称,∴OA=OB,∵AC⊥CB,∴∠ACB=90°,∴OC=AB=AO,∴∠OAC=∠OCA,∵AC为∠BAD的平分线,∴∠OAC=∠DAC,∴∠OCA=∠DAC,∴AD∥OC,∴S△AEO=S△ACE=,∴AE=DE,∴S△AOD=2S△AOE=3;(3)作EF⊥x轴于F,作AH⊥x轴于H,则EF∥AH,∵AD=2DE,∴DE=EA,∵EF∥AH,∴==1,∴DF=FH,∴EF是△DHA的中位线,∴EF=AH,∵S△OEF=S△OAH=﹣,∴OF•EF=OH•HA,∴OH=OF,∴OH=HF,∴DF=FH=HO=DO,∴S△OAH=S△ADO=3=1,∴﹣=1,∴k=﹣2,∴y=﹣,∵点A在y=﹣的图象上,∴把x=﹣1代入得,y=2,∴A(﹣1,2),∵点A在直线y=mx上,∴m=﹣2,∴P(﹣2,﹣2),在y轴上找到一点M,使得△OMP是直角三角形,当∠OMP=90°时,PM⊥y轴,则OM=2,∴点M的坐标为(0.﹣2);当∠OPM=90°时,过P作PG⊥y轴于G,则△OPM是等腰直角三角形,∴OM=2PG=4,∴点M的坐标为(0.﹣4);综上所述,点M的坐标为(0.﹣2)或(0,﹣4).19.解:(1)理由:∵∠ACB=90°,∴∠ACD=∠BCE=90°,又∵∠ADC=90°,∴∠ACD+∠DAC=90°,∴∠BCE=∠DAC,且∠ADC=∠BEC=90°,∴△ADC∽△CEB;(2)如图,过点O作ON⊥OM交直线CD于点N,分别过M、N作ME⊥x轴NF⊥x轴,由(1)可得:△NFO∽△OEM,∴,∵点M(2,1),∴OE=2,ME=1,∵tanα==,∴,∴NF=3,OF=,∴点N(﹣,3),∵设直线CD表达式:y=kx+b,∴∴∴直线CD的解析式为:y=﹣x+;(3)当∠CDP=90°时,如图,过点P作PH⊥BC,交BC延长线于点H,∵∠ADC+∠CDP=180°,∴点A,点D,点P三点共线,∵∠BAP=∠B=∠H=90°,∴四边形ABHP是矩形,∴AB=PH=3,∵将线段AE绕点E顺时针旋转90°,∴AE=EP,∠AEP=90°,∴∠AEB=∠PEH=90°,且∠BAE+∠AEB=90°,∴∠BAE=∠PEH,且∠B=∠H=90°,AE=EP,∴△ABE≌△EHP(AAS),∴BE=PH=3,当∠CPD=90°时,如图,过点P作PH⊥BC,交BC延长线于点H,延长HP交AD的延长线于N,则四边形CDNH是矩形,∴CD=NH=3,DN=CH,设BE=x,则EC=5﹣x,∵将线段AE绕点E顺时针旋转90°,∴AE=EP,∠AEP=90°,∴∠AEB=∠PEH=90°,且∠BAE+∠AEB=90°,∴∠BAE=∠PEH,且∠B=∠EHP=90°,AE=EP,∴△ABE≌△EHP(AAS),∴PH=BE=x,AB=EH=3,∴PN=3﹣x,CH=3﹣(5﹣x)=x﹣2=DN,∵∠DPC=90°,∴∠DPN+∠CPH=90°,且∠CPH+∠PCH=90°,∴∠PCH=∠DPN,且∠N=∠CHP=90°,∴△CPH∽△PDH,∴,∴∴x=∵点P在矩形ABCD外部,∴x=,∴BE=,综上所述:当BE的长为3或时,△DPC为直角三角形.20.解:(1)∵E(2,3)、F(4,﹣2),∴k EF==﹣,故答案为﹣.(2)∵G(1,3),H(﹣2,1),I(﹣1,6),∴k GH==,k GI==﹣,∴k GH•k GI=﹣1.(3)如图2中,过点K作KM⊥x轴于M,过点S作SN⊥x轴于N,连接KS交OR于J.∴S(6,8),∴ON=6,SN=8,∵四边形OKRS是正方形,∴OK=OS,∠KPS=∠KMO=∠SNO=90°,KJ=JS,JR=JO,∴∠KOM+∠SON=90°,∠SON+∠OSN=90°,∴∠KOM=∠OSN,∴△OMK≌△SNO(AAS),∴KM=ON=6,OM=SN=8,∴K(﹣8,6),∵KJ=JS,∴J(﹣1,7),∵JR=OJ,∴R(﹣2,14),∵k OR==﹣7,∵RT⊥OR,∴k RT=﹣=,设直线RT的解析式为y=x+b.。
广州、广东中考数学压轴题集锦

广州市历年中考压轴题2018年24.(14分)已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)证明:该抛物线与x轴总有两个不同的交点;(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;②若点C关于直线x=﹣mm2的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求ll rr的值.25.(14分)如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.2017年24.(14分)如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD 的对称图形为△CED.(1)求证:四边形OCED是菱形;(2)连接AE,若AB=6cm,BC=√5cm.①求sin∠EAD的值;②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA 匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.25.(14分)如图,AB是⊙O的直径,AAAA�=BBAA�,AB=2,连接AC.(1)求证:∠CAB=45°;(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD 所在的直线与AC所在的直线相交于点E,连接AD.①试探究AE与AD之间的是数量关系,并证明你的结论;②EEEE CCCC是否为定值?若是,请求出这个定值;若不是,请说明理由.2016年24.(14分)(2016•广州)已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B(1)求m的取值范围;(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3)当<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.25.(14分)(2016•广州)如图,点C为△ABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°(1)求证:BD是该外接圆的直径;(2)连结CD,求证:AC=BC+CD;(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.24.(14分)(2015•广州)如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.(1)试探究筝形对角线之间的位置关系,并证明你的结论;(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8,①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.25.(14分)(2015•广州)已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1•x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.(1)求点C的坐标;(2)当y1随着x的增大而增大时,求自变量x的取值范围;(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.24.(14分)(2014•广州)已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.(1)求抛物线的解析式和顶点C的坐标;(2)当∠APB为钝角时,求m的取值范围;(3)若m>,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.25.(14分)(2014•广州)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=3,BC=4,CD=5.点E为线段CD上一动点(不与点C重合),△BCE关于BE的轴对称图形为△BFE,连接CF.设CE=x,△BCF的面积为S1,△CEF的面积为S2.(1)当点F落在梯形ABCD的中位线上时,求x的值;(2)试用x表示,并写出x的取值范围;(3)当△BFE的外接圆与AD相切时,求的值.24.(14分)(2013•广州)已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.(1)当OC=时(如图),求证:CD是⊙O的切线;(2)当OC>时,CD所在直线于⊙O相交,设另一交点为E,连接AE.①当D为CE中点时,求△ACE的周长;②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE•ED的值;若不存在,请说明理由.25.(14分)(2013•广州)已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为B,且抛物线不经过第三象限.(1)使用a、c表示b;(2)判断点B所在象限,并说明理由;(3)若直线y2=2x+m经过点B,且与该抛物线交于另一点C(),求当x≥1时y1的取值范围.24.(14分)(2012•广州)如图,抛物线y=与x轴交于A、B两点(点A 在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.25.(14分)(2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).(1)当α=60°时,求CE的长;(2)当60°<α<90°时,①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.②连接CF,当CE2﹣CF2取最大值时,求tan∠DCF的值.24.(14分)(2011•广州)已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,点A的坐标是(1,0)(1)求c的值;(2)求a的取值范围;(3)该二次函数的图象与直线y=1交于C、D两点,设A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<a<1时,求证:S1﹣S2为常数,并求出该常数.25.(14分)(2011•广州)如图1,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角三角形DCE中∠DCE是直角,点D在线段AC上.(1)证明:B、C、E三点共线;(2)若M是线段BE的中点,N是线段AD的中点,证明:MN=OM;(3)将△DCE绕点C逆时针旋转α(0°<α<90°)后,记为△D1CE1(图2),若M1是线段BE1的中点,N1是线段AD1的中点,M1N1=OM1是否成立?若是,请证明;若不是,说明理由.24.(14分)(2010•广州)如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE 长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.(1)求弦AB的长;(2)判断∠ACB是否为定值?若是,求出∠ACB的大小;否则,请说明理由;(3)记△ABC的面积为S,若=4,求△ABC的周长.25.(14分)(2010•广州)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣x+b交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出该重叠部分的面积;若改变,请说明理由.24.(14分)(2009•广州)如图,边长为1的正方形ABCD被两条与边平行的线段EF、GH 分割为四个小矩形,EF与GH交于点P.(1)若AG=AE,证明:AF=AH;(2)若∠FAH=45°,证明:AG+AE=FH;(3)若Rt△GBF的周长为1,求矩形EPHD的面积.25.(14分)(2009•广州)如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣1),△ABC的面积为.(1)求该二次函数的关系式;(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC的外接圆有公共点,求m的取值范围;(3)在该二次函数的图象上是否存在点D,使四边形ACBD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由.24.(14分)(2008•广州)如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE(1)求证:四边形OGCH是平行四边形;(2)当点C在上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD2+3CH2是定值.25.(14分)(2008•广州)如图,在梯形ABCD中,AD∥BC,AB=AD=DC=2cm,BC=4cm,在等腰△PQR中,∠QPR=120°,底边QR=6cm,点B、C、Q、R在同一直线l上,且C、Q两点重合,如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动,t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米.(1)当t=4时,求S的值;(2)当4≤t≤10,求S与t的函数关系式,并求出S的最大值.24.(14分)(2007•广州)一次函数y=kx+k过点(1,4),且分别与x轴、y轴交于A、B 点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动,且PQ⊥AB.(1)求k的值,并在直角坐标系中画出一次函数的图象;(2)求a、b满足的等量关系式;(3)若△APQ是等腰三角形,求△APQ的面积.25.(12分)(2007•广州)已知:在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,连接EC,取EC的中点M,连接DM和BM.(1)若点D在边AC上,点E在边AB上且与点B不重合,如图1,探索BM、DM的关系并给予证明;(2)如果将图1中的△ADE绕点A逆时针旋转小于45°的角,如图2,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.广东省历年中考压轴题2018年24.(9分)如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.(1)证明:OD∥BC;(2)若tan∠ABC=2,证明:DA与⊙O相切;(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.25.(9.00分)已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如题图1,连接BC.(1)填空:∠OBC= °;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B 路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?2017年24.(9分)如图,AB是⊙O的直径,AB=4√3,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(1)求证:CB是∠ECP的平分线;(2)求证:CF=CE;(3)当CCCC CCCC=34时,求劣弧BBAA�的长度(结果保留π)25.(9分)如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2√3,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:点B的坐标为;(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)①求证:CCEE CCEE=√33;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.24.(9分)(2016•广东)如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A 作⊙O的切线AF,与直径BC的延长线交于点F.(1)求证:△ACF∽△DAE;(2)若S△AOC=,求DE的长;(3)连接EF,求证:EF是⊙O的切线.25.(9分)(2016•广东)如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.24.(9分)(2015•广东)⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.25.(9分)(2015•广东)如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt △ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm(1)填空:AD= (cm),DC= (cm)(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B方向运动,点N到AD的距离(用含x的式子表示)(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.(参考数据sin75°=,sin15°=)24.(9分)(2014•广东)如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB 于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F 点,连接PF.(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)(2)求证:OD=OE;(3)求证:PF是⊙O的切线.25.(9分)(2014•广东)如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.24.(9分)(2013•广东)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.25.(9分)(2013•广东)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF 沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= 度;(2)如图3,在三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.21.(2012•广东)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;(2)求tan∠ABG的值;(3)求EF的长.22.(2012•广东)如图,抛物线y=x2﹣x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省历年中考数学压轴题( 2)
姓名:
4.(2007 年 9 分 )已知等边 OAB 的边长为 a ,以 AB 边上的高 OA1 为边,按逆时 针方向作等边 OA1 B1 , A1B1 与 OB 相交于点 A2 .
(1)求线段 OA2 的长;
(2)若再以 OA2 为边按逆时针方向作等边 OA2B2 , A2B2 与 OB1 相交于点 A3 ,按
此作法进行下去,得到 OA3B3 , OA4 B4 ,…, OAnBn (如图 )。求 OA6B6
的周长.
B5
B4
B6 A7
A6
A5 B3
B7 O
A4 B2
A3 B1
A2
A
A1
B
解新方程 3
t 2
检验
3
t
0
2
求原方程的解
3 x
2 所以 x 9
4
x 2x 3 0
x x24 0
3.(2010 年 9 分 )某学校组织 340 名师生进行长途考察活动,带有行礼 170 件, 计划租用甲、乙两种型号的汽车共有 10 辆.经了解,甲车每辆最多能载 40 人和 16 件行李,乙车每辆最多能载 30 人和 20 件行李. ⑴请你帮助学校设计所有可行的租车方案; ⑵如果甲车的租金为每辆 2000 元,乙车的租金为每辆 1800 元,问哪种可行方 案使租车费用最省?
(2) 1 2 2 3 3 4
n ( n 1)
;
(3) 1 2 3 2 3 4 3 4 5
789
姓名:
.
2.(2009 年 9 分)小明用下面的方法求出方程 2 x 3 0 的解,请你仿照他的方
法求出下面两个方程的解,并把你的解答过程填写在下面的表格,
方程 2x 3 0
换元法得新方程 令x t
则 2t 3 0
广东省历年中考数学压轴题( 1)
1.(2010 年)阅读下列材料:
12 23 34
1 (1
2
3
0
1
2) ,
3
1 (2
3
4
1
2
3) ,
3
1 (3
4
5
2
3
4) ,
3
由以上三个等式相加,可得
12
23 34
1 34 5
20 .
3
读完以上材料,请你计算下各题:
(1) 1 2 2 3 3 4
10 11(写出过程);
