六年级比例的应用题和答案

合集下载

6年级比例应用题

6年级比例应用题一、简单比例关系应用题（1 10题）1. 一辆汽车3小时行驶180千米，照这样的速度，5小时行驶多少千米？解析：首先根据速度 = 路程÷时间，求出汽车的速度。

汽车3小时行驶180千米，速度为公式千米/小时。

然后根据路程 = 速度×时间，5小时行驶的路程为公式千米。

设5小时行驶公式千米，根据速度一定，路程和时间成正比例关系，可得公式，解得公式。

2. 配制一种农药，药粉和水的比是1:500，现有水6000千克，配制这种农药需要药粉多少千克？解析：药粉和水的比是公式，即水是药粉的500倍。

现有水6000千克，那么药粉的重量为公式千克。

设需要药粉公式千克，根据比例关系公式，解得公式。

3. 学校图书馆科技书与故事书的比是3:5，科技书有180本，故事书有多少本？解析：因为科技书与故事书的比是公式，设故事书有公式本，则公式，交叉相乘得公式，公式本。

思路是根据两种书数量的比例关系列方程求解。

4. 一块长方形菜地长和宽的比是5:3，长是40米，宽是多少米？解析：设宽是公式米，因为长和宽的比是公式，所以公式，交叉相乘得公式，公式米。

利用长和宽的比例关系来建立方程求解宽的长度。

5. 某工厂男职工与女职工的人数比是4:3，男职工有320人，女职工有多少人？解析：设女职工有公式人，根据男职工与女职工人数比是公式，可得公式，交叉相乘得公式，公式人。

依据给定的人数比例关系列方程求解女职工人数。

6. 一种混凝土是由水泥、沙子和石子按2:3:5配制而成的。

现在要配制150吨这种混凝土，需要水泥、沙子和石子各多少吨？解析：水泥、沙子和石子的比例为公式，总份数为公式份。

水泥占公式，沙子占公式，石子占公式。

水泥的重量为公式吨，沙子的重量为公式吨，石子的重量为公式吨。

先求出各成分占总量的比例，再根据总量求出各成分的量。

7. 小明和小红的零花钱之比是7:5，如果小明有56元零花钱，小红有多少元零花钱？解析：设小红有公式元零花钱，因为小明和小红零花钱之比是公式，所以公式，交叉相乘得公式，公式元。

六年级数学比应用题

六年级数学比应用题一、简单的比的计算应用题（1 - 5题）1. 已知甲、乙两数的比是3:5，甲数是12，求乙数。

- 解析：- 因为甲、乙两数的比是3:5，设乙数为x，则(甲)/(乙)=(3)/(5)。

- 已知甲数是12，即(12)/(x)=(3)/(5)。

- 根据比例的性质，内项之积等于外项之积，可得3x = 12×5。

- 解得x=(12×5)/(3)=20。

2. 某班男、女生人数比是4:3，男生有24人，女生有多少人？- 解析：- 设女生有x人，因为男、女生人数比是4:3，所以(24)/(x)=(4)/(3)。

- 由比例性质可得4x = 24×3。

- 解得x=(24×3)/(4)=18人。

3. 一种药水是把药粉和水按照1:100的比配成的。

要配制这种药水4040克，需要药粉多少克？- 解析：- 药粉和水的比是1:100，那么药水就是1 + 100=101份。

- 这种药水共4040克，那么一份就是4040÷101 = 40克。

- 药粉占1份，所以需要药粉40克。

4. 学校图书馆里科技书和故事书的比是3:4，科技书有180本，故事书有多少本？- 解析：- 设故事书有x本，因为科技书和故事书的比是3:4，所以(180)/(x)=(3)/(4)。

- 根据比例性质3x=180×4。

- 解得x=(180×4)/(3)=240本。

5. 甲、乙两个数的比是5:6，它们的和是66，求甲、乙两数。

- 解析：- 甲、乙两个数的比是5:6，设甲数是5x，乙数是6x。

- 它们的和是66，则5x + 6x=66。

- 即11x = 66，解得x = 6。

- 所以甲数5x = 5×6 = 30，乙数6x=6×6 = 36。

二、比在几何中的应用题（6 - 10题）6. 一个长方形的长和宽的比是5:3，长是25厘米，宽是多少厘米？- 解析：- 设宽是x厘米，因为长和宽的比是5:3，所以(25)/(x)=(5)/(3)。

苏教版数学六年级下册专项～比例解决问题【含答案】

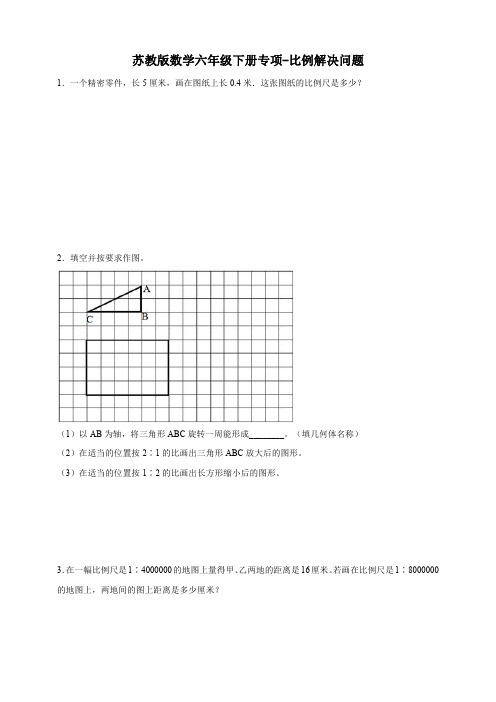
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。

（1）以AB为轴，将三角形ABC旋转一周能形成________。

（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。

（3）在适当的位置按1∶2的比画出长方形缩小后的图形。

3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。

若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。

（1）按3∶1的比画出图形A放大后得到的图形B。

（2）按1∶2的比画出图形B缩小后得到的图形C。

我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。

5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。

（单位：分米）12．根据图中提供的信息，完成下列问题。

（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。

（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。

广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。

乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。

比例的应用题六年级

比例的应用题六年级一、按比例分配问题。

1. 学校把栽70棵树的任务，按照六年级三个班的人数分配给各班，一班有46人，二班有44人，三班有50人。

三个班各应栽树多少棵？- 解析：首先求出三个班的总人数：46 + 44+50=140（人）。

然后计算各班人数占总人数的比例，一班：(46)/(140)，二班：(44)/(140)，三班：(50)/(140)。

最后用树的总数乘以各班所占比例得到各班应栽树的棵数。

- 一班应栽树：70×(46)/(140) = 23（棵）；- 二班应栽树：70×(44)/(140)=22（棵）；- 三班应栽树：70×(50)/(140)=25（棵）。

2. 一种混凝土是由水泥、沙子和石子按2:3:5的比例混合而成的。

如果要配制20吨这种混凝土，需要水泥、沙子和石子各多少吨？- 解析：首先求出总份数：2 + 3+5 = 10份。

然后计算每份的重量：20÷10 = 2吨。

最后根据各自的份数求出水泥、沙子和石子的重量。

- 水泥：2×2 = 4吨；- 沙子：2×3 = 6吨；- 石子：2×5 = 10吨。

3. 某工厂有三个车间，第一车间、第二车间、第三车间的人数比是8:12:21，第一车间比第二车间少80人，三个车间共有多少人？- 解析：设第一车间有8x人，第二车间有12x人。

根据第一车间比第二车间少80人，可列方程12x-8x = 80，解得x = 20。

则三个车间总人数为(8 +12+21)×20=41×20 = 820人。

二、比例尺问题。

4. 在比例尺是1:6000000的地图上，量得A、B两地的距离是5厘米。

一辆汽车以每小时75千米的速度从A地开往B地，需要多少小时？- 解析：根据比例尺公式，实际距离=图上距离÷比例尺，所以A、B两地的实际距离为5÷(1)/(6000000)=5×6000000 = 30000000厘米=300千米。

六年级比应用题及答案

六年级比应用题及答案一、题目：小明和小华共有120本故事书。

小明的故事书数量是小华的2倍。

请问小明和小华各有多少本故事书？答案：设小华有x本故事书，那么小明有2x本故事书。

根据题意，我们可以得到方程：x + 2x = 120。

解方程得：3x = 120，x = 40。

所以，小华有40本故事书，小明有2x = 80本故事书。

二、题目：一个长方形的长是宽的3倍，周长是40米。

求长方形的长和宽。

答案：设长方形的宽为x米，那么长为3x米。

根据周长公式，我们可以得到方程：2(x + 3x) = 40。

解方程得：2(4x) = 40，8x = 40，x = 5。

所以，长方形的宽为5米，长为3x = 15米。

三、题目：一个数的3倍加上4等于这个数的5倍减去6。

求这个数。

答案：设这个数为x。

根据题意，我们可以得到方程：3x + 4 = 5x - 6。

解方程得：3x - 5x = -6 - 4，-2x = -10，x = 5。

所以，这个数是5。

四、题目：一个班级有48名学生，男生人数是女生人数的2倍。

求男生和女生各有多少人？答案：设女生人数为x，那么男生人数为2x。

根据题意，我们可以得到方程：x + 2x = 48。

解方程得：3x = 48，x = 16。

所以，女生有16人，男生有2x = 32人。

五、题目：一个数的1/4加上这个数的1/3等于2。

求这个数。

答案：设这个数为x。

根据题意，我们可以得到方程：(1/4)x +(1/3)x = 2。

解方程得：(3/12)x + (4/12)x = 2，(7/12)x = 2，x = 24。

所以，这个数是24。

六年级关于比例的应用题

六年级关于比例的应用题一、比例应用题。

1. 一辆汽车3小时行驶180千米，照这样的速度，行驶300千米需要几小时？- 解析：首先根据速度 = 路程÷时间，求出汽车的速度。

已知汽车3小时行驶180千米，那么速度为180÷3 = 60（千米/小时）。

设行驶300千米需要x小时，因为速度一定，路程和时间成正比例，所以可列出比例式180:3 = 300:x，即180x=300×3，180x = 900，解得x = 5小时。

2. 用同样的方砖铺地，铺20平方米要320块，如果铺42平方米，要用多少块方砖？- 解析：因为每块方砖的面积是一定的，所以方砖的块数和铺地的面积成正比例。

设铺42平方米要用x块方砖。

可列出比例式20:320 = 42:x，20x=320×42，20x = 13440，解得x = 672块。

3. 配制一种农药，药粉和水的比是1:500。

- 现有水6000千克，配制这种农药需要药粉多少千克？- 解析：药粉和水的比是1:500，设需要药粉x千克，可列出比例式1:500=x:6000，500x = 6000，解得x = 12千克。

- 现有药粉3.6千克，配制这种农药需要水多少千克？- 解析：设需要水y千克，根据比例1:500 = 3.6:y，y=3.6×500 = 1800千克。

4. 学校操场长120米，宽80米，画在比例尺为1:4000的图纸上，长和宽各应画多少厘米？- 解析：因为比例尺=图上距离:实际距离，所以图上距离 = 实际距离×比例尺。

操场长120米=12000厘米，宽80米=8000厘米。

长应画12000×(1)/(4000)=3厘米，宽应画8000×(1)/(4000) = 2厘米。

5. 一个机器零件长5毫米，画在图纸上是4厘米，求这幅图纸的比例尺。

- 解析：首先统一单位，4厘米= 40毫米。

比例尺=图上距离:实际距离=40:5 = 8:1。

比例应用题(专项训练)数学六年级下册人教版

比例应用题（专项训练）20232024学年数学六年级下册人教版典例分析一．工程队修一段公路，原计划每天修4.8千米，18天修完。

实际提前2天修完，实际每天修多少千米？【答案】5.4千米【分析】根据题意可知：工作总量是一定的，工作效率和工作时间成反比例关系，设实际每天修x千米，据此列比例解答。

【详解】解：设实际每天修x千米。

（18－2）x＝4.8×1816x＝86.4x＝86.4÷16x＝5.4答：实际每天修5.4千米。

【点睛】明确工作总量一定，工作效率和工作时间成反比例关系，据此列出比例是解答本题的关键。

典例分析二．如图，学校大门在孔子雕像的正东方240米处。

1号教学楼在孔子雕像北偏东45°的200米处。

（1）分别计算出学校大门、1号教学楼到孔子雕像的图上距离。

（2）在图纸上画出学校大门和1号教学楼的位置。

【答案】（1）学校大门6厘米；1号教学楼5厘米（2）见详解【分析】（1）根据进率“1米＝100厘米”以及“图上距离＝实际距离×比例尺”，分别求出学校大门、1号教学楼到孔子雕像的图上距离。

（2）以图上的“上北下南，左西右东”为准，在孔子雕像的正东方画6厘米长的线段，即是学校大门；在孔子雕像的北偏东45°方向画5厘米长的线段，即是1号教学楼。

【详解】（1）240米＝24000厘米24000×14000＝6（厘米）200米＝20000厘米20000×14000＝5（厘米）答：学校大门到孔子雕像的图上距离是6厘米，1号教学楼到孔子雕像的图上距离是5厘米。

（2）如图：【点睛】本题考查比例尺的应用、根据比例尺画图以及根据方向、角度和距离确定物体的位置。

典例分析三．旗杆有多长？（1）操场上，同学们正在阳光下测量不同长度的竹竿、木棒、大树的长度及它们的影长，测量数据如表：实际长度（米）影长（米）实际长度与影长的比值跟踪训练1．在比例尺是1∶400000的地图上量得甲、乙两地的距离是6厘米。

六年级比例应用题50道含答案难

六年级比例应用题50道含答案难
一、题目
1. 小明有50元，买了一件衣服，价格是30元，小明还剩多少钱？
答案：小明还剩20元。

2. 小红有100元，买了一双鞋，价格是60元，小红还剩多少钱？
答案：小红还剩40元。

3. 小刚有120元，买了一件外套，价格是90元，小刚还剩多少钱？
答案：小刚还剩30元。

4. 小芳有150元，买了一件裙子，价格是100元，小芳还剩多少钱？
答案：小芳还剩50元。

5. 小强有200元，买了一件衬衫，价格是120元，小强还剩多少钱？
答案：小强还剩80元。

6. 小李有250元，买了一条裤子，价格是150元，小李还剩多少钱？
答案：小李还剩100元。

7. 小燕有300元，买了一件外套，价格是180元，小燕还剩多少钱？
答案：小燕还剩120元。

8. 小虎有350元，买了一双鞋，价格是210元，小虎还剩多少钱？
答案：小虎还剩140元。

9. 小龙有400元，买了一件衣服，价格是240元，小龙还剩多少钱？
答案：小龙还剩160元。

10. 小马有450元，买了一件裙子，价格是270元，小马还剩多少钱？
答案：小马还剩180元。

经典习题六年级比的应用57题(有答案)

比的应用题57题（有答案）1.沙、石共36吨，沙与石的比是1：8，沙、石各是多少吨？2.水泥、沙子和石子的比是2：3：5。

要搅拌20吨这样的混凝土，需要水泥、沙子和石子各是多少吨？3.甲、乙两数的平均数是56，甲与乙的比是4：3，甲、乙各是多少？4.一个长方形周长是88cm,长与宽的比是4：7。

长方形的长、宽各是多少厘米？面积是多少？5.等腰三角形的周长是70厘米，一条腰与底边长度的比是3：4，这个三角形的底边是多少厘米？6.用120厘米的铁丝做一个长方体的框架。

长、宽、高的比是3：2：1。

这个长方体的长、宽、高分别是多少？体积是多少？7. 一批图书有1200本，把其中的41分给低年级，余下的按4：5分给中、高年级，低、中、高年级各几本？8. 李惠家8月份共缴纳水费、电费、煤气费140元，其中电费占整个费用的74，水费与煤气费的比是1：3，李惠家水费、电费、煤气费各付多少元？9. 家里的菜地共800平方米，用52种西红柿。

剩下的按2：1的面积比种黄瓜和茄子。

三种蔬菜的面积分别是多少平方米?10.男工有40人，男工与女工的比是4：5，女工有多少人？一共有多少人？（1）如果先称20千克的水果糖，奶糖与软糖各需多少千克？（2）如果先称出15千克的奶糖，水果糖与软糖各需多少千克？12、男工与女工的比是4：5，女比男多4人，男、女各多少人？13、沙和石的比是7：9，沙比石少10吨，沙、石各多少吨？14、一桶油用去的量占剩下的73，已知这桶油共有50千克，用去了多少千克?还剩下多少千克？15、一套西装320元，其中裤子的价格是上衣的53，上衣和裤子的价格各是多少元？16、一个三角形的内角度数比为5：3：2，这个三角形的三个角的度数各是多少？这是一个什么三角形？17、一个长方形的周长是18米，长和宽的比是5：4，这个长方形的面积是多少平方米？18、某校六年级三个班的人数在100－150之间，在学校运动会上，六一班运动员占全年级人数的1/6，六二班占１/8，六三班占１/9，六年级共有多少人？19、商店运来一批电冰箱，卖了18台，卖出的台数与剩下的台数比是3：2，求运来电冰箱多少台？20、学校有足球蓝球共65个，其中足球和蓝球数量比是1：4，今年又买回一些足球，这时足球和篮球数量比是3：４，今年买回足球多少个？21、大母鸡和小母鸡的生蛋数量比是10：9，大母鸡比小母鸡多生２个鸡蛋，求大、小母鸡各生多少个蛋？22、甲乙两人下班回家，甲走的路程比乙多1/5，乙用的时间比甲多1/8，求甲乙两人的速度比23、建筑工地用2份水泥，3份沙子和5份石子配制一种混凝土，要配12吨这种混凝土需要水泥、沙子和石子各多少吨？24、一种混凝土的水泥、黄沙和石子的比是2:3:5,如果有2/5吨的水泥搅拌混凝土，需要黄沙、石子各多少吨？25、三个同学跑步，甲、乙、丙的速度比是4：3：2.甲跑了600米，乙比丙多跑多少米？26、工地用100千克水泥、150千克沙子、250千克石子配制一种混凝土。

小学六年级正反比例的应用题含答案

小学六年级正反比例的应用题含答案1、用同样的方砖铺地，铺20平方米要320块，如果铺42平方米，要用多少块方砖？2、一间教室，用面积是0.16平方米的方砖铺地，需要275块，如果用面积是0. 25平方米的方砖铺地，需要方砖多少块？3、建筑工地原来用4辆汽车，每天运土60立方米，如果用6辆同样的汽车来运，每天可以运土多少立方米？4我国发射的人造地球卫星绕地球运行3周约3.6小时，运行20周约需多少小时？5、一种铁丝，7.5米长重3千克，现在有19.5米长的这种铁丝，重多少千克？6、汽车在高速公路上3小时行240千米，照这样计算，5小时行多少千米？7、修一条公路，4天修了200米，照这样计算，又修了6天，又修了多少米？8、小明读一本书，每天读12页，8天可以读完。

如果每天多读4页，几天可以读完？9、今春分配给学校一些植树任务，每天栽200棵6天可以完成任务，现在需要4天完成任务，实际每天比原计划多栽多少棵？10、农场用3辆拖拉机耕地，每天共耕225公顷，照这样速度，用5辆同样拖拉机，每天共耕地多少公顷？11、一艘轮船，从甲地从开往乙地，每小时航行20千米，12小时到达，从乙地返回甲地时，每小时多航行4千米，几小时可以到达？12、100千克黄豆可以榨油13千克，照这样计算，要榨豆油6.5吨，需黄豆多少吨？13、学校计划买54张桌子，每张30元，如果这笔钱买椅子，可以买90张，每张椅子多少钱？14、一对互相咬合的齿轮，主动轮有20个齿，每分钟转60转，如果要使从动轮每分钟转40转，从动轮的齿数应是多少？15、把3米长的竹竿直立在地面上，测得影长1.2米，同时测得一根旗杆的影长为4.8米，求旗杆的高是多少米？16、一个机器零件长5毫米，画在图纸上是4厘米，求这幅图纸的比例尺。

（5分）17、地图上的26厘米，在比例尺为1∶1300000的地图上约是多少千米？（5分）18、李师傅计划生产450个零件，工作8小时后还差330个零件没有完成，照这样速度，共要几小时完成任务？19、用一批纸装订同样的练习本，如果每本30页，可以装订80本。

人教版六年级下册数学第四单元比例应用题专题训练(带答案)

人教版六年级下册数学第四单元比例应用题专题训练1．把一个长方形养鱼池按1：200 的比例尺画在图纸上，长是4d m，宽是3dm。

这个养鱼池的实际占地面积是多少平方米?2．两个互相咬合的齿轮，大齿轮有60个齿，每分钟转80圈，小齿轮有20个齿，每分钟转多少圈？3．一架飞机所带的燃料最多可以飞行6小时，飞机去时顺风，每小时可以飞行1500 km，返回时逆风，每小时可以飞行1200 km。

这架飞机最多能飞行多少千米就需要返回？4．制一批零件，甲单独完成要8小时，已知甲、乙的工作效率比是4：3，则乙单独完成要多长时间？5．有种钢管长6 m，把它锯成50 cm的小段，要锯44分钟，照这样计算，如果把它锯成40 cm的小段，要锯多少分钟？6．王大爷种了一块直角三角形的菜地，两条直角边共长10.8 m，它们的长度比是5：4。

将这块菜地用1：200的比例尺画在图上，这块菜地的图上面积是多少平方厘米？7．在比例尺为1 ：9000000的航空图上，甲、乙两地相距30cm，有两架飞机同时从甲、乙两地起飞，分别以810km/h和690km/h的速度相向飞行，经过几小时两架飞机在空中相遇？8．在比例尺是1：2500000的地图上，量得A、B两地相距12厘米。

如果李叔叔和王叔叔开车同时从两地相对出发，李叔叔开车每小时行105千米，王叔叔开车每小时行95千米，几小时后两人能相遇？9．为了加快推进美丽乡村建设，某工程队铺一条乡村公路，原计划每天铺320m，15天铺完。

实际施工时，由于改进了铺路方法，前4天就铺了1600m。

照这样计算，该工程队可以比原计划提前几天完成铺路任务？(用比例解答)10．一间房子用方砖铺地，如果用边长4分米的正方形地砖一共需要360块；如果改用边长为6分米的正方形地砖来铺，一共需要多少块？11．爸爸暑假准备开车带小明去上海迪士尼玩，他在一幅比例尺是1：4000000的中国地图上量得台州到上海的距离大约是8.5cm，如果爸爸开车平均每小时行驶85km，多少小时能到达？12．一间房子要用方砖铺地，用边长3分米的方砖，需要96块；如果改用边长是2分米的方砖，需要多少块？（用比例知识解答）13．在一幅比例尺是1∶5000000 的地图上，量得A地和B 地相距6 厘米。

六下数学正比例与反比例应用题训练30题带答案

则第二次相遇时，汽车经过的路程为：x+x-130=2x-130 摩托车经过的路程为：x+130
相同时间内，路程和速度成正比例，速度之比=路程之比
（2x-130）：（x+130）=3:2 解得x=650
8、一辆卡车与一辆小轿车同时从甲、乙两城相对开出，相遇后两车继续向前行驶．当小轿车到达甲地、卡车到达乙地后．立即返回，第二次相遇点距甲城120千米，已知：卡车与小轿车的速度比是3 ：4，甲、乙两城相距多少千米？
13、用方砖铺一间教室的地面，如果用边长为2dm的方砖，需要用60块，如果改用边长为3dm的方砖，需要用多少块？ 27块解析：解设需要用x块砖教室的面积一定，所用的方砖的块数和每块方砖的面积成反比例
2×2×60=3×3×x 解得 x=80/3 进一法，所以需要27块
14、有甲乙丙三个相互咬合的齿轮，当甲齿轮转动2圈时，乙齿轮转动3圈，丙齿轮转动4圈，这三个齿轮的齿数之比是（）：（）：（）。 6：4：3 解析：相互咬合的齿轮转动的总齿数是相同的，那么一圈的齿数和转动的圈数是成反比例的，设三个齿轮的齿数分别为x y z 则2x=3y=4z 得x：y ：z=6：4：3
16、学校组织同学参观爱国主义纪念展，每60名同学配2
X=18
4、某修路队修一条公路，前6天修了180米，照这样的速度，修路队又修了5天才全部修完，这条公路全长是多少米？
解设这条公路的全长是x米每天修的长度一定，路的全长和时间成正比例关系 180:6=x:(6+5)
X=330
5、甲乙丙三人进行200米赛跑（他们的速度保持不变），甲到终点时，乙还差20米，丙离终点还有25米，问乙到达终点时，丙还差多少米？
解设：甲乙两城相距x千米则第二次相遇时，卡车经过的路程为：x+x-120=2x-120 小轿车经过的路程为：x+120

人教版六年级下册数学第四单元比例应用题训练(含简单答案)

人教版六年级下册数学第四单元比例应用题训练1．曲港高速公路（曲阳至黄骅港）是河北省“东出西联”出海通道，其定州段连通京昆和京港澳高速，填补安国、博野两地无高速公路的空白，项目建设里程约为92千米，在一幅1∶4000000的地图上，这条高速公路的长度是多少？2．一个骑兵俑模型身高是18厘米，模型高度与实际高度的比是1∶10。

这个骑兵俑的实际身高是多少？（用比例解）3．在的地图上量得甲乙两地的距离是4厘米，甲乙两地的实际距离是多少？把它画在1∶4000000的地图上应画多长？4．在一幅比例尺为1∶2000000的地图上，量得甲乙两地之间的公路长10厘米。

一辆汽车和一辆货车从两地同时出发相向而行，汽车以每小时55千米的速度行驶，2小时后在超过中点10千米的地方相遇。

货车每小时行多少千米？5．在比例尺1∶4000000的地图上，量得天津到北京的距离是3厘米。

一辆汽车以每小时60千米的速度从天津开往北京，几小时能到达？6．一种药水，药液与水的比是1∶180，如果配制905千克的药水，需要药液多少千克？（用比例解）7．学校把制作爱心贺卡的任务按5∶4分配给六年级和五年级。

六年级实际制作了108张贺卡，超过原分配任务的20%，原计划五年级制作多少张爱心贺卡？8．小红去银行换港币，当天人民币与港币的兑换比是1∶1.25，小红要兑换1000元港币，她需要给银行多少元人民币？（用比例解）9．某市修一条道路，计划每天修120米，8天可以修完。

但因为天气原因，12天才完成任务，实际每天修多少米？（用比例方法解）10．一列动车从A城开往B城前3小时行了540千米，照这样的速度，动车还要行驶4小时才能到达B城，A城和B城相距多远？（用比例的方法解答）11．小明和小英住在同一个小区、小明家上个月用电102度，电费是61.2元。

小英家上个月用电85度，小英家上个月的电费是多少元？（用比例知识解答）12．小东家的客厅是正方形的，用边长0.6m的方砖铺地，正好需要100块。

六年级比例的应用题及答案

六年级比例的应用题及答案篇一：六年级数学按比分配应用题及答案】>1、把300 本作业按4∶5∶6 分给四、五、六年级的同学，四、五、六年级的同学各得多少本作业本？解：4＋5＋6＝15答：四年级得80 本，五年级得100 本，六年级得120 本。

2、一种生理盐水是把盐水和水按照1∶ 100 配制而成，要配制这种生理盐水5050 千克，需要盐水多少千克？解：1＋100＝101答：需要盐水50 千克。

答：山羊和绵羊一共有140 头。

4、一种石灰水是用石灰和水按1∶ 100 配成的，要配制5656 千克的石灰水，需石灰多少千克？解：1＋100＝101 答：需石灰56 千克。

5、体育室有200 根跳绳，按人数分配给六年级一、二两个班，一班有52 人，二班有48 人，两个班各得跳绳多少根？解：52 ＋48＝100 （人）答：一班可得跳绳104 根，二班可得跳绳96 根。

6、一个分数，它的分子和分母的和是40, 分子和分母的比是4∶ 6 ，这个分数是几分之几？解：4＋6＝10 答：这个分数是24 分之16。

7、一种药水是用药粉和水按 1 ∶80 配制成的。

⑴、40 千克药粉，可配制成多少千克的药水？3200 ＋40＝3240 （千克）答：40 千克药粉，可配制成3240 千克的药水。

⑵、60 千克水，需要药粉多少千克？答：60 千克水，需要药粉0.75 千克。

⑶、配制这种药水1620 千克，需要药粉多少千克？解：1＋80＝81答：配制这种药水1620 千克，需要药粉20 千克。

8、把96 分米长的铁丝焊成一个长方体框架，长、宽、和高的比是3∶2∶1，这个长方体的体积和表面各是多少？3＋2＋1＝6答：这个长方体的体积是384 立方分米，表面是352 平方分米。

9、五年级有140 人，六年级有130 人，从六年级调多少人到五年级，才能使五年级、六年级的人数比为5∶1？解：140 ＋130 ＝270 （人）5＋1＝6130 －45＝85（人）答：从六年级调85 人到五年级。

六年级比例奥数题及答案

六年级比例奥数题及答案六年级比例奥数题及答案 11、李明的爸爸经营个水果店，按开始的定价，每买出1千克水果，可获利0.2元。

后来李明建议爸爸降价销售，结果降价后每天的销量增加了1倍，每天获利比原来增加了50%。

问：每千克水果降价多少元?答案：设以前卖出X千克降价a元。

那么0.2X×(1+0.5)=(0.2-a)×2x则0.1X=2aXa=0.05答：每千克水果降价0.05元2、有5个小朋友，每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子.请你证明，这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。

解析与答案：首先要确定3枚棋子的颜色可以有多少种不同的情况，可以有：3黑，2黑1白，1黑2白，3白共4种配组情况，看作4个抽屉。

把每人的3枚棋作为一组当作一个苹果，因此共有5个苹果。

把每人所拿3枚棋子按其颜色配组情况放入相应的抽屉。

由于有5个苹果，比抽屉个数多，所以根据抽屉原理，至少有两个苹果在同一个抽屉里，也就是他们所拿棋子的颜色配组是一样的。

六年级比例奥数题及答案 2猎狗发现在离它10米的前方有一只奔跑着的兔子，马上追上去，兔跑9步的路程狗只需跑5步，但狗跑2步的时间，兔却跑3步。

问狗追上兔时，共跑了多少米路程?答案与解析：60米对于追及问题，我们知道：10米=速度差×追及时间狗追上兔时，所跑路程应为：总路程=狗的速度×追及时间这就是要弄清狗的速度与兔的速度差之间的倍数关系。

另一方面，在分析速度时，一定是相同时间内狗与兔的速度之间的倍数，而不是相同的步数或相同的路程。

只要分析清楚这些，就可以解出本题了。

详解1：为了看相同时间的路程关系，也就是速度关系，我们进行如下处理：狗跑2步的时间兔跑3步，则狗跑6步的时间兔子跑了9步，也就是兔子跑了狗的5步，那么在这段时间内，狗追上了兔子，狗的一步或狗兔间的距离缩短了狗的1步，而狗跑了6步，所以狗的速度是速度差的6倍。

人教版六年级下册数学第四单元比例应用题训练

人教版六年级下册数学第四单元比例应用题训练1．聪聪用240毫升的酸梅原汁加500毫升水调制了酸梅汤。

妈妈说，当酸梅原汁和水的比是3∶7时，口感最佳。

为了使调制的酸梅汤口感最佳，聪聪应再往酸梅汤中加水多少毫升?2．在比例尺是1∶5000000的地图上，量得甲、乙两地的距离是25厘米。

客车和货车同时从甲、乙两地相对开出，货车平均每时行驶80千米，货车和客车的速度比是2∶3，几时后两车相遇?3．小马骑自行车从家里到书店一共用了20分钟，每分钟行160米；返回时每分钟行100米，返回时用了多少分钟？（用比例解）4．一张精密零件图纸的比例尺是40：1，在图纸上量得零件的长是18厘米。

这个零件实际长多少毫米？5．一辆汽车的模型与实际长度的比是1：30，如果模型的长是15cm，汽车的长是多少米？（用方程解）6．海滨市计划修一条迎宾路，4天修了328米。

照这样计算，这条迎宾路一共修了20天，这条迎宾路全长是多少米？（用比例解）7．在比例尺1：20000000的地图上，量得甲、乙两地长4.2厘米，一辆客车分两天按3：4行完全程。

这辆客车第二天行了多少千米？8．甲地到乙地的公路全长225千米，2小时行驶90千米。

照这样计算，行驶完全程一共要多少小时？9．小华看一本书，4天看了48页。

照这样计算，他看完一本192页的书，需要多少天？10．甲、乙、丙三人跑200米（假设三人速度一定），甲到达终点时，乙距终点还有20米，丙距终点还有29米。

当乙到达终点时，丙距终点还有多少米？（用比例解）11．甲、乙两个仓库原有货物的质量比是6：5，后来甲仓库运出16吨货物，乙仓库运进4吨货物，这时甲、乙两个仓库货物的质量比是10：9。

原来甲、乙仓库各有多少吨货物？12．在比例尺是1：5000的图纸上，画一个长为5厘米宽为4厘米的长方形草坪，草坪的实际面积是多少平方米？13．北京的世界公园里有一座埃菲尔铁塔的模型，高度是32m。

与原塔高度的比是1：10。

小学六年级比例应用题及答案

小学六年级比例应用题及答案【篇一：人教版六年级数学《比例》试题及答案】一、填一填1、（）叫做比例。

2、在一个比例中，两个内项正好互为倒数，已知一个外项是3、北京到天津的实际距离是120千米，在比例尺是2，则另一个外项是（）。

51的地图上，两地的图上距离是（）厘米。

50000004、如果2a=3b，那么a:b=（）:（）。

5、用12的因数中的任意四个数组成一个比例是（）。

6、 3：（）=6：10=（）：357、在总价、单价和数量三种量中，当（）一定时，（）与（）成正比例当（）一定时，（）与（）成正比例当（）一定时，（）与（）成反比例8、配置一种淡盐水，盐占盐水的119，盐与水的比是（）。

二、判断对错1、如果甲数是乙数的15（甲、乙均不为0），甲与乙的比是1：5。

（）。

2、用同样的方砖铺地，铺地面积与方砖块数成反比例。

（）3、一项工程，甲独做要10小时，乙独做要8小时，甲、乙工作效率的之比是（）4、圆的面积与它的半径成正比例关系。

（）5、求比例中的未知项，叫做解比例。

（）6、一幅地图的比例尺是1：500000m。

（）三、选一选，将正确答案的序号填在括号里。

1、一个加数一定，和与另一个加数（）。

a、成正比例 b成反比例c不成比例2、出粉率一定，面粉质量与小麦质量成（）a、成正比例 b成反比例c不成比例3、在一副平面图上，用图上距离2cm表示实际距离200m,这幅图的比例尺是（）a、1：100b、 1：1000c 1：100005：4 14、按1：5将长方形缩小，就是将长方形的面积缩小到原来的（）a、111b、c、 525105、用3、4、16、12四个数组成比例，正确的是（）a、3：16=4：12b、3：4=12：16c、16：12=4：3四、算一算，解比例 x:10=11123: 0.4:x=1.2:2 = 432.4x五、画一画，操作题。

学校要建一个长100m,宽60m的长方形操场用1：1000的比例尺画出操场的平面图。

六年级比例应用题及答案

六年级比例应用题及答案题目：小明和小华在公园里比赛跑步，小明跑了全程的1/3，小华跑了全程的1/4。

如果小明跑了300米，那么小华跑了多少米？答案：1. 分析：首先，我们需要确定小明和小华跑步的比例关系。

题目中提到小明跑了全程的1/3，小华跑了全程的1/4。

2. 计算：已知小明跑了300米，这代表了全程的1/3。

我们可以通过除法计算出全程的距离。

全程距离 = 小明跑的距离 / 小明跑的比例全程距离 = 300米 / (1/3)3. 计算全程距离：全程距离 = 300米 * 3全程距离 = 900米4. 求小华跑的距离：现在我们知道了全程的距离，我们可以计算小华跑了多少米。

小华跑了全程的1/4。

小华跑的距离 = 全程距离 * 小华跑的比例小华跑的距离 = 900米 * (1/4)5. 计算小华跑的距离：小华跑的距离 = 900米 / 4小华跑的距离 = 225米6. 结论：所以，小华跑了225米。

题目：一个班级有60名学生，其中男生人数是女生人数的2倍。

如果男生人数增加了10人，那么男生和女生的人数比是多少？答案：1. 分析：题目中提到男生人数是女生人数的2倍，我们设女生人数为x，那么男生人数就是2x。

2. 计算：已知班级总人数为60人，可以建立方程：男生人数 + 女生人数 = 总人数2x + x = 603. 解方程：3x = 60x = 60 / 3x = 20所以，女生人数为20人，男生人数为2 * 20 = 40人。

4. 男生人数增加：题目中提到男生人数增加了10人，那么男生人数变为40 + 10 = 50人。

5. 求男生和女生的人数比：现在男生人数为50人，女生人数为20人。

男生和女生的人数比 = 男生人数 : 女生人数男生和女生的人数比 = 50 : 206. 简化比例：男生和女生的人数比 = 5 : 27. 结论：男生和女生的人数比是5:2。

题目：一个果园里有苹果树和梨树，苹果树的数量是梨树的3倍。

小学数学六年级上学期比的应用题30题带答案

19、工程队修一条路，上半月修好的米数与全长的比是1：5 ．如果再修360米，就正好修了这条路的一半．这条路全长多少米？
360÷（1/2-1/5）=1200（米）
20、一堆煤，第一天运走的吨数与总吨数的比是1：3，第二天运走4.5吨后，两天正好运走了总数的一半，这堆煤有多少吨？
4.5÷（1/2-1/3）=27（吨）
45÷3×（3+4）=105（千米）
10、医院的消毒酒精是由纯酒精和蒸馏水按3：1的比例配制而成的，现在有600克纯酒精，需要加入多少克蒸馏水？
600÷3×1=200(克)
11、甲、乙、丙三堆苹果共重280千克，甲堆苹果与乙堆苹果的质量比是3：4，乙堆苹果与丙堆苹果的质量比是6：7，三堆苹果的质量各是多少千克？
甲：乙：丙=9:12:14 甲：280÷（9+12+14）×9=72（千克）乙：280÷（9+12+14）×12=96（千克）丙：280÷（9+12+14）×14=112（千克）
12、一种饮料中橘汁与白糖的比是2:1，白糖和矿泉水的比是1:9，现在有60千克这种饮料，其中橘汁，白糖，与矿泉水各有多少千克？
21、两个厂在一月内生产的服装比为6：5，两种价格比为11 ：10，总产值为6960元，两个工厂的产值各为多少元？
1份：5050÷（1+100）=50（毫升）浓缩液：1×50=50（毫升）水：50×100=5000（毫升）
3、三个车间一共要生产零件1288个，第一车间有16人，第二车间有18人，第三车间有22人。按人数分配任务，三个车间各应生产多少个零件？
1份：1288÷（16+18+22）=23（毫升）第一车间：16×23=368（个）第二车间：18×23=414（个）第三车间：22×23=506（个）

六年级数学按比分配应用题及答案

六年级数学按比分配应用题及答案1.将300本作业按照4:5:6的比例分配给四年级、五年级和六年级的同学，每个年级分别得到80本、100本、120本作业本。

2.假设一种生理盐水是将盐水和水按照1:100的比例配制而成的。

需要配制5050千克这种生理盐水，那么需要多少千克的盐水？答案是50千克。

3.山羊和绵羊的头数比是2:5，山羊有40头。

那么山羊和绵羊的总头数是多少？答案是140头。

4.假设一种石灰水是将石灰和水按照1:100的比例配制而成的。

需要配制5656千克这种石灰水，那么需要多少千克的石灰？答案是56千克。

5.体育室有200根跳绳，需要按照人数分配给六年级一班和二班。

一班有52人，二班有48人。

那么一班和二班各得多少根跳绳？答案是一班得到104根跳绳，二班得到96根跳绳。

6.一个分数，它的分子和分母的和是40，分子和分母的比是4:6.那么这个分数是多少？答案是24/16.7.假设一种药水是将药粉和水按照1:80的比例配制而成的。

⑴如果有40千克的药粉，那么可以配制多少千克的药水？答案是3240千克。

⑵如果有60千克的水，那么需要多少千克的药粉？答案是0.75千克。

⑶如果需要配制1620千克的这种药水，那么需要多少千克的药粉？答案是20千克。

8.将96分米长的铁丝焊成一个长方体框架，长、宽、高的比例是3:2:1.那么这个长方体的体积和表面积分别是多少？答案是体积为384立方分米，表面积需要计算。

解析：1.第一段：没有明显格式错误，但是可以将“答”和“解”两个字加粗或者改为标题格式更加清晰。

改写如下：题目：长方体的体积和表面积答案：这个长方体的体积是384立方分米，表面积是352平方分米。

2.第二段：没有明显格式错误。

3.第三段：没有明显格式错误。

4.第四段：没有明显格式错误。

5.第五段：没有明显格式错误。

6.第六段：没有明显格式错误。

7.第七段：没有明显格式错误。

8.第八段：没有明显格式错误。