张量概念及其基本运算讲课讲稿
张量的运算方法

张量的运算方法**标题:张量的运算方法****一、引言**在许多数学和科学领域中,张量是一个重要的概念,它是一种多维数组,可以用于表示更复杂的数据结构。
张量的运算方法在数学、物理、计算机科学等领域中有着广泛的应用。
本篇文章将介绍张量的基本概念、运算规则以及一些常见的张量库。
**二、张量的基本概念**张量是一个可以表示任意维数数组的概念,它可以是一阶张量、二阶张量、高阶张量等。
在实际应用中,通常需要用到更高阶的张量,因为它们可以更好地表示复杂的数据结构。
**三、张量的基本运算**1. **标量与张量的乘法**:标量与一阶张量相乘,等同于将标量加在一阶张量上。
对于二阶或更高阶的张量,需要将标量与每一行或每列的对应元素相乘再相加。
2. **矩阵与张量的乘法**:矩阵与一阶或二阶张量相乘时,其结果为对应元素相乘后加在一阶或二阶张量的结果。
对于更高阶的张量,矩阵的乘积并不总是存在,取决于矩阵是否是子式的主对角线对称的幂。
3. **向量与张量的点积**:一维向量与一阶或二阶张量相乘,其结果为一维向量中每个元素与对应元素相乘后的和。
4. **张量的加法和减法**:同维度的张量可以相加或相减,执行这些操作时,需要考虑数据的一致性。
5. **张量的转置**:对于二阶或更高阶的张量,其转置是将主对角线上的元素与另一侧的对应元素交换位置。
对于一阶和二阶张量,转置操作还可以通过矩阵乘法实现。
6. **张量的共轭**:对于复数张量,可以通过取共轭来改变其复数元素的符号。
**四、常见张量库介绍**在Python中,有许多库可以用于处理和操作张量。
其中最常用的包括NumPy、TensorFlow和PyTorch等。
这些库提供了丰富的函数和方法来进行张量的创建、操作和运算。
**五、实例分析**以下是一个简单的例子,展示如何使用NumPy库进行一维张量的运算:```pythonimport numpy as np# 创建一个一维张量tensor = np.array([1, 2, 3])print("原始一维张量:", tensor)# 对一维张量进行加法和乘法运算result_add = tensor + 2 # 加法运算result_mul = tensor * 3 # 乘法运算print("加法运算结果:", result_add)print("乘法运算结果:", result_mul)```此外,我们还可以使用TensorFlow或PyTorch库来进行更高级的张量运算,例如矩阵乘法、向量化操作等。
《张量基础知识》课件

线性变换是指一个向量到另一个向量的映射,保持向量的加法和数乘运算。
3 奇异值分解(SVD)
奇异值分解是将矩阵分解为三个矩阵乘积的形式,被广泛应用于数据降维和信号处理。
总结
1 张量的概述
2 张量的运算和应用
张量是一种多维数组,用于表示和处理多 维数据。
《张量基础知识》PPT课 件
# 张量基础知识
什么是张量?
1 张量的定义
张量是一种多维数组, 用于表示和处理多维数 据。它具有多个轴和形 状,可以存储和计算多 维数据。
2 张量的基本特征
张量具有数据类型、维 度和形状。它可以是标 量、向量、矩阵或更高 维度的数组。
3 张量的分类
张量根据维度和形状的 不同可以分为标量、向 量、矩阵和高阶张量。
2 张量的象性
3 张量的幺模性
张量的象性描述了张量 在基向量变换下的行为。 张量的象性可以用来研 究线性变换和坐标变换。
张量的幺模性表示张量 在坐标变换中的不变性。 幺模张量在物理和拓扑 学中具有重要应用。
张量的相关概念
1 秩(rank)
秩是张量的非零元素的个数。秩为0的张量是标量,秩为1的张量是向量。
张量具有丰富的运算和广泛的应用,涵盖 物理学、数学和机器学习等领域。
3 张量的性质和相关概念的介绍
4 知识点总结
张量具有特定的性质和相关概念,如对称 性、象性和幺模性。
总结张量基础知识的关键概念和要点。
Q&A
1 相关问题解答
回答听众提出的与张量基础知识相关的问题。
2 课程结束
感谢听众参与本次张量基础知识课程, 张量乘法
张量加法是对应位置元素的相加操作。两 个形状相同的张量可以直接相加。
张量分解学习PPT课件

.
26
CP分解
张量的低秩近似
◦ 然而在低秩近似方面,高阶张量的性质比矩阵SVD差
Kolda给出了一个例子,一个立方张量的最佳秩-1近似并不 包括在其最佳秩-2近似中,这说明张量的秩-k近似无法渐进 地得到
下面的例子说明,张量的“最佳”秩-k近似甚至不一定存在
X a1ob 1oc2a1ob2oc1a2ob 1oc1
纤维:x i j :
.
6
基本概念及记号
切片(slice)
水平切片:X i : :
侧面切片:X : j :
正面切片:X ::k ( X k )
.
7
基本概念及记号
内积和范数
◦ 设 X,Y¡I1× I2× L× IN
内积:
I1 I2
IN
X,Y
L x y i1i2LiN i1i2LiN
i11i21 iN1
R
X§A,B,C¨arobrocr r1
X
c1 b 1
c2 b2
L
cR b R
a1
a2
aR
三阶张量的CP分解
.
20
CP分解
CP分解的矩阵形式
◦ 因子矩阵:秩一张量中对应的向量组成的矩阵,如
A a 1 a2 LaR
◦ 利用因子矩阵,一个三阶张量的CP分解可以写成展开形式
X (1) A C e B T X (2) B C e A T X (3) C B e A T
◦ 对于高阶张量,有
X ┈ λ ;A (1 ),A (2 ),L ,A (N ) Rra ( r 1 )o a ( r 2 )o L o a ( r N ) r 1
其展开形式为
X ( n ) A ( n ) d i a g ( λ ) A ( N ) e L e A ( n 1 ) e A ( n 1 ) e L e A ( 1 )T
【张量分析ppt课件】张量分析课件第三章 张量代数

按§2.5节三中(g)式面积矢量记法有:
dH 0 r u(r ) (r )dV
试证明物体 Ω 对o点的动量矩为:
H0 J ω
Ω
式中 称为物体 Ω 对o点的二阶惯性矩张量(注:J 不是四阶单位张量。但 J表达式中的 I是二阶单位张量)。 u (r ) ω r 证: H (r u) dV r (ω r ) dV (r r )ω (r ω)r ) dV
I u (ii ii ) (u j i j ) u j iiij ui ii u
设存在另一二阶张量 I ,且满足 u I I u 。则: u I u I o ; uo ∵ I I O ; I I (唯一性) ∴ 3.
A : J ( Amn imin ) : (ii i j ii i j ) Amnmi jn ii i j Amn imin A
二阶张量与二阶张量的(一)点乘:
A B (Aij ii i j) ( Bmn imin) (Aij Bmn )ii (i j im )in Aij Bjn ii in
二阶张量与二阶张量的(双)点乘:
A : B ( Aij ii i j ) : ( Bmn imin ) ( Aij Bmn )(ii im )(i j in ) Aij Bij
A P2 A P2
A0 P2 Φ0 P4
Φ0 P4
(3.1-11)
A : Φ0 A
0 0
的 n ; A ; A ; ; 分别称为一阶单位张量、二阶单位张量和四 阶单位张量。 上式定义的一阶、二阶和四阶单位张量具有性质: u u V n 1. u A0 A0 ii ii ij ii i j (3.1-12) 2. I 为单位二阶张量。 ii i j 且记 A ; A 为 I 。即 I ii ii ij。并称
张量定义(知识讲座)

§1 张量的定义张量:在三维笛卡儿〔Descartes〕坐标系中,一个含有三个与坐标相关的独立变量集合,通常可以用一个下标表示。
例如,对于位移分量u,v,w可以表示为u1,u2,u3,缩写记为u i,i=1, 2, 3。
对于坐标x,y, z可以表示为x i。
对于一个含有九个独立变量的集合,可以用两个下标来表示。
例如九个应力分量或应变分量〔由于对称,实际独立的仅有六个〕可以分别表示为σij和εij,其中σ11 , σ22分别表示σx, σxy〔就是τxy);ε11 , ε22分别表示εx,εxy(〕等。
同样,一个含有27个独立变量的集合可以用三个下标表示;而含有81个独立变量的集合可以用四个下标表示,依次可以类推。
为了给张量一个确切的定义,首先讨论矢量定义。
在坐标系Ox1x2x3中。
矢量OP的三个分量ζ 1, ζ 2,ζ3可以缩写作ζ i,同一矢量OP在新坐标系Ox'1x'2x'3中,写作ζ '1,ζ '2,ζ '3,缩写为ζ'i。
设坐标系Ox1x2x3与Ox'1x'2x'3的夹角方向余弦如下表所示方向余弦n i'j的第一下标对应于新坐标轴,而第二下标对应于原坐标轴。
则矢量在新老坐标系中的关系为或者上式可以缩写为或者。
a2, a3)和OP(ζ1, ζ2, ζ3),作它们的标量积,则考察矢量A(a1,显然,此标量积与坐标轴的选取无关,如果上述矢量作坐标变换,则反之,如ζ ' 为已知矢量,而a i为与坐标有关的三个标量,使一次形式在坐标变换时保持不变。
根据矢量定义,则a i 也是矢量。
推广上述的命题,可以给张量一个解析的定义。
设(ζ 1, ζ 2, ζ3)和(η 1, η 2, η3)是矢量,a ij是与坐标有关的九个量,假设当坐标变换时,双一次形式保持不变,则称由两个下标i,j确定的九个量的集合a ij为二阶张量。
张量分析课件-1.7 张量的代数运算
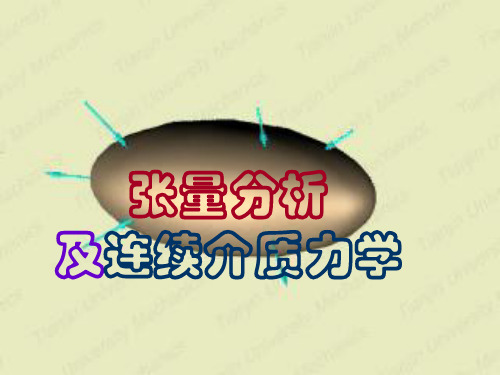
且 T ij S ij U ij ,
1.7.3 标量与张量相乘
若kT=U,则
kT ij U ij ,
且 kT ij U ij ,
张量相减:T-S=T + (-1)S
1.7.4 张量与张量并乘
若T,S 分别是m阶和n阶张量,则TS=U是m+n 阶张量。 U的分量指标的前后顺序和上下位置都与TS 的指标顺序和 上下位置相一致。例如
·
k l rs t ij rs l k t T S Tij g g g g S g g g T S δ g g g g g kl i j t r s kl t r i j s ls k t ij s k t Tij S g g g g g V g g g g g V kl t i j s k t i j s
·
S T T
·
ij kl
l k ij k i k gi g j g k g l Tij δ g g T g g S g g kl j i kj i k i
·
1.7.6 张量的点积
点积:若T,S分别是m阶和n阶张量,则 阶张量。例如: ·
TS U 是m+n-2
·
设S是T的转置。则有 1 A T S 为对称张量; 对称化运算: 2 1 反对称化运算: B T S 为反对称张量。 2
1.7.9 张量的商法则
设有一组数的集合(例如T(i, j, k, l, m)),如 果它满足对于任意一个q阶张量S(例如q=2,二阶张
量Slm)的内积均为一个p阶张量(例如p=3,三阶张量 Uijk),即在任意坐标系内以下等式均成立
t
张量定义及算法

1
可乘张量
设由逆变分量和协变分量所给定的两个矢量 a , b 是已知的,则由等式
i T ik a i b k , Tik ai bk , T.k a i bk , Tki ak b i
确定的都是二阶张量,称为可乘张量. 2
克罗内克尔符号
克罗内克尔符号 ij 是一阶逆变一阶协变的二阶混合张量,这是
[张量的商律] 任一指标 jk, j k' 使
' ' 1 m
k Tlm ail a jmT ijk , Tlmp ail a jm akpT ijk
i1 il il i i i 设 Tji11 jm 和 Tj ' j ' 各为一组 x 和 x 的函数,如果对任意逆变矢量 与 及
因为从
x i x i ij i j x x
可得
ij
x i x i x i x j i j x i x j x i x j
[二阶对称张量与反对称张量]
若张量满足等式
Tik Tki , T ik T ki , Tki Ti k
则分别称为二阶对称协变张量、二阶对称逆变张量和二阶对称混合张量.若张量满足等式
i
x j1 x jl x i1 x im j1 jl j j T i1im x 1 x l x i1 x im
N
j1 jl i1 im
jl 是 x i 的函数, 则量 Ti1j1 im (共有 n 个分量)称为 l 阶逆变(或抗变)m
r1 rl s1 s k r1 rl s1 s k Tp p t t T p p Tt t
1 m 1 h 1 m 1 h
《张量分析本科》课件
2
流体力学
流体力学中的张量可描述液体和气体的流动性质,从而帮助工程师设计和优化流体系 统。
3
材料科学
张量在材料的力学行为、热膨胀和磁性等方面的研究中起着重要作用,有助于材料性 能的改进。
经济学中的张量应用
金融风险评估 市场分析 关联性, 对风险评估和投资决策具有重要意义。
《张量分析本科》PPT课 件
这个课程将介绍张量的定义、基本概念、运算和性质,以及它在物理学、工 程学和经济学等领域的应用。
张量的定义和基本概念
张量是一个多维数组,具有特定的变换规律。它在数学和物理学中扮演着重 要角色,能够描述物体在各个方向上的变化。
张量的运算和性质
张量可以进行加法、乘法等运算,还具有一些特殊的性质,如对称性、反对称性和行列式等。这些运算 和性质是研究和应用张量的基础。
学科交叉
张量分析作为一门综合性学科, 促进了不同学科之间的交流与 合作,推动了学科发展的跨越 性进展。
学习资源推荐
1 书籍和教材推荐
2 网上教程和视频
《张量分析导论》、《张量分析教程》等 是学习和研究张量分析的重要参考资源。
有许多免费的网上教程和视频,可以帮助 初学者快速入门和掌握张量分析的基本概 念和应用。
张量在市场需求、价格和产量之间的关系分 析中,能够提供深入洞察和科学决策支持。
张量分析可以用于挖掘大规模数据集中的模 式和趋势,为经济预测和决策提供准确和可 靠的依据。
张量分析的重要性
科学研究
张量分析在各个学科的科学研 究中发挥着重要作用,帮助解 决复杂问题和揭示自然规律。
技术发展
随着科技的发展和应用领域的 拓展,张量分析为新技术的发 展提供了关键理论基础。
张量的坐标表示和变换规律
张量与张量积的定义与计算

张量与张量积的定义与计算张量是现代数学与物理学中非常重要的概念。
它广泛应用于各个领域,包括线性代数、微积分、物理学、工程学等。
在本文中,我们将介绍张量的基本概念、定义以及张量积的计算方法。
一、张量的定义张量可以看作是向量和矩阵的推广。
在物理学和工程学中,张量用于描述空间中的物理量。
在数学上,张量可以定义为多维数组,在不同的坐标系下有不同的分量表示。
在线性代数中,张量的定义可以从张量空间的角度看待。
假设V是一个n维向量空间,那么V的p阶张量空间可以表示为V ⊗ V ⊗⋯⊗V(一共p个V)。
其中⊗表示张量积,它是一种多重线性映射的二元运算。
二、张量积的定义张量积是以外积的方式组合两个向量的操作。
设有两个向量a和b,它们的张量积可以表示为a⊗b。
具体来说,张量积的结果是一个矩阵,其中每个元素由两个向量的对应元素相乘而得。
如果a是一个m维列向量,b是一个n维行向量,那么a⊗b的结果是一个m×n的矩阵。
矩阵中的每个元素由a和b的对应元素相乘得到。
三、张量积的计算计算张量积需要按照一定的规则进行。
具体来说,如果矩阵a和矩阵b的大小分别是m×n和p×q,那么它们的张量积可以通过以下步骤计算:1. 创建一个大小为(m×p)×(n×q)的零矩阵。
2. 遍历矩阵a的每个元素aij。
3. 将矩阵b的每个元素乘以aij,并将结果放入零矩阵中对应的位置。
计算完所有的元素后,得到的零矩阵就是矩阵a和矩阵b的张量积。
四、应用场景张量和张量积在各个领域都有重要的应用。
例如,在物理学中,张量用于描述力、能量、电磁场等物理量。
在工程学中,张量可用于描述应力、应变、磁场等。
此外,张量积还在机器学习和神经网络中扮演重要的角色。
在深度学习中,神经网络的参数可以表示为张量,通过计算张量积可以进行复杂的运算。
总结:本文介绍了张量与张量积的定义与计算方法。
张量是一种多维数组,在物理学和工程学中被广泛应用。
《张量基础知识》课件

提供数学工具
详细描述
弹性力学中的张量提供了丰富的数学工具,用于描述和 计算弹性材料的应力和变形,如弹性波传播、材料稳定 性等。
04
张量在机器学习中的应用
深度学习中的张量
深度学习中的张量用于表示多维 数据,如图像、语音和文本等。
张量可以高效地存储和计算大规 模数据,支持自动微分和反向传 播算法,使得深度学习模型能够
总结词
描述微观粒子的自旋和角动量
详细描述
量子力学中的张量也用于描述微观粒子的自旋和角动量等 性质,这些性质在量子力学中非常重要,是理解微观粒子 行为的关键。
总结词
提供数学工具
详细描述
量子力学中的张量提供了丰富的数学工具,用于描述和计 算微观粒子的状态和相互作用,如量子纠缠、量子门操作 等。
弹性力学中的张量
张量的分类
根据不同的分类标准,可以将张量分为多种类型。
根据张量的阶数,可以分为零阶张量(即标量)、一阶张量(即向量)、二阶张量(即矩阵)等。根据张量的变数个数,可 以分为纯量张量、二阶张量、三阶张量等。根据张量的对称性,可以分为对称张量、反对称张量、正交张量等。根据张量的 具体应用领域,可以分为物理张量、工程张量、医学张量等。
总结词
提供数学工具
详细描述
广义相对论中的张量提供了丰富的数学工具,用于描述 和计算引力场中的物理现象,如光线传播、星体运动等 。
量子力学中的张量
总结词
描述微观粒子的状态和相互作用
详细描述
在量子力学中,张量被用来描述微观粒子的状态和相互作 用,如狄拉克符号中的矩阵和向量等。这些张量提供了描 述微观粒子波函数的数学工具。
快速训练和优化。
张量在深度学习中还用于实现各 种复杂的神经网络结构,如卷积 神经网络、循环神经网络和注意
张量和应力张量PPT课件

1.1 角标符号
• 带有下角标的符号称为角标符号,可用来表 示成组的符号或数组。
• 例:
– 直角坐标系的三根轴
• x、y、z→x1、x2、x3 → xi(i=1,2,3);
– 空间直线的方向余弦
• l、m、n → lx、ly、lz → li(i=x,y,z);
– 表示一点应力状态的九个应力分量
• σxx、σxy… → σij(i,j=x,y,z);
a11b32
x13
a12b32 x23
a13b32
x33
y13
y33
1.3 张量的基本概念
• 只需一个实数就可以表示出来简单的物理量称为 标量。例如距离、时间、温度等。
• 需用空间坐标系中的三个分量来表示的物理量称 为矢量。 例如位移、速度、力等。
• 对于复杂的物理量,例如应力状态、应变状态等, 需要用空间坐标系中的三个矢量(也即九个分量) 才能完整地表示出来,这就是张量。
• 张量是矢量的推广,与矢量相类似,可以定义为: 由若干个当坐标系改变时满足转换关系的分量所 组成的集合称为张量。
• 物理量P
– 在j=1空,间2,坐3标);系xi (i=1,2,3)中存在九个分量Pij (i,
– 在新空间坐标系 xk(k=1’,2’,3’)中存在九个新 分量Pkr(k,r=1’,2’,3’)。
1.5 应力张量
• 外力确定后,受力物体内任意点的应力状态即已 确定。但表示该点应力状态的各个分量在不同坐 标系中将有不同的数值,因此在不同坐标系中该 点的应力分量之间应该存在一定的关系。
• 设受力物体内一点的应力状态为: – 在xi(i=x,y,z)坐标系中为σij(i,j=x,y,z);
– 在xk (k=x’,y’,z’)坐标系中为σkr(k,r=x’,y’,
【张量分析ppt课件】张量分析课件第一章 线性空间-50页精选文档

(2)∵ x y z ( x 1 y 1 ) z 1 , , ( x n y n ) z n
( x 1 y 1 z 1 , ,x n y n z n )
x ( y z ) ( x 1 ( y 1 z 1 ) , , ( x n ( y n z n ))
( x 1 y 1 z 1 , ,x n y n z n )
∴ x + (y + z )= ( x + y )+ z = x + y + z (4)∵ o(0, ,0)V0 x o (x 1 0 , x n 0 )(x1, ,xn)
∴ xox
(5)∵ ()x ()(x 1 , ,xn) (()x 1 , ,()xn)
∴
(x 1 , ,xn) (x 1 ), ,)xn)
第一章 线性空间
若记实数集合为F,F中的元素记为a、b、c、…。
则加法法则将F中的任意两个元素 a, bF ; c F
+ (a, b)c
abc
乘法法则将F中的任意两个元素 a, bF ; c F
× (a, b)c
abc
显然具有加法法则和乘法则所确定的实数集中元
素间确定关系使得实数集构成一个空间。并记为:
所有以x点为起点的矢量按:
u x yu x z(y 1 x 1 , ,y n x n ) (z 1 x 1 , ,z n x n )
(y 1 ( x 1 ) (z 1 x 1 ) ,,(y n x n ) (z n x n ))
u xy (y1x1, ,ynxn) ((y1x1) ,,(ynxn)) F
a, b,xF
(6) (a b ) x a x b x
a, b,xF
张量概念及其基本运算PPT课件

◆ 在运算中,括号内的求和标号应在进行其它运算前
优先求和。例:
aii2a121a222a323
(aii)2(a1 1a22 a3)32
.
7
★ 关于自由标号:
◆在同一方程式中,各张量的自由标号相同,
即同阶且标号字母相同。
◆自由标号的数量确定了张量的阶次。
张量可以用矩阵表示,称为张量矩阵,如:
a11 a12 a13
aij a21
a22
a23
a31 a32 a33
凡是同阶的两个或几个张量可以相加(或相减), 并得到同阶的张量,它的分量等于原来张量中标号 相同的诸分量之代数和。 即:
a ijb ijcij
其中各分量(元素)为:
aij bij cij
张量概念及其基本运算
1、张量概念
◆ 张量分析是研究固体力学、流体力学及连续介 质力学的重要数学工具 。
◆ 张量分析具有高度概括、形式简洁的特点。
◆ 所有与坐标系选取无关的量,统称为物理恒量。
◆ 在一定单位制下,只需指明其大小即足以被说明 的物理量,统称为标量。例如温度、质量、功等。
◆ 在一定单位制下,除指明其大小还应指出其方向 的物理量,称为矢量。例如速度、加速度等。
◆ 重复出现,且只能重复出现一次的下标符号称
为哑标号或假标号。哑标号在其方程内先罗列, 再求和。
.
4
3.求和约定
关于哑标号应理解为取其变程n内所有数值,然后再求和, 这就叫做求和约定。 例如:
3
aibi aibi a1b1a2b2a3b3 i1
3
aib j j aib j j ai1b1ai2b2ai3b3 j1
张量ppt

示多重求和。
例如:
33
aij xi xj
aij xi x j
i1 j1
★ 若要对在同项内出现两次以上的指标进行遍历求和,
一般应加求和号。如:
3
a 1b1c1 a 2b2c2 a 3b3c3 aibici i 1
24
张量基本概念
★ 一般说不能由等式
aibi aici
bi ci
两边消去ai导得
3. 换标符号,具有换标作用。例如:
d s2 ij d xi d xj d xi d xi d xj d xj
即:如果符号 的两个指标中,有一个和同项中其它
因子的指标相重,则可以把该因子的那个重指标换成
的另一个指标,而 自动消失。
29
符号ij 与erst
类似地有
ij a jk aik ; ij aik a jk ij akj aki ; ij aki akj ij jk ik ; ij jk kl il
符号ij 与erst
➢ 常用实例
1. 三个相互正交的单位基矢量构成正交标准化基。 它具有如下重要性质:
✓ 每个基矢量的模为1,即 ei e j 1 (当i=j时) ✓ 不同基矢量互相正交,即 ei e j 0 (当i≠j时)
上述两个性质可以用ij 表示统一形式:
2. 两个矢量 a 和 b 的分量的点积(或称数量积)为:
3
a b= a1b1 a2b2 a3b3 aibi i1
Appendix A.1
张量基本概念
➢求和约定
如果在表达式的某项中,某指标重复地出现两次, 则表示要把该项在该指标的取值范围内遍历求和。 该重复的指标称为哑指标,简称哑标。
3
0下载券文档一键搜索 VIP用户可在搜索时使用专有高级功能:一键搜索0下载券文档,下载券不够用不再有压力!
张量分析第二讲精品PPT课件

爱因斯坦求和约定
Sa 1x1a2x2anxn
n
n
S aixi ajxj
i1
j1
约定 Saixi ajxj
用拉丁字母表示3维,希腊字母表2
维
求和指
标与所用 的字母无
关
指标重
复只能一 次
指标范
围
33
Aij xi y j
i1 j1
双重求和
Aij xi yj A11x1y1A12x1y2 A13x1y3
i——自由指标,在每一项中只出现一次,一个公式 中必须相同
置换符号与克罗尼克尔记号
1 若i, j,k1,2,3,2,3,1,3,1,2 eijkeijk1 若i, j,k3,2,1,2,1,3,1,3,2
0 若有两个或三个等指
j i
1 0
当i j 当i j
ijaj i1a1i2a2i3a3ai imAmj i1A1j i2A2j i3A3j Aij
i
i
1 1
2 2
3 3
3
k
i
j
k
j i
j
i
i
j
i i
j j
3
j
i
k j
l k
l i
• 2. 张量相关的概念
P•g1(P1g1P2g2)•g1P1 P•g2(P1g1P2g2)•g2P2 P•g1(P1g1P2g2)•g1P1 P•g2(P1g1P2g2)•g2P2
gi gijgj
g i
gijg j
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a11 a12 a13
aij a21
a22
a23
a31 a32 a33
凡是同阶的两个或几个张量可以相加(或相减), 并得到同阶的张量,它的分量等于原来张量中标号 相同的诸分量之代数和。 即:
a ijb ijcij
其中各分量(元素)为:
aij bij cij
B、张量的乘积
◆ 对于任何阶的诸张量都可进行乘法运算。 ◆ 两个任意阶张量的乘法定义为:第一个张量的
、 、 、 当取n时,n阶张量,M = 3n。
◆ 张量的定义为:由若干坐标系改变时满足一定 坐标转化关系的有序数组成的集合。
◆ 张量是矢量和矩阵概念的推广。标量是0阶张量,
矢量是一阶张量,矩阵是二阶张量,而三阶张量 好比立体矩阵,更高阶张量则无法用图形表示
◆ 张量出现的背景:我们的目的是要用数学量来表示
张量概念及其基本运算
1、张量概念
◆ 张量分析是研究固体力学、流体力学及连续介 质力学的重要数学工具 。
◆ 张量分析具有高度概括、形式简洁的特点。
◆ 所有与坐标系选取无关的量,统称为物理恒量。
◆ 在一定单位制下,只需指明其大小即足以被说明 的物理量,统称为标量。例如温度、质量、功等。
◆ 在一定单位制下,除指明其大小还应指出其方向 的物理量,称为矢量。例如速度、加速度等。
(3) ijjk i11k i22k i33k ik
(4) aijij a1111a2222a3333 aii
(5) aiij a11j a22j a33j aj (即a1,或a2,或a3)
(6) ijlj li ijlj ijlj (ij i量的加减:
张量可以用矩阵表示,称为张量矩阵,如:
的张量;如果在微商中,下标符号是哑标号, 则作用的结果将产生一个新的降低一阶的张量。 例如:
' i
, xi x1
x2
,
x3
ui'i
ui u1u2u3 xi x1 x2 x3
是坐标参数xi的函数。
◆ 张量导数就是把张量的每个分量都对坐标参数
求导数。
◆ 对张量的坐标参数求导数时,采用在张量下标
符号前上方加“ ′”的方式来表示。例如 ,A i j 就表示对一阶张量 A的i 每一个分量对坐标参数
xj求导。
◆ 如果在微商中下标符号i是一个自由下标,则 算子 作i 用的结果,将产生一个新的升高一阶
a1b3 a2b3 a3b3
◆ 张量乘法不服从交换律,但张量乘法服从分配
律和结合律。例如:
( a i j b i) c j k a i c k j b i c k j; 或 ( a i b k j ) c m a i( b j k c m )
C、张量函数的求导:
◆ 一个张量是坐标函数,则该张量的每个分量都
物理量,可是标量加上向量都不能完整地表达所有 的物理量,所以物理学家使用的数学量的概念就 必须扩大,于是张量就出现了。
2.下标记号法
◆ 在张量的讨论中,都采用下标字母符号,来表
示和区别该张量的所有分量。
◆ 不重复出现的下标符号称为自由标号。自由标
号在其方程内只罗列不求和。以自由标号的数 量确定张量的阶次。
关于Kronecker
delta(
)符号:
ij
ij 是张量分析中的一个基本符号称为柯氏符号
(或柯罗尼克尔符号),亦称单位张量。其定义为:
ij 1 0,,
当 ij时
; 或
当 ij时 ;
1
: ij0
0
0 1 0
0 0 1
的作用与计算示例如下:
ij
(1) ii 112233 3
(2) ijij (11)2 (22)2 (33)2 3
◆ 求和约定只适用于字母标号,不适用于数字标号。
◆ 在运算中,括号内的求和标号应在进行其它运算前
优先求和。例:
aii2a121a222a323
(aii)2(a1 1a22 a3)32
★ 关于自由标号:
◆在同一方程式中,各张量的自由标号相同,
即同阶且标号字母相同。
◆自由标号的数量确定了张量的阶次。
★
◆ 重复出现,且只能重复出现一次的下标符号称
为哑标号或假标号。哑标号在其方程内先罗列, 再求和。
3.求和约定
关于哑标号应理解为取其变程n内所有数值,然后再求和, 这就叫做求和约定。 例如:
3
aibi aibi a1b1a2b2a3b3 i1
3
aib j j aib j j ai1b1ai2b2ai3b3 j1 3
每一个分量乘以第二个张量中的每一个分量, 它们所组成的集合仍然是一个张量,称为第一 个张量乘以第二个张量的乘积,即积张量。积 张量的阶数等于因子张量阶数之和。例如:
aibjk cijk
若 a i a 1 a 2 a 3 bjb 1 b 2 b 3
则:
a1b1 aibj a2b1
a3b1
a1b2 a2b2 a3b2
ai2i ai2ia121a222a323 i1
ii23
2 ii (
11
22
3)32
i1
33
ijij
ijij
i1 j1
11 1 1 12 1 2 13 13
21 21 22 22 23 23
31 31 32 32 33 33
★ 关于求和标号,即哑标有: ◆ 求和标号可任意变换字母表示。
◆ 绝对标量只需一个量就可确定,而绝对矢量则需 三个分量来确定。
◆ 若我们以r表示维度,以n表示幂次,则关于三维 空间,描述一切物理恒量的分量数目可统一地表
示成: M = 3n
◆ 现令 n 为这些物理量的阶次,并统一称这些物
理量为张量。
当n=0时,零阶张量,M = 1,标量; 当n=1时,一阶张量,M = 3,矢量;
