2.4 线段、角的轴对称性(3) 2
2.4 线段、角的轴对称性(4)

【练习】
如图,在△ABC中,AB=AC,点D在BC上, DE⊥AB,DF⊥AC,垂足分别为E、F,且 DE=DF.求证:D是BC的中点.
2.4 线段的轴对称性
【例3】
在三角形ABC中∠BAC的角平分线与BC的垂直平 分线相交于D点,DN⊥AC,DM⊥AB.求证: BM=CN.
2.3 设计Байду номын сангаас对称图案
2.4 线段的轴对称性
【练习】
已知:如图,在△ABC中,点O是∠ABC、∠ACB外 角的平分线的交点,那么点O在∠A的平分线上吗?证 明你的结论.
2.4 线段的轴对称性
【例2】
已知:如图,AD是△ABC的角平分线,DE ⊥ AB, DF ⊥ AC,垂足分别为E、F. 求证:AD垂直平分EF.
2.4 线段的轴对称性
初中数学 八年级(上册)
2.4 线段、角的轴对称 性(4)
2.4 线段的轴对称性
【活动】
在△ABC中,用直尺和圆规分别作角平分线AD、 BE,AD、BE相交于点P,再作∠C的角平分线, 你有什么发现?
2.4 线段的轴对称性
【例1】
已知:如图,△ABC的角平分线AD、BE相交于点P. 求证:点P在∠C的平分线上.
2.4线段-角的对称性

lQABP§线段,角的轴对称性(1)教学案主备人:赵廷尧自主学习问题1:如图,线段AB ,通过折叠,能否是使点A 与点B 重合问题2:线段是轴对称图形吗上面操作中的折痕是什么 <问题3:在折痕上任意取一点C ,连接AC 、BC ,AC 与BC 的数量关系怎样你能证明吗通过以上三个问题的解决你知道了什么 几何语言:∵MN ⊥AB ,AC =BC ,∴_______(线段垂直平分线上的点到线段两 端的距离相等). "探究活动例1、线段的垂直平分线外的点,到这条线段两端的距离相等吗为什么变形:在例1的条件下:1、若AP=6,BP=4,求△QPB 的周长;2、若△QPB 的周长为12,△APB 的周长为17,求AB ; %3、若△QPB 的周长为12,AB =7,求△APB 的周长。
4、若△QCB 的周长为24,△APB 的周长与四边形BPQC 的周长之差为12,求CQA BC例2、如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若BC=25cm ,求△AEG的周长D FC ·例3、如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂线分别与AD、BC相交于点E、F,连接AF.求证:AE=AF.(【课堂练习】:已知:如图,AB=AC=12 cm,AB的垂直平分线分别交AC、AB于D、E,△ABD的周长等于29 cm,求DC的长.\§线段,角的轴对称性(1)达 标 自 测班级 学号 姓名自测内容1.线段垂直平分线上的点到 距离相等。
2、如图,直线MN 是线段AB 的垂直平分线,垂足为D ,点P 是MN 上一点.若AB =10 cm ,则BD =_______cm ;若PA =10 cm ,则PB =_______cm .3.如图,在ΔABC 中,AB 的中垂线交AC 与点E ,若AC=9,AE:CE=2:1,则B 、E 两点间的距离是 。
苏教版八年级上册数学线段、 角的轴对称性补充习题答案【三篇】

苏教版八年级上册数学线段、角的轴对称性补充习题答案【三篇】2.4线段、角的轴对称性(1)答案1、由点D在线段AB的垂直平分线上,可知DA=DB.于是△BDC的周长=BD+DC+BC=DA+DC+BC=AC+BC=9.2、 (1)图略;(2)OA=OB=OC.∵点O在线段AB的垂直平分线m上,∴OA=OB(线段垂直平分线上的点到线段两端的距离相等).同理,OB=OC.∴OA=OB=OC.2.4线段、角的轴对称性(2)答案1、点D在线段AC的垂直平分线上,∵BC=BD+DC,BC=BD+AD,∴BD+DC=BD+AD.∴DC=DA.∴点D在线段AC的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上).2、∵∠1=∠2,AC=AC,∠3=∠4,∴△ABC≌△ADC,∴AB=AD,CB=CD.∴点A在线段BD的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上).同理,点C在线段BD的垂直平分线上,∴AC是线段BD的垂直平分线(两点确定一条直线).2.4线段、角的轴对称性(3)答案1、过点D作DE⊥AB,垂足为E.∵AD平分∠BAC,DC⊥AC,DE⊥AB,∴DE=DC(角平分线上的点到角两边的距离相等).根据题意,得DC=6.∴点D到AB的距离为6.2、 DE=DC.∵AD平分∠BAC,DB⊥AB,DF⊥AC,∴DB=DF(角平分线上的点到角两边的距离相等).又BE=CF,∴Rt△DBE≌Rt△DFC.∴DE=DC.3、∵∠FEB=∠FDC=90°,∠BFE=∠CFD,BE=CD,∴△BEF∽△CDF.∴FE=FD.∴点F在∠MAN的平分线上(角的内部到角两边距离相等的点在角的平分线上).。
第7讲线段与角的轴对称性

142
∴∠C=∠A=20°,∠BDC=90°, ∴∠CBD=90°﹣∠A=70°. 故选:D.
学习,为了追寻更好的自己!
例 3、如图,在△ABC 中,DE 和 DF 分别是边 AB 和 AC 的垂直平分线,且 D 点在 BC 边上,
连接 AD,则∠BAC=
°.
【分析】根据线段垂直平分线的性质得出 BD=AD,AD=CD,求出∠B=∠BAD,∠C
学习,为了追寻更好的自己!
第七讲 线段与角的轴对称性
一、知识梳理
要点一、线段的轴对称性 (1)线段是轴对称图形,线段的垂直平分线是它的对称轴. (2)线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等; (3)线段垂直平分线的性质定理的逆定理(判定定理):到线段两个端距离相等的点
在 线段的垂直平分线上. 要点诠释: 线段的垂直平分线的性质是证明两线段相等的常用方法之一.同时也给出了引辅助线的
பைடு நூலகம்
【点评】本题考查了线段垂直平分线的性质,等腰三角形的性质,三角形的内角和定理
等知识点,注意:线段垂直平分线上的点到线段两个端点的距离相等.
【变式 1】如图在△ABC 中 MP,NQ 分别垂直平分 AB、AC,若 BC 的长度为 9,则△APQ
的周长是
.
【分析】根据线段的垂直平分线的性质得出 AP=BP,AQ=CQ,求出△APQ 的周长=BC, 再代入求出即可.
145
学习,为了追寻更好的自己!
【详解】
解:作 OD⊥AB 于 D,OE⊥AC 于 E,OF⊥BC 于 F,连接 OC,
∵点 O 为∠ABC 与∠CAB 的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,
∴OE=OD=OF,
2.4线段、角的轴对称性(3)作业纸
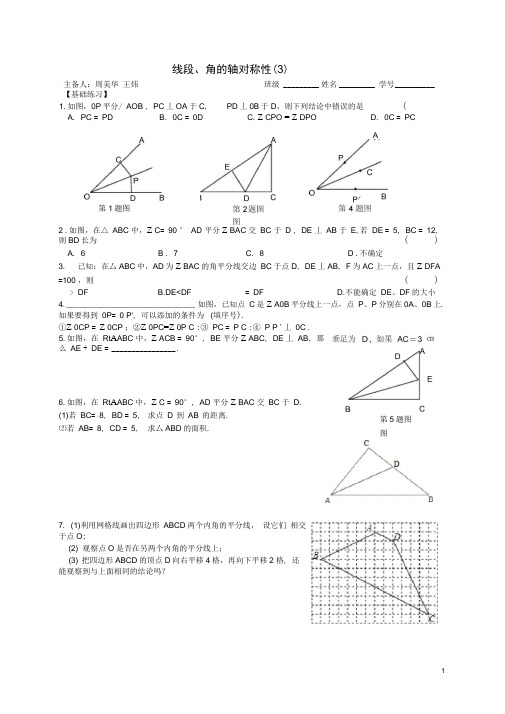
1线段、角的轴对称性(3)【基础练习】2 .如图,在△ ABC 中,Z C = 90 ° AD 平分Z BAC 交 BC 于 D , DE 丄 AB 于 E ,若 DE = 5, BC = 12, 则BD 长为 ( ) A . 6 B . 7C . 8D .不确定3. 已知:在厶ABC 中,AD 为Z BAC 的角平分线交边 BC 于点D , DE 丄AB , F 为AC 上一点,且Z DFA=100°,则 ()4. _____________________________ 如图,已知点 C 是Z A0B 平分线上一点,点 P 、P 分别在0A 、0B 上.如果要得到 0P = 0 P', 可以添加的条件为 (填序号).①Z 0CP = Z 0CP ;②Z 0PC =Z 0P C :③ PC = P C :④ P P '丄 0C .7. (1)利用网格线画出四边形 ABCD 两个内角的平分线, 设它们 相交于点O ;(2) 观察点O 是否在另两个内角的平分线上;(3) 把四边形ABCD 的顶点D 向右平移4格,再向下平移2 格, 还能观察到与上面相同的结论吗?主备人:周美华 王炜班级 _________ 姓名 _________ 学号 __________5.如图,在 Rt A ABC 中,Z ACB = 90°, BE 平分Z ABC , DE 丄 AB , 那么 AE + DE = ________________ .6.如图,在 Rt A ABC 中,Z C = 90°, AD 平分Z BAC 交 BC 于 D . (1)若 BC = 8, BD = 5, ⑵若 AB = 8, CD = 5, 求点D 到AB 的距离. 求厶ABD 的面积. 第5题图 图1.如图,0P 平分/ AOB , PC 丄OA 于C , PD 丄0B 于D ,则下列结论中错误的是 ( A . PC = PD B . 0C = 0DC . Z CPO = Z DPOD . 0C = PC> DFB.DE<DF= DFD.不能确定 DE 、DF 的大小第1题图A&已知:如图,点B、C分别在/ MAN的两边上,BD丄AM , CE丄AN,垂点分别为D、E, BD、CE相交于点F,且BF = CF .证明:点F在/ A的角平分线上.NOA, DN OB,9•如图,射线0C在/ AOB的内部,点D、E在射线OC上,DMEP OA, EQ OB,垂足分别为M、N、P、Q,且EP = EQ . 求证:DM =DN .【拓展提升】1 . △ ABC的周长为60,/ A和/B的角平分线相交于点P,若点P到边AB的距离为10,则厶ABC 的面积为.2 .如图,/ AOB= 90 °将三角尺的直角顶点落在/ AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与/ AOB的两边分别相交于点E、F.⑴求证:PE= PF.(2)若将三角板绕点P旋转,使得点E落在AO的延长线上,(1)中的结论还成立吗?请你画出相应的图形,并证明你的结论•完成时间: ____________家长签字: ____________2。
2.4-2 线段和角的轴对称性

用直尺、圆规作已知线段垂直平分线的一般步骤: 活动3 画一画 回顾作法:
1.分别以A 、B为圆心, 1 大于 AB长为半径画弧;
2
M
A
2. 两弧相交于点M、N;
B
3.过点M、N作直线.
∴直线MN即为线段AB 的 垂直平分线.
N
活动4
再画画 如图,任意三角形ABC,边AB、BC的 垂直平分线 l1 、 l2交于点O
.
画板 Z J G 反 共
P
A
B
在线段垂直平分线外, 不存在到线段两端距 离相等的点.
定理: 到线段两端距离相等的点 在线段的垂直 平分线上.
数量关系 位置关系
P
A B
推理格式:
∵ PA=PB
∴点P在线段AB的垂直平分线上
如图,点MN为直线l上两点,且满足 l MA=MB,NA=NB
GO
M B
完成以下填空:
A
∵MA=MB, N AB ∴点M在线段 的垂直平分线上. (理由是 到线段两端距离相等的点在线段 的垂直平分线上 又∵ NA=NB , ∴点N在线段AB的垂直平分线上. ∴直线MN是线段AB的 垂直平分线 . (理由是 两点确定一条直线 )
)
活动2
l
回顾、发现
如图,已知直线l 是线段AB的垂直平分线
作PO平分∠APB
1 2
共线
∵PO平分∠APB ∴ ∠1=∠2 在△POA和△POB中 PO=PO ∠1=∠2 PA=PB ∴△POA≌△POB(SAS) ∴∠AOP=∠BOP, OA=OB 又∵A、O、B三点共线 ∴∠AOP + ∠BOP=180° ∴∠AOP =90° ∴ PO⊥AB 又∵OA=OB ∴ PO垂直平分AB 即P在线段AB垂直平分线上
2.4线段、角的轴对称性(第1课时)(同步课件)八年级数学上册同步精品课堂(苏科版)

∵∠BAC=∠BAD+∠CAE+∠DAE
∴∠DAE=∠BAC-(∠BAD+∠CAE)=2α-180°
思维拓展
在△ABC中,∠BAC=α,边AB的垂直平分线交BC于点D,边AC的垂直平
分线交BC于点E,连接AD,AE,则∠DAE的度数为______________.
P
● 2
●
●
A●
●
P3
O
●
B(A)
新知归纳
线段的垂直平分线的性质定理:
线段的垂直平分线上的点到线段两端的距离相等.
符号语言:
l
∵点P在线段AB的垂直平分线上,
●
A●
∴ PA=PB
(线段的垂直平分线上的点到线段两端的距离相等).
用途:
相等的线段
P
●
O
B
操作与思考
思考4 线段的垂直平分线外的点,到这条线段两端的距离相等吗?
B
理由: 在l上另取一点P,连接PA、PB、PA'.
由作图可知,l是AA'的垂直平分线,
A
∴ AP=A'P,AM=A'M,
l
M
A'
∴ AM+BM=A'M+BM=A'B,
P
AP+BP=A'P+BP,
由“两点之间线段最短”可得:
A'B<A'P+BP.
即AM+BM最短.
课堂小结
线
段
垂
直
平
分
线
的
性
质
内容
2.4 线段、角的轴对称性(3) 2

在操作中感知角的轴 养口头表达能力.
3, 直线 OC 是∠AOB 的角平分线,
明确结论.
OC 翻折, 你有什么发现?角平分线
称轴吗?
第 1 页
共 3 页
2014-1-6
凤凰初中数学配套教学软件_教学设计
学生独立思考、积极探究.方法 不一,具体如下: 1.利用“AAS”证明△ODP≌ △OEP 后,说明 PD 与 PE 相等.
“角”的轴对称性又如何呢?与线段有什么异同和联
,我们就进入今天愉快的数学探究之旅.
:
积极思考, 动手操作, 提出猜想.
让学生动手操作,感
薄纸上画∠AOB,它是轴对称图形吗?如果是,对称
称性,猜想对称轴的位置
为什么?
究作铺垫,同时激发学 趣. 动手操作, 验证猜想, 描述发现,
A O 2-23 C B
相等,再结合证明两个
得到的结论.
实 “过一点有且只有一条直线与已知 路,让学生寻找到演绎推 直线垂直” ,说明 PD 与 PE 相等.
B
培养学生的动手能力和探 下面的证明积累经验.
讨论后共同小结:
师生互动,锻炼学生
线上的点有什么特点?
角平分线上的点到角两边的距 能力,培养学生勇于发表 离相等. 1. 猜想角平分线性质定理的逆 能力.
D O E 2-24 P A C
问题虽然比较简单,
线是否也有像线段垂直平分线一样的特殊性质呢?
受到 PD 与 PE 相等,但
在∠AOB 的角平分线 OC 任意取一点 P,PD⊥OA,
进行推理说明还是有困难
D 与 PE 相等吗?为什么?
学生从角平分线的定义入
明,你发现了什么?用
2.利用角的轴对称性和基本事
2.4 线段、角的轴对称性 课件(苏科版八年级上册) (6)

A
B D C
2、如图, NM是线段AB的中垂线, 下列说法正确的有:①②③ 。 ①AB⊥MN,②AD=DB, ③MN⊥AB, ④MD=DN,⑤AB是MN的垂直平分线
M
A
D
N
B
3、如图,若AC=12,BC=7,AB的垂直平
分线交AB于E,交AC于D,求△BCD的周长 。
A
1、因为
,所以AB=AC。
B
A D
C
理由:
2、如图, NM是线段AB的中垂 线, 下列说法正确的有: 。 ①AB⊥MN,②AD=DB, ③ MN⊥AB, ④MD=DN,⑤AB是 MN的垂直平分线
M
A
D N
B
1、因为 AD为BC的中垂线 ,所以AB=AC。 线段垂直平分线上的点与这条 理由:
第2章 图形的轴对称
2.4 线段的垂直平分线
如果一个图形沿着一条直线 对折 ,两侧的 图形能够 完全重合,这个图形就是轴对称图形。
对称轴。 折痕所在的这条直线叫做______
A
A′ B′
B C C′
把一个图形沿着某一条直线 折叠 ,如果 它能够 与另一个图形重合 ,那么就说这两个 图形关于这条直线对称,这条直线叫做对称轴, 折叠后重合的点是对应点,叫做 对称点 。
结论
线段垂直平分线性质定理。
线段垂直平分线上点,到
这条线段个端点的距离相 等.
相等的根据之一.
老师提示:这个结论是经常用来证明两条线段
你能说出“定理 线段垂直平分线上的 点到这条线段两个端点距离相等”的 逆命题吗?
组卷网
逆定理 到一条线段两个端点距离相等 的点,在这条线段的垂直平分线上.
2.4线段、角的轴对称性(2)课件ppt

说说你本节课你有什么收获?
2.4 线段、角的对称性(2)
作业
P57-58习题2.4,分析第5、6题的解法, 任选1题写出过程.
Q
A
M
B
2.4 线段、角的对称性(2)
定理 到线段两端的距离相等的点在线段垂直 平分线上. 因为QA=QB , 所以点Q是线段AB的、角的对称性(2)
试一试
你能用尺规画出任一条已知线段的垂直 平分线吗?如果能,说说你作图的依据.
A
B
2.4 线段、角的对称性(2)
初中数学 八年级(上册)
2.4
线段、角的对称性(2)
2.4 线段、角的对称性(2)
做一做
在一张薄纸上画一条线段AB. 你能找出与线段AB的端点A、B距离相 等的点吗? 这样的点有多少个?
A B
2.4 线段、角的对称性(2)
想一想
一个点到一条线段的两端的距离相等,那么这个 点在这条线段的垂直平分线上吗?
试一试
在直线AB外任取一点C,用刚学的方法 作出线段BC、AC的垂直平分线,你发现了 什么?
C
A
B
l2
2.4 线段、角的对称性(2)
例1 已知:如图2-22,在△ABC中,AB、AC的 垂直平分线l1,l2相交于点O.求证:点O在BC的 垂直平分线上. A
l1
O
l2
B
C
2.4 线段、角的对称性(2)
第2章 《轴对称图形》 :2.4 线段、角的轴对称性(2)(含答案)

第2章《轴对称图形》:2.4 线段、角的轴对称性(2)选择题1.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB:∠CAE=3:1,则∠C等于()A.28° B.25° C.22.5° D.20°2.三角形三边垂直平分线的交点是三角形的()A.外心 B.内心 C.重心 D.垂心(第1题)(第4题)3.与三角形三个顶点距离相等的点,是这个三角形的()A.三条中线的交点B.三条角平分线的交点C.三条高的交点D.三边的垂直平分线的交点4.如图,△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是()A.13cm B.14cm C.15cm D.16cm5.如图,在Rt△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB交BC于E,若BE=2 2 ,则AC=()A.1 B.2 C.3 D.4(第5题)(第6题)(第7题)填空题6.如图,点P到∠AOB两边的距离相等,若∠POB=30°,则∠AOB=度.7.如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是 cm.8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,BC=10cm,BD=6cm,则点D到AB的距离为 cm.(第8题)(第9题)(第10题)9.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是.10.如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长是 cm.11.在△ABC中,∠C=90°,BC=16cm,∠BAC的平分线交BC于D,且BD:DC=5:3,则D到AB的距离为 cm.12.如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是 cm.(第12题)(第14题)(第15题)13.在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=8,则点D 到斜边AB的距离等于.14.在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=15,且BD:DC=3:2,则D到边AB的距离是.15.如图,在△ABC中,∠C=90°,AD平分∠BAC,若CD=6 cm,则点D到AB 的距离是 cm.16.如图,已知∠C=90°,∠1=∠2,若BC=10,BD=6,则点D到边AB的距离为.(第16题)(第17题)(第18题)17.如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠ADC=度.18.如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AE C的度数是度.19.如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是 cm.(第19题)(第20题)(第21题)20.如图,△ABC中,DE是AC的垂直平分线,AE=6cm,△ABD的周长为26cm,则△ABC的周长为 cm.21.如图所示,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠A=35°,则∠CDB=度.22.如图,在Rt△A BC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是度.(第22题)(第23题)(第24题)23.△ABC中,∠BAC=100°,若DE、FG分别垂直平分AB和AC,则∠EAF=.24.如图,在△ABC中,AB的中垂线DE交AC于点D,交AB于点E,如果BC=10,△BDC的周长为22,那么AC= .25.如图,在△ABC中,AB=AC=12,EF为AC的中垂线,若EC=8,则BE的长为.26.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,垂足为E,交AC于D,连接BD,若∠ABD=50°,则∠C=度.(第25题)(第26题)27.如图,在△ABC中,BC边上的垂直平分线交AC于点D;已知AB=3,AC=7,BC=8,则△ABD的周长为.(第27题)(第28题)28.如图,在△ABC中,AB=AC=15cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC 的周长是25cm,则BC的长 cm .29.在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC 的度数是°.答案:1.故选A.考点:线段垂直平分线的性质.专题:计算题.分析:设∠CAE=x,则∠EAB=3x.根据线段的垂直平分线的性质,得AE=CE,再根据等边对等角,得∠C=∠CAE=x,然后根据三角形的内角和定理列方程求解.解答:解:设∠CAE=x,则∠EAB=3x.∵AC的垂直平分线交AC于D,交BC于E,∴AE=CE.∴∠C=∠CAE=x.根据三角形的内角和定理,得∠C+∠BAC=180°-∠B,即x+4x=140°,x=28°.则∠C=28°.故选A.点评:此题综合运用了线段垂直平分线的性质、等腰三角形的性质以及三角形的内角和定理.2.故选A.考点:线段垂直平分线的性质.分析:根据线段的垂直平分线的性质可知,三角形三边垂直平分线的交点到3个顶点的距离相等,所以是外心.解答:解:三角形三边垂直平分线的交点到3个顶点的距离相等,所以是外心.故选A.点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.3.故选D.考点:线段垂直平分线的性质.分析:可分别根据线段垂直平分线的性质进行思考,首先满足到A点、B点的距离相等,然后思考满足到C点、B点的距离相等,都分别在各自线段的垂直平分线上,于是答案可得.解答:解:如图:∵OA=OB,∴O在线段AB的垂直平分线上,∵OB=OC,∴O在线段BC的垂直平分线上,∵OA=OC,∴O在线段AC的垂直平分线上,又三个交点相交于一点,∴与三角形三个顶点距离相等的点,是这个三角形的三边的垂直平分线的交点.故选D.点评:此题考查了线段垂直平分线的性质;题目比较简单,只要熟知线段垂直平分线的性质即可.分别思考,两两满足条件是解答本题的关键.4.故选B.考点:线段垂直平分线的性质.分析:要求△ABC的周长,先有AE可求出AB,只要求出AC+BC即可,根据线段垂直平分线的性质可知,AD=BD,于是AC+BC=AC+CD+AD等于△ACD的周长,答案可得.解答:解:∵DE是AB的垂直平分线,∴AD=BD,AB=2AE=2又∵△ACD的周长=AC+AD+CD=AC+BD+CD=AC+BC=12∴△ABC的周长是12+2=14cm.故选B.点评:此题主要考查线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等;进行线段的等效转移,把已知与未知联系起来是正确解答本题的关键.5.故选B.考点:勾股定理;线段垂直平分线的性质.分析:利用线段的垂直平分线的性质计算.解答:解:∵DE垂直平分AB∴∠B=∠DAE,BE=AE∵∠B=22.5°,∠C=90°∴∠AEC=∠CAE=45°∴AC=CE∴2AC2=AE2∴AC=2.故选B.点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.填空题6.故答案为:60°.考点:角平分线的性质.分析:已知有点P到∠AOB两边的距离相等,根据角平分线的逆定理可知,可得OP为角的平分线,加上若∠POB=30°,答案可得.解答:解:∵点P到∠AOB两边的距离相等∴OP平分∠AOB∴∠AOB=2∠POB=60°.点评:此题主要考查角平分线性质的逆定理:到角的两边距离相等的点在角的平分线上;题目比较简单,从已知条件认真思考.7.故答案为:3cm..考点:角平分线的性质.专题:压轴题.分析:已知给出了角平分线,求的是D点到直线AB的距离,根据点到直线的距离,再根据角平分线的性质即可求得.解答:解:由∠C=90°,AD平分∠CAB作DE⊥AB于E所以D点到直线AB的距离是DE的长由角平分线的性质可知DE=CD又BC=8cm,BD=5cm所以DE=CD=3cm.所以D点到直线AB的距离是3cm.点评:本题主要考查平分线的性质,由已知能够注意到D点到直线AB的距离是CD的长是解决的关键.8.故答案为:4.考点:角平分线的性质.分析:要求点D到AB的距离利用角的平分线上的点到角的两边的距离相等可知,只要求得D到AC的距离即可,而D到AC的距离就是CD的值,答案可得.解答:解:∵∠C=90°,AD平分∠BAC,∴CD是点D到AB的距离,∵CD=10-6=4,∴点D到AB的距离为4.故答案为:4.点评:本题主要考查了角平分线上的一点到两边的距离相等的性质.做题前,要有分析过程,培养自己的分析能力.9.故填5.考点:角平分线的性质.分析:要求△ABD的面积,有AB=5,可为三角形的底,知求出底上的高即可,利用角的平分线上的点到角的两边的距离相等可知△ABD的高就是CD的长度,所以高是2,则可求得面积.解答:解:∵∠C=90°,AD平分∠BAC,∴点D到AB的距离=CD=2,∴△ABD的面积是5×2÷2=5.故填5.点评:本题主要考查了角平分线上的一点到两边的距离相等的性质.注意分析思路,培养自己的分析能力.10.故填10.考点:角平分线的性质.分析:由已知利用角的平分线上的点到角的两边的距离相等可得到DE=CD,AC=AE,加上BC=AC,三角形的周长为BE+BD+DE=BE+CB=AE+BE,于是周长可得.解答:解:CD=DE∵AC=BC∴∠B=45°∴DE=BE∵△DEB的周长=DB+DE+BE=AC+BE=AB=10.故填10.点评:本题主要考查角平分线上的点到角的两边距离相等的性质和线段的和差关系求值.利用线段相等,进行线段的转移是解决本题的关键.11.故填6.考点:角平分线的性质.分析:利用角的平分线上的点到角的两边的距离相等可知D到AB的距离为等于CD的长度,求CD长即可.解答:解:∵∠C=90°,BC=16cm,∠BAC的平分线交BC于D,∴CD就是D到AB的距离,∵BD:DC=5:3,BC=16cm,∴CD=6,即D到AB的距离为6cm.故填6.点评:本题主要考查角的平分线上的点到角的两边的距离相等的性质.利用线段相等学会线段的转移,利用相等的线段进行线段转移是一种很重要的方法,注意掌握.12.故填20.考点:角平分线的性质.分析:由已知条件,结合已知在图形上的位置,根据角平分线的性质可得M到AB的距离等于CM.解答:解:∵∠C=90°,AM平分∠CAB,∴M到AB的距离等于CM=20cm.故填20.点评:本题考查了角平分线的性质;注意题中隐含的条件:MC⊥AC的运用.本题比较简单,属于基础题.13.故填8.考点:角平分线的性质.分析:由已知条件开始思考,利用角的平分线上的点到角的两边的距离相等可知点D到斜边AB的距离等于8.解答:解:∵点D到斜边AB的距离等于CD∴D到斜边AB的距离为8.故填8.点评:本题主要考查了角平分线上的一点到两边的距离相等的性质.本题直接运用角平分线的性质就可,比较简单,属于基础题.14.故填6.考点:角平分线的性质.分析:首先由线段的比求得CD=6,然后利用角平分线的性质可得D到边AB的距离是.解答:解:∵BC=15,BD:DC=3:2∴CD=6∵∠C=90°AD平分∠BAC∴D到边AB的距离=CD=6.故填6.点评:此题主要考查角平分线的性质:角平分线上的任意一点到角的两边距离相等.做题时要由已知中线段的比求得线段的长,这是解答本题的关键.15.故填6.考点:角平分线的性质.分析:结合已知条件在图形上的位置,由角平分线的性质可得点D到AB的距离是6cm.解答:解:点D到AB的距离=CD=6cm.故填6.点评:此题主要考查角平分线的性质:角平分线上的任意一点到角的两边距离相等.比较简单,属于基础题.16.故填4.考点:角平分线的性质.分析:由已知条件首先求出线段CD的大小,接着利用角平分线的性质得点D 到边AB的距离等于CD的大小,问题可解.解答:解:∵BC=10,BD=6∴CD=4∵∠C=90°,∠1=∠2∴点D到边AB的距离=CD=4.故填4.点评:此题考查角平分线的性质:角平分线上的任意一点到角的两边距离相等;题目较为简单,属于基础题.17.故答案为:60°.考点:线段垂直平分线的性质;三角形的外角性质.专题:计算题.分析:由三角形的外角性质知∠ADC=∠BAD+∠B,又已知∠BAC=120°,根据三角形内角和定理易得∠B,而AB的垂直平分线交BC于点D,根据垂直平分线的性质知∠BAD=∠B,从而得解.解答:解:由AB=AC,∠BAC=120°,可得∠B=30°,因为点D是AB的垂直平分线上的点,所以AD=BD,因而∠BAD=∠B=30°,从而∠ADC=60度.点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.18.故答案为:115°.考点:线段垂直平分线的性质;三角形内角和定理;三角形的外角性质;角平分线的性质.专题:计算题.分析:先由题意得出垂直平分线垂直且平分BC,BE=EC,由题意可得∠C=∠EBC=12×50°=25度,所以∠AEC=90°+25°=115°.易求解.解答:解:∵AD垂直且平分BC于点,∴BE=EC,∴∠DBE=∠DCE,又∵∠ABC=50°,BE为∠ABC的平分线,∴∠EBC=∠C=12×50°=25°,∴∠AEC=∠C+∠EDC=90°+25°=115°,∴∠AEC=115°.点评:此题考查角的平分线、线段的垂直平分线及外角的相关知识,难度不大,19.故填19.考点:线段垂直平分线的性质.分析:由已知条件,根据垂直平分线的性质得到线段相等,进行线段的等量代换后可得到答案.解答:解:∵△ABC中,DE是AC的中垂线,∴AD=CD,AE=CE=12AC=3cm,∴△ABD得周长=AB+AD+BD=AB+BC=13---①则△ABC的周长为AB+BC+AC=AB+BC+6----②把②代入①得L△ABC=13+6=19cm.△ABC的周长为19cm.故填19.点评:本题考查了线段垂直平分线的性质;解答此题时要注意利用垂直平分线的性质找出题中的等量关系,进行等量代换,然后求解.20.故填38.考点:线段垂直平分线的性质.分析:由已知条件,利用线段的垂直平分线的性质,得到线段相等,结合周长,进行线段的等量代换可得答案.解答:解:因为DE垂直平分AC,根据线段垂直平分线的性质可得△ADB为等腰三角形.所以AD=CD.又因为周长△ABD=AB+BD+AD=AB+BD+CD=26∴周长△ABC=AB+BD+CD+AC=26+2×6=38.故填38.点评:本题考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等),难度一般.进行线段的等量代换是正确解答本题的关键.21.故填70.考点:线段垂直平分线的性质.分析:先利用三角形的内角和求出∠CBE的度数,再利用垂直平分线的性质求出∠DBC的度数,最后利用三角形的内角和求出∠CDB=70度.解答:解:∵△ABC中,∠C=90°,A=35°∴∠CBE=180°-∠C-∠A=180°-90°-35°=55°∵DE是AB的垂直平分线,∴AD=DB,∠A=∠DBE=35°,∴∠DBC=∠CBE-∠DBE=55°-35°=20°在△CDB中,∠C=90,∠DBC=20°,∠CDB=180°-∠C-∠DBC=180°-90°-20°=70°.∠CDB=70度.故填70.点评:此题主要考查线段的垂直平分线的性质及三角形内角和定理等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.22.故填10.考点:线段垂直平分线的性质.分析:根据垂直平分线的性质计算.∠BCD=∠BCN-∠DCA.解答:解:∵Rt△ABC中,∠B=90°,∠A=40°,∴∠BCN=180°-∠B-∠A=180°-90°-40°=50°,∵DN是AC的垂直平分线,∴DA=DC,∠A=∠DCA=40°,∠BCD=∠BCN-∠DCA=50°-40°=10°,∠BCD的度数是10度.故填10.点评:此题主要考查线段的垂直平分线的性质及等腰三角形的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.23.故答案为:20°.考点:线段垂直平分线的性质.分析:根据三角形内角和定理求出∠B+∠C=80°,再根据线段垂直平分线的性质求出∠BAE+∠CAF=∠B+∠C,然后便不难求出∠EAF.解答:解:∵∠BAC=100°,∴∠B+∠C=180°-100°=80°,∵DE、FG分别垂直平分AB和AC,∴∠BAE=∠B,∠CAF=∠C,∴∠BAE+∠CAF=80°,∴∠EAF=100°-80°=20°.故答案为:20°.点评:本题主要考查了线段垂直平分线的性质;得到∠BAE+∠CAF=∠B+∠C是正确解答本题的关键.24.故填12.考点:线段垂直平分线的性质.分析:由已知条件,利用线段的垂直平分线的性质得到线段相等,结合△BDC 的周长为22,可得答案.解答:解:因为DE垂直且平分AB⇒△ADB是等腰三角形⇒AD=BD已知△BDC=BC+BD+CD=22,BC=10⇒AC=12.故填12.点评:本题考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等);进行线段的等量代换是正确解答本题的关键.25.故填4.考点:线段垂直平分线的性质.分析:由已知条件,根据垂直平分线的性质得到EA=8,做差后得到BE的长度.解答:解:∵△ABC中,AB=AC=12,EF为AC的中垂线∴EC=EA=8,BE=12-8=4.BE的长为4.故填4.点评:此题主要考查线段的垂直平分线的性质等几何知识;进行线段的等量代换是正确解答本题的关键.26.故填65.考点:线段垂直平分线的性质.分析:由已知条件,根据垂直平分线的性质得出BD=AD,得到角相等,再根据三角形的内角和计算.解答:解:∵DE是AB的垂直平分线,∴BD=AD,∠A=∠ABD=50°,∵在△ABC中,AB=AC,∴∠ABC=∠C=12(180°-∠A)=12(180°-50°)=65°,∠C=65°.故填65.点评:此题主要考查线段的垂直平分线的性质等几何知识及三角形内角和定理.得到∠A=∠ABD=50°是正确解答本题的关键.27.故填10.考点:线段垂直平分线的性质.分析:由已知条件,运用垂直平分线的性质得到线段相等,进行等量代换后可得三角形的周长.解答:解:∵BC边上的垂直平分线交AC于点D,∴BD=CD.∴△ABD的周长=AB+AD+BD=AB+(AD+CD)=AB+AC=3+7=10.故填10.点评:此题主要考查线段的垂直平分线的性质等几何知识;进行线段的等量代换是正确解答本题的关键.28.故填10.考点:线段垂直平分线的性质.分析:由已知条件,根据垂直平分线性质,得到线段相等,进行线段的等量代换后得到答案.解答:解:∵△ABC中,AB=AC=15cm,D是AB的中点,DE⊥AB于D交AC于E,∴DE是AB的垂直平分线,EB=EA,∵△EBC的周长是25cm,即EB+EC+BC=25,EA+EC+BC=25,BC+AC=25,BC=25-AC=25-15=10.BC的长10cm.故填10.点评:此题主要考查线段的垂直平分线的性质等几何知识;进行线段的等量代换是正确解答本题的关键.29.故填15.考点:线段垂直平分线的性质;三角形内角和定理.分析:由已知条件,求出底角的度数,根据垂直平分线的性质计算可得答案.答:解:∵AB=AC,∠A=50°,∴∠ABC=∠C=(180°-50°)÷2=65°∵DE为AB的中垂线∴AD=BD∴∠ABD=∠A=50°∴∠CBD=∠ABC-∠ABD=15°.故填15.点评:本题考查了线段的垂直平分线的性质及三角形的内角和定理.解决本题的关键是利用线段的垂直平分线性质得到相应线段相等进而得到角相等.。
2.4线段、角的轴对称性(3)教学设计
让学生感受角平分线点的共性,几何画板的一般性图形验证,较好地进行了图形证明.
指导学生活动.
练习:课本P55练习.
延伸:在平面内确定一点M,使它到AB、AC的距离相等且MB=MC.
这题是线段垂直平分线性质和角平分线性质的综合应用.
借助网格画线段的垂直平分线和角平分线有利于学生明确其区别,也有利于学生动手操作,获得成功,调动学生学习的积极性.
小结
1.经历了画图、折纸、猜想、归纳的活动过程,探索得到了角的轴对称性:角是轴对称图形,对称轴是角平分线所在的直线.
2.本节课我们还证明了角平分线的性质定理:角平分线上的点到角的两边的距离相等;反过来,角的内部到角的两边距离相等的点在角的平分线上,从中我们可以发现图形的位置关系与数量关系的内在联系,你能举例说明这种内在的联系吗?
动手操作,验证猜想,描述发现,明确结论.
在操作中感知角的轴对称性,培养口头表达能力.
实践探索三
角平分线是否也有像线段垂直平分线一样的特殊性质呢?
如图,在∠AOB的角平分线OC任意取一点P,PD⊥OA,PE⊥OB,PD与PE相等吗?为什么?
通过证明,你发现了什么?用语言描述你得到的结论.
学生独立思考、积极探究.方法不一,具体如下:
总结
角平分线上的点有什么特点?
讨论后共同小结:
角平分线上的点到角两边的距离相等.
师生互动,锻炼学生的口头表达能力,培养学生勇于发表自己看法的能力.
实践探索四
如果任意一个点在角平分线上,那么这个点到这个角的两边距离相等.反过来,结合上节课所学⊥OA,QE⊥OB,且QD=QE,点Q在∠AOB的角平分线上吗?为什么?
2-4 线段、角的轴对称性(解析版)

姓名: 班级2.4 线段、角的轴对称性本课重点(1)垂直平分线与角平分线的性质与判定 本课难点 (2)利用垂直平分线与角平分线的性质与判定解决实际问题全卷共25题,满分:120分,时间:90分钟一、单选题(每题3分,共30分)1.(2021·河北保定市·八年级期末)ABC 内一点P 到三边距离相等,则点P 一定是ABC ( ) A .三条角平分线的交点B .三边垂直平分线的交点C .三条高的交点D .三条中线的交点【答案】A【分析】根据角平分线上的点到角两边的距离相等即可求解.【详解】解:∵点P 到三边距离相等,∴点P 一定在三条角平分线的交点上,故选:A .【点睛】本题考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键.2.(2021·河北保定市·八年级期末)如图,在ABC 中,BC 的垂直平分线分别交AC ,BC 于点D ,E ,若ABC 的周长为16,3BE =,则ABD △的周长为( )A .6B .10C .12D .20【答案】B 【分析】根据线段垂直平分线的性质可得BD CD =,BE CE =,即可得到10AB AC +=、ABD △的周长为AB AD BD AB AD CD AB AC ++=++=+,即可求解.【详解】解:∵DE 为BC 的垂直平分线,∴BD CD =,BE CE =,∵ABC 的周长为16,3BE =,∴10AB AC +=,∴ABD △的周长为10AB AD BD AB AD CD AB AC ++=++=+=,故选:B .【点睛】本题考查线段垂直平分线的性质,掌握线段垂直平分线的定义与性质是解题的关键.3.(2021·河南省实验中学八年级月考)元旦联欢会上,同学们玩抢凳子游戏,在与A 、B 、C 三名同学距离相等的位置放一个凳子,谁先抢到凳子谁获胜.如果将A 、B 、C 三名同学所在位置看作△ABC 的三个顶点,那么凳子应该放在△ABC 的( )A .三边中线的交点B .三条角平分线的交点C .三边上高的交点D .三边垂直平分线的交点 【答案】D【分析】为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边垂直平分线的交点上. 【详解】∵三角形的三条垂直平分线的交点到三角形三个顶点的距离相等,∴凳子应放在△ABC 的三条垂直平分线的交点最合适,故选:D . 【点睛】本题主要考查了线段垂直平分线的性质的应用,理解基本性质是解题关键.4.(2021·吉林九年级二模)如图,在锐角三角形ABC 中,BC BA >,按以下步骤作图:①以点B 为圆心,BA 长为半径作圆弧,交AC 于点D ;②分别以点A 、D 为圆心,大于12AD 长为半径作圆弧,计两弧交于点E ;③作射线BE ,交AC 于点P ,若60A ∠=︒,则ABP ∠的大小为( )A .20︒B .25︒C .30D .35︒【答案】C【分析】根据作图步骤可知BP ⊥AC ,根据直角三角形两锐角互余的性质即可得答案.【详解】由作图步骤可知:BP ⊥AC ,∴∠BP A =90°,∵60A ∠=︒,∴ABP ∠=90°-∠A =30°,故选:C .【点睛】本题考查尺规作图——作垂线,熟练掌握各基本作图的步骤是解题关键.5.(2021·成都西川中学八年级期中)如图,AD 是△ABC 的角平分线,DF ⊥AB 于点F ,且DE =DG ,S △ADG =24,S △AED =18,则△DEF 的面积为( )A .2B .3C .4D .6【答案】B 【分析】过点D 作DH ⊥AC 于H ,根据角平分线的性质得到DH =DF ,进而证明Rt △DEF ≌Rt △DGH ,根据全等三角形的性质得到△DEF 的面积=△DGH 的面积,根据题意列出方程,解方程得到答案.【详解】解:过点D 作DH ⊥AC 于H ,∵AD 是△ABC 的角平分线,DF ⊥AB ,DH ⊥AC ,∴DH =DF ,在Rt △DEF 和Rt △DGH 中,DF DH DE DG =⎧⎨=⎩,∴Rt △DEF ≌Rt △DGH (HL ), ∴△DEF 的面积=△DGH 的面积,设△DEF 的面积=△DGH 的面积=S ,同理可证,Rt △ADF ≌Rt △ADH ,∴△ADF 的面积=△ADH 的面积,∴24-S =18+S ,解得,S =3,故选:B .【点睛】本题考查的是全等三角形的判定与性质、角平分线的性质,作辅助线构造出全等三角形并利用角平分线的性质是解题的关键.6.(2021·辽宁九年级二模)如图,将△ABC 绕点A 逆时针旋转得到AB C ''△,点C 的对应点为点C ',C B ''的延长线交BC 于点D ,连接AD .则下列说法错误的是( )A .△ABC △ABC ''≅ B .//AB BC ' C .CDC CAC ∠∠''=D .AD 平分BDB '∠【答案】B【分析】A 、根据旋转的性质即可判断;B 、由旋转角的任意性可以判断;C 、由三角形内角和为180︒且两个角相等即可判断;D 、利用角平分线的判定定理即可证明. 【详解】解:A 、由旋转的性质可知:△ABC △ABC ''≅,故A 正确,不符合题意;B 、''ABC 由ABC 绕A 旋转任意角度得到,'//AB BC ∴只是特殊情况,故B 错误,符合题意;C 、''ABC AB C ≌,'C C ∴∠=∠,''1801C AC C ∠=︒-∠-∠,'1802CDC C ∠=︒-∠-∠,''12,CDC CAC ∠=∠∴∠=∠,故C 正确,不符合题意;D 、过A 分别作',C D CB 的垂线,垂直分别是,EF ,''ABC AB C ≌,''BC B C ∴=,''ABC AB C S S =△△; 11''22B C AE BC AF ∴⨯⨯=⨯⨯,AE AF ∴=, ',AE C D AF CB ⊥⊥,AD ∴平分BDB '∠,故D 正确,不符合题意;故选:B .【点睛】本题考查了,旋转的性质、平行线的判定定理、三角形内角和、角平分线,解题的关键是:掌握相关定理依次进行判断.7.(2021·湖南八年级期末)如图,在ABC 中,90C ∠=︒,30B ∠=︒,以A 为圆心,任意长为半径画弧交AB于M 、AC 于N ,再分别以M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,连接AP 并延长交BC 于D ,下列四个结论:①AD 是BAC ∠的平分线;②60ADC ∠=︒;③点D 在AB 的中垂线上;④:1:3ACD ACB S S =△△.其中正确的有( )A.只有①②③B.只有①②④C.只有①③④D.①②③④【答案】D【分析】利用角平分线的性质以及各内角度数和三角形面积求法分别得出即可.【详解】解:根据作图过程可知AD是BAC∠的角平分线,①正确;∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD是∠BAC的平分线,∴∠DAC=∠DAB=30°,∴∠ADC=60°,故②正确;∵∠B=30°,∠DAB=30°,∴AD=DB,∴点D在AB的中垂线上,故③正确;∵∠CAD=30°,∴CD=12AD,∵AD=DB,∴CD=12DB,∴CD=13CB,S△ACD=12CD•AC,S△ACB=12CB•AC,∴S△ACD:S△ACB=1:3,故④正确,故选D.【点睛】本题主要考查尺规作角平分线、角平分线的性质定理、三角形的外角以及等腰三角形的性质,熟练掌握有关知识点是解答的关键.8.(2021·广东七年级期末)如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE BC=,PG//AD交BC于F,交AB于G,①2ACB APB=∠∠;②S△P AC:S△P AB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有()A.①②④B.①③④C.②③④D.①③【答案】B【分析】利用角平分线的性质以及已知条件对①②③④进行一一判断,从而求解.【详解】解:∵P A平分∠CAB,PB平分∠CBE,∴∠P AB=12∠CAB,∠PBE=12∠CBE,∵∠CBE=∠CAB+∠ACB,∠PBE=∠P AB+∠APB,∴∠ACB=2∠APB;故①正确;过P作PM⊥AB于M,PN⊥AC于N,PS⊥BC于S,∴PM=PN=PS,∴PC平分∠BCD,∵S △P AC :S △P AB =(12AC •PN ):(12AB •PM )=AC :AB ;故②不正确;∵BE =BC ,BP 平分∠CBE ∴BP 垂直平分CE ,故③正确;∵PG ∥AD ,∴∠FPC =∠DCP ∵PC 平分∠DCB ,∴∠DCP =∠PCF ,∴∠PCF =∠CPF ,故④正确.本题正确的有:①③④故选:B .【点睛】此题主要考查了角平分线的性质和定义,平行线的性质,线段的垂直平分线的判定,等腰三角形的性质等.9.(2021·内蒙古中考真题)如图,在Rt ABC 中,90ACB ∠=︒,根据尺规作图的痕迹,判断以下结论错误的是( )A .BDE BAC ∠=∠B .BAD B =∠∠C .DE DC =D .AE AC =【答案】B 【分析】先通过作图过程可得AD 平分∠BAC ,DE ⊥AB ,然后证明△ACD ≌△AED 说明C 、D 正确,再根据直角三角形的性质说明选项A 正确,最后发现只有AE =EB 时才符合题意.【详解】解:由题意可得:AD 平分∠BAC ,DE ⊥AB ,在△ACD 和△AED 中∠AED =∠C ,∠EAD =∠CAD ,AD =AD∴△ACD ≌△AED (AAS )∴DE =DC ,AE =AC ,即C 、D 正确;在Rt △BED 中,∠BDE =90°-∠B 在Rt △BED 中,∠BAC =90°-∠B ∴∠BDE =∠BAC ,即选项A 正确;选项B ,只有AE =EB 时,才符合题意.故选B .【点睛】本题主要考查了尺规作图、全等三角形的性质与判定、直角三角形的性质,正确理解尺规作图成为解答本题的关键.10.(2021·江西八年级期末)如图,在ABC 中,DE 是边AC 的垂直平分线,交AC 于点D ,交AB 于点E ,点P 是直线DE 上的一个动点,若5AB =,则PB PC +的最小值为( )A .5B .6C .7D .8【答案】A 【分析】由条件可得点A 是点C 冠以ED 的对称点,即求PB+PC 的最小值就是求PB+PA 的最小值,在点P 运动的过程中,P 与E 重合时有最小值.【详解】解:∵ED 是AC 的垂直平分线,∴PC+PB=PA+PB ,∵P 运动的过程中,P 与E 重合时有最小值,∴PB+PC 的最小值=AB=5.故选:A 【点睛】本题主要考查动点最短路径问题,结合对称,寻找对称点,判断最值状态是解题的关键.二、填空题(每题3分,共24分)11.(2021·静宁县阿阳实验学校八年级期末)如图,123,,l l l 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 ____ 处.【答案】4.【分析】作直线l 1、l 2、l 3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P 1、P 2、P 3,内角平分线相交于点P 4,然后根据角平分线的性质进行判断.【详解】解:如图示,作直线l 1、l 2、l 3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P 1、P 2、P 3,内角平分线相交于点P 4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等. 故答案是:4.【点睛】本题考查了角平分线的性质,熟悉相关性质是解题的关键.12.(2021·全国九年级专题练习)如图,在△ABC中,AB=6,AC=8,BC=11,AB的垂直平分线分别交AB,BC于点D、E,AC的垂直平分线分别交AC,BC于点F、G,则△AEG的周长为__.【答案】11.【分析】根据线段垂直平分线的性质可得EA=EB,GA=GC,所以可求出△AEG的周长.【详解】解∵DE是线段AB的垂直平分线,∴EA=EB,同理,GA=GC,∴△AEG的周长=AE+EG+GA=EB+EG+GC=BC=11,故答案为:11.【点睛】本题考查了线段垂直平分线的性质.线段垂直平分线上的点到线段两端点的距离相等.13.(2021·全国八年级专题练习)已知:如图,点P在线段AB外,且P A=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则下列作法正确的是________.①作∠APB的平分线PC交AB于点C②过点P作PC⊥AB于点C且AC=BC③取AB中点C,连接PC④过点P作PC⊥AB,垂足为C【答案】①③④ 【分析】利用判断三角形全等的方法判断四个选项是否成立即可.【详解】解:①利用SAS 判断出△PCA ≌△PCB ,∴CA =CB ,∠PCA =∠PCB =90°,∴点P 在线段AB 的垂直平分线上,故正确; ②过线段外一点作已知线段的垂线,不能保证也平分此条线段,故错误;③利用SSS 判断出△PCA ≌△PCB ,∴∠PCA =∠PCB =90°,∴点P 在线段AB 的垂直平分线上,故正确;④利用HL 判断出△PCA ≌△PCB ,∴CA =CB ,∴点P 在线段AB 的垂直平分线上,故正确;故答案为:①③④.【点睛】此题主要考查了全等三角形的判定,线段垂直平分线的判定,熟练掌握全等三角形的判断方法是解本题的关键.14.(2021·广东八年级期末)在△ABC 中,AB =5,BC =8,AC =6,AD 平分∠BAC ,则S △ABD :S △ACD =___.【答案】5:6【分析】过D 作DE ⊥AB 于E ,DF ⊥AC 于F ,根据角平分线的性质得出DE =DF ,根据三角形的面积公式求出答案即可.【详解】解:过D 作DE ⊥AB 于E ,DF ⊥AC 于F ,∵AD 平分∠BAC ,∴DE =DF ,设DE =DF =R ,∵S △ABD =12AB DE ⨯⨯=152⨯⨯R ,S △ACD =12AC DF ⨯⨯=162R ⨯⨯, ∴S △ABD :S △ACD =5:6,故答案为:5:6.【点睛】本题考查了三角形的面积和角平分线的性质,注意:角平分线上的点到角的两边的距离相等. 15.(2021·四川八年级期末)如图,在Rt ABC 中,90C ∠=︒,利用尺规在BA ,BC 上分别截取BM BN =;分别以点M ,N 为圆心,以大于12MN 的长为半径作弧,两弧在CBA ∠内部交于点E ;作射线BE 交AC 于点F .若2CF =,点H 为线段AB 上的一动点,则FH 的最小值是______.【答案】2【分析】如图,过点F 作FG ⊥AB 于G .根据角平分线的性质定理证明GF =FC =2,利用垂线段最短即可解决问题.【详解】解:如图,过点F 作FG ⊥AB 于G .由作图可知,FB 平分∠ABC ,∵GF ⊥BA ,FC ⊥BC ,∴GF =FC =2,根据垂线段最短可知,HF 的最小值为2,故答案为:2.【点睛】本题考查作图-基本作图,垂线段最短,角平分线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.16.(2021·辽宁九年级二模)如图,在Rt ABC 中,90,22,C B PQ ∠∠=︒=︒垂直平分AB ,垂足为Q ,交BC 于点P .按以下步骤作图:以点A 为圆心,以适当的长为半径作弧,分别交边AC ,AB 于点D ,E ;分别以点D ,E 为圆心,以大于12DE 的长为半径作弧,两弧相交于点F ;作射线AF ,射线AF 与直线PQ 相交于点G ,则AGQ ∠的度数为__________度.【答案】56【分析】根据直角三角形两锐角互余得∠BAC =68°,由角平分线的定义得∠BAG =34°,由线段垂直平分线可得△AQG 是直角三角形,根据直角三角形两锐角互余即可求出∠AGQ .【详解】解:∵△ABC 是直角三角形,∠C =90°,∴∠B +∠BAC =90°,∵∠B =22°,∴∠BAC =90°−∠B =90°−22°=68°,由作法可知,AG 是∠BAC 的平分线,∴∠BAG =12∠BAC =34°,∵PQ 是AB 的垂直平分线,∴△AGQ 是直角三角形,∴∠AGQ +∠BAG =90°,∴∠AGQ =90°−∠BAG =90°−34°=56°,故答案为:56.【点睛】此题考查了直角三角形两锐角互余,角平分线的定义,线段垂直平分线的性质等知识,熟知角平分线和中垂线的尺规作法是解题的关键.17.(2021·山东济南市·七年级期末)如图,在ABC 中,120BAC ∠=︒,分别作AC ,AB 两边的垂直平分线PM 、PN ,垂足分别是点M 、N .以下说法正确的是______(填序号).①60P ∠=︒;②EAF B C ∠=∠+∠;③PE PF =;④点P 到点B 和点C 的距离相等.【答案】①②④【分析】根据垂直的定义、四边形内角和等于360°计算,判断①;根据线段垂直平分线的性质得到EC =EA ,FB =F A ,进而得到∠EAC =∠C ,∠F AB =∠B ,经过计算判断②;根据等腰三角形的性质判断③,根据线段垂直平分线的性质判断④.【详解】解:∵PM 垂直平分AC ,PN 垂直平分AB ,∴∠PMA =∠PNA =90°,∠BAC =120°∴∠P =360°-90°-90°-120°=60°,①说法正确;∵∠BAC =120°,∴∠B +∠C =180°-120°=60°,∵PM 垂直平分AC ,PN 垂直平分AB ,∴EC =EA ,FB =F A ,∴∠EAC =∠C ,∠F AB =∠B , ∴∠EAF =∠BAC -∠EAC -∠F AB =∠BAC -(∠B +∠C )=120°-60°=60°,∴ ∠EAF =∠B +∠C ,②说法正确;△ABC 不一定是等腰三角形,∴PE 与PF 的大小无法确定,③说法错误;连接PC 、P A 、PB ,∵PM 垂直平分AC ,PN 垂直平分AB ,∴PC =P A ,PB =P A ,∴PB =PC ,即点P 到点B 和点C 的距离相等,④说法正确,故答案为:①②④.【点睛】本题考查的是线段垂直平分线的性质、三角形内角和定理,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.18.(2021·四川成都铁路中学八年级期中)已知:△ABC 是三边都不相等的三角形,点P 是三个内角平分线的交点,点O 是三边垂直平分线的交点,当P 、O 同时在不等边△ABC 的内部时,那么∠BOC 和∠BPC 的数量关系是___.【答案】4360BPC ∠-︒【分析】根据三角形角平分线的性质以及三角形内角和定理,即可得到2180BAC BPC ∠=∠-︒;再根据三角形垂直平分线的性质以及三角形内角和定理,即可得到2BOC BAC ∠=∠,进而得出BOC ∠和BPC ∠的数量关系.【详解】解:BP 平分ABC ∠,CP 平分ACB ∠,12PBC ABC ∴∠=∠,12PCB ACB ∠=∠, 180()BPC PBC PCB ∴∠=︒-∠+∠180(=︒-11)22ABC ACB ∠+∠1180()2ABC ACB =︒-∠+∠ 1180(180)2BAC =︒-︒-∠1902BAC =︒+∠,即2180BAC BPC ∠=∠-︒; 如图,连接AO .点O 是这个三角形三边垂直平分线的交点,OA OB OC ∴==,OAB OBA ∴∠=∠,OAC OCA ∠=∠,OBC OCB ∠=∠,1802AOB OAB ∴∠=︒-∠,1802AOC OAC ∠=︒-∠,360()BOC AOB AOC ∴∠=︒-∠+∠360(18021802)OAB OAC =︒-︒-∠+︒-∠,22OAB OAC =∠+∠2BAC =∠2(2180)BPC =∠-︒4360BPC =∠-︒,故答案为:4360BPC ∠-︒.【点睛】本题考查了三角形的垂直平分线与角平分线,熟练掌握三角形的垂直平分线与角平分线的性质是解题的关键.三、解答题(19-22题每题9分,其他每题10分,共66分)19.(2021·山东八年级期末)某地有两所大学和两条相交的公路,如图所示(点M ,N 表示大学,OA ,OB 表示公路)现计划修建一座物资仓库到两所大学的距离相等,到两条公路的距离也相等.请你用尺规确定仓库所在的位置.【答案】作图见解析.【分析】根据题意,分别作AOB ∠的平分线和MN 的垂直平分线即可求得【详解】解:分别作AOB ∠的平分线和MN 的垂直平分线;作图步骤如下:①以O 为圆心,任意长度为半径作弧,交,OA OB 于两点,C D ,分别以,C D 为圆心,以大于12CD 为半径在角的内部分别作弧,交于一点E ,作射线OE ;②分别以,M N 为圆心,以大于12MN 为半径在MN 的两侧分别作弧,交于,F G ,作直线FG ;FG 与OE 的交点P 即为所求如图所示,P 在AOB ∠的平分线和MN 的垂直平分线的交点上,点P 就是仓库应该修建的位置.【点睛】本题考查了角平分线的性质,垂直平分线的性质,以及角平分线和垂直平分线的作图,熟练作图步骤是解题的关键.20.(2021·重庆南开中学七年级期末)如图,在Rt ABC 中,90ACB ∠=︒,点D 在BC 边上,连接AD ,点E 、F 分别为AB 边,AC 边上的点,连接DE 、DF ,使得DA 平分∠EDF ,且DE =DF ,过点D 作DG ⊥AB 于点G .(1)若DF //AB ,求证:AE =DE ;(2)求证:DG =CD .【答案】见详解【分析】(1)先利用平行线性质证得EAD ADF ∠=∠,再利用角平分线的定义证得EDA ADF ∠=∠,利用等量代换可得EDA EAD ∠=∠,即可得到答案AE =DE ;(2)先证AED AFD ≌,得EAD FAD ∠=∠,即可利用角平分线的性质得到答案.【详解】解:(1)∵//DF AB ∴EAD ADF ∠=∠∵DA 平分∠EDF ∴EDA ADF ∠=∠∴EDA EAD ∠=∠∴AE =DE .(2)∵EDA ADF ∠=∠,DE =DF ,AD=AD∴AED AFD ≌∴EAD FAD ∠=∠∵90ACB ∠=︒,DG ⊥AB ∴DG =CD .【点睛】本题考查了平行线的性质、角平分线的性质以及全等的应用,解题关键是利用性质找到角与角之间的关系.21.(2021·福建九年级一模)如图,将ABC 绕点A 按逆时针方向旋转DAC ∠的度数得到AED .(1)尺规作图:确定AED 的顶点E 的位置(保留作图痕迹,不写作法与证明过程);(2)连接AE,DE,设BC的延长线交DE于点G,连接AG.求证:AG平分DGB∠.【答案】(1)作图见解析,(2)证明见解析.【分析】(1)作∠EAB=∠DAC,截取AE=AB即可;(2)作AN⊥DE,AC⊥BC,交ED延长线于N,BG于M,证AN=AM即可.【详解】解:(1) 点E位置如图所示;(2)证明:作AN⊥DE,AC⊥BC,交ED延长线于N,BG于M,由旋转可知AED≌ABC,DE=BC,∴12AEDS DE AN=⋅,12ABCS BC AM=⋅,∴1122DE AN BC AM⋅=⋅,∴AN AM=,∴AG平分DGB∠.【点睛】本题考查了尺规作图和角平分线的判定,解题关键是明确尺规作图方法,熟练运用角平分线的判定证明.22.(2021.江苏八年级期中)如图,ABC中,边AB BC,的垂直平分线交于点P.==.(2)点P是否也在边AC的垂直平分线上?请说明理由.(1)求证:PA PB PC【答案】(1)见解析;(2)在,理由见解析【分析】(1)根据线段的垂直平分线的性质可求得,P A=PB,PB=PC,则P A=PB=PC.(2)根据线段的垂直平分线的性质的逆定理,可得点P在边AC的垂直平分线上.【详解】解:(1)证明:∵边AB、BC的垂直平分线交于点P,∴P A=PB,PB=PC.∴P A=PB=PC.(2)∵P A=PC,∴点P在边AC的垂直平分线上.【点睛】此题主要考查线段垂直平分线的性质定理及逆定理:(1)线段垂直平分线上的点和这条线段的两个端点的距离相等;(2)和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.23.(2021·湖南怀化市·八年级期末)如图.在△ABC中,∠C=90 °,∠A=30°.(1)用直尺和圆规作AB的垂直平分线,分别交AB、AC于D、E,交BC的延长线于F,连接EB.(不写作法,保留作图痕迹)(2)求证:EB平分∠ABC.(3)求证:AE=EF.【答案】见解析【分析】(1)先作线段AB的垂直平分线DE,再延长BC即可;(2)先利用直角三角形的性质求∠ABC= 60︒,再垂直平分线的性质得到∠ABE=∠A=30︒,再求出∠EBC=∠ABC-∠ABE=30︒,即可得到∠EBC=∠ABE,得到答案;(3)证明:先利用直角三角形的性质求∠DEB=90︒-∠ABE =60︒再利用三角形外角的性质求∠EFB=∠DEB-∠EBC=60︒-30︒=30︒,进而得∠EFB=∠EBC,证得BE=EF,又因为AE= BE,利用等量代换即可求得答案.【详解】(1)如图,即为所求;(2)证明:∵DE 是AB 的垂直平分线∴DE ⊥AB ∴AE=BE∵∠A=30︒,∠ACB=90︒∴∠ABE=∠A=30︒,∠ABC=90︒-∠A=60︒∴∠EBC=∠ABC-∠ABE=60︒-30︒=30︒∴∠EBC=∠ABE ∴EB 平分∠ABC .(3)证明:∵DE 是AB 的垂直平分线∴DE ⊥AB ∴∠DEB=90︒-∠ABE =60︒∴∠EFB=∠DEB-∠EBC=60︒-30︒=30︒∴∠EFB=∠EBC ∴BE=EF又∵AE= BE ∴AE=EF 【点睛】本题考查了尺规作图和垂直平分线性质得应用,解决此题的关键利用尺规作图,画出图形. 24.(2021·石家庄市第四十中学九年级二模)如图,在ABC 中,D 为BC 中点,DE BC ⊥交BAC ∠的平分线AE 于E ,EF AB ⊥于F ,EG AC ⊥交AC 的延长线于G .(1)求证:BF CG =;(2)若5AB =,3AC =,求AF 的长.【答案】(1)见解析;(2)4【分析】(1)连接BE 、EC ,证明Rt BFE △≌Rt CGE △即可;(2)证明Rt AEF Rt AEG △≌△,则AF AG =,继而求得AF 的长【详解】(1)证明:如图,连接BE 、EC ,∵ED BC ⊥,D 为BC 中点,∴BE EC =,∵EF AB ⊥,EG AG ⊥,且AE 平分FAG ∠,∴FE EG =,在Rt BFE △和Rt CGE △中,BE CE EF EG =⎧⎨=⎩,∴Rt BFE △≌Rt CGE △(HL )∴BF CG =. (2)解:在Rt AEF 和Rt AEG 中,AE AE EF EG =⎧⎨=⎩, ∴Rt AEF Rt AEG △≌△(HL ),∴AF AG =,∴2AB AC AF BF AG CG AF +=++-=,∴28AF =,∴4AF =.【点睛】本题考查了角平分线的性质,垂直平分线的性质,直角三角形全等的证明,全等三角形的性质,正确的作出辅助线是解题的关键.25.(2020·湖北)(1)模型:如图1,在ABC 中,AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,求证:::ADB ADC S S AB AC =△△.(2)模型应用:如图2,AD 平分EAC ∠交BC 的延长线于点D ,求证:::AB AC BD CD =.(3)类比应用:如图3,AB 平分DAE ∠,AE AD =,180D E ∠+∠=︒,求证:::BE CD AB AC =.【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析;【分析】(1)由题意得DE=DF,12ADBS AB DE∆=,12ADCS AC DF∆=,即可得出ADBS∆:ADCS∆=AB:AC;(2)在AB上取点E,使得AE=AC,根据题意可证△ACD≌△AED,从而可求出BD DEAB AE=,BD CDAB AD=,即可求解;(3)延长BE至M,使EM=DC,连接AM,根据题意可证△ADC≌△AEM,故而得出AE为∠BAM的角平分线,即AB AM ACBE EM DC==,即可得出答案;【详解】解:(1)∵AD平分∠BAC,DE⊥AB,DE⊥AC,∴DE=DF,∵12ADBS AB DE∆=,12ADCS AC DF∆=,∴ADBS∆:ADCS∆=AB:AC;(2)如图,在AB上取点E,使得AE=AC,连接DE 又∵AD平分∠CAE,∴∠CAD=∠DAE,在△ACD和△AED中,AC AECAD DAEAD AD=⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△AED(SAS),∴CD=DE且∠ADC=∠ADE,∴BD DEAB AE=,∴BD CDAB AD=,∴AB:AC=BD:CD;(3)如图延长BE至M,使EM=DC,连接AM,∵∠D+∠AEB=180°,又∵∠AEB+∠AEM=180°,∴∠D=∠AEM,在△ADC与△AEM中,AD AED AEMDC EM=⎧⎪∠=∠⎨⎪=⎩,∴△ADC≌△AEM(SAS),∴∠DAC=∠EAM=∠BAE,AC=AM,∴AE为∠BAM的角平分线,故AB AM ACBE EM DC==,∴BE:CD=AB:AC;【点睛】本题考查了全等三角形的判定与性质、角平分线的性质、以及三角形的面积的应用,正确掌握知识点是解题的关键;。
2.4线段、角的轴对称性(1)(2)

_________________________________.的周,厘米,的垂直平分线..如图,要在公路旁设一个公交车的停车站,停车站应设在什么地方,,边BC的垂直平分线分别交AB、AC于点2.4线段、角的轴对称性(2)课型:新授课主备人:董兰审核人:凌林授课时间:2014.9二次备课【学习目标】1.探索并证明线段垂直平分线的性质定理的逆定理,会用尺规作线段的垂直平分线;2.能利用所学知识提出问题并解决实际问题;3.经历探索线段的轴对称的过程,在“操作——探究——归纳——证明”的过程中培养思考的严谨性和表达的条理性.【学习重点】利用线段的轴对称性探索线段垂直平分线的性质定理的逆定理.【学习难点】灵活运用线段垂直平分线的性质解决实际问题.【预习作业】1.线段的垂直平分线上的点_____________________________________.2.到线段两端距离相等的点,在_________________________________.3.如图.∵QA=QB.∴____________________________.4.到三角形的三个顶点距离相等的点是()A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三条边的垂直平分线的交点5.如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F∵点P是AB边垂直平线上的一点∴_____ =_________ ().同理,PB=______.∴______ = ______(等量代换).∴点P在AC的垂直平分线上.(到线段两端距离相等的点,在这条线段的______________________)∴AB,BC,AC的垂直平分相交于同一点.6.有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在()A.在AC,BC两边高线的交点处B.在AC,BC两边中线的交点处C.在AC,BC两边垂直平分线的交点处D.在∠A,∠B两内角平分线的交点处)你能根据图形用符号语言表示你发现的结论吗?在线段的垂直平分线上的点都具有同一个性质而毫无例外;反之,具有这一性质的点都在这条线段的垂直平分线上而无一遗漏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O E Q
B
通过上述研究,你得到了什么结论?
2.4 线段、角的对称性(3)
说说你本节课你有什么收获?
2.4 线段、角的对称性(3)
作业:
P58习题2.4,分析第7、8题的思路,任 选1题写出过程.
初中数学
八年级(上册)
2.4
作
线段、角的对称性(3)
者:王正东(盐城市射阳县长荡初级中学)
AOB
2.4 线段、角的对称性(3)
做一做
在一张薄纸上画 ∠AOB,操作并思考: 它是轴对称图形吗? 为什么?
A O B
2.4 线段、角的对称性(3)
想一想
角是轴对称图形,它的对称轴在哪里?为什么?
A O
C
B
角是轴对称图形,角平分线所在的直线是它的对称轴.
2.4 线段、角的对称性(3)
想一想
如图,在∠AOB的角平分线OC任意取一点P, PD⊥OA,PE⊥OB,PD与PE相等吗?为什么?
D A P C E B
O
定理
角平分线上的点到角两边的距离相等.
2.4 线段、角的对称性(3)
想一想
角内部一点到角两边的距离相等,那么这个点 在这个角的角平分线上吗?
