1二进制及其转换
二进制及其转换教案

二进制及其转换教案 The document was prepared on January 2, 2021二进制及其转换[教学目标]1、认知目标(1)掌握进位制概念;(2)理解进制的本质;(3)掌握十进制和二进制的相互转换;(4)了解计算机所采用的数制及计算机采用二进制数的原因。
2、技能目标掌握二进制数和十进制数转换以及运算规则。
3、能力目标对学生思维能力进行拓展,激发他们探索计算机奥秘的欲望。
[教学重点](1)进制的本质组成(2)十进制与二进制间的相互转换[难点](1)进制的本质组成(2)十进制与二进制间的相互转换[教学方法]讲授法举例法[授课地点]普通教室,不用多媒体[教学过程]一、引入新课对计算机稍微了解的同学就知道计算机中使用的进位制是二进制,那什么是二进制,它跟我们数学上使用的十进制有什么联系。
这节课准备给大家补充点二进制的知识,这跟数学关系很密切,请同学务必认真听课。
二、切入课堂内容1、什么是进位制提出问题:什么是进位制最常见的进位制是什么学生普遍回答是十进制。
教师继续提问:那十进制为什么叫十进制引起学生的思考。
(部分经过思考的学生回答是约定的)教师提醒学生一起回忆幼儿园开始学习算术的情景。
当是我们是从最简单的个位数相加学起,比如2+3=,当时我们会数手指,2个手指+3个手指等于5个手指,答案为5。
那4+6呢4个手指+6个手指等于10个手指,10个手指刚好够用。
那6+9呢当时我们就困惑了。
记得当时老师是告诉我们把6拆成1+5,9+1=10,这时老师跟我们约定用一个脚趾表示10,另外用5个手指表示5。
这样通过脚趾,我们就成功解决了两个数相加超过10的问题。
教师提问:那当时我们为什么要约定10呢,为什么用9或11引起学生思考。
(部分经过思考的学生回答为了方便运算)教师提问:除此之外还有哪些常见的进位制请举例说明。
拓展学生的思维。
有学生回答60进制(时分秒的换算),360进制(1周=360度),二进制等等。
二进制数的基本概念与转换知识点总结

二进制数的基本概念与转换知识点总结二进制数是计算机科学中的重要概念,它在数据处理、储存和传输中起到至关重要的作用。
本文将介绍二进制数的基本概念与转换知识点,帮助读者更好地理解和运用二进制数。
一、二进制数的基本概念二进制数是一种由0和1组成的数制系统,与我们平常使用的十进制数制有所不同。
在二进制数中,每一位的权值是2的幂次方,从右向左依次增加。
例如,二进制数1101表示十进制数13。
二、二进制数的转换1. 十进制转换为二进制将给定的十进制数通过不断除以2,并记录余数,直到商为0为止。
最后将记录的余数从下往上依次排列,即为该十进制数的二进制表示。
例如,将十进制数27转换为二进制数:27 ÷ 2 = 13 (1)13 ÷ 2 = 6 (1)6 ÷ 2 = 3 03 ÷ 2 = 1 (1)1 ÷ 2 = 0 (1)所以,27的二进制表示为11011。
2. 二进制转换为十进制对于给定的二进制数,从右向左依次给每一位赋予对应的权值,并将其相加,即可得到该二进制数对应的十进制数。
例如,将二进制数11011转换为十进制数:(1 × 2^4) + (1 × 2^3) + (0 × 2^2) + (1 × 2^1) + (1 × 2^0) = 16 + 8 + 0 +2 + 1 = 27所以,二进制数11011表示的是十进制数27。
3. 八进制和十六进制转换为二进制八进制和十六进制数与二进制数之间存在对应关系。
将八进制数每一位转换为对应的三位二进制数,将十六进制数每一位转换为对应的四位二进制数,即可完成转换。
例如,将八进制数27转换为二进制数:2(八进制)= 010(二进制)7(八进制)= 111(二进制)所以,八进制数27对应的二进制数为010111。
将十六进制数AC转换为二进制数:A(十六进制)= 1010(二进制)C(十六进制)= 1100(二进制)所以,十六进制数AC对应的二进制数为10101100。
二进制转化换为十进制的公式

二进制转化换为十进制的公式二进制转化为十进制是一种常见的数值转换方法。
在计算机科学和信息技术领域中,二进制被广泛应用于数据存储和传输。
而在某些情况下,需要将二进制数转换为十进制以便于人们理解和使用。
下面将介绍二进制转化为十进制的公式及其应用。
一、二进制转化为十进制的公式要将一个二进制数转化为十进制,可以使用以下公式:十进制数 = a0 * 2^0 + a1 * 2^1 + a2 * 2^2 + ... + an * 2^n其中,a0, a1, a2, ..., an 表示二进制数中的每一位数字,n表示二进制数的总位数。
二、公式应用举例为了更好地理解二进制转化为十进制的过程,我们来看一个简单的例子。
假设有一个二进制数1101,我们要将其转换为十进制。
根据公式,我们可以得到:十进制数 = 1 * 2^0 + 0 * 2^1 + 1 * 2^2 + 1 * 2^3= 1 + 0 + 4 + 8= 13所以,二进制数1101转换为十进制为13。
三、二进制转化为十进制的应用场景二进制转化为十进制在计算机科学和信息技术领域中具有广泛的应用。
1. 数据存储和传输计算机中的数据以二进制形式存储和传输。
在某些情况下,需要将二进制数据转换为十进制以便于人们理解和使用。
例如,在计算机网络中传输的IP地址就是以二进制形式存储的,但在实际使用中我们更习惯使用十进制来表示。
2. 计算机编程在计算机编程中,二进制和十进制之间的转换也是常见的操作。
例如,在一些编程语言中,需要将用户输入的二进制数转换为十进制进行计算,或者将计算结果转换为十进制以便于输出。
3. 数字逻辑电路设计在数字逻辑电路设计中,二进制数常用于表示和操作电路的状态和信号。
而在设计过程中,需要将二进制数转换为十进制以进行分析和验证。
四、注意事项在进行二进制转化为十进制的过程中,需要注意以下几个问题。
1. 二进制数中的每一位只能是0或1,不能出现其他数字。
2. 二进制数的最高位对应的指数为n,最低位对应的指数为0。
二进制十进制和十六进制及其相互转换的公式

二进制十进制和十六进制及其相互转换的公式二进制、十进制和十六进制是计算机科学中常用的数制。
在计算机中,数据以二进制的形式表示,但是对于人类来说,二进制形式并不直观,因此使用十进制和十六进制进行数据展示和计算更为常见。
本文将介绍二进制、十进制和十六进制之间的转换公式。
一、二进制转十进制二进制是由0和1两个数字组成的数制。
每一位二进制位所代表的数值是2的n次方,其中n为该二进制位的位置,从右向左逐渐增加。
例如,二进制数1101,可以表示为:(1*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=8+4+0+1=13所以二进制数1101等于十进制数13二、十进制转二进制十进制数是由0-9这十个数字组成的数制。
将十进制数转换成二进制数的方法是不断地对十进制数进行除以2的整除运算,直到商为0,然后将每次的余数倒序排列。
例如,将十进制数53转换成二进制数:53÷2=26余126÷2=13余013÷2=6余16÷2=3余03÷2=1余11÷2=0余1三、十六进制和二进制、十进制的转换十六进制数是由0-9这十个数字和A-F这六个字母组成的数制,其中A代表10,B代表11,依此类推,F代表15、十六进制数可以很方便地将二进制数字转换成较短的字符表示,同时也更加直观。
1.二进制转十六进制:将二进制数每四位一组,从右向左进行分组,并将每个分组转换成对应的十六进制字符。
0110(6)1101(D)0101(5)1011(B)转换结果为6D5B。
2.十六进制转二进制:将十六进制数中的每个字符逐个转换成对应的四位二进制数。
例如,将十六进制数3A转换成二进制数:3->0011A->10103.十六进制转十进制:将十六进制数中的每个字符逐个转换成对应的十进制数,然后将这些十进制数相加即可得到结果。
例如,将十六进制数1F转换成十进制数:1*16^1+F*16^0=16+15=31所以十六进制数1F等于十进制数314.十进制转十六进制:将十进制数不断地进行除以16的整除运算,直到商为0,然后将每次的余数倒序排列,并将每个余数转换成对应的十六进制字符。
七年级上册二进制及其转换

七年级上册二进制及其转换一、二进制的概念。
1. 定义。
- 在数学和数字电路中,二进制(binary)是一种以2为基数的记数法,通常用0和1来表示。
它是计算机技术中广泛采用的一种数制。
例如,在二进制中,10表示的是十进制中的2(因为1×2^1 + 0×2^0=2)。
2. 与十进制的对比。
- 十进制是我们日常生活中最常用的数制,它以10为基数,有0 - 9十个数字。
而二进制只有0和1两个数字。
这是因为计算机的硬件基础是电子元件,这些元件通常只有两种稳定的状态,如电路的通和断、电压的高和低等,正好可以用0和1来表示。
二、二进制转换为十进制。
1. 转换方法。
- 按位权展开法。
对于一个二进制数b_nb_n - 1·s b_1b_0(其中b_i为0或1),它转换为十进制数的公式为D=∑_i = 0^nb_i×2^i。
- 例如,将二进制数101转换为十进制:- 这里n = 2,b_2=1,b_1=0,b_0=1。
- 根据公式D = b_2×2^2+b_1×2^1+b_0×2^0=1×2^2+0×2^1+1×2^0=4 + 0+1=5。
三、十进制转换为二进制。
1. 除2取余法。
- 把十进制数除以2,取余数,然后将商继续除以2,再取余数,直到商为0。
最后将所有的余数从右到左排列,就得到了对应的二进制数。
- 例如,将十进制数13转换为二进制:- 13÷2 = 6·s·s1(余数为1)- 6÷2 = 3·s·s0(余数为0)- 3÷2 = 1·s·s1(余数为1)- 1÷2 = 0·s·s1(余数为1)- 从右到左排列余数得到1101,所以十进制数13转换为二进制是1101。
1-2数制及其转换

3
一. 计算机中的数制
数制的基本要素 Decimal , Binary, Hexadecimal
2
但,一味的把数写成二进制又不符合人类的书写习惯 如,二进制代码 00010010001101000101 由于代码太长,写起来麻烦,而且容易出错。 由于代码太长,写起来麻烦,而且容易出错。 所以,在计算机中引入了多种计数法,常见的数制有: 所以,在计算机中引入了多种计数法,常见的数制有:
Decimal , Binary, Hexadecimal
20
5. 二进制数→十六进制数 6. 十六进制数→二进制数
四合一 一分为四
以小数点为界, 位十六进制数对应4 以小数点为界,1位十六进制数对应4位二进制数
( A7B8.C9)16 = ( 1010 0111 1011 1000 .1100 1001 )2 11001001
【方法】将每一位十六进制数用对应的4位二进制数来 方法】将每一位十六进制数用对应的 位二进制数来 表示,其最左侧和最右侧的 可以省去 可以省去。 表示,其最左侧和最右侧的0可以省去。
简化算法: 简化算法:
1111B =10000B - 1 1× = 1 ×2 4 - 1 = 16 -1 = 15
8
~~~
课堂练习3:把二进制数转换成十进制
1111 1111B = (
255 ) D
简化算法: 简化算法:
1111 1111B = 1 0000 0000B - 1 1× = 1 ×2 8 - 1 = 256 -1 = 255
数字的进制小学数学中的二进制八进制与十六进制

数字的进制小学数学中的二进制八进制与十六进制数字的进制——小学数学中的二进制、八进制与十六进制数字的进制是数学中一个非常重要的概念。
在小学数学教学中,除了常用的十进制之外,还有其他进制数的概念,如二进制、八进制和十六进制。
本文将介绍这三种进制数的基本概念、表示方法及其在计算机领域的应用。
一、二进制的概念二进制是一种基础的计数系统,使用的数字只有0和1。
在二进制中,每一位数字的权值是2的幂次方,从右至左依次增加。
例如,二进制数1101表示为(1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (1 × 2^0) = 13。
二、八进制的概念八进制是一种计数系统,使用的数字有0-7共八个。
在八进制中,每一位数字的权值是8的幂次方,从右至左依次增加。
例如,八进制数725表示为(7 × 8^2) + (2 × 8^1) + (5 × 8^0) = 469。
三、十六进制的概念十六进制是一种计数系统,使用的数字有0-9十个和A-F六个,共十六个。
在十六进制中,每一位数字的权值是16的幂次方,从右至左依次增加。
例如,十六进制数A5B表示为(10 × 16^2) + (5 × 16^1) + (11 × 16^0) = 2643。
四、进制间的转换方法在小学数学中,了解不同进制的转换方法有助于提升学生的数学运算能力。
下面将介绍二进制、八进制和十六进制之间的转换方法。
1. 二进制转换为十进制:按权展开法,将每一位数字的权重相加即可得到十进制数。
2. 十进制转换为二进制:将十进制数逐步除以2,得到的余数从下往上组成二进制数。
3. 八进制转换为十进制:按权展开法,将每一位数字的权重相加即可得到十进制数。
4. 十进制转换为八进制:将十进制数逐步除以8,得到的余数从下往上组成八进制数。
5. 十六进制转换为十进制:按权展开法,将每一位数字的权重相加即可得到十进制数。
二进制及其转换PPT课件

2020/10/13
3
中国与十进制
中国是世界上第一个同时使用“十进制”和 “位值制”的国家。古埃及、古希腊和古罗马都没 有发明位值制。古代美洲玛雅人和两河流域的古巴 比伦人虽然发明了位值制,却分别使用的是20进制 和60进制计数法。
今天通用的十进制阿拉伯数字系统,实际上是 10世纪后由印度传入地中海沿岸及西欧各国。 考证 历史,直到6世纪末以后,印度才开始使用十进制 计数法。于是,有学者认为,印度的十进制计数法 可能源自中国,古代中国才是今天通行的十进制计 数法的真正源头。
2020/10/13
2
中国与十进制
中国古代使用的是十进制计数法,即每满10个 数目就进一个单位,如10个1进为10,10个10进为 100等。十进制起源于何时已不可考,但至迟春秋时 期,中国古人就已经能够熟练使用十进制进行计数 和运算了。
中国古代的十进制计数方法实际包括了“位值
制”十进制”和“位值制”两种计数方法。位值制 就是以位置定数目,如22,同样是两个2,第一个2 因位于十位上,故代表20,第二个2因位于个位上, 故代表2。可以看出,由于使用了位值制,就可以很 简捷地记录较大的数目。
104 万 1028 穰 1052 恒河沙 1076 全仕祥 10-23 阿摩罗
108 亿 1032 沟 1056 阿僧祇
10-24 涅盘寂静
5
十进制的定义
把0,1,2,3,4,5,6,7,8,9这十个数码放到相应的位 置来表示数。
数码所在的位置叫做数位,个位、十位、百位、 千位……等等。
每个数位上可以使用的数码的个数叫做这种计数 制的基数,十进制的基数是10。
每个数位所代表的数叫做位权数,进位规则“逢 十进一”。
2020/10/13
二进制及其转换教案

二进制及其转换教案本节课将介绍二进制及其转换。
我们知道计算机中使用的进位制是二进制,但是什么是二进制,它与我们数学上使用的十进制有什么关系?本节课将为大家补充二进制的知识,这对于理解计算机原理非常重要。
首先,我们来了解什么是进位制。
进位制是人们为了计数和运算方便而约定的记数系统。
最常见的进位制是十进制,它由10个数码组成,进位方法是逢十进一。
在幼儿园时,我们从最简单的个位数相加学起,逐渐学会了进位。
这是我们约定了10作为进位基数,以方便运算。
除了十进制,还有其他常见的进位制,比如60进制(时分秒的换算)、360进制(1周=360度)等。
接下来我们将重点介绍二进制。
二进制是一种进位制,由0和1两个数码组成,进位方法是逢二进一。
计算机中使用二进制是因为计算机的内部电路只能识别0和1,所以采用二进制能够更方便地进行运算。
我们将介绍十进制和二进制的相互转换,以及二进制的运算规则。
通过本节课的研究,我们可以拓展思维能力,激发探索计算机奥秘的欲望。
由于数学知识的复杂性,学生的数学要求较高,因此不同班级的课堂效果略有差异。
那些数学成绩较好的班级通常表现出更高的听课热情,而且学生研究新知识的速度也有所不同。
在板书设计方面,老师需要注意让内容简明易懂。
一、进位制是为了方便计数和运算而约定的记数系统。
它由十个数码组成,基数为10.进位方法是逢十进一,并采用位权表示法,即一个数码在不同位置上所代表的值不同。
二、二进制是另一种记数系统,同样由三部分组成:1和0两个数码来描述,基数为2,逢二进一,位权大小为2-n、2-n-1、2-n-2、……、2、21、22、……、2n。
三、在二进制和十进制之间进行转换时,有两种方法。
首先,将二进制转换为十进制,可以按照权位展开的方式进行。
其次,将十进制转换为二进制,则可以使用除2取余法。
四、课后思考:如何将45转化为5进制?。
二进制的单位换算关系

二进制的单位换算关系一、引言在计算机科学中,二进制是一种重要的计数系统,它由0和1两个数字组成。
二进制单位换算关系是计算机领域中的基础知识,它可以帮助我们理解计算机内部数据的存储和处理方式。
本文将详细介绍二进制单位换算关系,包括位(bit)、字节(byte)、千字节(kilobyte)、兆字节(megabyte)、千兆字节(gigabyte)和太字节(terabyte)等单位的换算及其在计算机中的应用。
二、位与字节的关系在二进制计数系统中,最小的单位是位(bit)。
一个位只能表示0或1两个数字。
8个位组成一个字节(byte),一个字节可以表示256个不同的数字。
字节是计算机中最常用的数据单位之一,它可以存储一个字符或一个整数。
三、字节与千字节的关系千字节(kilobyte)是字节的一千倍,即1千字节等于1024字节。
这是因为计算机中的存储容量通常以2的幂次进行表示。
千字节是计算机存储容量的基本单位之一,它可以存储大约1000个字符或一个小型文档。
四、千字节与兆字节的关系兆字节(megabyte)是千字节的一百万倍,即1兆字节等于1024千字节。
兆字节是计算机存储容量的另一个重要单位,它可以存储大约1000兆个字符或一个较大的文件。
五、兆字节与千兆字节的关系千兆字节(gigabyte)是兆字节的一千倍,即1千兆字节等于1024兆字节。
千兆字节是计算机存储容量的较大单位,它可以存储多个大型文件或一个较长的视频。
六、千兆字节与太字节的关系太字节(terabyte)是千兆字节的一千倍,即1太字节等于1024千兆字节。
太字节是计算机存储容量的巨大单位,它可以存储非常大的数据集合,例如整个互联网上的信息。
七、二进制单位换算实例为了更好地理解二进制单位换算关系,我们来看几个实际的例子。
例1:将1000字节转换为千字节。
1000字节等于1000/1024 ≈ 0.976千字节。
例2:将2兆字节转换为千兆字节。
2兆字节等于2*1024/1024 ≈ 2千兆字节。
计算机数制及转化
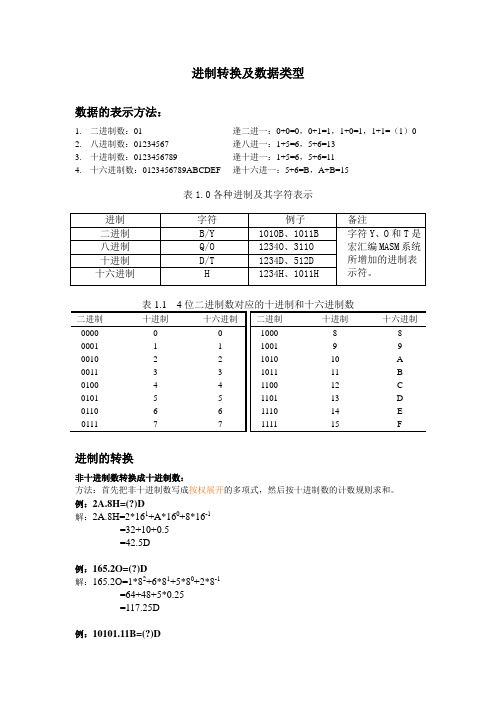
进制转换及数据类型数据的表示方法:1.二进制数:01 逢二进一:0+0=0,0+1=1,1+0=1,1+1=(1)02.八进制数:01234567 逢八进一:1+5=6,5+6=133.十进制数:0123456789 逢十进一:1+5=6,5+6=114.十六进制数:0123456789ABCDEF 逢十六进一:5+6=B,A+B=15表1.0各种进制及其字符表示进制的转换非十进制数转换成十进制数:方法:首先把非十进制数写成按权展开的多项式,然后按十进制数的计数规则求和。
例:2A.8H=(?)D解:2A.8H=2*161+A*160+8*16-1=32+10+0.5=42.5D例:165.2O=(?)D解:165.2O=1*82+6*81+5*80+2*8-1=64+48+5*0.25=117.25D例:10101.11B=(?)D解:10101.11B=1*24+0*23+1*22+0*21+1*20+1*2-1+1*2-2=16+0+4+0+1+0.5+0.25=21.75D十进制数转换其它进制数:1.整数转换方法:整数转换,采用基数连除法。
把十进制整数N 转换成R 进制数的步骤:1) 将N 除以R ,记下所得的商和余数2) 将上一步所得的商再除以R ,记下所得商和余数 3) 重复做第2步直到商为04) 将各个余数转换成R 进制的数码,并按照和运算过程相反的顺序把各个余数排列起来,即为R 进制数。
例:427D=(?)H 解:427D=1ABH 例:427D=(?)O 解:427D=653O 例:11D=(?)B 解:11D=1011B2.纯小数转换纯小数转换,采用基数连乘法。
把十进制的纯小数M 转换成R 进制数的步骤: 1) 将M 乘以R ,记下整数部分2) 将上一步乘积中的小数部分再乘以R ,记下整数部分3) 重复做第2步,直到小数部分为0或者满足精度要求为止4) 将各步求得的整数转换成R 进制的数码,并按照和运算过程相同的顺序排列起来,即为所求的R 进制数。
二进制及其转换2014

这种逢几进一的计数法,称为进位计数制。 简称“数制”或“进制”。
3
十进制特点是逢十进一
(3333)=3×103+3×102+3×101+3×100
十进制数位就是个位、十位、百位、千位、 万位、十分位、百分位,千分位等等。 每个数位可以使用0,1,2,3,4,5,6,7,8,9 十个数码, 基数是10。 十进制位权数:
13
四、知识背景介绍
莱布尼兹 (Gottfriend Wilhelm von Leibniz 1646.7.1.—1716.11.14.) 德国最重要的自然科学家、数学家、 物理学家、历史学家和哲学家,一个举世 罕见的科学天才,和牛顿同为微积分的创 建人。在数学史上,他应该是第一个明确 提出二进制数这个概念的科学家。
第11章 逻辑代数初步
11.1 二进制及其转换
1
网购:
日常生活中, 我们经常会使用各 种数字,如一部苹 果iPhone 4S手机淘 宝不同卖家的价格 分别为3440.67元、 4080.32元、4080.10 元、3350.38元等。 这些数都是十进制 数。
2
在实际应用中,还使用其他的计数制, 如三双鞋(两只鞋为一双)、两周实习(七 天为一周)、4打信封(十二个信封为一打)、 半斤八两(一斤十六两)、三天(72小时)、 一刻钟(15分)、二小时(120分)等等。
2
1
0
9
三、例题与练习
练习:将下列二进制数换算成十进制数 (1)(101)2 ; (2)(101011)2 解:(1) (101)2 = 1×22+0×21+1×20=4+0+1=(5)10 (2)(101011)2 = 1×25+0×24+1×23 +0×22 +1×21 +1×20= 32+0+8+0+2+1=(43)10
计算机数值之间的转换

计算机数值之间的转换计算机数值之间的转换是计算机科学中一个非常基础且重要的知识点。
在计算机编程和算法设计中,常常需要进行不同数值之间的转换,比如整数到浮点数的转换、二进制到十进制的转换等等。
本文将介绍常见的数值转换方法及其实现原理。
1.十进制到二进制的转换:十进制数转换为二进制数的方法是通过不断除以2并记录余数,直到商为0为止,然后将记录下来的余数倒序排列,即为二进制数。
例如,将十进制数27转换为二进制数:27÷2=13余113÷2=6余16÷2=3余03÷2=1余11÷2=0余12.二进制到十进制的转换:1×2^4+1×2^3+0×2^2+1×2^1+1×2^0=16+8+0+2+1=273.十进制到十六进制的转换:十进制数转换为十六进制数的方法是通过不断除以16并记录余数,直到商为0为止,然后将记录下来的余数倒序排列,并将10、11、12、13、14、15分别表示为A、B、C、D、E、F,即为十六进制数。
例如,将十进制数255转换为十六进制数:255÷16=15余15(F)15÷16=0余15(F)倒序排列余数:FF,即将十进制数255转换为十六进制数FF。
4.十六进制到十进制的转换:十六进制数转换为十进制数的方法是将十六进制数按权相加。
例如,将十六进制数FF转换为十进制数:15×16^1+15×16^0=240+15=255即将十六进制数FF转换为十进制数255浮点数是计算机中用来表示实数的一种方式,一般由符号位、指数位和尾数位组成。
在计算机中,浮点数的表示采用IEEE754标准。
1.十进制到浮点数的转换:十进制数转换为浮点数的方法是通过科学计数法,将实数部分转换为二进制,并使用指数表示小数点的位置。
例如,将十进制数2.5转换为单精度浮点数:2.浮点数到十进制的转换:浮点数到十进制数的转换是将浮点数的各个部分按照IEEE754标准进行计算和转换。
二进制_精品文档

二进制引言:二进制是一种使用数字0和1表示的计数系统,广泛用于计算机科学和信息技术领域。
它是一种基于二的单位制,与我们常见的十进制(基数为10)不同。
在本文中,我们将介绍二进制的基本概念、如何进行二进制转换以及其在计算机科学中的重要性。
一、二进制的基本概念二进制使用0和1两个数字表示数值。
每个数字位被称为一个比特(bit),而每8个比特组成一个字节(byte)。
例如,十进制数值7在二进制中表示为111,其中最右边的1表示2^0(1的0次方),接下来的1表示2^1(1的1次方),最左边的1表示2^2(1的2次方)。
因此,111可以计算为1×2^0 + 1×2^1 +1×2^2 = 7。
二进制有很多有趣的特性。
首先,只有两个数字使得运算更为简单。
其次,二进制数字转换到十进制非常直观,只需计算每位上1所代表的十进制值,再求和即可。
最后,二进制位可以用来表示各种信息,如逻辑状态、图像、音频等。
二、二进制转换在实际应用中,我们常常需要将十进制数值转换为二进制,或者进行反向转换。
下面是一些常见的转换方法。
1. 十进制转二进制:将十进制数值除以2并记录余数,然后将商再次除以2,重复此过程,直到商为0为止。
最后,将每次的余数依次排列,即可得到二进制结果。
例如,将十进制数值42转换为二进制:42 ÷ 2 = 21 余 021 ÷ 2 = 10 余 110 ÷ 2 = 5 余 05 ÷ 2 = 2 余 12 ÷ 2 = 1 余 01 ÷2 = 0 余 1逆序排列余数,得到二进制数值101010。
所以,十进制数值42的二进制表示为101010。
2. 二进制转十进制:将二进制数值的每位上的1所代表的十进制值相加,即可得到十进制结果。
例如,二进制数值101010转换为十进制:1×2^0 + 1×2^2 + 1×2^4 = 1 + 4 + 16 = 21。
11.1二进制及其转换

方法二、数值后面加特定的字母区分
新授
十进制和二进制进行类比
十进制 二进制
0、1
每个数位上可以使用的数码 基数 进位规则
0、1、2、3、4、5、6、7、8、9 10 “逢十进一”
2
“逢二进一”
二进制位权数表
整数部分 位置 位权数 … … 第3位 第2位 第1位
22
21
20
二进制特点与缺点: 便于实现,不便记忆
余0 余0 余0 余1
读 数 方 向 由 下 往 上
810
(1000 ) 2
除2 取余,逆序输出
例题
例2 将十进制数(101)10换算成二进制 数。
问题解决
八进制 每个数位上可以使用的数码 基数 进位规则 0、1、2、3、4、5、6、7 8
“逢八进一”
问题解决
1、八进制位权数表
整数部分 位置 位权数 … … 第3位 82 第2位 81 第1位 80
新授
进位制是人们为了计数和运算方便而约定的计数系统。 你还知道哪些常见的进位制?请举例。
二进制:计算机采用的计数制。
只有“0”、“1”两个状态,容易实现,运算简单
新授
思考:如何区别不同进位制的数? 进制数的表示方法: 方法一、用一个下标来表明 例:(101)10 (101)2 十进制 例: 101D 十进制 (D可以省略) 二进制 101B 二进制 (101)16 十六进制 101H 十六进制
新授
将十进制数换算成二进制数,通常使用“除2取余法”。
具体做法:不断用2去除要换算的十进制数,若余数为
1,则相应数位的数码为1,若余数为0,则相应数位的 数码为0,一直除到商是1为止,然后按照从高位到低位 的顺序写出换算结果。
二进制及其运算规则作了简单介绍

一、二进制及其运算规则简介二进制是一种计算机和电子系统中常用的数字表示方式,其基数为2,只包含0和1两个数字。
在计算机科学和数字电路中,二进制具有重要的地位和作用。
二进制数可以通过不同的进制转换公式和运算规则进行运算,包括加法、减法、乘法和除法等。
二、深度探讨二进制在计算机中的应用1. 二进制转换在计算机系统中,二进制常用于表示数据、指令和存储位置区域。
为了方便计算和显示,二进制可以转换为其他进制,如八进制、十进制和十六进制。
转换规则和方法可以通过移位操作和逐位相加确定。
2. 二进制运算规则二进制的运算规则包括加法、减法、乘法和除法。
这些规则与十进制的运算类似,都需要对齐相应位置的数字进行计算。
对于减法和除法,需要借位和补位的操作。
在计算机系统中,这些运算规则被硬件电路和逻辑门实现。
3. 二进制的逻辑运算除了数值运算外,二进制还可以进行逻辑运算,包括与、或、非、异或等。
这些运算常用于逻辑电路、布尔运算和逻辑推理中。
通过逻辑运算,计算机可以进行复杂的逻辑判断和条件分支。
三、总结和回顾通过本文的介绍和探讨,我们对二进制及其运算规则有了更深入的理解。
二进制作为计算机系统中的基本表示方式,具有重要的地位和作用。
我们可以通过二进制转换和运算规则实现多样的计算和逻辑操作,从而完成复杂的计算任务和逻辑推理。
在学习计算机科学和数字电路时,深入理解二进制及其运算规则是非常重要的。
个人观点与理解:二进制作为计算机系统中的基础之一,对于理解计算机的运行原理和设计逻辑非常重要。
深入学习二进制及其转换规则和运算规则,有助于我们更好地理解计算机的内部结构和运行方式。
二进制的逻辑运算在编程语言和算法设计中也扮演着重要角色。
对于计算机科学相关专业的学生来说,深入学习二进制是必不可少的一部分。
关于二进制的深度探讨可以继续从以下几个方面进行扩展和深入探讨:1. 二进制在计算机内部的表示方式二进制在计算机内部是如何表示和存储的呢?这涉及到计算机的数据存储结构和内存管理。
数制及其相互转换

数制及其相互转换要点各种计数制二进制、八进制、十六进制对照表数制间的相互转换各种计数制二进制:由0,1组成,逢二进一八进制:由0,1,2,3,4,5,6,7八个数字组成,逢八进一十进制:由0,1,2,3,4,5,6,7,8,9十个数字组成,逢十进一十六进制:由0~9十个数字、A、B、C、D、E、F六个字母组成,逢十六进一二进制、八进制、十六进制对照表十进制二进制八进制十六进制十进制二进制八进制十六进制0 0000 0 0 8 1000 81 0001 1 1 9 1001 92 0010 2 2 10 1010 A3 0011 3 3 11 1011 B4 0100 4 4 12 1100 C5 0101 5 5 13 1101 D6 0110 6 6 14 1110 E7 0111 7 7 15 1111 F数制间的相互转换•转换原则:如果两个有理数相等,则它们的整数部分和小数部分分别相等。
•一、非十进制数间的转换•二、十进制数转换成非十进制数•三、非十进制数转换成十进制数•总结一、非十进制数间的转换1.二进制数与八进制数间的转换以小数点为界,向左或向右,三位二进制数一组用一位八进制数取代。
注意:不足三位二进制数用0补足三位。
基本关系:一位八进制数 = 三位二进制数八进制数 二进制数一分三三合一转换原则:将(714.431)8转换成二进制数例1:7 1 4 . 4 3 1 111 1 0 0 100 100 11 0 10 0 即:(714.431)8=(111001100.100011001)2 例:将二进制数(1111101.11001)2转换成八进制数1 111 101. 110 01 0 0 0 175 .62即:(1111101.11001)2=(175.62)82. 二进制数与十六进制数间的转换基本关系:一位十六进制数 = 四位二进制数转换原则:一分四十六进制数二进制数四合一将十六进制数1AC0.6D H 转换成相应的二进制数1 A C 0. 6 D 1 0 0 0 1010 1100 0000 . 110 0 1101 即:(1AC0.6D )16=(1101011000000.01101101)2例3:将二进制数(1100011.10111)2转换成相应的十六进制数110 0011. 1011 1 0 0 0 063 . B 8 即:(1100011.10111)2=(63.B8)16例2:二、十进制数转换成非十进制数十进制数转换R进制数转换原则:将十进制数分成整数部分和小数部分,分别采用不同的方法换算,然后将两部分相加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二进制的位权数表:
位置 … 位权数 … 整数部分 第3 位 第2 位 第1位
20
22
21
例如,二进制数1100100的意义是
1 26 1 25 0 24 0 23 1 22 0 21 0 20
3)二进制数换算成了十进制数将这些数字计 算出来,就把二进制数换算成了十进制数.
3)数位:数码在数中的位置(个位,十位,百 位。。。)
4)位权数:每个数位所代表的数叫做位权数
1、十进制位权数表
位置 整数部分 小数部分
……
……
第3 位
第2 位
第1 位
第1 位
第2 位
……
……
位权 数
10
2
10
1
10
0
10
-1
10
-2
按权展开:
365= 3 10 6 10 5 10
二进制及其转换
数值型数据在计算机中如何表示?
二进制
引入新课
日常生活中,我 们经常会使用各种数 字,如一部苹果 iphone 6p手机淘宝不 同卖家的价格分别为 5228.00元、 5138.00元、 5188.00元和 4155.20元等。这些 数都是十进制数
1、十进制与十进制数
1)数码:采用是十个基本数码 2)基数:每个数位上可以使用的数码符号的个数 (十进制的基本数码为0,1,2,3,4,5,6,7,8,9,共10个, 所以十进制的基数为10)
2 1 0 1 0
2.68= 2 10 6 10 8 10 这样的式子叫按权展开式
2
十进制数的特点
(1)采用十个基本数码: 0,1,2,3,4,5,6,7,8,9,基数是10
(2)进位规则是“逢十进一”
练习:
写出下列十进制数的按权展开式 1)3241 2)45.2
2、二进制
在电路中,电子元件与电路都具有两种对 立的状态.如电灯的“亮”与“不亮”, 电路的“通”与“断”,信号的“有”和 “无”.采用数码0和1表示相互对立的两 种状态十分方便,因此,在数字电路中普 遍采用二进制.
二进制数的特点
(1)采用2个基本数码(每个数位只有 两个不同的数码符号0和1),基数为2.
例如:1100100 1100100
6
= 1 2 1 2 0 2 0 2 1 2 0 2 0 2 =100
5 4 3 2 1
0
4)为区别不同进位制的数,通常用下标指明 基数. 如 (100) 2 表示二进制中的数, (100)10 表示十进制中的数. 由上面的计算知 (1100100 )2 (100)10 因此二进制数100与十进制数100表示的不 是同一个数.
10
2
练习:
将十进制数 (97)10 换算为二进制数
巩固练习:
P5 习题1
课堂小结:
本节课主要学习了二进制十进制之间的 相互转换,按权展开的内容
课堂作业:பைடு நூலகம்
教材P5习题2,3
3、十进制与二进制数的互化
例1 将下列二进制数换算为十进制数.
( 101 ) 2
( 101011 ) 2
练习: P3练习1,2
3、十进制与二进制数的互化
整数部分:按 “倒序除2取余 例2:将十进制数(101)10 换算为二进制数. 0 解 2 101 余 1 2 位 法”的原则进 行转换。即用2 2 余021 位 读 连续去除十进 25余122 位 数 制数,直至商 3 方 12 余 0 2 位 等于0为止,逆 序排列余数即 6余024 位 向 可得到与该十 3余125 位 进制相对应的 6 余12 位 二进制数各位 的数值。 ) (101 ) 1 26 1 25 0 24 0 23 1 22 0 21 1 20 (1100101
