11.1二进制及其转换
二进制十进制数的转换

二进制十进制数的转换
二进制和十进制都是数字表示方式,二进制是计算机中常用的数字表示方式,十进制则是我们平常使用的数字表示方式。
在计算机领域,需要经常进行二进制和十进制数之间的转换。
1. 二进制转十进制
二进制数是由 0 和 1 组成的数字表示方式,每一位上的数都是2 的幂次方。
例如,二进制数 1011,其各位数值分别为 1、0、1、1,代表的十进制数为:
1×2+0×2+1×2+1×2=8+0+2+1=11
因此,二进制数 1011 转换成十进制数为 11。
2. 十进制转二进制
十进制数是由 0 到 9 这十个数字组成的数字表示方式,每一位上的数都是 10 的幂次方。
将十进制数转换成二进制数,可以用连续除以 2 的方法。
例如,将十进制数 22 转换成二进制数:第一步:22 ÷ 2 = 11 0
第二步:11 ÷ 2 = 5 (1)
第三步: 5 ÷ 2 = 2 (1)
第四步: 2 ÷ 2 = 1 0
第五步: 1 ÷ 2 = 0 (1)
将上述步骤中每一个余数从下往上排列,得到的二进制数为10110。
以上就是二进制和十进制数之间的转换方法。
在计算机编程中,
经常需要用到这些转换方式。
各个进制之间的转换

各个进制之间的转换各个进制之间的转换是计算机科学中非常重要的一部分。
我们知道,在数学中,我们使用十进制系统,也就是以 10 作为基数。
但是计算机在处理数据时使用的是二进制系统,以 2 作为基数。
因此,当我们需要在计算机中进行数据处理时,就需要进行各个进制之间的转换。
首先,让我们来介绍二进制转换。
二进制是由 0 和 1 组成的数字系统。
为了将一个十进制数转换为二进制数,我们可以使用除以 2 的方法。
例如,将十进制数 10 转换为二进制数的步骤如下:1. 用 2 整除 10 得到商 5 和余数 0;2. 将余数 0 记为二进制位的最后一位;3. 用 2 整除 5 得到商 2 和余数 1;4. 将余数 1 记为二进制位的倒数第二位;5. 用 2 整除 2 得到商 1 和余数 0;6. 将余数 0 记为二进制位的倒数第三位;7. 将商 1 记为二进制位的倒数第四位;8. 最终得到二进制数 1010。
接下来,我们介绍八进制和十六进制数的转换。
八进制是由 0~7 组成的数字系统,而十六进制是由 0~9 和 A~F 组成的数字系统。
将一个十进制数转换为八进制或十六进制数的步骤与二进制相似,只是将除数变为 8 或 16,余数范围变为 0~7 或 0~15。
最后,我们介绍各个进制之间的相互转换。
可以使用十进制作为中转,例如将二进制数转换为十六进制数的步骤如下:1. 将二进制数分为 4 位一组,不足的补 0;2. 将每组二进制数转换为十进制数;3. 将十进制数转换为十六进制数。
通过以上的介绍,相信大家已经了解了各个进制之间的转换方法,希望对大家有所帮助。
二进制与十进制转换

二进制与十进制转换在计算机科学和数学领域,二进制(binary)和十进制(decimal)是两个常见且重要的数制系统。
二进制是一种基于2的系统,只包含0和1两个数字,而十进制是一种基于10的系统,包含0到9这10个数字。
在计算机中,二进制是最基本的数制系统,而十进制是人们通常使用的数制系统。
一、二进制转换为十进制二进制转换为十进制的方法相对简单,只需要按照权重相加即可。
下面以一个示例来说明具体的转换过程。
假设有一个八位的二进制数字11011010,我们要将其转换为十进制。
第一步,从右到左给每一位二进制数字分配不同的权重,从0开始依次增加。
第二步,将每一位二进制数字与对应的权重相乘,并将结果相加。
1 * 2^7 + 1 * 2^6 + 0 * 2^5 + 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0* 2^0 = 218所以,二进制数11011010转换为十进制后为218。
二、十进制转换为二进制十进制转换为二进制相对于二进制转换为十进制稍微复杂一些。
下面以一个示例来说明具体的转换过程。
假设有一个十进制数218,我们要将其转换为二进制。
第一步,找到离218最接近的2的乘方,该乘方最大但不超过218。
在本例中,2的乘方为2^7=128。
第二步,将2的乘方减去离218最接近的2的乘方,将结果记为余数。
218 - 128 = 90 (余数为90)第三步,重复第一步和第二步,直到余数为0。
2^6=64,余数为262^4=16,余数为102^3=8,余数为22^1=2,余数为0第四步,将每一步的结果(余数)以相反的顺序排列起来,得到二进制数。
218的二进制表示为11011010。
通过以上的示例,我们可以看到,二进制和十进制之间的转换并没有太多的难度。
掌握了转换的方法之后,可以轻松地在二进制和十进制之间进行转换。
总结:二进制和十进制是计算机科学和数学领域中常见的数制系统。
二进制由0和1组成,而十进制由0到9这10个数字组成。
进制之间的转换关系表

进制之间的转换关系表进制是数学中重要的概念,用于表示数字的一种方式。
常见的进制包括十进制、二进制、八进制和十六进制。
在不同进制之间进行转换是计算机科学和信息技术领域中的基础操作之一。
本文将介绍进制之间的转换关系表,帮助读者更好地理解和应用进制转换。
在十进制系统中,我们使用的是基数为10的进制。
它是人类社会中最常用的进制,因为我们有十根手指,可以按照个位、十位、百位等顺序进行计数。
相对于十进制,其他进制系数的基数不同。
二进制是计算机内部使用的进制,它的基数是2。
在二进制中,只有两个数字,即0和1。
转换二进制到十进制的方法是每一位的数字乘以2的幂次方,然后将结果相加。
例如,二进制数1001可以转换为十进制数9,计算方式是1*2^3 + 0*2^2+ 0*2^1 + 1*2^0 = 9。
八进制是基数为8的进制系统。
八进制中使用的数字是0到7。
转换八进制到十进制的方法类似于二进制。
每一位的数字乘以8的幂次方,然后将结果相加。
例如,八进制数123可以转换为十进制数83,计算方式是1*8^2 + 2*8^1 + 3*8^0 = 83。
十六进制是基数为16的进制系统。
除了0到9的数字,十六进制还使用A到F的六个字母表示10到15的数字。
转换十六进制到十进制的方法和前面两种进制类似。
每一位的数字乘以16的幂次方,然后将结果相加。
例如,十六进制数1A可以转换为十进制数26,计算方式是1*16^1 + 10*16^0 = 26。
除了从较低的进制转换到较高的进制,我们还可以从较高的进制转换到较低的进制。
转换的方法与前面相反,即将原数除以对应基数并取余数,然后将余数从低位到高位排列。
这样可以得到新的进制表示。
在计算机科学中,进制转换是一个基础的操作。
计算机内部的运算都是使用二进制进行的,但人们更习惯于使用十进制进行计算。
因此,在数据传输和存储中,常常需要将十进制转换为二进制,然后再进行处理。
同样地,在计算机程序中,十六进制经常用于表示内存地址和数据的编码。
十进制与二进制的转换

十进制与二进制的转换在计算机科学和信息技术领域中,十进制和二进制之间的转换是一个常见的操作。
十进制是我们通常使用的数字系统,而二进制则是计算机使用的数字系统。
在本文中,我将详细介绍如何进行十进制与二进制的转换。
一、十进制与二进制的基本概念十进制是一种基数为10的数字系统,由0-9十个数字组成。
每个位置上的数字表示该位置上的值乘以对应的权重,从右到左权重递增,最右边的位置权重为0,然后递增1。
例如,数字1234表示1乘以1000,2乘以100,3乘以10,4乘以1,再将它们相加得到1234。
二进制是一种基数为2的数字系统,由0和1两个数字组成。
每个位置上的数字表示该位置上的值乘以对应的权重,从右到左权重递增,最右边的位置权重为0,然后递增1。
例如,二进制数字1101表示1乘以8,1乘以4,0乘以2,1乘以1,再将它们相加得到13。
二、十进制转换为二进制要将十进制数转换为二进制数,我们可以使用除2取余的方法。
具体步骤如下:1. 将十进制数除以2,得到商和余数。
2. 将余数写在二进制数的最右边。
3. 将商作为新的十进制数,重复步骤1和步骤2,直到商为0为止。
4. 将所有的余数按照从下到上的顺序排列,得到的就是对应的二进制数。
举例说明,将十进制数19转换为二进制数:1. 19除以2,商为9,余数为1。
2. 9除以2,商为4,余数为1。
3. 4除以2,商为2,余数为0。
4. 2除以2,商为1,余数为0。
5. 1除以2,商为0,余数为1。
将得到的余数从下到上排列,得到的二进制数为10011。
三、二进制转换为十进制要将二进制数转换为十进制数,我们可以使用加权求和的方法。
具体步骤如下:1. 从二进制数的最右边开始,将每位上的值乘以对应的权重。
2. 权重从右到左递增,从0开始。
3. 将所有位上的乘积相加,得到的和就是对应的十进制数。
举例说明,将二进制数10111转换为十进制数:1. 1乘以2的0次方,得到1。
2. 1乘以2的1次方,得到2。
二进制及其转换PPT课件

2020/10/13
3
中国与十进制
中国是世界上第一个同时使用“十进制”和 “位值制”的国家。古埃及、古希腊和古罗马都没 有发明位值制。古代美洲玛雅人和两河流域的古巴 比伦人虽然发明了位值制,却分别使用的是20进制 和60进制计数法。
今天通用的十进制阿拉伯数字系统,实际上是 10世纪后由印度传入地中海沿岸及西欧各国。 考证 历史,直到6世纪末以后,印度才开始使用十进制 计数法。于是,有学者认为,印度的十进制计数法 可能源自中国,古代中国才是今天通行的十进制计 数法的真正源头。
2020/10/13
2
中国与十进制
中国古代使用的是十进制计数法,即每满10个 数目就进一个单位,如10个1进为10,10个10进为 100等。十进制起源于何时已不可考,但至迟春秋时 期,中国古人就已经能够熟练使用十进制进行计数 和运算了。
中国古代的十进制计数方法实际包括了“位值
制”十进制”和“位值制”两种计数方法。位值制 就是以位置定数目,如22,同样是两个2,第一个2 因位于十位上,故代表20,第二个2因位于个位上, 故代表2。可以看出,由于使用了位值制,就可以很 简捷地记录较大的数目。
104 万 1028 穰 1052 恒河沙 1076 全仕祥 10-23 阿摩罗
108 亿 1032 沟 1056 阿僧祇
10-24 涅盘寂静
5
十进制的定义
把0,1,2,3,4,5,6,7,8,9这十个数码放到相应的位 置来表示数。
数码所在的位置叫做数位,个位、十位、百位、 千位……等等。
每个数位上可以使用的数码的个数叫做这种计数 制的基数,十进制的基数是10。
每个数位所代表的数叫做位权数,进位规则“逢 十进一”。
2020/10/13
二进制转换的实用技巧

二进制转换的实用技巧在当今数字化的时代,二进制作为计算机和电子设备的基础语言,理解和掌握二进制转换的技巧变得越来越重要。
无论是对于计算机科学的学生,还是对电子技术感兴趣的爱好者,亦或是从事相关工作的专业人士,熟练进行二进制转换都能带来很大的便利。
什么是二进制呢?简单来说,二进制就是一种以2 为基数的记数法,通常用 0 和 1 来表示。
在计算机中,所有的数据和指令最终都以二进制的形式进行存储和处理。
我们先从二进制转换为十进制说起。
这个过程其实有一个比较简单的方法。
假设我们有一个二进制数 1010 ,要将其转换为十进制,就从右往左依次用每个数字乘以 2 的相应次方(次方从 0 开始),然后将所有结果相加。
对于 1010 来说,最右边的 0 乘以 2 的 0 次方等于 0 ,第二个 1 乘以 2 的 1 次方等于 2 ,第三个 0 乘以 2 的 2 次方等于 0 ,最左边的 1 乘以 2 的 3 次方等于 8 ,最后将这几个结果相加: 0 + 2+ 0 + 8 = 10 ,所以二进制 1010 转换为十进制就是 10 。
再来说说十进制转换为二进制。
常见的方法是“除 2 取余,逆序排列”。
比如我们要把十进制数 13 转换为二进制。
首先用 13 除以 2 ,商是 6 ,余数是 1 ;再用 6 除以 2 ,商是 3 ,余数是 0 ;接着用 3 除以2 ,商是 1 ,余数是 1 ;最后 1 除以 2 ,商是 0 ,余数是 1 。
然后将所有的余数从下往上排列,得到 1101 ,这就是十进制 13 对应的二进制数。
二进制和八进制、十六进制之间的转换也很实用。
先看二进制转八进制,因为 8 等于 2 的 3 次方,所以我们可以将二进制数从右往左每 3 位一组进行分组(不足 3 位的在左边补 0 ),然后将每组转换为对应的八进制数字。
例如,二进制数 101011 ,分组后为 010 101 ,010 转换为八进制是 2 ,101 转换为八进制是 5 ,所以转换后的八进制数是25 。
二进制转化规则

二进制转化规则在计算机科学中,二进制是一种非常常用的数制,它由0和1组成,具有简洁、运算规则简单、适合逻辑运算等特点。
在计算机内部,所有的信息都被表示为二进制形式。
然而,在实际应用中,我们经常需要将十进制数转换为二进制数,或者将二进制数转换为十进制数。
本文将介绍二进制转化的规则。
一、十进制转二进制将十进制数转换为二进制数的方法是采用“除2取余法”。
具体步骤如下:1. 将十进制数的整数部分除以2,得到商和余数(1或0);2. 将商再次除以2,得到新的商和余数;3. 重复上述步骤,直到商为0为止;4. 将每一步的余数从低位到高位依次排列,即为该十进制数的二进制表示。
例如,将十进制数23转换为二进制数的过程如下:23 ÷ 2 = 11 余 111 ÷ 2 = 5 余 15 ÷ 2 = 2 余 12 ÷ 2 = 1 余 01 ÷2 = 0 余 1将每一步的余数从低位到高位依次排列,得到23的二进制表示为10111。
二、二进制转十进制将二进制数转换为十进制数的方法是采用“乘权求和法”。
具体步骤如下:1. 从二进制数的最低位开始,每个位上的数字乘以该位的权值(2的幂次方),得到每个位的值;2. 将每个位的值相加,得到该二进制数的十进制表示。
例如,将二进制数10111转换为十进制数的计算过程如下:1×2^4 + 0×2^3 + 1×2^2 + 1×2^1 + 1×2^0 = 23因此,二进制数10111等于十进制数23。
三、注意事项在进行二进制转化时,需要注意以下几点:1. 在不同的场合下,二进制数的表示可能采用不同的基数和字母表示。
例如,在计算机科学中,常用的基数为2,字母表示为0和1;而在物理学中,常用的基数为8,字母表示为0、1、2、3、4、5、6和7。
因此,在进行转换时,需要明确所采用的基数和字母表示;2. 在进行转换时,需要注意进位或借位的处理。
二进制及其转换教案

二进制及其转换教案本节课将介绍二进制及其转换。
我们知道计算机中使用的进位制是二进制,但是什么是二进制,它与我们数学上使用的十进制有什么关系?本节课将为大家补充二进制的知识,这对于理解计算机原理非常重要。
首先,我们来了解什么是进位制。
进位制是人们为了计数和运算方便而约定的记数系统。
最常见的进位制是十进制,它由10个数码组成,进位方法是逢十进一。
在幼儿园时,我们从最简单的个位数相加学起,逐渐学会了进位。
这是我们约定了10作为进位基数,以方便运算。
除了十进制,还有其他常见的进位制,比如60进制(时分秒的换算)、360进制(1周=360度)等。
接下来我们将重点介绍二进制。
二进制是一种进位制,由0和1两个数码组成,进位方法是逢二进一。
计算机中使用二进制是因为计算机的内部电路只能识别0和1,所以采用二进制能够更方便地进行运算。
我们将介绍十进制和二进制的相互转换,以及二进制的运算规则。
通过本节课的研究,我们可以拓展思维能力,激发探索计算机奥秘的欲望。
由于数学知识的复杂性,学生的数学要求较高,因此不同班级的课堂效果略有差异。
那些数学成绩较好的班级通常表现出更高的听课热情,而且学生研究新知识的速度也有所不同。
在板书设计方面,老师需要注意让内容简明易懂。
一、进位制是为了方便计数和运算而约定的记数系统。
它由十个数码组成,基数为10.进位方法是逢十进一,并采用位权表示法,即一个数码在不同位置上所代表的值不同。
二、二进制是另一种记数系统,同样由三部分组成:1和0两个数码来描述,基数为2,逢二进一,位权大小为2-n、2-n-1、2-n-2、……、2、21、22、……、2n。
三、在二进制和十进制之间进行转换时,有两种方法。
首先,将二进制转换为十进制,可以按照权位展开的方式进行。
其次,将十进制转换为二进制,则可以使用除2取余法。
四、课后思考:如何将45转化为5进制?。
二进制及其转换2014

这种逢几进一的计数法,称为进位计数制。 简称“数制”或“进制”。
3
十进制特点是逢十进一
(3333)=3×103+3×102+3×101+3×100
十进制数位就是个位、十位、百位、千位、 万位、十分位、百分位,千分位等等。 每个数位可以使用0,1,2,3,4,5,6,7,8,9 十个数码, 基数是10。 十进制位权数:
13
四、知识背景介绍
莱布尼兹 (Gottfriend Wilhelm von Leibniz 1646.7.1.—1716.11.14.) 德国最重要的自然科学家、数学家、 物理学家、历史学家和哲学家,一个举世 罕见的科学天才,和牛顿同为微积分的创 建人。在数学史上,他应该是第一个明确 提出二进制数这个概念的科学家。
第11章 逻辑代数初步
11.1 二进制及其转换
1
网购:
日常生活中, 我们经常会使用各 种数字,如一部苹 果iPhone 4S手机淘 宝不同卖家的价格 分别为3440.67元、 4080.32元、4080.10 元、3350.38元等。 这些数都是十进制 数。
2
在实际应用中,还使用其他的计数制, 如三双鞋(两只鞋为一双)、两周实习(七 天为一周)、4打信封(十二个信封为一打)、 半斤八两(一斤十六两)、三天(72小时)、 一刻钟(15分)、二小时(120分)等等。
2
1
0
9
三、例题与练习
练习:将下列二进制数换算成十进制数 (1)(101)2 ; (2)(101011)2 解:(1) (101)2 = 1×22+0×21+1×20=4+0+1=(5)10 (2)(101011)2 = 1×25+0×24+1×23 +0×22 +1×21 +1×20= 32+0+8+0+2+1=(43)10
二进制、数制及其相互转换PPT课件

• ②加1,得100000000,进位1被丢弃(因为一个字节只
能容纳8位,28只能被存储为00000000),因此-0的补码
.
38
•
负数:最高位为1,其余各位为原码的相应位取反,然后对整
个数加1。例如:
•
-7 的原码:
10000111
•
-7 的补码:第①步
变,对其余各位取反。)
11111000(最高位不
•
第②步
+1
•
结果
11111001
• 即对+7各位取反加1。
• 数值原码反码补码
.
39
• 由负数的补码求其原码,只须按由负数的原码求其补码的
• N2 = B7B6B5 B4 B3B2B1B0 •
• N16 = H1
H0
.
23
• 例:(1111111000111.100101011)2
(
)16
• 解:
• 0001 1111 1100 0111.1001 0101 1000
• 1 F C 7. 9 5 8
• 答 : (1111111000111.100101011)2 = (1FC7.958)16
80 = 2560 + 384 + 56 + 5 = (3005)10
.
13
• (3)(3B)16 ( )10 • (3B)16 = 3 161 + 11 160 = 48 + 11
= (59)10 • (4)(1011.11)2 ( )10 • (1011.11)2 =1 24-1+0 23-1+ 1
• 因此,最好能做到将符号位和其它位统一 处理。对减法也按加法来处理。这就是 “补码”。
第2讲 二进制数及数制转换(1)汇总
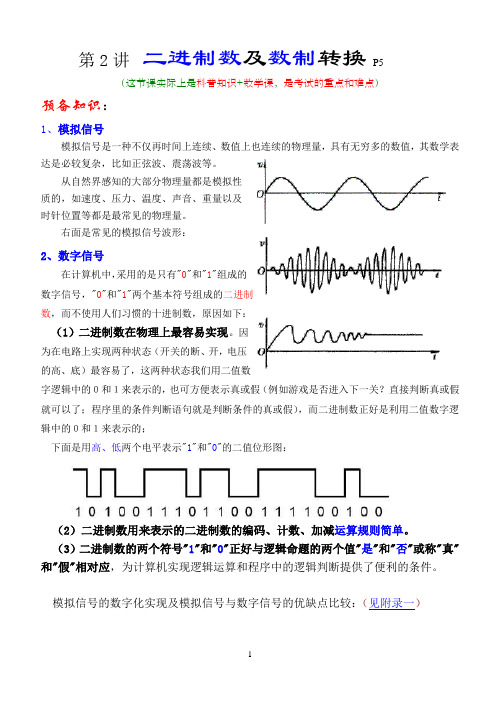
第2讲二进制数及数制转换P5(这节课实际上是科普知识+数学课,是考试的重点和难点)预备知识:1、模拟信号模拟信号是一种不仅再时间上连续、数值上也连续的物理量,具有无穷多的数值,其数学表达是必较复杂,比如正弦波、震荡波等。
从自然界感知的大部分物理量都是模拟性质的,如速度、压力、温度、声音、重量以及时针位置等都是最常见的物理量。
右面是常见的模拟信号波形:2、数字信号在计算机中,采用的是只有"0"和"1"组成的数字信号,"0"和"1"两个基本符号组成的二进制数,而不使用人们习惯的十进制数,原因如下:(1)二进制数在物理上最容易实现。
因为在电路上实现两种状态(开关的断、开,电压的高、底)最容易了,这两种状态我们用二值数字逻辑中的0和1来表示的,也可方便表示真或假(例如游戏是否进入下一关?直接判断真或假就可以了;程序里的条件判断语句就是判断条件的真或假),而二进制数正好是利用二值数字逻辑中的0和1来表示的;下面是用高、低两个电平表示"1"和"0"的二值位形图:(2)二进制数用来表示的二进制数的编码、计数、加减运算规则简单。
(3)二进制数的两个符号"1"和"0"正好与逻辑命题的两个值"是"和"否"或称"真"和"假"相对应,为计算机实现逻辑运算和程序中的逻辑判断提供了便利的条件。
模拟信号的数字化实现及模拟信号与数字信号的优缺点比较:(见附录一)把声音、图象等模拟量信息,首先要变成离散化的数字(0和1)后,计算机系统就可以进行处理、传送。
因此,信息的数字化是信息化社会的基础。
人们发现在对信号的存储、分析和传输中,数字电路更具优越性。
为了能够处理存储连续变化的模拟信号,数字电路采用二进制数首先对其进行量化处理后,再使用复杂的数字系统来实现信号的存储、分析和量化。
进制之间的转换

进制之间的转换--进制之间的转换--介绍:进制也就是进位计数制,是人为定义的带进位的计数方法(有不带进位的计数方法,比如原始的结绳计数法,唱票时常用的“正”字计数法,以及类似的tally?mark计数)。
?对于任何一种进制---X进制,就表示每一位置上的数运算时都是逢X进一位。
十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x进制就是逢x进位。
--常见的几种进制二进制(B)十进制(D)十六进制(H)八进制(O)二进制二进制有两个特点:它由两个数码0、1组成,二进制的规律是逢二进一。
-转换。
将二进制转换为十进制。
例子:将二进制数10111.1011转换为十进制解析:小数点前1011------转换为十进制1×230×221×211×20------8+0+2+1=11小数点后1011------转换为十进制1×2-10×2-21×2-31×2-4----0.5+0+0.125+0.0625=0.6875则,二进制1011.1011转换为十进制数为11+0.6875=11.6875.(1011.1011)B=(11.6875)D将二进制转换为八进制。
例子:将二进制数10111.1011转换为八进制解析:1011.1011(由小数点开始,向两边每3个分为一组)001011.101100(按照二进制转十进制的算法,算出每三个所对应的十进制数)13.54则,(1011.1011)B=(13.54)O将二进制转换为十六进制。
例子:将二进制数10111.1011转换为八进制解析:1011.1011(从小数点开始向两边每四个分为一组)1101.1011(按照二进制转十进制的算法,算出每四个所对应的十进制数)13.13则,(1101.1101)B=(D.D)H(在十六进制中将10,11,12,13,14,15分别表示为字母A,B,C,D,E所以13,对应的则为D)八进制-八进制的规律是逢八进一将八进制转换为其他进制时,需要先将它化为二进制。
二进制转换算法

二进制,八进制,十进制,十六进制之间的转换算法一、十进制与二进制之间的转换(1) 十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000 ) 2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2) 小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2, 一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1 :将0.125换算为二进制得出结果:将0.125换算为二进制(0.001 ) 2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步,将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步,将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8, 0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制是怎样换算的?

二进制是Hale Waihona Puke 样换算的?二进制是怎样换算的?
二进制,比如,十进制中的0、l、2、3、4,在二进制中用0、10、11、100来表示,所以0和1之外的.数字在二进制中就不需要了。二进制不仅可以表示出来所有的数字,还可以进行加、减、乘、除运算。电路中通电和断电的两种情况,可以用开关的ON(开)、OFF(关)来表示。如果把这种开、关作用理解成二进制的0和1,就能明白在电子计算机中运用二进制的优越性了。
二进制及其转换教案

二进制及其转换[教学目标]1、认知目标(1)掌握进位制概念;(2)理解进制的本质;(3)掌握十进制和二进制的相互转换;(4)了解计算机所采用的数制及计算机采用二进制数的原因。
2、技能目标掌握二进制数和十进制数转换以及运算规则。
3、能力目标对学生思维能力进行拓展,激发他们探索计算机奥秘的欲望。
[教学重点](1)进制的本质组成(2)十进制与二进制间的相互转换[难点](1)进制的本质组成(2)十进制与二进制间的相互转换[教学方法]讲授法???举例法?[授课地点]普通教室,不用多媒体[教学过程]一、? 引入新课对计算机稍微了解的同学就知道计算机中使用的进位制是二进制,那什么是二进制,它跟我们数学上使用的十进制有什么联系。
这节课准备给大家补充点二进制的知识,这跟数学关系很密切,请同学务必认真听课。
二、? ?切入课堂内容1、什么是进位制提出问题:什么是进位制?最常见的进位制是什么?学生普遍回答是十进制。
教师继续提问:那十进制为什么叫十进制?引起学生的思考。
(部分经过思考的学生回答是约定的)教师提醒学生一起回忆幼儿园开始学习算术的情景。
当是我们是从最简单的个位数相加学起,比如2+3=?,当时我们会数手指,2个手指+3个手指等于5个手指,答案为5。
那4+6呢?4个手指+6个手指等于10个手指,10个手指刚好够用。
那6+9呢?当时我们就困惑了。
记得当时老师是告诉我们把6拆成1+5,9+1=10,这时老师跟我们约定用一个脚趾表示10,另外用5个手指表示5。
这样通过脚趾,我们就成功解决了两个数相加超过10的问题。
教师提问:那当时我们为什么要约定10呢,为什么用9或11?引起学生思考。
(部分经过思考的学生回答为了方便运算)教师提问:除此之外还有哪些常见的进位制?请举例说明。
拓展学生的思维。
有学生回答60进制(时分秒的换算),360进制(1周=360度),二进制等等。
教师和学生一起归纳进位制的概念,学生和老师形成共识:进位制是人们为了计数和运算方便而约定的记数系统。
二进制转换规则

二进制转换规则二进制是一种只包含0和1的数字系统,它被广泛应用于计算机科学和电子工程领域中。
二进制数可以表示数字、字符、图像和声音等信息。
在计算机系统中,所有数据都以二进制形式存储和处理。
二进制转换是将一个数字、字符或其他数据从十进制或其他进制表示形式转换为二进制表示形式的过程。
下面介绍一些二进制转换的规则。
1. 十进制转二进制规则:将十进制数不断除以2,得到的商和余数就是二进制数的各个位。
具体步骤如下:- 将要转换的十进制数除以2,得到商和余数;- 将余数记录下来,作为二进制数当前位的值;- 将商作为新的十进制数,重复以上步骤,直到商为0为止; - 将所有余数倒序排列,得到的就是转换后的二进制数。
例如,将十进制数19转换为二进制数的过程如下:19 ÷ 2 = 9 (1)9 ÷ 2 = 4 (1)4 ÷ 2 = 2 02 ÷ 2 = 1 01 ÷ 2 = 0 (1)所以,19的二进制表示形式为10011。
2. 二进制转十进制规则:将二进制数各个位上的值乘以对应的权值,然后相加即可得到十进制表示形式。
具体步骤如下:- 从二进制数的最右边一位开始,将每一位的值乘以2的幂次方,幂次方从0开始,每次增加1;- 将上述乘积相加,得到的就是转换后的十进制数。
例如,将二进制数101101转换为十进制数的过程如下:1 × 2^5 + 0 × 2^4 + 1 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 45所以,101101的十进制表示形式为45。
以上就是二进制转换的规则,掌握这些规则可以更好地理解和应用二进制数。
二进制与其他进制之间的转换.

各数制的权
各数制中整数部分不同位的权为“基的n-1次 方(n为数值所在的位数,n的最小值取1)”, 小数部分不同位的权值为“基的-n次方”。
一个十进制数(135.7)可表示为: 135=1×102+3×101+5×100+7×10-1 如:十进制中,各位的权为10n-1
二进制中,各位的权为2n-1 十六进制中,各位的权为16n-1
十进制与二进制的相互转换
1.十进制转换为二进制 整数部分:按“倒序除2取余法”的原则进行转换。
即用2连续去除十进制数,直至商等于0为止,逆 序排列余数即可得到与该十进制相对应的二进制 数各位的数值。
小数部分:按“顺序乘2取整法”的原则进行转换。
小数乘以目标数制的基数,第一次相乘结果的整数部 分为目的数的最高位,将其小数部分再乘基数依次 记下整数部分,反复进行下去,直到乘积的小数部 分为“0”,或满足要求的精度为止。(如2-5,只要求 到小数点后第五位)。
二进制与八进制转换
转换方法:从小数点开始,将二进制数的整数和小 数部分每三位分为一组,不足三位的分别在整数的 最高位前和小数的最低位后加“0”补足,然后每组 用等值的八进制码替代,即得八进制数。
例:(11010111.0100111)2 = (327.234)8
二进制转与十六进制的相互转换
2.二进制数与十六进制数的相互转换 由于16=24,所以在将二进制数转换成十六进
【例1】将(236)D转换成二进制。 转换过程如图1所示。
2 2 36 2 118 2 59 2 29 2 14 27 23 21 0
…………… 0 …………… 0 …………… 1 …………… 1 …………… 0 …………… 1 …………… 1 …………… 1
二进制转换算法

一、概念1.十进制十进制使用十个数字(0、1、2、3、4、5、6、7、8、9)记数,基数为10,逢十进一。
历史上第一台电子数字计算机ENIAC是一台十进制机器,其数字以十进制表示,并以十进制形式运算。
设计十进制机器比设计二进制机器复杂得多。
而自然界具有两种稳定状态的组件普遍存在,如开关的开和关,电路的通和断,电压的高和低等,非常适合表示计算机中的数。
设计过程简单,可靠性高。
因此,现在改为二进制计算机。
2. 二进制二进制以2为基数,只用0和1两个数字表示数,逢2进一。
二进制与遵循十进制数遵循一样的运算规则,但显得比十进制更简单。
例如:(1)加法:0+0=0 0+1=1 1+0=1 1+1=0(2)减法:0-0=0 1-1=0 1-0=1 0-1=1(3)乘法:0*0=0 0*1=0 1*0=0 1*1=1(4)除法:0/1=0 1/1=1,除数不能为0二、进制转换1.二进制与十进制数间的转换(1)二进制转换为十进制将每个二进制数按权展开后求和即可。
请看例题:把二进制数(101.101)2=1*22+0*21+1*20+1*2-1+0*2-2+1*2-3=(5.625)10二进制数转换为十进制数:二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制第0位 0 * 20= 0第1位 0 * 21= 0第2位 1 * 22= 4第3位 0 * 23= 0第4位 0 * 24= 0第5位 1 * 25= 32第6位 1 * 26= 64第7位 0 * 27= 0+---------------------------100用横式计算为:0 * 20 + 0 * 21 + 1 * 22 + 1 * 23 + 0 * 24 + 1 * 25 + 1 * 26 + 0 * 27 = 100 0乘以多少都是0,所以我们也可以直接跳过值为0的位:1 * 22 + 1 * 23 + 1 * 25 + 1 * 26 = 100(2)十进制转换为二进制一般需要将十进制数的整数部分与小数部分分开处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在实际运用中,我们经常会遇到各种各样的开关电路设计问题。对于一个实际问题, 通常是先对问题作必要的理论分析,建立相应的数学模型,然后才进入实际解决问 题的阶段。建立开关电路数学模型所用的工具就是逻辑代数的知识。
日常生活中,我们经常会使用各种数字,如
一年5天,一瓶洗发水卖33.8元等,这些数字都是十进 制
例2 将十进制数(101)10换算成二进制数
探究
你一定也听说过二进制,与十进制类比,你能回答下面的问题 吗? (1)二进制的基数是什么? (2)二进制每个数位上有几个不同的数 码?分别是什么? (3)二进制的进位规则是什么?
位置
位权数
整数部分
…
…
第3位
22
第2位
21
第1位
20
为了区别不同进位制的数,通常用下标指明基数。 例如,(101)10表示十进制的数,(101)2表 示二进制的数 例1 将下列二进制数换算成十进制数: (1)(101)2, (2)(101011)2
十进制是我们最熟悉的一种计数方式。它把 0,1,2,3,4,5,6,7,8,9这十个数码放到相应的位置来表 示数。
数码所在的位置叫做数位,也就是我们常说的个位、 十位、百位、千位、万位、亿位及十分位、百分位、 千分位等。 每个数位上可以使用的数码的个数叫做这种计数制 的基数。十进制的每一个数位上都可以用10个数码。 因此十进制的基数是10. 每个数位所代表的数叫做位权数。十进制数 的进位规则是 “逢十进一”
整数部分 位置 … … 第3位 102 第2位 101 第1位 100
小数部分 第1位 10-1 第2位 10-2 … …
位权数
十进制数的意义是各个数位的数码与其位权数乘积之和。 例如,
365=3X 102+6X101+5X100
2.68=2X100 +6X10-1 +8X10-2
这种式子叫做按权展开式
二进制------十进制
将这个二进制数写成各个数位的数码与其位权数 乘积之和的形式,然后计算出结果。
如何将一个十进制数换算成二进制数?
把十进制化成2的各次幂之和的形式,并且各次幂的系 数只能去0和1
十进制------二进制
除2取余法:不断用2去除要换算的十进制数,若 余数为1,则相应数位的数码为1,若余数为0, 则相应数位的数码为0,一直除到商是1为止,然 后按照从高位到地位的顺序写出换算结果。
逻辑代数的产生: 1849年英国数学家乔治.布尔(George Boole)首先提出, 用来描述客观事务逻辑关系的数学方法——称为布尔代数。 后来被广泛用于开关电路和数字逻辑电路的分析与设计, 所以也称为开关代数或逻辑代数。 逻辑代数中用字母表示变量——逻辑变量,每个逻辑变量的 取值只有两种可能——0和1。它们也是逻辑代数中仅有的两个 常数。0和1只表示两种不同的逻辑状态,不表示数量大小。
