均数差异显著性检验EXCEL
利用Excel进行数据比较与差异分析通过对比数据进行差异分析和发现问题

利用Excel进行数据比较与差异分析通过对比数据进行差异分析和发现问题利用Excel进行数据比较与差异分析在数据处理和分析的领域中,Excel是一种广泛使用的工具。
其强大的数据比较和分析功能可帮助我们深入挖掘数据,发现其中的差异并解决问题。
本文将介绍如何利用Excel进行数据比较与差异分析的方法和步骤。
一、数据准备在进行数据比较和差异分析之前,我们首先需要准备好数据。
假设我们有两个数据集A和B,分别表示两个不同时间段或者不同实验条件下的数据。
确保数据集的格式一致,并存储在Excel的不同工作表或者不同的工作簿中。
二、数据比较1. 打开Excel,并在两个数据集的工作表中选择需要进行比较的数据范围。
2. 在主菜单栏中选择“条件格式”,然后选择“新规则”。
3. 从弹出的对话框中选择“使用公式确定哪些单元格要进行格式设置”。
4. 在“格式值”输入框中,输入公式“=A1<>B1”(其中A1和B1为两个数据集中的对应单元格)。
5. 在“设置格式”中选择要应用的格式,可以选择不同的填充颜色来突出显示差异。
6. 单击“确定”按钮,然后将格式应用到整个数据范围。
这样,Excel会根据设定的规则对两个数据集进行比较,并将不同的部分以突出显示的形式展现出来。
三、差异分析数据比较之后,我们可以进一步进行差异分析,以深入了解数据之间的差异并找到问题所在。
1. 使用Excel的数据透视表功能可以帮助我们更好地分析数据差异。
选择两个数据集中的所有数据,并在主菜单栏中选择“插入”-“透视表”。
2. 在弹出的对话框中,选择要分析的数据集范围并确定透视表的位置。
3. 在透视表字段列表中,将需要比较的指标和维度字段拖拽到相应的区域。
4. 使用透视表的行和列字段可以对数据进行分类和分组,从而更好地显示数据之间的差异。
5. 可以利用透视表的值字段选项,选择并应用统计函数,如求和、平均值等,以便对数据进行更详细的分析。
6. 根据透视表的分析结果,我们可以对差异进行深入研究,并找出可能的问题所在。
Excel中的单因素方差分析
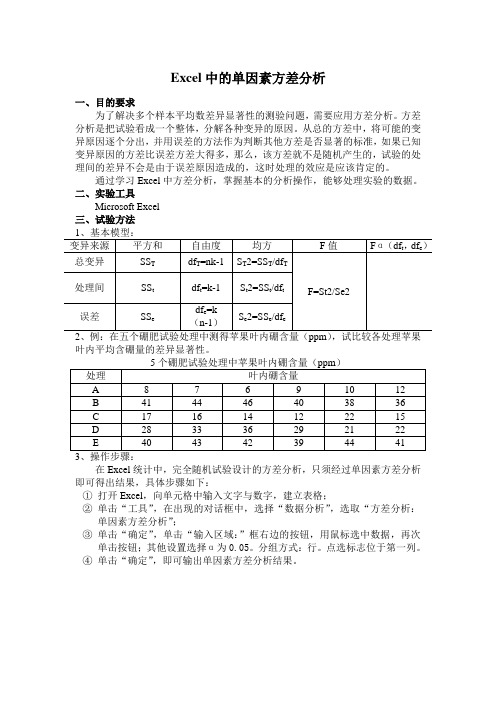
Excel中的单因素方差分析一、目的要求为了解决多个样本平均数差异显著性的测验问题,需要应用方差分析。
方差分析是把试验看成一个整体,分解各种变异的原因。
从总的方差中,将可能的变异原因逐个分出,并用误差的方法作为判断其他方差是否显著的标准,如果已知变异原因的方差比误差方差大得多,那么,该方差就不是随机产生的,试验的处理间的差异不会是由于误差原因造成的,这时处理的效应是应该肯定的。
通过学习Excel中方差分析,掌握基本的分析操作,能够处理实验的数据。
二、实验工具Microsoft Excel三、试验方法叶内平均含硼量的差异显著性。
在Excel统计中,完全随机试验设计的方差分析,只须经过单因素方差分析即可得出结果,具体步骤如下:①打开Excel,向单元格中输入文字与数字,建立表格;②单击“工具”,在出现的对话框中,选择“数据分析”,选取“方差分析:单因素方差分析”;③单击“确定”,单击“输入区域:”框右边的按钮,用鼠标选中数据,再次单击按钮;其他设置选择α为0.05。
分组方式:行。
点选标志位于第一列。
④单击“确定”,即可输出单因素方差分析结果。
4、方差分析输出结果:SUMMARY组观测数求和平均方差A 6 52 8.666667 4.666667B 6 245 40.83333 13.76667C 6 96 16 11.6D 6 169 28.16667 34.96667E 6 249 41.5 3.5差异源SS df MS F P-value F crit 组间5160.467 4 1290.117 94.1691 1.07E-14 2.75871 组内342.5 25 13.7总计5502.967 295、多重比较:由方差分析的结果,采用新复极差测验法,再稍加计算比较处理,即可得出:60.05显著,并可知除E与B二处理间无极显著差异外,其他均有极显著差异。
SPSS中的单因素方差分析一、基本原理单因素方差分析也即一维方差分析,是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题,如各组之间有显著差异,说明这个因素(分类变量)对因变量是有显著影响的,因素的不同水平会影响到因变量的取值。
应用电子表格Excel宏功能进行计量资料比较的显著性检验

得 了可行 的效果 _ 。另有学 者 应用 Ecl内置 函数 进 5 ] xe
行 方 差齐性 检验 及 t 检验 J 。
入 “ 碱 酯 酶 含 量 ” B : 4各 单 元 格 中输 入胆 碱 脂 胆 ,2 G
酶 各数 值 。 点 H1单元 格一 工 具 一 数 据 分 析 一 方 差 分 析 : 单 因素方 差 分 析 一 确 定 一 输 入 区 域 : 鼠标 选 中 B : 用 2 B , 组 方 式选 择 “ ” = . 5 输 出新 工 作 表 组 一 5分 行 , 00 , 确定 一结 果见 表 9 。
见表 3 。
两总 体均 数 的 比较 由参 考文 献 [ ] 3 中的 数 据 , 药 物 治 疗 绝 经 后 妇 两 女 骨 质 疏 松 症 第 24腰 椎 ( 2 4 骨 密 度 的改 善 值 见 _ L _)
表 1 。
Байду номын сангаас
D I1 .9 9 ji n 10  ̄2 3 2 1 .4 0 8 O :0 36 /.s .0 6 5 .0 20 .2 s
用 E cl xe 进行计量资料 的显著 性检验 , 方便直观 快速 , 以用于 医学统计 学处理。 可
【 关键词 】 E cl 统计 xe
宏 显著性检验
统 计 分析是 医学 工作 者 探 讨 真 理 、 现 真 理 的 有 发
表 1 两药物治疗绝经后妇女骨质疏松症 L _ 密度改善值 24骨
鲳
2 软件 安排及 宏 的加 载 2 1 安 装 办 公 软 件 mi oo fc x e 2 0 采 用 . c sf of eE cl 0 3, r t i 典 型安 装 。 2 2 打 开 E cl, 工 具一 加 载宏 一 放 人 安装 光 盘 . xe 点 一加 载 数据分 析 工具 。 3 应 用宏 功能 进行 计量 资料 比较 的显 著性 检验
如何在Excel中灵活运用ttest函数

如何在Excel中灵活运用ttest函数Excel是一款广泛应用于数据分析和计算的电子表格软件。
其中,ttest函数是一种用于假设检验的函数,能够帮助用户判断两个样本的均值是否有显著差异。
在本文中,我们将介绍如何在Excel中灵活运用ttest函数进行数据分析。
一、ttest函数简介ttest函数是Excel中的一个统计函数,用于进行t检验,即根据样本数据判断两个总体均值是否存在显著差异。
该函数的语法为:TTEST(array1, array2, tails, type),其中:- array1:表示第一个样本的数据范围;- array2:表示第二个样本的数据范围;- tails:表示假设检验的尾数,可以选择1或2。
当tails为1时,表示单尾检验;当tails为2时,表示双尾检验;- type:表示ttest函数的类型,可以选择1、2或3。
当type为1时,表示两个样本的方差相等;当type为2时,表示两个样本的方差不等且样本大小相等;当type为3时,表示两个样本的方差不等且样本大小不等。
二、ttest函数的应用下面以一个实例来说明如何在Excel中灵活运用ttest函数。
假设我们有两组数据,分别为X组和Y组,在Excel的两列中分别输入这两组数据。
然后,在Excel的任意一个单元格中输入以下公式:=TTEST(A1:A10, B1:B10, 2, 3)其中,A1:A10表示X组的数据范围,B1:B10表示Y组的数据范围,2表示双尾检验,3表示两个样本的方差不等且样本大小不等。
按下Enter键后,Excel会自动计算出ttest函数的结果,包括t值、自由度、双尾概率等信息。
根据这些信息,我们可以判断这两组数据的均值是否存在显著差异。
三、ttest函数的结果解读ttest函数的结果包括t值、自由度、双尾概率等信息。
其中,t值越大表示两个样本的均值差异越显著,自由度越大表示样本数据越多,双尾概率表示根据t值和自由度计算得出的两个样本均值差异的概率。
EXCEL均数差异显著性检验

无法控制的随机因素引起的误差。
现在,我们假设有这样一个情况: 从一批同质(相同品种、相同日龄、 相同饲料、相同饲养管理等)的20000只肉 鸡中随机抽取各含100只肉鸡的两个样本, 分别称量其42天出栏重,结果发现:
样本1平均出栏重为:2.24kg/只 样本2平均出栏重为:2.31kg/只
确定性事件
必然事件(U) (certain event)
不可能事件(V) (impossible event)
在一定条件下可能发生也可能不发生。
随机事件(random event) 不确定事件(indefinite event) 为了研究随机现象,需要进行大量重复的调查、实验、 测试等,这些统称为试验。
下面以两均数差异显著性检验为例具体说 明操作步骤。
例1: 随机抽测9头内江猪和9头荣昌猪经产母猪的产仔 数,得到如下数据资料:
内江猪 荣昌猪
产仔数 14 15 12 11 13 17 14 14 13 12 14 13 13 12 14 10 10 10
试比较内江猪与荣昌猪两品种经产母猪产仔数 是否存在显著差异。
根据以上公式可导出以下结论:
由此可知,当总体平均数落在已知的样本均数置 信概率为(1-)的置信区间以外时,就表明在显著 水平时差异显著。
例5.2:母猪的怀孕期为114d,现抽测12头大白猪母猪的怀孕期分别 为115,113,114,112,116,115,114,118,113、115、114、113,试 检验所得样本的平均数与总体平均数114d有无显著差异?
1 、提出假设
H0
无效假设 /零假设 /检验假设
1 = 2
误差 效应
备择假设 /对应假设
excel anova 函数

excel anova 函数【原创实用版】目录1.EXCEL ANOVA 函数的概述2.ANOVA 函数的适用场景3.ANOVA 函数的基本语法4.ANOVA 函数的实例解析5.ANOVA 函数的结论解读正文1.EXCEL ANOVA 函数的概述在 EXCEL 中,ANOVA 函数是一种用于分析数据方差的函数,其全称为“分析方差”,主要用于单因素方差分析。
它可以帮助我们判断不同样本均值之间是否存在显著性差异,从而为我们提供数据分析的依据。
2.ANOVA 函数的适用场景ANOVA 函数主要适用于以下场景:- 对比三个或以上样本均值的差异;- 分析各样本均值间是否存在显著性差异;- 评估样本数据是否符合正态分布。
3.ANOVA 函数的基本语法在 EXCEL 中,ANOVA 函数的基本语法如下:```=ANOVA(range1, range2, range3,...)```其中,range1、range2、range3 等表示需要进行方差分析的数据范围。
需要注意的是,数据范围需要用逗号分隔,且各数据范围的大小应相同。
4.ANOVA 函数的实例解析假设我们有一组数据,需要分析不同品牌饮料的口感评分是否存在显著性差异。
数据如下:```品牌 | 口感评分----|-------A | 85, 90, 88, 92B | 80, 82, 85, 88C | 87, 90, 89, 91```我们可以使用 ANOVA 函数进行分析,具体操作如下:```=ANOVA(C1:C4, D1:D4, E1:E4)```函数结果显示,p 值为 0.05,小于 0.05,说明各品牌饮料的口感评分存在显著性差异。
5.ANOVA 函数的结论解读根据 ANOVA 函数的结果,我们可以得出以下结论:- 如果 p 值小于 0.05,说明各样本均值之间存在显著性差异;- 如果 p 值大于等于 0.05,说明各样本均值之间不存在显著性差异。
如何在Excel中进行统计假设检验和推断分析

如何在Excel中进行统计假设检验和推断分析在Excel中进行统计假设检验和推断分析是经济学、统计学和数据分析领域的基础技能之一。
统计假设检验常用于判断数据样本是否符合某种分布或是否有显著的差异,而推断分析则用于从样本数据中得出总体的特征。
本文将介绍如何在Excel中进行这两种分析,并给出具体示例和操作步骤。
第一章:统计假设检验1.1 单样本均值检验单样本均值检验用于判断样本均值是否与已知的总体均值有显著的差异。
在Excel中,可以使用T.TEST函数进行单样本均值检验。
具体操作步骤如下:(1)在输入数据所在列中输入样本数据;(2)选择一个空白单元格,输入=T.TEST(数据范围,已知均值);(3)按下回车键,即可得到检验的结果。
1.2 配对样本均值检验配对样本均值检验用于判断配对样本的均值差异是否显著。
在Excel中,可以使用T.TEST函数和数据分析工具进行配对样本均值检验。
具体操作步骤如下:(1)在两个列中输入配对样本数据;(2)点击“数据”选项卡,在“分析”工具中选择“数据分析”;(3)从弹出窗口中选择“t-检验:配对两样本”的选项,点击“确定”;(4)在对话框中输入“输入范围”和“相关系数”;(5)点击“确定”,即可得到检验结果。
1.3 独立样本均值检验独立样本均值检验用于判断两个独立样本的均值是否有显著差异。
在Excel中,可以使用T.TEST函数和数据分析工具进行独立样本均值检验。
具体操作步骤如下:(1)在两个列中分别输入两个独立样本数据;(2)点击“数据”选项卡,在“分析”工具中选择“数据分析”;(3)从弹出窗口中选择“t-检验:两独立样本的方差不等”的选项,点击“确定”;(4)在对话框中输入“输入范围”和“类型”;第二章:推断分析2.1 单样本推断单样本推断用于从一个样本数据中得出总体的特征。
在Excel 中,可以使用T.INV函数进行单样本推断。
具体操作步骤如下:(1)在输入数据所在列中输入样本数据;(2)选择一个空白单元格,输入=T.INV(置信水平, 自由度);(3)按下回车键,即可得到推断结果。
图表中平均数差异显著性检验结果的规范表达

表 2 各组肉鸡心脏腹水指数的变化 ( x ? s, n = 64 )
组别
28日龄
35 日龄42日龄来自C10. 197 ? 0. 006Bc 0. 210 ? 0. 006B b 0. 213 ? 0. 010Bb
T1
0. 220 ? 0. 013AB bc 0. 230 ? 0. 007ABb 0. 251 ? 0. 007Bb
1 图表中存在的问题
平均数差异显著性检验常见有 2个平均数间的差
异显著性检验 ( 成组检验 ) 和多个平均数间的差异显 著性检验 (多重比较 ) 。用于成组检验的方法有 t检验 等, 而用于多重比较的方法有 Duncan 和 q 检验等; 但 许多论文的图表中对这 2种检验结果的表达和描述却 是多种多样的, 有的表述甚至欠妥。 111 图表中显著性检验结果表达存在的问题
12 0
A CTA ED ITO LOG ICA
20( 2)
图表中平均数差异显著性检验结果的规范表达
郝拉娣 1)
何 平2)
( 1 )大连水产学院学报编辑部, 116023; 2) 水产科学杂志编辑部, 116023: 辽宁大连 )
摘 要 科技论文图 表中 平均数 差异 显著性 检验 结果的 表达 存在很多问题, 如图表中不标出检验结果、表达 符号多样、符号 标注位置不统一、检验 结果描 述缺 项等, 以及 图表 注释中 对检 验结果的表述不 全面, 甚 至描述 有错。 通过分 析存 在的问 题, 提出了规范表达的建 议。 关键词 科技论文; 显著性检验; 平均数 S tandard expression of statistica l an alysis of sign if ican t d ifference b etw een m ean valu es in f igu re s and tab lesM HAO Lad,i HE P ing Abstrac t M any incorrect expressions o f statistica l ana lys is of significant d ifference between m ean va lues are found in figures and tab les in sc-i tech pub lications, including no symbo,l incomp le te or va riation, even w rong in types and lo ca tion for sta tistica l analysis. Standard expression of sta tistica l ana lys is is recomm ended on the basis o f exam ina tion and evaluation o f the problem s in significant d ifference betw een m ean va lues in figures and tab les. K ey word s sc -i tech publica tion; sign ificance test; m ean F ir st-Auth or. s address Edito rial O ffice of Journa l of Da lian F isheries U niversity, 116023, D alian, Ch ina
如何在Excel中使用ANOVA进行方差分析

如何在Excel中使用ANOVA进行方差分析方差分析(ANOVA)是一种常用的统计分析方法,用于比较两个或多个样本之间的均值是否存在统计显著性差异。
在Excel中,我们可以利用内置的数据分析工具paketo进行ANOVA分析,具体步骤如下:1. 数据准备首先,我们需要将待分析的数据准备好。
假设我们要比较三种不同药物对某种疾病的治疗效果,我们可以将每种药物的治疗结果记录在Excel的不同列中,每个样本的观测值放在不同行中,确保数据排列整齐。
2. 打开数据分析工具paketo点击Excel工具栏上的“数据”选项卡,在“数据分析”组中找到“数据分析”按钮,点击打开数据分析对话框。
3. 选择ANOVA工具在数据分析对话框中,找到并选中“方差分析(ANOVA)”工具,然后点击“确定”按钮。
4. 填写输入范围在ANOVA工具的对话框中,需要填写“输入范围”和“Alpha”值。
“输入范围”即为待分析的数据范围,可以手动输入或通过点击选择数据表中的相关数据区域。
“Alpha”值用于设置显著性水平,默认为0.05,可以根据需要适当调整。
5. 设置输出选项在ANOVA工具的对话框中,可以对输出结果进行设置。
一般情况下,选择“新工作表里输出”即可,这样可以在新的工作表中查看分析结果。
6. 点击确定,进行分析完成以上设置后,点击“确定”按钮开始进行ANOVA分析。
7. 分析结果解读分析完成后,Excel将会在指定的输出位置生成ANOVA的结果。
通过观察各个因素的P值,我们可以判断各组间的均值是否存在显著差异。
从ANOVA结果中,我们可以查看总体方差(Between groups)和误差方差(Within groups),并计算出F值和P值。
若P值小于显著性水平,则可以认为各个样本之间的均值存在显著差异。
总结:通过Excel中的数据分析工具paketo,我们可以轻松地进行ANOVA方差分析。
只需将待分析数据准备好,选择合适的工具,填入相应的参数,即可得到分析结果。
excel假设检验方法

excel假设检验方法Excel可以使用多种方法进行假设检验。
以下是一些常见的假设检验方法,并为每种方法提供了Excel中的函数示例:1. 单样本t检验:使用T.TEST函数。
例如,=T.TEST(range, sample_mean, tails)用于检验一个样本平均值与一个给定的总体平均值之间是否存在显著差异。
2. 双样本t检验:使用T.TEST函数。
例如,=T.TEST(range1, range2, tails, type)用于检验两个样本均值之间是否存在显著差异。
3. 配对样本t检验:使用T.TEST函数。
例如,=T.TEST(range1, range2, 2, 1)用于检验一组相关的配对观测值之间是否存在显著差异。
4. 方差分析(ANOVA):使用ANOVA函数。
例如,=ANOVA(range1, range2, range3, ...)用于检验多个样本均值之间是否存在显著差异。
5. 卡方检验:使用CHISQ.TEST函数。
例如,=CHISQ.TEST(observed_range, expected_range)用于检验观测频数与期望频数之间是否存在显著差异。
6. 相关性检验:使用CORREL函数计算相关系数,然后使用T.TEST函数检验相关系数是否显著。
例如,=T.TEST(CORREL(range1, range2), sample_size-2, tails)用于检验两个变量之间的相关性是否显著。
这些是Excel中常用的假设检验方法和相应函数的示例。
根据具体的假设检验问题,你可以选择合适的方法并使用相应的函数进行分析。
均数差异显著性考验EXCEL

方差分析
用于比较两个或多个独立样本的平均值是否 存在显著差异。
假设检验的逻辑
提出假设
假设两组数据的平均值无显著差异(H0),或存在显著差异(H1)。
确定显著性水平
选择一个合适的显著性水平(如0.05或0.01),用于判断假设是否成立。
计算检验统计量
根据样本数据计算检验统计量,如t值、Z值或F值。
做出决策
总结词
用于检验两组数据是否具有相似的方差。
详细描述
FTEST函数用于进行方差齐性检验,判断两 组数据的方差是否相似。它需要输入两组数 据的标准差和样本数量,并返回F统计量和 p值。
CHITEST函数:卡方检验
总结词
用于检验两个分类变量是否独立。
详细描述
CHITEST函数用于进行卡方检验,判断两个 分类变量之间是否存在关联或独立关系。它 需要输入观察频数和期望频数,并返回卡方
人工智能的介入
自动化和智能化
人工智能技术将应用于均数差异显著性 检验,实现自动化和智能化的数据处理 和分析,提高分析效率和准确性。
VS
数据挖掘与预测
人工智能将通过数据挖掘和机器学习技术 ,发现隐藏在数据中的规律和趋势,为均 数差异显著性检验提供新的思路和方法。
THANKS
感谢观看
03
Excel中常用的均数差异 显著性检验函数
TTEST函数:双样本t检验
总结词
用于比较两组数据的均值是否存在显著差异。
详细描述
TTEST函数可以对两个独立样本或配对样本进行t检验,以判断两组数据的均值是否存 在显著差异。它需要输入样本数据和自由度,并返回t统计量和p值。
FTEST函数:方差齐性检验
均数差异显著性检验 (Excel实现
Excel表格如何做差异分析报表

●在日常生活和工作中,我们经常需要对比两个事物,哪个是好的,哪个是不好的。
这种对比差异的分析,则是【差异分析】●10 个差异分析可视化的技巧,让你的报告不再只是枯燥的数字和百分比。
方法1:用括号标记负数方法2:自定义数字格式,设置数字颜色方法3:使用箭头方法4:使用单元格颜色方法5:使用箭头–条件格式方法6:使用数据条方法7:「单元中」的图表方法8:使用按比例缩小的图表方法9:制作更好的差异分析图方法10:在图表中突出显示实例方法11:漂亮的「实际与目标」差异对比图方法12:带有浮动条的「实际与目标」差异对比图方法13:使用条形图进行自上而下的垂直差异对比图●01●用括号标记负数把数字放在括号中,和负号比起来,更容易识别是正数还是负数。
❶选择要设置格式的单元格;❷按下【Ctrl+1】,打开「单元格格式」对话框;❸在对话框中选择「数字」选项卡,选择最下面的「自定义」;❹设置单元格的格式代码【类型】为:0;(0);0如果是百分比,那么需要修改一下格式的代码,加上%,具体如下:0-00%;(0.00)%;0%想要让数字都对齐,不会受到括号的影响,让报告更加美观,可以把格式代码改成下面的样子:0-00 _)%;(0.00)%; 0 _)%●02●自定义数字格式,设置数字颜色❶选择要设置格式的单元格;❷按下【Ctrl+1】,打开「单元格格式」对话框;❸在对话框中选择「数字」选项卡,选择最下面的「自定义」;❹设置单元格的格式代码【类型】为:[Blue]0;[Red]0;0这样正数会显示为蓝色,负数会变成红色(显示为正数),0 则保持默认的颜色。
结合方法一,[Blue]0_);[Red](0);0_),负数带括号并且标红●03●使用箭头上下箭头,也可以直观的呈现正数、负数的数值,或者好的、不好的数据。
❶选择数据,然后按下【Ctrl+1】打开「单元格格式」窗口。
❷设置「自定义」格式代码如下:0 ▲;0 ▼;0让箭头靠右对齐,而数字靠左对齐,这样会更加的美观。
excle折线图图中怎么显示差异显著性
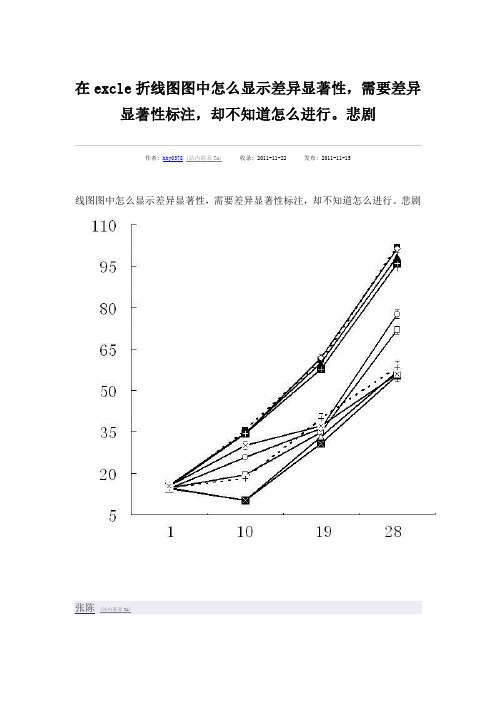
在excle折线图图中怎么显示差异显著性,需要差异显著性标注,却不知道怎么进行。
悲剧作者: hhy0378(站内联系TA)收录: 2011-11-22 发布: 2011-11-15线图图中怎么显示差异显著性,需要差异显著性标注,却不知道怎么进行。
悲剧张陈(站内联系TA)你可以添加文本框,但是你的处理这么多加文本框也不会好看,如果非要加显著志”,在“值”的对话框中打勾,点确定。
你会在图形中看到线条上出现数据,6楼: Originally posted by luojiang_925 at 2011-11-16 1949:我也遇到这方面的问题3楼: Originally posted by honghailuo at 2011-11-15 1630:在Excel中图的线条上点右键,选择“数据系列格式”,在其中选择“数据标志”,在“值”的对话框中打勾,点确定。
你会在图形中看到线条上出现数据,然后依据你方差分析的结果,将相关的数据修改成字母“a,b,c... ...误差线之间重合,就表明处理价差异不显著,一般不用标abc,直接可以看出来3楼: Originally posted by honghailuo at 2011-11-15 1630:在Excel中图的线条上点右键,选择“数据系列格式”,在其中选择“数据标志”,在“值”的对话框中打勾,点确定。
你会在图形中看到线条上出现数据,然后依据你方差分析的结果,将相关的数据修改成字母“a,b,c... ...正解哈作图还是要用ORIGIN作图软件,小木虫里有破解版!EXCEL做出来的图不10楼: Originally posted by dxxjhl at 2011-11-17 1151:正解哈作图还是要用ORIGIN作图软件,小木虫里有破解版!EXCEL做出来的图不太好看,而且需要需改很多东西!!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机事件(random event) 随机事件 不确定事件(indefinite event) 不确定事件 为了研究随机现象,需要进行大量重复的调查、实验、 为了研究随机现象,需要进行大量重复的调查、实验、 测试等,这些统称为试验。 测试等,这些统称为试验。
二、频率(frequency) 频率( )
P(A) = p
统计概率
抛掷一枚硬币发生正面朝上的试验记录 实验者 蒲丰 投掷次数 4040 发生正面朝上的次数 频率(m/n) 频率 2048 6019 12012 0.5069 0.5016 0.5005
K 皮尔逊 12000 K 皮尔逊 24000
随着实验次数的增多, 随着实验次数的增多,正面朝上这个事件发生的频率稳定 接近0.5,我们称0.5作为这个事件的概率 作为这个事件的概率。 接近 ,我们称 作为这个事件的概率。
第四章 均数差异显著性检验 — t检验
河南农业职业学院 孙攀峰
目的要求
显著性检验的目的、 显著性检验的目的、 方法以及步骤 Excel进行 Excel进行t检验的步 进行t 骤、方法
第一节 概率及分布概述
一、事件
定义:在一定条件下, 定义:在一定条件下,某种事物出现与否 就称为是事件。 就称为是事件。 自然界和社会生活上发生的现象是各 种各样的,常见的有两类。 种各样的,常见的有两类。
若在相同的条件下,进行了n次试验,在这n 若在相同的条件下,进行了 次试验,在这 次试验 次试验中,事件 出现的次数 称为事件A出现的 出现的次数m称为事件 次试验中,事件A出现的次数 称为事件 出现的 频数,比值 称为事件A出现的频率 频数,比值m/n称为事件 出现的频率 称为事件 出现的频率(frequency), , 记为W(A)=m/n。 。 记为
即假设两品种经产母猪产仔数的总体平均数µ 即假设两品种经产母猪产仔数的总体平均数µ1 和µ2 不相等,亦即存在处理效应, 不相等,亦即存在处理效应,其意义是指两品种经产母 猪产仔数存在本质上的差异。 猪产仔数存在本质上的差异。
(2)备择假设HA : µ1 ≠µ2 备择假设H
2 、 确定显著水平
能否定H 人为规定的概率标准称为显著水平, 规定的概率标准称为显著水平 能否定 0的人为规定的概率标准称为显著水平,记作α。
统计学中,一般认为概率小于 统计学中,一般认为概率小于0.05或0.01的事件 或 的事件 为小概率事件,所以在小概率原理基础上建立的假设 为小概率事件 所以在小概率原理基础上建立的假设 检验也常取α 检验也常取α=0.05和α=0.01两个显著水平 。 和 两个显著水平
=0.05 α=0.05
显著水平*
P< α
α=0.01
极显著水平**
选定检验方法,计算检验统计量, 3 、选定检验方法,计算检验统计量,确定概率值 根据研究设计的类型和统计推断的目的选 择使用不同的检验方法。 例:
这里是对两品种经产母猪产仔数的总体 平均数进行比较, 平均数进行比较,因此为均数差异显著性检 ------t检验。 验------t检验。
1
2
3
4
5
6
7
8
9
10
随机抽取一个球,求下列事件的概率 随机抽取一个球,求下列事件的概率; (1)事件 =抽得一个编号< 4 事件A=抽得一个编号 事件 事件B 抽得一个编号是2的倍数 (2)事件 =抽得一个编号是 的倍数 事件 抽得一个编号是 该试验样本空间由10个等可能的基本事件构成, 该试验样本空间由 个等可能的基本事件构成,即n=10,而 个等可能的基本事件构成 , 事件A所包含的基本事件有 所包含的基本事件有3个 即抽得编号为1、 、 中的任 事件 所包含的基本事件有 个,即抽得编号为 、2、3中的任 何一个,事件A便发生 便发生。 何一个,事件 便发生。 P(A)=3/10=0.3 P(B)=5/10=0.5
四、小概率事件原理
概念: 如果某事件发生的概率很小 很小, 概念: 如果某事件发生的概率很小,在大量 重复试验中事件发生的频率也很小, 重复试验中事件发生的频率也很小, 在1次试验中该事件被看做是不会发 次试验中该事件被看做是不会发 生的。 生的。 应用:是假设检验时进行统计推断的理论依据。 应用:是假设检验时进行统计推断的理论依据。
通常将5%,1%认为是小概率的标准,又称 通常将 , 认为是小概率的标准, 认为是小概率的标准 显著水平。 显著水平。
第二节 均数差异显著性检验
一、复习回顾
生物统计的本质: 生物统计的本质: 研究如何从样本推断总体 样本抽取的原则: 样本抽取的原则: 随机抽样 试验误差的概念: 试验误差的概念: 由样本推断总体时, 由样本推断总体时,由各种 无法控制的随机因素引起的误差。 无法控制的随机因素引起的误差。
六、显著性检验的步骤
1、提出假设 提出假设 2、确定显著水平 、 3、选定检验方法,计算检验统计量, 、选定检验方法,计算检验统计量, 确定概率值作出推断 确定概率值 4、结论:是否接受假设
下面以两均数差异显著性检验为例具体说 明操作步骤。 明操作步骤。
例1: 随机抽测9头内江猪和9 随机抽测9头内江猪和9头荣昌猪经产母猪的产 仔数,得到如下数据资料:
一、概率基本概念 1 6 2 7 3 8 4 9 5 10
A=“一次取一个球,取得红球的概率” = 一次取一个球,取得红球的概率”
10个球中取一个球,其可能结果有10个基本事件(即每个球 个球中取一个球,其可能结果有 个基本事件 个基本事件( 个球中取一个球 被取到的可能性是相等的), ),即 被取到的可能性是相等的),即n=10 事件A:取得红球, 事件包含3个基本事件 事件 :取得红球,则A事件包含 个基本事件,即m=3 事件包含 个基本事件, P(A)=3/10=0.3
处理 效应 误差 效应
三、显著性检验的任务
分析误差产生的原因 排除误差干扰 确定差异的性质 对总体特征做出正确判断
四、显著性检验的原理
小概率原理: 小概率原理: 统计假设:对总体的某些未知或不完全知道 统计假设:
的性质提出待考查的命题,通常包括无效假 的性质提出待考查的命题, 设和备择假设。 设和备择假设。根据样本资料对假设的成立 与否进行推断就是假设检验, 与否进行推断就是假设检验,也称显著性检 验。
一、概率基本概念
在一定条件下必然出现某种结果或必然不出现某种结果。 在一定条件下必然出现某种结果或必然不出现某种结果。
确定性事件
必然事件( 必然事件(U) (certain event)
不可能事件( 不可能事件(V) (impossible event)
在一定条件下可能发生也可能不发生。 在一定条件下可能发生也可能不发生。
差异
在试验进行过程中,尽管尽量排除随机误差的影响,以 在试验进行过程中,尽管尽量排除随机误差的影响, 突出试验的处理效应,但由于生物个体间无法避免的差异, 突出试验的处理效应,但由于生物个体间无法避免的差异, 以及诸多无法控制的随机因素, 以及诸多无法控制的随机因素,使得试验结果最后表现的观 察值除了处理效应以外,还包括试验误差的效应。 察值除了处理效应以外,还包括试验误差的效应。
在无效假设H 成立的前提下计算t 在无效假设H0成立的前提下计算t值
注:由于计算过程复杂,这里不再重复书上内容,在下 由于计算过程复杂,这里不再重复书上内容, 面将具体讲解如何用Excel来进行统计分析。 来进行统计分析。 面将具体讲解如何用 来进行统计分析
三、概率(probabห้องสมุดไป่ตู้lity,P) 概率(
m m P(A) = p=lim ≈ n n
在一般情况下,随机事件的概率 是不可 在一般情况下,随机事件的概率P是不可 能准确得到的。通常以试验次数n充分大 充分大, 能准确得到的。通常以试验次数 充分大,随 机事件A的频率作为该随机事件概率的近似值 的频率作为该随机事件概率的近似值。 机事件 的频率作为该随机事件概率的近似值。
一、概率基本概念
频率表明了事件频繁出现的程度, 频率表明了事件频繁出现的程度,因而其稳定 性说明了随机事件发生的可能性大小, 性说明了随机事件发生的可能性大小,是其本身固 有的客观属性,提示了隐藏在随机现象中的规律性。 有的客观属性,提示了隐藏在随机现象中的规律性。
定义:设在相同的条件下,进行大量重复试验, 定义:设在相同的条件下,进行大量重复试验, 若事件A的频率稳定地在某一确定值 的附近摆动 若事件 的频率稳定地在某一确定值p的附近摆动, 的频率稳定地在某一确定值 的附近摆动, 则称p为事件 出现的概率 则称 为事件A出现的概率。 为事件 出现的概率。
0≤W(A) ≤1
抛掷一枚硬币发生正面朝上的试验记录 实验者 蒲峰 皮尔逊 皮尔逊 投掷次数 ( n) 4040 12000 24000 发生正面朝上次数 频率 (m/n) m/n) (m) 2048 6019 12012 0.5069 0.5016 0.5005
从表中可以看出,试验随着 值的不同 值的不同, 从表中可以看出,试验随着n值的不同,正面朝上出现 的频率也不相同, 越大时, 的频率也不相同,当n越大时,频率越接近 越大时 频率越接近0.50。 。
五、显著性检验的分类
t 检验——主要用于检验两个处理平均数差 检验——主要用于检验两个处理平均数差 异是否显著; 异是否显著; 方差分析——主要用于检验多个处理平均 方差分析——主要用于检验多个处理平均 数间差异是否显著; 数间差异是否显著; 检验 —— 主要用于由质量性状得来的次 数资料的显著性检验等。 数资料的显著性检验等。
处理 效应 误差 效应
表 面 效 应
二、显著性检验的目的
对两个样本进行比较时, 对两个样本进行比较时,必须判断样本 间差异主要是随机误差造成的, 间差异主要是随机误差造成的,还是本质不 同或处理效应引起的? 同或处理效应引起的? 处理 效应 误差 效应
