传送带模型练习(带答案)
(完整版)高中物理传送带模型(解析版)
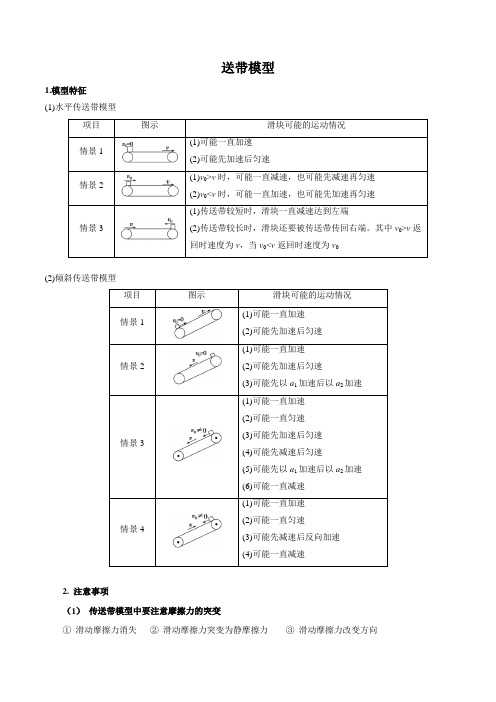
送带模型1.模型特征(1)水平传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景3(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v0>v返回时速度为v,当v0<v返回时速度为v0(2)倾斜传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速情景3(1)可能一直加速(2)可能一直匀速(3)可能先加速后匀速(4)可能先减速后匀速(5)可能先以a1加速后以a2加速(6)可能一直减速情景4(1)可能一直加速(2)可能一直匀速(3)可能先减速后反向加速(4)可能一直减速2. 注意事项(1)传送带模型中要注意摩擦力的突变①滑动摩擦力消失②滑动摩擦力突变为静摩擦力③滑动摩擦力改变方向(2)传送带与物体运动的牵制。
牛顿第二定律中a 是物体对地加速度,运动学公式中S 是物体对地的位移,这一点必须明确。
(3) 分析问题的思路:初始条件→相对运动→判断滑动摩擦力的大小和方向→分析出物体受的合外力和加速度大小和方向→由物体速度变化再分析相对运动来判断以后的受力及运动状态的改变。
【典例1】如图所示,传送带的水平部分长为L ,运动速率恒为v ,在其左端无初速放上木块,若木块与传送带间的动摩擦因数为μ,则木块从左到右的运动时间可能是( )A.L v +v 2μgB.L vC.2L μgD.2L v【答案】 ACD【典例2】如图所示,倾角为37°,长为l =16 m 的传送带,转动速度为v =10 m/s ,动摩擦因数μ=0.5,在传送带顶端A 处无初速度地释放一个质量为m =0.5 kg 的物体.已知sin 37°=0.6,cos 37°=0.8,g =10 m/s 2.求:(1)传送带顺时针转动时,物体从顶端A 滑到底端B 的时间; (2)传送带逆时针转动时,物体从顶端A 滑到底端B 的时间. 【答案】 (1)4 s (2)2 s【典例3】如图所示,与水平面成θ=30°的传送带正以v =3 m/s 的速度匀速运行,A 、B 两端相距l =13.5 m 。
传送带模型--2024年高三物理二轮常见模型含参考答案

2024年高三物理二轮常见模型专题传送带模型特训目标特训内容目标1水平传送带模型(1T -5T )目标2倾斜传送带模型(6T -10T )目标3电磁场中的传送带模型(11T -15T )【特训典例】一、水平传送带模型1如图所示,足够长的水平传送带以v 0=2m/s 的速度沿逆时针方向匀速转动,在传送带的左端连接有一光滑的弧形轨道,轨道的下端水平且与传送带在同一水平面上,滑块与传送带间的动摩擦因数为μ=0.4。
现将一质量为m =1kg 的滑块(可视为质点)从弧形轨道上高为h =0.8m 的地方由静止释放,重力加速度大小取g =10m/s 2,则()A.滑块刚滑上传送带左端时的速度大小为4m/sB.滑块在传送带上向右滑行的最远距离为2.5mC.滑块从开始滑上传送带到第一次回到传送带最左端所用的时间为2.5sD.滑块从开始滑上传送带到第一次回到传送带最左端的过程中,传动系统对传送带多做的功为12J 2如图甲所示,一足够长的水平传送带以某一恒定速度顺时针转动,一根轻弹簧一端与竖直墙面连接,另一端与工件不拴接。
工件将弹簧压缩一段距离后置于传送带最左端无初速度释放,工件向右运动受到的摩擦力F f 随位移x 变化的关系如图乙所示,x 0、F f 0为已知量,则下列说法正确的是(工件与传送带间的动摩擦因数处处相等)()A.工件在传送带上先做加速运动,后做减速运动B.工件向右运动2x 0后与弹簧分离C.弹簧的劲度系数为F f 0x 0D.整个运动过程中摩擦力对工件做功为0.75F f 0x 03如图所示,水平传送带AB 长L =10m ,以恒定速率v 1=2m/s 运行。
初速度大小为v 2=4m/s 的小物块(可视为质点)从与传送带等高的光滑水平地面上经A 点滑上传送带。
小物块的质量m =1kg ,物块与传送带间的动摩擦因数μ=0.4,g取10m/s2,则()A.小物块离开传送带时的速度大小为2m/sB.小物体在传送带上的运动时间为2sC.小物块与传送带间的摩擦生热为16JD.小物块和传送带之间形成的划痕长为4.5m4如图甲所示,水平传送带在电机的作用下,t=0时刻由静止开始向右做匀加速直线运动,物块(视为质点)在t=0时刻以速度v0从左轮中心的正上方水平向右滑上传送带,t0时刻物块与传送带的速度相等均为0.4v0,物块和传送带运动的v-t图像如图乙所示,t0时刻前后物块的加速度大小变化量为53m/s2,物块从右轮中心正上方离开传送带时速度为0.8v0,整个过程中物块相对传送带的位移为1.5m。
(完整版)高中物理传送带模型典型例题(含答案)【经典】,推荐文档

难点形成的原因:1、对于物体与传送带之间是否存在摩擦力、是滑动摩擦力还是静摩擦力、摩擦力的方向如何,等等,这些关于摩擦力的产生条件、方向的判断等基础知识模糊不清;2、对于物体相对地面、相对传送带分别做什么样的运动,判断错误;3、对于物体在传送带上运动过程中的能量转化情况考虑不全面,出现能量转化不守恒的错误过程。
1、水平传送带被广泛地应用于机场和火车站,如图所示为一水平传送带装置示意图.绷紧的传送带AB 始终保持恒定的速率v =1 m/s 运行,一质量为m =4 kg 的行李无初速度地放在A 处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数μ=0.1,A 、B 间的距离L =2 m ,g 取10 m/s 2.(1)求行李刚开始运动时所受滑动摩擦力的大小与加速度的大小;(2)求行李做匀加速直线运动的时间;(3)如果提高传送带的运行速率,行李就能被较快地传送到B 处,求行李从A 处传送到B 处的最短时间和传送带对应的最小运行速率.解析 (1)行李刚开始运动时,受力如图所示,滑动摩擦力:F f =μmg =4 N 由牛顿第二定律得:F f =ma 解得:a =1m/s 2(2)行李达到与传送带相同速率后不再加速,则:v =at ,解得t ==1 sv a (3)行李始终匀加速运行时间最短,且加速度仍为a =1 m/s 2,当行李到达右端时,有:v =2aL 解得:v min ==2 m/s 2min2aL 故传送带的最小运行速率为2 m/s 行李运行的最短时间:t min ==2 sv mina 2:如图所示,传送带与地面成夹角θ=37°,以10m/s 的速度顺时针转动,在传送带下端轻轻地放一个质量m=0.5㎏的物体,它与传送带间的动摩擦因数μ=0.9,已知传送带从A→B 的长度L=50m ,则物体从A 到B 需要的时间为多少?【解析】物体放上传送带以后,开始一段时间,其运动加速度2m/s 2.1sin cos =-=m mg mg a θθμ。
(完整版)高中物理传送带模型(解析版)

送带模型1.模型特征(1)水平传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景3(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v0>v返回时速度为v,当v0<v返回时速度为v0(2)倾斜传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速情景3(1)可能一直加速(2)可能一直匀速(3)可能先加速后匀速(4)可能先减速后匀速(5)可能先以a1加速后以a2加速(6)可能一直减速情景4(1)可能一直加速(2)可能一直匀速(3)可能先减速后反向加速(4)可能一直减速2. 注意事项(1)传送带模型中要注意摩擦力的突变①滑动摩擦力消失②滑动摩擦力突变为静摩擦力③滑动摩擦力改变方向(2)传送带与物体运动的牵制。
牛顿第二定律中a 是物体对地加速度,运动学公式中S 是物体对地的位移,这一点必须明确。
(3) 分析问题的思路:初始条件→相对运动→判断滑动摩擦力的大小和方向→分析出物体受的合外力和加速度大小和方向→由物体速度变化再分析相对运动来判断以后的受力及运动状态的改变。
【典例1】如图所示,传送带的水平部分长为L ,运动速率恒为v ,在其左端无初速放上木块,若木块与传送带间的动摩擦因数为μ,则木块从左到右的运动时间可能是( )A.L v +v 2μgB.L vC.2L μgD.2L v【答案】 ACD【典例2】如图所示,倾角为37°,长为l =16 m 的传送带,转动速度为v =10 m/s ,动摩擦因数μ=0.5,在传送带顶端A 处无初速度地释放一个质量为m =0.5 kg 的物体.已知sin 37°=0.6,cos 37°=0.8,g =10 m/s 2.求:(1)传送带顺时针转动时,物体从顶端A 滑到底端B 的时间; (2)传送带逆时针转动时,物体从顶端A 滑到底端B 的时间. 【答案】 (1)4 s (2)2 s【典例3】如图所示,与水平面成θ=30°的传送带正以v =3 m/s 的速度匀速运行,A 、B 两端相距l =13.5 m 。
高中物理-传送带模型

传送带模型1.水平传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景3(1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端。
其中v0>v,返回时速度为v;当v0<v,返回时速度为v02.倾斜传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速*情景3(1)可能一直加速(2)可能先加速后匀速(3)可能一直匀速(4)可能先以a1加速后以a2加速*情景4(1)可能一直加速(2)可能一直匀速(3)可能先减速后反向加速①水平传送带问题:求解的关键在于正确分析出物体所受摩擦力.判断摩擦力时要注意比较物体的运动速度与传送带的速度,也就是分析物体在运动位移x(对地)的过程中速度是否和传送带速度相等.物体的速度与传送带速度相等的时刻就是物体所受摩擦力发生突变的时刻.②倾斜传送带问题:求解的关键在于正确分析物体与传送带的相对运动情况,从而判断其是否受到滑动摩擦力作用.如果受到滑动摩擦力作用应进一步确定其大小和方向,然后根据物体的受力情况确定物体的运动情况.当物体速度与传送带速度相等时,物体所受的摩擦力有可能发生突变.小结:分析处理传送带问题时需要特别注意两点:一是对物体在初态时(静止释放或有初速度的释放)所受滑动摩擦力的方向的分析;二是对物体与传送带共速时摩擦力的有无及方向的分析.对于传送带问题,一定要全面掌握上面提到的几类传送带模型,尤其注意要根据具体情况适时进行讨论,看一看受力与速度有没有转折点、突变点,做好运动过程的划分及相应动力学分析.3.传送带问题的解题思路模板[分析物体运动过程]例1:(多选)如图所示,足够长的传送带与水平面夹角为θ,在传送带上某位置轻轻放置一小木块,小木块与传送带间动摩擦因素为μ,小木块速度随时间变化关系如图所示,v 0、t 0已知,则( )A .传送带一定逆时针转动B .00tan cos v gt μθθ=+C .传送带的速度大于v 0D .t 0后滑块的加速度为002sin v g t θ-[求相互运动时间,相互运动的位移] 例2:如图所示,水平传送带两端相距x =8 m ,工件与传送带间的动摩擦因数μ=0.6,工件滑上A 端时速度v A =10 m/s ,设工件到达B 端时的速度为v B 。
高考一轮微专题训练【10】“传送带”模型(含答案)

微专题训练10 “传送带”模型1.(单选)物块M 在静止的传送带上匀速下滑时,传送带突然转动,传送带转动的方向如图1中箭头所示.则传送带转动后 ( ).图1A .物块将减速下滑B .物块仍匀速下滑C .物块受到的摩擦力变小D .物块受到的摩擦力变大解析 当传送带静止时,物块匀速下滑,物块受力平衡可得:mgsin θ=μmgcos θ;当传送带转动起来时,由于物块与传送带之间运动方向相反,可判断物块所受的滑动摩擦力方向并没有发生变化,仍然沿斜面向上,大小仍为μmgcos θ,物块受力仍然是平衡的,所以物块仍匀速下滑.答案 B2.(多选)如图2所示,一质量为m 的小物体以一定的速率v 0滑到水平传送带上左端的A 点,当传送带始终静止时,已知物体能滑过右端的B 点,经过的时间为t 0,则下列判断正确的是 ( ).图2A .若传送带逆时针方向运行且保持速率不变,则物体也能滑过B 点,且用时为t 0B .若传送带逆时针方向运行且保持速率不变,则物体可能先向右做匀减速运动直到速度减为零,然后向左加速,因此不能滑过B 点C .若传送带顺时针方向运行,当其运行速率(保持不变)v =v 0时,物体将一直做匀速运动滑过B 点,用时一定小于t 0D .若传送带顺时针方向运行,当其运行速率(保持不变)v>v 0时,物体一定向右一直做匀加速运动滑过B 点,用时一定小于t 0解析 传送带静止时,有12mv 2B -12mv 20=-μmgL ,即v B =v 20-2μgL ,物体做匀减速运动,若传送带逆时针运行,物体仍受向左的摩擦力μmg ,同样由上式分析,一定能匀减速至右端,速度为v B ,用时也一定仍为t 0,故选项A 对,而B 错;若传送带顺时针方向运行,当其运行速率(保持不变)v =v 0时,物体将不受摩擦力的作用,一直做匀速运动滑至B 端,因为匀速通过,故用时一定小于t 0,故选项C 正确;当其运行速率(保持不变)v>v 0时,开始物体受到向右的摩擦力的作用,做加速运动,运动有两种可能:若物体加速到速度v 还未到达B 端时,则先匀加速运动后匀速运动,若物体速度一直未加速到v 时,则一直做匀加速运动,故选项D 不对.答案 AC3.(多选)如图3甲为应用于机场和火车站的安全检查仪,用于对旅客的行李进行安全检查.其传送装置可简化为如图乙的模型,紧绷的传送带始终保持v =1 m/s 的恒定速率运行.旅客把行李无初速度地放在A 处,设行李与传送带之间的动摩擦因数μ=0.1,A 、B 间的距离为2 m ,g 取10 m/s 2.若乘客把行李放到传送带的同时也以v =1 m/s 的恒定速率平行于传送带运动到B 处取行李,则 ( ).图3A .乘客与行李同时到达B 处B .乘客提前0.5 s 到达B 处C .行李提前0.5 s 到达B 处D .若传送带速度足够大,行李最快也要2 s 才能到达B 处解析 行李放在传送带上,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.加速度为a =μg =1 m/s 2,历时t 1=v a =1 s 达到共同速度,位移x 1=v 2t 1=0.5 m ,此后行李匀速运动t 2=2 m -x 1v =1.5 s 到达B ,共用2.5 s ;乘客到达B ,历时t =2 m v=2 s ,故B 正确.若传送带速度足够大,行李一直加速运动,最短运动时间t min =2×21 s =2 s ,D 项正确. 答案 BD4.(2018·郑州检测)(单选)如图4所示为粮袋的传送装置,已知AB 间长度为L ,传送带与水平方向的夹角为θ,工作时其运行速度为v ,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A 点将粮袋放到运行中的传送带上,关于粮袋从A 到B 的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力) ( ).图4A .粮袋到达B 点的速度与v 比较,可能大,也可能相等或小B .粮袋开始运动的加速度为g(sin θ-μcos θ),若L 足够大,则以后将一定以速度v 做匀速运动C .若μ≥tan θ,则粮袋从A 到B 一定一直是做加速运动D .不论μ大小如何,粮袋从A 到B 一直做匀加速运动,且a>gsin θ解析 开始时,粮袋相对传送带向上运动,受重力、支持力和沿传送带向下的摩擦力,由牛顿第二定律可知,mgsin θ+μF N =ma ,F N =mgcos θ,解得a =gsin θ+μgcos θ,故B 项错;粮袋加速到与传送带相对静止时,若mgsin θ>μmgcos θ,即当μ<tan θ时粮袋将继续做加速运动,C 、D 项错,A 项对. 答案 A5.(2018·江西盟校二联,24)如图5所示,一水平传送装置有轮半径均为R =1πm 的主动轮O 1和从动轮O 2及传送带等构成.两轮轴心相距8.0 m ,轮与传送带不打滑.现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数为μ=0.4,这袋面粉中的面粉可不断地从袋中渗出.(g 取10 m/s 2)图5(1)当传送带以4.0 m/s 的速度匀速运动时,将这袋面粉由左端O 2正上方的A 点轻放在传送带上后,这袋面粉由A 端运送到O 1正上方的B 端所用的时间为多少?(2)要想尽快将这袋面粉由A 端送到B 端(设初速度仍为零),主动轮O 1的转速至少应为多大?解析 设这袋面粉质量为m ,其在与传送带产生相对滑动的过程中所受摩擦力f =μmg.故而其加速度为:a =f m=μg =4.0 m/s 2 (1)若传送带的速度v 带=4.0 m/s ,则这袋面粉加速运动的时间t 1=v 带/a =1.0 s ,在t 1时间内的位移s 1为:s 1=12at 21=2.0 m 其后以v =4.0 m/s 的速度做匀速运动s 2=l AB -s 1=vt 2,解得:t 2=1.5 s运动的总时间为:t =t 1+t 2=2.5 s(2)要想时间最短,这袋面粉应一直向B 端做加速运动,由l AB =12at′2可得:t′=2.0 s 此时传送带的运转速度为:v′=at′=8.0 m/s由v′=ωR =2πnR 可得:n =4 r/s =240 r/min答案 (1)2.5 s (2)4 r/s 或240 r/min6.如图6所示,绷紧的传送带,始终以2 m/s 的速度匀速斜向上运行,传送带与水平方向间的夹角θ=30°.现把质量为10 kg 的工件轻轻地放在传送带底端P 处,由传送带传送至顶端Q 处.已知P 、Q 之间的距离为4 m ,工件与传送带间的动摩擦因数为μ=32,取g =10 m/s 2.图6(1)通过计算说明工件在传送带上做什么运动;(2)求工件从P 点运动到Q 点所用的时间.解析 (1)工件受重力、摩擦力、支持力共同作用,摩擦力为动力由牛顿第二定律得:μmgcos θ-mgsin θ=ma代入数值得:a =2.5 m/s 2则其速度达到传送带速度时发生的位移为x 1=v 22a =222×2.5 m =0.8 m<4 m可见工件先匀加速运动0.8 m ,然后匀速运动3.2 m(2)匀加速时,由x 1=v 2t 1得t 1=0.8 s匀速上升时t 2=x 2v =3.22 s =1.6 s所以工件从P 点运动到Q 点所用的时间为t =t 1+t 2=2.4 s答案 (1)先匀加速运动0.8 m ,然后匀速运动3.2 m (2)2.4 s。
高中物理---传送带模型-----典型例题(含答案)【经典】

难点形成的原因:1、对于物体与传送带之间是否存在摩擦力、是滑动摩擦力还是静摩擦力、摩擦力的方向如何,等等,这些关于摩擦力的产生条件、方向的判断等基础知识模糊不清;2、对于物体相对地面、相对传送带分别做什么样的运动,判断错误;3、对于物体在传送带上运动过程中的能量转化情况考虑不全面,出现能量转化不守恒的错误过程。
1、水平传送带被广泛地应用于机场和火车站,如图所示为一水平传送带装置示意图.绷紧的传送带AB 始终保持恒定的速率v =1 m/s 运行,一质量为m =4 kg 的行李无初速度地放在A 处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数μ=,A 、B 间的距离L =2 m ,g 取10 m/s 2. (1)求行李刚开始运动时所受滑动摩擦力的大小与加速度的大小; (2)求行李做匀加速直线运动的时间;(3)如果提高传送带的运行速率,行李就能被较快地传送到B 处,求行李从A 处传送到B 处的最短时间和传送带对应的最小运行速率. |解析 (1)行李刚开始运动时,受力如图所示,滑动摩擦力:F f =μmg =4 N 由牛顿第二定律得:F f =ma 解得:a =1 m/s 2 (2)行李达到与传送带相同速率后不再加速,则:v =at ,解得t =v a=1 s(3)行李始终匀加速运行时间最短,且加速度仍为a =1 m/s 2,当行李到达右端时, 有:v 2min =2aL 解得:v min =2aL =2 m/s故传送带的最小运行速率为2 m/s 行李运行的最短时间:t min =v mina=2 s 2:如图所示,传送带与地面成夹角θ=37°,以10m/s 的速度顺时针转动,在传送带下端轻轻地放一个质量m=㎏的物体,它与传送带间的动摩擦因数μ=,已知传送带从A →B 的长度L=50m ,则物体从A 到B 需要的时间为多少【解析】物体放上传送带以后,开始一段时间,其运动加速度2m/s 2.1sin cos =-=mmg mg a θθμ。
牛顿第二定律传送带模型含答案

7.如图5所示,水平传送带A、B两端相距x=4 m,以v0=2 m/s的速率顺时针转动,将一小煤块无初速度地放到A点,已知小煤块与传送带间的动摩擦因数为0.4,取g=10 m/s2,由于小煤块与传送带之间有相对滑动,故会在传送带上留下划痕,则小煤块从A运动到B的过程中()图5A.所用的时间为2.25 sB.所用的时间为0.5 sC.划痕长度为4 mD.划痕长度为0.5 m解析小煤块在传送带上滑动时,根据牛顿第二定律有:μmg=ma,解得a=4 m/s2,当小煤块和传送带速度相同时,位移为x1=v202a=0.5 m<4 m,因此小煤块先加速后匀速,加速时间为t1=v0a =0.5 s,匀速运动时间t2=x-x1v0=1.75 s,小煤块从A运动到B的过程中所用时间为t=t1+t2=2.25 s,故选项A正确,B错误;在加速阶段相对位移产生划痕,故有Δx=v0t1-x1=0.5 m,故选项C错误,D正确。
答案AD【例1】如图1所示,水平长传送带始终以v匀速运动,现将一质量为m的物体轻放于A端,物体与传送带之间的动摩擦因数为μ,AB长为L,L足够长。
问:图1(1)物体从A到B做什么运动?(2)当物体的速度达到传送带速度v时,物体的位移多大?传送带的位移多大?(3)物体从A到B运动的时间为多少?(4)什么条件下物体从A到B所用时间最短?解析(1)物体先做匀加速直线运动,当速度与传送带速度相同时,做匀速直线运动。
(2)由v=at和a=μg,解得t=v μg物体的位移x1=12at 2=v22μg传送带的位移x2=vt=v2μg (3)物体从A到B运动的时间为t总=vμg +L-x1v=Lv+v2μg(4)当物体从A到B一直做匀加速直线运动时,所用时间最短,所以要求传送带的速度满足v≥2μgL。
答案(1)先匀加速,后匀速(2)v22μgv2μg(3)Lv+v2μg(4)v≥2μgL【拓展延伸1】若在【例1】中物体以初速度v0(v0≠v)从A端向B端运动,则:(1)物体可能做什么运动?(2)什么情景下物体从A到B所用时间最短,如何求最短时间?解析(1)①若v0<v,物体刚放到传送带上时将做a=μg的匀加速运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1:如图所示,绷紧的传送带,始终以2 m/s 的速度匀速斜向上运行,传送带与水平方向间的夹角 0 = 30°。
现把质量为10 kg 的工件轻轻地放在传送带底端P 处,由传送带传送至顶端 Q 处。
■'3 2口 = 2,取 g = 10 m/s 。
(1) 通过计算说明工件在传送带上做什么运动;(2) 求工件从P 点运动到Q 点所用的时间。
[答案](1)先匀加速运动0.8 m,然后匀速运动3.2 m (2)2.4 s解析(1)工件受重力、摩擦力、支持力共同作用,摩擦力为动力由牛顿第二定律得:j mcos 旷mgsin 尸ma 代入数值得:a =2.5 m/s 22v -则其速度达到传送带速度时发生的位移为X 1= = --------- m = 0.8 m<4 m 可见工件先匀加速运动0.8 m ,然后匀速运动3.2 m 2a 2X 2.5已知P 、Q 之间的距离为4 m 工件与传送带间的动摩擦因数 22(2)匀加速时,由X 1 =尹得t 1 = 0.8 sX 2 3 2匀速上升时t 2= _=可s = 1.6 s 所以工件从v 2P 点运动到Q 点所用的时间为t = t 1 +t 2= 2.4 s2:如图,倾角为37 °,长为 擦因数j = 0.5,在传送带顶端 体.已知 sin 37° =6, cos 37 (1) 传送带顺时针转动时,物体从顶端 (2) 传送带逆时针转动时,物体从顶端 答案 (1)4 s (2)2 s解析(1)传送带顺时针转动时,物体相对传送带向下运动,则物体所受滑动摩擦力沿斜面向上,相对传送带向l = 16 m 的传送带,转动速度为 A 处无初速度地释放一个质量为=.8, g = 10 m/s 2.求: A 滑到底端B 的时间; A 滑到底端B 的时间.v = 10 m/s ,动摩 m = 0.5 kg 的物下匀加速运动,根据牛顿第二定律有 mg(sin 37 ° 37 ° )nra 则a =gsin 37 ° 37 °= m/s 2,根据11= 2at 2得 t = 4 s.(2传送带逆时针转动,当物体下滑速度小于传送带转动速度时,物体相对传送带向上运动,则物体所受滑动摩擦力沿传送带向下,设物体的加速度mgsin 37+ rrcps 37大小为 a 1,由牛顿第二得,mgsin 37 ° + m^s 37 ° =ms !则有 &== 10 m/s 2v 10 1设当物体运动速度等于传送带转动速度时经历的时间为「位移为X1,则有t1= a= 10 s = 1 s, X 1 = 2a 1t2= 5 m <= 16 m当物体运动速度等于传送带速度瞬间, 有mgsin 37 ° j mcgis 37 °,则下一时刻物体相对传送带向下运动, 受到传送带向上的滑动摩擦力一一摩擦力发生突变.设当物体下滑速度大于传送带转动速度时物体的加速度为 mgsin 37 — m?Ps 37a 2,则 a 2=---------------------- = 2mQX 2= l — X 1 = 11 m1又因为 X 2= Vt 2 +2业2,则有 1Ct 2+ t 2= 11,解得:t 2= 1 s(t 2=— 11 s 舍去)所以上总=t 〔+ t 2= 2 s.3•如图所示,足够长的传送带与水平面倾角 037 °,以12m/s 的速率逆时针转动。
在传送带底部有一质量 m = 1.0kg 的物体,物体与斜面间动摩擦因数片0.25,现用轻细绳将物体由静止沿传送带向上拉动,拉力F = 10.0N ,方向平行传送带向上。
经时间t = 4.0s 绳子突然断了,求: (1) (2) 绳断时物体的速度大小;绳断后物体还能上行多远从绳断开始到物体再返回到传送带底端时的运动时间(3) (g = 10m/s 2, sin 37 ° = 0.6 ,$7° = 0.8 答案:1、8.0m/s2、 【解析】(1)物体开始向上运动过程中,受重力 mg,摩擦力F f ,拉力F ,设加速度为&,则有F 4.0m3、3.3s-mgsin — F f = ma 〔 又 F f = j N F N = mgcos 0得 a = 2.0m / s 2所以,t = 4.0s 时物体速度 V 1=a* = 8.0m/s(2)绳断后,物体距传送带底端si =a i t 2 /2= 16m.设绳断后物体的加速度为 念由牛顿第二定律得-mgsin - j mgcos 0 玄m a? = -8.0m / s 2物体做减速运动时间t 2 = -v i /a 2= 1.0s 减速运动位移S 2=V i t 2+ S 2t 22/2 = 4.0m(3)此后物体沿传送带匀加速下滑,设加速度为a 3,由牛顿第二定律得mgsin j mgco= ma ? a= 8.0m / s 2当物体与传送带共速时向下运动距离S 3= v 2/(2a 3)=9m用时t 3 = v / a 3=1.5s 共速后摩擦力反向,由于mgsin 大于j mgcos 物体继续沿传送带匀加速下滑,设此时加速度为a 4,由牛顿第二定律得 Mgsin - J mgcos 0 4=ma下滑到传送带低部的距离为S 1+S 2-s=11m 设下滑的时间为t4,由得t 4=0.8s 最后得t=t 2+t 3+t 4=3.3s上,若小煤块与传送带之间的动摩擦因数为□,求:小煤块在传送带上留下的痕迹长度是多少?2V x' Vt — 传送带运动的位移g5: 一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为。
初始时,传送带与煤块都是静止的。
现让传送带以恒定的加速度 a o 开始运动,当其速度达到V o 后,便以此速度做匀 速运动。
经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动。
求此黑色 痕迹的长度。
方法一:根据“传送带上有黑色痕迹”可知,煤块与传送带之间发生了相对滑动,煤块的加速度a 小于传送带的加速度 a@根据牛顿运动定律,可g设经历时间t ,传送带由静止开始加速到速度等于 V0,煤块则由静止加速到V ,有V ° a °t由于a<a0,故V <V 0,煤块继续受到滑动摩擦力的作用。
再经过时间t',煤块的速度由V 增加到V 0,有V °V a t此后,煤块与传送带运动速度相同,相对于传送带不再滑动,不再产生新的痕迹。
设在煤块的速度从 0增加到v0的整个过程中,传送带和煤块移动的距离分别为16、如图所示。
水平传送装置由轮半径均为R 米的主动轮01和从动轮02及传送带等构成。
两轮轴心相距L=8.0米,轮与传送带不打滑。
现用此装置运送一袋面粉,已知面粉袋与传送带间的动摩擦因数 为卩=0.4,这袋面粉中间的面粉可不断地从袋中渗出。
(1) 当传送带以v °==4.0m/s 的速度匀速运动时,将这袋面粉由左端 。
2正上方的A 点轻放在传送带上后, 这袋面粉由A 端运送到O 1正上方的B 端所用时间为多少?(2) 要想尽快将这带面粉由 A 端送到B 端(设初速度仍为零),传送带的速度至少应为多大? (3) 由于面粉的渗漏,在运送这袋面粉的过程中会在深色传送带上留 下白色的面粉的痕迹。
这袋面粉在传送带上留下的痕迹最长能有多 长(设袋的初速度仍为零)?此时传送带的速度至少应为多大?【解析】设面粉袋的质量为 m,其在与传送带产生相当滑动的过程中所受的摩擦力f= g m®故而其加速度为:a丄 g 4.0m/s2m(1) 若传送速带的速度v 带=4.0m/s ,则面粉袋加速运动的时间t 空 1 0s ,在t 1时间内的位移为1a匀速运动S 2=|AB — si=Vt 2,解得t 2=1.5s ,运动的总时间为t=t 1+t 2=2.5s(2) 要想时间最短,m 应一直向B 端做加速运动,由] 丄■ 2可得t 2 0s 此时传送带的运转速度为 v at 8 0m/ sl AB 〜at2(3)传送带的速度越大,“痕迹”越长。
当面粉的痕迹布满整条传送带时,痕迹达到最长。
即痕迹长为△1+2 n R=18.0m=2在面粉袋由A 端运动到B 端的时间内,传送带运转的距离s 带 s I AB 26.0m【解析】在煤块从开始加速至与传送带达到共同速度的过程中F 摩 F N mgmgm2由公式v 2ax2 2V V x 可得: 2a 2 g从煤块静止至煤块与传送带达到相对静止的过程中煤块加速运动的时x' x木块相对传送带滑动的位移s0和s ,有a °t 222 vo2a传送带上留下的黑色痕迹的长度S 0 ! IQ 。
g)由以上各式得2 a 0g1at 122.0m ,其后以V =4.°m/s的速度做又由(2)中已知t/=2.0s 此时传送带的运转速度为V〃=13m/s(3 分)7:如图所示,倾角为370的传送带以4m/s的速度沿图示方向匀速运动。
已知传送带的上、下两端间的距离为L=7m。
现将一质量m=0.4kg的小木块放到传送带的顶端,使它从静止开始沿传送带下滑,已知木块与传送带间的动摩擦因数为卩=0.25,取g=10m/s2。
求木块滑到底的过程中,摩擦力对木块做的功以及产生的热各是多少?【解析】刚开始时,合力的大小为 F i = mgsin370+[mgcos37),由牛顿第二定律,加速度大小a1= ?? = 8m/s2,该过程所用时间t1= Z? = 0.5s,位移大小s1=_?L = 1mm ?? 2??|二者速度大小相同后,合力的大小为 F 2= mgsin37o—mgcos3TO加速度大小a= -? =4m/s2 ,m位移大小s前L-s1= 6m,所用时间s前v°t2 +畀儿2得:t2= 1s。
(另一个解t2=—3s舍去)摩擦力所做的功= ^mgcos37o • (s1-s2) = —4.0J,全过程中生的热Q= f • s相对=^gcos3To •【(v0t1-s1)+ (s2-v0t2)】=0.8N x 3m=2.4J。
&如图甲所示,倾斜的传送带以恒定的速率逆时针运行•在t= 0时刻,将质量为1.0 kg的物块(可视为质点)无初速度地放在传送带的最上端A点,经过1.0 s,物块从最下端的B点离开传送带.取沿传送带向下为速度的正方向,则物块的对地速度随时间变化的图象如图乙所示(g= 10 m/s2),求:(1)物块与传送带间的动摩擦因数;⑵从A到B的过程中,传送带对物块做的功. 4. (1)*3(2)— 3.75 JV1 V2 —V1解析(1)由题图乙可知,物块在前0.5 s的加速度为:ai= =8 m/s2,后0.5 s的加速度为:a>=---------------------- = 2 m/s2物块在前0.5 s受到的滑动摩擦力沿传送t1 t2带向下,由牛顿第二定律得:mgsin 0+伏mcos 0=mai物块在后0.5 s受到的滑动摩擦力沿传送带向上,由牛顿第二定律得:mgsin —ncos =ma?联立解得:[1= 学V1⑵由v —t图线与t轴所围面积意义可知,在前0.5 s,物块对地位移为:X1= 2t1则摩擦力对物块做功:在后0.5 s物块对地位移为:V1 + V2X2=—2一t2则摩擦力对物块做功W2= 1 mcos 0' X2所以传送带对物块做的总功:W= W1 + W2联立解得:W —3.75 J9.如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动,质量为m的滑块从传送带右端以水平向左的速率V2滑上传送带,且V2>V1,最终滑块又返回至传送带的右端,对于此过程,求:(1)滑块返回传送带右端时的速率一(2)传送带对滑块做功(3)滑块与传送带间摩擦产生的热量(4)电动机做的功【解析】:(1)由于传送带足够长,滑块先向左减速至0再向右加速,由于V1<V2,当速度增大到等于传送带速度时,滑块还在传送带上,之后与传1 1送带一起向右匀速运动,有V2‘= V1 (2)根据动能定理,传送带对滑块做功W=A E k= 2mV12—2mV22V2 V2 1(3)滑块向左运动x1= 2打,摩擦力对滑块做功:W1=—F f X1=—F f2t1①又摩擦力做功等于滑块动能的变化量,即:W1=—2mV22②该过程中传送带的位移:X2= V1t1摩擦力对传送带做功:W2 = —F f z X2=—F f z V1t1③传送带对滑块的摩擦力与滑块对传送带的摩擦力为作用力与反作一V1 1用力,则有F f =F f‘④联立①②③④得:W2= —mV1V2设滑块向右匀加速运动的时间为为t2,位移为X3,贝U:X3 = 2上2摩擦力对滑块做功:W3= F f X3= 2 mV12该过程中传送带的位移:X4—V1t2—2X3滑块相对传送带的总位移:X相对—X1+ X2 + X4 —X3 —X1 + X2 + X3系统克服滑动摩擦力做功:1 1如总=F f X相对TW1I +| W2I + W3= 2m(V1 + V2)2滑块与传送带间摩擦产生的热量大小等于系统克服滑动摩擦力做功,Q =如总=2口©1 +V2)2,不计轮轴处的摩擦。
