物流管理定量分析方法试卷(答案)
物流管理定量分析方法形成性考核册(第3版)答案

第一次作业物资调运方案优化的表上作业法1.若某物资的总供应量大于总需求量,则可增设一个(A ),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。
(A)虚销地(B)虚产地(C)需求量 (D)供应量2。
将下列某物资的供求不平衡运输问题(供应量、需求量单位:吨;运价单位:元/吨)化为供求平衡运输问题:量与总供应量的差额,并取该产地到各销地的单位运价为0,并将供不应求运输问题化为供求平衡运输问题。
(A)大于 (B)小于 (C)等于(D)大于等于4.将下列某物资的供求不平衡运输问题(供应量、需求量单位:吨;运价单位:元/吨)化为供求平衡运输问题:5A,B,C,D四个仓库中收存,四仓库收进的数量分别为100吨、1500吨、400吨和1100吨,仓库和发货点之间的单位运价如下表所示:/吨)试用最小元素法确定一个初始调运方案,再调整寻求最优调运方案,使运输总费用最小。
解:6。
某物资要从产地A1,A2,A3调往销地B1,B2,B3,运输平衡表(单位:吨)和运价表(单位:元/吨)如下表所示:试用最小元素法编制初始调运方案,并求最优调运方案。
所有检验数全为正,此调运方案最优.最低运输总费用:(元)7。
设某物资要从产地A1,A2,A3调往销地B1,B2,B3,B4,运输平衡表(单位:吨)和运价表(单位:百元/吨)如下表所示:试问应怎样调运才能使总运费最省?所有检验数全为正,初始调运方案就是最优调运方案.最小运输总费用为(元)8.有一运输问题,涉及3个起始点A1,A2,A3和4个目的点B1,B2,B3,B4,3个起始点的供应量分别为50吨、50吨、75吨,4个目的点的需求量分别为40吨、55吨、60吨、20吨.运输平衡表及各起始点与目的点之间的距离(公里)如下表所示:假设每次装车的额外费用不计,运输成本与所行驶的距离成正比。
试求最优的调运方案,并求最小吨公里数。
检验数全为正,达到最优调运方案。
2023国家开放大学电大专科《物流管理定量分析方法》期末试题及答案

2023国家开放大学电大专科《物流管理定量分析方法》期末试题及答案(试卷号:2320) 盗传必究一、单项选择题(每小题4分,共20分)1.可通过增设一个虚(),能将下面的物资不平薇运输问题(供应量,需求量单位,吨;运价单位:元/吨)化为平衡逐输何供需■«!据衰A.钥地 C.产销地2.某物流公司有三种化学原料A|.A,.A 」.每公斤原料A,含三种化学成分 的含fit 分别为。
.7公斤,0.2公斤和0.1公斤)每公斤原料A,含B,・B,•&的含IR 分别为0.】 公斤・。
.3公斤和0.6公斤j每公斤原料A,含的含ft 分别为0.3公斤.0.4公斤和 0.3公斤.每公斤原料A*.A :・A3的成本分别为,00元,200元和300元.今需要B.成分至 少11。
公斤,出成分至少60公斤,&成分至少9。
公斤.为列出使总成本最小的线性规划模 型•设原料A|.A,.A,的用It 分别为百公斤,门公斤和队公斤•则化学成分B,应清足的约 束条件为《 ).A. 0. l«r | +0. 6心+0・ 3xt =9。
C. 0. I Xi 4-0. 6xj+0> 3xj^90A. -I G 2D. 14.设运输某物品的成本函数为('g )= q‘+50q,则运输嫉物品的固定成本为《A. 50B. 0C.qD. 15.由曲线/ = ”・・直线工=1与± = 16.以及工轴围成的曲边梯形的面枳表示为(x H <Lrx H dLx ii7. 设 '+xlnj •,求8.什 JI 定税分• +e-)(Lr3.设人井且A = B ・则工=(•求 M+28'B.产地 D.铜产地B.。
. 1 x | + 0. 6B + 0.3.cM90D ・ mmS = 400x| -h200jr : ). D. x H (Lr.共27分)E0 0 02 0 0一I 2(1 什W»»AiSxt A ' + H‘ 的命今.10.试耳出用MATLAB软件计算函数的yN《e・+/)htr二阶导敬的命令诵句.U. fit岛出用MATLAB软件it算定枳分£ /1 + 2, di的命令遍句.lE.jfi用IH第12 H 18分,第13 ■»分.共26分)12. JI公司机三个产Jt A、.、4远愉菜肉说品三个制Jt ,.石产地的供宸■(单位m)qs»堆的n求位,晚)及各产地到A钥堆的单位/价(革位'百元僵)如F厦所示、爆■平畜豪与1S价我B.B,B*B, B.At13242A<7a128At 需求■IS68128171035(!)在上表中写出用最小元素法编制的初始调运方案(用共它方法不汁成绩”(】2分)(2)检验上述初始词运方案是否最优,若非最优•求最优调运方案•并计算最低运墙总费用•(6分)13.已知运送基物品运输量为q吨时的成本函散C(q) = 10Q0 + 4Ug(百元),运摇该物品的市场需求函数为q=iooo-io小其中/>为价格,单位为百元/吨州为需求SI,单位为吨),求获皴大利润时的运输大利润.试题答案及评分标准(仅供参考)一•♦项法捧H(每小底[分.共20分)1. A2.C3.D小・9分.共27分)4.B1 0 0*0 0"6. A +2『= 0 2 0+0 2 20 0 3io 0 4■ ■5.C7分三、MSfllC小分.共”分)评&人・试写出用MATLAB «poo-042.10 0 K7.« (x 1 )* 4- (J* )*lnx + x (Iru )'=3x' + Inx + 18.J:d +/〉<U -(Zx1+«-) I;«14-e三,««■(«小IB9分.共27分)9.H算A " + B,的M ATI. AB命令奇旬为‘»dw>>A=[2 0 0 Oil 2 0 Oil -1 2 -hl - I -】2】»B«[1 1 I 1I2000I32 1 0i4 3 -I 1]»C«inv(A)>>D・C+B'10.»clear>>»ytns x»y-(exp(x) + x-2) • log(x)»diH(y.2>H.»deiir>>・yms x»y— sqrtf JT2+ZF IIS、阻用■(第12 1 18分,第13・B分,共26分)12.(1)用♦小元Xtttfi制的初怕■运方案知下表所示, 场■平街寰与垣价豪找空格时成的用回路・计算检弟散•<[到出度负A rt--2巳出现负幢趋散.方案需W曜«h凋# ■为0・2咤.H整后的第二个黄运方宴如F表所示.运•平衡*与运价H9分6分9分7分9分12分14分16分求第二个id运方案的检验数:M=0 •& = 2,山=0・人=6 所有检殿敷非负.第二个周运方案最优.最低运18 总费用为e8X2+2X4+3X2 + 7 *8 + 15X8 = 206(有元)13.由g = 10。
《物流管理定量分析方法》形成性考核册作业 参考答案
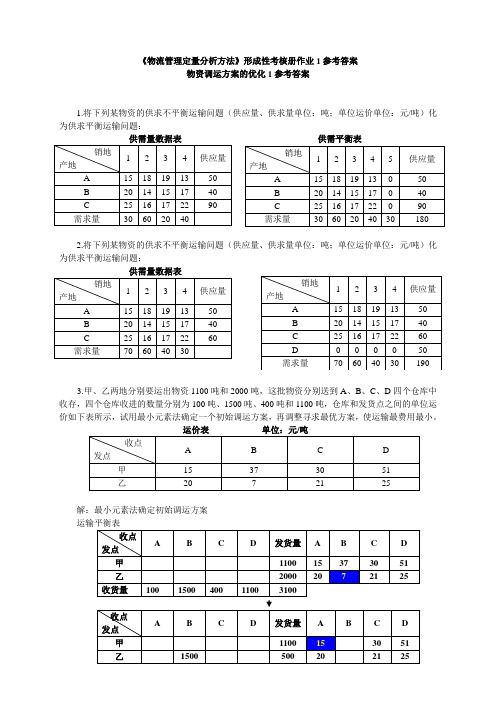
《物流管理定量分析方法》形成性考核册作业1参考答案物资调运方案的优化1参考答案1.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;单位运价单位:元/吨)化为供求平衡运输问题:供需量数据表 供需平衡表2.将下列某物资的供求不平衡运输问题(供应量、供求量单位:吨;单位运价单位:元/吨)化为供求平衡运输问题:供需量数据表3.甲、乙两地分别要运出物资1100吨和2000吨,这批物资分别送到A 、B 、C 、D 四个仓库中收存,四个仓库收进的数量分别为100吨、1500吨、400吨和1100吨,仓库和发货点之间的单位运价如下表所示,试用最小元素法确定一个初始调运方案,再调整寻求最优方案,使运输最费用最小。
运价表 单位:元/吨解:最小元素法确定初始调运方案 运输平衡表应用闭回路方法计算检验数:λ12 = 37—51+25—7 = 4﹥0 λ= 30—51+25—21 = —17﹤013λ23 = 21—30+51—25 = 21 ﹥0这样,所有的检验数已全部非负,因此调整后的调运方案就是最优方案。
最小运输费用为:S = 100×15+400×30+600×51+1500×7+500×25 = 56300(元)4.某物资要从产地A、B、C调往销地一、二、三,运输平衡表(单位:吨)与运价(单位:元/吨)如下表所示,试用最小元素法编制初始调运方案,并求最调运方案。
解:用编制初始调运方案,过程如下:运输平衡表与运价表运输平衡表与运价表运输平衡表与运价表5.某物资要从产地A、B、C调往销地一、二、三、四,运输平衡表(单位:吨)与运价表(单位:百元/吨)如下表所示,试问应怎样调运才能使总运费最省?解:用最小元素法编制初始运输方案运输平衡表与运价表运输平衡表与运价表运输平衡表与运价表运输平衡表与运价表初始物资调运方案为:应用闭回路方法计算检验数λ11= 3 —3 + 2 —1 = 1 ﹥0λ12= 11 —3 + 2 —9 = 1 ﹥0λ24= 9 —2 + 3 —12 = -2﹤0λ31= 7 —1 + 2 —3 + 12 —5 = 12 ﹥0 λ32= 4 —9 + 2 —3 + 12 —5 = 1 ﹥0 λ33= 10 —3 + 12—5 = 15 ﹥0= 2 —3 + 12 —9 = 2 ﹥023故调整后的运输方案为最优方案,其运费为:6. 有一3个其始点A、B、C和4个目的点一、二、三、四的运输问题,3个起始的供应量分别为50吨、50吨、75吨,4个目的点的需求量分别为40吨、55吨、60吨、和20吨。
国家开放大学电大本科《物流管理定量分析方法》期末试题标准题库及答案

国家开放大学电大本科《物流管理定量分析方法》期末试题标准题库及答案(试卷号:2320)盗传必究《物流管理定量分析方法》题库一-、单项选择题(每小题4分,共20分)l.若某物资的总供应最( )总需求量.则可增设一个虚销地,其需求最取兑需求量与 总供应51的差额.并取各产地到诙销地的运价为0,可将供过于求运悔间题化为供求平衡运输 何能,A .大于a 小于 C 等于D.不等于2.菜肉流公司有三抻化学说料A,・Az ・A>.每公斤原料A|含三种化学成分 的含呆分别为0・7公斤,0.2公斤WO.]公斤;每公斤原料A,含的含跟分别为0.1 公斤、。
.3公斤和0.6公斤,每公斤说料A,含的含KI 分别为0.3公斤,0.4公斤和 。
・3公斤.再公斤原料A,.A,・A,的成本分别为500元、300元和400元.今需要成分至 少忆心公斤成分至少50公斤成分至少80公斤.为列出使总成本最小的纹性规划锁 型•设原利A Jt A |t A.的用星分别为心公斤公斤和q 公斤.则化学成分3应满足的约 束条件为( ).A. 0» 'Li t 4-0. 3X 24-Q. 4XJ ^50。
•:? r i +。
. 3.“+。
. =50o -n B ・-1 oI.设f (X )在以的某个邻域内有定义,如果对于该邻域内任何异于工。
的工■郡 成/ (x )>/ (xj 成立.则称了。
为/ (工)的《 ).A.极大值点B.根小值 C 极大值D.极小值点5.某物品运输it 为g 单位时的边际成本为MC Q )= 3g + 5O (箪位,万元/单位〉,已知固 定成本为2万元,则运输JR 从3单位增加到5单位时成本的增).7.设y =《工'+ 3)1心,求2’10'0 2 [-1 1Y1 3 ,求 $3A +2B6.巳知矩阵A0. 2xt +0. 3x : +0<4xj^5OD. 0. 2.”+0. +0. 4»>503.设A.根据逆矩阡的定义.判断逆逅阵A ,=(A.A. (3q+5O)dgB. (3g+ 50 心 C L (5q+5O)dq + 2D. j :MC(g)dq+C(0)二■计小赃9分.共27分)二,针算・1国小119分.共27分)8. 计算定枳分■,(2 + 3W +K )<Lr钦件计筒炬阡表达式A '十RL 的命令.10.试可出用MATLAH 牧件什筑函数》-e*ln (j +/T + 16)的卧散的命分而小. 儿试写出用MATLAH 状件H 算定机分山的命令g四,应用B5(第12 IB 18分.策13歌8分,共26分)12.某物流公司从三个产地A|.A,.A.送榆景物质到三个仍地出•&.B,,各产他的伉应 缺(机位8吨),各钠地的需求量《垂位,吨)及各产地到各销地的氧仲.运价(单位。
物流管理定量分析方法形成性考核册(第3版)答案

第一次作业物资调运方案优化的表上作业法1.若某物资的总供应量大于总需求量,则可增设一个(A ),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。
(A)虚销地(B)虚产地(C)需求量(D)供应量2. 将下列某物资的供求不平衡运输问题(供应量、需求量单位:吨;运价单位:元/吨)化为供求平衡运输问题:供需量数据表供需平衡表3. 若某物资的总供应量()总需求量,则可增设一个虚产地,其供应量取总需求量与总供应量的差额,并取该产地到各销地的单位运价为0,并将供不应求运输问题化为供求平衡运输问题。
(A) 大于(B)小于(C)等于(D)大于等于4.将下列某物资的供求不平衡运输问题(供应量、需求量单位:吨;运价单位:元/吨)化为供求平衡运输问题:供需量数据表供需量平衡表5. 甲、乙两产地分别要运出物资1100吨和2000吨,这批物资分别送到A,B,C,D四个仓库中收存,四仓库收进的数量分别为100吨、1500吨、400吨和1100吨,仓库和发货点之间的单位运价如下表所示:运价表(单位:元/吨)试用最小元素法确定一个初始调运方案,再调整寻求最优调运方案,使运输总费用最小。
解:构造运输平衡表与运价表,并编制初始调运方案第一次检验:17,41312-==λλ<0。
已出现负检验数,方案需要调整,调整量为: 400=θ(吨)调整后的第二个调运方案为:第二次检验:17,31,4232112===λλλ 。
所有检验数都为正,所以此调运方案最优。
6.某物资要从产地A 1,A 2,A 3调往销地B 1,B 2,B 3,运输平衡表(单位:吨)和运价表(单位:元/吨)如下表所示:运输平衡表与运价表试用最小元素法编制初始调运方案,并求最优调运方案。
解:编制初始调运方案第一次检验:10,100,70,1032231312-====λλλλ<0 已出现负检验数,方案需要调整,调整量为=θ15第二次检验:10,90,60,1032231312====λλλλ所有检验数全为正,此调运方案最优。
电大《物流管理定量分析方法》国家开放大学历届试题含答案

1
、 ‘ ,
0
, ,
B
同r I
M
25叫 u‘ n h u
l i l -」
r j
仁 } (
3ZT
求
FZ
求
qJA 十 BT
0
0
算 积分
b d,
三、编程题{每小题 9 分,共 27 分)
,2
9. 设 A=11
•1
1 3 -1
,2
20i , B= 卜 1
2 - 2J
L3
算 X=YB 的命令语句。
II
01 , Y = A~l ,试写出用 MATLAB 软件计
12 分 14 分
已出现负检验数,方案需要调整,调整量为 8=500 吨。 调整后的第二个调运方案如下表所示:
运输平衡表与运价表
二♂变 I
E
皿
供应量
I
EE
A
700
200
900
6
9 10
B
500 100
600
7
3
8
C
需求量
500 700 500 800
500 2000
4
6
5
求第二个调运方案的检验数:
=3x 2 1nx 十三 +X2 Z
J: I: 8. (eI 一川x = (eX - x 2)
2019 年 1 月
5. C
9分 5分 9分 5分
=e2 - 5
三、编程题(每小题 9 分,共 27 分) 9. >>cl 巳 ar
>>A=[2 3 -1;1 2 0; 一 1 2 -2J; >>B=[2 1; 一 1 0;3 1J; >>Y=inv(A);
物流管理定量分析方法试题答案

物流管理定量分析方法试题答案IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】《物流管理定量分析方法》期末复习题一、线性规划法 1. 设⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=011101,132031B A ,求:AB T . 解:⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡---=1121011011132031T AB 2.已知矩阵⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-=2101111412210101C B A ,,,求:AB +C. 解:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡-=+3702210116012101111412210101C AB 3.已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=131211203012011B A ,,求:AB. 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=531421131211203012011AB 4. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:B T A. 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1723422011201110011653042001T A B 5.设110012212601A B ⎡⎤-⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,,求:(1) 2B T -A ;(2) AB . 解:12000122121126TB A -⎡⎤⎡⎤-=-⎢⎥⎢⎥-⎣⎦⎣⎦240001241242126164-⎡⎤⎡⎤⎡⎤=-=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦6. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011B A ,,求:AB. 解: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=600540321201110011AB 7. 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=321212113101012111B A ,,求:AB .解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=434014646321212113101012111AB 二、导数方法1.设y =(x 2-3) ln x ,求:y '解:xx x x x x x x y 3ln 2)(ln )3(ln )3(22-+='⋅-+⋅'-=' 2.设y =(1+x 3) ln x ,求:y '解:22331ln 3)(ln )1(ln )1(x xx x x x x x y ++='⋅++⋅'+=' 3.设y =(1+x 2)ln x ,求:y '解:xx x x x x x x y 2221ln 2))(ln 1(ln )1(++='++'+='4. 设xx y e 4=,求:y '解:x x x x x x x y )e 4()e (e )(4344+='⋅+⋅'=' 5.设31ln xxy +=,求:y ' 解:23232333)1(ln 31)1()1()(ln )1()(ln x x x x x x x x x x y +-+=+'+⋅-+⋅'='6.设xy x+=1e ,求:y '解:22)1(e )1()1(e )1()e (x x x x x y xx x +=+'+-+'='7.设y =x 3ln x ,求:y '解:2233ln 3)(ln ln )(x x x x x x x y +='⋅+⋅'='三、微元变化累积 1.计算定积分:⎰+1d )e 3(x x x解:25e 3)e 321(d )e 3(|1021-=+=+⎰x x x x x 2.计算定积分:⎰+312d )2(x xx解:3ln 2326|)|ln 231(d )2(|313312+=+=+⎰x x x x x3.计算定积分:⎰+103d )e 24(x x x 解: 1e 2)e 2(d )e 24(|1413-=+=+⎰x x x x x4.计算定积分:⎰+13d )e 2(x x x解:47e 2)e 241(d )e 2(|1413-=+=+⎰x x x x x5.计算定积分:⎰+21d )12(x xx解:2ln 3|)|ln (d )12(|21221+=+=+⎰x x x xx6..计算定积分:⎰+21d )1e (x xx解:2ln e e |)|ln e (d )1e (22121|+-=+=+⎰x x xx x7.计算定积分:⎰+212d )1(x xx解:2ln 37|)|ln 31(d )1(|213212+=+=+⎰x x x x x 四、表上作业法1.某公司从三个产地A1,A2,A3运输某物资到三个销地B1,B2,B3,各产地的供应量(单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表所示:(1)在下表中写出用最小元素法编制的初始调运方案:(2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费用。
物流管理定量分析方法试卷01

1. 若某物资的总供应量大于总需求量,则可增设一个( A ),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。
(A) 虚销地 (B) 虚产地 (C) 需求量 (D) 供应量2.某物流企业用甲、乙两种原材料生产A ,B ,C 三种产品。
企业现有甲原料30吨,乙原料50吨。
每吨A 产品需要甲原料2吨;每吨B 产品需要甲原料1吨,乙原料2吨;每吨C 产品需要乙原料4吨。
又知每吨A ,B ,C 产品的利润分别为3万元、2万元和0.5万元。
为列出获得最大利润的线性规划问题,设生产A ,B ,C 三种产品的产量分别为x 1吨、x 2吨和x 3吨,则目标函数为( D )。
(A) max S =30x 1+50x 2 (B) min S =3x 1+2x 2+0.5x 3 (C) min S =30x 1+50x 2 (D) max S =3x 1+2x 2+0.5x 33. 设⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=721,7421x B x A ,并且A =B ,则x =( B )。
(A) 1 (B) 2(C) 3 (D) 44. 设某公司运输某物品的总成本(单位:百元)函数为C (q )=500+2q +q 2,则运输量为100单位时的总成本为( C )百元。
(A) 202 (B) 107 (C) 10700 (D) 7025. 已知运输某物品q 吨的边际成本函数(单位:元/吨)为MC(q )=200+5q ,则运输该物品从100吨到300吨时成本的增加量为( D )。
(A) 100300(2005)d q q +⎰ (B) (2005)d q q +⎰(C)300100(2005)d (0)q q C ++⎰(D)300100(2005)d q q +⎰二、计算题(每小题7分,共21分)6. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=101201 , 4321B A ,求:AB T.⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=41032411100214321T AB 7分7. 设5e x y x =,求:y '5545()e (e )(5)e x x xy x x x x'''=⋅+⋅=+ 8. 计算定积分:311(e )d x x x-⎰333111(e )d (e ln ||)e e ln3|x x x x x -=-=--⎰ 三、编程题(每小题6分,共12分)9. 试写出用MATLAB软件计算函数y = >>clear;>>syms x y;>>y=(3+sqrt(x))/log(x); >>dy=diff(y)10. 试写出用MATLAB 软件计算定积分21||e d x x x -⎰的命令语句。
物流管理定量分析方法形成性考核册(第3版)答案

第一次作业物资调运方案优化的表上作业法1.若某物资的总供应量大于总需求量,则可增设一个(A ),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。
(A)虚销地(B)虚产地(C)需求量 (D)供应量2。
将下列某物资的供求不平衡运输问题(供应量、需求量单位:吨;运价单位:元/吨)化为供求平衡运输问题:量与总供应量的差额,并取该产地到各销地的单位运价为0,并将供不应求运输问题化为供求平衡运输问题。
(A) 大于(B)小于(C)等于 (D)大于等于4.将下列某物资的供求不平衡运输问题(供应量、需求量单位:吨;运价单位:元/吨)化为供求平衡运输问题:5A,B,C,D 四个仓库中收存,四仓库收进的数量分别为100吨、1500吨、400吨和1100吨,仓库和发货点之间的单位运价如下表所示::元/吨)试用最小元素法确定一个初始调运方案,再调整寻求最优调运方案,使运输总费用最小. 解: 构造运输平衡表与运价表,并编制初始调运方案第一次检验:17,41312-==λλ〈0。
已出现负检验数,方案需要调整,调整量为: 400=θ(吨)调整后的第二个调运方案为:第二次检验:17,31,4232112===λλλ 。
所有检验数都为正,所以此调运方案最优。
6.某物资要从产地A 1,A 2,A 3调往销地B 1,B 2,B 3,运输平衡表(单位:吨)和运价表(单位:元/吨)如下表所示:试用最小元素法编制初始调运方案,并求最优调运方案。
第一次检验:10,100,70,1032231312-====λλλλ<0 已出现负检验数,方案需要调整,调整量为=θ15第二次检验:10,90,60,1032231312====λλλλ所有检验数全为正,此调运方案最优。
最低运输总费用:355020453015101530355020min =⨯+⨯+⨯+⨯+⨯=S (元)7. 设某物资要从产地A 1,A 2,A 3调往销地B 1,B 2,B 3,B 4,运输平衡表(单位:吨)和运价表(单位:百元/吨)如下表所示:试问应怎样调运才能使总运费最省?解:编制初始调运方案:第一次检验数为13,11,3,0,1,1333124221211======λλλλλλ所有检验数全为正,初始调运方案就是最优调运方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 若某物资的总供应量大于总需求量,则可增设一个( A ),其需求量取总供应量与总需求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。
(A) 虚销地 (B) 虚产地 (C) 需求量 (D) 供应量
2.某物流企业用甲、乙两种原材料生产A ,B ,C 三种产品。
企业现有甲原料30吨,乙原料50吨。
每吨A 产品需要甲原料2吨;每吨B 产品需要甲原料1吨,乙原料2吨;每吨C 产品需要乙原料4吨。
又知每吨A ,B ,C 产品的利润分别为3万元、2万元和0.5万元。
为列出获得最大利润的线性规划问题,设生产A ,B ,C 三种产品的产量分别为x 1吨、x 2吨和x 3吨,则目标函数为( D )。
(A) max S =30x 1+50x 2 (B) min S =3x 1+2x 2+0.5x 3 (C) min S =30x 1+50x 2 (D) max S =3x 1+2x 2+0.5x 3
3. 设⎥⎦
⎤
⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=721,7421x B x A ,并且A =B ,则x =( B )。
(A) 1 (B) 2
(C) 3 (D) 4
4. 设某公司运输某物品的总成本(单位:百元)函数为C (q )=500+2q +q 2,则运输量为100单位时的总成本为( C )百元。
(A) 202 (B) 107 (C) 10700 (D) 702
5. 已知运输某物品q 吨的边际成本函数(单位:元/吨)为MC
(q )=200+5q ,则运输该物品从100吨到300吨时成本的增加量为( D )。
(A) 100300(2005)d q q +⎰ (B) (2005)d q q +⎰
(C)
300100
(2005)d (0)q q C ++⎰
(D)
300100
(2005)d q q +⎰
6. 设⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=101201 , 4321B A ,求:AB T ⎥⎦
⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=41032411100214321T AB
7. 设5e x
y x =,求:y '
5545()e (e )(5)e x x x y x x x x '''=⋅+⋅=+
8. 计算定积分:3
1
1(e )d x x x
-⎰
3
33111(e )d (e ln ||)e e ln3|x x
x x x -=-=--⎰ 9. 试写出用MA TLAB
软件计算函数y = >>clear;
>>syms x y;
>>y=(3+sqrt(x))/log(x); >>dy=diff(y)
10. 试写出用MATLAB 软件计算定积分2
1||e d x x x -⎰的命令语句。
>>clear; >>syms x y; 2分 >>y=abs(x)*exp(x); 4分 >>int(y,-1,2) 6分 11.已知某商品运输量为q 单位的总成本(单位:元)函数为C
(q )=2000+100q +0.01q 2,总收入(单位:元)函数为R
(q )=150q -0.01q 2,求使利润最大时的运输量和最大利润。
11. 利润函数为:
L (q )=R (q )-C (q )=50q -0.02q 2-2000 令()500.040L q q '=-=得惟一驻点q =1250 故当运输量为1250单位时,利润最大。
最大利润为L (1250)=29250元。
12. 某物流公司下属企业欲制定生产A 和B 两种产品的生产计划。
已知生产一件A 产品需要原材料1吨,动力1单位,生产设备3工时;生产一件B 产品需要原材料2吨,动力1单位,生产设备1工时。
在一个生产周期内,可用原材料16吨,动力10单位,生产设备24工时。
每件A 产品利润3千元,每件B 产品利润4千元。
试建立使企业能获得最大利润的线性规划模型,并写出用MATLAB 软件计算该线性规划问题的命令语句。
12. 设生产A ,B 两种产品分别为x 1件和x 2件,显然,x 1,x 2≥0。
线性规划模型为:⎪⎪⎩⎪⎪⎨
⎧≥≤+≤+≤++=0
2431016
243max 212121212
1x x x x x x x x x x S ,
计算该线性规划模型的MATLAB 命令语句为: >>clear;
>>C=-[3 4];
>>A=[1 2; 1 1; 3 1]; >>B=[16 10 24]; >>LB=[0 0];
>>[X,fval]=linprog(C,A,B,[],[],LB)
13. 某物流公司从A 1,A 2和A 3三个产地,运送一批物资到B 1,B 2,B 3和B 4四个销地。
已知各产地的供应量(单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:元/吨)如下表所示:
运输平衡表与运价表
(1)在上表中写出用最小元素法编制的初始调运方案;
(2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费用。
运输平衡表与运价表
找空格对应的闭回路,计算检验数,直到出现负检验数:
λ11=0,λ12=80,λ13=20,λ23=-10
已出现负检验数,方案需要调整,调整量为θ=200吨。
调整后的第二个调运方案如下表所示:
运输平衡表与运价表
求第二个调运方案的检验数:
λ11=0,λ12=70,λ13=20,λ21=10,λ24=30,λ32=60
所有检验数非负,第二个调运方案最优。
最低运输总费用为:
300×20+500×10+200×40+400×50+100×30+300×40=54000(元)。
