分析力学基础-第二类拉格朗日方程
合集下载
第二类拉格朗日方程的初积分PPT课件
j 1
L q j
q j
L ) 0 q j
②
式②代入到式①
d
dt
k
(q j
j 1
L q j
)
dL dt
0
d
dt
[
k j 1
(q j
L q j
)
L]
0
得:
k j 1
(q j
L q j
)
L
常量
③
将L=T-V=T2+T1+T0-V代入式③
第4页/共29页
其中：
k
j 1
(q j
T2 q j
)
2T2
V mg(R r) cosj
因为 L T V L(j,j,q)
q为循环坐标，有
L
q
(J
2 3
mr2 )q
2 5
m(R
r)Rj
C1
又L中不显含时间t，且T=T2，存在能量积分，由
T2 V C2
即：
1 2
(JO
2 5
mR2
)q2
1 2
7 5
m(R
r)j
2
保守系统
2 m(R r)Rjq mg(R r) cosj 0
哈密尔顿力学是哈密尔顿于1833年 建立的经典力学的重新表述。它由拉格 朗日力学演变而来，那是经典力学的另 一表述，由拉格朗日于1788年建立。但 它可以使用辛空间不依赖于拉格朗日力 学表述。
第13页/共29页
哈密顿原理
哈密顿原理是一种积分形式的变分原理，是哈密顿于1834年建立的。
哈密顿原理为：在相同的 始终位置、相同，约束条件下， 完整、主动力有势的系统在所 有的可能运动中，真实运动使 哈密顿作用量取驻值。
L q j
q j
L ) 0 q j
②
式②代入到式①
d
dt
k
(q j
j 1
L q j
)
dL dt
0
d
dt
[
k j 1
(q j
L q j
)
L]
0
得:
k j 1
(q j
L q j
)
L
常量
③
将L=T-V=T2+T1+T0-V代入式③
第4页/共29页
其中：
k
j 1
(q j
T2 q j
)
2T2
V mg(R r) cosj
因为 L T V L(j,j,q)
q为循环坐标，有
L
q
(J
2 3
mr2 )q
2 5
m(R
r)Rj
C1
又L中不显含时间t，且T=T2，存在能量积分，由
T2 V C2
即：
1 2
(JO
2 5
mR2
)q2
1 2
7 5
m(R
r)j
2
保守系统
2 m(R r)Rjq mg(R r) cosj 0
哈密尔顿力学是哈密尔顿于1833年 建立的经典力学的重新表述。它由拉格 朗日力学演变而来，那是经典力学的另 一表述，由拉格朗日于1788年建立。但 它可以使用辛空间不依赖于拉格朗日力 学表述。
第13页/共29页
哈密顿原理
哈密顿原理是一种积分形式的变分原理，是哈密顿于1834年建立的。
哈密顿原理为：在相同的 始终位置、相同，约束条件下， 完整、主动力有势的系统在所 有的可能运动中，真实运动使 哈密顿作用量取驻值。
拉格朗日第一类和第二类方程
拉格朗日第一类和第二类方程
拉格朗日第一类方程和第二类方程是经典力学中的两个重要概念。
拉格朗日第一类方程可以用于描述有约束的系统，它将约束力引入到系统的动力学方程中，从而更准确地描述了系统的运动。
而拉格朗日第二类方程则是经典力学的基本动力学方程之一，它通过引入拉格朗日量来描述系统的运动。
拉格朗日第二类方程具有广泛的应用，包括描述多自由度系统、非保守系统和相对论性力学系统等。
在实际应用中，我们可以利用拉格朗日第一类方程和第二类方程来解决各种问题，包括机械系统的运动、电磁场的传播和量子力学系统的行为等。
因此，深入理解拉格朗日第一类方程和第二类方程对于研究物理学、工程学和应用数学等领域都具有重要意义。
- 1 -。
分析力学基础8.5拉格朗日第二类方程0806
δ
T r& + Q j = 0 &k
& ∂rk ∂rk = & ∂w j ∂ w j
d ∂rk d t ∂w j
T
∂rk & = ∂w j
r& & k
T
∂rk ∑ mk ∂w j k =1
& & y = (l0 − vt )ψ cosψ − v sinψ
小球动能
1 1 1 & & 2 + y 2 ) = m(l0 − vt ) 2ψ 2 + mv 2 & T = m( x 2 2 2 V = mgx
主动力
r x
r mg
r mg
关于ψ 广义力
T2
T0
= mg (l0 − vt ) cosψ
rk = rk ( w, t )
导数
T n ∂rk − m && + Qj = 0 δwj ∑ k ∑ k=1 ∂w rk j =1 j
δ
∂r ∂r &k = ∑ k w j + k & r ∂t j =1 ∂w j
δ
& ∂rk ∂rk = & ∂wj ∂wj
1 & T& T = ∑ mk rk rk k =1 2
n
(
)
d ∂ = d t ∂w j &
2011年1月6日
1 ∂ T & & mk rk rk − ∑2 ∂w j k =1
n
T r& + Q j = 0 &k
& ∂rk ∂rk = & ∂w j ∂ w j
d ∂rk d t ∂w j
T
∂rk & = ∂w j
r& & k
T
∂rk ∑ mk ∂w j k =1
& & y = (l0 − vt )ψ cosψ − v sinψ
小球动能
1 1 1 & & 2 + y 2 ) = m(l0 − vt ) 2ψ 2 + mv 2 & T = m( x 2 2 2 V = mgx
主动力
r x
r mg
r mg
关于ψ 广义力
T2
T0
= mg (l0 − vt ) cosψ
rk = rk ( w, t )
导数
T n ∂rk − m && + Qj = 0 δwj ∑ k ∑ k=1 ∂w rk j =1 j
δ
∂r ∂r &k = ∑ k w j + k & r ∂t j =1 ∂w j
δ
& ∂rk ∂rk = & ∂wj ∂wj
1 & T& T = ∑ mk rk rk k =1 2
n
(
)
d ∂ = d t ∂w j &
2011年1月6日
1 ∂ T & & mk rk rk − ∑2 ∂w j k =1
n
第2章 拉格朗日方程
z
O
l
2
x2 y2 z 2 l 2 0
x
M m
x vt
2
y z l 0
2 2
y
x2 y2 z 2 l 2 0
拉格朗日科学研究所涉及的领域极其广泛。他在数学上最突出的贡献是使数学分析与几何与力学脱离开来，使数学的独立性更为清楚， 从此数学不再仅仅是其他学科的工具。 拉格朗日总结了18世纪的数学成果，同时又为19世纪的数学研究开辟了道路，堪称法国最杰出的数学大师。同时，他的关于月球 运动(三体问题)、行星运动、轨道计算、两个不动中心问题、流体力学等方面的成果，在使天文学力学化、力学分析化上，也起到了 历史性的作用，促进了力学和天体力学的进一步发展，成为这些领域的开创性或奠基性研究。 在柏林工作的前十年，拉格朗日把大量时间花在代数方程和超越方程的解法上，作出了有价值的贡献，推动了代数学的发展。他 提交给柏林科学院两篇著名的论文：《关于解数值方程》和《关于方程的代数解法的研究》 。把前人解三、四次代数方程的各种解法， 总结为一套标准方法，即把方程化为低一次的方程(称辅助方程或预解式)以求解。 他试图寻找五次方程的预解函数，希望这个函数是低于五次的方程的解，但未获得成功。然而，他的思想已蕴含着置换群概念，对后 来阿贝尔和伽罗华起到启发性作用，最终解决了高于四次的一般方程为何不能用代数方法求解的问题。因而也可以说拉格朗日是群论 的先驱。 在数论方面，拉格朗日也显示出非凡的才能。他对费马提出的许多问题作出了解答。如，一个正整数是不多于4个平方数的和的问 题等等，他还证明了圆周率的无理性。这些研究成果丰富了数论的内容。 在《解析函数论》以及他早在1772年的一篇论文中，在为微积分奠定理论基础方面作了独特的尝试，他企图把微分运算归结为代数运 算，从而抛弃自牛顿以来一直令人困惑的无穷小量，并想由此出发建立全部分析学。但是由于他没有考虑到无穷级数的收敛性问题， 他自以为摆脱了极限概念，其实只是回避了极限概念，并没有能达到他想使微积分代数化、严密化的目的。不过，他用幂级数表示函 数的处理方法对分析学的发展产生了影响，成为实变函数论的起点。 拉格朗日也是分析力学的创立者。拉格朗日在其名著《分析力学》中，在总结历史上各种力学基本原理的基础上，发展达朗贝尔、 欧拉等人研究成果，引入了势和等势面的概念，进一步把数学分析应用于质点和刚体力学，提出了运用于静力学和动力学的普遍方程， 引进广义坐标的概念，建立了拉格朗日方程，把力学体系的运动方程从以力为基本概念的牛顿形式，改变为以能量为基本概念的分析 力学形式，奠定了分析力学的基础，为把力学理论推广应用到物理学其他领域开辟了道路。他还给出刚体在重力作用下，绕旋转对称 轴上的定点转动(拉格朗日陀螺)的欧拉动力学方程的解，对三体问题的求解方法有重要贡献，解决了限制性三体运动的定型问题。拉 格朗日对流体运动的理论也有重要贡献，提出了描述流体运动的拉格朗日方法。 拉格朗日的研究工作中，约有一半同天体力学有关。他用自己在分析力学中的原理和公式，建立起各类天体的运动方程。在天体 运动方程的解法中，拉格朗日发现了三体问题运动方程的五个特解，即拉格朗日平动解。此外，他还研究了彗星和小行星的摄动问题， 提出了彗星起源假说等。 近百余年来，数学领域的许多新成就都可以直接或间接地溯源于拉格朗日的工作。所以他在数学史上被认为是对分析数学的发展 产生全面影响的数学家之一。被誉为“欧洲最大的数学家”。
拉格朗日第二类方程
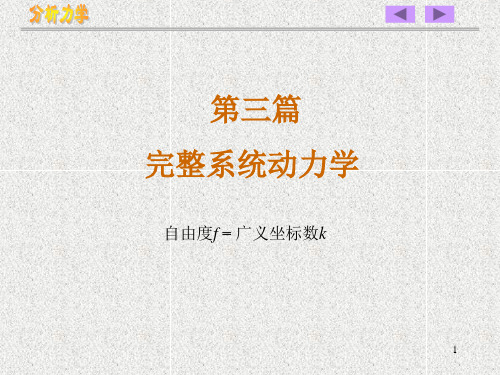
代入初始条件，t =0 时， 0 0 , 0 0 得 C1 C2 0
故：
3M
gt 2
(2P9Q)( Rr)2
20
[例]图示系统，物块C质量为m1 ，均质轮A、B质量均为m2， 半径均为R，A作纯滚动，求系统的运动微分方程。 解：系统具有一自由度，保守
系统。以物块C的平衡位置为
原点，取x为广义坐标：
AF q j
（4）不含约束力。
二、保守系统的拉格朗日方程
如果作用于质点系的力是有势力，则：
Qj
V q j
而拉氏方程为：
15
d dt
T q j
T q j
V q j
由于V=V（q1，q2，...，qk），不含广义速度，所以
V q j
0,
d dt
V q j
0
上式为：
d dt
T q j
T q j
d dt
V q j
V q j
或：d dt
(T V q j
)
(T V q j
)
0
令L=T-V——拉格朗日函数
d dt
(
L q j
)
L q j
0 ( j1,2,,k )
保守系统的拉格朗日第二类方程。
16
应用拉氏方程解题的步骤：
1. 判定质点系的自由度 f，选取适宜的广义坐标。必须注意： 不能遗漏独立的坐标，也不能有多余的（不独立）坐标。
Q
A
M
T
1 2P 6
9Q (R g
r ) 2
;
d T
dt
1 2P 9Q (R r)2
6
g
;
T 0
19
理论力学：第二类拉格朗日方程的总结
θ&&(θ ) = ? x&(θ ) = ?
L中无 x, t
∂T ∂x&
=
5 2
mx& +
1 2
mLθ& cosθ
=
C
&x&(θ ) = ?
5 mx&2 + 1 mL2θ&2 + 1Lmg(1− cosθ ) = E
4
6
2
2014-3-25
8
理论力学
习题课
∂T ∂x&
2014-3-25
根据对z轴的动量矩守恒和初始条件，可得关系式： ϕ&
=
1
sin2 θ
15
理论力学
习题课
问题：B 点的运动轨迹？
θ0
=
π
4
=
0.7854,ϕ0
=
0,θ&0
=
0,ϕ&0
=
2.0rad/s
m = 1kg L = 1m k = 10N/m
∂T
∂ϕ&
=
1 mL2 3
sin2 θϕ&
=
C1
2014-3-25
mL&x&cosθ
+
1 mL2θ&&+
3
1 2
mgL sinθ
=
0
2014-3-25
10
理论力学
习题课
x
A
aA
θ&&= −15 2 g,
17L
&x&
=3g 17
求地面的约束力
F
aCt A
分析力学基础第一章(4-6节)
T q
m1
m2 x m2 Lcos
px
循环积分——系统的水平动量守恒
T V C
能量积分——机械能守恒
x
F t
vA
m1 g
CvCA
m2 g
§1-6 第一类拉格朗日方程
§1-6 第一类拉格朗日方程
设描述系统的位形坐标：q1 , q2 , , qn
系统的约束方程为： fk r1, r2 , , rn , t 0 k 1,2, , s
i 1
k 1
代入动力学普遍方程：
n
Fi FIi
ri
n
Fi
miri ri
0
i 1
i 1
有：
n i 1
Fi
miri ri
N Qk
k1
n i 1
miri
ri qk
qk
§ 1-4 第二类拉格朗日方程
n
i 1
Fi
miri ri
N Qk
k1
n i 1
miri
解：1、系统的自由度为k=1
2、系统的广义坐标：
3、系统的动能： T 1 1 m l22 1 m l22
23
6
4、系统的势能：
V
mg
l
1
cos
5、拉格朗日函数： 2
L T V 1 ml22 mg l 1 cos
OB
6
2
d dt
L qk
L qk
0
1 m l2 l m gsin
3
2
mg A
i 1
Fi
miri
s
k
k 1
fk ri
ri
第1章 分析力学基础 1-6拉格朗日第二类方程的积分汇总
解：研究楔形体与圆柱体组成 的系统。系统受理想、完整、 定常约束，具有两个自由度。 取广义坐标为x, s ；各坐标原点 均在初始位置。
M1-8
我们已知道系统动能和势能为
V
1 3
Ph
Q(h
s sin
r cos )
T
1 2
P
g
Q
x&2
3 4
Q g
s&2
Q g
x&s&cos
1 2
P
g
Q
x&2
3 4
M1-10
[例] 一均质圆柱体可绕其垂直中心轴自由
转动，圆柱表面刻有倾角为 的螺旋槽。
小球M自静止沿槽下滑，已知小球质量为 m1圆柱体质量为m2，半径为R， 试求：小球下降高度为h时，小球相对圆
柱体的速度，圆柱体的角速度。 解：系统受理想、完整、定常约束，
具有两个自由度。取广义坐标为, s ；
各坐标原点均在初Leabharlann 位置。当ssin =h ，得
2m12 sin2 m2 s&2 2gh 0
(2m1 m2 )
s&
(2m1 m2 )2gh
2m1 sin2 m2
& 2m1 cos
R
2gh
(2m1 m2 )(2m1 sin2 m2)
q&k
L qk
q&k
0
N k 1
d dt
L q&k
q&k
L q&k
q&&k
L qk
q&k
d dt
N
k 1
L q&k
q&k
M1-8
我们已知道系统动能和势能为
V
1 3
Ph
Q(h
s sin
r cos )
T
1 2
P
g
Q
x&2
3 4
Q g
s&2
Q g
x&s&cos
1 2
P
g
Q
x&2
3 4
M1-10
[例] 一均质圆柱体可绕其垂直中心轴自由
转动，圆柱表面刻有倾角为 的螺旋槽。
小球M自静止沿槽下滑，已知小球质量为 m1圆柱体质量为m2，半径为R， 试求：小球下降高度为h时，小球相对圆
柱体的速度，圆柱体的角速度。 解：系统受理想、完整、定常约束，
具有两个自由度。取广义坐标为, s ；
各坐标原点均在初Leabharlann 位置。当ssin =h ，得
2m12 sin2 m2 s&2 2gh 0
(2m1 m2 )
s&
(2m1 m2 )2gh
2m1 sin2 m2
& 2m1 cos
R
2gh
(2m1 m2 )(2m1 sin2 m2)
q&k
L qk
q&k
0
N k 1
d dt
L q&k
q&k
L q&k
q&&k
L qk
q&k
d dt
N
k 1
L q&k
q&k
06分析力学基础第二类拉格朗日方程
将Qk代入拉格朗日方程式，得
d dt
(
T qk
)
T qk
V qk
0
势能V不包含广义速度，引入拉格朗日函数
L T V L(qk , qk , t)
为拉格朗日函数（动势），是表征体系约束运动状态和相互作用 等性质的特征函数。
保守体系的拉格朗日方程为：
d dt
(
L qk
)
系统的运动微分方程。
(m1 m2 )x m2l kx 0 x l g 0
上式为系统在平衡位置(x =0, =0)附近微幅运动的微分方程。
M1-23
M1-24
变换 1.
ri qk
ri qk
由 ri ri (q1, q2, qN , t) (i 1, 2, n)
d dt
n i1
mi ri
ri qk
qk
n i1
1 2
mi
ri
ri
d dt
qk
n1 2
i1
mivi2
qk
n i1
1 2
mivi2
d dt
T qk
T qk
M1-3
由
Qk
n
miri
i1
ri qk
k 1, 2, N
可得
d dt
T qk
T qk
Qk
k 1, 2, N
为理想完整系的拉格朗日方程，方程数等于质点系的自由度数。 其中：
Qk
§4 完整约束的第二类拉格朗日方程
§4 完整约束的第二类拉格朗日方程上一次课我们从牛顿第二定律出发导出达朗伯——拉格朗日方程：0)(=⋅-∑i i ii r a m F δ ，并推证了两个数学关系式一、两个数学关系式：ααq r qr i ∂∂=∂∂ ，ααq r q r dt d i i ∂∂=∂∂ 其中第i 个质点的位矢是广义坐标αq 的函数：1,2,()i i s t r r q q q =……，这些正是为我们这次课推导拉格朗日方程而准备的基础和工具。
二.方程推导：将达朗伯-拉格朗日方程展开写成两部分：0=-∑∑i i i i i i i r r m r F δδ这个方程中的虚位移i r δ，用高等数学中的全微分公式很容易推出它就等于αααδδq q r r s i i ∑∂∂= 。
因为dt t r dq q r r d i s i i ∂∂+∂∂=∑= ααα1，我们将此式中的实位移改成虚位移i r δ，再考虑到虚位移的改变与时间无关，即0=t δ，于是就由上式可以得出虚位移αααδδq q r r s i i ∑∂∂=。
我们将这个关系式代到达朗伯—拉格朗日方程的展开式中去，则有：011=∂∂⋅-∂∂⋅∑∑∑∑∂∂∂=∂=∂∂αδδq q r r m q q r F i i i i n i i i ，由于这里的两个求和运算，一个是对指标i 求和，一个是对指标α求和，它们是互不关联的，所以两个求和符号可以写在一起的。
所以上式也可以写成为：0=∂∂-∂∂⋅⋅∑∑∑∑ααααααδδq q r r m q q r F i i i i i i i …(1) ααααααααααδδδq q r dt d r m q r r m dtd q q r r m q q r r m i i i i i i i i i i i i i i i ⋅∂∂-∂∂=∂∂=∂∂⋅⋅∑∑∑∑∑∑)]()([)( αααααααδδq r m q r m q dt d q q r dt d r m q r r m dt d i i i ii i i i i i i ⋅∂∂-∂∂=⋅∂∂-∂∂∑∑∑∑∂)]21()21([)]()([22 =ααααδq r m q r m q dt d i i i i i i ⋅∂∂-∂∂∑∑∑]2121[22. [∑=i i i T r m 221 正好是力学体系的动能T 。
8-1第二类拉格朗日方程
例1
解
取曲柄的转角为广义坐标。
T11 2(2m9m 2)(r1r2)22
Q
M
M
T1 6(2m9m 2)(r1r2)2
d dt
T
T
Q
1 6(2m9m2)(r1r2)2M
6M
(2m9m2)(r1r2)2
例2
用拉格朗日方程求椭圆摆的运动微分方程
y
mA g
x
O
A
x
B
mBg
例2
解
取x和为广义坐标
ri qk
d dti n1m iri q riki n1m irid dt q rik
d dti n1m iriq riki n1m iriqrik
d dt qki n12 1m iri2 qki n12 1m iri2
ddt
T qk
T qk
第二类拉格朗日方程
Qk Qk* 0
Qk*
ddt
T qk
qTk
d dt q T k q T k Q k,
k1,2,
,N
第二类拉格朗 日方程
如主动力都是有势力： Qk
V qk
ddtqTk qTk qVk
V 0 qk
d dt q L k q L k0, k1,2, ,N主的动拉力格为朗势日力方时程
L = T – V — 拉格朗日函数，或动势
➢ 判断系统是否为完整约束，主动力是否 有势，以决定能否应用拉格朗日方程以 及应用何种形式的拉格朗日方程。
➢ 确定系统的自由度数，选择合适的广义 坐标。
➢ 按所选的广义坐标，写出系统动能、势 能或广义力。
➢ 把动能、广义力或拉格朗日函数代入拉格 朗日方程。
06-分析力学基础-第二类拉格朗日方程资料
保守体系的拉格朗日方程为：
d dt
(qLk)qLk
0
想一想：上式的成立、适用条件是什么？
M1-6
3. 对拉格朗日方程的评价
(1) 拉氏方程的特点（优点）： 是一个二阶微分方程组，方程个数与体系的自由度相同。形式简 洁、结构紧凑。而且无论选取什么参数作广义坐标，方程形式不变。 方程中不出现约束反力，因而在建立体系的方程时，只需分析已 知的主动力，不必考虑未知的约束反力。体系越复杂，约束条件越 多，自由度越少，方程个数也越少，问题也就越简单。
M1-10
系统动能：
T1 2m 1x21 2JBB 21 2JI
2 A
1 2 m 1 x 2 1 2 1 2 m 2 R 2B 2 1 2 2 3 m 2 R 2A 2
m1
2m2 2
x2
系统的拉格朗日函数（动势）
LTV m 1 2 2 m 2x 2 1 2 k (0 x )2 m 1 g x
5. 求出上述一组微分方程的积分。
M1-9
[例] 物块C的质量为m1，A，B两轮 皆为均质圆轮，半径R，质量为m2， 求系统的运动微分方程。
解：图示机构只有一个自由度，所受
约束皆为完整、理想、定常的，以物 块平衡位置为原点，取x 为广义坐标。
系统势能： (以弹簧原长为弹性势能零点)
V1 2k(0x)2m1gx
2. 计算质点系的动能T，表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j(j 1 ,2 , ,k)，计算公式为：
Q j i n1(Xi q xijYi q yijZi q zij) 或
Qj
W ( j) qj
若主动力为有势力，也可将势能 V 表示为广义坐标的函数。
07-分析力学基础-第二类拉格朗日方程的应用
Q ∂L 3 Q & & = s − x cosα & g ∂s 2 g Q d ∂L 3 Q && − &&cosα = s x & dt ∂s 2 g g
∂L =0 ∂x
∂L = Qsinα ∂s
代入保守系统拉氏方程，并适当化简， 代入保守系统拉氏方程，并适当化简，得到系统的运动微分方 程。
& & (P+Q)& −Q⋅& cosα =0 x s & & 3& −2& cosα =2gsinα s x
拉格朗日函数
L = T −V
1 m(x2 -xθlsinθ + 1 l 2θ 2 ) & & && = 2 3 1 kx2 + mg(x + l cosθ ) 2 2
4、应用拉格朗日方程建立系统的运动微分方程
∂L = － + mgx kx ∂x
∂L = mx- 1 m &lsinθ & θ & ∂x 2
2 2 −mgl(θ12 +θ2 )/2 − kl 2 (θ12 −2θ1 θ2 +θ2 )/2
∂L =−mglθ −kl 2 (θ −θ ) =−(mgl + kl 2 )θ + kl 2θ 1 1 2 1 2 ∂θ1
∂L = ml 2θ & 1 & ∂θ1 d ∂L = ml 2θ && 1 & dt ∂θ1
O
r0
B k A
解：1、系统的约束为完整约束，且主动 系统的约束为完整约束， O θ B' W
r0 r
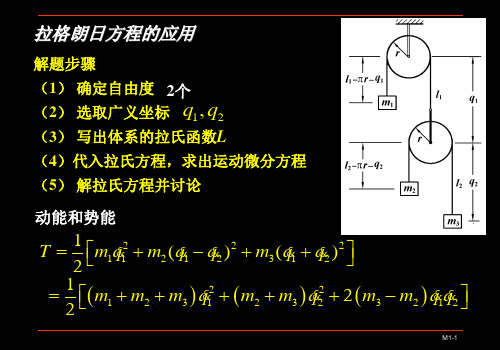
∂L =0 ∂x
∂L = Qsinα ∂s
代入保守系统拉氏方程，并适当化简， 代入保守系统拉氏方程，并适当化简，得到系统的运动微分方 程。
& & (P+Q)& −Q⋅& cosα =0 x s & & 3& −2& cosα =2gsinα s x
拉格朗日函数
L = T −V
1 m(x2 -xθlsinθ + 1 l 2θ 2 ) & & && = 2 3 1 kx2 + mg(x + l cosθ ) 2 2
4、应用拉格朗日方程建立系统的运动微分方程
∂L = － + mgx kx ∂x
∂L = mx- 1 m &lsinθ & θ & ∂x 2
2 2 −mgl(θ12 +θ2 )/2 − kl 2 (θ12 −2θ1 θ2 +θ2 )/2
∂L =−mglθ −kl 2 (θ −θ ) =−(mgl + kl 2 )θ + kl 2θ 1 1 2 1 2 ∂θ1
∂L = ml 2θ & 1 & ∂θ1 d ∂L = ml 2θ && 1 & dt ∂θ1
O
r0
B k A
解：1、系统的约束为完整约束，且主动 系统的约束为完整约束， O θ B' W
r0 r
§14.2、第二类拉格朗日方程
v1 r55 v4 v2 r44 r55 v3 r44 r55 1 1 1 2 2 2 2 T m1r5 5 m2 (r4 4 r55 ) m3 (r4 4 r55 ) 2 2 2 w 5 (m1 m2 m3 ) gr5 3) 确定广义力; Q5 5 w 4 m2 g r4 4 m3 g r4 4 Q4 (m2 m3 ) gr4 4 4
x r cos (r L) sin y r sin (r L) cos
1 2 2 T m(r L) 2
12
w m g y Q m g(r L) sin
4) 列拉格朗日方程;
3) 确定广义力;
(m1 m2 )a2 m1ar cos 0 2(m1 m2 ) sin 5) 联立求解; ar g 2 m1 2m1 sin 3m2
2
3) 确定广义力;
10
m1 sin( 2 ) a2 g 2 m1 2m1 sin 3m2
评论,在应用第二类拉格朗日方程求解动力学问题 时,解题思路/解题步骤都相同: 第一步、确定系统的自由度数与相应的系统参数 即广义坐标; 第二步、进行速度分析,确定系统动能; 第三步、确定各系统参数(广义坐标) 的广义力; 第四步、依次列各广义坐标对应的拉格朗日方程; 第五步、联立求解;
1) 确定系统参数:轮1轮心O点相对位移和三角 块向左的位移(xr /xe);
9
wxr m1 g sin xr wx 2 m1 g sin Qx 2 0 Qxr xr xr x2 T 3 4) 列拉格朗日方程; m1vr m1v2 cos vr 2 T 3 0 m1ar m1a2 cos m1 g sin xr 2 T T 0 (m1 m2 )v2 m1vr cos x2 v
分析力学基础 第二类拉格朗日方程
2. 计算质点系的动能T，表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j(j 1 ,2 ,L,k)，计算公式为：
Q j i n1(Xi q xijYi q yijZi q zij) 或
Qj
W ( j) qj
若主动力为有势力，也可将势能 V 表示为广义坐标的函数。
4. 建立拉氏方程并加以整理，得出k个二阶常微分方程。
i n1(F im i& r& i) q rik0 k1,2,LN
M1-2
变换
1.
ri qk
r&i q&k
2.
d dt
ri qk
r&i qk
3. i n 1m i& r & i q r ik i n 1m id d t r & i q r ik i n 1m ir & id d t q r ik
T
n
1 2
mivi2
——体系相对惯性系的动能
i1
pk
T q&k
——广义动量，可为线动量、角动量或其他物理量
M1-4
2. 保守体系的拉格朗日方程
如果主动力都是保守力，即 FV，则为广义力
Q k i n 1 F ri q r r ik i n 1 V r r i q r r ik q V k Q k i n 1F ri q r r ik i n 1 F ix q x k i F iy q y k i F iz q z k i
两边再对 q&k 求偏导即可得
ri qk
r&i q&k
３—5 第二类拉格朗日方程
1. 基本形式的拉格朗日方程
质点 i 的虚位移
拉格朗日第二类方程
n 1 1 2 2 ( m v ) ( m v i i i i ) k d i 1 2 i 1 2 [ ]q j j q q j j 1 dt n
d T T [ ]q j j q j j 1 dt q
k
( m)
13
将（d）（m）代入（c）得：
9
j — 广义速度 式中：q
ri ri , 由（a）知 只是广义坐标和时间的函数，与广义速 q j t
j 求偏导： 度无关，故将上式对q
ri vi j q j q
②将（g）对任一广义坐标ql 求偏导：
( h)
k k vi 2 ri 2 ri ri ri j j ( )q ( ) q ql j 1 ql q j ql t tql j 1 ql q j
故：
3M 2 gt ( 2 P 9Q )( R r ) 2
20
[例]图示系统，物块C质量为m1 ，均质轮A、B质量均为m2， 半径均为R，A作纯滚动，求系统的运动微分方程。 解：系统具有一自由度，保守 系统。以物块C的平衡位置为 原点，取x为广义坐标：
1 1 1 1 2 2 2 2 T m1 x J A A m2 v A J B B 2 2 2 2 2 1 2 11 2 1 11 x x 2 2 2 x m1 x m2 R ( ) m2 ( ) m2 R ( ) 2 22 2R 2 2 22 R 1 2 (8m1 7m2 ) x 16
v A ( R r ) vA Rr A r r
18
1 1Q 2 1 2 2 T J O v A J A A 2 2g 2 2 11 P 1 Q 1 1 Q ( R r ) 2 2 2 (R r)2 (R r)2 r2 23 g 2g 2 2g r2 1 2 P 9Q 2 (R r)2 12 g
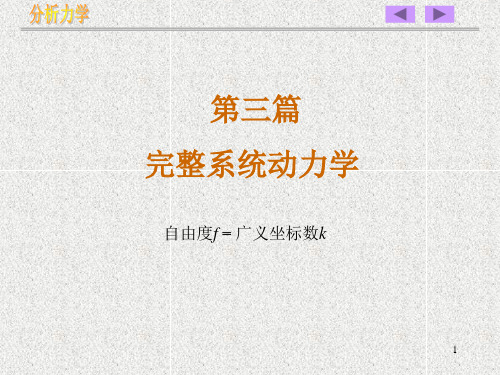
d T T [ ]q j j q j j 1 dt q
k
( m)
13
将（d）（m）代入（c）得：
9
j — 广义速度 式中：q
ri ri , 由（a）知 只是广义坐标和时间的函数，与广义速 q j t
j 求偏导： 度无关，故将上式对q
ri vi j q j q
②将（g）对任一广义坐标ql 求偏导：
( h)
k k vi 2 ri 2 ri ri ri j j ( )q ( ) q ql j 1 ql q j ql t tql j 1 ql q j
故：
3M 2 gt ( 2 P 9Q )( R r ) 2
20
[例]图示系统，物块C质量为m1 ，均质轮A、B质量均为m2， 半径均为R，A作纯滚动，求系统的运动微分方程。 解：系统具有一自由度，保守 系统。以物块C的平衡位置为 原点，取x为广义坐标：
1 1 1 1 2 2 2 2 T m1 x J A A m2 v A J B B 2 2 2 2 2 1 2 11 2 1 11 x x 2 2 2 x m1 x m2 R ( ) m2 ( ) m2 R ( ) 2 22 2R 2 2 22 R 1 2 (8m1 7m2 ) x 16
v A ( R r ) vA Rr A r r
18
1 1Q 2 1 2 2 T J O v A J A A 2 2g 2 2 11 P 1 Q 1 1 Q ( R r ) 2 2 2 (R r)2 (R r)2 r2 23 g 2g 2 2g r2 1 2 P 9Q 2 (R r)2 12 g
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
广义坐标vA 。(Rr)
A
vA r
R r
r
M1-16
T
1 2
JO&2
1 2
Q g
v
2 A
1 2
J AA2
1 2
1 3
P g
(R
r)2&2
1 2
Q g
(R
r)2&2
1 2
1 2
Q g
r2
(R
r)2 r2
&2
1 2P 9Q (R r)2&2
12 g
W ( ) M
Q
W ( )
M
T&
1 6
2P
得
(m1 m2 )&x&1 m2l&&cos m2l&2 sin 0
M1-14
同理：
T& m2l2& m2lx&1 cos
T
m2lx&in
d dt
T x&1
m2l(l&&
cos &x&1
x&1&sin )
由拉格朗日方程d
dt
(
T q&k
)
T qk
Qk
得
m2l(l&& cos&x&1 x&1&sin) m2gl sin
)
M1-13
系统势能：（选质点 M2 在最低位置为零势能位
置）
V m2gl(1 cos)
求导运算可得：
T x&1
(m1
m2
)
x&1
m2l&cos
T x1
0
Qx1
V x1
0
d dt
T x&1
(m1
m2 )&x&1
m2l&&cos
m2l&2 sin
由拉格朗日方程ddt
(
T q&k
)
T qk
Qk
zi q j
)
或
Qj
W ( j) qj
若主动力为有势力，也可将势能 V 表示为广义坐标的 函数。
4. 建立拉氏方程并加以整理，得出k个二阶常微分方程。
5. 求出上述一组微分方程的M积1-9分。
[例] 物块C的质量为m1，A，B两 轮皆为均质圆轮，半径R，质量为 m2，求系统的运动微分方程。
解：图示机构只有一个自由度，所
M1-15
[例] 水平面内运动的行星齿轮机构。均质杆OA：重P，可 绕O点转动；均质小齿轮：重Q，半径 r ，沿半径为R的固定 大齿轮滚动。系统初始静止，系杆OA位于图示OA0位置。 系杆OA受大小不变力偶M作用后，求系杆OA的运动方程。
解：图示机构只有一个自由度，
所受约束皆为完整、理想、
定常的，可取OA杆转角 为
惯性虚功项，使之与系统的动能的变化联系起来。
n
(Fi
i1
mi
&r&i )
ri qk
0
k 1, 2, L N
M1-2
变换
1.
ri qk
r&i q&k
2.
d dt
ri qk
r&i qk
3.
n i1
mi&r&i
ri qk
n
mi
i1
d dt
r&i
ri qk
n
mi
r&i
d dt
i1
ri qk
受约束皆为完整、理想、定常
的，以物块平衡位置为原点，
取系统x 势为能广：义坐标。
(以弹簧原长为弹性势能零点)
V
1 2
k ( 0
x)2
m1gx
M1-10
系统动能：
T
1 2
m1x&2
1 2
J BB2
1 2
J IA2
1 2
m1x&2
1 2
1 2
m2 R 2B2
1 2
3 2
m2 R 2A2
m1 2m2 x&2 2
态和相互作用等性质的特征函数。 保守体系的拉格朗日方程为：
d dt
(
L q&k
)
L qk
0
想一想：上式的成立、适用条件是什么？
M1-6
3. 对拉格朗日方程的评价
(1) 拉氏方程的特点（优点）： 是一个二阶微分方程组，方程个数与体系的自由度 相同。形式简洁、结构紧凑。而且无论选取什么参数 作 方广程义中坐不标出，现方约程束形反式力不，变因。而在建立体系的方程时， 只需分析已知的主动力，不必考虑未知的约束反力。 体系越复杂，约束条件越多，自由度越少，方程个数 也 ➢ 拉越氏少方，程问是题从也能就量越的简角单度。来描述动力学规律的，能量 是整个物理学的基本物理量而且是标量，因此拉氏方 程为把力学规律推广到其他物理学领域开辟了可能性， 成为力学与其他物理学分支相联系的桥梁。
Fiz
zi qk
n i1
V xi
xi qk
V yi
yi qk
V zi
zi qk
V qk
M1-5
2. 保守体系的拉格朗日方程
将Qk代入拉格朗日方程式，得
d dt
(
T q&k
)
T qk
V qk
0
势能V不包含广义速度，引入拉格朗日函数
L T V L(qk , q&k , t)
为拉格朗日函数（动势），是表征体系约束运动状
i1
pk
T q&k
——广义动量，可为线动量、角动量或其他物理量
M1-4
2. 保守体系的拉格朗日方程
如果主动力都是保守力F，即 V ，则为广义力
Qk
n i 1
r Fi
rri qk
i
n 1
Vrri
rri qk
V qk
Qk
n i1
r Fi
rri qk
n Fix
i1
xi qk
Fiy
yi qk
n i1
mi
d dt
r&i
q&r&ik
n i1
mir&i
r&i qk
d dt
n i1
mi
r&i
q&r&ik
qk
n
1 2
mi
r&i
r&i
i1
d dt
q&k
n i1
1 2
mivi2
qk
n i1
1 2
mivi2
d dt
T q&k
T qk
M1-3
由
Qk
n i1
自然长度位置， 逆时针
转向为正。
M1-19
系统动能：
vB2 ( x& l&cos )2 (l&sin )2 x&2 l2&2 2x&l&cos
T
1 2
m1x&2
1 2
m2vB2
1 2
m1x&2
1 2
m2 (x&2
l 2&2
2 x&l&cos )
1 2
(m1
m2 )x&2
1 2
m2l 2&2
M1-7
3. 对拉格朗日方程的评价 (2) 拉氏氏方方程程的在价理值论上、方法上、形式上和应用上 用高度统一的规律，描述了力学系统的动力学规律， 为解决体系的动力学问题提供了统一的程序化的方 法，不仅在力学范畴有重要的理论意义和实用价值， 而且为研究近代物理学提供了必要的物理思想和数 学技巧。
M1-8
m2 x&l&cos
M1-20
系统势能： (以弹簧原长为弹性势能零点， 滑块A所在平面为重力势能零 点)
V
1 2
kx2
m2gl cos
拉格朗日函数：
L T V
1 2
(m1
m2
) x&2
1 2
m2l 2&2
m2 x&l&cos
1 2
kx2
m2 gl
cos
M1-21
L
1 2
(m1
m2
) x&2
1 2
m2l 2&2
m2 x&l&cos
1 2
kx2
m2 gl
cos
Lx& (m1 m2 )x& m2l&cos
,
L x
kx
d dt
Lx&
(m1
m2 )&x&
m2l&&cos
m2l&2 sin
L& m2l2& m2 x&l cos,
L
m2 x&l&sin
m2gl sin
d dt
(
L&)
m2l
2&&
dri
dt
r&i
N ri k1 qk
q&k
ri t
两可边 得再对q&k 求偏导即
ri qk
r&i q&k
M1-25
变换 2.
d dt
ri qk
r&i qk