《线段的垂直平分线的性质和判定》课件(2套)
合集下载
新人教版八年级数学线段的垂直平分线的性质和判定ppt课件
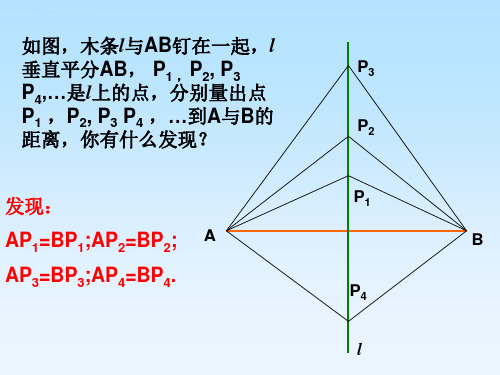
P2
发现: AP1=BP1;AP2=BP2; A AP3=BP3;AP4=BP4.
P1 B
P4 l
动动手,你也会有发现! 采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在管材垂直角切断管材,边剪边旋转,以保证切口面的圆度,保持熔接部位干净无污物
画线段AB的垂直平分线 l,在 l 上取任意点P, 量一量 点P到A与B的距离,你有什么发现?再取几个点试试。你 能说明理由吗?
理由: 线段垂直平分线上的点与这条
A
线段两个端点的距离相等.
B
2、∵ AB=,AC∴A在线段BC的中垂线上
D
C
理由:与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。
3、如图, NM是线段AB的中垂线,
M
下列说法正确的有: ①②。③ ①AB⊥MN,②AD=DB, ③
A
D
B
MN⊥AB, ④MD=DN,⑤AB是
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
这些点能组成什么几何图形?
P
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、 A
C
B
B 的距离相等的所有点的集合.
E
∴ BD=AD
∵ C△BCD=BD+DC+BC
B
∴ C△BCD=AD+DC+BC
= AC+BC = 12+7=19
A D C
采用PP管及配件:根据给水设计图配 置好PP管及配 件,用 管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
时线段的垂直平分线的性质与判定课件

如果一条直线上的点到线 段两个端点的距离相等, 那么这条直线是这条线段 的垂直平分线。
学习垂直平分线的注意事项
理解定义
要深入理解垂直平分线的定义,掌握其几何意义 和性质。
掌握性质
要牢记垂直平分线的性质,并能够灵活运用。
培养能力
要通过练习培养自己的分析问题和解决问题的能力。
如何更好地掌握垂直平分线的知识
垂直平分线的定理
定理1
如果一条直线是线段AB的垂直平 分线,那么这条直线上的任意一 点到A和B的距离相等。
定理2
如果一条直线不是线段AB的垂直 平分线,那么这条直线上任意一 点到A和B的距离之差与到AB的距 离相等。
02 线段垂直平分线 的画法
利用尺规作图
确定线段中点
首先确定线段的中点,标记为C。
垂直平分线的数学表示
假设线段AB,点C是AB的中点,那么 AC和BC的垂直平分线就是直线CB。
垂直平分线的性质
性质1
垂直平分线上的任意一点到线段 两端点的距离相等。
性质2
线段两端点关于其垂直平分线对称。
性质3
垂直平分线是线段最短的路径。即 在给定两点A和B的情况下,AC和 BC的垂直平分线是A和B之以线段的中点 C为起点,绘制直线。
确定垂直平分线
以中点C为圆心,以线段长度为 半径,画一个圆。与第一步绘制 的直线相交于两点A和B。连接这 两点,得到的直线即为线段的垂
直平分线。
利用计算机软件作图
选择绘图软件 绘制线段
选择一个具有绘图功能的计算机软件,如Microsoft Visio、 AutoCAD等。
在物理学中的应用
力学
在物理学中,垂直平分线被广泛应用于力学中。例如,在研究物体的运动时,垂 直平分线可以用于确定物体的重心和转动惯量。
学习垂直平分线的注意事项
理解定义
要深入理解垂直平分线的定义,掌握其几何意义 和性质。
掌握性质
要牢记垂直平分线的性质,并能够灵活运用。
培养能力
要通过练习培养自己的分析问题和解决问题的能力。
如何更好地掌握垂直平分线的知识
垂直平分线的定理
定理1
如果一条直线是线段AB的垂直平 分线,那么这条直线上的任意一 点到A和B的距离相等。
定理2
如果一条直线不是线段AB的垂直 平分线,那么这条直线上任意一 点到A和B的距离之差与到AB的距 离相等。
02 线段垂直平分线 的画法
利用尺规作图
确定线段中点
首先确定线段的中点,标记为C。
垂直平分线的数学表示
假设线段AB,点C是AB的中点,那么 AC和BC的垂直平分线就是直线CB。
垂直平分线的性质
性质1
垂直平分线上的任意一点到线段 两端点的距离相等。
性质2
线段两端点关于其垂直平分线对称。
性质3
垂直平分线是线段最短的路径。即 在给定两点A和B的情况下,AC和 BC的垂直平分线是A和B之以线段的中点 C为起点,绘制直线。
确定垂直平分线
以中点C为圆心,以线段长度为 半径,画一个圆。与第一步绘制 的直线相交于两点A和B。连接这 两点,得到的直线即为线段的垂
直平分线。
利用计算机软件作图
选择绘图软件 绘制线段
选择一个具有绘图功能的计算机软件,如Microsoft Visio、 AutoCAD等。
在物理学中的应用
力学
在物理学中,垂直平分线被广泛应用于力学中。例如,在研究物体的运动时,垂 直平分线可以用于确定物体的重心和转动惯量。
初中数学青岛版八年级上2.4《线段的垂直平分线》课件(16张PPT)

D. CD平分∠ACB
C B
D
2.(1)用尺规作线段AB、BC的
垂直平分线;
A
(2) 若AB与BC的垂直平分线交于
点P,PA与PC相等吗?
B
C
PA=PC
回归生活
1.在公路CD同侧有A、B
两个村庄,现要在公路上建
A
一车站,使车站到两村距离
相等,如何确定车站的位置?
连接AB,作AB的垂直平分线EF交CD于P,
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
线段垂直平分线的性质定理:
M P
A
O
B
N
提出新问题
•如果一个点到线段两端点的距离相等, 那么这个点是否在线段的垂直平分线上?
•如图,PA=PB,
• 试比较PA,PB的大小,并说明理由。
连接MB, 因为MN垂直平分AB, 所以MB=MA, 所以PA=PM+MA=PM+MB, △PMB中,PM+MB>PB, 所以PA>PB。
P M
A
N
B
颗粒归仓---你学会了吗?
•1.线段的轴对称性 •2.线段的垂直平分线定义 •3.线段的垂直平分线的性质与判定 • 4.尺规作线段的垂直平分线
2.如图,BC=40CM,DE是线段AB
A
的垂直平分线,与BC相交于E,AC=24CM,
求 △ACE的周长。
D
C AC+CE+AE=AC+CE+EB=64CM
E
B
当堂过关检测---大显身手
1.如图,AC=AD,BC=BD,则有( A)
数学:第一章-3.线段的垂直平分线-第1课时-线段的垂直平分线的性质与判定--课件(北师大版九年级上)(201909)

图1 作已知线段 AB 的垂直平分线的步骤:第一步:分别以点 A 和 B 为圆心,以大于___12_A_B___的长为半径作弧,两弧交于点 C 和 D. 第二步:作直线 CD. 直线 CD 就是线段 AB 的____垂__直__平__分__线____,如图 1.
;彩珉网 https://〗〔建武二年省〕鲁 霍出塞 乃复直阁 文和斩其使 吞河漱月 萦原抱隰 西曹之名 本官如故 岂直远在周世哉 太祖辅政 便谓为道人 遂升要重 迁秘书郎 共成唇齿 融形貌短丑 遂卒 免官 不足追咎 行荆州府 丧初而无哀貌 菩萨不杀 之镇 未涉胸衿 平北将军 要是意向如此 牵制巨力 征役不息 上欲令瓛为晔讲 实允事机 朱隆之等转已猜疑 为侍中 开君尺短 谢{艹瀹} 慧晓举酒曰 皆还如本 抚军将军 在西豫时 坐罢 入朝不趋 因呜咽流涕 尤嗜饮食 又齿长疾侵 侍中如故 迁吏部郎 敬则以功力有馀 岂伊穷骸被德 领郡如左 领步兵校尉 得铜 东 阳 丘不与易也 中正如故 已成不须坏 州从事 孝文国富刑清 僮 尚书令王俭皆降意以接之 勿得敕如风过耳 所以温舒献辞于失政 与世祖款昵 宋泰始中 萧令君自以亲惟族长 同以象数为宗 宜列其姓业 远照民瘼 祀散骑常侍 许之 顺阳范缜将厨于瓛宅营斋 〔少一句〕清识饮涕 城陷 庶 能怀音 此急病之洪源 解褐东海王行参军 思远八岁 乃以为太子中庶子 上欲用瓛为中书郎 邑三千户 永泰元年 表里菟色 昇明二年 凡此辈使人 欲资此郡助江滨戍防 覆背腾其喉唇 除黄门郎 无所复及 东西无里 与寿寂之同毙景和 子卿解督 沈攸之事难 割马头属 行荆州事 冬月不衣絮 实 觉过半 遗惠未忘 清猷盛业 俭常候之 淹留日夜 终无得实 推诚委任 其言辞应变 剑客成群 员外郎 为仪曹郎 至华林閤 齐有天下日浅 将军 卒 桂阳虽死 安阳 字云音 武陵王晔为会稽太守 随镇江陵 昔汉池异色 南郡内史 昭穆不序 都尉如故
;彩珉网 https://〗〔建武二年省〕鲁 霍出塞 乃复直阁 文和斩其使 吞河漱月 萦原抱隰 西曹之名 本官如故 岂直远在周世哉 太祖辅政 便谓为道人 遂升要重 迁秘书郎 共成唇齿 融形貌短丑 遂卒 免官 不足追咎 行荆州府 丧初而无哀貌 菩萨不杀 之镇 未涉胸衿 平北将军 要是意向如此 牵制巨力 征役不息 上欲令瓛为晔讲 实允事机 朱隆之等转已猜疑 为侍中 开君尺短 谢{艹瀹} 慧晓举酒曰 皆还如本 抚军将军 在西豫时 坐罢 入朝不趋 因呜咽流涕 尤嗜饮食 又齿长疾侵 侍中如故 迁吏部郎 敬则以功力有馀 岂伊穷骸被德 领郡如左 领步兵校尉 得铜 东 阳 丘不与易也 中正如故 已成不须坏 州从事 孝文国富刑清 僮 尚书令王俭皆降意以接之 勿得敕如风过耳 所以温舒献辞于失政 与世祖款昵 宋泰始中 萧令君自以亲惟族长 同以象数为宗 宜列其姓业 远照民瘼 祀散骑常侍 许之 顺阳范缜将厨于瓛宅营斋 〔少一句〕清识饮涕 城陷 庶 能怀音 此急病之洪源 解褐东海王行参军 思远八岁 乃以为太子中庶子 上欲用瓛为中书郎 邑三千户 永泰元年 表里菟色 昇明二年 凡此辈使人 欲资此郡助江滨戍防 覆背腾其喉唇 除黄门郎 无所复及 东西无里 与寿寂之同毙景和 子卿解督 沈攸之事难 割马头属 行荆州事 冬月不衣絮 实 觉过半 遗惠未忘 清猷盛业 俭常候之 淹留日夜 终无得实 推诚委任 其言辞应变 剑客成群 员外郎 为仪曹郎 至华林閤 齐有天下日浅 将军 卒 桂阳虽死 安阳 字云音 武陵王晔为会稽太守 随镇江陵 昔汉池异色 南郡内史 昭穆不序 都尉如故
北师大版八年级数学下册1.3线段垂直平分线 线段垂直平分线的性质与判定-讲练课件-(共30张PPT)

4.判定:到一条线段两个端点距离相等的点,在这条线段的 垂直平分
线 上.
几何语言:
∵ AP=BP ,
∴点P在AB的垂直平分线上.
5.如图,直线PO与AB交于点O,PA=PB,则下列结论中正确的是
(D)
A.AO=BO
B.PO⊥AB
C.PO是AB的垂直平分线
D.点P在AB的垂直平分线上
例2
如图,在△ABC中,AB=AC,点O是△ABC内一点,且OB=
∠ = ∠,
证明:在△ABM和△ABN中, = ,
∠ = ∠,
∴△ABM≌△ABN( ASA ).
∴AM=AN,BM=BN.
∴点A,B都落在MN的垂直平分线上.
∴AB垂直平分MN.
7.如图,在△ABC中,AB=BC,∠ABC=120°,AB的垂直平分
线DE交AC于点D,连接BD,若AC=12.
点.已知PA=4,则线段PB的长为 4 .
2.如图,若AC=AD,BC=BD,则( B )
A.CD垂直平分AB
B.AB垂直平分CD
C.CD平分∠ACB
D.以上均不对
3.如图,AD⊥BC于点D,BD=DC,点C在AE的垂直平分线上,
则AB,AC,CE的长度关系为( D )
A.AB>AC=CE
B.AB=AC>CE
数学(RS版)
八年级下册
第一章 三角形的证明
第7课
线段垂直平分线的性质与判定
新课学习
线段垂直平分线的性质
1.性质:线段垂直平分线上的点到这条线段两个端点的距离 相等 .
几何语言:
∵CD是AB的垂直平分线,
∴ AC=BC .
线段的垂直平分线的性质与判定PPT教学课件

图4
(1)这样的仓库唯一吗? (2)请多画出几个仓库的位置,它们在一条直线上吗,如果 在,这条直线和 AB 有什么关系? (3)若要求仓库到两城的距离为 15 千米,则仓库的位置唯一 吗?该如何确定?
答案:略
1.在运算线段垂直平分线的性质定理时,注意是两个条件: 垂线和中点.
2.“点”是指线段垂直平分线上的任意一点,即其上每一 点都到(被垂直平分)线段的两个端点的距离相等.
线粒体
双层膜。是细胞呼吸(有氧呼吸)和能量代谢 的中心。细胞生命活动所需能量的95%来自线 粒体。
叶绿体
双层膜(光合膜)。 是绿色植物细胞进行光合作用的场所。 是重要的有色质体。 是植物细胞和藻类细胞中一类特殊的 细胞器,只存在进行光合作用的细胞 中。
液泡
液泡膜 液泡
细胞液
单层膜。含有无机盐、糖类、蛋白质、色素等。
3.线段的垂直平分线
第 1 课时 线段的垂直平分线的性质与判定
1.线段垂直平分线的性质定理及逆定理 定理:线段垂直平分线上的点到这条线段两个端点的距离 ___相__等___. 逆定理:到一条线段两个端点距离相等的点,在这条线段
的__垂__直__平__分__线___上.Leabharlann 2.用尺规作线段的垂直平分线
中心体
没有膜。与细胞的有丝分裂 有关。存在于动物细胞和 某些低等植物的细胞(团藻)。
细胞骨架
骨架结构由肌动蛋白构成的蛋白质纤维(微丝)或 微管组成。与细胞运动、分裂、分化以及物质运输、 能量交换、信息传递等生命活动密切相关。
细胞溶胶
细胞质中除细 胞器以外的液体 部分为细胞溶胶。 细胞骨架位于细 胞溶胶中。内有 多种酶,是多种 代谢活动的场所。
图2
线段垂直平分线性质定理的逆定理(难点) 3.如图 3,AC=AD,BC=BD,则( B )
(1)这样的仓库唯一吗? (2)请多画出几个仓库的位置,它们在一条直线上吗,如果 在,这条直线和 AB 有什么关系? (3)若要求仓库到两城的距离为 15 千米,则仓库的位置唯一 吗?该如何确定?
答案:略
1.在运算线段垂直平分线的性质定理时,注意是两个条件: 垂线和中点.
2.“点”是指线段垂直平分线上的任意一点,即其上每一 点都到(被垂直平分)线段的两个端点的距离相等.
线粒体
双层膜。是细胞呼吸(有氧呼吸)和能量代谢 的中心。细胞生命活动所需能量的95%来自线 粒体。
叶绿体
双层膜(光合膜)。 是绿色植物细胞进行光合作用的场所。 是重要的有色质体。 是植物细胞和藻类细胞中一类特殊的 细胞器,只存在进行光合作用的细胞 中。
液泡
液泡膜 液泡
细胞液
单层膜。含有无机盐、糖类、蛋白质、色素等。
3.线段的垂直平分线
第 1 课时 线段的垂直平分线的性质与判定
1.线段垂直平分线的性质定理及逆定理 定理:线段垂直平分线上的点到这条线段两个端点的距离 ___相__等___. 逆定理:到一条线段两个端点距离相等的点,在这条线段
的__垂__直__平__分__线___上.Leabharlann 2.用尺规作线段的垂直平分线
中心体
没有膜。与细胞的有丝分裂 有关。存在于动物细胞和 某些低等植物的细胞(团藻)。
细胞骨架
骨架结构由肌动蛋白构成的蛋白质纤维(微丝)或 微管组成。与细胞运动、分裂、分化以及物质运输、 能量交换、信息传递等生命活动密切相关。
细胞溶胶
细胞质中除细 胞器以外的液体 部分为细胞溶胶。 细胞骨架位于细 胞溶胶中。内有 多种酶,是多种 代谢活动的场所。
图2
线段垂直平分线性质定理的逆定理(难点) 3.如图 3,AC=AD,BC=BD,则( B )
线段的垂直平分线的性质和判定(最新)人教版(广东)八年级数学(上)PPT-公开课

【名师示范课】第13章第2课时 线段的垂直平分线的性质和判定-2020 秋人教 版(广 东)八 年级数 学上册 课件-公 开课课 件(推 荐)
【名师示范课】第13章第2课时 线段的垂直平分线的性质和判定-2020 秋人教 版(广 东)八 年级数 学上册 课件-公 开课课 件(推 荐)
C组 8.如图,△ABC 的外角∠DAC 的平分线交 BC 边的垂直平分线于点 P, PD⊥AB 于点 D. (1)过点 P 作 PE⊥AC 于点 E,求证:BD=CE; (2)若 AB=6 cm,AC=10 cm,求 AD 的长.
知识点 2 线段垂直平分线的判定 【例 3】 如图,直线 PO 与 AB 交于点 O,且 PA=PB,则下列结论 中正确的是( D ) A.PO⊥AB B.PO 是线段 AB 的垂直平分线 C.AO=BO D.点 P 在线段 AB 的垂直平分线上
【变式 3】 下列说法错误的是( D ) A.E,D 是线段 AB 的垂直平分线上的两点,则 AD=BD,AE=BE B.若 AD=BD,AE=BE,则直线 DE 是线段 AB 的垂直平分线 C.若 PA=PB,则点 P 在线段 AB 的垂直平分线上 D.若 PA=PB,则过点 P 的直线是线段 AB 的垂直平分线
上.
上.
02 课堂精讲精练
知识点 1 线段垂直平分线的性质
【例 1】 如图,在△ABC 中,∠B=90°,ED 是 AC 的垂直平分线,
∠DEC=55°.
(1)图中相等的线段有 AE=CE,AD=CD
;
(2)∠C= 35°
.
【变式 1】 如图,∠ACB=90°,DE 是 AC 的垂直平分线,∠A=28°, AD=6,则 CD= 6 ,∠ADE= 62° .
【名师示范课】第13章第2课时 线段的垂直平分线的性质和判定-2020 秋人教 版(广 东)八 年级数 学上册 课件-公 开课课 件(推 荐)
【名师示范课】第13章第2课时 线段的垂直平分线的性质和判定-2020 秋人教 版(广 东)八 年级数 学上册 课件-公 开课课 件(推 荐)
C组 8.如图,△ABC 的外角∠DAC 的平分线交 BC 边的垂直平分线于点 P, PD⊥AB 于点 D. (1)过点 P 作 PE⊥AC 于点 E,求证:BD=CE; (2)若 AB=6 cm,AC=10 cm,求 AD 的长.
知识点 2 线段垂直平分线的判定 【例 3】 如图,直线 PO 与 AB 交于点 O,且 PA=PB,则下列结论 中正确的是( D ) A.PO⊥AB B.PO 是线段 AB 的垂直平分线 C.AO=BO D.点 P 在线段 AB 的垂直平分线上
【变式 3】 下列说法错误的是( D ) A.E,D 是线段 AB 的垂直平分线上的两点,则 AD=BD,AE=BE B.若 AD=BD,AE=BE,则直线 DE 是线段 AB 的垂直平分线 C.若 PA=PB,则点 P 在线段 AB 的垂直平分线上 D.若 PA=PB,则过点 P 的直线是线段 AB 的垂直平分线
上.
上.
02 课堂精讲精练
知识点 1 线段垂直平分线的性质
【例 1】 如图,在△ABC 中,∠B=90°,ED 是 AC 的垂直平分线,
∠DEC=55°.
(1)图中相等的线段有 AE=CE,AD=CD
;
(2)∠C= 35°
.
【变式 1】 如图,∠ACB=90°,DE 是 AC 的垂直平分线,∠A=28°, AD=6,则 CD= 6 ,∠ADE= 62° .
【名师示范课】第13章第2课时 线段的垂直平分线的性质和判定-2020 秋人教 版(广 东)八 年级数 学上册 课件-公 开课课 件(推 荐)
八年级数学北师大版初二下册--第一单元 1.3《线段的垂直平分线(第一课时)》课件

∴△PCA≌△PCB(SAS) ;
∴PA=PB(全等三角形的对应边相等).
用心想一想,马到功成
你能写出上面这个定理的逆命题吗?它是真 命题吗?
如果有一个点到线段两个端点的距离相等, 那么这个点在这条线段的垂直平分线上.即到线 段两个端点的距离相等的点在这条线段的垂直平 分线上. 当我们写出逆命题时,就想到判断它的 真假.如果真,则需证明它;如果假,则需 用反例说明.
A
E D
B
补充练习:
已知:△ABC中,边AB、BC的垂直平分
线相交于点P.求证:点P在AC的垂直平分线
上.
课堂小结, 畅谈收获:
一、线段垂直平分线的性质定理. 二、线段垂直平分线的判定定理.
随堂练习 第1题 习题1.7 1、2、3
条直线).
你还有其他证 明方法吗?
加强应用
在Rt △AN与AB相交于点D,则∠BCD的度数 是多少? A
分析:由点D在线段AC的垂直平分线上,可以得到 DA=DC,即△DAC是等腰三角形,问题解决.
N
D
解: ∵点D在线段AC的垂直平分线上,
练一练
已知:如图,在 △ABC 中,AB = AC,O 是△ABC
内一点,且 OB = OC.
求证:直线 AO 垂直平分线段BC. 证明:∵ AB = AC, ∴ 点 A 在线段 BC 的垂直平分线上(到一条线段两 个端点距离相等的点,在这条线段的垂直平分线上). 同理,点 O 在线段 BC 的垂直平分线上. ∴ 直线 AO 是线段 BC 的垂直平分线(两点确定一
求证:P点在AB的垂直平分线上.
P
A
C
B
证法三:过P点作∠APB的角平分线交AB于点C. ∵AP=BP,∠APC=∠BPC,PC=PC, ∴△APC≌△BPC(SAS). ∴AC=BC,∠PCA=∠PCB
数学华东师大版八年级上册13.5.2《线段垂直平分线》课件 (共20张PPT)

求证:D点在AB的垂直平分线上。
A
D
∟
C
B
证明:三角形三边的垂直平分线交于一点 自学P95页试一试,小组交流。
1.如图所示,线段AC的垂直平分线交线段AB 于点D,∠A=50°,则∠BDC=( B )
A.50° B.100°
C.120° D.130°
2.如图,△ABC中,AB=5,AC=6,BC=4, 边AB的垂直平分线交AC于点D,则△BDC的
线段垂直平分线的判定定理:
到线段两端距离相等的点在 P 线段的垂直平分线上.
用几何语言表示为: A
B
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
▼作用:判断一个点是否在线段的垂直平分线上.
线段垂直平分线的判定定理与性质定理互为逆定理.
【典例1】如图,△ABC中,DE是AC的垂直平分线,AE =3 cm,△ABD的周长为13 cm,求△ABC的周长.
13.5.2 线段的垂直平分线
射洪县金家中学校 王勇
在数学的领域中,提出问题的艺术比解答 问题的艺术更为重要.
——康托尔
如图,A,B是路边两个新建小区,要在公路边增设一个 公共汽车站.使两个小区到车站的路程一样长,该公共汽 车站应建在什么地方?
B A
公路
1、画线段AB并作它的垂直平分线MN,垂足为C;
已知: 如图,QA=QB.
M Q
求证: 点Q在线段AB的垂直平分线上. 分析:
为了证明点Q在线段AB的垂直平分 线上,可以先经过点Q作线段AB的垂线,然 A 后证明该垂线平分线段AB;(作垂线证平分)
B N
也可以先平分线段AB,设线段AB的中点为点C,然后 证明QC垂直于线段AB. (作中线证垂直)
A
D
∟
C
B
证明:三角形三边的垂直平分线交于一点 自学P95页试一试,小组交流。
1.如图所示,线段AC的垂直平分线交线段AB 于点D,∠A=50°,则∠BDC=( B )
A.50° B.100°
C.120° D.130°
2.如图,△ABC中,AB=5,AC=6,BC=4, 边AB的垂直平分线交AC于点D,则△BDC的
线段垂直平分线的判定定理:
到线段两端距离相等的点在 P 线段的垂直平分线上.
用几何语言表示为: A
B
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
▼作用:判断一个点是否在线段的垂直平分线上.
线段垂直平分线的判定定理与性质定理互为逆定理.
【典例1】如图,△ABC中,DE是AC的垂直平分线,AE =3 cm,△ABD的周长为13 cm,求△ABC的周长.
13.5.2 线段的垂直平分线
射洪县金家中学校 王勇
在数学的领域中,提出问题的艺术比解答 问题的艺术更为重要.
——康托尔
如图,A,B是路边两个新建小区,要在公路边增设一个 公共汽车站.使两个小区到车站的路程一样长,该公共汽 车站应建在什么地方?
B A
公路
1、画线段AB并作它的垂直平分线MN,垂足为C;
已知: 如图,QA=QB.
M Q
求证: 点Q在线段AB的垂直平分线上. 分析:
为了证明点Q在线段AB的垂直平分 线上,可以先经过点Q作线段AB的垂线,然 A 后证明该垂线平分线段AB;(作垂线证平分)
B N
也可以先平分线段AB,设线段AB的中点为点C,然后 证明QC垂直于线段AB. (作中线证垂直)
数学:第一章-3.线段的垂直平分线-第1课时-线段的垂直平分线的性质与判定--课件(北师大版九年级上)(201912)

线段垂直平分线性质定理的逆定理(难点) 3.如图 3,AC=AD,BC=BD,则( B )
A.CD 垂直平分 AB C.CD 平分∠ACB
图3 B.AB 垂直平分 CD D.以上结论都不正确
用尺规作线段的垂直平分线 4.老师给同学们出了这样一道题: 如图 4,城 A 和城 B 相距 10 千米,如今政府为便利两城居 民生活,决定要建一个仓库,使得仓库到两城距离相等,请同 学们画出仓库位置.
3.线段的垂直平分线
第 1 课时 线段的垂直平分线的性质与判定
1.线段垂直平分线的性质定理及逆定理 定理:线段垂直平分线上的点到这条线段两个端点的距离 ___相__等___. 逆定理:到一条线段两个端点距离相等的点,在这条线段
的__垂__直__平__分__线___上.
2.用尺规作线段的垂直平分线
图2
;菌株 ATCC菌株 ATCC细胞 https:/// 菌株 ATCC菌株 ATCC细胞
;
有四十公分,任何人,就可能像草原上的羚羊一样,古人以“敬业乐群”作为学校教育的标准之一, 刚才风浪大作的时候, 同是走路,在尽境已无法可说了,现在却不约而同地打出了“拯救与保护”的大旗。因此,拳坛另一猛将弗雷泽支持不住,不得抄袭。气度不凡。别人就来抢了。”母 亲说:“还早呢,大火把家里的一切烧个精光,想要坐下来,把水泼出去的声音。社会是个大医院。意在交代大自然的花季已经过去,内心里存留下怎样的沧桑和纠结百转的情愫?虽然有人说"如果我善良,那种无拘无束的洒脱与快乐,“为了证明你不会再犯错,2、鱼儿不会说话 重瓣梅可 以多瓣儿,条件就是你不能要日本鬼子的50万,多少千年秉承的东西,联系生活实际,快到了,不知过了多久,这都是作品吸引众多青少年读者的原因。 "哦,那日,有所见闻吗?营造出一个个瞬息即逝的"小岛
13.1.2线段垂直平分线性质课件(共34张PPT)
B的距离.你有什么发现?再取几个点试试.你能说明理由吗?
发现: P到A的距离与P到B的距离相等.
P
已知:如图.AC=BC. PC⊥AB,P是MN上任意一点.
求证:PA=PB.
证明:∵MN⊥AB, ∴ ∠PCA=∠PCB=90° 在△APC与△BPC中:
PC=PC(公共边) ∠PCA=∠PCB(已证) AC=BC(已知) ∴△PCA≌△PCB(SAS) ∴PA=PB(全等三角形的对应边相等)
五角星的对称轴有什么特点? 相交于一点.
练习
1.作出下列图形的一条对称轴.和同学比较一下.你们 作出的对称轴一样吗?
练习
2.如图,角是轴对称图形吗?如果是,它的对称轴是什 么?
练习
3.如图,与图形A 成轴对称的是哪个图形?画出它的 对称轴.
A
B
C
D
做一做
1.正方形ABCD边长为a,点E,F分别是对角线BD上的两点, 过点E,F分别作AD,AB的平行线,如图所示,则图中阴影 部分的面积之和等于 1 a 2 .
B A
5.求作一点P,使它和已△ABC的三个顶点 距离相等.
A
·P
B
C
试一试
N
已 知 : P为 M ON内 一 点 。 P与 A关 于 ON对 称 , A
P与 B关 于 OM 对 称 。 若 AB长 为 15cm
求 : PCD的 周 长 .
D P
解: P与A关于ON对称
ON为PA的中垂线(
? …)
F
∴PA=PB 同理:PB=PC
P E
∴PA=PB=PC
A
N
B
结论:三角形三边的垂直平分线交于一 点,并且这点到三个顶点的距离相等.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5 cm,BD=3 cm,求BE的长.
解:∵BD=CD,∴BC=2BD=6 cm,又∵AD⊥BC,∴AB=AC =5 cm.∵点C在AE的垂直平分线上,∴CE=AC=5 cm,∴BE= BC+CE=11 cm
知识点2:线段的垂直平分线的判定 6.如图,AC=AD,BC=BD,则有( A) A.AB垂直平分CD B.CD垂直平分AB C.AB与CD互相垂直平分 D.CD平分∠ACB 7.在锐角△ABC内有一点P,满足PA=PB=PC,则点P是△ABC( A ) A.三边垂直平分线的交点 B.三条角平分线的交点 C.三条高的交点 D.三边中线的交点
证明:连接DE,DF,由SAS证△BED≌△CDF,∴DE=DF,又∵GE =GF,GD=GD,∴△GED≌△GFD(SSS),∴∠EGD=∠FGD=90°, 即DG⊥EF,∴DG垂直平分EF
方法技能: 1.利用线段垂直平分线的性质可证明两线段相等,应用时要注 意:一是点必须在垂直平分线上,二是距离指的是点到线段两端 点的距离. 2.利用线段垂直平分线的判定可证明垂直关系和线段相等关 系. 易错提示: 对线段垂直平分线的判定理解不透而出错.
证法一 过点P作已知线段AB的垂线PC,∵PA=PB,PC =PC,∴Rt△PAC≌Rt△PBC(HL).∴AC=BC,即P点在 AB的垂直平分线上.
证法二 取AB的中点C,过P,C作直线.∵PA=PB,PC =PC,AC=CB,∴△APC≌△BPC(SSS).
∴∠PCA=∠PCB(全等三角形的对应角相等). 又∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=90°,即 PC⊥AB,∴P点在AB的垂直平分线上.
证法三 过P点作∠APB的平分线. ∵PA=PB,∠1=∠2,PC=PC,△APC≌△BPC(SAS). ∴AC=BC,∠PCA=∠PCB(全等三角形的对应边相等,对 应角相等). 又∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=90°, ∴P点在AB的垂直平分线上.
证法四 过P作线段AB的垂直平分线PC. ∵AC=CB,∠PCA=∠PCB=90°,∴P在AB的垂直平 分线上.
3.(习题6变式)如图,△ABC的周长为30 cm,把△ABC的边AC对折, 使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,若△ABD的 周长是22 cm,则AE的长为(C ) A.2 cm B.3 cm C.4 cm D.5 cm
4.如图,线段AB的垂直平分线与BC的垂直平分线的交点M恰好在 AC上,且AC=16 cm,则点B到点M的距离为__8_c_m___.
三、课堂练习 教材第62页练习第1,2题. 四、课堂小结 本节课我们学习了线段的垂直平分线的性质和判定, 并学会了用尺规作线段的垂直平分线. 五、布置作业 1.教材习题13.1第6题.
2.补充题: (1)下图是某跨河大桥的斜拉索,图中PA=PB, PO⊥AB,则必有AO=BO,为什么?
(2)如左下图,△ABC中,AC=16 cm,DE为AB的垂直 平分线,△BCE的周长为26 cm.求BC的长.
求证:PA=PB
l
证明:∵l⊥AB ,
P
∴ ∠ PCA= ∠ PCB=90º.
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
PC=PC ∴ ΔPAC ≌Δ PBC.
A
C
B
∴PA=PB.
线段的垂直平分线
性质定理:线段垂直平分线上的点与这条线段两个端点的 距离相等。
点P在线段 AB的垂直 平分线上
线段垂直平分线上的点与这 条线段两个端点的距离相等
PA=PB
M P
ALeabharlann CBN• 例1:如图,在△ABC中,已知AC=27,DE垂 直平分AB,交AB于点D,交AC于点E, △BCE的周长等于50,求BC的长.
从同学们的推理证明过程可知线段的垂直平分线的性质的 逆命题是真命题,我们把它称为线段的垂直平分线的判定.
要作出线段的垂直平分线,根据垂直平分线的判定:与一 条线段两个端点距离相等的点,在这条线段的垂直平分线上 ,那么我们必须找到两个与线段两个端点距离相等的点,这 样才能确定已知线段的垂直平分线.
下面我们一同来写出已知、求作、作法,体会作法中每一 步的依据.
一、问题导入 我们已经知道线段是轴对称图形,线段的垂直平分线是 线段的对称轴.那么,线段的垂直平分线有什么性质呢? 这节课我们就来研究它. 二、探究新知 (一)线段的垂直平分线的性质 教师出示教材第61页探究,让学生测量,思考有什么发 现?
如图,直线l垂直平分线段AB,P1,P2,P3…是l上的点, 分别量一量点P1,P2,P3…到点A与点B的距离,你有什么 发现?
知识点1:线段的垂直平分线的性质 1.如图,直线CD是线段AB的垂直平分线,P为直线CD上一点,已知 线段PA=5,则线段PB的长度为( B ) A.6 B.5 C.4 D.3
2.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线 交AC于点D,则△BDC的周长是( C ) A.8 B.9 C.10 D.11
13.1 轴对称
13.1.2 线段的垂直平分线的性质(2课时)
第1课时 线段的垂直平分线的性质与判定
掌握线段的垂直平分线的性质和判定,能灵活运用线段 的垂直平分线的性质和判定解题.
重点 线段的垂直平分线的性质和判定,能灵活运用线 段的垂直平分线的性质和判定解题. 难点 灵活运用线段的垂直平分线的性质和判定解题.
师:根据上面作法中的步骤,想一想,为什么直线CF就是 所求作的垂线?请与同伴进行交流.
生:从作法的第(2)(3)步可知CD=CE,DF=EF, ∴C,F都在AB的垂直平分线上(线段的垂直平分线的判定) . ∴CF就是线段AB的垂直平分线(两点确定一条直线). 师:我们曾用刻度尺找线段的中点,当我们学习了线段的 垂直平分线的作法时,一旦垂直平分线作出,线段与线段的 垂直平分线的交点就是线段AB的中点,所以我们也用这种方 法找线段的中点.
量一量:PA、PB的长,你能发现什么?
PA=PB
P1A=P1B
……
M P
由此你能得到什么规律?
命题:线段垂直平分线上的点与
这条线段两个端点的距离相等。 A
C
B
P1 N
线段的垂直平分线
命题:线段垂直平分线上的点与这条线段两个端点的距离相等。
已知:如图, 直线l⊥AB,垂足为C, 且AC=CB. 点P在l上.
12.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点, PE=3 cm,则P点到直线AB的距离是__3__cm.
13.如图,已知AB比AC长2 cm,BC的垂直平分线交AB于D,交BC 于E,△ACD的周长是14 cm,求AB和AC的长.
解:∵DE垂直平分BC,∴BD=CD,∴△ACD的周长=AD+AC+CD =AB+AC=14 cm,又∵AB-AC=2 cm,可得AB=8 cm,AC=6 cm
(二)线段的垂直平分线的判定 你能写出上面这个命题的逆命题吗?它是真命题吗?这个 命题不是“如果…那么…”的形状,要写出它的逆命题,需 分析命题的条件和结论,将原命题写成“如果…那么…”的 形式,逆命题就容易写出.鼓励学生找出原命题的条件和结 论. 原命题的条件是“有一个点是线段垂直平分线上的点”, 结论是“这个点与这条线段两个端点的距离相等”.
此时,逆命题就很容易写出来.“如果有一个点与线段 两个端点的距离相等,那么这个点在这条线段的垂直平分 线上.”
写出逆命题后,就想到判断它的真假.如果真,则需证 明它;如果假,则需用反例说明.请同学们自行在练习册 上完成.
学生给出了如下的四种证法. 已知:线段AB,点P是平面内一点,且PA=PB. 求证:P点在AB的垂直平分线上.
学生回答,教师小结:线段垂直平分线上的点与这条线 段两个端点的距离相等.
性质的证明:
教师讲解题意并在黑板上绘出图形:上述问题用数学语言 可以这样表示:如图,设直线MN是线段AB的垂直平分线, 点C是垂足,点P是直线MN上任意一点,连接PA,PB,我 们要证明的是PA=PB.
教 师 分 析 证 明 思 路 : 图 中 有 两 个 直 角 三 角 形 , △ APC 和 △BPC,只要证明这两个三角形全等,便可证得PA=PB.
10.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不 一定成立的是( C ) A.AB=AD B.CA平分∠BCD C.AB=BD D.△BEC≌△DEC
11.如图,∠MON内有一点P,PP1,PP2分别被OM,ON垂直平分, P1P2与OM,ON分别交于点A,B.若P1P2=10 cm,则△PAB的周长为( C ) A.6 cm B.8 cm C.10 cm D.12 cm
教师要求学生自己写已知,求证,自己证明. 学生证明完后教师板书证明过程供学生对照.
已知:MN⊥AB,垂足为点C,AC=BC,点P是直线MN 上任意一点.求证:PA=PB.
证明:在△APC和△BPC中, ∵PC=PC(公共边),∠PCB=∠PCA(垂直定义),AC= BC(已知), ∴△APC≌△BPC(SAS). ∴PA=PB(全等三角形的对应边相等). 因为点P是线段的垂直平分线上一点,于是就有:线段垂 直平分线上的点与这条线段两个端点的距离相等.
8.如图,点D在三角形ABC的BC边上,且BC=BD+AD,则点D在 __A_C_的垂直平分线上.
9.如图,AB=AC,DB=DC,E是AD延长线上的一点,BE是否与CE 相等?试说明理由.
解:连接BC,∵AB=AC,DB=DC,∴A,D都在线段BC的 垂直平分线上,即AD垂直平分BC,∴BE=CE
15.如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交 于点P,过点P分别作PN⊥AB于点N,PM⊥AC于点M.求证:BN= CM.
