2017年上海中考二模24题专练(学生版)
2017年上海市松江区中考二模考试(含听力文本和答案)

2017年上海市松江区中考二模考试(含听力文本和答案)————————————————————————————————作者:————————————————————————————————日期:2017年松江区初中毕业生学业模拟考试初三英语2017.4Part1 Listening (第一部分听力)I. Listening comprehension (听力理解)(共30 分)A. Listen and choose the right picture (根据你听到的内容,选出相应的图片)(6分)1._______2._______3._______4._______5._______6. _______B. Listen to the dialogue and choose the best answer to the question you hear (根据你听到的对话和问题,选出最恰当的答案)(8分)7. A) Tom’s.B) Peter's.C) Jane’s.D) Mike’s.8. A) This morning. B) Yesterday morning.C) This afternoon. D) Yesterday afternoon.9. A) To the museum. B) To Jack’s house.C) To the cinema. D) To Sams home.10. A) One. B) Three.C) Five. D) Seven.11. A) Teacher and student. B) Husband and wife.C) Manager and secretary. D) Father and daughter.12. A) Animals. B) Hobbies.C) Sports. D) Friends.13. A) A jacket. B) A raincoat.C) A T-shirt. D) A sweater.14. A) He moved to Beijing when he was very young.B) He will ask someone else to help the woman.C) He will show the woman around Beijing.D) He can provide little useful information.C. Listen to the passage and tell whether the following statements are true or false (判断下列句子是否符合你听到的短文内容,符合的用“T”表示,不符合的用“F”表示)(6分)15. We decided to sell our house because we are in great need of money.16. The house was still not sold after it was put on the market for three weeks.17. The house was kept clean and tidy with my effort so that it could be sold.18. The house agent called me before he came to visit my house with a couple.19. Everything in my house was in perfect order when the three people walked around it.20. The couple bought the house probably because it provided the same feeling as their own.D. Listen to the passage and complete the following sentences (听短文,完成下列内容。
2017年上海市崇明县中考数学二模试题(解析版)

C、6,8,9,8,9,众数是8和9,此选项错误;
D、由C的判断知本选项正确;
故选D.
【点睛】本题考查了平均数、中位数和众数的定义,属于基础题型,熟练掌握平均数、中位数和众数的定义是解题的关键.
4.商场将某种商品按原价的8折出售,仍可获利20元.已知这种商品的进价为140元,那么这种商品的原价是( )
A.160元B.180元C.200元D.220元
【答案】C
【解析】
【分析】
利用打折是在标价的基础之上,利润是在进价的基础上,进而得出等式求出即可.
【详解】解:设原价为x元,根据题意可得:
80%x=140+20,
解得:x=200.
所以该商品的原价为200元;
故选C.
【点睛】此题主要考查了一元一次方程的应用,根据题意列出方程是解决问题的关键.
理由:∵四边形ABCD是平行四边形,∴ , ,
∵AE=AB,∴ , ,
∴四边形DEAC是平行四边形,
∵AB=DE,AE=AB,
∴AE=DE,
∴平行四边形DEAC是菱形.
故选B.
【点睛】本题考查了平行四边形的判定和性质以及菱形的判定方法,熟练掌握平行四边形的判定与性质和菱形的判定是解此题的关键.
二、填空题
【答案】
【解析】
【分析】
先判断掷一次骰子,向上的一面的点数为素数的情况,再利用概率公式求解即可.
【详解】解:∵掷一次这枚骰子,向上的一面的点数为素数的有2,3,5共3种情况,
∴掷一次这枚骰子,向上的一面的点数为素数的概率是: .
故答案为 .
【点睛】本题考查了求简单事件的概率,根据题意判断出素数的个数是解题的关键.
2017届上海市黄浦区初三数学、语文、英语二模卷(含答案)

C C
B
E
A(D)
(图 1)
B
E
(图 2) D
A
C
B
E (图 3) D
A
九年级数学 共 4 页 第 4页
黄浦区 2017 年九年级学业考试模拟考评分标准参考
一、选择题(本大题 6 小题,每小题 4 分,满分 24 分)
1.D ;
2.D ;
3.A;
4.B;
5.C;
6.A.
二、填空题:(本大题共 12 题,每题 4 分,满分 48 分)
三、解答题:(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
0
1
计算: 2017 1 2 2 2 1 2sin 30 .
20.(本题满分 10 分)
解方程:
x2 x2
16 x2 4
x
1 2.
21.(本题满分 10 分)
如图,在△ABC 中,∠ACB=90°,∠A=15°,D 是边 AB 的中点,DE⊥AB 交 AC 于点 E.
答:设定扫地时间为 60 分钟. —————————————————————(1 分)
23. 证:(1)联结 AE、AF. ————————————————————————(1 分) 由菱形 ABCD,得∠ACE=∠ACF. ——————————————————(1 分) 又∵点 E、C、F 均在圆 A 上, ∴AE=AC=AF,——————————————————————————(1 分) ∴∠AFC=∠ACF=∠ACE=∠AEC. —————————————————(1 分) ∴△ACE≌△ACF,————————————————————————(1 分) ∴CE=CF. ———————————————————————————(1 分) (2)∵E 是弧 CG 中点,
2017年上海市奉贤区中考语文二模试卷(解析版)

2017年上海市奉贤区中考语文二模试卷一、文言文1.默写(1)欲把西湖比西子,(《饮湖上初晴后雨》)(2),清泉石上流。
(《山居秋暝》)(3)了却君王天下事,。
(《破阵子•为陈同甫赋壮词以寄之》)(4),小桥流水人家……(《天净沙•秋思》)(5)黄发垂髫,。
(《桃花源记》)2.阅读下面的诗,完成下列各题东临碣石,以观沧海。
水何澹澹,山岛竦峙。
树木丛生,百草丰茂。
秋风萧瑟,洪波涌起。
日月之行,若出其中。
星汉灿烂,若出其里。
幸甚至哉,歌以咏志。
(1)诗中“竦峙”的意思是(2)对这首诗理解错误的一项是A.全诗借大海雄伟壮丽的景象,表达了诗人豪迈乐观的积极进取精神。
B.“东临碣石”两句以“观”字总领全篇,点名了观沧海的地点。
C.“水何澹澹”两句,动静相衬,写出了大海的全景。
D.“日月之行”四句具体描写了大海吞吐日月星汉的真实景象。
3.阅读下文,完成下列各题黄生借书说书非借不能读也。
子不闻藏书者乎?七略、四库,天子之书,然天子读书者有几?汗牛塞屋,富贵家之书,然富贵人读书者有几?其他祖父积、子孙弃者无论焉。
非独书为然,天下物皆然。
非夫人之物而强假焉,必虑人逼取,而惴惴焉摩玩之不已,曰:“今日存,明日去,吾不得而见之矣。
”若业为吾所有,必高束焉,庋藏焉,曰“姑俟异日观”云尔。
(1)上文的作者是(朝代)的文学家(人名)。
(2)用现代汉语翻译下列句子。
其他祖父积、子孙弃者无论焉。
(3)下列理解不正确的一项是A.选文阐明了“书非借不能读也”的观点。
B.上文先用了“天子读书”和“富贵人读书”这两个常见的事实来论证了观点。
第1页(共18页)C.上文再以“非读书为然,天下物皆然”一句深化了论点,扩展了论题。
D.上文最后以对比论证来证明“天下物皆然”4.阅读下文,完成下列各题楚王使魏逐张仪①.陈轸②曰:“王何逐张子?”曰:“为臣不忠不信。
”曰:“不忠,王无以为臣;不信,王勿与为约。
且魏臣不忠不信,于王何伤?忠且信,于王何益?逐而听则可,若不听,是王令困也。
英语_2017年上海市静安区中考英语二模试卷(含答案)

2017年上海市静安区中考英语二模试卷一、Part 2 Phonetics, Vocabulary and Grammar(第二部分语音、词汇和语法)1. How is your l________nch at school ? Which is correct for the underlined part ?()A /u/B /ʌ/C /ɔ:/D /a:/2. More and more young people are trying to do something for ________old at weekends.()A aB anC theD /3. Jack left __________Germany last year and found a job in a big company a month ago.()A forB inC toD after4. Donald Trump was elected as President of the United States _________November 9tℎ,2016.()A inB ofC atD on5. I don't think the honour is ___________. It really belongs to all the teachers and friends around.()A meB myC mineD myself6. Some students like to be volunteers in the community and _________prefer to do part﹣time jobs.()A otherB the otherC othersD the others7. The more careful you are , _________mistakes you will make in the coming test/()A fewerB the fewerC fewestD the fewest8. Though Mr. Liu is over sixty , he works as __________as those young people in the office.()A hardB harderC hardestD the hardest9. After Jenny's mother had a conversation with the teacher , she seemed very________.()A happinessB happyC happilyD happiest10. ________is your home to the nearest underground station?__________About ten minutes' walk.()A How soonB How longC How oftenD How far11. Online games are very attractive , ____________we shouldn't spend too much time on it.()A butB orC soD because12. The fireman set out immediately __________they received the phone call for help.()A unlessB whileC as soon asD until13. Passengers _________show their passports and have their luggage checked before boarding.()A mustB needC canD may14. Fred knows a lot about Chinese tea culture and its history , _________?()A isn't heB doesn't heC hasn't heD won't he15. By the year of 2010. the ten﹣year﹣old girl _______her first collection of poems()A publishedB was publishingC has publishedD had published16. The news our football team lost an important game again made our fans ________for hours.()A criedB cryC to cryD crying17. The workers on the construction site are used to __________at 5:30in the morning.()A get upB got upC getting upD have got up18. ___________piece of good advice our teacher gave up before we entered for the contest!()A HowB WhatC What anD What a19. Would you like to teach me how to make vegetable salad?___________I' ll teach you.()A Of courseB Thanks a lotC Never mindD You are welcome.20. My family plan to visit the Oxford University this summer.___________()A That's all rightB I don't think soC It's my pleasureD Sounds great二、.Complete the following passage with the words or phrases in the box. Each can only be used once(将下列单词或词组填入空格.每空格限填一词,每个单词或词组只能填一次):(共8分)21. A. sweet B. pretty C. rarely D. distance E. fruitThere was a man who had four sons. He wanted his sons to learn not to reach a conclusion too quickly. So he sent them , to go and look at a pear tree that was a great(1)_______away. The first son went in the winter , the second in the spring , the third in the summer , and the youngest son in the autumn. When they had all gone and come back ,the first son said that the tree didn't look a bit(2)_______or straight. The second son said no ﹣﹣﹣﹣﹣it was covered with green buds (萌芽) and full of hope. The third son disagreed and said it was loaded with flowers that smelt so(3)_______, and it was themost amazing thing he had ever seen. The last son disagreed with all of them. He said it was drooping (下垂) with(4)_______, full of life and satisfaction.22. A. produce B. all the rest C. at the end D. miss E. judgeThe man then explained to his sons that they were all right because they had each seen but one season in the tree's life. He told them that they cannot(1)_______a tree , or a person ,by only one season , and that the key points of who they are ﹣﹣﹣﹣﹣and the pleasure ,joy and love that come from that life ﹣﹣﹣can only be measured(2)_______, when all the seasons are up.If you give up when it's winter , you will(3)_______the hope of your spring , the beautyof your summer , excitement of your autumn. Don't let the pain of one season destroy the joy of(4)_______.Don't decide a life by one difficult season.三、 Complete the sentences with the given words in their proper forms(用括号中所给单词的适当形式完成下列句子,每空格限填一词)(8分)23. She prepared many colored stars to praise the________for their excellent work in class.(child)24. Look at the________stamp from the left! It's about the 2008Beijing Olympic Games.(five)25. Lily , only eight , is able to take care of________when her parents are out on business.(she)26. We know having no dinner isn't a healthy way for fat people to lose________.(weight)27. People are becoming more and more________in reading e﹣novels in the spare time.( interest)28. Could you________give me a hand before I take part in the English speech contest ?( possible )29. One can easily find________excuse for what he does when facing the difficulties.(variety )30. It's doctors' duty to________their patients carefully and give the best treatment.(治疗).(exam)四、. Rewrite the following sentences as required(根据所给要求,改写下列句子.62-67题,每空格限填一词.)(14分)31. Our headmaster usually has a meeting on Monday morning.(改为一般疑问句)________your headmaster usually________a meeting on Monday morning?32. The company apologized to the public for its terrible service.(保持句意不变)The company________the public for its terrible services.33. You can finish the work on computer. You needn't write anything on paper.(合并为一句)You can finish the work on computer________ writing anything on paper.34. The girl________is introducing her new school to the foreign guests.(对划线部分提问)________ is introducing her new school to the foreign guests?35. " John , will you go abroad to continue your study next year?" Susan asked.(改为宾语从句)Susan asked John________ he________go abroad to continue his study the next year.36. Grandma Li plants different kinds of vegetables in her small yard.(改为被动语态)Different kinds of vegetables________by Grandma Li in her small yard.37. the problem , ourselves , we , to work out , within two days , can depend on(连词成句)五. Part 3Reading and Writing(第三部分读写) Reading comprehension(阅读理解):(共50分) A. Choose the best answer(根据短文内容,选择最恰当的答案):(12分)38. Nothing in Wiley Post's early years suggests that he would become a famouspilot. His family were farmers. In 1913, Wiley saw something that forever changed his life ﹣an airplane. Wiley Post began to study everything he could find about flying. Post finally rode in an airplane in 1919. After his first ride, Wiley Post knew that flying was something he could learn to do.Wiley Post began his career in flying, not as a pilot, but as a performer who jumps from airplanes using a parachute. He did this with a group that performed flying tricks to earn money.Wiley Post then decided the only way to become a good pilot was to buy an airplane of his own. He needed more money than he earned in the flying show. He went to work in the oil﹣producing areas of Texas. But he damaged his left eye in an accident. Doctors had to remove his eye. Judging distance is difficult without two eyes. Wiley Post began teaching himself to judge distance with only one eye. It took a long time, but he succeeded. In 1928, he got a job flying the plane that belonged to a rich oil producer from Oklahoma called F.C.Hall. In 1930, Post entered the National Air Races in this plane and won.On June 23, 1931, Post and Gatty had flown around the world. But many people said Gatty was the real hero. He had guided the flight. This hurt Post. Wiley Post began to plan another flight around the world. This time he would go alone.On July 15, 1933, Post took off from Floyd Bennett Field in New York. He became the first person to fly from New York to Berlin without stopping. He had flown around the world in seven days, eighteen hours and forty﹣nine minutes.(1). In 1913Wiley Post saw________which forever changed his life.A nothing.B an airplane.C a farmer.D a famous pilot.(2). Wiley Post began his career in flying and earned money by________.A being a pilot.B flying a plane.C performing flying tricks.D making a parachute.(3). In order to earn more money to buy an airplane of his own , Wiley Post________.A went to work in Texas.B went on doing the flying show.C damaged his left eye.D got rid of one of his eyes.(4). Who taught him to judge distance with only one eye ?________A Doctors.B Gatty.C A rich oil producer.D He himself.(5). What does the word " This " probably stand for the sentence "This hurt Post."________A Post flew F. C People say Gatty was the real hero.B Post and Gatty flew together. D Post failed to plan another flight alone.(6). Which of the following is NOT Correct according to the passage ?________A Post rode an airplane for the first time in 1919.B In 1928, Post got a job and started to fly his own airplane.C Post entered the National Air Races in 1930and own.D In 1933, Post became the first one to fly from New York to Berlin without stopping.39. B. Choose the words of expressions and complete the passagewhy do leaves(树叶) change colour?One of nature's most beautiful(1)_______is a forest full of bright autumn colors. Imagine making art with all those colours of paint!Leaves in their autumn colours are beautiful. Did you ever wonder why a tree's leaves change colour? To answer this question , you need to(2)_______the important job thatleaves do.Leaves make food so the tree can grow and have energy. This process is called photosynthesis (光合作用). Leaves need three things to do their job.1)Leaves need water , which they get from the tree(3)_______their stem (茎).2)Leaves need a gas called carbon dioxide. They take it in from the air around them. 3)All plants(4)_______a chemical called chlorophyll(叶绿素), which gives leaves their green colour. Leaves need sunlight , too. Sunlight and chlorophyll work together to turn water and carbon dioxide into a kind of sugar. This sugar is the food that provides plants (5)_______energy. When they make food , trees give off a gas called oxygen. Animals need oxygen to live.Photosynthesis doesn't just help plants stay alive. Photosynthesis(6)_______makes food for all living things. Some animals , such as mice , eat plants. Other animals , such as hawks , eat the plant eaters. Without plants , what would hawks do for food ?(1)A recordsB animalsC sightsD manners(2)A preventB includeC controlD understand(3)A throughB withC aboveD beside(4)A keep offB rely onC turn intoD give up(5)A impossibleB uselessC convenientD necessary(6)A almostB alsoC hardlyD seldom40. Read the passage and fill in the blanks with proper words(在短文的空格内填入适当的词,使其内容通顺,每空格限填一词,首字母已给)Attending a university is an important part of a person's life. Today , many people go to a university to study and train for a future job in subjects like law , medicine , or education. But , the university isn't a modern invention. An important o(56)________started in Egypt a thousand years ago.The world's oldest surviving university , Al﹣Azhar , is in Cario , Egypt. It was first built as a mosque (清真寺) in A. D.972to(57)________the daughter of the king Muhammad. A few years later learners and teachers began meeting in the mosque. They read and talked about the subjects of religion(宗教) and law. Around the year 988 ,leaders in the city of Cario decided to create a school for learning and soon a(58)________that , Al﹣Azhar University was started.Because a university was a new idea , the teachers at Al﹣Azhar needed to think aboutwhat courses to teach and(59)________to teach them. The earliest courses were in lawand religions. In a course , students read and studied with the teacher , but there were hot and free d(60)________among them , too. Often , there was no" correct" answer toa question. In the years that followed , the new university attracted scholars from around the world who came to teach and do research. At Al﹣Azhar , people not only studied the past , but it was a place for s(61)________new ideas with each others as wellOver a thousand years later, Al﹣Azhar is still an important university in the world.Its library contains more than 250,000of the world's oldest and most valuable books.Today,many of the world's most i(62)________universities such as Oxford and Harvard still follow the traditions started at Al﹣Azhar.41. Answer the questions(根据短文内容回答下列问题)More than one million international students are studying in the United States. Many of them find it helpful to have a smartphone and an American credit (信用卡),These things make it easy to pay for many kinds of goods and services. But getting a credit card as an international student is not a simple process. Normal U.S. lenders ask for a social security number(社会保障号码). In addition, They ask to see a person's credit history. This helps the lenders trust that someone is responsible and will make timely payments. These are the ________ most international students do not have.But one company is trying to make the process easier and fairer for them.Jack Guo is from China. He now studies at a university in California. He says having an American credit card makes it easier for students to get around town. And, he says,credit cards are important for international students who hope to live in the country in the future.Kalpesh Kapadia came from India to study at Carnegie Mellon University in Pittsburgh,Pennsylvania. He faced the same difficulties that many international students face when trying to get an American credit card. He decided to open SelfScore(万事达信用卡).Without asking for crediting history and a social number , SelfScore looks at materials such as passports , visas ,and acceptance letters to American school. ________About 10,000international students from more than 66countries now have credit cards through SelfScore. Kapadia says less than one percent of Self Score's credit card holders are late for their payments because of different kinds of reasons.(1)_______. Is it easy for an international student to get a credit card in the U.S. A?________(2)_______. What do " the things "in the second paragraph refer to ?________(3)_______. What can Jack Guo do in America if he has a credit card?________(4)_______. How did Kapadia get rid of his difficulties in getting an American credit card ?________(5)_______. How many SelfScore's credit card holders pay on time according to Kapadia?________(6)_______. SelfScore considers a student's ability to pay when he/she wants to get a credit card.Do you think it is important ? Why or why not ?________六、. Writing(作文)(20分)42. Write at least 60words about the topic "________, a new way of life !"(请以"________,一种崭新的生活方式"为题,从以下图片中选取其中一张图片,举例表述你的思考和理由,写一篇不少于60 个词的短文,标点符号不占格.(注意:文中不得出现考生的姓名、校名及其他相关信息,否则不予评分)Points for reference :• Which way do you choose to write about ?• Why do you think it a new way of life ?• Could you give some suggestions in order to make better use of it ?2017年上海市静安区中考英语二模试卷答案1. B2. C3. A4. D5. C6. C7. B8. A9. B10. D11. A12. C13. A14. B15. D16. B17. C18. D19. D20. D21. D,B,A,E22. E,C,D,B23. children24. fifth25. herself26. weight27. interested28. possibly29. various30. examine31. Does,have32. said sorry to33. instead of34. in red ,Which girl35. if,would36. are planted37. 先找到人称代词 We作句子的主语放在句首,再找动词 can depend on 作句子的谓语,ourselves 作句子的宾语,放在动词depend on的后面;to work out不定式作目的状语. the problem 放在动词work out 后面做宾语、within two days时间状语放在句末.故答案为 We can depend on ourselves to work out the problem within two days.38. BCADCB39. CDABDB40. ne,remember/recall,fter,how,iscussions,haring,important41. things,The company also consider a student's ability to pay.,No, itisn't,Asocialsecuritynumberandaperson'scredithistory,He can get around the town easily. He can live in the country in the future,ByopeningSelfScore,More than 99 percent,Yes,IdoBecausetheSelfScorealsowantstogetitsmoneyback42. mobike,mobike。
(完整)上海市虹口区2017年中考数学二模试卷含答案,推荐文档
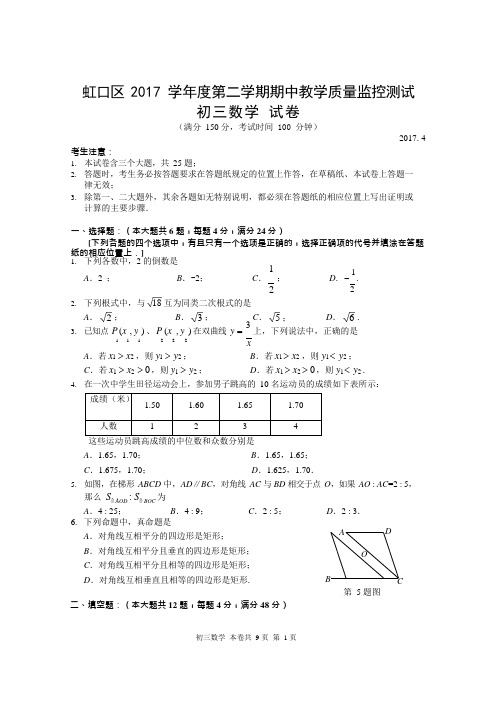
18 2 3 5 6 ADO虹口区 2017 学年度第二学期期中教学质量监控测试初三数学 试卷(满分 150 分,考试时间 100 分钟)2017.4考生注意:1. 本试卷含三个大题,共 25 题;2. 答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共 6 题,每题 4 分,满分 24 分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.]1. 下列各数中,2 的倒数是1 A .2 ; B .-2; C . ;D . - 1. 22 2. 下列根式中,与互为同类二次根式的是A . ;B . ;C . ;D . .3. 已知点 P (x , y ) 、 P (x , y ) 在双曲线 y = 3上,下列说法中,正确的是1 11222xA .若 x 1 > x 2 ,则 y 1 > y 2 ;B .若 x 1 > x 2 ,则 y 1 < y 2 ;C .若 x 1 > x 2 > 0 ,则 y 1 > y 2 ;D .若 x 1 > x 2 > 0 ,则 y 1 < y 2 .4. 在一次中学生田径运动会上,参加男子跳高的 10 名运动员的成绩如下表所示:成绩(米) 1.50 1.60 1.65 1.70 人数1234A .1.65,1.70;B .1.65,1.65;C .1.675,1.70;D .1.625,1.70.5. 如图,在梯形 ABCD 中,AD ∥BC ,对角线 AC 与 BD 相交于点 O ,如果 AO : AC =2 : 5,那么 S AOD : S BOC 为A .4 : 25;B .4 : 9;C .2 : 5;D .2 : 3. 6. 下列命题中,真命题是 A .对角线互相平分的四边形是矩形; B .对角线互相平分且垂直的四边形是矩形; C .对角线互相平分且相等的四边形是矩形; D .对角线互相垂直且相等的四边形是矩形.二、填空题:(本大题共 12 题,每题 4 分,满分 48 分)BC第 5 题图5 频数(人)3x + 4 2 [请将结果直接填入答题纸的相应位置] 7.计算: (-a )3 =▲.8. 不等式-x + 4 < 0 的解集是▲ .9. 如果一元二次方程 x 2 + 4x + m = 0 没有实数根,那么 m 的取值范围是 ▲.10.= x 的解为▲ . 11. 直线 y = -x + 2 不经过第▲象限.12. 如果将抛物线 y = 2x 2 向右平移 3 个单位,那么所得新抛物线的表达式是▲.13. 一副 52 张的扑克牌(无大王、小王),从中任意取出一张牌,抽到 K 的概率是 ▲.14. 为了支援地震灾区同学,某校开展捐书活动,九(1)班同学积极参与.现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在 3.5~4.5 组别的频率是 0.3,那么捐书数量在 4.5~5.5 组别的人数是 ▲ .12842.53.54.55.56.5 第 14 题图本数(本) B A第 16 题图C A P Q B第 17 题图 15. 边心距为 4 的正三角形的边长为 ▲ . 16. 如图,在△ABC 中,DE ∥BC ,AD =2BD ,如果 = , = ,那么 = ▲(用a 、b 表示).AB a AC b DE17. 定义:如图,点 P 、Q 把线段 AB 分割成线段 AP 、PQ 和 BQ ,若以 AP 、PQ 、BQ 为边的三角形是一个直角三角形,则称点 P 、Q 是线段 AB 的勾股分割点.已知点 P 、Q 是线段 AB 的勾股分割点,如果 AP =4,PQ =6(PQ >BQ ),那么 BQ = ▲.18. 如图,在 Rt △ABC 中,∠C =90°,AB =10,sin B = 4,点 5 D 在斜边 AB 上,把△ACD 沿直线 CD 翻折,使得点 A 落在同一平面内的 A ′处,当 A ′D 平行 Rt △ABC 的直角边时,AD 的 长 为 ▲ . 三、解答题(本大题共 7 题,满分 78 分) 19.(本题满分 10 分)ABC第 18 题图x + 2 先化简,再求值:x + 4 - 4) ,其中 x = .xx 2 - 2x x - 2D E ÷ (20.(本题满分 10 分)⎧x 2 - 4xy + 3y 2 = 0, ①解方程组: ⎨⎩2x + y = 21.② 21.(本题满分 10 分,第(1)小题 5 分,第(2)小题 5 分)如图,⊙A 、⊙B 、⊙C 两两外切,AB=10,BC=21, sin B = 4.5(1) 求AC 的长; (2) 求⊙A 、⊙B 、⊙C 的半径.22.(本题满分 10 分,第(1)小题 4 分,第(2)小题 6 分)某市为鼓励市民节约用水,自来水公司按分段收费标准收费,下图反映的是每月水费 y (元)与用水量 x (吨)之间的函数关系. (1) 当用水量超过 10 吨时,求 y 关于 x 的函数解析式(不写定义域); (2) 按上述分段收费标准,小聪家三、四月份分别交水费 38 元和 27 元,问四月份比三月份节约用水多少吨?23.(本题满分 12 分,第(1)小题 6 分,第(2)小题 6 分)如图,在□ABCD 中,过点 A 作 AE ⊥BC 、AF ⊥DC ,垂足分别为点 E 、F ,AE 、AF 分别交 BD 于点 G 、H 且 AG=AH . (1) 求证:四边形 ABCD 是菱形;(2) 延长 AF 、BC 相交于点 P ,求证: BC 2 = DF ⋅ BP .ADHGFAB C第 21 题图yBP AOx24.(本题满分 12 分,第(1)小题 4 分,第(2)小题 4 分,第(3)小题 4 分)如图,在平面直角坐标系 xOy 中,抛物线 y = 1x 2 + bx + c 经过点 A (-2,0)和原点,4点 B 在抛物线上且tan ∠BAO = 1 2,抛物线的对称轴与 x 轴相交于点 P .(1) 求抛物线的解析式,并直接写出点 P 的坐标; (2) 点 C 为抛物线上一点,若四边形 AOBC 为等腰梯形且 AO ∥BC ,求点 C 的坐标; (3) 点 D 在 AB 上,若△ADP ∽△ABO ,求点 D 的坐标.第 24 题图25.(本题满分 14 分,第(1)小题 4 分,第(2)小题 5 分,第(3)小题 5 分)4如图,在△ABC 中,AB=AC =5,cos B = ,点 P 为边 BC 上一动点,过点 P 作射线 PE5交射线 BA 于点 D ,∠BPD=∠BAC .以点 P 为圆心,PC 长为半径作⊙P 交射线 PD 于点 E , 联结 CE ,设 BD=x ,CE=y . (1) 当⊙P 与 AB 相切时,求⊙P 的半径; (2) 当点 D 在 BA 的延长线上时,求 y 关于 x 的函数解析式,并写出定义域;5(3)如果⊙O 与⊙P 相交于点 C 、E ,且⊙O 经过点 B ,当 OP= 4时,求 AD 的长.DAEBPC5 5 + 25 - 25说 明 :2017 年虹口区中考数学模拟练习卷答案要点与评分标准1. 解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;2. 第一、二大题若无特别说明,每题评分只有满分或零分;3. 第三大题中各题右端所注分数,表示考生正确做对这一步应得分数;4. 评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半; 5.评分时,给分或扣分均以 1 分为基本单位. 一、选择题:(本大题共 6 题,满分 24 分)1.C ;2.A ;3.D ;4.A ;5.B ;6.C . 二、填空题:(本大题共 12 题,满分 48 分)7. -a 3 ; 8. x > 4 ; 9. m > 4 ; 10. x = 4 ; 11.三; 12. y = 2(x - 3)2 ;13. 1 ;14.16; 2 213 15. 8 3 ;16. - a + b ;17. 2 3 3;18.4 或 8.三、解答题:(本大题共 7 题,满分 78 分)19.解:原式= x + 2 ÷ x 2+ 4 - 4x .......................................................................... (3 分)x x (x -2)= x + 2 ⋅x (x - 2) ......................................................................................... (2 分) x = x + 2 x - 2(x - 2)2 ………………………………………………………………………(2 分) 把 x = 代入,原式= = 9 + 4 ................................................................ (3 分)20.由①得: (x - y )(x - 3y ) = 0 ,∴ x - y = 0 或 x - 3y = 0 .............................................................................. (2 分) 将它们与方程②分别组成方程组,得:5⎪⎩⎪⎩⎩ ⎧x - y = 0, ⎨2x + y = 21; ⎧x - 3y = 0 ,⎨2x + y = 21 .................................................................................... (4 分) ⎩⎩ 分别解这两个方程组,⎧x 1 = 7, 得原方程组的解为⎨ y = 7;⎧x 2 = 9,y =3. . .................................................................(4 分) ⎩ 1 ⎩ 2(代入消元法参照给分)21.解:(1)过点 A 作 AD ⊥BC ,垂足为点 D∵ sin B = 4 5 ∴ cos B = 35………………………………………………(1 分)在 Rt △ABD 中, BD = AB ⋅cos B = 10 ⨯ 3= 6 .............................................(1 分)5 AD = AB ⋅sin B = 10 ⨯ 4 = 8 ................................................. (1 分) 5∴CD =21-6=15在 Rt △ACD 中, AC === 17 ............................... (2 分) (2)设⊙A 、⊙B 、⊙C 的半径长分别为 x 、y 、z∵⊙A 、⊙B 、⊙C 两两外切∴AB=x+y ,BC=y+z ,AC=x+z ....................................................................... (2 分)⎧x + y =10, 根据题意得⎨ y + z = 21,⎪x + z = 17. ⎧x = 3, 解得⎨ y = 7, ⎪z = 14. …………………………………(3 分)∴⊙A 、⊙B 、⊙C 的半径长分别为 3、7、14.22. 解:(1)设函数解析式为 y =kx +b ( k ≠ 0 ) .......................................................... (1 分)⎧30 = 10k + b由题意得: ⎨70 = 20k + b ⎧k = 4解得: .⎨........................................................................................................(2 分) ⎩b = -10∴y 与 x 之间的函数解析式为 y = 4x -10 . ................................................. (1 分)(2)把 y =38 代入 y = 4x -10 得38 = 4x -10 解得 x =12 ....................................................................... (2 分) 当 0≤x ≤10 时,设函数解析式为 y =k’x ( k ≠ 0 ) 由题意得30 = 10k ' 解得 k’=3 ∴函数解析式为 y =3x ......................................................................... (2 分) 把 y=27 代入 y =3x , 得 27=3x 解得 x =9 .......................................................................................(1 分)∴ 12-9=3答:四月份比三月份节约用水 3 吨. ..................................................................... (1 分)23.(1)证明:在□ABCD 中,∠ABC =∠ADC .............................................................. (1 分) ∵AE ⊥BC ,AF ⊥DC ∴∠BAE +∠ABC=90° ∠DAF+∠ADC =90°∴∠BAE =∠DAF .................................................................................................. (1 分) ∵AG=AH ∴∠AGH =∠AHG ............................................................................ (1 分) ∵∠AGH =∠BAE+∠ABG ∠AHG =∠DAF +∠ADH∴∠ABG=∠ADH ................................................................................................... (1 分) ∴AB=AD ............................................................................................................... (1 分) 又∵四边形 ABCD 是平行四边形 ∴四边形 ABCD 是菱形 ...................................................................................... (1 分) (2) 在□ABCD 中,AD ∥BC ,AB ∥CD ............................................................... (1 分)∴ DF = AF DC AP ,AF = BC ................................................................................ (2 分)AP BP∴ DF = BC ....................................................................................................... (1 分) DC BP∵四边形 ABCD 是菱形 ∴BC=DC .................................................................... (1 分) ∴ DF = BC BC BP即 BC 2 = DF ⋅ BP ............................................................................... (1 分) 24.解:(1)把 A (-2,0)、O (0,0)⎧ 代入1 ⎧0 = 1- 2b + c , 得⎨0 = c . ⎩b = 解得⎪⎨ ,2 .......................................................... (2 分) ⎩c = 0.∴ y = 1 x 2 + 1x .................................................................................... (1 分)4 2P (-1,0) .................................................................................................... (1 分) (2) 过点 B 作 BM ⊥x 轴,垂足为点 M由tan ∠BAO = 1 可得 BM = 1 AM22设点 B (2a -2,a ) .......................................................................................... (1 分)把点 B 代入,得a = 1 (2a - 2)2 + 1(2a - 2)4 2解得 a =2 或 0(舍去) ∴点 B (2,2) .............................................................................................. (1 分) ∵四边形 AOBC 为等腰梯形,AO ∥BC把 y=2 代入 y = 1 x 2 + 1x 4 2得 2 = 1 x 2 + 1x42解得 x=-4 或 2(舍) ...........................................(1 分)∵BO= 2 ∴BO =AC AC= 2 ∴点 C (-4,2) ...............................................................................................(1 分)222 5(3) ∵△ADP ∽△ABO∠BAO =∠DAPAB = 2 5 ,AO =2 AP =1 ① AD = APAO AB∴ AD = 2 ∴ AD =5 .................................................................(1 分) 5 由tan ∠BAO = 1 得 D ( - 8 , 1) .......................................................................(1 分)2 5 5② AD = AP AB AO ∴ AD = 1 2∴ AD = 5..................................................................... (1 分) 由tan ∠BAO = 1 得 D (0,1) ....................................................................... (1 分)2综合①②,点 D 的坐标为( - 8 , 1)或(0,1)5 525.(1)过点 A 作 AM ⊥BC ,垂足为点 M在 Rt △ABM 中, BM = AB ⋅ cos B = 4 ∵AB=AC ∴BC=2BM=8 ................................................................................... (1 分) 过点 P 作 PN ⊥AB ,垂足为点 N 设⊙P 的半径为 r ,则 BP =8-r在 Rt △BPQ 中, PN = BP ⋅sin B = 3(8 - r ) ............................................. (1 分)5∵⊙P 与 AB 相切 ∴PN=PC3∴ (8 - r ) = r 5…………………………………………………………………(1 分) 解得 r =3 ................................................................................................................... (1 分)(2) ∵∠BPD=∠BAC ,∠B=∠B∴△BPD ∽△BAC x BP∴ BD = BPBC BA ∴ BP = 5 x8 即 =8 5 ∴ CP = 8 - 5 x ........................................................................ (1 分) 8 过点 P 作 PQ ⊥CE ,垂足为点 Q∵PE=PC ∴∠CPE =2∠CPQ可得∠B=∠D ∠CPE=∠B+∠D=2∠B∴∠CPQ=∠B ...................................................................................................... (1 分)在 Rt △CPQ 中, CQ = CP ⋅sin ∠CPQ = 3 (8 - 5 x ) = 24 - 3x ........................ (1 分)5 8 5 8∵PQ ⊥CE ∴CE=2CQ∴ y = 48 - 3x ( 5 < x < 64 ) ............................................................... (1 分,1 分)5 4 5(3)根据题意可得圆心 O 为 EC 与 BC 垂直平分线的交点,即直线 AM 与 PQ 的交点1 2 5在 Rt △OPM 中, PM = OP ⋅ cos ∠OPM = 1 .................................................. (1 分) ①点 P 在线段 MC 上时,BP = 4 +1 = 5∴ x = 8 BP = 8 ........................................................................ (1 分) 5∴AD =3 .................................................................................................................. (1 分) ②点 P 在线段 MB 上时BP = 4 -1 = 3 ∴ x = 8 BP =24 ....................................................................(1 分) 5 5∴AD = 1 ...............................................................................................................(1 分)5综合①②可得 AD = 3 或 15“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
上海市2017年中考二模语文试题(卷)与答案(参考)

上海市2017年中考二模语文试题(卷)与答案上海市2017年中考二模语文试题及答案【上海市2017年中考二模语文试题及答案】一、文言文(39分)(一)默写(15分)1、乱花渐欲好看眼,_____________________。
(《钞票塘湖春行》)2、_____________________,五十弦翻塞外声。
(《破阵子?为陈同甫赋壮词以寄之》)3、晨兴理荒秽,_____________________。
(《归园田居》)4、_____________________ ,水降而石出者。
(《醉翁亭记》)5、然往来视之,______________________ ___。
(《黔之驴》)(二)阅读下面的诗词,完成第6-7题(4分)山居秋暝空山新雨后,天气晚来秋。
明月松间照,清泉石上流。
竹喧归浣女,莲动下渔舟。
随意春芳歇,王孙自可留。
天净沙?秋思孤村降日残霞,轻烟老树寒鸦,一点飞鸿影下。
青山绿水,白草红叶黄花。
6、下列对两首诗的明白正确的一项是( )(2分)A.两首诗词都写了雨后山村的景象。
B.两首诗词中都有直截了当点名季节的诗句。
C.两首诗词都写到了秋天山水的特点D. 两首诗词都经过色彩来描绘景物。
7、两首诗词的作者借赏心悦目的秋景都表达了___________ ____________ _。
(2分)(三)阅读下文,完成第8-9题(8分)臣本布衣,躬耕于南阳,苟全性命于乱世,别求闻达于诸侯。
先帝别以臣卑鄙,猥自枉屈,三顾臣于草庐之中,咨臣以当世之事,由是感激,遂许先帝以驱驰。
后值倾覆,受任于败军之际,奉命于危难之间,尔来二十有一年矣。
先帝知臣慎重,故临崩寄臣以大事也。
受命以来,夙夜忧叹,恐委托别效,以伤先帝之明,故五月渡泸,深入别毛。
今南方已定,兵甲已脚,当奖率三军,北定中原,庶竭驽钝,攘除奸凶,兴复汉室,还于旧都。
此臣因此报先帝而忠陛下之职分也。
至于斟酌损益,进尽忠言,则攸之、棉、允之任也。
8、请按要求完成下面的基础积存表。
2017年上海市各区数学二模压轴题图文解析

本解析由华东师范大学出版社《挑战压轴题》作者马学斌老师独家提供。
可作学习材料,切勿做其他用途。
更多信息,欢迎关注“挑战压轴题”微信公众号(ti ao z han y azho u ti).《2017年上海市各区中考数学二模压轴题图文解析》目录2017 年上海市宝山区中考模拟第 24、25 题/ 22017 年上海市崇明区中考模拟第 24、25 题/ 62017 年上海市奉贤区中考模拟第 24、25 题/ 102017 年上海市虹口区中考模拟第 24、25 题/ 142017 年上海市黄浦区中考模拟第 24、25 题/ 182017 年上海市嘉定区中考模拟第 24、25 题/ 232017 年上海市静安区中考模拟第 24、25 题/ 272017 年上海市闵行区中考模拟第 24、25 题/ 312017 年上海市浦东新区中考模拟第 24、25 题/ 342017 年上海市普陀区中考模拟第 24、25 题/ 382017 年上海市松江区中考模拟第 24、25 题/ 422017 年上海市徐汇区中考模拟第 24、25 题/ 472017 年上海市杨浦区中考模拟第 24、25 题/ 522017 年上海市长宁区青浦区金山区中考模拟第 24、25 题/ 552017 年上海市宝山区中考模拟第 18 题/ 592017 年上海市崇明区中考模拟第 18 题/ 602017 年上海市奉贤区中考模拟第 18 题/ 612017 年上海市虹口区中考模拟第 18 题/ 622017 年上海市黄浦区中考模拟第 18 题/ 632017 年上海市嘉定区中考模拟第 18 题/ 642017 年上海市静安区中考模拟第 18 题/ 652017 年上海市闵行区中考模拟第 18 题/ 662017 年上海市浦东新区中考模拟第 18 题/ 672017 年上海市普陀区中考模拟第 18 题/ 682017 年上海市松江区中考模拟第 18 题/ 692017 年上海市徐汇区中考模拟第 18 题/ 702017 年上海市杨浦区中考模拟第 18 题/ 712017 年上海市长宁区青浦区金山区中考模拟第 18 题/ 722015 年上海市中考第 24、25 题/ 732016 年上海市中考第 24、25 题/ 77例2017年上海市宝山区中考模拟第24题如图 1,已知直线y x与x轴交于点B,与y轴交于点C,抛物线1 22 12y x b x2 2与x 轴交于A、B 两点(A 在B 的左侧),与y 轴交于点C.(1)求抛物线的解析式;(2)点M 是上述抛物线上一点,如果△ABM 和△ABC 相似,求点M 的坐标;(3)联结AC,求顶点D、E、F、G 在△ABC 各边上的矩形DEFG 面积最大时,写出该矩形在AB 边上的顶点的坐标.图 1动感体验请打开几何画板文件名“17 宝山 24”,拖动点D 在BC 上运动,可以体验到,当点D是BC 的中点时,矩形DEFG 的面积最大,最大值是△ABC 面积的一半.思路点拨1.第(2)题△ABM 和△ABC 相似,只存在这两个三角形全等的情形,此时M、C 关于抛物线的对称轴对称.2.第(3)题的矩形DEFG 存在两种情况.用二次函数表示矩形的面积,求二次函数的最大值,然后看看最大值时矩形顶点的位置具有什么特殊性.图文解析(1)由1y x 2 ,得B(4, 0),C(0,-2).2将点B(4, 0)代入y 1 x2 bx 2 ,得 8+4b-2=0.解得 3b .2 2所以抛物线的解析式为 1 2 3 2 1 ( 1)( 4)y x x x x .所以A(-1, 0).2 2 2(2)如图 2,由A(-1, 0)、B(4, 0)、C(0,-2),可得 tan∠CAO=tan∠BCO=2.又因为∠CAO 与∠ACO 互余,所以∠BCO 与∠ACO 互余.所以△ABC 是直角三角形.过点A、B 分别作x 轴的垂线,不可能存在点M.所以只存在∠AMB=90°的情况,此时点M 在x 轴的下方(如图 3 所示).图 2 图 32如图 3,如果△ABM 和△ABC 相似,那么△ABM ≌△BAC .所以点 M 与点 C 关于抛物线的对称轴对称,点 M 的坐标为(3,-2).(3)矩形 DEFG 有两种情况:1①如图 4,在 AB 边上的顶点有两个,坐标分别为(2, 0)和( ,0) .23②如图 5,在 AB 边上的顶点有一个,坐标为( ,0).2考点伸展第(3)题的解题思路是这样的:在 Rt △ABC 中,AB =5,高 CO =2.情形一,如图 4,F 、G 两点在 AB 上.设 DE =m ,DG =n .根据相似三角形对应高的比等于对应边的比,得 2 .所以 5(2 )n m nm . 2 52 所以 S =mn = 5 2 n n = 5 ( 1)2 5 (2 )n . 2 2所以当 n =1 时,矩形 DEFG 的面积最大.几何意义是 D 为 BC 的中点时,矩形的面积 最大,最大值是△ABC 面积的一半.情形二,如图 5,点 G 在 AB 上.同样的,设 DE =m ,DG =n .由 BD DG ,得 2 5.所以 2 5 n . m n m BE EA 22 55 所以 S =m n = (2 5 ) m m 2 = 1 ( 5)2 5 m .2 2所以当 m 5 时,矩形 DEFG 的面积最大.几何意义是 D 为 BC 的中点时,矩形的面 积最大,最大值也是△ABC 面积的一半.此时点 G 为 AB 的中点.图 4 图 53例2017年上海市宝山区中考模拟第25题如图 1,在△ABC 中,∠ACB 为直角,AB=10,∠A=30°,半径为 1 的动圆Q 的圆心从点C 出发,沿着CB 方向以 1 个单位长度/秒的速度匀速运动,同时动点P 从点B 出发,沿着BA 方向也以 1 个单位长度/秒的速度匀速运动,设运动时间为t 秒(0<t≤5),以P 为圆心、PB 为半径的⊙P 与AB、BC 的另一个交点分别为E、D,联结ED、EQ.(1)判断并证明ED 与BC 的位置关系,并求当点Q 与点D 重合时t 的值;(2)当⊙P 和AC 相交时,设CQ 为x,⊙P 被AC 解得的弦长为y,求y 关于x 的函数解析式,并求当⊙Q 过点B 时⊙P 被AC 截得的弦长;(3)若⊙P 与⊙Q 相交,写出t 的取值范围.图 1动感体验请打开几何画板文件名“17 宝山 25”,拖动Q 由C 向B 运动,可以体验到,⊙P 与⊙Q 的位置关系依次为外离、外切和相交.思路点拨1.第(1)题Q、D 重合时,根据CQ+BD=BC 列关于t 的方程.2.第(2)题⊙Q 过点B 时,CQ=5-1=4.3.第(3)题求⊙P 与⊙Q 相交,先求临界位置外切时t 的值.图文解析(1)如图 2,根据直径所对的圆周角是直角,可以知道ED⊥BC.在 Rt△ABC 中,AB=10,∠A=30°,所以BC=5.在 Rt△BDE 中,BE=2BP=2t,∠BED=30°,所以BD=t,DE= 3 t.如图 3,当点Q 与点D 重合时,BD+CQ=BC=5.所以 2t=5.解得t=2.5.图 2 图 3(2)如图 4,设⊙P 和AC 相交于M、N 两点.作PH⊥MN 于H,那么MH=NH.在 Rt△PAH 中,PA=10-t,∠A=30°,所以PH=12(10t)t.=5 12在 Rt△PMH 中,PM=PB=t,由勾股定理,得MH2=PM2-PH2= 2 (5 1 )2t t .2 于是得到y=MN=2MH=3t2 20t 100 .4如图 5,当⊙Q 过点B 时,CQ=x=4,此时MN=y=316 20 4 100 =2 7 .图 4 图 5<t≤5.(3)当⊙P与⊙Q相交时,t的取值范围是17974考点伸展第(3)题的解题过程分三步:第一步,罗列三要素.对于圆P,r P=t;对于圆Q,r Q=1;圆心距PQ 需要求一下.如图 6,作PF⊥BC 于F.在Rt△PFQ 中,由勾股定理,得PQ=( 3 )2 (5 3 )2t t .2 2第二步,列方程.如图 7,当⊙P 与⊙Q 外切时,r P+r Q=PQ.所以t 1( 3 t)2 (5 3t)2 .整理,得 2t2-17t+24=0.解得17 97t .2 2 4第三步,写结论.图 6 图 75例2017年上海市崇明区中考模拟第 24题 如图 1,已知抛物线 y =ax 2-2x +c 经过△ABC 的三个顶点,其中点 A (0, 1),点 B (9, 10),AC //x 轴. (1)求这条抛物线的解析式;(2)求 tan ∠ABC 的值;(3)若点 D 为抛物线的顶点,点 E 是直线 AC 上一点,当△CDE 与△ABC 相似时,求 点 E 的坐标.图 1动感体验请打开几何画板文件名“17 崇明 24”,拖动点 E 在点 C 左侧运动,可以体验到,△CDE 与△ABC 相似存在两种情况.思路点拨1.求 tan ∠ABC 的值,首先要将∠ABC 放在某个直角三角形中.作 AB 边上的高 CH 以 后,有两种解法:一种解法是∠BAC =45°为特殊值;另一种解法是一般性的,已知三角形 的三边,作高不设高,设 AH =m .2.探究△CDE 与△ABC 相似,首选的方法是寻找一组等角,然后按照对应边成比例分 两种情况列方程.图文解析 c1,(1)将 A (0, 1)、B (9, 10)两点分别代入 y =ax 2-2x +c ,得81a 18 c 10.1 3 解得 a = ,c =1.所以这条抛物线的解析式为 12 2 1y x x . 3(2)由于 AC //x 轴,抛物线的对称轴为 x =3,所以 C (6, 1).如图 2,作 BM ⊥AC ,垂足为 M .作 CH ⊥AB 于 H .由 A (0, 1)、B (9, 10),可知 AM =BM =9,所以∠BAC =45°,AB =9 2 .在 Rt △ACH 中,AC =6,所以 AH =CH =3 2 .在 Rt △BCH 中,BH =AB -AH =6 2 ,所以 tan ∠ABC = C H B H= 3 2 6 2 = 1 2 . 6(3)由 1 2 2 1 1 ( 3)2 2y x x x ,得顶点D 的坐标为(3,-2).3 3由C(6, 1)、D(3,-2),可知∠ACD=45°,CD=3 2 .当点E 在点C 左侧时,∠DCE=∠BAC.分两种情况讨论△CDE 与△ABC 相似:①当C E A B时,CE 9 2 .解得CE=9.此时E(-3, 1)(如图 3 所示).C D A C32 6②CE AC 时,CE 6 .解得CE=2.此时E(4, 1)(如图 4 所示).C D A B329 2图 2 图 3 图 4考点伸展第(2)题还有一般的解法:如图 2,△ABC 的三边长是确定的,那么作AB 边上的高CH,设AH=m,就可以求得AH,进而求得CH、BH 的长.由A(0, 1)、B(9, 10)、C(6, 1),可得AB=9 2 ,BC=3 10 ,AC=6.由CH2=CA2-AH2,CH2=CB2-BH2,得CA2-AH2=CB2-BH2.解方程62 m2 (3 10)2 (9 2 m)2 ,得m 3 2 .于是得到BH=6 2 ,CH=3 2 .7例 2017年上海市崇明区中考模拟第 25题如图,梯形 ABCD 中,AB //CD ,∠ABC =90°,AB =6,BC =8,tan D =2,点 E 是射线 CD 上一动点(不与点 C 重合),将△BCE 沿着 BE 进行翻折,点 C 的对应点记为点 F .(1)如图 1,当点 F 落在梯形 ABCD 的中位线 MN 上时,求 CE 的长;S (2)如图 2,当点 E 在线段 CD 上时,设 CE =x , △BFCS△E F C=y ,求 y 与 x 之间的函数关系式,并写出定义域;(3)如图 3,联结 AC ,线段 BF 与射线 CA 交于点 G ,当△CBG 是等腰三角形时,求 CE 的长.图 1 图 2 图 3动感体验请打开几何画板文件名“17 崇明 25”,拖动点 E 运动,可以体验到,等腰三角形 BCG 存在三种情况,每种情况的点 G 的位置都具有特殊性.思路点拨1.第(1)题点 F 到 AB 的距离等于 BF 的一半,得到∠FBA =30°.2.第(2)题△BFC 与△EFC 的面积比等于 BH 与 EH 的比,通过 Rt △BCH ∽Rt △CEH 得到 BH 与 EH 的比.3.第(3)题先求 CG 的长,再求 CE 的长.延长 BF 交 CD 的延长线于 K ,得到△KEF ∽△KBC .图文解析(1)如图 4,在 Rt △FNB 中,BN = 所以∠B F N =30°. 1 2 B C = 1 2B F ,所以∠FBA =30°.所以∠FBC =60°. 所以∠FBE =∠CBE =30°.= 8 3 3所以 C E =B C t a n 30°=83 3. 图 4(2)如图 5,设 BE 垂直平分 FC 于点 H ,那么∠CBH =∠ECH . 所以△CBH ∽△ECH .S 所以CBH△S△ECHBH = ( )2EH= 64 x 2 S .所以 y = BFC △S△EFC= 2S △CBHC2S △ECH = 64 x2. 定义域是 0<x ≤10.8图 5图 6(3)①如图 6,当 CG =CB =8 时,AG =2.CK CG 延长 BF 交 CD 的延长线于 K .由 4 ,得 CK =4AB =24.AB AG1 3在 Rt △KBC 中,BC =8,CK =24,所以 tan ∠K =.所以 sin ∠K = 10 10. 在 Rt △KEF 中,FE =CE =x ,EK =CK -CE =24-x .由 sin ∠K =F E E K = 10 10,得10 x 24 x 10.解得 x =CE = 8 10 83.②如图 7,当 GC =GB 时,点 G 在 BC 的垂直平分线上,此时四边形 ABCK 为矩形. 在 Rt △EKF 中,sin ∠EKF =B C B K = 8 10 = 4 5,FE =CE =x ,KE =CK -CE =6-x .所以 4 x6 x 5.解得 x =CE = 8 3.③如图 8,当 BG =BC =8 时,由于 BC =BF ,所以 F 、G 重合.此时 BE ⊥AC .由 tan ∠CEB =tan ∠ACB = 3 4 ,得B C C E 3 .所以 CE = 432 3.图 7 图 8考点伸展第(3)题的①、②两种情况,解 Rt △KEF ,可以用勾股定理列方程.9例 2017年上海市奉贤区中考模拟第 24题如图 1,在平面直角坐标系中,抛物线 y =-x 2+bx +c 经过点 A (3, 0)和点 B (2, 3),过点1 3A 的直线与 y 轴的负半轴相交于点 C ,且 tan ∠CAO =(1)求这条抛物线的表达式及对称轴;. (2)联结 AB 、BC ,求∠ABC 的正切值;(3)若点 D 在 x 轴下方的对称轴上,当 S △ABC =S △ADC 时,求点 D 的坐标.图 1动感体验请打开几何画板文件名“17 奉贤 24”,可以体验到,△ABC 是等腰直角三角形,B 、D 两点到直线 AC 的距离相等.思路点拨1.直觉告诉我们,△ABC 是直角三角形.2.第(3)题的意思可以表达为:B 、D 在直线 AC 的两侧,到直线 AC 的距离相等.于 是我们容易想到,平行线间的距离处处相等.图文解析(1)将 A (3, 0)、B (2, 3)两点分别代入 y =-x 2+bx +c ,得93b c 0,4 2b c 3.解得 b =2,c =3.所以 y =-x 2+2x +3.对称轴是直线 x =1.O C OA (2)由 t a n ∠C A O == 1 3,OA =3,得 OC =1.所以 C (0,-1). 由两点间的距离公式,得 AB 2=12+32=10,AC 2=32+12=10,BC 2=22+42=20. 所以∠BAC =90°,且 AB =AC .所以△ABC 是等腰直角三角形,tan ∠ABC =1.(3)因为△ABC 与△ADC 有公共底边 AC ,当 S △ABC =S △ADC 时,B 、D 到直线 AC 的距离相等.如图 2,因为点 B (2, 3)关于点 A (3, 0)的对称点为 E (4,-3),那么过点 E 作 AC 的平行线 与抛物线的对称轴的交点即为所求的点 D .由 A (3, 0)、C (0,-1)可得直线 AC 的解析式为1y x 1.3设直线 DE 的解析式为y x b ,代入点 E (4,-3),得 13 1b .3 3 10所以直线DE 的解析式为11 3 y x .当x=1 时,y=-4.3 3所以点D 的坐标为(1,-4).考点伸展第(2)题也可以构造 Rt△ABM 和 Rt△CAN(如图 3),用“边角边”证明△ABM≌△CAN,从而得到等腰直角三角形ABC.图 2 图 3第(3)题也可以这样思考:如图 4,过点B 与直线AC 平行的直线为y 1 x 7 ,与y 轴交于点F(0, 7)33 3.F、C 两点间的距离为710(1) .3 3把直线AC:y 1 x 向下平移1013 3个单位,得到直线113y x .3 3感谢网友上海交大昂立教育张春莹老师第(3)题的解法:如图 5,如果把BL、KD 分别看作△ABC 和△ADC 的底边,那么它们的高都是A、C 两点间的水平距离,当△ABC 与△ADC 的面积相等时,BL=KD.1 ),K(1,2 ).所以3 ( 1) ( 2) 由直线AC 的解析式可以求得L (y .2,D3 3 3 3解得y D=-4.所以D(1,-4).图 4 图 511例2017年上海市奉贤区中考模拟第25题如图 1,线段AB=4,以AB 为直径作半圆O,点C 为弧AB 的中点,点P 为直径AB 上一点,联结PC,过点C 作CD//AB,且CD=PC,过点D 作DE//PC,交射线PB 于点E,PD 与CE 相交于点Q.(1)若点P 与点A 重合,求BE 的长;PD=y,当点P 在线段AO 上时,求y 关于x 的函数关系式及定义域;C E(2)设P C=x,(3)当点Q 在半圆O 上时,求PC 的长.图 1 备用图动感体验请打开几何画板文件名“17 奉贤 25”,拖动点P 在AO 上运动,可以体验到,PD 与CE的比就是菱形的对角线的比,可以转化为PQ 与EQ 的比,进而转化为∠PEQ 的正切值.拖动点P 在OB 上运动,可以体验到,当点Q 落在圆上时,点Q 到AB 的距离等于圆的半径的一半.思路点拨1.四边形PCDE 是菱形,对角线互相垂直平分.2.第(2)题根据∠PEQ 和∠CEO 是同一个角,用正切值得到关系式.3.第(3)题画图的步骤是:点Q 在OC 的中垂线与圆的交点处,延长CQ 交AB 的延长线于点E,过点Q 作CE 的垂线得到点P、D.图文解析(1)如图 2,由CD//AB,DE//PC,得四边形PCDE 是平行四边形.又因为CD=PC,所以四边形PCDE 是菱形.在等腰直角三角形AOC 中,AC= 2 OA=2 2 .当点P 与点A 重合,PE=AC=2 2 .所以BE=AB-PE=4-2 2 .图 2 图 3(2)如图 3,在 Rt△CPO 中,PC=x,CO=2,所以PO=x 2 4 .所以EO=PE-PO=PC-PO=x x 2 4 .12因为PD 与CE 互相垂直平分于Q,所以y=P DC E=PQE Q =tan∠PEQ=tan∠CEO=C OE O.所以y2x x 42x x2 442.定义域是2≤x≤22 .(3)如图 4,作QH⊥AB 于H.因为菱形PCDE 的对边CD 与PE 间的距离保持不变,等于圆的半径CO=2,当点Q在半圆O 上时,QH=12OQ=1.所以∠QOH=30°.此时∠COQ=60°,△COQ 是等边三角形.所以∠DCE=30°.所以∠PCE=30°.在 Rt△COP 中,∠OCP=30°,CO=2,所以PC=C O= 2c o s3032=4 33.图 4 图 5考点伸展在本题情境下,当点P 从A 运动到B 的过程中,求点Q 运动过的路径长.因为点Q 是CE 的中点,所以点Q 的运动轨迹与点E 的运动轨迹平行,点Q 的路径长等于点E 路径长的一半.如图 2,当点P 与点A 重合时,AE=AC=2 2 .如图 5,当点P 与点B 重合时,BE=BC=2 2 .所以点E 运动的路径长为 4,点Q 运动的路径长为 2.13例2017年上海市虹口区中考模拟第24题如图 1,在平面直角坐标系中,抛物线1y x bx c 经过点A(-2, 0)和原点,点B 在4抛物线上且 tan∠BAO=12,抛物线的对称轴与x 轴相交于点P.(1)求抛物线的解析式,并直接写出点P 的坐标;(2)点C 为抛物线上一点,若四边形AOBC为等腰梯形且AO//BC,求点C 的坐标;(3)点D 在AB 上,若△ADP 与△ABO 相似,求点D 的坐标.图 1动感体验请打开几何画板文件名“17 虹口 24”,拖动点D 在AB 上运动,可以体验到,△ADP与△ABO 相似存在两种情况.点击屏幕左下角的按钮“第(2)题”,可以体验到,以A、O、B、C 为顶点的等腰梯形存在三种情况,其中AO//BC 时,点C 与点B 关于抛物线的对称轴对称.思路点拨1.已知二次函数的二次项系数和抛物线与x 轴的两个交点,可以直接写出交点式.2.等腰梯形AOBC 当AO//BC 时,C、B 两点关于抛物线的对称轴对称.3.分两种情况讨论△ADP 与△ABO 相似.由于∠A 是公共角,根据夹∠A 的两边对应成比例,分两种情况列方程,先求AD 的长,再求点D 的坐标.图文解析(1)因为抛物线1y x bx c 与x 轴交于点A(-2, 0)和原点,所以411 1y x(x2)x x.244 2抛物线的对称轴是直线x=-1,点P 的坐标为(-1, 0).1(2)作BH⊥x 轴于H.设点B 的坐标为(x, x(x 2)) .4由 tan∠BAO=B HA H=121,得AH=2BH.所以(x 2) 2x(x 2) .4解得x=2,或x=-2(B、A 重合,舍去).所以B(2, 2).若四边形AOBC 为等腰梯形且AO//BC,那么B、C 关于抛物线的对称轴x=-1 对称.所以点C 的坐标为(-4, 2).图 2 图 314(3)作DE⊥x 轴于E.在 Rt△ADE 中,已知 tan∠A=12,所以DE=55A D,AE=2 55 A D.由于△ADP 与△ABO 有公共角∠A,分两种情况讨论相似:①当AD AB 时,AD 2 5 .所以AD=5 .A P A O1 2此时DE=1,AE=2.所以点D 的坐标为(0, 1).②当A D A O时,A D 2.所以A D= 5 A P A B125 5.此时DE=15,AE=25.所以OE=OA-AE=858 1(,).5 5.所以点D的坐标为图 4 图 5考点伸展如果第(2)题改为以A、O、B、C 为顶点的四边形是等腰梯形,那么就要分三种情况:△AOB 的三边的垂直平分线都可以是等腰梯形的对称轴.第二种情况:如果OC//AB,那么点C 与点O 关于直线AB 的垂直平分线对称.点C 在直线1y x 上,设C(2m, m).2由CB=OA=2,得CB2=4.所以(2m-2)2+(m-2)2=4.解得m=254 2 ,或m=2(此时四边形AOCB 是平行四边形).所以C( , ).5 5第三种情况:如果AC//OB,那么点C 与点A 关于直线OB 的垂直平分线对称.点C 在直线y=x+2 上,设C(n, n+2).由CB=AO=2,得CB2=4.所以(n-2)2+n2=4.解得n=2,或n=0(舍去).所以C(2, 4).图 6 图 715例2017年上海市虹口区中考模拟第25题如图 1,在△ABC 中,AB=AC=5,cos B=45,点P 为边BC 上一动点,过点P 作射线PE 交射线BA 于点D,∠BPD=∠BAC.以点P 为圆心,PC 长为半径作⊙P 交射线PD 于点E,联结CE,设BD=x,CE=y.(1)当⊙P 与AB 相切时,求⊙P 的半径;(2)当点D 在BA 的延长线上时,求y 关于x 的函数解析式,并写出定义域;(3)如果⊙O 与⊙P 相交于点C、E,且⊙O 经过点B,当O P=54时,求AD 的长.图 1动感体验请打开几何画板文件名“17 虹口 25”,拖动点P 运动,可以体验到,△BPD 与△BAC 保持相似,PN 与BD 保持平行.观察度量值,可以体验到,OP=1.25 存在两种情况.思路点拨1.作圆P 的弦CE 对应的弦心距PN,把图形中与∠B 相等的角都标记出来.2.第(3)题的圆O 经过B、C、E 三点,事实上OP 与BD 是平行的.图文解析(1)如图 2,作AM⊥BC 于M,那么BM=CM.在 Rt△ABM 中,AB=5,cos B=B MA B=45,所以BM=4,sin B=35.如图 3,设⊙P 与AB 切于点H,那么 sin B=PHBP=35.所以r8 r 35=.解得r=3.图 2 图 3 图 4 (2)如图 4,由于∠B=∠B,∠BPD=∠BAC,所以△BPD∽△BAC.因为AB=AC,所以PB=PD.如图 5,设圆P 与BC 的另一个交点为F,因此所以F E//B D.所以∠E F C=∠B.P F P E.P B P D在△PBD 中,B P B A 5,所以5 5BP BD x .B D B C888在△EFC 中,由PC=PE=PF,可知∠FEC=90°,所以 sin∠EFC=C EC F3.516所以CF5 CE 5 y .所以 PC = 13 3 2 CF = 5 6y .由 BC =BP +PC =8,得5 x 5 y .整理,得 48 3 y x .定义域是 5<x < 64886545.(3)因为⊙O 经过 B 、C 、E 三点,所以圆心 O 是 BC 和 CE 的垂直平分线的交点. 如图 6,设 CE 的中点为 N ,那么 OP ⊥CE 于 N . 所以 OP //FE //BA .所以 cos ∠OPM =cos B = 4 5 .当 OP = 5 4时,MP =1.①如图 6,当 P 在 M 右侧时,BP =4+1=5.此时 BD = 所以 A D =B D -B A =8-5=3.8 5BP =8.②如图 7,当 P 在 M 左侧时,BP =4-1=3.此时 BD = 8 5 B P = 24 5.2 4 所以 AD =BA -BD = 5 = 51 5.图 5 图 6 图 7考点伸展第(2)题不证明 FE //BA 的话,可以证明∠CPN =∠B .如图 8,由于∠CPE =∠B +∠D =2∠B ,∠CPE =2∠CPN ,所以∠CPN =∠B .在 Rt △CPE 中, 1 2 3 5 C E =PC .所以 PC =5 6 C E = 5 6 5 y .所以 BP =8 y .6 在△BPD 中, 1 2 B D = 4 5 BP .所以 1 x 4 5 y .整理,得 48 3 (8 ) y x .2 5 6 5 4定义域中 x = 64 5的几何意义如图 9 所示.图 8 图 917例 2017年上海市黄浦区中考模拟第 24题如图 1,点 A 在函数 y4(x >0)的图像上,过点 A 作 x 轴和 y 轴的平行线分别交函 x数 y 1的图像于点 B 、C ,直线 BC 与坐标轴的交点为 D 、E . x(1)当点 C 的横坐标为 1 时,求点 B 的坐标;(2)试问:当点 A 在函数 y4(x >0)的图像上运动时,△ABC 的面积是否发生变 x 化?若不变,请求出△ABC 的面积;若变化,请说明理由;(3)试说明:当点 A 在函数 y4(x >0)的图像上运动时,线段 BD 与 CE 的长始终 x相等.图 1动感体验请打开几何画板文件名“17 黄浦 24”,拖动点 A 运动,可以体验到,△DBM 与△CEN 保持全等,MN 与 BC 保持平行.思路点拨1.设点 A 的横坐标为 m ,A 、C 两点的横坐标相等,A 、B 两点的纵坐标相等,用 m 表 示 A 、B 、C 三点的坐标和 AB 、AC 的长.2.证明 BD =CE ,因为四点共线,只要证明 B 、D 两点间的竖直距离等于 C 、E 两点间 的竖直距离就可以了.图文解析(1)当点 C 的横坐标为 1 时,C (1, 1),A (1, 4).由 1 x4 ,得x 1 .所以点 B 的坐标为(1 ,4) 4 4 . (2)△ABC 的面积为定值.计算如下:4 如图 2,设点 A 的坐标为(m , ) m 1 ,那么 C (m , ) mm 4 ,B ( , ). 4 m3m 所以 A B = 4 ,AC = 3 m .所以 S △ABC = 1 2 A B A C = 1 3 3 = m2 4 m9 8 . (3)如图 3,延长 AB 交 y 轴于 M ,延长 AC 交 x 轴于 N .在 Rt △DBM 中,tan ∠DBM =tan ∠ABC = A C A B = 3 3m = m 44 m 2 ,BM = m 4,所以DM=BM tan∠DBM=m44=m21m.所以DM=CN.18又因为 sin∠DBM=sin∠CEN,所以DB=CE.图 2 图 3考点伸展如图 4,第(2)题中,面积为定值的有:矩形AMON、△ABC、△BOM、△CON,所以△BOC 的面积也为定值.如图 5,联结MN,那么MN 与BC 保持平行,这是因为M B N C 1.M A N A 4还有一个有趣的结论,随着点A 的运动,直线MN 与双曲线y 1(x>0)保持相切.x直线MN 的解析式为44,与y1y x 联立方程组,消去y,得m m x214 4x.x m m2整理,得(2x-m)2=0.所以直线MN 与双曲线有一个交点,保持相切.感谢网友上海交大昂立教育张春莹老师提供的第(3)题的简练解法:如图 4,因为B D B M 1,C E C N 1,所以B D=C E.B C B A3C B C A 3图 4 图 519例2017年上海市黄浦区中考模拟第25题已知 Rt△ABC 斜边AB 上的D、E 两点满足∠DCE=45°.(1)如图 1,当AC=1,BC= 3 ,且点D 与点A 重合时,求线段BE 的长;(2)如图 2,当△ABC 是等腰直角三角形时,求证:AD2+BE2=DE2;(3)如图 3,当AC=3,BC=4 时,设AD=x,BE=y,求y 关于x 的函数关系式,并写出定义域.图 1 图 2 图 3动感体验请打开几何画板文件名“17 黄浦 25”,可以体验到,四边形CMEN 是正方形.点击屏幕左下方的按钮“第(2)题”,可以体验到,直角三角形DEF 的边FD=AD,FE=BE.点击按钮“第(3)题”,可以体验到,△CDP∽△ECQ.思路点拨1.第(1)题过点E 向两条直角边作垂线段,围成一个正方形,然后根据对应线段成比例求正方形的边长,再得到BE 的长等于正方形边长的 2 倍.2.第(2)题的目标是把AD、BE 和DE 围成一个直角三角形.经典的解法有翻折和旋转两种.图文解析(1)当AC=1,BC= 3 时,AB=2,∠B=30°.如图 4,作EM⊥BC 于M,作EN⊥AC 于N,那么四边形CMEN 是正方形.设正方形的边长为a.由EM BM,得a 3 a .AC BC 1 3解得 3 3a .2所以BE=2EM=3 3 .图 4【解法二】如图 4,因为1C B E MS C B△C B E21S C A E N C A△C B E2S B E,△C B ES E A△C B E,所以C B B E.C A E A.解得BE=3 3 .所以3B E12B E20(2)如图5,以CE 为对称轴,构造△CFE≌△CBE,那么FE=BE,∠CFE=∠B=45°.联结DF.由“边角边”证明△CFD≌△CAD,所以FD=AD,∠CFD=∠A=45°.所以△DEF 是直角三角形,FD2+FE2=DE2.所以AD2+BE2=DE2.【解法二】如图 6,绕点C 将△CBE 逆时针旋转 90°得到△CAG,那么AG=BE,CE =CG,∠CAG=∠B=45°.由“边角边”证明△CDG≌△CDE,所以DG=DE.在 Rt△GDA 中,AD2+AG2=DG2.所以AD2+BE2=DE2.图 5 图 6(3)如图 7,作CH⊥AB 于H.在 Rt△ABC 中,AC=3,BC=4,所以AB=5.于是可得CH 12 ,BH 16 ,9AH .5 5 5所以DH 9 x,16EH y .5 5如图 8,以H 为旋转中心,将点D 逆时针旋转 90°得到点P,将点E 顺时针旋转 90°得到点Q.于是可得△CDP∽△ECQ.由PD QC,得PD QE PC QC .PC QE所以2(9 x) 2(16 y ) 12 (9 x )12 (16 y )5 5 5 5 5 5.整理,得2860xy5x 21.157 定义域是0≤x≤15 7.当B、E 重合时x=.图 7 图 821考点伸展第(3)题解法多样,再介绍三种解法:如图 9,过点C 作AB 的平行线KL.构造等腰直角三角形KDD′和LEE′.由△CDE∽△KCD,△CDE∽△LEC,得△KCD∽△LEC.所以KC DK,即KC CL=LE DK .LE CL所以12 (9 )12 (16 ) 12 2 12 2x y55555 5.整理即可.如图 10,分别以CD、CE 为对称轴,作CH 的对应线段CK、CL,再围成正方形CKRL.在 Rt△DER 中,由DR2+ER2=DE2,得2 2129121 6(x)(y)(5x y)25555.整理即可.如图 11,类似第(2)题的第一种解法,在 Rt△A′B′T 中,A′B′=CB-CA=1,所以A′T=35 ,B′T= 4 5.在 Rt△DET 中,DE=5-x-y,TE=y 4,T D= 3x ,由勾股定理,得5 52 4 23 2(5x y ) (y ) (x ) .整理即可.5 5图 9 图 10 图 1122例2017年上海市嘉定区中考模拟第24题如图 1,在平面直角坐标系中,已知点A 的坐标为(3, 1),点B 的坐标为(6, 5),点C 的坐标为(0, 5),某二次函数的图像经过A、B、C 三点.(1)求这个二次函数的解析式;(2)假如点Q 在该二次函数图像的对称轴上,且△ACQ 是等腰三角形,请直接写出点Q 的坐标;(3)如果点P 在(1)中求出的二次函数的图像上,且 tan∠PCA=12,求∠PCB 的正弦值.图 1动感体验请打开几何画板文件名“17 嘉定 24”,可以体验到,当AD⊥AC,且AC=2AD 时,点D 的位置是确定的,射线CD 与抛物线的交点就是点P.思路点拨1.由B、C 两点的坐标可知抛物线的对称轴是直线x=3,再由点A 的坐标可知点A 就是抛物线的顶点,因此设顶点式比较简便.2.分三种情况讨论等腰三角形ACQ:AQ=AC,CQ=CA,QA=QC.3.第(3)题的解题策略是:根据 tan∠PCA=12,过点A 作AC 的垂线,在垂线上截取AD=12AC,那么点P 就是射线CD 与抛物线的交点,∠DCB 就是∠PCB.不用求点P的坐标,求点D 的坐标就好了.图文解析(1)由B(6, 5)、C(0, 5),可知抛物线的对称轴是直线x=3.由A(3, 1),可知点A 是抛物线的顶点.设二次函数的解析式为y=a(x-3)2+1,代入点B(6, 5),得 9a+1=5.4 4 4 8解得a .所以y (x 3)2 1x 2 x 5.9 9 9 33 3(2)点Q 的坐标为(3, 6),(3,-4),(3, 9)或(3, )8.(3)如图 2,绕着点A 将线段AC 的中点旋转 90°得到点D,那么射线CD 与抛物线的交点就是要求的点P.当点D 在CA 左侧时,射线CD 与抛物线没有交点.如图 3,当点D 在CA 右侧时,作DE⊥x 轴于E,那么∠DCE 就是∠PCB.过点A 作x 轴的平行线交y 轴于M,过点D 作DN⊥AM 于N.CM MA AC由△CMA∽△AND,得 2 .AN ND DA所以A N 1C M ,1 32N D M A .22 223在 Rt△CDE 中,CE=MA+AN=3+2=5,ED=CM-ND=3 5 4,2 2所以 tan∠DCE=E DC E=12.所以 sin∠DCE=55,即 sin∠PCB=55.图 2 图 3考点伸展第(2)题分三种情况讨论等腰三角形ACQ:①如图 4,当AQ=AC=5 时,以A 为圆心、以AC 为半径的圆与对称轴有两个交点,所以点Q 的坐标为(3, 6) 或(3,-4).②如图 5,当CQ=CA 时,点C 在AQ 的垂直平分线上,此时点Q 的坐标为(3, 9).③如图 6,当QA=QC 时,点Q 在AC 的垂直平分线上,此时1 4A C A Q.2 5所以AQ=58AC =2583 3.此时点Q 的坐标为(3, )8.图 4 图 5 图 6 24例2017年上海市嘉定区中考模拟第25题已知AB=8,⊙O 经过点A、B,以AB 为一边画平行四边形ABCD,另一边CD 经过点O(如图 1).以点B 为圆心,BC 长为半径画弧,交线段OC 于点E(点E 不与点O、点C 重合).(1)求证:OD=OE;(2)如果⊙O 的半径长为 5(如图 2),设OD=x,BC=y,求y 与x 的函数解析式,并写出它的定义域;(3)如果⊙O 的半径长为 5,联结AC,当BE⊥AC 时,求OD 的长.图 1 图 2 备用图动感体验请打开几何画板文件名“17 嘉定 25”,拖动点D 运动,可以体验到,四边形ABED 保持等腰梯形的形状,△BCE 保持等腰三角形的形状,垂足H 的位置保持不变,MH 的位置保持不变.双击按钮“AC⊥BE”,可以体验到,点C 恰好落在圆上,MH 等于EC 与AB 和的一半.思路点拨1.根据等腰梯形是轴对称图形,很容易知道点O 是DE 的中点.2.第(2)题中,等腰三角形BCE 的高BH 为定值,先用x 表示EC,再用勾股定理就可以表示BC 了.3.第(3)题如何利用BE⊥AC,常规的方法是过点C 作BE 的平行线得到直角三角形.图文解析(1)如图 3,因为四边形ABCD 是平行四边形,所以AD=BC.又因为BE=BC,所以AD=BE.所以四边形ABED 是等腰梯形.因为圆心O 在弦AB 的垂直平分线上,所以点O 是上底DE 的中点,即OD=OE.图 3 图 425例2017年上海市静安区中考模拟第24题如图 1,已知二次函数 1 2y x bx c 的图像与x 轴的正半轴交于点A(2, 0)和点B,2与y 轴交于点C,它的顶点为M,对称轴与x 轴相交于点N.(1)用b 的代数式表示点M 的坐标;(2)当 tan∠MAN=2 时,求此二次函数的解析式及∠ACB 的正切值.图 1动感体验请打开几何画板文件名“17 静安 24”,拖动点N 运动,观察∠MAN 的正切值的度量值,可以体验到,当 tan∠MAN=2 时,△OBC 是等腰直角三角形.思路点拨1.第(1)题分三步:根据抛物线的解析式写出对称轴x=b;代入点A 的坐标,用b表示c;求x=b 时y 的值,得到顶点的纵坐标.2.第(2)题先根据 tan∠MAN=2 求b 的值,确定点B、C 的坐标,再作BC 边上的高AH,解直角三角形ABH 和直角三角形ACH.图文解析(1)由 1 2y x bx c ,得抛物线的对称轴为直线x=b.2将点A(2, 0)代入 1 2y x bx c ,得-2+2b+c=0.所以c=2-2b.2当x=b 时, 1 2 2 2 1 2 2 2 1 ( 2)2y x bx b b b b .2 2 2所以抛物线的顶点M 的坐标可以表示为( , 1 ( 2)2 )b b .2MN(2)当 tan∠MAN=2 时, 2 ,即MN=2AN.AN解方程1 ( 2)2 2( 2)b b ,得b=6,或b=2(与A 重合,舍去).2此时抛物线的解析式为 1 2 6 10y x x ,A(2, 0),B(6, 0),C(0,-10).2所以AB=8,OB=OC=10.所以BC=10 2 ,∠B=45°.27作AH⊥BC 于H,那么AH=BH=4 2 .在 Rt△ACH 中,CH=BC-BH=6 2 ,所以 tan∠ACB=A HC H=23 .图 2考点伸展第(2)题上面的解法是利用“边角边”,作高先求高.也可以利用“边边边”,作高不设高.由A(2, 0),B(6, 0),C(0,-10),得AB=8,BC=10 2 ,AC=104 .设CH=m,那么BH=10 2 m.由AH2=AC2-CH2,AH2=AB2-BH2,得AC2-CH2=AB2-BH2.解方程( 104)2 m2 82 (10 2 m)2 ,得m CH 6 2 .所以AH2=AC2-CH2=( 104)2 (6 2)2 =32.所以AH=4 2 .28例2017年上海市静安区中考模拟第25题如图 1,已知⊙O 的半径OA 的长为 2,点B 是⊙O 上的动点,以AB 为半径的⊙A 与线段OB 相交于点C,AC 的延长线与⊙O 相交于点D.设线段AB 的长为x,线段OC 的长为y.(1)求y 关于x 的函数解析式,并写出定义域;(2)当四边形ABDO 是梯形时,求线段OC 的长.图 1图文解析(1)如图 1,因为OA=OB,所以∠OAB=∠B.因为AC=AB,所以∠ACB=∠B.所以∠OAB=∠ACB.所以△OAB∽△ACB.所以B O B A,即2xB A B Cx 2 y.整理,得 2 1 2y x .定义域是 0≤x≤2.x=2 的几何意义如图 2 所示.2图 1 图 2(2)梯形ABDO 存在两种情况:①如图 3,当AB//OD 时,A B C B,即x2y.整理,得(x+2)y=4.D O C O2y代入y 2 1 x2 ,得( 2)(2 1 2 ) 4x x .整理,得x2+2x-4=0.2 2解得x= 5 1,或x= 5 1(舍去).所以CO=y=2 1 2 =2 1 ( 5 1)2x= 5 1.事实上,此时点C 是线段OB 的黄2 2金分割点.。
2017年上海市松江区中考数学、语文、英语二模试卷及答案

2017 年上海市松江区中考数学二模试卷
参考答案与试题解析
一、选择题(共 6 小题,每小题 4 分,满分 24 分) 1.﹣8 的绝对值是( ) A.﹣8 B.8 C.﹣ D. 【考点】15:绝对值. 【分析】依据绝对值的性质解答即可. 【解答】解:﹣8 的绝对值是 8. 故选:B. 【点评】本题主要考查的是绝对值的性质,掌握绝对值的性质是解题的关键.
11.在一个袋中,装有除颜色外其它完全相同的 2 个红球、3 个白球和 4 个黑球,
从中随机摸出一个球,摸到的球是红球的概率是
.
【考点】X4:概率公式. 【分析】根据题意可得袋中共有 9 个球,其中有 2 个红球,再由概率公式可得答 案.
【解答】解:从中随机摸出【点评】此题主要考查了概率公式,关键是掌握概率=所求情况数与总情况数之 比.
4.对于二次函数 y=(x+1)2﹣3,下列说法正确的是( ) A.图象开口方向向下 B.图象与 y 轴的交点坐标是(0,﹣3) C.图象的顶点坐标为(1,﹣3) D.抛物线在 x>﹣1 的部分是上升的 【考点】H3:二次函数的性质. 【分析】根据二次函数的性质对各选项进行判断. 【解答】解:二次函数 y=(x+1)2﹣3 的图象的开口向上,顶点坐标为(﹣1, ﹣3),函数有最大值﹣3, ∵对称轴为直线 x=﹣1, ∴当 x>﹣1 时,y 随着 x 的增大而增大. 故选 D. 【点评】本题考查了二次函数的性质,能够顺利得到顶点式表达的函数的顶点坐 标、对称轴及开口方向是解答本题的关键.
2017年上海市徐汇区中考英语二模试卷(含答案)

2016学年第二学期徐汇区初三模拟考英语试卷2017.4(满分150分,考试时间100分钟)Part 2 Phonetics, Vocabulary and Grammar(第二部分语音、词汇和语法)II. Choose the best answer (选择最恰当的答案): (共20分)26. Which of the following words matches the sound / nju:/?A) now B) nor C) new D) near27. Brooklyn Beckham, ________ eldest child of the Beckhams, will sell his photo book in May, 2017.A) a B) an C) the D) /28. Nobody can stop a person with a strong will ________ realizing his dreams.A) of B) from C) with D) by29. If they don’t prepare ________ well for the interview, they may fail to get the offer.A) they B) them C) theirs D) themselves30. When Frank complained about the cold winter, Jane________ the sunny summer days in Australia.A) enjoys B) was enjoying C) has enjoyed D) will enjoy31. Joe can only take two of his family members into the studio and leave ________ waiting outside.A) the others B) others C) other D) the other32. ________ the end of yesterday, there had been more than 10 car accidents because of the typhoon.A) By B) From C) At D) To33. The old ________ enjoy the convenience of technologies because they don’t accept new things quickly.A) mustn’t B) needn’t C) can’t D) shouldn’t34. The panda ________ to get used to the new environment since he returned from America.A) learns B) is learning C) learned D) has learnt35. The audience were attracted by ________ the stories and the readings at the new program “Readers”.A) both B) neither C) either D) none36. After the operation on Grandma’s heart, she becomes much ________ at present.A) good B) well C) better D) best37. Every picture in the coloring book Secret Garden was not drawn by computer ________ all by hand.A) and B) so C) but D) or38. The year’s best picture was wrongly awarded to La La Land, which ________ never ________ before.A) would…happen B) was…happening C) has…happened D) had…happened39. A: ________ can we get the chance to join the party?B: To join this party, you have to dress up like a Superhero.A) Why B) What C) How D) Where40. Jenny is an independent girl and she is considering ________ a boarding school(寄宿学校).A) enter B) entering C) to enter D) entered41. Every Monday morning all the staff members have a meeting to report their recent work, ________?A) haven’t they B) don’t they C) aren’t they D) won’t they42. Alex had no interest in painting ________ he met a creative and patient art teacher one day.A) when B) because C) until D) if43. ________ good chance those teenagers were given to experience different cultures!A) How B) What C) What a D) What an44. A: The dishes you cooked tonight are really delicious.B: ________A) Of course! B) I’m glad you like them!C) That’s all right! D) Never mind!45. A: Excuse me, can I ask you some questions about the changes in Shanghai?B: ________A) Sure, go ahead! B) Congratulations!C) I am so sorry! D) Nice to meet you!III. Complete the following passage with the words or phrases in the box. Each can only be used once (将下列单词或词组填入空格。
2017年上海市松江区中考二模试卷(含答案)---2017.04.21

2017年松江区初中毕业生学业模拟考试初三英语2017.4 Part 2 Phonetics, Vocabulary and Grammar(第二部分语音、词汇和语法)II. Choose the best answer(选择最恰当的答案)(共20分)26. Which of the following underlined parts is different in pronunciation from the others?A. You just leave the door open.B. He passed the driving test out of luck.C. Don’t p ush me with your hand.D. It is not allowed to hunt for wild animals.27. All of us opened our mouths in ________ surprise at the unexpected news.A. aB. anC. theD. /28. Jerry goes to the swimming class ________ Saturday afternoons.A. inB. atC. onD. for29. The twins look really alike. It’s difficult for me to tell one ________ the other.A. fromB. betweenC. amongD. as30. My pen is out of ink. May I use ________?A. youB. yourC. yoursD. yourself31. I was hurt badly in the accident. Unluckily, Jane was ________ injured than me.A. more seriouslyB. the more seriouslyC. most seriouslyD. the most seriously32. Grandma sometime felt ________ after all her children left the village for the city.A. naturallyB. safelyC. sadlyD. lonely33. Alice is such a kind and helpful student that ________ in our school thinks well of her.A. nobodyB. everybodyC. anybodyD. somebody34. --________ times have you read the book Harry Potter and the Chamber of Secrets?-- Twice.A. How manyB. How oftenC. How soonD. How long35. Thanks for your offer of help, ________ I want to try it again by myself.A. orB. butC. andD. so36. Your eyesight may become poorer ________ you still spend much time on computer games.A. unlessB. thoughC. whileD. if37. Mum, you ________ pick me up at school this afternoon. I will take the bus home myself.A. mustn’tB. shouldn’tC. needn’tD. can’t38. Now Artificial Intelligence(人工智能)________ in many ways of our life.A. is usedB. was usedC. will be usedD. had been used39. I missed the train. It ________ the platform already when I got to the station.A. would leaveB. has leftC. is leavingD. had left40. I hope Mr. and Mrs. Smith ________ together with their lost son in no time.A. getB. will getC. would getD. have got41. All of the fans are looking forward to ________ their favorite star at the stadium.A. seeB. seeingC. be seenD. being seen42. With repeated efforts, I managed ________ the baby stop crying.A. makeB. to makeC. to makingD. making43. A couple of parents ________ invited to attend the teacher-parent meeting every month.A. isB. amC. areD. be44. -- I had a very good time at the party. Thanks for your invitation.--________A. Your are welcome.B. All right.C. Good luck to you!D. Not too bad!45. -- I think students should be allowed to take their cellphones to school.--________. It does no good. They may spend too long time on them.A. I think soB. That’s all rightC. No problemD. I don’t agreeIII. Complete the following passage with the words or phrases in the box. Each can only be used once (将下列单词或词组填入空格。
2017年上海市初三二模分类汇编2425题

2017.4 1徐汇2普陀3松江区4崇明5黄埔6闵行7静安8嘉定1徐汇区24、如图10,已知抛物线y= ax2 + 4(a工0)与x 轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点。
(1)当厶ABD的面积为4时,①求点D的坐标;②联结OD,点M是抛物线上的点,且/ MDO =/ BOD,求点M的坐标;(2)直线BD、AD分别与y轴交于点E、F,那么OE+OF的值是否变化,请说明理由。
ffl 1025、如图11,已知△ ABC中,AB= AC=5,BC=6,点0是边BC上的动点,以点O为圆心,OB为半径作圆O ,交AB边于点D,过点D作/ ODP=/ B,交边AC于点P,交圆O与点E。
设OB= x。
(1)当点P与点C重合时,求PD的长;(2)设AP-EP= y,求y关于x的解析式及定义域;(3)联结OP,当OP丄OD时,试判断以点P为圆心,PC为半径的圆P与圆O的位置关系。
2普陀区24.如图9,在平面直角坐标系xOy中,二次函数y X2 2x m ( m > 0 )的对称轴与比例系数为5 的反比例函数图像交于点A,与x轴交于点B,抛物线的图像与y轴交于点C,且OC 3OB .(1)求点A的坐标;(2)求直线AC的表达式;(3)点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、B、E、F为顶点的四边形是菱形,直接写出点F 的坐标.25•如图10,半圆0的直径AB = 10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上, EC丄CD , FD丄CD •(1)求证:EO OF ;(2)联结0C,如果△ ECO中有一个内角等于45°,求线段EF的长;(3)当动弦CD在弧AB上滑动时,设变量CE X,四边形CDFE面积为S,周长为I,问:S与I是否分别随着x的变化而变化?试用所学的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.3松江区已知抛物线y x2bx c与x轴交于点A和点B (3, 0),与y轴交于点C (0, 3) , P是线段BC上一点,过点P作PN// y轴交X轴于点N,交抛物线于点M .(1)求该抛物线的表达式;(2)如果点P的横坐标为2,点Q是第一象限抛物线上的一点,且△ 标;QMC和厶PMC的面积相等,求Q的坐3(3)如果PM -PN,求tan/CMN 的值.225 .如图,已知在Rt A ABC中,/3/ ACB=90 ° cosB=# , BC=3, P是射线AB上的一个动点,以P为圆心,PA为5半径的O P与射线AC的另一个交点为D,直线PD交直线BC于点E.(1)当PA=1时,求CE的长;(2)如果点P在边AB的上,当O P与以点C为圆心,CE为半径的O C内切时,求O P的半径;(3)设线段BE的中点为Q,射线PQ与O P相交于点F,点P在运动过程中,当PE// CF时,求AP的长.4崇明24如图,已知抛物线y ax22x c经过ABC的三个顶点,其中点A(0,1),点B(9,10) , AC II x轴.(1) 求这条抛物线的解析式;(2) 求tan ABC 的值;(3)若点D为抛物线的顶点,点E是直线AC上一点,当CDE与ABC相似时,求点E的坐标.x(第24题图)25 .如图,梯形 ABCD 中,AB II CD , ABC 90 , AB 6 , BC 8 , tanD 2,点 E 是射线 CD 上一动点 (不与点C 重合),将 BCE 沿着BE 进行翻折,点C 的对应点记为点 F .写出定义域;(1) 如图1,当点F 落在梯形ABCD 的中位线 MN 上时,求CE 的长; (2) 如图2,当点E 在线段CD 上时,设CESBFCS EFCy ,求y 与X 之间的函数关系式,并(3) 如图3,联结 AC ,线段BF 与射线CA 交于点G , CBG 是等腰三角形时,求 CE 的长.(第25题图1)(第25题图2) (第 25题图3) (第 25题备用图)4 15黄埔区如图,点A在函数y — x 0图像上,过点A作x轴和y轴的平行线分别交函数y —图像于点B、x x C,直线BC与坐标轴的交点为D、E.(1)当点C的横坐标为1时,求点B的坐标;4(2)试问:当点A在函数y — x 0图像上运动时,△ ABC的面积是否发生变化?若不变,请求出△ ABCx的面积;若变化,请说明理由;4(3)试说明:当点A在函数y x 0图像上运动时,线段BD与CE的长始终相等•x25 .已知:Rt △ ABC 斜边AB 上点D 、E ,满足/ DCE=45(1) 如图1,当AC=1 , BC=、一3,且点D 与A 重合时,求线段 B E 的长;(2) 如图2,当厶ABC 是等腰直角三角形时,求证: AD 2+BE 2=DE 2;⑶如图3,当AC=3,BC=4时,设AD=x ,BE=y ,求y 关于x 的函数关系式,并写出定义域(图3)(图1) (图2)A6闵行24•如图,在平面直角坐标系 xOy 中,抛物线y X 2 1 m x 3m 经过点A 1,0,且与y 轴相交于点B .(1) 求这条抛物线的表达式及点 B 的坐标;(2) 设点C 是所求抛物线上一点,线段 BC 与x 轴正半轴相交与点 D ,如果-BD -,求点C 的坐标;CD 5(3) 在(2)的条件下,联结 AC ,求 ABC 的度数.第24题图25•如图,在梯形ABCD 中,AD//BC , B 90 , AB 4 , BC 9 , AD 6。
2017年上海市各区数学二模压轴题——图文解析

2017 年上海市浦东新区中考模拟第 24、25 题 / 34 2017 年上海市普陀区中考模拟第 24、25 题 / 38 2017 年上海市松江区中考模拟第 24、25 题 / 42 2017 年上海市徐汇区中考模拟第 24、25 题 / 47 2017 年上海市杨浦区中考模拟第 24、25 题 / 52 2017 年上海市长宁区青浦区金山区中考模拟第 24、25 题 / 55 2017 年上海市宝山区中考模拟第 18 题 / 59 2017 年上海市崇明区中考模拟第 18 题 / 60 2017 年上海市奉贤区中考模拟第 18 题 / 61 2017 年上海市虹口区中考模拟第 18 题 / 62 2017 年上海市黄浦区中考模拟第 18 题 / 63 2017 年上海市嘉定区中考模拟第 18 题 / 64 2017 年上海市静安区中考模拟第 18 题 / 65 2017 年上海市闵行区中考模拟第 18 题 / 66 2017 年上海市浦东新区中考模拟第 18 题 / 67 2017 年上海市普陀区中考模拟第 18 题 / 68 2017 年上海市松江区中考模拟第 18 题 / 69 2017 年上海市徐汇区中考模拟第 18 题 / 70 2017 年上海市杨浦区中考模拟第 18 题 / 71 2017 年上海市长宁区青浦区金山区中考模拟第 18 题 / 72 2015 年上海市中考第 24、25 题 / 73 2016 年上海市中考第 24、25 题 / 77
心从点 C 出发,沿着 CB 方向以 1 个单位长度/秒的速度匀速运动,同时动点 P 从点 B 出发, 沿着 BA 方向也以 1 个单位长度/秒的速度匀速运动,设运动时间为 t 秒(0<t≤5) ,以 P 为 圆心、PB 为半径的⊙P 与 AB、BC 的另一个交点分别为 E、D,联结 ED、EQ. (1)判断并证明 ED 与 BC 的位置关系,并求当 点 Q 与点 D 重合时 t 的值; (2)当⊙P 和 AC 相交时,设 CQ 为 x,⊙P 被 AC 解得的弦长为 y,求 y 关于 x 的函数解析式,并求 当⊙Q 过点 B 时⊙P 被 AC 截得的弦长; (3)若⊙P 与⊙Q 相交,写出 t 的取值范围. 图1
2017初三数学二模汇编24题

(长宁青浦)24.(本题满分12分)已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.(1)求点A、B的坐标;等腰直角三角形时,求抛物线的解析式;(3)设半径为2的⊙P与直线OA交于M、N两点,已知MN=P(m,2)(m>0),求m的值.第24题图(杨浦)24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)如图,已知抛物线2y ax x c =-+的对称轴为直线x =1,与x 轴的一个交点为A (-1,0),顶点为B . 点C (5,m )在抛物线上,直线BC 交x 轴于点E . (1) 求抛物线的表达式及点E 的坐标; (2) 联结AB ,求∠B 的正切值;(3) 点G 为线段AC 上一点,过点G 作CB 的垂线交x 轴于点M (位于点E 右侧),当△CGM 与△ABE 相似时,求点M 的坐标.x yA BE C O (第24题图)(徐汇)24.(本题满分12分)如图10,已知抛物线)0(42≠+=a ax y 与x 轴交于点A 和点)0,2(B ,与y 轴交于点C ,点D 是抛物线在第一象限的点. (1)当ABD ∆的面积为4时,① 求点D 的坐标; (4分)② 联结OD ,点M 是该抛物线上的点,且BOD MDO ∠=∠,求点M 的坐标;(4分)(2)直线BD 、AD 分别交y 轴于点E 、F ,那么OF OE +的值是否变化,请说明理由. (4分)(松江)24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)已知抛物线c bx x y ++-=2与x 轴交于点A 和点B (3,0),与y 轴交于点C (0,3),P 是线段BC 上一点,过点P 作PN ∥y 轴交x 轴于点N ,交抛物线于点M . (1)求该抛物线的表达式;(2)如果点P 的横坐标为2,点Q 是第一象限抛物线上的一点,且△QMC 和△PMC 的面积相等,求点Q 的坐标; (3)如果PN PM 23=,求tan ∠CMN 的值.(第24题图)(普陀)24.(本题满分12分)如图9,在平面直角坐标系xOy 中,二次函数22y x x m =-+(m >0)的对称轴与比例系数为5的反比例函数图像交于点A ,与x 轴交于点B ,抛物线的图像与y 轴交于点C ,且3OC OB =. (1)求点A 的坐标;(2)求直线AC 的表达式;(3)点E 是直线AC 上一动点,点F 在x 轴上方的平面内,且使以A 、B 、E 、F 为顶点的四边形是菱形,直接写出点F 的坐标.图9(闵行)24.(本题共3小题,其中每小题各4分,满分12分)如图,在平面直角坐标系xOy中,抛物线2(1)3y x m x m=--+经过点A(1-,0),且与y轴相交于点B.(1)求这条抛物线的表达式及点B的坐标;(2)设点C是所求抛物线上一点,线段BC与x轴正半轴相交于点D.如果35BDCD=,求点C的坐标;(3)在(2)条件下,联结AB.求∠ABC的度数.O xy(第24题图)(静安)24.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知二次函数c bx x y ++-=221的图像与x 轴的正半轴相交于点A (2,0)和点B 、 与y 轴相交于点C ,它的顶点为M 、对称轴与x 轴相交于点N . (1) 用b 的代数式表示顶点M 的坐标; (2) 当tan ∠MAN =2时,求此二次函数的解析式 及∠ACB 的正切值.(嘉定)24.(本题满分12分,每小题4分)在平面直角坐标系xOy (如图7)中,已知点A 的坐标为(3,1),点B 的坐标为(6,5),点C 的坐标为(0,5);某二次函数的图像经过点A 、点B 与点C . (1)求这个二次函数的解析式;(2)假如点Q 在该函数图像的对称轴上,且△ACQ 是等腰三角形,直接..写出点Q 的坐标; (3)如果第一象限内的点P 在(1)中求出的二次函数 的图像上,且21tan =∠PCA ,求PCB ∠的正弦值.图7(黄浦)24.(本题满分12分)如图,点A 在函数()40y x x =>图像上,过点A 作x 轴和y 轴的平行线分别交函数xy 1=图像于点B 、C ,直线BC 与坐标轴的交点为D 、E .(1)当点C 的横坐标为1时,求点B 的坐标; (2)试问:当点A 在函数()40y x x=>图像上运动时,△ABC 的面积是否发生变化?若不变,请求出△ABC 的面积;若变化,请说明理由;(3)试说明:当点A 在函数()40y x x=>图像上运动时,线段BD 与CE 的长始终相等.E BCA DxyO图8(奉贤)24.(本题满分12分,每小题4分)如图8,在平面直角坐标系xOy 中,抛物线y 2经过点A (3,0)和点B (2,3),过点A 的直线与y 轴的负半轴相交于点C ,且(1)求这条抛物线的表达式及对称轴; (2)联结AB 、BC ,求∠ABC 的正切值;(3)若点D 在x 轴下方的对称轴上,当ABC S ∆= 求点D 的坐标.(崇明)24.(本题满分12分,其中每小题各4分)如图,已知抛物线22y ax x c =-+经过ABC ∆AC x ∥轴.(1)求这条抛物线的解析式;(2)求tan ABC ∠的值;(3)若点D 为抛物线的顶点,点E 是直线AC 上一点,当CDE ∆与ABC ∆相似时,求点E 的坐标.(第24题图)(宝山)24. (本题满分12分,每小题满分各4分)如图7,已知直线221-=x y 与x 轴交于点B ,与y 轴交于点C ,抛物线2212-+=bx x y 与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C.(1)求抛物线的解析式;(2)点M 是上述抛物线上一点,如果△ABM 和△ABC 相似,求点M 的坐标;(3)连接AC ,求顶点D 、E 、F 、G 在△ABC 各边上的矩形DEFC面积最大时,写出该矩形在AB 边上的顶点的坐标.图7(浦东)24.(本题满分12分,其中第(1)小题3分,第(2)小题4分,第(3)小题5分)已知抛物线23y ax bx =+-经过点(7,3)A -,与x 轴正半轴交于()(,0)6,0B m C m 、两点,与y 轴交于点D .(1)求m 的值;(2)求这条抛物线的表达式;(3)点P 在抛物线上,点Q 在x 轴上,当90PQD ∠=,且2PQ DQ =时,求点P Q 、的坐标。
上海市各区2017届中考物理二模试卷按考点分类汇编 凸透镜成像实验(含答案)

凸透镜成像实验宝山:24.“测定物质的密度”和“探究物质质量与体积的关系”实验需要测量的物理量____;多次测量的意义_____。
(均选填“相同”或“不同”)在“探究凸透镜成像规律”实验中,移动光屏找像时,要保持光具座上__________的位置不变,在移动过程中,眼睛要注意观察______上像,直到出现清晰的像为止。
相同;不同;发光物和凸透镜;光屏上的像。
奉贤:24.小朱同学在做“探究凸透镜成像的规律”实验中,首先依次将蜡烛、凸透镜和光屏放在水平放置的光具座上,接着调整它们的中心大致在__________,目的是___________________________。
若用凸透镜的焦距为10 厘米,蜡烛、凸透镜和光屏的位置如图13所示,此时光屏上的像一定是__________像;若保持凸透镜的位置不变,将蜡烛放置在36 厘米刻度处,则光屏在光具座的__________厘米刻度处时可得到一个清晰的像(选填:“79”、“81”或“85”)。
24、同一高度;为了使像清晰地成在光屏的中央;倒立;放大;实;85黄浦:24. 在图13中,凸透镜焦距为10厘米。
保持透镜位置不变,当蜡烛在15厘米刻度处时,为了在光屏的中心找到像,应调整光屏的________,并将光屏向_______(选填“远离透镜”或“靠近透镜”)方向移动,此时所成像的大小与物体相比是_______的。
若要得到烛焰的虚像,应使蜡烛与透镜间的距离________10厘米。
24. 高度;远离透镜;放大;小于嘉定:6.某凸透镜焦距为15厘米。
当物体沿主光轴从距透镜25厘米处向50厘米处移动时则()BA.像变大,像距变大 B.像变小,像距变小C.像先变小后变大,像距变大 D.像先变小后变大,像距变小普陀:6.某凸透镜的焦距为 10 厘米,物体经凸透镜能在离凸透镜 15 厘米的光屏上成像,所成的像是()B A.倒立、放大、实像 B.倒立、缩小、实像C.正立、放大、虚像 D.正立、缩小、实像青浦:7.物体沿主光轴逐步靠近凸透镜的过程中,在另一侧,光屏在距离凸透镜16厘米和24厘米处时分别能得到缩小和放大的像,则该透镜的焦距可能为()BA.8厘米 B.10厘米C.12厘米 D.16厘米松江:24.在焦距为5厘米、10厘米和20厘米的凸透镜中选择一个放置在图17所示的位置,将蜡烛、光屏分别置于光具座上透镜两侧,调整透镜和光屏的中心大致与烛焰的中心在(5)。
上海市杨浦区2017届中考数学二模试卷(解析版)

2017年上海市杨浦区中考数学二模试卷一、选择题(本大题共6小题,每小题4分,共24分)1.与平面直角坐标系中的点具有一一对应关系的是()A.实数B.有理数C.有序实数对D.有序有理数对2.化简(a≠0)的结果是()A.a B.﹣a C.﹣a D.a3.通常在频率分布直方图中,用每小组对应的小矩形的面积表示该小组的组频率.因此,频率分布直方图的纵轴表示()A.B.C.D.4.如果用A表示事件“若a>b,则a+c>b+c”,用P(A)表示“事件A发生的概率”,那么下列结论中正确的是()A.P(A)=1 B.P(A)=0 C.0<P(A)<1 D.P(A)>15.下列判断不正确的是()A.如果=,那么||=||B. +=+C.如果非零向量=k•(k≠0),那么∥D. +=06.下列四个命题中真命题是()A.矩形的对角线平分对角B.平行四边形的对角线相等C.梯形的对角线互相垂直D.菱形的对角线互相垂直平分二、填空题(本大题12小题,每小题4分,共48分)7.两个不相等的无理数,它们的乘积为有理数,这两个数可以是.8.化简:=.9.在实数范围内分解因式:a3﹣2a=.10.不等式组的解集是.11.方程的解是:x=.12.已知点A(2,﹣1)在反比例函数y=(k≠0)的图象上,那么当x>0时,y随x的增大而.13.如果将抛物线y=x2向左平移4个单位,再向下平移2个单位后,那么此时抛物线的表达式是.14.如表记录的是某班级女生在一次跳绳练习中跳绳的次数及相应的人数,则该班级女生本次练习中跳绳次数的平均数是次数40506070人数234115.如图,已知:△ABC中,∠C=90°,AC=40,BD平分∠ABC交AC于D,AD:DC=5:3,则D点到AB的距离是.16.正十二边形的中心角是度.17.如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A 处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB=米(用含α,β的代数式表示)18.如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为.三、解答题(本大题共7小题,共78分)19.(10分)计算:27﹣()﹣1÷3+80﹣(﹣2)2.20.(10分)解方程:.21.(10分)已知:如图,在△ABC中,∠ABC=45°,tanA=,AB=14,(1)求:△ABC的面积;(2)若以C为圆心的圆C与直线AB相切,以A为圆心的圆A与圆C相切,试求圆A的半径.22.(10分)水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x 千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.(1)当x的取值为时,在甲乙两家店所花钱一样多?(2)当x的取值为时,在乙店批发比较便宜?(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.23.(12分)已知:如图,四边形ABCD中,DB⊥BC,DB平分∠ADC,点E为边CD的中点,AB⊥BE.(1)求证:BD2=AD•DC;(2)连结AE,当BD=BC时,求证:ABCE为平行四边形.24.(12分)如图,已知抛物线y=ax2﹣x+c的对称轴为直线x=1,与x轴的一个交点为A(﹣1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.(1)求抛物线的表达式及点E的坐标;(2)联结AB,求∠B的正切值;(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.25.(14分)已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;(2)当扇形的半径长为5,且AC=6时,求线段DE的长;(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由.2017年上海市杨浦区中考数学二模试卷参考答案与试题解析一、选择题(本大题共6小题,每小题4分,共24分)1.与平面直角坐标系中的点具有一一对应关系的是()A.实数B.有理数C.有序实数对D.有序有理数对【考点】D1:点的坐标.【分析】根据平面直角坐标系与有序实数对的关系,可得答案.【解答】解:有序实数对与平面直角坐标系中的点具有一一对应关系,故选:C【点评】本题考查了点的坐标,平面直角坐标系与有序实数对是一一对应关系.2.化简(a≠0)的结果是()A.a B.﹣a C.﹣a D.a【考点】73:二次根式的性质与化简.【分析】二次根式有意义,则a<0,根据二次根式的性质解答.【解答】解:有意义,则a<0,﹣a>0,原式=﹣a.故选C.【点评】本题考查了二次根式的化简,注意二次根式的结果为非负数及题目的隐含条件a<0.二次根式的性质:=|a|.3.通常在频率分布直方图中,用每小组对应的小矩形的面积表示该小组的组频率.因此,频率分布直方图的纵轴表示()A.B.C.D.【考点】V8:频数(率)分布直方图.【分析】根据频率分布直方图中纵横坐标的意义,易得长方形的面积为长乘宽,即组距×频率/组距=频率;即答案.【解答】解:在频率直方图中纵坐标表示频率/组距,横坐标表示组距,则小长方形的高表示频率/组距,小长方形的长表示组距,则长方形的面积为长乘宽,即组距×频率/组距=频率;故选:B.【点评】本题考查频率直方图中横纵坐标表示的意义.4.如果用A表示事件“若a>b,则a+c>b+c”,用P(A)表示“事件A发生的概率”,那么下列结论中正确的是()A.P(A)=1 B.P(A)=0 C.0<P(A)<1 D.P(A)>1【考点】X3:概率的意义.【分析】根据不等式的基本性质1知事件A是必然事件,由概率的意义可得答案.【解答】解:若a>b,根据不等式的基本性质知a+c>b+c必然成立,∴事件A是必然事件,∴P(A)=1,故选:A.【点评】本题主要考查概率的意义及不等式的基本性质,熟练掌握必然事件的定义是解题的关键.5.下列判断不正确的是()A.如果=,那么||=||B. +=+C.如果非零向量=k•(k≠0),那么∥D. +=0【考点】LM:*平面向量.【分析】根据模的定义,可确定A正确;根据平面向量的交换律,可判定B正确,又由如果非零向量非零向量=k•(k≠0),那么∥或共线,可得C错误;利用相反向量的知识,可判定D正确.【解答】解:A、如果=,那么||=||,故此选项正确;B、+=+,故本选项正确;C、如果非零向量=k•(k≠0),那么∥或共线,故此选项错误;D、+=0,故此选项正确;故选:C.【点评】此题考查了平面向量的知识.注意理解平面向量有关的定义是关键.6.下列四个命题中真命题是()A.矩形的对角线平分对角B.平行四边形的对角线相等C.梯形的对角线互相垂直D.菱形的对角线互相垂直平分【考点】O1:命题与定理.【分析】由矩形、菱形、梯形和平行四边形对角线的性质作出判断,从而利用排除法得出答案.【解答】解:矩形的对角线不能平分对角,A错误;平行四边形的对角线平分,但不一定相等,B错误.梯形的对角线不一定互相垂直,C错误;根据菱形的性质,菱形的对角线互相垂直平分,D正确;故选:D.【点评】本题考查了命题与定理;熟记矩形、菱形、梯形和平行四边形对角线的性质是解决问题的关键.二、填空题(本大题12小题,每小题4分,共48分)7.两个不相等的无理数,它们的乘积为有理数,这两个数可以是和﹣(答案不唯一).【考点】26:无理数.【分析】由于无理数就是无限不循环小数.初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及0.1010010001…,等有这样规律的数.由此即可求解【解答】解:∵两个不相等的无理数,它们的乘积为有理数,这两个数可以是和﹣.(答案不唯一).【点评】此题主要考查了无理数的定义和性质,解题时注意无理数的积不一定是无理数.8.化简:=﹣.【考点】66:约分.【分析】先将分子与分母进行因式分解,再根据分式的基本性质,将分子与分母的公因式约去,即可求解.【解答】解:==﹣,故答案为:﹣.【点评】此题考查了约分,约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去.9.在实数范围内分解因式:a3﹣2a=a(a+)(a﹣).【考点】55:提公因式法与公式法的综合运用.【分析】先提取公因式a,再根据平方差公式进行二次分解即可求得答案.【解答】解:a3﹣2a=a(a2﹣2)=a(a+)(a﹣).故答案为:a(a+)(a﹣).【点评】本题考查了提公因式法,公式法分解因式.注意提取公因式后利用平方差公式进行二次分解,注意分解要彻底.10.不等式组的解集是4<x<5.【考点】CB:解一元一次不等式组.【分析】根据不等式分别求出x的取值范围,画出坐标轴,在其上表示出来x.【解答】解:不等式组可以化为:,在坐标轴上表示为:∴不等式组的解集为:4<x<5.【点评】本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x大于较小的数、小于较大的数,那么解集为x 介于两数之间.11.方程的解是:x=±2.【考点】AG:无理方程.【分析】对方程左右两边同时平方,可得x2+5=9,进而解可得x的值.【解答】解:根据题意,有,左右两边同时平方可得x2+5=9;解之,可得:x=±2.故答案为:±2.【点评】本题考查含二次根式的无理方程的解法,一般先化为一次或二次方程,再求解,答案注意根式有意义的条件.12.已知点A(2,﹣1)在反比例函数y=(k≠0)的图象上,那么当x>0时,y随x的增大而增大.【考点】G4:反比例函数的性质.【分析】首先将点A的坐标代入解析式求得k值,然后根据反比例函数的性质确定其增减性即可.【解答】解:∵点A(2,﹣1)在反比例函数y=(k≠0)的图象上,∴k=2×(﹣1)=﹣2<0,∴在每一象限内y随着x的增大而增大,故答案为:增大.【点评】本题考查了反比例函数的性质,解题的关键是利用待定系数法确定比例系数的值,难度不大.13.如果将抛物线y=x2向左平移4个单位,再向下平移2个单位后,那么此时抛物线的表达式是y=(x+4)2﹣2.【考点】H6:二次函数图象与几何变换.【分析】根据二次函数图象左加右减,上加下减的平移规律进行求解.【解答】解:函数y=x2向左平移4个单位,得:y=(x+4)2;再向下平移2个单位后,得:y=(x+4)2﹣2.【点评】主要考查的是函数图象的平移,用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.14.如表记录的是某班级女生在一次跳绳练习中跳绳的次数及相应的人数,则该班级女生本次练习中跳绳次数的平均数是54次数40506070人数2341【考点】W2:加权平均数.【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.【解答】解:该班级女生本次练习中跳绳次数的平均数是==54.故答案为54.【点评】本题考查的是加权平均数的求法.本题易出现的错误是求40,50,60,70这四个数的平均数,对平均数的理解不正确.15.如图,已知:△ABC中,∠C=90°,AC=40,BD平分∠ABC交AC于D,AD:DC=5:3,则D点到AB的距离是15.【考点】KF:角平分线的性质.【分析】先求出CD的长,再根据角平分线的性质即可得出结论.【解答】解:∵AC=40,AD:DC=5:3,∴CD=40×=15.∵BD平分∠BAC交AC于D,∴D点到AB的距离是15.故答案为:15.【点评】本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.16.正十二边形的中心角是30度.【考点】MM:正多边形和圆.【分析】根据正多边形的中心角的定义,可得正六边形的中心角是:360°÷12=30°.【解答】解:正十二边形的中心角是:360°÷12=30°.故答案为:30.【点评】此题考查了正多边形的中心角.此题比较简单,注意准确掌握定义是关键.17.如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A 处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB= +10米(用含α,β的代数式表示)【考点】TA:解直角三角形的应用﹣仰角俯角问题.【分析】作AH⊥CD交CD的延长线于H,根据正切的概念分别求出DC、DH,计算即可.【解答】解:作AH⊥CD交CD的延长线于H,在Rt△DBC中,tan∠DBC=,则AH=BC=,在Rt△AHD中,tan∠DAH=,DH=AH×tanβ=,∴AB=CH=CD+DH=+10,故答案为: +10.【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.18.如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为.【考点】PB:翻折变换(折叠问题);KW:等腰直角三角形.【分析】作DG⊥AE,先根据翻折变换的性质得到△DEF≌△BEF,再根据等腰三角形的性质及三角形外角的性质可得到∠AED=CDF,设CF=x,则DF=FB=4﹣x,根据勾股定理求出CF,可知tan∠AED=tanCDF,在Rt△ADG和Rt△EDG分别求出DG、EG,然后根据勾股定理即可得到结论.【解答】解:作DG⊥BE,∵△DEF是△BEF翻折而成,∴△DEF≌△BEF,∠B=∠EDF,∵△ABC是等腰直角三角形,∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠AED+45°,∴∠AED=∠CDF,∵CA=CB=4,CD=AD=2,设CF=x,∴DF=FB=4﹣x,∴在Rt△CDF中,由勾股定理得,CF2+CD2=DF2,即x2+4=(4﹣x)2,解得x=,∵∠A=45°,AD=2,∴AG=DG=,∵tan∠AED=tanCDF==,∴=,∴=,∴EG=,∴DE=BE==.故答案为:.【点评】本题考查的是图形翻折变换的性质、等腰直角三角形的性质、勾股定理、三角形外角的性质以及锐角三角函数的综合运用,涉及面较广,但难易适中.三、解答题(本大题共7小题,共78分)19.(10分)(2017•杨浦区二模)计算:27﹣()﹣1÷3+80﹣(﹣2)2.【考点】2C:实数的运算;2F:分数指数幂;6E:零指数幂;6F:负整数指数幂.【分析】原式利用分数指数幂,零指数幂、负整数指数幂法则,以及完全平方公式化简即可得到结果.【解答】解:原式=3﹣1+1﹣7+4=7﹣7.【点评】此题考查了实数的运算,分数指数幂,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.20.(10分)(2017•杨浦区二模)解方程:.【考点】B3:解分式方程.【分析】分式方程去分母转化为一元二次方程,求出一元二次方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:3(1﹣x)﹣(x+3)=(1﹣x)(x+3),整理得:x2﹣2x﹣3=0,即(x+1)(x﹣3)=0,解得:x1=﹣1,x1=3,经检验x1=﹣1,x1=3都是原方程的根.【点评】此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.21.(10分)(2017•杨浦区二模)已知:如图,在△ABC中,∠ABC=45°,tanA=,AB=14,(1)求:△ABC的面积;(2)若以C为圆心的圆C与直线AB相切,以A为圆心的圆A与圆C相切,试求圆A的半径.【考点】MJ:圆与圆的位置关系;MC:切线的性质;T7:解直角三角形.【分析】(1)过C作CD⊥AB于D,解直角三角形得到CD=,根据三角形的面积公式即可得到结论;(2)根据圆C与直线AB相切,得到⊙C的半径=,根据勾股定理得到AC==,设⊙A的半径为r,当圆A与圆C内切时,当圆A与圆C外切时即可得到结论.【解答】解:(1)过C作CD⊥AB于D,∵tanA==,∴AD=,∵∠ABC=45°,∴BD=CD,∵AB=14,∴+CD=15,∴CD=,∴△ABC的面积=AB•CD=×15×=;(2)∵以C为圆心的圆C与直线AB相切,∴⊙C的半径=,∵AD=,∴AC==,设⊙A的半径为r,当圆A与圆C内切时,r﹣=,∴r=,当圆A与圆C外切时,r+=,∴r=,综上所述:以A为圆心的圆A与圆C相切,圆A的半径为:或.【点评】本题考查了圆与圆的位置关系,勾股定理,三角形的面积的计算,解直角三角形,注意分类讨论思想的应用.22.(10分)(2017•杨浦区二模)水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.(1)当x的取值为20千克时,在甲乙两家店所花钱一样多?(2)当x的取值为0<x<20时,在乙店批发比较便宜?(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.【考点】FH:一次函数的应用.【分析】(1)利用两个函数图象的交点坐标即可解决问题.(2)根据y2的图象在y1的下方,观察图象即可解决问题.(3)设AB的解析式为y=kx+b,由题意OC的函数解析式为y=10x,可得方程组,解方程组即可.【解答】解:(1)由图象可知,x=20千克时,y1=y2,故答案为20千克.(2)由图象可知,0<x<20时,在乙店批发比较便宜.故答案为0<x<20.(3)设AB的解析式为y=kx+b,由题意OC的函数解析式为y=10x,∴,解得,∴射线AB的表达式y=5x+100(x≥10).【点评】本题考查一次函数的应用、二元一次方程组等知识,解题的关键是灵活运用一次函数的性质解决问题,学会利用图象解决实际问题,属于中考常考题型.23.(12分)(2017•杨浦区二模)已知:如图,四边形ABCD中,DB⊥BC,DB 平分∠ADC,点E为边CD的中点,AB⊥BE.(1)求证:BD2=AD•DC;(2)连结AE,当BD=BC时,求证:ABCE为平行四边形.【考点】S9:相似三角形的判定与性质;L6:平行四边形的判定.【分析】(1)根据直角三角形的性质得到BE=DE,由等腰三角形的性质得到∠DBE=∠BDE,根据角平分线的定义得到∠ADB=∠BDE,等量代换得到∠ADB=∠DBE,根据平行线的判定定理得到AD∥BE,根据相似三角形的性质即可得到结论;(2)由已知条件得到△BDC是等腰直角三角形,根据等腰直角三角形的性质得到∠BDC=45°,求得∠ADE=90°,推出四边形ADEB是矩形,根据矩形的性质得到AB=DE,AE=BD,于是得到结论.【解答】(1)证明:∵DB⊥BC,点E为边CD的中点,∴BE=DE,∴∠DBE=∠BDE,∵DB平分∠ADC,∴∠ADB=∠BDE,∴∠ADB=∠DBE,∴AD∥BE,∵AB⊥BE,∴∠A=∠ABE=90°,∵∠DBC=90°,∴∠A=∠DBC,∴△ADB∽△BDC,∴,∴BD2=AD•DC;(2)解:∵BD=BC,∴△BDC是等腰直角三角形,∴∠BDC=45°,∴∠ADE=90°,∴四边形ADEB是矩形,∴AB=DE,AE=BD,∴AB=CE,AE=BC,∴四边形ABCE为平行四边形.【点评】本题考查了相似三角形的判定和性质,等腰直角三角形的判定和性质,平行四边形的判定,平行线的判定和性质,正确的理解题意是解题的关键.24.(12分)(2017•杨浦区二模)如图,已知抛物线y=ax2﹣x+c的对称轴为直线x=1,与x轴的一个交点为A(﹣1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.(1)求抛物线的表达式及点E的坐标;(2)联结AB,求∠B的正切值;(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.【考点】HF:二次函数综合题.【分析】(1)由对称轴可求得a的值,再把A点坐标代入可求得c的值,则可求得抛物线表达式,则可求得B、C的坐标,由待定系数法可求得直线BC的解析式,可求得E点坐标;(2)由A、B、C三点的坐标可求得AB、AC和BC的长,可判定△ABC是以BC 为斜边的直角三角形,利用三角形的定义可求得答案;(3)设M(x,0),当∠GCM=∠BAE时,可知△AMC为等腰直角三角形,可求得M点的坐标;当∠CMG=∠BAE时,可证得△MEC∽△MCA,利用相似三角形的性质可求得x的值,可求得M点的坐标.【解答】解:(1)∵抛物线对称轴为x=1,∴﹣=1,解得a=,把A点坐标代入可得+1+c=0,解得c=﹣,∴抛物线表达式为y=x2﹣x﹣,∵y=x2﹣x﹣=(x﹣1)2﹣2,∴B(1,﹣2),把C(5,m)代入抛物线解析式可得m=﹣5﹣=6,∴C(5,6),设直线BC解析式为y=kx+b,把B、C坐标代入可得,解得,∴直线BC解析式为y=2x﹣4,令y=2可得2x﹣4=0,解得x=2,∴E(2,0);(2)∵A(﹣1,0),B(1,﹣2),C(5,6),∴AB=2,AC==6,BC==4,∴AB2+AC2=8+72=80=BC2,∴△ABC是以BC为斜边的直角三角形,∴tan∠B===3;(3)∵A(﹣1,0),B(1,﹣2),∴∠CAE=∠BAE=45°,∵GM⊥BC,∴∠CGM+∠GCB=∠GCB+∠ABC=90°,∴∠CGM=∠ABC,∴当△CGM与△ABE相似时有两种情况,设M(x,0),则C(x,2x﹣4),①当∠GCM=∠BAE=45°时,则∠AMC=90°,∴MC=AM,即2x﹣4=x+1,解得x=5,∴M(5,0);②当∠GMC=∠BAE=∠MAC=45°时,∵∠MEC=∠AEB=∠MCG,∴△MEC∽△MCA,∴=,即=,∴MC2=(x﹣2)(x+1),∵C(5,6),∴MC2=(x﹣5)2+62=x2﹣10x+61,∴(x﹣2)(x+1)=x2﹣10x+61,解得x=7,∴M(7,0);综上可知M点的坐标为(5,0)或(7,0).【点评】本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、勾股定理及其逆定理、三角函数的定义、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(1)中注意利用对称轴求得a的值是解题的关键,在(2)中证得△ABC为直角三角形是解题的关键,在(3)中利用相似三角形的性质得到关于M点坐标的方程是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强,难度适中.25.(14分)(2017•杨浦区二模)已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC 于点E,联结AE.(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;(2)当扇形的半径长为5,且AC=6时,求线段DE的长;(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由.【考点】MR:圆的综合题.【分析】(1)利用矩形的性质,只要证明△OAC是等边三角形,即可解决问题.(2)如图2中,作OH⊥AD于H.由△AOH∽△ADO,推出=,推出=,可得AD=,CD=AD﹣AC=,由DE∥OA,可得=,求出DE即可.(3)如图3中,结论:∠BCD的值是确定的.∠BCD=45°.连接AB、BC,由∠BCD=∠BAC+∠ABC,又∠BAC=∠BOC,∠ABC=∠AOC,即可推出∠BCD=∠BOC+∠AOC=(∠BCO+∠AOC)=×90°=45°.【解答】解:(1)如图1中,∵四边形ABCD是矩形,∴AD=EC,AC=CD,OC=CE,∠AOD=90°∴AC=OC=OA,∴△AOC是等边三角形,∴∠OAD=60°,∴∠ADO=90°﹣∠OAD=30°.(2)如图2中,作OH⊥AD于H.∵OA=OC,OH⊥AC,∴AH=HC=3,∵∠OAH=∠OAD,∠AHO=∠AOD,∴△AOH∽△ADO,∴=,∴=,∴AD=,∴CD=AD﹣AC=,∵DE⊥OD,∴∠EDO=90°,∴∠AOD+∠EDO=180°,∴DE∥OA,∴=,∴=,∴DE=.(3)如图3中,结论:∠BCD的值是确定的.∠BCD=45°.理由:连接AB、BC.∵∠BCD=∠BAC+∠ABC,又∵∠BAC=∠BOC,∠ABC=∠AOC,∴∠BCD=∠BOC+∠AOC=(∠BCO+∠AOC)=×90°=45°.【点评】本题考查圆综合题、矩形的性质、圆周角定理、平行线的判定和性质、相似三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考压轴题.。
上海市崇明县2017届中考数学二模试卷(含解析)

2017年上海市崇明县中考数学二模试卷一、选择题(本大题共6题,每题4分,满分24分)1.下列运算错误的是()A.x+2x=3x B.(x3)2=x6C.x2•x3=x5D.x8÷x4=x22.一次函数y=﹣3x+2的图象不经过()A.第一象限 B.第二象限 C.第三象限 D.第四象限3.在一次引体向上的测试中,小强等5位同学引体向上的次数分别为:6,8,9,8,9,那么关于这组数据的说法正确的是()A.平均数是8.5 B.中位数是8.5 C.众数是8.5 D.众数是8和94.商场将某种商品按原价的8折出售,仍可获利20元.已知这种商品的进价为140元,那么这种商品的原价是()A.160元B.180元C.200元D.220元5.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转()A.15° B.30° C.45° D.60°6.如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是()A.AB=AD B.AB=ED C.CD=AE D.EC=AD二、填空题(本大题共12题,每题4分,满分48分)7.16的平方根是.8.分解因式:x2﹣9x= .9.方程的解为.10.不等式组的解集是.11.已知函数f(x)=,那么自变量x的取值范围是.12.已知关于x的方程x2﹣4x+m=0有两个不相等的实数根,那么m的取值范围是.13.如果将抛物线y=3x2+5向右平移4个单位后,那么所得新抛物线的顶点坐标是.14.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷一次骰子,向上的一面出现的点数是素数的概率是.15.某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如图所示的两幅不完整的统计图,已知该校有1200名学生,估计全校最喜爱文学类图书的学生有人.16.一商场内的一座自动扶梯所在的斜边的坡度为i=1:2.4,小明站在自动扶梯上,当他沿着斜坡向上方向前进了13米时,他在铅垂方向升高了米.17.在Rt△ABC中,∠B=90°,BC=3,cosA=,以点A为圆心,为半径作圆,再以点C为圆心,2为半径作圆,那么这两圆的位置关系是.18.如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为.三、解答题(本大题共7题,满分78分)19.(10分)计算:27+(+1)2﹣()﹣2+.20.(10分)解方程组:.21.(10分)已知△ABC中,AD⊥BC,垂足为D,且AD=4,以AD为直径作圆O,交AB边于点G,交AC边于点F.如果点F恰好是的中点.(1)求CD的长度;(2)当BD=3时,求BG的长度.22.(10分)在一条笔直的公路上有AB两地,小明骑自行车从A地去B地,小刚骑电动车从B地去A地然后立即原路返回到B地,如图是两人离B地的距离y(千米)和行驶时间x (小时)之间的函数图象.请根据图象回答下列问题:(1)AB两地的距离是,小明行驶的速度是;(2)若两人间的距离不超过3千米时,能够用无线对讲机保持联系,那么小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系的x的取值范围是.23.(12分)如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,联结DE并延长至点F,使EF=AE,联结AF,CF,联结BE并延长交CF于点G.(1)求证:BC=DF;(2)若BD=2DC,求证:GF=2EG.24.(12分)如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.(1)求这条抛物线的解析式;(2)求tan∠ABC的值;(3)若点D为抛物线的顶点,点E是直线AC上一点,当△CDE与△ABC相似时,求点E的坐标.25.(14分)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=6,BC=8,tanD=2,点E是射线CD上一动点(不与点C重合),将△BCE沿着BE进行翻折,点C的对应点记为点F.(1)如图1,当点F落在梯形ABCD的中位线MN上时,求CE的长;(2)如图2,当点E在线段CD上时,设CE=x, =y,求y与x之间的函数关系式,并写出定义域;(3)如图3,联结AC,线段BF与射线CA交于点G,当△CBG是等腰三角形时,求CE的长.2017年上海市崇明县中考数学二模试卷参考答案与试题解析一、选择题(本大题共6题,每题4分,满分24分)1.下列运算错误的是()A.x+2x=3x B.(x3)2=x6C.x2•x3=x5D.x8÷x4=x2【考点】48:同底数幂的除法;35:合并同类项;46:同底数幂的乘法;47:幂的乘方与积的乘方.【分析】根据合并同类项的法则、幂的乘方、同底数幂相乘、同底数幂相除逐一判断可得.【解答】解:A、x+2x=3x,正确,不符合题意;B、(x3)2=x6,正确,不符合题意;C、x2•x3=x5,正确,不符合题意;D、x8÷x4=x4,原式错误,符合题意;故选:D.【点评】本题主要考查幂的运算和合并同类项法则,熟练掌握幂的运算法则和合并同类项的法则是解题的关键.2.一次函数y=﹣3x+2的图象不经过()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】F7:一次函数图象与系数的关系.【分析】由于k=﹣3<0,b=2>0,根据一次函数图象与系数的关系得到一次函数y=﹣3x+2的图象经过第二、四象限,与y轴的交点在x轴上方,即还要过第一象限.【解答】解:∵k=﹣3<0,∴一次函数y=﹣3x+2的图象经过第二、四象限,∵b=2>0,∴一次函数y=﹣3x+2的图象与y轴的交点在x轴上方,∴一次函数y=﹣3x+2的图象经过第一、二、四象限,即一次函数y=﹣3x+2的图象不经过第三象限.故选C.【点评】本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).3.在一次引体向上的测试中,小强等5位同学引体向上的次数分别为:6,8,9,8,9,那么关于这组数据的说法正确的是()A.平均数是8.5 B.中位数是8.5 C.众数是8.5 D.众数是8和9【考点】W5:众数;W1:算术平均数;W4:中位数.【分析】根据平均数、中位数、众数的定义判断各选项正误即可.【解答】解:A、平均数==8,此选项错误;B、6,8,8,9,9中位数是8,此选项错误;C、6,8,9,8,9众数是8和9,此选项错误;D、正确;故选D.【点评】本题主要考查了平均数、中位数以及众数的知识,解答本题的关键是熟练掌握各个知识点的定义以及计算公式,此题难度不大.4.商场将某种商品按原价的8折出售,仍可获利20元.已知这种商品的进价为140元,那么这种商品的原价是()A.160元B.180元C.200元D.220元【考点】8A:一元一次方程的应用.【分析】利用打折是在标价的基础之上,利润是在进价的基础上,进而得出等式求出即可.【解答】解:设原价为x元,根据题意可得:80%x=140+20,解得:x=200.所以该商品的原价为200元;故选:C.【点评】此题主要考查了一元一次方程的应用,根据题意列出方程是解决问题的关键.5.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转()A.15° B.30° C.45° D.60°【考点】J9:平行线的判定.【分析】先根据邻补角的定义得到∠3=60°,根据平行线的判定当b与a的夹角为45°时,b∥c,由此得到直线b绕点A逆时针旋转60°﹣45°=15°.【解答】解:∵∠1=120°,∴∠3=60°,∵∠2=45°,∴当∠3=∠2=45°时,b∥c,∴直线b绕点A逆时针旋转60°﹣45°=15°.故选:A.【点评】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.6.如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是()A.AB=AD B.AB=ED C.CD=AE D.EC=AD【考点】L9:菱形的判定;L5:平行四边形的性质.【分析】直接利用平行四边形的判定方法得出四边形DEAC是平行四边形,进而利用菱形的判定方法得出答案.【解答】解:添加AB=ED能使四边形ACDE成为菱形,理由:∵四边形ABCD是平行四边形,∴ABDC,∵AE=AB,∴AEDC,∴四边形DEAC是平行四边形,∵AB=DE,AE=AB,∴AE=DE,∴平行四边形DEAC是菱形.故选:B.【点评】此题主要考查了平行四边形的判定以及菱形的判定,正确掌握平行四边形的判定与性质是解题关键.二、填空题(本大题共12题,每题4分,满分48分)7.16的平方根是±4 .【考点】21:平方根.【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a 的平方根,由此即可解决问题.【解答】解:∵(±4)2=16,∴16的平方根是±4.故答案为:±4.【点评】本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.8.分解因式:x2﹣9x= x(x﹣9).【考点】51:因式分解的意义.【分析】首先确定多项式中的两项中的公因式为x,然后提取公因式即可.【解答】解:原式=x•x﹣9•x=x(x﹣9),故答案为:x(x﹣9).【点评】本题考查了提公因式法因式分解的知识,解题的关键是首先确定多项式各项的公因式,然后提取出来.9.方程的解为 3 .【考点】AG:无理方程.【分析】首先把方程两边分别平方,然后解一元二次方程即可求出x的值.【解答】解:两边平方得:2x+3=x2∴x2﹣2x﹣3=0,解方程得:x1=3,x2=﹣1,检验:当x1=3时,方程的左边=右边,所以x1=3为原方程的解,当x2=﹣1时,原方程的左边≠右边,所以x2=﹣1不是原方程的解.故答案为3.【点评】本题主要考查解无理方程,关键在于首先把方程的两边平方,注意最后要把x的值代入原方程进行检验.10.不等式组的解集是3<x<5 .【考点】CB:解一元一次不等式组.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式3x﹣15<0,得:x<5,解不等式3﹣x<0,得:x>3,∴不等式组的解集为:3<x<5,故答案为:3<x<5.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.11.已知函数f(x)=,那么自变量x的取值范围是.【考点】E4:函数自变量的取值范围.【分析】根据分式有意义的条件进行计算即可.【解答】解:∵2x+3≠0,∴;故答案为.【点评】本题考查了函数自变量的取值范围问题,掌握分式有意义的条件是解题的关键.12.已知关于x的方程x2﹣4x+m=0有两个不相等的实数根,那么m的取值范围是m<4 .【考点】AA:根的判别式.【分析】由方程有两个不相等的实数根结合根的判别式即可得出△=16﹣4m>0,解之即可得出结论.【解答】解:∵关于x的方程x2﹣4x+m=0有两个不相等的实数根,∴△=(﹣4)2﹣4m=16﹣4m>0,解得:m<4.故答案为:m<4.【点评】本题考查了根的判别式,熟练掌握“当△>0时,方程有两个不相等的实数根”是解题的关键.13.如果将抛物线y=3x2+5向右平移4个单位后,那么所得新抛物线的顶点坐标是(4,5).【考点】H6:二次函数图象与几何变换.【分析】根据抛物线的平移规律,可得答案.【解答】解:由将抛物线y=3x2+5向右平移4个单位,得y=3(x﹣4)2+5,顶点坐标为(4,5),故答案为:(4,5).【点评】本题考查了二次函数图象与几何变换,利用平移规律:左加右减,上加下减是解题关键.14.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷一次骰子,向上的一面出现的点数是素数的概率是.【考点】X4:概率公式.【分析】由一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,掷一次这枚骰子,向上的一面的点数为素数的有3种情况,直接利用概率公式求解即可求得答案.【解答】解:∵一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,掷一次这枚骰子,向上的一面的点数为素数的有3种情况,∴掷一次这枚骰子,向上的一面的点数为素数的概率是: =.故答案为:.【点评】此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.15.某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如图所示的两幅不完整的统计图,已知该校有1200名学生,估计全校最喜爱文学类图书的学生有480 人.【考点】VC:条形统计图;V5:用样本估计总体;VB:扇形统计图.【分析】首先求出样本中喜爱文学类图书所占百分比,进而估计全校最喜爱文学类图书的学生数.【解答】解:∵被调查的学生人数为:12÷20%=60(人),喜欢文学类的有24人,∴全校1200名学生中喜欢艺体类的有1200×=480人,故答案为:480.【点评】此题主要考查了条形统计图的应用以及扇形统计图应用、利用样本估计总体等知识,利用图形得出正确信息求出样本容量是解题关键.16.一商场内的一座自动扶梯所在的斜边的坡度为i=1:2.4,小明站在自动扶梯上,当他沿着斜坡向上方向前进了13米时,他在铅垂方向升高了 5 米.【考点】T9:解直角三角形的应用﹣坡度坡角问题.【分析】根据坡度,可以求得竖直高度与斜坡的比值,然后根据斜坡的长为13米,从而可以解答本题.【解答】解:∵自动扶梯所在的斜边的坡度为i=1:2.4,∴竖直高度与斜坡的比值为:1:2.6,设竖直高度为x米,x:13=1:2.6,解得,x=5,故答案为:5.【点评】本题考查解直角三角形的应用﹣坡度坡角问题,解答本题的关键是明确题意,明确什么是坡度,找出所求问题需要的条件.17.在Rt△ABC中,∠B=90°,BC=3,cosA=,以点A为圆心,为半径作圆,再以点C为圆心,2为半径作圆,那么这两圆的位置关系是外离.【考点】MJ:圆与圆的位置关系;T7:解直角三角形.【分析】先解直角三角形求出BC=5,再利用无理数的估算得到2+<5,然后利用圆与圆的位置关系进行判断.【解答】解:∵∠B=90°,∴cosA==,设AB=4x,BC=5x,∴BC=3x,∴3x=3,解得x=1,∴BC=5,∵<3,∴2+<5,∴以点A为圆心,为半径作圆和以点C为圆心,2为半径作圆相离.故答案为外离.【点评】本题考查了圆与圆的位置关系:两圆的圆心距为d、两圆半径分别为R、r,若两圆外离⇔d>R+r;两圆外切⇔d=R+r;两圆相交⇔R﹣r<d<R+r(R≥r);两圆内切⇔d=R﹣r (R>r);两圆内含⇔d<R﹣r(R>r).也考查了解直角三角形.18.如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为.【考点】R2:旋转的性质;KQ:勾股定理.【分析】根据勾股定理得到AB=5,根据旋转的性质得到AC1=AC=4,AB1=AB=5,∠CAC1=∠BAB1,推出AB′∥BC,根据平行线的性质得到∠B1AC=∠ACB=90°,根据相似三角形的性质得到AD=,CD=,根据勾股定理求得BB1=4,根据相似三角形的性质即可得到结论.【解答】解:∵∠C=90°,BC=3,AC=4,∴AB=5,∵将△ABC绕着点A旋转后得△AB1C1,∴AC1=AC=4,AB1=AB=5,∠CAC1=∠BAB1,∴∠AB1B=∠ABB1,∵BD平分∠ABC,∴∠ABB1=∠CBB1,∴∠AB1B=∠CBB1,∴AB1∥BC,∴∠B1AC=∠ACB=90°,∴△AB1D∽△CBD,∴==,∴AD=,CD=,∴B1D==,BD==,∴BB1=4,∵∠C1AC=∠B1AB,AC=AC1,AB=AB1,∴△ACC1∽△ABB1,∴=,∴CC1=,故答案为:.【点评】本题考查了旋转的性质,等腰三角形的判定和性质,平行线的判定和性质,勾股定理,正确的作出图形是解题的关键.三、解答题(本大题共7题,满分78分)19.(10分)(2017•崇明县二模)计算:27+(+1)2﹣()﹣2+.【考点】2C:实数的运算;2F:分数指数幂;6F:负整数指数幂;T5:特殊角的三角函数值.【分析】原式利用立方根定义,完全平方公式,负整数指数幂法则,以及特殊角的三角函数值计算即可得到结果.【解答】解:原式=3+4+2﹣4+﹣1=3+2.【点评】此题考查了实数的运算,负整数指数幂,分数指数幂,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.20.(10分)(2017•崇明县二模)解方程组:.【考点】AF:高次方程.【分析】组中第一个方程可因式分解为两个一元一次方程,这两个方程与组中的另一个方程组成新的方程组,解二元一次方程组得到原方程组的解.【解答】解:由①得:(x﹣4y)(x﹣y)=0,∴x﹣4y=0或x+y=0.原方程组可化为,.解,得;解,得,.∴原方程组的解为,【点评】本题考查了二元一次方程组的解法.解决本题的关键是把方程组中的二元二次方程变形为两个二元一次方程.21.(10分)(2017•崇明县二模)已知△ABC中,AD⊥BC,垂足为D,且AD=4,以AD为直径作圆O,交AB边于点G,交AC边于点F.如果点F恰好是的中点.(1)求CD的长度;(2)当BD=3时,求BG的长度.【考点】S9:相似三角形的判定与性质;KQ:勾股定理.【分析】(1)由点F恰好是的中点.可得出FO⊥AD,结合AD⊥BC,可得出OF∥CD,进而可得出.结合AD的长度即可求出CD的长度;(2)过点O作OH⊥AG,垂足为H,则△OAH∽△BAD,在Rt△ABD中可求出AB的长度,由垂径定理可得出AG=2AH,再根据相似三角形的性质可求出AH的长度,进而可得出AG、BG的长度,此题得解.【解答】解:(1)∵点F是的中点,OF是半径,∴OF⊥AD.∵AD⊥BC,∴OF∥CD,∴.∵OF=OA,AD=4,∴CD=4.(2)过点O作OH⊥AG,垂足为H,如图所示.∵在⊙O中,OH⊥AG,∴AG=2AH.∵∠ADB=90°,∴AD2+BD2=AB2.∵BD=3,AD=4,∴AB=5.∵∠OAH=∠BAD,∠ADB=∠AHO,∴△OAH∽△BAD,∴,∴AH=,AG=,BG=AB﹣AG=.【点评】本题考查了相似三角形的判定与性质、勾股定理、平行线的判定与性质以及垂径定理,解题的关键是:(1)根据“垂直于同一条直线的两条直线互相平行”找出OF∥CD;(2)利用相似三角形的性质以及勾股定理求出AH、AB的长度.22.(10分)(2017•崇明县二模)在一条笔直的公路上有AB两地,小明骑自行车从A地去B地,小刚骑电动车从B地去A地然后立即原路返回到B地,如图是两人离B地的距离y (千米)和行驶时间x(小时)之间的函数图象.请根据图象回答下列问题:(1)AB两地的距离是30km ,小明行驶的速度是15km/h ;(2)若两人间的距离不超过3千米时,能够用无线对讲机保持联系,那么小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系的x的取值范围是≤x≤2 .【考点】FH:一次函数的应用.【分析】(1)根据x=0时,甲距离B地30千米;小明行驶的速度=30÷2,由此即可解决问题.(2)根据两人间的距离不超过3千米时,能够用无线对讲机保持联系,那么小刚从A地原路返回到B地途中,则15x﹣30(x﹣1)=3,解方程即可.【解答】解:(1)x=0时,小明距离B地30km,所以,A、B两地的距离为30km;由图可知,小明行驶的速度:30÷2=15(km/h),小刚行驶的速度:30÷1=30(km/h),(2)设x小时,小明、小刚两人相距3km,若小刚从A地原路返回到B地途中,则15x﹣30(x﹣1)=3,解得x=,所以,当≤x≤2时,小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系.故答案为:(1)30km;15km/h;(2).【点评】本题考查一次函数的应用、相遇问题等知识,理解题意是解题的关键,考虑问题要全面,不能漏解,属于中考常考题型.23.(12分)(2017•崇明县二模)如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,联结DE并延长至点F,使EF=AE,联结AF,CF,联结BE并延长交CF于点G.(1)求证:BC=DF;(2)若BD=2DC,求证:GF=2EG.【考点】S9:相似三角形的判定与性质;KD:全等三角形的判定与性质;KK:等边三角形的性质.【分析】(1)根据等边三角形的性质得到AB=AC=BC,∠ABC=∠ACB=60°,由于CD=CE,得到△CDE是等边三角形,求得∠CDE=∠ABC=60°,CD=DE,推出四边形ABDF是平行四边形,根据平行四边形的性质得到AB=DF,即可得到结论;(2)根据等边三角形的性质得到∠CDE=∠DCE=60°,CE=CD=DE,根据全等三角形的性质得到∠CBE=∠DFC,由相似三角形的性质得到,即可得到结论.【解答】证明:(1)∵△ABC是等边三角形,∴AB=AC=BC,∠ABC=∠ACB=60°,∵CD=CE,∴△CDE是等边三角形,∴∠CDE=∠ABC=60°,CD=DE,∴DF∥AB,∵EF=AE,CD=DE,∴,∴AF∥BC,∴四边形ABDF是平行四边形,∴AB=DF,又∵AB=BC,∴BC=DF;(2)∵△CDE是等边三角形,∴∠CDE=∠DCE=60°,CE=CD=DE,又∵BC=DF,在△BCE和△FDC中,,∴△BCE≌△FDC,∴∠CBE=∠DFC,又∵∠BED=∠FEG,∴△BDE∽△FGE,∴,又∵CD=DE,BD=2CD,∴,∴GF=2EG.【点评】本题考查全等三角形的判定和性质、等边三角形的性质、相似三角形的判定和性质、平行四边形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,需要正确寻找全等三角形,属于中考常考题型.24.(12分)(2017•崇明县二模)如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.(1)求这条抛物线的解析式;(2)求tan∠ABC的值;(3)若点D为抛物线的顶点,点E是直线AC上一点,当△CDE与△ABC相似时,求点E的坐标.【考点】HF:二次函数综合题.【分析】(1)将点A和点B的坐标代入抛物线的解析式求得a、c的值即可;(2)过点B作BH⊥AC,垂足为H.过点C作CG⊥AB,垂足为点G.先证明△ABH和△ACG 均为等腰直角三角形,然后再求得AC的长,然后利用特殊锐角三角函数可求得BG、GC的长,最后依据锐角三角函数的定义求解即可;(3)过点D作DK⊥AC,垂足为K,先证明△DCK为等腰直角三角形,则∠DCK=∠BAC,当或时,△CDE与△ABC相似,然后可求得CE的长.【解答】解:(1)∵抛物线y=ax2﹣2x+c经过点A(0,1)和点B(9,10),∴,解得.∴这条抛物线的解析式为y=x2﹣2x+1.(2)过点B作BH⊥AC,垂足为H.∵AC∥x轴,A(0,1),B(9,10),∴H(9,1).∴BH=AH=9.又∵∠BHA=90°,∴△HAB是等腰直角三角形.∴∠HAB=45°.∵AC∥x轴,A(0,1),点C也在该抛物线上.∴C(6,1)过点C作CG⊥AB,垂足为点G.∵∠GAC=45°,∠AGC=90°,∴CG=AC•sin45°=3.∴AG=3.又∵在Rt△ABH中,AB==9.∴BG=9﹣3=6.∴在Rt△BCG中,tan∠ABC==.(3)如图2所示:过点D作DK⊥AC,垂足为K.∵点D是抛物线y=x2﹣2x+1的顶点,∴D(3,﹣2).∴K(3,1)∴CK=DK=3.又∵∠CKD=90°,∴△CDK是等腰直角三角形∴∠DCK=45°又∵∠BAC=45°,∴∠DCK=∠BAC.∴要使△CDE与△ABC相似时,则点E在点C的左侧.当时,则,∴EC=2,∴E(4,1).当时,则,∴EC=9.∴E(﹣3,1).综上所述,当△CDE与△ABC相似时,点E的坐标为E(4,1)或E(﹣3,1).【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、等腰直角三角形的性质和判定,锐角三角函数的定义,相似三角形的判定,找出△CDE与△ABC相似的条件是解题的关键.25.(14分)(2017•崇明县二模)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=6,BC=8,tanD=2,点E是射线CD上一动点(不与点C重合),将△BCE沿着BE进行翻折,点C的对应点记为点F.(1)如图1,当点F落在梯形ABCD的中位线MN上时,求CE的长;(2)如图2,当点E在线段CD上时,设CE=x, =y,求y与x之间的函数关系式,并写出定义域;(3)如图3,联结AC,线段BF与射线CA交于点G,当△CBG是等腰三角形时,求CE的长.【考点】LO:四边形综合题.【分析】(1)把BE与MN的交点记为点O,根据折叠的性质以及梯形中位线定理,可判定△EFO是等边三角形,即可得出∠FEB=60°,∠CEB=60°,即可得出在Rt△ECB中,;(2)把BE与CF的交点记为点P,根据BE是CF的垂直平分线,可得S△EFC=2S△EPC,S△BFC=2S,进而得到,再判定△ECP∽△CBP,可得,即可得出(0<x≤10);△BPC(3)当△CBG是等腰三角形时,分三种情况进行讨论:①GB=GC;②CB=CG;③BC=BG,分别根据折叠的性质以及直角三角形的边角关系,求得CE的长.【解答】解:(1)把BE与MN的交点记为点O,∵梯形ABCD中,AB∥CD,∠ABC=90°,∴∠C=90°,由翻折得∠CEB=∠FEB,∠EFB=∠C=90°,∵MN是梯形ABCD的中位线,∴MN∥AB∥CD,∴∠CEB=∠FOE,,∴∠FEB=∠FOE,∴FE=FO,∵∠EFB=90°,EO=BO,∴FO=EO,∴FE=FO=EO,∴△EFO是等边三角形,∴∠FEB=60°,∴∠CEB=60°,∴在Rt△ECB中,;(2)把BE与CF的交点记为点P,由翻折得,BE是CF的垂直平分线,即∠EPC=∠BPC=90°,,∴S△EFC=2S△EPC,S△BFC=2S△BPC,∴,∵∠ECP+∠BCP=90°,∠CBP+∠BCP=90°,∴∠ECP=∠CBP,又∵∠EPC=∠BPC=90°,∴△ECP∽△CBP,∴∴(0<x≤10);(3)当△CBG是等腰三角形时,存在三种情况:①GB=GC,延长BF交CD于点H,∵GB=GC,∴∠GBC=∠GCB,∵∠HCB=90°,∴∠CHB+∠GBC=90°,∵∠ABC=90°,∴∠CAB+∠GCB=90°,∴∠CHB=∠CAB,∴sin∠CHB=sin∠CAB=,∵∠ABC=90°,∴∠ACB+∠CAB=90°,∠ABG+∠GBC=90°,∴∠CAB=∠GBA,∴GA=GB,∴GA=GC,∵AB∥CD,∴,∴CH=AB=6,∵CE=x,∴EF=x,HE=6﹣x,∵∠HFE=90°,∴,②CB=CG,当CB=CG=8时,AG=10﹣8=2,∵AB∥CD,∴,∴CH=4AB=24,∵CE=x,∴EF=x,HE=24﹣x,∵∠HFE=∠HCB=90°,∴,解得,即;③BC=BG,当BC=BG时,F点与G点重合,由翻折可得,BE垂直平分线段GC,∵∠CBE+∠BCA=90°=∠CAB+∠BCA,∴∠CBE=∠CAB,∵∠ECB=∠CBA=90°,∴,∴,解得CE=,综上所述,CE的长为、、.【点评】本题属于四边形综合题,主要考查了梯形的性质,等边三角形的判定与性质,相似三角形的判定与性质,线段垂直平分线的性质以及平行线分线段成比例定理的综合应用,解决问题的关键是画出图形,并进行分类讨论.解题时注意:相似三角形的面积之比等于相似。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、(宝山)如图,已知直线22
1
-=
x y 与x 轴交于点B ,与y 轴交于点C ,抛物线22
12
-+=
bx x y 与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C . (1)求抛物线的解析式;
(2)点M 是上述抛物线上一点,如果△ABM 和△ABC 相似,求点M 的坐标;
(3)连接AC ,求顶点D 、E 、F 、G 在△ABC 各边上的矩形DEFG 面积最大时,写出该矩形在AB 边上的顶点的坐标.
2、(崇明)如图,已知抛物线c x ax y +-=22
经过△ABC 的三个顶点,其中点A (0,1),点B (9,10),AC ∥x 轴. (1)求这条抛物线的解析式; (2)求tan ∠ABC 的值;
(3)若点D 为抛物线的顶点,点E 是直线AC 上一点,当△CDE 与△ABC 相似时,求点E 的坐标.
3、(奉贤)如图,在平面直角坐标系xOy 中,抛物线c bx x y ++-=2
经过点A (3,0)和点B (2,3),过点A 的直线与y 轴的负半轴相交于点C ,且3
1tan =∠CAO . (1)求这条抛物线的表达式及对称轴; (2)联结AB 、BC ,求∠ABC 的正切值;
(3)若点D 在x 轴下方的对称轴上,当S △DBC=S △ADC 时,求点D 的坐标.
4、(虹口)如图,在平面直角坐标系xOy 中,抛物线c bx x y ++=2
4
1经过点A (-2,0)和原点,点B 在抛物线上且2
1
tan =
∠BAO ,抛物线的对称轴与x 轴相交于点P . (1)求抛物线的解析式,并直接写出点P 的坐标;
(2)点C 为抛物线上一点,若四边形AOBC 为等腰梯形且AO ∥BC ,求点C 的坐标; (3)点D 在AB 上,若△ADP 相似于△ABP ,求点D 的坐标.
5、(黄浦)如图,点A 在函数)0(4
>=x x
y 图像上,过点A 作x 轴和y 轴的平行线分别交函数x
y 1
=
图像于点B 、C ,直线BC 与坐标轴的交点为D 、E. (1)当点C 的横坐标为1时,求点B 的坐标; (2)试问:当点A 在函数)0(4
>=
x x
y 图像上运动时,△ABC 的面积是否发生变化?若不变,请求出△ABC 的面积;若变化,请说明理由; (3)试说明:当点A 在函数)0(4
>=x x
y 图像上运动时,线段BD 与CE 的长始终相等.
E
B
C A D
x
y
O
6、(嘉定)在平面直角坐标系xOy (如图7)中,已知点A 的坐标为)1,3(,点B 的坐标为),(56,点C 的坐标为)5,0(;某二次函数的图像经过点A 、点B 与点C . (1)求这个二次函数的解析式;
(2)假如点Q 在该函数图像的对称轴上,且△ACQ 是等腰三角形,直接写出点Q 的坐标; (3)如果第一象限内的点P 在(1)中求出的二次函数 的图像上,且2
1
tan =∠PCA ,求PCB ∠的正弦值.
图7
7、(静安)已知二次函数c bx x y ++-
=2
2
1的图像与x 轴的正半轴相交于点A (2,0)和点B 、与y 轴相交于点C ,它的顶点为M 、对称轴与x 轴相交于点N . (1) 用b 的代数式表示顶点M 的坐标; (2) 当tan ∠MAN=2时,求此二次函数的解析式 及∠ACB 的正切值.
8、(闵行)如图,在平面直角坐标系xOy 中, 抛物线m x m x y 3)1(2
+--=经过点)0,1(-A ,且与y 轴相交于点B .
(1)求这条抛物线的表达式及点B 的坐标;
(2)设点C 是所求抛物线上一点,线段BC 与x 轴正半轴相交于点D ,如果5
3
=CD BD ,求点C 的坐标;
(3)在(2)条件下,联结AC ,求ABC ∠的度数.
9、(浦东)已知:抛物线32
-+=bx ax y 经过点A (7,﹣3),与x 轴正半轴交于点B (m ,0)、C (6m 、0)两点,与y 轴交于点D . (1)求m 的值;
(2)求这条抛物线的表达式;
(3)点P 在抛物线上,点Q 在x 轴上,当∠PQD=90°且PQ=2DQ 时,求点P 、Q 的坐标.
10、(普陀)如图,在平面直角坐标系xOy 中,二次函数)0(22
>+-=m m x x y 的对称轴与比例系数为5的反比例函数图象交于点A ,与x 轴交于点B ,抛物线的图象与y 轴交于点C ,且OB OC 3=. (1)求点A 的坐标; (2)求直线AC 的表达式;
(3)点E 是直线AC 上一动点,点F 在x 轴上方的平面内,且使以A 、B 、E 、F 为顶点的四边形是菱形,直接写出点F 的坐标.
11、(青浦)已知OAB ∆在直角坐标系中的位置如图,点A 在第一象限,点B 在x 轴正半轴上,6OA OB ==,30AOB ∠=︒.
(1)求点A 、B 的坐标;
(2)开口向上的抛物线经过原点O 和点B ,设其顶点为E ,当OBE ∆为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的EP 与直线OA 交于M N 、两点,
已知MN ()2P m ,(0m >),求m 的值.
12、(松江)已知抛物线c bx x y ++-=2与x 轴交于点A 和点B (3,0),与y 轴交于点C (0,3),P 是线段BC 上一点,过点P 作PN ∥y 轴交x 轴于点N ,交抛物线于点M .
(1)求该抛物线的表达式;
(2)如果点P 的横坐标为2,点Q 是第一象限抛物线上的一点,且△QMC 和△PMC 的面积相等,求点Q 的坐标;
(3)如果PN PM 2
3=,求tan ∠CMN 的值.
13、(徐汇)如图,已知抛物线)0(42
≠+=a ax y 与x 轴交于点A 和点B (2,0),与y 轴交于点C ,点D 是抛物线在第一象限的点.
(1)当△ABD 的面积为4时,
①求点D 的坐标;
②联结OD ,点M 是抛物线上的点,且∠MDO=∠BOD ,求点M 的坐标;
(2)直线BD 、AD 分别与y 轴交于点E 、F ,那么OE+OF 的值是否变化,请说明理由.
14、(杨浦)如图,已知抛物线c x ax y +-=2
的对称轴为直线x=1,与x 轴的一个交点为A (﹣1,0),顶点为B .点C (5,m )在抛物线上,直线BC 交x 轴于点E .
(1)求抛物线的表达式及点E 的坐标;
(2)联结AB ,求∠B 的正切值;
(3)点G 为线段AC 上一点,过点G 作CB 的垂线交x 轴于点M (位于点E 右侧),当△CGM 与△ABE 相似时,求点M 的坐标.
15、(长宁金山)已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
2,P(m,2)(m>0),(3)设半径为2的⊙P与直线OA交于M、N两点,已知MN=3
求m的值.。
