流体力学大作业计算题答案-2
(完整版)流体力学习题解析
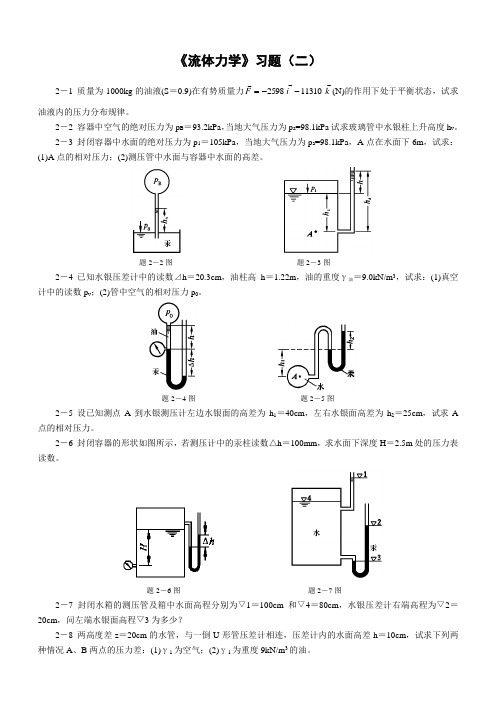
《流体力学》习题（二）2－1 质量为1000kg 的油液(S ＝0.9)在有势质量力k i F 113102598--=(N)的作用下处于平衡状态，试求油液内的压力分布规律。
2－2 容器中空气的绝对压力为p B ＝93.2kPa ，当地大气压力为p a =98.1kPa 试求玻璃管中水银柱上升高度h v 。
2－3 封闭容器中水面的绝对压力为p 1＝105kPa ，当地大气压力为p a =98.1kPa ，A 点在水面下6m ，试求：(1)A 点的相对压力；(2)测压管中水面与容器中水面的高差。
题2－2图 题2－3图 2－4 已知水银压差计中的读数⊿h ＝20.3cm ，油柱高h ＝1.22m ，油的重度γ油＝9.0kN/m 3，试求：(1)真空计中的读数p v ；(2)管中空气的相对压力p 0。
题2－4图 题2－5图 2－5 设已知测点A 到水银测压计左边水银面的高差为h 1＝40cm ，左右水银面高差为h 2＝25cm ，试求A 点的相对压力。
2－6 封闭容器的形状如图所示，若测压计中的汞柱读数△h ＝100mm ，求水面下深度H ＝2.5m 处的压力表读数。
题2－6图 题2－7图 2－7 封闭水箱的测压管及箱中水面高程分别为▽1＝100cm 和▽4＝80cm ，水银压差计右端高程为▽2＝20cm ，问左端水银面高程▽3为多少？2－8 两高度差z ＝20cm 的水管，与一倒U 形管压差计相连，压差计内的水面高差h ＝10cm ，试求下列两种情况A 、B 两点的压力差：(1)γ1为空气；(2)γ1为重度9kN/m 3的油。
题2－8图题2－9图2－9 有一半封闭容器，左边三格为水，右边一格为油(比重为0.9)。
试求A、B、C、D四点的相对压力。
2－10 一小封闭容器放在大封闭容器中，后者充满压缩空气。
测压表A、B的读数分别为8.28kPa和13.80kPa，已知当地大气压为100kPa，试求小容器内的绝对压力。
流体力学课后习题答案第二章
第二章 流体静力学2-1 密闭容器测压管液面高于容器内液面h=1.8m,液体密度为850kg/m3, 求液面压强。
解：08509.8 1.814994Pa p gh ρ==⨯⨯=2-2 密闭水箱，压力表测得压强为4900Pa,压力表中心比A 点高0.4米，A 点在液面下1.5m ，液面压强。
解：0()490010009.8(0.4 1.5) 49009800 1.15880PaM B A p p g h h ρ=+-=+⨯⨯-=-⨯=-2-3 水箱形状如图，底部有4个支座。
试求底面上的总压力和四个支座的支座反力，并讨论总压力和支座反力不相等的原因。
解：底面上总压力（内力，与容器内的反作用力平衡）()10009.81333352.8KN P ghA ρ==⨯⨯+⨯⨯=支座反力支座反力（合外力）3312()10009.8(31)274.4KN G g V V ρ=+=⨯⨯+=2-4盛满水的容器顶口装有活塞A ，直径d=0.4m ，容器底直径D=1.0m ，高h=1.8m 。
如活塞上加力为2520N(包括活塞自重)。
求容器底的压强和总压力。
解：压强2252010009.8 1.837.7kPa (0.4)/4G p gh A ρπ=+=+⨯⨯= 总压力 237.71/429.6KN P p A π=⋅=⨯⋅=2-5多管水银测压计用来测水箱中的表面压强。
图中高程单位为m ，试求水面的绝对压强。
解：对1-1等压面02(3.0 1.4)(2.5 1.4)p g p g ρρ+-=+-汞对3-3等压面 2(2.5 1.2)(2.3 1.2)a p g p g ρρ+-=+-汞将两式相加后整理0(2.3 1.2)(2.5 1.4)(2.5 1.2)(3.0 1.4)264.8kPap g g g g ρρρρ=-+-----=汞汞绝对压强 0.0264.8+98=362.8kPa abs a p p p =+=2-6水管A 、B 两点高差h 1=0.2m ，U 形管压差计中水银液面高差h 2=0.2m 。
流体力学课后答案
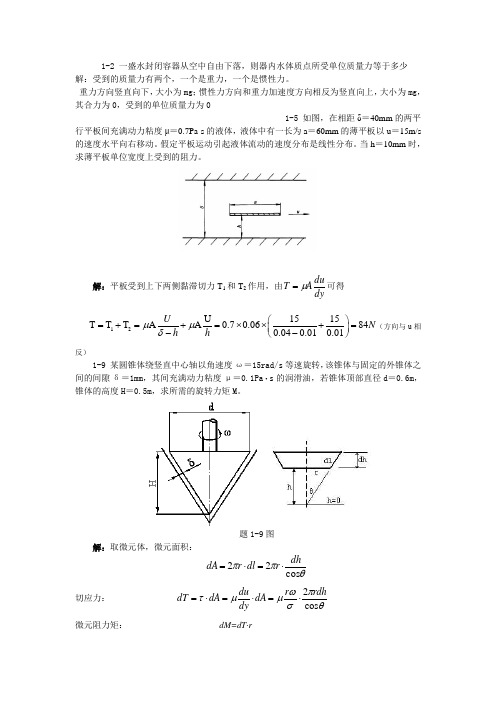
1-2 一盛水封闭容器从空中自由下落，则器内水体质点所受单位质量力等于多少 解：受到的质量力有两个，一个是重力，一个是惯性力。
重力方向竖直向下，大小为mg ；惯性力方向和重力加速度方向相反为竖直向上，大小为mg ，其合力为0，受到的单位质量力为01-5 如图，在相距δ＝40mm 的两平行平板间充满动力粘度μ＝0.7Pa·s 的液体，液体中有一长为a ＝60mm 的薄平板以u ＝15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h ＝10mm 时，求薄平板单位宽度上受到的阻力。
解：平板受到上下两侧黏滞切力T 1和T 2作用，由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭（方向与u 相反）1-9 某圆锥体绕竖直中心轴以角速度ω＝15rad/s 等速旋转，该锥体与固定的外锥体之间的间隙δ＝1mm ，其间充满动力粘度μ＝0.1Pa ·s 的润滑油，若锥体顶部直径d ＝0.6m ，锥体的高度H ＝0.5m ，求所需的旋转力矩M 。
题1-9图解：取微元体，微元面积：θππcos 22dhr dl r dA ⋅=⋅= 切应力： θπσωμμτcos 2rdh r dA dy du dA dT ⋅=⋅=⋅= 微元阻力矩： dM=dT·r阻力矩：2-12 圆柱形容器的半径cm R 15=，高cm H 50=，盛水深cm h 30=，若容器以等角速度ω绕z 轴旋转，试求ω最大为多少时不致使水从容器中溢出。
解：因旋转抛物体的体积等于同底同高圆柱体体积的一半，因此，当容器旋转使水上升到最高时，旋转抛物体自由液面的顶点距容器顶部h’= 2(H-h)= 40cm等角速度旋转直立容器中液体压强的分布规律为0222p gz r p +⎪⎪⎭⎫⎝⎛-=ωρ对于液面，p=p 0 , 则gr z 222ω=，可得出22r gz =ω 将z=h ’,r=R 代入上式得s R gh /671.1815.04.08.92'222=⨯⨯==ω2-13装满油的圆柱形容器，直径cm D 80=，油的密度3/801m kg =ρ，顶盖中心点装有真空表，表的读数为Pa 4900，试求：（1）容器静止时，作用于顶盖上总压力的大小和方向；（2）容器以等角速度120-=s ω旋转时，真空表的读数值不变，作用于顶盖上总压力的大小和方向。
流体力学计算题（有答案）
《流体力学》计算题及答案。
2、当压强增加4×104Pa 时，某种液体的密度增长0.015%，求该液体的压缩系数。
解：0=+=⇒=dV Vd dM V M ρρρρρd dV V -=N m dp d dp V dV p /1075.3104%015.011294-⨯=⨯==-=ρρβ3、将一根长度L 为800mm ，直径d 为45mm 的圆轴水平放置于内径D 为50mm 的圆管中央，圆柱体与圆管的间隙充满密度为925kg/m 3、运动粘度s m /105.624-⨯=ν的油液。
求将圆柱体以0.8m/s 的速度作水平移动时所需的拉力F 为多少牛顿？（间隙中的速度分布可认为是线性分布）。
答案： N F 8.21=4、(将一根长度L 为1m ，直径d 为200mm 的圆柱体水平放置于内径D 为206mm 的圆管中央，圆柱体与圆管的间隙充满密度为920kg/m 3的油液。
测得将圆柱体以1m/s 的速度作水平移动时的拉力F 为108牛顿，求该油液的运动粘度（间隙中的速度分布可认为是线性分布）。
答案：运动粘度s m /106.524-⨯=ν6、液体通过装置DV 的阻力损失由倒置U 形差压计测量。
液体的密度为1500kg/m 3。
差压计中的指示液体使用密度为750 kg/m 3的油。
求如图所示标定值时，A 和B 的压强水头变化。
解：设差压计中的工作液体密度为Pam8、已知速度场⎪⎩⎪⎨⎧-=-=)/()/(2222x y ax x y ay u υ，其中a 为常数。
（１）试求流线方程（２）判断流动是否无旋，若无旋则求速度势ϕ。
答案：（１）流线方程C y x =-22（２）因为22y x x y u +=∂∂-∂∂υ除了０点外，022≠+=∂∂-∂∂y x xy u υ，所以是有旋的，不存在速度势。
9、在平面不可压缩流动中，已知速度势函数233xy x -=ϕ，求相应的流函数。
答案：10、已知某不可压缩流体平面流动的速度分布规律为：⎩⎨⎧--=-+=yxy yx x u 22422υ判断说明该流动是否连续？是否无旋？并求出流函数。
西工大-计算流体力学大作业
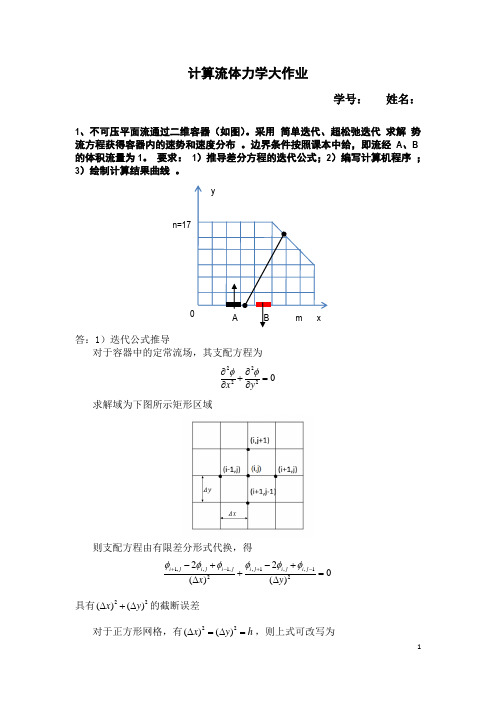
计算流体力学大作业学号： 姓名：1、不可压平面流通过二维容器（如图）。
采用 简单迭代、超松弛迭代 求解 势流方程获得容器内的速势和速度分布 。
边界条件按照课本中给，即流经 A 、B 的体积流量为1。
要求： 1）推导差分方程的迭代公式；2）编写计算机程序 ； 3）绘制计算结果曲线 。
答：1）迭代公式推导对于容器中的定常流场，其支配方程为22220x yφφ∂∂+=∂∂ 求解域为下图所示矩形区域则支配方程由有限差分形式代换，得1,,1,,1,,122220()()i j i j i ji j i j i j x y φφφφφφ+-+--+-++=∆∆具有22()()x y ∆+∆的截断误差对于正方形网格，有22()()x y h ∆=∆=，则上式可改写为n=17,1,1,,1,11()4i j i j i j i j i j φφφφφ+-+-=+++若采用简单迭代公式，即Liebmann 公式，则有(1)()(1)()(1),1,1,,1,11()4n n n n n i j i j i j i j i j φφφφφ++++-+-=+++若采用超松弛迭代，即SOR 公式，则有(1)()()(1)()(1),,1,1,,1,1(1)()4n n n n n n i j i j i j i j i j i j ωφωφφφφφ++++-+-=-++++其中松弛因子12ω<<。
ω最佳值opt ω为opt ω=式中cos(/)cos(/)m n αππ=+，m ，n 分别表示在网格系统中垂直线和水平线的总数。
2）计算机程序本程序采用C 语言编写。
程序源代码如下： #include<stdio.h> #include<math.h> void main() { int m=25,n=17,ilast[17],jlast[25]; int step1,step2; double h=0.25; double psi_j[25][17],psiprv_j,vel_j[25][17],velx_j[25][17],vely_j[25][17]; double psi_c[25][17],psiprv_c,vel_c[25][17],velx_c[25][17],vely_c[25][17]; double Pi,Alpha,Omega,Error; int i,j; for(i=0;i<17;i++) jlast[i]=17; for(i=17;i<m;i++) jlast[i]=17-(i-16); for(j=0;j<9;j++) ilast[j]=25; for(j=9;j<n;j++) ilast[j]=25-(j-8); //数据初始化 for(j=0;j<n;j++) { psi_j[0][j]=1.0; psi_c[0][j]=1.0;}for(i=1;i<m;i++){psi_j[i][jlast[i]-1]=1.0;psi_c[i][jlast[i]-1]=1.0; }for(j=0;j<8;j++){psi_j[m-1][j]=1.0;psi_c[m-1][j]=1.0;}for(i=1;i<m-1;i++){if(i>6 && i<21){psi_j[i][0]=0.0;psi_c[i][0]=0.0;}else{psi_j[i][0]=1.0;psi_c[i][0]=1.0;}}for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psi_j[i][j]=0.5;psi_c[i][j]=0.5;}}//处理右上角数据for(i=0;i<m;i++){for(j=0;j<n;j++){if(j>jlast[i]-1){psi_j[i][j]=0;vel_j[i][j]=3;psi_c[i][j]=0;vel_c[i][j]=3;}}}Pi=4.0*atan(1.0);Alpha=cos(Pi/m)+cos(Pi/n);Omega=(8.0-4*sqrt(4-pow(Alpha,2)))/pow(Alpha,2);//计算速势step1=0;step2=0;//简单迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_j=psi_j[i][j];psi_j[i][j]=(psi_j[i-1][j]+psi_j[i+1][j]+psi_j[i][j-1]+psi_j[i][j+1])/4.0;Error=Error+fabs(psi_j[i][j]-psiprv_j);}}step1++;if(step1>1000)break;if(Error<=0.001)break;}//超松弛迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_c=psi_c[i][j];psi_c[i][j]=(1-Omega)*psi_c[i][j]+Omega*(psi_c[i-1][j]+psi_c[i+1][j]+psi_c[i][j-1]+psi_c[i][j+1])/4.0;Error=Error+fabs(psi_c[i][j]-psiprv_c);}}step2++;if(step2>1000)break;if(Error<=0.001)break;}//计算速度for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){if(j==0){vely_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i][j+1]-psi_j[i][j+2])/2/h;vely_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i][j+1]-psi_c[i][j+2])/2/h;}else if(j==jlast[i]-1){vely_j[i][j]=(psi_j[i][j-2]-4*psi_j[i][j-1]+3*psi_j[i][j])/2/h;vely_c[i][j]=(psi_c[i][j-2]-4*psi_c[i][j-1]+3*psi_c[i][j])/2/h;}else{vely_j[i][j]=(psi_j[i][j+1]-psi_j[i][j-1])/2/h;vely_c[i][j]=(psi_c[i][j+1]-psi_c[i][j-1])/2/h;}}}for(j=0;j<n;j++){for(i=0;i<ilast[j];i++){if(i==0){velx_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i+1][j]-psi_j[i+2][j])/2/h;velx_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i+1][j]-psi_c[i+2][j])/2/h;}else if(i==ilast[j]-1){velx_j[i][j]=(psi_j[i-2][j]-4*psi_j[i-1][j]+3*psi_j[i][j])/2/h;velx_c[i][j]=(psi_c[i-2][j]-4*psi_c[i-1][j]+3*psi_c[i][j])/2/h;}else{velx_j[i][j]=(psi_j[i+1][j]-psi_j[i-1][j])/2/h;velx_c[i][j]=(psi_c[i+1][j]-psi_c[i-1][j])/2/h;}}}for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){vel_j[i][j]=sqrt(pow(velx_j[i][j],2)+pow(vely_j[i][j],2));vel_c[i][j]=sqrt(pow(velx_c[i][j],2)+pow(vely_c[i][j],2));}}//输出结果分布FILE *fp;fp=fopen("f:\\ESL\\YFresult.txt","w");fprintf(fp,"简单迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_j[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_j[i][j]);}}fprintf(fp,"超松弛迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_c[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_c[i][j]);}}fclose(fp);//输出tecplot数据FILE *fp1;fp1=fopen("f:\\ESL\\TECPLOT-result.txt","w");fprintf(fp1,"title=erwei grid\n");fprintf(fp1,"variables=x, y, psi_easy, velocity_easy, psi_SOR\n, velocity_SOR\n");fprintf(fp1,"zone t=grid,i=25,j=17,f=point\n");for(j=0;j<n;j++){for(i=0;i<m;i++){fprintf(fp1,"%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f\n",i*h,j*h,psi_j[i][j],vel_j[i][j],p si_c[i][j],vel_c[i][j]);}}fclose(fp1);}3）计算结果采用简单迭代，容器内的速势和速度分布速势分布（简单迭代）速度分布（简单迭代）采用超松弛迭代，容器内的速势和速度分布速势分布（SOR ） 速度分布（SOR ）2、用点源（汇）分布在对称轴的源汇模拟流体绕过NACA0012旋称体的二维轴对称势流解。
流体力学课后习题及答案
第二章2-2解：由P gh ρ=得h 水 =Pg ρ水=3350101109.8⨯⨯⨯=5.1m 335010=3.21.6109.8Ph m gρ⨯==⨯⨯四氯化碳四氯化碳 335010=0.37513.6109.8Ph m g ρ⨯==⨯⨯水银水银2-3 解：（1）体积弹性模量 /dpEv d ρρ=+在重力场中流体的压强形式为：dpg dzρ=- d dp gdz Evρρρ∴=-=两边积分，带入边界条件：00,0,z p ρρ===0lnEvp Ev Ev ghρ∴=- 11222212.5*160N F *40000NF L L s F s ==⎛⎫=== ⎪⎝⎭题解：有杠杆原理知：F 所以： 6、如题2-6图所示，封闭容器中盛有ρ=800kg/3m的油，1300h mm =，油下面为水，2500h mm =，测压管中水银液位读数400hmm =，求封闭容器中油面上的压强p 的大小。
解：12g 0p h gh gh ρρρ++-=油水水银12g p gh h gh ρρρ=--水银油水333313.6109.840010109.8500100.8--=⨯⨯⨯⨯-⨯⨯⨯-⨯=44.6110pa ⨯2-7：解：（1）、2224F gh s 10009.81001010101098Nρ--==⨯⨯⨯⨯⨯=2）m 121216G [s h h s h ]1000199109.81.95g Nρ-=⨯⨯=⨯⨯⨯=（-）+02h（3）因为在21h h -处谁对容器有向上的压力2-8，解：由同一液面压强相等可列：(0)()gh sin /6p(0)1239.21/^3p p h l kn m θθπ===∴=液2-9 解：设A 点距左U 形管测压计水银页面高度为H 则B 点距右U 型管测压计水银高度为H+hB A B h gh g H h gh gh gh m ag ρρρρρρA P -P -+P P -P =-=-⨯⨯P 水水水水则（+）=则（）=（13600-1000）9.80.3=370442.10，解：选取右侧U 形管汞柱高作为等压面，有：1132()m B P g h h gh gh gh p ρρρρ++-+=+酒汞汞水B p 42.7410pa =-⨯2-11解:左边液面压强与右边液面压强相等知，.66g .66.89g .82g .8211g ⨯+-⨯=⨯+-⨯未知水未知水）（）（ρρρρ解得333102.31m kg 103.85⨯=⋅⨯=-未知ρ3m kg -⋅2-12 解：设左支管液面到另一液体分界面的距离为1h ，右支管为2h ，则有：1112222P gh P gh gh ρρρ+=++或121122121221()()P P g h h ghP P gh gh ghρρρρρρ-=--+-=-+=-得 1221()P P h gρρ-=-2-13解：gh P gh ρρ+=水水银P=gh gh ρρ∴-水银水127400.07891.8F PS N∴==⨯=2-14解：以闸门与液面交点为O 点，沿闸门向下方向建立坐标S ，取微元ds ，在面积bds 内，液体压力对链轴取矩()()0.2sin600.2dM ghbds s g s sdsρρ=-+=-+ 所以)0sin 600.2Mgb s sds ρ=-+Q对链轴取矩)cos600.2Q M Q =由力矩平衡得 0Q M M +=化简)1.*1.9320.302Q -=得 26778Q N=()()D 33352.151y y *1132***2*4121232,8832**10*10*12*89.6*10xcC c xc cD c I y sI b a y s d y F g h s ρ=+==========题解：依题意知又即:*16、一个很长的铅垂壁面吧海水和淡水隔开，海水深7m ；试确定淡水多深时壁面所受液体作用力合力为零。
流体力学大作业
一.选择题1.牛顿内摩擦定律适用于（）。
A．任何流体B．牛顿流体C．非牛顿流体2.液体不具有的性质是（）。
A．易流动性B．压缩性C．抗拉性D．粘滞性3连续介质假定认为流体（）连续。
A．在宏观上B．在微观上C．分子间D．原子间4.在国际单位制中流体力学基本量纲不包括（）。
A．时间B．质量C．长度D．力．5.在静水中取一六面体，作用在该六面体上的力有（）A．切向力、正压力B．正压力 C．正压力、重力 D．正压力、切向力、重力6．下述哪些力属于质量力 ( )A．惯性力B．粘性力C．弹性力D．表面张力 E．重力7．某点存在真空时，（）（）A．该点的绝对压强为正值B．该点的相对压强为正值 c.该点的绝对压强为负值D．该点的相对压强为负值8.流体静压强的（）。
A．方向与受压面有关 B．大小与受压面积有关 B．大小与受压面方位无关9.流体静压强的全微分式为（）。
A．B．C．10.压强单位为时，采用了哪种表示法（）。
A．应力单位B．大气压倍数C．液柱高度11.密封容器内液面压强小于大气压强，其任一点的测压管液面（）。
A．高于容器内液面B．低于容器内液面C．等于容器内液面12.流体运动的连续性方程是根据（）原理导出的。
A.动量守恒B. 质量守恒C.能量守恒D. 力的平衡13. 流线和迹线重合的条件为（）。
A.恒定流B.非恒定流C.非恒定均匀流14.总流伯努利方程适用于（）。
A.恒定流B.非恒定流C.可压缩流体15. 总水头线与测压管水头线的基本规律是：（）、（）A.总水头线总是沿程下降的。
B.总水头线总是在测压管水头线的上方。
C.测压管水头线沿程可升可降。
D.测压管水头线总是沿程下降的。
16 管道中液体的雷诺数与（）无关。
A. 温度B. 管径C. 流速D. 管长17.. 某圆管直径d=30mm，其中液体平均流速为20cm/s。
液体粘滞系数为0.0114cm3/s，则此管中液体流态为（）。
A. 层流B. 层流向紊流过渡C.紊流18.等直径圆管中紊流的过流断面流速分布是（） A呈抛物线分布 B. 呈对数线分布 C.呈椭圆曲线分布 D. 呈双曲线分布19.等直径圆管中的层流，其过流断面平均流速是圆管中最大流速的（）A 1.0倍 B.1/3倍 C. 1/4倍 D. 1/2倍20.圆管中的层流的沿程损失与管中平均流速的（）成正比.A. 一次方B. 二次方C. 三次方D. 四次方21..圆管的水力半径是 ( )A. d/2B. d/3C. d/4D. d/5.22谢才公式中谢才系数的单位是（） A. 无量纲 B. C. D. .23. 判断层流和紊流的临界雷诺数是（）A.上临界雷诺数B.下临界雷诺数C.上下临界雷诺数代数平均D.上下临界雷诺数几何平均24.. 对于管道无压流，当充满度分别为（）时，其流量和速度分别达到最大。
流体力学计算题练习及答案
练习题1. 如右图所示，在一密闭容器中，上部装有密度ρ1=0.8×103kg/m 3的油，下部为密度ρ2=103 kg/m 3的水，已知h 1=0.4m ，h 2=0.2m 。
测压管中水银柱的读数h =0.5m ，水银的密度为ρ1=13.6×103 kg/m 3。
求密闭容器中油液面上的压强p 0。
2. 图示为一水暖系统，为了防止水温升高时体积膨胀将水管胀裂，在系统顶部设一膨胀水箱，使水有膨胀的余地。
若系统内水的总体积为8m3，加温前后温差为50℃，在其温度范围内水的膨胀系数为βT ＝9×10－4 1/℃，求膨胀水箱的最小容积。
3. 当温度不变，压强从0.20 MPa 增加到10 MPa 时，某种液体的体积减小0.49%，求该液体的体积模量。
4. 两个充满空气的封闭容器互相隔开，左边压力表M 的读数为100kPa ，右边真空计V 的读数为 3.5mH2O ，试求连接两容器的水银压差计中h 的读值。
5. 已知流体运动的速度场为：3231yv xy v y x ==，，试求t=2时过点()()x y z ，，，，=312处的流线方程。
hp ap 0h 1h 2ρ1ρ2ρ36. 如图所示，水在压强作用下从密封的下水箱沿竖直管道流入上水箱中，已知h ＝50cm ，H ＝3m ，管道直径D ＝25mm ，λ＝0.02，各局部阻力系数分别为ζ1＝0.5，ζ2＝5.0，ζ3＝1.0，求：为维持稳定的管中流速V ＝1m/s ，下水箱的液面压强应保持在多少Pa?7. 右图为毕托管示意图。
液体自左向右流动，直管和直角弯管直接插入管道内的液体中，弯管开口迎着流动方向。
测得A 点的液柱高度为hA =170 mm ，B 点的液柱高度为hB = 230 mm ，已知液体的密度为 =990 kg/m3，忽略阻力损失，试计算管内液体的流速uA 。
8. 如右图所示为一壁厚可以忽略的大容器，在其下部开一直径为d =12mm 的小孔口，水自孔口流出后进入另一液面比大容器液面低H =1.2m 的容器中，两容器内的水位始终保持不变。
《流体力学》课后习题答案.pdf
得：T1 = t1 + 273 = 50 + 273 = 323K ，T2 = t2 + 273 = 78 + 273 = 351K
根据
p
=
mRT V
，有：
p1
=
mRT1 V1
，
p2
=
mRT2 V2
得： V2 V1
=
p1 p2
T2 T1
=
9.8067 104 5.8840 105
351 323
=
0.18
设管段长度 l，管段表面积： A = dl
单位长度管壁上粘滞力： = A u = dl u − 0 = 3.14 0.025 0.03
l y l
0.001
1-8 解： A = 0.8 0.2 = 0.16m2 ，u=1m/s， = 10mm ， = 1.15Pa s
T = A u = A u − 0 = 1.15 0.16 1 = 18.4N
1
=
T1 b
=
A b
u
−0 −h
=
0.7 0.06b b
15 − 0 0.04 − 0.01
=
21N
/m，方向水平向左
下表面单位宽度受到的内摩擦力：
2
=
T2 b
=
Au−0 b h−0
=
0.7 0.06b 15 − 0
b
0.01− 0
= 63N
/m，方向水平向左
平板单位宽度上受到的阻力：
= 1 + 2 = 21+ 63 = 84N ，方向水平向左。
h1 = 5.6m
2.4 解：如图 1-2 是等压面，3-4 是等压面，5-6 段充的是空气，因此 p6 = p5 ，6-7 是等压面，
流体力学--习题解答及习题课讲义
流 体 力 学习题解答及习题课第2章2-1 解：A B p p gh ρ=+ 则()()4442.710 2.9100.421.36109.807e a a v A B Hg e v p p p p p p h g g p p m g ρρρ+---==+⨯+⨯===⨯⨯2-2 解：111a p gh p gh ρρ++煤水＝ 则：()11a p p gh ρρ=+-水煤 同理：222a p gh p gh ρρ++煤水＝ 则：()22a p p gh ρρ=+-水煤而：12p p gH ρ=+煤 则：()()12a a p gh p gh gH ρρρρρ+-=+-+水煤水煤煤可得：第一章 流体及其主要物理性质例1：已知油品的相对密度为0.85，求其重度。
解：3/980085.085.0m N ⨯=⇒=γδ例2：当压强增加5×104Pa 时，某种液体的密度增长0.02%，求该液体的弹性系数。
解：0=+=⇒=dV Vd dM V M ρρρρρd dV V -=Pa dp d dp V dV E p84105.2105%02.01111⨯=⨯⨯==-==ρρβ例3：已知：A ＝1200cm 2，V ＝0.5m/sμ1＝0.142Pa.s ，h 1＝1.0mm μ2＝0.235Pa.s ，h 2＝1.4mm 求：平板上所受的内摩擦力F绘制：平板间流体的流速分布图及应力分布图 解：（前提条件：牛顿流体、层流运动）dy du μτ= ⎪⎪⎩⎪⎪⎨⎧-=-=⇒2221110h u h u V μτμτ 因为 τ1＝τ2 所以sm h h Vh u h uh u V /23.02112212211=+=⇒=-μμμμμN h uV A F 6.411=-==μτ第二章 流体静力学例1：如图，汽车上有一长方形水箱，高H ＝1.2m ，长L ＝4m ，水箱顶盖中心有一供加水用的通大气压孔，试计算当汽车以加速度为3m/s 2向前行驶时，水箱底面上前后两点A 、B 的静压强（装满水）。
流体力学第二章参考答案
第二章 流体静力学2-1 将盛有液体的U 形小玻璃管装在作水平加速运动的汽车上(如图示)，已知L ＝30 cm ，h ＝5cm ，试求汽车的加速度a 。
解：将坐标原点放在U 形玻璃管底部的中心。
Z 轴垂直向上，x 轴与加速度的方向一致，则玻璃管装在作水平运动的汽车上时，单位质量液体的质量力和液体的加速度分量分别为0,0,,0,0x y z x y z g g g ga a a a ===-===代入压力全微分公式得d (d d )p a x g z ρ=-+因为自由液面是等压面，即d 0p =，所以自由液面的微分式为d d a x g z =- 积分的：a z x c g=-+，斜率为a g -，即a g h L = 解得21.63m/s 6g a g h L ===2-2 一封闭水箱如图示，金属测压计测得的压强值为p ＝4.9kPa(相对压强)，测压计中心比A 点高z ＝0.5m ，而A 点在液面以下h ＝1.5m 。
求液面的绝对压强和相对压强。
解：由0p gh p gz ρρ+=+得相对压强为30() 4.91010009.81 4.9kPa p p g z h ρ=+-=⨯-⨯⨯=-绝对压强0( 4.998)kPa=93.1kPa abs a p p p =+=-+2-3 在装满水的锥台形容器盖上，加一力F ＝4kN 。
容器的尺寸如图示，D ＝2m ，d ＝l m ，h ＝2m 。
试求(1)A 、B 、A ’、B ’各点的相对压强；(2)容器底面上的总压力。
解：(1)02 5.06kPa 4F F p D A π===,由0p p gh ρ=+得：0 5.06kPa A B p p p ===''0 5.06kPa+10009.82Pa 24.7kPa A B p p p gh ρ==+=⨯⨯=(2) 容器底面上的总压力为2'24.7kPa 77.6kN 4A D P p A π==⨯= 2-4 一封闭容器水面的绝对压强p 0＝85kPa ，中间玻璃管两端开口，当既无空气通过玻璃管进入容器、又无水进人玻璃管时，试求玻璃管应该伸入水面下的深度h 。
(完整版)流体力学练习题及答案
(完整版)流体力学练习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN流体力学练习题及答案一、单项选择题1、下列各力中，不属于表面力的是（ ）。
A ．惯性力B ．粘滞力C ．压力D ．表面张力2、下列关于流体粘性的说法中，不准确的说法是（ ）。
A ．粘性是实际流体的物性之一B ．构成流体粘性的因素是流体分子间的吸引力C ．流体粘性具有阻碍流体流动的能力D ．流体运动粘度的国际单位制单位是m 2/s3、在流体研究的欧拉法中，流体质点的加速度包括当地加速度和迁移加速度，迁移加速度反映（ ）。
A ．由于流体质点运动改变了空间位置而引起的速度变化率B ．流体速度场的不稳定性C ．流体质点在流场某一固定空间位置上的速度变化率D ．流体的膨胀性4、重力场中平衡流体的势函数为（ ）。
A ．gz -=πB ．gz =πC ．z ρπ-=D ．z ρπ=5、无旋流动是指（ ）流动。
A ．平行B ．不可压缩流体平面C ．旋涡强度为零的D ．流线是直线的6、流体内摩擦力的量纲[]F 是（ ）。
A . []1-MLtB . []21--t MLC . []11--t ML D . []2-MLt 7、已知不可压缩流体的流速场为xyj zi x 2V 2+= ，则流动属于（ ）。
A ．三向稳定流动B ．二维非稳定流动C ．三维稳定流动D ．二维稳定流动8、动量方程 的不适用于(??? ??) 的流场。
A ．理想流体作定常流动B ．粘性流体作定常流动C ．不可压缩流体作定常流动D ．流体作非定常流动9、不可压缩实际流体在重力场中的水平等径管道内作稳定流动时，以下陈述错误的是：沿流动方向 ( ) 。
A ．流量逐渐减少B ．阻力损失量与流经的长度成正比C ．压强逐渐下降D ．雷诺数维持不变10、串联管道系统中,其各支管内单位质量流体的能量损失（ ）。
A ．一定不相等B ．之和为单位质量流体的总能量损失C ．一定相等D ．相等与否取决于支管长度是否相等11、边界层的基本特征之一是（ ）。
流体力学习题及答案.doc
第一章 绪论1-1 连续介质假设的条件是什么？答：所研究问题中物体的特征尺度L ,远远大于流体分子的平均自由行程l ,即l/L<<1。
1-2 设稀薄气体的分子自由行程是几米的数量级 ,问下列二种情况连续介质假设是否成立？（1）人造卫星在飞离大气层进入稀薄气体层时； （2）假象地球在这样的稀薄气体中运动时。
答：（1）不成立。
（2）成立。
1-3 粘性流体在静止时有没有切应力？理想流体在运动时有没有切应力？静止流体没有粘性吗？ 答：（1）由于0=dy dv ,因此0==dydv μτ ,没有剪切应力。
（2）对于理想流体 ,由于粘性系数0=μ ,因此0==dydvμτ ,没有剪切应力。
（3）粘性是流体的根本属性。
只是在静止流体中 ,由于流场的速度为0 ,流体的粘性没有表现出来。
1-4 在水池和风洞中进行船模试验时 ,需要测定由下式定义的无因次数（雷诺数）νUL=Re ,其中U 为试验速度 ,L 为船模长度 ,ν为流体的运动粘性系数。
如果s m U /20= ,m L 4= ,温度由C ︒10增到C ︒40时 ,分别计算在水池和风洞中试验时的Re 数。
（C ︒10时水和空气的运动粘性系数为410013.0-⨯和410014.0-⨯ ,C ︒40时水和空气的运动粘性系数为4100075.0-⨯和410179.0-⨯）。
答：C ︒10时水的Re 为：()()72410154.6/10013.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒10时空气的Re 为：()()72410714.5/10014.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒40时水的Re 为：()()82410067.1/100075.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒40时空气的Re 为：()()62410469.4/10179.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
流体力学习题解答(参考)
习题解答2-9解L H L H H ⋅⋅=⋅⋅⋅=αγαγsin 2sin 2P 2左()()()αααααααsin 32sin 6sin 2 sin /sin /2/12/sin /sin 2 3H H H L H H H HAZ J ZC Z C C D =+=+=+= ααsin 3sin H x Z H x x D D -=⎪⎭⎫⎝⎛--= ⎪⎭⎫ ⎝⎛-⋅⋅⋅=⎪⎭⎫ ⎝⎛-⋅=⋅ααγαsin 3sin 2sin 3P P 2H x L H H x x D 左左L h ⋅⋅=αγsin 2P 2右 αs i n 32'h Z D = ⎪⎭⎫ ⎝⎛-⋅⋅⋅=⎪⎭⎫ ⎝⎛-⋅=⋅ααγαsin 3sin 2sin 3P P 2'h x L h h x x D右右平衡时有：⎪⎭⎫ ⎝⎛-⋅⋅⋅⎪⎭⎫ ⎝⎛-⋅⋅⋅ααγααγsin 3sin 2sin 3sin 222h x L h H x L H ＝ 所以 ⎪⎭⎫⎝⎛-⋅⎪⎭⎫ ⎝⎛-⋅ααs i n 3s i n 322h x h H x H ＝有 m h H h H x 795.060sin )4.02(34.02sin )(322332233=︒--=--=α2-13解L d L d L d Ry 22216316181γπγπγπ=+=()L d d d L H H L H L H Rx 22222212221834121212121γγγγγ=⎪⎭⎫ ⎝⎛-=-=+=N 9236100.49.810001632=⨯⨯⨯⨯=π＋Ry N 5880100.49.81000832=⨯⨯⨯⨯=RxN 588010949923658802222==+=+=y x R R R︒=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=50.5758809236arctg arctg x yR R θ 2-16解（不能直接利用教材上的公式）盖板上任意点上的压力()⎪⎪⎭⎫⎝⎛+=︒+=z h z h p 2245sin γγ ()A z J J J A z h dA z dA z h zdA z h z p c c z z c A AAD ⋅+=⋅+⋅⋅⋅+=︒+=⋅⎰⎰⎰22 222245sin ，＝γγγγγ其中：42244332322542213223222224442 22d d d d J d d d b a J d ab A d z z c c ππππππππ=⋅+==⋅⎪⎪⎭⎫ ⎝⎛=====，434232543225224222d d h d d d h z p D γππγπγπγ+⋅⋅=⋅+⋅⋅⋅=⋅433254d hd z p d T D γπγπ+=⋅=⋅ ()()6587N0.6528320.69.81000 583232542232＝＝⨯+⨯⨯⨯⨯⨯+=+=h d h d d hd T ππγγπγπ2-17解r d r H 3 4==，，由图可知 21h h =球冠edc 和fgh 的体积分别为：()321 2456/41r r r r V ππ=-=球冠edc 曲面上的压力体为abedc ，重量为γπγππγπ33221244924533411341r r r r V r d F =⎪⎭⎫⎝⎛-⋅⋅=⎪⎭⎫ ⎝⎛-⋅=部分球面ef －rg 上作用力等于同体积水的重量。
流体力学第二章
第二章习题简答2-1 题2-1图示中的A 、B 点的相对压强各为多少？(单位分别用N/m 2和mH 2O 表示)题2-1图解：()OmH Pa gh P O mH Pa gh P B B A A 2232940038.910005.0490035.38.91000==⨯⨯==-=-=-⨯⨯==ρρ2-2 已知题2-2图中z = 1m ， h = 2m ，试求A 点的相对压强。
解：取等压面1-1，则Pagh gz P ghgz P A A 3108.9)21(8.91000⨯-=-⨯⨯=-=-=-ρρρρ2-3 已知水箱真空表M 的读数为0.98kPa ，水箱与油箱的液面差H =1.5m ，水银柱差m 2.02=h ，3m /kg 800=油ρ，求1h 为多少米？解：取等压面1-1，则()()()()()mgh H g P gh h gh gh P h h H g P P Hg Hg a a 6.58.980010002.05.198009802.01332802212121=⨯-+⨯-+⨯=-+-+=++=+++-油油ρρρρρρρ2-4 为了精确测定密度为ρ的液体中A 、B 两点的微小压差，特设计图示微压计。
测定时的各液面差如图示。
试求ρ与ρ'的关系及同一高程上A、B 两点的压差。
解：如图取等压面1-1，则()a b g gb -=ρρ' （对于a 段空气产生的压力忽略不计）得()⎪⎭⎫ ⎝⎛-=-=b a ba b 1'ρρρ取等压面2-2，则gHbagH gH p p p gHp gH p B A B A ρρρρρ=-=-=∆-=-''2-5 图示密闭容器，压力表的示值为4900N/m 2，压力表中心比A 点高0.4m ，A 点在水面下1.5m,求水面压强。
解：PagH gh P P ghP gH P 5880)5.14.0(9800490000-=-⨯+=-+=+=+ρρρρ2-6 图为倾斜水管上测定压差的装置，已知cm 20=z ，压差计液面之差cm 12=h ，求当（1）31kg/m 920=ρ的油时;（2）1ρ为空气时;A 、B 两点的压差分别为多少？解：（1）取等压面1-1OmH Pa ghgZ gh P P gh gZ P gh P A B B A 21119.092.1865)12.02.0(980012.08.9920==-⨯+⨯⨯=-+=---=-ρρρρρρ（2）同题（1）可得OmH Pa ghgZ P P gZ P gh P A B B A 208.0784)12.02.0(9800==-⨯=-=--=-ρρρρ（第2小题跟课本后的答案不一样，课本为0.05mH 2O ）2-7 已知倾斜微压计的倾角︒=30α，测得0.5m =l ，容器中液面至测压管口高度m 1.0=h ,求压力p 。
流体力学课后重点题型答案
∴p 1 − p 2 = ρga − ρgb + ρ ' gc
将上式右边 ± ρgc 得：
p 1 − p 2 = ρga − ρgb + ρ ' gc ± ρgc
是管轴线上的速度。求：流过该流管的体积流量和流管横截面上平均流速的大小。
7
解： qV = ∫ υdA = ∫ υ ⋅ 2π ⋅ rdr
A 0 r0 r ＝ ∫ υ m [1 − ( ) 2 ]2π ⋅ rdr 0 r0 r0 r ＝ 2πυm ∫ [1 − ( ) 2 ]rdr 0 r0
r0
＝ υ m r0 2
1
h2
F 1 1 Aυ x ( + ) h1 h 2
h1
υx
试求水在管中上升的高度。 解： h =
4σ cos θ ρgd
20℃水的密度 ρ = 998.23 kg/m3, σ = 0.07275 N/m
所以 h =
4 × 0.07275 × cos10 D = 0.0029 ≈ 3 mm 998.23 × 9.806 × 0.01
∫
t + Δt
t
β t dt = ∫
V ''
V
1 dV V
整理得： β t Δt = ln V '− ln V
ΔV = V '−V = V × (e Δtβ t − 1) =8×（e50×0.0005－1）＝0.203
m3
1-4 绝对压强为 3.329×105Pa 的空气的等温体积模量和等熵体积模量各为多少？（提示：空气
《流体力学》课后习题答案详解
习题【1】1-1 解：已知：120t =℃，1395p kPa '=，250t =℃ 120273293T K =+=，250273323T K =+= 据p RT ρ=，有：11p RT ρ'=，22p RT ρ'= 得：2211p T p T '='，则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解：受到的质量力有两个，一个是重力，一个是惯性力。
重力方向竖直向下，大小为mg ；惯性力方向和重力加速度方向相反为竖直向上，大小为mg ，其合力为0，受到的单位质量力为01-3 解：已知：V=10m 3，50T ∆=℃，0.0005V α=℃-1根据1V V V Tα∆=⋅∆，得：30.000510VVV Tα∆=⋅⋅∆=⨯⨯1-4 解：已知：419.806710Pa p '=⨯，52 5.884010Pa p '=⨯，150t =℃，278t =℃得：1127350273323T t K=+=+=，G ＝mg自由落体： 加速度a ＝g2227378273351T t K =+=+=根据mRTp V=，有：111mRT p V '=，222mRT p V '=得：421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯，即210.18V V = 体积减小了()10.18100%82%-⨯=1-5 解：已知：40mm δ=，0.7Pa s μ=⋅，a =60mm ，u =15m/s ，h =10mm根据牛顿内摩擦力定律：uT Ayμ∆=∆ 设平板宽度为b ，则平板面积0.06A a b b =⋅=上表面单位宽度受到的内摩擦力：1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ，方向水平向左下表面单位宽度受到的内摩擦力： 2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ，方向水平向左平板单位宽度上受到的阻力：12216384N τττ=+=+=，方向水平向左。
流体力学作业2答案
作业2答案（第3章、第4章）第3章一、选择题1、流体运动的连续性方程是根据（C）原理导出的。
A、动量守恒B、质量守恒C、能量守恒D、力的平衡2、流线和迹线重合的条件为（ C ）A、恒定流B、非恒定流C、非恒定均匀流二、判断题1、以每个流体质点运动规律为研究对象的方法称为拉格朗日法。
（正确）2、恒定流一定是均匀流。
（错误）3、涡流是指流体质点在运动中不绕自身轴旋转的流动。
（正确）4、无旋流就是无涡流。
（正确）5、非均匀流一定是非恒定流。
（错误）三、简答题1、述流体运动的两种方法是什么？简述其内容。
答：研究流体运动有两种不同的观点，因而形成两种不同的方法：一种方法是从分析流体各个质点的运动着手，即跟踪流体质点的方法来研究整个流体的运动，称之为拉格朗日法；另一种方法则是从分析流体所占据的空间中各固定点处的流体的运动着手，即设立观察站的方法来研究流体在整个空间里的运动，称其为欧拉法2. 流体微团体运动分为哪几种形式?答：①平移②线变形③角变形④旋转变形。
3. 写出恒定平面势流中流函数、势函数与流速的关系。
（改为：写出恒定平面势流中流函数具有的性质，流函数与流速势的关系。
）答：流函数具有的性质（1）流函数相等的点组成的线即流线，或曰，同一流线上个点的流函数为常数。
（2）两流线间的函数值之差为为单宽流量。
（3）平面势流的流函数为一个调和函数。
答：流函数与流速势的关系（1）流函数与势函数为调和函数。
（2）等势线与等流函数线正交。
4．什么是过流断面和断面平均流速？为什么要引入断面平均流速？答：与流线正交的断面叫过流断面。
过流断面上点流速的平均值为断面平均流速。
引入断面平均流速的概念是为了在工程应用中简化计算。
5．如图所示，水流通过由两段等截面及一段变截面组成的管道，试问：(1)当阀门开度一定，上游水位保持不变，各段管中，是恒定流还是非恒定流？是均匀流还是非均匀流？(2)当阀门开度一定，上游水位随时间下降，这时管中是恒定流还是非恒定流？(3)恒定流情况下，当判别第II 段管中是渐变流还是急变流时，与该段管长有无关系？答：（1）是恒定流。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一.选择题
1.牛顿内摩擦定律适用于（）。
A．任何流体B．牛顿流体C．非牛顿流体
2.液体不具有的性质是（）。
A．易流动性B．压缩性C．抗拉性D．粘滞性
3.连续介质假定认为流体（）连续。
A．在宏观上B．在微观上C．分子间D．原子间
4.在国际单位制中流体力学基本量纲不包括（）。
A．时间B．质量C．长度D．力．
5.在静水中取一六面体，作用在该六面体上的力有（） A．切向力、正压力B．正压力 C．正压力、重力 D．正压力、切向力、重力
6．下述哪些力属于质量力 ( ) ( ) A．惯性力B．粘性力C．弹性力D．表面张力 E．重力
7．某点存在真空时，（）（） A．该点的绝对压强为正值B．该点的相对压强为正值 c.该点的绝对压强为负值D．该点的相对压强为负值
8.流体静压强的（）。
A．方向与受压面有关 B．大小与受压面积有关 B．大小与受压面方位无关
9.流体静压强的全微分式为（）。
A．B．C．
10.压强单位为时，采用了哪种表示法（）。
A．应力单位B．大气压倍数C．液柱高度
11.密封容器内液面压强小于大气压强，其任一点的测压管液面（）。
A．高于容器内液面B．低于容器内液面C．等于容器内液面
12.流体运动的连续性方程是根据（）原理导出的。
A.动量守恒 B. 质量守恒 C.能量守恒 D. 力的平衡
13. 流线和迹线重合的条件为（）。
A.恒定流 B.非恒定流 C.非恒定均匀流
14.总流伯努利方程适用于（）。
A.恒定流 B.非恒定流 C.可压缩流体
15. 总水头线与测压管水头线的基本规律是：（）、（） A.总水头线总是沿程下降的。
B.总水头线总是在测压管水头线的上方。
C.测压管水头线沿程可升可降。
D.测压管水头线总是沿程下降的。
16 管道中液体的雷诺数与（）无关。
A. 温度 B. 管径 C. 流速 D. 管长
17.某圆管直径d=30mm，其中液体平均流速为20cm/s。
液体粘滞系数为0.0114cm3/s，则此管中液体流态为（）。
A. 层流 B. 层流向紊流过渡 C.紊流
18.等直径圆管中紊流的过流断面流速分布是（） A呈抛物线分布 B. 呈对数线分布 C.呈椭圆曲线分布
D. 呈双曲线分布
19.等直径圆管中的层流，其过流断面平均流速是圆管中最大流速的（） A 1.0倍 B.1/3倍 C. 1/4倍 D. 1/2倍
20.圆管中的层流的沿程损失与管中平均流速的（）成正比. A. 一次方 B. 二次方 C. 三次方 D. 四次方
21.圆管的水力半径是 ( ) A. d/2 B. d/3 C. d/4 D. d/5.
22谢才公式中谢才系数的单位是（） A. 无量纲 B. C. D. .
23.判断层流和紊流的临界雷诺数是（） A.上临界雷诺数 B.下临界雷诺数 C.上下临界雷诺数代数平均 D.上下临界雷诺数几何平均
24.对于管道无压流，当充满度分别为（）时，其流量和速度分别达到最大。
A. 0.5, 0.5 B. 0.95, 0.81
C. 0.81, 081
D. 1.0, 1.0
25.对于a, b, c三种水面线，下列哪些说法是错误（）（） A．所有a、c型曲线都是壅水曲线，即，水深沿程增大。
B．所有b型曲线都是壅水曲线，即，水深沿程增大。
C．所有a、c型曲线都是降水曲线，即，水深沿程减小。
C．所有b型曲线都是降水曲线，即，水深沿程减小。
二.判断题
1.压强和切应力属表面力。
（）
2.流体惯性力与加速度方向相同。
（）
3.粘滞性可以制止流体流动。
（）
4.理想流体与实际流体的区别仅在于，理想流体具有不可压缩性。
（）
5.等压面与质量力垂直。
（）
6.某点存在真空，是指该点的绝对压强小于大气压强。
（）
7.静止流体中某点压强的大小，不仅与其淹没深度有关还与受压面的方位有关。
( )
8.相对压强的数值可为正值，也可以是正值。
( )
9.静止液面下的闸板的总压力作用中心与闸板形心重合。
（）
10.和大气相通容器的测压管液面一定与容器内液面高度相同。
（）
11.相对静止液体的等压面一定是水平面。
（）
12.以每个流体质点运动规律为研究对象的方法称为拉格朗日法。
（）
13.恒定流一定是均匀流。
( )
14.涡流是指流体质点在运动中不绕自身轴旋转的流动。
( )
15.无旋流就是无涡流。
（）
16.非均匀流一定是非恒定流。
（）
17.N-S方程为理想流体运动的微分方程。
（）
18.毕托管是量测流体点流速的一种仪器。
（）
19.层流的沿程水头损失系数仅与雷诺数有关。
( )
20.壁面光滑的管道一定是水力光滑管。
( )
21.在过流断面突变处一般发生局部水头损失。
( )
22.等直径圆管中的层流,其过流断面平均流速是圆管中最大流速的1/2倍（）
23.流体内切应力方向与流体运动方向相同。
（）
24.阻力平方区内阻力系数与雷诺数无关。
（）
25.计算阻力损失时，短管既要考虑局部阻力损失，也要考虑沿程阻力损失，长管计算同样也要考虑这两项损失。
（）
26.长管是指几何长度很长的管道。
（）
27.孔口淹没出流时，孔口淹没越深，其出流的流速和流量就越大。
（）
28.管嘴收缩断面的真空度与作用水头成正比，作用水头越大，收缩断面的真空度越大，泄流量也越大。
（）
29.同一短管，在自由出流和淹没出流条件下，流量计算公式的形式及流量系数的数值均相同。
（）
30.若两孔口形状、尺寸完全相同，作用水头相同，一个为自由出流，一个为淹没出流，二者的流量是相同的。
（）
三.简答题
1．为什么可将流体作为连续介质处理？
2．什么是流体的粘滞性？它对流体流动起什么作用？
3.动力粘滞系数和运动粘滞系数有什么区别？
4.等压面是水平面的条件是什么？
5.同一容器中装两种液体，且，在容器侧壁装了两根测压管。
试问：图中所标明的测压管中液面位置对吗？为什么？
6.描述流体运动的两种方法是什么？简述其内容。
7.流体微团体运动分为哪几种形式?
8.写出恒定平面势流中流函数、势函数与流速的关系。
9.什么是过流断面和断面平均流速？为什么要引入断面均流速？
10.如图所示，水流通过由两段等截面及一段变截面组成的管道，试问： (1)当阀门开度一定，上游水位保持不变，各段管中，是恒定流还是非恒定流？是均匀流还是非均匀流？ (2)当阀门开度一定，上游水位随时间下降，这时管中是恒定流还是非恒定流？ (3)恒定流情况下，当判别第II段管中是渐变流还是急变流时，与该段管长有无关系？
11.说明总流能量方程中各项的物理意义。
12.写出实际流体恒定元流的伯努利方程和实际流体恒定总流的伯努利方程，并指出他们的区别？
13.应用恒定总统能量方程时，为什么把过流断面选在渐变流段或均匀流段？
14.在写总流能量方程时，过流断面上的代表点、基准面是否可以任意选取？为什么？
15.关于水流流向问题有如下一些说法：“水一定由高处向低处流”；“水是从压强大向压强小的地方流”；“水是从流速大的地方向流速小的地方流”。
这些说法是否正确？为什么？如何正确描述？
16总流的动量方程为，试问：（1）中包括哪些力？（2）如果由动量方程求得的力为负值说明什么问题？
17.圆管中层流与紊流，其流速分布有什么不同？
18 简述尼古拉兹实验中沿程阻力系数λ的变化规律。
19.写出管流和明渠水流雷诺数的表达式，并说明其层流、紊流的判别标准？
20.雷诺数的物理意义？它为什么能用来判别流态？
21.当输水管直径一定时，随流量增大，雷诺数是增大还是减少？当输水管流量一定时，随管径加大，雷诺数是增大还是减少？
22.两个不同管径的管道，通过不同粘滞性的液体，它们的临界雷诺数是否相同？
23.能量损失有几种形式？产生能量损失的物理原因是什么？
24.为什么管嘴出流时，阻力增加了，泄流量反而增大？
25.写出薄壁小孔口出流的收缩系数，流速系数和流量系数的表达式。
26.外延管嘴正常工作的条件是什么？
27.为什么外延管嘴出流比同等条件下孔口出流的流量大？
28.简述明渠均匀流的水力特征及其形成条件。
29.简述明渠水流的三种流态及其四个判别方法及标准。
30.简述明渠恒定非均匀流的水力特征。