清华大学理论力学课后习题答案-虚位移原理及其应用习题解(内容参考)
理论力学-第12章 虚位移原理及其应用

约束方程中包含质点速度,即
f ri ,ri 0 i 1,, n
1,, s
而且约束方程不可积分成有限形式,这种约束则称为非完整 约束(non -holonomic constraint)。
基本概念
约束
约束的分类-完整约束与非完整约束
沿直线轨道作纯滚动的圆轮,C* 点为轮上一点,即速度瞬心。圆轮的 约束为
这是虚位移原理的最简单的例子。
第12章 虚位移原理及其应用
基本概念
返回
基本概念
约束 广义坐标与自由度 虚位移与虚功 理想约束
基本概念
约束
基本概念
约束
静力学中曾经从对运动的限制和受力两个方面对 约束作了定义和描述。现在需要对约束的定义加以 扩展。
基本概念
约束
约束定义的扩展
为了用分析的方法研究物体的平衡规律,必须将约束分析化, 也就是用数学表达式描述约束。这时,约束对物体运动预加的限 制条件,将被表示为
基本概念
约束
约束的分类-双侧约束与单侧约束
被约束在双面滑道中的滑 块(B)运动的约束方程为
yB 0
基本概念
约束
约束的分类-双侧约束与单侧约束
被约束在单面滑道的滑块(B) 运动的约束方程为
yB 0
基本概念
约束
约束的分类-双侧约束与单侧约束
用刚性杆悬挂的单摆为双面 约束
x2 y2 l2
MC (F) 0
F1l1 F2l2
引言
M C (F ) 0 F1l1 F2l2
上述结论也可以从力作功得 到。杠杆工作的过程中,其初始 角速度与最终角速度一般均为零。 如 果 令 δd1 和 δd2 分 别 表 示 A 点 和 B 点满足约束的任意上升和下降的 距离,不考虑C铰的摩擦力,则据 动能定理可以写出
清华大学本校用理论力学课件4-1 虚位移原理

2
P2
W
解
第4章
虚 位 移 原 理 及 应 用
约束是理想的,可用虚功原理。 r3 y tan r2 r3 x r2 r tan tan r3 y 1 r3 y tan r3 x r 1
虚功原理: P r P r2 W r3 y 0 1 1 2
虚功原理: A P rA Q rB 0
P rB tan Q rA
P
y
A
rA
O
l
rB
B
x
Q
解
解析法
第4章
2 2 约束方程: xB yA l 2
虚 位 移 原 理 及 应 用
变分得: 2 xB xB 2 yA yA 0 xB yA xB cot xB yA 虚功原理: y Q xB P yA 0
第1节
虚位移原理
2013年8月23日
虚位移原理
第4章
虚 位 移 原 理 及 应 用
具有理想约束的质点系,在给定位置处于平 衡的充分必要条件是:主动力系在质点系的 任意虚位移上所作的虚功等于零,即:
( F r 0 F δx F δy F δz ) 0
i i
xi i yi i zi i
P
P Q tan
A l
O
B Q
x
例5
第4章
虚 位 移 原 理 及 应 用
已知:a, P, M; 求:约束反力NB
a
a
M A
C
a
a
P B
解
第4章
(1) 解除B水平约束,求NBx
理论力学:第13章 虚位移原理及分析力学基础
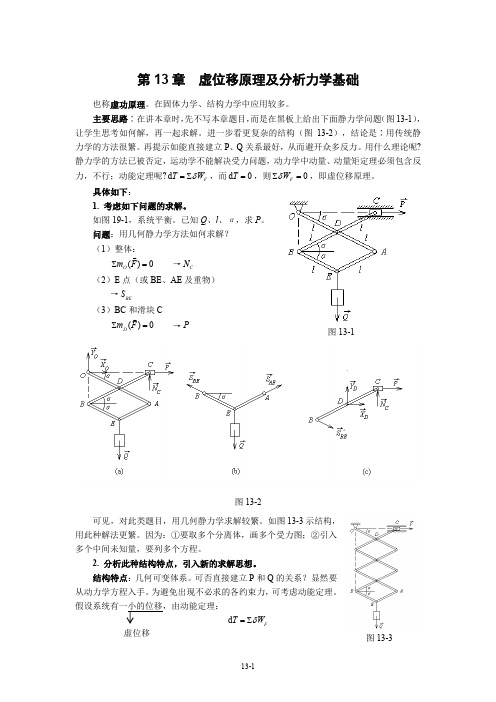
第13章 虚位移原理及分析力学基础也称虚功原理。
在固体力学、结构力学中应用较多。
主要思路∶在讲本章时,先不写本章题目,而是在黑板上给出下面静力学问题(图13-1),让学生思考如何解,再一起求解。
进一步看更复杂的结构(图13-2),结论是∶用传统静力学的方法很繁。
再提示如能直接建立P 、Q 关系最好,从而避开众多反力。
用什么理论呢?静力学的方法已被否定,运动学不能解决受力问题,动力学中动量、动量矩定理必须包含反力,不行;动能定理呢?d F T W δ=∑,而d 0T =,则0F W δ∑=,即虚位移原理。
具体如下:1. 考虑如下问题的求解。
如图19-1,系统平衡。
已知Q 、l 、α,求P 。
问题:用几何静力学方法如何求解? (1)整体:()0O m F ∑=→C N (2)E 点(或BE 、AE 及重物)→BE S(3)BC 和滑块C()0D m F ∑=→P图13-2可见,对此类题目,用几何静力学求解较繁。
如图13-3示结构,用此种解法更繁。
因为:①要取多个分离体,画多个受力图;②引入多个中间未知量,要列多个方程。
2. 分析此种结构特点,引入新的求解思想。
结构特点:几何可变体系。
可否直接建立P 和Q 的关系?显然要从动力学方程入手。
为避免出现不必求的各约束力,可考虑动能定理。
假设系统有一小的位移,由动能定理:d F T W δ=∑图13-1图13-3虚位移由于系统平衡,动能无变化,d 0T =,则0F W δ∑= → 虚功方程此方程中只包含P 和Q ,故建立了简单的方程,可求P 。
此便是虚位移原理的思想。
严格建立虚位移原理,需有诸多基本概念。
13.1 约束 约束的运动学分类静力学中讲的约束——约束的力的性质(约束的力的方面),用约束力表示,常指物体; 此处讲的约束——约束的运动的性质(约束的运动的方面),用约束方程表示,指限制条件。
一、 约束和约束方程自由质点系:运动不受任何限制。
非自由质点系:运动受到限制——约束。
《理论力学》第十三章--虚位移试题及答案
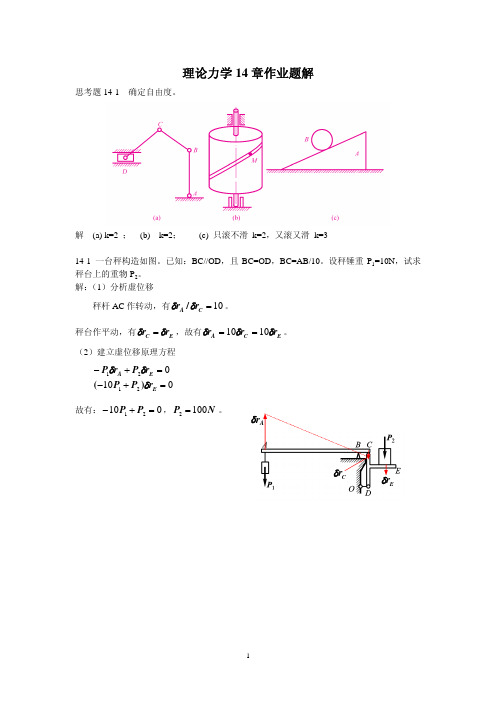
理论力学14章作业题解思考题14-1 确定自由度。
解 (a) k=2 ; (b) k=2; (c) 只滚不滑 k=2,又滚又滑 k=314-1 一台秤构造如图。
已知:BC//OD ,且BC=OD ,BC=AB/10。
设秤锤重P 1=10N ,试求秤台上的重物P 2。
解:(1)分析虚位移 秤杆AC 作转动,有10=C A r r d d /。
秤台作平动,有E C r r d d =,故有E C A r r r d d d 1010==。
(2)建立虚位移原理方程1002121=+-=+-E E A r P P r P r P d d d )(故有:01021=+-P P ,N P 1002=。
Cr d Er14-5 OA=l ,OC=R满足的条件。
解: (用虚位移原理求解)(1) 运动分析(虚位移关系分析)A 处虚位移关系用合成运动的理论分析。
A 为动点,OC 为动系。
r e A r r r r r r d d d +=f d d cos A e r r =另外:R r l r C e /d d = (2) 虚功方程fd f f d d d d cos /)cos /(cos /R l F F r R l F F R r l F r F r F r F C C C A C 21212121000==-=-=-14-9 已知:AC=BC=EC=GC=DE=DG=l ,荷载F 2。
求平衡时的F 1。
解 用解析法,1个自由度,选q 为广义坐标。
建立坐标,如图。
(1) 计算虚位移qdqd q qdq d q sin ,cos cos ,sin l y l y l x l x A A D D 2233-====(2) 计算力的投影 2211F F F F x y -=-= , (3) 建立虚位移原理方程qqdq q q d d sin cos )cos sin (230320212121F F l F l F x F y F D x A y ==×-×=+Oxy14-12 F=4kN, AO=OE=5m. 求D 解:(1) 接触D 处水平约束,代之约束力。
15 理论力学--虚位移原理及其应用

(i = 1, 2,⋯, n )
O θ1 l1 M1(x1,2) y θ2 y l2 M2(x2,y2) x
如图15-5所示双摆。质点系由两个 质点组成,受到两个几何约束,广义坐 标数(或自由度数)为 2 ,可以选取角
ϕ 1和 ϕ 2作为广义坐标, ϕ 1和 ϕ 2相互
独立。
图 15-5
15.2.4 虚位移分析 15.2.4.1 几何法 应用几何学或运动学的方法求各点虚位移间的关 系。首先根据系统的约束条件,确定自由度,给定虚 位移,画出虚位移图,然后应用运动学的方法求有关 点虚位移间的关系。 质点的无限小位移与该点的速度成正比,即dr = v dt。 两质点无限小位移大小之比等于两点速度大小之比。 两质点虚位移大小之比等于对应点虚速度大小之比。 可以应用运动学中的速度分析方法(如瞬心法、速度 投影法、速度合成定理等)去建立虚位移间的关系。
本章重点 虚位移、理想约束的概念,应用虚位移原理 求解物体系的平衡问题。 本章难点 广义坐标、广义力的概念,广义坐标形式的 虚位移原理。
15.1 约束及其分类 . 15.1.1 约束与约束方程 位形(Configuration): 位形 质点系内各质点在空间的位置的集合。 约束(Constraints): 约束 在非自由质点系中,那些预先给定的限制质点系 位形或速度的运动学条件。 例如,限制刚体内任意两点间的距离不变的条件 ,限制车轮在直线轨道上滚动而不滑动的条件 约束方程(Contraint equations): 约束方程 限制条件的数学方程式。
f j ( x1 , y1 , z1 ; ⋯; xn , yn , zn ) = 0
( j = 1, 2,⋯, s )
(15-3)
15.2 虚位移与自由度 . 15.2.1 虚位移 质点或质点系在给定位置(或瞬时),为约束所 容许的任何无限小位移,称为质点或质点系在该位置 的虚位移 虚位移(Virtual displacement)。 虚位移 虚线位移:δ r , δ r = δ x i + δ y j + δ z k 。 虚角位移:δϕ , δθ 。
理论力学答案完整版(清华大学出版社)9

F1 = F1(sinϑ i − cosϑ j) , F2 = F2i
点 A 和 B 的坐标及其变分为
rA = −(l1 − l2 )cosϑ i + (l1 + l2 )sinϑ j
,
rB = −2l1 cosϑ i
δrA = (l1 − l2 )sinϑ ⋅δϑ i + (l1 + l2 )cosϑ ⋅δϑ j ,
Fδ re − G1δ ra = 0 按速度合成定理,虚位移存在如下关系:δ ra = δ re tan β ,于是
(a)
题 9-9 图
导出 F = G1 tan β .
(2)水平面有摩擦时,当水平力 F 较小,斜面 D 有向左运动趋势,此时摩擦力方向向右,
临界平衡时,虚功方程为
(F + ) Fmax δ re − G1δ ra = 0 , 其中 Fmax = (G1 + G2 ) f 。求得: F ≥ G1 tan β − (G1 + G2 ) f .
i =1
解题要领 1) 对于自由度不为零的系统,求其平衡时主动力满足的关系可用虚功原理. 2) 对于自由度为零的系统,为求其约束力,可以依次解除一个约束,使自由度为 1,即将
此约束力作为主动力应用虚功原理. 3) 独立的坐标变分个数与系统的自由度相同,可以用解析或虚速度的方法建立不独立的坐
标变分满足的关系.
三 广义坐标表示的虚位移原理
广义坐标:确定质点系位形的独立坐标。
虚功原理的广义坐标表述:受理想约束的质点系,其平衡的充分必要条件是系统所有与广义
坐标对应的广义力为零
Qj = 0 ( j = 1,2,L, m)
∑ 其中
Qj
=
理论力学(机械工业出版社)第四章虚位移原理习题解答

习 题4-1 如图4-19所示,在曲柄式压榨机的销钉B 上作用水平力F ,此力位于平面ABC 内,作用线平分∠ABC 。
设AB =BC ,∠ABC =θ2,各处摩擦及杆重不计,试求物体所受的压力。
图4-190δ)90cos(δδN =--︒=∑C B F s F s F W θ)90cos(δ)902cos(δθθ-︒=︒-C B s s θθsin δ2sin δC B s s = 虚位移原理0δ)90cos(δδN =--︒=∑C B F s F s F W θ 0δsin δN =-C B s F s F θθθθθtan 2)2sin(sin sin δδ2N F F s s F F C B ===4-2 如图4-20所示,在压缩机的手轮上作用一力偶,其矩为M 。
手轮轴的两端各有螺距同为h ,但方向相反的螺纹。
螺纹上各套有一个螺母A 和B ,这两个螺母分别与长为l 的杆相铰接,四杆形成棱形框,如图所示,此棱形框的点D 固定不动,而点C 连接在压缩机的水平压板上。
试求当棱形框的顶角等于2f 时,压缩机对被压物体的压力。
图4-20ϕϕcos δ)290cos(δC A s s =-︒ C A s s δsin δ2=ϕ而 θϕδπ2c o s δP s A =ϕθϕθϕtan δπsin δcos π22δPP s C ==虚位移原理0δδδN =-=∑C F s F M W θ 0tan δπδN =⨯-ϕθθPF M ϕcot πN PMF =4-3 试求图4-21所示各式滑轮在平衡时F 的值,摩擦力及绳索质量不计。
图4-21虚位移原理0δδδ=+-=∑A B F s G s F W(a) A B s s δ2δ= 2G F =(b) A B s s δ8δ= 8G F = (c) A B s s δ6δ= 6G F =(d) A B s s δ5δ= 5G F =4-4 四铰连杆组成如图4-22所示的棱形ABCD ,受力如图,试求平衡时θ应等于多少?图4-22θθcos δ)290cos(δC B s s =-︒ C B s s δsin δ2=θ 虚位移原理0δcos δ2δ=-=∑C B F s G s F W θ0sin δ2cos δ2=⨯-θθB B s G s Fθtan =GF4-5 在图4-23所示机构中,曲柄OA 上作用一力偶矩为M 的力偶,滑块D 上作用一水平力F ,机构尺寸如图。
理论力学-虚位移原理

因此,在虚位移原理中,首先要研究加在质点系上的 各种约束,以及约束所许可的位移的普遍性质。
第六章 虚位移原理
§6-2 约束和约束方程
约束与约束方程 约束的类型
第六章 虚位移原理
§6-2 约束和约束方程
式中xA,yA和xB,yB分别为A,B两点的直角坐标。上述方程表明这四 个坐标并非都独立。可以消去其中的某三个,从而只剩下一个独立坐标,
这一坐标完全确定了此质点系的位置。
以后我们改称系统的位置为位形。
第六章 虚位移原理
§6-2 约束和约束方程
约束实例
曲面
图示质点A在曲面上运动,质点A的约束方程就是曲面 的曲面方程:
z
f (x, y, z) 0
A(x, y, z)
z
y
x
x
y
第六章 虚位移原理
§6-2 约束和约束方程
约束类型
三、约束的类型
按照约束对质点系运动限制的不同情况,可将约束分类如下:
1.完整约束和非完整约束
其约束方程的一般形式为
f j (x1, y1, z1; ...; xn , yn , zn; x1, y1, z1, ...; xn, yn, zn; t) 0
约束类型
第六章 虚位移原理
非完整约束
§6-2 约束和约束方程
约束类型
2.定常约束和非定常约束
● 如果约束方程中不含时间t,这种约束称为定常约束或稳 定约束。
定常约束一般形式为
f j (x1, y1, z1; ...; xn, yn, zn; x1, y1, z1,...; xn, yn, zn;) 0
理论力学课件 虚位移原理

N
设AB杆与BC杆在B点用光滑
铰链连接.由N = -N 得
A
C Nr + Nr = Nr - Nr = 0
24
(3)连接两质点的无重刚杆
连接两质点的刚杆由于不
计自重,均为二力杆. 设质点
M1和M2的虚位移分别为 r1
M2
与r2 则有:
r1cos 1 = r2cos 2 N1r1 + N2r2
n
Fi ri 0
i 1
n
或:
Fxixi Fyiyi 0
i 1
27
五、虚位移原理的应用 1.求解复杂系统(运动机构)的平衡条件.
1)画虚位移图.
2)利用几何法或解析法求各虚位移之 间的关系.
3)计算各主动力的虚功. 4)利用虚位移原理求解平衡条件.
28
例题5. 套筒分别置于光 滑水平面上互相垂直的 滑道中,受力分别为P和 Q如图所示.长为 l 的连 杆和水平方向夹角为 , 摩擦均不计.求系统的平 衡条件.
以Ni表示质点系中质点Mi的约束力的合 力 , ri表示该质点的虚位移 , 则质点系的理想 约束条件可表示为
n
Ni·ri = 0
i 1
23
(1)光滑接触面
光滑接触面的约束反力恒垂直
N
于接触面的切面 , 而被约束质点的
r
虚位移总是沿着切面的 , 即N r
Nr = 0
r B N (2)连接两刚体的光滑铰链
l
A(x,y) x 图1-3
6
O
y 左图中摆锤A的约束方程为
l
(细绳)
x2 + y2 l 2
A(x,y) x
图1-4
理论力学解答(清华版)

第一章 静力学基本概念1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2FB.2F - 1FC.1F +2F图1-18 图1-191-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体;B. 变形体;C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.-F/31-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21第二章力系的简化2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A指向B的力F,在z轴上投影为,对z轴的矩的大小为。
答:F/2;62F/5。
2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b,c,则力F在轴z和y上的投影:Fz= ;Fy= ;F对轴x的矩M x(F)= 。
答:Fz=F·sinφ;Fy=-F·cosφ·cosφ;Mx(F)=F(b·sinφ+c·cosφ·cosθ)图2-40 图2-412-3.力通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力在x轴上的投影为,对x轴的矩为。
理论力学13虚位移原理

在分析力学中,拉格朗日方程是描述系统动力学的关键方程。通过应用虚位移原理,可以推导出拉格朗日方程的形式和求解方法。
拉格朗日方程的推导
在分析力学中的应用
04
CHAPTER
虚位移原理的推导过程
定义
01
虚功是系统在虚位移上所做的功,等于作用力与虚位移的点积。
虚功原理表述
02
对于一个处于平衡状态的力学系统,所有外力在任何虚位移上所做的虚功总和为零。
理论与其他物理场的结合
在多物理场问题中,可以将虚位移原理与热力学、电磁学等领域的基本原理结合起来,以解决更为复杂的工程问题。
对理论的发展和推广
THANKS
感谢您的观看。
理论力学13虚位移原理
目录
虚位移原理的概述 虚位移原理的基本概念 虚位移原理的应用 虚位移原理的推导过程 虚位移原理的限制和推广
01
CHAPTER
虚位移原理的概述
虚位移
在理想约束条件下,系统发生的微小位移。
虚位移原理
在平衡状态下,系统所受的外力对任意虚位移所做的总虚功为零。
虚功
在虚位移过程中,作用力对机构所做的功称为虚功。
虚速度和虚加速度的推导
05
CHAPTER
虚位移原理的限制和推广
VS
虚位移原理主要适用于分析力学中,特别是对刚体和弹性体的平衡问题进行分析。
限制条件
虚位移原理仅适用于保守系统,即系统中不存在非保守力(如摩擦力)的情况。同时,该原理假定系统处于平衡状态,对于动态问题不适用。
适用范围
适用范围和限制条件
虚位移原理在工程领域中也有广泛应用,如机构分析、机器人学、车辆动力学等领域。
01
02
第15章 虚位移原理_例题

δ y D = − 2 a sin ϕδϕ − b sinψδψ x B = 2 a sin ϕ + 2 b sinψ , δ x B = 2 a cos ϕδϕ + 2 b cosψδψ
代入(a)式,得:
( − P a sin ϕ − P2 2a sin ϕ + F 2a cos ϕ )δϕ + ( − P2b sin ψ + F 2b cosψ )δψ = 0 1
h 4、列虚功方程: δW = 2 Flδϕ − FN δs = (2 Fl − FN ) ⋅ δϕ = 0 2π
δϕ 是任意的,有: 2 Fl − h F = 0 由于 N 2π 也即:
l ∴ FN = 4π F h
讨论: 1)利用约束力不做功避免了所有约束力的出现, 这是虚位移原理解题与矢量静力学解题相比的巨大优点。 2)本题求虚位移间关系的方法为:由物理关系直接给 出法。
− M δθ − F δx B = 0
注意:几何法时,主动力与虚位移方向一致为正;
力偶、角度逆时针为正 解析法时主动力、坐标变分各自沿坐标轴方向为正,力偶、角度逆时针为正。 力偶
例4 均质杆OA及AB在A点用铰连接,并在O点用固定铰 支座,如图所示。两杆各长2a和2b,各重P1及P2,设在B点 加水平力 F 以维持平衡,求两杆与铅直线所成的角ϕ及ψ 。
而
δ rC = a δϕ , δ rB = δ rD = δ rA = 2 a δϕ
代入上式后,得:
( F cosϕ ⋅2a − P1 ⋅asinϕ − P2 ⋅2asinϕ )δϕ = 0
tgϕ =
2F P1 + 2 P2
讨论:其它可能虚位移与真实位移
例5 :升降机构,
理论力学(刘又文 彭献)答案第8章

5.如图 8.6a、b、c、d 中虚线所示的虚位移是否对?
F
A
FQ
Cv δs A
δs B
δs A δsD D
B δs E C δ sC
B O δs B
(a)
C
A
δs D
E
(b)
δs A δs A O
F
A
C
v
F
A
δs A
δs B
B
B
C
δs B
O1
δs B
O
(d)
δ sC
δ sC
M
(c)
图 8.6 257
7.如图 8.8 a 所示桁架,在用虚位移原理求 CD 杆内力时,给实线虚位移如
258
图 b 所示。对吗?
G A C D B A F
图 8.8
G
C δ sC δ s D D δ sC E δs E F
(b)
δs D B F δs F F
E F
(a)
F
答:不对。 δsC 、 δsD 如图 b 中虚线所示是正确的。因为,ACF 部分绕 A 点 定轴转动, C 点虚位移应垂直 AC 连线; BDF 部分作平面运动且 B 点为速度瞬心, 所以 D 点虚位移应垂直 BD。 虚位移关系
第8章
一.约束与虚位移 虚位移
虚位移原理与能量法
§8.1 概念答疑
1.“虚位移是一种假想的位移,不可能是真实位移”,这种说法对吗? 答: 不对。 因为虚位移是约束允许的微小位移。 实位移也必须是约束允许的, 是在一定的外力和初始条件下实现的确定位移。在定常约束下,实位移一定是虚 位移中的一个。例如,图 8.1 所示单摆的虚位移可为 δϕ1 和 δϕ 2 ,而真实移只取其 一。
【工程力学 课后习题及答案全解】第25章虚位移原理在弹性静力学中的应用习题解

S表面
S表面
由功的互等定理(1)=(2)
(2)
习题 25-4 图
F
(a)
q(∆V ) F
= 1 − 2ν E
Fql
所以 (∆V ) F
=
1 − 2ν E
Fl
25-5 具有中间铰的线弹性材料梁,受力如图 a 所 示,两段梁的弯曲刚度均为 EI。用莫尔法确定中间铰两侧 截面的相对转角有下列四种分段方法,试判断哪一种是正 确的。
θ wmax
θM wmax θ
(a)
示。若集中力 F 和集中力偶 M 数值相等,试判断下列等
式(数值相等)中哪一个是正确的。
(A) ∆ yC (M ) = ∆ yC (F ) ;
(B)θ B (M ) = θ B (F ) ; (C) θ B (M ) = ∆ yC (F ) ;
— 15 —
(D) θ B (F ) = ∆ yC (M ) 。
=
11ql 3 24EI
(→)
∆Cy
=
1 EI
(M C3 AΩ3) =
1 EI
⎡ ⎢( ⎣
1 2
⋅
ql 2 2
)(
1 2
⋅
l 4
⋅
⎤ l)⎥
⎦
=
ql 4 32EI
(↓)
(b)θ A
=
1 EI
(M C1AΩ1) =
1 EI
⎡ ⎢( ⎣
1 2
)(
2 3
⋅
ql 2 8
⎤ ⋅l)⎥ =
⎦
ql 3 24EI
(逆)
习题 25-8 图(a)
习题 25-8 图(b)
习题 25-8 图(c)
M
虚位移原理习题解答

7-1. 在图示机构中,曲柄OA 上作用一力偶,其矩为M ,另在滑块D 上作用水平力F 。
机构尺寸如图所示。
求当机构平衡时,力F 与力偶矩M 的关系。
解 设OA 杆虚位移为δϕ,则A 、B 、C 、D 各点虚位移如图,θδθδθδθδδϕδcos 2cos cos 2cos D B A B A r r r r a r ===由上述各式和虚功方程0=+-D r F M δδϕ解出θ2tan Fa M =7-2. 图示桁架中,已知AD=DB=6m ,CD=3m ,节点D 处载荷为P 。
试用虚位移原理求杆3的内力。
解 B 、C 、D 各点虚位移如图所示,θδδθδθδcos ,2sin cos C D c B r r r r ==代入虚功方程 03=-B D r F r P δδ解得杆3的内力 P PF ==θcot 23 7-3. 组合梁由铰链C 铰接AC 和CE 而成,载荷分布如图所示。
已知跨度l=8m ,P=4900N ,均布力q=2450N/m ,力偶矩M=4900N ⋅m ;求支座反力。
N 2450N 14700N 2450==-=E B A F F F ,,7-4 组合梁由水平梁AC 、CD 组成,如图所。
已知:F 1= 20kN ,F 2 = 12kN ,q = 4kN/m ,M = 2kN ·m 。
不计梁自重,试求:固定端A 和支座B 处的约束力。
组合梁由水平梁AC 、CD 组成,如图12-16a 所。
已知:F 1= 20kN ,F 2 = 12kN ,q = 4kN/m ,M = 2kN ·m 。
不计梁自重,试求:固定端A 和支座B 处的约束力。
(a)(b)2 222(d )(e)图12-16 例题12-5图解:组合梁为静定结构,其自由度为零,不可能发生虚位移。
为能应用虚位移原理确定A 、B 二处的约束力,可逐次解除一个约束,代之以作用力,使系统具有一个自由度,并解除约束处的正应力视为主动力;分析系统各主动力作用点的虚位移以及相应的虚功,应用虚位移原理建立求解约束力的方程。
虚位移原理

同样可得
二、虚位移的计算
或者,由于 为AB的瞬心,故
由正弦定理
16.2
虚 位 移 及 其 计 算
二、虚位移的计算
2、解析法
解析法是利用对约束方程或坐标表达式进行变分以求出虚位移之间的关系。例如
椭圆规机构如图,坐标
有约束方程
对上式进行变分运算得
16.2
虚 位 移 及 其 计 算
或者把 表示成 的函数,也可求出虚位移间的关系。
因为
作变分运算
所以
比较以上两种方法,可以发现,几何法直观,且较为简便,而解析法比较规范。
选广义坐标为φ
(解析法)
在x、y轴上的 分量:
各质点虚位移之间的关系的几何法
理论力学:第十六章 分析力学基础
16.1.4完整约束与非完整约束
完整约束 —— 约束方程不包含质点速度,或者包含质点 速度但约束方程是可以积分的约束(几何约束以及可以积分的运动约束);
非完整约束 —— 约束方程包含质点速度、且约束方程不 可以积分的约束(不能积分的运动约束)。
理论力学:第十六章 分析力学基础
在本例中:可以选择 θ 为质点的广义坐标, A的直角坐标可以表示为:
y
x
O
A(x1, y1)
B(x2, y2)
a
b
理论力学:第十六章 分析力学基础
例如:双摆中摆的约束方程只有2个
其确定摆位置的两个坐标X1、X2、Y1、Y2中 只有2个是独立的
所以一般选择2个独立参量来确定摆的位置,
在本例中:可以选择 θ φ为质点的广义坐标, 摆锤的直角坐标可以表示为:
1. 虚位移
x
y
O
理论力学---第十五章虚位移原理

由于 任意,故 PQ tg 24
[练习15-1] 该机构在图示位置平衡,求F1和 F2的关系。
(题2-14)
B
解:建立F1和F2的虚功方程:
A
δrA
90°
45°30°
F2
F1
60°
δrB
F1 rA F2 cos30rB 0
rA cos45 rB
F1 rA F2 cos30rA cos45 0
xC asin , yC acos xA lsin , y A lcos xB 2asin , yB 0
14
三、虚功
力 F 在质点发生的虚位移r 上所作的功称为虚功,记为W。
W F r W XxYy Zz
15
理想约束
如果在质点系的任何虚位移上,质点系的所有约束反力的 虚功之和等于零,则称这种约束为理想约束。
(Fi Ni ) ri Ri ri 0
对质点系: (Fi Ni ) ri 0 (理想约束下, Ni ri 0 )
Fi ri 0 与前题条件矛盾 故 Fi ri 0 时质点系必处于平衡。
20
二、虚位移原理的应用 1、系统在给定位置平衡时,求主动力之间的关系; 2、求系统在已知主动力作用下的平衡位置; 3、求系统在已知主动力作用下平衡时的约束反力; 4、求平衡构架内二力杆的内力。
l
角时 ,
l
0.6
0.3
cos
弹簧变形量 l0 l 0.3(co1s 1) (m)
弹簧力:F F k 1.(5 co1s 1) (kN)
l
sin
0.3 co
s2
由虚位移原理,得: M Fl 0
M 1.5(co1s 1)(0.3csoisn2 ) 0
理论力学习题详细解答 第12章 虚位移原理及其应用习题解

第12章 虚位移原理及其应用12-1 图示结构由8根无重杆铰接成三个相同的菱形。
试求平衡时,主动力F 1与F 2的大小关系。
解:应用解析法,如图(a ),设OD = lθsin 2l y A =;θsin 6l y B =θθδcos 2δl y A =;θθδcos 6δl y B =应用虚位移原理:0δδ12=⋅-⋅A B y F y F02612=-F F;213F F =12-2图示的平面机构中,D 点作用一水平力F 1,求保持机构平衡时主动力F 2之值。
已知:AC = BC= EC = DE = FC = DF = l 。
解:应用解析法,如图所示:θcos l y A =;θsin 3l x D = θθδsin δl y A -=;θθδcos 3δl x D =应用虚位移原理:0δδ12=⋅-⋅-D A x F y F0cos3sin 12=-θθF F ;θcot 312F F =12-3 图示楔形机构处于平衡状态,尖劈角为θ和β,不计楔块自重与摩擦。
求竖向力F 1与F 2的大小关系。
解:如图(a ),应用虚位移原理:0δδ2211=⋅+⋅r F r F 如图(b ):βθtan δδtan δ2a 1r r r ==;12δtan tan δr r θβ=0δtan tan δ1211=⋅-⋅r θβF r F ;θβtan tan 21⋅=F F12-4 图示摇杆机构位于水平面上,已知OO 1 = OA 。
机构上受到力偶矩M 1和M 2的作用。
机构在可能的任意角度θ下处于平衡时,求M 1和M 2之间的关系。
习题12-1图(a )习题12-2解图习题12-3(a )r a(b )解:应用虚位移原理:0δδ2211=⋅-⋅ϕϕM M (1)如图所示,e a δcos δr r =θ其中:`1a δδϕ⋅=OA r ;2e δcos 2δϕθ⋅⋅=OA r 所以:21δ2δϕϕ=,代入式(1)得:122M M =12-5 等长的AB 、BC 、CD 三直杆在B 、C 铰接并用铰支座A 、D 固定,如图所示。
理论力学课件习题虚功原理

2a
W
例5、质量为m的质点在光滑的水平桌上运动。此质点 上系一根轻绳,绳子穿过桌面上一小孔O,另一端挂一 质量为m’ 的质点,试讨论质点m的运动情况。
M
M’
Q m g[2 R sin 2 (2 R cos l ) cos ] 0
D O C
B
A
例2(p39-2.3)
• 解:体系自由度为取ACO()为广义坐标,以c点为坐标原 点,ABC( ).主动力为P和Q,由虚功原理得:
y A
w P rB Q rA Px B Qy A 0 x B l1 cos l 2 cos y A l 2 sin P l1 sin l 2 sin Ql2 cos 0 Q l1 sin l 2 sin P l 2 cos O l1 sin l 2 sin l 2 cos l1 cos Q tan tan P
Q
O
பைடு நூலகம்
P
c
B
x
例3 三个相同的匀质球,求平 衡时α的关系
O
α l O1 O3 O2
A
2个自由度 , r sin l sin 2r sin w m gy1 2m gy 2 y 2 l cos r cos y1 y 2 2r cos l cos r cos 2r cos
w 3l (sin cos tan ) 2r (sin 3 cos tan ) 0 1 tan tan tan 3 即O2 应该在过 A点的竖直线外侧,而且 与A,O在一条直线上
例4:长度为L的轻棒四根,光滑地连成一菱形ABCD。 AB,AD两边支于同一水平线上相距为2a的两个钉上,BD 间用一轻绳联接,C点上系一重量W。设A点的顶角为2a, 试用虚功原理求绳长中张力T。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12章 虚位移原理及其应用
12-1 图示结构由8根无重杆铰接成三个相同的菱形。
试求平衡时,主动力F 1与F 2的大小关系。
解:应用解析法,如图(a ),设OD = l
θsin 2l y A =;θsin 6l y B = θθδcos 2δl y A =;θθδcos 6δl y B =
应用虚位移原理:0δδ12=⋅-⋅A B y F y F
02612=-F F
;213F F =
12-2图示的平面机构中,D 点作用一水平力F 1,求保持机构平衡时主动力F 2之值。
已知:AC = BC
= EC = DE = FC = DF = l 。
解:应用解析法,如图所示:
θcos l y A =;θsin 3l x D = θθδsin δl y A -=;θθδcos 3
δl x D =
应用虚位移原理:0δδ12=⋅-⋅-D A x F y F
0cos
3sin 12=-θθF F ;θcot 312F F =
12-3 图示楔形机构处于平衡状态,尖劈角为θ和β,不计楔块自重与摩擦。
求竖向力F 1与F 2的大小关系。
解:如图(a ),应用虚位移原理:0δδ2211=⋅+⋅r
F r F 如图(b ):
β
θt a n δδt a n δ2
a 1r r r ==
;12
δtan tan δr r θ
β
=
0δtan tan δ1211=⋅
-⋅r θβF r F ;θ
β
tan tan 21⋅=F F
12-4 图示摇杆机构位于水平面上,已知OO 1 = OA 。
机构上受到力偶矩M 1和M 2的作用。
机构在可
习题12-1图
(a )
习题12-2解图
习题12-3
(a )
r a
(b )
能的任意角度θ下处于平衡时,求M 1和M 2之间的关系。
解:应用虚位移原理:0δδ2211=⋅-⋅ϕϕM M (1)
如图所示,e a δcos δr r =θ
其中:`1a δδϕ⋅=OA r ;2e δcos 2δϕθ⋅⋅=OA r 所以:21δ2δϕϕ=,代入式(1)得:122M M =
12-5 等长的AB 、BC 、CD 三直杆在B 、C 铰接并用铰支座A 、D 固定,如图所示。
设在三杆上各有一力偶作用,其力偶矩的大小分别为M 1 、M 2和M 3。
求在图示位置平衡时三个力偶矩之间的关系(各杆重不计)。
解:应用虚位移原理:
0δδδ332211=⋅+⋅+⋅ϕϕϕM M M (1)
如图所示,B C r r δ60sin δ=︒;CB C r r δ60cos δ=︒
设三杆长均为l ,则有:`1δδϕl r B =;3δδϕl r C =;2δδϕl r CB =
所以:
13δδ23ϕϕ=,23δδ2
1
ϕϕ=代入式(1)得: 02
1
23321=++M M M ;023321=++M M M 12-6 图示三根均质杆相铰接,AC = b ,CD = BD = 2b ,AB = 3b ,AB 水平,各杆重力与其长度成正比。
求平衡时θ、β与γ间的关系。
解:应用解析法,如图所示:
θsin 2
b y E =
; θθδcos 2δb
y E =
γθsin sin b b y F +=;γγθθδcos δcos δb b y F +=
βsin b y G =; ββδcos δb y G =
应用虚位移原理:0δ2δ2δ=++⋅G F E y mg y mg y mg 即:0δcos 2)δcos δcos (2δcos 2
=+++⋅
ββγγθθθθmgb b b mg b
mg (1) 根据几何关系:βγθsin 2sin 2sin b b b =+;βγθcos 2cos 2cos 3b b b b ++=
e 习题12-4解图
r C
r B 习题12-5解图
习题12-6解图
对上两式求变分:;ββγγθθδcos 2δcos 2δcos b b b =+;γβ
γ
θβθβδcos cos δcos 2cos δ+=
0δsin 2δsin 2δsin =---ββγγθθb b b ;
γβθθβγγθδtan cos sin tan cos sin 2
δ++-=;=βδγβ
θθβ
γγθγβδ)tan cos sin tan cos sin cos (cos cos 1++-=
将上式代入式(1),有:
0tan tan sin cos tan 2cos 2tan tan tan cos sin 5=+-++++-β
θγ
γθγβθβγγmg mg mg
0)sin cos (tan 2)tan (tan cos 2)tan cos (sin 5=-++++-γγθβθγβγγ 0)tan (tan 2)tan (tan 2)tan (tan 5=-++++-γθβθβγ 0tan 3tan 7tan 4=--βγθ
12-7 计算下列机构在图示位置平衡时主动力之间的关系。
构件的自重及各处摩擦忽略不计。
解:图(a ):0δδ=⋅
-⋅l r M r F D
C ;︒=︒30cos δ60cos δ
D C r r 0δδ3=⋅-⋅l
r
M r F D D ;Fl M 3=
图(b ):0δδ2a e =⋅-⋅l r
M r F ;e a δ60cos δr r =︒
0δδa a =⋅-⋅l r
M r F ;Fl M =
图(c ):0δδ=⋅-⋅r
r
M r F A C ;)cos(δcos δθϕϕ-=B A r r ;θθ2sin δcos δB C r r =
C A r r δ2tan cot δϕθ+=;0δ2cot tan δ=+⋅-⋅C C r r
M r F θϕ
习题12-7解图
(a )
θ
ϕcot tan 2+=
rF
M
12-8 机构如图,已知OA = O 1B = l ,O 1B ⊥OO 1,力偶矩M 。
试求机构在图示位置平衡时,力F 的大小。
解:应用虚位移原理:0δδ=⋅-⋅θM r F B (1)
如图所示,e a δsin δr r =θ;其中:θδδa l r =;
δδe l l
r
r B =所以:B r l δsin sin δθθθ=, 代入式(1)得:l
M F =
12-9 机构如图,已知OA = 20cm ,O 1D = 15cm ,O 1D // OB ,弹簧的弹性系数k = 1000N/cm ,已经拉伸变形cm 2s =λ,M 1 = 200N · m 。
试求系统在θ = 30º、β
解:应用虚位移原理:
0δδδ121=⋅-⋅-⋅
D
O r
M r F OA r M D B A (1) 如图所示,B C A r r r δδδ==
θθcos δsin δD C r r =
代入式(1)得:0δtan δδ121=⋅-⋅-⋅
D
O r M r F OA r M A
A A θ m N 8.259)210002
.0200(30tan 15.0)(tan s 112⋅-=⨯-︒=-=
λθk OA M D O M
12-10 在图示结构中,已知铅垂作用力F ,力偶矩为M 的力偶,尺寸l 。
试求支座B 与C 处的约束力。
解:解除B 处约束,系统的虚位移如图(a ),
应用虚位移原理:
0δδδ=⋅+⋅-⋅ϕM r F r F D B B (1)
其中:B D r r δ2δ=;l r l r B D δ2δδ==ϕ
代入式(1)得:
0δ2δ2δ=⋅
+⋅-⋅
l
r M r F r F B
B B B
习题12-8解图
习题12-9解图
习题12-10图
(a )。
