几何光学的习题ppt课件
合集下载
第十一章几何光学ppt - 加入收藏

近视眼的配镜:凹透镜的作用是把无穷远处物体成 像在近视眼远点,使眼不调节可看清远物。 凹透镜 远点
远点距离
此时有:p =∞, p′=-(远点距离)
由透镜成像公式得: f= p′ 凹透镜焦度:Φ =1/f=1/ p′凹透镜片度数= -100D(度)
远视眼的配镜:凸透镜的作用是把近点之内(或 明视距离处)的物体成像在远视眼近点。
y f1 y
f2
显微镜的放大率:
tg
y 25
y 25 M y / 25 y f2
y/ f2
25cm
2.光学系统的分辨本领
光学仪器的圆孔衍射现象限制了光学系统分辨物体细 节的能力。 A B’
两物点
B 物镜
相应两象点
A’ 艾里斑
分辨极限:光学系统能分辨开两物点的最短距离。 分辨本领:最短距离的倒数称为光学系统的分辨本领。
凸透镜 近点 物
25cm 此时有: p = 25cm, 由透镜成像公式得: 凸透镜焦度:Φ=1/f
p′=近点距离
f pp p p
凸透镜片度数=+100D(度)
散光眼和配镜
C
A B
若AB>CD
D 原因:角膜的各个方向子午线的半径不相等
即散光眼为非对称折射系统
矫正:配戴适当焦度的柱面透镜 •凸柱面透镜 •凹柱面透镜
17 mm
f2
n 2r n 2 - n1
22 . 7 mm
2、眼的调节
眼的调节:眼睛改变自身焦度使远近不同的物体均能在视网 膜上成清晰像的本领。眼的调节是通过改变晶状体表面的 曲率来完成。 对近物:
增大晶状体表面曲率(即曲率 半径减小), 焦度增大。
几何光学习题课 学生版PPT课件
9
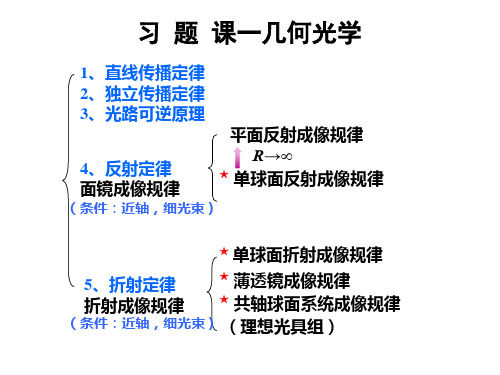
5. 如图所示,一光线射入折射率为n的一球形水滴,求(1)此光线在水滴内
球面另一侧的入射角a;此光线被全反射还是部分反射?(2)偏向角(出射 光线与入射光线之间的夹角)的d 表达式;(3)求偏向角d最小时的入射角i1.
i1 i2 a i2
d
10
6.一虚物PQ位于凹透镜右侧二倍焦距处,用作图法求它经透镜成的像。
入瞳、孔径光阑、出瞳相互共轭
将系统中各光阑逐个地对其前面光学系统成像,将所有这些像对入瞳中心
张角,其中最小张角者所对应的光阑即系统的视场光阑F.S.。
入窗—视场光阑经前面 出窗—视场光阑经后面
光学系统的像。---限制物 光学系统的像。---限制
方视场(PQ1)的大小
像方视场(P’Q1’)的大小
视场光阑、入窗、 出窗相互共轭
F
O
Q
F
P
11
7.一玻璃空盒的两端是共轴球面,一端是半径r1= —1.65cm的凹面,另一 端是半径为r2= 1.65cm的凹面,两顶点间距1.85cm。将盒在空气中密封 后放入水中。一高为1cm的物体距前凹球面的顶点10cm,与光轴垂直。
求物体经玻璃盒所成的像。(玻璃厚度忽略不计)
Q
P
C1
O1 O2
入窗 出窗
A.S. D
'0
O2
D
出瞳 E x .P .
将系统中各光阑 分别经其前面的光 学元件成像于系统 的物空间,其中对 轴上物点张角最小 的那个像所对应的
光阑即为孔径光 阑A.S.。
入瞳—孔径光阑通过其前面光学系统所成的像-----决定进入系统光束的大小 出瞳—孔径光阑通过其后面光学系统所成的像-----决定从系统出射光束的大小
5. 如图所示,一光线射入折射率为n的一球形水滴,求(1)此光线在水滴内
球面另一侧的入射角a;此光线被全反射还是部分反射?(2)偏向角(出射 光线与入射光线之间的夹角)的d 表达式;(3)求偏向角d最小时的入射角i1.
i1 i2 a i2
d
10
6.一虚物PQ位于凹透镜右侧二倍焦距处,用作图法求它经透镜成的像。
入瞳、孔径光阑、出瞳相互共轭
将系统中各光阑逐个地对其前面光学系统成像,将所有这些像对入瞳中心
张角,其中最小张角者所对应的光阑即系统的视场光阑F.S.。
入窗—视场光阑经前面 出窗—视场光阑经后面
光学系统的像。---限制物 光学系统的像。---限制
方视场(PQ1)的大小
像方视场(P’Q1’)的大小
视场光阑、入窗、 出窗相互共轭
F
O
Q
F
P
11
7.一玻璃空盒的两端是共轴球面,一端是半径r1= —1.65cm的凹面,另一 端是半径为r2= 1.65cm的凹面,两顶点间距1.85cm。将盒在空气中密封 后放入水中。一高为1cm的物体距前凹球面的顶点10cm,与光轴垂直。
求物体经玻璃盒所成的像。(玻璃厚度忽略不计)
Q
P
C1
O1 O2
入窗 出窗
A.S. D
'0
O2
D
出瞳 E x .P .
将系统中各光阑 分别经其前面的光 学元件成像于系统 的物空间,其中对 轴上物点张角最小 的那个像所对应的
光阑即为孔径光 阑A.S.。
入瞳—孔径光阑通过其前面光学系统所成的像-----决定进入系统光束的大小 出瞳—孔径光阑通过其后面光学系统所成的像-----决定从系统出射光束的大小
最新【物理课件】第三章 几何光学PPT课件

n1 x x1 2 y12 n2 x2 x2 y22
由费马原理有:
d n1x x1 n2 x2 x 0
dx
x x1 2 y12
x2 x2 y22
x x1 0 必有x2 x 0 x2 x
故 : x1 x x2 即: 折射线、 入射线分居法线两侧
Y
Ax1, y1
同理:也可证 明反射定律。
n1 A 'C AC
n 2 CB CB
'
n1 sin
i1 n 2 sin
i2
0
n 2 sin i2 n 2 sin i1
由于反射、折射定律是实 验定律,是公认的正确的 结论,所以,费马原理是
Y
Ax1, y1
M
O n1 A’
i1 Cx,0 B‘
i2
P O’ X
正确的。
Z
若光线实际发自于某点,则称该点为实发光点;
若某点为诸光线反向延长线的交点,则该点称为虚发光点。
2、单心光束:只有一个交点的光束,亦称同心光束。
该唯一的交点称为光束的顶点。
发散单心光束
会聚单心光束
3、实像、虚像
• 当顶点为光束的发出点时,该顶点称为光源、物点。
• 当单心光束经折射或反射后,仍能找到一个顶点,称光束保持了其
n2
B x2,y2
§3.3 单心光束 实像和虚像
成像问题是几何光学研究的主要问题之 一。光学元件质量的高低是 以成像质量来衡量的。为学习研究成像规律,首先介绍几个基本概念。
一、单心光束、实像、虚像
1、发光点:只有几何位置而没有大小的发射光束的光源。
它也是一个抽象概念,一个理想模型,有助于描述物和像的 性质。点光源就是一个发光点。
第五章几何光学PPT课件
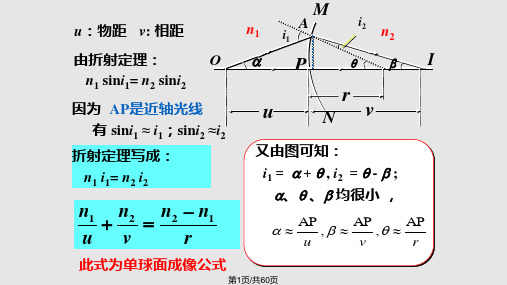
1 u
1 v
n
n0 n0
1 r1
1 r2
如薄透镜周围媒质是空气,即n0 =1,上式变为:
1 u
1 v
n
1
1 r1
1 r2
以上两式称为薄透镜成像公式,适用于各种形状 的凸凹透镜,符号规则同前.
第17页/共60页
1 u
1 v
n n0 n0
1 r1
1 r2
当薄透镜前后的媒质相同时两个焦距相等,其值为:
n1 n2
F2
第二焦度 2
2
n2 f2
n2
n1 r
n1 n2 n2 n1
f2
r
f1
n1 n2 n1
r
f2
n2 n2 n1
r
u
F2
u
f2
n1 n2
f2
1
2
n2
n1 r
n2 f2
n1 f1
f1 、 f2 为正值,折射面有会聚光线,反之发散光线
对同一折射面尽管两侧焦矩不相等,但其焦度相等。 第7页/共60页
u:物距 v: 相距
M
n1
A
i1
i2 n2
由折射定理:
O
n1 sini1= n2 sini2
因为 AP是近轴光线 有 sini1 ≈ i1;sini2 ≈i2
折射定理写成:
n1 i1= n2 i2
n1 n2 n2 n1
uv
r
P
I
r
u
Nv
又由图可知:
i1= + , i2 = - ; 、 、 均很小 ,
uv
r
n1 n2
第一焦点F1:
F1
第一焦距f1:
《几何光学综合复习》PPT课件
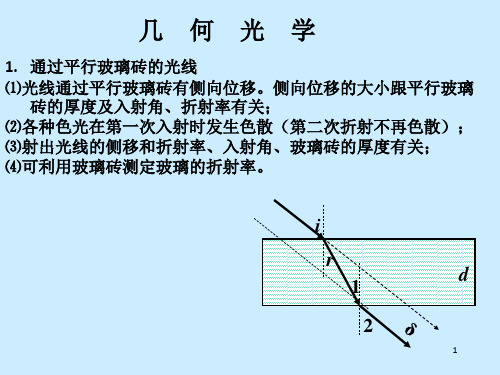
16.(15分)如图所示,一束光线以60o 的入射角射到一水平放置的平
面镜上,反射后在正上方与平面镜平行的光屏上留下一光点P,
现将一块上下两面平行的透明体平放在平面镜上,则进入透明体
的光线经平面镜反射后再从透明体的上表面射出,在光屏上留下
一光点 P‘ (图中未画出)。已知 PP 2 3 cm。透明体对光的折射
6
07届南京市综合检测题(三) 5
5.如图所示,有三块截面为等腰直角三角形的透明材料(图 中的Ⅰ、Ⅱ、Ⅲ)恰好拼成一个正方形棱镜.从E点垂直于边 射入的单色光在F处发生全反射,在G、H连续发生两次折射后 射出.若该单色光在三块材料中的传播速率依次为v1、v2、v3,
下列关系式中正确的是 ( )D
A.v3>v1>v2 B.v2>v3>v1 C.v3>v2>v1 D.v1>v2>v3
( A)
A.内芯的折射率比外套大,光传播时在内芯与外套的界 面上发生全反射
B.内芯的折射率比外套小,光传播时在内芯与外套的界 面上发生全反射
C.内芯的折射率比外套小,光传播时在内芯与外套的界 面上发生折射
D.内芯的折射率与外套的相同,外套的材料有韧性,可 以起保护作用
内芯
外套 5
06年广东东莞中学高考模拟试题2 2.对下列自然现象的描述正确的是: ( ) C
A
标 尺
B
S L0 LP
K
13
解: 设拔掉K稳定时,m下移△x,两次反射角分别为α和β,
弹簧的劲度系数为k,由力的平衡:
k△x=mg
根据反射光线得: △x+Ltanα-Ltanβ=h
根据入射光线得:
L0tanα-L0tanβ=△x
几何光学完整PPT课件
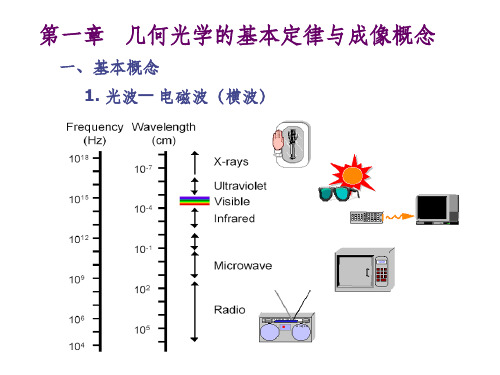
3. 物空间(不论是实物还是虚物)介质的折射率是指实际入射光 线所在空间介质折射率,像空间(不论是实像还是虚像)介质的 折射率是指实际出射光线所在空间介质的折射率。
4. 物和像都是相对某一系统而言的,前一系统的像则是后一系统 的物。物空间和像空间不仅一一对应,而且根据光的可逆性,若 将物点移到像点位置,使光沿反方向入射光学系统,则像在原来 物点上。这样一对相应的点称为“共轭点”。
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
精选
31
2. 转面公式
原则:前一折射面的象为后一面的物 ,前一面的象空间为后一面的物空间
4. C-球心 r-球面曲率半径 I 、I′-入、折射角
5. A 、A′-物点、象点 L、L′-物距、象距
精选
20
2. 符号法则(便于统一计算) 规定光线从左向右传播
a)沿轴线段 L、L′、r 以O为原点, 与光线传播方向相同,为“+” 与光线传播方向相反,为“-”
b)垂轴线段 h 在光轴之上,为“+” 在光轴之下,为“-”
例:某物体通过一透镜成像后在透镜内部,透镜材 料为玻璃,透镜两侧均为空气。问该像所处的空间 介质是玻璃还是空气?
4 5
6
3 2 1
位标器动平衡调试系统光源
第二章 球面与共轴球面系统
§ 2-1 光线光路计算与共轴光学系统
共轴球面系统— 光学系统一般由球面和平面组成, 各球面球心在一条直线(光轴)上。
精选
28
2. 轴向放大率:光轴上一对共轭点沿轴移动量之间的比值
4. 物和像都是相对某一系统而言的,前一系统的像则是后一系统 的物。物空间和像空间不仅一一对应,而且根据光的可逆性,若 将物点移到像点位置,使光沿反方向入射光学系统,则像在原来 物点上。这样一对相应的点称为“共轭点”。
1. 共轴球面系统的结构参量: 各球面半径:r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔:d1 、 d2 …… dk-1 各球面间介质折射率:n1 、 n2 …… nk-1 、 nk n 、 k+1
精选
31
2. 转面公式
原则:前一折射面的象为后一面的物 ,前一面的象空间为后一面的物空间
4. C-球心 r-球面曲率半径 I 、I′-入、折射角
5. A 、A′-物点、象点 L、L′-物距、象距
精选
20
2. 符号法则(便于统一计算) 规定光线从左向右传播
a)沿轴线段 L、L′、r 以O为原点, 与光线传播方向相同,为“+” 与光线传播方向相反,为“-”
b)垂轴线段 h 在光轴之上,为“+” 在光轴之下,为“-”
例:某物体通过一透镜成像后在透镜内部,透镜材 料为玻璃,透镜两侧均为空气。问该像所处的空间 介质是玻璃还是空气?
4 5
6
3 2 1
位标器动平衡调试系统光源
第二章 球面与共轴球面系统
§ 2-1 光线光路计算与共轴光学系统
共轴球面系统— 光学系统一般由球面和平面组成, 各球面球心在一条直线(光轴)上。
精选
28
2. 轴向放大率:光轴上一对共轭点沿轴移动量之间的比值
66几何光学习题讲解1PPT课件

It'S An Honor To Walk With You All The Way
演讲人:XXXXXX
时 间:XX年XX月XX日
17
7
例3:一个直径为200mm的玻璃球,折射率为1.53。 球内有两个小气泡,看上去恰好在球心,另一个从 最近的方向看去,好像在球表面和中心的中间,求 两气泡的实际位置。
8
解:如上图可知,气泡A的像A’在球心,则根据折射 率定律,A也在球心。对于气泡B有
解之得:
气泡离球心实际位置:
9
例4:有一玻璃半球,折射率为1.5,半径为50mm, 其中平面镀银。一个高为10mm的小物放在球面顶点 前方100mm,求经过这个系统最后所成像的位置、大 小、虚实和正倒。
2
例2:一束平行细光束入射到一半径r=30mm、折射 率n=1.5的玻璃球上,求其会聚点的位置。
3
解:该题可以应用单个折射面的高斯公式来解决
4
(1)考虑光束射入玻璃球的状态,用高斯公式:
5
会聚点位于第二面后15mm处。
6
进一步可以讨论:像的属性:虚实、放缩; 再进一步可以考虑镀膜的情况(凹面、凸面)。
例1:一厚度为200mm的平行平板玻璃(设n=1.5), 下面放一直径为1mm的金属片。若在玻璃板上盖一 圆形纸片,要求在玻璃板上方任何方向上都看不到 该金属片,问纸片最小直径应为多少?
1
解:令纸片最小半径为x, 全反射临界角求取方法为: 其中n2=1, n1=1.5, 根据几何关系有: 联立两式可以求出纸片最小直径为358.77mm。
10
第一次成像有:
解之得:
11
对于第二个平面而言,因为
,所以
其物方光线垂直入射到该平面上,经过反射后,
演讲人:XXXXXX
时 间:XX年XX月XX日
17
7
例3:一个直径为200mm的玻璃球,折射率为1.53。 球内有两个小气泡,看上去恰好在球心,另一个从 最近的方向看去,好像在球表面和中心的中间,求 两气泡的实际位置。
8
解:如上图可知,气泡A的像A’在球心,则根据折射 率定律,A也在球心。对于气泡B有
解之得:
气泡离球心实际位置:
9
例4:有一玻璃半球,折射率为1.5,半径为50mm, 其中平面镀银。一个高为10mm的小物放在球面顶点 前方100mm,求经过这个系统最后所成像的位置、大 小、虚实和正倒。
2
例2:一束平行细光束入射到一半径r=30mm、折射 率n=1.5的玻璃球上,求其会聚点的位置。
3
解:该题可以应用单个折射面的高斯公式来解决
4
(1)考虑光束射入玻璃球的状态,用高斯公式:
5
会聚点位于第二面后15mm处。
6
进一步可以讨论:像的属性:虚实、放缩; 再进一步可以考虑镀膜的情况(凹面、凸面)。
例1:一厚度为200mm的平行平板玻璃(设n=1.5), 下面放一直径为1mm的金属片。若在玻璃板上盖一 圆形纸片,要求在玻璃板上方任何方向上都看不到 该金属片,问纸片最小直径应为多少?
1
解:令纸片最小半径为x, 全反射临界角求取方法为: 其中n2=1, n1=1.5, 根据几何关系有: 联立两式可以求出纸片最小直径为358.77mm。
10
第一次成像有:
解之得:
11
对于第二个平面而言,因为
,所以
其物方光线垂直入射到该平面上,经过反射后,
几何光学PPT【2024版】

只与两种介质有关,折射率
i 介质1
1
分界面
介质2
i2
像 物
13
折射光在入射面内
入射面
n
i1 i1
界面
i2
n1 sin i1 n2 sin i2 Snell定律
Descartes 定律 14
光的色散
• 一束平行的白光(复色光)从一种媒质 (例如真空或空气)射入另一种媒质时, 只要入射角不等于0,不同颜色的光在空间 散开来。
这种情况就是全反射,也称全内反射
30
全反射临界角
• 光线从光密介质射向光疏介质,折射角比
入射角大
•
入射角满足
i1
arcsin
n2 n1
就会出现全反射
• 出现全反射的最小入射角
称作全反射临界角
n1
iC
iC
arcsin
n2 n1
n2
31
4.全反射棱镜
屋脊形五棱镜
67.5
67.5
倒转棱镜(阿米西棱镜) 32
• 根据这一事实,也可以得出这样的结论, 既然在媒质中,光总是沿直线、折线、或 曲线传播,那么就可以用一条几何上的线 来描述和研究光的传播,这就是“光线”。
8
几何光学的局限
• 几何光学是关于光的唯象理论。 • 不涉及光的物理本质。 • 对于光线,是无法从物理上定义其速度的。 • 在几何光学领域,也无法定义诸如波长、
51
n n n n s s r
平行光入射 s n
n
M
n n
r
Q
O
C
Q
r
n
s
s
s nr f n
n n
O
Q
i 介质1
1
分界面
介质2
i2
像 物
13
折射光在入射面内
入射面
n
i1 i1
界面
i2
n1 sin i1 n2 sin i2 Snell定律
Descartes 定律 14
光的色散
• 一束平行的白光(复色光)从一种媒质 (例如真空或空气)射入另一种媒质时, 只要入射角不等于0,不同颜色的光在空间 散开来。
这种情况就是全反射,也称全内反射
30
全反射临界角
• 光线从光密介质射向光疏介质,折射角比
入射角大
•
入射角满足
i1
arcsin
n2 n1
就会出现全反射
• 出现全反射的最小入射角
称作全反射临界角
n1
iC
iC
arcsin
n2 n1
n2
31
4.全反射棱镜
屋脊形五棱镜
67.5
67.5
倒转棱镜(阿米西棱镜) 32
• 根据这一事实,也可以得出这样的结论, 既然在媒质中,光总是沿直线、折线、或 曲线传播,那么就可以用一条几何上的线 来描述和研究光的传播,这就是“光线”。
8
几何光学的局限
• 几何光学是关于光的唯象理论。 • 不涉及光的物理本质。 • 对于光线,是无法从物理上定义其速度的。 • 在几何光学领域,也无法定义诸如波长、
51
n n n n s s r
平行光入射 s n
n
M
n n
r
Q
O
C
Q
r
n
s
s
s nr f n
n n
O
Q
几何光学讲解PPT课件

i2 i2 '
2、最小偏向角
i1 i1',i2 i2 '
偏向角最小,称为最小偏向角。n sin ( m) / sin / 2
第5页/共69页
2
3、三棱镜的色散
法线
i1
i2
白光
三棱镜的色散
第6页/共69页
红
青 紫
第7页/共69页
第8页/共69页
§2 惠更斯原理
一、波的几何描述 波面(波阵面)、平面波、球面波的概念
第44页/共69页
第45页/共69页
四、薄透镜傍轴成像的牛顿公式 :
s, s 高斯公式中 是从O点算起的 ,薄透镜傍轴成像时也可以将物像方的焦
点
作为计算起点,此时成像的符号法则也要做如下的调整:
F , F
若入射光从左向右传播、计算起点分别是薄透镜的物方焦点
F F ' 和像方焦点
,物像点分别为
Q、Q ' 以及物像
二、实象 虚象 实物 虚物
实象(物):有实际光线会聚(发出)的点。 虚象(物):无实际光线会聚(发出)的点。
第17页/共69页
成 像 实 例
第18页/共69页
第19页/共69页
实物、实象、虚象的联系与区别
实物与实象: 联系:均为有光能量存在的光束顶点。 区别:光能量的传播范围不同。
实象与虚象: 联系:均为经反射、折射后所得的象点。 区别:象点处光能量有无状态不同。
平面反射能实现理想成象。
四、物像之间的等光程性 虚光程 等光程面
第21页/共69页
§5 共轴球面组傍轴成像
一、 球面的几个概念 符号法则
r
C
O
球面顶点:O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O
Hale Waihona Puke M‘4.某人山高为h,站在安在墙上的镜前,求该 人能够从头到脚看到自己全身像的镜子大小L 是多少? 5.某人身高180cm,一平面镜放在他身前 120cm处,为了看到他自己的全身像镜子大 小应该是多少
第四章 光学系统中 的光束限制 1.照相镜头焦距f=35mm,底片像幅尺寸为24mm*36mm, 求该相机的最大视场角,视场光阑位在何处? 2.6倍双目望远镜系统中,物镜焦距为108mm,物镜口径 为30mm,目镜口径为20mm,如果系统中没有视场光阑, 问该望远镜最大极限视场角为多少?渐晕系数Kd=0.5时的 视场角等于多少? 3.7倍望远系统,视场2w=8度,目镜焦距为25mm出瞳直径 为5mm假定无渐晕求孔径光阑入瞳和出瞳位置,物镜和目 镜的口径,视场光阑的口径。 4.照相物镜焦距为50mm,相对孔径1:5,对2m远处目标 照相,假定底片上像点弥散斑直径小于0.05mm仍可认为 成像清晰,问物空间能清晰成像的最远最近距离是多少米
4.一个正透镜焦距f‘,使物体成像于屏上,试求物和像之间最小距离时的垂轴放大 率β。 5.用作图法求图中位于空气中各薄透镜的焦点F,F‘的位置
B
A A H,H’ B
B
B A H,H’
A
第三章 平面与平面系统
1.判断图中棱镜系统的成像方向
y x z
2.判断下面图形的成像方向。
y x z 3.作图找出图中的箭头OP先通过平面反射MV,再经过M’V所成的像 P M V
几何光学的习题
第一章 几何光学基本定律与成像概念
1.人眼垂直看水池1m深处的物体,水的折射率为 1.33,试问该物体的像到水面的距离是多少? 2.为了从坦克内部观察外边目标需要在坦克壁上开 一个孔。假定坦克壁厚200mm,孔宽为120mm,在 孔内安装一块折射率n=1.5163的玻璃,厚度与装甲 厚度相同,问在观察者眼睛允许左右移动的条件下, 能看到外界多大角度范围? 3.试用费马原理导出反射和折射定律
第二章 理想光学系统 1.某照相机可拍摄最近距离为1m,装上两个屈光度 (f‘=500mm)的近拍镜后,能拍摄的最近距离是多少? (假设近拍镜与照相镜头密接) 2.由已知f‘1=50mm,f’2= —150mm的两个薄透镜组成 的光学系统,对一实物成放大4倍的实像,并且第一透镜 的放大率β1=—2,试求:1.两透镜的距离2.物象之间的距 离3.保持物面位置不变,移动第一透镜至何处时,仍能 在原像面位置得到物体的清晰像?与此相应的垂轴放大 率为多大? 3.有一光学系统,已知f‘=—f=100mm,总厚度(第一面 到最后一面的距离)为15mm,lf’=96mm,lf=—97mm。 求此系统对实物成放大十倍的实像时物距(离第一面) l1,像距(离最后一面)lk‘及物像共轭距L。并画图表示
4.有一架开普勒望远镜,视放大率为6,物方视场 角2w=8度,出瞳直径D’=5mm,物镜和目镜之间距 离L=140mm假定孔径光阑与物镜框重合,系统无 渐晕,求: 1.物镜焦距和目镜焦距2.物镜口径和目镜口径3.分 划板直径4.出瞳距离5.画出光 路图 5.有一显微镜,物镜的放大率β=—40,目镜 的倍率 为Γ目=15(均为薄透镜),物镜的共轭距为 195mm,求物镜和目镜的焦距,物体的位置,光 学筒长,物镜和目镜的间距,系统的等效焦距和 总倍率。
第七章 典型光学系统 1.已知显微镜的视放大率为—300,目镜的焦距为20mm, 求显微镜的倍率。假定人眼的视角分辨率为60“,问使用 该显微镜观察时,能分辨的两物点的最小距离等于多少? 2.用一架5倍的开普勒望远镜,通过一个观察窗观察位于 距离500mm远处的目标,假定该望远镜的目镜和物镜之间 有足够的调焦可能,该望远镜物镜焦距f‘物=100mm,求 此时仪器的实际视放大率Γ等于多少? 3.在一个2倍伽利略望远镜物镜前,加一个焦距为100mm 的正透镜,构成一个组合放大镜。问此组合放大镜的视放 大率等于多少倍?对一个近视度的观察者,需要调节视度, 目镜应向哪个方向移动(靠近还是远离物镜)?若目镜焦 距为20mm,目镜移动量是多少?
