光学教程几何光学部分
合集下载
光学 第3章 几何光学的基本原理
(1) 偏向角
i1
又
i2
i2
i2 '
i1'i2
A
'
i1 i1' A
(2) 最小偏向角0
当i1改变时 、i1'均随之而改变，当 i1 i1'时，偏向角取最小 0。
0 2i1 A
A
此时在棱镜内传播的光线平行于底边，有:
i2
i2 '
A 2
，i1
i1'
0
2
A
2. 棱镜的折射率
3、折射定律：(1) 折射线在入射线和法线决定的平面内； (2) 折射线、入射线分居法线两侧； (3) 折射角和入射角满足斯涅尔定律：n1sini1=n2sini2
i1 i1'
n1
n2
i2
7 反射和折射定律光路图
3、光的独立传播定律：几个光源发出的光在空间传播并相遇后， 它们将各自保持自己原有的特性(频率、波长、偏振状态)沿原来 的方向继续传播，互不影响。 4、光路可逆原理：当光线的方向反转时，它将逆着同一路径传 播，称为光路可逆原理。
i2 i2
A2 x2,0
i1 i1
B2 n2
x
n1
晰，像的深度由上式确定，y‘ 叫做像似深度 ，y是物的实际深度。
20
(3)像散现象：当i1≠0，即入射光束倾斜入射时，折射光线会发生像散现象。如沿 着倾斜的角度观察水中的物体时，像的清晰度由于像散而被破坏。
例1: 使一束向P点会聚的光在到达P点之前通过一平行玻璃板。如果将玻璃板 垂直于光束的轴竖放，问会聚点将朝哪个方向移动？移动的距离为多少？
A1 A2
P
P'
M
光学教程(重要)第3章几何光学1
x x1 y12
2 ' '
n2 x2 x
2 x2 x y2 2
n A C n2 CB 1 n1 sin i1 n2 sin i2 0 AC CB n2 sin i2 n2 sin i1
z
O n1 n2
O’
B x2 , y2
B1
z O
P2 P1
●
i2 A1
i2＋△i2 A2
B2
n2
●
P'
i1
n1 x
i1+△i1
P
y
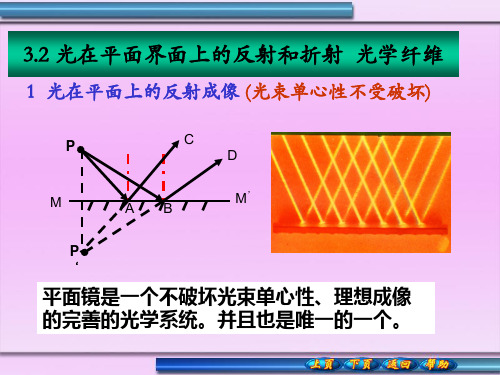
折射后，光束的单心 性已被破坏。
n2 y n1
2、像似深度
当i1 0，即光束垂直入射到分界时，x 0 y y1 y2 P、P2、和P三点重合在一点，光束保持其单心性。 1 像似深度：y n2 y n1
A
四、棱镜
棱镜是一种由多个平面界面组合而 成的光学元件。光通过棱镜时，产生两 个或两个以上界面的连续折射，传播方 向发生偏折。最常用的棱镜是三棱镜 （如图示）。
2 2 n12 n2
n2 sin ic n1
2 故 : i sin 1 n12 n2
说明： (1)当n1、n2一定时，i一定，即一定的光纤所允许传播的光线范围是一定的；
(2) 要扩大传播的范围，必须增大n1、n2的差值； (3) 光纤的特点：A. 可同时传输多路信号而互不影响； B. 轻便、柔软、防震、可弯曲折叠。
• 这种撇开光的波动本性，而仅以光的直线传播为基础，研究光在透明 介质中有传播规律的学科称为几何光学，也称为光线光学。
• 由于直线传播仅是波动的近似，所以，几何光学只能用于有限的范围 和给出近似的结论。
《光学教程》姚启钧原著-第三章-几何光学的基本原理
第三章
3.4 光连续在几个球面界面上的折射
子系统1
子系统m
子系统N
物
像
y1 y
y’N y’
一、共轴光具组
1、光轴 (optical axis) ---- 光学系统的对称轴 各球面的球心位于同一条直线上 连接各球心的直线为光轴
共轴光具组
实际成像系统通常由多个折射球面级联构成
r
n
n’
F
F’
O
C
像方焦点F’：与光轴上无穷远处物点对应的像点 像方焦距f’：与像方焦点对应的像距 像方焦平面：过F’点垂直于光轴的平面
像方焦距:
四、球面折射对光束单心性的破坏
物方焦点F : 与光轴上无穷远处像点对应的物点 物方焦距f ：与物方焦点对应的物距。 物方焦平面：过F点垂直于光轴的平面。
1
1’
O
二、几何光学的基本实验定律
1
1’
O
2
（3）光的折射定律
二、几何光学的基本实验定律
（4）光的独立传播定律和光路可逆原理
二、几何光学的基本实验定律
适用条件： R远大于光波长λ （否则，用衍射光学）
二、几何光学的基本实验定律
三、 费马原理
（一）、概念 光程:
B
A
低损耗
玻璃 几千dB/km
石英光纤 0.2 dB/km
2) 信带宽、容量大、速度快
3) 电气绝缘性能好 无感应 无串话
5) 资源丰富 价格低
4) 重量轻 耐火 耐腐蚀 可用在许多恶劣环境下
折射棱镜
四、棱镜
四、棱镜
五脊棱镜
直角棱镜
使像转过900
反射棱镜
： 借助光在棱镜中的全反射，改变光进行的方向.
光学教程几何光学部分
第1章 几何光学基础
以光线概念为基础、 用三大实验定律和几何 方法讨论光的传播及光 成像的规律。
1
第4章 几何光学基础
几何光学的基本定律 物像基本概念 球面和球面系统 平面和平面系统 光学材料（自学）
2
1.1 几何光学的基本定律
基本概念 发光点与发光体
当发光体（光源）的大小和其辐射作用距离 相比可略去不计时，该发光体可视为是发光 点或点光源。 任何发光体（光源）可视为由无数个这样的 发光点的集合。
28
1.2 物像基本概念
光
Q
具
组
实物成实像
Q 光 具 组
虚物成实像
QQ '
光 具 Q' 组
实物成虚像
Q
Q'
'
光
具
Q
组
虚物成虚像
29
1.2 物像基本概念
物与像：
物视为无数物点的集合，若每一物点经光学系 统后都有对应的像点，像点的集合就称为光学系 统对该物所成的完善像（理想像）。 物和像的对应关系光学
47
1.3 单球面和共轴球系统的傍轴成像
轴向放大率
dl dl
由物像公式 nnnn l l r
得 dlnl2n2
dl nl2 n
恒为正值，表示物点沿轴移动，其
像点以同方向沿轴移动。
48
1.3 单球面和共轴球系统的傍轴成像
当物点沿轴移动有限距离
l l
2
1
l l
2
1
由
nnnnnn l2 l2 r l1 l1
1.3 单球面和共轴球系统的傍轴成像
符号规则
光路方向 规定光线从左到右的传播方向为 正，即正向光路，反之为反向光路。
以光线概念为基础、 用三大实验定律和几何 方法讨论光的传播及光 成像的规律。
1
第4章 几何光学基础
几何光学的基本定律 物像基本概念 球面和球面系统 平面和平面系统 光学材料（自学）
2
1.1 几何光学的基本定律
基本概念 发光点与发光体
当发光体（光源）的大小和其辐射作用距离 相比可略去不计时，该发光体可视为是发光 点或点光源。 任何发光体（光源）可视为由无数个这样的 发光点的集合。
28
1.2 物像基本概念
光
Q
具
组
实物成实像
Q 光 具 组
虚物成实像
QQ '
光 具 Q' 组
实物成虚像
Q
Q'
'
光
具
Q
组
虚物成虚像
29
1.2 物像基本概念
物与像：
物视为无数物点的集合，若每一物点经光学系 统后都有对应的像点，像点的集合就称为光学系 统对该物所成的完善像（理想像）。 物和像的对应关系光学
47
1.3 单球面和共轴球系统的傍轴成像
轴向放大率
dl dl
由物像公式 nnnn l l r
得 dlnl2n2
dl nl2 n
恒为正值，表示物点沿轴移动，其
像点以同方向沿轴移动。
48
1.3 单球面和共轴球系统的傍轴成像
当物点沿轴移动有限距离
l l
2
1
l l
2
1
由
nnnnnn l2 l2 r l1 l1
1.3 单球面和共轴球系统的傍轴成像
符号规则
光路方向 规定光线从左到右的传播方向为 正，即正向光路，反之为反向光路。
应用光学第一章几何光学基本原理
种性质更加突出。——波粒二象性 • 一般情况下，把光作为电磁波看待，称为“光波”
λ
第六页，讲稿共五十七页哦
第1节 光波和光线
三、光的特性
• 光的本质是电磁波
• 光的传播实际上是波动的传播 • 物理光学
研究光的本性，并由此来研究各种光学现象
• 几何光学 不考虑光的本性，研究光的传播规律和传播现象
第七页，讲稿共五十七页哦
v2
v
第十八页，讲稿共五十七页哦
第3节 折射率与光速
四、用绝对折射率表示折射定律
• 折射定律：
sin I 1 n1, 2 sin I 2
• 相对折射率与绝对折射率的关系：
n1, 2 n 2 n1
• 所以， sin I 1 n 2 sin I 2 n1
•或
n 1 sinI1 n 2sinI2
第十九页，讲稿共五十七页哦
• 三、透镜
• 透镜的作用——成像
– 正透镜成像：中心比边缘厚，光束中心走的慢，边缘走的快—— 成实像。
– 负透镜成像：边缘比中心厚，光束中心走的快，边缘走的慢—— 成虚像。
PP’AQ源自Q’P’ PA’
A A’
Q Q’
第二十八页，讲稿共五十七页哦
第6节 光学系统类别和成像的概念
四、成像的概念
• 像：出射光线的交点 – 实像点：出射光线的实际交点
同心光束
平行光束
像散光束
第十二页，讲稿共五十七页哦
第2节 几何光学基本定律
一、光的传播现象分类
• 光的传播可以分为两类：
– 光在同一种均匀透明介质中传播：
直线传播定律
– 光在两种均匀介质分界面上传播：
➢ 反射定律，折射定律
A
λ
第六页，讲稿共五十七页哦
第1节 光波和光线
三、光的特性
• 光的本质是电磁波
• 光的传播实际上是波动的传播 • 物理光学
研究光的本性，并由此来研究各种光学现象
• 几何光学 不考虑光的本性，研究光的传播规律和传播现象
第七页，讲稿共五十七页哦
v2
v
第十八页，讲稿共五十七页哦
第3节 折射率与光速
四、用绝对折射率表示折射定律
• 折射定律：
sin I 1 n1, 2 sin I 2
• 相对折射率与绝对折射率的关系：
n1, 2 n 2 n1
• 所以， sin I 1 n 2 sin I 2 n1
•或
n 1 sinI1 n 2sinI2
第十九页，讲稿共五十七页哦
• 三、透镜
• 透镜的作用——成像
– 正透镜成像：中心比边缘厚，光束中心走的慢，边缘走的快—— 成实像。
– 负透镜成像：边缘比中心厚，光束中心走的快，边缘走的慢—— 成虚像。
PP’AQ源自Q’P’ PA’
A A’
Q Q’
第二十八页，讲稿共五十七页哦
第6节 光学系统类别和成像的概念
四、成像的概念
• 像：出射光线的交点 – 实像点：出射光线的实际交点
同心光束
平行光束
像散光束
第十二页，讲稿共五十七页哦
第2节 几何光学基本定律
一、光的传播现象分类
• 光的传播可以分为两类：
– 光在同一种均匀透明介质中传播：
直线传播定律
– 光在两种均匀介质分界面上传播：
➢ 反射定律，折射定律
A
光学教程(重要)第3章几何光学2
l r 2 r s2 2r r s cos l r 2 s r 2 2r s r cos
光程PAP nl nl
P
n r 2 r s2 2r r s cos
由P点所发出的单心光束经球面反射后，单心性被破坏
三、近轴光线条件下球面反射的物像公式
1、近轴光线条件
当 很小时，cos 1
l r 2 r s2 2 r r s r r s 2 s
l r 2 s r 2 2 r s r r s r 2 s
2
1 1 1 s s f
——球面反射物像公式
说明：1、它是球面反射成像的基本公式，只在近轴条件下成立；
2、式中各量必须严格遵从符号法则；
3、对凸球面反射同样适用；
4、当光线从右至左时同样适用。
例题：3-1 P129[例3-3] 一个点状物放在凹面镜前0.05m处，凹面镜的曲率半径为0.20m， 试确定像的位置和性质。
§3.3 光在球面上的反射和折射
一、球面的几个概念 符号法则
1、基本概念：
球面顶点：O 球面曲率中心：C 球面曲率半径：r 球面主轴：连接O、C的直线。 主截面：通过主轴的平面。
r
C
O
主轴
主轴对于所有的主截面具有对称性，因而只须讨论一个 主截面内光线的反射和折射情况即可。
2、符号法则：为使计算结果普遍适用，对线段和角度正负取法的规定。
由P点所发出的单心光束经球面折射后，单心性被破坏
五、近轴光线条件下球面折射的物像公式
1、物像公式:
当 很小时，cos 1
l r2 r s2 2r r s r r s2 s
光程PAP nl nl
P
n r 2 r s2 2r r s cos
由P点所发出的单心光束经球面反射后，单心性被破坏
三、近轴光线条件下球面反射的物像公式
1、近轴光线条件
当 很小时，cos 1
l r 2 r s2 2 r r s r r s 2 s
l r 2 s r 2 2 r s r r s r 2 s
2
1 1 1 s s f
——球面反射物像公式
说明：1、它是球面反射成像的基本公式，只在近轴条件下成立；
2、式中各量必须严格遵从符号法则；
3、对凸球面反射同样适用；
4、当光线从右至左时同样适用。
例题：3-1 P129[例3-3] 一个点状物放在凹面镜前0.05m处，凹面镜的曲率半径为0.20m， 试确定像的位置和性质。
§3.3 光在球面上的反射和折射
一、球面的几个概念 符号法则
1、基本概念：
球面顶点：O 球面曲率中心：C 球面曲率半径：r 球面主轴：连接O、C的直线。 主截面：通过主轴的平面。
r
C
O
主轴
主轴对于所有的主截面具有对称性，因而只须讨论一个 主截面内光线的反射和折射情况即可。
2、符号法则：为使计算结果普遍适用，对线段和角度正负取法的规定。
由P点所发出的单心光束经球面折射后，单心性被破坏
五、近轴光线条件下球面折射的物像公式
1、物像公式:
当 很小时，cos 1
l r2 r s2 2r r s r r s2 s
第十一章 几何光学181212
n1 n2 n2 n1
uv
r
f2
n2 r n2 n1
f1
n1 r n2 n1
f2
n2 r n2 n1
①f1 、f2可正可负， F1、F2可以是实焦点，也可 以是虚焦点，单球面对光线可以起到会聚作用， 也可以起到发散作用。
②当f1 、f2为正时， F1、F2是实际光线交汇点， 就是实焦点，对光线起会聚作用；
1 1 n 1( 1 1 )
uv
r1 r2
透镜有两个焦点；若薄透镜两侧介质n不同时，
两焦距不等；当薄透镜两侧介质n相同时，两焦
距也相等。
薄透镜焦距公式
f
n
n0 n0
1 ( r1
1 1
r2
)
比
薄透镜公式 1 1 n n0 ( 1 1 )
较
例11-2 从几何光学的角度来看，人眼可简化为 高尔斯特兰简化眼模型。这种模型将人眼成像归 结成一个曲率半径为5.7mm、媒质折射率为1.33 的单球面折射成像。⑴试求这种简化眼的焦点位 置和焦度；⑵若已知某物在膜后24.02mm处视网 膜上成像，求该物应放在何处。
解⑴：已知n1=1.0, n2=1.33, r=5.7mm
ur
a.从F1到折射面顶点的距离(物距)叫第一焦距，f1 u=f1，v =∞
n1 n2 n2 n1
uv
r
f1
n1 r n2 n1
n1
n2
平行主光轴光线成像 于F2处，F2称为折 射面的第二焦点。
F2
v r
b.从F2到折射面顶点的距离(像距)叫第二焦距，f2
u= ∞ ，v =f2
光学教程___第3章_几何光学的基本原理
i2 ic的光线折射出光纤;i2 ic 的光线在两层介质间多次全
反射从一端传到另一端.
内窥镜、光导通讯……
为了使更大范围内的光束能在纤维中传播，应选择n1和n2的差
值较大的材料去制造光学纤维。
/ 77
20
四.棱镜
主截面：垂直于两界面的截面. 偏向角：出射线与入射线间的夹角.
＝(i1-i2 )+(i1 -i2 )= i1 +i1 -A
由P点所发出的单心光束经球面反射后，单心性被破坏
/ 77
26
三、近轴光线条件下球面反射的物像公式
当φ很小时，cosφ 1
l r2 r s2 2 rr s r r s2 s
l' r2 s' r 2 2 r s' r r s' r 2 s'
由:
A
d l
n 2rs rsin 0 P
l
l
-u
i
-i′ l '
-u`
C
P` -s` O
化简有：r l
s
s r l'
0
-r -s
即：1 l'
1 l
1 r
s l'
s l
对一定的球面和发光点P（S一定），不同的入射点对应有不同的S‘。
即：同一个物点所发出的不同光线经球面反射后不再交于一点。
第三章 几何光学的基 本原理
/ 77
1
干涉和衍射现象揭示了光的波动性，所有 光学现象都能够用波动概念解释。但是在波面 线度远大于波长时，研究光的反射，折射成象 等问题，如果不用波长、位相等波动概念而代 之以光线和波面等概念，即用几何的方法来研 究，将更为方便。
《光学教程》第一章几何光学概述
光焦度的单位称为屈光度，以字母D表 示。若球面的曲率半径以米为单位，其 倒数的单位便是D
如果发光点的位置在P′点，它的像便在 P点。换句话说，如果P和P′之一为物， 则另一点为其相应的像。物点和像点的 这种关系称为共轭，相应的点称为共轭 点，相应的光线称为共轭光线。应该指 出，物像共轭是光路可逆原理的必然结
练习P161 3.10 3.12 3.13
六、球面反射对光束单心性的破坏
从物点发散的单心光束经球面反射后， 将不再保持单心性(即使平行光束入射 时也不例外)。
七、近轴光线条件下球面反 射的物像公式
在球面反射的情况中，物空间与像空间 重合，且反射光线与入射光线的进行方 向恰恰相反。这一情况，在数学处理上 可以认为像方介质的折射率n′等于物方 介 质 折 射 率 n 的 负 值 ， 即 n′=-n( 这 仅 在 数学上有意义)。
问题：平面镜反射能否成虚像？
二、光在平面界面上的折射 光 束单心性的破坏
当x不变时，像点S′的位置x′随y而变， 即 从 S 点 发 出 的 不 同 光 线 经 OM 面 折 射 后并不能相交于同一点。
进一步研究可知折射光线在空间也无同 一交会点，这说明折射光束的单心性已 被破坏。
比较光在平面上的反射
单独的球面不仅是一个简单的光学 系统，而且是组成光学仪器的基本 元素；
研究光经过球面的反射和折射，是 研究一般光学系统成像的基础。
一、基本概念
球面的中心点O称为顶点； 球面的球心C称为曲率中心； 球面的半径称为曲率半径； 连接顶点和曲率中心的直线CO称为主轴；
通过主轴的平面称为主截面；
主轴对于所有的主截面具有对称性，因 而只须讨论一个主截面内光线的反射 和折射。
省略一套公式.
第十一章 几何光学
（2）如果从折射点到像点的方向，与折射光线的方向相同， 该像称为实像，像距p′为正。反之像为虚像，像距为负。
（3）如果从折射点到曲率中心的方向，与折射光线的方向相 同曲率半径r为正，反之r为负。
25
2 、2 、薄透薄镜透镜的的焦焦距距(fo和cus焦)和度焦度(degree focus)
如透镜前后媒质相同则焦距
解：
n1=1.3
n2=1.5
O
I
P
p′
p 11
n1=1.3, n2=1.5, p= + 40cm, p′= -32cm, 代入球面成像公式，有
1.3 1.5 1.5 1.3 40 32 r
解得曲率半径为
r = -13.9 cm.
由于 r 是负的，说明凹面对着入射光线，即玻璃处于折射面 的凸侧。
20
按结构分类
凸透镜 (convex lens)
薄
中间厚 边缘薄
透
镜
凹透镜 (concave lens)
中间薄 边缘厚
21
透镜种类(按光学性质分): 会聚透镜 发散透镜
如果组成透镜材料的 折射率大于镜外介质 的折射率
凸透镜 凹透镜
22
一、薄透镜成像公式
1、薄透镜成像公式
n
<< r
n0
n0
O
之，若是入射光线对着凹球面，则r取负值。
规定：
（1）如果从物点到折射点的方向，与入射光线的方向相同，该物
称为实物，物距p为正。反之物为虚物，物距为负。
（2）如果从折射点到像点的方向，与折射光线的方向相同，
该像称为实像，像距p′为正。反之像为虚像，像距为负。
（3）如果从折射点到曲率中心的方向，与折射光线的方向相同，
（3）如果从折射点到曲率中心的方向，与折射光线的方向相 同曲率半径r为正，反之r为负。
25
2 、2 、薄透薄镜透镜的的焦焦距距(fo和cus焦)和度焦度(degree focus)
如透镜前后媒质相同则焦距
解：
n1=1.3
n2=1.5
O
I
P
p′
p 11
n1=1.3, n2=1.5, p= + 40cm, p′= -32cm, 代入球面成像公式，有
1.3 1.5 1.5 1.3 40 32 r
解得曲率半径为
r = -13.9 cm.
由于 r 是负的，说明凹面对着入射光线，即玻璃处于折射面 的凸侧。
20
按结构分类
凸透镜 (convex lens)
薄
中间厚 边缘薄
透
镜
凹透镜 (concave lens)
中间薄 边缘厚
21
透镜种类(按光学性质分): 会聚透镜 发散透镜
如果组成透镜材料的 折射率大于镜外介质 的折射率
凸透镜 凹透镜
22
一、薄透镜成像公式
1、薄透镜成像公式
n
<< r
n0
n0
O
之，若是入射光线对着凹球面，则r取负值。
规定：
（1）如果从物点到折射点的方向，与入射光线的方向相同，该物
称为实物，物距p为正。反之物为虚物，物距为负。
（2）如果从折射点到像点的方向，与折射光线的方向相同，
该像称为实像，像距p′为正。反之像为虚像，像距为负。
（3）如果从折射点到曲率中心的方向，与折射光线的方向相同，
物理竞赛光学教程_第一讲几何光学
物理课件网（ ）欢迎您！第一讲 几 何 光 学 §1.1 几何光学基础1、光的独立传播：几束光在交错时互不妨碍，仍按原来各自的方向传播。
2、光的直线传播：光在同一均匀介质中沿直线传播。
3、光的折射定律：①折射光线在入射光线和法线所决定平面内； ②折射光线和入射光线分居法线两侧；③入射角1i 与折射角2i 满足2211sin sin i n i n =；④当光由光密介质向光疏介质中传播，且入射角大于临界角C 时，将发生全面反射现象（折射率为1n 的光密介质对折射率为2n 的光疏介质的临界角12sin n n C =）。
4、光的反射定律：①反射光线在入射光线和法线所决定平面内； ②反射光线和入射光线分居法线两侧； ③反射角等于入射角。
§1.2 光的反射1.2.1、组合平面镜成像：1.组合平面镜 由两个以上的平面镜组成的光学系统叫做组合平面镜，射向组合平面镜的光线往往要在平面镜之间发生多次反射，因而会出现生成复像的现象。
先看一种较简单的现象，两面互相垂直的平面镜（交于O 点）镜间放一点光源S （图1-2-1），S 发出的光线经过两个平面镜反射后形成了1S 、2S 、3S 三个虚像。
用几何的方法不难证明：这三个虚像都位于以O 为圆心、OS 为半径的圆上，而且S 和1S 、S 和2S 、1S 和3S 、2S 和3S之间都以平面镜（或它们的延长线）保持着对称关系。
用这个方法我们可以容易地确定较复杂的情况中复像的个数和位置。
两面平面镜AO 和BO 成60º角放置（图1-2-2），用上述规律，很容易确定像的位置：①以O 为圆心、OS 为半径作圆；②过S 做AO 和BO 的垂线与圆交于1S 和2S ；③过1S 和2S 作BO 和AO 的垂线与圆交于3S 和4S ；④过3S 和4S 作AO 和BO 的垂线与圆交于5S，3图1-2-2S S 2图1-2-1高中物理竞赛电学光学教程 第一讲几何光学51~S S 便是S在两平面镜中的5个像。
[理学]《光学教程》姚启钧第三章几何光学的基本原理
![[理学]《光学教程》姚启钧第三章几何光学的基本原理](https://img.taocdn.com/s3/m/0d8df0f1b14e852458fb5780.png)
(a) 原理
光学纤维:中央折射率 大,表层折射率小的透 明细玻璃丝.
光进入光学纤维后,多次 在内壁上发生全内反射, 光从纤维的一端传向另 一端.
n
n
r
a 阶跃型光纤 b
r
梯度型光纤
阶跃型多模光纤
梯度型多模光纤
2 i
阶跃光学纤维的端面
n0
B A
n2
n2 n1
i
i
n1
n2
2 n12 n2 )
2、焦点与焦距
F 和物方焦距 f 物方焦点
F
F
f
f
将s f，s 代入(3)式，可得
f
透
n1
（5）
薄透镜物像距公式
n2 n1 n n1 n2 n 透 （3） s s r r2 1 F 和像方焦距 f 像方焦点
F
F
f
f
将s ，s f
代入(3)式，可得
f
透
f n 2 0 f n1
n2
（6）
由（ 5）、（ 6）式可知：
结论：物方焦点和像方焦点肯定在透镜的两侧。
三、高斯公式
将焦距公式（5）、（6）代入物像距公式（3）中，可得
高斯公式：
f f 1 s s
o
f
f
F
（7）
P
F
P
s
s
1 1 1 当n1 n2时，有 s s f
错：
（8）
f f 1 s s
1 1 1 s s f
四、垂轴放大率
Q
y P
①
三棱镜
三棱镜两折射面的夹角称三棱镜顶角A。 出射光与入射光之间的夹角称棱镜的偏向角。
光学纤维:中央折射率 大,表层折射率小的透 明细玻璃丝.
光进入光学纤维后,多次 在内壁上发生全内反射, 光从纤维的一端传向另 一端.
n
n
r
a 阶跃型光纤 b
r
梯度型光纤
阶跃型多模光纤
梯度型多模光纤
2 i
阶跃光学纤维的端面
n0
B A
n2
n2 n1
i
i
n1
n2
2 n12 n2 )
2、焦点与焦距
F 和物方焦距 f 物方焦点
F
F
f
f
将s f，s 代入(3)式，可得
f
透
n1
（5）
薄透镜物像距公式
n2 n1 n n1 n2 n 透 （3） s s r r2 1 F 和像方焦距 f 像方焦点
F
F
f
f
将s ，s f
代入(3)式，可得
f
透
f n 2 0 f n1
n2
（6）
由（ 5）、（ 6）式可知：
结论：物方焦点和像方焦点肯定在透镜的两侧。
三、高斯公式
将焦距公式（5）、（6）代入物像距公式（3）中，可得
高斯公式：
f f 1 s s
o
f
f
F
（7）
P
F
P
s
s
1 1 1 当n1 n2时，有 s s f
错：
（8）
f f 1 s s
1 1 1 s s f
四、垂轴放大率
Q
y P
①
三棱镜
三棱镜两折射面的夹角称三棱镜顶角A。 出射光与入射光之间的夹角称棱镜的偏向角。
光学教程第一章New-
(L)
B
ndl 0
A
9
光学教程第一篇 几何光学
正则邻域：
费马原理中，光线的比较曲线应该属于该 光线的正则邻域内。
正则邻域：可以被光线覆盖的一个邻域， 其中每一点有且仅有一条光线通过。
实际光线与其他曲线的差别：积分是一个
稳定值。当不满足正则邻域条件时，光线的光
程可能不再是一个极小。
M 反射、
折射
P
故: n1siin 1n2siin 2
2020/8/21
19
光学教程第一篇 几何光学
例题：
媒质中光线路径方程： 当媒质折射率n沿x方向
dx dl
连续改变时，光线路径如何？
dz
（海市蜃楼……）
由折射定律（为入射角）：
n (x)sin (x)n 1si1 n
而：(dl)2 (dx)2 (dz)2
11
光学教程第一篇 几何光学
nld在r小Q2三角n形dQ1Q Ql22Q2'中：
Q1Biblioteka nl drQ1 Q2'
0
Q1
O1
Q2
Q 2' Q2
P2 O2
ndQl2' ndOl2
Q1
O1
P1 费马原理证明图示
根据拉格朗日积分不变式：
n ld r Q 2n ld r Q 2'nQ d 2' l0
Q 1
Q 2
后面还将看到偏振棱镜；
2020/8/21
28
光学教程第一篇 几何光学
反射棱镜：
利用玻璃介质面与空气介质 面的折射率差异，用全反射原理 或镀银的方式进行反射。
1. 直角棱镜：
直角棱镜通常来实现光 束 的 90 转 向 和 180 的 转 向 。 图 为 通 过 90 转 向 的 棱 镜 成 象。即为全反射棱镜。
《光学教程》第五版姚启钧第一章几何光学PPT课件
新 笛 卡 儿 符 号 法 则
以主轴转向考虑的光线 顺时针为正 逆时针为负
｛Leabharlann (4) 全正图形 图中标记的是线段或角度的绝对值（如上)
二、傍轴条件下单球面折射的物象公式
二. 费马原理
A
B
dl=nds
L n ds
A
B
光在指定的两点间传播，实际的光程总是一个极值。 也就是说，光沿光程为最小值、最大值或恒定值的路程传播。 这就称为费马原理。
公式：
L n ds =极值（最大、最小或稳定值）
A
B
三. 应用举例
由费马原理可以直接推出直线传播定律以及反射和折射定律。 • 最小光程 • 恒定值 • 最大光程 反射定律
P’
·
同心光束
2. 折射
例1：处于液体中深度为y处有一点光源P,作PO垂直于液面，试 求射出液面折射线的延长线与PO交点P′的深度y′与入射角的 关系
n2 n1
y
o
i2 y' i1
y y
P
· P’ ·
y
tgi1 sin i1 cosi2 y tgi2 sin i2 cosi1
yn2 1 (
*共轭关系 由光路可逆原理，光线方向逆转，物像互换。 物像一一对应 物像共轭 物像互换（光线逆转） 入射光线、出射光线一一对应 光线共轭 入射光线、出射光线互换 （光线逆转）
*物像间所有光线光程相等
1.5 单球面上的傍轴成像
一、符号法则
y
P
1. 几个基本物理量
主
n1
n2
╭ u'
•
-u ╮
-p
O
P’ •
二. 几何光学的基本定律
《光学教程》第五版 姚启钧 第一章 几何光学
B'
B'
利用 物方焦平面 作图 光心
利用 物方焦点 作图 象方焦平面
利用 象方焦平面 作图 光心
四、 物像之间的等光程性
物点和像点之间各光线的光程相等。
F
F'
例1-3. p36 已知薄透镜 f ' 12cm, 问：
（1） 球面完全对称，折射率n=1.5，求曲率半径R；
（2） n1=4/3, n2=1 r2=R， f ' 12cm求, 曲率半径r1。
A ╭r φ-li''u'╭ n' P′
P -p
O
-y'
p'
笛 卡 儿 符 号 法
则
(3) 角度（以锐角量度）
｛ 以主轴转向考虑的光线 顺时针为正 逆时针为负
(4) 全正图形 图中标记的是线段或角度的绝对值（如上)
二、傍轴条件下单球面折射的物象公式
在下图中，当u,u’ 很小时， 称为傍轴条件
n -i
n
P
F’
P’
x'
-p’
-f ’ -p
-x
n′
F
f
六、 傍轴物点成像的放大率 亥姆霍兹-拉格朗日定理
1. 横向放大率
y pi y' p'i'
ni n'i'
n
y -x • P F•
-f i
-p
y' y
n p' n' p
利用-p=-(f+x),p'=(f '+x')
及牛顿公式，得
f x'
第一章几何光学基础11几何光学基本规律12光程费马原理13棱镜和最小偏向角全内反射和光学纤维14同心光束和象散光束物和象15单球面上的傍轴成象内容16薄透镜的成象规律17理想光学系统的基点和基面18共轴球面系统组合的理论19空气中的厚透镜薄透镜组110一般理想光具组的作图求像法和物像公式11几何光学的基本原理11光源
B'
利用 物方焦平面 作图 光心
利用 物方焦点 作图 象方焦平面
利用 象方焦平面 作图 光心
四、 物像之间的等光程性
物点和像点之间各光线的光程相等。
F
F'
例1-3. p36 已知薄透镜 f ' 12cm, 问：
（1） 球面完全对称，折射率n=1.5，求曲率半径R；
（2） n1=4/3, n2=1 r2=R， f ' 12cm求, 曲率半径r1。
A ╭r φ-li''u'╭ n' P′
P -p
O
-y'
p'
笛 卡 儿 符 号 法
则
(3) 角度（以锐角量度）
｛ 以主轴转向考虑的光线 顺时针为正 逆时针为负
(4) 全正图形 图中标记的是线段或角度的绝对值（如上)
二、傍轴条件下单球面折射的物象公式
在下图中，当u,u’ 很小时， 称为傍轴条件
n -i
n
P
F’
P’
x'
-p’
-f ’ -p
-x
n′
F
f
六、 傍轴物点成像的放大率 亥姆霍兹-拉格朗日定理
1. 横向放大率
y pi y' p'i'
ni n'i'
n
y -x • P F•
-f i
-p
y' y
n p' n' p
利用-p=-(f+x),p'=(f '+x')
及牛顿公式，得
f x'
第一章几何光学基础11几何光学基本规律12光程费马原理13棱镜和最小偏向角全内反射和光学纤维14同心光束和象散光束物和象15单球面上的傍轴成象内容16薄透镜的成象规律17理想光学系统的基点和基面18共轴球面系统组合的理论19空气中的厚透镜薄透镜组110一般理想光具组的作图求像法和物像公式11几何光学的基本原理11光源
光学教程(叶玉堂)第1章几何光学基础综述
应用光学几何光学基础几何光学基础光学仪器的基本光学仪器的基本原理1几何光学的基本定律1几何光学的基本定律2物像基本定律2物像基本定律3球面和球面系统3球面和球面系统1理想光学系统的基本特性1理想光学系统的基本特性理想光学系统理想光学系统2理想光学系统的物像关系2理想光学系统的物像关系平面和平面系统3理想光学系统的组合3理想光学系统的组合放大镜3显微镜3显微镜望远镜11几何光学的基本定律一发光点光线和光束1发光点
克莱门德（公元50年）和托勒玫（公元90～168年） 研究了光的折射现象，最先测定了光通过两种介质 分界面时的入射角和折射角。 罗马的塞涅卡（公元前3～公元65年）指出充满水 的玻璃泡具有放大性能。
阿拉伯的马斯拉来、埃及的阿尔哈金（公元 965 ～ 1038年）认为光线来自被观察的物体，而光是以球 面波的形式从光源发出的，反射线与入射线共面且 入射面垂直于界面。
（1）
E点，由折射定律可得：
sin I ' n sin I ' n
（2） （3）
利用
U' I U I '
sin U ' sin I ' ' r L r
三角形A‘EC中，利用正弦定理亦有：
（4） （5）
则有：
sin I ' L rr sin U '
'
由式（1）－（5）就可确定折射光线的特性
光波的波长范围
几何光学
以光的直线传播为基础，以光学的四大基 本定律为支柱 ;
光学
波动光学
以光的电磁性质为基础，以光波的干涉、 衍射为主干
量子光学
以光的量子理论为基础，以爱因斯坦 的光电子理论为依据
§0-2 光学发展简史 一、萌芽时期 世界光学的（知识）最 早记录，一般书上说是古希 腊欧几里德关于“人为什么 能看见物体”的回答，但应 归中国的墨翟。从时间上看， 墨翟（公元前468～376年）， 要比欧几里德（公元前330～ 墨翟（公元前468～376年） 275年）关于光学现象的解释 早一百多年。
克莱门德（公元50年）和托勒玫（公元90～168年） 研究了光的折射现象，最先测定了光通过两种介质 分界面时的入射角和折射角。 罗马的塞涅卡（公元前3～公元65年）指出充满水 的玻璃泡具有放大性能。
阿拉伯的马斯拉来、埃及的阿尔哈金（公元 965 ～ 1038年）认为光线来自被观察的物体，而光是以球 面波的形式从光源发出的，反射线与入射线共面且 入射面垂直于界面。
（1）
E点，由折射定律可得：
sin I ' n sin I ' n
（2） （3）
利用
U' I U I '
sin U ' sin I ' ' r L r
三角形A‘EC中，利用正弦定理亦有：
（4） （5）
则有：
sin I ' L rr sin U '
'
由式（1）－（5）就可确定折射光线的特性
光波的波长范围
几何光学
以光的直线传播为基础，以光学的四大基 本定律为支柱 ;
光学
波动光学
以光的电磁性质为基础，以光波的干涉、 衍射为主干
量子光学
以光的量子理论为基础，以爱因斯坦 的光电子理论为依据
§0-2 光学发展简史 一、萌芽时期 世界光学的（知识）最 早记录，一般书上说是古希 腊欧几里德关于“人为什么 能看见物体”的回答，但应 归中国的墨翟。从时间上看， 墨翟（公元前468～376年）， 要比欧几里德（公元前330～ 墨翟（公元前468～376年） 275年）关于光学现象的解释 早一百多年。
《光学教程》(姚启钧)第三章 几何光学的基本原理
3 全反射 光学纤维
(1) 全反射：只有反射而无折射的现象称为全折射。
i2
O
A1 i1 ic
A2
n A3 2
x
n1
P y
全反射条件 : ⑴ n1 n2
1
⑵ i1 ic
临界角
n2 n 0 s in 1 2 其中 : ic s in s in 90 n1 n1
三棱镜
三棱镜两折射面的夹角称三棱镜顶角A。 出射光与入射光之间的夹角称棱镜的偏向角。
A
（1）偏向角
n
1
偏向角 i1 i2 i i
' 1 ' 2 ' 1
' 2
nD
2
i2 i A i1 i A
i1
B
i
' 2
i2
E
C
i1'
（2）最小偏向角：
n=1.5
P -s1 O1 R s2’ s2 s1’ O2 P’
P1’
n=1.5
解：
-s1
O1
n' n n' n s' s r
(1). O1面：s1=-, r1=+R, n1=1, n1’=1.5
O2 P’ s2’ R s2 s1’
P1’
s1’ = 3R
O2面：s2=R, r2= -R, n2=1.5, n2’=1
1、光焦度：表征曲折光线的本领；
（3）
透
n n1 n n 2 r r2 1
（4）
透 1 2
透 0 透 0
正透镜或会聚透镜 负透镜或发散透镜
光学教程 第三章
∆ PAP ' = n[(− r ) 2 + (r − s ) 2 + 2(− r )(r − s ) cos ϕ ]1/ 2 + n[(− r ) + ( s '− r ) − 2(− r )( s '− r ) cos ϕ ]
2 2 1/ 2
当A点移动时，半径r是常量，角度ϕ是位置的变量。 根据费马原理，上式对ϕ求导，并令导数等于零，即
点光源
.
n′
全内反射
n
ic
由折射定律:
n ′ sin 90 0 = n sin i c
i c 称作临界角.
n′ ic = arcsin . n
内反射，全内反射：
n1 > n2
n2
入射角大 于临界角 的光线发 生全反射
ic
n1
2. 光学纤维 利用全反射原理制成的光能量的传输线
光学纤维:中央折射率 大,表层折射率小的透 明细玻璃丝.
n d∆ PAP ' n = [−2r (r − s ) sin ϕ ] + [2r ( s '− r ) sin ϕ ] = 0 l' dϕ l
由此可得： 或者：
r − s s '− r − =0 l l'
1 1 1 s' s + = ( + ) l l' r l' l (1)
s → s ′ 随 ϕ 而变，光束的单心性被破坏。
P'
− s'
o
PO = − s PA = l
P' O = − s' AP' = l '
ϕ：半径AC与主轴的夹角
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对于椭球，光程为恒定值 对于内切面，光程为最大值 对于外切面，光程为最小值
22
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
23
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光路可逆原理 在几何光学中，任何光路都是可逆的。 意义：利用此原理可以通过简单的推理获 得某些发结论。
B
L n(s)ds A
ds
A
B n
19
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
费马原理
表述：光在空间两定点间传播时，实际 光程为一特定的极值。
数学表达式
A Bn(s)ds极 值 极 大 、 极 小 、 恒 定 、 拐 点 或 LA Bn(s)ds0
意义：费马原理是几何光学的基本原理。由 费马原理可以导出在均匀介质中的直线传播 定律、反射定律和折射定律，
几何光学的基本定律 物像基本概念 球面和球面系统 平面和平面系统 光学材料（自学）
3
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
基本概念 发光点与发光体
当发光体（光源）的大小和其辐射作用距离 相比可略去不计时，该发光体可视为是发光 点或点光源。 任何发光体（光源）可视为由无数个这样的 发光点的集合。
20
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
21
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
说明 光在均匀介质中的直线传播及在平面界面 上的反射和折射，都是光程最短的例子。 光线也可能按光程极大的路程传播，或按 某一稳定值的路程传播。
如图三反射面，通过F、F的光线：
数学处理上，反射定律可视为折射定律的特 例
在折射定律 sin I n 中 sin I n
令 n n 得 I I
此即反射定律。
这表明，凡是由折射定律导得的公式中，只要
令 n n，便可适用于反射的场合。
13
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
独立传播定律 从不同光源发出的光线同时通过空间某 点时，彼此互不影响，各光线独立传播。 利用这条定律，研究某一光线传播时， 可不考虑其它光线的影响。这可使对光 线传播情况的研究大为简化。
24
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
习题 P39 1-1, 1-2
25
第4章 光的电磁理论1章 几何
1.2 物像基本概念
光学系统（由多个反射面、折射面组成）
界面
传播特性：反射面、折射面 几何形状：平面、球面
26
第4章 光的电磁理论1章 几何
1.2 物像基本概念
sin I n sin I n
n c/v
11
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
确定反射光 线与折射光 线方向的几 何作图法
2 n1
n2
i1 -i1' B 1
O i2 A
C
图1.2-4 确定反射光线与折射光线的几何作图法
12
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
几何光学
第1章 第2章 第3章
几何光学基础 理想光学系统 光学仪器的基本原理
1
第4章 光的电磁理论1章 几何
第1章 几何光学基础
以光线概念为基础、 用三大实验定律和几何 方法讨论光的传播及光 成像的规律。
2
第4章 光的电磁理论1章 几何
第4章 几何光学基础
1.1 1.2 1.3 1.4 1.5
4
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光线
代表光能的传播路径的有向几何线。 在各向同性介质中点光源的光线：
光线 波面
球面波
第4章 光的电磁理论1章 几何
平面波 5Βιβλιοθήκη 1.1 几何光学的基本定律
光束 大量光线的集合。
6
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
基本实验定律和原理 直线传播定律 在均匀介质中，光线按直线传播。 光直线传播定律是几何光学的基础， 只有光在均匀介质中无阻拦地传播的 情况下才成立。
光学系统的分类
非成像光学系统 成像光学系统
非球面成像光学系统 球面成像光学系统（含平面）
非共轴球面成像光学系统 共轴球面成像光学系统
14
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
全反射 只有反射而无折射的现象。 条件：
光线由光密介质
到光疏介质（n>n ）
入射角大于或等于 临界角（I Im）
n' sin I
mn
应用：棱镜、光纤等。
15
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
增大视场角
例：水（n=4/3）→空气（n=1）：
9
1.1 几何光学的基本定律
反射定律 反射光线、入射光线和法线在同一平面内; 入射光线与反射光线分别位于法线的两侧; 入射光线与法线夹角和反射光线与法线夹角 大小相同，即
I I
10
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
折射定律 折射光线、入射光线和法线定同一平面内； 入射光线与反射光线分别位于法线的两侧; 折射角正弦与入射角正弦之比为一常数，等于前 一介质与后一介质的折射率之比， 即
ic=48.59o
玻璃（n=1.5）→
空气（n=1）：ic=41.81o
48.6o 48.6o
鱼眼在水中的视场
第4章 光的电磁理论1章 几何
水中的针孔成像
16
1.1 几何光学的基本定律
导光
转向
n1 z
纤芯
n2 包层
17
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光程： 光在均匀介质中经过的几何路程S和 该介质折射率n的乘积
LnScvtct v
即光程为光在介质中传播时间内在真空 中所传播的路程，也称为“折合路程”。
18
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光在非均匀介质中传播，即介质的折射率n是 位置的函数，则光在该介质中所经过的几何 路程不是直线而是一空间曲线，如图所示。 这时，从A点到B点的光程为：
7
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
在非均匀介质中光线是曲线
8
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
反射定律和折射定律
当光传播到两种不同介质的理想光滑分 界面时，通常会发生反射和折射，其传 播的方向遵循折射定律和反射定律。
第4章 光的电磁理论1章 几何
夹角为代数量， 顺时为正。由此 导出的公式具有 普适性。
22
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
23
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光路可逆原理 在几何光学中，任何光路都是可逆的。 意义：利用此原理可以通过简单的推理获 得某些发结论。
B
L n(s)ds A
ds
A
B n
19
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
费马原理
表述：光在空间两定点间传播时，实际 光程为一特定的极值。
数学表达式
A Bn(s)ds极 值 极 大 、 极 小 、 恒 定 、 拐 点 或 LA Bn(s)ds0
意义：费马原理是几何光学的基本原理。由 费马原理可以导出在均匀介质中的直线传播 定律、反射定律和折射定律，
几何光学的基本定律 物像基本概念 球面和球面系统 平面和平面系统 光学材料（自学）
3
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
基本概念 发光点与发光体
当发光体（光源）的大小和其辐射作用距离 相比可略去不计时，该发光体可视为是发光 点或点光源。 任何发光体（光源）可视为由无数个这样的 发光点的集合。
20
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
21
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
说明 光在均匀介质中的直线传播及在平面界面 上的反射和折射，都是光程最短的例子。 光线也可能按光程极大的路程传播，或按 某一稳定值的路程传播。
如图三反射面，通过F、F的光线：
数学处理上，反射定律可视为折射定律的特 例
在折射定律 sin I n 中 sin I n
令 n n 得 I I
此即反射定律。
这表明，凡是由折射定律导得的公式中，只要
令 n n，便可适用于反射的场合。
13
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
独立传播定律 从不同光源发出的光线同时通过空间某 点时，彼此互不影响，各光线独立传播。 利用这条定律，研究某一光线传播时， 可不考虑其它光线的影响。这可使对光 线传播情况的研究大为简化。
24
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
习题 P39 1-1, 1-2
25
第4章 光的电磁理论1章 几何
1.2 物像基本概念
光学系统（由多个反射面、折射面组成）
界面
传播特性：反射面、折射面 几何形状：平面、球面
26
第4章 光的电磁理论1章 几何
1.2 物像基本概念
sin I n sin I n
n c/v
11
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
确定反射光 线与折射光 线方向的几 何作图法
2 n1
n2
i1 -i1' B 1
O i2 A
C
图1.2-4 确定反射光线与折射光线的几何作图法
12
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
几何光学
第1章 第2章 第3章
几何光学基础 理想光学系统 光学仪器的基本原理
1
第4章 光的电磁理论1章 几何
第1章 几何光学基础
以光线概念为基础、 用三大实验定律和几何 方法讨论光的传播及光 成像的规律。
2
第4章 光的电磁理论1章 几何
第4章 几何光学基础
1.1 1.2 1.3 1.4 1.5
4
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光线
代表光能的传播路径的有向几何线。 在各向同性介质中点光源的光线：
光线 波面
球面波
第4章 光的电磁理论1章 几何
平面波 5Βιβλιοθήκη 1.1 几何光学的基本定律
光束 大量光线的集合。
6
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
基本实验定律和原理 直线传播定律 在均匀介质中，光线按直线传播。 光直线传播定律是几何光学的基础， 只有光在均匀介质中无阻拦地传播的 情况下才成立。
光学系统的分类
非成像光学系统 成像光学系统
非球面成像光学系统 球面成像光学系统（含平面）
非共轴球面成像光学系统 共轴球面成像光学系统
14
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
全反射 只有反射而无折射的现象。 条件：
光线由光密介质
到光疏介质（n>n ）
入射角大于或等于 临界角（I Im）
n' sin I
mn
应用：棱镜、光纤等。
15
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
增大视场角
例：水（n=4/3）→空气（n=1）：
9
1.1 几何光学的基本定律
反射定律 反射光线、入射光线和法线在同一平面内; 入射光线与反射光线分别位于法线的两侧; 入射光线与法线夹角和反射光线与法线夹角 大小相同，即
I I
10
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
折射定律 折射光线、入射光线和法线定同一平面内； 入射光线与反射光线分别位于法线的两侧; 折射角正弦与入射角正弦之比为一常数，等于前 一介质与后一介质的折射率之比， 即
ic=48.59o
玻璃（n=1.5）→
空气（n=1）：ic=41.81o
48.6o 48.6o
鱼眼在水中的视场
第4章 光的电磁理论1章 几何
水中的针孔成像
16
1.1 几何光学的基本定律
导光
转向
n1 z
纤芯
n2 包层
17
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光程： 光在均匀介质中经过的几何路程S和 该介质折射率n的乘积
LnScvtct v
即光程为光在介质中传播时间内在真空 中所传播的路程，也称为“折合路程”。
18
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
光在非均匀介质中传播，即介质的折射率n是 位置的函数，则光在该介质中所经过的几何 路程不是直线而是一空间曲线，如图所示。 这时，从A点到B点的光程为：
7
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
在非均匀介质中光线是曲线
8
第4章 光的电磁理论1章 几何
1.1 几何光学的基本定律
反射定律和折射定律
当光传播到两种不同介质的理想光滑分 界面时，通常会发生反射和折射，其传 播的方向遵循折射定律和反射定律。
第4章 光的电磁理论1章 几何
夹角为代数量， 顺时为正。由此 导出的公式具有 普适性。