小学奥数教程:比例应用题(一)
(完整版)小学奥数--比的应用(学生版)

【题型概述】今天,我们学习有连比的应用题。
解决此类应用题应该先将两个比转化成连比,然后按比例分配。
【典型例题】希望小学六年级有三个班,共195名学生。
六(1)班和六(2)班的人数比是7:8,六(2)班与六(3)班的人数比是6:5,你知道三个班各有多少名学生吗?【举一反三】1.小芳和小灵步行的速度比是2:3,小灵和小红步行的速度比是4:5,三人一分钟所行的路程和是175米,三个伙伴每分钟各行了多少米?2.某学校学生阅览室里有236本童话故事书,分三层摆放,第一层与第二层的本数比是3:4,第二层与第三层的本数比是5:6,三层各有多少本童话故事书?【拓展提高】春节快来了!水果批发商张老板购进了1420箱苹果、香蕉和梨,苹果和香蕉的箱数比是4;3,梨比香蕉少180箱。
苹果、香蕉和梨三种水果各购进了多少箱?【奥赛训练】1.培育花圃的李阿姨培育了850株菊花、玫瑰花和月季花,菊花、玫瑰花的株数比是5:2,月季花比玫瑰花多40株。
菊花、玫瑰花和月季花三种话各有多少株?2.2008年8月第29届奥运会子啊首都北京召开。
育才小学六年级三个班的同学分别进行募捐。
学校学生处共收到捐款18000元,六(1)班和六(2)班捐款数额比是6:7,六(3)班比六(2)班少捐400元,六年级三个班的同学各捐款多少元?3.甲乙两数的比是5:7,乙丙两数的比是3:4,已知甲乙两数的和是84,求乙丙两数的和是多少?【典型例题】甲乙两个长方形的周长相等,甲的长与宽的比是3:2,乙的长与宽的比是2:1,那么甲乙两个的长方形的面积比是多少?【举一反三】1.有两个长方形,大长方形的长比小长方形的长多41,而小长方形的宽比大长方形的宽多51,求这两个长方形的面积比。
2.某外贸公司有三批货物共值152万元,三批货物的重量比是2:4:3,单价比是6:5:2,这三批货物各值多少万元?【拓展提高】甲乙两个服装厂12月份生产服装的数量比是6:7,两个厂服装的单价比是11:10,并且这两个厂这个月的总产值是8160万元。
(完整)六年级奥数思维训练比例应用题

六年级奥数思维训练比例应用题
一、尝试练习
1.甲乙两人走同一段路, 甲要20分钟, 乙要15分钟, 现在甲、乙两人分别同时从相距840米的两地相向而行, 相遇时, 甲、乙各走了多少米?
2.盒子里共有红、白、黑三种颜色的彩球共68个, 红球与白球个数的比是1:2, 白球与黑球个数的比是3:4, 红球有多少个?
二、训练营地
1.甲、乙、丙三个平行四边形的底之比是4:5:6, 高之比是3:2:1, 已知三个平行四边形的面积和是140平方分米, 那么甲、乙、丙三个平行四边形的面积各是多少?
2.某校四、五年级参加数学竞赛的人数相等, 四年级获奖人数与未获奖人数的比是1:4, 五年级获奖人数与未获奖人数的比是2:7;两个年级中获奖与未获奖人数的比是多少?
3.光明小学有三个年级, 一年级学生占全校学生人数的25%, 二年级与三年级学生人数的比是3: 4, 已知一年级比三年级学生少40人, 一年级有学生多少人?
4.五年级举行数学竞赛, 一班占参加比赛总人数的1/3, 二班与三班参加比赛人数的比是11: 13, 二班比三班少8人, 则三班有多少人参加比赛?。
小学奥数比的应用

甲工厂有120名工人,乙工厂有80名工人。
从乙工厂调几名工人到甲工厂才能使甲工厂与乙工厂工人的数量比是5:3?讲解题:1.甲班有60名学生,乙班有80名学生。
从甲班调几名学生到乙班才能使甲、乙两班学生数量的比是2:3?2.小明有25元钱,小华有35元钱。
小华给小明几元钱才能使小明与小华的钱数比是2:1?光明小学将五年级的140名学生分成三个小组进行植树活动。
已知第一小组和第二小组学生的比是3:2,第二小组和第三小组学生的比是4:5。
这三个小组各有多少名学生?讲解题:1.某农场把61600平方米耕地划分为粮田、棉田与其他作物区,粮田与棉田的面积比是7:2,棉田与其他作物面积的比是6:1。
每种作物的面积各是多少平方米?2.光明小学将五年级的140名学生分成三个小组进行植树活动。
已知第一小组和第二小组学生的比是2:3,第二小组和第三小组学生的比是4:5。
这三个小组各有多少名学生?黄山小学六年级的同学分三组参加植树活动。
第一组与第二组学生数量的比是5:4,第二组与第三组学生数量的比是3:2。
已知第一组的学生数量比二、三两组学生数量的总和少15名。
六年级参加植树活动的一共有多少名学生?讲解题:1.嘉名小学参加科技组与作文组的学生数量的比是9:10,参加作文组与数学组的学生数量的比是5:7。
已知数学组与科技组共有69名学生。
数学组比作文组多多少名学生?2.两块一样重的合金,一块合金中铜与锌的质量比是2:5,另一块合金中铜与锌的质量比是1:3。
现将两块合金合成一块,求新合金中铜与锌的质量比。
甲、乙两校原有图书的数量比是7:5,如果甲校给乙校650本,甲、乙两校图书的数量比就是3:4。
原来甲校有图书多少本?讲解题:1.小明读一本书,已读部分和未读部分的比是1:5。
如果再读30页,则已读部分和未读部分的比是3:5。
这本书一共有多少页?2.甲、乙两包糖的质量比是4:1,从甲包取出130克放入乙包后,甲、乙两包糖的质量比为7:5。
小学奥数教程之比例应用题(一).教师版 (127)

1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化,有目的的转化;4、单位“1”变化的比例问题5、方程解比例应用题比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用,这一部分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有:一、比和比例的性质性质1:若a : b =c :d ,则(a + c ):(b + d )= a :b =c :d ; 性质2:若a : b =c :d ,则(a - c ):(b - d )= a :b =c :d ;性质3:若a : b =c :d ,则(a +x c ):(b +x d )=a :b =c :d ;(x 为常数) 性质4:若a : b =c :d ,则a ×d = b ×c ;(即外项积等于内项积) 正比例:如果a ÷b =k (k 为常数),则称a 、b 成正比; 反比例:如果a ×b =k (k 为常数),则称a 、b 成反比.二、主要比例转化实例①xa yb =⇒y b x a =; x ya b =; a b x y=; ②x a y b = ⇒ mx a my b =; x ma y mb =(其中0m ≠); ③x a y b = ⇒ x a x y a b =++; x y a bx a --=; x y a b x y a b++=-- ;④x a yb=,y c z d = ⇒ x a c z b d =;::::x y z ac bc bd =;⑤ x 的c a等于y 的d b ,则x 是y 的ad bc ,y 是x 的bcad .三、按比例分配与和差关系⑴按比例分配例如:将x 个物体按照:a b 的比例分配给甲、乙两个人,那么实际上甲、乙两个人各自分配到的物体数量与x 的比分别为():a a b +和():b a b +,所以甲分配到ax a b +个,乙分配到bxa b+个. 知识点拨教学目标比例应用题(一)⑵已知两组物体的数量比和数量差,求各个类别数量的问题例如:两个类别A 、B ,元素的数量比为:a b (这里a b >),数量差为x ,那么A 的元素数量为axa b-,B 的元素数量为bxa b-,所以解题的关键是求出()a b -与a 或b 的比值.四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“l ”。
比例和反比例 (奥数)(1)

比例和反比例 (奥数)(1)一、比例和反比例1.工人铺一条路,用边长4分米的方砖铺需要500块,如果改用边长5分米的方砖铺,需要多少块?【答案】解:设需要x块,4×4×500=5×5×x25x=8000x=320答:如果改用边长5分米的方砖铺地,需要320块。
【解析】【分析】此题主要考查了反比例应用题,这条路的总面积是一定的,每块砖的面积与铺的块数成反比例,据此列比例解答.2.京沪高铁的火车行驶路程与时间如下表:路程/千米80160240480……时间/时1236……(1)在上图中描出表示路程与时间相对应的点,然后把它们按顺序连起来。
(2)利用画出的图像估计一下,时间3.5小时的路程是________千米。
【答案】(1)根据分析,作图如下:(2)280【解析】【解答】(2)利用画出的图像估计一下,时间 3.5小时的路程是:3.5×80=280(千米).故答案为:280。
【分析】(1)观察统计图可知,纵轴表示路程,横轴表示时间,根据表中数据先描点,再连线,据此作图;(2)根据题意,用时间×速度=路程,据此列式解答.3.服装厂要加工一批服装,一共有4500套,头5天加工了750套,照这样计算,一共要多少天才能加工完这批报装?(用比例解)【答案】解:设一共要x天才能加工完这批服装。
750:5=4500:x750x=5×4500x=22500÷750x=30答:一共要30天才能加工完这批服装。
【解析】【分析】每天加工服装的套数不变,加工的总数与天数成正比例关系;设出未知数,根据每天加工的套数不变列出比例,解比例即可解决问题。
4.一辆汽车在公路上行驶,行驶的时间和路程如下图。
(1)这辆车10小时行驶多少千米?(2)行驶600千米要多少时?【答案】(1)解:10×80=800(千米)答:这辆车10小时行驶800千米。
(2)解:600÷80=7.5(小时)答:行驶600千米要7.5时。
(小学奥数)比例应用题(一)

1、比例的基本性質2、熟練掌握比例式的恒等變形及連比問題3、能夠進行各種條件下比例的轉化,有目的的轉化;4、單位“1”變化的比例問題5、方程解比例應用題比例與百分數作為一種數學工具在人們日常生活中處理多組數量關係非常有用,這一部分內容也是小升初考試的重要內容.通過本講需要學生掌握的內容有:一、比和比例的性質性質1:若a : b =c :d ,則(a + c ):(b + d )= a :b =c :d ; 性質2:若a : b =c :d ,則(a - c ):(b - d )= a :b =c :d ;性質3:若a : b =c :d ,則(a +x c ):(b +x d )=a :b =c :d ;(x 為常數) 性質4:若a : b =c :d ,則a ×d = b ×c ;(即外項積等於內項積) 正比例:如果a ÷b =k (k 為常數),則稱a 、b 成正比; 反比例:如果a ×b =k (k 為常數),則稱a 、b 成反比. 二、主要比例轉化實例 ①x ay b = ⇒ y b x a =; x ya b=; a b x y =;② x ay b = ⇒mx a my b =; x ma y mb =(其中0m ≠); ③ x ay b = ⇒x a x y a b =++; x y a bx a--=; x y a b x y a b ++=-- ;④ x a y b =,y c z d=⇒ x acz bd=;::::x y z ac bc bd =;知識點撥教學目標比例應用題(一)⑤ x 的c a 等於y 的d b ,則x 是y 的ad bc ,y 是x 的bc ad. 三、按比例分配與和差關係⑴按比例分配例如:將x 個物體按照:a b 的比例分配給甲、乙兩個人,那麼實際上甲、乙兩個人各自分配到的物體數量與x 的比分別為():a a b +和():b a b +,所以甲分配到ax a b +個,乙分配到bxa b+個. ⑵已知兩組物體的數量比和數量差,求各個類別數量的問題例如:兩個類別A 、B ,元素的數量比為:a b (這裏a b >),數量差為x ,那麼A 的元素數量為ax a b -,B 的元素數量為bxa b-,所以解題的關鍵是求出()a b -與a 或b 的比值.四、比例題目常用解題方式和思路解答分數應用題關鍵是正確理解、運用單位“l ”。
【精品奥数】六年级下册数学思维训练讲义-第四讲 比例(一) 人教版(含答案)

第四讲比例(一)第一部分:趣味数学开心蛙摘桃子开心蛙摘了一筐桃子,第一天吃掉这筐桃子的一半,第二天吃剩下的一半,第三天又吃了再剩下的一半,这时候筐里还有3个桃子,开心蛙一共摘了几个桃子?【答案】24个第二部分:习题精讲例题1:在比例“30:20=48:32”中,从30里减去18,而20、48这两项不变,要使比例成立,应把32加上多少?思路点拨:在比例30:20=48:32中,两个内项没有发生变化,而两个外项都发生了变化,而其中一个外项的变化是已知的,另外一个外项32的变化是未知的,所以,我们可以设32加上的数是x,这样就构成一个新的比例:(30-18):20=48:(32+x),用解比例的知识可求出x的值所以(30-18):20=48:(32+x), 12:20=48:(32+x),12×(32+x)=48×20,(32+x)=48×20,32+x=80,x=48答:应把32加上48.练习1:1.在比例“18:24=27:36”中,从24里减去12,而18、27这两项不变,要使比例成立,应在36上减去多少?2.在比例“4.5:6=5.1:6.8”中,两个外项不变,内项6减去0.6,要使比例成立,另外一个内项5.1应加上多少?3.在比例“:=:”中,两个外项不变,内项加上,要使比例成立,另外一个内项应减去多少?例题2:小明读一本300页的故事书,前2天读了全书的,照这样计算,读完全书还要多少天?思路点拨:这是一道带有分数的比例应用题,我们既可以根据具体的页数列比例式,也可根据相对应的分数列比例式。
解:设读完全书还需要x天:2=(1-):xX=4答:读完全书还需要4天练习2:1.一辆汽车从A地开往300千米外的B地,前2小时已经行了全程的,照这样计算,行完全程还需要几小时?2.工厂接到生产2000个零件的任务,前3天完成了总任务的45%,剩下的任务还需要多少天才能完成?3.小明计划在6天内读完一本240页的故事书,实际每天多读了原计划的,实际多少天就能读完?例题3:甲、乙两辆汽车分别从两地相向开出,它们的速度比是5:7,在距中点18千米处相遇两地相距多少千米?思路点拨:因为两车同时出发,相遇时间一定,所以,路程与速度成正比,即相遇时甲、乙两车行驶的路程比为5:7.然后由“距中点18千米处相遇”可以知道,相遇时乙车比甲车多行18×2=36(千米)。
六年级奥数-11比的应用(一)

比的应用(一)1.理解比和按比例分配的意义2.学会解比例分配问题1.确定分配的比例2.按比例分配的解法按比例分配基本题型在实际生活中,有时并不是把一个数量平均分,而常常需要把一个数量按一定的比进行分配,这种就叫做按比例分配。
1、按比例分配的方法通常有两种:(1)把比看作分成的份数,先求出每一份是多少,再解答。
(2)转化成分数解答:先求出个部分占总量的几分之几,再解答。
2、按比例分配的基本出题方式通常是:已知两个或几个数量的和,这两个或几个数量的比,求这两个或这几个数量是多少?例1.甲乙丙三人共同生产100个零件,甲完成了三成,乙和丙完成的数量是2:5,乙和丙各完成了多少个?练习1.小明调查了本地区11月份每天的天气情况,把它们分为晴天、阴天、雨天三类,从统计结果来看,晴天占了,阴天和雨天的天数比为2:1,这个月晴天、阴天、雨天各有多少天?已知两个或几个数量的和,这两个或几个数量的比,求这两个或这几个数量是多少。
遇到这种题型时,需要先求出每份是多少。
例2.小华准备用60cm长的铁丝围成一个长方形,若围成的长方形的长与宽的比是3︰2,那么这个长方形的面积是多少?练习1.一个长方形菜园周长是96米,长和宽的比是7:5.菜园的面积是多少平方米?当比例涉及到长方形周长、长方体棱长和时,需要注意先算出各部分的和。
例3.一个三角形的三个内角的比是2:3:4,这三个内角的度数分别是多少?练习1.一个长方体棱长总和为96厘米,高为4厘米,长与宽的比是3∶2,这个长方体的体积是多少?有时候题目会有隐含信息告知我们各部分的和,这要求我们仔细读题,掌握好基础知识。
按比例分配变化题型1、按比例分配变化题型有:(1)已知两个数量的差,两个数的比,求这两个数是多少?(2)已知一个数量是多少,两个或几个数的比,求另外几个数量是多少?注意:遇到这种题型时,需要求出每一份的量。
例1.一块长方形的地,长和宽的比是5:3,长比宽多24米,这块地的面积是多少平方米?练习1.把一根绳子按5:3截成甲、乙两段,已知乙比甲短1.2米.这根绳子原来全长多少米?已知两个数量的差,两个数的比,求这两个数是多少。
奥数第九讲比的应用1学生版

例1. 甲工厂有120人,乙工厂有80人.从乙工厂调几人到甲工厂才能使甲工厂与乙工厂人数的比是答案解:,,,(人);答:从乙工厂调5人到甲工厂才能使甲工厂与乙工厂人数的比是.解析因为总人数不变,因此根据总人数以及后来两厂人数比,求出后来乙厂人数,然后用原来乙工厂人数减去后来的人数,即为所求.举一反三:1. 甲班有60人,乙班有80人.从甲班调几人到乙班才能使甲、乙两班人数的比是2. 小明有25元,小华有35元.小华给小明几元才能使小明与小华的钱数比是甲筐有50个苹果,乙筐有70个苹果,从乙筐拿几个苹果放入甲筐才能使甲、乙两筐苹果个数的比是7:5?例2. 光明小学将五年级的140名学生,分成三个小组进行植树活动,已知第一小组和第二小组人数的比是,第二小组和第三小组人数的比是.这三个小组各有多少人?答案解:,,第一小组、第二小组和第三小组人数的比是,,(人),(人),(人);答:第一小组有32人,第二小组有48人,第三小组有60人.解析根据第一小组和第二小组人数的比是,第二小组和第三小组人数的比是,可以得到第一小组、第二小组和第三小组人数的比是,总人数是140人,根据按比例分配求出各小组的人数.举一反三:某农场把61600平方米耕地划归为粮田、棉田与其他作物,粮田与棉田之间的面积比是,棉田与其他作物面积的比是.每种作物的面积各是多少平方米?黄山小学六年级的同学分三组参加植树.第一组与第二组的人数的比是,第二组与第三组人数的比是.已知第一组的人数比二、三组人数的总和少15人.六年级参加植树的共有多少人?科技小组与作文小组的人数比是,作文小组与数学小组人数比是.已知数学小组与科技小组共有69人.数学小组比作文小组多多少人?例3. 甲乙两校原有图书本数的比是,如果甲校给乙校650本,甲、乙两校图书本数的比就是.原来甲校有图书多少本?答案解:份,份, 两校图书总数:,,(本);原来甲校有图书:(本);答:原来甲校有图书2450本.解析甲乙两校原有图书本数的比是,两校图书总数是份,甲校占总数的,如果甲校给乙校650本,甲、乙两校图书本数的比就是,这时的两校图书总数不变即单位“1”不变,两校图书总数是份,甲校占总数的,甲校由原来的占图书总数的变为,是因为甲校给乙校650本,就是两校图书总数的是650本,据此可求出两校图书总数,求原来甲校有图书多少本,用两校图书总数,两校图书总数已求出.举一反三:小明读一本书,已读与未读的页数比是,如果再读30页,则已读和未读的页数为.这本书共有多少页?甲、乙两包糖的质量比是,从甲包取出130克放入乙包后,甲、乙两包糖的质量比为.原来甲包有多少克糖?五年级三个班举行数学竞赛,一班参加比赛的占全年级参赛人数的.二班与三班参加比赛的人数比是,二班比三班少8人,一班有多少人参加了数学竞赛?例4. 例子:甲乙丙三人同时从A向B跑,当甲跑到B时,乙离B还有35米,丙离B还有68米;当乙跑到B时,丙离B还有40米,A、B相距多少米?思路导航:乙跑最后35米时,丙跑68-40=28(米),丙与乙速度的比为28:35=4:5,把AB的距离看做“1”,当乙跑完单位“1”,丙跑完了5分之4,距离B还有1-5分之四=5分之一算式:68-40=28(米)40÷(1-35分之28)=200(米)题目:小刚和小明进行了100米短跑比赛(假定2人速度均不变)。
比例和反比例 (奥数)(1)
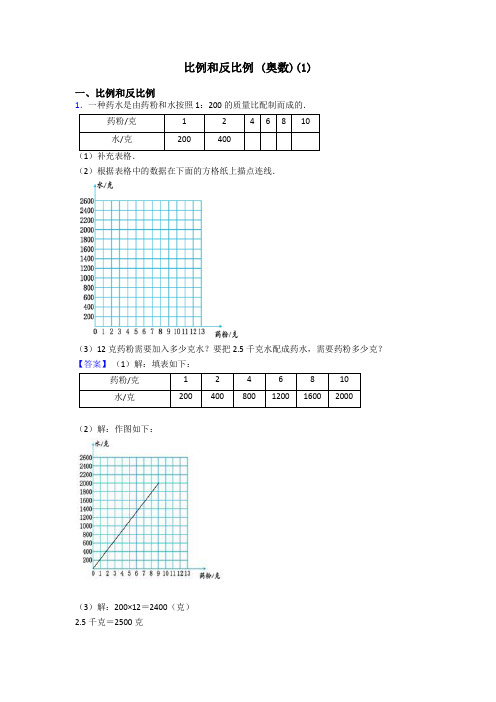
比例和反比例 (奥数)(1)一、比例和反比例1.一种药水是由药粉和水按照1:200的质量比配制而成的.药粉/克1246810水/克200400(1)补充表格.(2)根据表格中的数据在下面的方格纸上描点连线.(3)12克药粉需要加入多少克水?要把2.5千克水配成药水,需要药粉多少克?【答案】(1)解:填表如下:药粉/克1246810水/克200400800120016002000(2)解:作图如下:(3)解:200×12=2400(克)2.5千克=2500克2500× =12.5(克)答:12克药粉需要加水2400克,要把2.5千克水配成药水,需要药粉12.5克.【解析】【分析】(1)根据条件“ 一种药水是由药粉和水按照1:200的质量比配制而成的”可知,用药粉:水=1:200,据此列比例解答,然后填表即可;(2)根据统计表中的数据,在统计图中先描点,然后再连线,图中的统计图纵轴每格代表200克,据此作图;(3)根据条件可知,1克药粉要加入200克水,用药粉的质量×200=水的质量,据此用乘法计算;要把2.5千克水配成药水,需要药粉多少克,先统一单位,1千克=1000克,然后用水的质量×药粉占水的分率=药粉的质量,据此列式解答。
2.同一时间、同一地点测得的树高和它的影长如下表:树高/米2346…影长/米1.62.43.24.8…(2)树高和影长成什么比例?为什么?(3)量得一颗大树的影长是10.4米,这棵大树有多高?【答案】(1)(2)解:成正比例。
因为 =1.25, =1.25, =1.25, =0.8(一定),所以,树高和影长成正比例。
(3)解:设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答:这棵大树的高度是13米。
【解析】【分析】(1)观察统计图可知,横轴表示树高,竖轴表示影长,据此先描点,再连线,据此作图;(2)分别用树高:影长,求出比值,当比值一定时,成正比例,据此判断;(3)根据题意可知,设这棵大树的高度是x米,用树高:影长=树高:影长,据此列正比例解答.3.王叔叔开车从甲地到乙地,一共用了3小时,每小时行80km,原路返回每小时行100km。
比例的应用1——小学六年级奥数题

比例的应用(1)例1:甲乙两个长方形,它们的周长相等,甲的长与宽之比是3:2,乙的长与宽之比是4:3,那么,甲与乙的面积之比是多少?练习:1、甲乙两人步行的速度比是7:5,甲乙分别由A、B两地同事出发,如果相向而行,0.5小时相遇。
如果他们同时同向而行,那么甲追上乙需要多少小时?2、客车和货车从甲、乙两地同时出发,相向而行,在距中点30千米处相遇。
已知货车与客车的速度比是5:8,求甲、乙两地的距离。
例2:一种大米每千克1.08元,另一种大米每千克1.48元,把这种大米混合后,售价为每千克1.23元,求两种大米混合的重量比?练习:1、用奶糖和水果糖混合在一起酿成一种礼品糖,已知奶糖每千克5.4元,水果糖每千克3元。
现在要想配出的礼品糖每千克为4.8元,那么奶糖和水果糖应该按怎样的比例混合?2、例3:两只蜡烛长度相等,粗蜡烛可以点5小时,细蜡烛可以点4小时,同时点燃一段时间后,粗蜡烛长度是细蜡烛长度的2倍。
此时已经点燃了多少小时?练习:1、有长度相同,粗细不同的两支蜡烛,细蜡烛点完需1小时,粗蜡烛点完需2小时。
有一次停电,将这两支蜡烛同时点燃,来电时,发现粗蜡烛是细蜡烛的2 倍时,问停电多长时间?2、两支粗细,长短都不相同的蜡烛,长的一支能燃4小时,短的一支能燃6小时,将它们同时点燃2小时后,两支蜡烛剩下的长度相等。
求两支蜡烛原来的长度比。
3、两支蜡烛粗细不同,细蜡烛之长是粗蜡烛之长的2倍,细蜡烛点完要1小时,粗蜡烛点完要2小时,有一次停电,将这两支蜡烛同时点燃,来电时发现两支蜡烛所剩的长度一样。
问:停电多长时间?能力检测:1、甲和乙同时分别从A、B两站相对出发,在离中点 8千米处相遇,已知乙的速度与甲的速度比是3:4,问A、B两站相距多少千米?2、话梅糖每千克5.1元,奶糖每千克8.9元,现把这两种糖混合后,要求混合后的糖价为每千克5.4元,话梅糖和奶糖应用怎样的重量比才合适?3、一个底面直径是24厘米的圆柱形玻璃中装有水,水里放着一个底面直径12厘米,高18厘米的圆锥形铅块,当铅块从水中取出时,杯里的水面会下降多少厘米?4、一个正方体的表面积是54平方厘米,如果以这个正方体一个面的对角线为棱长做一个新的正方体,如图所示。
奥数比例的应用题

奥数比例的应用题奥数比例的应用题国际数学奥林匹克是一项以数学为内容,以中学生为对象的国际性竞赛活动,至今已有30余年的历史。
下面是小编收集的奥数比例的应用题,希望大家认真阅读!奥数比例的应用题1知识点1.份数思想甲:乙=a:b,可以看成甲为a份,乙为b份。
份数是可以相加减的,如甲、乙的总和为a+b份,甲比乙多a-b份。
2.量份对应如果a份对应的量是x,那么1份对应的量就是x÷a。
而如果1份对应的量是x,那么a份对应的量就是x×a3.统一比(化连比)在两个比中,1份代表的量可能是不同的。
例如甲:乙=2:3,乙:丙=2:5,这里乙在前面的比中代表3份,在后面的比中代表2份,应该取3、2最小公倍数6,两个比分别化为甲:乙=4:6,乙:丙=6:15,这样就统一了两个比,可以写成甲:乙:丙=4:6:15.例题:(1)艾迪和大宽的糖数之比为4:5,艾迪有20块糖,那么大宽有块糖.(2)艾迪和大宽一共有45块糖,而且两人糖数之比为4:5,那么艾迪有块糖,大宽有块糖.(3)艾迪、大宽和薇儿一共有45块糖,而且三人糖数之比为4:5:6,那么艾迪有块糖,大宽有块糖,薇儿有块糖.(4)艾迪、大宽和薇儿三人糖数之比为4:5:6,并且知道薇儿比艾迪多10块糖,那么三人共有块糖.【解析】(1)艾迪4份是20块,因此1份是20÷4=5块,大宽是5份,因此大宽有5×5=25块;(2)艾迪4份,大宽5份,总共9份,对应45块糖,所以1份是45÷9=5块糖,所以艾迪有5×4=20块糖,大宽有5×5=25块糖;(3)一共有4+5+6=15份,对应45块糖,所以1份是45÷15=3块糖,所以艾迪有3×4=12块糖,大宽有3×5=15块糖,薇儿有3×6=18块糖;(4)薇儿比艾迪多6-4=2份,对应10块糖,所以1份是10÷2=5块糖,三人一共有4+5+6=15份,所以共有5×15=75块糖。
小学奥数教程∶比例 计算题

小学奥数教程∶比例计算题一、比例1.一个计算机芯片的实际尺寸是8mm×8mm,按一定比例所画的图如下图,图中所用的比例尺是()。
A. 1:5B. 25:1C. 2:1D. 5:1【答案】 D【解析】【解答】4cm:8mm=40mm:8mm=(40÷8):(8÷8)=5:1故答案为:D.【分析】已知图上距离和实际距离,求比例尺,用图上距离:实际距离=比例尺,据此解答.2.比例尺一定,实际距离扩大到原来的5倍,则图上距离( )。
A. 缩小到原来的B. 扩大到原来的5倍C. 不变【答案】 B【解析】【解答】解:因为图上距离=实际距离×比例尺,所以当比例尺一定时,实际距离扩大到原来的5倍,则图上距离也将扩大到原来的5倍。
故答案为:B。
【分析】图上距离=实际距离×比例尺。
3.下面( )组中的两个比不能组成比例。
A. 10:12和35:42B. 20:10和60:20C. :和12:8D. 0.6:0.2和:【答案】 B【解析】【解答】解:A、10:12=, 35:42=,能组成比例;B、20:10=2,60:20=3,不能组成比例;C、=1.5,12:8=1.5,能组成比例;D、0.6:0.2=3,=3:1,不能组成比例。
故答案为:B。
【分析】比值相等的两个比能组成比例,由此计算出两个比的比值即可确定能否组成比例。
4.把一个直径4毫米的手表零件,画在图纸上的直径是8厘米,这幅图纸的比例尺是( )。
A. 1:2B. 2:1C. 1:20D. 20 2 1【答案】 D【解析】【解答】解:8厘米=80毫米,比例尺是80:4=20:1。
故答案为:D。
【分析】把图上距离换算成毫米,然后写出图上距离与实际距离的比并把比化成后项是1的比就是这幅图的比例尺。
5.在比例尺是1:50000的图纸上,量及两点之间的距离是18厘米,这两点的实际距离是________千米.【答案】 9【解析】【解答】解:18÷=900000厘米=9千米,所以这两点的实际距离是9千米。
【精品】比例 (奥数)

【精品】比例 (奥数)一、比例1.一个零件的高是4mm,在图纸上的高是2cm.这幅图纸的比例尺是()A. 1:5B. 5:1C. 1:2D. 2:1【答案】 B【解析】【解答】解:2cm=20mm,比例尺:20:4=5:1。
故答案为:B。
【分析】把2cm换算成mm,然后写出图上距离与实际距离的比并化成后项是1的比就是这幅图的比例尺。
2.下面各比中,能与:6组成比例的是()A. 2.5:16B. 0.1:C. 3:2.4D. :4【答案】 D【解析】【解答】解:;A、2.5:16=2.5÷16=0.15625,不能组成比例;B、,不能组成比例;C、3:2.4=1.25,不能组成比例;D、,能组成比例。
故答案为:D。
【分析】比例是表示两个比相等的式子,因此比值相等的两个比才能组成比例。
3.下面各比中与:组成比例的比是()。
A. 3:4B. 4:3C. 1:12【答案】 B【解析】【解答】:=÷=,选项A,3:4=3÷4=,≠,不能组成比例;选项B,4:3=4÷3=,=,能组成比例;选项C,1:12=1÷12=,≠,不能组成比例。
故答案为:B.【分析】判断两个比是否能组成比例,可以求出比值,用前项÷后项=比值,如果比值相等,就能组成比例,否则不能组成比例.4.如果5x=8y(x、y≠0),那么________:________=5:8.【答案】 y;x【解析】【解答】如果5x=8y(x、y≠0),那么y:x=5:8。
故答案为:y;x。
【分析】根据比例的性质:在比例里,两外项之积等于两内项之积,将相乘的两个数同时做外项或内项即可解答。
5.一幅地图的比例尺是1:400000,把它改成线段比例尺是________,已知AB两地的实际距离是24千米,在这幅地图上应画________厘米。
【答案】;6【解析】【解答】400000厘米=4千米,图上1厘米代表实际4千米,线段比例尺为:, 24÷4=6(厘米).故答案为:;6.【分析】先把400000厘米化为4千米,比例尺就是图上1厘米表示实际4千米;实际距离×比例尺=图上距离,据此解答.6.在3,15,12,5,9,30,20把可以组成的比例写出两组________、________。
五年级奥数比和比例应用题

五年级奥数比和比例应用题五年级奥数比和比例应用题无论是在学校还是在社会中,我们最不陌生的就是试题了,通过试题可以检测参试者所掌握的知识和技能。
那么一般好的试题都具备什么特点呢?下面是店铺为大家整理的五年级奥数比和比例应用题,欢迎阅读与收藏。
五年级奥数比和比例应用题 1某车间要加工2220个零件,单独做,甲、乙、丙三人所需工作时间的比是4∶5∶6。
现在由三人共同加工,问完成任务时,三人各加工了多少个?错解由甲、乙、丙三人单独做所需工作时间的比是4∶5∶6,推出甲、乙、丙三人工作效率的比是6∶5∶4,用按比例分配的思路解。
评析上述解答错在把甲、乙、丙三人工作效率的比看成是6∶5∶4。
诚然,如果甲、乙二人工作时间的比是4∶5,那么,甲、乙二人工作效率的比就是5∶4,这是正确的。
但是,把甲、乙、丙三人工作时间的连比是4∶5∶6转化成甲、乙、丙三人工作效率的连比是6∶5∶4,那就大错了!不错,工作效率的比等于工作时间比的反比。
从已知条件看,甲、乙二人工作时间的比是4∶5,所以,甲、乙二人工作效率的比是5∶4;乙、丙二人工作时间的比是5∶6,所以,乙、丙二人工作效率的比是6∶5。
这里的“5∶4”表示甲5份,乙4份,“6∶5”表示乙6份,丙5分,两个比都是两重相比,其中同样表示“乙”有几份的数在前后两个比中并不相同,我们怎么能将这两个比直接变成甲、乙、丙三人工作效率的连比呢?显然,上述解答中把甲、乙、丙三人工作效率的连比看成是6∶5∶4,是错误的。
容易看出,因为5∶4=15∶12,6∶5=12∶10,所以,由上述“甲、乙二人工作效率的比是5∶4,乙、丙二人工作效率的比是6∶5”,也可以得到甲、乙、丙三人工作效率的比是是15∶12∶10。
五年级奥数比和比例应用题 2有两瓶同样重的盐水,甲瓶盐水盐与水重量的比是1∶8,乙瓶盐水盐与水重量的比是1:5。
现将两瓶盐水并在一起,问在混合后的盐水中盐与水重量的比是多少?错解认为在甲瓶盐水中,盐的重量是“1”,水的重量是“8”,在乙瓶盐水中,盐的重量是“1”,水的重量是“5”,于是,将两瓶盐水并在一起,便得到盐的重量是(1+1=)2,水的重量是(8+5=)13。
小学六年级奥数-第14讲比的应用(一)后附答案

第14讲比的应用(一)我们已经学过比的知识,都知道比和分数、除法其实是一回事,所有比与分数能互相转化。
运用这种方法解决一些实际问题可以化难为易,化繁为简。
二、精讲精练24【例题1】甲数是乙数的2,乙数是丙数的4,甲、乙、丙三数的比是():():35练习1:1、甲数是乙数的4,乙数是丙数的5,甲、乙、丙三数的比是():():()582、甲数是乙数的4,甲数是丙数的4,甲、乙、丙三数的比是():():()593、甲数是丙数的3,乙数是丙数的 2 1,甲、乙、丙三数的比是():():()。
72【例题2】光明小学将五年级的140 名学生,分成三个小组进行植树活动,已知第一小组和第二小组人数的比是2:3,第二小组和第三小组人数的比是4:5。
这三个小组各有多少人?练习2:1、某农场把61600公亩耕地划归为粮田与棉田,它们之间的比是7:2,棉田与其他作物面积的比6:1。
每种作物各是多少公亩?2、黄山小学六年级的同学分三组参加植树。
第一组与第二组的人数的比是5:4,第二组与第三组人数的比是3:2。
已知第一组的人数比二、三组人数的总和少15 人。
六年级参加植树的共有多少人?【例题3】甲、乙两校原有图书本数的比是7:5,如果甲校给乙校650 本,甲、乙两校图书本数的比就是3:4。
原来甲校有图书多少本?练习3:1、小明读一本书,已读的和未读的页数比是1:5。
如果再读30 页,则已读和未读的页数之比为3:5。
这本书共有多少页?2、甲、乙两包糖的重量比是4:1。
从甲包取出130克放入乙包后,甲、乙两包糖7:5。
原来甲包有多少克糖?【例题4】从前有个农民,临死前留下遗言,要把17 头牛分给三个儿子,其中大111儿子分得1,二儿子分得1,小儿子分得1,但不能把牛卖掉或杀掉。
三个儿子按照老239人的要求怎么也不好分。
后来一位邻居顺利地把17 头牛分完了,你知道这到底是怎么回事吗?练习4:1 、图书室取出一批书,按照一年级得 1 ,二年级得 1 ,三年级得1 ,正好是 41 本,各年级各得多237少本?2、古罗马富豪约翰逊再临终前,对怀孕的妻子写下这样一份遗嘱:如果生下来是个男孩,就把遗产的三分之二给儿子,母亲拿三分之一;如果生下来的是女孩就把遗产的三分之一给女儿,三分之二给母亲。
小学奥数教程∶比例和反比例 计算题(1)

小学奥数教程∶比例和反比例计算题(1)一、比例和反比例1.工人铺一条路,用边长4分米的方砖铺需要500块,如果改用边长5分米的方砖铺,需要多少块?【答案】解:设需要x块,4×4×500=5×5×x25x=8000x=320答:如果改用边长5分米的方砖铺地,需要320块。
【解析】【分析】此题主要考查了反比例应用题,这条路的总面积是一定的,每块砖的面积与铺的块数成反比例,据此列比例解答.2.妈妈有一辆自行车,A和B是自行车的两个齿轮(如图),骑车时用脚驱动A带动B,从而使自行车前进。
(1)这辆自行车,齿轮A有50个齿,齿轮B有20个齿。
当齿轮A转动1圈时,齿轮B 转动多少圈?(2)这辆自行车的车轮直径约是60cm,妈妈每天上班的路程大约是3000m。
妈妈骑车上班大约要置多少圈(即齿轮A转动的圈数)?(计算时π取3,最后结果保留整数)【答案】(1)解:50×1÷20=2.5(圈)答:齿轮B转动2.5圈。
(2)解:60cm=0.6m3000÷(0.6×3×2.5)≈667(圈)答:妈妈骑车上班大约要置667圈。
【解析】【分析】(1)根据题意可知,用齿轮A的齿数×转动的圈数÷齿轮B的齿数=齿轮B转动的圈数,据此列式解答;(2)根据题意可知,先求出自行车齿轮B每圈走过的路程,用周长公式:C=πd,然后根据齿轮A转1圈,齿轮B转2.5圈,可以求出齿轮A每圈走过的路程,用齿轮B每圈走过的路程×齿轮B转动的圈数=齿轮A每圈走过的路程,最后用上班的总路程÷齿轮A每圈走过的路程=齿轮A转动的圈数,据此列式解答,结果保留整数.3.乐乐买了一个军舰模型,包装盒上写着“按1:400制作”,他量了一下,模型长45cm。
这艘军舰实际有多长?【答案】解:设这艘军舰实际长xcm.x=45×400x=1800018000cm=180m答:这艘军舰实际长180米.【解析】【分析】先设出未知数,然后根据1:400的比列出比例,解比例求出实际的长度,注意换算单位.4.用边长15厘米的方砖给房间铺地需要2000块,如果改用边长为25厘米的方砖铺地,需要多少块?【答案】解:设需要x块。
小学奥数教程:比例应用题(一)

⼩学奥数教程:⽐例应⽤题(⼀)1、⽐例的基本性质2、熟练掌握⽐例式的恒等变形及连⽐问题3、能够进⾏各种条件下⽐例的转化,有⽬的的转化;4、单位“1”变化的⽐例问题5、⽅程解⽐例应⽤题⽐例与百分数作为⼀种数学⼯具在⼈们⽇常⽣活中处理多组数量关系⾮常有⽤,这⼀部分内容也是⼩升初考试的重要内容.通过本讲需要学⽣掌握的内容有:⼀、⽐和⽐例的性质性质1:若a : b =c :d ,则(a + c ):(b + d )= a :b =c :d ;性质2:若a : b =c :d ,则(a - c ):(b - d )= a :b =c :d ;性质3:若a : b =c :d ,则(a +x c ):(b +x d )=a :b =c :d ;(x 为常数)性质4:若a : b =c :d ,则a ×d = b ×c ;(即外项积等于内项积)正⽐例:如果a ÷b =k (k 为常数),则称a 、b 成正⽐;反⽐例:如果a ×b =k (k 为常数),则称a 、b 成反⽐.⼆、主要⽐例转化实例① x a y b = ? y b x a =; x y a b=; a b x y =;② x a y b = ? mx a my b =; x ma y mb=(其中0m ≠);③ x a y b = ? x a x y a b =++; x y a b x a--=; x y a b x y a b ++=-- ;④ x a y b =,y c z d = ? x a c z b d=;::::x y z ac bc bd =;⑤ x 的c a等于y 的d b ,则x 是y 的ad bc ,y 是x 的bc ad .三、按⽐例分配与和差关系⑴按⽐例分配例如:将x 个物体按照:a b 的⽐例分配给甲、⼄两个⼈,那么实际上甲、⼄两个⼈各⾃分配到的物体数量与x 的⽐分别为():a a b +和():b a b +,所以甲分配到ax a b +个,⼄分配到bx a b+个. ⑵已知两组物体的数量⽐和数量差,求各个类别数量的问题例如:两个类别A 、B ,元素的数量⽐为:a b (这⾥a b >),数量差为x ,那么A 的元素数量为ax a b -,B 的元素数量为bx a b-,所以解题的关键是求出()a b -与a 或b 的⽐值.知识点拨教学⽬标⽐例应⽤题(⼀)四、⽐例题⽬常⽤解题⽅式和思路解答分数应⽤题关键是正确理解、运⽤单位“l ”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化,有目的的转化;4、单位“1”变化的比例问题5、方程解比例应用题比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用,这一部分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有:一、比和比例的性质性质1:若a : b =c :d ,则(a + c ):(b + d )= a :b =c :d ;性质2:若a : b =c :d ,则(a - c ):(b - d )= a :b =c :d ;性质3:若a : b =c :d ,则(a +x c ):(b +x d )=a :b =c :d ;(x 为常数)性质4:若a : b =c :d ,则a ×d = b ×c ;(即外项积等于内项积)正比例:如果a ÷b =k (k 为常数),则称a 、b 成正比;反比例:如果a ×b =k (k 为常数),则称a 、b 成反比.二、主要比例转化实例①x a y b = ⇒ y b x a =; x y a b =; a b x y =; ② x a y b = ⇒ mx a my b =; x ma y mb=(其中0m ≠); ③ x a y b = ⇒ x a x y a b =++; x y a b x a--=; x y a b x y a b ++=-- ;④ x a y b =,y c z d = ⇒ x ac z bd=;::::x y z ac bc bd =; ⑤ x 的c a等于y 的d b ,则x 是y 的ad bc ,y 是x 的bc ad . 三、按比例分配与和差关系 ⑴按比例分配例如:将x 个物体按照:a b 的比例分配给甲、乙两个人,那么实际上甲、乙两个人各自分配到的物体数量与x 的比分别为():a a b +和():b a b +,所以甲分配到ax a b +个,乙分配到bx a b+个. ⑵已知两组物体的数量比和数量差,求各个类别数量的问题 例如:两个类别A 、B ,元素的数量比为:a b (这里a b >),数量差为x ,那么A 的元素数量为ax a b -,B 的元素数量为bx a b-,所以解题的关键是求出()a b -与a 或b 的比值. 知识点拨 教学目标比例应用题(一)四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“l ”。
题中如果有几个不同的单位“1”,必须根据具体情况,将不同的单位“1”,转化成统一的单位“1”,使数量关系简单化,达到解决问题的效果。
在解答分数应用题时,要注意以下几点:1. 题中有几种数量相比较时,要选择与各个已知条件关系密切、便于直接解答的数量为单位“1”。
2. 若题中数量发生变化的,一般要选择不变量为单位“1”。
3. 应用正、反比例性质解答应用题时要注意题中某一数量是否一定,然后再确定是成正比例,还是成反比例。
找出这些具体数量相对应的分率与其他具体数量之间的正、反比例关系,就能找到更好、更巧的解法。
4. 题中有明显的等量关系,也可以用方程的方法去解。
5. 赋值解比例问题模块一、比例转化 【例 1】 甲、乙、丙三个数,已知甲:(乙+丙)4:3=,乙:丙2:7=,求甲:乙:丙。
【考点】比例应用题 【难度】2星 【题型】解答【解析】 由:2:7=乙丙可得到():2:9+=乙乙丙,():7:9+=丙乙丙,而():4:3+=甲乙丙, 所以:427::::12:2:7399==甲乙丙. 【答案】12:2:7【例 2】 已知甲、乙、丙三个数,甲的一半等于乙的2倍也等于丙的23,那么甲的23、乙的2倍、丙的一半这三个数的比为多少?【考点】比例应用题 【难度】2星 【题型】解答【解析】 甲的一半、乙的2倍、丙的23这三个数的比为1:1:1,所以甲、乙、丙这三个数的比为()121:12:123⎛⎫⎛⎫÷÷÷ ⎪ ⎪⎝⎭⎝⎭即132::22,化简为4:1:3,那么甲的23、乙的2倍、丙的一半这三个数的比为()214:12:332⎛⎫⎛⎫⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭即83:2:32,化简为16:12:9. 【答案】16:12:9【例 3】 已知甲、乙、丙三个数,甲等于乙、丙两数和的13,乙等于甲、丙两数和的12,丙等于甲、乙两数和的57,求甲:乙:丙. 【考点】比例应用题 【难度】2星 【题型】解答【解析】 由甲等于乙、丙两数和的13,得到甲等于三个数和的113+14=,同样的乙等于甲、丙两数和的112+13=,同样的丙等于甲、乙两个数和的557512=+ ,所以甲:乙:丙115::3:4:54312==. 【答案】3:4:5【例 4】 甲、乙两个工人上班,甲比乙多走15的路程,而乙比甲的时间少111,甲、乙的速度比是 . 【考点】比例应用题 【难度】2星 【题型】解答【关键词】2008年,清华附中例题精讲【解析】 甲走的路程是乙走的路程的65,甲用的时间是乙用的时间的1110,所以甲的速度是乙的速度的6111251011÷=,即甲、乙的速度比是12:11. 【答案】12:11【例 5】 右图是一个园林的规划图,其中,正方形的43是草地;圆的76是竹林;竹林比草地多占地450平方米. 问:水池占多少平方米? 【考点】比例应用题 【难度】2星 【题型】解答【解析】 正方形的43是草地,那如果水池占1份,草地的面积便是3份;圆的76是竹林,水池占1份,竹林的面积是6份。
从而竹林比草地多出的面积是(6-3=)3份。
3份的面积是450平方米,可见1份面积是450÷3=150(平方米),即水池面积是150平方米。
【答案】150【例 6】 如下图所示,圆B 与圆C 的面积之和等于圆A 面积的45,且圆A 中的阴影部分面积占圆A 面积的16,圆B 的阴影部分面积占圆B 面积的15,圆C 的阴影部分面积占圆C 面积的13.求圆A 、圆B 、圆C 的面积之比.CB A【考点】比例应用题 【难度】3星 【题型】解答【解析】 设A 与B 的共同部分的面积为x ,A 与C 的共同部分的面积为y ,则根据题意有()()564A B C x y =+=+,5B x =,3C y =,于是得到()56453B C B C ⎛⎫+=+ ⎪⎝⎭,这条式子可化简为15B C =,所以()5204A B C C =+=.最后得到::20:15:1A B C =. 【答案】::20:15:1A B C =【例 7】 地球表面的陆地面积和海洋面积之比是29∶71,其中陆地的四分之三在北半球,那么南、北半球海洋面积之比是( )A . 284∶29B . 284∶87C . 87∶29D . 171∶113【考点】比例应用题 【难度】2星 【题型】选择【关键词】华杯赛,六年级【解析】 解:设地球表面积为1,则北半球海洋面积为:0.5-0.29×34=1.134南半球海洋面积为:0.71-1.134=1.714南北半球海洋面积之比为:1.714∶1.134=171∶113 答案:D【答案】D【例 8】 某俱乐部男、女会员的人数之比是3:2,分为甲、乙、丙三组.已知甲、乙、丙三组的人数比是10:8:7,甲组中男、女会员的人数之比是3:1,乙组中男、女会员的人数之比是5:3.求丙组中男、女会员人数之比.【考点】比例应用题 【难度】3星 【题型】解答【解析】 以总人数为1,则甲组男会员人数为103310873110⨯=+++,女会员为31110310⨯=,乙组男会员为8511087535⨯=+++,女会员为1335525⨯=;丙组男会员为33113+210510⎛⎫-+= ⎪⎝⎭,女会员为21393+2102550⎛⎫-+= ⎪⎝⎭;所以,丙组中男、女会员人数之比为19:5:91050=. 【答案】5:9【巩固】 某团体有100名会员,男女会员人数之比是14:11,会员分成三组,甲组人数与乙、丙两组人数之和一样多,各组男女会员人数之比依次为12:13、5:3、2:1,那么丙组有多少名男会员?【考点】比例应用题 【难度】3星 【题型】解答【解析】 会员总人数100人,男女比例为14:11,则可知男、女会员人数分别为56人、44人;又已知甲组人数与乙、丙两组人数之和一样多,则可知甲组人数为50人,乙、丙人数之和为50人,可设丙组人数为x 人,则乙组人数为()50x -人,又已知甲组男、女会员比为12:13,则甲组男、女会员人数分别为24人、26人,又已知乙、丙两组男、女会员比例,则可得:5224(50)5683x x +-+=,解得18x =.即丙组会员人数为18人,又已知男、女比例,可得丙组男会员人数为218123⨯=人. 【答案】12【例 9】 一项公路的修建工程被平均分成两份承包给甲、乙个工程队建设,两个工程队建设了相同多的一段时间后,分别剩下60%、40%的任务没有完成,已知两个工程队的工作效率(建设速度)之比3:1,求这两个工程队原先承包的修建公路长度之比.【考点】比例应用题 【难度】3星 【题型】解答【解析】 (法一)甲工程队以3倍乙工程队建设速度,仅完成了40%的承包任务,而乙工程队完成了60%,所以甲工程队承包任务的40%等于乙工程队承包任务的60%3180%⨯=,所以甲工程队的承包的任务是乙工程队承包任务的180%40%450%÷=,所以两个工程队承包的修建公路长度之比为450%:19:2=.(法二)两个工程队完成的工程任务(修建公路长度)之比等于工作效率之比,等于3:1,而他们分别完成了各自任务的40%和60%,所以两个工程队承包的修建公路长度之比为()()340%:160%9:2÷÷=.【答案】9:2【例 10】 A 、B 、C 三项工程的工作量之比为1:2:3,由甲、乙、丙三队分别承担.三个工程队同时开工,若干天后,甲完成的工作量是乙未完成的工作量的二分之一,乙完成的工作量是丙未完成的工作量的三分之一,丙完成的工作量等于甲未完成的工作量,则甲、乙、丙队的工作效率的比是多少?【考点】比例应用题 【难度】4星 【题型】解答【关键词】2007年,华杯赛,总决赛【解析】 根据题意,如果把A 工程的工作量看作1,则B 工程的工作量就是2,C 工程的工作量就是3. 设甲、乙、丙三个工程队的工作效率分别为x 、y 、z .经过k 天,则:()()()22133213kx ky ky kzkz kx =-⎧⎪=-⎨⎪=-⎩将⑶代入⑵,得()243kx ky +=,将⑷代入⑴,得2223kx kx +=-,47x k =, 将47x k =代入⑴,得67y k =.代入⑶,得37z k=. 甲、乙、丙三队的.工作效率的连比是463::4:6:3777k k k=. 【答案】4:6:3【巩固】 某次数学竞赛设一、二、三等奖.已知:①甲、乙两校获一等奖的人数相等;②甲校获一等奖的人数占该校获奖总人数的百分数与乙校相应的百分数的比为5:6;③甲、乙两校获二等奖的人数总和占两校获奖人数总和的20%;④甲校获三等奖的人数占该校获奖人数的50%;⑤甲校获二等奖的人数是乙校获二等奖人数的4.5倍.那么,乙校获一等奖的人数占该校获奖总人数的百分数等于多少?【考点】比例应用题 【难度】3星 【题型】解答【解析】 由①、②可知甲、乙两校获奖总人数的比为6:5,不妨设甲校有60人获奖,则乙校有50人获奖.由③知两校获二等奖的共有(6050)20%22+⨯=人;由⑤知甲校获二等奖的有22(4.51) 4.518÷+⨯=人;由④知甲校获一等奖的有606050%1812-⨯-=人,那么乙校获一等奖的也有12人,从而所求百分数为1250100%24%÷⨯=.【答案】24%【例 11】 ①某校毕业生共有9个班,每班人数相等.②已知一班的男生人数比二、三班两个班的女生总数多1;③四、五、六班三个班的女生总数比七、八、九班三个班的男生总数多1.那么该校毕业生中男、女生人数比是多少?【考点】比例应用题 【难度】3星 【题型】解答【解析】 如下表所示,由②知,一、二、三班的男生总数比二、三班总人数多1;由③知,四至九班的男则女生总数等于四个班的人数之和.所以,男、女生人数之比是5:4.【答案】5:4=模块二、按比例分配与和差关系(一)量倍对应【例 12】 一些苹果平均分给甲、乙两班的学生,甲班比乙班多分到16个,而甲、乙两班的人数比为13:11,求一共有多少个苹果?【考点】比例应用题 【难度】2星 【题型】解答【解析】 一共有()()1613111311192÷-⨯+=个苹果.【答案】192个【巩固】 甲、乙两个班共种树若干棵,已知甲班种的棵数的14等于乙班种的棵数的15,且乙班比甲班多种树24棵,甲、乙两个班各种树多少棵?【考点】比例应用题 【难度】2星 【题型】解答【解析】 甲、乙两班种树棵数之比为:11:4:554=,甲班种树棵数为:()2454496÷-⨯=(棵),乙班种树棵数为:()24545120÷-⨯=(棵).【答案】120棵【例 13】 甲乙两校参加数学竞赛的人数之比是7:8,获奖人数之比是2:3,两校各有320人未获奖,那么两校参赛的学生共有 人。
