3-4图乘法及其应用
合集下载
图乘法及其应用
38
4 128EI
温 度
4. 图乘法及其应用
(Graphic Multiplication Method and its Applications)
已有基础： 1. 静定结构的内力计算； 2. 利用位移计算公式求静定结构的位移； 3. 杆件结构在荷载作用下的位移计算公式,即:
P
MM Pds EI
FN FNds EA
1 EI
( l ql 2 28
l 1 22
1 l 3ql 2 32 8
3 l) 42
1 (ql 4 3ql 4 ) 5ql 4 ( )
EI 64 128 128EI
?
解法一、
q
ql 2
2
ql 2
A
l2
C l2
B
8
B
A
C
MP 图
Cy
1 EI
[( l ql 2 28
38
2
1 ql 3 24 EI
（
）
例 2. 已知 EI 为常数，求刚架C、D两点
距离的改变 CD 。
解：作荷载内力图和单位荷载内力图
p117
2
yc h
CD
yc
EI
1 EI
2 ql 2 l h 38
qhl 3 ( ) 12 EI
例 3. 已知 EI 为常数，求刚架A点的竖向位
4k
由此可得有弹簧支座的一般情况位移公式为
MMP ds Fk FPk
EI
k
例 5. 已知 EI 为常数，求 Cy 。
q
A
l2
结构力学(第三章)-图乘法
( M x tan ) 1 x tan M P dx EI tan
xM P dx
图乘法求位移公式为:
图乘法的 适用条件是 什么?
EI tan 1 xc yc EI EI
ip
yc
EI
例. 试求图示梁B端转角.
A
P
B B
MP
A
M 1 B 1
B
c
y c
ql 2 / 2
ql 2 / 8
例 4. 图示梁 EI 为常数，求C点竖向位移 。 q ql 2 / 8 ql 2 / 2
MP
A
l/2 C
1
q q
l/2
B
l/2
Mi
c
y c
C ql / 2 ql 2 / 8
ql 2 / 8 ql 2 / 4 ql 2 / 8
ql / 2
§3.4 图乘法及其应用
(Graphic Multiplication Method and its Applications)
刚架与梁的位移计算公式为：
iP MM P ds EI
在杆件数量多的情况下,不方便. 下面介绍 计算位移的图乘法.
一、图乘法
MM P ds EI 1 图乘法是Vereshagin于 M M P ds (对于等 截面杆) EI 1925年提出的，他当时 1 为莫斯科铁路运输学院 MM P dx (对于直杆) EI 的学生。
1 1
B
Mi
l
ql / 4
2
l
ql 2 / 4
1/ l
0 解：作荷载弯矩图和单位荷载弯矩图
q
MP
人教版二年级数学上册《2、3、4的乘法口诀》表内乘法PPT优秀课件
你是怎么想的 ？
1×1就是一个1 ，所以口诀是 一一得一。
一一得一
看图直接说口诀。
二二得四
三五十五
看图列乘法算式。
4×5=20
2×4=8
射击怪兽
3
1
4
2
2×1= 2
2
5
15
10
2×5= 10
五 十
二十
十五
四五 二十
二四
。
得六
得八
得五
得四
一四 。
得二
得六
全课总结，提升能力
总结：今天学习了4的乘法口诀，一四得四、二 四得八、三四十二、四四十六。每句口诀对应两道乘 法算式（“四四十六”除外）。
想一想，你会编 上面乘法算式的 口诀吗？
想法你口一发诀想现，，了自什你能己么编照？出着23 的乘法口诀吗？
1捆棒棒糖有3个, 一共有3捆。
四行有16个，用点子图表示是 ，你 能列式计算吗？
那么四行有几个豆沙汤圆呢？
8
12
16
164个×4。＝16。
记忆口诀
（1）学生齐读。 （2）同桌对口诀。 （3）开火车背口诀。
2.3.4的乘法口诀
课前复习
3×5＝ 15 5＋5＋5＋5＝ 20 5×5＝ 25
5×2＝ 10 5×1＝ 5
3＋3＋3＝ 9
熟记2、3的乘法口诀，能运用口诀计算相关的乘法 算式，提高概括和语言表达能力；
经历2、3和1的乘法口诀的编制过程，理解这些口诀 的意义； 感受数学与生活的密切联系，培养学习数学的兴趣， 增强学好数学的自信心。
初步感知
一行有4个，用点子图表示是 ，你能 列式计算吗？
我们先看看一行豆沙汤圆有几个？
结构力学(王焕定第三版)教材习题第三章到第十章习题答案全解——哈工大老师提供
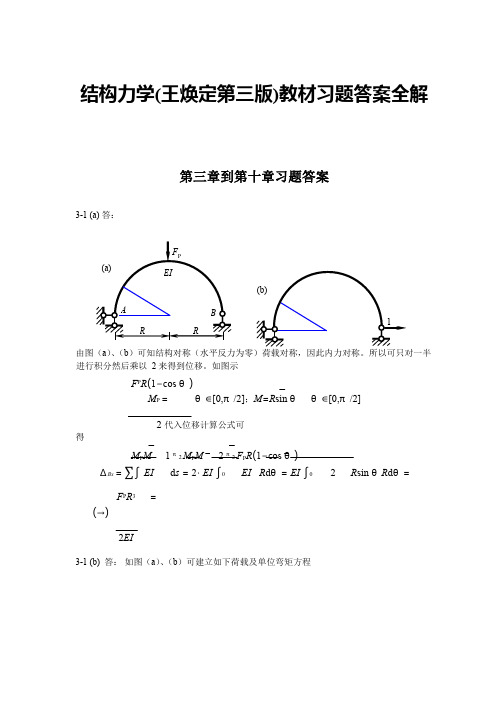
结构力学(王焕定第三版)教材习题答案全解第三章到第十章习题答案3-1 (a) 答：由图（a）、（b）可知结构对称（水平反力为零）荷载对称，因此内力对称。
所以可只对一半进行积分然后乘以2 来得到位移。
如图示F P R(1−cos θ)M P = θ∈[0,π/2]；M=R sin θθ∈[0,π/2]2 代入位移计算公式可得M P M 1 π2 M P M 2 π2 F P R(1−cos θ)∆Bx = ∑∫ EI d s = 2⋅EI ∫0 EI R dθ= EI ∫0 2 R sin θR dθ=F P R3 =(→)2EI3-1 (b) 答：如图（a）、（b）可建立如下荷载及单位弯矩方程pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R d θ= q EI 4∫0π2 (1−2cos θ+cos 2θ)R d θqR 4 ⎡ θ 1 ⎤3π ⎞ qR 4= EI ×⎢θ−2sin θ+ 2 + 4sin2θ⎥⎦0 =⎝⎜ 4 − 2⎠⎟ 2EI (→)2 ⎣3-2 答：作M P 图和单位力弯矩图如下图： 由此可得内力方程代入位移公式积分可得2 2 P0 s i n ( ) d (1 c o s ) (1 c os ) q M R q R M R θθ α α θ θ − = = − = − ∫( a )根据题意EI(x) = EI (l + x)2l 代入位移公式并积分（查积分表）可得M P M l 2 q0x4∆Bx =∑∫ EI d x =∫0 6EI(l + x) d x7 q0l4 0.07 ql4= (ln 2−)×= (→)12 3EI EI3-3 答：分别作出荷载引起的轴力和单位力引起的轴力如下图所示：由此可得C 点的竖向为移为：M图3pxqM M xl==xPM图lq05 83 8F NP F N1 F NP F N1 ∆Cy =∑∫ EAd s=∑ EA l =6 5112.5 kN× ×6 m+2×(62.5 kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 8 8EA=8.485×10−4 m当求CD 和CE 杆之间的夹角改变使：施加如图所示单位广义力并求作出F N2 图，则F∆=∑∫ F NP EA F N2 ds =∑ NP EAF N2 l2×62.5 kN×(−0.15)×5 m+(−112.5 kN)×0.25×6 m =EA=−1.4×10−4 rad ( 夹角减小）3-4 （a）答：先作出M p和M 如右图所示。
《结构力学图乘法》PPT课件
EI
E1I1 E2 I 2 E3 I3
Ei Ii
对于等直杆有
Δ
1 EI
l M ( x)M ( x)dx
M(x)
MC
EI
ω
C
即 积分可用M(x)图的面积 ω 和与M(x)
xc
x
图形心C对应的 Mc 的乘积来代替
M(x)
当M图为正弯矩时，
Δ MC
EI
ω应代以正号. 当M图为负弯矩时， ω应代以负号.
（3）图 M 图 M P中至少有一个是直线
图形。
3、图乘法公式
KP
Ap yc EI
M M P ds EI
←杆轴为直线
M M P dx EI
←杆段EI为常数
1 EI
M M Pdx
(M x tan α)
1
EI x tan α M Pdx
tan α EI
注意
有时M(x)图为连续光滑曲线，而 M(x) 为折线，则应以 折线的转折点为界，把积分分成几段，逐段使用图乘法， 然后求其和.
例1 求CV , EI等于常数。
解：
2kN/m
作 M 图 MP 图，如右图所示。 A 2m C 2m B
分段：M ，M P 分为AC、CB两段。16
分块： M P图的AC段分为两块。
还记得 吗？
（3）同侧弯矩图相乘为正，反之为负；
（4）拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解；
（5）应用图乘法首先熟练掌握常用图形面积及形心 位置。
几中常见图形的面积和形心的计算公式
a
b
C
lb
la
3
结构力学位移法
例:求图示悬臂梁C 点的竖向位移。
(a) 54 C MP (c) 24 C 3kN/m (d) 30 3kN/m (b) 4 C M1 3kN/m F =1
4m
2m
6 M P2 C
M P1
解 在C点施加竖向单位力，作出M1图和MP图，再 用图乘法求位移。但图乘结果不能直接得出，需要采用 叠加法， 将MP图分解为MP1和MP2叠加，见图c、图d， 然后令MP1 和MP2 图分别与M1图图乘后再相加。
4. 图乘法及其应用
(Graphic Multiplication Method and its Applications)
已有基础： 1. 静定结构的内力计算； 2. 利用位移计算公式求静定结构的位移；
3. 杆件结构在荷载作用下的位移计算公式,即:
kFQ FQds FN FNds MM P ds P EI EA GA
Dy
3 1 FP a 2 2a ( 1 2 2 ) F a 4 F a P ( FP a 2 a ) P () E2 I 2 2 3 E1 A1 3 E2 I 2
例 7. 已知 EI 为常数，求 Cy 。
解：作荷载和单位荷载的内力图
返回
MP
分解
M
Cy
1 1 ql l 3l 1 ql l [( ) ( l) EI 3 8 2 8 2 8 3 2 ql 2 l ql 4 ( l) ] () 温 3 8 4 128 EI 度
ql 4
ql 2 M 8 2
ql 2 8
解法二、
ql 2 2
ql 2 8
ql 2 2
A
ql 2 32
ql 2 8
1 1 l ql l Cy [( ) EI 2 2 2 3 A 2 1 l ql l ( ) 2 2 8 6 2 4 2 l ql l 17ql ( )] () 3 2 32 4 384 EI
人教版二年级上册数学(新插图) 4-3 2、3的乘法口诀 教学课件
4.连出小动物的过河路线。（教材P57“练习十一”第5题）
四、课堂小结
1×4=4 2×4=8 3×4=12 4×4=16
一四得四 二四得八 三四十二 四四十六
4×1=4 4×2=8 4×3=12
五、课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题。
到今天为止我们已经学习了哪些数的乘法口诀？
二、自主探究
同学们读一读这些乘法口诀！
一一得一 一二得二 二二得四 一三得三 二三得六 三三得九 一四得四 二四得八 三四十二 四四十六 一五得五 二五一十 三五十五 四五二十 五五二十五
仔细观察，你有什么发现？
三、巩固深化
1.对口诀。（教材P55“做一做”第1题）
二、自主探究
（教材P54 例题2）
你发现了 什么？
1副乒乓球拍有2个 球拍，2副乒乓球 拍有4个球拍。
想一想 你能编制出2的乘法口诀吗？
二、自主探究
（教材P54 例题2）
一副乒乓球拍有几个？ 能列出乘法算式吗？
我们可以编制出哪句 口诀呢？
1×2=2 2×1=2
一二得二
二、自主探究
（教材P54 例题2）
一一……
得一。
二三……
得六。
四四……
十六。
三、巩固深化
2.吃饭时每人需要一双筷子，请填空：
（教材P55“做一做”第2题）
2个人需要（ 4 ）根筷子； 3个人需要（ 6 ）根筷子； 4个人需要（ 8 ）根筷子； 你发现了什么？
三、巩固深化
3.边画边说口诀。（教材P56“练习十一”第1题）
三、巩固深化
4×4= 16 12 +4 16
四四十六
二、自主探究
四、课堂小结
1×4=4 2×4=8 3×4=12 4×4=16
一四得四 二四得八 三四十二 四四十六
4×1=4 4×2=8 4×3=12
五、课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题。
到今天为止我们已经学习了哪些数的乘法口诀？
二、自主探究
同学们读一读这些乘法口诀！
一一得一 一二得二 二二得四 一三得三 二三得六 三三得九 一四得四 二四得八 三四十二 四四十六 一五得五 二五一十 三五十五 四五二十 五五二十五
仔细观察，你有什么发现？
三、巩固深化
1.对口诀。（教材P55“做一做”第1题）
二、自主探究
（教材P54 例题2）
你发现了 什么？
1副乒乓球拍有2个 球拍，2副乒乓球 拍有4个球拍。
想一想 你能编制出2的乘法口诀吗？
二、自主探究
（教材P54 例题2）
一副乒乓球拍有几个？ 能列出乘法算式吗？
我们可以编制出哪句 口诀呢？
1×2=2 2×1=2
一二得二
二、自主探究
（教材P54 例题2）
一一……
得一。
二三……
得六。
四四……
十六。
三、巩固深化
2.吃饭时每人需要一双筷子，请填空：
（教材P55“做一做”第2题）
2个人需要（ 4 ）根筷子； 3个人需要（ 6 ）根筷子； 4个人需要（ 8 ）根筷子； 你发现了什么？
三、巩固深化
3.边画边说口诀。（教材P56“练习十一”第1题）
三、巩固深化
4×4= 16 12 +4 16
四四十六
二、自主探究
《2、3、4的乘法口诀》表内乘法PPT精品课件
四只乌龟，十六条腿， 四四十六。
同学们都学过哪些 乘法口诀？
一一得一 一二得二 一三得三 一四得四 一五得五
1×1＝1 一一得一
二二得四 二三得六 二四得八 二五一十
三三得九 三四十二 三五十五
四四十六 四五二十
五五二十五
一共有多少个气球？
我知道 4的乘 法口诀：
一四得四 二四得八 三四十二 四四十六
10＋10＝
2＋2＝
4＋4＝
4×2＝
3×4＝
2×2＝
5×4＝
6＋6＝
4
8
12
20
3的乘法口诀
1个3 2个3 3个3
1×3=3 2×3=6 3×3=9
一三得三 二三得六 三三得九
每相邻两句口诀的得数相差3。
看图：写出口诀。
4 × 4 ＝ 16
口诀 ： 四四十六
看蝴蝶下面藏着什么，把口诀补充完整。
3×2＝（ 6 ） 口诀：二三得六
2×2＝（ 4 ） 口诀：二二得四
4×5＝（20） 口诀：四五二十
3×3＝（ 9 ） 口诀：三三得九
课堂小结
一一得一 一二得二 二二得四 一三得三 二三得六 三三得九 一四得四 二四得八 三四十二 四四十六
教材练习十一第4、6、7题。
谢谢大家！！
连一连。 5×5
2×3
2×2
二三得六
五五二十五
二二得四
1×3=3 2×3=6 3×3=9
一三得三 二三得六 三三得九
3×1=3 3×2=6
填一填。
3只小兔拔（ 15 ）个。 4只小兔拔（ 20 ）个。 5只小兔拔（ 25 ）个。 两只乌龟，八条腿， 二四得八。 三只乌龟，十二条腿， 三四十二。
同学们都学过哪些 乘法口诀？
一一得一 一二得二 一三得三 一四得四 一五得五
1×1＝1 一一得一
二二得四 二三得六 二四得八 二五一十
三三得九 三四十二 三五十五
四四十六 四五二十
五五二十五
一共有多少个气球？
我知道 4的乘 法口诀：
一四得四 二四得八 三四十二 四四十六
10＋10＝
2＋2＝
4＋4＝
4×2＝
3×4＝
2×2＝
5×4＝
6＋6＝
4
8
12
20
3的乘法口诀
1个3 2个3 3个3
1×3=3 2×3=6 3×3=9
一三得三 二三得六 三三得九
每相邻两句口诀的得数相差3。
看图：写出口诀。
4 × 4 ＝ 16
口诀 ： 四四十六
看蝴蝶下面藏着什么，把口诀补充完整。
3×2＝（ 6 ） 口诀：二三得六
2×2＝（ 4 ） 口诀：二二得四
4×5＝（20） 口诀：四五二十
3×3＝（ 9 ） 口诀：三三得九
课堂小结
一一得一 一二得二 二二得四 一三得三 二三得六 三三得九 一四得四 二四得八 三四十二 四四十六
教材练习十一第4、6、7题。
谢谢大家！！
连一连。 5×5
2×3
2×2
二三得六
五五二十五
二二得四
1×3=3 2×3=6 3×3=9
一三得三 二三得六 三三得九
3×1=3 3×2=6
填一填。
3只小兔拔（ 15 ）个。 4只小兔拔（ 20 ）个。 5只小兔拔（ 25 ）个。 两只乌龟，八条腿， 二四得八。 三只乌龟，十二条腿， 三四十二。
结构力学第3章习题及参考答案
（1）在 作用下A点的转角为
由此解得
按上述思路，再求C截面两侧的转角，为此作出单位弯矩图，如图(c)所示，则
3-15已测得在图示荷载作用下各点竖向位移为H点1.2 cm，G、I点0.1 cm，F、C、J点0.06 cm，D、B点0.05 cm。试求当10 kN竖向力平均分布作用于15个结点上时，H点的竖向位移。
3-6 (a)
解将悬臂梁在K截面切开，取左边部分，并将K截面内力作为荷载作用在K截面上，如图(a-1)所示。(a-1)所示结构悬臂端的竖向位移就是原结构K截面的竖向位移。作出(a-1)所示结构的Mp和 图，并将Mp图按荷载分解。图乘结果为
3-6 (b)
解
3-6 (c)
解
3-6 (d)
解
3-6 (e)
解
3-9试求图示刚架在温度作用下产生的D点的水平位移。梁为高度h=0.8m的矩形截面梁，线膨胀系数为 =10-5 oC-1。
解
3-10图示桁架各杆温度上升t，已知线膨胀系数 。试求由此引起的K点竖向位移。（画出需要的图）
解
*3-11图示梁截面尺寸为b×h=0.2m×0.6m，EI为常数，线膨胀系数为 ，弹簧刚度系数k=48EI/l3(l=2m)。梁上侧温度上升10℃，下侧上升30℃，并有图示支座移动和荷载作用。试求C点的竖向位移。
解
3-6 (f)
解（1)相对水平位移
（2)相对竖向位移
对称结构在对称荷载作用下的反对称位移等于零
解
3-7试求图示结构在支座位移下的指定位移。
3-7 (a)
解
3-7 (b)
解
3-8图示结构各杆件均为截面高度相同的矩形截面，内侧温度上升t，外侧不变。试求C点的竖向位移。线膨胀系数为 。
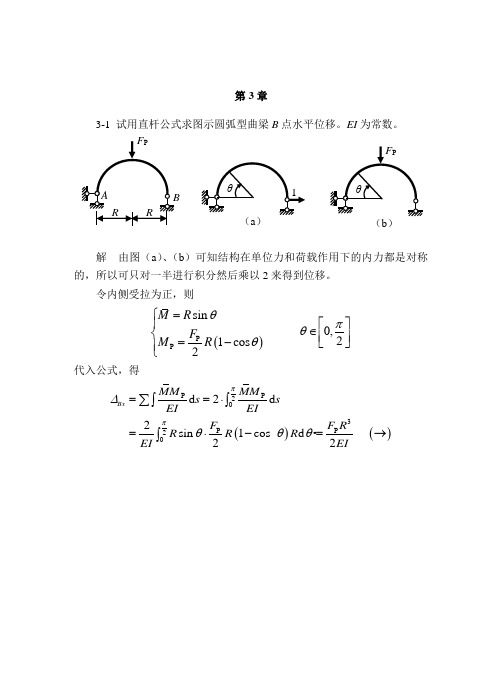
由此解得
按上述思路，再求C截面两侧的转角，为此作出单位弯矩图，如图(c)所示，则
3-15已测得在图示荷载作用下各点竖向位移为H点1.2 cm，G、I点0.1 cm，F、C、J点0.06 cm，D、B点0.05 cm。试求当10 kN竖向力平均分布作用于15个结点上时，H点的竖向位移。
3-6 (a)
解将悬臂梁在K截面切开，取左边部分，并将K截面内力作为荷载作用在K截面上，如图(a-1)所示。(a-1)所示结构悬臂端的竖向位移就是原结构K截面的竖向位移。作出(a-1)所示结构的Mp和 图，并将Mp图按荷载分解。图乘结果为
3-6 (b)
解
3-6 (c)
解
3-6 (d)
解
3-6 (e)
解
3-9试求图示刚架在温度作用下产生的D点的水平位移。梁为高度h=0.8m的矩形截面梁，线膨胀系数为 =10-5 oC-1。
解
3-10图示桁架各杆温度上升t，已知线膨胀系数 。试求由此引起的K点竖向位移。（画出需要的图）
解
*3-11图示梁截面尺寸为b×h=0.2m×0.6m，EI为常数，线膨胀系数为 ，弹簧刚度系数k=48EI/l3(l=2m)。梁上侧温度上升10℃，下侧上升30℃，并有图示支座移动和荷载作用。试求C点的竖向位移。
解
3-6 (f)
解（1)相对水平位移
（2)相对竖向位移
对称结构在对称荷载作用下的反对称位移等于零
解
3-7试求图示结构在支座位移下的指定位移。
3-7 (a)
解
3-7 (b)
解
3-8图示结构各杆件均为截面高度相同的矩形截面，内侧温度上升t，外侧不变。试求C点的竖向位移。线膨胀系数为 。
结构力学图乘法
FN FPb M FQ 状态II FPa
M ds ds EI FN ds ds EA
ds 0
kFQ GA
ds
令状态I的平衡力系在状态II的位移上做虚功，得到：
0 ds FN ds W12 FP M ds FQ FQ kFQ FN FN M M ds ds ds EI GA EA
yc
几中常见图形的面积和形心的计算公式
a b 顶点
C
lb 3
C
5l 8
la 3
3l 8
l
l
三角形
l h AP 2
二次抛物线
2 Ap h l 3
顶点
c
顶点
( n 1) l n2
c
l n2
3l/4 l
l/4
l
二次抛物线
l h Ap 3
N 次抛物线
lh n1
3. 图形相乘的几种情况
1
作业：
4-3 (a)；(c)
§4-5 互等定理
互等定理适用于线性变形体系，即体系产生的 是小变形，且杆件材料服从虎克定律。
一、 功的互等定理
功的互等本质上是虚功互等。
下图给出状态I和状态II。
FP1 2 FP
FPa
FPb
A
1 2 a b
a
b
B
A
1 2 B a 1 b 2
所以
即
F F
P P
11 FP 2 FP 2 FPa a FPb b
在任一线性变形体系中，第一状态的外力 在第二状态的位移上所做的虚功W12等于第二状 态的外力在第一状态的位移上所做的虚功W21。
《2、3、4的乘法口诀》表内乘法PPT
历史课件： . /kejian/lishi/
填一填
吃饭时每人需要一双筷 子，4个人需要（ 8 ） 根筷子。
课堂小结
一一得一 一二得二 二二得四 一三得三 二三得六 三三得九 一四得四 二四得八 三四十二 四四十六
ppt下载： . /xiazai/
ppt教程： . /powerpoint/
资nwen/
试卷下载： . /shiti/
教案下载： . /jiaoan/
ppt论坛： . .cn
ppt课件： . /kejian/
语文课件： . /kejian/yuwen/ 数学课件： . /kejian/shuxue/
方框里有几个汤圆？
8个汤圆
2个 4
2×4＝8 4×2＝8
二四得八
8
乘法口诀
2的乘法口诀
1个2
1×2=2 一二得二
2个2
2×2=4 二二得四
每相邻两句乘法口诀的得数相差2。
3 4 12 4 3 12
三四十二
小动物过河
4
8
12
16
中等练习
1个秋千坐2人,2个秋千坐（ 4 ）人，3个秋千坐 （ 6 ）人，4个秋千坐（ 8 ）人。
英语课件： . /kejian/yingyu/ 美术课件： . /kejian/meishu/
科学课件： . /kejian/kexue/ 物理课件： . /kejian/wuli/
化学课件： . /kejian/huaxue/ 生物课件： . /kejian/shengwu/
地理课件： . /kejian/dili/
2、3、4的乘法口诀
-.
本节目标 01 1. 掌握2、3、4的乘法口诀,并能运用口诀计算有关的乘法算式题。 02 2.通过学生摆一摆、说一说、比一比等活动，培养操作能力和归纳意识。 03
结构力学：第5章 静定结构位移计算3(图乘法)
（3） yc 应取自直线图中。
2. 若 与 yc 在杆件的同侧，yc取正值；
反之，取负值。
3. 如图形较复杂，可分解为简单图形.
(1) 曲-折组合
例如
Mi MKdx 1 y1 2 y2 3 y3 j y j
(2) 梯-梯同侧组合
1
2
Mi MKdx 1 y1 2 y2
y1
(2c 3
FP
A
C
l
l
2
2
a
B
解：作荷载内力图和单位荷载内力图
FNP
FP 2
D
A C FP
l
l
2
2
a
B
FN
1 2
D
1 AC
a
B
l
l
2
2
l
MP
FP l
4
Cy
0l
MM P EI
ds
0a
FN FNP EA
ds
M请对计算结4 果 C进y 行4F适8PEl当3I (讨1 论1l！23aAI )
2 [(1 l FPl ) 2 l ] 1 1 FP a FPl 3 FPa
1 EI
yc
必须注意 适用条件
图乘法是Vereshagin于1925年提出的，他 当时为莫斯科铁路运输学院的学生。
二、几种常见图形的面积和形心位置的 确定方法
顶点指曲 线切线与 杆轴重合 或平行
hl
n1
(n 1)l n2
h
C
l n2
三、注意事项：
1. 图乘法的应用条件： （1）等截面直杆，EI为常数； （2）两个M图中应有一个是直线；
q A
MP 图
1 ql 2 8
2. 若 与 yc 在杆件的同侧，yc取正值；
反之，取负值。
3. 如图形较复杂，可分解为简单图形.
(1) 曲-折组合
例如
Mi MKdx 1 y1 2 y2 3 y3 j y j
(2) 梯-梯同侧组合
1
2
Mi MKdx 1 y1 2 y2
y1
(2c 3
FP
A
C
l
l
2
2
a
B
解：作荷载内力图和单位荷载内力图
FNP
FP 2
D
A C FP
l
l
2
2
a
B
FN
1 2
D
1 AC
a
B
l
l
2
2
l
MP
FP l
4
Cy
0l
MM P EI
ds
0a
FN FNP EA
ds
M请对计算结4 果 C进y 行4F适8PEl当3I (讨1 论1l！23aAI )
2 [(1 l FPl ) 2 l ] 1 1 FP a FPl 3 FPa
1 EI
yc
必须注意 适用条件
图乘法是Vereshagin于1925年提出的，他 当时为莫斯科铁路运输学院的学生。
二、几种常见图形的面积和形心位置的 确定方法
顶点指曲 线切线与 杆轴重合 或平行
hl
n1
(n 1)l n2
h
C
l n2
三、注意事项：
1. 图乘法的应用条件： （1）等截面直杆，EI为常数； （2）两个M图中应有一个是直线；
q A
MP 图
1 ql 2 8
图乘法
？ Δ = 1 1 3a ⋅3a×Pa EI 2 4
Pa
Δ
=
1 EI
⎡ ⎢⎣
Pa×a 2
×
2 3
a 2
×2+
a
2
+3a 2
4
×
a 2
×2×
Pa⎥⎦⎤
a
= 23Pa3
a/2
24EI
例：求图示梁C点的挠度。
？ D = 1 Pl 2 l = Pl 3 C EI 2 6 12 EI
Δ C
=
ωy0
EI
=
⎜⎛ ⎝
= 1 (220⋅0.533− 555⋅0.4 + 53.3⋅0.6) = −2×10−3m = −0.2cm
3.6465
例：求B点竖向位移。
21
3ql2/2
ql2/8
MP
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ ql
EI l
B
l
M1
Δ BV
=
1 EI
⎡1 ⎢⎣ 2
3ql 2 2
l
2l 3
− 2l 3
ql 2 8
A2 b 侧的两个三角形，分别与另
一图形相乘，然后叠加。
c y1
y2 d
A⋅ yc EI
=
1 EI
(A1 ⋅
y1 +
A2 ⋅
y2 )
=
=
1 EI
⎡al ⎢⎣ 2
(−
2 3
c
+
1 3
d)
+
bl 2
(1 3
c
−
2 3
d)⎥⎦⎤
=
1 EI
⎡l ⎢⎣6
3-4图乘法及其应用
为常数，求 Dy 。
C
a
E1A1
解：作荷载和单位荷载的内力图
FP D
+ FP FP
+1
1
a
E1A1
2FP
2
B
FP a
a
a E2I2
A
DyFE NF 1A N 1 PlE 2yIc21FPa( E12 A )1 ( 2FP) 2a
E2 1I2(FP 2a223aFPa2a)(12 E1A 21 )FPa4 3F EP 2a I2 3()
例 7. 已知 EI 为常数，求 Cy 。
解：作荷载和单位荷载的内力图
返回 MP
分解
M
CyE 1I[(1 3q82l2l)38l(1 2q82ll)3l
(2q2ll)l] q4l () 3 8 4 12E 8I
温 度
FP 2k
。因此，弹簧对位移的贡献为
FB
FP 2k
FP 4k
。
由此可得有弹簧支座的一般情况位移公式为
M M PdsF kF Pk
EI
k
例 5. 已知 EI 为常数，求 Cy 。
q
A
l2
C l2
B
解：作荷载内力图和单位荷载内力图
ql 2
2
ql 2
8
A
C
MP 图
l 2
B A ql 2 2
2[1 (lFPl)2l]11FPaFPl3FPa
EI2 2 4 3 4 EA 2 2 4E 8 I4EA
讨论:如果B支座处为刚度k的弹簧，该如何
计算？
A C FP
l
l
2
2
B
A
k
结构力学图乘法
nl注意折线的转折点为界把积分分成几段逐段使用图乘法有时mx图为连续光滑曲线而为折线则应以mx然后求其和
§4-4 图乘法
1.图乘法原理
梁、刚架等弯曲变形为主的构件位移计算公式：
KP
M K M P ds 称莫尔积分 EI
建立方程，逐杆积分，在杆件数量多的情况 下不方便。
图乘法的思想：利用图形静矩的概念将图 形积分变为图形相乘。
M M EI
ds
kFQ FQ GA
ds
FN FN EA
ds
同样，令状态II的平衡力系在状态I的位移上 做虚功，得到：
W21 FP M ds FQ 0ds FNds
M M EI
1 EI
(1 y1
2 y2
3 y3 )
1 EI
(64 1 2
4
20 3
32 3 ) 34
1 (32 80 8) 13.33 ( )
EI
3
EI
例3 求 ,B EI等于常数。
解： A
作 M 图及M P 图，
如右所示。
7kN
B 2m
6kN/m
C
6kN.m
3
l
顶点
C
5l
3l
8
8
l
三角形
AP
l
h 2
二次抛物线
2 Ap 3 h l
c
顶点
3l/4
l/4
l
二次抛物线
Ap
lh 3
顶点
(n 1) l n2
§4-4 图乘法
1.图乘法原理
梁、刚架等弯曲变形为主的构件位移计算公式：
KP
M K M P ds 称莫尔积分 EI
建立方程，逐杆积分，在杆件数量多的情况 下不方便。
图乘法的思想：利用图形静矩的概念将图 形积分变为图形相乘。
M M EI
ds
kFQ FQ GA
ds
FN FN EA
ds
同样，令状态II的平衡力系在状态I的位移上 做虚功，得到：
W21 FP M ds FQ 0ds FNds
M M EI
1 EI
(1 y1
2 y2
3 y3 )
1 EI
(64 1 2
4
20 3
32 3 ) 34
1 (32 80 8) 13.33 ( )
EI
3
EI
例3 求 ,B EI等于常数。
解： A
作 M 图及M P 图，
如右所示。
7kN
B 2m
6kN/m
C
6kN.m
3
l
顶点
C
5l
3l
8
8
l
三角形
AP
l
h 2
二次抛物线
2 Ap 3 h l
c
顶点
3l/4
l/4
l
二次抛物线
Ap
lh 3
顶点
(n 1) l n2
二年级上册数学青岛版3和4的乘法口诀(课件)
3、4的乘法Байду номын сангаас诀
—— 帮助商贩快速算出货物总量
一、情境感知
有一天，高帽子客人来到了水果商铺，你能帮助老板计算卖出了多少水果吗？
二、操作探究
一共卖出了多少水果？
要求： 1.用学具小棒代替苹果摆一摆， 用○表示苹果画一画。 2.尝试列出乘法算式，说出算式 的意义。
二、操作探究
一共卖出了多少水果？
你能接着编下去吗？
二、操作探究
一起记口诀。 一二三 三 三 三三三 四 五 得得得 十 十 三六九 二 五
3 333 3
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
二、操作探究
一共卖出了多少根香蕉？
要求： 1.用学具小棒代替香蕉摆一摆， 用 表示香蕉画一画。 2.尝试列出乘法算式，说出算式 的意义。
4个3相加是12 4×3＝12 或 3×4＝12
5个3相加是15 5×3＝15 或 3 ×5＝15
二、操作探究
编口诀。
乘法算式 1×3＝3 或 3×1＝3
乘法口诀 一三得三
2×3＝6 或 3×2＝6
二三得六
3×3＝9 或 3×3＝9 4×3＝12 或 3×4＝12 5×3＝15 或 3×5＝15
三三得九 三四十二 三五十五
三、游戏闯关
小青蛙，本领大，吃害虫，顶呱呱， 我们都要爱惜它。 小朋友，学数学，我们一起数青蛙。
三、游戏闯关
一只青蛙一张嘴，两只眼睛四条腿; 两只青蛙两张嘴，四只眼睛八条腿; 三只青蛙三张嘴，六只眼睛十二条腿; 四只青蛙四张嘴，八只眼睛十六条腿; 五只青蛙五张嘴，十只眼睛二十条腿。
谢谢同学们
二、操作探究
1-5 的乘法口诀表：竖着读一读。
—— 帮助商贩快速算出货物总量
一、情境感知
有一天，高帽子客人来到了水果商铺，你能帮助老板计算卖出了多少水果吗？
二、操作探究
一共卖出了多少水果？
要求： 1.用学具小棒代替苹果摆一摆， 用○表示苹果画一画。 2.尝试列出乘法算式，说出算式 的意义。
二、操作探究
一共卖出了多少水果？
你能接着编下去吗？
二、操作探究
一起记口诀。 一二三 三 三 三三三 四 五 得得得 十 十 三六九 二 五
3 333 3
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
二、操作探究
一共卖出了多少根香蕉？
要求： 1.用学具小棒代替香蕉摆一摆， 用 表示香蕉画一画。 2.尝试列出乘法算式，说出算式 的意义。
4个3相加是12 4×3＝12 或 3×4＝12
5个3相加是15 5×3＝15 或 3 ×5＝15
二、操作探究
编口诀。
乘法算式 1×3＝3 或 3×1＝3
乘法口诀 一三得三
2×3＝6 或 3×2＝6
二三得六
3×3＝9 或 3×3＝9 4×3＝12 或 3×4＝12 5×3＝15 或 3×5＝15
三三得九 三四十二 三五十五
三、游戏闯关
小青蛙，本领大，吃害虫，顶呱呱， 我们都要爱惜它。 小朋友，学数学，我们一起数青蛙。
三、游戏闯关
一只青蛙一张嘴，两只眼睛四条腿; 两只青蛙两张嘴，四只眼睛八条腿; 三只青蛙三张嘴，六只眼睛十二条腿; 四只青蛙四张嘴，八只眼睛十六条腿; 五只青蛙五张嘴，十只眼睛二十条腿。
谢谢同学们
二、操作探究
1-5 的乘法口诀表：竖着读一读。
结构力学(I)-结构静力分析篇3 结构位移计算
26 / 42
第三章
练习
结构位移计算
K B l
k EI l2
如图具有弹性支座的梁，求K点竖向位移。
A l C l
27 / 42
第三章
练习
结构位移计算
如图桁架的上弦杆均做长8mm，求由此引 起的K点竖向位移。
E K F
8m
A
C
B
68m
D
28 / 42
第三章
结构位移计算
§3-6 互等定理
δWe Pi Pi q j qi ds
i i
δWi (FN δ FQδ Mδ M Z δ )d s
l i 0
P
i i
Pi
q j qi ds
i
l i 0
(FN δ FQδ Mδ M Z δ )d s
在变形虚位移上所作功的总和，将它理解为虚 内力功是有偏颇的。
由虚功原理派生出的虚位移原理和虚力原理是 在加进新的条件下的应用，所以多少还是有 所区别的。 平衡的变形体上的广义力和相对应的广义位移 之积形成虚功。“虚”表明作功的双方是相互 独立无关的。
7 / 42
第三章
结构位移计算
3-2-2 杆系结构的虚功方程
第三章
方法使用条件
结构位移计算
1、等刚直杆
2、至少有一直线图 3、yc应取自直线图中
3-4-2 需要的注意问题
和 yc取若在杆轴线同侧，则乘积为正； 反之为负。 拱、曲杆结构和连续变截面的结构只能通 过积分的方式求解
应用图乘法首先熟练掌握常用图形面积及 形心位置
17 / 42
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
讨论:如果B支座处为刚度k的弹簧，该如何
计算？
A C FP
l
l
2
2
B
A
k
FBP
FP 2
C FP=1
l
l
2
2
B k
FB
1 2
MP
FPl
4
M
l 4
显然，按弹簧刚度定义，荷载下弹簧变形为
FP 2k
。因此，弹簧对位移的贡献为
FB
FP 2k
FP 。
4k
由此可得有弹簧支座的一般情况位移公式为
M M Pd s F kF P k
图乘法是Vereshagin于1925年提出的，他 当时为莫斯科铁路运输学院的学生。
二、几种常见图形的面积和形心位置的 确定方法
顶点指曲 线切线与 杆轴重合 或平行
hl
n1
(n 1)l n2
h
C
l n2
三、注意事项：
1. 图乘法的应用条件： （1）等截面直杆，EI为常数； （2）两个M图中应有一个是直线；
例 7. 已知 EI 为常数，求 Cy 。
解：作荷载和单位荷载的内力图
谢谢！
绘制变形图时，应根据弯矩图判断杆件的 凹凸方向，注意反弯点的利用。如：
FPl/2 FPl/2 FPl/2
FP
FP
FPl/4 MP 图
FPl/4
例 4. 已知： E、I、A为常数，求 Cy 。
D
FP
A
C
l
l
2
2
a
B
解：作荷载内力图和单位荷载内力图
FNP
FP 2
D
A C FP
l
l
2
2
a
B
FN
1 2
（3） y c 应取自直线图中。
2. 若 与 y c 在杆件的同侧，yc取正值；
反之，取负值。
3. 如图形较复杂，可分解为简单图形.
(1) 曲-折组合
例如
M i M K d x 1 y 1 2 y 2 3 y 3 j y j
(2) 梯-梯同侧组合
1
2
M iM K d x 1 y 1 2 y 2 yy12
D
1 AC
a
B
l
l
2
2
l
MP
FPl
4
M
4
请对计算结果
C y0 lM E M PIds0 aF N E F N P A ds C 进y行4F 适PE 8l当3 (讨I1论1l！3a A 2)I
2[1 (lF Pl)2l]11F PaF Pl3F Pa
EI22 4 34 EA 2 2 4E 8 I4EA
解法二、
ql 2 2
ql 2
ql 2
2
8
A
l
Cy
1 EI
[(1 2
l ql 2 22
l) 3
2
(1 l ql2 l )
A
22 8 6
( 2 l ql 2 l )] 17ql 4 ( ) 3 2 32 4 384EI
ql 2 32 ql 2 8
1
M图
例 6. 已知 CD、BD杆的E1A1和AC杆的 E2I2
四、应用举例
例 1. 设 EI 为常数，求Cy 和 B 。
l
l
2
2
解：作荷载内力图和单位荷载内力图
q
对吗？
FP=1
A
BA
C
B
1 ql 2
MP 图 8
l
应分段！ M 图 4
CyE1I[(322l 18ql2)(854l)]2
5 q4l () 384EI
q A
1 ql 2
MP 图 8
1
2
1
B
A
EI64 12812E8I
?
解法一、
q
ql 2
2
ql 2
A l2
C l2
B
8
B
A
C
MP 图
Cy
1 [( l ql2 EI 2 8
l) 4
A
(1 l ql2 l )
22 4 3
A
q
FQ
ql 2
M ql 2
ql 2 ql 2
8
8
4
ql 2
8
(1 l ql2 3 l )] 17ql4 ( ) 3 2 8 4 2 384EI
EI k
例 5. 已知 EI 为常数，求 Cy 。
q
A
l2
C l2
B
解：作荷载内力图和单位荷载内力图
ql 2
2
ql 2
8
A
C
MP 图
l 2
B A ql 2 2
1
M图
ql 2
一种算法：
结果正确否？ A
8
B
C
CyE 1(I2 lq82l2 l1 21 32 l3q 82l4 32 l)
1(q4l3q4l)5q4l ()
移 Ay ，并绘出刚架的变形曲线。
FP
解：作荷载内力图和单位荷载内力图
FPl/2 FPl/2 FPl/2 EI
FP
FPl/4 MP 图
FPl/4
2EI M图
在 M 图求面积，在 MP图取竖标，有：
A y E yc IE 1 I2 llF 2 Pl2E 1 Il3 2lF 4 Pl
F Pl3() 1E 6 I
这部分主要内容：
1.
图乘法；
MMP EI
ds
MEMIPdsEycI
C MP
yC M
2. 几种常见图形的面积和形心 位置的确定方法；
3. 注意事项；
4. 应用举例。
一、图乘法
MMP EI
ds
E1IMMPds
E 1IxtanM Pdx
tE anIxM Pdx
tE an IxcE 1Iyc
必须注意 适用条件
为常数，求 Dy 。
C
a
E1A1
解：作荷载和单位荷载的内力图
FP D
+ FP FP
+1
1
a
E1A1
2FP
2
B
FP a
a
a E2I2
A
D yF E N F 1A N 1 PlE 2 yIc21F Pa( E 12 A )1 ( 2F P) 2a
E2 1I2(F P 2a22 3 aF Pa2a)(12 E 1A 21 )F Pa4 3F E P 2a I2 3()
(2 (c
cd 3 2d 3
) )
(3) 梯-梯异侧组合
A
a 1
C
2
y2 y1 c
B b MK 图 D
d M图
M iM K d x 1 y 1 2 y 2 yy12
(2 (c
cd 3 2d 3
) )
b
c 取 负 值
(4) 阶梯形截面杆
M E iM K d I x E 1 1 I y 1 1 E 2 2 I y 2 2 E 3 3 I y 3 3 E jjI y jj
C
B
M图
B
1 [(2l EI 3
1ql2)1] 82
1 ql3 24EI
（
）
例 2. 已知 EI 为常数，求刚架C、D两点
距离的改变 CD 。
解：作荷载内力图和单位荷载内力图
p117
2
yc h
CDEycIE1I32q8l2 lh
qh3l() 12EI
例 3. 已知 EI 为常数，求刚架A点的竖向位